Abstract
Pain management is a crucial part in Sickle Cell Disease treatment. Accurate pain assessment is the first stage in pain management. However, pain is a subjective response and hard to assess via objective approaches. In this paper, we proposed a system to map objective physiological measures to subjective self-reported pain scores using machine learning techniques. Using Multinomial Logistic Regression and data from 40 patients, we were able to predict patients’ pain scores on an 11-point rating scale with an average accuracy of 0.578 at the intra-individual level, and an accuracy of 0.429 at the inter-individual level. With a condensed 4-point rating scale, the accuracy at the inter-individual level was further improved to 0.681. Overall, we presented a preliminary machine learning model that can predict pain scores in SCD patients with promising results. To our knowledge, such a system has not been proposed earlier within the SCD or pain domains by exploiting machine learning concepts within the clinical framework.
Keywords: physiological sensing, decision support, machine learning, health informatics
1. Introduction
Sickle Cell Disease (SCD) is an inherited blood disorder that affects one in 396 African Americans and one in 1,200 Hispanic Americans in the United States (US) (Lorey et al., 1996). Although medical treatment for SCD has improved dramatically, median survival age for SCD patients is 61 years (Elmariah et al., 2014), significantly lower than for African-Americans without SCD. In SCD, red blood cells (RBCs) become adherent and dehydrated, as well as sickle-shaped when deoxygenated which decreases blood flow and leads to frequent vasoocclusive painful episodes and chronic organ damage (Schnog et al., 2004). Currently, there is no standard treatment available for pain and patients currently attempt to manage their pain symptoms to avoid hospitalization. Moreover, their pain levels are reported during intermittent clinic visits and often difficult to manage due to the subjective nature of pain.
Pain caused by SCD is not only an excruciating experience, but also could be the precursor of a serious complication in some patients (Ballas, 2005). Therefore, an improved understanding of pain as well as an effective pain management approach is critical in SCD treatment. Although accurate pain assessment is the cornerstone of pain management, there is currently no gold standard for comparison. While pain is a highly subjective experience, its assessment and management are difficult. In clinical practice, medical providers use additional objective indicators, such as vital signs and non-verbal cues to improve their assessment of pain and create a balance between pain tolerance and medication dosage.
Physiological measurements of patients are potential objective indicators for patients’ pain levels. Current clinical guidelines recommend frequent vital signs during assessment and treatment of painful episodes. These physiologic measurements include: blood pressure, respiratory rate, oxygen saturations, temperature and pulse (Rees et al., 2003). It has also been previously reported that acute pain leads to changes in vital signs such as heart rate, blood pressure and respiratory rate (Macintyre et al., 2010). Therefore, the goal of this study is to develop an objective pain assessment model based on physiological measurements using machine learning techniques. Specifically, we take the novel approach of using real patient data from 40 patients admitted for pain to build pain prediction models using objective physiological measures as features at both the intra- and inter-individual levels based on a 11-point numeric rating scale (NRS) (Downie et al., 1978). We further create pain prediction models to assess different ways of establishing the pain scale, with a goal of finding the optimum pain scale for future usage. To our knowledge, such a system has not been rigorously analyzed in the SCD or pain population so far. To this end, our study proposes to address the following key research questions:
RQ1. How do these physiological features relate to one another?
RQ2. How well do the features predict pain levels in individual patient models?
RQ3. How well do the features predict pain levels in generalized (or inter-individual) patient models?
RQ4. How does the system performance change for different pain scales?
RQ5. Finally, how does a pain change detector perform using the same features?
Using the research questions posed above, we try to address the main research hypothesis of our study: Can physiological measures be indicators of pain in sickle cell disease (SCD) patients?
2. Related work
There is a growing trend of applying machine learning techniques in various clinical and medical areas. Physiological measurements, especially vital signs, are widely used in these studies as indicators for certain phenomena. Forkan et al. (2015) developed a fuzzy-rule based model to detect behavioral and health-related abnormality of patients by monitoring their daily activities, location routine behaviors, and vital signs (e.g. blood pressure, heart rate, temperature) with wearable sensors. The system achieved a high accuracy of 95.10% in detecting four types of abnormal changes. Churpek et al. (2014) described a multinomial logistic regression model to forecast cardiac arrests (CAs) and intensive care unit (ICU) transfers using Electronic Health Record (EHR) data. Vital sign, demographic, location, and laboratory data were extracted from the EHR data and utilized as potential predictors. The performance of the model was evaluated by area under the receiver operating characteristic curve (AUC). A receiver operating characteristic curve (ROC curve) is a plot of the true positive rate (TPR) against the false positive rate (FPR) at various decision threshold settings (Bradley, 1997). AUC is the metric used to summarize the ROC curve in one number, which can be used to represent the discrimination ability of a model between classes. An AUC of 1.0 represents a prediction model with perfect discrimination, while an AUC of 0.5 represents a prediction model with random guessing. In the paper of Churpek et al., AUC measures of 0.88 and 0.77 were achieved for prediction of CAs and ICU transfer, respectively. Gultepe et al. (2014) developed a machine learning based system to predict lactate levels and mortality risk based on vital signs and white blood cell count (WBC) from EHR data. Multiple classification methods were used by Gultepe et al. (2014), including Naïve Bayes, Support Vector Machine, Gaussian Mixture model, Hidden Markov model. An accuracy of 99% and AUC of 1.00 were obtained for lactate level prediction. An accuracy of 73% and AUC of 0.73 were achieved for mortality prediction. Austin et al. (2013) compared multiple classification methods, including Bootstrap aggregation, boosting, Random Forests, and Support Vector Machines, in distinguishing two subtypes of heart failure. The ability of these methods to predict the probability of the presence of one subtype heart failure was also investigated in the study. The dataset they used contained patient demographics, vital signs and physical examination at presentation, medical history, and results of laboratory tests. Acharya et al. (2015) developing a system for classifying normal and diabetes by using the heart rate information extracted from the Electrocardiogram (ECG) signals. They tested different classifiers, including Decision Trees, K-Nearest Neighbors, Naïve Bayes and Support Vector Machines, and obtained an average accuracy of 92.02%, sensitivity of 92.59% and specificity of 91.46% by using Decision Trees.
Furthermore, machine learning approaches have also demonstrated effectiveness in SCD related studies. Milton et al. (2014) developed an ensemble system including a collection of 14 models to predict Fetal Hemoglobin (HbF) in SCD using genetic risk score (GRS) composed of different numbers of single nucleotide polymorphisms (SNPs). The ensemble system was able to explain 23.4% of the variability in HbF, and the correlation between predicted HbF from the system and observed HbF ranged between 0.28 to 0.44 in three independent test cohorts. In paper (Desai et al., 2012), a machine learning algorithm based on support vector machines was adopted to identify a 10-gene signature that discriminates between patients with and without increased tricuspid regurgitation jet velocity (TRV), and validated it as a potential biomarker for an elevated TRV in SCD. Khalaf et al. (2016) presented various neural network models for classifying the level of dosage for SCD medication. They used 13 features, including body weight, Hemoglobin, and Mean Corpuscular Volume to recommend one out of 6 levels of hydroxyurea medication dosage the patient needs to take, and obtained the best performance with AUC of 0.989. The same research group (Khalaf et al., 2017) further applied other machine learning architectures, such as random forest, support vector machines, and recurrent neural network to a similar problem, and found random forest produced the highest performance overall.
As mentioned earlier, pain is subjective and individualized in nature. However, the use of physiological measurements to study pain is not new. In paper (Brown et al., 2011), individuals were exposed to painful and non-painful thermal stimuli and the authors were able to successfully utilize Support vector machine to distinguish the two groups with an accuracy of 80.6% based on functional magnetic resonance imaging (fMRI) data. Huang et al. (2013) proposed a machine learning approach based on Naïve Bayes classifier to predict both binary level of pain (low pain and high pain) and continuous numerical value of pain (from 0 to 10) from single-trial laser-evoked potentials (LEPs). Their approach provided an accuracy of 86.3% at intra-individual level, and 80.3% at inter-individual level for binary pain prediction. Kächele et al. (2016) utilized multiple bio-physiological measurements such as electromyography (EMG), electrocardiogram (ECG), and skin conductance level (SCL) to predict pain intensity with two levels (no pain and high pain), as well as five levels using the random forest algorithm. The authors placed great effort into creating specialized classifiers for a patient by using only the most similar individuals as input data. Shankar et al. (2009) attempted to measure pain empirically using electrocardiogram (ECG), heart rate (HR), blood pressure (BP) and galvanic skin response (GSR) as artificial pain inducement with an apparatus that they designed called Pain Inducer. While they were able to find differences in the cardiac and GSR parameters between pain and non-pain conditions, they were not able to measure statistical differences in the two population groups. Tousignant-Laflamme et al. (2005) explored the relationship between HR and pain perception, and found that the relationship was significant only in the male participants (19 out of 29 participants). In paper (Harrison et al., 2006), the researchers explored the skin conductance as a measure of pain and stress in hospitalized infants. In this study, they did not find statistical differences in the skin conductance values between non-painful tasks like feeding and painful tasks like heel lancing.
One key point that was highlighted from all these studies is that pain is multifaceted, and the relationship between physiological symptoms and pain depends strongly on the patient cohort. Moreover, several of the described studies utilized artificial pain stimuli to study the relationship between pain and physiology. The relationships between pain and physiology were often inconclusive, mostly owing to the limited number of participants in the studies.
3. Material and methods
In this section, we discuss the techniques we used for data analysis, as well as handling missing data from our EHR dataset.
3.1. Data description
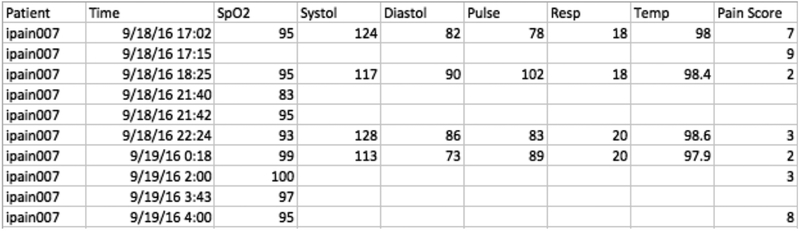
Our study used data collected from 40 in-patient participants with their clinical data recorded on admission at Duke University Hospital, from June 2015 to April 2017. There were total 5363 records from the 40 patients in the dataset. Each data entry contained six vital signs measured at the same time. These were: (i) peripheral capillary oxygen saturation (SpO2), (ii) systolic blood pressure, (iii) diastolic blood pressure, (iv) pulse (aka heart rate), (v) respiratory rate (Resp), and (vi) temperature. Along with the physiological measures, the patient’s self-reported pain score was included with each data entry. This pain score was the current pain experienced by the patient with an ordinal range from 0 (no pain) to 10 (severe and unbearable pain). The data were anonymized using study labels to label the patient without identification and the timestamp for each data entry was recorded. Fig. 1 shows a sample of the Electronic Health Record (EHR) data. The blank area in the sample dataset is indicative of missing values. In our dataset, the data missing rate among all seven variables (six vital signs and the pain score) for all patients is 54.09%. The most direct approach to handle missing data is list-wise deletion, which means excluding all cases with any missing value. The percentage of complete cases in our dataset is only 6.34%, making it necessary to implement an imputation method to predict and impute missing data values.
Fig. 1.
Sample Electronic Health Record
3.2. Intra-individual level and inter-individual level analysis
Prediction of pain scores by using vital signs can be realized at two levels: intra-individual and inter-individual. At the intra-individual level, a personal prediction model is created by using data from a single patient, and can be applied to the same patient only. At the inter-individual level, a general prediction model is created by using data from a group of patients, and can be applied to any patient. The intra-individual analysis can be applied to patients having enough data to create their own models, while the general inter-individual analysis can be utilized for new patients that do not have sufficient data initially to create their personal models, eventually moving to the intra-individual model as more data for the individual patient is collected.
3.3. Imputation method
A variety of imputation methods of varying complexity are available. Single imputation is the simplest and most common method for handling missing data. It generates a single replacement value for each missing data point. According to the value used to replace the missing value, there are several single imputation methods. One is mean imputation, in which missing values of each variable are replaced with the arithmetic mean of that variable. Mean imputation has the benefit of not changing the variable mean, but leads to an artificial decrease in variable variances. A better single imputation approach is regression imputation. In this method, each missing value in the dataset is replaced by a predicted value from a regression model based on complete cases. Regression imputation provides a more reliable value for missing data by including more information from the observed data. However, it overestimates the correlations between variables, and still underestimates variable variances. Therefore, the main disadvantage of single imputation is that the single value being imputed cannot reflect the variability and uncertainty of the actual value.
For these reasons, we chose to implement multiple imputation by Fully Conditional Specification (FCS). Multiple imputation is a method in which missing values are replaced by multiple simulated values (Rubin, 2004). Therefore, it takes into account for uncertainty in the missing values and improves the validity of the results when analyzing datasets with missing observations (Blankers et al., 2010). FCS is one of the implementation techniques for multiple imputation. It is an iterative Markov Chain Monte Carlo (MCMC) method that can be used for a dataset with an arbitrary missing data pattern. FCS provides flexibility in creating imputation models and generally yields unbiased and appropriate estimates of missing values (Van Buuren, 2007). Additionally, multiple imputation has been successfully utilized in many healthcare related researches. For example, Fullerton et al. (2012) applied multiple imputation to impute missing data for respiratory rate, heart rate, temperature, systolic blood pressure, oxygen saturation and AVPU score; Shah et al. (2015) implied multiple imputation to replace missing data in body mass index, total cholesterol, blood pressure, smoking status, and other parameters. Multiple imputation involves three steps:
Each missing value is imputed M times from a distribution, which leads to M completed datasets.
Each of the M completed datasets is analyzed using standard complete-case procedures independently.
The M results are pooled into one result (Rubin, 2004). According to our data missing rate (~50%), M = 40 were chosen following the existing recommendation (Graham et al., 2007).
In our intra-individual level analysis, six vital signs and the pain score were used for imputation as well as pain prediction. However, for the inter-individual level analysis, the treatment of individual-level differences becomes a problem. By considering individual-level differences in the imputation phase, then patient labels should be used as a predictor in imputation. By considering individual-level differences in the prediction phase, the patient labels should then be included in the prediction model beyond six vital signs. Therefore, we presented our inter-individual results in four cases: (1) Case 1: imputation with patient labels and prediction with patient labels; (2) Case 2: imputation with patient labels and prediction without patient labels; (3) Case 3: imputation without patient labels and prediction with patient labels; (4) Case 4: imputation without patient labels and prediction without patient labels.
3.4. Prediction method
We implemented a series of classification algorithms to predict patients’ pain scores based on their vital signs, all of which belong to the category of supervised machine learning. In supervised machine learning, the task is inferring a function to model the relationship between the target variable (pain score), and predictor variables (vital signs) from a training dataset. The training dataset contains series of training samples. Each sample is a pair of target variable and predictor variables, which can be used to estimate parameters of the inferred function. After the training process, the inferred function can be used to predict the value of the target variable from a new sample of predictor variables.
We adopted four widely used classification algorithms for pain prediction: Multinomial Logistic Regression (MLR), K-Nearest Neighbors (KNN), Support Vector Machine (SVM), and Random Forest (RF). The former two approaches are easier to implement and interpret; the latter two methods are more advanced and reported to have higher prediction accuracy. Moreover, as mentioned in section 2 related work, it is clear that all four algorithms are also prevailing machine learning approaches in healthcare related areas.
The first prediction model we applied was Multinomial Logistic Regression (MLR). Logistic Regression is a simple type of supervised machine learning approach for binary classification. The inferred function used in Logistic Regression is called the logistic or sigmoid function. The output of logistic function is bounded between 0 and 1, which can be interpreted as the conditional probability of each possible value of the target variable by giving the input predictor variables. Therefore, Logistic Regression is commonly used to predict a binary category target variable. MLR can be considered as an extension of binary Logistic Regression, which can be used to predict the probabilities of the category membership of a nominal target variable with more than two classes. The final outcomes of a MLR model will be the probability assignments for each class, and the decision is made by choosing the class with the highest probability. In our case, the outcomes are the class membership of 11 pain scores. The main advantages of using MLR are its simple implementation, fast computation, and that we can draw qualitative conclusions about the phenomenon based on the value and significance of each predictor variable in the model.
K-Nearest Neighbors (KNN) is a simple, easy to interpret machine learning algorithm with high predictive power. In KNN classification, the category of a data point is determined by a majority of its k nearest neighbors. In other words, the data point is assigned with the most common class among its k nearest neighbors.
Support Vector Machine (SVM) (Cortes & Vapnik, 1995) is another widely used supervised machine learning algorithm. In a classification problem, an SVM model maps data points from input space to feature space, then finds a decision surface among classes that has the largest distance to any data point. New samples then can be mapped into the same feature space, and their categories can be predicted based on which side of the decision surface they fall on. In addition to performing linear classification like MLR, which means the decision surface is a hyperplane, SVM can effectively perform nonlinear classification using a kernel trick that maps inputs into high-dimensional feature spaces.
As suggested by Caruana & Niculescu-Mizil (2006), Random Forest (RF) has an overall excellent performance in many machine learning tasks. The basic principle of RF is that a group of weak learners can get together to establish a strong learner. Decision tree is the weak learner used in the RF algorithm, with tree leaves representing classes and branches representing combinations of features that lead to those classes. An RF model recruits a collection of decision trees at training time and predicts the class of a data sample as the majority voting from all trees. We used the method of 10 fold cross-validation to evaluate all our prediction results. This is a common technique for assessing the performance of the prediction model on an independent dataset in order to ensure generalizability (Kohavi, 1995). As measures of classification utility, we reported accuracy and weighted average F1 score based on precision and recall as evaluation metrics. Accuracy is the ratio of correctly predicted pain scores over total number of pain scores. We then computed precision and recall for each of 11 pain scores. Precision is the ratio of the number of correctly identified entities with this pain score over the total number of this particular pain score predicted by the model. On the other hand, recall is the ratio of the number of correctly identified entities with this pain score over the total number entities with this pain score in the dataset. F1 score is the harmonic mean of precision and recall for each pain score (Mitchell, 1997). The weighted average F1 score, a better choice for evaluating multiple classes datasets, is the average of F1 score among all pain scores weighted by the number of instances of each pain score (Larsen & Aone, 1999).
4. Results
4.1. Feature analysis (RQ1)
We first examined the Pearson correlation between each two of the six vital signs we plan to use as indicators for pain scores. Additionally, the correlation between each vital sign and the pain score was also inspected. Tables 1A and 1B shows the correlations for the dataset imputed with patient labels (intra-individual level) and the dataset imputed without patient labels (inter-individual level), respectively. All correlations are statistically significant (p-value < 0.001). Only systolic and diastolic blood pressure have a moderate positive correlation with each other with r = 0.626 in Table 1A (or 0.640 in Table 1B), and the other variables are poorly correlated or uncorrelated with one another (Udovičić et al., 2007). The correlations of vital signs indicate that they can contribute to the prediction model by carrying information from different perspectives. Therefore, it is reasonable to utilize all six vital signs as predictors in the prediction models. We will further discuss the predictor importance in Section 4.3. For the correlations between pain score and vital signs at both the intra-individual and inter-individual levels, none of the parameters show a strong correlation. This indicates that the pain score is not linearly related to any of the six vital signs. Therefore, a linear model is not utilized for pain prediction.
Table 1A.
Pearson correlation of six vital signs in imputed dataset with patient labels (Note: SpO2 = oxygen saturation, Resp = respiratory rate, and BP = blood pressure)
| SpO2 | Systolic BP |
Diastolic BP |
Pulse | Resp | Temperature | Pain Scores | |
|---|---|---|---|---|---|---|---|
| SpO2 | 1.000 | −0.095 | −0.058 | −0.147 | −0.046 | −0.102 | −0.015 |
| Systolic BP | 1.000 | 0.626 | −0.001 | 0.019 | 0.012 | 0.090 | |
| Diastolic BP | 1.000 | 0.078 | 0.084 | −0.005 | 0.033 | ||
| Pulse | 1.000 | 0.361 | 0.458 | −0.203 | |||
| Resp | 1.000 | 0.217 | −0.126 | ||||
| Temperature | 1.000 | −0.075 | |||||
| Pain | 1.000 |
Table 1B.
Pearson correlation of six vital signs in imputed dataset without patient labels (Note: SpO2 = oxygen saturation, Resp = respiratory rate, and BP = blood pressure)
| SpO2 | Systolic BP |
Diastolic BP |
Pulse | Resp | Temperature | Pain Scores | |
|---|---|---|---|---|---|---|---|
| SpO2 | 1.000 | −0.072 | −0.058 | −0.161 | −0.047 | −0.094 | 0.088 |
| Systolic BP | 1.000 | 0.640 | −0.019 | 0.017 | −0.0154 | 0.134 | |
| Diastolic BP | 1.000 | 0.058 | 0.065 | −0.042 | 0.039 | ||
| Pulse | 1.000 | 0.380 | 0.450 | −0.212 | |||
| Resp | 1.000 | 0.204 | −0.121 | ||||
| Temperature | 1.000 | −0.098 | |||||
| Pain Scores | 1.000 |
4.2. Intra-individual analysis (RQ2)
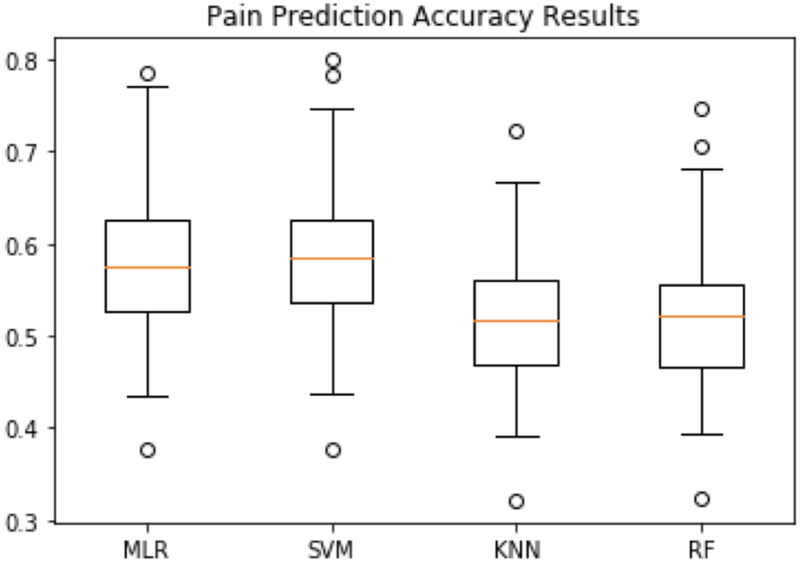
Fig. 2 and Fig. 3 show the intra-individual pain prediction results for 38 patients in terms of accuracy and weighted average F1 score respectively. Two patients have too few data for intra-individual analysis, since the suggested minimum sample size required for multinomial classification is 3.3 times of the number of classes, which is 37 samples in our case (Raudys & Jain, 1991). For each patient, the accuracy and weighted average F1 score were defined as described in section 3.4, and obtained by pooling (i.e. taking the average) over 40 imputations. The four boxplots in Fig. 2 represent the accuracy distribution of predictions for 38 patients by applying MLR, SVM, KNN and RF classifiers, respectively. Among all four prediction methods, SVM achieved the highest accuracy result ranging from 0.377 to 0.800, and an average accuracy of 0.582. MLR obtained a little bit lower performance than SVM ranging from 0.377 to 0.786, and an average accuracy of 0.578. KNN and RF had lower average performances of 0.522 and 0.523, respectively.
Fig. 2.
Intra-individual pain prediction accuracy results using MLR, SVM, KNN and RF
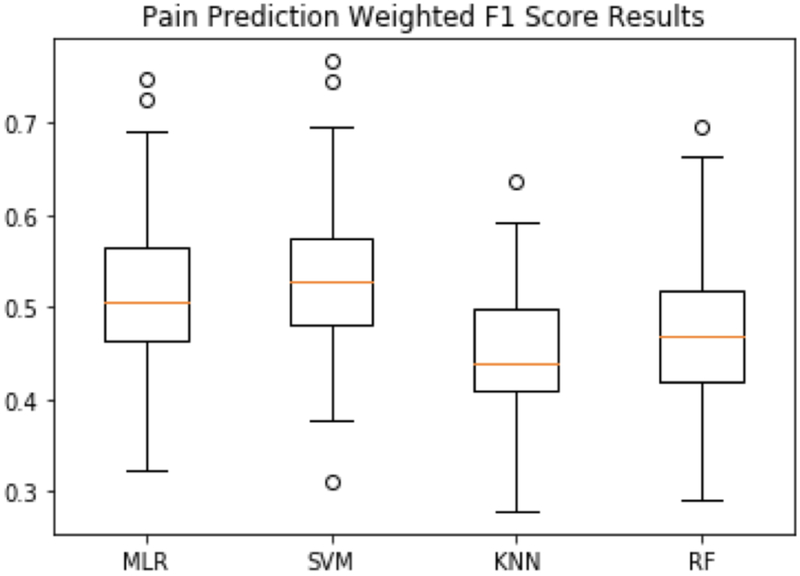
Fig. 3.
Intra-individual pain prediction weighted average F1 score results using MLR, SVM, KNN and RF
Fig. 3 illustrates the intra-individual prediction results with respect to weighted average F1 score. Due to the class imbalance problem (since the pain levels are not distributed equally over all the 11 pain levels), weighted F1 scores were lower than accuracy measures, but show a similar trend among the four algorithms. Once again, SVM outperformed other classifiers based on an average weighted F1 score of 0.529. MLR also had a similar performance with an average weighted F1 score of 0.520. KNN and RF obtained an average weighted F1 score of 0.454 and 0.477 respectively.
4.3. Inter-individual analysis (RQ3)
Tables 2A and 2B summarize the pooled accuracy results and weighted average F1 score results of two prediction methods at the inter-individual level in the four cases defined in section 3.3. We tested the same four prediction algorithms as we used in the intra-individual level analysis, and MLR and SVM still outperformed KNN and RF. Therefore, we only reported MLR and SVM results for convenience. Among four inter-individual cases, the best performance was achieved by considering individual-level differences in both the imputation phase and the prediction phase (aka Case 1 that utilizes intra-individual imputation as well as intra-individual prediction). We describe the interpretation of these cases in more detail in Section 3.3. In Case 1, the accuracy was 0.429 for MLR, 0.421 for SVM, and the weighted average F1 score was 0.422 for MLR, 0.410 for SVM. A lower performance appeared in Case 4 with MLR (accuracy: 0.257, weighted average F1 score: 0.209) and SVM (accuracy: 0.246, weighted average F1 score: 0.156). In general, MLR obtained better performance than SVM. Considering that there are total 11 pain scores to predict, the model will obtain a 0.091 (1/11) accuracy by random guessing. Therefore, the prediction model can still be considered useful even though the accuracy is not as high as many classifiers with fewer levels.
Table 2A.
Inter-individual pain prediction accuracy results using MLR and SVM
| Imputation with labels [MLR, SVM] |
Imputation without labels [MLR, SVM] |
|
|---|---|---|
| Prediction with labels | Case1: [0.429, 0.421] | Case 3: [0.313, 0.305] |
| Prediction without labels | Case 2: [0.215, 0.236] | Case 4: [0.257, 0.246] |
Table 2B.
Inter-individual pain prediction weighted average F1 score results using MLR and SVM
| Imputation with labels [MLR, SVM] |
Imputation without labels [MLR, SVM] |
|
|---|---|---|
| Prediction with labels | Case 1: [0.422, 0.410] | Case 3: [0.301, 0.290] |
| Prediction without labels | Case 2: [0.173, 0.193] | Case 4: [0.209, 0.156] |
In order to measure the importance of each feature in predicting the pain score, a likelihood ratio test was performed in Case 4, which means we evaluated the feature importance on the general population without considering individual-level differences (Hosmer et. al 2013). In this test, the value of deviance with and without a specific feature in the model are compared. The deviance is equal to −2lnL, where L is the likelihood of the fitted model. The difference between the deviances is the chi-square value shown in Table 3. It follows a chi-square distribution with degrees of freedom equal to the difference in the number of parameters estimated. From the results shown in Table 1, we can find that all features have contributed to the prediction of pain scores (p-value < 0.001). By comparing the chi-squared value associated with each feature, we can estimate the relative importance of the six vital signs. Although the order of chi-squared values of six vital signs vary due to imputation, we can still find that SpO2, systolic blood pressure, pulse and temperature significantly affect pain prediction. Diastolic blood pressure has lower impact than the previous four features. Resp seems to have the smallest impact among all six features. However, since all the features were found to be significant parameters to measure pain, we have retained the six physiological measures for building pain prediction models.
Table 3.
Likelihood ratio tests of MLR for Case 4 (vital signs are sorted according to their importance as predictors using the average chi-squared values among all imputed dataset)
| Vital Signs | Average among all imputed dataset | Imputed dataset with highest accuracy (imp 13) | Imputed dataset with lowest accuracy (imp 35) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Chi-squared | Degree of freedom | Significant level | Chi-squared | Degree of freedom | Significant level | Chi-squared | Degree of freedom | Significant level | |
| Temperature | 784.498 | 10 | <0.001 | 1284.547 | 10 | <0.001 | 583.525 | 10 | <0.001 |
| Systolic BP | 396.486 | 10 | <0.001 | 296.514 | 10 | <0.001 | 338.438 | 10 | <0.001 |
| SpO2 | 366.134 | 10 | <0.001 | 309.031 | 10 | <0.001 | 362.161 | 10 | <0.001 |
| Pulse | 357.173 | 10 | <0.001 | 642.612 | 10 | <0.001 | 435.084 | 10 | <0.001 |
| Diastolic BP | 315.559 | 10 | <0.001 | 214.835 | 10 | <0.001 | 212.067 | 10 | <0.001 |
| Resp | 115.448 | 10 | <0.001 | 130.301 | 10 | <0.001 | 83.806 | 10 | <0.001 |
4.4. Other pain rating scales (RQ4)
In the original EHR dataset, there are 11 different pain scores. There is a lot of uncertainty in how patients report their pain, and even in how a single patient will report their pain from one time to the next with such a dense rating scale. Moreover, there are other pain rating scales in use with fewer levels (Hjermstad et al., 2011). Therefore, we further created pain prediction models based on a 6-point rating scale, a 4-point rating scale, and a binary rating scale. Ten pain scores, except pain score 0, are divided evenly into five categories in the 6-point rating scale (new levels are: 0, 1–2, 3–4, 5–6, 7–8, 9–10). Different cut-points may be applied for pain caused by different diseases (Boonstra et al., 2014; Zelman et al., 2005). In the 4-point rating scale, NRS scores can be categorized as none (0), mild (1–3), moderate (4–6), and severe (7–10) (Krebs et al., 2007). Cut-point 5 is considered as the optimal solution for binary division of NRS scores (Zelman et al., 2003). Table 4 illustrates the transformation rules of pain rating scales from the original 11-point scale and the prediction performances in the four inter-individual analysis cases among these different scales. Only MLR results were listed in these tables, since we have demonstrated that MLR was the best among the four algorithms we have tested in section 4.2 and section 4.3. As shown in Table 4, accuracies and weighted average F1 scores increased significantly with the decreasing number of pain levels. The performance of the four cases showed a similar trend as in inter-individual analysis with 11 pain scores.
Table 4.
Inter-individual pain prediction results with varying pain scales
| Number of Pain Ratings | Transformation Rules | Imputation with labels & Prediction with labels (Case 1) Accuracy/Weighted F1 |
Imputation with labels & Prediction without labels (Case 2) Accuracy/Weighted F1 |
Imputation without labels & Prediction with labels (Case 3) Accuracy/Weighted F1 |
Imputation without labels & Prediction without labels (Case 4) Accuracy/Weighted F1 |
|---|---|---|---|---|---|
| 11 Pain Scores | N/A | 0.429 / 0.422 | 0.215 / 0.173 | 0.313 / 0.301 | 0.257 / 0.209 |
| 6 Pain Scores | None:0 | 0.546 / 0.540 | 0.347 / 0.262 | 0.449 / 0.423 | 0.397 / 0.313 |
| Very mild: 1–2 | |||||
| Mild: 3–4 | |||||
| Moderate: 5–6 | |||||
| Severe: 7–8 | |||||
| Very severe:9–10 | |||||
| 4 Pain Scores | None: 0 | 0.681 / 0.673 | 0.521 / 0.421 | 0.607 / 0.578 | 0.563 / 0.483 |
| Mild: 1–3 | |||||
| Moderate: 4–6 | |||||
| Severe: 7–10 | |||||
| 2 Pain Scores | No/mild | 0.821 / 0.819 | 0.680 / 0.647 | 0.730 / 0.718 | 0.678 / 0.616 |
| Pain: 0–5 | |||||
| Severe | |||||
| Pain: 6–10 |
4.5. Pain change detection using physiology (RQ5)
In this study, pain change is defined as increase, decrease and no change, marked as 1, −1 and 0, respectively. When the difference between next pain score and current pain score is larger than 0, it is an increase; when the difference is smaller than 0, it is a decrease; otherwise, it is no change. Current physiological measurements were used to predict the pain change direction from current pain score to next pain score. The same six vital signs were used as predictors for pain change detection. The prediction results are summarized in Table 5. Only MLR results were listed due to its best performance.
Table 5.
Pain change prediction results using MLR
| Accuracy | Imputation with labels Accuracy/Weighted F1 |
Imputation without labels Accuracy/Weighted F1 |
|---|---|---|
| Prediction with labels | Case 1:0.403 / 0.386 | Case 3: 0.390 / 0.374 |
| Prediction without labels | Case 2: 0.363 / 0.315 | Case 4: 0.404 / 0.347 |
5. Discussion
In this section, we discuss the implications and challenges of the different experiments, and results we obtained in the previous sections.
5.1. Feature analysis (RQ1)
The relationship between systolic and diastolic blood pressure has been well reported in healthy patients with correlations ranging around 0.6–0.7 (Soergel et al., 1997). It was interesting to see a similar relationship even within our SCD patient cohort. Since the coefficient of determination between systolic and diastolic blood pressure (r sq. = 0.38) was low, we concluded that they could be treated as independent variables for the prediction analysis. The other physiological measures appeared poorly correlated or uncorrelated with one another. Hence, we retained all the features to evaluate the pain prediction models as multicollinearity (when independent variables are dependent on each other) did not take place in our dataset. However, at this point, it was still not clear whether physiological measures can really be used to predict pain levels in SCD patients or not. We discuss the prediction results further in the next sections.
5.2. Intra-individual pain prediction (RQ2)
Pain is a subjective experience and really hard to assess except using patients’ own self-reports according to its definition (McCaffery, 1968). However, as shown in our intra-individual pain prediction results, we were able to predict pain scores of each patient using only six objective physiological measurements. An average accuracy of 0.582, and a maximum accuracy of 0.800 were obtained among 38 individuals’ analysis results in our study comparing to their self-reported values.
Among all four machine learning algorithms, SVM with linear kernel had the best performance, but the results of the relatively simpler MLR were comparable to those from the SVM. Moreover, MLR is a probabilistic algorithm, as opposed to SVM which is more geometrically inspired. SVM tries to learn support vectors that best separate the classes by a hyperplane, hence SVM is a more complex and less explainable model (Cortes & Vapnik, 1995). Based on these findings, we rationalized that MLR might be adopted as the optimal algorithm for our remaining experiments. For the other machine learning methods, it is not surprising that KNN had the worst performance since it just considered the local neighborhood of the current data point. Physiological measurements are not only affected by pain, but also affected by other things like patients’ activity. For the same pain score, there may not always be the same combination of vital signs. Therefore, a simple algorithm like KNN is less likely to perform as well as other techniques for this dataset. The reason why the accuracy of RF was not as good as in some other applications was that the number of data samples used for training from each patient were limited, which was not sufficient to leverage the predictive power of RF.
Considering the evaluation metrics, accuracy is the most commonly used one. However, when the dataset has a class imbalance challenge, then just using accuracy to evaluate the results biases the evaluation toward the majority class, since accuracy measures the ratio of the number of accurate predictions to the total predictions. Precision and recall are two measures generally used in these circumstances. For example, precision could be used to represent the fraction of correctly predicted pain score 8 among all claimed pain score 8 by the prediction model; recall could be used to represent the fraction of correctly predicted pain score 8 among all actual pain score 8 in the dataset. To represent these two metrics with one quantifier, we used F1 score, the harmonic mean of precision and recall, as our evaluation metric for each single class. Furthermore, since we had total 11 classes (pain scores), we used one single weighted average F1 score to represent the general prediction results among all 11 classes. We found that due to the class imbalance problem, the weighted F1 scores were lower than the accuracies, but still provided comparable, as well as unbiased performances. The weighted F1 score further showed similar trends as the accuracy results among the four machine learning algorithms, indicating that both metrics were effective for this dataset.
5.3. Inter-individual pain prediction (RQ3)
Due to the inherent individual differences in physiological data and the subjective nature of pain, inter-individual prediction will tend to have lower performance than intra-individual pain prediction. However, in real clinical conditions, when a new patient is enrolled, there are no data to build an intra-individual level model for the new patient, in which case the inter-individual level model should be applied. Furthermore, the performance of inter-individual prediction was still much better than the baseline random guess (accuracy of 1/11), which indicates that the six vital signs are still strong predictors for pain scores at inter-individual level. Similar patterns of results in inter-individual pain predictions were observed as compared to the intra-individual pain predictions of accuracies and weighted average F1 scores using the four machine learning algorithms: MLR and SVM achieved the best and comparable performance, and weighted average F1 scores were lower than accuracies. Due to the limited number of features (six vital signs) and a moderate-sized dataset (5363 samples), it turned out that more complex algorithms like RF did not improve the prediction accuracy. Overall, MLR should be considered the optimal algorithm at both intra-individual and inter-individual levels due to its prediction accuracy, ease of implementation and explanatory power. The better performance of MLR may be due to the fact that there are high variances in the corresponding training samples among different imputed datasets, thus a simpler algorithm that needs less tuning of parameters is more robust and able to obtain a better and generalizable performance among 40 different imputed datasets.
As described in section 3.3, there were four different cases in inter-individual pain prediction. Among all four cases, two cases are worth further attention: Case 1, considering individual differences in both imputation phase and prediction phase; Case 4, not considering individual differences in either imputation phase or prediction phase. Case 1 is important as it had the highest performance by utilizing patient labels in both the imputation phase and the prediction phase. Case 4 is also important because it didn’t employ patient labels in any phases. The remaining two cases fall in between these two extreme conditions with applying patient labels in only one of the two phases. A typical scenario in practical application is, when a new patient X is enrolled in the system, no vital signs and pain scores are recorded for this patient, then the Case 4 model could be applied first which assumes no prior information about patient X. With the increase of data records from patient X, we could then apply the Case 1 model to obtain a more personalized model with improved performance.
5.4. Other pain rating scales (RQ4)
In the practical clinical application, there is a very fine line between consecutive pain levels such as 5 and 6 making it extremely challenging for machine learning techniques to achieve that degree of precision. Not surprisingly, as shown from the prediction with other pain scales (Table 3), we found that with a decreasing number of pain levels, the prediction accuracies increased significantly, but meanwhile we also lost some sensitivity in distinguishing different pain intensities. When the pain prediction system was applied with the 4-point rating scale, we were able to reach a “sweet spot”, where a good balance was achieved between prediction accuracy (0.681 in Case 1, 0.563 in Case 4 as shown in Table 3) and pain assessment sensitivity. This was further corroborated by our clinical collaborators who either used the 11-point scale from 0 to 10, or the 4-point scale (None, Mild, Moderate, Severe).
Furthermore, the 11-point prediction model and the 4-point prediction model can be applied to patients in different pain scenarios. For example, patients hospitalized routinely use the 0 to 10 point visual analog scale to monitor patient pain levels and response to interventions. Patients using this scale was found useful in the titration of analgesics during pain crisis and used to assist in discharge planning (Ballas, 1993). It is possible to use the 4-point model for this case as well, but we lose granularity by doing so. That said, for patients with sparser data, the 11-point model maybe too complex a model, creating issues like under-fitting due to less training data.
Medical providers more often use the 4-point model for outpatients with SCD to assist with clinical decision making. Based on classification of pain (none, mild, moderate or severe), patients can be advised to treatment of their pain with oral medications (WHO guidelines). In addition, when the pain levels of a patient are sparse, the 4-point model is appropriate for pain prediction. For example, one of the patients in our dataset only had self-reported pain scores as [0, 4, 5, 7], which is an ideal case for applying the 4-point model. Similarly, if a patient was newly admitted to the hospital and had reported pain levels for a single day, then the 4-point model would be initially used until more data were obtained for that patient.
As mentioned in section 2, the feasibility of pain prediction using objective physiological measurements has been explored by several research studies. Huang et al. (2013) reported their results for both intra-individual level and inter-individual level with accuracies of 0.863 and 0.803 respectively for binary pain prediction using LEPs. Kächele et al. (2016) reported their accuracy for inter-individual binary pain prediction of 0.857. Furthermore, they also provided their inter-individual prediction for five pain levels with accuracy of 0.395. These accuracy results for inter-individual binary prediction were comparable to our results (0.821 in Case 1 as shown in Table 3) with vital signs as predictors. Meanwhile the accuracy of five pain levels (0.395) from Kächele et al. was comparable to our inter-individual prediction results with six pain levels of Case 4 (as shown in Table 3) where the accuracies were 0.397.
5.5. Pain change detection using physiology (RQ5)
In pain change detection, we defined pain change as increase, decrease and no change which made it a three-class classification problem. The baseline accuracy in this case would then be 0.33 (1/3). However, the highest accuracy we achieved in our experiments was 0.404. It indicated that the current dataset we used was not sufficient for accurate pain change detection as the results were not much improved from the baseline. The main reason of the low performance was that other pain related information, such as medication usage, was not included in the analysis. For example, if patients take pain relief medications, their pain scores will decrease. However, the prediction model has no clue of the medication usage, hence the pain change cannot be predicted correctly. Moreover, the magnitude of pain change were not utilized by the prediction model, which further affected the algorithm performance.
5.6. Importance in clinical practice
We believe our findings are crucial to clinical providers of patients with pain. Due to the subjective nature of the pain, assessment and management is currently difficult. Clinicians often rely on other indicators, such as vitals and non-verbal cues, to improve their assessment of the pain. Evaluating the predictive ability of objective physiologic measurements is therefore critical. Although studies have shown independent associations between heart rate and blood pressure with pain, there have been no significant efforts reported on the attempt to predict pain. Clifton et.al. (2017) reported modeling of symptoms of pain in relation to pain medication administration. The model was a new hybrid model for the dynamics of subjective pain that involves a dynamical systems approach using both differential equations to predict future pain levels and a statistical approach to combine system parameters to patient data (both personal characteristics and medication response history). We are now reporting our initial efforts to build predictive techniques for pain based on vital signs.
We recognize the limitations in a pilot study, including sample size and potential confounders to changes in vital signs outside of pain (such as dehydration and infection). We attempted to include patients similar in admission diagnosis and exclude patients with active infection or receiving transfusions. Patients with an admission diagnosis of uncomplicated pain crisis were included and received standard of care treatments including intravenous fluids and narcotic pain medications.
6. Conclusion
Using only physiological measurements for patients with SCD, we estimated the pain scores of the individuals without including their medication information. Using multiple imputation, we utilized missing data in the machine learning algorithms. We proposed pain prediction models in various scenarios: (i) intra-individual pain prediction with 11 pain scores, (ii) inter-individual pain prediction with 11 pain scores, and (iii) inter-individual pain prediction with condensed pain levels numbering less than 11 (6,4 and 2 pain levels). In each of these experiments, MLR gave the optimal performance among the four algorithms we tested (MLR, SVM, KNN, RF), striking a balance between accuracy and model simplicity. Our test results addressed the main research hypothesis regarding the feasibility of using objective physiological measurements to predict subjective pain in SCD patients.
For future work, patients’ personal and demographic information like age, gender and baseline pain score will be included in the prediction model to further improve the system performance. Medication usage will be included in the pain change detection model. We also plan to incorporate wearable device data into the model, replacing the physiological measures from the EHR data with the wearable physiological information. We are currently in the process of collecting wearable data from SCD patients with the Microsoft Band 2 device, where we will utilize the data from the Band to predict the pain levels of the patients. This is a step towards continuous and non-invasive pain management for SCD patients during hospitalization and after they are discharged from the hospital. Doing so will allow us to create a remote pain management system that can hopefully reduce re-hospitalization and improve the quality of life for patients with SCD.
Acknowledgment
This work was supported in part by the NIH under grant K01 LM012439–01. We thank Dr. Daniel Abrams and Dr. William Romine for their valuable feedback on the manuscript.
References
- Acharya UR, Vidya KS, Ghista DN, Lim WJE, Molinari F, & Sankaranarayanan M (2015). Computer-aided diagnosis of diabetic subjects by heart rate variability signals using discrete wavelet transform method. Knowledge-based systems, 81, 56–64. [Google Scholar]
- Austin PC, Tu JV, Ho JE, Levy D, & Lee DS (2013). Using methods from the data-mining and machine-learning literature for disease classification and prediction: a case study examining classification of heart failure subtypes. Journal of clinical epidemiology, 66(4), 398–407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ballas SK (2005). Pain management of sickle cell disease. Hematology/oncology clinics of North America, 19(5), 785–802. [DOI] [PubMed] [Google Scholar]
- Blankers M, Koeter MW, & Schippers GM (2010). Missing data approaches in eHealth research: simulation study and a tutorial for nonmathematically inclined researchers. Journal of medical Internet research, 12(5). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boonstra AM, Preuper HRS, Balk GA, & Stewart RE (2014). Cut-off points for mild, moderate, and severe pain on the visual analogue scale for pain in patients with chronic musculoskeletal pain. PAIN®, 155(12), 2545–2550. [DOI] [PubMed] [Google Scholar]
- Bradley AP (1997). The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern recognition, 30(7), 1145–1159. [Google Scholar]
- Brown JE, Chatterjee N, Younger J, & Mackey S (2011). Towards a physiology-based measure of pain: patterns of human brain activity distinguish painful from non-painful thermal stimulation. PloS one, 6(9), e24124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caruana R, & Niculescu-Mizil A (2006, June). An empirical comparison of supervised learning algorithms In Proceedings of the 23rd international conference on Machine learning (pp. 161–168). ACM. [Google Scholar]
- Churpek MM, Yuen TC, Park SY, Gibbons R, & Edelson DP (2014). Using electronic health record data to develop and validate a prediction model for adverse outcomes on the wards. Critical care medicine, 42(4), 841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clifton SM, Kang C, Li JJ, Long Q, Shah N, & Abrams DM (2017). Hybrid statistical and mechanistic mathematical model guides mobile health intervention for chronic pain. Journal of Computational Biology. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cortes C, & Vapnik V (1995). Support-vector networks. Machine learning, 20(3), 273–297. [Google Scholar]
- Desai AA, Zhou T, Ahmad H, Zhang W, Mu W, Trevino S, … & Thiruvoipati T (2012). A novel molecular signature for elevated tricuspid regurgitation velocity in sickle cell disease. American journal of respiratory and critical care medicine, 186(4), 359–368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Downie WW, Leatham PA, Rhind VM, Wright V, Branco JA, & Anderson JA (1978). Studies with pain rating scales. Annals of the rheumatic diseases, 37(4), 378–381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elmariah H, Garrett ME, Castro LM, Jonassaint JC, Ataga KI, Eckman JR, … & Telen MJ (2014). Factors associated with survival in a contemporary adult sickle cell disease cohort. American journal of hematology, 89(5), 530–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forkan ARM, Khalil I, Tari Z, Foufou S, & Bouras A (2015). A context-aware approach for long-term behavioural change detection and abnormality prediction in ambient assisted living. Pattern Recognition, 48(3), 628–641. [Google Scholar]
- Fullerton JN, Price CL, Silvey NE, Brace SJ, & Perkins GD (2012). Is the Modified Early Warning Score (MEWS) superior to clinician judgement in detecting critical illness in the pre-hospital environment?. Resuscitation, 83(5), 557–562. [DOI] [PubMed] [Google Scholar]
- Graham JW, Olchowski AE, & Gilreath TD (2007). How many imputations are really needed? Some practical clarifications of multiple imputation theory. Prevention science, 8(3), 206–213. [DOI] [PubMed] [Google Scholar]
- Gultepe E, Green JP, Nguyen H, Adams J, Albertson T, & Tagkopoulos I (2014). From vital signs to clinical outcomes for patients with sepsis: a machine learning basis for a clinical decision support system. Journal of the American Medical Informatics Association, 315–325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrison D, Boyce S, Loughnan P, Dargaville P, Storm H, & Johnston L (2006). Skin conductance as a measure of pain and stress in hospitalised infants. Early human development, 82(9), 603–608. [DOI] [PubMed] [Google Scholar]
- Hjermstad MJ, Fayers PM, Haugen DF, Caraceni A, Hanks GW, Loge JH, … & European Palliative Care Research Collaborative (EPCRC. (2011). Studies comparing Numerical Rating Scales, Verbal Rating Scales, and Visual Analogue Scales for assessment of pain intensity in adults: a systematic literature review. Journal of pain and symptom management, 41(6), 1073–1093. [DOI] [PubMed] [Google Scholar]
- Hosmer DW Jr, Lemeshow S, & Sturdivant RX (2013). Applied logistic regression (Vol. 398). John Wiley & Sons. [Google Scholar]
- Huang G, Xiao P, Hung YS, Iannetti GD, Zhang ZG, & Hu L (2013). A novel approach to predict subjective pain perception from single-trial laser-evoked potentials. Neuroimage, 81, 283–293. [DOI] [PubMed] [Google Scholar]
- Kächele M, Thiam P, Amirian M, Schwenker F, & Palm G (2016). Methods for person-centered continuous pain intensity assessment from bio-physiological channels. IEEE Journal of Selected Topics in Signal Processing, 10(5), 854–864. [Google Scholar]
- Khalaf M, Hussain AJ, Al-Jumeily D, Keight R, Keenan R, Fergus P, … & Idowu IO (2016, August). Training Neural Networks as Experimental Models: Classifying Biomedical Datasets for Sickle Cell Disease In International Conference on Intelligent Computing (pp. 784–795). Springer International Publishing. [Google Scholar]
- Khalaf M, Hussain AJ, Keight R, Al-Jumeily D, Fergus P, Keenan R, & Tso P (2017). Machine learning approaches to the application of disease modifying therapy for sickle cell using classification models. Neurocomputing, 228, 154–164. [Google Scholar]
- Kohavi R (1995, August). A study of cross-validation and bootstrap for accuracy estimation and model selection In Ijcai (Vol. 14, No. 2, pp. 1137–1145). [Google Scholar]
- Krebs EE, Carey TS, & Weinberger M (2007). Accuracy of the pain numeric rating scale as a screening test in primary care. Journal of General Internal Medicine, 22(10), 1453–1458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larsen B, & Aone C (1999, August). Fast and effective text mining using linear-time document clustering In Proceedings of the fifth ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 16–22). ACM. [Google Scholar]
- Lorey FW, Arnopp J, & Cunningham GC (1996). Distribution of hemoglobinopathy variants by ethnicity in a multiethnic state. Genetic epidemiology, 13(5), 501–512. [DOI] [PubMed] [Google Scholar]
- Macintyre PE, Scott DA, Schug SA, Visser EJ, & Walker SM (Eds.). (2010). Acute pain management: scientific evidence(pp. 35–45). Melbourne: ANZCA & FPM. [Google Scholar]
- McCaffery M (1968). Nursing practice theories related to cognition, bodily pain, and man-environment interactions. University of California Print. Office. [Google Scholar]
- Milton JN, Gordeuk VR, Taylor JG, Gladwin MT, Steinberg MH, & Sebastiani P (2014). Prediction of fetal hemoglobin in sickle cell anemia using an ensemble of genetic risk prediction models. Circulation: Cardiovascular Genetics, CIRCGENETICS-113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell TM (1997). Machine learning. WCB. [Google Scholar]
- Raudys SJ, & Jain AK (1991). Small sample size effects in statistical pattern recognition: Recommendations for practitioners. IEEE Transactions on pattern analysis and machine intelligence, 13(3), 252–264. [Google Scholar]
- Rees DC, Olujohungbe AD, Parker NE, Stephens AD, Telfer P, & Wright J (2003). Guidelines for the management of the acute painful crisis in sickle cell disease. British journal of haematology, 120(5), 744–752. [DOI] [PubMed] [Google Scholar]
- Rubin DB (2004). Multiple imputation for nonresponse in surveys (Vol. 81). John Wiley & Sons. [Google Scholar]
- Schnog JB, Duits AJ, Muskiet FA, Ten Cate H, Rojer RA, & Brandjes DP (2004). Sickle cell disease; a general overview. Neth J Med, 62(10), 364–74. [PubMed] [Google Scholar]
- Shah AD, Langenberg C, Rapsomaniki E, Denaxas S, Pujades-Rodriguez M, Gale CP, … & Hemingway H (2015). Type 2 diabetes and incidence of cardiovascular diseases: a cohort study in 1· 9 million people. The lancet Diabetes & endocrinology, 3(2), 105–113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shankar K, Subbiah BV, & Jackson D (2009). An empirical approach for objective pain measurement using dermal and cardiac parameters In 13th International Conference on Biomedical Engineering (pp. 678–681). Springer Berlin Heidelberg. [Google Scholar]
- Soergel M, Kirschstein M, Busch C, Danne T, Gellermann J, Holl R, … & Rascher W (1997). Oscillometric twenty-four-hour ambulatory blood pressure values in healthy children and adolescents: a multicenter trial including 1141 subjects. The Journal of pediatrics, 130(2), 178–184. [DOI] [PubMed] [Google Scholar]
- Tousignant-Laflamme Y, Rainville P, & Marchand S (2005). Establishing a link between heart rate and pain in healthy subjects: a gender effect. The Journal of Pain, 6(6), 341–347. [DOI] [PubMed] [Google Scholar]
- Udovičić M, Baždarić K, Bilić-Zulle L, & Petrovečki M (2007). What we need to know when calculating the coefficient of correlation?. Biochemia Medica, 17(1), 10–15. [Google Scholar]
- Van Buuren S (2007). Multiple imputation of discrete and continuous data by fully conditional specification. Statistical methods in medical research, 16(3), 219–242. [DOI] [PubMed] [Google Scholar]
- Zelman DC, Hoffman DL, Seifeldin R, & Dukes EM (2003). Development of a metric for a day of manageable pain control: derivation of pain severity cut-points for low back pain and osteoarthritis. Pain, 106(1), 35–42. [DOI] [PubMed] [Google Scholar]
- Zelman DC, Dukes E, Brandenburg N, Bostrom A, & Gore M (2005). Identification of cut-points for mild, moderate and severe pain due to diabetic peripheral neuropathy. Pain, 115(1), 29–36. [DOI] [PubMed] [Google Scholar]