Characterizing Highly Benefited Patients in Randomized Clinical Trials

Abstract

Physicians and patients may choose a certain treatment only if it is predicted to have a large effect for the profile of that patient. We consider randomized controlled trials in which the clinical goal is to identify as many patients as possible that can highly benefit from the treatment. This is challenging with large numbers of covariate profiles, first, because the theoretical, exact method is not feasible, and, second, because usual model-based methods typically give incorrect results. Better, more recent methods use a two-stage approach, where a first stage estimates a working model to produce a scalar predictor of the treatment effect for each covariate profile; and a second stage estimates empirically a high-benefit group based on the first-stage predictor. The problem with these methods is that each of the two stages is usually agnostic about the role of the other one in addressing the clinical goal. We propose a method that characterizes highly benefited patients by linking model estimation directly to the particular clinical goal. It is shown that the new method has the following two key properties in comparison with existing approaches: first, the meaning of the solution with regard to the clinical goal is the same, and second, the value of the solution is the best that can be achieved when using the working model as a predictor, even if that model is incorrect. In the Citalopram for Agitation in Alzheimer’s Disease (CitAD) randomized controlled trial, the new method identifies substantially larger groups of highly benefited patients, many of whom are missed by the standard method.

1. Introduction

Patients often differ in their response to treatment, and characterizing this variation is crucial for the development of evidence-based, personalized treatment plans. In practice, treatments may be costly or may pose harm to patients (e.g. through adverse side effects or drug toxicity) and clinicians must balance treatment recommendations with each patient’s probability of response. Thus, there is considerable interest in the development and refinement of statistical methods capable of identifying patients with high versus low average treatment effect. For example, a recent randomized controlled trial in psychiatry evaluated the efficacy of citalopram for reducing agitation in patients with probable Alzheimer’s disease [1]. Although the estimated average treatment effect in the trial was positive, an adverse cardiac event occurred in a small proportion of people, and the treatment was associated with slight cognitive worsening. Additionally, only 40% of participants assigned to citalopram had a moderate or marked response compared to 26% of those assigned to placebo, and thus it would clearly be desirable to identify strong predictors of response. In this setting, the preferred clinical goal is to target the treatment to patients who are predicted to experience a large clinical benefit. In addition to providing practical recommendations regarding who should be targeted for treatment, identifying patients whose response to citalopram is large could help clarify the biological mechanisms for citalopram’s action in this population.

Several approaches have been employed to estimate heterogeneity in treatment effects in the setting of randomized controlled trials. One general approach is to posit outcome regression models in which the effect of treatment assignment on response can differ depending on baseline covariates. A major limitation of this approach is that the posited outcome regression model may be misspecified. Zhang et al. [2] (see also Zhao et al. [3], Rubin and van der Laan [4]) adapt this regression framework and develop a robust method for identifying an optimal treatment regime, which, when followed, maximizes the empirical treatment effect in the study population. However, this optimal treatment regime does not necessarily identify highly benefited patients; indeed, it assigns treatment to a patient even when their expected treatment effect is small, as long as it is positive. In addition, one cannot directly adapt Zhang et al.’s [2] method to identify highly respondent subgroups of patients, for the following reason. That method maximizes the empirical treatment effect in the entire study population. If instead the goal is to maximize the treatment effect over particular subsets of patients, there will almost always be some small subsets that appear to achieve a treatment effect higher than a particular threshold chosen. Therefore, parameter estimation in this setting is ill-defined because it reduces to selecting the subgroup with the highest estimated treatment effect, regardless of the size of this subgroup. This issue illustrates that balance needs to be addressed between the magnitude of the treatment effect in a particular subgroup and the number of patients in that subgroup.

Cai et al. [5] proposed an alternative method for estimating heterogeneity in the treatment effect. In a two-stage approach, the first stage posits a working regression model (fitted by maximum likelihood, for example), and estimates each subject’s model-based expected response under each treatment arm, and hence the model-based subject’s effect is estimated as the difference between the two estimates. In a second stage, the approach uses the model-based effect estimate as a scalar index score for grouping patients. Then, a local likelihood approach is used to obtain non-parametric estimates of the treatment effect within each strata of the index score. This approach produces consistent estimates of the treatment effect within strata defined by the estimated regression model. However, because the working model in the first stage of the procedure may be misspecified, maximum likelihood or ordinary least squares estimators of model parameters may not be the best approach (even in large samples) to characterize the largest subgroup possible whose empirical treatment effect is greater than some pre-specified threshold.

In this paper we propose a method that characterizes large subgroups who experience a large treatment effect. Section 2 formulates the goal and further reviews the existing approaches. Section 3 develops the new approach. The essence of this approach is that it connects the estimation of parameters from the working model directly to the clinical goal – to identify large subgroups that experience a large empirical treatment effect. We show theoretically, and also by application to the CitAD trial throughout, that the proposed approach characterizes different highly benefited groups that can be much larger than those characterized by the existing approach. Section 4 concludes with remarks.

2. Goal and motivating background

2.1. Problem and limitations of existing methods

For the general framework, consider a study of a random sample of n individuals from a population and for each of whom we can measure a vector of covariates X_i, which we assume have finite although possibly many levels. Each individual can be assigned a standard treatment t = 0, in which case we would measure a potential outcome Y_i(t = 0), or a new treatment t = 1, in which case we would measure a potential outcome Y_i(t = 1) [6]. Actual assignment Treat_i(= 0, 1) is assigned at random, that is, Treat_i is independent of (Y_i(0), Y_i(1), X_i), and then the outcome Y_i := Y_i(Treat_i) corresponding to the actual assignment is observed. Based on the information of the study, the overall population average potential outcome E{Y_i(t)} can be estimated without further assumptions by the sample analogue E(Y_i | Treat_i = t) of the average observed outcomes among those assigned Treat_i = t.

Even if the new treatment is the best (on average, or for a particular patient, Zhang et al. [2]), its effect may be small and its administration associated with burden or adverse effects. Then, for subsequent clinical practice, physicians may wish to only give the new treatment to patients for whom the above study suggests the effect is large enough. To do this, for example, in the psychiatric trial we discuss in Section 2.2, the physicians wanted to characterize a subgroup of patients based on covariates, for whom the treatment effect is, on average, greater than a chosen clinically important value, say eff_min. Taking here the absolute difference as the causal effect of interest, the physicians’ goal is as follows:

$$\text{find a group of patients,}\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array},\text{that maximizes the proportion},\text{pr}\left\{X_i\in \underset{\text{ benefited }}{\text{ highly }}\right\},\text{subject to having large average effect,}E\left\{Y_i(1)-Y_i(0)|X_i\in \underset{\text{ benefited }}{\text{ highly }}\right\}\ge {\text{eff}}_{\text{min}}.$$ (1)

If it is possible to estimate well the conditional effect (X_i) := E{Y_i(1) – Y_i(0) | X_i} for all X_i without further assumptions, then the goal eq. (1) is easily addressable. To see this, consider, for any indicator function in(X_i), the quantity effect {in(X_i) = 1} := E{Y_i(1) – Y_i(0) | in(X_i) = 1}. We prove the following result in the Appendix.

Result 1. Among all indicator functions in(X_i) such that effect {in(X_i) = 1} ≥ eff_min, the indicator that maximizes the size pr{in(X_i) = 1} is of the form

$$i{n}_0\left(X_i\right):=1\text{ if and only if effect }\left(X_i\right)\ge k$$

where k is a constant determined by effect {in₀(X_i) = 1} = eff_min, provided that such a k exists.

In other words, the largest group $\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}$ satisfying eq. (1) is {x : in₀(x) = 1} and is obtained if we start including in the group patients from the larger down to the smaller values of the conditional effect (X_i), and stop when including the covariate with the next smallest value of effect (X_i) in $\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}$ would first produce an average effect $E\left\{Y_i(1)-Y_i(0)|X_i\in \underset{\text{ benefited }}{\text{ highly }}\right\}$ smaller than eff_min.

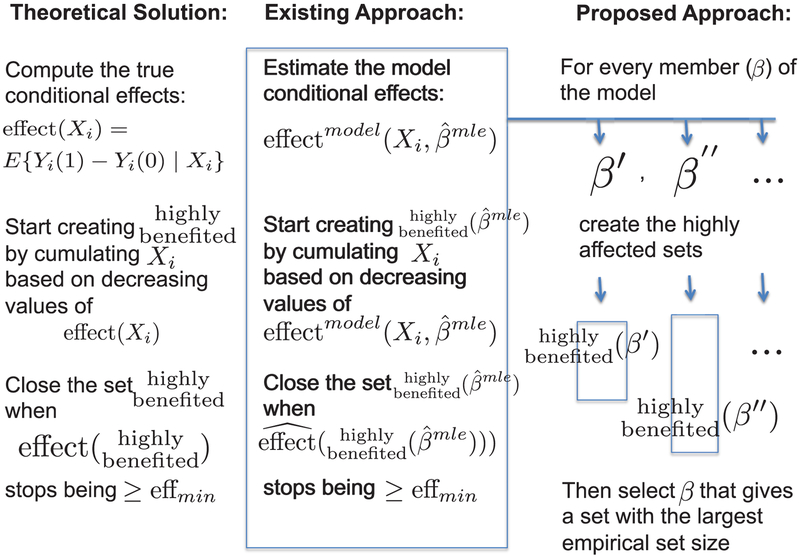
More realistically, when the levels of X_i are many, the conditional effects are not estimable without further assumptions, and the above direct approach is not feasible. An existing approach [5] mirrors the theoretical approach using a working model (see Figure 1, first two columns). Specifically, here the existing approach in a first stage fits a parametric working model (which may not be correct): pr(Y_i(t) | X_i, β) (= pr(Y_i | X_i, Treat_i = t, β), by random assignment), by the MLE ${\widehat{\beta }}^{mle}$ or a solution to another standard estimating equation. Based on this fit, the approach obtains an initial, model-based estimate of the effect E(Y_i | X_i, Treat_i = 1)- E(Y_i | X_i, Treat_i = 0) using

$${\text{effect}}^{model}\left(X_i,{\widehat{\beta }}^{mle}\right):=E\left(Y_i|X_i,{\text{ Treat }}_i=1,{\widehat{\beta }}^{mle}\right)-E\left(Y_i|X_i,{\text{ Treat }}_i=0,{\widehat{\beta }}^{mle}\right).$$ (2)

This approach can attempt to approximate goal eq. (1) by mimicking the theoretical solution given above, as follows: first, sort the covariates by the values of estimated effects, effect ${\text{effect}}^{model}\left(X_i,{\widehat{\beta }}^{mle}\right)$; then, start creating the set $\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\widehat{\beta }}^{mle}\right)$ by cumulating X_i from larger to smaller values of ${\text{effect}}^{\text{model}}\left(X_i,{\widehat{\beta }}^{mle}\right)$; and close the set $\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\widehat{\beta }}^{mle}\right)$ when the empirical (non-parametric) estimated effect (difference in sample averages of treated minus control) in that set would stop being ≥ eff_min. This gives

$$\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\widehat{\beta }}^{mle}\right)=\begin{array}{c}\text{the largest-fraction }\left\{X_i:{\text{ effect }}^{\text{ thodel }}\left(X_i,{\widehat{\beta }}^{mle}\right)\ge e\right\}\\ \text{over all values }e\end{array}$$ (3)

such that the empirical treatment effect in the set is at least eff_min. By largest-fraction set we mean a set that has the largest probability based on the empirical distribution of X_i in the study.

Figure 1:

Schematic representation of the theoretical solution, the existing approach, and the proposed approach, for a given eff_min.

A useful property of this approach, resulting from the empirical estimation at the second stage, is that the effect among the estimated highly benefited set in eq. (3) is approximately the desired clinical effect eff_min, even if the working model is incorrect. Specifically, [5] show that, allowing for the working model to be incorrect, the estimator ${\widehat{\beta }}^{mle}$ will converge to a value, say ${\overline{\beta }}^{mle}$, and the set $\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\widehat{\beta }}^{mle}\right)$ will converge to

$$\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\overline{\beta }}^{mle}\right)=\begin{array}{c}\text{ the largest-probability set }\left\{X_i:{\text{effect}}^{model},{\overline{\beta }}^{mle})\ge e\right\}\\ \text{ over }e\end{array}$$

such that the effect within the set is at least eff_min. Therefore, the empirical $\widehat{\text{effect}}\left\{\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\widehat{\beta }}^{mle}\right)\right\}$, defined as the difference between the empirical averages of the highly benefited set assigned Treat = 1 versus those assignd Treat = 0, converges to at least the nominal effect eff_min. The above assumes that ${\text{effect}}^{model}\left(X_i,{\overline{\beta }}^{mle}\right)$ is not constant in X_I; if it is, then the convergence may not hold, for example, because the sets may be empty.

For a trial with small to moderate sample size, the set of patients $\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\widehat{\beta }}^{mle}\right)$ may have a true effect that is smaller than the limit. For this reason, we can use a modified set ${\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}}^{calib}\left({\widehat{\beta }}^{mle}\right)$, that uses a resampling method to calibrate its effect to the nominal eff_min (Appendix B).

A problem with the above approach, however, is that it still uses the estimate (e.g., MLE) of the working model as if the model were correct. In Section 3, we show that, by using a different estimation of the same working model, a different highly benefited group can be identified, which can be much larger than the one identified by the existing approach. First, however, we illustrate the existing approach using data from the Citalopram for Agitation in Alzheimer Disease Study (CitAD) [1].

2.2. A motivating example

CitAD was a randomized placebo-controlled trial designed to evaluate the efficacy of citalopram in reducing agitation in patients with probable Alzheimer’s disease [1]. The estimated average treatment effect was a 13.6% (se=7.1%) reduction in the probability of agitation symptoms in the citalopram versus the placebo group, as measured by the modified Alzheimer Disease Cooperative Study-Clinical Global Impression of Change Score (hereafter, mADCS-CGIC, Schneider et al. [7], Drye et al. [8]).

As agitation in Alzheimer’s disease (AD) is a heterogeneous clinical syndrome that encompasses many underlying pathologies, a secondary aim of the study was to characterize which patients were more likely to respond to citalopram, potentially elucidating which dysfunctional pathways might respond to citalopram. Characterizing heterogeneity in citalopram’s effect is also important because its use is associated with an adverse cardiac complication (long QT syndrome and cognitive worsening), and a preferred clinical goal would be to target highly respondent patients for treatment [9]. We hypothesized that agitation in AD might involve disturbances in affective and/or executive control which might further reflect different disturbances in underlying brain circuits. One hypothesized type of agitation reflects affective disturbance, manifested by mood lability, irritability, anxiety, dysphoria, and/or other affective/mood symptoms. Another hypothesized type reflects agitation from loss of inhibitory control resulting in disinhibition, disorganization, apathy, or other clinical manifestations of loss of executive control. Given the substantial evidence for the involvement of serotonergic deficits in affective dysregulation in mood disorders, we hypothesized that participants with primarily affective type of agitation would respond better to citalopram treatment. To this end, one of the authors (CGL) derived two categorical scales, the affective dysregulation scale (ADS, ranging from 0–7), and the exective dyscontrol scale (EDS, ranging from 0 to 6), where higher values indicate more dysfunction. These scales were derived by examining the CitAD dataset for items that appeared to be a priori associated with affective or executive dysregulation (see Appendix A for detailed derivation). Table 1 is a cross-tabulation of the number of patients in each arm of the study with different combinations of ADS and EDS scores at baseline.

Table 1:

Patients falling in each ADS and EDS categories; values in red are patients assigned to the placebo group, values in blue are patients assigned to the treatment group. Values are shown for the 167 patients for whom outcome data were available.

	7	0/0	0/0	0/0	0/0	0/2	1/0	0/0
	6	0/0	0/0	0/0	1/0	0/0	0/0	0/0
	5	0/1	1/2	2/2	3/2	0/3	1/3	3/2
	4	2/1	2/0	5/3	1/2	4/9	3/3	2/3
ADS	3	0/1	5/1	4/4	6/6	1/2	8/3	2/1
	2	1/1	1/6	1/5	3/3	2/2	2/2	2/0
	1	1/1	1/4	4/3	1/1	0/0	0/1	0/1
	0	0/0	1/0	0/0	2/0	1/0	0/0	1/0
		0	1	2	3	4	5	6
	EDS

Our goal here is to assess if there exist patient profiles, based on the ADS and EDS covariates, that experience a high citalopram versus placebo effect eff_min, examining this question for eff_min = 30%, 35% and 40% (by comparison the overall average was estimated at 13.6%). Table 1 shows that each cell is populated by a relatively small number (if any) of patients, so direct implementation of the theoretical approach described in Section 2.1 is not feasible.

To address the goal, consider first the approach of positing a working model, also described in Section 2.1. In particular, consider the logistic regression working models for the binary outcome Y_i, with value 1 signifying a reduction in agitation symptoms:

$$\begin{gathered} \text{logit}E\left(Y_i|{\text{ADS}}_i,{\text{EDS}}_i,{\text{ Treat }}_i=1,\beta \right)={\beta }_{10}+{\beta }_{11}{\text{ADS}}_i+{\beta }_{12}{\text{EDS}}_i+{\beta }_{13}{\text{ADS}}_i\times {\text{EDS}}_i \\ \text{logit}E\left(Y_i|{\text{ADS}}_i,{\text{EDS}}_i,{\text{ Treat }}_i=0,\beta \right)={\beta }_{00}+{\beta }_{\text{01}}{\text{ADS}}_i+{\beta }_{02}{\text{EDS}}_i+{\beta }_{03}{\text{ADS}}_i\times {\text{EDS}}_i. \end{gathered}$$

In this first approach, the parameters, β, were estimated by the MLE ${\widehat{\beta }}^{mle}$, and effect ^model(X_i, β) in eq. (2) was estimated by ${\text{effect}}^{model}\left(X_i,{\widehat{\beta }}^{mle}\right)$. The latter takes 41 unique values, each corresponding to a non-empty cell in Table 1 (provided no two elements of ${\widehat{\beta }}^{mle}$ are the same). Next, patients were ranked by their values effect ${\text{effect}}^{model}\left(X_i,{\widehat{\beta }}^{mle}\right)$, and for each of the three values of eff_min = 30%, 35% and 40%, first we identified the uncalibrated set, say $\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\widehat{\beta }}^{mle};{\text{ eff }}_{\text{min}}\right)$, of the highly benefited patients based on the description in Section 2.1.

We evaluated the properties of these sets, by conducting a simulation as described in Appendix B. First, we found that the true effects experienced by the uncalibrated sets were approximately 5% lower than their corresponding three nominal values. Then, for each nominal value, we searched for the value that the empirical effect should have in order that the simulated true effects be equal to the nominal. These resulting values were 35%, 40% and 45%, respectively, and the corresponding sets, which we call ${\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}}^{calib}\left\{{\widehat{\beta }}^{mle};{\text{ eff }}^{emp}\left({\text{ eff }}_{\text{min}}\right)\right\}$ in Appendix B, are shown on the top three panels in Figure 2.

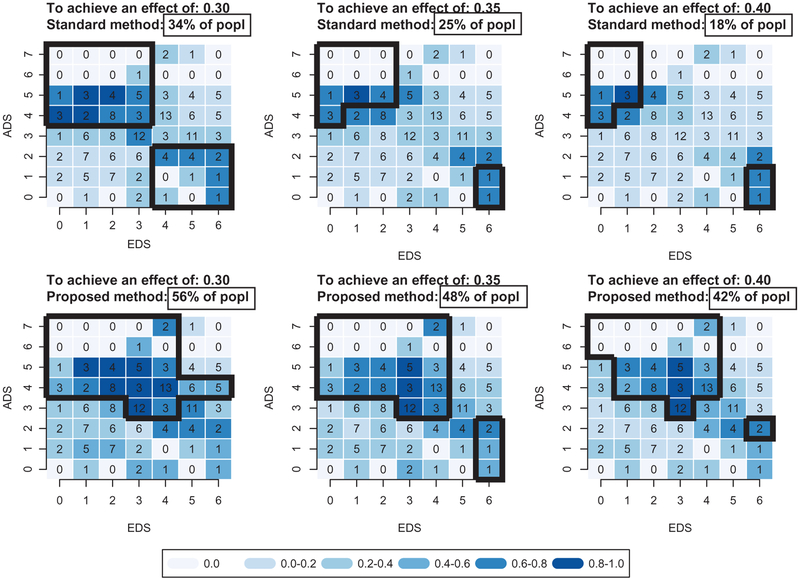
Figure 2:

ADS-EDS profile of patients (black contours) that have large treatment effect (30% in left panels, 35% in middle panels, and 40% in right panels), as found by the standard two-stage method (top panels) and by the new proposed method (bottom panels). Both methods are calibrated as described in Appendix B. The percents given in boxed rectangles are determined over 500 simulation samples of the process in Appendix B; and the intensity of the blue color of a particular ADS-EDS cell represents the proportion of times, over the same 500 samples, that the cell is included in the highly benefited group. The number provided in each cell displays the number of patients in the dataset in each category.

For example, the set ${\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}}^{calib}\left\{{\widehat{\beta }}^{mle};{\text{ eff }}^{emp}\left({\text{ eff }}_{\text{min}}=30\%\right)\right\}$ of patients who experience an average effect of 30% are the patients with EDS ≤ 3 & ADS ≥ 4 or with EDS ≥ 4 & ADS ≤ 2. This group is estimated to form 34% of the study population.

3. Proposed approach

The proposed approach is motivated by re-examining the parallelism that a better estimation approach should try to draw to the theoretical solution. In the theoretical solution (left column of Figure 1), the largest set $\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}$ is achieved by cumulatively including covariates based on the order of the true conditional effects effect (X_i). The model-based approach of Section 2.1 tries to parallel this by, first, estimating the conditional effects based on the MLE of a model ${\widehat{\beta }}^{mle}$, and then cumulating these ordered effects, effect ${\text{effect}}^{model}\left(X_i,{\widehat{\beta }}^{mle}\right)$, as in eq. (3).

While the above set of patients does experience the desired effect eff_min in large samples, this is not, of course, the largest such set if the working model is incorrect. In fact, it is not even the largest achievable set when using the same working model. This is because, if the model is incorrect, the member of the model $\left({\widehat{\beta }}^{mle}\right)$ that maximizes the (incorrect) likelihood does not necessarily have the invariance property with respect to the truth, and so it is not necessarily the same as the member of the model that achieves the largest set.

The proposed approach is to find the largest such set that can be achieved. To do this, the model should be left free at the first stage, so that one can consider all values of the parameter β, that can predict effect (X_i) by effect ^model(X_i, β). Then,

(i) for each value β of the parameter, find

$$\begin{array}{c}\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}(\beta )\text{as the largest-fraction set}\left\{X_i:{\text{ effect }}^{model}\left(X_i,\beta \right)\ge e\right\}\\ \text{ over }e\end{array}$$ (4)

and such that the empirical effect within the set is at least eff_min; then

(ii) find

$$\begin{array}{c}\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\widehat{\beta }}^{best}\right)\text{ as the largest-fraction set}\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}(\beta ),\\ \text{ over }\beta \end{array}$$ (5)

where, $\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}(\beta )$ is as obtained in eq. (4).

By construction in eq. (5), the proposed set $\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\widehat{\beta }}^{best}\right)$ is the largest possible set of the type in eq. (4) that can be achieved by using the working model, and so it is also at least as large as the one obtained in eq. (3) by the standard approach. Also by construction, the set $\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\widehat{\beta }}^{best}\right)$ will converge to

$$\begin{array}{c}\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}({\overline{\beta }}^{\text{best}})=\text{ the largest-probability set }\left\{X_i:{\text{ effect }}^{model}\left(X_i,\beta \right)\ge e\right\},\\ \text{ over }e\text{ and }\beta \end{array}$$

such that the effect within the set is at least eff_min, where ${\overline{\beta }}^{\text{best}}$ is the maximizer of the right-hand-side of the last expression. Thus we have:

$$\text{Pr}\left\{X_i\in \begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}({\overline{\beta }}^{\text{best}})\right\}\ge \text{Pr}\left\{X_i\in \begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}({\overline{\beta }}^{mle})\right\}$$

Moreover, with finitely many levels of x, the empirical effect, say $\widehat{\text{effect}}\left\{\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\overline{\beta }}^{best}\right)\right\}$ on the new highly benefited set converges, in large samples, to at least the nominal effect eff_min, and the empirical proportion, say $\widehat{\text{Pr}}\left\{X_i\in \begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}({\overline{\beta }}^{\text{best}})\right\}$ converges to the probability $\text{Pr}\left\{X_i\in \begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}({\overline{\beta }}^{\text{best}})\right\}$. A formal proof of this result would be more involved, due in part to having to deal with the estimators of parameters within functions (such as empirical estimates of probabilities and effects), and also due to the appearance of non-smooth indicator functions in both the probability statement and the effect function. Nonetheless, this heuristic argument seems to suggest that, under some regularity conditions and in sufficiently large samples, the new method will correctly produce a larger set of highly benefited patients than the standard method.

In small to moderate samples, and as with empirical maximization of other objective functions (e.g., sum of squares), the above convergence happens, by construction, from values of the effect that can be larger than the nominal one. For this reason, it is better to consider a modified set ${\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}}^{calib}\left({\widehat{\beta }}^{best}\right)$ that uses the resampling approach to calibrate to the nominal minimal effect (see Appendix B).

We evaluated the properties of this new method by an analogous simulation to that for the standard method of Section 2 and as described in detail in Appendix B. We found that the true effects experienced by the uncalibrated sets of the new method were approximately 10% lower than their corresponding three nominal values. Then, for each nominal value, we searched for the value that the empirical effect should have in order that the simulated true effects be equal to the nominal. These three values were approximately 40%, 45% and 50%, respectively, and these resulting sets, which we call ${\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}}^{calib}\left\{{\widehat{\beta }}^{best};{\text{ eff }}^{emp}\left({\text{ eff }}_{\text{min}}\right)\right\}$ in Appendix B, are shown on the bottom three panels in Figure 2.

For example, the set ${\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}}^{calib}\left\{{\widehat{\beta }}^{mle};{\text{ eff }}^{emp}\left({\text{ eff }}_{\text{min}}=30\%\right)\right\}$ of patients that experiences an average effect of 30% are the patients with EDS ≤ 4 & ADS ≥ 4 and the following (EDS,ADS) cells: (3,3), (4,3), (5,4), (6,4), as shown within the black contour of the bottom left panel of Figure 2. This group is estimated to form 56% of the study population. Therefore, even after adjusting for overfitting, the new method is estimated to characterize substantially larger groups of patients with high benefit.

4. Discussion

We have illustrated a new method of characterizing groups of patients with high benefit. We believe the new method can have important clinical implications regarding which patients are targeted for treatment, as well as important methodological implications for characterizing such groups in observational studies.

The example of CitAD illustrates the potential of these methods. The ADS and EDS covariates are indeed predictive of effect regardless of whether standard methods or the new methods presented above are used, but the proportion of participants is much higher with the new method. For example, using a 30% effect size as the minimum difference of clinical significance, 34% of participants fall into ADS/EDS categories with clinically significant effects using standard methods compared to 56% with the new method. Thus, using ADS/EDS categories a clinician could identify 20% more patients with AD and agitation who would be predicted to have a clinically significant response to citalopram, an undoubtedly clinically meaningful difference. Given the potential toxicity of medications (for example, QTc prolongation observed with citalopram treatment in CitAD, [9]), identifying patients most likely to respond to drug represents a substantial improvement in maximizing benefit over risk. It is particularly impressive that ADS/EDS categories are so useful for predicting response because these subscales were derived from first principles, i.e. examining instruments at the item level and deriving the instruments pre hoc, independently of results, not as the result of cluster analytic techniques. This suggests the potential utility of applying these methods to other trials to improve clinicians’ ability to predict response to drug treatment.

A number of areas regarding the proposed method warrant further exploration. First, it is possible that the largest subgroup that, on average, has an effect larger than a constant may include finer subgroups with a negative effect. This is difficult to know, however, because a method that would search for this would be also subject to the difficulty of fitting effects given the high dimensional X. Perhaps an expert’s opinion on whether the finer parts of the subgroup make sense would be useful. Second, making the clinical objective the same as the statistical objective function to maximize, while scientifically desirable, is prone to overfitting. Here, we addressed this in part by calibration through simulation. Additional work is needed to develop accessible inference methods for confidence intervals, and for finding if and how a semiparametric efficient estimator can be achieved for the set $\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}({\overline{\beta }}^{\text{best}})$, for example using theory of van der Laan and Rubin [10], van der Laan and Rose [11]. Further, one can build additional parsimony into the estimation by regularizing the objective function through adding a condition that, for example, the magnitude of the coefficients be restricted. Thus, the contribution of the proposed method is not in competition with regularization, but is, instead, to emphasize the change of the core objective function - from a statistical one (e.g., least squares or likelihood) to a clinically meaningful one such as of the proportion of highly benefited patients. Working with this objective function analytically is not as straightforward because its complexity suggests it may not be convex. In practice we searched for maxima using simulated annealing.

Usefully, the new method can be applied to also characterize highly benefited groups in observational studies. Specifically, if treatment assignment is ignorable [6] and the propensity score [12] is reliably estimable, then, in principle, similar methods to these presented here can be applied to the population of potential outcomes after adjusting through the propensity score. This would provide an alternative way of fitting, for example, a structural mean model [13, 14], where the coefficients are chosen to maximize group of patients that are benefited beyond a minimum effect desired by physicians and patients.

Table 2:

Items comprising the affective (ADS) and dysexecutive (EDS) indicators at baseline.

ADS (Affective), Range = 0–7	EDS (Dysexecutive), Range = 0–6
1. Family history of mood disorder in first-degree relative	1. Inattention
a. form EH ‒ 1, item 19 scored as C, D, E, or F	a. form NR item 7 scored ≥3 (NBRS)
2. Personal history of mood disorder	2. Aberrant motor behavior
a. form EH ‒ 1, item 21 scored as C, D, E, or F	a. form NP item 101a times item 101b scored ≥4 (NPI)
3. Depression	OR
a. form CS total score of ≥ 6 (Cornell Depression Scale total)	b. form CM item 12 scored ≥4 will (CMAI)
OR	3. Disinhibition
b. form NR item 19 scored ≥3 (NBRS)	a. form NP item 83a times item 83b scored ≥4 (NPI)
OR	OR
c. form NP item 46a × item 46b scored ≥4 (NPI)	b. form CM item 11 scored ≥4 will (CMAI)
4. Mood liability	OR
a. form NR, item 31 scored ≥3	c. form NR item 14 scored ≥3 (NBRS)
5. Anxiety	4. Apathy
a. form NR, item 10 scored ≥3 (NBRS)	a. form NP item 74a times item 74b scored ≥4 (NPI)
OR	OR
b. form NP item 55a times item 55b scored ≥4 (NPI)	b. form NR item 12 will will scored ≥3 (NBRS)
6. Irritability	5. Poor planning
a. form NP item 92a × item 92b scored ≥4 (NPI)	a. form NR item 30 scored ≥3 (NBRS)
7. Somatic	6. Disorganization
a. form NR item 8 scored ≥3 (NBRS)	a. form NR item 13 scored ≥3 (NBRS)

Appendix

Appendix A: Characterization of the largest highly benefited subgroup

We prove the result for the case where X_i has finite though possibly many levels. Consider the indicator in₀(X_i) and the constant k defined in Result 1; and consider any other indicator in(X_i) whose subgroup size is strictly larger than that of in₀, i.e., suppose P := pr{in(X_i) = 1} > P₀ := pr{in₀(X_i) = 1}. Then it is useful to consider the quantity

$$q(x):=\left\{\frac{i{n}_0(x)}{P_0}-\frac{in(x)}{P}\right\}\{\text{ effect }(x)-k\}p(x),$$

where effect (x) is as defined in Section 2.1 and p(x) = pr(X_i = x). Specifically, q(x) is non-negative because if in₀(x) = 1, both of the first two terms are non-negative; and if in₀(x) = 0, both of the first two terms are non-positive. Moreover, q(x) is strictly positive with positive probability because, when effect (x) > k (and in₀(x) = 1), then the first two terms are strictly positive regardless of in(x). Now, if q(x) is summed over x, we get

$$0<\sum _{x}q(x)=E_0-k-E+k,\text{ so }E<E_0$$

where E₀ and E are the effects effect {in₀(X_i) = 1} and effect {in(X_i) = 1}, respectively, within the subgroups defined by the indicators. Thus, if E ≥ E₀ we must have P ≤ P₀. By assumption, E₀ = eff_min, and thus the maximum size is attained at P₀ by in₀.

Appendix B: Evaluation and calibration of highly benefited sets through simulation

We sought to evaluate the properties of estimated highly benefited subgroups derived through fitting data D^obs from a trial, utilizing both the standard and proposed methods. To do so, we applied the estimated sets to the target population from which the data are sampled. In order to do this, for example, for the proposed method and for a nominal minimum effect eff^nom equal to, say 30%, we did the following.

For both the standard and the proposed methods for characterizing a highly benefited subgroup, we evaluated properties of the estimated sets based on X_i – derived through fitting data D^obs from a trial – are applied to the target population from which the data are sampled. In order to do this, for example, for the proposed method and for a nominal minimum effect eff^nom equal to, say 30%, we did the following.

1. Treat D^obs as the target source population, and obtain a bootstrap data sample, D^rep with replacement.

2. For D^rep, derive $\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\widehat{\beta }}^{best};{\text{ eff }}^{emp}{\text{eff }}_{\text{min}}=30\%;D^{rep}\right)$ in order to reach a minimum empirical effect eff^emp = 30% on data D^rep, as described in Section 3 (here, the explicit notation for the empirically achieved minimum effect and for the data D^rep is important).

3. Apply $\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\widehat{\beta }}^{best};{\text{ eff }}^{emp};D^{rep}\right)$ back to the target source population D^obs, and find the true effect on these patients $\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\widehat{\beta }}^{best};{\text{ eff }}^{emp};D^{rep}\right)$, which, based on the notation of Section 2.1, is $\widehat{\text{effect}}\left\{\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\widehat{\beta }}^{best};{\text{ eff }}^{emp};D^{rep}\right)\right\}$.

4. Repeat steps (1)–(3) and find the true average effect

   $$E\left[\widehat{\text{effect}}\left\{\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left({\widehat{\beta }}^{best};{\text{ eff }}^{emp};D^{rep}\right)\right\}|D^{obs}\right],$$

   averaged over the simulated data sets D^rep given D^obs.

5. If the true effect as verified in step 4 is different from the nominal 30% then search, using a bijection method, for what value we should require the empirical effect in step 2 to be, so that the true effect in step 4 is equal to the nominal. Call that empirical effect eff^emp(eff^nom) (this function can be different between the proposed method and the standard method).

6. for the data D^obs define the calibrated highly benefited group for the nominal eff^nom = 30% effect, as

   $${\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}}^{calib}\left({\widehat{\beta }}^{best};{\text{ eff }}^{nom};D^{obs}\right):=\begin{array}{c}\text{ highly }\\ \text{ benefited }\end{array}\left\{{\widehat{\beta }}^{best};{\text{ eff }}^{emp}\left({\text{eff }}^{nom}\right);D^{obs}\right\}$$

   We used the same approach to evaluate and produce calibration also for the standard method.

Appendix C: Derivation of the affective and executive scales

Items were derived from medical/psychiatric history and from neuropsychiatric instruments including Cornell Scale for Depression in Dementia (CSDD, Alexopoulos et al. [15]), Neurobehavioral Rating Scale (NBRS, Levin et al. [16]), Neuropsychiatric Inventory (NPI, Cummings et al. [17]), and Cohen-Mansfield Agitation Inventory (CMAI, Cohen-Mansfield [18]). The ADS consisted of 7 items: (1) family history of mood disorder;(2) personal history of mood disorder; (3) Depression defined as CSDD score ≥ 6 or NBRS depression item ≥ 3 or NPI Depression score ≥ 4; (4) Mood lability defined as NBRS mood lability item ≥ 3; (5) Anxiety defined as NBRS anxiety ≥ 3 or NPI Anxiety ≥ 4; (6) Irritability defined as NPI Irritability ≥ 4; and Somatic defined as NBRS somatic symptoms item ≥ 3. Each ADS item was scored as 0 or 1 and summed for total range of 0 to 7. The EDS consisted of 6 items: (1) Inattention defined as NBRS inattention item ≥3; (2) Aberrant Motor Behavior defined as NPI Aberrant Motor Behavior ≥ 4 or CMAI aberrant motor behavior item ≥ 4; (3) Disinhbition defined as NPI Disinhibition ≥ 4 or CMAI disinhibition ≥ 4 or CMAI disinhibition ≥ 4; (4) Apathy defined as NPI Apathy ≥ 4 or NBRS apathy item ≥3; (5) Poor planninag as defined by NBRS poor planning item ≥ 3; (6) Disorganization defined as NBRS disorganization item ≥3. Each EDS item was scored as 0 or 1 and summed for total range of 0 to 6.