Abstract
Causal mediation analysis seeks to decompose the effect of a treatment or exposure among multiple possible paths and provide casually interpretable path-specific effect estimates. Recent advances have extended causal mediation analysis to situations with a sequence of mediators or multiple contemporaneous mediators. However, available methods still have limitations and computational and other challenges remain. The present paper provides an extended causal mediation and path analysis methodology. The new method, implemented in the new R package, gmediation (described in a companion paper), accommodates both a sequence (two stages) of mediators and multiple mediators at each stage, and allows for multiple types of outcomes following generalized linear models. The methodology can also handle unsaturated models and clustered data. Addressing other practical issues, we provide new guidelines for the choice of a decomposition, and for the choice of a reference group multiplier for the reduction of Monte Carlo error in mediation formula computations. The new method is applied to data from a cohort study to illuminate the contribution of alternative biological and behavioral paths in the effect of socioeconomic status on dental caries in adolescence.
Keywords: Causal Inference, Dental caries, Mediation analysis, Mediation formula, Generalized linear model, Potential outcome, Sensitivity analysis
1. Introduction
Mediation analysis seeks to decompose the total effect of a treatment or exposure on a final outcome into alternative paths. The goal of such an analysis is to illuminate the mechanisms through which the exposure affects the outcome. In the simplest scenario, the exposure effect is apportioned between the direct effect and the indirect effect through a single mediator. However, in many health contexts, exposure effects are more realistically described with multiple mediators, in some cases occurring in multiple ‘stages’ involving a sequence of mediators. The more general situation has been referred to as path analysis.
Classically, mediation and path analysis have relied on linear regression models. More recently, causal mediation analysis using a potential outcomes framework has provided a principled foundation allowing for causally interpretable mediation (direct, indirect and path-specific) effects under flexible model specifications. One of the most popular causal model approaches is based on the mediation formula.1,2 This approach, as originally developed in the single mediator setting, provides inference for natural direct and indirect effects3,4 yielding an exact decomposition of the total exposure effect. The mediation formula approach accommodates flexible models for the mediator and final outcome, for example allowing interactions and mixed types of variables following generalized linear models. A key assumption of this approach is ‘sequential ignorability’.1
Recent papers have extended the original (single mediator) parametric mediation formula to allow a sequence of mediators, thus accommodating more complex causal models.5,6 This approach, which uses extended versions of the mediation formula and assumes an extended version of sequential ignorability, has a number of limitations. As the approach relies on parametric models for each outcome (including the mediators) it may lack robustness to violations of the assumed models.7,8 As noted by several researchers,9,10 the separate specification of models for each outcome will generally not provide a straightforward model for the natural direct or indirect effects. For example, mediation effects may vary over different levels of covariates, even in the absence of interaction terms in the models. A further challenge in the case of multiple mediators is that some paths may not be identifiable even under sequential ignorability.11,5
A number of alternative methods have been proposed that circumvent one or more of the limitations of the parametric mediation formula approach. Direct and (natural) indirect effect models have been proposed that provide parsimonious descriptions of these mediation effects.9,12 Other researchers have provided semiparametric approaches to avoid parametric model assumptions or to improve robustness. For example, Albert7 provided an inverse probability of exposure weighting approach, that uses a logistic regression model for exposure in place of a model for the mediator. Nguyen et al.10 (see also Tchetgen Tchetgen13) offered an approach using inverse odds ratio weighting. As noted by Nguyen et al.,10 the weighting approach is advantageous for situations with multiple mediators as a single exposure model takes the place of the multiple mediator models needed in the mediation formula approach. Other researchers, using a graphical model framework, have provided nonparametric (discrete probability) formulae for certain path-specific effects.14,15
Despite its limitations, the parametric mediation formula framework still has important advantages. First, the semiparametric and alternative parametric approaches7–10,12,13 are generally limited to a single mediator, or multiple contemporaneous (non causally-ordered) mediators. In contrast, the generalized mediation formula approach allows for causal models with multiple ‘stages’ of mediation, that is, paths with more than two links. (The nonparametric theoretical results mentioned above11,14,15 accommodate multiple causally-ordered mediators, but this work does not elaborate on inference issues or provide data examples.) Structural equation model (SEM) based approaches (as implemented, for example, in MPlus16) would seem to offer similar advantages, but tend to be limited to linear (or ‘linearized’, e.g., probit) models. In contrast, the mediation formula approach, as implemented in the R mediation package17 for the single mediator case, offer flexible model specifications, typically including a choice among a number of generalized linear models for each outcome. Such models tend to be appealing to health researchers, due in part to their familiarity, and because they naturally allow for conditioning on baseline covariates, unlike the standard covariance structure analysis approach to SEM which considers the entire variable vector as random. Further, the mediation formula approach has been successfully used in a number of recent applications.18,19 Nevertheless, the use of the extended mediation formula has been hampered by some remaining limitations, by practical and technical difficulties, and by a lack of suitable user-friendly software.
The goal of the present paper is to present a further development of the extended parametric mediation formula approach to causal mediation and path analysis, with special attention to its practical use and implementation. As in previously described approaches,5,6 our extended method allows for two stages of mediation, and a generalized linear model for each outcome. New contributions of the present paper include extensions to: 1) multiple mediators at each stage, 2) unsaturated models, and 3) clustered data. In addition, we elucidate some important practical issues, including the choice of a decomposition, the choice of a reference group, and number of needed Monte Carlo draws in the mediation formula. All of the extensions described in this paper are incorporated in a newly developed R package called gmediation. The latter is described in a companion paper.20
2. Background
2.1. Causal mediation analysis – single mediator
We begin with some notational and theoretical background. The mediation formula approach to mediation analysis uses a potential outcomes framework. We let Y(x) denote the potential outcome of Y if exposure X were set to level x. We also define nested potential outcomes; for example, Y(x,M(x’)) is the potential outcome of Y if X were set to x and variable (e.g., mediator) M set to its potential outcome if X = x’. Variables without parentheses (e.g., Y) in expressions given here on in will refer to observed values. This notation extends to multiple contemporaneous and multiple stages of mediators as shown below. We focus on natural direct and indirect effects, though other types of mediation effects (e.g., controlled and randomized interventional effects) have been described in the literature.21,22 We also restrict attention to the common situation of a binary treatment or exposure (X). We further let C denote a vector of observed baseline covariates (not affected by X).
Causal mediation effects may be defined in terms of expected potential outcomes. For example, in the single mediator case, the natural direct and indirect effects are defined as:
| (1) |
| (2) |
We further note that the total effect, , can be decomposed into natural direct and indirect effects in two ways: or . Thus, in the single mediator case there are two versions of each effect, corresponding to the two possible decompositions.
Researchers taking a causal model approach have given close attention to the identification of causal mediation effects. Imai et al.1 showed that (1) and (2) are identified under the consistency assumption (see Supplementary Material, Appendix A) and the following sequential ignorability assumptions,
| (3) |
| (4) |
for x, x’ = 0,1 and all m and c (that is over the support of M and C). Note that a positivity assumption is also made, namely, P(X = x | C = c ) > 0 and P(M(x) = m | X = x, C = c) > 0, for x = 0,1 and all m, c. Condition (3) states that the observed exposure, X, is independent of potential outcomes of Y and M conditional on C, while (4) amounts to the requirement that there are no unobserved confounders (and no confounders affected by X) of the M-Y relationship.
Under the above assumptions, any expected potential outcome for Y can be identified (that is, expressed in terms of estimable parameters) using the mediation formula as follows:
| (5) |
Imai et al.1 also discussed the important issue of sensitivity analysis for the sequential ignorability assumption, with a focus on (4) as this condition is not assured under a randomized treatment or exposure, even if the levels of the mediator were also randomized.
2.2. Causal Mediation with Multiple Causally-Unordered Mediators
Often, one wishes to provide a decomposition through multiple mediators with no assumed causal ordering. We refer to such a set of causally-unordered mediators as ‘contemporaneous’, regardless of whether they are actually measured at (or close to) the same time. The situation of multiple contemporaneous mediators was addressed by Wang et al.23 taking an extended mediation formula approach while allowing for the mediators to be correlated (as may be induced by an unobserved confounder among them) by incorporating a model involving multivariate normally-distributed latent variables. An alternative mediation formula approach24 allowed for interactions among mediators while assuming potential outcomes of contemporaneous mediators to be conditionally independent (conditional on observed baseline covariates).
The situation of multiple causally-unordered mediators was also addressed in papers taking a natural effect model approach.9,10,13 This approach assumes that the contemporaneous mediators are ‘nonintertwined’,9 that is, that mediators do not causally affect one another, and there are no confounders affected by exposure.
2.3. Generalized Causal Mediation
Albert and Nelson5 and Daniel et al.6 extended the parametric mediation formula approach to the situation of a causally-ordered sequence of mediators, considering a single mediator at each stage. As noted by these researchers, even under an extended sequential ignorability assumption, some of the expected potential outcomes, thus some path-specific effects, are not identified, a result obtained theoretically by Avin et al.11 The problem occurs for a nested potential outcome that involves a ‘cross-world discrepancy’, that is, potential outcomes of the same mediator at different exposure levels (also referred to as ‘counterfactuals’). An example is the potential outcome Y(0, M1(0), M2(0, M1(1))), which involves both M1(0) and M1(1). Consequently, the effect for the path X → M1 → M2 → Y, which can be expressed, for example, as a contrast between expected values of Y(0, M1(0), M2(0, M1(1))) and Y(0, M1(0), M2(0, M1(0))) = Y(0), is not identifiable even under sequential ignorability. Identification of such path-specific effects requires a further assumption regarding the joint distribution of M1(0) and M1(1). As any such assumption will not generally be testable, it is typically incorporated within a sensitivity analysis.
Daniel et al.6 provided formal identifiability results for the general expected potential outcome in the case of one mediator per stage. They also discussed the case of multiple contemporaneous mediators considered as a ‘group’, implying that for any intervention, all mediators in the group would be affected in the same manner (either exposed or not exposed). Taguri at al.24 also addressed this situation, noting that this grouping approach would allow the (nominally) contemporaneous mediators to have an arbitrary causal ordering as well as unobserved confounders. Considering the contemporaneous mediators as a group allows the notation and theory for the case of a single mediator at each stage6 to go through as before. These approaches are limited, though, in that they do not allow consideration of separate paths (corresponding to distinct hypothesized mechanisms) among the multiple contemporaneous mediators.
3. Extensions of Generalized Causal Mediation
3.1. Multi-stage Model with Multiple Contemporaneous Mediators
A key extension of interest is to allow multiple stages of mediation with distinct contemporaneous mediators, that is, mediators on separate paths, at each stage. The flexibility provided by the combination of multiple stages and multiple mediators per stage would have considerable advantages. First, a departure from the no causal ordering assumption among multiple mediators in a single-stage model, may be resolved by including multiple stages. This extension allows the construction of a more elaborate causal, specifically, directed acyclic graph (DAG), model in which the conditional independence assumption among contemporaneous mediators is more plausible, allowing one to avoid complicated multivariate models.23
We consider the two-stage mediation model, as represented in Figure 1, and address inference for each path-specific effect (providing the ‘finest decomposition’ of the total exposure effect).6 Identifiability of the path-specific effects requires extensions of the consistency and sequential ignorability assumptions given above. The approach, representing an extension of the mediation formula, extends earlier results.6,24 Our assumptions and derivations focus on the case of two mediators per stage. Highlights follow with details provided in the Supplementary Material (Web Appendix A). The extension to an arbitrary number of mediators at each stage would be straightforward though notationally cumbersome.
Figure 1.
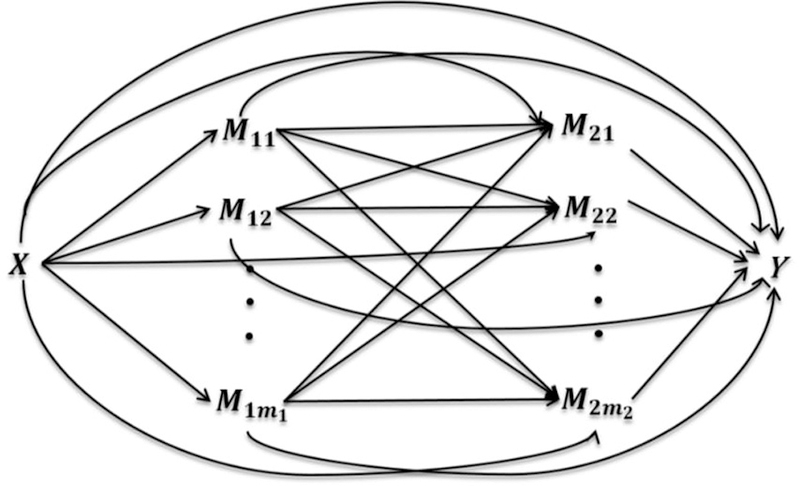
Causal graph for two-stage mediation model
For two mediators per stage, all path-specific effects can be defined in terms of expected values of the following nested potential outcome:
| (6) |
(Note, as in the above expression, that we occasionally use square and curly brackets in place of parentheses to enhance readability of nested potential outcomes.) The d’s in (6), and in other potential outcomes shown below, represent exposure indicators with indicating the exposure status for the path involving the ith first-stage mediator and the jth second-stage mediator, i = 0,…, m1, and j = 0,…, m2, where an index equal to 0 means that the path does not involve a mediator at the corresponding stage. Note that this notation for the d’s can be extended to an arbitrary number of stages by using a corresponding number of digits in the subscript. In particular, for the single-stage case with one mediator there would only be two d’s: d0 and d1. Contrasts between expected values for the above potential outcome with selected values for the d’s provide the path-specific effects. In Section 3.3, we define different path-specific effects and show how they are obtained in particular decompositions.
We distinguish two cases. Case 1 involves potential outcomes without cross-world discrepancies for the first-stage mediators, namely, d10 = d11 = d12, d20 = d21 = d22. Case 2 includes potential outcomes not following the Case 1 restrictions, that is, with one or more cross-world discrepancies. For example, a potential outcome with d10 = 1 and d11 = 0 would involve both counterfactuals for the first first-stage mediator, M11(0) and M11(1). The required joint density for such counterfactuals cannot be estimated from the data as subjects are either exposed or not exposed, but not both.
For Case 1, we assume the following, with C as before representing a vector of baseline covariates (not affected by X) and Mk denoting the vector of mediators at stage k:
A1. No unmeasured confounding of the X-(M1,M2,Y) relationships
A2. No unmeasured confounding of the M1-(M2,Y) relationships
A3. No unmeasured confounding of the M2-Y relationships
where the above conditional independence statements hold for all .
We note that we are also making the assumptions implied by the graph (as in Figure 1) under the nonparametric structural equation model interpretation of Pearl.25 Namely, we assume conditional independence of (potential outcomes of) contemporaneous variables as follows,
A4.
A5. for all c, x, d’s and m’s.
For Case 1, under assumptions A1-A5 as well as consistency (see Supplementary Material, Web Appendix A), we obtain the identifiable expression,
| (7) |
where M represents the vector of all mediators, and , a vector of values for M. We note that here, and elsewhere in the paper, integrals may be interpreted as summations for discrete variables. For the covariates (C) this may be summation over the empirical distribution as done in our simulations and data example.
Our identifiability results for Case 1 can be seen as a special case of previous results11, 14 that use a graphical model framework. Case 2 requires stronger assumptions than those for Case 1. Previous researchers11,14,15 noted the lack of identifiability for Case 2 under sequential ignorability, or analogous graphical assumptions, but did not show how supplementary assumptions can be used to provide identifiability. Aside from consistency and A3, we assume extended versions of assumptions A1, A2, A4, and A5 that include both counterfactuals for each first-stage mediator. We derive the following expression (see Web Appendix A for details):
| (8) |
where if , otherwise, , and if , otherwise, , for j = 1, 2; and the term (and corresponding integral) is removed when for j = 1, 2.
Under the assumptions for Case 2 noted above, all the terms in expression (8) are identifiable with the exception of the f* terms, which represent conditional distributions of counterfactuals (conditional on the other counterfactual for each first-stage mediator). To carry out the estimation, in the parametric framework discussed below, we introduce additional model assumptions in a copula model approach5,6 in conjunction with a sensitivity analysis. The sensitivity parameter, ρ, is the ‘cross-world correlation’ between normally-distributed latent versions of the counterfactuals for each first-stage mediator. The approach is described in detail in the Supplementary Material (Web Appendix A).
We take a parametric approach to inference in which a generalized linear (association) model is specified for each mediator and for the final outcome, providing flexibility in the types of variables that can be handled. Steps in the estimation of path-specific effects are as follows: 1) fit each association model, 2) for a given choice of decomposition, compute estimates of relevant expected potential outcomes using the mediation formula, plugging in estimates for parameters, 3) obtain estimated path-specific effects as appropriate contrasts (i.e., differences or ratios) of the estimated expected potential outcomes. For standard errors and/or confidence intervals, bootstrap resampling may be used. Further details and issues involved in these steps are discussed below.
3.2. Nonsaturated Causal Mediation/Path Models
The causal mediation analysis literature has so far focused on saturated models, that is, models in which the final outcome and each mediator have a link from (are causally affected by) the exposure and all mediators at each prior stage. Thus, the final outcome, Y, would have a link from all the other (prior) variables; the second-stage mediators would have a link from all first-stage mediators as well as the exposure, and the first-stage mediators would all have a link from the exposure. (Note that links - or non-links - from baseline covariates do not affect whether a model is considered as saturated or unsaturated according to the above definition.) However, it will often be desirable to allow more flexibility in the modeling. For example, a particular first-stage mediator may not be hypothesized to affect every second-stage mediator. Removing such links (thus, producing an unsaturated model) is a way to provide a simpler, more parsimonious model.
Allowing for unsaturated models raises additional issues. Whereas in a saturated model all paths involving first-stage mediators are non-identifiable without further cross-world assumptions, this is not always the case with unsaturated models. The general rule in the present two-stage mediation context is that a path involving a first-stage mediator is identifiable if and only if it is the only path going through that mediator.11 The use of unsaturated models thus requires additional attention in the estimation algorithm, as identifiability for a given path may be affected by the deletion of a link. Another, perhaps obvious, implication is that the absence of links in the model will produce ‘null’ paths, i.e., some paths that may otherwise exist will have an a priori zero effect due to the model specification. Specific implications when using the gmediation R package are discussed in Cho and Albert.20
3.3. Decompositions
While only two distinct decompositions exist for the single mediator case, this number increases dramatically with the number of mediators. This fact is highlighted by Daniel et al.6 who considered the case of a sequence of mediators with an arbitrary number of stages and one mediator per stage. For m mediators, the number of possible decompositions is 2m. In the case of m1 (contemporaneous) mediators in a single-stage model, the number of possible decompositions is (m1+1)!. In the case of m1 first-stage and m2 second-stage mediators the number is {(m1+1) × (m2+1)}!. For example, with two mediators at each stage the number of possible decompositions is (3 × 3)! = 362,880. Daniel et al.6 provided some suggestions for dealing with the daunting number of decompositions. Here, we provide some new guidelines, the first of which is based on a compelling identifiability consideration that can greatly reduce the number of candidate decompositions.
We first formulate a compact way to characterize different decompositions, focusing on the case of two stages of mediation (and considering saturated models for now). To obtain a decomposition we start, without loss of generality, with all d’s (defined in Section 3.1) set equal to 1 (corresponding to E{Y(1)}); we then set one d at a time to 0, obtaining the corresponding expected potential outcome for the resulting array of d’s after each change. Path-specific effects are obtained using successive expected potential outcomes. For example, if the first d set to 0 is d00, we obtain, using a difference scale,
This contrast, involving only a change in d00, represents a (natural) direct effect. Of course, this is one of many possible versions of the natural direct effect, which are obtained by using different sets of values - common to both terms in the contrast - for the other d’s besides d00. Supposing that the next d set to 0 is d01, the resulting contrast is,
which represents a natural indirect effect occurring through mediator M21 alone. This process continues until all the d’s are equal to 0, providing Q = (m1 + 1) × (m2 + 1) path-specific effects. These path-specific effects sum to the total exposure effect by construction, thus providing a proper decomposition.6 The number of possible decompositions is thus equal to the number of possible orderings in which the d’s are set to 0, which is Q! as noted above. A particular ordering (thus, decomposition) may be represented by listing the ordered d’s in an ‘order vector’. For example, in the case of two stages and one mediator per stage, the order vector (d00, d01, d10, d11) would indicate the decomposition obtained by first setting d00 to 0, then d01, and so on.
We propose that some orderings be ruled out as they unnecessarily increase the number of non-identifiable paths (that is, non-identifiable without additional cross-world assumptions – see Web Appendix A). Consider the d’s corresponding to paths through a given first-stage mediator, M11, say, in the scenario of two mediators at each of two stages; these d’s would be d10, d11, and d12. When the first (and second) of these d’s are set to zero this produces a potential outcome for Y involving cross-world potential outcomes for M11, namely, M11(1) and M11(0), and thus a non-identifiable path-specific effect. This is resolved once the last d in the group is set to zero. Non-identifiability for paths involving a first-stage mediator is unavoidable (in a saturated two-stage mediation model), regardless of the choice of decomposition. However, if a d not involving a first stage mediator, for example, d01, were set to zero in between the d’s for a first-stage mediator this would unnecessarily result in a non-identifiable effect - in this case, for the path through the first second-stage mediator. Therefore, it is preferable to keep the group of d’s for any given first-stage mediator (for example, d10, d11, and d12, for first-stage mediator M11) together in the ordering of setting d’s to 0. This consideration, in the case of two stages and one mediator per stage, would thus suggest (d00, d01, d10, d11) and (d11, d10, d01, d00) as possible orderings but not, for example, (d00, d10, d01, d11) since in this ordering d01 (corresponding to the path through the second-stage mediator alone) occurs between d10 and d11 (representing paths through the first-stage mediator). In the former orderings, the direct and indirect (through the second-stage mediator) effects are both identifiable, while in the latter ordering only the direct effect is identifiable.
The second consideration that we propose for selecting a decomposition involves the context of the data and the interventional interpretation of the potential outcome. From this perspective, we will prefer decompositions representing more practical and acceptable (possible future) interventions. There are two premises of this approach: 1) if the exposure is beneficial, a desirable intervention would involve the introduction of the exposure (for those unexposed), while if the exposure is detrimental, interventions would involve removing the exposure (for those exposed); 2) in a sequence of interventions, one would first intervene to affect the mediator (before affecting the direct effect). The reason for the latter is because the direct effect represents ‘all other’ (unobserved) mediators; targeting ‘all other’ mediators would be impractical, whereas if the mediator in question has already been intervened on, then the direct effect can be affected as well in a subsequent intervention by simply exposing the person. Based on these premises, the rule we propose (in terms of the ordering of setting d’s to zero) is to start with d00 (and generally proceed with paths with an increasing number of links) for a beneficial exposure, and end with d00 (go from longer to short paths) for a detrimental exposure.
As a simple example, consider a single mediator (say, M = frequency of dental visits) of the relationship between SES (X=1 for low SES; X=0 for high SES) and dental caries (Y=DMFT). Choosing between the two possible decompositions (as shown in Section 2.1) essentially involves the choice between the potential outcomes Y(0,M(1)) and Y(1,M(0)). Here, the exposure (low SES) is detrimental. Thus, a future intervention will seek to remove this exposure (in whole or in part). Targeting the mediator, the intervention of interest would correspond to Y(1,M(0)), representing the partial removal of the effect of low SES – i.e., an intervention for a low SES person that produces a dental visit frequency as if the person were high SES, for example by enabling increased access to dental care. This corresponds to setting d1 equal to zero first, and d0 = 0 last, in accordance with the rule. Using Y(0,M(1)) instead (contrary to our rule) would amount to an intervention for a high SES person in which dental visits were affected as if the person were low SES; this intervention is unlikely to be of interest for the reasons expressed in the two premises above. For a beneficial exposure, the reasoning is reversed and we would be interest in Y(0,M(1)) (and the corresponding decomposition) rather than Y(1,M(0)). This rule applies in a similar manner to the more complex situation involving a sequence of mediators.
We note that this rule should be reinterpreted when paths are not all in the same direction. For example, a generally beneficial drug may have a negative path, for example through a mediator representing an unwelcome side effect. In this case, a future intervention of interest might block the path through this mediator (for example, by adding an auxiliary agent that ameliorates the side effects). Here, then, the interest will be in the potential outcome Y(1,M(0)). Thus, in this sort of case, the exposure should be considered as ‘detrimental’ since it has a negative effect through the mediator.
Combining the above two principles, we propose the following rule (expressed for the two-stage mediation case):
Combined Rule:
For a beneficial exposure, use order
for a detrimental exposure, use order
where , and the elements/sets within parentheses follow the displayed order, but elements within brackets can follow any order.
For convenient reference, we will refer to the two broad schemes in this rule as the ‘increasing exposure’ and ‘decreasing exposure’ decompositions, respectively. The combined rule reduces the number of candidate decompositions considerably. We note that for simplicity the rule expressed above may be more restrictive than necessary. For example, for a beneficial exposure and two first-stage mediators, a permissible ordering (according to the above rule) is ; however, the ordering , which is not consistent with the above rule, may also be suitable according to our two principles. A remaining indeterminacy is in the order of d’s corresponding to multiple mediators at a particular mediation stage. These orderings can be decided based on context-specific considerations, for example, of the most likely, practical or desirable order of a sequence of future interventions affecting the mediators. The implementation of the above rules is illustrated in an example provided in Web Appendix C.
3.4. Clustered Data
Often studies involve individuals within larger units (clusters) whereby individuals within the same cluster tend to be similar in unmeasured characteristics that may be relevant to the response. Two broad approaches are commonly used for clustered data. The marginal model (or generalized estimating equations (GEE)) approach, which provides inference for population-level fixed effects, considers the within-cluster correlation as a nuisance parameter and seeks to account for it only in the estimation of variances of fixed effect estimates. The other approach, using random effects models, estimates fixed effects while conditioning on the random effects (representing cluster effects) providing cluster-level inference.
The mediation formula approach to mediation analysis would be more complicated with the introduction of random effects (though a related approach26 considered a latent mediator). On the other hand, an explicit variance formula (such as the sandwich estimator in the GEE framework) is not available for mediation effect estimates obtained via the mediation formula.
Some scholars27 have expressed a preference for the marginal model approach to avoid the more stringent assumptions of the random effects model. To maintain a marginal model approach for inference regarding path-specific effects, we propose to account for clustering by using a modification of the standard bootstrap approach. A relatively simple approach is to use the cluster bootstrap method which samples (with replacement) clusters rather than individuals. This approach has been shown to work well in a regression context when there are a sufficient number of clusters.28 Alternative techniques have been proposed that seek to provide greater efficiency, particularly with a relatively small number of clusters.28 These approaches include a ‘residual bootstrap’ technique in which residuals are bootstrapped, and then used to obtain bootstrap samples of the outcomes. Field and Welsh28 focused on the linear model case, though a version of the residual bootstrap has been proposed for the generalized linear model,29 albeit for non-clustered data. Clearly, further investigation and development of bootstrap techniques is needed for complex mediation models.
3.5. Reference group
An issue that has received little attention for mediation analysis, particularly for the mediation formula, is the choice of the reference group. We use the term ‘reference group’ to indicate the subset of individuals to which inference is performed. An implication is that the joint distribution of the covariates for the reference group is used in the mediation formula. In practice, the evaluation of the mediation formula may involve the summation over the empirical distribution of the covariate vector, C, for the subjects in the reference group. Note that the selection of a reference group need not affect the model fitting; for the latter, which is done prior to the computation of the mediation formula, it is generally advisable to use the entire sample.
A natural choice for the reference group may arise from a particular design. For example, a group-matched cohort study may seek to recruit patients with a particular risk factor (for example, very low birth weight) along with matched (normal) controls. Here, the implied target population to which inference will be made is the subpopulation with the risk factor; it may therefore be reasonable to use the corresponding subgroup in the sample as the reference group.
Another consideration for the reference group is the possibility of reducing assumptions or simplifying inference. For example, Albert7 provided a simple formula for the natural direct and indirect effects for the subpopulation of exposed individuals. Similarly, Vanderweele and Vansteelandt30 showed that reduced assumptions are needed for inference regarding natural direct and indirect effects for the exposed. These papers addressed the situation of a single mediator. In the case of multiple mediation stages, it has not yet been established that inference for the exposure group (or any other reference group in general) will allow weaker assumptions.
An extension of the idea of the reference group is to use sampling weights in the mediation formula. This is discussed in the single (albeit latent) mediator case in Albert et al.,26 but may be employed in the same manner in more general mediation models. The inclusions of such weights in the extended mediation formula may allow inference to a population of interest when, for example, the sample is obtained from a known probability sampling scheme.
3.6. Computational Issues
The mediation formula approach to causal mediation and path analysis tends to be computationally intensive. The problem is magnified considerably for multiple stages and multiple mediators per stage. This is seen by the fact that the mediation formula itself involves a multi-dimensional integration (or approximation, such as via Monte Carlo); further, this computation is carried out for each person in the reference group and then repeated for each bootstrap sample (and re-estimation of model parameters).
As was done previously for less complex mediation models, we consider algorithms that compute the mediation formula via Monte Carlo simulation. Daniel et al.6 suggested that the reference group be multiplied to reduce error in the Monte Carlo estimation. However, how large a multiplier is needed for a given application may be unclear.
Another issue is how to conduct inference for non-identifiable paths. As noted in Section 3.1, we use a sensitivity parameter representing the cross-world correlation between (possibly latent versions of) counterfactuals for each first-stage mediator. Fortunately, being a correlation, this parameter is bounded by −1 and 1. However, the relationship between the cross-world correlation and estimates of path-specific effects has received little study. In the likely case that the user does not have much prior information about the cross-world correlation, the user may wish to have an idea of the range of sensitivity parameter values that need to be examined in order to get reasonable bounds on the otherwise non-identifiable mediation effects.
With the above motivation, we conducted a simulation study with the following two goals, in addition to that of examining validity of inference for the extended causal mediation/path analysis: 1) to investigate the relationship between the reference group multiplier and precision of path-specific effect (Monte Carlo based) estimators, and 2) to examine the relationship between the cross-world correlation and estimated path-specific effects. We considered two overall scenarios, one mimicking a dental data set (to be analyzed in the next section), the other, constructed to have approximately equal path-specific effects. Saturated models with one mediator at each stage (a special case of the causal model in Figure 1) were considered throughout. As in the dental data, the simulation models involved a mix of variable types; namely, the first-stage mediator and final outcome (as well as exposure) were binary (Bernoulli distributed), while the second-stage mediator was generated as normally distributed. Generalized linear models with canonical links were used to generate each mediator and the final outcome. Each model included a single common continuous (normally distributed) covariate representing a confounder. A variation of this model was also considered in which the final outcome is distributed as negative binomial. Total sample sizes of 200 (roughly that of the dental dataset) and 1000 were used. The parameter values used for the simulations are given in the Supplementary Material, Web Table B1.
For each generated dataset we conducted the method described above using the gmediation R package.20 The ‘decreasing exposure’ decomposition was used and the whole sample was designated as the reference group. We studied the Monte Carlo accuracy by varying the reference group multiplier (using 1, 10, 100, and 1000 for the n=200 case, 1 and 10 for the n=1000 case). In addition, we used values for ρ ranging from −0.9 to 0.9 by 0.1 to study the effect of this parameter on inferences for non-identifiable paths; this was done for n=200 and reference group multiplier equal to 1000. Effects for each of the four possible paths were estimated using the extended mediation formulae (7) and (8) (see also Web Appendix A) in conjunction with fitting of correctly specified regression models. Five-hundred bootstrap samples were drawn for each generated dataset to obtain 95% confidence intervals for each path-specific effect using the bootstrap percentile method. For each scenario 500 replications were performed.
The true values for each path-specific effect were obtained by applying the extended mediation formulae using the true values for the regression parameters. The generated (empirical) covariate distribution for a dataset was considered as the true covariate distribution. These dataset-specific true values were used in computing the biases and coverage probabilities as described below. For each scenario, we computed (averaging over replications): bias (average estimate minus the true value), relative bias (average ratio of the bias and the true value), simulation standard error of the bias (noting that true values vary over replicates), coverage (percent of 95% confidence intervals that cover the true value) and power (percent of 95% confidence intervals that do not cover 0).
Figure 2 displays the simulation-estimated standard error of bias (se(bias)) as a function of the reference group multiplier (‘mult’) for the ‘dental data’ and equal path-specific effects scenarios with binary Y and n=200. The results show decreases in the se(bias) for each path-specific effect as ‘mult’ increases from 1 to 1000. The downward trend is modest for most of the paths in the dental data scenario (Figure 2A), with a noticeable ‘elbow’ (from mult = 1 to mult = 10) only for the two-mediator (M1, M2) path. The decrease in se(bias) is somewhat more pronounced, with less leveling off with increasing multiplier, in the equal path-specific effect scenario (Figure 2B), though most paths (with the exception of the direct path) still show the greatest decline between multipliers 1 and 10. (Note, though, that the Y axes for the plots for the two scenarios are on different scales.) The results for negative binomial Y (dental data scenario) similarly show an elbow at mult = 10 with results for all paths being very similar; see Supplementary Material, Figure B1. The results (not included) for n=1000 (binary Y) show similar relative declines, reflective of the five-fold increase in sample size, though changes on an absolute scale are smaller relative to the results for n=200. In summary, most examined scenarios show a substantial (up to around 50%) reduction in the standard error of bias when increasing the reference group multiplier from 1 to 10. The reduction in Monte Carlo error may be particularly important for smaller sample sizes in which cases absolute errors will tend to be reduced substantially with an increasing multiplier. Depending on the scenario and path, further error reduction may occur with higher multiplier values (even up to 1000 or more); it may thus be advisable to use such higher multiplier values, computational time permitting.
Figure 2.
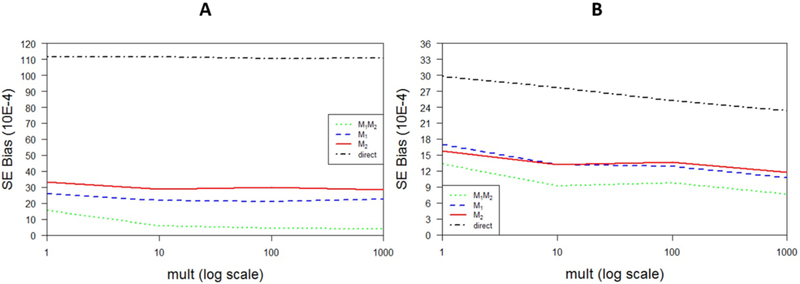
Standard error of bias by reference group multiplier (log scale) for each path from simulations: A) mimicked dental data, B) equal path-specific effects scenario
The plots relating ρ and the simulation average effect estimates (with multiplier of 1000 and n=200) for binary Y are provided in Web Appendix B (Figures B2 and B3). Both the dental data and equal path-specific effects scenarios show little effect of ρ on estimates. This is particularly so for the dental data scenario which shows a very flat trend, while the results for the equal path-specific effects scenarios show a slightly decreasing trend for the M1 alone path and increasing trend for the M1→ M2 path. Thus, the effect of the sensitivity parameter (ρ) on average path-specific effect estimates is remarkably small across multiple scenarios. While the results for our scenarios indicate low sensitivity to the choice of ρ, this may not hold in all situations. Also, there may be substantial variability due to Monte Carlo error over varying values of ρ for a given dataset. Additional results, including relative biases and confidence interval coverages revealing good properties for the included scenarios, are provided in the Supplementary Material (Tables B2 and B3).
4. Data Example
We applied the generalized causal path analysis to data from an observational cohort study of dental caries in adolescents.31 In this study, subjects were assessed on a number of dental and behavioral outcomes at around age 14 years. Baseline demographic information included socioeconomic status (SES), gender, race, and birth status (normal weight or very low birth weight with or without bronchopulmonary dysplasia). The study contained some siblings, so subjects were considered as clustered within ‘family’ (specifically, same mother), although many such ‘clusters’ contained just a single child. Of major interest in this study were the possible behavioral and biological mechanisms leading to dental caries. For the present analysis, we investigated possible paths in the relationship between SES and DMFT (decayed, missing, or filled teeth). Mediators of interest include brushing behavior (‘Brush’, at least once per day brushing versus less), frequency of dental visits (‘Visit’, at least once a year regular visits versus fewer), use of sealants (‘Sealant’, yes or no), and the oral hygiene index (‘OHI’, a clinical measure of oral hygiene or cleanliness of teeth, scored from 0 to 3, higher scores indicating worse hygiene). Scientific considerations led to the two-stage model (with Brush and Visit at the first stage and Sealant and OHI at the second stage) illustrated in Figure 3.
Figure 3:
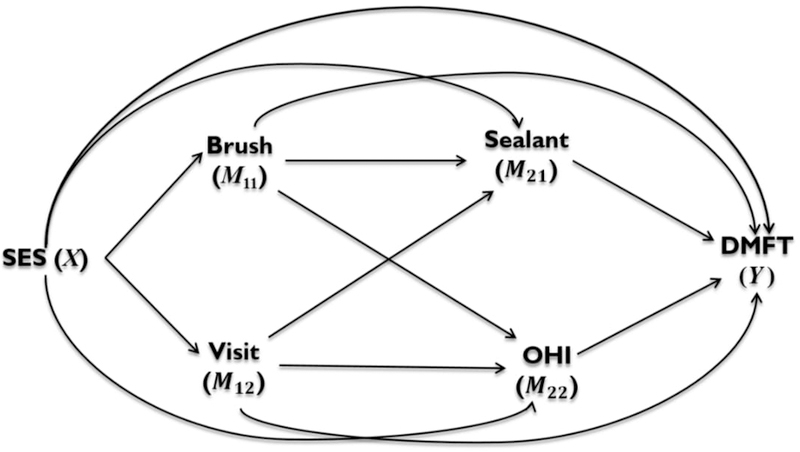
Causal graph for dental data example
We implemented the generalized causal path analysis methodology with the following specifications. We fit logistic regression models for dichotomized DMFT (DMFTD, coded as 0 for none, 1 for any DMFT) and for the binary mediators (Brush, Visit, and Sealant), and a linear regression model for OHI. As a first approach, a saturated model was used (with each outcome/mediator model including all causally preceding variables). Also, all of the demographic variables mentioned above were included in each outcome model as potential confounders. A ‘decreasing exposure’ decomposition was chosen in accordance with the combined rule described in Section 3.3, based on the exposure, low SES, being considered as detrimental. The detailed specification of the decomposition is provided in Web Appendix C. The reference group was taken to be the whole sample, and a multiplier of 10,000 was used. One thousand cluster (family) bootstrap samples were drawn to obtain percentile method 95 percent confidence intervals. In addition, p-values, corresponding to (confidence interval based) tests of each path-specific effect equal to zero, were computed. Aside from assuming the above regression models and consistency, we are making the sequential ignorability (or no omitted confounder) and contemporaneous mediator conditional independence assumptions of Section 3.1 (with the stronger versions for paths through first-stage mediators).
Table 1 provides the estimated path-specific effects and estimated mean proportion of the total SES effect due to each path (that is, the estimated path-specific effect divided by the estimated total effect) along with 95% confidence intervals. The results show that most (an estimated 0.73 or 73%) of the effect of SES on DMFTD is direct (or through unidentified mediators). The direct effect is not statistically significant at α = 0.05 though the total effect is (p = 0.016). However, there is a statistically significant estimated effect of 0.054 (p=0.012) for the path through OHI alone, corresponding to an estimated 0.33 of the total SES effect. The interpretation of this effect estimate is that there would be an estimated decrease of 0.054 in the probability of any caries (DMFTD=1) due to an intervention, provided to low SES subjects whose first-stage mediator (Brush and Visit) levels are as if the subjects were high SES, that produces OHI levels as if the subjects were high SES. All the other paths show small estimated effects (and proportions) not found to be statistically significant. A more comprehensive discussion of the interpretation of path-specific effects (including all those in the decomposition used) is provided in Web Appendix C. Note that alternative decompositions may have different path-specific effect interpretations.
Table 1.
Estimated Path-Specific Effects and Proportions (of Total Effect) with 95% Confidence Intervals for Dental Data Analysis
| Path-Specific Effects | Proportion | ||
|---|---|---|---|
| Path | Estimate (95% CI) | Estimate (95% CI) | p-value |
| ses→visit→ohi→dmft | −0.008 (−0.019, 0.025) | −0.051 (−0.096, 0.13) | 0.82 |
| ses→visit→sealant→dmft | 0.015 (−0.020, 0.023) | 0.093 (−0.27, 0.32) | 0.87 |
| ses→visit→dmft | −0.003 (−0.015, 0.052) | −0.019 (−0.15, 0.53) | 0.26 |
| ses→brush→ohi→dmft | 0.009 (−0.024, 0.022) | 0.053 (−0.17, 0.16) | 0.97 |
| ses→brush→sealant→dmft | −0.005 (−0.023, 0.023) | −0.031 (−0.14, 0.14) | 0.96 |
| ses→brush→dmft | −0.008 (−0.030, 0.023) | −0.046 (−0.16, 0.12) | 0.79 |
| ses→ohi→dmft | 0.054 (0.009, 0.090) | 0.33 (0.055, 0.561) | 0.012 |
| ses→sealant→dmft | −0.009 (−0.031, 0.021) | −0.054 (−0.912, 0.623) | 0.82 |
| ses→dmft | 0.12 (−0.026, 0.222) | 0.729 (−0.287, 2.410) | 0.13 |
| Total Effect | 0.17 (0.036, 0.278) | 0.016 | |
Secondarily, we examined an unsaturated model obtained by removing Brush from the model for Sealant, as there is no compelling reason to presume a link between these variables. A further analysis considered the DMFT count, assumed to be distributed as negative binomial, as the final outcome. Here, a loglinear, rather than logistic regression, model was used for Y; otherwise, specifications for both saturated and unsaturated (removing the link between Brush and Sealant) models were as before. Substantially similar conclusions were obtained for all these analyses (results not shown).
A limitation of this analysis is the possibility of omitted mediators and confounders, and the lack of a sensitivity analysis for the sequential ignorability assumptions. Also, there is the possibility of measurement error or bias, particularly in the brushing variable which was obtained via questionnaire. Such measurement error may affect some of the path-specific effect estimates and possibly help explain the relatively large effect for the path going directly from SES to OHI, as we do not consider there to be obvious omitted mediators.
5. Discussion
This paper presents extensions of the generalized causal mediation/path analysis methodology. The extended methodology is able to handle multiple mediators at each of two stages of mediation and provides increased flexibility by allowing unsaturated models, clustered data, and choice of reference group. The data analysis presented in this paper was conducted using the gmediation R package. This package, along with the dental data analyzed in the present paper, can be downloaded from the web: https://cran.r-project.org/web/packages/gmediation/index.html
The two-stage mediation model, relative to reduced (one-stage) models, will entail a greater number of sequential ignorability assumptions; this is to be expected as a greater number of path-specific effects are being estimated. It should be noted, though, that a flexible feature of the two-stage model is that certain confounders affected by exposure may be included as first-stage “mediators”. Although the corresponding path-specific effects may not be of interest, inclusion of such confounders may avoid what would otherwise be a violation of sequential ignorability in the corresponding one-stage model.
We note that more complex models may quickly lead to a large number of paths and corresponding estimates and significance tests. These may need to be interpreted with care, and adjustments for multiplicity considered depending on the context and objectives of the study. Generally, without adjusting for multiplicity, results should be considered as exploratory as opposed to confirmatory.
This paper by no means exhausts the important issues in the assessment of causal mediation and path-specific effects. For example, missing data issues were not discussed in this paper. Multiple imputation may be readily implemented with the present method, but further work is needed, particularly on approaches for informative missing data. Model fit is an important issue for parametric data analysis. Our approach involves the separate fit of models to each mediator and to the final outcome; thus, standard model fit criteria and diagnostics (for generalized linear models) are available to the user, and appropriate model criticism should be conducted before using the models in a causal mediation analysis. A sensitivity analysis for possible violation of the extended sequential ignorability assumption would be desirable, but unfortunately a method for such is not available. Albert and Wang32 proposed two new approaches to sensitivity analysis for a single mediator model that allow for different types of mediators and final outcome variables following generalized linear models. It may be possible to extend these approaches to the multiple stage and/or multiple mediators per stage situations.
Supplementary Material
Acknowledgements
The authors are grateful to the Editor and two reviewers for insightful and constructive comments that helped greatly in improving the paper. The authors would like to thank Jingxiao Chen, Yuchen Han, and Youjun Li for assistance with graphs, simulations, and manuscript preparation. Thanks also go to Dr. Lynn Singer for providing access to the longitudinal cohort of VLBW and NBW adolescents, supported by the Maternal and Child Health Program, Health Resources and Services Administration, Department of Health and Human Services [grant numbers MC-390592, MC-00127, MC-00334].
Funding
This work was supported by the National Institute of Dental and Craniofacial Research, National Institutes of Health [grant numbers R01DE022674 (J. Albert) and R21DE16469 (S. Nelson)].
Footnotes
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
References
- 1.Imai K, Keele L, Yamamoto T. Identification, inference and sensitivity analysis for causal mediation effects. Statistical Science 2010; 25: 51–71. [Google Scholar]
- 2.Pearl J The causal mediation formula—a guide to the assessment of pathways and mechanisms. Prevention Science 2012; 13: 426–436. [DOI] [PubMed] [Google Scholar]
- 3.Robins JM, Greenland S. Identifiability and exchangeability for direct and indirect effects. Epidemiology 1992; 3:143–155. [DOI] [PubMed] [Google Scholar]
- 4.Pearl J Direct and indirect effects. In Proceedings of the seventeenth conference on uncertainty in artificial intelligence Morgan Kaufmann Publishers Inc, 2011, pp411–420. [Google Scholar]
- 5.Albert JM, Nelson S. Generalized causal mediation analysis. Biometrics 2011; 67:1028–1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Daniel RM, De Stavola BL, Cousens SN, Vansteelandt S. Causal mediation analysis with multiple mediators. Biometrics 2015; 71: 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Albert JM. Mediation analysis for nonlinear models with confounding. Epidemiology 2012; 23: 879–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tchetgen EJ, Shpitser I. Semiparametric theory for causal mediation analysis: efficiency bounds, multiple robustness, and sensitivity analysis. Annals of Statistics 2012; 40:1816–1845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lange T, Vansteelandt S, Bekaert M. A simple unified approach for estimating natural direct and indirect effects. American Journal of Epidemiology 2012; 176:190–195. [DOI] [PubMed] [Google Scholar]
- 10.Nguyen QC, Osypuk TL, Schmidt NM, Glymour MM, Tchetgen Tchetgen EJ. Practical guidance for conducting mediation analysis with multiple mediators using inverse odds ratio weighting. American Journal of Epidemiology 2015; 181:349–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Avin C, Shpitser I, Pearl J. Identifiability of path-specific effects. In Proceeding of the 19th Joint Conference on Artificial Intelligence San Francisco, CA: Morgan Kaufmann Publishers Inc, 2005, pp357–363. [Google Scholar]
- 12.van der Laan MJ, Petersen ML. Direct effect models. The International Journal of Biostatistics 2008; 4: Article 23, 1–27. [DOI] [PubMed] [Google Scholar]
- 13.Tchetgen Tchetgen EJ. Inverse odds ratio‐weighted estimation for causal mediation analysis. Statistics in Medicine 2013; 32: 4567–4580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shpitser I Counterfactual graphical models for longitudinal mediation analysis with unobserved confounding. Cognitive Science 2013; 37, 1011–1035. [DOI] [PubMed] [Google Scholar]
- 15.Shpitser I, Tchetgen Tchetgen E. Causal inference with a graphical hierarchy of interventions. Annals of Statistics 2016; 44: 2433–2466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Muthén B, Asparouhov T. Causal effects in mediation modeling: An introduction with applications to latent variables. Structural Equation Modeling: A Multidisciplinary Journal 2015; 22:12–23. [Google Scholar]
- 17.Tingley D, Yamamoto T, Hirose K, Imai K, Keele L. Mediation: R package for causal mediation analysis. Journal of Statistical Software 2014; 59: 1–38.26917999 [Google Scholar]
- 18.Westreich D, Cole SR, Young JG, Palella F, Tien PC, Kingsley L, Gange SJ, Hernán MA. The parametric g‐formula to estimate the effect of highly active antiretroviral therapy on incident AIDS or death. Statistics in Medicine 2012; 31:2000–2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Young JG, Cain LE, Robins JM, O’Reilly EJ, Hernán MA. Comparative effectiveness of dynamic treatment regimes: an application of the parametric g-formula. Statistics in Biosciences 2011; 3:119–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cho JI, Albert JM. (2017). gmediation: An R Package for Generalized Causal Mediation and Path Analysis Unpublished manuscript. [DOI] [PMC free article] [PubMed]
- 21.Didelez V, Dawid AP, Geneletti S. Direct and indirect effects of sequential decisions In:Proc. 22nd UAI Conference UAI Press, Corvallis, Oregon, 2006, pp138–146. [Google Scholar]
- 22.VanderWeele TJ, Tchetgen Tchetgen EJ. Mediation analysis with time varying exposures and mediators. Journal of the Royal Statistical Society: Series B 2017; 79:917–938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wang W, Nelson S, Albert JM. Estimation of causal mediation effects for a dichotomous outcome in multiple‐mediator models using the mediation formula. Statistics in Medicine 2013; 32:4211–4228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Taguri M, Featherstone J, Cheng J. Causal mediation analysis with multiple causally non-ordered mediators. Statistical Methods in Medical Research 2015; 0: 1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pearl J. Causality 2nd Edition. New York: Cambridge University Press, 2009. [Google Scholar]
- 26.Albert JM, Geng C, Nelson S. Causal mediation analysis with a latent mediator. Biometrical Journal 2016; 58: 535–548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hubbard AE, Ahern J, Fleischer NL, Van der Laan M, Lippman SA, Jewell N, Bruckner T, Satariano WA. To GEE or not to GEE: comparing population average and mixed models for estimating the associations between neighborhood risk factors and health. Epidemiology 2010; 21:467–474. [DOI] [PubMed] [Google Scholar]
- 28.Field CA, Welsh AH. Bootstrapping clustered data. Journal of the Royal Statistical Society: Series B 2007; 69: 369–390. [Google Scholar]
- 29.Moulton LH, Zeger SL. Bootstrapping generalized linear models. Computational Statistics & Data Analysis 1991; 11: 53–63. [Google Scholar]
- 30.Vansteelandt S, VanderWeele TJ. Natural direct and indirect effects on the exposed: effect decomposition under weaker assumptions. Biometrics 2012; 68:1019–1027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Nelson S, Albert JM, Lombardi G, Wishnek S, Asaad G, Kirchner HL, Singer LT. Dental caries and enamel defects in very low birth weight adolescents. Caries Research 2010; 44: 509–518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Albert JM, Wang W. Sensitivity analyses for parametric causal mediation effect estimation. Biostatistics 2014; 16:339–351. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


