Abstract
The process of platelet adhesion is initiated by glycoprotein (GP)Ib and GPIIbIIIa receptors on the platelet surface binding with von Willebrand factor on the vascular walls. This initial adhesion and detachment of a single platelet is a complex process that involves multiple bonds forming and breaking and is strongly influenced by the surrounding blood-flow environment. In addition to bond-level kinetics, external factors such as shear rate, hematocrit, and GPIb and GPIIbIIIa receptor densities have also been identified as influencing the platelet-level rate constants in separate studies, but this still leaves a gap in understanding between these two length scales. In this study, we investigate the fundamental relationship of the dynamics of platelet adhesion, including these interrelating factors, using a coherent strategy. We build a, to our knowledge, novel and computationally efficient multiscale model accounting for multibond kinetics and hydrodynamic effects due to the flow of a cellular suspension. The model predictions of platelet-level kinetics are verified by our microfluidic experiments, which systematically investigate the role of each external factor on platelet adhesion in an in vitro setting. We derive quantitative formulas describing how the rates of platelet adhesion, translocation, and detachment are defined by the molecular-level kinetic constants, the local platelet concentration near the reactive surface determined by red-blood-cell migration, the platelet effective reactive area due to its tumbling motion, and the platelet surface receptor density. Furthermore, if any of these aspects involved have abnormalities, e.g., in a disease condition, our findings also have clinical relevance in predicting the resulting change in the adhesion dynamics, which is essential to hemostasis and thrombosis.
Introduction
Understanding the biophysics of platelet adhesion is a long-standing challenge in the study of hemostasis and thrombosis. At the interface of vessel walls and flowing blood, platelet adhesion involves a complex mechanism including multiple steps. At the site of vascular injury where the subendothelial layer is exposed to an arterial flow, platelet adhesion is initiated by glycoprotein (GP)Ib receptors on its surface forming transient bonds with von Willebrand factor (VWF) immobilized on the subendothelial matrix. This initial tethering captures single platelets from flowing blood, slows them, and triggers their activation (1, 2). Subsequently, GPIIbIIIa receptors on the platelet surface react with VWF and fibrinogen, leading to stable platelet adhesion (3). The adhesion process proceeds until multiple platelets aggregate to form clots. In this study, we focus on the initial adhesion of single platelets mediated by GPIb and GPIIbIIIa receptors. These two steps together define the rate of platelet adhesion often reported from experimental studies (4, 5) as well as the rate of platelet detachment from the vessel wall. Such platelet-level kinetics can be measured in terms of the number of adhered platelets or the surface coverage in minute-long experiments (4, 5). The rate of platelet adhesion/detachment, however, does not equal the rate of association and/or dissociation between a single GPIb or GPIIbIIIa receptor and a ligand such as VWF because more than 10,000 copies of GPIb and GPIIbIIIa receptors are located on the surface of each platelet (6). Single-molecule studies have been frequently used to directly measure bond-level kinetics (7, 8, 9). Remarkably, despite an abundance of experimental data, the relationship between platelet-level kinetics and bond-level kinetics remains underexplored and has, to the authors’ knowledge, only been considered in one specific experimental study estimating the size of a VWF-GPIb encounter complex (7). The gap in knowledge between these two length scales prevents us from gaining a fundamental understanding of platelet adhesion and, ultimately, the ability to control hemostasis and thrombosis.
Despite involving only two types of platelet surface receptors, the initial platelet adhesion is still a complex process influenced by several external factors that present a major obstacle to any simple linkage of bond- and platelet-level kinetics. In addition to the obvious factors such as the number of GPIb and GPIIbIIIa receptors, the environment in which platelet adhesion occurs, i.e., the effects of flowing blood at physiological shear rates, must also be considered. It is well known that platelet adhesion is a shear-induced phenomenon (10); it occurs much faster in the presence of shear flow than in quiescent fluid. Moreover, red blood cells are the dominant species in blood by both number as well as mass and thus play a significant role in the cross-flow transport of platelets via hydrodynamic interactions (11, 12, 13, 14, 15). In short, red blood cells migrate away from vessel walls under shear because of their unique deformable shapes, thus forming a cell-free layer (i.e., the Fahraeus-Lindqvist layer) near the wall (16). As a result, platelets, which are much more rigid and dilute, marginate toward vessel walls and have a near-wall excess concentration influenced by the hematocrit (the volume fraction of red blood cells). Note that abnormally low hematocrit may cause prolonged bleeding times (17) in part because of reduced platelet margination. On the other hand, an elevated hematocrit enhances platelet accumulation and thrombus formation (18). Thus, because of all these interrelated factors—especially the hydrodynamic effects—it is challenging to perform controlled variable experiments at the platelet level in an in vitro environment. Among existing publications, we have not seen a study systematically investigating the role of each factor and presenting quantitative results that can be compared with model predictions.
Existing simulation studies of platelet adhesion utilize techniques such as the boundary element method (12, 19, 20, 21), the immersed boundary method (22), and dissipative particle dynamics (23). In these simulations, platelets are modeled as rigid oblate spheroids. Because of their aspherical shapes, near-wall platelets undergo wall-hindered tumbling motion in shear flow, which is referred to as the modified Jefferey orbit (19, 24). This unique tumbling motion of platelets influences the contact area between a platelet and the channel wall, and thus a spherical platelet model is not sufficient for the study of platelet adhesion (19, 25). In addition to the adhesion kinetics, the deformable red blood cells are included in these simulations to account for their influence on platelets (12, 23). It is now feasible to simulate hemostasis from the initial single-platelet adhesion to the eventual clot formation in a whole-blood suspension. However, such full-scale blood simulations typically take weeks to complete, limiting their role in the planning and interpretation of experiments. Therefore, lower-order models have also been developed that capture most of the physics regarding platelet transport across the channel and can estimate relevant rate constants with reduced computation time (21). Like experimental studies, a challenge in existing models is the lack of a fundamental relationship linking platelet adhesion to the binding kinetics at the molecular level. The bond-level reaction constants have been chosen simply to produce platelet-level kinetics that are comparable to experimental measurements (12, 19, 21). Such fitted values, however, have not been compared to direct measurements at the molecular level, calling into question the validity of these models.
In this study, we use both experiments and a multiscale computational model to explore the complex mechanism of platelet adhesion in microchannel flow. To better characterize the translocation behavior of adhered platelets, our in vitro microfluidic experiments measure the detachment rate and the stable adhesion rate of platelets on VWF-coated surfaces in addition to the rate of adhesion that is commonly measured. These platelet-level rate constants are predicted by our model, which includes bond-level kinetics referenced from single-molecule measurements, hydrodynamic effects determined from small-scale simulations, and finally, multibond kinetics. We therefore bridge the gap in knowledge between bond-level and platelet-level kinetics, which is essential to fundamentally understand hemostasis and thrombosis. The near-quantitative agreement between experimental and model results demonstrates that our coarse-grained approach is a promising alternative to time-consuming whole-blood simulations. We perform controlled variable studies to systematically investigate the roles of shear rate, hematocrit, and GPIb and GPIIbIIIa receptor densities on platelet adhesion, which unify findings from previous separate studies. Abnormalities in these platelet properties or blood-flow characteristics may be associated with disease conditions, and thus the clinical relevance of our model is also discussed.
Methods
Sample preparation
Healthy volunteers were recruited by the Royal College of Surgeons in Ireland at Beaumont Hospital, Dublin, Ireland. These donors had not taken any medication known to affect platelet function within the previous 14 days. All donors gave informed consent. Blood was drawn from the antecubital vein through a 19-gauge Sarstedt Safety Needle into an S-Monovette 9NC blood collection tube (Sarstedt, Wexford, Ireland) containing the anticoagulant solution trisodium citrate dihydrate (final concentration of 0.32%, 1:9 ratio of citrate/blood). Hematocrit and platelet count were routinely recorded (Sysmex KX21N; Sysmex, Kobe, Japan). All donors we recruited had hematocrit and platelet counts within the reference range for healthy individuals.
For experiments with varying hematocrit, a two-step centrifugation was used to separate red blood cells, platelet-rich plasma (PRP), and platelet-poor plasma (PPP). Whole blood was first centrifuged at 170 × g for 10 min at room temperature. Red blood cells and PRP were thus separated. The top 90% of PRP was aspirated into a fresh tube, and platelets were allowed to rest for a minimum of 15 min before use. Subsequently, PPP was prepared by centrifugation of PRP at 21,000 × g for 2 min. Assuming PPP contains no platelets, these three components of blood can be remixed to vary the hematocrit while keeping platelet concentration constant.
Blood samples were incubated with 1 μM DiOC6 at 37°C for 30 min before each experimental run. DiOC6 is a green fluorescent, lipophilic dye that labels platelets (26). When antibodies were used, they were added at the desired concentration along with DiOC6 in the incubation stage. After incubation, all experiments were conducted within 3 h of blood draw.
DPFA
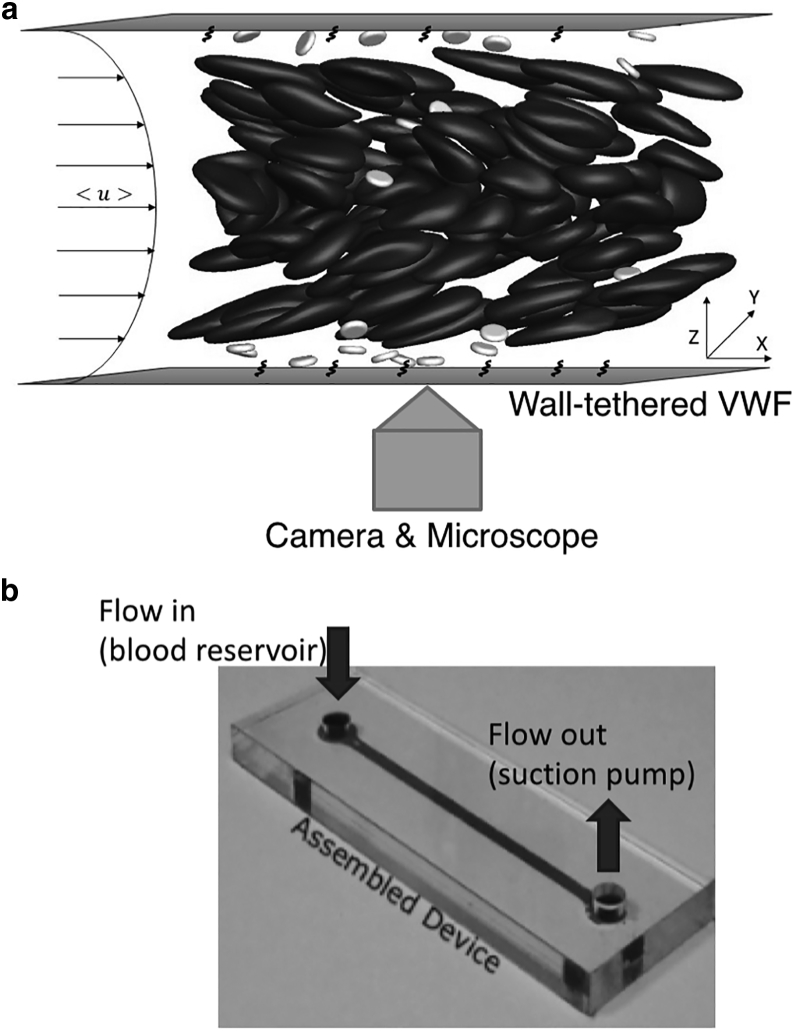
We utilized an existing experimental setup called the Dynamic Platelet Function Assay (DPFA) for our platelet adhesion experiments (27) as shown in Fig. 1. This device primarily consists of a custom-made microfluidic chamber (Fig. 1 b). It is a rectangular channel 30 mm long (Lx), 2 mm wide (Ly), and 50 μm high (Lz). The channel height (Lz) is comparable to the diameter of human arterioles. The interior coverslip surface of the chamber was coated with a monolayer of VWF (100 μg/mL, Haemate-P; CSL-Behring, Marburg, Germany) overnight at 4°C. The channel walls can thus be treated as a homogeneous surface (28). Before each experimental run, the channel was washed with phosphate-buffered saline, blocked with 1% bovine serum albumin for 1 h at room temperature, and rinsed again in phosphate-buffered saline.
Figure 1.
Schematic of the DPFA (27) showing (a) setup of the flow chamber and (b) microfluidic chip design.
During each experimental run, the blood sample was drawn through biocompatible platinum-cured silicone tubing (Nalgene, 0.0625 in internal diameter; Thermo Fisher Scientific, Hvidovre, Denmark) and perfused through the VWF-coated flow chamber using a NEMESYS syringe pump (Cetoni, Korbussen, Germany). The pump controls the flow rate ranging from 25 to 100 μL/min, corresponding to a characteristic shear rate of 500 to 2000 s−1 and matching the range of arteriole shear rates. This characteristic shear rate is the wall shear rate for parabolic flow and is lower than the actual wall shear rate because of the presence of red blood cells (29). At 30% hematocrit and a characteristic shear rate of 2000 s−1, we estimate from whole-blood simulations that the actual wall shear rate is 2800 s−1, with the difference being smaller than those reported in smaller channels (11).
Images were captured using a vacuum-cooled (−80°C) digital electron multiplying-CCD camera (iXON EM+; Andor Technology, Belfast, Ireland) connected to MetaMorph software (version 7.7; Molecular Devices, Wokingham, UK) and illuminated with an Osram 103-W mercury light source and a fluorescein isothiocyanate filter set providing excitation and emission at 490 and 528 nm, respectively (Chroma Technology, Rockingham, VT). Images were acquired in the x-y plane at z = 0 (channel bottom) at 19 frames/s for 500 frames using a 63× objective (500 × 500 pixels, 185 × 185 μm) field of view for visualization of platelet interactions with VWF in real time. A sample image is shown in Fig. 2, and a sample video is provided in the Supporting Material (Video S1). Because of the high wall shear rate (>500 s−1), only adhered platelets, i.e., those forming at least one GPIb-VWF bond, were captured by the camera. Because images were taken at the bottom wall, red blood cells were out of focus and were not captured. White blood cells rarely appeared in the imaging window and were excluded in the image analysis.
Figure 2.
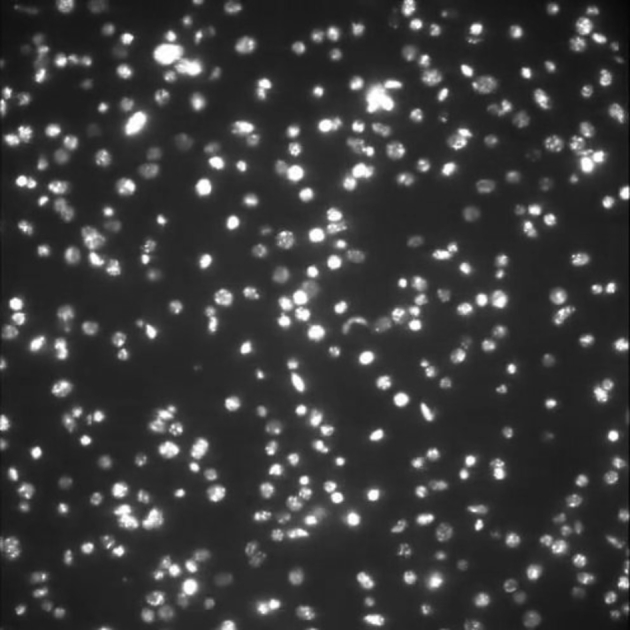
Sample image showing platelets that adhere to VWF tethered to the bottom wall. Image was taken at the end of the experiment, representing the highest surface density of platelets.
A total of 1000 frames are shown, but only the first 500 frames are used for analysis.
Controlled variables
Similar to previous experiments (27, 28), the standard operating condition used in our experiments was 1500 s−1 characteristic shear rate (75 μL/min) with untreated whole blood. This control case matches the physiological flow conditions in arterioles (30). To investigate the effects of platelet and flow properties on adhesion kinetics, we selected the following four independent variables and performed controlled variable studies with each experiment repeated three times per donor.
AK2 dosage
The monoclonal antibody AK2 binds to the platelet GPIb receptor and inhibits platelets binding to VWF (31). In our experiments, we varied AK2 dosage below the saturating dose determined by light transmission platelet aggregation (N = 5 donors) to control the degree of inhibition (32), thus reducing GPIb receptor density on platelet surfaces.
Hematocrit
To confirm the role of red-blood-cell migration on platelet adhesion, we varied the hematocrit between 20 and 35% (N = 7).
Shear rate
We varied the characteristic shear rate ranging from 500 to 2000 s−1 by changing the flow rate Q (N = 7).
ReoPro
Similar to the role of AK2, ReoPro inhibits GPIIbIIIa-VWF binding (33). We used ReoPro at sub-saturation dosages determined by light transmission platelet aggregation to specifically reduce GPIIbIIIa receptor density (N = 5).
Reaction pathways
Based on our experimental setup and flow conditions, we consider the following reactions as the dominant platelet adhesion mechanisms:
| (1) |
and
| (2) |
In addition to the reactions shown in Eqs. 1 and 2, platelet adhesion can also occur through alternative pathways that are not included in our analysis as well as our model. In this section, we briefly discuss how these possibilities are less likely in our experiments and do not significantly influence our results.
First of all, we ignore the small amount of freely flowing VWF present in the blood sample. Under abnormal circumstances, these VWFs can react with flowing platelets and form aggregates without any wall interactions. Our microscope can only focus on the near-wall region (z ∼ 0), and any blood clots in flowing blood are unlikely to be visualized. Nevertheless, by creating a monolayer of VWF on the channel walls, the concentration contrast between wall-bound VWF and freely flowing VWF is magnified greatly.
If GPIIbIIIa is triggered before GPIb-VWF binding, platelet adhesion can occur directly through GPIIbIIIa-VWF interactions (Eq. 2) and bypass GPIb-VWF interactions (Eq. 1). We tested this possibility in experiments at high AK2 concentrations (>2.5 μg/mL) such that GPIb-VWF interactions are completely inhibited. The amount of adhered platelets was less than 5% of that in control cases.
GPIIbIIIa-VWF interaction is considered irreversible in our analysis (Eq. 2) because of its long lifetime compared to the duration of our experiments (<30 s). This assumption is supported by the results of ReoPro experiments to be discussed later. We found that the rate of platelet detachment (Koff) does not change significantly with ReoPro dosage. Therefore, the detachment of platelets is dominated by breaking GPIb-VWF bonds.
In all platelet adhesion experiments, extra care was taken to prevent platelet activation because activated platelets undergo a conformational change, and the resulting shapes are difficult to model. In addition, platelet activation triggers platelet aggregation, which is beyond the scope of this study at the single-platelet level. Platelet activation levels before perfusion were less than 5% as quantified by p-selectin expression levels (see Supporting Materials and Methods for the flow cytometry method). The addition of AK2 or ReoPro did not induce platelet activation either. During our experiments, platelets remained discoidal with no obvious change in shape, and thus we assume neither GPIb-VWF nor GPIIbIIIa-VWF interactions are affected by platelet preactivation within our system.
Finally, we assume GPIb and GPIIb receptors are distributed homogeneously on platelet surfaces. We further assume that AK2 and ReoPro reduce receptor densities in a uniform fashion. Recent studies reveal that GPIb receptors undergo shear-induced clustering (34), which contradicts this assumption of homogeneity. The clustering effect could be another mechanism for shear-enhanced platelet adhesion and is not considered in our model and analysis.
Data analysis
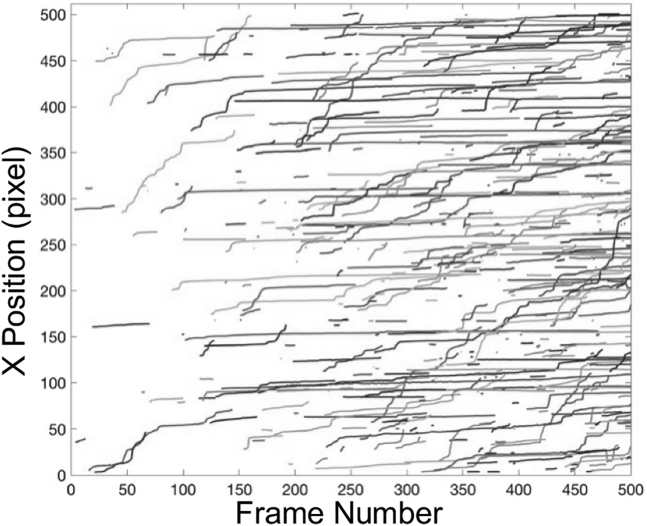
The stack of images from each experimental run was analyzed in MATLAB (The MathWorks, Natick, MA) using an existing algorithm (35) to extract useful information about platelet motion. The trajectories (flow direction, x vs. t) of individual adhered platelets are shown in Fig. 3. After initial adhesion, platelets continue to move along the flow direction in a stop-go motion, i.e., translocation. Some platelets slow down and become stationary, whereas others eventually detach from the VWF-coated surface.
Figure 3.
Sample platelet tracks obtained from one experimental run at standard operating conditions. Only 20% of the total number of platelet tracks (randomly selected and colored) are shown. Colored sample tracks for other operating conditions can be found in Fig. S1.
We denote the instantaneous number of adhered platelets in the viewing window as Nplatelet, which can be further characterized as transiently adhered platelets Nplatelet,1 and stably adhered platelets Nplatelet,2 depending on whether they eventually detach from the surface. We denote the cumulative number of adhered platelets at a particular time, i.e., the total number of platelet tracks that have appeared in the video so far, as Ntrack. Platelet tracks obtained from image analysis contain not only actual platelet tracks that first appear inside the viewing window but also extra tracks because of platelets rolling into the viewing window. By assuming a homogeneous distribution of adhered platelets in the vicinity of the small viewing area, Nplatelet does not need to be corrected. However, Ntrack is corrected by a factor ω. We consider a square area equaling one-fourth of the area of the viewing window located at the center and calculate the fraction of platelets rolling into this small square among all tracks in this area. We use this ratio to estimate ω. Because of the slow translocating speed of platelets, we do not consider the possibility of platelets rolling into the viewing window and eventually rolling out of the viewing window.
The process of platelet adhesion involves reversible and irreversible reactions which are approximated in previous computational models (21, 25). Based on these studies, we use the following differential model to estimate the rate constants at the platelet level from experimental measurements of Ntrack and Nplatelet:
| (3) |
| (4) |
| (5) |
and
| (6) |
Kon is commonly referred to as the adhesion rate and is by convention defined with respect to the bulk platelet concentration. N0 is set to the product of the measured bulk platelet concentration (∼150,000–450,000/μL) and the controlled volume (30 mm × 2 mm × 25 μm). Koff is the detachment rate or the inverse of the translocation lifetime. Kon,2 is the rate of stable adhesion due to the irreversible GPIIbIIIa-VWF binding.
The integration of Eqs. 3, 4, 5, and 6 results in unknown constants that can be set using proper initial conditions. Because of the experimental setup, there always exists a time lag Δt such that Nplatelet > 0 at t = 0. Therefore, we use the conditions Ntrack = Nplatelet,1 = Nplatelet,2 = Nplatelet = 0 at t = −Δt to obtain the integrated rate equations as follows:
| (7) |
| (8) |
| (9) |
and
| (10) |
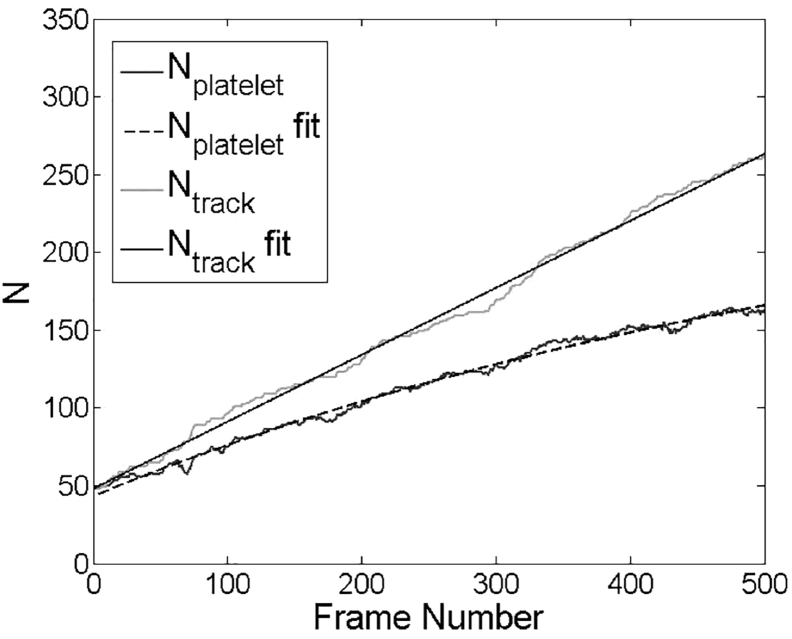
These integrated equations can then be used to fit experimental data as shown in Fig. 4 using MATLAB (The MathWorks). Equation 7 is first used to fit Ntrack versus t data and calculate Kon and Δt. To ensure a linear growth of Ntrack due to single-platelet adhesion, we use first 200 frames of images for this first step of fitting. Equation 10 is then used to fit Nplatelet versu t up to 500 frames and calculate Koff and Kon,2. The three macroscopic rate constants Kon, Koff, and Kon,2 can therefore be determined uniquely.
Figure 4.
Number of platelets (Nplatelet, lower) in the image viewing window and number of total platelet tracks (Ntrack, upper) versus t, with fitted lines according to Eqs. 7, 8, 9, and 10.
Mathematical modeling
Governing equation
Based on our previous studies (13, 14), the number density of platelets nP in flowing blood can be written as a function of z and t in the following form because of the combined effects of hydrodynamic fluxes FCP and FPP and near-wall adhesion reactions R:
| (11) |
The hydrodynamic fluxes FCP and FPP are written in Boltzmann-like form to account for binary shear-induced hydrodynamic collisions between a red blood cell and a platelet (FCP) or two platelets (FPP) in Eqs. 12a and 12b (13, 14):
| (12a) |
| (12b) |
To account for platelet adhesion onto channel walls (R), we define the number densities of transiently adhered nP,s1 and stably adhered platelets nP,s2. We assume that the difference between nP,s1 (measured as Nplatelet,1) and nP,s2 (measured as Nplatelet,2) is dependent upon the creation of irreversible GPIIbIIIa-VWF bonds. The summation of these two quantities yields the concentration of adhered platelets nP,s. Note that nP,s1, nP,s2, and nP,s are surface concentrations instead of volume concentrations defined for nP and nC (red blood cell). The rate equations linking platelets in flowing blood to platelets adhered to channel walls can thus be written as
| (13) |
| (14) |
and
| (15) |
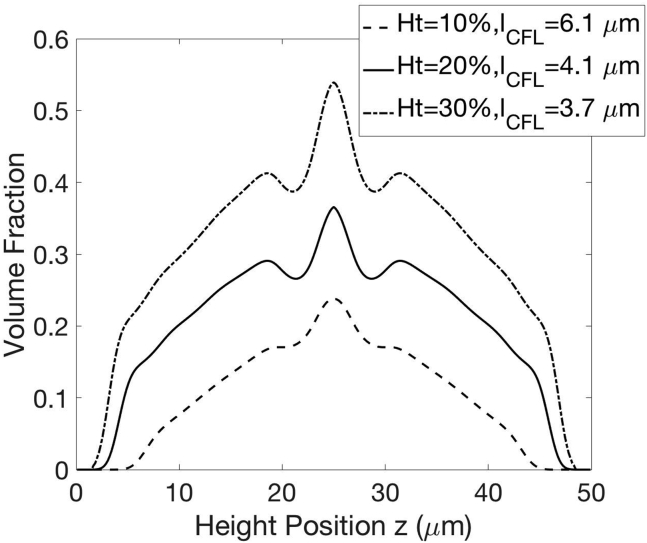
Our goal is to solve nP(z, t), nP,s1(t), and nP,s2(t). In our previous studies (13, 14), we considered the case of no adhesion reactions (R = 0, nP,s1(t) = 0, nP,s2(t) = 0). The red-blood-cell concentration nC was determined based on the balance between shear-induced diffusion due to two cell interactions similar to Eq. 12a and a hydrodynamic lift due to red blood cells’ deformability. We determined these hydrodynamic contributions from small-scale simulations using the boundary integral method (11). Our coarse-grained model is therefore more computationally efficient than full-scale simulations, as we have discussed elsewhere (13). The resulting concentration distributions of red blood cells nC and platelets nP have been verified with whole-blood simulations and show nonmonotonic variation with the cross-flow position z, mainly due to the complex shapes of red blood cells in pressure-driven flow. The decoupling of red-blood-cell migration from platelet motion enables us to quickly evaluate the influence of platelet properties on adhesion dynamics without repeating the calculation for red blood cells. In this study, the model inputs in Eqs. 12a and 12b corresponding to hydrodynamic contributions are set to values determined in our previous studies (13, 14). The red-blood-cell concentration distribution nC(z) is set to its steady-state value at a given hematocrit (Fig. 5). We assume platelets are fully marginated before adhesion and nP at t = 0 is thus set to its steady-state value at a given hematocrit when R = 0 (13). nP,s1 and nP,s2 are set to 0 at t = 0.
Figure 5.
Red-blood-cell concentration profile and cell-free layer thicknesses at varying hematocrits, .
In addition to the hydrodynamic contributions defined above, various quantities in Eqs. 13, 14, and 15 are related to GPIb-VWF and GPIIb-VWF binding kinetics and will be explained in Binding Model. We use a finite volume scheme to solve Eq. 11, and the numerical method is similar to our previous time-dependent study on platelet margination (14).
Binding model
A summary of key variables that appeared in Eqs. 13, 14, and 15 is provided in Table 1. Their values are chosen to match the corresponding average values for healthy platelets. As mentioned before, the units of nP,s and nP differ by one length scale. Because only platelets within the proximity of top and bottom channel walls are able to interact with VWF, we impose a cutoff distance L for platelet adhesion. It is defined with respect to the platelet’s center of mass and equals the platelet radius aP plus l, which is the cutoff bond formation distance. The size of VWF is O(100 nm) and is much bigger than the sizes of GPIb and GPIIbIIIa receptors (∼7 nm). Therefore, we approximate l using the VWF size. It is well known that VWF undergoes a conformational change from a globular form to an extended form under flow shear (9, 36). The shape change has been well characterized for freely flowing VWF for a wide range of flow rates and hematocrit conditions (36), but little information is known for tethered VWF, which is expected to elongate more easily (37). According to the measurement by Siedlecki et al. for tethered VWF (38), l is estimated to be 373 nm at a shear rate of 3300 s−1 and reduces to 149 nm in a globular form in a quiescent fluid. Based on the limited information available, we assume (nm), where is the dimensional characteristic shear rate (s−1). This linear correlation is a crude approximation, and mechanisms such as the internal association are not accounted for (36). For the control case of 1500 s−1, l is calculated to be 251 nm, which is between previous estimates of 200 nm (21) and 280 nm (12) used in similar computational models and agrees with experimental estimates of ∼150–400 nm (37). The resulting L is 1.7 μm, which is smaller than the cell-free layer thickness (>3.6 μm).
Table 1.
Summary of Variables in the Binding Model
| Variables | Description | Method |
|---|---|---|
| L | reactive distance | literature (38) |
| α, β | receptor density | literature (6, 39) |
| molecular-level kinetic constants | literature (7, 12, 42) | |
| reactive area fraction | BEM simulations | |
| ξ | height distribution of adhered platelets | BEM simulations |
BEM, boundary element method.
α and β are the numbers of GPIb and GPIIbIIIa receptors per platelet and are assumed to be homogenously distributed. Unless noted otherwise, α is set to 25,000 (6) and β is chosen to be 50,000 (39). kon is the binding rate between a single GPIb and VWF. kon versus loading force F has been measured using an optical tweezer by Kim et al. (7). They extrapolated the following correlation (lower loading, state 1): . The loading force can be related to the extension of VWF (40). At maximal bond formation distance l, the force experienced by the VWF before binding is estimated to be 8.6 pN at 1500 s−1, assuming 12 VWF monomer units. The exact conformation of wall-tethered VWF in our experiments under appropriate flow conditions is unknown. If we assume that the bond length, i.e., the VWF size, is equal to the distance (z) between a point on the platelet surface and the channel wall, kon is a function of z, and we refer to this as the first binding scenario. Alternatively, we can assume that the bond length always equals l at a given shear rate and is thus independent of z. We refer to this as the second binding scenario. Because kon decreases with the elongation force and thus the bond length, the minimal value of kon is obtained at the maximal bond length l, and therefore the first scenario always has a higher binding rate. We will present results for both binding scenarios. Our calculated kon values based on experimental measurement are ∼0.01/s and are smaller than those used in previous computational models (21). We will discuss the consequences of using different binding models and values for kinetic constants in our discussion in Effects of AK2, Hematocrit, Shear Rate, and ReoPro on Adhesion Rate Constants and Sensitivity Analysis.
The rate κoff for platelets detaching from VWF-tethered surfaces in Eq. 14 is not to be confused with the dissociation rate of GPIb-VWF bonds koff. In fact, κoff depends on the competition between forming new bonds (kon) and breaking existing bonds (koff). In the limit of abundant VWF bonds, the detachment rate κoff can be approximated analytically (41):
| (16) |
and
| (17) |
In the expressions above, nα is the number of GPIb-VWF bonds and pn(t) is the probability of having nα bonds at time t. The probability of detachment within time t thus corresponds to p0(t). We refer to single-molecule measurement of bond dissociation rate koff (42), which first shows a decrease with tensile force F (<20 pN) and then increases with F (catch-slip-bond behavior). Other experimental studies report slip-bond or flex-bond (two slip-bond states) behaviors of GPIb-VWF binding (7). In our simulations as well as in previous studies (21), the loading force on a GPIb-VWF bond exceeds 20 pN as a result of balancing the hydrodynamic drag on a platelet. This loading force is much greater than the force experienced by an unbound VWF. In this high loading regime, it is agreed among various studies that koff decreases with F (slip bond). koff is estimated to be O(1 s−1), consistent with values used in previous models (21). Both kon and koff in Eq. 17 are functions of z. Therefore, we also need to estimate a height z at which the platelet reenters the flow. This height cannot be a single value, which may cause numerical instability. From simulations of adhered platelets, we approximate a normal distribution ξ(z) for the height with an average κoff. Molecular-level measurement of GPIIbIIIa-VWF binding is limited (43). Because of the lack of data suitable for our model, we assume kon,2 = 0.01kon based on previous modeling studies (12). For simplicity, we estimate an average rate of GPIIbIIIa-VWF binding based on boundary integral simulations.
Aα(z) is the area fraction of a platelet in flowing blood that is within the reactive distance l whose center of mass is at height z. This quantity is related to the very first GPIb-VWF binding event and thus results in platelet (transient) adhesion. We determine Aα from boundary integral simulations detailed in Model Inputs: Boundary Integral Simulations. Once the platelet is adhered, the average platelet effective reactive area increases, and we again estimate an average effective area fraction from boundary integral simulations. This quantity describes the configuration of transiently adhered platelets and is relevant for the first GPIIbIIIa-VWF binding event that leads to stable platelet adhesion.
With all kinetic constants determined, we can write down the expressions for Kon, Koff, and Kon,2 using model parameters as follows:
| (18) |
| (19) |
and
| (20) |
These platelet-level rate constants can therefore be compared with those obtained from experimental measurements for verification. According to our model, Koff and Kon,2 are independent of time and can be readily calculated based on boundary integral simulations. Kon is a time-dependent variable based on the concentration of platelets in flowing blood nP, which changes with time because of adhesion reactions.
Model inputs: Boundary integral simulations
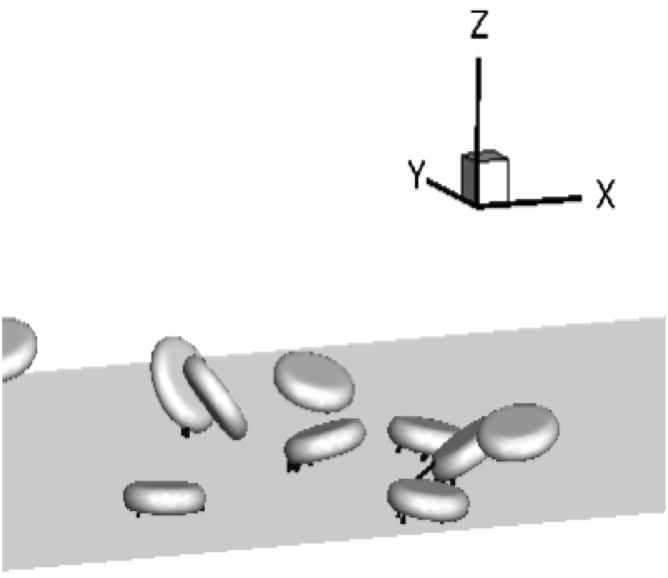
To understand the dynamics of platelets in flowing blood, we performed simulations of red blood cells and platelets in channel flow which match experimental flow conditions as shown in Fig. 6. Our simulation method is adopted from existing studies (11, 12). All key parameters used in our simulations are summarized in Table 2. The deformability of red blood cells is modeled using the Skalak law (44). Platelets are modeled as rigid oblate spheroids with a 1:4 aspect ratio. Therefore, we fully account for the presence of red blood cells instead of making approximations (21) or completely ignore them (19). Because of the low concentration of platelets, the size of the computation domain needed to contain enough platelets for statistical significance is large. In addition, the slow rate of reactions makes it difficult to simulate the entire process of a single-platelet adhesion within reasonable computation time. These challenges make it necessary for us to wisely choose our simulation setup to extract useful information that can be used in our model.
Figure 6.

Snapshot of simulating freely flowing platelets inside the cell-free layer. Only the near-wall region is shown; Ht = 30%, Ca = 0.75 ( s−1).
Table 2.
Key Parameters Used in Simulations for RBCs and PLTs
| Parameter | Scaled Units | Physical Units | Description |
|---|---|---|---|
| a | 1 | 2.82 μm | RBC equivalent radius |
| aP | 0.5 | 1.41 μm | PLT radius |
| Lx | 32 | 90.24 μm | |
| Ly | 9 | 25.38 μm | |
| Lz | 17.73 | 50 μm | |
| μ | 1 | 1.2 cP | plasma viscosity |
| 1 | ∼500–2000 s−1 | ||
| ES | 2000/ | 6.8 μN/m | RBC shear modulus |
| ED | RBC dilatational modulus | ||
| EB | 3.3 × 10−3a2ES | RBC bending modulus | |
| ν | 0.65 | RBC reduced volume | |
| λ | 1 | RBC viscosity ratio | |
| Ca | ∼0.25–1 | capillary number |
PLT, platelet; RBC, red blood cell.
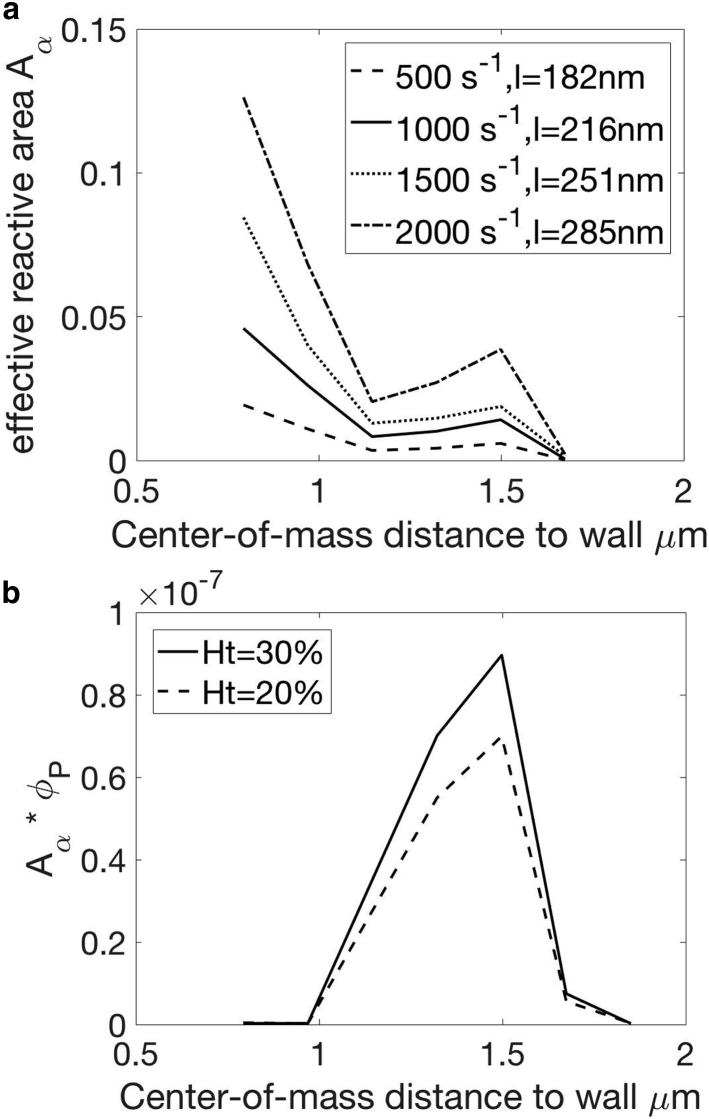
We assume that at a volume fraction exceeding its actual value (ϕP = 2%), platelets are still dilute enough such that they do not interact with each other once adhered. Therefore, we can increase the density of platelets in our simulations for computational efficiency. A simulation video is provided in the Supporting Material (Video S2). We perform two sets of simulations to obtain model inputs Aα(z), , and ξ, with the channel height matching a 50 micron channel (Lz) used in our experiments. We set the hematocrit to 30%, and red blood cells are assumed to be fully migrated. In the first set of simulations, we are interested in freely flowing platelets before forming any GPIb-VWF bonds as shown in Fig. 6. The center-of-mass positions of platelets are chosen randomly between aP/4 (short axis of the platelet) and L. The orientation angles of platelets are chosen randomly as well. At each time step, we record the center-of-mass z of each platelet and its corresponding effective area Aα within the bond distance l. Each simulation lasts for at least 400 dimensionless time and is repeated until the Aα vs. z correlation converges (Fig. 7 a). Because l depends on the shear rate, i.e., capillary number when ES is constant for healthy red blood cells, we performed simulations at various shear rates.
Figure 7.
Results from simulations of freely flowing platelets. (a) Average Aα vs. z at various shear rates, corresponding to different cutoff bond formation distance l, is shown. (b) The product of Aα and ϕP as a function of z— ϕP = 0.5%, Ca = 0.75 (1500 s−1)—is shown.
Ht = 30%, only platelets near one wall are shown.
Results obtained from our simulations are shown in Fig. 7. We observe the tumbling motion of platelets near the wall (24). Aα is maximal when the platelet’s center of mass is 1.5 μm from the wall, which is slightly bigger than the platelet radius (1.4 μm). The location of this maximal peak agrees with previous observations that platelets undergo modified Jefferey orbit motion when located at least 1.2 radii away from the wall (45). Similar to “Jefferey orbits” in unbound simple shear flow, the tumbling motion also depends on the shear rate. This change in tumbling frequency (45), along with the increase in l, contributes to the increase of Aα with the shear rate. As the platelet gets closer to the wall, its tumbling motion is hindered and Aα decreases. When the wall distance drops below 1.2 μm, tumbling motion is completely suppressed, and the platelet undergoes wobbling motion with its two long axes (radii) almost parallel to the wall. Aα thus increases again. The product of Aα and ϕP (Fig. 7 b) is proportional to the rate of adhesion at position z. Even though Aα is very high when z < 1.2 μm, the concentration of platelets is very low in this region, and so is the product of these two quantities.
In the second set of simulations, we study transiently adhered platelets and investigate their dynamics before either detachment or the formation of GPIIbIIIa-VWF bonds for stable adhesion as shown in Fig. 8. GPIb-VWF bonds are modeled as Hookean springs with a spring constant of 10 pN/nm (19). The equilibrium length is 149 nm (38). The kinetic constants kon and koff are specified as in Binding Model. Platelets are initialized with configurations similar to the freely flowing case, with the addition of one GPIb bond chosen at a random position on platelet surface within l. At each time step, in addition to Aα and z, we also record nα as the number of GPIb-VWF bonds and lα as the average GPIb-VWF bond length for every platelet.
Figure 8.
Snapshot of simulating transiently adhered platelets. Only platelets and GPIb-VWF bonds are shown; Ht = 30%.
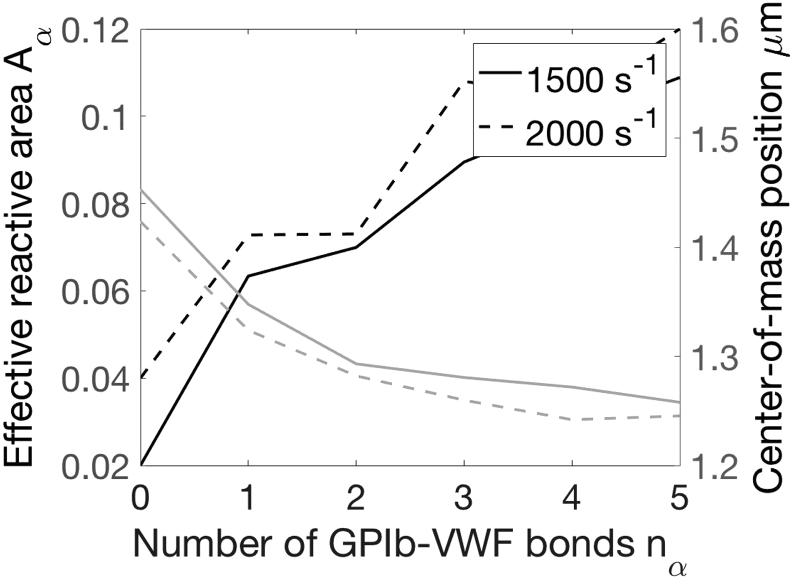
Based on our observations, once platelets are adhered, i.e., nα > 0, the bond spring force increases to balance the drag force on the platelet and slows the flowing platelet (Fig. 9). As a result, adhered platelets not only are pulled closer to the wall but also orient such that their two long axes align with the flow direction. Aα thus triples even when only one bond is formed. The increase of the reactive area upon initial adhesion has not been discussed in previous literature and is important for accelerating subsequent binding reactions. This increase of Aα and the decrease of the center-of-mass distance to the wall (z) saturate as multiple bonds are formed (nα > 6). At this time, platelets lose their freedom to move and become less sensitive to the breakup and formation of a single bond. Because the wall shear rate influences the fluid drag experienced by adhered platelets, it also plays a role in the dynamics of adhered platelets.
Figure 9.
Effect of GPIb-VWF bond count on the effective reactive area (black) and the center-of-mass distance (gray); nα = 0 values are obtained from simulations of freely flowing platelets as shown in Fig. 7.
Platelet detachment is related to the nα = 1 stage. Therefore, we approximate κoff and ξ(z) based on the configuration of platelets with nα = 1 from our simulations. The formation of GPIIbIIIa-VWF bonds may occur at various nα values. The average area and height z for GPIIbIIIa-VWF binding is estimated as the average of Aα for an attached platelet over nα = 1,2,…6 GPIb-VWF bonds. This crude estimate can potentially be replaced with better approximations using more advanced techniques. However, because of the lack of accurate determination of kon,2 (Binding Model), we are limited in the overall estimation of Kon,2 and we choose to continue with this simple approximation.
Results and Discussion
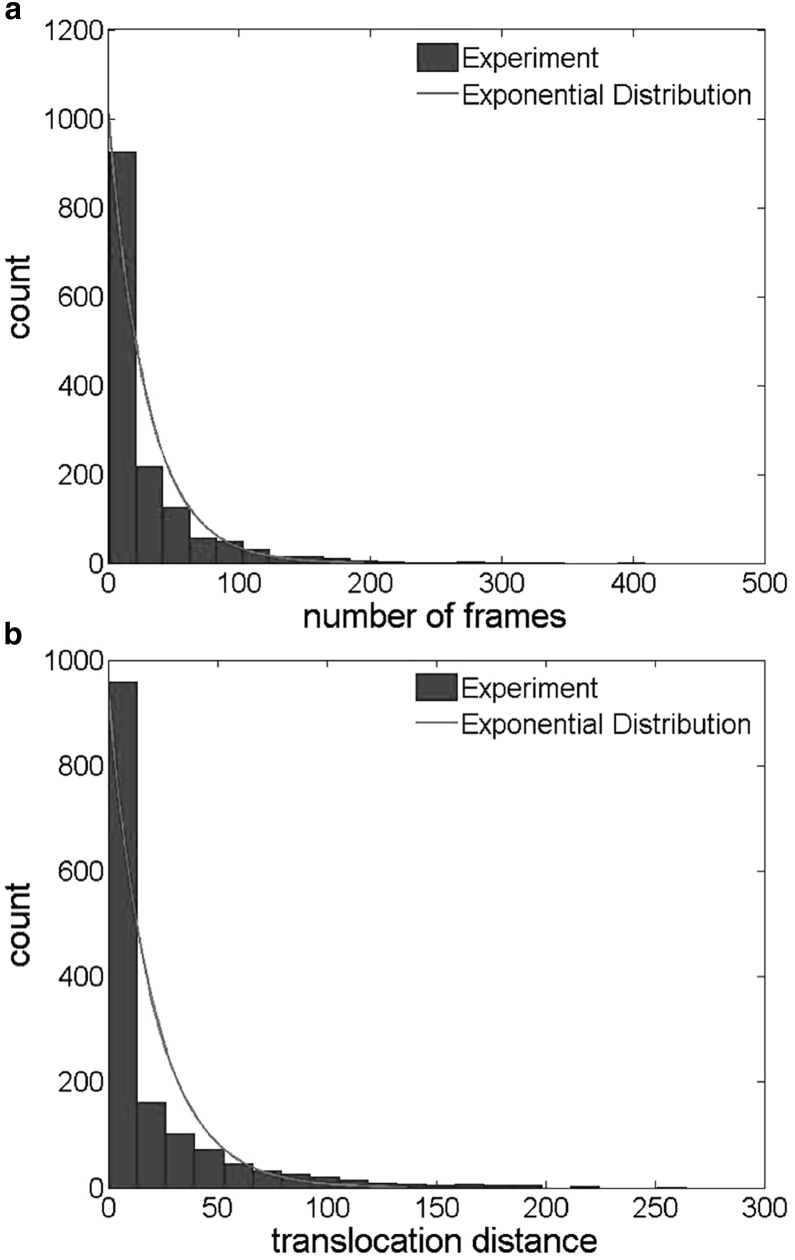
Experiments: Platelet translocation dynamics
As shown in Fig. 3, transiently adhered platelets undergo stop-go motion along the flow direction, commonly referred to as platelet translocation (20). In our rate equation (Eq. 4), we estimate Koff assuming that the process of platelet detachment is exponential in nature. We verified this assumption by plotting the histogram of platelet translocation lifetime as shown in Fig. 10 a, which indeed follows an exponential distribution. The rate constant fitted from this exponential distribution Koff, i.e., the inverse of translocation lifetime, is equivalent to Koff fitted from Eq. 10. In addition to translocation lifetime, previous studies reported that the translocation distance also follows an exponential distribution (21). We plot our experimental results in Fig. 10 b, which shows a near-exponential distribution.
Figure 10.
Sample distributions from one experimental run showing (a) translocation lifetime at 19 frames/s and (b) translocation distance (pixel).
The discussion above justifies using Eqs. 7, 8, 9, and 10 to approximate the rate constants for single-platelet adhesion. As shown in Fig. 4, although Ntrack grows linearly with time, the increase of Nplatelet slows until the number of transiently adhered platelets reaches a steady-state balance with the number of platelets in the flowing blood available for binding. For control cases at standard operating conditions (N = 13), we calculated Kon, Koff, and Kon,2 to be 0.07 ± 0.02, 0.16 ± 0.03, and 0.48 ± 0.08 s−1, respectively. These constants are small compared to the characteristic shear rate (1500 s−1) and the frame rate (19 s−1). Although we cannot probe transient adhesion and detachment events lasting shorter than 0.05 s, we assume the resolution of our camera is high enough for us to calculate accurate rate constants.
Model: Evolution of platelet margination profile due to adhesion
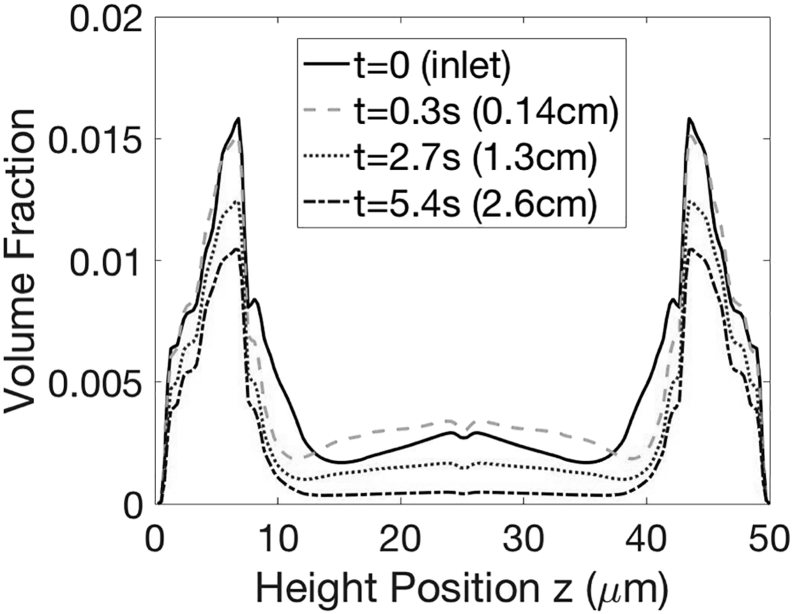
The concentration distribution of platelets in flowing blood at 30% hematocrit, solved according to Eq. 11, is shown in Fig. 11. The distribution of platelets in the cross-flow direction is governed by pairwise interactions between a red blood cell and a platelet in the cell-laden region and near-wall reactions between platelets and the tethered VWF. In addition, a weak platelet-platelet interaction exists inside the cell-free layer. As mentioned before, the concentration distribution of red blood cells differs from that of rigid particles and has unique nonmonotonic characteristics defined by the deformable cell membrane. Therefore, the concentration distribution of platelets also has a complex shape and cannot be approximated in any available analytical form to our knowledge. As binding reactions proceed, near-wall platelet concentration decreases. Platelets away from the wall, especially those near the edge of the cell-free layer, move toward the wall to replenish the reactive region. In our experimental setup, the inlet is always supplied by marginated platelets, and therefore the concentration profile remains fixed. Because of platelet adhesion, we expect the concentration profile to vary with the distance downstream. The difference between temporal variation and axial variation has been reconciled in our previous study (14), and the temporal evolution we predict with our model can be used to estimate the variation in the flow direction in experiments using the average platelet velocity in the flow direction uP. At 30% hematocrit and 1500 s−1 characteristic shear rate, the elapse time of 5 s in our model corresponds to 2.4 cm downstream and results in a 50% reduction in the concentration of freely flowing platelets compared to the inlet. However, the viewing window is 185 μm wide (x) in our experiments, and therefore the platelet concentration in flowing blood decreases by only 5% and drainage is not a concern. The corresponding Damköhler number is O(0.1). For a similar experimental setup, Fitzgibbon et al. (21) estimated the rate of platelets entering the cell-free layer at 20% hematocrit to be 0.2 s, which is greater than the rate of platelet adhesion and also suggests that the platelet adhesion is reaction limited. Because of the slow reaction rate compared to the flow rate and the platelet replenishment rate in the near-wall region, our governing equation for freely flowing platelets (11), which does not include axial variation, remains valid for our experimental setup. Because Kon depends on nP, which does not vary significantly during the experiment, we do not observe any axial variation in the adhesion kinetics.
Figure 11.
Model prediction of the temporal evolution of platelet concentration at 30% hematocrit after the induction of platelet-VWF binding at t = 0. Based on the average velocity in the flow direction of marginated platelets, the elapse of 1 s corresponds to 0.5 cm downstream in the experiments, Ca = 0.75 (1500 s−1). The concentration profile at the inlet is equivalent to the black solid curve (t = 0). The distance downstream corresponding to each time point is listed in the parenthesis.
The comparison of rate constants between the multiscale model and experimental measurements for the control case is shown in Table 3. These values we measured agree with previous estimations (21, 46). Because the hydrodynamic effects determining nP contain no fitting parameters and the binding model relies on literature values and various assumptions, we consider the agreement, for which the model predictions are less than twofold of the experimental values, to be good, especially for the estimation of Kon. In a previous model estimating the adhesion kinetics in the absence of flow (7), the model prediction is more than threefold the experimental measurement. In the constant kon model, kon is set to the smallest value, obtained at the maximal bond formation distance. Kon is always lower than the variable kon case (model 1). Koff, as a result of the competition between kon and koff, is therefore higher for model 2. Once adhered, platelets are pulled closer to the wall in model 2 because of longer bond formation distance. Kon,2 depends on the configuration of adhered platelets and is thus higher in model 2.
Table 3.
Comparison of the Platelet-Level Rate Constants between Experimental Measurements and the Multiscale Model for the Control Case
| Variables | Experiment (s−1) | Model 1 (Variable kon) (s−1) | Model 2 (Constant kon) (s−1) |
|---|---|---|---|
| Kon | 0.07 ± 0.02 | 0.07 | 0.039 |
| Koff | 0.16 ± 0.03 | 0.071 | 0.083 |
| Kon,2 | 0.48 ± 0.08 | 0.2 | 0.71 |
Error bars represent SD due to variation among several donors (N = 13).
We now move on to investigate the effects of platelet properties and flow properties using controlled variable studies (Controlled Variables). Because of the variation in rate constants measured among multiple donors, we will normalize all rate constants by those for control cases for each donor to demonstrate the effects of independent variables and compare our experimental results with model predictions.
Effects of AK2, hematocrit, shear rate, and ReoPro on adhesion rate constants
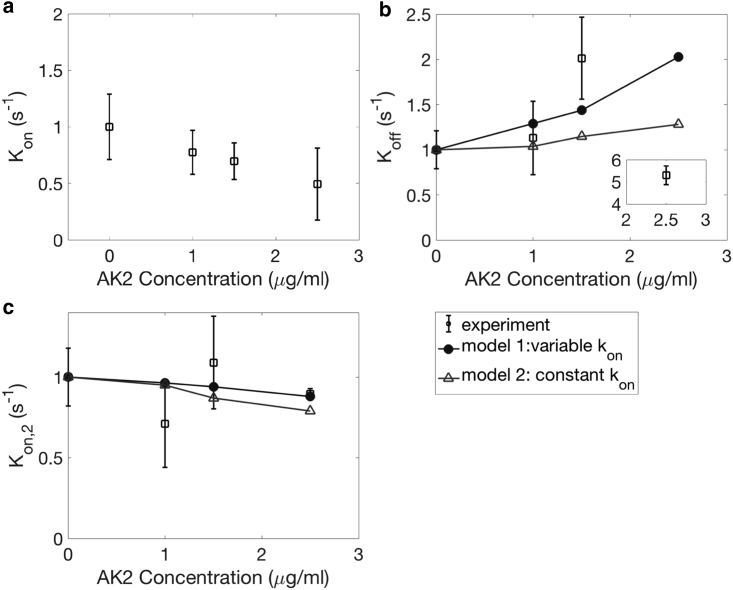
In our experiments, the effect of AK2 on platelet adhesion is demonstrated in Figs. 12 and S1 a. Compared to the control case, we observed a significant reduction in the number of adhered platelets and an increase in translocation velocity. The rate constants from our model and experiments are summarized in Fig. 12. In accordance with our experimental observations, the measured value of Kon decreases with AK2 concentration in a nearly linear manner. In our model, we consider the effect of AK2 as reducing α, which causes a change in the simulations of adhered platelets. We do not know a priori the percentage of reduction in GPIb receptor densities due to drug inhibition at a given dosage. Therefore, we estimate the percentage of reduction in GPIb receptor density α at a given AK2 dosage based on the experimental measurement of Kon as shown in Fig. 12 a, and we use this correlation in our model for the estimation of Koff and Kon,2. The reduced α-value is still large enough that Eqs. 16 and 17 are valid. In addition, Koff increases with AK2 dosage. As platelets are transiently adhered, they are less likely to form subsequent bonds because of the reduction in α. This reduction in the bond formation rate is related to platelet detachment according to Eq. 17. In our experiments, Kon,2 does not show a significant change, consistent with no visible differences for stably adhered platelets. Our model predicts a weak decrease of Kon,2 because the configuration of adhered platelets with fewer GPIb receptor binding sites is less favorable for slowing down platelets for stable adhesion, i.e., the platelets are less “sticky.” Our findings can thus help to understand the mechanism of Bernard Soulier syndrome, which is a bleeding disorder due to a deficiency in the number of GPIb receptors (47).
Figure 12.
The effect of AK2 dosage on Kon (a), Koff (b), and Kon,2 (c). N = 5 donors, repeated three times per donor. Error bars represent SD.
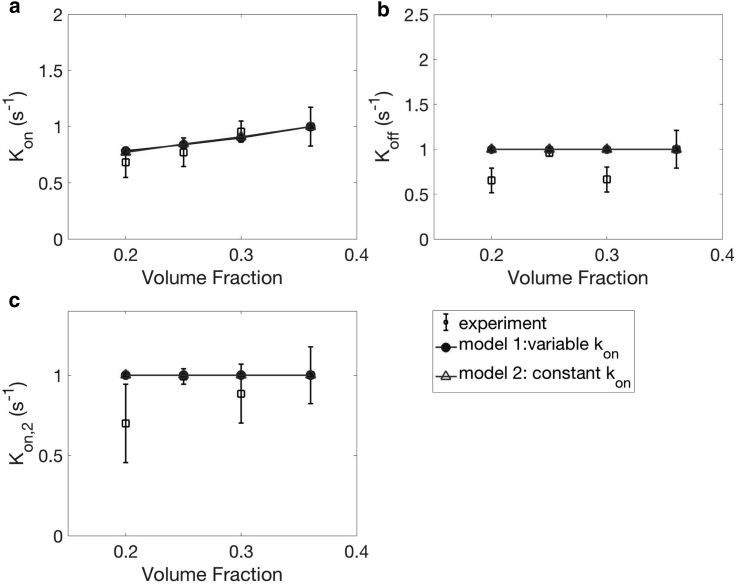
Similar to the case of AK2, we also observed a reduction in the number of adhered platelets when hematocrit is reduced in our experiments (Fig. 13; Fig. S1 b). In our model, the hematocrit influences cell-platelet collisions (FCP) and the initial platelet concentration distribution nP(t = 0) in Eq. 11. Unlike the AK2 case, however, we did not observe any significant changes in Koff or Kon,2, which is consistent between experiments and our model. If we examine individual platelet tracks (Fig. S1 b), they look similar to those under standard operating conditions (Fig. 3). This confirms the role of red blood cells on influencing the near-wall concentration of platelets but not directly on platelet adhesion. In our model, an increase in hematocrit results in platelets being more concentrated and closer to the walls because of the reduced cell-free layer thickness. To save computation time, we did not simulate freely flowing platelets at varying hematocrits, i.e., the hematocrit is fixed at 30%, which may contribute to the slight discrepancy between our model and experiments in Fig. 13 a. The hematocrit does not alter platelet properties such as kon, koff, α, β, Aα, and . Once adhered, platelets only feel a weak influence of red blood cells located far from the reactive region. Because Koff and Kon,2 are defined in terms of nP,s1, the theoretical results do not show any variation. The influence of hematocrit on platelet adhesion that we discuss in this section can explain the clinical findings of how bleeding time is related to the hematocrit level (17). Because red blood cells do not influence platelet functions directly, we expect subsequent reactions after single-platelet adhesion to be less sensitive to the hematocrit. Thus, we believe our model captures most of the effect of hematocrit on bleeding.
Figure 13.
The effect of hematocrit on Kon (a), Koff (b), and Kon,2 (c). N = 7 donors, repeated three times per donor. Error bars represent SD.
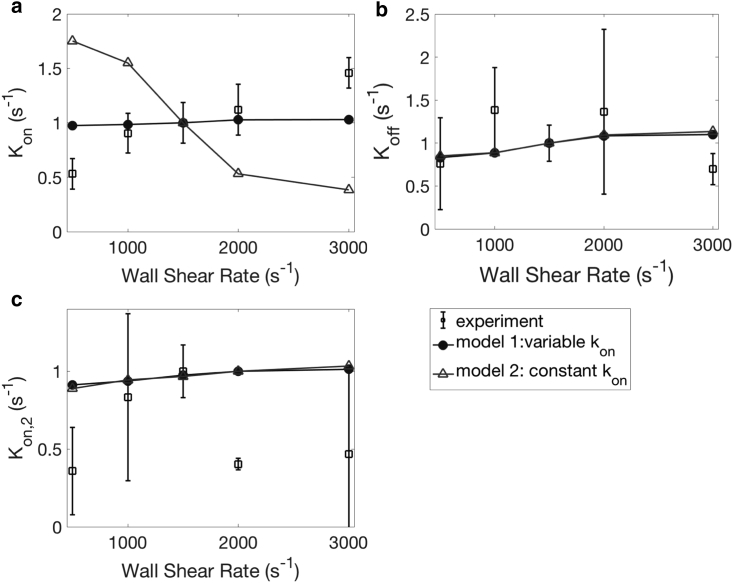
The effect of shear rate is demonstrated in Figs. 14 and S1 c. In our experiments, we observed that Kon increases weakly with the shear rate. The trends of Koff and Kon,2 are less clear. It is worth pointing out that the range of shear rates that we investigate is smaller than those in previous experimental studies (up to 5000 s−1) (48). Such high shear rates are seen in stenosed arteries, and the effect of shear rate is more dramatic. In addition to GPIb, it is known that other platelet surface receptors can also interact with VWF. We chose our shear rate to be within the physiological range such that GPIb-VWF interactions dominate, and platelet activation is prevented. Unlike previous cases where the two models of kon give similar qualitative trends, we see distinct trends of Kon versus shear rate (Fig. 14 a) here. The variable-reaction-rate model (model 1) captures the increase of Kon with shear rate seen in experiments, whereas the constant kon model shows a decrease in the rate of adhesion. The shear rate manifests itself in various aspects of platelet adhesion. For the healthy red blood cells that we consider in our study, the effect of the shear rate is equivalent to the effect of the capillary number (Ca) defined in Table 2. For Ca ≥ 0.5, red blood cells are in the tank-treading regime and have saturated shapes at steady state (11). We anticipate that shear-induced diffusion of platelets due to platelet-cell hydrodynamic collisions (FCP) does not change significantly and the platelet distribution nP(z) in Eq. 14 is not affected by the shear rate. On the other hand, for a fixed z, Aα increases weakly with the shear rate because of the change in tumbling dynamics (45) and an increase in l, as shown in Fig. 7 a. kon decreases with the spring force based on existing studies (7) and thus decreases with z. The combined effects of these factors result in different trends in Kon(z) depending on the binding model used. We observe an increase in Koff for both binding models. In addition to the change in kon with the shear rate, koff also increases. As a result, κoff increases, which is not obvious in the experiments. We observe a weak increase in Kon,2 with the shear rate as well, which can be explained using a similar argument as the AK2 case because of the change in configuration of transiently adhered platelets. More experimental runs are needed to reduce uncertainties and achieve a quantitative comparison.
Figure 14.
The effect of shear rate on Kon (a), Koff (b), and Kon,2 (c). N = 7 donors, repeated three times per donor. Error bars represent SD.
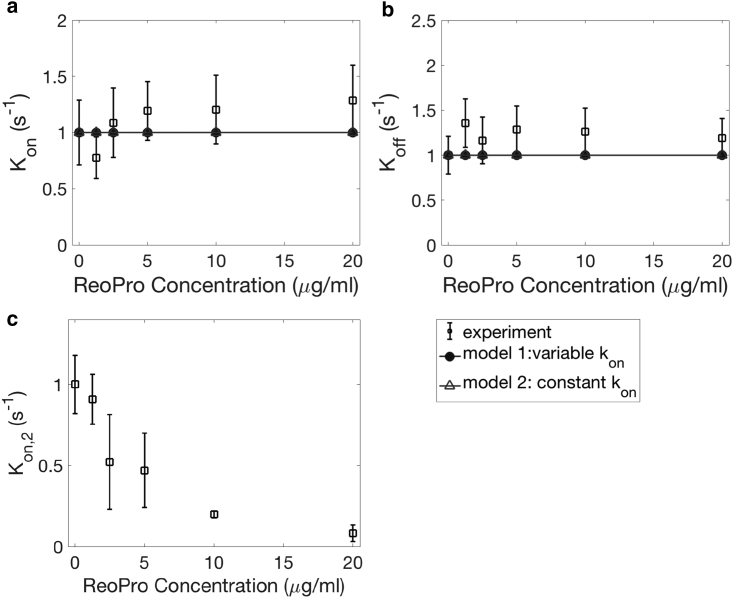
Unlike the previous three cases in which the independent variables influence platelet adhesion from an early stage as indicated by the number of adhered platelets, we do not see the effect of ReoPro until approaching the end of the experiments, as shown in Fig. S1 d. As time progresses, we observed a significant increase in the fraction of translocating, i.e., moving platelets. As a result, Kon,2 decreases with increasing ReoPro dosage, whereas Kon and Koff remain unchanged. Similar to the case of AK2, we vary β in our model to study the effect of ReoPro as shown in Fig. 15. We predict no change in Kon or Koff based on Eqs. 18 and 19. Kon,2, however, decreases based on Eq. 20. Again, the degree of reduction in β is estimated based on ReoPro experiments (Fig. 15 c) because Kon,2 is directly proportional to β. GPIIbIIIa deficit is associated with Glanzmann’s throbasthenia (49). Our findings can thus indicate the consequence of this bleeding disorder.
Figure 15.
The effect of ReoPro on Kon (a), Koff (b), and Kon,2 (c). N = 5 donors, repeated three times per donor. Error bars represent SD.
Sensitivity analysis
The accuracy of our model depends on the approximation of several variables, which are subject to a variety of errors. As mentioned previously, the hydrodynamic contributions contain no fitting parameters. The margination profile of platelet concentration has been verified against various experiments (13), and the comparison is limited by the resolution of experimental measurements. On the other hand, the kinetic information is extracted from either existing studies or boundary integral simulations. Whether these quantities are applicable to our model and experiments remains unknown. For example, we consider fixed values of α = 25,000 and β = 50,000 in our model. Their actual values vary from person to person. We measured GPIb and GPIIbIIIa counts for four blood donors using flow cytometry (Biocytex, Marseille, France, Table S1), and the measured GPIb count α differs from the α value in our model by up to 50%. It is worth considering the validity of using a fixed value in the model rather than a distribution for a select parameter, which may be a more realistic representation of the parameter value.
To evaluate the effects of these uncertainties, we perform a sensitivity analysis as summarized in Table 4. We choose to analyze the effects related to GPIb-VWF interactions that are most representative of our model sensitivity and to which sources of error can be traced. Variables such as β are not analyzed because the effects are similar to α according to Eqs. 18 and 20. By varying a select parameter symmetrically about the value used for the control case in our model, we evaluate the change in Kon and Koff. If the resulting variation is no longer symmetric about the original value, we also vary the select parameter as the weighted average of the upper bound (25%), mean (50%), and lower bound (25%) and calculate the resulting rate constants. This method measures the deviation due to a distribution of parameter values instead of a single value.
Table 4.
Sensitivity Analysis for the Mathematical Model Evaluated at Standard Operating Conditions
| Variable | Variation | Kon | Koff | Source of Error |
|---|---|---|---|---|
| α | ±50% | ±50% | ∼−36%–56% (5%) | individual differences (Table S1) |
| kon | ±50% | ±50% | ∼−36%–56% (5%) | SM experiments (7) |
| Aα | ±5% | ±5% | ∼−4%–5% | BEM simulations |
| κoff | ±5% | ND | ±4% | SM experiments (42) |
| L | ±10% | ∼−6%–2% (−1%) | ND | SM experiments (38), variable kon |
| ∼−54%–46% (−2%) | ND | SM experiments (38), fixed kon |
The percentage value listed in the parenthesis represents the change in mean rate constant when the variation about a select parameter results in asymmetric change in the rate constant, calculated from a weighted average of the upper bound (25%), mean (50%), and lower bound (25%) of the select parameter. ND, no data; SM, single molecule; BEM, boundary element method.
Quantities containing the largest uncertainty are α, kon, and L, which await more single-molecule measurements to accurately determine their values. The value of L can also be studied using novel simulations of wall-tethered VWF, similar to existing simulations of freely flowing VWF (36). Our model allows arbitrary binding models, and therefore kinetic variables can be updated based on the state-of-art measurements to re-evaluate platelet-level rate constants in future studies.
Conclusions
Using a combination of modeling and experimental approaches, we study the initial platelet adhesion onto vascular walls in channel flow, which signals the onset of clot formation and ultimately hemostasis and thrombosis. Although this process is mediated by platelet surface receptors GPIb and GPIIbIIIa interacting with wall-tethered VWF, multibond kinetics and the blood-flow environment also play critical roles. We build a multiscale model that accounts for these various factors and is thus more complete than previous lower-order models. Instead of studying a single controlled variable, the complementary microfluidic experiments systematically investigate the effects of shear rate, hematocrit, and GPIb and GPIIb receptor densities using a coherent strategy. In addition to qualitative observations which are consistent with previous findings, we characterize the adhesion dynamics in terms of multiple rate constants. The agreement between our model and experimental results, though semiquantitative, shows the feasibility of using both kinetic and mechanical information to fundamentally understand the process of platelet adhesion from a molecular level.
The results of this investigation provide new, to our knowledge, insights in the initial steps of platelet adhesion. We conclude that fluid dynamics manifests itself in almost every aspect of platelet adhesion. Bond-level kinetics are force dependent and thus are sensitive to fluid drag, which changes with the shear rate. Depending on the assumptions made for binding, different trends are observed for the platelet adhesion rate at varying shear rates. Near-wall platelets undergo wall-hindered tumbling motion (modified Jefferey orbit) due to blood flow, which influences the reactive area of freely flowing platelets forming initial contact with the wall. As the platelet becomes adhered to the VWF-tethered wall, the balance between the bond force and the drag force becomes the new mechanism governing the platelet motion and results in an increase in the reactive area. Finally, the near-wall concentration of platelets is largely influenced by the distribution of red blood cells, which are the dominating species in the blood suspension. The effects of red-blood-cell migration and platelet margination can be explained by the deforming shapes of red blood cells due to fluid shear. Therefore, red blood cells also play a role in the initial steps of thrombosis and hemostasis. Thus far, we have only considered blood samples from healthy donors with flow conditions matching those in human arteriole vessels, but we can predict changes in the adhesion dynamics if any variables in the model are set to abnormal values. Such abnormalities may be associated with diseases, e.g., bleeding disorders, and thus giving clinical relevance to our model.
The novel, to our knowledge, coarse-grained model we have built is much more computationally efficient than large-scale whole-blood simulations because cell-platelet interactions are captured at the suspension level instead of the particle level. We fully account for the hydrodynamic effects of red blood cells, which is essential to accurately determine the near-wall platelet concentration. The sensitivity of this model is discussed, with the majority of uncertainties in the kinetic information referenced from single-molecule measurements. These uncertainties, along with assumptions we made in both our experiments and model, may be investigated in more detail in future studies to improve the model.
Author Contributions
Q.M.Q. is the first author, who designed the research and wrote the manuscript. Q.M.Q., E.D., and I.O. conducted experiments. I.S. performed image analysis. Q.M.Q. performed modeling study. A.J.R. and D.K. advised experimental setup (DPFA). E.S.G.S. is the principal investigator.
Acknowledgments
The authors acknowledge the support from Dr. Johnathan Cowman and Dr. Nigel Kent.
The authors acknowledge support from the US Army High Performance Computing Research Center and support from Stanford University’s Certainty computer cluster, which is funded by the American Recovery and Reinvestment Act of 2009 (grant number: W911NF07200271). Q.M.Q. is supported by Stanford Graduate Fellowship in Science and Engineering (SGF).
Editor: Mark Alber.
Footnotes
Supporting Materials and Methods, one figure, one table, and two videos are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(19)30111-0.
Supporting Material
References
- 1.Li Z., Delaney M.K., Du X. Signaling during platelet adhesion and activation. Arterioscler. Thromb. Vasc. Biol. 2010;30:2341–2349. doi: 10.1161/ATVBAHA.110.207522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gibbins J.M. Platelet adhesion signalling and the regulation of thrombus formation. J. Cell Sci. 2004;117:3415–3425. doi: 10.1242/jcs.01325. [DOI] [PubMed] [Google Scholar]
- 3.Weiss H.J., Hawiger J., Hoffmann T. Fibrinogen-independent platelet adhesion and thrombus formation on subendothelium mediated by glycoprotein IIb-IIIa complex at high shear rate. J. Clin. Invest. 1989;83:288–297. doi: 10.1172/JCI113871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Savage B., Saldívar E., Ruggeri Z.M. Initiation of platelet adhesion by arrest onto fibrinogen or translocation on von Willebrand factor. Cell. 1996;84:289–297. doi: 10.1016/s0092-8674(00)80983-6. [DOI] [PubMed] [Google Scholar]
- 5.Baumgartner H.R., Tschopp T.B., Meyer D. Shear rate dependent inhibition of platelet adhesion and aggregation on collagenous surfaces by antibodies to human factor VIII/von Willebrand factor. Br. J. Haematol. 1980;44:127–139. doi: 10.1111/j.1365-2141.1980.tb01190.x. [DOI] [PubMed] [Google Scholar]
- 6.Bergmeier W., Piffath C.L., Wagner D.D. The role of platelet adhesion receptor GPIbalpha far exceeds that of its main ligand, von Willebrand factor, in arterial thrombosis. Proc. Natl. Acad. Sci. USA. 2006;103:16900–16905. doi: 10.1073/pnas.0608207103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kim J., Hudson N.E., Springer T.A. Force-induced on-rate switching and modulation by mutations in gain-of-function von Willebrand diseases. Proc. Natl. Acad. Sci. USA. 2015;112:4648–4653. doi: 10.1073/pnas.1501689112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kim J., Zhang C.Z., Springer T.A. A mechanically stabilized receptor-ligand flex-bond important in the vasculature. Nature. 2010;466:992–995. doi: 10.1038/nature09295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fu H., Jiang Y., Springer T.A. Flow-induced elongation of von Willebrand factor precedes tension-dependent activation. Nat. Commun. 2017;8:324. doi: 10.1038/s41467-017-00230-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wootton D.M., Ku D.N. Fluid mechanics of vascular systems, diseases, and thrombosis. Annu. Rev. Biomed. Eng. 1999;1:299–329. doi: 10.1146/annurev.bioeng.1.1.299. [DOI] [PubMed] [Google Scholar]
- 11.Zhao H., Shaqfeh E., Narsimhan V. Shear-induced particle migration and margination in a cellular suspension. Phys. Fluids. 2012;24:011902. [Google Scholar]
- 12.Spann A.P., Campbell J.E., Shaqfeh E.S.G. The effect of hematocrit on platelet adhesion: experiments and simulations. Biophys. J. 2016;111:577–588. doi: 10.1016/j.bpj.2016.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Qi Q., Shaqfeh E. Theory to predict particle migration and margination in the pressure-driven channel flow of blood. Phys. Rev. Fluids. 2017;2:093102. [Google Scholar]
- 14.Qi Q., Shaqfeh E. Time-dependent particle migration and margination in the pressure-driven channel flow of blood. Phys. Rev. Fluids. 2018;3:034302. [Google Scholar]
- 15.Fitzgibbon S., Spann A.P., Shaqfeh E.S.G. In vitro measurement of particle margination in the microchannel flow: effect of varying hematocrit. Biophys. J. 2015;108:2601–2608. doi: 10.1016/j.bpj.2015.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Secomb T.W. Hemodynamics. Compr. Physiol. 2016;6:975–1003. doi: 10.1002/cphy.c150038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Valeri C.R., Cassidy G., Loscalzo J. Anemia-induced increase in the bleeding time: implications for treatment of nonsurgical blood loss. Transfusion. 2001;41:977–983. doi: 10.1046/j.1537-2995.2001.41080977.x. [DOI] [PubMed] [Google Scholar]
- 18.Walton B.L., Lehmann M., Wolberg A.S. Elevated hematocrit enhances platelet accumulation following vascular injury. Blood. 2017;129:2537–2546. doi: 10.1182/blood-2016-10-746479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mody N.A., King M.R. Platelet adhesive dynamics. Part II: high shear-induced transient aggregation via GPIbalpha-vWF-GPIbalpha bridging. Biophys. J. 2008;95:2556–2574. doi: 10.1529/biophysj.107.128520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wang W., Mody N.A., King M.R. Multiscale model of platelet translocation and collision. J. Comput. Phys. 2013;244:223–235. doi: 10.1016/j.jcp.2012.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fitzgibbon S., Cowman J., Shaqfeh E.S. Examining platelet adhesion via Stokes flow simulations and microfluidic experiments. Soft Matter. 2015;11:355–367. doi: 10.1039/c4sm01450b. [DOI] [PubMed] [Google Scholar]
- 22.Vahidkhah K., Bagchi P. Microparticle shape effects on margination, near-wall dynamics and adhesion in a three-dimensional simulation of red blood cell suspension. Soft Matter. 2015;11:2097–2109. doi: 10.1039/c4sm02686a. [DOI] [PubMed] [Google Scholar]
- 23.Zhang P., Zhang L., Bluestein D. A multiscale biomechanical model of platelets: correlating with in-vitro results. J. Biomech. 2017;50:26–33. doi: 10.1016/j.jbiomech.2016.11.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Vahidkhah K., Diamond S.L., Bagchi P. Platelet dynamics in three-dimensional simulation of whole blood. Biophys. J. 2014;106:2529–2540. doi: 10.1016/j.bpj.2014.04.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Skorczewski T., Griffith B., Fogelson A. Multi-bond models of platelet adhesion and cohesion. In: Layton A.T., Olson S.D., editors. AMS Contemporary Mathematics: Biological Fluid Dynamics: Modeling, Computations, and Applications. 2014. pp. 149–172. [Google Scholar]
- 26.Sabnis R.W., Deligeorgiev T.G., Dalvi T.S. DiOC6(3): a useful dye for staining the endoplasmic reticulum. Biotech. Histochem. 1997;72:253–258. doi: 10.3109/10520299709082249. [DOI] [PubMed] [Google Scholar]
- 27.Lincoln B., Ricco A.J., Meade G. Integrated system investigating shear-mediated platelet interactions with von Willebrand factor using microliters of whole blood. Anal. Biochem. 2010;405:174–183. doi: 10.1016/j.ab.2010.05.030. [DOI] [PubMed] [Google Scholar]
- 28.Kent N.J., Basabe-Desmonts L., Ricco A.J. Microfluidic device to study arterial shear-mediated platelet-surface interactions in whole blood: reduced sample volumes and well-characterised protein surfaces. Biomed. Microdevices. 2010;12:987–1000. doi: 10.1007/s10544-010-9453-y. [DOI] [PubMed] [Google Scholar]
- 29.Sugii Y., Nishio S., Okamoto K. In vivo PIV measurement of red blood cell velocity field in microvessels considering mesentery motion. Physiol. Meas. 2002;23:403–416. doi: 10.1088/0967-3334/23/2/315. [DOI] [PubMed] [Google Scholar]
- 30.Lipowsky H.H., Kovalcheck S., Zweifach B.W. The distribution of blood rheological parameters in the microvasculature of cat mesentery. Circ. Res. 1978;43:738–749. doi: 10.1161/01.res.43.5.738. [DOI] [PubMed] [Google Scholar]
- 31.Cauwenberghs N., Vanhoorelbeke K., Deckmyn H. Structural determinants within platelet glycoprotein Ibalpha involved in its binding to von Willebrand factor. Platelets. 2000;11:373–378. doi: 10.1080/09537100020019157. [DOI] [PubMed] [Google Scholar]
- 32.Wu Y.P., van Breugel H.H., Sixma J.J. Platelet adhesion to multimeric and dimeric von Willebrand factor and to collagen type III preincubated with von Willebrand factor. Arterioscler. Thromb. Vasc. Biol. 1996;16:611–620. doi: 10.1161/01.atv.16.5.611. [DOI] [PubMed] [Google Scholar]
- 33.Coller B.S. GPIIb/IIIa antagonists: pathophysiologic and therapeutic insights from studies of c7E3 Fab. Thromb. Haemost. 1997;78:730–735. [PubMed] [Google Scholar]
- 34.Gitz E., Koopman C.D., Urbanus R.T. Platelet interaction with von Willebrand factor is enhanced by shear-induced clustering of glycoprotein Ibα. Haematologica. 2013;98:1810–1818. doi: 10.3324/haematol.2013.087221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Izeddin I., Boulanger J., Sibarita J.B. Wavelet analysis for single molecule localization microscopy. Opt. Express. 2012;20:2081–2095. doi: 10.1364/OE.20.002081. [DOI] [PubMed] [Google Scholar]
- 36.Rack K., Huck V., Gompper G. Margination and stretching of von Willebrand factor in the blood stream enable adhesion. Sci. Rep. 2017;7:14278. doi: 10.1038/s41598-017-14346-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Springer T.A. von Willebrand factor, Jedi knight of the bloodstream. Blood. 2014;124:1412–1425. doi: 10.1182/blood-2014-05-378638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Siedlecki C.A., Lestini B.J., Marchant R.E. Shear-dependent changes in the three-dimensional structure of human von Willebrand factor. Blood. 1996;88:2939–2950. [PubMed] [Google Scholar]
- 39.Nair S., Ghosh K., Mohanty D. Glanzmann’s thrombasthenia: updated. Platelets. 2002;13:387–393. doi: 10.1080/0953710021000024394. [DOI] [PubMed] [Google Scholar]
- 40.Müller, J. P., S. Mielke, …, M. Benoit. Force sensing by the vascular protein von Willebrand factor is tuned by a strong intermonomer interaction. Proc. Natl. Acad. Sci. USA. 113:1208–1213. [DOI] [PMC free article] [PubMed]
- 41.Chesla S.E., Selvaraj P., Zhu C. Measuring two-dimensional receptor-ligand binding kinetics by micropipette. Biophys. J. 1998;75:1553–1572. doi: 10.1016/S0006-3495(98)74074-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ju L., Chen Y., Zhu C. Von Willebrand factor-A1 domain binds platelet glycoprotein Ibα in multiple states with distinctive force-dependent dissociation kinetics. Thromb. Res. 2015;136:606–612. doi: 10.1016/j.thromres.2015.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Weisel J.W., Shuman H., Litvinov R.I. Protein-protein unbinding induced by force: single-molecule studies. Curr. Opin. Struct. Biol. 2003;13:227–235. doi: 10.1016/s0959-440x(03)00039-3. [DOI] [PubMed] [Google Scholar]
- 44.Skalak R., Ozkaya N., Skalak T.C. Biofluid mechanics. Annu. Rev. Fluid Mech. 1989;21:167–200. [Google Scholar]
- 45.Mody N.A., King M.R. Three-dimensional simulations of a platelet-shaped spheroid near a wall in shear flow. Phys. Fluids. 2005;17:113302. [Google Scholar]
- 46.Dopheide S.M., Maxwell M.J., Jackson S.P. Shear-dependent tether formation during platelet translocation on von Willebrand factor. Blood. 2002;99:159–167. doi: 10.1182/blood.v99.1.159. [DOI] [PubMed] [Google Scholar]
- 47.Weiss H.J., Tschopp T.B., Egan J.J. Decreased adhesion of giant (Bernard-Soulier) platelets to subendothelium. Further implications on the role of the von Willebrand factor in hemostasis. Am. J. Med. 1974;57:920–925. doi: 10.1016/0002-9343(74)90170-3. [DOI] [PubMed] [Google Scholar]
- 48.Reininger A.J., Heijnen H.F., Ruggeri Z.M. Mechanism of platelet adhesion to von Willebrand factor and microparticle formation under high shear stress. Blood. 2006;107:3537–3545. doi: 10.1182/blood-2005-02-0618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.French D.L., Seligsohn U. Platelet glycoprotein IIb/IIIa receptors and Glanzmann’s thrombasthenia. Arterioscler. Thromb. Vasc. Biol. 2000;20:607–610. doi: 10.1161/01.atv.20.3.607. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
A total of 1000 frames are shown, but only the first 500 frames are used for analysis.
Ht = 30%, only platelets near one wall are shown.