Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Feb 14;6(3):720–727. doi: 10.1021/acsphotonics.8b01595

Experimental Demonstration of Ultrafast THz Modulation in a Graphene-Based Thin Film Absorber through Negative Photoinduced Conductivity

Anna C Tasolamprou †,*, Anastasios D Koulouklidis †, Christina Daskalaki †, Charalampos P Mavidis †,‡, George Kenanakis †, George Deligeorgis †, Zacharias Viskadourakis †, Polina Kuzhir ¶,§, Stelios Tzortzakis †,‡,∥, Maria Kafesaki †,‡, Eleftherios N Economou †,⊥, Costas M Soukoulis †,#
PMCID: PMC6429433  PMID: 30918912

Abstract

graphic file with name ph-2018-01595t_0007.jpg

We present an experimental demonstration and interpretation of an ultrafast optically tunable, graphene-based thin film absorption modulator for operation in the THz regime. The graphene-based component consists of a uniform CVD-grown graphene sheet stacked on an SU-8 dielectric substrate that is grounded by a metallic ground plate. The structure shows enhanced absorption originating from constructive interference of the impinging and reflected waves at the absorbing graphene sheet. The modulation of this absorption, which is demonstrated via a THz time-domain spectroscopy setup, is achieved by applying an optical pump signal, which modifies the conductivity of the graphene sheet. We report an ultrafast (on the order of few ps) absorption modulation on the order of 40% upon photoexcitation. Our results provide evidence that the optical pump excitation results in the degradation of the graphene THz conductivity, which is connected with the generation of hot carriers, the increase of the electronic temperature, and the dominant increase of the scattering rate over the carrier concentration as found in highly doped samples.

Keywords: THz graphene, hot carrier generation, ultrafast THz tunable grapheme metasurface, grapheme photoexcitation, experimental grapheme absorber, flat optics modulation

1. Introduction

Graphene, the acclaimed two-dimensional (2D) material made of carbon atoms arranged in a honeycomb lattice, exhibits unique mechanical, thermal, electrical, and optical properties; these stem from the linear dispersion of its 2D Dirac fermions, which allows wide tunability. In particular, graphene optical properties can be modified by imposing a kind of stimulus. The stimuli include, among others, chemical doping, thermal tuning, external electrostatic or magnetic field, and optical pumping.1−6 Due to its reconfigurable optical properties, graphene has been examined and employed in a large number of photonic and plasmonic applications,7 whereas its significance as a constituent element in metasurface configurations, substituting or accompanying thin metallic parts, has been previously demonstrated.8 The vast majority of the currently existing or investigated graphene-based metasurfaces consist of one or more graphene layers, patterned or unpatterned, combined with other materials and/or structures, dielectrics and/or metallic. Depending on the meta-atom architecture in those metasurfaces and the control stimuli, one can achieve a variety of tunable functionalities that span over a vast part of the electromagnetic spectrum, from microwaves to the visible.9,10,48 Particularly in the THz spectrum, graphene predominantly exhibits a Drude-like response due to its easily generated and controlled free carriers and, therefore, is considered a suitable platform for dynamically tunable metasurface components.11,12 Some interesting graphene-based implementations involve broadband modulators, filters and absorbers,13−16 biosensors,17 polarizers,18 light detectors,19,20 cloaks,21 and many others.

A simple but yet remarkable graphene component/metasurface is based on the classical Salisbury screen22 and the coherent absorption principle. It consists of a single uniform sheet of graphene placed on top of a dielectric film, which is placed on a metallic plate. The only source of losses in the system is the graphene sheet assuming negligible losses in the dielectric film and almost perfect reflection by the metallic plate. In a freestanding state (i.e., without the back-reflector), graphene absorbs only a small percentage of the impinging wave. However, if two waves come in phase at the lossy sheet, enhanced and even perfect absorption may occur. In this simple structure one wave is the impinging wave and the second is the wave reflected by the metallic back plate. Due to its simplicity and the tunability capability, the specific graphene-based absorbing metasurface and its variations have been intensively investigated.23−28 Recently it has been demonstrated experimentally that electrostatic gate-tunable perfect absorption in a structure consisting of a large area of monolayer graphene over a grounded electrolytic medium is possible.29 Electrostatic tunability though cannot provide an ultrafast response as is required in advanced modulation devices.

In this work we demonstrate experimentally a graphene-based ultrathin absorber that exhibits ultrafast (on the order of few ps) intensity modulation. This ultrafast modulation is achieved by photoexcitation via an optical pump signal. Our absorber metasurface consists of a simple graphene sheet deposited on a grounded dielectric substrate of micrometer thickness and provides tunable absorption (or reflection) functionality in the terahertz regime. The sample is fabricated by stacking a chemical vapor deposition (CVD)-grown graphene monolayer on a dielectric SU-8 spacer supported by a Pt back plate. The electromagnetic response characterization and the demonstration of the ultrafast THz absorption modulation of the structure are conducted by using a THz time-domain spectroscopic system (THz-TDS) coupled with an IR-pump laser used for the photoexcitation. It is found that photoexcitation dynamically modulates the conductivity of the graphene sheet in the sample with decay of 2.79 ps, resulting in absorption tuning on the order of 40%. The time scale is comparable and even smaller with respect to other emerging or established platforms;30−32 that is, a germanium-based metasurface with a full recovery time of 17 ps has been recently demonstrated.31 Our system holds additionally the advantage of the 2D nature of the material, which is ideal for the realization of minimized components. Thus, among the established platforms, our system provides a promising, ultrathin, ultrafast modulation scheme appropriate for the demanding future flat optics modulation applications.

Moreover we provide a thorough interpretation of our experimental findings by discussing in detail the mechanism of the photoinduced modulation of the terahertz conductivity in the graphene sheet under an IR pump laser with variable fluence. In particular, we provide experimental evidence that the optical signal leads to the degradation of the THz graphene conductivity, which varies with the square root of fluence. The terahertz photoinduced conductivity dynamics of graphene is an issue of much discussion. The underlying relaxation and recombination dynamics of the photogenerated electrons and holes, the cooling dynamics of the hot electrons, the appearance of carrier multiplication and optical gain, the saturation effects, etc., appear to be involved phenomena, affected among others by parameters such as growing methods, substrate materials, and ambient temperature.33−37 Remarkably, it has been demonstrated that the sign of the photoinduced conductivity dynamics depends greatly on the doping level in the graphene. In particular, it has been demonstrated that photoexcitation in graphene of neutral charge point results in a rise of the carrier concentration and an increase of conductivity, whereas when the initial doping level is high, photoexcitation affects the scattering rate of the carriers. Depending on the detailed conditions, the modification of the scattering rate can be the dominant effect and can lead to a conductivity decrease,38−41 as is also found in our experiments.

The paper is organized as follows: Initially we present the proposed structure and the origins of the enhanced absorption in the graphene-based component. Then we describe the fabrication procedure and present the experimental results that reveal the tunable absorption function. Finally we discuss the observed negative photoinduced conductivity and conclude our work.

2. Principle of Coherent Absorption Operation

Our metasurface is shown in Figure 1. It is designed for tunable absorption operation based on the coherent absorption principle. To maximize absorption, we need on one hand to minimize the reflection from the top surface and on the other hand to enforce coherence, i.e., constructive interference of incident and reflected (from back-reflector) wave at the lossy graphene sheet (which would ideally be the only source of losses in the system). This is achieved when the impedance of the freespace, Z0 = 120π, and the metasurface is matched, which provides two conditions for the graphene surface conductivity, σ, and the details of the dielectric substrate (acting as cavity). For normal incidence the conditions are Re{σ(ω)Z0} = 1 and 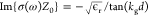Inline graphic, where ϵr is the relative permittivity of the substrate and Inline graphic is the wavenumber in the cavity.23,24 The first condition is satisfied for various doping levels at the vicinity of 2 THz and assuming an ideal, lossless, SU-8 dielectric film of ϵr = 3.9, while the second condition requires a thickness equal to d = 20 μm. The conditions and subsequently the structure parameters can be properly adjusted for different angles and polarization.23,29

Figure 1.

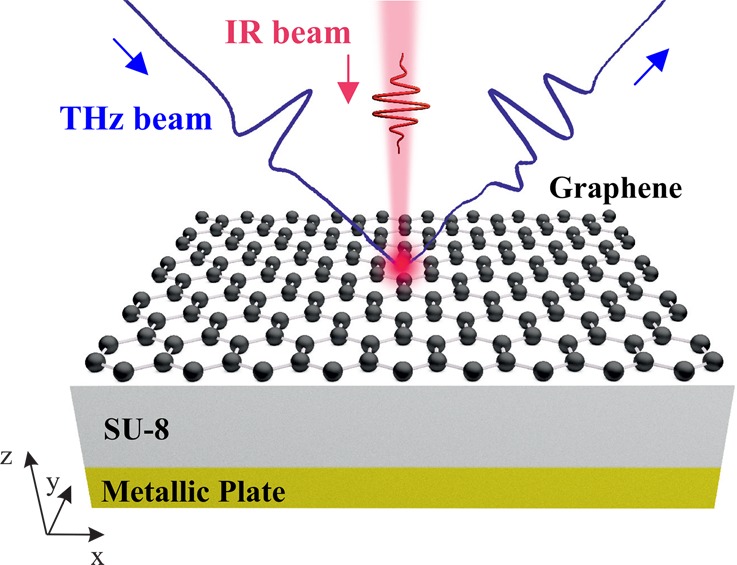
Figure 1

Open in a new tab

Schematic representation of the graphene absorber structure. It is composed of a graphene monolayer on top of a dielectric (SU-8) film of thickness d = 20 μm placed on a metallic back-reflector. The THz beam illuminates the sample at an angle θ while the sample is optically excited by a near-IR beam at normal incidence.

The principle and results of coherent absorption operation are described in Figure 2, where we present the absorption spectra (see Figure 2a) of three structures: (i) a freestanding graphene sheet, (ii) a back-plated dielectric, loss-free slab (ϵr = 3.9), and (iii) the proposed metasurface. The spectra are calculated in the frequency range 1–4 THz (Figure 2a) assuming normal incidence, for two different graphene conductivities, one (σ1) fulfilling the previously mentioned perfect absorption conditions and a second one (σ2) that does not fulfill those conditions. Figure 2b shows the distribution of the absolute electric field across the metasurface, along the z-axis.

Figure 2.

Figure 2

Open in a new tab

(a) Comparison of absorption spectra versus frequency for the optimum frequency-dependent complex graphene conductivity (σ1) and for another case (σ2): (i) a free-standing graphene sheet in air (blue curves), (ii) a loss-free dielectric slab standing on top of a grounded perfect metallic layer (magenta curves), and (iii) a graphene sheet on top of a grounded, ohmic loss-free dielectric/metal slab (green curves). The THz beam is normally incident. (b) Absolute value of the electric field (|E|) along the metasurface (xy plane) versus the z-axis at frequency f = 1.86 THz [green curves corresponding to conductivities σ1 (solid curve) and σ2 (dashed curves)] and at frequency f = 3.65 THz (blue curve) for the σ2 conductivity.

The conductivities σ1 and σ2 are complex, frequency-dependent functions, obtained from the Kubo formula42 (see also eq 1 and eq 2) assuming EF = 1 eV and τ = 18 fs (values producing maximum absorption) for σ1 and EF = 350 meV and τ = 20 fs for σ2. The standalone graphene sheet absorption is presented in Figure 2a with the cyan curves. Absorption due to a single pass of the impinging field from the graphene sheet is as low as ∼2%. Absorption changes drastically if we place the graphene sheet on the dielectric substrate as seen in Figure 2a. The constructive interference of the incident and reflected waves on the lossy sheet leads to a large increase of the absorption for both σ1 and σ2 scenarios. In fact, for the case of σ1, where the details for the graphene have been selected such that the impedance matching condition and the cavity size conditions are exactly met, perfect absorption is achieved. In these proof of concept calculations, the only source of losses is the graphene sheet; this is also observed in Figure 2a and the middle case of no graphene sheet (magenta lines), where no absorption is observed.

The coherent absorption mechanism is further clarified in Figure 2b, where we plot the profile of the absolute value of the electric field (uniform in the xy plane) versus the z-axis at two distinct frequencies, f = 1.86 THz (green curves for both σ1 and σ2, solid and dashed, respectively) and f = 3.65 THz (blue curve for σ2). On resonance, that is at f = 1.86 THz and for σ2, the absolute value of the field at the graphene sheet is significantly higher than at f = 3.65 THz (which is practically zero); this shows increased interaction of the field with the lossy surface and hence increased absorption. For the optimum σ1 case, the absorption is maximized and no field is reflected, which is evident form the flat profile of the wave at the air region. (In the case of σ2 the incident field experiences partial reflection, which adds up to the incident profile.)

3. Sample Preparation

The measured sample is fabricated as follows: A silicon wafer is used for mechanical support. A Pt thick layer (400 nm) is evaporated using e-gun evaporation on the entire surface of the sample. This is used to act as the bottom ground plane depicted in Figure 1 with yellow color. On top of the ground plane, a layer of SU-8 is spin coated and exposed to UV and heating (300 °C for 60 min) to fully cure the material. The process was tuned to produce a postcuring thickness of 20 μm. Finally a PlanarTech Dual CVD system was used to grow a graphene monolayer on copper foil. To transfer the graphene layer onto SU-8, a poly(methyl methacrylate) (PMMA) layer was spin coated on top of the graphene/copper stack and copper was etched using a mixture of HCl acid with H2O2 in water at 50 °C. After full removal of Cu, the PMMA/graphene membrane was rinsed thoroughly with deionized water and was wet transferred on the SU-8 layer. A mild annealing process at 100 °C was used to remove any remaining water residues and ensure graphene is fully attached on the SU-8 surface.

4. Optically Tunable Graphene Absorption: Setup and Experimental Demonstration

For the experimental study of the graphene-based absorber we use a powerful THz-TDS system that provides the ability of measurements in reflection mode. It is based on a pump–probe, coherent detection approach and uses an amplified kHz Ti:sapphire laser system delivering 35 fs pulses at 800 nm central wavelength and a maximum energy of 2.3 mJ/pulse. The most intense part of the initial beam is focused in ambient air after partial frequency doubling in a beta-barium-borate (BBO) crystal (50 m thick) to produce a two-color filament and, subsequently, THz radiation (>200 kV/cm).

The emitted THz pulses (Figure 3a) are focused at the sample and after being reflected are guided to the detection stage, where an air-biased coherent detection (ABCD) scheme is applied providing a useful THz spectrum up to 13 THz (inset of Figure 3a). Another part of the initial laser beam is used to excite the sample in an IR-pump/THz-probe configuration. The angle of incidence of the THz beam on the sample is equal to 45°, while the pump beam illuminates it at normal incidence. The angle of incidence is selected in order to facilitate the characterization procedure, while s polarization is selected since it is characterized by higher absorption in the graphene sheet for oblique incidence.28 Our theoretical results for p polarization show a similar response but with lower absorption levels. The whole experimental setup is enclosed in a purge gas chamber to avoid water vapor absorption of the THz radiation, and all measurements are performed at low levels of humidity.

Figure 3.

Figure 3

Open in a new tab

(a) THz electric field and its corresponding spectrum (inset). (b) Optical pump induced THz relative reflectivity change (DR/R) as a function of pump delay. The measurement refers to the peak of the first pulse reflected by the graphene sheet, prior to cavity insertion. The red dashed curve corresponds to the fitted exponential decay of the experimental data.

Figure 3b shows the free carriers’ dynamics of the graphene layer by measuring the optical pump induced THz field relative reflectivity change (DR/R) as a function of pump delay. In this measurement we record the peak of the THz electric field reflected by the first surface of the sample, the graphene sheet, for the maximum available pump fluence of 0.690 mJ/cm2. The red dashed curve corresponds to the fitted exponential decay of the experimental data. The instantaneous rise and the rapid decay equal to ∼2.79 ps of the excited carriers demonstrate the fast switching capability of our device, while the negative sign of DR/R implies a negative pump-induced photoconductivity, as reported in, for example, ref (39). All the following measurements are performed at a fixed THz-optical pump time delay corresponding to the maximum change of relative reflectivity.

Figure 4a shows the absorption spectra of the metasurface for variable fluence values up to 0.690 mJ/cm2 in the frequency regime from 0.75 to 8 THz. Without photoexcitation, the graphene-based structure absorbs a maximum of 75% of the incoming radiation at f = 2.17 THz. Interestingly, when photoexcited, the properties of the graphene sheet are modified and the maximum absorption drops to 45% of the incoming radiation, for maximum fluence 0.690 mJ/cm2, providing ultrafast modulation of the absorption on the order of 40%. For the second absorption peak, at f = 6.38 THz, the structure absorbs a maximum of 62.5% of the incoming radiation, dropping to 47% when photoexcited, corresponding to a modulation of 25%. The enhanced absorption in the first resonance originates from the coherent superposition of incident and reflected wave at the absorbing graphene sheet, as discussed in Figure 2. Perfect absorption is not achieved since the conditions mentioned in the discussion of Figure 2 are not exactly met. The same coherent superposition is the effect behind the second resonance, but there the graphene and the free space impedance mismatch is larger, making the absorption smaller. In Figure 4b, the absorption at resonance peaks (2.17 and 6.38 THz) is shown as a function of the fluence. The gradient of the absorption peak is large for small values of fluence and becomes smaller as fluence increases. The absorption peak approximately varies with 1/I1/2. The decrease of the absorption in the metasurface implies a decrease of the real part of the conductivity and points to negative dynamics, a response that is discussed in the next section.

Figure 4.

Figure 4

Open in a new tab

Measurements of the photoinduced absorption modulation for incoming wave of s polarization and angle of incidence equal to 45°. (a) Absorption spectra for variable values of fluence, I, in the range 0–0.690 mJ/cm2 in the frequency range 0.75–8 THz. Without the photoexcitation the graphene-based structure absorbs a maximum of 75% of the incoming wave at f = 2.17 THz. With photoexcitation the properties of the graphene sheet are modified and the maximum absorption drops; for maximum I = 0.690 mJ/cm2 the absorption drops to 45%, providing thus an ultrafast modulation of the absorption on the order of 40%. (b) On-resonance absorption amplitude as a function of the imposed fluence in the range 0–0.690 mJ/cm2. Inset shows the measured reflected signal by the structure when fluence equals I = 0 mJ/cm2 (blue curve) and I = 0.690 mJ/cm2 (orange curve).

5. Discussion and Interpretation

For analyzing the experimental results we initially perform a numerical study of the structure’s absorbing properties, aiming at the required graphene conductivity as to reproduce the experimentally observed response. The simulations are performed in the frequency domain using the commercial finite element method electromagnetic solver Comsol Multiphysics.43 Graphene is simulated as a conductive sheet by imposing a boundary condition in the corresponding interface. The surface conductivity of the graphene is given by the Kubo formula and can be written as a sum a two terms, σintra, describing the intraband response, and σinter, describing the interband transitions, with

5. 1
5. 2

where the function Inline graphic reads

5. 3

ω is the angular frequency, ℏ the reduced Planck constant, kB the Boltzmann constant, e the electron charge, τ the electron relaxation time, and T the temperature. In the THz frequency range under investigation the interband contribution is much smaller than the intraband contribution (on the order of 10–3) and is completely omitted in our calculations. We use the Kubo formula for the initial state and properly adjust our model in order to account for the negative pump-induced observed photoconductivity.

As is reported in many recent works, the photoinduced THz conductivity may be either positive or negative.38−41 Positive photoconductivity is observed in graphene samples close to the neutral charge point and stems from a rise of the carrier concentration, modeled with an increase of the Fermi level. Negative photoconductivity, the phenomenon that we also observe, is found in highly doped samples, and it seems to be connected with relaxation of the photoexcited carriers through (a) generation of hot electrons (i.e., increase of carrier temperature), (b) enhanced carrier–carrier scattering, and (c) enhanced carrier scattering with lattice vibrations. These mechanisms in highly doped graphene seem to dominate photoconductivity over the increase of carrier concentration (initial concentration, in any case, is high for large values of the Fermi level) and lead to negative photoinduced conductivity. To quantify this negative photoinduced conductivity, various approaches have been proposed; the majority of them promote an enhancement of the scattering rate, connected with an increase in the effective electronic temperature, Te.

Our numerical study indeed showed that the experimentally observed response can be understood and reproduced by considering reduction of the graphene conductivity by photoexcitation. Moreover the observed change of the absorption intensity without a considerable shift of the absorption peak frequency implies change mostly in the real part of the photoinduced conductivity. Thus, to analyze our experimental data and reproduce them numerically, we use the model reported in ref (41), where, in accordance with our case, the authors record a decrease in the photoinduced THz conductivity for the same frequency range and similar fluence intensity values (their analysis refers to experimental data up to 2.5 THz, whereas our main resonance is at 2.17 THz). This decrease is attributed to the above-mentioned relaxation mechanisms and, since it is also much greater in the real part of the conductivity than in the imaginary part (as in our case), points to a Drude behavior. In their case they also observe a zero crossing of the imaginary part of the photoinduced conductivity, which suggests a Lorentzian oscillator. Thus, a Drude–Lorentz model is used to describe the frequency dependence of the conductivity decrease:

5. 4

with the modification term Δσ(ω) reading

5. 5

In the state where there is no pump applied to the graphene sample, we consider that the Fermi energy is equal to EF = 250 meV and that the relaxation time is equal to τ = 25 fs, values frequently reported in highly doped graphene samples.

The first part of the dynamic conductivity Δσ(ω), as is already mentioned, affects mainly its real part; its weight 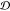Inline graphic accounts for all the dynamic phenomena that lead to the negative photoinduced conductivity and subsequently to the modulation of the absorption level in our metasurface. The second part of eq 5 is the Lorentz term with oscillation strength F, line width γ, and ω0 as the resonant frequency. In the literature the resonant frequency ω0 appears to be influenced by various effects such as the stimulated emission of THz photons in photoexcited graphene in the presence of atmospheric gases,44 the excitation of plasmons,45 laser-induced two-photon oxidation,46 etc. For our implementation, the Lorentzian term affects slightly the position of the resonance and serves mainly as a fine-tuning parameter.

Figure 5 presents the results of fitting the experimental data to the selected model of the conductivity via the simulation and the measured absorption data by the structure shown in Figure 1. The experimental measurement for the case where no optical pump is applied is plotted in black. For the graphene in the initial state, without the pump, we assume EF = 250 meV, τ = 25 fs, and temperature T = 300 K. The real part of the surface conductivity is calculated by the intraband term of the Kubo formula, eq 1, equal to σno pump = 2.1 G0 at the main resonance (f = 2.17 THz), where G0 = e2/h is the quantum of conductance. The corresponding calculated absorption spectra are plotted in red. The agreement is excellent for the first resonance where the maximum modulation is recorded and remains good also for the second resonance. Green curve corresponds to the experimentally measured absorption spectrum when the pump is on and the fluence is maximum and equal to I = 0.690 mJ/cm2. To simulate the absorption spectra with the optical pump on and the fluence up to I = 0.690 mJ/cm2, we add to the fluence-free Kubo formula the model of eq 5, where the optimized parameters are F = 5.9 × 108 Ω–1 s–1, γ = 16 THz, ω0/2π = 2.7 THz, and Inline graphic varies between 0 and 18.3 × 109 Ω–1 s–1.

Figure 5.

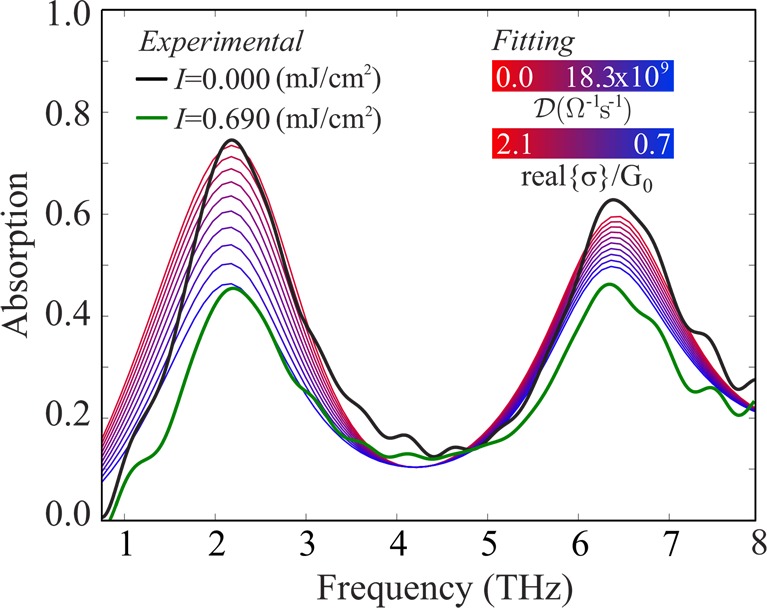
Figure 5

Open in a new tab

Fitted absorption spectra corresponding to the experimental measurements of Figure 4a. The black curve corresponds to the experimentally measured absorption spectra of the metasurface before the application of the optical pump and the green curve to the experimentally measured absorption spectra when the pump is on and fluence is equal to I = 0.690 mJ/cm2. All other curves (red to blue) correspond to the fitted data of the conductivity according to eq 1 and eq 5 and the simulation of the subsequent absorption by the structure shown in Figure 1. For the graphene sample before the pump excitation, the graphene Fermi energy is equal to |Ef| = 250 meV and the relaxation time is equal to τ = 25 fs (red curve). To fit the absorption data versus fluence, we have chosen F = 5.9 × 108 Ω–1 s–1, γ = 16 THz, and ω0/2π = 2.7 THz for all nine values of fluence, while the weight Inline graphic was varied almost linearly in the range Inline graphic Ω–1 s–1 as the fluence was changed from 0 to 0.690 mJ/cm2. The real part of the conductivity on the main resonance (f = 2.17 THz) varies from 2.1 G0 to 0.8 G0. In fitting, emphasis was focused on reproducing as accurate as possible the peaks, especially the main resonance, and their fluence dependence.

Figure 6 presents the fitted data for the real part of the conductivity on the main resonance, f = 2.17 THz (both the total, Figure 6a, and its drop, Figure 6b) versus the experimental values of the fluence (the continuous curves are a guide to the eye). The green curve (inset in Figure 6a) shows the calculated on-resonance absorption versus the fitted real part of the conductivity, demonstrating an almost linear relation as expected when the elevated effective temperature is its main cause. In Figure 6b the drop of the real part of the fitted conductivity is plotted versus the fluence, showing an almost squared root dependence. Some small discrepancies are attributed to the imaginary part. For the maximum fluence, I = 0.690 mJ/cm2, the real part of the surface conductivity is calculated to be equal to approximately σmax pump = 0.8 G0 (Figure 6a). In comparison to the no pump case, this corresponds to a drop of approximately Re{Δσ} = 1.3 G0 which stands in agreement with many works involving THz pump probe spectroscopy. All the intermediate spectra are derived by varying the weight Inline graphic in the range Inline graphic Ω–1 s–1, fitting the fluence that varies from 0 to I = 0.690 mJ/cm2 in the experiment. For the parameters of the Lorentzian term F, γ, and ω0 we assume no variation for increasing fluence; the reported variation in the literature is very low, and in our case the term has only a small affect on the position of the resonance.

Figure 6.

Figure 6

Open in a new tab

(a) Fitted values (as described in Figure 5) of the real part of the conductivity on the main resonance frequency (2.17 THz), real{σ}/G0, versus the experimental values of fluence. Inset shows the almost linear relation of absorption versus the real part of the conductivity. (b) Real part of the conductivity drop, real{Δσ}/G0, versus the fluence I values measured in the experiment; it varies approximately as I1/2.

In the range under investigation, the drop in the real part of the conductivity is linear with the weight Inline graphic. The drop of the on-resonance absorption is also linear with conductivity, as seen in the inset of Figure 6a. We observe that as fluence increases, the real part of the conductivity experiences the same type of drop as the experimental on-resonance absorption shown in Figure 4b. In Figure 6b we present the evolution of the photoinduced dynamic conductivity, Re{Δσ}/G0, versus fluence I, exhibiting an I1/2 reported in ref (41). Beyond that, recent works report the exact same behavior of the electron temperature with fluence, I1/2, in highly doped samples,39,47 which is a product of the hot carrier dynamics that affect the scattering rate and reflect the terahertz conductivity.

6. Conclusion

We investigated both experimentally and theoretically a graphene-based thin film absorber exhibiting ultrafast tunable THz operation. The structure consists of a uniform graphene sheet grown by CVD on a grounded dielectric substrate; it is designed to provide enhanced absorption. The latter occurs due to the coherent interference of the impinging and reflected waves when they are in phase at the lossy graphene sheet at the frequency of 2.17 THz. Our sample was characterized by a broadband THz time-domain-spectroscopic system in an IR pump–THz probe configuration. The THz absorption modulation was achieved by photoexcitation, which modulated the conductivity of the graphene. Our results provided evidence that in our highly doped sample photoexcitation leads to a reduction of the THz conductivity with decay of 2.79 ps, resulting in an absorption intensity decrease of 40%, with maximum fluence equal to approximately 0.7 mJ/cm2. We have thoroughly discussed the dynamics of the photoinduced reduction of the conductivity, which is connected with the generation of hot carriers, the increase of the electronic temperature, and the overall increase of the scattering rate. Our system provides ultrathin, ultrafast modulation appropriate for the demanding future flat optics modulation applications.

Acknowledgments

This work was supported by the European Union’s Horizon 2020 Project 696656 Graphene Flagship, the European Research Council under ERC Advanced Grant no. 320081 (project PHOTOMETA), and the European Union’s Horizon 2020 Future Emerging Technologies call (FETOPEN-RIA) under grant agreement no. 736876 (project VISORSURF), the Hellenic Foundation for Research and Innovation (HFRI), and the General Secretariat for Research and Technology (GSRT), under the HFRI PhD Fellowship grant (GA. no. 4894). This work was also partially supported by the National Priorities Research Program grant no. NPRP9-329-1-067 from the Qatar National Research Fund (member of The Qatar Foundation), the H2020 Laserlab-Europe (EC-GA 654148), and H2020 MIR-BOSE (EC-GA 737017) projects. P.K. is thankful to Tomsk State University Competitive Programme and H2020-MSCA-RISE-2014 Project ID 644076 CoExAN.

The authors declare no competing financial interest.

References

  1. Liu H.; Liu Y.; Zhu D. Chemical doping of graphene. J. Mater. Chem. 2011, 21, 3335–3345. 10.1039/C0JM02922J. [DOI] [Google Scholar]
  2. Das A.; Pisana S.; Chakraborty B.; Piscanec S.; Saha S. K.; Waghmare U. V.; Novoselov K. S.; Krishnamurthy H. R.; Geim A. K.; Ferrari A. C.; Sood A. K. Monitoring dopants by Raman scattering in an electrochemically top-gated graphene transistor. Nat. Nanotechnol. 2008, 3, 210–215. 10.1038/nnano.2008.67. [DOI] [PubMed] [Google Scholar]
  3. Sun D.; Aivazian G.; Jones A. M.; Ross J. S.; Yao W.; Cobden D.; Xu X. Ultrafast hot-carrier-dominated photocurrent in graphene. Nat. Nanotechnol. 2012, 7, 114–118. 10.1038/nnano.2011.243. [DOI] [PubMed] [Google Scholar]
  4. Tielrooij K. J.; Song J. C. W.; Jensen S. A.; Centeno A.; Pesquera A.; Zurutuza Elorza A.; Bonn M.; Levitov L. S.; Koppens F. H. L. Photoexcitation cascade and multiple hot-carrier generation in graphene. Nat. Phys. 2013, 9, 248–252. 10.1038/nphys2564. [DOI] [Google Scholar]
  5. Winzer T.; Malić E. Impact of Auger processes on carrier dynamics in graphene. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 85, 241404. 10.1103/PhysRevB.85.241404. [DOI] [Google Scholar]
  6. Fan Y.; Shen N.-H.; Zhang F.; Zhao Q.; Wei Z.; Zhang P.; Dong J.; Fu Q.; Li H.; Soukoulis C. Photoexcited Graphene Metasurfaces: Significantly Enhanced and Tunable Magnetic Resonances. ACS Photonics 2018, 5, 1612–1618. 10.1021/acsphotonics.8b00057. [DOI] [Google Scholar]
  7. Koppens F.; Chang D.; García De Abajo F. Graphene plasmonics: A platform for strong light-matter interactions. Nano Lett. 2011, 11, 3370–3377. 10.1021/nl201771h. [DOI] [PubMed] [Google Scholar]
  8. Tassin P.; Koschny T.; Kafesaki M.; Soukoulis C. M. A comparison of graphene, superconductors and metals as conductors for metamaterials and plasmonics. Nat. Photonics 2012, 6, 259–264. 10.1038/nphoton.2012.27. [DOI] [Google Scholar]
  9. De Abajo F. Graphene plasmonics: Challenges and opportunities. ACS Photonics 2014, 1, 133–152. 10.1021/ph400147y. [DOI] [Google Scholar]
  10. Kuzhir P.; Paddubskaya A.; Volynets N.; Batrakov K.; Kaplas T.; Lamberti P.; Kotsilkova R.; Lambin P. Main principles of passive devices based on graphene and carbon films in microwave - THz frequency range. J. Nanophotonics 2017, 11, 032504. 10.1117/1.JNP.11.032504. [DOI] [Google Scholar]
  11. Abadal S.; Llatser I.; Mestres A.; Lee H.; Alarcon E.; Cabellos-Aparicio A. Time-domain analysis of graphene-based miniaturized antennas for ultra-short-range impulse radio communications. IEEE Trans Commun 2015, 63, 1470–1482. [Google Scholar]
  12. Mousavi S.; Kholmanov I.; Alici K.; Purtseladze D.; Arju N.; Tatar K.; Fozdar D.; Suk J.; Hao Y.; Khanikaev A.; Ruoff R.; Shvets G. Inductive tuning of fano-resonant metasurfaces using plasmonic response of graphene in the mid-infrared. Nano Lett. 2013, 13, 1111–1117. 10.1021/nl304476b. [DOI] [PubMed] [Google Scholar]
  13. Kakenov N.; Ergoktas M.; Balci O.; Kocabas C.. Graphene based terahertz phase modulators. 2D Mater. 2018, 5, 035018. 10.1088/2053-1583/aabfaa. [DOI] [Google Scholar]
  14. Liu M.; Yin X.; Ulin-Avila E.; Geng B.; Zentgraf T.; Ju L.; Wang F.; Zhang X. A graphene-based broadband optical modulator. Nature 2011, 474, 64–67. 10.1038/nature10067. [DOI] [PubMed] [Google Scholar]
  15. Polat E. O.; Kocabas C. Broadband Optical Modulators Based on Graphene Supercapacitors. Nano Lett. 2013, 13, 5851–5857. 10.1021/nl402616t. [DOI] [PubMed] [Google Scholar]
  16. Shen N.-H.; Tassin P.; Koschny T.; Soukoulis C. M. Comparison of gold- and graphene-based resonant nanostructures for terahertz metamaterials and an ultrathin graphene-based modulator. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 115437. 10.1103/PhysRevB.90.115437. [DOI] [Google Scholar]
  17. Liang G.; Hu X.; Yu X.; Shen Y.; Li L. H.; Davies A. G.; Linfield E. H.; Liang H. K.; Zhang Y.; Yu S. F.; Wang Q. J. Integrated Terahertz Graphene Modulator with 100% Modulation Depth. ACS Photonics 2015, 2, 1559–1566. 10.1021/acsphotonics.5b00317. [DOI] [Google Scholar]
  18. Shao Y.; Wang J.; Wu H.; Liu J.; Aksay I.; Lin Y. Graphene based electrochemical sensors and biosensors: A review. Electroanalysis 2010, 22, 1027–1036. 10.1002/elan.200900571. [DOI] [Google Scholar]
  19. Fan Y.; Shen N.-H.; Zhang F.; Wei Z.; Li H.; Zhao Q.; Fu Q.; Zhang P.; Koschny T.; Soukoulis C. M. Electrically Tunable Goos-Hänchen Effect with Graphene in the Terahertz Regime. Adv. Opt. Mater. 2016, 4, 1824–1828. 10.1002/adom.201600303. [DOI] [Google Scholar]
  20. Koppens F. H. L.; Mueller T.; Avouris P.; Ferrari A. C.; Vitiello M. S.; Polini M. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat. Nanotechnol. 2014, 9, 780–793. 10.1038/nnano.2014.215. [DOI] [PubMed] [Google Scholar]
  21. Zhang B. Y.; Liu T.; Meng B.; Li X.; Liang G.; Hu X.; Wang Q. J. Broadband high photoresponse from pure monolayer graphene photodetector. Nat. Commun. 2013, 4, 1811. 10.1038/ncomms2830. [DOI] [PubMed] [Google Scholar]
  22. Chen P.-Y.; Soric J.; Alú A. Invisibility and cloaking based on scattering cancellation. Adv. Mater. 2012, 24, OP281–OP304. 10.1002/adma.201202624. [DOI] [PubMed] [Google Scholar]
  23. Salisbury W. W.Absorbent body of electromagnetic waves. U.S. Patent 2,599,944, 1952.
  24. Andryieuski A.; Lavrinenko A. V. Graphene metamaterials based tunable terahertz absorber: effective surface conductivity approach. Opt. Express 2013, 21, 9144. 10.1364/OE.21.009144. [DOI] [PubMed] [Google Scholar]
  25. Batrakov K.; Kuzhir P.; Maksimenko S.; Paddubskaya A.; Voronovich S.; Lambin P.; Kaplas T.; Svirko Y. Flexible transparent graphene/polymer multilayers for efficient electromagnetic field absorption. Sci. Rep. 2015, 4, 7191. 10.1038/srep07191. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Huidobro P. A.; Kraft M.; Maier S. A.; Pendry J. B. Graphene as a Tunable Anisotropic or Isotropic Plasmonic Metasurface. ACS Nano 2016, 10, 5499–5506. 10.1021/acsnano.6b01944. [DOI] [PubMed] [Google Scholar]
  27. Batrakov K.; Kuzhir P.; Maksimenko S.; Volynets N.; Voronovich S.; Paddubskaya A.; Valusis G.; Kaplas T.; Svirko Y.; Lambin P. Enhanced microwave-to-terahertz absorption in graphene. Appl. Phys. Lett. 2016, 108, 123101. 10.1063/1.4944531. [DOI] [Google Scholar]
  28. Galiffi E.; Pendry J.; Huidobro P. Broadband Tunable THz Absorption with Singular Graphene Metasurfaces. ACS Nano 2018, 12, 1006–1013. 10.1021/acsnano.7b07951. [DOI] [PubMed] [Google Scholar]
  29. Zhan T.; Shi X.; Dai Y.; Liu X.; Zi J. Transfer matrix method for optics in graphene layers. J. Phys.: Condens. Matter 2013, 25, 215301. 10.1088/0953-8984/25/21/215301. [DOI] [PubMed] [Google Scholar]
  30. Kakenov N.; Balci O.; Takan T.; Ozkan V. A.; Altan H.; Kocabas C. Observation of Gate-Tunable Coherent Perfect Absorption of Terahertz Radiation in Graphene. ACS Photonics 2016, 3, 1531–1535. 10.1021/acsphotonics.6b00240. [DOI] [Google Scholar]
  31. Srivastava Y.; Manjappa M.; Cong L.; Krishnamoorthy H.; Savinov V.; Pitchappa P.; Singh R. A Superconducting Dual-Channel Photonic Switch. Adv. Mater. 2018, 30, 1801257. 10.1002/adma.201801257. [DOI] [PubMed] [Google Scholar]
  32. Lim W.; Manjappa M.; Srivastava Y.; Cong L.; Kumar A.; MacDonald K.; Singh R. Ultrafast All-Optical Switching of Germanium-Based Flexible Metaphotonic Devices. Adv. Mater. 2018, 30, 1705331. 10.1002/adma.201705331. [DOI] [PubMed] [Google Scholar]
  33. Bakoz A.; Liles A.; Gonzalez-Fernandez A.; Habruseva T.; Hu C.; Viktorov E.; Hegarty S.; ÓFaolain L. Wavelength stability in a hybrid photonic crystal laser through controlled nonlinear absorptive heating in the reflector. Light: Sci. Appl. 2018, 7, 39. 10.1038/s41377-018-0043-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. George P.; Strait J.; Dawlaty J.; Shivaraman S.; Chandrashekhar M.; Rana F.; Spencer M. Ultrafast optical-pump terahertz-probe spectroscopy of the carrier relaxation and recombination dynamics in epitaxial graphene. Nano Lett. 2008, 8, 4248–4251. 10.1021/nl8019399. [DOI] [PubMed] [Google Scholar]
  35. Strait J.; Wang H.; Shivaraman S.; Shields V.; Spencer M.; Rana F. Very slow cooling dynamics of photoexcited carriers in graphene observed by optical-pump terahertz-probe spectroscopy. Nano Lett. 2011, 11, 4902–4906. 10.1021/nl202800h. [DOI] [PubMed] [Google Scholar]
  36. Huang L.; Gao B.; Hartland G.; Kelly M.; Xing H. Ultrafast relaxation of hot optical phonons in monolayer and multilayer graphene on different substrates. Surf. Sci. 2011, 605, 1657–1661. 10.1016/j.susc.2010.12.009. [DOI] [Google Scholar]
  37. Tielrooij K.; Massicotte M.; Piatkowski L.; Woessner A.; Ma Q.; Jarillo-Herrero P.; Hulst N.; Koppens F. Hot-carrier photocurrent effects at graphene-metal interfaces. J. Phys.: Condens. Matter 2015, 27, 164207. 10.1088/0953-8984/27/16/164207. [DOI] [PubMed] [Google Scholar]
  38. Mihnev M.; Kadi F.; Divin C.; Winzer T.; Lee S.; Liu C.-H.; Zhong Z.; Berger C.; De Heer W.; Malic E.; Knorr A.; Norris T. Microscopic origins of the terahertz carrier relaxation and cooling dynamics in graphene. Nat. Commun. 2016, 7, 11617. 10.1038/ncomms11617. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Jnawali G.; Rao Y.; Yan H.; Heinz T. Observation of a transient decrease in terahertz conductivity of single-layer graphene induced by ultrafast optical excitation. Nano Lett. 2013, 13, 524–530. 10.1021/nl303988q. [DOI] [PubMed] [Google Scholar]
  40. Shi S.-F.; Tang T.-T.; Zeng B.; Ju L.; Zhou Q.; Zettl A.; Wang F. Controlling graphene ultrafast hot carrier response from metal-like to semiconductor-like by electrostatic gating. Nano Lett. 2014, 14, 1578–1582. 10.1021/nl404826r. [DOI] [PubMed] [Google Scholar]
  41. Winnerl S.; Göttfert F.; Mittendorff M.; Schneider H.; Helm M.; Winzer T.; Malic E.; Knorr A.; Orlita M.; Potemski M.; Sprinkle M.; Berger C.; De Heer W. Time-resolved spectroscopy on epitaxial graphene in the infrared spectral range: Relaxation dynamics and saturation behavior. J. Phys.: Condens. Matter 2013, 25, 054202. 10.1088/0953-8984/25/5/054202. [DOI] [PubMed] [Google Scholar]
  42. Kar S.; Mohapatra D.; Freysz E.; Sood A. Tuning photoinduced terahertz conductivity in monolayer graphene: Optical-pump terahertz-probe spectroscopy. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 165420. 10.1103/PhysRevB.90.165420. [DOI] [Google Scholar]
  43. Falkovsky L.; Varlamov A. Space-time dispersion of graphene conductivity. Eur. Phys. J. B 2007, 56, 281–284. 10.1140/epjb/e2007-00142-3. [DOI] [Google Scholar]
  44. Multiphysics C.COMSOL Multiphysics, www.comsol.com.
  45. Docherty C.; Lin C.-T.; Joyce H.; Nicholas R.; Herz L.; Li L.-J.; Johnston M. Extreme sensitivity of graphene photoconductivity to environmental gases. Nat. Commun. 2012, 3, 1228. 10.1038/ncomms2235. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Parkinson P.; Joyce H.; Gao Q.; Tan H.; Zhang X.; Zou J.; Jagadish C.; Herz L.; Johnston M. Carrier lifetime and mobility enhancement in nearly defect-free core-shell nanowires measured using time-resolved terahertz spectroscopy. Nano Lett. 2009, 9, 3349–3353. 10.1021/nl9016336. [DOI] [PubMed] [Google Scholar]
  47. Aumanen J.; Johansson A.; Koivistoinen J.; Myllyperkiö P.; Pettersson M. Patterning and tuning of electrical and optical properties of graphene by laser induced two-photon oxidation. Nanoscale 2015, 7, 2851–2855. 10.1039/C4NR05207B. [DOI] [PubMed] [Google Scholar]
  48. Graham M.; Shi S.-F.; Ralph D.; Park J.; McEuen P. Photocurrent measurements of supercollision cooling in graphene. Nat. Phys. 2013, 9, 103–108. 10.1038/nphys2493. [DOI] [Google Scholar]

Articles from ACS Photonics are provided here courtesy of American Chemical Society

RESOURCES