 Phosphofructokinases catalyze the ATP-dependent phosphorylation of fructose-6-phosphate and they are highly regulated.
Phosphofructokinases catalyze the ATP-dependent phosphorylation of fructose-6-phosphate and they are highly regulated.
Abstract
Phosphofructokinases (Pfks) catalyze the ATP-dependent phosphorylation of fructose-6-phosphate (F6P) and they are regulated in a wide variety of organisms. Although numerous aspects of the kinetics and regulation have been characterized for Pfks, the knowledge about the mechanism of the phosphoryl transfer reaction and the transition state lags behind. In this work, we describe the X-ray crystal structure of the homodimeric Pfk-2 from E. coli, which contains products in one site and reactants in the other, as well as an additional ATP molecule in the inhibitory allosteric site adjacent to the reactants. This complex was previously predicted when studying the kinetic mechanism of ATP inhibition. After removing the allosteric ATP, molecular dynamic (MD) simulations revealed conformational changes related to domain packing, as well as stable interactions of Lys27 and Asp256 with donor (ATP) and acceptor (fructose-6-) groups, and of Asp166 with Mg2+. The phosphoryl transfer reaction mechanism catalyzed by Pfk-2 was investigated through Quantum Mechanics/Molecular Mechanics (QM/MM) simulations using a combination of the string method and a path-collective variable for the exploration of its free energy surface. The calculated activation free energies showed that a dissociative mechanism, occurring with a metaphosphate intermediate formation followed by a proton transfer to Asp256, is more favorable than an associative one. The structural analysis reveals the role of Asp256 acting as a catalytic base and Lys27 stabilizing the transition state of the dissociative mechanism.
1. Introduction
Phosphoryl transfer reactions are crucial for metabolic pathways and cellular signaling transduction.1–4 These reactions are catalyzed by kinases that transfer the terminal phosphate group from the phosphoryl donor (most commonly ATP) to nucleophilic groups on the acceptor molecule, which could be small molecules such as sugars and lipids, or the side chains of particular residues in proteins.5–11 The ATP-dependent phosphorylation of fructose-6-phosphate (F6P) to yield fructose-1,6-bisphosphate (FBP) is catalyzed by phosphofructokinase (fructose-6-P kinase, Pfk), which is believed to have an important role in glycolysis regulation.12 In Escherichia coli, this reaction is performed by two non-homologous isoenzymes, Pfk-1 and Pfk-2.12 Pfk-2, the minor isoenzyme, is one of the most extensively characterized member of the ribokinase-like superfamily,13,14 which includes ribokinases, fructokinases, fructose-1-P kinases, tagatose-6-P kinases and nucleoside kinases, among others.13,15 In this superfamily the phosphoryl transfer process has been studied by in vacuo QM calculations of a reduced active site of thiazole kinase, ThiK, a distant homologue of Pfk-2.16,17 Although a QM/MM calculation was not performed in that contribution, their findings help to identify residues important for transition state stabilization, albeit noting that a more realistic catalytic environment should be considered. In the light of this prior information, however, the phosphoryl transfer for Pfks has not been studied so far.
X-ray structures of Pfk-2 with the F6P substrate (PDB ID: 3N1C) and with two MgATP2– (PDB ID: ; 3CQD) have been previously reported. There are few kinase structures in the Protein Data Bank (PDB) that are bound to both reactants and products, namely the xylulose kinase from Lactobacillus acidophilus (PDB ID: ; 3LL3), phosphoglycerate kinase from Homo sapiens (PDB ID: ; 2X15) and adenylate kinase from Plasmodium falciparum (PDB ID: ; 3TLX), which has not been associated to any publication, and, noteworthy, the Pfk-1 from E. coli with its reaction products.18 In this work, for the first time, we report the structure of a member of the ribokinase family (Pfk-2) solved with both reactants and products in the same crystal (PDB ID: ; 3UQD). Thus, this crystallographic structure could serve as a model to study the chemical reaction catalyzed by the enzyme, as it provides information not only about the position of each ligand at the beginning and the end of the phosphorylation reaction but also about the residues performing key interactions that could be relevant for the catalytic activity of the enzyme.
The ribokinase superfamily has been studied in terms of evolution, showing that the overall fold and reaction machinery are strongly conserved over a wide range of species and substrate specificities.19 In this family, the general chemical reaction consists of the ATP-dependent phosphorylation of a hydroxymethyl group in the substrates.13 Although the sequence similarities of these proteins are in the range of 18–22%,20 the alignment of different protein–ligand complexes reveals conserved regions that are important for catalysis and protein stabilization.14,21–24 These conserved regions have been targets of multiple studies, with Pfk-2 being the most studied phosphosugar kinase member at the biochemical and structural level.12,14,24–34 Noteworthy, the GXGD14,35 motif contains a highly conserved aspartate residue, for which the D256N mutation in Pfk-2 produced a striking 15 000-fold decrease in the catalytic constant with no variation in the KM values for F6P or MgATP2–. This result indicates that Asp256 participates specifically in catalysis but not in substrate binding in Pfk-2.14 This residue has also been proposed to have a catalytic role in d-tagatose-6-P kinase (LacC), which is closely related to Pfk-2. In 2007, Miallau36et al. proposed a mechanism for LacC in which the side chain of the GXGD aspartate residue (Asp254) removes a proton from the substrate C1 hydroxyl group to activate the oxygen atom as a nucleophile, which then attacks the γ-phosphate of ATP to yield the phosphorylated product. Another residue involved in catalysis is present in the conserved “motif-I” located at the N-terminal region that ends with a lysine residue, as in 1-phosphofructokinase from E. coli (Lys41), LacC from S. aureus (Lys38) and ribokinase from Lactococcus lactis (Lys40).14,36 Thus, they also proposed that the nearby conserved lysine residue (Lys38) likely stabilizes the negative charge of the transition state.36 Following this reasoning, we present a mechanistic model for Pfk-2 in which the equivalent GXGD aspartate residue (Asp256) abstracts the proton from the substrate (see Fig. S1 in the ESI,† upper mechanism).
In general, two kinds of limiting mechanisms have been proposed for phosphoryl transfer reactions,4,37 which can be considered as the extremes across a spectrum of possible concerted (ANDN) mechanisms. On the one hand, in the associative or addition–elimination (AN + DN) mechanism, a nucleophilic attack occurs prior to the departure of the leaving group, and the reaction proceeds via a pentavalent phosphorane intermediate. If Pfk-2 performed this mechanism, the proton of the sugar phosphate substrate would be transferred to one of the non-bridging oxygen atoms of the phosphate group (see Fig. S1 in the ESI,† lower mechanism), decreasing its charge and favoring the approach to the nucleophile. On the other hand, in the dissociative or elimination–addition (DN + AN) mechanism, the reaction proceeds via an expansive transition state (TS) with metaphosphate character, where bond cleavage of the leaving group occurs prior to bond formation with the nucleophile. If the phosphoryl transfer of Pfk-2 followed this mechanism, the carboxylate group in a side chain would act as the base responsible for substrate deprotonation. In this case, the formal negative charges born by both the phosphate group and the nucleophile would then favor a dissociative mechanism. This same carboxylate group would then act as an acid to protonate the transferred phosphoryl group and thus regenerate the enzyme to its original state. This last step has been studied at the quantum mechanics/molecular mechanics (QM/MM) level in protein kinases, demonstrating its feasibility.38
In this work, we describe the crystallographic structure of Pfk-2 with products in one active site and reactants in the other, plus an additional MgATP2– positioned in the allosteric site adjacent to reactants. With this structure we performed an in-depth theoretical study of the phosphorylation reaction mechanism, using highly parallelized computational techniques. The comparison of the interactions observed in the crystal, and during MD simulations of the active sites containing reactants and products, allows the identification of a conformational change in the chain bearing the products that is essential for the reaction to take place. Furthermore, Lys27 adopts a better conformation for the reaction and Asp166 joins the coordination sphere of Mg2+, replacing a water molecule. QM/MM calculations were performed considering the effect of the protein environment and its flexibility.39 We determined that Pfk-2 follows a dissociative phosphorylation mechanism during catalysis, and we also clarified the role of some conserved residues within the ribokinase family, particularly those participating in enzyme catalysis.
2. Methods
2.1. Crystallization, data collection, structure determination and refinement
The enzyme was purified as described by Parducci et al. (2006).27 All details related with crystallization, data collection and structure determination are widely described in the ESI.† The structure of E. coli Pfk-2 in complex with the products (FBP and MgADP–) in one active site and the reactants (F6P and MgATP2–) in the other active site, which is coterminous with the inhibitor MgATP2– in the allosteric site, are deposited in Protein Data Bank, code ; 3UQD. Full statistics for data collection and refinement are given in Table S1 in the ESI.†
2.2. Classical and QM/MM molecular dynamics simulations
2.2.1. System building and MD simulations
The starting structure for our calculations was built from the X-ray crystal of Pfk-2 in complex with reactants and products (PDB ID: 3UQD) reported in this communication. It is known that this enzyme performs its catalytic activity in the dimeric state,26,40,41 therefore, we chose to work with only one of the two dimers (named as chains B and D, following the nomenclature used by prior crystal structure of this enzyme).29 The chains A and C, which complete the tetramer in the asymmetric unit, were removed. In this selected dimer, chain B contained the products (FBP and MgADP–), and chain D contained the reactants (F6P and MgATP2–). The allosteric inhibitor MgATP2–, originally bound to the active site containing the reactants, was removed prior to the simulation in order to eliminate any possible effect for the presence of this inhibitor. Once the appropriate chains and ligands were selected, the system was prepared as described in the ESI.† The ESI† also contains a more detailed account of the computational proceedings for the 100 ns of fully unrestrained MD simulations that we performed after system equilibration and Table S2† with the protonation states of histidines.
2.2.2. QM/MM calculations
After the classical MD simulation, QM/MM calculations were performed using the fDynamo program.42 For that purpose we selected the active site containing the products because, as discussed below, it might reflect better the catalytically competent arrangement of interactions for phosphoryl transfer (see Results and discussion). We assumed that only one Mg2+ ion participates in catalysis; although the active site with reactants has an additional Mg2+ ion, this additional ion participates only in the formation of the inhibitory complex as it is demonstrated that the complex MgATP2– is the actual inhibitor for Pfk-2 (ref. 25) and it is not involved in catalysis. Moreover, in the products-containing chain, there was just one Mg2+ ion forming the MgADP– complex (an actual product), without any signal about a potential location for a second ion. Using the active site containing the products as a scaffold, we made the appropriate modifications to generate the reactant structure, leaving chain D unaltered. This procedure can be viewed as a follow up of the reverse reaction (from products to reactants), considering that the mechanism of the forward and reverse reactions is the same (the principle of microscopic reversibility). For the sake of clarity, the results of the simulations are discussed considering the direction from reactants to products.
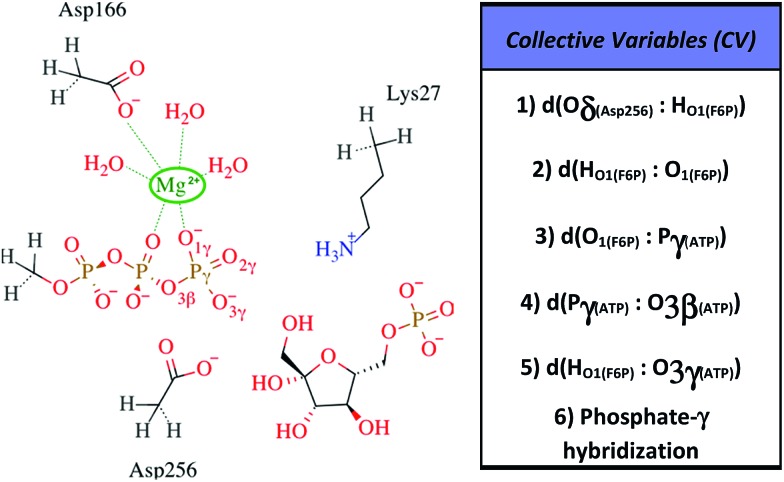
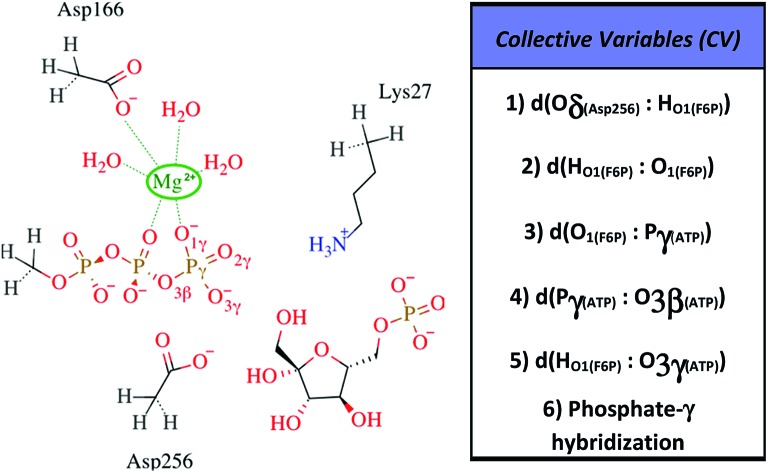
All information related with the selected QM subsystem and computational methods used are described in the ESI.† Briefly, the AM1d-PhoT Hamiltonian43,44 was selected for the QM subsystem. The atoms included in the selected QM subsystem are represented in Fig. 1. QM/MM MD simulations were carried out in order to obtain the Minimum Free Energy Paths (MFEPs) by means of the on-the-fly string method.39,45,46 These MFEPs were obtained in the space of Collective Variables (CVs) that define the most important changes taking place during the chemical reaction (see Fig. 1). Once the converged MFEPs were determined, the corresponding potentials of mean force (PMFs) were obtained using the umbrella sampling method47 along the path CVs39,45 that define the progress of the system along these paths. This methodological combination has proven to be an efficient approach for studying the free energy landscapes of complex enzymatic reactions.39,48,49 Details related with the simulations performed are widely described on the ESI.†
Fig. 1. Selected QM region for the F6P phosphorylation reaction is shown to the left, the hydrogen-link atoms are represented using dashed bonds. To the right, the collective variables used to explore the reaction mechanisms are defined.
3. Results and discussion
3.1. Interactions of Pfk-2 with substrates and products revealed by crystal structure
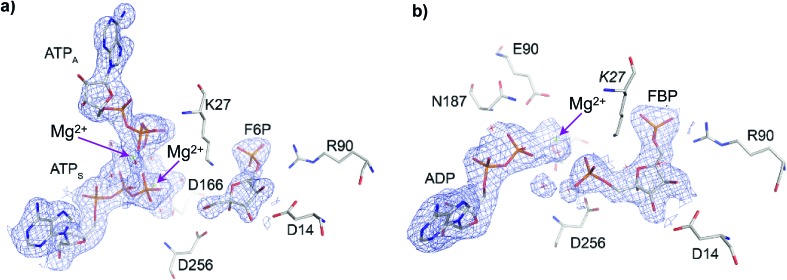
The crystallographic structure of Pfk-2 was obtained in the presence of reactants and products (PDB ID: 3UQD). As previously described for the Pfk-2:F6P complex (PDB ID: ; 3N1C),31 we observed four monomers in the asymmetric unit, which were related by a 222 symmetry (a dimer of dimers), with chains A and C, or B and D, composing the dimeric form observed in solution. The difference electron density map clearly showed the presence of the products FBP and MgADP– in one active site of the dimer (chains B and C), and the reactants F6P and MgATP2– in the other active site (chains D and A). Interestingly, an additional MgATP2– was found at the inhibitory allosteric site in chains D and A, in close contact with MgATP2–. Fig. 2 shows the active sites of chains B and D. The presence of F6P and ATP in the crystallographic structure was unexpected because the crystallization conditions were established to contain only the products; therefore, we suggest that the enzyme might have catalyzed the reverse reaction, at least to the extent needed for binding (both substrate sites and the allosteric site) and for complex crystallization. Notably, in the kinetic mechanism of Pfk-2 substrate inhibition31 proposed on the basis of protein–ligand complexes determined by X-ray crystallography, such as Pfk-2:(MgATP)2 (PDB ID: ; 3CQD) and Pfk-2:F6P (PDB ID: ; 3N1C), the occurrence of the species Pfk-2:F6P:(MgATP)2 was predicted. Taken together, the structure described in this report provides the opportunity to study one crucial intermediate in the allosteric inhibition mechanism of the enzyme, as well as the conformational changes occurring upon phosphoryl transfer.
Fig. 2. Active sites of Pfk-2 in chains (a) D and (b) B, containing F6P and FBP, respectively. In (a) the electron density omit map (Fo–Fc) contoured at 2σ for F6P and both MgATP2– is shown in blue (where ATPS is the substrate ATP and ATPA is the allosteric ATP). Residues surrounding F6P are represented. In (b) the corresponding electron density omit map for FBP and MgADP– is shown in blue. Residues surrounding FBP are represented. The arrows indicate the Mg2+ ions positions.
As previously described for Pfk-2 and other ribokinase family members,21,29,36 the overall fold of the monomer consists of two domains, which perform different roles in substrate binding and oligomerization. The major domain is formed by a central β-sheet surrounded by α-helices, where a long furrow along the C-terminal edge of the sheet provides residues for the active site that contact F6P, ATP4– and Mg2+. The minor domain consists of a four-stranded β-sheet that acts as a lid over the active site and provides residues mainly involved in contacting F6P. This domain forms the monomer–monomer interface by orthogonal β-sheet packing, and shares part of the β3 strand with the complementary sheet in an arrangement called a β-clasp. The first half of β3 provides residues to the active and allosteric sites in the adjacent subunit of the dimer.31 It has been observed that the major and minor domains change their relative orientation upon substrate binding.26 For instance, whereas the chains in the crystal structure of the Pfk-2:F6P complex present variable relative orientations, in the Pfk-2:(MgATP)2 complex they adopt a fixed position. This induced fit upon sugar binding was also observed in the present structure, in which different relative orientations between domains are observed among the four monomers in the asymmetric unit.
In the active site bearing reactants the F6P molecule is oriented by electrostatic interactions between the 6-phosphate group and the positive charges of Arg90 and Arg29 (from the complementary chain) in a similar fashion as observed in the Pfk-2:F6P complex (PDB ID: 3N1C, chain D). In addition, hydroxyl groups OH3 and OH4 of the sugar phosphate sustained a bidentate coordination with the carboxylate group of Asp14 (as observed in Fig. 2a) that, although conserved in the Pfk-2:F6P complex, is somewhat pushed apart, decreasing the observed restraint on the torsion angle along the C3–C4 bond.31 As a consequence of the change in the sugar ring conformation, the Hydrogen Bond (HB) network around groups OH1, OH2 and OH3 is rearranged. Moreover, the oxygen atom of the hydroxyl group OH2 comes closer to the carboxylate oxygens of Asp256 (dO2(F6P):Oδ(Asp256) = 3.68 Å) than the oxygen atom of the group to be phosphorylated, OH1 (dO1(F6P):Oδ(Asp256) = 3.89 Å). Additionally, more solvent molecules can be found around the sugar phosphate, indicating more solvent accessibility than in the Pfk-2:F6P complex, consistent with a more open enzyme conformation. Moreover, Lys27 from the complementary chain is slightly displaced away from the 6-phosphate group and the fructose OH1. Regarding the substrate and inhibitor nucleotides, they are bound in a similar fashion as seen in the Pfk-2:(MgATP)2 complex.29 The β-phosphoryl group interacts with Asn187, whereas one Mg2+ ion is coordinated by oxygen atoms belonging to the β- and γ-phosphates (as seen in Fig. 2a) and through water molecules to Lys185, Glu190 and Asp166, similar to the Pfk-2:(MgATP)2 complex.29 The second Mg2+ ion belongs to the inhibitor MgATP2– and is coordinated with β- and γ-phosphoryl groups of ATPS and ATPA (as seen in Fig. 2a). Although the inhibitor MgATP2– forms π–π stacking with Tyr23, this nucleotide is displaced compared to the Pfk-2:(MgATP)2 complex29 because of the minor domain movement. Another important difference is that Lys27 is not able to interact with the γ-phosphate of the nucleotide, due to the interactions established with the 6-phosphate group of the sugar. These observations indicate a mutual negative effect of the binding of F6P and the allosteric MgATP2–.
In the active site containing the products (FBP and ADP, see Fig. 2b) only one Mg2+ ion has been found, and it forms the MgADP– product. The loop β13–α8 that surrounds the adenine moiety is slightly displaced towards the minor domain, according to the compaction of the whole subunit. Interactions with the 6-phosphate group are close to those described for the active site with reactants. However, HB interactions between the carboxylate oxygens of Asp14 and OH3 or OH4 hydroxyl groups of the sugar are strengthened, although without the constrained torsion observed in the Pfk-2:F6P complex.31 OH1 is closer to the Asp256 carboxylate group than OH2, similar to the disposition found in the Pfk-2:F6P complex. The guanidinium group of Arg105 is bound to the 1-phosphate group. The side chain nitrogen from Lys27 is tightly coordinated to phosphoryl groups 1 and 6.
Multiple sequence alignments of ribokinase family members show that a conserved lysine residue, associated with a catalytic role,21,36 is located at the N-terminus of the α1-helix29 belonging to the so-called “motif I,” with a conserved sequence XGKG. It has been stated that the combination of main-chain amide nitrogens and the conserved positively charged side-chains create an anion hole that helps to stabilize the transition state.21 For Pfk-2, this residue has been replaced by a glycine in the primary structure, mainly to make room for the OH2 group of the substrate.31 However, Lys27 of the complementary chain has its –NH3+ group at the same spatial location as the abovementioned conserved lysine side-chain.31 It is known that dimer formation is essential for catalysis in this family. In the case of Pfk-2, this seems to be due to the requirement of Lys27 from the complementary subunit to be present in the active site. The spatial location of this residue creates a charge-relay network that ultimately conducts the phosphorylation reaction. Some relevant distances and energy values are collected on the ESI (Tables S3 and S4†).
3.2. Classical MD reveals conformational diversity in the active sites
The presence of reactants and products in different active sites provides valuable information about conformational changes during Pfk-2 catalysis, because these configurations represent the initial and final states of the reaction pathway. However, the whole structure must be relaxed from the strains imposed by interactions that arise from crystal packing. Therefore, we performed 100 ns MD simulation as we described in the ESI.† MD provided information about (i) the overall structural changes of the system, (ii) the stability of interactions between Pfk-2 residues and ligands at each active site, and (iii) the stability of the relative position of the ligands in each active site.
Interactions in the active sites of each complex seem to depend on the relative orientations of the domains, which in turn could be affected by the presence of the inhibitor MgATP2–, because it bridges the minor and major domains, stabilizing the overall conformation as we previously stated in Section 3.1. Thus, in order to assess changes in the level of compaction between both chains along the trajectory, we calculated the distance between the center of mass (COM) of the two domains (Fig. S3, see ESI†) using the VMD plug-in DisRg developed by Falsafi-Zadeh et al.50 These results showed that a closed conformation is favored in the product-containing chain.
After crystal packing relaxation, it is worthy to evaluate any change in the most relevant interactions within the active site. In this way, F6P conserved a very stable network of interactions with Arg90 and Asp14 residues that explains the recognition and affinity of this substrate in the active site (see Fig. S4 and S5, ESI†). Moreover, the interaction made with the conserved Asp256 residue (that belongs to the GXGD motif13,14) keeps stable during the entire MD simulation, although during the system construction, the PROPKA51 program determined that residue Asp256 in chain B should be protonated according to its chemical environment (Fig S5, ESI†). Additionally, the triphosphate moiety of MgATP2– performed stable interactions with Lys27, Lys185, Asn187 and Ser224 residues (Fig. S6 and S7, ESI†). Furthermore, the coordination sphere of Mg2+ keeps stable during the simulation; with the only change that Asp166 enters this coordination sphere replacing one water molecule with respect to the crystal structure. Finally, the distance between ligands in each chain was measured, revealing that in the reactants-containing chain, the distance between ligands constantly fluctuated approximately 5.2 Å, but in the case of the chain containing products, this distance was more stable and remained constant at an average value of 4.3 Å in the last 40 ns. Further details related with all these interactions are given in the ESI.†
To analyze the phosphoryl transfer pathway, we could have used either the active site with reactants, removing the inhibitor MgATP2–, or the active site with products. Considering that the monomer containing the reactants was initially prepared from an inhibited structure, some features seem to indicate that it could be further away from the catalytic conformation. The proximity between the phosphorous atom of the transferred phosphate group and the oxygen atom of the leaving ADP indicates a shorter path for phosphoryl transfer in the active site with products. The closed conformation observed in Pfk-2:F6P31 and Pfk-2:FBP:ADP complexes also argues in favor of this as the catalytic, and thus the best, conformation for QM/MM simulations of the reaction mechanisms.
3.3. QM/MM simulations show the preference for a dissociative mechanism in Pfk-2
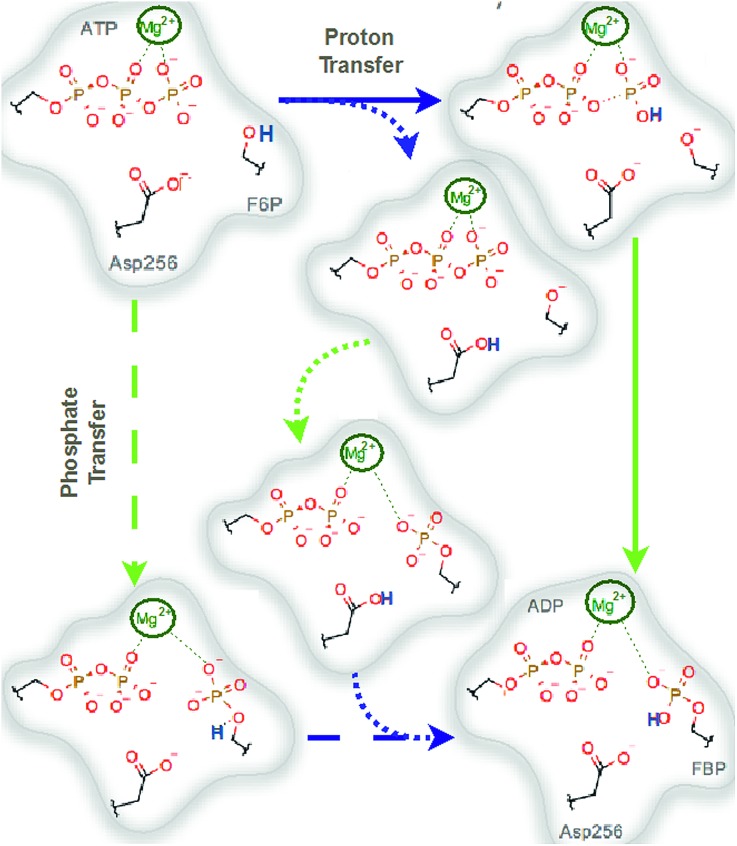
We explored different phosphoryl transfer reaction mechanisms using a hybrid QM/MM potential as described in the Method section above, and determined the most reliable one in terms of free energy barriers. The reaction catalyzed by Pfk-2 consists of two chemical steps: (i) phosphoryl transfer from MgATP2– to the 1-hydroxyl (OH1) of F6P, and (ii) abstraction of the proton from this acceptor group by a surrounding base, which could be either the Asp256 residue or a non-bridging oxygen atom of the transferred phosphate group. Accordingly, we explored different mechanistic proposals schematically shown in Fig. 3. Considering different options for the base in charge of proton abstraction (Asp256 or the phosphate group itself) we have: (i) direct proton transfer to the non-bridging oxygen atom followed by phosphate transfer (upper right corner of Fig. 3) or (ii) vice versa (lower left corner), and (iii) proton transfer via Asp256 followed by phosphate transfer (along the diagonal). A MFEP calculation was performed with initial guesses corresponding to these mechanistic variants and the results of the string method converged to two possible mechanisms presented in Fig. 4–7. In the first one (Path 1) the catalytic residue Asp256 acts as a general base and deprotonates the OH1 group of the sugar substrate (F6P), which further attacks the MgATP2– γ-phosphate.35 The second path (Path 2) resulted in a substrate-assisted mechanism in which one of the non-bridging γ-phosphate oxygen atoms acts as a general base.
Fig. 3. Schematic representation of possible reaction mechanisms catalyzed by Pfk-2. The arrows indicate the possible paths. Starting for the reactants (upper left corner), the reaction could proceed from: (i and ii) a proton transfer (to both Asp256 or γ-phosphate) followed by a phosphate transfer or (iii) by a phosphate transfer followed by a proton transfer. Blue arrows indicate proton transfer events and green arrows indicate phosphate transfer.
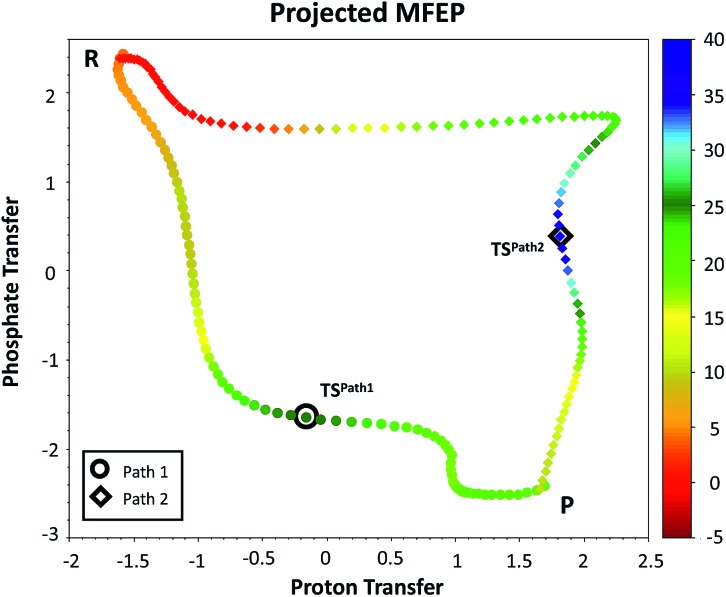
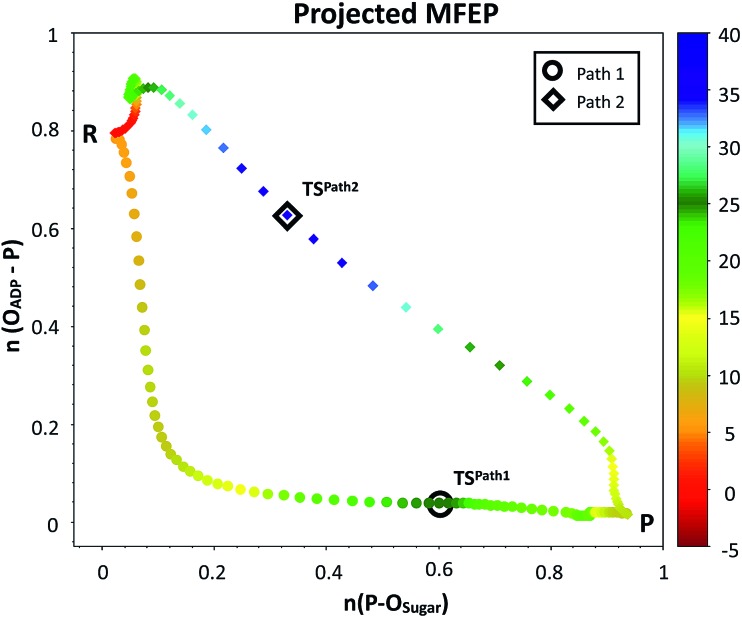
Fig. 4. Minimum free energy paths obtained with the string method for two possible reaction mechanisms observed for F6P phosphorylation catalyzed reaction. The paths are projected on the plane defined by the two antisymmetric combinations of distances defining the proton (d[(O1(F6P)–HO1(F6P)) – (HO1(F6P)–OAcc)], in Å) and the phosphate transfer (d[(O1(F6P)–Pγ(ATP)) – (Pγ(ATP)–O3β(ATP))], in Å). Where OAcc is Oδ(Asp256) for Path 1 with filled circles and O3γ(ATP) for Path 2 in filled diamonds. The colouring scheme represents the free energy coordinate in kcal mol–1.
Fig. 5. Minimum free energy paths obtained with the string method for the phosphorylation character of both converged solutions. The paths are projected on the plane defined by the bond order between the transferred phosphate and the donor oxygen d(Pγ–O1(Sugar)) on the x-axis, and the bond order between the transferred phosphate and the acceptor oxygen d(Pγ–O3β(Nucleotide)) on the y-axis. The colouring scheme represents the free energy of both converged Paths in kcal mol–1.
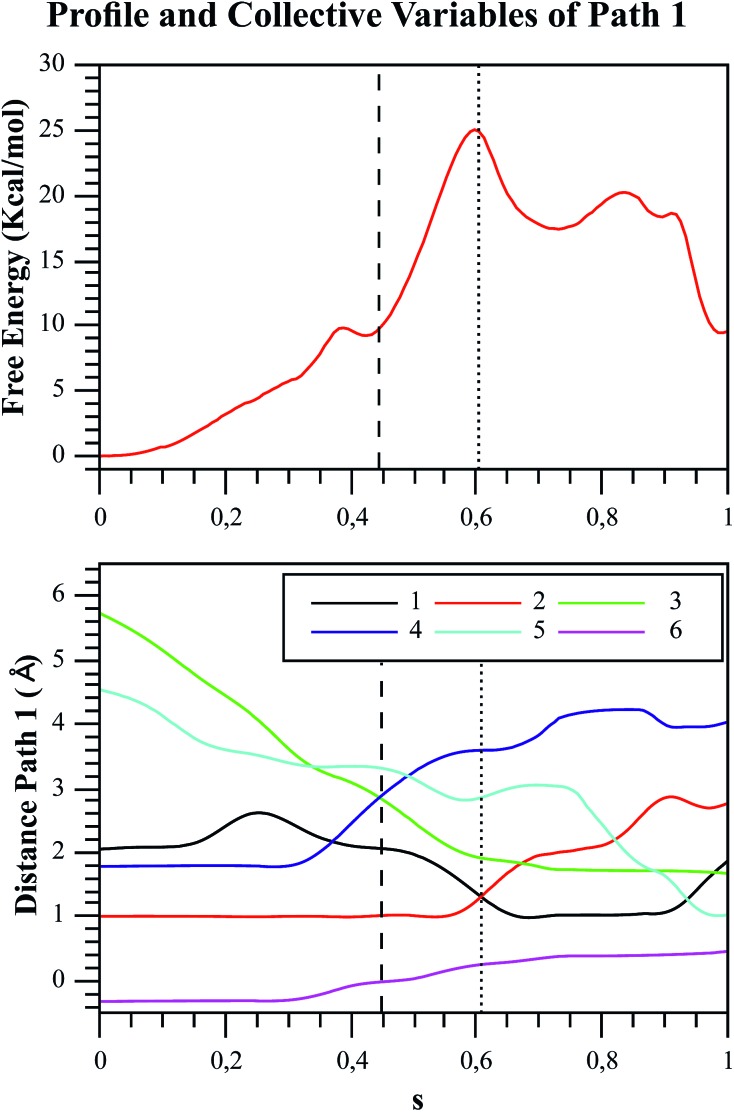
Fig. 6. Free energy profile of Path 1 along the s coordinate, obtained with the string method under the AM1/d-PhoT/OPLS level (upper chart). The collective variables obtained on each node are also depicted (lower chart). Each number represents the following CVs: (1) d(Oδ(Asp256):HO1(F6P)); (2) d(HO1(F6P):O1(F6P)); (3) d(O1(F6P):Pγ(ATP)); (4) d(Pγ(ATP):O3β(ATP)); (5) d(HO1(F6P):O3γ(ATP)); (6) phosphate-γ hybridization. The phosphate and proton transfers are indicated with dashed and pointed lines, respectively.
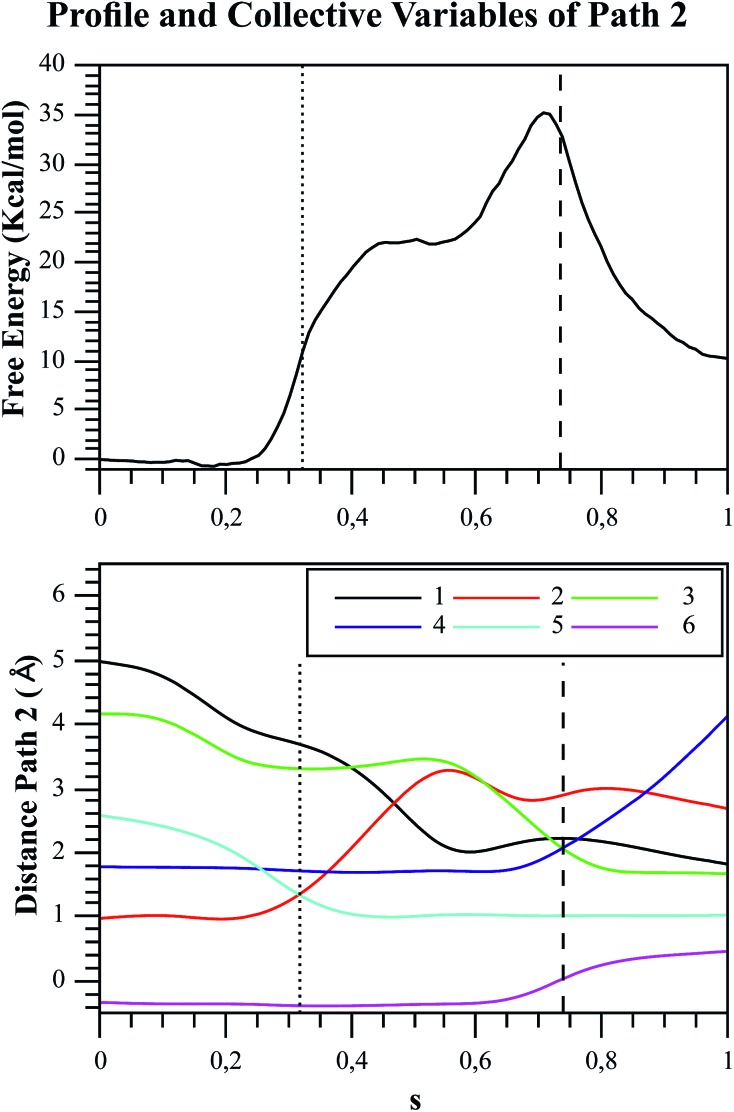
Fig. 7. Free energy profile of Path 2 along the s coordinate, obtained with the string method under the AM1/d-PhoT/OPLS level (upper chart). The collective variables obtained on each node are also depicted (lower chart). Each number represents the following CVs: (1) d(Oδ(Asp256):HO1(F6P)); (2) d(HO1(F6P):O1(F6P)); (3) d(O1(F6P):Pγ(ATP)); (4) d(Pγ(ATP):O3β(ATP)); (5) d(HO1(F6P):O3γ(ATP)); (6) phosphate-γ hybridization. The proton and phosphate transfers are indicated with pointed and dashed lines, respectively.
3.3.1. The role of Asp256 and Lys27 in the converged mechanisms
Fig. 4 depicts the minimum free energy path obtained for the converged mechanisms projected on the phosphate and proton transfer coordinates. At the beginning of Path 1, Asp256 is well-positioned for the proposed proton abstraction, as has been also found in other phosphosugar kinases.36 In this mechanism, the γ-phosphate group transfer to the O1 atom of F6P takes place first and, only when this is very advanced, the Asp256 residue removes the F6P OH1 proton. At the last stage of this mechanism, the abstracted proton is transferred from Asp256 to the phosphate, completing the process. For Path 2, the process is initiated by a F6P OH1 proton transfer to one of the non-bridging γ-phosphate oxygens followed by a nucleophilic attack on the Pγ atom of MgATP2– by the F6P hydroxyanion.
In order to rationalize the different ordering between proton and phosphate transfers in the two converged mechanisms, we looked at the environment in which the process was taking place. Specifically, we analyzed the distance from Lys27 to the γ-phosphate group along the reaction pathway. In Fig. S10 in the ESI,† the evolution along the MFEPs of the distance between the nitrogen atom of the ε-amino group of Lys27 (NZ(Lys27)) and the phosphorous atom of the γ-phosphate of MgATP2– (Pγ(ATP)) for both converged pathways are depicted, together with the percentage of frames with a HB found between these two groups. We found that Lys27 assists the charge of the transferred phosphate in Path 1 establishing a close interaction with it. On the contrary, Lys27 has a minor role during the first stages of Path 2. Lys27 is found further away of the phosphate group during these first stages of the mechanism described by Path 2. Thus, the nature of the reaction mechanism is strongly coupled to the conformational diversity of the enzymatic active site and, in particular, to the electrostatic complementarity between the reacting fragments (the transferred phosphate group) and the protein (Lys27).
3.3.2. Nature of the phosphoryl transfer
Having obtained a sketch of both converged paths, we sought information about the character of the phosphoryl transfer in each mechanism. There is no clear data about the phosphorylation character prevalence within the ribokinase family. Previous results suggest that this type of kinase follows an associative AN + DN type mechanism,16,17 but this suggestion is based on vacuum QM calculations applied to model systems where the reacting fragments were simplified by eliminating the adenine and the ribose moieties. Although analysis of the system using QM methods is required, it is also essential to consider the environmental effects (protein and/or solvent) on the chemical reaction, as they control and modify the possible reaction mechanisms and energetic profiles, especially when charged species are involved.
The plausible mechanisms for phosphate transfer reactions may be placed on a continuum between a completely associative mechanism and a completely dissociative one as described in the introduction. The nature of these mechanisms can be differentiated by the degree of bond formation and bond cleavage at the TS. In that sense, it is possible to construct a More O'Ferrall–Jencks52–54 diagram, choosing the bond orders (see ESI† for details)55 between the phosphorus atom of the transferred phosphate and either the donor or acceptor oxygen atoms as coordinates. Fig. 5 depicts the MFEPs projected on these bond orders, showing that phosphoryl transfer in Path 1 follows a dissociative-type mechanism. This is characterized by longer bond distances, required for the approach of the negatively charged phosphate to the hydroxyl group of the sugar. The sum of the distances of the phosphorous atom to both the acceptor and donor oxygens is always larger than 5.0 Å to reduce the electrostatic repulsion. Conversely, the phosphoryl transfer in Path 2 follows an associative-type mechanism, in which the phosphate transfer occurs with smaller distances to the donor and acceptor oxygen atoms. The proton is transferred to the γ-phosphate, reducing its charge and increasing the nucleophilicity of the O1 atom. This allows a closer approach between the reacting fragments. Accordingly, the TS in Path 2 appears considerably earlier than the TS in Path 1, in terms of the phosphorus distances to the leaving and nucleophilic oxygen atoms.
3.3.3. Evolution of key distances along the reaction paths
One of the advantages of exploring the free energy landscape instead of potential energy is that it allows the system to be flexible. Therefore, the substrates can change their conformation, helping to cross the free energy barrier, as explained by Ma and Nussinov.56 Additionally, the string method gives us valuable information about the evolution of the CVs, and the corresponding free energy changes along the reaction path. Fig. 6 and 7 depict the free energy profile along the path CV (the s coordinate that measures the advance of the system along the reaction path) and the evolution of the CVs used to define the free energy surface for the two paths. Focusing on Path 1 (Fig. 6), we observed that the initial distance between ligands was very large, reaching a value of almost 5.7 Å. It was reported by Mildvan that the optimal distance between the entering oxygen atom and the attacked phosphorus atom for a dissociative TS should be 4.5–6 Å,57 which is consistent with our results. Looking closely at Fig. 6, there are some crossing points related to important structures drawn from the energetic profile. Around s = 0.45, the crossing between CVs 3 and 4 (d(O1(F6P):Pγ(ATP)) and d(Pγ(ATP):O3β(ATP))), corresponds to the moment when the distances of the transferred phosphoryl group to the donor and acceptor oxygen atoms are exactly the same. At s = 0.6 the CVs 1 and 2 (d(Oδ(Asp256):HO1(F6P)) and d(HO1(F6P):O1(F6P))) cross, corresponding to the moment when the phosphosugar proton is located midway between F6P and the aspartate residue (Asp256). The proton transfer to this residue is the most demanding step energetically speaking, corresponding to the highest TS or bottleneck of the mechanism (see Fig. 6, top), though this process is still coupled to the phosphate transfer, i.e. phosphoryl transfer is not totally completed when proton transfer starts. The asynchronicity between both events (proton and phosphate transfer) has been recently stressed by the results of Lopata et al.58 These authors showed that mutants of dUTPase decouple both processes occurring during the catalytic reaction. At s = 0.95, the final migration of the proton from Asp256 to the O3γ(ATP) oxygen atom of the transferred phosphate takes place, leading to the final reaction products. This last stage of the reaction has a small free energy barrier, although the corresponding TS lies below than that corresponding to the proton transfer from the sugar to Asp256. Unlike the other mechanism, in Path 2 (Fig. 7), the initial distance between the ligands is approximately 4.2 Å, in accordance with the more associative character of the phosphoryl transfer for this path.57 The first intersection is observed at s = 0.3, where the CVs 2 and 5 cross (d(HO1(F6P):O1(F6P)) and d(HO1(F6P):O3γ(ATP))), accounting for the moment when the sugar proton is transferred to one of the non-bridging oxygens of the γ-phosphate group at MgATP2–. At s = 0.5, the CVs 1 and 2 cross (d(Oδ(Asp256):HO1(F6P)) and d(HO1(F6P):O1(F6P))), because residue Asp256 approaches the transferred proton until reaching a distance of approximately 2.0 Å. Although this residue never receives the proton, it assists the stabilization of the protonated phosphate by HB. Finally, the last crossing between CVs 3 and 4 (d(O1(F6P):Pγ(ATP)) and d(Pγ(ATP):O3β(ATP))) takes place at s = 0.75, corresponding to the final phosphate transfer. The crossing point is observed at oxygen–phosphorous 5distances much shorter than in Path 1; being 2.85 and 2.07 Å in Path 1 and Path 2 respectively, which is consistent with the different nature of the phosphoryl transfer shown in Fig. 5. This sequence of events is also consistent with the prior information (see Fig. 4.), in which the proton transfer to the γ-phosphate occurs first in Path 2. Then the protonated phosphate starts its migration following an associative-type mechanism.
3.3.4. Activation free energies and the preferred mechanism of Pfk-2
Once the possible reaction pathways were characterized, the energetics for both mechanisms can be discussed to determine which one is preferred by Pfk-2. Although the associative mechanism obtained for Path 2 appears more chemically intuitive, the free energy barrier for the dissociative mechanism (Path 1) is lower: the difference between the activation free energies is ≈8 kcal mol–1 (27.0 kcal mol–1 for Path 1 and 35.2 kcal mol–1 for Path 2, see Fig. 6 and 7). However, both calculated free energy barriers are still far from the experimental value, estimated from the catalytic rate constant to be of approximately 15.2 kcal mol–1.14,24,27
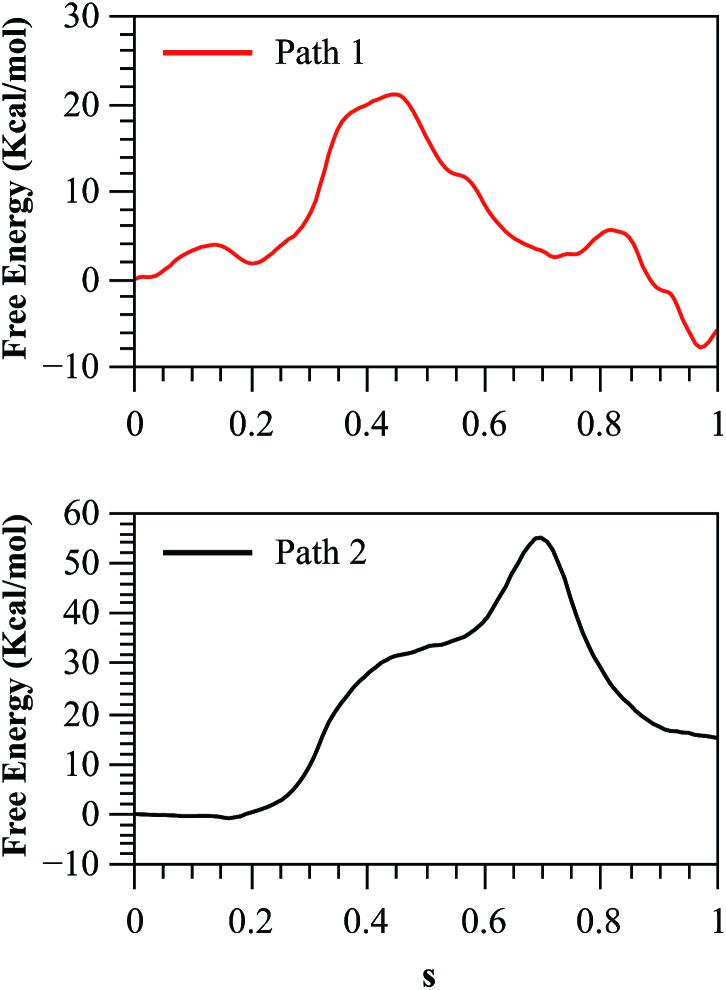
As we described in the Method section and ESI,† QM/MM simulations were performed using the AM1d-PhoT semiempirical Hamiltonian to describe the QM region. Although this semiempirical Hamiltonian was parameterized specifically to consider phosphate transfer reactions,43 a higher level of theory is required to obtain a precise estimation of energetics.59 Therefore, we corrected the converged strings by means of single point calculations on optimized geometries obtained at different values of the path CV coordinate s. For this purpose, we used the hybrid B3LYP/6-311++G**/OPLS Hamiltonian, and obtained the corrected free energy profiles, as depicted in Fig. 8. After this correction, the calculated free energy barriers were 21.0 and 55.2 kcal mol–1 for Paths 1 and 2, respectively. According to both the corrected and uncorrected free energy profiles, the preferred mechanism is the dissociative mechanism described by Path 1.
Fig. 8. Free energy profile for both paths, obtained with the string method and corrected at the B3LYP/6-311++G**/OPLS level.
The free energy profile for this path is still 5.8 kcal mol–1 higher than the experimental value. The discrepancy with the experimentally derived value can also be partially reduced considering the zero-point energy correction to the activation free energy. Once the ZPE is included our best estimation of the activation free energy for the dissociative mechanism (Path 1) is 19.1 kcal mol–1. The remaining error is consistent with the observed reaction energy: although the experimental results show that the reaction is nearly thermoneutral,12 we found that in the corrected free energy profile the products where 4 kcal mol–1 higher than reactants. This could be due to an incomplete relaxation of the environment or inherent errors in our QM/MM description. As a further test we obtained the free energy profile after adding corrections with other functionals and/or basis sets (see Fig. S12†) obtaining results very similar to those presented here.
The larger free energy barrier obtained after corrections for Path 2 could be attributed to the limitations of the semiempirical Hamiltonian to describe this type of mechanisms. In a comparative QM/MM study of the catalytic mechanism of hairpin ribozyme with different quantum treatments,59 the authors concluded that when a non-bridging oxygen atom of the phosphate group acts as the base that activates the nucleophile, the AM1d-PhoT Hamiltonian predicts that proton transfer precedes phosphate transfer in a clearly asynchronous reaction pathway, just as was found in our case. However, at higher theoretical levels (either using density functional theory or ab initio approaches) the reaction proceeds in the reverse order, with the phosphate transfer preceding the proton transfer. Thus, semiempirical structures appear in high-energy regions of the Potential Energy Surface (PES) obtained at better levels of theory, explaining the large barrier obtained in the corrected free energy profile for Path 2. However, it is worth noting that though the AM1d-PhoT method doesn't correctly describe the structures for Path 2, the obtained activation energy is expected to resemble similar values when higher QM levels are used, as was observed in the previous cited study in hairpin ribozyme,59 where AM1d-PhoT still could reproduce the energetics in reasonable agreement with respect to higher level QM data. This would mean that the energy barrier obtained for Path 2 at a higher QM level should lie not far from 35 kcal mol–1. In fact, QM/MM studies at a DFT level in protein kinase A (PKA)17,60 have shown that potential energy barriers for the associative mechanism are within a range of 25–35 kcal mol–1. Instead, when the reaction takes place with proton transfer to another base (Asp256 in our case), the PES obtained at higher levels of theory shows that the reaction proceeds through a less asynchronous pathway, where the phosphate transfer precedes proton transfer. This is precisely the kind of mechanism described by Path 1 in our AM1d-PhoT/MM treatment.
In order to further investigate the relative energetics of Paths 1 and 2 and the possible dependence with respect to the chosen computational level, we performed an exploration of the potential energy surface at the B3LYP/MM level. In particular, we carried out a relaxed B3LYP/MM scan along the tightness coordinate (the distance between the donor and acceptor oxygen atoms, O3β–O1) for structures where the phosphorous atom is equidistant to both oxygens. In this scan we moved the system from the dissociative pathway region (where the tightness coordinate takes values of around 5 Å) to the associative one (with values of about 4 Å for the tightness coordinate), see Fig. S11.† Our results clearly demonstrate that the associative pathway (Path 2) presents relative energies that would be 15–20 kcal mol–1 larger than for the dissociative mechanism (Path 1), in good agreement with the difference observed between the activation free energies. We are thus confident that the representation of the reaction mechanism provided by Path 1 obtained from our QM/MM simulations correctly reproduces the main characteristics of the reaction between F6P and ATP catalyzed by Pfk-2.
Conclusions
In this contribution we have presented valuable information regarding the structure and reaction mechanism of Pfk-2 from E. coli. We have reported the structure of the intermediate Pfk-2:F6P:(MgATP)2 that was previously suggested from the analysis of substrate inhibition of the enzyme. After performing a classical MD simulation, we observed that Pfk-2 must undergo a conformational transition between “open” and “closed” states, in order to perform its catalytic activity. We found that the chain containing products (chain B) becomes more compact than the chain bearing the reactants without inhibitor (chain D). In this domain closure, Lys27 approached the γ-phosphate of MgATP2– substrate in the subunit that contains substrates without inhibitor. The results presented here indicate a mutual negative effect of the binding of F6P and the allosteric MgATP2– for the interactions established between the reacting fragments and the residues of the active site.
Altogether, these characteristics prompted us to select the subunit containing products for QM/MM calculations: the ligands and residues in the active site were better oriented and the subunit conformation was in the closed state needed for the enzymatic reaction to take place. The exploration of the phosphoryl transfer mechanism with the string method showed that the preferred path in Pfk-2 is a dissociative mechanism where Asp256 acts as a general base. After phosphorylation of F6P, Asp256 acts as an acid to protonate the transferred phosphoryl group, recovering in this way the original state of the enzyme. During this process, Lys27 from the complementary chain stabilizes the transition state, forming a HB contact with the γ-phosphate during transfer. A second path was also obtained in which the phosphorylation is mainly associative, following a non-concerted mechanism, with the proton transfer preceding the phosphate transfer. However, this mechanism was found to be unfavorable due to a prohibitively high free energy barrier.
The methodology used in this work opens the possibility to study other members of the ribokinase family since relevant information regarding the kinetic mechanism of Pfk-2 is provided. In addition, the specific roles of Asp256 and Lys27 residues, which belong to the conserved enzymatic machinery of the family, were clarified. Furthermore, the reported crystal structure could serve as a model to reconstruct the active sites of other members of the family, as it provides detailed information about the relative position and specific interactions of both reactants and products embedded in their corresponding chemical environment.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
J. M. acknowledges CONICYT for her postdoctoral project FONDECYT/Postdoctorado-2015 No. 3150041. K. Z. and I. T. gratefully acknowledge financial support from Ministerio de Economía y Competitividad and FEDER funds (project CTQ2015-66223-C2-2-P). K. Z. acknowledges a FPU fellowship from Ministerio de Educación. R. R. acknowledges support from a doctoral fellowship CONICYT-PCHA/Folio 21130949. The authors acknowledge computational facilities of the Servei d'Informàtica de la Universitat de València in the `Tirant' supercomputer. R. C. and J. B. acknowledge to FONDECYT 1090336. J. C. acknowledges to FONDECYT 1170718. I. T. acknowledges the financial support from Generalitat Valenciana, grant number AICO/2018/238.
Footnotes
†Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc00094a
References
- Knowles J. R. Annu. Rev. Biochem. 1980;49:877–919. doi: 10.1146/annurev.bi.49.070180.004305. [DOI] [PubMed] [Google Scholar]
- Lipmann F. Adv. Enzymol. Relat. Subj. Biochem. 1941;1:99–162. [Google Scholar]
- Westheimer F. H. Science. 1987;235:1173–1178. doi: 10.1126/science.2434996. [DOI] [PubMed] [Google Scholar]
- Kamerlin S. C. L., Sharma P. K., Prasad R. B., Warshel A. Q. Rev. Biophys. 2013;46:1–132. doi: 10.1017/S0033583512000157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagata R., Fujihashi M., Kawamura H., Sato T., Fujita T., Atomi H., Miki K. ACS Chem. Biol. 2017;12:1514–1523. doi: 10.1021/acschembio.7b00064. [DOI] [PubMed] [Google Scholar]
- Vasu D., Kumar P. S., Prasad U. V., Swarupa V., Yeswanth S., Srikanth L., Sunitha M. M., Choudhary A., Sarma P. V. G. K. Iran. Biomed. J. 2017;21:94–105. doi: 10.18869/acadpub.ibj.21.2.94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith G. K., Ke Z., Guo H., Hengge A. C. J. Phys. Chem. B. 2011;115:13713–13722. doi: 10.1021/jp207532s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter T. Cell. 2000;100:113–127. doi: 10.1016/s0092-8674(00)81688-8. [DOI] [PubMed] [Google Scholar]
- Ingram-Smith C., Wharton J., Reinholz C., Doucet T., Hesler R., Smith K. Life. 2015;5:861–871. doi: 10.3390/life5010861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato M., Arakawa T., Nam Y.-W., Nishimoto M., Kitaoka M., Fushinobu S. Biochim. Biophys. Acta, Proteins Proteomics. 2015;1854:333–340. doi: 10.1016/j.bbapap.2015.01.011. [DOI] [PubMed] [Google Scholar]
- Cheek S., Ginalski K., Grishin N. V. BMC Struct. Biol. 2005;5:6. doi: 10.1186/1472-6807-5-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babul J. J. Biol. Chem. 1978;253:4350–4355. [PubMed] [Google Scholar]
- Bork P., Sander C., Valencia A. Protein Sci. 2008;2:31–40. doi: 10.1002/pro.5560020104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cabrera R., Babul J., Guixé V. Arch. Biochem. Biophys. 2010;502:23–30. doi: 10.1016/j.abb.2010.06.024. [DOI] [PubMed] [Google Scholar]
- Spychala J., Datta N. S., Takabayashi K., Datta M., Fox I. H., Gribbin T., Mitchell B. S. Proc. Natl. Acad. Sci. U. S. A. 1996;93:1232–1237. doi: 10.1073/pnas.93.3.1232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyguda E., Szefczyk B., Sokalski W. Int. J. Mol. Sci. 2004;5:141–153. [Google Scholar]
- Dyguda-Kazimierowicz E., Sokalski W. A., Leszczyński J. J. Mol. Model. 2007;13:839–849. doi: 10.1007/s00894-007-0192-9. [DOI] [PubMed] [Google Scholar]
- Shirakihara Y., Evans P. R. J. Mol. Biol. 1988;204:973–994. doi: 10.1016/0022-2836(88)90056-3. [DOI] [PubMed] [Google Scholar]
- Newman J. A., Das S. K., Sedelnikova S. E., Rice D. W. J. Mol. Biol. 2006;363:520–530. doi: 10.1016/j.jmb.2006.08.013. [DOI] [PubMed] [Google Scholar]
- Arnfors L., Hansen T., Schönheit P., Ladenstein R., Meining W. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2006;62:1085–1097. doi: 10.1107/S0907444906024826. [DOI] [PubMed] [Google Scholar]
- Sigrell J. A., Cameron A. D., Jones T. A., Mowbray S. L. Structure. 1998;6:183–193. doi: 10.1016/s0969-2126(98)00020-3. [DOI] [PubMed] [Google Scholar]
- Schumacher M. A., Scott D. M., Mathews I. I., Ealick S. E., Roos D. S., Ullman B., Brennan R. G. J. Mol. Biol. 2000;298:875–893. doi: 10.1006/jmbi.2000.3753. [DOI] [PubMed] [Google Scholar]
- Maj M. C., Singh B., Gupta R. S. Biochemistry. 2002;41:4059–4069. doi: 10.1021/bi0119161. [DOI] [PubMed] [Google Scholar]
- Caniuguir A., Cabrera R., Báez M., Vásquez C. C., Babul J., Guixé V. FEBS Lett. 2005;579:2313–2318. doi: 10.1016/j.febslet.2005.02.078. [DOI] [PubMed] [Google Scholar]
- Guixé V., Babul J. J. Biol. Chem. 1985;260:11001–11005. [PubMed] [Google Scholar]
- Cabrera R., Fischer H., Trapani S., Craievich A. F., Garratt R. C., Guixe V., Babul J. J. Biol. Chem. 2003;278:12913–12919. doi: 10.1074/jbc.M212137200. [DOI] [PubMed] [Google Scholar]
- Parducci R. E., Cabrera R., Baez M., Guixé V. Biochemistry. 2006;45:9291–9299. doi: 10.1021/bi060026o. [DOI] [PubMed] [Google Scholar]
- Baez M., Cabrera R., Guixé V., Babul J. Biochemistry. 2007;46:6141–6148. doi: 10.1021/bi7002247. [DOI] [PubMed] [Google Scholar]
- Cabrera R., Ambrosio A. L. B., Garratt R. C., Guixé V., Babul J. J. Mol. Biol. 2008;383:588–602. doi: 10.1016/j.jmb.2008.08.029. [DOI] [PubMed] [Google Scholar]
- Rivas-Pardo J. A., Caniuguir A., Wilson C. A. M., Babul J., Guixé V. Arch. Biochem. Biophys. 2011;505:60–66. doi: 10.1016/j.abb.2010.09.020. [DOI] [PubMed] [Google Scholar]
- Cabrera R., Baez M., Pereira H. M., Caniuguir A., Garratt R. C., Babul J. J. Biol. Chem. 2011;286:5774–5783. doi: 10.1074/jbc.M110.163162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baez M., Wilson C. A. M., Babul J. FEBS Lett. 2011;585:2158–2164. doi: 10.1016/j.febslet.2011.05.041. [DOI] [PubMed] [Google Scholar]
- Ramírez-Sarmiento C. A., Baez M., Zamora R. A., Balasubramaniam D., Babul J., Komives E. A., Guixé V. Biophys. J. 2015;108:2350–2361. doi: 10.1016/j.bpj.2015.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villalobos P., Soto F., Baez M., Babul J. Biochimie. 2016;128–129:209–216. doi: 10.1016/j.biochi.2016.08.013. [DOI] [PubMed] [Google Scholar]
- Guixé V., Merino F. IUBMB Life. 2009;61:753–761. doi: 10.1002/iub.217. [DOI] [PubMed] [Google Scholar]
- Miallau L., Hunter W. N., McSweeney S. M., Leonard G. A. J. Biol. Chem. 2007;282:19948–19957. doi: 10.1074/jbc.M701480200. [DOI] [PubMed] [Google Scholar]
- Lassila J. K., Zalatan J. G., Herschlag D. Annu. Rev. Biochem. 2011;80:669–702. doi: 10.1146/annurev-biochem-060409-092741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pérez-Gallegos A., Garcia-Viloca M., González-Lafont À., Lluch J. M. ACS Catal. 2015;5:4897–4912. [Google Scholar]
- Zinovjev K., Ruiz-Pernía J. J., Tuñón I. J. Chem. Theory Comput. 2013;9:3740–3749. doi: 10.1021/ct400153r. [DOI] [PubMed] [Google Scholar]
- Guixé V., Rodríguez P. H., Babul J. Biochemistry. 1998;37:13269–13275. doi: 10.1021/bi980576p. [DOI] [PubMed] [Google Scholar]
- Cabrera R., Guixé V., Alfaro J., Rodríguez P. H., Babul J. Arch. Biochem. Biophys. 2002;406:289–295. doi: 10.1016/s0003-9861(02)00435-6. [DOI] [PubMed] [Google Scholar]
- Field M. J., Albe M., Bret C., Proust-De Martin F., Thomas A. J. Comput. Chem. 2000;21:1088–1100. [Google Scholar]
- Nam K., Cui Q., Gao J., York D. M. J. Chem. Theory Comput. 2007;3:486–504. doi: 10.1021/ct6002466. [DOI] [PubMed] [Google Scholar]
- Marcos E., Anglada J. M., Crehuet R. Phys. Chem. Chem. Phys. 2008;10:2442. doi: 10.1039/b719792f. [DOI] [PubMed] [Google Scholar]
- Zinovjev K., Martí S., Tuñón I. J. Chem. Theory Comput. 2012;8:1795–1801. doi: 10.1021/ct300070b. [DOI] [PubMed] [Google Scholar]
- Maragliano L., Vanden-Eijnden E. Chem. Phys. Lett. 2007;446:182–190. [Google Scholar]
- Torrie G. M., Valleau J. P. J. Comput. Phys. 1977;23:187–199. [Google Scholar]
- Roca M., Aranda J., Moliner V., Tuñón I. Curr. Opin. Chem. Biol. 2012;16:465–471. doi: 10.1016/j.cbpa.2012.10.014. [DOI] [PubMed] [Google Scholar]
- Aranda J., Zinovjev K., Roca M., Tuñón I. J. Am. Chem. Soc. 2014;136:16227–16239. doi: 10.1021/ja5077124. [DOI] [PubMed] [Google Scholar]
- Falsafi-Zadeh S., Karimi Z., Galehdari H. Bioinformation. 2012;8:341–343. doi: 10.6026/97320630008341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olsson M. H. M., Søndergaard C. R., Rostkowski M., Jensen J. H. J. Chem. Theory Comput. 2011;7:525–537. doi: 10.1021/ct100578z. [DOI] [PubMed] [Google Scholar]
- O'Ferrall R. A. M. J. Chem. Soc. B. 1970:274–277. [Google Scholar]
- Jencks W. P. Chem. Rev. 1972;72:705–718. [Google Scholar]
- Jencks D. A., Jencks W. P. J. Am. Chem. Soc. 1977;99:7948–7960. [Google Scholar]
- Pauling L. J. Am. Chem. Soc. 1947;69:542–553. [Google Scholar]
- Ma B., Nussinov R. Curr. Opin. Chem. Biol. 2010;14:652–659. doi: 10.1016/j.cbpa.2010.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mildvan A. S. Proteins. 1997;29:401–416. [PubMed] [Google Scholar]
- Lopata A., Jambrina P. G., Sharma P. K., Brooks B. R., Toth J., Vertessy B. G., Rosta E. ACS Catal. 2015;5:3225–3237. [Google Scholar]
- Mlýnský V., Banáš P., Šponer J., van der Kamp M. W., Mulholland A. J., Otyepka M. J. Chem. Theory Comput. 2014;10:1608–1622. doi: 10.1021/ct401015e. [DOI] [PubMed] [Google Scholar]
- Pérez-Gallegos A., Garcia-Viloca M., González-Lafont À., Lluch J. M. J. Comput.-Aided Mol. Des. 2014;28:1077–1091. doi: 10.1007/s10822-014-9786-3. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.