Analysis of dual solution for MHD flow of Williamson fluid with slippage

Abstract

This study investigates the numerical solutions of MHD boundary layer and heat transfer of the Williamson fluid flow on the exponentially vertical shrinking sheet, having variable thickness and thermal conductivity under effects of the velocity and thermal slip parameters. It is also assumed that shrinking/stretching velocity, as well as the wall temperature, has the exponential function form. In this study, the continuity, momentum and energy equations with buoyancy parameter and Hartmann number are incorporated especially in the Williamson fluid flow case. Similarity transformation variables have been employed to formulate the ordinary differential equations (ODEs) from partial differential equations (PDEs). The resultant ODEs are solved by shooting method with Runge Kutta of fourth order method in Maple software. The effects of the different applied non-dimensional physical parameters on the boundary layer and heat transfer flow problems are presented in graphs. The effects of Williamson parameter, Prandtl number, and slip parameters on velocity and temperature profiles have been thoroughly demonstrated and discussed. The numerical results show that the buoyancy force and the slip parameters contribute to the occurrence of the dual solutions on the boundary layer and heat transfer flow problems. Furthermore, the stability analysis suggests that the first solution is stable and physically possible.

1. Introduction

The boundary layer pseudo-plastic fluids flows have vast industrial applications such as solutions of the polymers with higher molecular weight, emulsion covered sheets such as polymer sheets extrusion and photographic films etc. Since Navier-Stokes equations are not able to define all kinds of fluid flows, a comprehensive study is required to explore the rheological characteristics of all kind of fluids such type of the deficiency different type of the rheological models have been introduced. To study the behavior of the pseudo-plastic (shear thinning) fluids several models are introduced such as Cross model, Ellis model, Carreaus model, the power law models any many other non-Newtonian models, see [1, 2, 3, 4, 5]. However, there has been a little attention given to investigate the multiple solutions of Williamson fluid over a shrinking/stretching surface in presence of MHD.

The Williamson fluid was firstly introduced by Williamson [6] in his pioneer research of pseudo-plastic materials flow. He described the flow of pseudo-plastic fluids by developing a model equation and verified this hypothesis with the experiment. Since then, many other researchers worked on the Williamson fluid, such as [7, 8, 9]. A flow of a thin layer of the Williamson fluid in the presence of a gravitational field over an inclined surface was studied by Lyubimov and Perminov [10]. The perturbation method to the Williamson fluid inserted in the fracture of the rock was developed by Dapra and Scarpi [11]. The effect of the presence of an inclined magnetic field over the Williamson peristaltic flow fluid in the inclined asymmetric or symmetric channel was analyzed by Nadeem and Akram [12, 13]. Meanwhile, the Williamson peristaltic pumping fluid flow and heat transfer over the porous medium was studied by Vasudev et al., [14]. Cramer et al. [15], indicated that the Williamson fluid model is perfect for the experimental data of the polymeric solutions as well as suspensions of the particle as compared to the other previous fluid models. Mixed convection flow of different fluids has been considered by many researchers such as Mabood [16] and Turkyilmazoglu [17]. For the shear thinning fluids, power law model indicates that the dynamic viscosity decreases indefinitely when shear rate increases. This implies that there will be zero viscosity when shear rate tends infinity and infinite viscosity when the shear rate is zero or at the rest. Each real fluid may have both maximum and minimum dynamic viscosities depending on the fluid's molecular structure. In the present Williamson model, both viscosities maximum (${\mu }_0$) and the minimum (${\mu }_{\infty }$) are taken into account. But in the case of pseudo-plastic fluids, the apparent viscosity cannot be zero at infinity, so this model gives better results.

Due to numerous applications in engineering and industries, MHD fluid flows on shrinking sheet have gained much attention nowadays [18, 19, 20, 21]. Such applications include liquid coating on photographic films, extrusion of the polymeric sheet from expire, boundary layer through the liquid film in the concentration process, aerodynamic extrusion of plastic sheets, etc. Turkyilmazoglu [22] dealt with the MHD flow through analytical approach. Mabood et al. [23], considered MHD flow of rotating fluid over a vertical surface. Akbar et al. [24] studied “partial slip and heat transfer peristaltic flow behavior of the Williamson fluid through the inclined asymmetric channel”. This study was later extended by incorporating nanoparticle. Vajravelu et al. [25] analyzed Williamson fluid flow (peristaltic) in asymmetric channels with permeable walls having different amplitudes and phases. They have also discussed the effect of the various waveforms on the fluid flow pattern. Akram et al. [26], analyzed the effects of an induced magnetic field over the peristaltic flow of the Williamson fluid by analytical and numerical techniques. Bhatti and Rashidi [27] suggested the thermal radiation and thermos diffusion effects of the flow pattern of the Williamson nanofluid on shrinking/stretching porous sheet.

The aim of this study is to investigate the multiple solutions numerically of MHD mixed convectional flow of the Williamson fluid on an exponentially shrinking/stretching sheet with combined effects of the velocity and the thermal slip conditions. The nonlinear coupled governing equations in partial differential equations form are transformed into ordinary differential equations form by using similarity transformations. Then, the equations are solved by applying the shooting method, it is already implicated successfully such as [28, 29]. The calculations are obtained for the different applied physical parameters until the desired level of the accuracy obtained. The results of the shear stress, as well as the temperature gradient, are calculated at the wall of the solid surface. It is expected that the findings of the present study will prove fruitful in the future research to enhance the development in science and technology.

2. Model

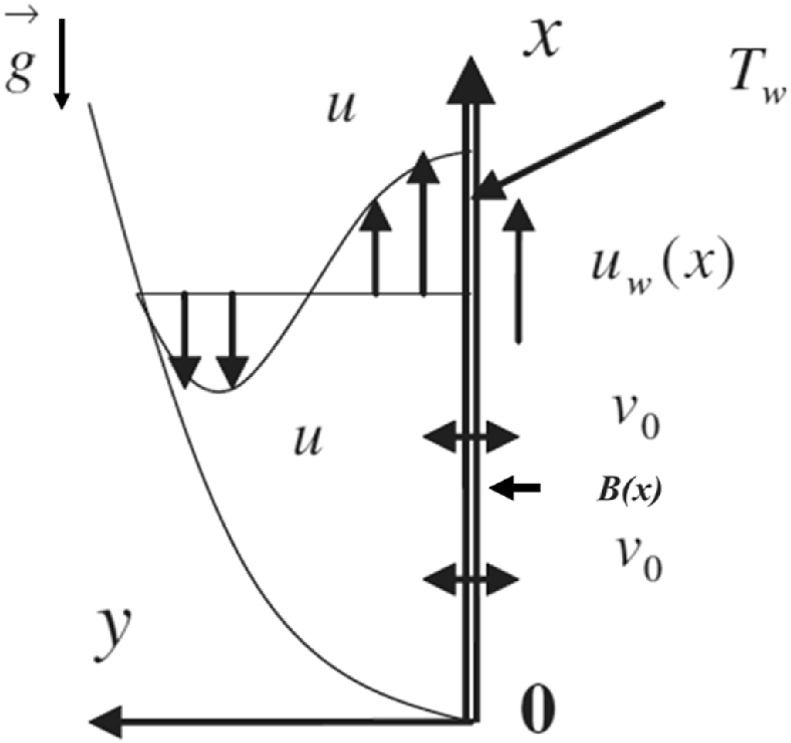
Let us consider the MHD two-dimensional incompressible steady laminar Williamson fluid flow on the vertical exponential shrinking/stretching sheet along with slip boundary condition placed in the plane$y=0$. The plate is shrieked and stretched exponentially along $x$-axis at the velocity$u_w=C{e}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$l$}\right.}$ with a wall temperature $T_w$. The fluid taken into account is electrically conducting and the applied magnetic field is perpendicular to the sheet. Due to the small Reynolds number, the polarization of magnetic field is ignored. The rheological equations of Williamson fluid are taken as mentioned by Reddy et al., [30]. In case of Williamson fluid flow, Cauchy stress tensor (S) will be written as

$$\mathit{S}=-p\mathit{I}+\tau$$ (1)

$$\tau =\left({\mu }_{\infty }+\frac{{\mu }_0-{\mu }_{\infty }}{1-\sqrt{\dot{\gamma }}}\right)A_1$$ (2)

where S stands for the extra stress tensor,${\mu }_{\infty }$ restrictive viscosity with infinite shear rate, ${\mu }_0$ restrictive viscosity with zero shear rate,$A_1$ first Rivlin Erickson tensor, Γ > 0 is the constant of time and $\dot{\gamma }$ will be written as

$$\dot{\gamma }=\sqrt{\frac{\pi }{2}},\pi =trace\left(A_1^2\right)\text{.}$$ (3)

It is considered that

$${\mu }_{\infty }=0,\sqrt{\dot{\gamma }}<1$$ (4)

which leads to

$$\tau =\left(\frac{{\mu }_0}{1-\sqrt{\dot{\gamma }}}\right)A_1.$$ (5)

Applying binomial expansion on (5), which gives

$$\tau ={\mu }_0\left(1-\sqrt{\dot{\gamma }}\right)A_1.$$ (6)

Under the given conditions, the boundary layer and heat transfer flow equations without viscous dissipation with magnetic force will be (refer [31])

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$ (7)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\vartheta \frac{{\partial }^{2}u}{\partial y^2}+\sqrt{2}v\text{Γ}\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial y^2}+g\beta \left(T-T_{\infty }\right)-\frac{\sigma B^{2}u}{\rho }$$ (8)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{{\partial }^{2}T}{\partial y^2}$$ (9)

subjected to initial and boundary conditions below

$$v=v_w,u=u_w+N\vartheta \frac{\partial u}{\partial y}T=T_w\left(x\right)+K\frac{\partial T}{\partial y},aty=0$$

$$u\to 0,T\to T_{\infty }\text{as}y\to \infty$$ (10)

where, $(u_w=C{e}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$l$}\right.})$ and $T_w=T_{\infty }+T_0{e}^{\raisebox{1ex}{$2x$}\!\left/ \!\raisebox{-1ex}{$l$}\right.}$. In the above mentioned conditions $N=N_1{e}^{\raisebox{1ex}{$-x$}\!\left/ \!\raisebox{-1ex}{$2l$}\right.}$ and $K=K_1{e}^{\raisebox{1ex}{$-x$}\!\left/ \!\raisebox{-1ex}{$2l$}\right.}$ indicate the velocity slip and the thermal slip factors that vary with x (but at the values $N=0$ and $K=0$, the no-slip cases are examined), $N_1$and $K_1$ are values of initial velocity and thermal slips factors respectively, $u_w$ is shrinking/stretching velocity with $U_w$ as a shrinking/stretching constant, the velocity components are u and v along x and the y-directions, respectively. l is characteristic length of the sheet and B=$B_0{e}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$l$}\right.}$is a magnetic field in which $B_0$ is the constant of magnetic field.

Velocity components will be written as

$$u=\frac{\partial \psi }{\partial y},v=-\frac{\partial \psi }{\partial x},$$ (11)

For relations of (11), (7) is satisfied automatically and (8, 9) takes the form:

$$\frac{\partial \psi }{\partial y}\frac{{\partial }^2\psi }{\partial x\partial y}-\frac{\partial \psi }{\partial x}\frac{{\partial }^2\psi }{\partial y^2}=\vartheta \frac{{\partial }^3\psi }{\partial y^3}+\sqrt{2}v\text{Γ}\frac{{\partial }^2\psi }{\partial y^2}\frac{{\partial }^3\psi }{\partial y^3}+g\beta \left(T-T_{\infty }\right)-\frac{\sigma B^2}{\rho }\frac{\partial \psi }{\partial y}$$ (12)

$$\frac{\partial \psi }{\partial y}\frac{\partial T}{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial T}{\partial y}=\alpha \frac{{\partial }^{2}T}{\partial y^2}$$ (13)

The boundary conditions in (10) will then be reduced to

$-\frac{\partial \psi }{\partial x}=v_w;\frac{\partial \psi }{\partial y}=u_w+N\vartheta \frac{{\partial }^2\psi }{\partial y^2};T=T_w\left(x\right)+K\frac{\partial T}{\partial y},$ at $y=0$

$$\frac{\partial \psi }{\partial y}\to 0,T\to T_{\infty }asy\to \infty$$ (14)

To get the similarity solutions, the following similarity transformations are used

$$\psi =\sqrt{2\vartheta l{U}_w}{e}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2l$}\right.}f\left(\eta \right),\theta \left(\eta \right)=\frac{\left(T-T_{\infty }\right)}{\left(T_w-T_{\infty }\right)},\eta =y\sqrt{\frac{U_w}{2\vartheta l}}{e}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2l$}\right.}$$ (15)

where $\eta$ represents the similarity variable and $v_w\left(x\right)$ is denoted by

$$v_w\left(x\right)=-\sqrt{\frac{\vartheta U_w}{2l}}{e}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2l$}\right.}S$$ (16)

Using similarity transformations in Equations (12), (13) produces,

$$f^{″\prime }\left(\eta \right)+\lambda f^{\prime \prime }\left(\eta \right)f^{\prime \prime \prime }\left(\eta \right)-2f^{\prime 2}\left(\eta \right)+f\left(\eta \right)f^{\prime \prime }\left(\eta \right)-M{f}^{\prime }\left(\eta \right)+2\sigma \theta \left(\eta \right)=0$$ (17)

$${\theta }^{\prime \prime }\left(\eta \right)+Prf\left(\eta \right){\theta }^{\prime }\left(\eta \right)-4Pr{f}^{\prime }\left(\eta \right)\theta \left(\eta \right)=0$$ (18)

The related boundary conditions will be,

$$f\left(0\right)=S,f^{\prime }\left(0\right)=\xi +\delta f^{\prime \prime }\left(0\right);(where\xi =\frac{c}{U_w}),\theta \left(0\right)=1+\beta {\theta }^{\prime }\left(0\right)$$

$$f^{\prime }\left(\eta \right)\to 0,\theta \left(\eta \right)\to 0as\eta \to \infty$$ (19)

where $\beta =K_1\sqrt{\frac{U_w}{2\vartheta l}}$ and $\delta =N_1\sqrt{\frac{\vartheta U_w}{2l}}$ are thermal and velocity slip parameters [32], $M=\frac{2\sigma B_0^{2}l}{\rho U_w}$ is Hartmann number, $\lambda =\text{Γ}\sqrt{\frac{U_w^{3}exp(3x/l)}{\vartheta l}}$ is dimensionless Williamson fluid parameter, the mixed convection parameter is $\sigma =\frac{Gr}{R{e}^2}$(Gr=$\frac{g\beta l^2{T}^2}{{\vartheta }^2},Re=\frac{U_{w}l}{\vartheta }$), and $Pr=\frac{\vartheta }{\alpha }$ is Prandtl number. At λ = 0, the Eq. (13) will be reduced to the form of the classical boundary layer equation in case of viscous fluid flow. The parameter $\lambda =\text{Γ}\sqrt{\frac{U_w^{3}exp(3x/l)}{\vartheta l}}$ does not allow the problem to be self-similar, henceforth, this analysis is considered as a local similar. $N_u$ represents the gradient of the wall temperature and $C_f$ for the coefficient of the skin friction are important interesting physical quantities that are to be measured. The coordinate system and flow regime are illustrated in Fig. 1. By boundary layer approximations, ${\tau }_w$ and $q_w$take the form

$${\tau }_w={\mu }_0\left(\frac{\partial u}{\partial y}+\frac{\Gamma }{\sqrt{2}}{\left(\frac{\partial u}{\partial y}\right)}^2\right)\text{and}{q}_w=-\alpha {\left(\frac{\partial T}{\partial y}\right)}_{y=0}$$ (20)

Fig. 1.

Physical model and coordinate system.

That are written as,

$$C_f=\frac{{\tau }_w}{\rho U_w^2};N_u=\frac{x{q}_w}{\alpha \left(T_w-T_{\infty }\right)}$$ (21)

In the dimensionless form, both parameters above can be written as

$$\sqrt{2Re}{e}^{-3x/2l}{C}_f=\left(f^{\prime \prime }\left(0\right)+\frac{\lambda }{2}{(f^{\prime \prime }\left(0\right))}^2\right);-{\theta }^{\prime }\left(0\right)=\sqrt{\frac{2}{Re}}{e}^{-x/2l}{N}_u$$ (22)

2.1. Stability analysis

In this regard, unsteady state of our governing model has been considered to do a stability analysis on the present problem. While Eq. (7) continues as before, Eqs. (8) and (9) supplanted by as pursues:

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\vartheta \frac{{\partial }^{2}u}{\partial y^2}+\sqrt{2}v\text{Γ}\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial y^2}+g\beta \left(T-T_{\infty }\right)-\frac{\sigma B^{2}u}{\rho }$$ (23)

$$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{{\partial }^{2}T}{\partial y^2}$$ (24)

subjected to new boundary conditions

$$v=v_w,u=u_w+N\vartheta \frac{\partial u}{\partial y}T=T_w\left(x\right)+K\frac{\partial T}{\partial y},aty=0$$

$$u\to 0,T\to T_{\infty }asy\to \infty$$ (25)

Another dimensionless variable τ is presented, where τ is uniform with the problem of which solutions will be related with problem of an initial value and physically feasible. With the presentation of new dimensionless variable τ in Eq. (15), we now have

$$\psi =\sqrt{2\vartheta l{U}_w}{e}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2l$}\right.}f\left(\eta ,\tau \right);\theta (\eta ,\tau )=\raisebox{1ex}{$\left(T-T_{\infty }\right)$}\!\left/ \!\raisebox{-1ex}{$\left(T_w-T_{\infty }\right)$}\right.;$$

$$\eta =y\sqrt{\frac{U_w}{2\vartheta l}}{e}^{\frac{x}{2l}};\tau =\frac{U_w}{2l}{e}^{\frac{x}{l}}.t$$ (26)

Substituting Eq. (26) into Eqs. (23) and (24) yields

$$\frac{{\partial }^{3}f\left(\eta ,\tau \right)}{\partial {\eta }^3}+\lambda \frac{{\partial }^{2}f\left(\eta ,\tau \right)}{\partial {\eta }^2}\frac{{\partial }^{3}f\left(\eta ,\tau \right)}{\partial {\eta }^3}-2{\left(\frac{\partial f\left(\eta ,\tau \right)}{\partial \eta }\right)}^2+f\left(\eta ,\tau \right)\frac{{\partial }^{2}f\left(\eta ,\tau \right)}{\partial {\eta }^2}+2\sigma \theta (\eta ,\tau )-M\frac{\partial f\left(\eta ,\tau \right)}{\partial \eta }-\frac{{\partial }^{2}f\left(\eta ,\tau \right)}{\partial \tau \partial \eta }=0$$ (27)

$$\frac{1}{Pr}\frac{{\partial }^2\theta \left(\eta ,\tau \right)}{\partial {\eta }^2}+f\left(\eta ,\tau \right)\frac{\partial \theta \left(\eta ,\tau \right)}{\partial \eta }-4\frac{\partial f\left(\eta ,\tau \right)}{\partial \eta }\theta \left(\eta ,\tau \right)-\frac{\partial \theta \left(\eta ,\tau \right)}{\partial \tau }=0$$ (28)

The boundary conditions, in Eq. (25), become

$$f\left(0,\tau \right)=S;\frac{\partial f\left(0,\tau \right)}{\partial \eta }=\xi +\delta \frac{{\partial }^{2}f\left(0,\tau \right)}{\partial {\eta }^2};\theta \left(0,\tau \right)=1+\beta \frac{\partial {\theta }^{\prime }\left(0,\tau \right)}{\partial \eta }$$

$$\frac{\partial f\left(\eta ,\tau \right)}{\partial \eta }\to 0;\theta \left(\eta ,\tau \right)\to 0;as\eta \to \infty$$ (29)

The stability of solution of $f\left(\eta \right)=f_0\left(\eta \right)$ and $\theta \left(\eta \right)={\theta }_0\left(\eta \right)$ is tested in order to satisfy the boundary value problems in Eq. (19) as proposed by Merkin [33] and Weidman et al., [34]

$$f\left(\eta ,\tau \right)=f_0\left(\eta \right)+e^{-\epsilon \tau }F\left(\eta ,\tau \right)$$

$$\theta \left(\eta ,\tau \right)={\theta }_0\left(\eta \right)+e^{-\epsilon \tau }G\left(\eta ,\tau \right)$$ (30)

where the unknown eigenvalue is $\epsilon$ or likewise can be depicted as the rate of development or disturbances decay. A set of infinite eigenvalues ${\epsilon }_1<{\epsilon }_2<{\epsilon }_3\mathrm{...}$ is given by the eigenvalue solutions. Furthermore, if the values of smallest eigenvalue are positive (initial decay of disturbances) which means that solution is stable and physical possible. On the other hand, the negative values of smallest eigenvalue show the initial disturbances growth which mean flow is unstable.

Substituting Eq. (30) into Eqs. (27) and (28); gives

$$F_0^{\prime \prime \prime }+\lambda f_0^{\prime \prime }{F}_0^{\prime \prime \prime }+\lambda F_0^{\prime \prime }{f}_0^{\prime \prime \prime }-4f_0^{\prime }{F}_0^{\prime }+f_0{F}_0^{\prime \prime }+F_0{f}_0^{\prime \prime }+2\sigma G_0-M{F}_0^{\prime }+\epsilon F_0^{\prime }=0$$ (31)

$$\frac{1}{Pr}{G}_0^{\prime \prime }++f_0{G}_0^{\prime }+F_0{\theta }_0^{\prime }-4f_0^{\prime }{G}_0-4F_0^{\prime }{\theta }_0+\epsilon G_0=0$$ (32)

subjected to boundary conditions below

$$F_0\left(0\right)=0,F_0^{\prime }\left(0\right)=\delta F_0^{\prime \prime }\left(0\right),G_0\left(0\right)=\beta G_0^{\prime }\left(0\right),$$

$$F_0^{\prime }\left(\eta \right)\to 0,G_0\left(\eta \right)\to 0,as\eta \to \infty .$$ (33)

The smallest number of eigenvalue $\epsilon$ determines the stability of dual solutions. According to Rehman et al. [35], we have to relax the $G_0\left(\eta \right)$ on our initial boundary condition. In this manner, we solved the equations with new boundary condition of $G_0^{\prime }\left(\eta \right)=1$, which is relaxed from $G_0\left(\eta \right)\to 0$ as η → ∞. Finally, we determine a fixed smallest value of $\epsilon$, which is called smallest eigen value.

3. Result & discussion

The computation of Eqs. (17) and (18) with initial and boundary conditions given by (19) have been done by applying shooting method. The results of the skin friction coefficient$f^{\prime \prime }\left(0\right)$ and the heat transfer rate $-{\theta }^{\prime }\left(0\right)$ at various values of applied parameters as Hartmann number (M), velocity slip parameter ($\delta )$ and the thermal slip parameter $\left(\beta \right)$ are obtained numerically. Furthermore, the velocity and temperature profiles are determined by solving nonlinear ordinary differential equations. Numerical solutions are presented with the help of graphs to examine the effects of the different parameters such as velocity slip parameter ($\delta$), thermal slip parameter ($\beta$), magnetic parameter (M), Williamson fluid parameter ($\lambda$) Prandtl number (Pr). Variation of the skin friction coefficient $f^{\prime \prime }\left(0\right)$ and heat transfer rate$-\theta \prime \left(0\right)$ with respect to Hartmann number (M) for various values of all the mentioned parameters are presented in Table 1. In order to verify our applied numerical method, our results have been compared with the results of bvp4c method in Table 2. Table 2 shows an excellent agreement between shooting method and three-stage labatoo three-A-formula in bvp4c solver in MATLAB.$f^{\prime \prime }\left(0\right)$and$-\theta \prime \left(0\right)$ are presented graphically in Figs. 10 and 11 respectively.

Table 1.

The values of the skin friction coefficient and rate of the heat transfer of considered Parameters.

M	$\delta$	$\beta$	$\lambda$	S	$\sigma$	Pr	$\xi$	$f^{\prime \prime }\left(0\right)$		$-{\theta }^{\prime }\left(0\right)$
								1st Solution	2nd Solution	1st Solution	2nd Solution
0.8	0	0	0.1	2	-0.25	2	-1	1.213807	1.038613	0.252532	-0.67397
	0.1	0.1						1.376217	0.725463	1.515805	-1.60832
	0.5	0.5						0.984085	0.382931	1.201361	-1.07531
2	0	0						2.273161	0.889304	1.815061	-11.4029
	0.1	0.1						1.924793	0.656778	1.948979	-9.32232
	0.5	0.5						1.119306	0.323239	1.239023	-5.02345
1	0.1	0.1	0.1					1.510519	0.688307	1.65597	-2.93329
			0					1.382296	0.7017285	1.538828	2.667072
			0.1	2.5				2.04788	-0.1605	2.7438	-12.4147
				4				3.194703	-4.53368	4.26351	4.77032
				2	0			1.70550	-----	1.80370	-----
					-0.5			1.237112	0.813012	1.36303	0.076830
					-0.25		1	-2.085813	-3.46665	3.35283	-8.370184

Table 2.

Comparison of numerical methods for various values of different parameters.

M	$\mathit{\delta }$	$\mathit{\beta }$	$\mathit{\lambda }$	S	$\mathit{\sigma }$	Pr	$\mathit{\xi }$	${\mathit{f}}^{\prime \prime }\left(0\right)$
								Shooting Results	BVP4C Results
0	0	0	0	0	0	1	1	-1.28181638	-1.28181639
0.5	0	0	0	0	0	1	1	-1.46644548	-1.46644548
1	0.1	0.1	0.1	2	-0.25	1	1	-2.12641933	-2.12641933
0	0	0	0	2.5	0	1	-1	1.64190906	1.64190906
1	0.1	0.1	0.1	2	0	1	-1	1.705508323	1.70550832
1	0	0	0	2	0	1	-1	1.70939369	1.70939368
1	0.1	0.1	0.5	2	-0.25	2	-1	1.55546734	1.55546685

Fig. 10.

Variation of Temperature profile $f^{\prime }\left(\eta \right)$ at various values of suction parameter (S) over stretching surface.

Fig. 11.

The profile of coefficient of skin friction $f^{\prime \prime }\left(0\right)$ with different values of M and $\delta ,\beta$ when λ = 0.1, S = 2, ζ = -1, Pr = 2 and σ = -0.25.

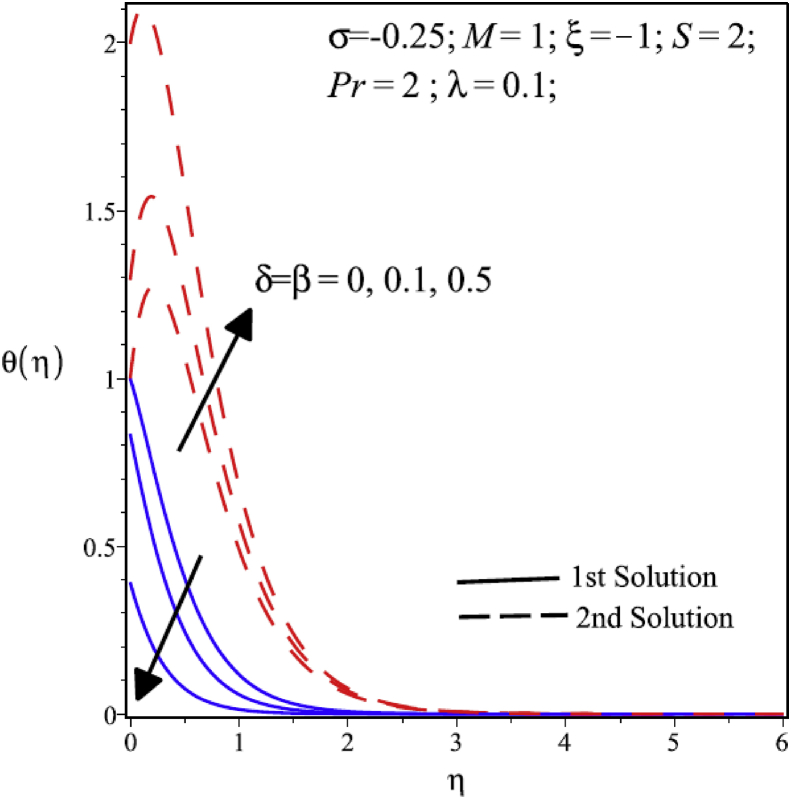
Fig. 2: demonstrates the impact of the momentum (hydrodynamic) slip parameter $\delta$ on the velocity distribution profiles. It can clearly be examined that the velocity distribution profiles are decreasing as the slip parameter are increasing and momentum boundary layer thickness decreases in first solution. On the other hand, the numerical result show that no change occurs in momentum boundary layer thickness in second solution with increments in velocity slip parameter$\left(\delta \right)$. The effect of thermal slip parameter $\beta$ over temperature distribution is enlightened in Fig. 3. In the case of the 1st solution, the increment in thermal slip parameter $\beta$ decreases the temperature and the thickness of the thermal boundary layer that is also mostly observed in literature. In the second solution, the heat transfer rate and thickness of the thermal boundary layers increase by increasing thermal slip parameter.

Fig. 2.

Variation of velocity profile $f^{\prime }\left(\eta \right)$ at various values of slip parameters.

Fig. 3.

Variation of temperature profile $\theta \left(\eta \right)$ at various values of slip parameters.

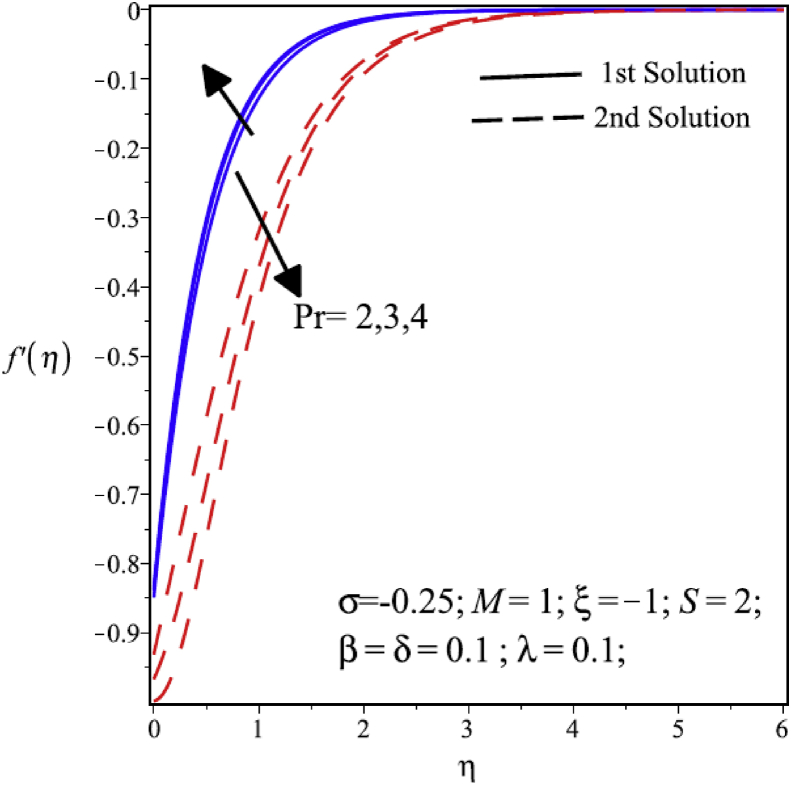
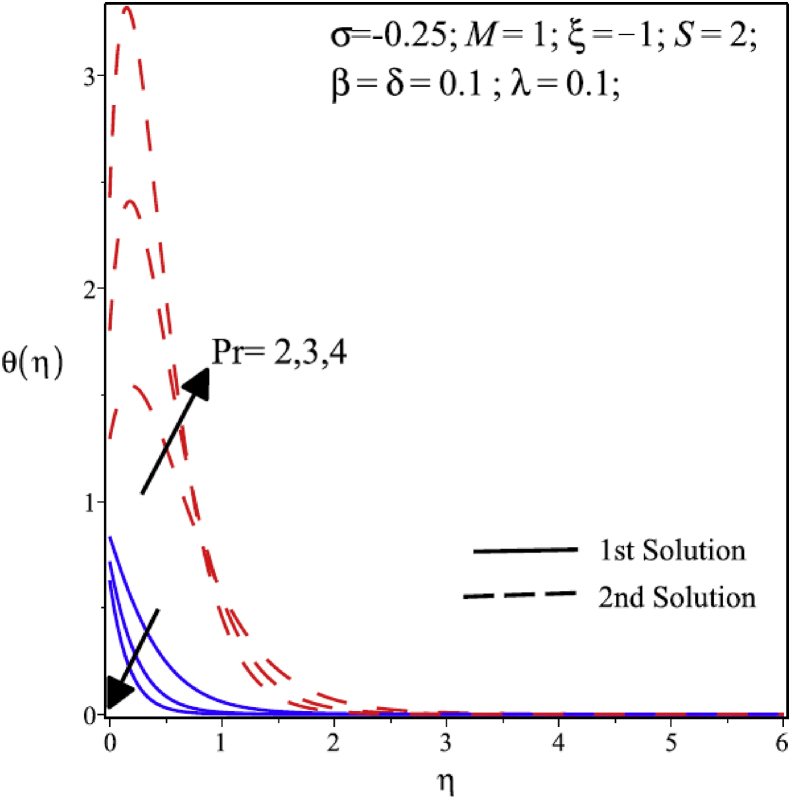
The effects of Prandtl number (Pr) over velocity distribution profile is represented in Fig. 4. The figure shows that velocity and thickness of momentum boundary layer reduce as the Prandtl number (Pr) is increasing in the first solution. On contrary, in the second solution the reverse effect is observed. Fig. 5 shows that in the first solution the heat transfer rate decreases as the Prandtl number increase. As a sample, MATLAB program for Fig. 5 is given in Appendix A. This behavior resembles with the first solution observed in Fig. 3. It is examined that the increasing value of Pr decreases rate of the heat transfer in fluid considerably and the boundary layer comes closer to wall because the increasing value of the Prandtl number decreases rate of thermal diffusivity so in the result thinning boundary layer. However, thickness of thermal boundary layer and temperature rise in the first solution. However, in the second solution at start it is rising but after a point it is decreasing by increasing in Prandtl number.

Fig. 4.

Variation velocity profile $f^{\prime }\left(\eta \right)$ at various values of Prandtl number.

Fig. 5.

Variation of temperature profile $\theta \left(\eta \right)$ at various values of Prandtl number.

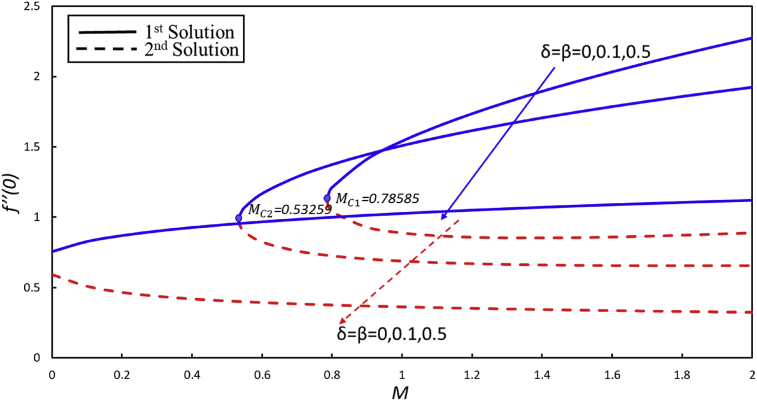
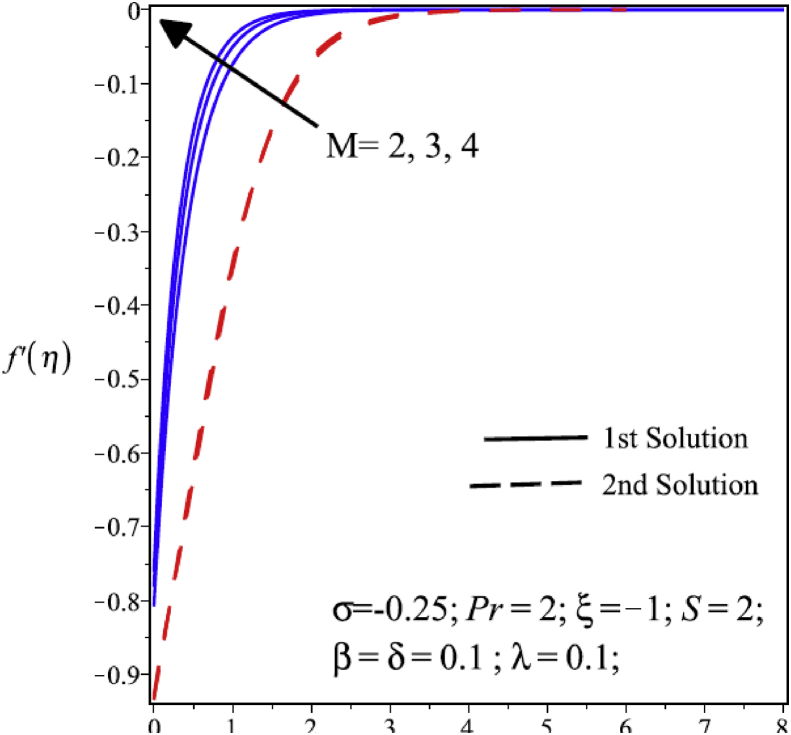
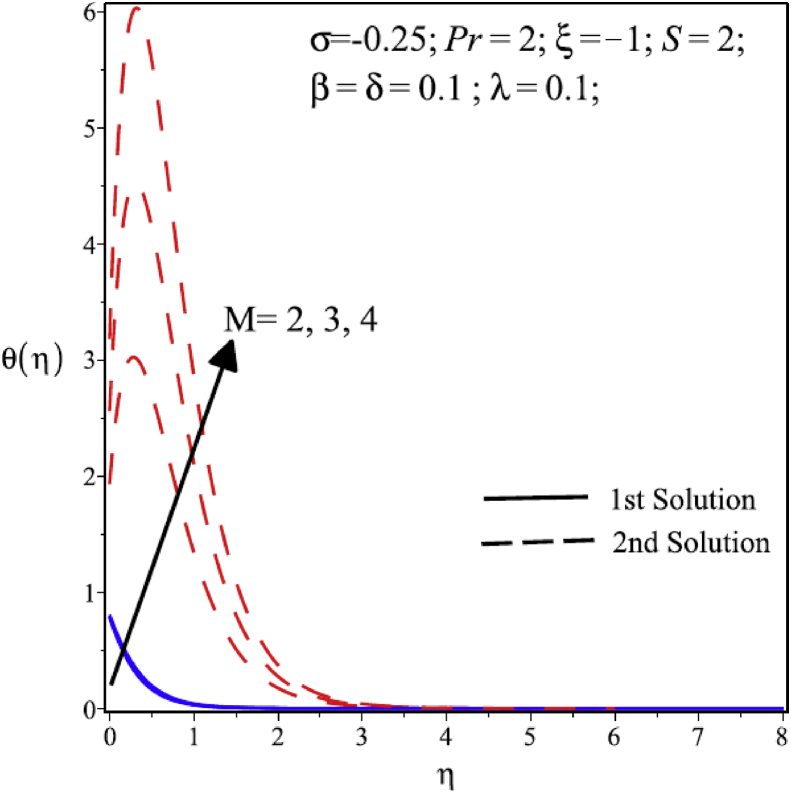
Fig. 6 represents the effect of the Hartman number (M) over the velocity distribution profile. Figure shows that the velocity and thickness of momentum boundary layer decline by the increasing value of the Hartmann number (M), the one of the reason is that the Lorentz force is increasing by increasing in Hartman number (M) that produce resistance in flow of the fluid. Furthermore, the thickness of boundary layer and velocity distribution has remained same when Hartmann number increases in second solution. Fig. 7 shows that the heat transfer rate is increasing as magnetic parameter (M) is increased in both solutions. The influence of the magnetic field is main reason behind the rise of thermal boundary layer thickness as well as rate of the heat transfer.

Fig. 6.

Variation of velocity profile $f^{\prime }\left(\eta \right)$ at various values of the Hartmann number.

Fig. 7.

Variation of temperature profile $\theta \left(\eta \right)$ at various values of the Hartmann number (M).

Fig. 8 illustrates the influence of dimensionless Williamson fluid parameter $\lambda$on velocity profile. This number $\lambda$is present only in momentum equation in combined derivative form as $\lambda f^{\prime \prime }\left(\eta \right)f^{\prime \prime \prime }\left(\eta \right)$. This is number also named as Weissenberg number ($\lambda$) which measures the relative effects of viscosity to elasticity. The $\lambda =0\text{and}\lambda =\infty$represent Newtonian fluid and elastic solid respectively. The middle values stand for polymeric viscoelastic fluid properties. The magnitude of the velocity is increased along the boundary layer as value of $\lambda$ is increased, so it decreases the cohesive forces between the fluid molecules and flowing layer therefore flowing fluid is accelerated with greater Weissenberg number. In present study, it is observed that the dual solution exists only in range of $0\le \lambda \le 0.1$. The velocity distribution profile decreases in first solution as $\lambda$ increases but no effect is observed in the second solution in spite of increasing $\lambda$.

Fig. 8.

Variation of Velocity profile $f^{\prime }\left(\eta \right)$ at various values of Williamson parameter (λ).

In order to show the existing of dual solutions over stretching surface, Figs. 9 and 10 are drawn. Velocity profile decreases in first solution when suction is increased in Fig. 9. On the other hand, dual behavior of velocity profile has been noticed. Fig. 10 demonstrated the effect of suction parameter on temperature profile. When suction increased, temperature and thickness of thermal boundary layer decrease in the first solution. However, dual behavior of increasing and decreasing of temperature profile can be seen in the second solution.

Fig. 9.

Variation of Velocity profile $f^{\prime }\left(\eta \right)$ at various values of suction parameter (S) over stretching surface.

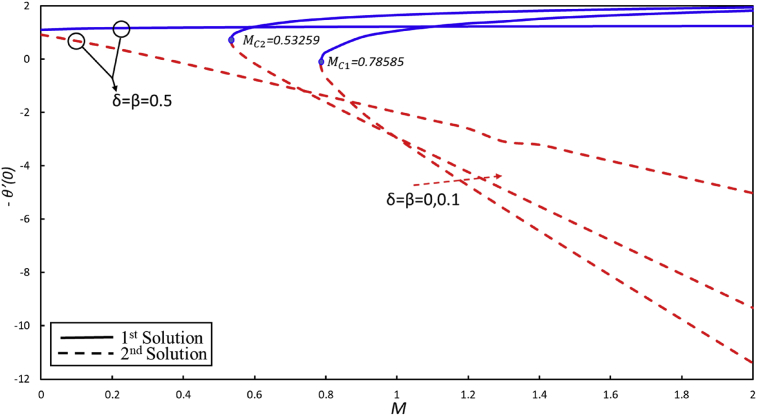
Fig. 11, shows the coefficient of skin friction; skin friction diminutions as velocity slip effect increases in both solutions. However, skin friction is increased in first solution and the reverse behavior is observed in second solution in which skin friction is decreasing by increment in the magnetic parameter (M).

Graph of local Nusselt number is plotted in Fig. 12, which demonstrates that as the slip parameter increases heat transfer rate increases in the second solution and declines monotonically as the Hartmann number is increased. In first solution, no more change occurs in the heat transfer rate when thermal slip parameters increase.

Fig. 12.

The profile of heat transfer rate $-{\theta }^{\prime }\left(0\right)$ with different values of M and $\delta ,\beta$ when λ = 0.1, S = 2, ζ = -1, Pr = 2 and σ = -0.25.

In like way, because of the presence of double solutions in a chose limit of parameters, as appeared in our separate numerical outcomes, an investigation of stability has been performed to decide the most stable solution between them by verdict the smallest eigen value $\epsilon$. With the help of bvp4c solver in MATLAB software, the Eqs. (31) and (32) along with boundary conditions (33) has been solved numerically. The certain values of $\delta ,\beta$ and $\xi$ together with the smallest eigenvalue $\epsilon$ properly listed in Table 3, when other parameters are fixed such as $\sigma =-0.25;\lambda =0;M=1;S=2;\text{and}Pr=2;$. From this table, it is seen that the second solutions demonstrate negative values, while the first solutions indicate positive values. At that point, it is concluded that the second solution is not stable and not physically feasible, on the other side, the first solution is stable and physically possible.

Table 3.

List of several values of the smallest eigenvalue $\epsilon$ when ξ < 0 (for Shrinking surface) and ξ > 0 (for Stretching surface).

$\mathit{\delta }$	$\mathit{\beta }$	$\mathit{\xi }$	$\mathit{\epsilon }$
			1st Solution	2nd Solution
0.1	0.1	-1	1.0994	-0.94705
0	0.1	-1	0.81561	-0.72048
0	0	-1	0.8375	-0.73862
0.1	0	-1	1.10014	-0.94768
0.1	0.1	1	3.0857	-2.16463
0	0.1	1	3.26891	-2.29312

4. Conclusion

The MHD flow of Williamson fluid and heat transfer with exponentially vertical shrinking/stretching sheet is examined unanimously into consideration of velocity and thermal slip effect. The similarity solutions are obtained by applying similarity transformations over governing boundary layer partial differential equations in form of the ordinary differential equations which have been solved by applying shooting method with maple software. Moreover, stability equations are derived from unsteady equations of basic governing equations. The summarized conclusion of the study is presented here.

• 1.The magnitude of the coefficient of the skin-friction is decreasing with Hartmann number.
• 2.The slip parameters are caused to decrease the velocity and temperature distribution inside the boundary layer in the first solution.
• 3.The velocity boundary layer thickness of the Williamson fluid is smaller as compare to the Newtonian fluid.
• 4.The magnetic parameter reduces the thickness of the velocity boundary layer.
• 5.The magnetic parameter increases the thickness of the thermal boundary layer.
• 6.The first solution is stable and physically possible.

Declarations

Author contribution statement

Liaquat A. Lund: Analyzed and interpreted the data; Wrote the paper.

Zurni Omar: Conceived and designed the analysis; Wrote the paper.

Ilyas Khan: Contributed analysis tools or data; Wrote the paper.

Funding statement

This work was supported by Universiti Utara Malaysia (UUM).

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.

Appendix A. Supplementary data

The following are the supplementary data related to this article: