Robustness and Efficiency of Poisson-Boltzmann Modeling on GPUs

Abstract

Poisson-Boltzmann equation (PBE)-based continuum electrostatics models have been widely used in modeling electrostatic interactions in biochemical processes, particularly in estimating protein-ligand binding affinities. Fast convergence of PBE solvers is crucial in binding affinity computations as numerous snapshots need to be processed. Efforts have been reported to develop PBE solvers on graphics processing units (GPUs) for efficient modeling of biomolecules, though only relatively simple successive over-relaxation and conjugate gradient methods were implemented. However, neither convergence nor scaling properties of the two methods are optimal for large biomolecules. On the other hand, geometric multigrid (MG) has been shown to be an optimal solver on CPUs, though no MG was reported for biomolecular applications on GPUs. This is not a surprise as it is a more complex method and depends on simpler but limited iterative methods such as Gauss-Seidel in its core relaxation procedure. The robustness and efficiency of MG on GPUs are also unclear. Here we present an implementation and a thorough analysis of MG on GPUs. Our analysis shows that robustness is a more pronounced issue than efficiency for both MG and other tested solvers when the single precision is used for complex biomolecules. We further show how to balance robustness and efficiency by utilizing MG’s overall efficiency and conjugate gradient’s robustness, pointing to a hybrid GPU solver with a good balance of efficiency and accuracy. The new PBE solver will significantly improve the computational throughput for a range of biomolecular applications on the GPU platforms.

Graphical Abstract

1. Introduction

Poisson-Boltzmann equation (PBE)-based continuum electrostatics modeling has gained wide acceptance in biomolecular applications, given the crucial roles played by electrostatic interactions in biochemical processes such as protein-protein and protein-ligand recognitions.^1–18 For example, PBE-based models have been widely used in the binding affinity computations, such as in the Molecular Mechanics Poisson-Boltzmann Surface Area (MMPBSA) method.^19–24 Because of the extremely complex geometries of biomolecules, it is vital to increase the accuracy and efficiency of PBE-based models for nontrivial applications in biomolecular simulations.^25–33

For biomolecular applications, it is impossible to solve the PBE analytically. Instead, we rely on numerical solutions. The most widely adopted numerical method is the finite-difference method,^34–46 where finite-difference grids are used to discretize the space and build up a set of linear/nonlinear equations. Other traditional numerical schemes include the finite-element method,^47–55 the box method,⁴⁰ the boundary element method,^56–71 and the boundary integral method.^{72, 73} Different from these direct numerical methods, indirect methods such as a free energy functional variational formulation have also been explored to solve PBE,^{12, 74} where the solution is obtained by searching for the minimum in the functional space. Among these approaches, FDM solvers for the PBE have been incorporated in several programs such as DelPhi,^{34, 36, 43, 75, 76} APBS,^{38, 40, 77} UHBD,^{35, 37} CHARMM/PBEQ,^{36, 42} and Amber/PBSA.^{30, 44–46, 78, 79} Numerical PBE schemes have been applied to the prediction of pKa values,^80–85 solvation free energies,^86–91 and binding free energies,^92–98 and the analysis of protein folding and biosynthesis,^99–111 and the design of new functional proteins.^{112, 113}

As the computational studies shift to larger and more complex biomolecular systems, both program efficiency and convergence rate become more challenging to address on conventional CPU-based computing platforms. These challenges are more pronounced when incorporating the PBE in typical biomolecular applications such as post processing binding free energy calculations and modeling amino acid mutation effects^{114, 115} that involve tens of thousands of snapshots. An interesting direction to address these challenges is to explore alternative hardware, such as the graphics processing units (GPUs), which have gradually been employed in a range of computational chemistry problems with impressive speedup, for example in MD simulations^116–118 and ab initio quantum mechanical (QM) calculations.^119–121 Several publications have also reported to use GPUs to accelerate linear PBE solutions for biomolecular systems with impressive speedup.^122–124 However, different from MD or QM simulations, various PBE solvers behave with markedly different efficiency on CPUs.^{45, 46} This is an important issue to consider when porting PBE calculations to GPUs.

To date only relatively simple PBE solvers were implemented on GPUs, including the successive over-relaxation (SOR) method,^{122, 123} the conjugate gradient methods (CG),¹²⁴ and the direct-sum boundary integral method with algebraic GMRES.¹²⁵ However, our prior analysis of various PBE solvers have shown that the convergence rate of many simple methods is not optimal on CPUs for large systems or tight convergence criteria even if they are simple to implement.^{45, 46} Specifically for SOR, there are two disadvantages. Firstly, a parallel (i.e. red-black) SOR has to be used on GPUs. However, the convergence rate of the red-black SOR is slower than SOR due to its color-ordered updating approach. Secondly, for most consumer-level GPU cards, single precision operations are widely supported with high efficiency. Double precision operations are at a significant disadvantage. Unfortunately, use of single precision further reduces the convergence rate of the red-black SOR. CG, as one of the best known Krylov subspace methods, has shown to be more stable but its scaling was not optimal for large biomolecular systems.¹²⁴

Multigrid methods are known to be optimal for solving many linear and nonlinear systems on CPUs. Typically there are two classes of multigrid methods: geometric multigrid and algebraic multigrid.¹²⁶ Geometric multigrid requires prior physical/mathematical knowledge of the underlying discretization and grid hierarchy, whereas algebraic multigrid only requires the coefficient matrix. Previous studies have shown that geometric multigrid is an optimal PBE solver for biomolecular applications.^{38, 45, 46, 127, 128} Algebraic multigrid can be used both as a direct PBE solver and as a preconditioner for a CG PBE solver.^{124, 129} However, its performance was not promising for biomolecules as our previous testing has shown.^{45, 124} Algebraic multigrid^{130, 131} and specialized multigrid^132–134 were also ported to GPUs on the Nvidia platform for various elliptic partial differential equation problems.

To date, there has been no report of geometric multigrid (MG) as a PBE solver on GPUs. This is not a surprise, as there are many implementation issues, particularly for applications to large and complex biomolecules. What further complicates the issue is the use of iterative methods such as SOR or Gauss-Seidel in its core relaxation procedure, as these simple methods are limited in the widely used single-precision mode as reviewed above. In addition, the robustness and efficiency of MG on GPUs are unclear. Therefore, a thorough analysis of MG on GPUs is a necessary step to realize marked overall efficiency improvement.

In the following, we present an implementation and a thorough analysis of the MG PBE solver for complex biomolecules on GPUs based on the Nvidia Compute Unified Device Architecture (CUDA). Our results show the robustness is a more pronounced issue than efficiency among the tested GPU PBE solvers in the widely used single precision mode. We further show how to balance robustness and efficiency in MG solver for complex biomolecular applications.

2. Methods

2.1. Poisson-Boltzmann Equation

In Poisson-Boltzmann continuum solvent models, both solute and solvent molecules are represented as continua: the solute molecule is treated as a low-dielectric cavity embedded in a high-dielectric continuum representing the solvent molecules collectively. For an electrolyte solution, a Boltzmann term describing the salt effect can be used in the Poisson equation, leading to the well-known Poisson-Boltzmann equation (PBE)

$$\nabla \cdot \epsilon (\mathit{r})\nabla u(\mathit{r})+\lambda (\mathit{r}){\Sigma }_i{n}_i{q}_i\exp [-q_{i}u(\mathit{r})/kT]=-\rho (\mathit{r}),$$ (1)

where ε is the dielectric constant, u is the electrostatic potential, ρ is the charge density, and λ is a masking function for the Stern layer. All variables are functions of position vector r. In the salt related term, n_i is the number density of ion type i in the bulk electrolyte, q_i is the charge of ion type i, k is the Boltzmann constant, and T is the temperature. Obviously the PBE is a non-linear partial differential equation. When q_iu(r)/kT is small, the PBE can be linearized as

$$\nabla \cdot \epsilon (\mathit{r})\nabla u(\mathit{r})-\lambda (\mathit{r}){\Sigma }_i{n}_i{q}_i^{2}u(\mathit{r})/kT=-\rho (\mathit{r}).$$ (2)

Only numerical solutions of equation (1) or (2) can be obtained for biomolecules. In this development the equations are discretized with a simple finite-volume scheme. The linearized PBE, for example, can be written at each grid point as follows

$$\begin{gathered} -h^{-2}{\epsilon }_i(i-1,j,k)[u(i-1,j,k)-u(i,j,k)]-h^{-2}{\epsilon }_i(i,j,k)[u(i+1,j,k)-u(i,j,k)] \\ -h^{-2}{\epsilon }_i(i,j-1,k)[u(i,j-1,k)-u(i,j,k)]-h^{-2}{\epsilon }_i(i,j,k)[u(i,j+1,k)-u(i,j,k)] \\ -h^{-2}{\epsilon }_i(i,j,k-1)[u(i,j,k-1)-u(i,j,k)]-h^{-2}{\epsilon }_i(i,j,k)[u(i,j,k+1)-u(i,j,k)] \\ +{\kappa }^{2}u(i,j,k)=h^{-3}q(i,j,k), \end{gathered}$$ (3)

where h is the grid spacing, i, j, and k are grid indexes along x, y, and z axes, respectively. ε_i(i, j, k) is the dielectric constant between grid points (i, j, k) and (i+1, j, k). ε_j(i, j, k) and ε_k(i, j, k) are defined similarly. κ² absorbs all related coefficients in the Boltzmann term. q(i, j, k) is the total solute charge within a cubic volume h³ centered at (i, j, k). The linear system can then be denoted symbolically as

$$\mathit{A}u=f,$$ (4)

where A is the left-hand-side coefficient matrix and f is the right-hand-side constant in equation (3).

To solve equation (4), a number of solvers have been developed for biomolecular applications, such as successive over-relaxation,¹³⁵ conjugate gradient,¹³⁵ (modified) incomplete Cholesky conjugate gradient ((M)ICCG),^136–139 geometric multigrid,¹⁴⁰ and algebraic multigrid.¹⁴¹ All solvers proceed from an initial guess of u(i, j, k) to approach the solution iteratively. In this manuscript, we present an implementation of the geometric multigrid method on the CUDA GPU platform and a detailed analysis of its performance along with other GPU-friendly methods.

2.2. Geometric Multigrid Method

Geometric multigrid (MG) methods are highly efficient techniques to solve linear equations or nonlinear equations with an algorithm complexity of O(N) for a system of N grid points.¹⁴² In the following the basic ideas of MG are first introduced before discussion of their GPU-specific issues.

In MG, a multigrid hierarchy is constructed by partitioning the system into coarse and fine grid levels. Spectral analysis of some of the basic iterative methods such as Gauss-Seidel shows that they are very good at eliminating both high-frequency or oscillatory components of the error on fine grids, and low-frequency or smooth components of the error on coarse grids.¹⁴² Therefore, the multigrid hierarchy can be utilized to solve the linear system by using the same basic iterative methods as smoothers on every level. The coarse grid points form a coarse level, and an interpolation operator, defined as a weighted sum of the coarse grid points, is used to interpolate a coarse level solution to a fine level. A restriction operator, usually taken as the transpose of the interpolation operator, is used to restrict a fine-level solution to a coarse level.^{143, 144} Worth noting is that in our implementation, the restriction and interpolation operators were implemented as harmonic averaging as proposed by Holst et al.³⁸

There are basic and nested strategies for the MG methods, leading to the V-Cycle and F-Cycle algorithms, respectively. By combining relaxation, restriction and interpolation operators, a V-Cycle scheme can be constructed as shown in Figure 1(a), and a recursive V-Cycle scheme is provided in Algorithm 1. The linear restriction and interpolation operators are denoted as ${\mathit{I}}_h^{2h}$ and ${\mathit{I}}_{2h}^h$, respectively, below.

Figure 1.

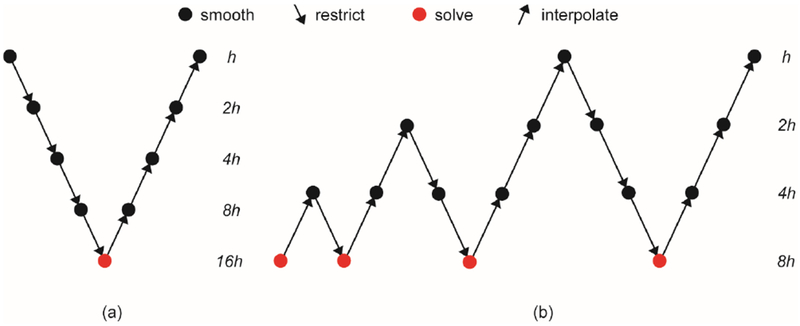
Illustrations of (a) V-Cycle and (b) F-Cycle.

Algorithm 1. MG V-Cycle (Recursive):

$${\nu }^h\leftarrow V^h({\nu }^h,f^h)$$

1. Relax ν₁ times on A^hu^h=f^h with a given initial guess ν^h.

2. If Ω^h = coarsest grid, then go to step 4.

   Else

   $$\begin{gathered} f^{2h}\leftarrow {\mathit{I}}_h^{2h}(f^h-{\mathit{A}}^h{\nu }^h), \\ {\nu }^{2h}\leftarrow 0, \\ {\nu }^{2h}\leftarrow V^{2h}({\nu }^{2h},f^{2h}). \end{gathered}$$

3. Correct ${\nu }^h\leftarrow {\nu }^h+{\mathit{I}}_{2h}^h{\nu }^{2h}$.

4. Relax ν₂ times on A^hu^h=f^h with a given initial guess ν^h.

The idea of using coarsest-grid solutions to obtain improved initial guesses for the finest-grid solutions is called nested iteration, as relaxation on the coarsest grid is not expensive. The algorithm that joins the nested iteration with the V-Cycle leads to the full multigrid V-Cycle, or F-Cycle for short. An F-Cycle scheme is illustrated in the Figure 1(b) and a recursive F-Cycle algorithm is shown in Algorithm 2. In this study, we implemented both V-Cycle and combined F-V-Cycle MG solvers on GPUs and analyzed their performance.

Algorithm 2. MG F-Cycle (Recursive):

$${\nu }^h\leftarrow F^h(f^h)$$

1. If Ω^h=coarsest grid, set ν^h ← 0 and go to step 3.

   Else

   $$\begin{gathered} f^{2h}\leftarrow {\mathit{I}}_h^{2h}(f^h), \\ {\nu }^{2h}\leftarrow F^{2h}(f^{2h}). \end{gathered}$$

2. Correct ${\nu }^h\leftarrow {\mathit{I}}_{2h}^h{\nu }^{2h}$.

3. Solve ν^h ← V^h (ν^h, f^h) with ν₀ cycles.

2.3. Red-Black Gauss-Seidel/SOR Relaxations

As reviewed above, a core routine of the MG method is to relax all grids using an iterative relaxer. There are many basic iterative methods such as Gauss-Seidel and SOR that can be utilized.

The basic idea of SOR is that components of a new approximated solution are used as soon as they are computed.¹⁴² To solve the linear equation (4) Au = f, we first introduce a decomposition of A, such as A = D − L − U, where D is the diagonal of A, U and L are the negative upper and lower triangular parts of A, respectively. Equation (4) can then be rewritten as

$$u={(\mathit{D}-\omega \mathit{L})}^{-1}\left\{[\omega \mathit{U}+(1-\omega )\mathit{D}]u+\omega f\right\},$$

where ω is an over-relaxation factor. Note that when ω = 1, SOR reduces to Gauss-Seidel. This representation corresponds to solving the jth equation for u_j and using latest approximations for components 1, 2, …, j−1.

Defining the Gauss–Seidel/SOR iteration matrix as

$${\mathit{R}}_{\mathit{G}}={(\mathit{D}-\omega \mathit{L})}^{-1}[\omega \mathit{U}+(1-\omega )\mathit{D}],$$

we can express the method as the following given an approximate solution v,

$$v\leftarrow {\mathit{R}}_{\mathit{G}}v+{(\mathit{D}-\omega \mathit{L})}^{-1}\omega f.$$

The order in which the components of v are updated can be ascending or descending.

Another effective alternative is to update all the even components first and then update all the odd components next. This strategy leads to the red-black Gauss-Seidel/SOR method,¹⁴⁵ as illustrated in Figure 2. Notice that the red points only depend on the black points and vice versa. This leads to some significant advantage for parallel computation, as shown in several MPI implementations.^{75, 146} Here in our MG implementation, the red-black Gauss-Seidel is used as the relaxer at every level except the coarsest level where the red-black SOR is used.

Figure 2.

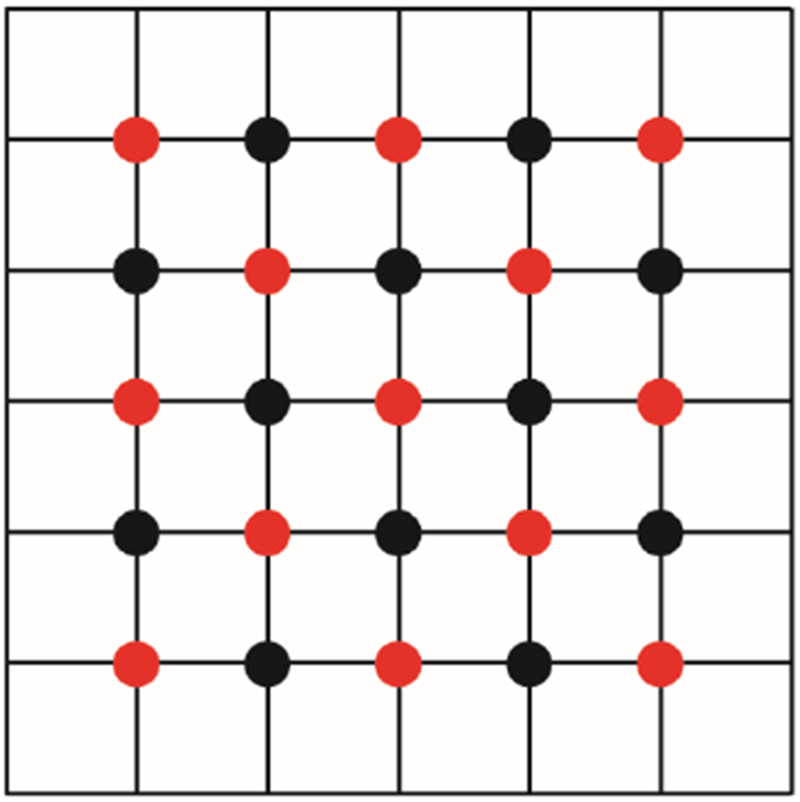
Illustration of a 2-D red-black grid.

2.4. CUDA Unified Memory and Array Optimization

Unified Memory was introduced in CUDA 6. It provides a new programming framework that allows GPU applications to use a single pointer in both CPU functions and GPU kernels. This markedly simplifies memory management. Later CUDA 8 and the Pascal architecture significantly improves the Unified Memory functionalities by introducing 49-bit virtual addressing and on-demand page migration. The large 49-bit virtual addresses are sufficient to enable GPUs to access the entire system memory plus the memory of all GPUs in the system. The Page Migration engine allows GPU threads to fault on non-resident memory accesses, so that the system can migrate pages from anywhere in the system to the GPUs memory on-demand for efficient processing.¹⁴⁷

However, page faults and migration can be expensive. To avoid the overhead, data prefetching and usage hint functionalities may be used. In our MG implementations on Pascal architectures, we utilized CUDA Unified Memory and optimized memory access with cudaMemAdvise and cudaMemPrefetchAsync application programming interfaces. On pre-Pascal architectures, we used zero-copy memory to avoid data migrations.¹³⁴

Similar to CPU implementation of FDPB solvers,⁴⁴ the matrix arrays were stored in the matrix-free style with padded zeros at grid boundaries so that fast stencil access can be achieved and the conditional branch was avoided in all GPU kernels. When the MG solver is combined with the Jacobi-PCG solver implemented with the CUSP library,¹⁴⁸ the matrix-free arrays were transformed into the diagonal matrix format first, which is suited for PBE seven-banded coefficient matrix computation, before feeding into later phase iterations.

2.5. Computational Details

All CUDA PBE solvers were implemented in both single and double precisions in the PBSA program^{45, 46, 78, 79, 149–161} of the Amber/AmberTools 18 packages.^{162, 163} The double precision was implemented for the robustness analysis only, and the single precision was used throughout the study unless otherwise specified. The largest 144 biomolecular structures from the Amber PBSA benchmark suite were used in our test.⁴⁵ The number of atoms in these molecules range from 4,240 to 37,421. Their geometries are quite different, requiring at least 1 million grid points with the default setup. The atomic charges were assigned to those of Cornell et al¹⁶⁴ and the atomic radii to the modified Bondi radius set.

All testing runs were performed with the following conditions unless specified otherwise. The convergence criteria of 10⁻⁴ and 10⁻⁶ were used for low- and high-precision applications, respectively, unless specified otherwise. The grid spacing of 0.5 Ǻ was used. The ratio of the grid dimension over the solute dimension (the fillratio keyword in Amber) was set to 1.5. No electrostatic focusing was applied. The potential values on all grid points were initialized to zero. The dielectric constants were set to 1 and 80 for solute and solvent, respectively. The weighted harmonic average of the solute and solvent dielectric constants was used as the boundary dielectric constants. Therefore, the symmetric and positive-definite coefficient matrices were obtained and suitable for all tested linear solvers. Finally, the conductor boundary condition was used to minimize the setup cost of boundary conditions. All other parameters were set as default in the PBSA module in the Amber/AmberTools 18 package.¹⁶²

All testing was conducted on a dedicated compute node with two NVIDIA TITAN Xp GPU cards and one Intel Xeon E5-1620 v3 CPU and 16GB main memory. Our time measurements for each solver include all execution time of the core routine code, i.e. time elapsed on device (GPU) and on host (CPU) and also for transferring data between the device and the host.

3. Results and Discussion

In the following we first investigated the robustness of the GPU solvers with a diverse set of large and complex biomolecules and analyzed the cause of observed failures with the MG solver as the focus. Based on the analysis, we proposed to balance algorithm robustness and computational efficiency with a hybrid MG-PCG iteration scheme on GPUs. This is followed by further optimization of the MG iteration. Finally the performance of various GPU solvers is presented, along with a sanity check to confirm the numerical accuracy of the new implementation. We end this section with a discussion of implementation details and potential future improvements.

3.1. Robustness of GPU Solvers

We first tested three representative GPU solvers, SOR, Jacobi-PCG, and MG, in the single-precision modes on a set of 144 large biomolecules. The testing statistics are summarized in Table 1. With a convergence criterion 10⁻⁴ (or looser), all solvers were found to converge in all test cases. Once the convergence criterion is tightened to 10⁻⁵, SOR fails to converge with all test cases and MG fails to converge with five test cases. Interestingly Jacobi-PCG stands out by passing all tests. With the tightest tested convergence criterion of 10⁻⁶, even MG fails almost all except one case. Once again Jacobi-PCG passes all tests.

Table 1.

Number of failures in the test of different GPU solvers with a convergence criterion of 10⁻⁴, 10⁻⁵, and 10⁻⁶, respectively. The maximum allowed iteration steps is 3,000. S/D denotes the single/double precision mode. A total of 144 cases were used.

Solver	SOR(S)	Jacobi-PCG(S)	MG(S)	SOR(D)	Jacobi-PCG(D)	MG(D)
10−4	0	0	0	0	0	0
10−5	144	0	5	27	0	0
10−6	144	0	143	65	0	0

As a comparison all tests were rerun in the double precision mode. Under this condition, SOR still fails to converge in 27 cases at the criterion of 10⁻⁵ and 65 cases at that of 10⁻⁶. On the other hand, both Jacobi-PCG and MG are able to converge in all cases in all tested convergence criteria (Table 1). It is clear that MG has a better convergence behavior than SOR, but worse than Jacobi-PCG in the single-precision mode, apparently due to its dependence on SOR/Gauss-Seidel as the relaxers.

Inspection of the failed MG test cases shows that these failures are not due to their extra-large system sizes but due to their high net charges. Here we use protein 1TZY to illustrate the common characteristics of all failures. The protein contains 152 positive residues and 68 negative residues among a total of 755 residues and 12,321 atoms; and is discretized onto a finite-difference grid of 16,393,727 points. The residual L2-norm of the finest grid was observed to decrease from the initial 4.27×10³ to 7.97×10⁻² in eight V-Cycles, then halted around 7.30×10⁻² in the following 144 V-Cycles until hitting the maximum relaxation iteration cycles allowed. Specifically, the iteration cycles needed at each level increased from the default setting of ten cycles to the maximum of 1,000 cycles, as shown in the Figure 3. In contrast, MG in the double precision mode was able to converge with a final L2-norm of 3.98×10⁻² within seven V-Cycles.

Figure 3.

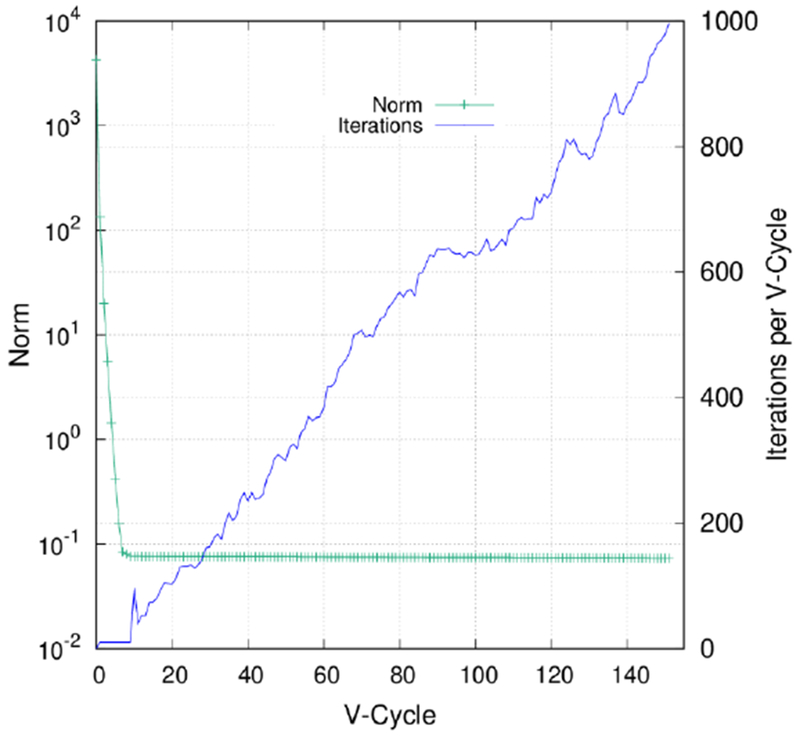
Decreasing L2-norm of the finest grid and increasing iteration cycles needed per V-Cycle of 1TZY. The single precision was used.

We also investigated whether the use of the red-black SOR/Gauss-Seidel instead of the original SOR/Gauss-Seidel was causing the failures by MG. Our test shows that MG with the original Gauss-Seidel also fails in the single precision, with the L2-norm oscillating around 6.50×10⁻² after nine V-Cycles. Considering the error-smoothing nature of the MG algorithm, we can conclude that in charge-rich systems, the single-precision SOR/Gauss-Seidel iterations result in too much numerical noise that is too hard to reduce. Worth noting is that at the coarsest level, where the systems are always small, the single-precision SOR/Gauss-Seidel can be used to solve the linear system in exactly ten iterations. Thus, the difficulty faced in the single-precision MG runs is in the relaxation phase at the fine grid levels, but not in the final solution phase at the coarsest grid level.

3.2. Hybrid GPU Solver

Since MG solver is much faster than other GPU solvers if it can converge (most 10⁻⁵ cases as shown above) and Jaocbi-PCG is more robust with tighter convergence criteria, we introduced the Jacobi-PCG solver as a backup to address the MG solver’s convergence issue. For the same test case of 1TZY as shown in Figure 4, Jacobi-PCG was able to reduce the L2-norm to 5.43×10⁻³ in 259 iterations after MG V-Cycles fail to reduce the L2-norm further. Interestingly oscillation in L2-norm occurs at the switching point between the two solvers, but the L2-norm decreases thereafter. This is reasonable since the MG and CG solvers follow very different ideas (iterative vs. Krylov subspace) and thus approach the solution through different paths.

Figure 4.

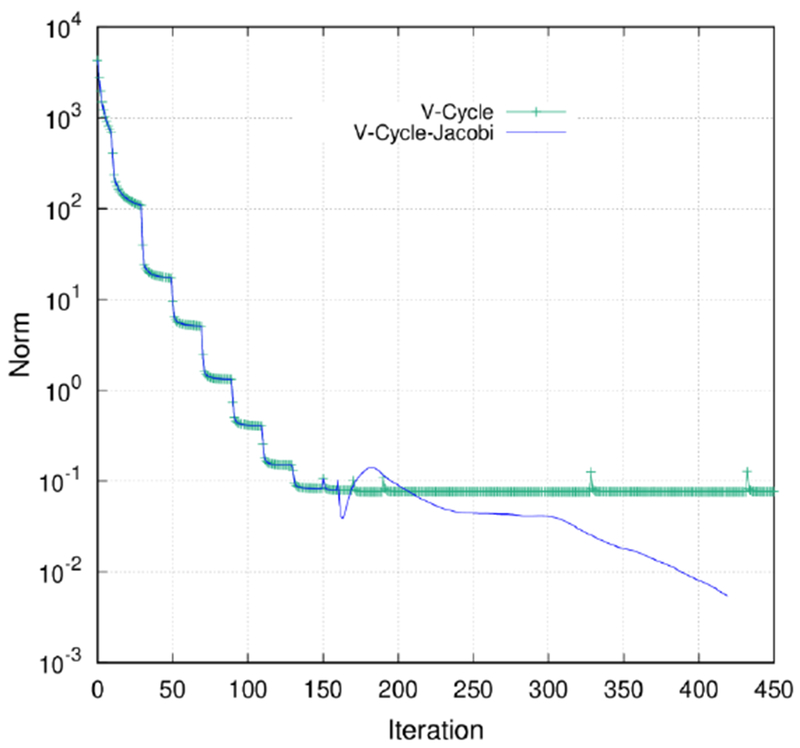
L2-norm of the finest grid versus number of iterations (either Gauss-Seidel iterations or PCG iterations) for 1TZY. Green is for V-Cycle solver. Blue is for V-Cycle-Jacobi-PCG hybrid solver.

Next we investigated the proper switching point between the two solvers. By monitoring the instant un-convergence rate (r_uc) in the MG iteration, which is defined as the ratio of the L2-norm of the current step to that of the previous step (r_uc = curent_norm/previous_norm), the solver scheduler smoothly switches from MG to Jacobi-PCG when r_uc is larger than a preset cutoff. Our analysis shows that V-Cycles generally stop to converge after r_uc becomes larger than 0.95, but different cutoff value may lead to different overall performance. To find the optimal cutoff, we analyzed the performance of the hybrid MG-Jacobi solver for twelve randomly selected test cases versus the r_uc cutoff at the tight convergence criterion of 10⁻⁶. As shown in Figure 5, the cutoff value of 0.9 is a reasonable choice for most test cases.

Figure 5.

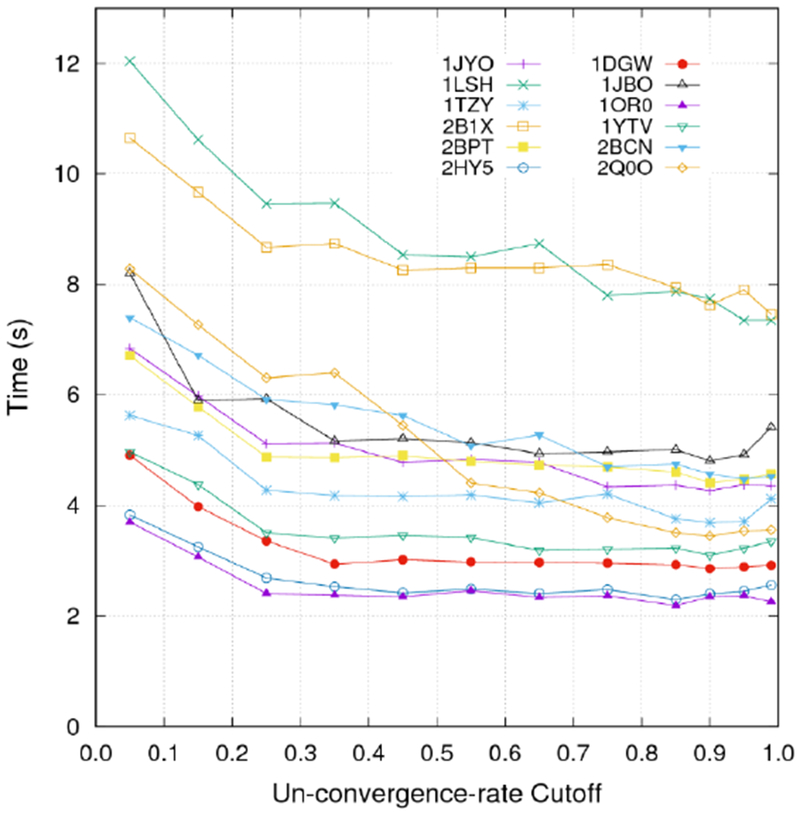
Performances of the hybrid MG-Jacobi-PCG solver for twelve randomly selected test cases versus the cutoff used for r_uc. The convergence criterion was set to 10⁻⁶.

To illustrate the performance of the hybrid GPU solver, a detailed timing analysis is provided in Table 2 for the five test cases previously failed in the MG (single precision) runs. Worth noting is that the performance of the hybrid GPU solver is still better than the GPU/Jacobi-PCG solver, and the speedup factor is ~2.0. More thorough tests with all 144 protein systems show that the overall speedup ratio of the hybrid MG over Jacobi-PCG can be higher as ~5.0 as shown in Section 3.4.

Table 2.

Timing (in seconds) of the five test cases that previously failed in MG (single precision) runs by GPU/Jacobi-PCG and GPU/MG-Jacobi-PCG at the convergence criterion of 10⁻⁶.

Protein	Ngrid	Jacobi-PCG	MG-Jacobi
1TZY	16393727	7.87	3.71
1JYO	19433295	8.61	4.31
2BPT	18727455	8.97	4.46
1LSH	29984175	16.54	8.08
2B1X	27740559	15.23	7.98

3.3. Efficiency Tuning of MG on GPUs

The V-Cycle used in the MG solver usually starts with zero initial potentials. However, it would be beneficial if a better initial guess than the default zero solution is used. The straightforward way is to solve the system on the coarsest grid first and interpolate the solution back to the finest level as the initial guess. To realize this idea, we embedded one F-Cycle at the beginning of the MG cycle to provide a better initial guess for the subsequent V-Cycles. As shown in Figure 6, improvement from 0.8% to 28% was observed compared to the V-Cycle-only MG at least at the tested condition on GPUs. Here the convergence criterion was set to 10⁻⁵ to make the problems more challenging while still without many convergence failures. Our analysis shows that one embedded F-Cycle on average saves three or four V-Cycles later.

Figure 6.

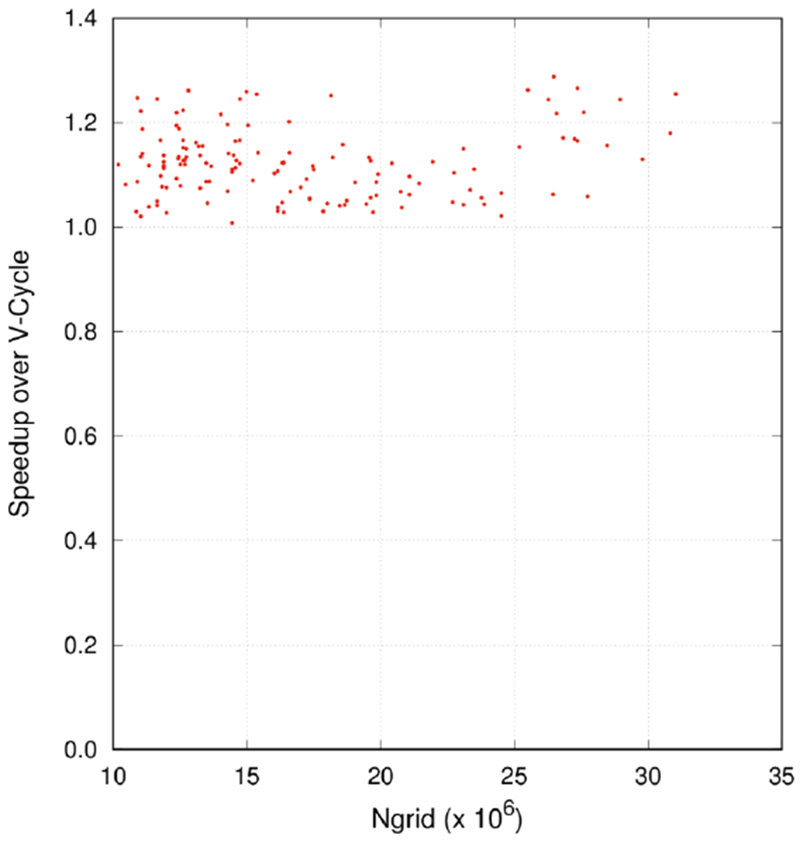
Speedup of 1F-V-Cycle over V-Cycle for the protein test set. The convergence criterion was set to 10⁻⁵.

Interestingly, however, using multiple F-Cycles as iterative engine deteriorates the convergence of MG (data not shown). This is reasonable considering that in one F-Cycle (see Figure 1(b)) a better initial guess is already obtained and used for the largest V-Cycle (the final cycle inside F-Cycle) to smooth errors. The solution obtained here should be fed directly into a subsequent V-Cycle to continue smoothing. If, however, another F-Cycle is applied subsequently, the solution would be restricted all way down to provide an initial guess for the coarsest level. This cancels the contribution of the first F-Cycle since on the coarsest level the system is small enough to be easily solved with any initial guess.

3.4. Efficiency Comparison of Various CUDA Solvers

As discussed in Methods, the red-black Gauss-Seidel was used as the smoother and the red-black SOR as the coarsest-level solver in the GPU MG cycles. Thus the performance gain of the GPU MG over the CPU MG can never be higher than that of the GPU SOR over the CPU SOR. Fortunately, it is good to note that the SOR can be implemented with extremely high efficiency as shown in Figure 7: a very high speedup ratios ranging from ~87 to ~109 can be obtained if the problem can be solved with the tested single precision condition. This is consistent with a previous development (Luty and Walker, Personal communication).

Figure 7.

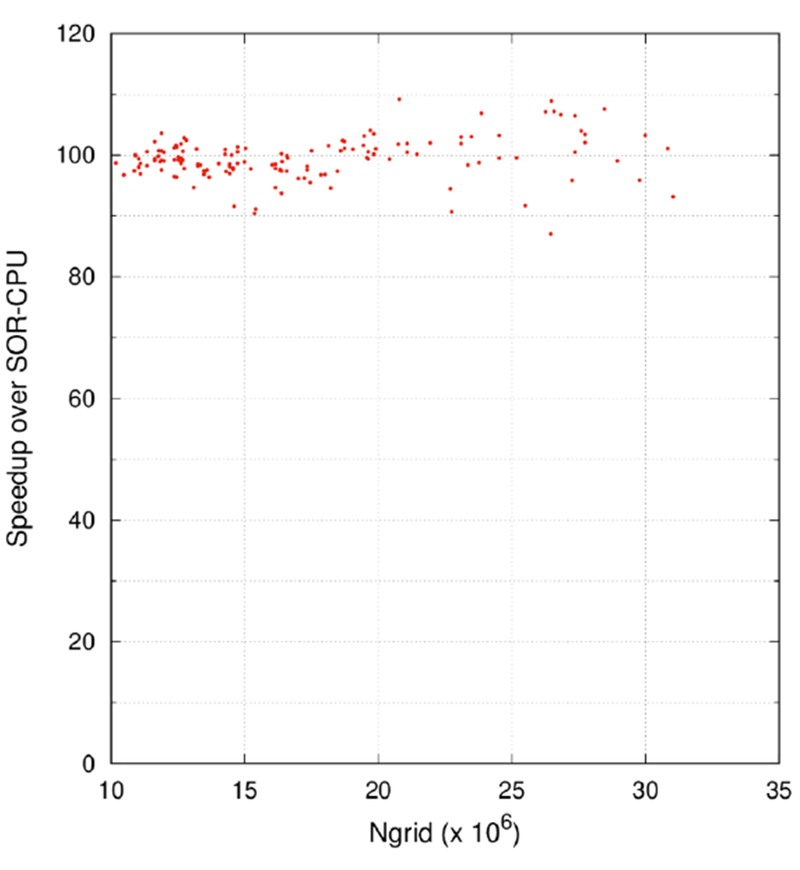
SOR speedup of GPU runs over CPU runs for the protein test set. The convergence criterion was set to 10⁻⁴, with which no failure was observed. Here the CPU version is the single-thread version without the red-black labeling.

Next a natural question is how much faster MG can achieve over the already very highly efficient SOR solver on GPUs. As a reference, we also compared the CG-based GPU (Jacobi-PCG) solver.¹²⁴ Here eight representative proteins that cover from ~12 to ~30 million grid points were selected to measure their solver time with 10⁻⁴ and 10⁻⁶ convergence criteria. Table 3 shows that the hybrid MG solver overall performs the best among the three solvers with Jacobi-PCG as the second and SOR as the third. With the convergence criterion of 10⁻⁴ where SOR can converge, the speedup ratios of the hybrid MG and Jacobi-PCG solvers over SOR are ~3.0 to ~9.0 and ~0.9 to ~1.9, respectively. With the convergence criterion of 10⁻⁶ where SOR and pure MG mostly cannot converge, the speedup ratios of the hybrid MG solver over the Jacobi-PCG solver are ~1.9 to ~2.7.

Table 3.

Average time (in seconds) used by GPU solvers for eight selected proteins. The measurement is the time elapsed both on device (GPU) and on host (CPU) and on transferring data between the device and the host. The criteria of 10⁻⁴ and 10⁻⁶ were used.

	Protein	Ngrid	GPU
			SOR	Jacobi-PCG	MG
Convergence 10−4	1OR0	12615615	3.44	3.94	0.92
	3EHU	12737983	4.16	4.27	1.05
	1YTV	15039999	4.22	4.31	1.19
	1DGW	15368463	3.74	4.13	1.15
	2BCN	19625007	6.91	5.97	1.34
	2Q0O	21077567	6.81	6.01	1.33
	1JBO	25502607	14.61	7.66	1.86
	1E6Y	29788591	12.80	10.01	1.86
Convergence 10−6	1OR0	12615615	-	5.88	2.47
	3EHU	12737983	-	5.78	2.71
	1YTV	15039999	-	6.23	3.14
	1DGW	15368463	-	6.21	3.05
	2BCN	19625007	-	8.91	4.75
	2Q0O	21077567	-	10.04	3.78
	1JBO	25502607	-	11.44	4.84
	1E6Y	29788591	-	15.57	6.91

Finally, it is interesting to see how the three tested GPU solvers scale with system sizes. Figure 8 shows the overall performances of the three GPU solvers on all 144 test cases. With the convergence criterion of 10⁻⁴ (Figure 8(a)), speedup ratios of MG over SOR solvers are from ~2.4 to ~10.4. Clearly the ratios depend on system sizes, but the scaling is roughly linear. This shows the advantage of the MG solver on larger systems, consistent with the original MG development on CPUs as reported in the literature.^{38, 45} Finally, with the convergence criterion of 10⁻⁶ (Figure 8(b)), the hybrid MG performs better than the Jacobi PCG at speedup ratios of ~2.0 to ~5.0, clearly showing the added benefit of incorporating the Jacobi PCG into the hybrid MG solver.

Figure 8.

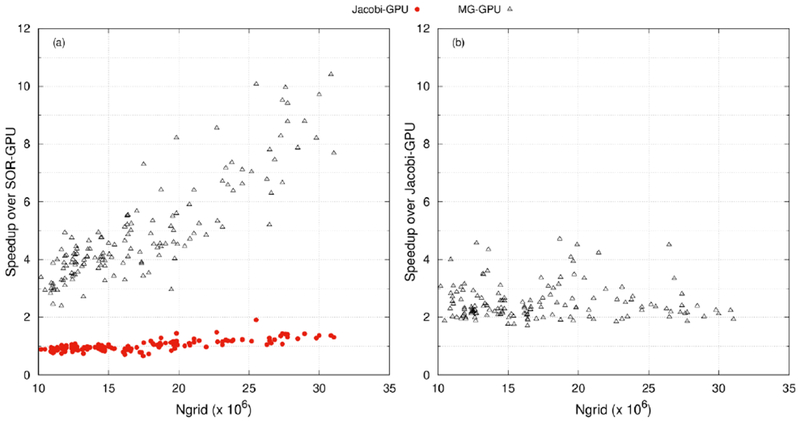
Comparison between GPU solvers SOR, Jacobi-PCG, and MG for the protein test set with (a) SOR-GPU and (b) Jacobi-GPU as the reference, respectively. The convergence criteria were set to 10⁻⁴ for (a) and 10⁻⁶ for (b), respectively.

3.5. Accuracy of CUDA MG Implementation

Given the default use of single precision on GPUs for optimal efficiency, it is important to confirm that our MG GPU implementation can achieve consistent numerical results with its CPU counterpart. Specifically, the electrostatic solvation energies by both solvers were compared for the large set of biomolecules. As shown in Figure 9, the energies between GPU and CPU implementations correlate quite well with both 10⁻⁴ and 10⁻⁶ convergence criteria. The final fitting slopes are 1.00016 and 0.999997, respectively, and the asymptotic standard errors are 0.0024% and 0.000025%, respectively. The maximum relative energy errors between the two implementations are 8.76×10⁻⁴ and 6.27 ×10⁻⁶, respectively, which are consistent with the convergence criteria chosen.

Figure 9.

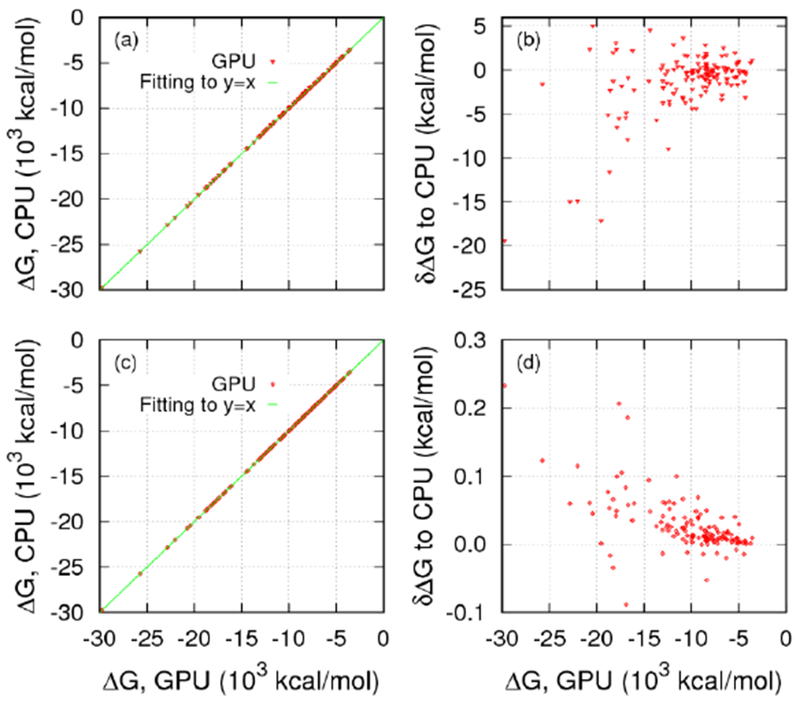
Correlations (a), (c) and differences (b), (d) of electrostatic solvation energies by the MG solver on GPU and on CPU for the protein test set. The convergence criterion was set to 10⁻⁴ in (a) and (b) and 10⁻⁶ in (c) and (d). The linear regression slopes are 1.00016 and 0.999997, respectively. The asymptotic standard errors are 0.0024% and 0.000025% for the 10⁻⁴ and 10⁻⁶ criteria, respectively.

3.6. Memory Considerations

Memory usage is crucial for GPU implementations since memory is often limited on most consumer-grade GPUs. In the MG implementation, the typical GPU memory usage is about 75 × Ngrid bytes, where Ngrid is the number of grid points when discretizing the system with the finite difference method. If the MG-Jacobi-PCG hybrid solver is involved in the computation with tighter convergence criteria, the typical GPU memory usage is about 135 × Ngrid bytes. Our analysis of the MG solver showed that NVIDIA Titan Xp cards, which have 12 GB GPU memory, are sufficient to successfully run all our 144 stress tests until host memory hit the limit first. On the older NVIDIA GTX 980 Ti cards with ∼ 6 GB GPU memory, the MG implementation is able to successfully complete calculations with ~ 75.0 million grid points given sufficient host memory. Worth noting is that for extremely large grids, for example those with at least one billion grid points, the MG implementation generally requires about 70 GB memory, which is far beyond the available memory on most consumer-grade GPU cards.

3.7. Future Directions

In the MG cycles, the computation bottleneck is the red-black Gauss-Seidel/SOR relaxation, so that it would be most beneficial to gain further optimization on those operations. In the color-labeled storage patterns, the matrix elements of the same color are accessed nonconsecutively by parallel threads, which causes performance loss. A possible strategy to improve locality and coalescing of memory accesses is to split the matrix storage into two separate red/black groups.¹⁶⁵ In this way, bandwidth utilization can be improved by accessing array elements continuously.

Another direction for further optimization is to utilize the on-chip fast shared memory that is private for each thread block, its latency is two orders of magnitude lower than that of the global memory. However, shared memory is more complicated to use and needs careful management. For example, data prefetching is required and comes with a cost when moving data from the global memory to the shared memory of a thread block. In addition, unfavorable overhead may also result from accessing overlapping data between neighboring thread blocks since the shared memory of a thread block is not visible outside the thread block.

Finally, only the linear system solver, i.e. the multi-grid setup and the solution (both F- and V-cycles) have been implemented on GPUs in this study, while the discretization of PBE is still carried out on the host CPU. Porting the entire PBSA program onto GPUs would clearly accelerate the overall efficiency of the program. The remaining bottlenecks in the program are the molecular surface determination and the reaction field energy calculation (as it requires looping over all pairwise terms between surface charges and atomic charges). These two steps dominate roughly 96% of the remaining CPU time, which we expect to be reduced by at least 2/3 after being ported to GPUs. The additional development and other fine-grained optimizations are in progress in our lab. We expect our full GPU implementation of both PBSA and MMPBSA programs to be available along with the release of Amber 2019.

4. Conclusions

In this study, we implemented a PBE MG solver to harvest the computing powers on GPU platforms, and investigated the robustness and efficiency of multiple GPU solvers using a large set of realistic biomolecules. Our analysis shows that the tested GPU solvers have different convergence behaviors when a tight acceptance criterion ≥ 10⁻⁵ is used in the single precision mode. SOR was found to be the worst in this regard while Jacobi-PCG the best, and MG in the middle. Failures in MG were found not due to large system sizes but significant numbers of charged residues. It is clear that the use of single precision in the Gauss-Seidel relaxation introduces too much numerical noise that is too hard to reduce. This is in contrast to its much-better convergence behavior when the tests were conducted in the double-precision mode. We therefore developed a hybrid MG/PCG solver to utilize the advantages of high efficiency of MG and robustness of Jacobi-PCG for the widely used single-precision mode on GPUs.

The MG solver was further improved by embedding one F-Cycle before the initiation of V-cycles to provide a better initial guess. Our analysis shows that the strategy on average saves three or four V-Cycles. After incorporating this and other improvements, we further compared the efficiency of three representative GPU solvers. Our analysis shows that GPU/SOR speedup over CPU/SOR can be very impressive with ratios ~100 if the problem can be solved with the tested single precision condition. MG solver overall performs best among the three solvers with Jacobi-PCG as the second and SOR as the third when they all can converge. With the tight convergence criterion of 10⁻⁶ where SOR and pure MG mostly cannot converge, the speedup ratios of the hybrid MG solver over Jacobi-PCG are ~2.0 to ~5.0.

Finally, the implementation of the MG solver was validated by comparing electrostatic solvation energies computed on both GPU and CPU. The energies between the two sets correlate quite well with both loose and tight convergence criteria. The maximum relative energy errors between the two are consistent with the convergence criteria chosen. Future directions to improve the PBE calculations were also discussed. The new developments, together with other fine-grained optimizations in progress as implemented in the latest Amber package, will greatly benefit a wide range of biomolecular applications, such as those in MMPBSA binding affinity simulations on the GPU platforms.