Self-organized mechano-chemical dynamics in amoeboid locomotion of Physarum fragments

Abstract

The aim of this work is to quantify the spatio-temporal dynamics of flow-driven amoeboid locomotion in small (~100 µm) fragments of the true slime mold Physarum polycephalum. In this model organism, cellular contraction drives intracellular flows, and these flows transport the chemical signals that regulate contraction in the first place. As a consequence of these non-linear interactions, a diversity of migratory behaviors can be observed in migrating Physarum fragments. To study these dynamics, we measure the spatio-temporal distributions of the velocities of the endoplasm and ectoplasm of each migrating fragment, the traction stresses it generates on the substratum, and the concentration of free intracellular calcium. Using these unprecedented experimental data, we classify migrating Physarum fragments according to their dynamics, finding that they often exhibit spontaneously coordinated waves of flow, contractility and chemical signaling. We show that Physarum fragments exhibiting symmetric spatio-temporal patterns of endoplasmic flow migrate significantly slower than fragments with asymmetric patterns. In addition, our joint measurements of ectoplasm velocity and traction stress at the substratum suggest that forward motion of the ectoplasm is enabled by a succession of stick-slip transitions, which we conjecture are also organized in the form of waves. Combining our experiments with a simplified convection-diffusion model, we show that the convective transport of calcium ions may be key for establishing and maintaining the spatiotemporal patterns of calcium concentration that regulate the generation of contractile forces.

1. Introduction

Amoeboid locomotion is a fast type of cellular locomotion that involves large shape changes mediated by cell contractility, and does not require biochemically regulated adhesion to the extracellular environment [1–4]. In addition to its conspicuous biomedical applications, the study of amoeboid locomotion has been recently applied to the bio-mimetic design of fluid filled, highly deformable robots [5, 6]. Amoeboid organisms such as Amoeba proteus and Physarum polycephalum are particularly interesting model organisms for biomimetic design because they develop significant intracellular pressure-driven flows [7,8]. Because diffusion across these giant cells is slow, intracellular flows are important not only to drive motility but also for the transport of chemical signals and nutrients (see §3.4 below and [9]). The non-linear feedback between pressure-driven flow, molecular transport and cell contractility can lead to rich dynamics that differ from those observed in smaller cells, and which are yet poorly understood.

This study examines the spatio-temporal dynamics of flow driven amoeboid locomotion in the true slime mold Physarum polycephalum. The Physarum plasmodium is a multi-nucleated slime mold that is composed of a gel-like ectoplasm and a sol-like endoplasm [10]. During locomotion, the endoplasm flows back and forth in a periodic manner, which is customarily characterized as shuttle flow [7, 11]. This flow is driven by periodic contractions of cross linked actomyosin fibrils in the ectoplasm [12–14]. The contraction is regulated by waves of calcium ions [15,16], whose propagation is notably influenced by the endoplasmic flow [17, 18]. The interactions between these physical phenomena can be associated with the complex spatio-temporal patterns observed in a variety of Physarum preparations, including non-locomoting protoplasmic droplets, and locomoting plasmodial fragments of small (~ 100 µm) [13] and intermediate (~ 1 µm) size [19]. These experiments reported homologous spatio-temporal patterns for a range of different geometries, biological strains and environmental conditions, implying that the spatio-temporal coordination of motility in Physarum plasmodia could be achieved via remarkably robust physical mechanisms. However, investigating the details of these mechanisms has been difficult since the vast majority of previous experiments recorded a limited amount of data, namely the fragment thickness as estimated indirectly from image brightness. In particular, there is very limited information about the spatio-temporal dynamics of calcium ions and their relation with endoplasmic flow and ectoplasmic contractility [18].

Mathematical models facilitate investigating the spatio-temporal coordination of Physarum motility by integrating the available experimental data into quantitative frameworks including variables that may be hard to measure experimentally. Various models have been constructed under this premise, and the numerical results have reproduced a variety of experimentally observed spatio-temporal patterns [13, 20–22]. However, these models have been so far limited to fixed simple geometries or have neglected key aspects of the mechano-chemical feedback present in locomoting Physarum fragments.

This paper presents novel multi-channel measurements of mechanical and chemical variables in plasmodial fragments of Physarum polycephalum undergoing directional migration. These measurements provide simultaneous spatio-temporal maps of the contractile forces generated by the fragments on their substratum, the velocities of their endoplasm and ectoplasm, and the distribution of free intracellular calcium concentration ([Ca²⁺]i). The experimental data are analyzed to study how a biological system like Physarum coordinates the generation of mechanical forces with their shape changes and internal flows via adhesion to its substratum, and how these pressure driven flows transport the chemical signals that regulate force generation in the first place. The ultimate goal of the analysis is to understand how these phenomena are spontaneously organized to enable the directional flow driven locomotion of amoeboid organisms.

2. Methods

2.1. Preparation of Physarum fragments

Motile Physarum fragments of approximately 500 µm in length were prepared as in our previous study [13]. Physarum plasmodia were grown on 1% agar gel (Granulated; BD) using 150 × 15 mm culture plates (BD), fed with oat flakes (QUAKER) and kept in a dark humid environment at room temperature. Small portions of ~ 0.2 × 0.2 mm² were cut from the parent plasmodia, transfered to collogen coated polyacrylamide (PA) gels embedded with fluorescent beads. A cap made of agarose was placed over the Physarum fragments immediately after. After several hours, the fragments adapted to tadpole like shape and perfomed directed migration, with noticeable intracellular streaming.

2.2. Gel Fabrication

Collagen-coated PA gels were prepared for traction force microscopy as previously described [23]. The gel was ~ 1.5 mm thick and consisted of two layers, the top layer was thin (~ 10 µm) and contained 0.5 µm florescent beads (FluoSperes; Molecular Probes). The gels were fabricated using 5% acrylamide and 0.3% bisacrylamide (Fisher BioReagents), resulting in a Young’s modulus value equals to 8.73 kPa [24]. The Poisson’s ratio of the gel was measured to be 0.46 using the forces generated by the Physarum fragments themselves, following an elastographic traction force microscopy method recently developed by our group [25]. The cap, made of 0.8% agarose with thickness of 3 mm, prevented the PA gel from drying out and generate gentle confinement (a ~ 30 Pa and a ~ 1 KPa Young’s modulus) to facilitate the measurement of intracellular flow. More details about the effect of the agar cap on our measurements and the migration of Physarum fragments can be found in [13, 25].

2.3. Microscopy

A Leica DMI 6000B inverted microscope and a PC running Micro-Manager software were used for image acquisition [26]. Time-lapse sequences were acquired at 16× in both bright-field and fluorescent-field. First, 10 images were acquired in the bright field at a frame rate of 5 Hz for flow quantification. Then, a 40-image fluorescence z-stack (Δz = 1 µm) was acquired over 10 sec for traction force microscopy. This 12-second acquisition cycle was repeated until the cell moved out of the field of view, providing quasi-simultaneous recordings of intracellular streaming and traction stresses, given that the variables oscillate with a much longer period of ~ 100 sec [11].

2.4. Flow Quantification

The cytoplasm of Physarum amoebae is densely packed with intracellular vesicles, which were used as fiduciary markers to quantify the intracellular streaming velocity by particle image velocimetry (PIV) [11,27]. The intracellular domain can be separated as endoplasmic flow phase and ectoplasmic gel phase with respective characteristic velocities of 10 µm/s and 0.15 µm/s. Different algorithms were used to determine the velocities range across 2 orders of magnitude. For V⃗_sol, we pre-process the raw image sequences using high-pass, band-pass and low-pass temporal filters as described in our previous paper [13]. Then we ran an in-house PIV algorithm on each filtered image sequences and asigned the velocity vector resulting from the sequences that maximizes the PIV signal-to-noise ratio at each point. As for V⃗_gel, we ran PIV on image pair consists of the first and last image in bright field of each acquisition cycle. The rather long time interval (1.8 second) allowed us to detect the low velocities of the ectoplasmic gel phase. Points with velocity lower than 0.2 µm/s were considered as ectoplasm. The PIV interrogation window size and spacing were respectively 32 and 8 pixels, yielding a spatial resolution of 6.5 µm.

2.5. Traction force microscopy

The 3D deformation of the PA substrate was measured at its top surface on which the Physarum amoebae were migrating as reported by del Álamo et al. [23]. Each instantaneous fluorescence z-stack was cross-correlated with a reference z-stack which was recorded at the end of experiment once the amoebae moved out of the field of view. Using these measurements as boundary conditions, we computed the three-dimensional deformation field in the whole polyacrylamide substrate by solving the elasto-static equation. We then compute the traction stress τ⃗ = (τ_xz, τ_yz, τ_zz) exerted by the cell on the substrate using Fourier TFM methods described elsewhere [23, 28]. The spatial resolution of τ⃗ was 13 µm in x,y and 1 µm in z.

2.6. Measurement of free calcium concentration

Single-wave length calcium indicators like Calcium Green-1 (Molecular Probes) exhibit an increase in fluorescence upon binding calcium ions and have been successfully applied to monitor the dynamics of [Ca²⁺]i. However, the recorded intensity of these indicators can vary with other factors such as cell thickness. In our experiments, the local thickness of Physarum fragments can vary up to 50% during migration. Dual-wavelength ratiometric dyes, with distinct spectra of calcium free and calcium bond forms, can be used to minimize the effect of variation in cell thickness. However, dual-wavelength dyes require excitation in the UV range, for which Physarum fragments exhibit significant auto-fluorescence. To solve this problem, Texas Red (Molecular Probes), which is a calcium insensitive fluorescent dye, is co-injected into the sample together with Calcium Green-1. The ratio of fluorescent intensity between calcium sensitive dye and background dye are used to monitor the variation of [Ca²⁺]i. Both dyes were dextran-conjugated and had a molecular weight of 10 kDa, which dramatically reduced leakage and compartmentalization compared to their non-conjugated forms. The dyes were coinjected into the parent mold under a Nikon SMZ-10 microscope using a PM 1000 cell micro-injection system (MicroData Instrument, Inc). Time-lapse sequences were acquired under 20× in bright-field, FITC and TRITC. 10 images in bright field were acquired first at 5 Hz for flow quantification, followed by one snapshot in FITC for Calcium Green-1 and another one in TRITC for Texas Red. This 5-second acquisition cycle was repeated for at least 10 minutes, allowing us to obtain a quasi-simultaneous quantification of intracellullar flow and [Ca²⁺]i during Physarum migration. Preliminary results obtained from this acquisition protocol were presented in [18].

2.7. Fragment shape statistics

Cell contours are extracted from bright-field microscopy time-lapse sequences as described previously [28]. Raw images are digitally thresholded, eroded and dilated in order to obtain a time-dependent scalar field Ω_c(t, x, y) containing ones inside the fragment and zeroes outside of it. The statistical distributions of fragment shape are determined from Ω_c(t, x, y) following the method outlined in ref. [29]. At each instant of time, Ω_c(t, x, y) is rotated so that the major axis of the fragment coincides with the x direction, and translated so that the origin (x, y) = (0, 0) is set at the centroid of the fragment. The probability density function of a point belonging to the interior of the fragment in this reference frame is calculated simply as

$$P(x,y)=\frac{1}{N_c}\sum _{i=1}^{N_c}\frac{1}{N_{t,i}}\sum _{j=1}^{N_{t,i}}{\mathrm{\Omega }}_{c,i}(t_j,x,y),$$ (1)

where N_c is the number of cells and N_t,i is the number of temporal observations corresponding to the i-th cell. According to this definition, the median cell shape is defined by the iso-contour P(x, y) = 0.5.

2.8. Kymographic representation

To facilitate the analysis of the spatio-temporal organization of endoplasmic flow, traction stresses, free intracellular calcium, etc., we generated kymographs for the quantities of interest. We followed the approach introduced by Bastounis et al [30] for migrating amoeboid cells. At each instant of time (t) the major axis of cell is aligned vertically (x), and the measured quantity (q(t, x, y)) is projected and the averaged over the cross section of the Physarum fragment, i.e.

$$\overline{q}(t,x)=\frac{\int {\mathrm{\Omega }}_c(t,x,y)\mathbf{q}(t,x,y)·{\mathbf{u}}_{\mathbf{x}}\mathrm{d}y}{\int {\mathrm{\Omega }}_c(t,x,y)\mathrm{d}y},$$ (2)

where Ω_c denotes the interior of the Physarum fragment, and u_x is a unit vector oriented towards the fragment’s front. Plotting two-dimensional maps of q⃗ produces kymographs that can reveal patterns of organization in the spatio-temporal dynamics of migrating Physarum fragments.

3. Results and Discussion

3.1. The spatio-temporal organization of endoplasmic flow and traction stresses reveals distinct dynamical modes in migrating Physarum fragments

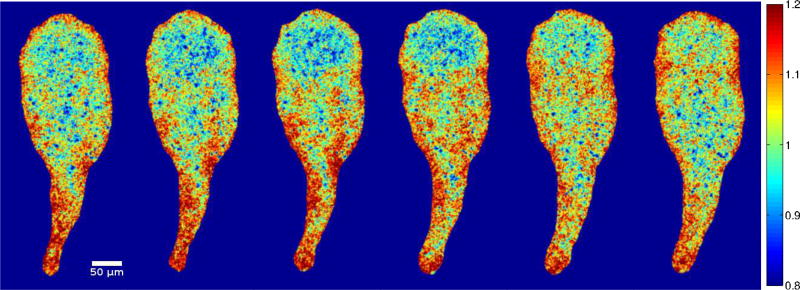
A few hours after seeding the Physarum fragments on PA gel, we observed that fragments of diameter larger than ~ 100 µm performed persistent locomotion. Fragments larger than ~ 500 µm formed complex branched structures markedly different from an amoeboid shape, and were not considered in this study. We focused our investigation on fragments of size ~ 300 µm, which generally adopted a tadpole-like shape, with a more rounded head and a tapering tail.

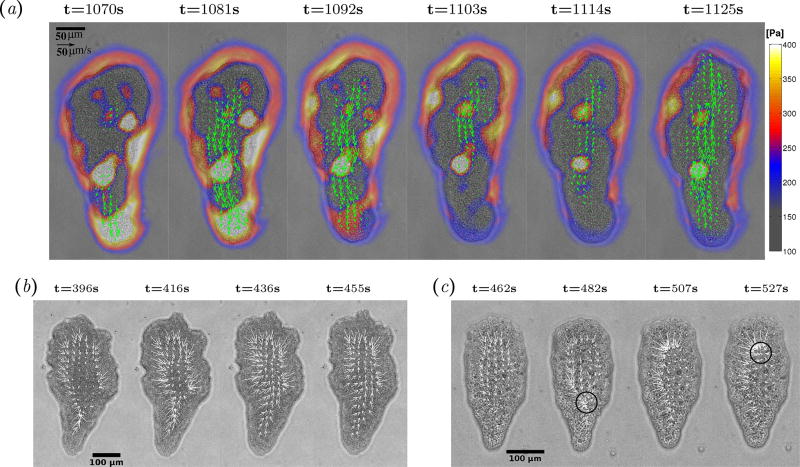
Directional locomotion of Physarum fragments requires the spatio-temporal coordination of endoplasmic flows and traction stresses exerted on a contact surface [13]. Most of the fragments analyzed in this study developed organized endoplasmic flows that oscillated between forward and backward motion with a well defined periodicity (Figure 1a). The traction stresses exerted by these locomoting fragments oscillated with a similar period, all the time showing an inward contractile pattern with larger stresses along the cell periphery. This pattern has been proposed to be analogous to a surface tension [14, 31], and has been recently linked to the cortical F-actin filaments and their cross-linkers in Dictyostelium amoebae [32]. Removing the stress vectors near each fragment’s boundary renders the traction stress generated under the fragment’s body easier to analyze, and unmasks waves of contraction with distinct spatio-temporal dynamics (Figure 1b, c).

Figure 1.

(a) Instantaneous endoplasmic flow speed and traction stresses exerted on the substrate by a migrating Physarum fragment. Arrows exhibit the flow speed and colormap shows the magnitude of traction stresses. (b, c) Instantaneous traction stresses exerted by two Physarum fragments with different dynamical behaviors, with the stress vectors along the cell boundary removed. Black circles indicate the location of contraction centers.

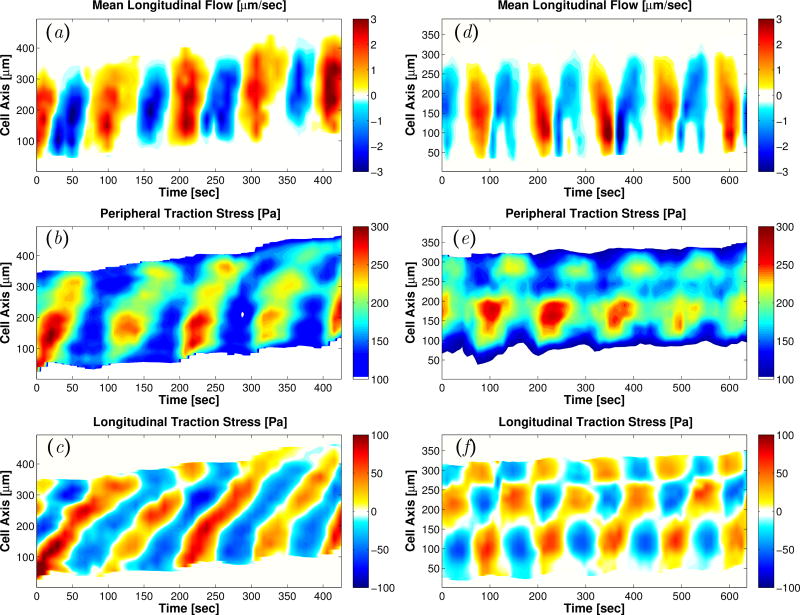
The most common organized pattern consisted of traveling waves that propagated forward along the center line of the motile fragment (Figure 2a–c). We labeled this migration mode as peristaltic because their motion was driven by forward traveling waves of contraction and relaxation (Figures 1b and 2b,c). This terminology is based on previous studies of Physarum migration [10, 11, 33], in which peristaltic fragments were designated by analyzing the dynamics of fragment width change rather than their force generation dynamics. In Physarum fragments undergoing peristaltic locomotion, both the forward and backward endoplasmic flow waves are generated from the tail and propagate forward in an approximately linear fashion. This mode has drawn more attention in previous studies because it occurs more often and leads to faster migration than other modes [7,11,13,34]. However, it is not the only migration mode of Physarum locomotion with organized spatio-temporal dynamics.

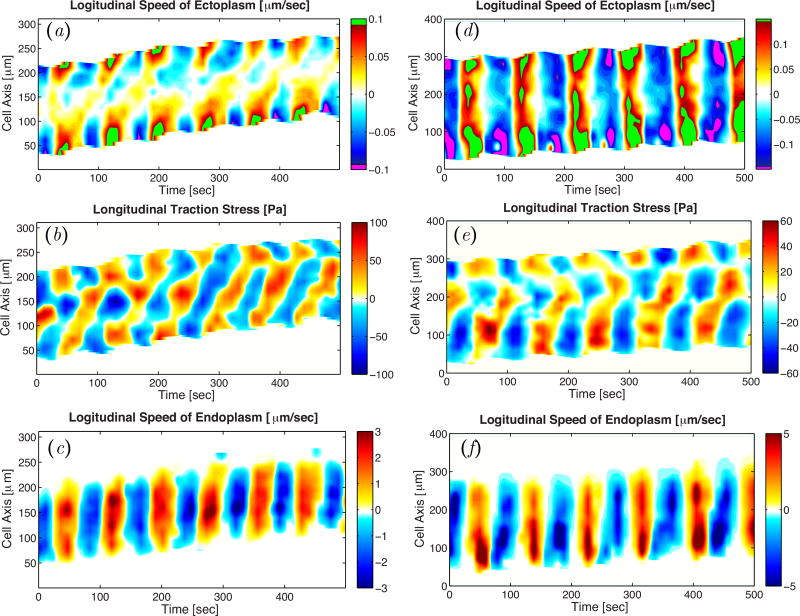
Figure 2.

Kymographs of longitudinal endoplasm flow velocity (a, d), peripheral traction stress (b, e), and longitudinal traction stress (c, f) for a peristaltic (a–c) and an amphistaltic (d–f) Physarum fragment.

We also observed a less frequent yet distinct mode of locomotion in which the head and tail contracted and relaxed in an anti-phase manner, and which we named the amphistaltic mode. This mode sustains waves of forward and backward endoplasmic flow that alternate periodically, similar to the peristaltic mode. However, in Physarum fragments undergoing amphistaltic locomotion, the waves of forward endoplasmic flow originate at the fragment’s front and propagates backward, whereas the waves of backward flow originate at the fragment’s back and travel forward. This dynamics leads to evident ‘V’-shaped patterns in the flow kymograph (Figure 2d). The instantaneous spatial patterns of traction stresses in amphistaltic Physarum fragments showed inward contraction similar to peristaltic ones (Figure 1c). However, the traction stress kymographs revealed remarkable differences in their spatio-temporal dynamics. Instead of traveling waves, amphistaltic fragments sustained standing waves of traction stress with alternating peaks and valleys at the front and rear of the fragment (Figure 2e, f). Consistently, traction stress snapshots of amphistaltic fragments show localized contraction centers in the front and rear part of the fragment (black circles in Figure 1c). This pattern of contraction resembles that of the Physarum “dumbbells” previously described by others [14,35–37]. These dumbbells form two thick round heads connected by a tube that contract alternatively while the fragment stays in place. We also observed a few contractile dumbbells in our experiments. However, the amphistaltic Physarum fragments reported here always adopted a tadpole-like shape and were able to move persistently.

Out of the 40 fragments in our study, 20 exhibited peristaltic behavior, 8 were amphistaltic, and 2 alternated between peristaltic and amphistaltic. In addition, 5 fragments had organized spatio-temporal dynamics that did not match either the peristaltic or amphistaltic patterns, and 5 more fragments had disorganized dynamics. Once a Physarum fragment began migrating either by the peristaltic or by the amphistaltic mode, the fragment would sustain the same mode for the duration of the whole experiment, i.e. ≳ 30 mins ≳ 20 cycles. Thus, the spatio-temporal dynamics of migrating Physarum fragments appear to settle into relatively robust oscillatory behaviors. This observation generally agrees with Rodiek et al [19], who measured the height oscillations of ~ 1 mm–long Physarum fragments while they were migrating freely without being constrained by an agarose cap. These authors reported two spatio-temporal patterns in their measurements that resemble the peristaltic and amphistaltic behaviors found in our experiments: traveling waves that propagated at ~ 5µm/s, and standing waves with multiple spatial nodes separated by wavelength of ~ 100 µm with period of 10 minutes. We observed a few fragments that shifted spontaneously between the peristaltic and the amphistaltic mode while migrating, as well as other organized spatiotemporal patterns including 2-to-1 backward/forward flow waves (Figure 3a,b,c) and disorganized patterns (Figure 3d,e,f). This type of behavior is typical for systems with complex non-linear dynamics. Consistently, previous experimental studies on Physarum protoplasm droplets found traveling waves, standing waves, and chaos in local droplet thickness [38,39]. In addition, recent mathematical models that include feedback between contraction, endoplasmic flow and calcium signaling in simplified non-migratory geometries have predicted a number of dynamical regimes depending on the level of mechano-chemical feedback and the rheological properties of the endoplasm [22, 40].

Figure 3.

Kymographs of flow and traction stress of two Physarum that exhibited uncommon spatio-temporal dynamics. (a, b, c) Kymographs for a fragment exhibiting organized dynamics with two consecutive backward flow waves for each forward flow wave (reminiscent of a period doubling state). (d, e, f) Kymographs for a fragment exhibiting disorganized dynamics.

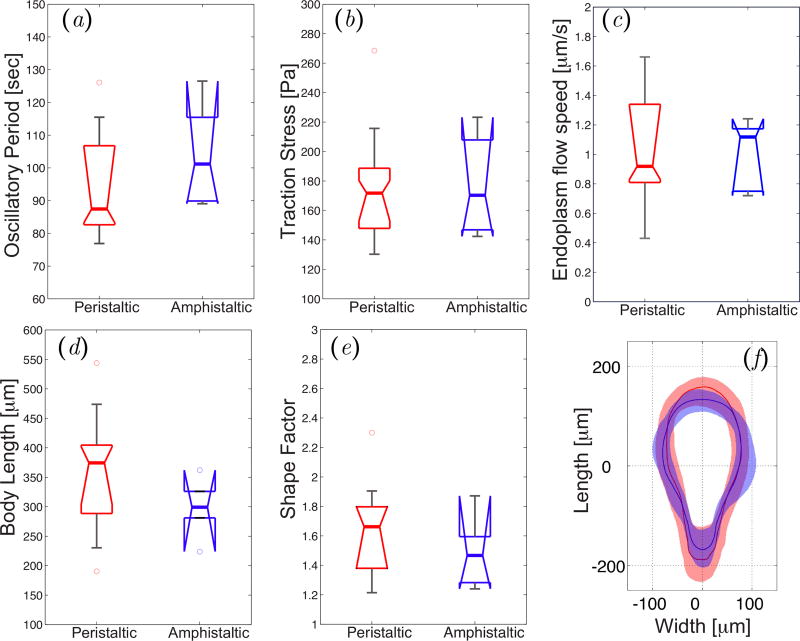
In an attempt to find differences in the properties of peristaltic and amphistaltic Physarum fragments that could explain their distinct dynamics, we compared their oscillation period, average traction stress magnitudes and average endoplasmic flow speeds. However, we did not find any significant difference in these parameters between the two types of fragments (Figure 4a–c). Furthermore, both peristaltic and amphistaltic fragments adopted a similar tadpole-like shape during migration (Figure 4f). Rieu et al previously reported that Physarum fragments with distinct dynamics of force generation can be differentiated by the number of membrane invaginations [14]. To quantify whether there were differences in the number of membrane invaginations of Physarum fragments undergoing peristaltic and amphistaltic locomotion, we measured the shape factor S_f = P²(4πA)⁻¹, where P is each fragment’s perimeter and A is its area. This parameter is unity for a perfect circle and increases as the number of lobes and invaginations in the perimeter of the fragment increases. No significant difference was found between the two types of fragments (Figure 4e). Ongoing measurements of the endoplasmic rheological properties [41] should clarify if these properties play an important role in establishing the spatio-temporal dynamical state of migrating Physarum fragments, as predicted by some mathematical models [22,40]. Despite these similarities, the average migration speeds of peristaltic and amphistaltic fragments were significantly different, as shown in the next section.

Figure 4.

(a)–(e) Box plots of motility parameters corresponding to peristaltic (N = 20) and amphistaltic (N = 8) Physarum fragments. (a) Average oscillation period. (b) Average magnitude of the traction stresses. (c) Average endoplasmic flow speed. (d) Average fragment length. (e) Shape factor. (f) Average shape of peristaltic (red line) and amphistaltic (blue line) types. Shaded regions contain 90% of the statistical distribution of shapes for each fragment type.

3.2. The spatiotemporal dynamics of endoplasmic and ectoplasmic flows affect the migration speed of Physarum fragments

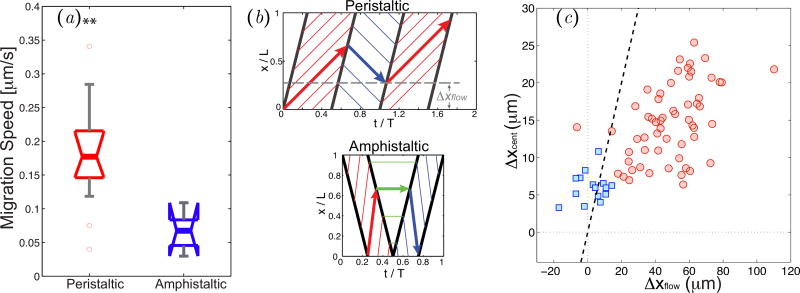
We found that Physarum fragments undergoing peristaltic migration were in average ~ 3 times faster than those undergoing amphistaltic migration (Figure 5a). This difference in locomotion speed is particularly remarkable considering that both peristaltic and amphistaltic fragments have similar sizes and shapes, and that their traction stresses and internal flow speeds have similar magnitudes and oscillation periods (Figure 5). A possible explanation can be found by noting the different asymmetries in the motion of endoplasmic fluid particles that arise from the different spatio-temporal dynamics of flow waves in each locomotion mode. Figure 5 presents this idea by plotting spatio-temporal particle trajectories in a simplified model in which the endoplasmic flow has constant speed and waves propagate forward and backward with constant wave speeds along the Physarum fragment. In peristaltic fragments, Matsumoto et al [11] noted that fluid particles spend longer times traveling forward than backward, yielding net forward displacement every cycle period (Δx_flow > 0, Figure 5c). Extending this argument to amphistaltic Physarum fragments predicts that fluid particles approximately return to their original location at the end of each period (Figure 5c). Consistent with this reasoning, a scatter plot of the net forward motion of the centroid of a fragment (Δx_cent) vs. Δx_flow clearly segregates the amphistaltic and peristaltic locomotion modes (Figure 5b).

Figure 5.

(a) Box plot of average migration speeds in peristaltic (N = 20) and amphistaltic (N = 8) Physarum fragments. Two asterisks denote statistically significant differences between medians (p < 0.01). (b) Simplified model schematic for the distance traveled by endoplasmic fluid particles per oscillation cycle. Top panel, peristaltic fragments; bottom panel, amphistaltic fragments. (c) Scatter plot of the distance Δx_cent traveled by the centroid of the Physarum fragment per oscillation cycle vs. the net distance Δx_flow traveled by an endoplasmic fluid particle. , peristaltic fragments; , amphistaltic fragments. The dashed line is Δx_cent = Δx_flow.

It should be noted that the flow kinematics argument hold as long as the Physarum fragments do not experience shape changes over time scales longer than their ~ 100 s oscillation period. This could explain Rodiek’s et al [19] observation that unconstrained Physarum fragments that sustain traveling waves in their height advance their front slower than fragments that sustain multi-nodal standing waves, because their fragments undergo substantial elongation and flattening during the duration of the experiment. In our experiments, this secular thickness variations are constrained by agarose cap placed on top of the sample.

While it provides a plausible explanation for the major differences in migration speed found between peristaltic and amphistaltic fragments, the flow kinematics hypothesis also poses a paradox because it predicts that amphistaltic fragments should not be able to migrate. Furthermore, we previously used mathematical modeling to show that the asymmetry of endoplasmic flow velocity alone cannot determine the migration speed of migrating Physarum fragments [13]. The data in figure 5(b), which shows that Δx_cent is significantly lower than Δx_flow, agrees with this idea. Physarum plasmodia are often conceptualized as being composed of a two-phase fluid in which the sol and gel phases respectively represent the endoplasm and the ectoplasm. Therefore, it is reasonable to expect that the dynamics of the ectoplasm may contribute to the net migration speed of the plasmodium.

We still know little about the dynamics of the ectoplasm because its motion is significantly slower and harder to measure than that of the endoplasm. In this study, we expanded the image processing algorithm for the quantification of intracellular flow [13], in order to measure the flow velocity of the ectoplasm in addition to that of the endoplasm (see §2 and Figure 6).

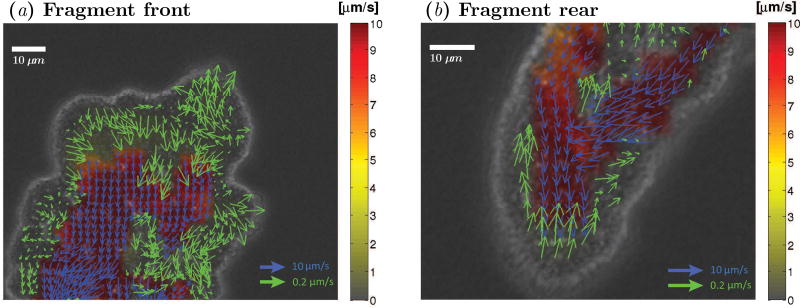
Figure 6.

Instantaneous snapshots showing velocity vectors for endoplasm (blue) and ectoplasm (green) flows in a migrating Physarum, superimposed on the bright field image of the fragment. The pseudo-color map indicates the magnitude of velocity according to the colorbar in the right hand side of the panel. (a) Frontal part of the fragment. (b) Rear part of the fragment.

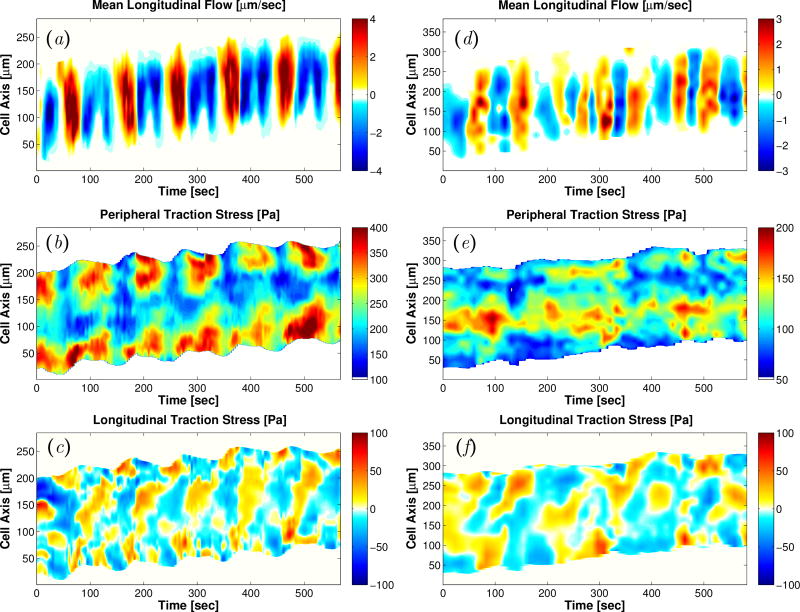
Ectoplasm velocity is organized spatio-temporally in the form of traveling waves and standing waves in peristaltic and amphistaltic fragments respectively (Figure 7a,d), consistent with the dynamics of the traction stresses generated by the fragments (Figure 7b,e) and their endoplasm flow velocity (Figure 7c,f). However, in both types of fragments the ectoplasm velocity is asymmetric reaching substantially higher values during forward motion than during backward motion, particularly in the rear. These results suggest that the dynamics of the ectoplasm also contribute to the net motion of Physarum fragments.

Figure 7.

Kymographs of longitudinal ectoplasm flow velocity (a, d), longitudinal traction stress (b, e), and longitudinal endoplasm flow velocity (c, f) for a peristaltic (a–c) and an amphistaltic (d–f) Physarum fragment. In panels (a, d), we have added bright green and purple at the floor and ceiling of the colormaps to emphasize asymmetries in the velocity data.

3.3. Dynamics of substratum adhesion experience smooth slip-stick transitions

Inspection of Figure 7 suggests that traction stresses generation is closely related to the motion of the ectoplasm over the substratum, which is sound considering that the ectoplasm forms a cortical layer directly in contact with the plasmodial membrane. We explored this relationship in more detail in order to gain insight about the regulation of substratum adhesion in migrating Physarum fragments, which is not well understood since integrin-like adhesion proteins have not been identified yet for this organism.

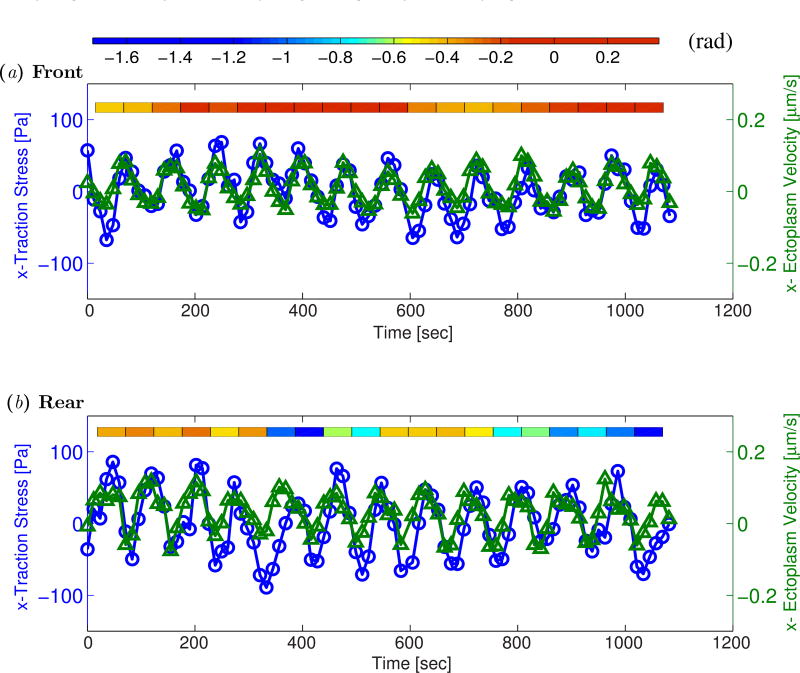
We plotted the time evolution of the ectoplasm speed together with that of the traction stresses at the front of a fragment (Figure 8a), and with the phase difference between these two variables. The time lag between the two signals was calculated by maximizing their cross-correlation over interrogation windows of 95 seconds and 50% overlap. The instantaneous phase difference was then obtained as the ratio of time lag and the averaged oscillation period (83 seconds). This analysis revealed that the traction stresses and ectoplasm velocity oscillate in phase for the most part. This result suggest that adhesion in this region follows the viscous-like regime τ = ξυ where τ is the adhesion stress, υ the ectoplasm velocity and ξ is a friction factor. This result is in agreement with theoretical studies describing biological friction as the consequence of the thermally driven formation and rupture of molecular bonds [42].

Figure 8.

Time histories of longitudinal ectoplasm velocity ( ) and longitudinal traction stresses ( ) at two specific locations in the front (panel a) and the back (panel b) of the peristaltic Physarum fragment shown in Figure 7. The tiled bars at the top of the plots represent the time-dependent phase differences (in radians) between the ectoplasm velocity and the traction stresses. Blue and orange tiles represent phase differences near −π/2 (cell and substrate stick) and zero (cell and substrate slip) respectively, as indicated by the color scale at the top of the figure.

In contrast to our observations at the front of the fragments, the time evolutions of ectoplasm speed and traction stresses have a complex relationship at the rear, alternating intervals at which they oscillate in phase with intervals in which the ectoplasm velocity precedes the traction stresses by approximately 1/4 of an oscillation period. Since a time integration of endoplasm velocity (i.e. endoplasm displacement) would generate the same phase difference of 1/4 period, we interpret this result as indicative of the occurrence of stick-slip transitions at the rear of Physarum fragments. Slip-stick transitions occur when ξ has a non-monotonic dependence with the ectoplasm velocity, which is a common behavior in biological friction [42]. This type of transitions have been linked to the dramatic shape oscillations experienced by cells such as keratocytes when crawling on flat substrata [43], and it has been proposed that the frequency of these oscillations correlates with the speed of cell crawling [28, 29, 43, 44]. In the present experiments, we did not observe sharp changes in traction stress, ectoplasm speed or fragment length occurring at the stick-slip transitions, suggesting that these transitions are mild in migrating Physarum fragments. We analyzed kymographs of the phase difference between the time evolutions of traction stress and ectoplasm speed (not shown). While these data were somewhat noisy, they suggested that periodic stick-slip transitions propagate from the rear to the front of peristaltic fragments, while a standing stick-slip transition seems to form near the front of amphistaltic fragments. The dynamics of these transitions could provide a mechanism for Physarum to regulate the strength of their substrate adhesion in a way that supports asymmetry in the motion of the ectoplasm. However, additional experiments and further analysis are needed to confirm these ideas.

3.4. Dynamics of free intracellular calcium

The transport of calcium ions in Physarum fragments occurs in a complex regime that likely couples convection, diffusion and a time-dependent geometry caused by fluid-structure interactions at the fragment’s lengthscale. Using reported values of cytoplasmic Ca²⁺ diffusivity, D = 5.3 × 10⁻¹⁰m²/s [45], and our measurement of intracellular flow speed υ ~ 5µm/s, we estimate that characteristic timescales for Ca²⁺ diffusion and convection over a cell length (l ~ 100µm) are the same, t_D = t_C = 20s. Furthermore, this transport timescale is similar to the period of cellular shape changes (T ≈ 100s) observed in our experiments.

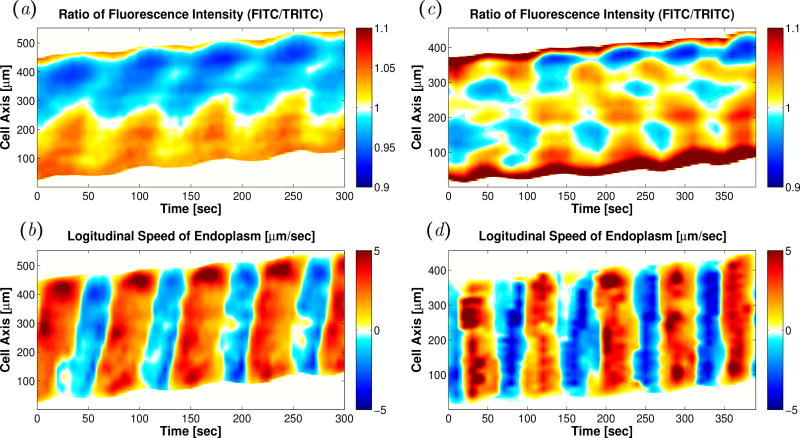
In order to study the relation between endoplasmic flow and the distribution of free intracellular calcium, we performed ratiometric measurements of free ion concentration, [Ca²⁺]i, jointly with intracellular flow. Figure 9 shows a time sequence of [Ca²⁺]i throughout one oscillation cycle of a typical peristaltic cell. Although this type of measurement is inherently noisy, it is possible to discern waves of high calcium concentration propagating from the rear to the front of the Physarum fragment. The spatio-temporal dynamics of these waves are clearly observed when [Ca²⁺]i is represented in kymographic form. Figure 10 shows kymographs of [Ca²⁺]i and intracellular flow that are representative of the peristaltic and amphistaltic migration modes.

Figure 9.

Time sequence of ratiometric measurememt of [Ca²⁺]i during the locomotion of a typical peristaltic cell showing a Ca²⁺ wave propagating forward.

Figure 10.

(a) Kymograph of ratiometric measurement of [Ca²⁺]i in a typical peristaltic fragment. (b) Kymograph of instantaneous longitudinal velocities of endoplasmic flow of the same peristaltic fragment in Figure 10(a). (c) Kymograph of ratiometric measurement of [Ca²⁺]i in a typical amphistaltic fragment. (d) Kymograph of instantaneous longitudinal velocities of endoplasmic flow of the same amphistaltic fragment in Figure 10(]c).

Both for the peristaltic and amphistaltic modes, the spatio-temporal patterns of calcium concentration are consistent with the dynamics of the traction stress, endoplasmic flow and ectoplasmic motion. In Physarum fragments undergoing peristaltic migration, we found waves of [Ca²⁺]i that traveled from the rear to the front of the fragment (Figure 10a), whereas patterns of [Ca²⁺]i standing waves were observed for Physarum fragments undergoing amphistaltic locomotion (Figure 10c). The phase speed of the traveling waves was found to agree well with the measured endoplasmic flow velocity, υ₀ ≈ 5 µm/s, suggesting that endoplasmic flows may be important in sustaining the dynamics of [Ca²⁺]i transport.

To test this hypothesis, we considered a simple 1-D model for the transport of a passive scalar in non-dimensional form,

$$\text{St }{\partial }_{t}c+{\upsilon }_{\mathit{\text{endo}}}{\partial }_{x}c={\text{Pe}}^{-1}{\partial }_{\mathit{\text{xx}}}c$$ (3)

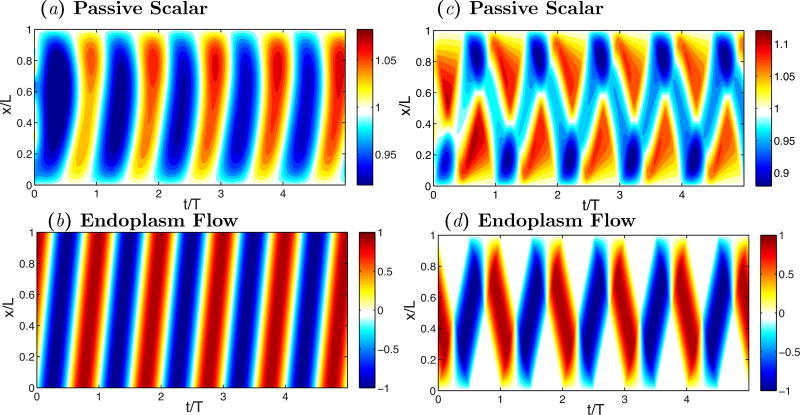
where υ_endo is a prescribed velocity normalized with υ₀, the spatial variable xε[0, 1] is normalized with the fragment length L, and the time variable t is normalized with the period of the flow oscillations T. The two non-dimensional parameters in this equation are the Strouhal number St = L/(υ₀T) and the Péclet number Pe = Lυ₀/D, both of which have values of order unity in migrating Physarum fragments according to our experimental measurements and [45]. The solution to this transport equation exhibits traveling waves of passive scalar when υ_endo is set to mimic our experimental measurements for peristaltic fragments, e.g. υ_endo = sin[2π(x − ζt)] where the non-dimensional phase velocity ζ ≈ 5 (Figure 11a–b). Likewise, this simple model generates standing waves of passive scalar when the endoplasmic velocity is set to mimic our measurements for amphistaltic fragments (Figure 11c–d). Qualitatively, these results are robust with respect to changes in the parameter values, and in the boundary conditions (e.g. Neumann vs. Dirichlet) and initial conditions. For instance, the passive scalar in Figure 11 evolves from random initial conditions into temporally periodic pattern in about one oscillation cycle.

Figure 11.

(a) Kymograph of concentration of passive scalar in a mimic peristaltic fragment. (b) Kymograph of longitudinal velocities of endoplasmic flow representative of a peristaltic fragment. (c) Kymograph of concentration of passive scalar in a mimic amphistaltic fragment. (d) Kymograph of longitudinal velocities of endoplasmic flow of endoplasmic flow representative of an amphistaltic fragment.

It is evident that a flow-transport-only model for the dynamics of intracellular calcium does not capture many of the quantitative features observed in our measurements of Figure 10. It is also evident that such a simplistic model neglects potentially relevant phenomena such as chemical kinetics of phosphorylation/dephosphorylation of the myosin light chain, Ca²⁺ influx through various calcium channels on plasma membrane, Ca²⁺ release from the sarcoplasmic reticulum and endoplasmic reticulum through IP₃ channels, etc [46–51]. Nevertheless, the ability of such a simple model to generate traveling waves and standing waves of a passive scalar highlight the importance of endoplasmic flow in the self-organization of dynamical patterns in migrating Physarum fragments.

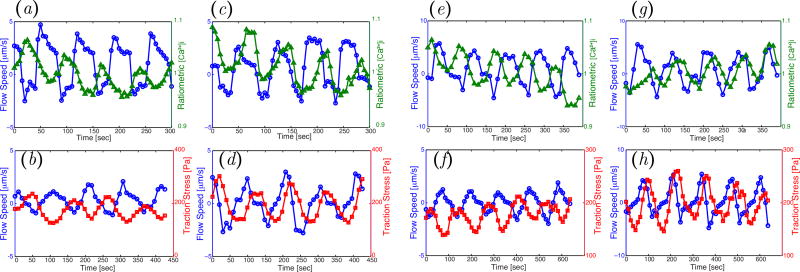
The molecular regulation of acto-myosin contractility by calcium should be the same for Physarum fragments following the peristaltic and amphistaltic migration modes, given that we prepared all the fragments using the same protocol and the emergence of these modes was spontaneous. Thus, we hypothesized that the phase coordination between the dynamics of calcium and contractility waves would be the same for both migratory modes. While it was not possible to measure [Ca²⁺]i and traction stresses simultaneously in our experiments, we measured both [Ca²⁺]i jointly with endoplasmic flow, and traction stresses jointly with endoplasmic flow. The flow data were then used as reference to temporally align the oscillations of [Ca²⁺]i and traction stress for Physarum fragments following the same migration mode. We plotted time profiles at specific locations at the front and rear of each fragment (Figure 12), and juxtaposed the time evolution of endoplasmic flow velocity to that of [Ca²⁺]i or traction stresses (Figure 12).

Figure 12.

Top row (a, c, e, g): Time histories of endoplasmic flow velocity ( ) and ratiometric measurement of [Ca²⁺]i ( ), averaged along the width of a peristaltic fragment (panels a and c) and an amphistaltic fragment (panels e and g). Bottom row (b, d, f, h): Time histories of endoplasmic flow velocity ( ) and peripheral traction stress ( ), averaged along the width of a peristaltic fragment (panels b and d) and an amphistaltic fragment (panels f and h). Panels (a, b, e, f): Fragment front. Panels (c, d, g, h): Fragment rear.

For the peristaltic migration mode, the time evolutions of endoplasmic flow and [Ca²⁺]i were found to have opposite phases at the front of the Physarum fragment (Figure 12a). The time evolutions of endoplasmic flow and traction stress also had opposite phases at the fragment front (Figure 12b), implying that the oscillations in [Ca²⁺]i and traction stress were in phase. The same relationship between [Ca²⁺]i, endoplasmic flow and the traction stresses can be deduced from the time profiles of these variables recorded at the rear of peristaltic Physarum fragments (Figure 12c, d). In amphistaltic fragments (Figure 12e–h), the phase coordination between the waves of [Ca²⁺]i, flow speed and traction stress was the same as in peristaltic fragments. Our finding that the calcium concentration is in phase with traction stresses agrees with previous observations [17, 52, 53]. Yoshiyama et al [17] interpreted this result as an indication that calcium inhibits acto-myosin contractility in Physarum because the maximum calcium concentration coincides with the onset of relaxation. However, the kinetics of the involved biochemical reactions could make this response more complicated [54].

4. Conclusion

The multi-nucleated slime mold Physarum polychephalum can be used to generate amoeboid-like motile cells by excision of ~ 100 µm-long fragments from the parent mold. These fragments are formed by a cortical gel-like ectoplasm that surrounds a sol-like endoplasm. Periodic contractions of the ectoplasm drive shuttle flows in the endoplasm, which transport the nutrients and calcium ions necessary for contraction. The feedback among these processes can lead to rich spatio-temporal dynamics that significantly affect the migration behavior of Physarum fragments. However, our understanding of these dynamics is limited by a lack of direct measurements of quantitative variables. This study provides detailed concurrent measurements of the spatio-temporal distribution of endoplasmic and ectoplasmic flow, contractile forces and [Ca²⁺]i in migrating fragments of Physarum plasmodia. To the best of our knowledge, this is the first experimental quantification of mechano-chemical dynamics in a model organism of flow-driven amoeboid migration.

The spatio-temporal patterns found in the measured quantities suggests that the mechano-chemical dynamics of these fragments can lead to a variety of both disorganized and organized states. We focused our attention on two particularly stable organized states associated with periodic oscillations in flow, contractile forces and [Ca²⁺]i. In the most stable (i.e. frequently observed) state, the mechano-chemical dynamics of the fragment are organized in the form of traveling waves that propagate from the rear to the front of the fragment, in good agreement with the peristaltic behavior studied in previous works [11, 13]. We also investigated a second stable dynamical state that we termed amphistaltic because it consists of alternate anti-phase contractions and relaxations of the fragment’s front and back (from αμϕı in Greek meaning “on both sides”). These anti-phase contractions are associated with standing waves of traction stresses and [Ca²⁺]i, but they lead to traveling waves of endoplasmic flow with alternating propagation directions; waves of forward flow propagate backward and viceversa, leading to clear V-shape patterns in spatio-temporal flow kymographs.

Our data suggest that the transport of calcium ions by the endoplasmic flows observed in Physarum fragments may be fundamental to coordinate the spatio-temporal patterns of traction stresses that drive their locomotion. Specifically, we showed that the forward traveling waves of endoplasmic flow found in peristaltic fragments can sustain traveling waves of calcium concentration, consistent with our experimental measurements of [Ca²⁺]i. In a similar fashion, the flow waves of alternating propagation direction observed in amphistaltic fragments can sustain standing waves of [Ca²⁺]i, also consistent with our experimental measurements. Furthermore, we showed that the patterns of concentration of calcium ions evolve in space and time with the same phase as those of the traction stresses.

Apart from the organization of their mechano-chemical dynamics, we did not observe significant differences between the properties of peristaltic and amphistaltic Physarum fragments. Both types of fragments were found to have similar sizes and shapes, and their traction stresses and internal flow speeds were found to have similar magnitudes and oscillation periods. Nevertheless, the average migration speed of peristaltic fragments was measured to be 3 times higher than the migration speed of amphistaltic fragments. We argued that this difference could be caused in part by the spatio-temporal dynamics of the endoplasmic flows in the two types of fragments. In peristaltic fragments both positive and negative endoplasmic velocity waves propagate forward, which allows for positive net endoplasmic motion every oscillation cycle [11]. On the other hand, in amphistaltic fragments positive and negative velocity waves propagate in opposite directions, which leads to zero net endoplasm motion.

Albeit slowly, amphistaltic fragments undergo peristent directional migration over long periods of time. Thus, it is evident that analyzing the symmetry of endoplasm flow is not sufficient to capture the migratory behavior of Physarum fragments. In contrast to the endoplasm, we observed that the ectoplasm of both peristaltic and amphistaltic fragments flows faster forward than it does backward, leading to a significant amount of net motion per cycle. In a previous study [13], we used numerical modeling to illustrate that this type of asymmetry in ectoplasm motion would require tight coordination between the generation of contractile forces and the adhesion of the ectoplasm to the substratum. We explored this coordination by comparing the time evolutions of the traction stresses generated by the Physarum fragments and of the motion of their ectoplasm. Our experimental results suggest that the spatio-temporal coordination between these two quantities may be realized by means of stick-slip transitions. We occasionally observed stationary hotspots in the measured traction stresses (see e.g. Figure 1a), which might be associated with the stick-slip transitions observed at the fragment tail. These stationary adhesions are however more common in other types of amoeboid cells such as Amoeba proteus or Dyctiostelium discoideum. In both cell types, the adhesion sites remain stationary as the cells migrate over them, leaving a clear signature in the kymographs that consists of horizontal bands (see Supplementary Information and refs. [30, 32]) This behavior significantly contrasts with the dynamics of the traction stresses observed in migrating Physarum fragments. Finally, our data provide preliminary evidence that these transitions might be organized in the form of traveling or standing waves, consistent with the dynamics of endoplasmic flow, contractility and calcium distribution. Further experiments and analyses are needed to confirm and expand this mechanistic model.