A Theory of Socio-economic Disparities in Health over the Life Cycle

Abstract

Motivated by the observation that medical care explains only a relatively small part of the SES-health gradient, we present a life-cycle model that incorporates several additional behaviours that potentially explain (jointly) a large part of observed disparities. As a result, the model provides not only a conceptual framework for the SES-health gradient but more generally an improved framework for the production of health. We derive novel predictions from the theory by performing comparative dynamic analyses. More generally, our comparative dynamic method can be applied to models of similar form, e.g., human capital, health deficits, firm investment, to name a few.

Disparities in health across socioeconomic status (SES) groups – often called the SES-health gradient – are substantial. For example, Case and Deaton (2005) show how in the United States, a 20 year old low-income (bottom quartile of family income) male, on average, reports to be in similar health as a 60 year old high-income (top quartile) male. In cross sectional data the disparity in health between low and high SES groups appears to increase over the life cycle until ages 50–60, after which it narrows. These patterns exist across a wide range of measures of SES, such as education and wealth, and across all indicators of health, including the onset of chronic diseases, disability and mortality (e.g., Adler et al., 1994; Marmot, 1999). The pattern is also remarkably similar between countries with relatively low levels of protection from loss of work and health risks, such as the U.S., and those with stronger welfare systems, such as the Netherlands (Case and Deaton, 2005; Smith, 2007; Van Kippersluis et al., 2010).

Recent significant contributions to the understanding of socioeconomic disparities in health have concentrated on the identification of causal effects, but have stopped short of uncovering the underlying mechanisms that produce the causal relationships. For example, education is found to have a causal protective effect on mortality (Lleras-Muney, 2005) but it is not known exactly how the more educated achieve their health advantage (Cutler and Lleras-Muney, 2010).

Case and Deaton (2005) argue that it is extremely difficult to understand the relationships between health, education, income, wealth and labor-force status without some guiding theoretical framework. Integrating the roles of proposed mechanisms and their long-term effect into a theoretical framework allows researchers to disentangle the differential patterns of causality and assess the interaction between mechanisms. Such understanding is essential in designing effective policies to reduce disparities (Deaton, 2002). It is no surprise then that several authors (e.g., Case and Deaton, 2005; Cutler, Lleras-Muney and Vogl, 2011) have pointed to the absence of a theory of SES and health over the life cycle and have emphasised the importance of developing one.

This paper develops a conceptual framework for health and SES in which the SES-health gradient is the outcome of rational (constrained) individual choices made over the life cycle. The paper makes two main contributions. The first main contribution is of a fundamental nature and consists of extending the canonical human-capital model for the demand for health (Grossman, 1972a,b) in two ways. First, we employ a relatively straightforward extension by allowing for decreasing returns to scale in health investment of the health-production process (see Galama and Kapteyn, 2011; Galama and Van Kippersluis, 2013, and Galama, 2015, for the reasoning behind this extension). Second, motivated by the observation that differences in medical care usage explain only a small part of the health gradient (e.g., Adler et al., 1993), we conduct an extensive review of the literature from multiple disciplines to identify the most important mechanisms through which socioeconomic characteristics such as wealth, earnings, and education, interact with health. We then include several additional decisions regarding health (besides health investment), such as choices regarding lifestyle (exercise, healthy/unhealthy consumption), working conditions, labor-force participation, and longevity, as mechanisms generating disparities in health. In doing so, we develop a comprehensive theory of the SES-health gradient, by integrating the most important interactions between health, longevity, health behaviour, and SES (wealth, education, and earnings) during adulthood.¹

Because of the inclusion of a rich set of endogenous health behaviours, endogenous health, and endogenous longevity, the theory can be employed to analyze the value of health as well as the value of life. Previous papers employing a life-cycle model for the value of life include Rosen (1988), Ehrlich (2000), Becker (2007), and Kuhn et al. (2015). In contrast to these papers, but in line with Murphy and Topel (2006), we distinguish between the value of health and the value of longevity. We go beyond Murphy and Topel (2006) by treating health and longevity endogenously: individuals seek to optimise both health and longevity. We find that the value of health and the value of life are distinct concepts that vary with age and by SES in distinct ways. For example, calibrated simulations suggest the value of life decreases near the end of life whereas the value of health increases. Assessments of the value of a statistical life generally involve investigating how much individuals need to be paid for taking a certain risk of death (usually in a setting of hazardous work). In practice, such estimates may capture the monetary value (compensating variation) of both the effect of changes in health and changes in longevity. In our theory, individuals are willing to engage in a certain amount of unhealthy consumption or job hazards for the instantaneous benefits it provides, as long as these benefits outweigh the associated health cost: the reduction in life-time utility due to health loss. Our theory suggests that unhealthy job conditions as well as risky health behaviours may be used in empirical work to evaluate both the value of health and the value of life.

Our second main contribution consists of deriving detailed predictions from the theory by performing comparative dynamic analyses of the effects of wealth, earnings, education, and health on health behaviour and longevity. We are the first to perform such analyses analytically for a comprehensive theory with multiple health behaviours (to better model health) and multiple dimensions of SES (to model disparities in health for several measures of SES).² The comparative dynamic analyses not only deliver novel predictions regarding the SES-health gradient (see below), but more generally provide an alternative and complementary method to calibration and / or estimation in exploring model characteristics. They provide a method for researchers to explore their own research questions of interest. The method can be applied to models of similar form, for example, human capital, health deficits, firm investment, rational addiction, habit formation, and resource extraction, to name a few. This work is therefore potentially also relevant to these and other areas of economics.

The comparative dynamic analyses provide insight into the mechanisms through which SES and health interact, and generate novel testable predictions. We highlight a few here and discuss these and several others more extensively in section 3.

First, wealth, earnings, and education affect health behaviour by increasing the marginal value of health relative to the marginal value of wealth. Intuitively, wealth, earnings, and the higher earnings associated with education relax the budget constraint. At higher levels of wealth, and hence consumption, only limited marginal utility is gained from additional consumption and it is not beneficial to consume more. In contrast, health extends length of life, providing additional time during which consumption, leisure, and health can be enjoyed. This leads higher SES individuals to place a higher value on their health and to invest more in it (Becker, 2007; Hall and Jones, 2007).

A higher marginal value of health, in turn, increases the marginal benefits of healthy consumption, and the marginal costs of unhealthy working (and living) environments, and unhealthy consumption. This leads to healthier behaviour and gradually to greater health advantage with age. The more rapidly worsening health of low SES individuals may lead to early withdrawal from the labour force and associated lost earnings, further widening the gradient in early- and mid-age. The model allows for a subsequent narrowing of the SES-health gradient, due to mortality selection and potentially because low SES individuals increase their health investment and improve their health behaviour faster as a result of their more rapidly worsening health. Our model is thus able to replicate the life-cycle patterns of the SES-health gradient.

Second, we predict a central role for our concept of a “health cost” of unhealthy behaviours. The health cost is the marginal value (in terms of life-time utility) of health lost due to detrimental health behaviours. It takes into account all future consequences of current health behaviour. As a result of differences in the health cost, our theory predicts that high SES individuals are more likely to drink moderately but less likely to drink heavily (Van Kippersluis and Galama, 2014); and that individuals are willing to accept unhealthy working conditions in mid-life, given the high monetary benefits during those years, but that their willingness declines later in life due to an increasing health cost. Thus, the concept of a health cost has potential for explaining variation in health behaviours over the life cycle and across SES groups.³

Third, we predict that the ability to postpone death (endogenous longevity) is crucial in explaining observed associations between SES and health. Absent the ability to extend life (fixed horizon), associations between SES and health are small. If, however, life can be extended, SES and health are positively associated and the greater the degree of life extension, the greater is their association. The intuition behind this result is that the horizon (longevity) is a crucial determinant of the return to investments in health. This suggests that in settings where it is difficult for wealthier, higher income and higher educated individuals to increase life expectancy (e.g., due to a high disease burden, competing risks, low efficiency of health investment, etc.), health disparities across socioeconomic groups would be smaller.

These are just a few examples of how the theory can be used as a conceptual framework in conjunction with the comparative dynamic analyses to generate testable predictions for the complex relationships between SES and health. The theory is rich, and it is impossible to produce an exhaustive list of its possible uses. Researchers can use the theory and detailed comparative dynamic analyses presented here as a template to study their own questions of interest.

The paper is organised as follows. Section 1 reviews the literature on health disparities by SES to determine the essential components required in a theoretical framework. Developing a theory requires simplification and a focus on the essential mechanisms relating SES and health. To keep the model relatively simple we focus on explaining health disparities in adulthood.⁴ We highlight potential explanations for the SES-health gradient that a) explain a large part of the gradient and b) are relatively straightforward to include in our theoretical framework. Based on these principles we develop our theoretical formulation in section 2. Section 3 presents dynamics and calibrated simulations, section 4 presents comparative dynamic analyses and makes predictions, and section 5 summarises and concludes.

1 Components of a Theory of the Gradient

In this section we review the empirical literature to determine the essential components of a theory of health disparities by SES in adulthood. Based on these findings we present our theoretical formulation.

A significant body of research across multiple disciplines (including epidemiology, sociology, demography, psychology, evolutionary biology, and economics) has been devoted to documenting and explaining the substantial disparity in health between low and high SES groups. The pathways linking the various dimensions of SES to health are diverse: some cause health, some are caused by health and some are jointly determined with health (e.g., Cutler et al., 2011). Several key findings can be identified.

Medical care

Utilization of medical services and access to care explain only a relatively small part of the association between SES and health (e.g., Adler et al., 1993). Therefore, additional mechanisms, besides medical care, have to be included in the model.

Work environment and lifestyle

Epidemiological research highlights the importance of lifestyles (e.g., smoking, drinking, caloric intake, and exercise), psychosocial and environmental risk factors, neighborhood social environment, acute and chronic psychosocial stress, social relationships and supports, sense of control, fetal and early childhood conditions, and physical, chemical, and psychosocial hazards and stressors at work (e.g., House et al., 1994; Lynch, Kaplan and Shema, 1997).

During adulthood, two of those mechanisms appear to be of particular importance: (i) working conditions, and (ii) lifestyles. Using three different datasets from the U.K. and the U.S., House et al. (1994) find that features of the psychosocial working environment, social circumstances outside work, and health behaviour jointly account for much of the social gradient in health. Some epidemiological studies suggest that around two thirds of the social gradient in health deterioration could be explained by working environment and lifestyle factors alone (Borg and Kristensen, 2000). Low SES individuals more often perform risky, manual labour than high SES individuals, and their health deteriorates faster as a consequence (Marmot et al., 1997; Ravesteijn et al., 2013). Case and Deaton (2005) find that those who are employed in manual occupations have worse health than those who work in professional occupations and that the health effect of occupation operates at least in part independently of the personal characteristics of the workers. Extensive research further suggests an important role of lifestyle factors, particularly smoking, in explaining SES disparities in health (Mackenbach et al., 2004). Fuchs (1986) argues that in developed countries, it is personal lifestyles that cause the greatest variation in health.

Education

Education appears to be a key dimension of SES and studies suggest education has a causal protective effect on health and mortality (Lleras-Muney, 2005; Conti et al., 2010; Van Kippersluis et al., 2011).⁵ Education increases wages (e.g., Mincer, 1974), thereby enabling purchases of health investment goods and services (though higher wages also increase the opportunity cost of time). Education potentially increases the efficiency of medical and preventive care usage and time inputs into the production of health investment (Grossman, 1972a; 1972b). The higher educated are also better able at managing their diseases (Goldman and Smith, 2002), and benefit more from new knowledge and new technology (Lleras-Muney and Lichtenberg, 2005; Glied and Lleras-Muney, 2008).

Financial measures of SES

Financial measures of SES may have a more limited impact on health than education. Smith (2007) finds no effect of financial measures of SES (income, wealth, and change in wealth) on changes in health. Cutler, Lleras-Muney and Vogl (2011) provide an overview of empirical findings and conclude that the evidence points to no, or a very limited, impact of income or wealth on health (see also Michaud and Van Soest, 2008). Yet, this view is not unequivocally accepted. For example, Lynch, Kaplan and Shema (1997) suggest that accumulated exposure to economic hardship causes bad health, and Herd, Schoeni and House (2008) argue that there might be causal effects of financial resources on health at the bottom of the income or wealth distribution. Income and wealth enable purchases of medical care and thereby potentially allow for better health maintenance. Further, more affluent workers may choose safer working and living environments since safety is a normal good (Viscusi, 1978). But, higher wages are also associated with higher opportunity costs, which would reduce the amount of time devoted to health maintenance.

Health and labor-force withdrawal

In the other direction of causality, studies have shown that perhaps the most dominant causal relation between health and dimensions of SES in adulthood is the causal impact that poor health has on one’s ability to work and hence produce income and wealth (e.g., Case and Deaton, 2005; Smith, 2007). Healthy individuals are also more productive and earn higher wages (Currie and Madrian, 1999).

Joint determination

Fuchs (1986) has argued that the strong correlation between SES and health may be due to differences in the time preferences of individuals, which affects investments in both education and health. Cutler and Lleras-Muney (2008) argue that differences in individual preferences (risk aversion and discount rates) appear to explain only a small portion of the SES-health gradient, but they also note that preferences are difficult to measure, and that preferences with respect to health may differ from preferences with respect to finance. Other third factors known to contribute to the correlation between SES and health are cognitive and non-cognitive skills, in particular conscientiousness and self-esteem (Auld and Sidhu, 2005; Chiteji, 2010; Conti et al., 2010; Savelyev, 2014).

Gradient over the life cycle

Health inequalities are largest in mid-life and narrow in later life. The literature provides competing explanations for this pattern. The cumulative advantage hypothesis states that health inequalities emerge by early adulthood and subsequently widen as economic and health advantages of higher SES individuals accumulate (House et al., 1994; Ross and Wu, 1996; Lynch, 2003). Any apparent narrowing of SES inequalities in late life is largely attributed to mortality selection, i.e., lower SES people are more likely to die which results in an apparently healthier surviving disadvantaged population.⁶ The competing age-as-leveler hypothesis maintains that later in life deterioration in health becomes more closely associated with age than with any other predictor, i.e. through a greater equalization of health risks (House et al., 1994), with the result that the SES-health gradient narrows.

2 Theory

2.1 Theoretical Formulation

In this section we formalise the above discussion on the features of a theoretical framework for the SES-health gradient over the life cycle. The aim is to understand the SES-health gradient as the outcome of rational constrained individual behaviour.

A natural starting point for a theory of the relation between health and SES is a model of life cycle utility maximization. Our model is based on the Grossman model of the demand for health (Grossman, 1972a; 1972b; 2000) in continuous time (see also Wagstaff, 1986a; Ehrlich and Chuma, 1990; Zweifel and Breyer, 1997; Galama, 2015). The Grossman model provides a framework for the interrelationship between health, financial measures of SES (wealth, wages, and earnings), the demand for consumption, the demand for medical goods and services, and the demand for time investments in health (e.g., visits to the doctor, exercise). Health increases earnings (through reduced sick time) and provides utility. We add six additional features to the model.

First, we assume decreasing-returns-to-scale (DRTS) in investment of the health-production process. This addresses the degeneracy of the solutions for investment and health that characterises commonly employed linear investment models (Ehrlich and Chuma, 1990; Galama, 2015). It is further attractive in that the health-production process is generally thought of as being subject to diminishing returns (Wagstaff, 1986b).

Second, individuals choose their level of “job-related health stress”, which can be interpreted broadly, ranging from physical working conditions (e.g., hard or risky labor) to psychosocial aspects of work (e.g., low social status, lack of control, repetitive work, etc.) that are detrimental to health. Individuals may accept risky and/or unhealthy work environments, in exchange for higher pay (Muurinen, 1982; Case and Deaton, 2005), i.e. a compensating wage differential (Smith, 1776; Viscusi, 1978).

Third, we allow consumption patterns to affect the health deterioration rate (Grossman, 1972b; Forster, 2001; Case and Deaton, 2005; see Cawley and Ruhm, 2012, for a review of theoretical models of health behaviours). We distinguish healthy consumption (such as the consumption of healthy foods, sports and exercise) from unhealthy consumption (such as smoking, excessive alcohol consumption). Healthy consumption provides utility, and is associated with health benefits in that it lowers the health deterioration rate. We interpret healthy consumption broadly to include decisions regarding housing and neighborhood.⁷ Unhealthy consumption provides consumption benefits (utility) but increases the health deterioration rate.

Fourth, the effect of education on income is included in a straightforward manner by assuming a Mincer-type wage relation, in which earnings are increasing in the level of education and in the level of experience of workers (e.g., Mincer, 1974).

Fifth, individuals endogenously optimise length of life (Ehrlich and Chuma, 1990). Longevity is an important health outcome and differential mortality by SES may explain part of the narrowing of the gradient in late life. Moreover, length of life is an essential horizon that determines the duration over which the benefits of health investments and healthy behaviours can be reaped.

Last, we include leisure, which jointly with sick time and time inputs into health investment and into health behaviour allows for the modelling of an implicit retirement decision. As health declines, increased sick time and increased demand for time inputs into health investment and healthy behaviour reduce the amount of time that can be devoted to work, capturing possible reverse causality from health to labour force participation, and thereby financial measures of SES.

Individuals maximise the life-time utility function

$${\displaystyle {\int }_0^{T}U(t)e^{-\beta t}dt,}$$ (1)

where time t is measured from the time an individual has completed her education and joined the labour force (e.g., around age 25 or so), T denotes total lifetime (endogenous), β is a subjective discount factor, and individuals derive utility U(t) ≡ U[C_h(t), C_u(t), L(t), H(t)] from healthy consumption C_h(t), unhealthy consumption C_u(t), leisure L(t), and health H(t). Utility is assumed to be strictly concave and increasing in its arguments.

Healthy C_h(t) and unhealthy C_u(t) consumption are produced following a Becker (1965) home-production model by combining goods, X_h(t) and X_u(t), purchased in the market and own time inputs, ${\tau }_{C_h}(t)$ and ${\tau }_{C_u}(t)$

$$C_h(t)\equiv C_h[X_h(t),{\tau }_{C_h}(t);{\mu }_{C_h}(t)],$$ (2)

$$C_u(t)\equiv C_u[X_u(t),{\tau }_{C_u}(t);{\mu }_{C_u}(t)],$$ (3)

where ${\mu }_{C_h}(t)$ and ${\mu }_{C_u}(t)$ are (exogenous) efficiency factors.

The objective function (1) is maximised subject to three constraints. The first relates to the production of health capital

$$\frac{\partial H(t)}{\partial t}=I[m(t),{\tau }_m(t);E]-d(t).$$ (4)

Health H(t) can be improved through health production I[m(t), τ_m(t); E]. Goods and services m(t) (e.g., medical care) as well as own time inputs τ_m(t) (e.g., exercise, time spent visiting a doctor, etc.) are used in the production of health I[m(t), τ_m(t); E]. We assume the following functional form

$$I[m(t),{\tau }_m(t);E]\equiv {\mu }_I(t;E)m{(t)}^{{\alpha }_I}{\tau }_m{(t)}^{{\beta }_I},$$ (5)

where the efficiency of the health-production process μ_I (t;E) is assumed to be a function of the consumer’s stock of knowledge E as the more educated are assumed to be more efficient consumers and producers of health (Grossman, 1972a; 1972b). The health-production function I[m(t), τ_m(t), E] is assumed to exhibit DRTS (0 < α_I + β_I < 1).

Health (equation 4) deteriorates at the health deterioration rate d(t) ≡ d[t, C_h(t), C_u(t), z(t), H(t); ξ(t)]. The health deterioration rate depends endogenously on healthy consumption C_h(t), unhealthy consumption C_u(t), job-related health stress z(t), and health H(t).⁸ Consumption can be healthy (∂d/∂C_h ≤ 0; e.g., healthy foods, healthy neighborhood) or unhealthy (∂d/∂C_u > 0; e.g., smoking). Greater job-related health stress z(t) accelerates the “aging” process (∂d/∂z > 0). The deterioration rate depends in a flexible way on health, instead of the usual assumption of a linear relationship d(t) = δ(t)H(t) as in Grossman (1972a;b) and the related literature (but see Dalgaard and Strulik, 2014, for an exception), and ξ(t) denotes a vector of exogenous environmental conditions. Last, we have a fixed initial H(0) = H₀ and a fixed end condition H(T) = H_min for health.⁹

The second constraint is the total time budget Ω,

$$\Omega ={\tau }_w(t)+L(t)+{\tau }_m(t)+{\tau }_{C_h}(t)+{\tau }_{C_u}(t)+s[H(t)],$$ (6)

where the total time available in any period Ω is the sum of all possible uses τ_w(t) (work), L(t) (leisure), τ_m(t) (health investment), ${\tau }_{C_h}(t)$ (healthy consumption), ${\tau }_{C_u}(t)$ (unhealthy consumption) and s[H(t)] (sick time).

The third constraint concerns the dynamic relation for financial assets:

$$\frac{\partial A(t)}{\partial t}=rA(t)+Y(t)-p_{X_h}(t)X_h(t)-p_{X_u}(t)X_u(t)-p_m(t)m(t).$$ (7)

Assets A(t) provide a return r (the return on capital), increase with income Y (t) and decrease with purchases in the market of healthy consumption goods X_h(t), unhealthy consumption goods X_u(t), and medical care m(t), at prices $p_{X_h}(t)$, $p_{X_u}(t)$, and p_m(t), respectively. We have a fixed initial A(0) = A₀ and a fixed end condition A(T) = A_T for wealth, and assume that individuals face no borrowing constraints.¹⁰

Income Y (t) ≡ Y [H(t), z(t); E, x(t)] is assumed to be an increasing function of health H(t) (∂Y/∂H > 0) and of job-related health stress z(t) (∂Y/∂z > 0; Case and Deaton, 2005). We follow Grossman (1972b,a; 1972b,a; 2000) and model income Y (t) as the product of the wage rate w(t) and time spent working τ_w(t),

$$Y[H(t)]\equiv w(t)\{\Omega -L(t)-{\tau }_m(t)-{\tau }_{C_h}(t)-{\tau }_{C_u}(t)-s[H(t)]\}.$$ (8)

Individuals receive wages w(t) ≡ w[t, z(t); E, x(t)], which are a function of job-related health stress z(t)

$$w(t)=w_{\ast }(t){[1+z(t)]}^{{\gamma }_w},$$ (9)

where γ_w ≥ 0 and w_*(t) ≡ w_*[E, x(t)] represents the “stressless” wage rate, i.e., the wage rate associated with the least job-related health stress z(t) = 0.¹¹ The stressless wage rate w_*(t) is a function of the consumer’s education E and experience x(t) (e.g., Mincer, 1974),

$$w_{\ast }(t)=w_E{e}^{{\rho }_{E}E+{\beta }_{x}x(t)-{\beta }_{x^2}x{(t)}^2},$$ (10)

where education E is expressed in years of schooling, x(t) is years of working experience, and ρ_E, β_x and ${\beta }_{x^2}$ are coefficients, assumed to be positive.

Thus, we have the following optimal control problem: the objective function (1) is maximised with respect to the control functions L(t), X_h(t), ${\tau }_{C_h}(t)$, X_u(t), ${\tau }_{C_u}(t)$, m(t), τ_m(t), z(t), the parameter T, and subject to the constraints (4), (6) and (7).

The Hamiltonian (see, e.g., Seierstad and Sydsaeter, 1987) of this problem is:

$$\mathfrak{J}=U(t)e^{-\beta t}+q_H(t)\frac{\partial H(t)}{\partial t}+q_A(t)\frac{\partial A(t)}{\partial t},$$ (11)

where q_H(t) is the marginal value of remaining life-time utility (from t onward) derived from additional health capital

$$q_H(t)=\frac{\partial }{\partial H(t)}{\displaystyle {\int }_t^{T^{\ast }}U(\ast )e^{-\beta s}ds},$$ (12)

and q_A(t) is the marginal value of remaining life-time utility derived from additional financial capital

$$q_A(t)=\frac{\partial }{\partial A(t)}{\displaystyle {\int }_t^{T^{\ast }}U(\ast )e^{-\beta s}ds,}$$ (13)

T* denotes optimal length of life, and U(∗) denotes the maximised utility function (see, e.g., Caputo, 2005).

The condition for optimal longevity T follows from the dynamic envelope theorem (e.g., Caputo, 2005, p. 293):

$$\frac{\partial }{\partial T}{\displaystyle {\int }_t^{T^{\ast }}U(\ast )e^{-\beta s}ds=\frac{\partial }{\partial T}{\displaystyle {\int }_0^T\mathfrak{J}(t)dt}}=\mathfrak{J}(T)=0.$$ (14)

The marginal value of life extension is given by $\mathfrak{J}(T)=U(T)e^{-\beta T}+q_H(T){\partial H(t)/\partial t|}_{t=T}+{q_A(T)\partial A(t)/\partial t|}_{t=T}$. When dividing by the marginal value of wealth, one obtains a measure for the monetary value of life, $\mathfrak{J}(T)/q_A(T)=U(T)/U_C(T)+q_{h/a}(T){\partial H(t)/\partial t|}_{t=T}+{\partial A(t)/\partial t|}_{t=T}$. The monetary value of life is similar to the expressions obtained in Rosen (1988) (his equation 16) and Murphy and Topel (2006) (their equations 7 and 8), for health-neutral consumption. Our measure is richer since it additionally takes into account asset accumulation and health depreciation.

2.2 First-Order Conditions

In this section we discuss the first-order conditions for optimization. We assume that an interior solution to the optimization problem exists. Detailed derivations are provided in Appendix A. The first-order condition for health investment is given by

$$q_{h/a}(t)={\pi }_I(t),$$ (15)

where q_h/a(t) represents the marginal benefit of health investment, defined as the ratio of the marginal value of health, q_H(t), to the marginal value of wealth, q_A(t) (throughout the paper we refer to q_h/a(t) as the relative marginal value of health):

$$q_{h/a}(t)\equiv \frac{q_H(t)}{q_A(t)},$$ (16)

and π_I(t) represents the marginal cost of health investment,

$${\pi }_I(t)\equiv \frac{p_m(t)}{\partial I/\partial m}=\frac{w(t)}{\partial I/\partial {\tau }_m}.$$ (17)

The marginal benefit of health investment increases in the marginal value of health q_H(t) and decreases in the marginal value of wealth q_A(t). If the marginal value of health is high individuals invest more in health, and if the marginal value of wealth is high individuals invest less, consume less, and save more.

For the functional form (5) we can express the marginal cost of health investment π_I(t) as follows (see Appendix B for detail)

$${\pi }_I(t)=\frac{p_m{(t)}^{1-{\beta }_I}w{(t)}^{{\beta }_I}}{{\mu }_I(t;E){\alpha }_I^{1-{\beta }_I}{\beta }_I^{{\beta }_I}}m{(t)}^{1-{\alpha }_I-{\beta }_I},$$ (18)

$${\pi }_I(t)=\frac{p_m{(t)}^{{\alpha }_I}w{(t)}^{1-{\alpha }_I}}{{\mu }_I(t;E){\alpha }_I^{{\alpha }_I}{\beta }_I^{1-{\alpha }_I}}{\tau }_m{(t)}^{1-{\alpha }_I-{\beta }_I}.$$ (19)

The marginal cost of health investment π_I(t) increases with the level of health investment goods and services m(t) and time inputs τ_m(t) due to decreasing returns to scale 0 < α_I + β_I < 1,¹² with the price of medical goods and services purchased in the market p_m(t), and with the opportunity cost of time w(t), where the latter is a function of job-related health stress, z(t).

The first-order condition for leisure is

$$\frac{\partial U}{\partial L}=q_A(0)w(t)e^{(\beta -r)t},$$ (20)

a standard result equating the marginal utility of leisure ∂U/∂L to the marginal cost of leisure, which is a function of the marginal value of initial wealth q_A(0), the individual’s wage rate w(t), and the difference between the time preference rate β and the return on capital r.

The first-order condition for healthy consumption is

$$\frac{\partial U}{\partial C_h}=q_A(0)\left[{\pi }_{C_h}(t)-{\phi }_{d{C}_h}(t)\right]e^{(\beta -r)t},$$ (21)

where ${\pi }_{C_h}(t)\equiv {\pi }_{C_h}(t)[t,C_h(t),z(t);E,x(t)]$ is the marginal monetary cost of healthy consumption C_h(t)

$${\pi }_{C_h}(t)\equiv \frac{p_{X_h}(t)}{\partial C_h/\partial X_h}=\frac{w(t)}{\partial C_h/\partial {\tau }_{C_h}},$$ (22)

and ${\phi }_{d{C}_h}(t)\equiv {\phi }_{d{C}_h}[t,H(t),C_h(t),C_u(t),z(t);E,x(t),\xi (t)]$ is the marginal health benefit of healthy consumption

$${\phi }_{d{C}_h(t)}\equiv -q_{h/a}(t)\frac{\partial d}{\partial C_h}.$$ (23)

The marginal monetary cost of healthy consumption ${\pi }_{C_h}(t)$ (equation 22) is a function of the price of healthy consumption goods and services $p_{X_h}(t)$ and the opportunity cost of time w(t), and represents the direct monetary cost of consumption. The marginal health benefit of healthy consumption ${\phi }_{d{C}_h}(t)$ (equation 23), is equal to the product of the relative marginal value of health q_h/a(t) and the “amount” of health saved ∂d/∂C_h, and represents the marginal value of health saved.

Similarly, the first-order condition for unhealthy consumption is

$$\frac{\partial U}{\partial C_u}=q_A(0)[{\pi }_{C_u}(t)+{\pi }_{d{C}_u}(t)]e^{(\beta -r)t},$$ (24)

where ${\pi }_{C_u}(t)\equiv {\pi }_{C_u}(t)[t,C_u(t),z(t);E,x(t)]$ is the marginal monetary cost of unhealthy consumption C_u(t) (direct monetary cost)

$${\pi }_{C_u}(t)\equiv \frac{p_{X_u}(t)}{\partial C_u/\partial X_u}=\frac{w(t)}{\partial C_u/\partial {\tau }_{C_u}},$$ (25)

and ${\pi }_{d{C}_u}(t)\equiv {\pi }_{d_{C_u}}[t,H(t),C_h(t),C_u(t),z(t);E,x(t),\xi (t)]$ is the marginal health cost of unhealthy consumption (marginal value of health lost)

$${\pi }_{d{C}_u}(t)\equiv q_{h/a}(t)\frac{\partial d}{\partial C_u}.$$ (26)

The first-order condition for unhealthy consumption (24) is similar to the condition for healthy consumption (21). The difference lies in the marginal health cost (rather than health benefit) of unhealthy consumption, which has to be added rather than subtracted from the marginal monetary cost of unhealthy consumption ${\pi }_{C_u}(t)$.

Last, the first-order condition for job-related health stress is

$${\phi }_z(t)={\pi }_{dz}(t),$$ (27)

where φ_z(t) ≡ φ_z[t, H(t), z(t); E, x(t)] is the marginal production benefit of job-related health stress

$${\phi }_z(t)\equiv \frac{\partial Y}{\partial z},$$ (28)

reflecting the notion that job-related health stress is associated with a compensating wage differential (greater earnings), and π_dz(t) ≡ π_dz[t, H(t), C_h(t), C_u(t), z(t); E, x(t), ξ(t)] is the marginal health cost of job-related health stress (marginal value of health lost)

$${\pi }_{dz}(t)\equiv q_{h/a}(t)\frac{\partial d}{\partial z}.$$ (29)

2.3 The Health Cost and Health Benefit of Health Behaviour

From the first-order conditions follows that lifestyle decisions regarding consumption and occupation provide utility (directly or indirectly), and are associated with a monetary cost and with an opportunity cost. However, in contrast to conventional economic models, in our theory, these lifestyle decisions are additionally associated with a “health benefit” or a “health cost”. The health cost (benefit) is given by

$$q_{h/a}(t)=\frac{\partial d}{\partial x},$$ (30)

where the variable x represents the relevant health behaviour (e.g., unhealthy consumption, or hard physical labor), and the definition of q_h/a(t) is given by (12), (13), and (16). From (16), (43) and (44) follows

$$q_{h/a}(t)=q_{h/a}(T)e^{-{\displaystyle {\int }_t^T\left[r+\frac{\partial d}{\partial H}\right]dx}}+{\displaystyle {\int }_t^T{e}^{-{\displaystyle {\int }_t^s\left[r+\frac{\partial d}{\partial H}\right]dx}}}\left(\frac{1}{q_A(0)}\frac{\partial U}{\partial H}{e}^{-(\beta -r)s}+\frac{\partial Y}{\partial H}\right)ds.$$ (31)

The health cost (benefit) is the amount of health “lost” (“saved”) due to the health behaviour ∂d/∂x times the relative marginal value of health q_h/a(t) (the “price” or “value” of health, measured in life-time monetary units [e.g., US dollars] per unit of health, see 31). In simple terms, unhealthy consumption worsens health, and the health cost is the value one attaches to the lifetime consequences of reduced health. These lifetime consequences consist of the discounted additional (marginal) utility (q_A(0)⁻¹ ∂U/∂He^−(β−r)s in 31) plus the additional earnings (production benefit) derived from better health (∂Y/∂H in 31), over the remainder of life (from t till T). They are discounted at the rate r+∂d/∂H, where ∂d/∂H represents the cost of holding the stock of health and r represents the opportunity cost (i.e. one could alternatively invest in assets).

There are assymetries between health costs and health benefits. For healthy consumption the time investments and monetary costs are incurred today (and so is utility, if any, from its consumption), while the health benefits are reaped in the future. For unhealthy consumption the opposite holds: it provides pleasure (and requires time investments and monetary costs) today, while the health costs occur in the future. This implies that discount rates matter, as well as information on the healthiness or unhealthiness of the good ∂d/∂x. Individuals who discount the future heavily (large β in 31) or who underestimate the health consequences, will engage more in unhealthy consumption. Likewise, individuals who discount the future or underestimate the health gains from healthy consumption will engage less in healthy consumption.

Assessments of the value of a statistical life (VSL, see Viscusi and Aldy, 2003, for a review) generally involve investigating the risk of death that people are willing to take (usually in a setting of hazardous work) and how much they should be paid for taking these risks. An analogous concept is captured in, e.g., the first-order condition for job-related health stress (27), which weighs the wage premium of engaging in unhealthy / risky jobs today with the costs in terms of the lifetime consequences of reduced health (and associated longevity). In our theory, individuals are also willing to engage in a certain amount of unhealthy consumption for the utility it provides, as long as this benefit outweighs the associated health cost: the reduction in life-time utility due to health loss associated with unhealthy consumption. Thus, our theory provides a framework for determining the value of life and the value of health in settings outside of hazardous work, e.g., by exploiting unhealthy behaviours.

As we discuss in the remainder of the paper, the health cost and health benefit of behaviour are promising concepts for understanding a wide range of health behaviours, as well as the socioeconomic disparities in these behaviours.

2.4 Assumptions

Apart from the earlier mentioned assumptions of diminishing returns to scale (DRTS) of investment m(t), τ_m(t), in the health-production function I[m(t), τ_m(t); E] (0 < α_I +β_I < 1), and diminishing marginal utilities of healthy C_h(t) and unhealthy consumption C_u(t), of leisure L(t), and of health H(t), we further assume:

1. Diminishing marginal production benefit of health ∂²Y/∂H² < 0, diminishing marginal production benefit of job-related health stress ∂²Y/∂z² < 0, diminishing marginal health benefit of healthy consumption ${\partial }^{2}d/\partial C_h^2>0$, and diminishing returns to longevity (see 14)

   $$\frac{\partial \mathfrak{J}(T)}{\partial (T)}=\frac{{\partial }^2}{\partial T^2}{\displaystyle {\int }_t^{T^{\ast }}U(\ast )e^{-\beta s}ds>0,}$$ (32)

   where T* denotes optimal length of life and U(∗) denotes the maximised utility function (see, e.g., Caputo, 2005).

2. Increasing or constant returns to scale in the marginal health cost of unhealthy consumption ${\partial }^{2}d/\partial C_u^2\ge 0$ (as in Forster, 2001)¹³ and in the marginal health cost of job-related health stress ∂²d/∂z² ≥ 0.

3. Cobb-Douglas CRTS relations between the inputs (goods/services purchased in the market and own-time) and the outputs healthy consumption C_h(t), and unhealthy consumption $C_u(t):C_h(t)={\mu }_{C_h}(t)X_h{(t)}^{{\kappa }_{C_h(t)}}{\tau }_{C_h}{(t)}^{1-{\kappa }_{C_h}}$, and $C_u(t)={\mu }_{C_u}(t)X_u{(t)}^{{\kappa }_{C_u}}{\tau }_{C_u}{(t)}^{1-{\kappa }_{Cu}}$, where ${\kappa }_{C_h}$, ${\kappa }_{C_u}$ are the elasticities of the outputs with respect to goods and services, and $1-{\kappa }_{C_h}$, $1-{\kappa }_{C_u}$ are the elasticities of the outputs with respect to time inputs. As a result we have (see equations 22 and 25):

   $${\pi }_{C_h}(t)=\frac{p_{C_h}{(t)}^{{\kappa }_{C_h}}w{(t)}^{1-{\kappa }_{C_h}}}{{\kappa }_{C_h}^{{\kappa }_{C_h}}{(1-{\kappa }_{C_h})}^{1-{\kappa }_{C_h}}{\mu }_{C_h}(t)},$$ (33)

   $${\pi }_{C_u}(t)=\frac{p_{C_u}{(t)}^{{\kappa }_{C_u}}w{(t)}^{1-{\kappa }_{C_u}}}{{\kappa }_{C_u}^{{\kappa }_{C_u}}{(1-{\kappa }_{C_u})}^{1-{\kappa }_{C_u}}{\mu }_{C_u}(t)}.$$ (34)

4. First-order direct effects dominate higher-order indirect effects for control variables. For example, wealth affects healthy consumption directly, but also indirectly through its effect on unhealthy consumption, since unhealthy consumption affects healthy consumption through its effect on utility and on health deterioration. The assumption, in this particular example, is that the direct effect of wealth on healthy consumption dominates any indirect wealth effect that operates through unhealthy consumption or through any other control variable.

   Second- and higher-order terms are often ignored since they tend to be quantitatively less important (e.g., first-order Taylor series approximations). Moreover, additively separable utility functions are fairly conventional in the literature (e.g., Zeckhauser, 1970; Gjerde et al., 2005; Hall and Jones, 2007), and assuming that utility is additively separable, and that the health deterioration rate is additively separable, would lead to similar results. The difference is that we require second-order terms to be small, not that they are identical to zero, and we do not make the assumption for state variables since small differences can grow large over time. Thus, e.g., the marginal utility of healthy consumption is still a function of health (e.g., Finkelstein et al., 2013). Therefore, our assumption is less restrictive than the fairly conventional assumption of functions being additively separable in their arguments. We provide more detail in Appendix D.

In addition to these four assumptions, we need further information to be able to conduct the comparative dynamic analyses (section 4). In particular, we need the sign of ∂d/∂H, ∂q_A(t)/∂A(t), and ∂q_A(t)/∂H(t). For this reason, in the next section, we calibrate a simple version of the model to establish which signs are plausible. We obtain these as our “benchmark” relationships. From the calibrated model we have

1. ∂d/∂H > 0,

2. ∂q_A(t)/∂A(t) < 0; ∂q_A(t)/∂w_E < 0; ∂q_A(t)/∂E < 0,

3. ∂q_A(t)/∂H(t) < 0.

The calibrated model suggests that health increases aging at a diminishing rate, i.e. ∂d/∂H ≥ 0 and ∂²d/∂H² ≤ 0. This suggests that the health of healthy individuals deteriorates faster in absolute terms (since they have more of it) but not in relative terms (as a percentage of total health). Further, the calibrated model suggests diminishing returns to wealth ${\partial }_{q_A}(t)/\partial A(t)={\partial }^2[{\displaystyle {\int }_t^{T^{\ast }}U(\ast )}{e}^{-\beta s}ds]/\partial A{(t)}^2<0$, i.e. poorer individuals derive greater benefits from an additional increment of wealth than wealthier individuals. Finally, the calibrated model suggests unhealthier individuals derive greater benefits from an additional increment of wealth $\partial q_A(t)/\partial H(t)={\partial }^2[{\displaystyle {\int }_t^{T^{\ast }}U(\ast )}{e}^{-\beta s}ds]/\partial A(t)\partial H(t)<0$).¹⁴ This suggests health and wealth are to some extent substitutable in financing consumption and leisure (e.g., Muurinen, 1982; Case and Deaton, 2005).¹⁵

In the Appendix we also explicitly investigate the sensitivity of our predictions to the opposite signs of the above relations to assess the robustness of our results.

3 Dynamics and Numerical Calibration

In this section we begin with a study of the life-cycle profiles of health and health investment. Theoretically, the model’s predictions for these life-cycle patterns are ambiguous. We therefore calibrate a simple version of the model to investigate whether for a realistic set of parameter values it is able to reproduce empirical stylised facts. We then use findings from the calibrated simulations to make predictions for the life-cycle trajectories of healthy and unhealthy consumption and job-related health stress.

3.1 Health Investment and Health Over the Life Cycle

A quick glance at the first-order conditions in section 2.2 shows that the relative marginal value of health q_h/a(t) is an important driver of health investment (and more generally of health behaviour). Specifically, note that from (15), (18) and (19) we obtain

$$m(t)\propto q_{h/a}{(t)}^{1/(1-{\alpha }_I-{\beta }_I)},$$ (35)

$${\tau }_m(t)\propto q_{h/a}{(t)}^{1/(1-{\alpha }_I-{\beta }_I)}.$$ (36)

Thus, health investment increases with the marginal value of health. Hence, to understand health investment we first investigate the dynamics of the relative marginal value of health q_h/a(t) and of health H(t). We then discuss the implications of these dynamic patterns for health behaviours.¹⁶

Individuals start life generally in good health at H(0) = H₀, while the terminal health stock H(T) is constrained to the minimum health level H_min, below which life cannot be sustained. This implies that health decreases over the life cycle. Indeed, empirical evidence suggests that health falls over the life cycle, first slowly and then more rapidly in old age (e.g., Deaton and Paxson, 1998; Van Kippersluis et al., 2009; Dalgaard and Strulik, 2014).

The evolution of the relative marginal value of health q_h/a(t) is given by

$$\frac{\partial q_{h/a}(t)}{\partial t}=q_{h/a}(t)\left[r+\frac{\partial d}{\partial H}\right]-\frac{1}{q_A(0)}\frac{\partial U}{\partial H}{e}^{-(\beta -r)t}-\frac{\partial Y}{\partial H}$$ (37)

(combine equations 43 and 44 of Appendix A). Recall that the relative marginal value of health q_h/a(t) is the ratio of the marginal value of health q_H(t) and the marginal value of wealth q_A(t). The marginal value of wealth depreciates with age at the rate of return on capital r (see 43). The marginal value of health q_H(t) however, may increase or decrease with age. As long as q_H(t) appreciates, or depreciates more slowly than q_A(t), the relative marginal value of health q_h/a(t) will increase with age.

Empirical evidence suggests that health investments increase with age: medical expenditures peak in the final phase of life (Zweifel, Felder and Meiers, 1999),¹⁷ and other components of health investment either increase or stay relatively flat with age (Podor and Halliday, 2012). This suggests that the relative marginal value of health increases with age (see 15).

Theoretically our model allows for these patterns, but does not unambiguously predict them. In the next section, therefore, we resort to calibrated simulations to investigate whether our model, for a realistic set of parameter values, is able to reproduce these empirical stylised facts.

3.2 Calibrated Simulations

Our calibrated simulations proceed in several steps. First, we compute five-year averages for a health index and for health investment and treat these as the data “moments” for our calibration. Following Poterba, Venti and Wise (2011; 2013), we construct a health index using 1999–2013 U.S. Panel Study of Income Dynamics (PSID) data of a rich set of health measures, including: (i) a binary indicator of poor self-reported health; (ii) diseases such as acute myocardial infarctions (AMI), arthritis, asthma, cancer, diabetes, heart conditions, high blood pressure, learning disorders, lung disease, and stroke; (iii) mental health problems, (iv) activities of daily living (ADLs), and (v) body-mass index (BMI). We arbitrarily scale this health index such that initial health is equal to 100 and health at age 80 is equal to 15. We obtained age profiles for health investment from Halliday et al. (2017) who computed health investment expenditures from the U.S. Medical Expenditure Survey (MEPS). Figure 1 shows the life-cycle patterns of health and health investment, where the dots indicate the average of the health index and of health investment in 5 year age groups. As the Figure shows, health declines in a concave manner over the life cycle, while health investment increases rapidly in old age. These are stylised facts our model of health production ought to reproduce.

Figure 1.

Model simulation of health (left figure) and health investment (right figure) using calibrated parameter values in Table 1. The solid lines indicate the model simulations, and the dots indicate the empirical data moments constructed from PSID (health) and MEPS (health investment).

Second, we estimate the hourly wage profile using the PSID data and a Mincer equation of log hourly wages on dummies for each educational level and a quadratic polynomial in age. The estimated parameters are as follows

$$w_t=e^{2.3366+0.3731\times D+0.0314\times t-0.0006\times t^2},$$ (38)

where D is a dummy for a college degree, t measures age, and we multiply by 2 to obtain the yearly wages in thousands of dollars (assuming individuals work for 40 hours, 50 weeks per year). This Mincer-type wage equation for a college graduate starts with annual wages of $30, 000 per year at age t = 20 and peaks at $45, 000 per year at age t = 50 after which wages gradually decline.

Third, we numerically simulate a simplified version of our model (see Appendix C for details). Since the aim is to investigate whether our model is capable of reproducing the stylised facts regarding the life-cycle profiles of health and health investment, we omit the time inputs into consumption and health investment, omit the distinction between healthy and unhealthy consumption, and omit job-related health stress.

We assume a constant relative risk aversion (CRRA) utility function with scale parameter μ_U of the form

$$U[H_t,C_t]=\frac{1}{1-\rho }{\mu }_U{\left[C_t^{\zeta }{H}_t^{1-\zeta }\right]}^{1-\rho }+B,$$ (39)

where 0 ≤ ζ ≤ 1 is the relative “share” of consumption versus health, ρ is the coefficient of relative risk aversion, and B is a constant to ensure that utility is positive (Hall and Jones, 2007). We follow Scholz and Seshadri (2016) in modelling sick time as $s[H_t]=H_t^{-\gamma }$, and use a flexible functional form for health production

$$H_{t+1}-H_t={\mu }_I{m}_t^{\alpha }-d_t^{\ast }{H}_t^v,$$ (40)

where 0 < α < 1, and $d_t^{\ast }=e^{a+bt}$ following Cropper (1981) and Wagstaf (1986a). This functional form is flexible enough to capture various possible relationships between the deterioration rate ( $d_t=d_t^{\ast }{H}_t^v$) and health. For example, ν = 1 represents the Grossman case, while ν < 0 is akin to the health-deficit model by Dalgaard and Strulik (2014), in which the health of unhealthy individuals deteriorates faster. The functional form also depends in a flexible way on calendar age t.

No consensus exists over what causes aging with many theories attempting to explain what drives it. Two important classes of theories are prominent. The first class consists of “deficit-based theories”, where aging occurs predominantly as a result of the accumulation of deficits (or “damage”). For example, Arking (2006) advocates a theory of aging in which health decline is independent of calendar age, depending solely on the level of health, i.e. as in a model of aging due to wear and tear (see also Dalgaard and Strulik, 2014). The second class consists of “programmed theories of aging”, where aging is predominantly the result of genetically regulated or predetermined processes (Longo et al., 2005, de Magalhaes 2003, 2011, 2014). Such processes exhibit “pure” calendar age effects. De Magalhaes (2011) writes for example: ‘… it is now largely recognised that ageing (…) is not primarily the result of damage to irreplaceable body parts’ and that there is a role for ‘… genetically regulated processes or predetermined mechanisms’ (de Magalhaes, 2011). Further, Longo et al. (2005) provide evidence for genetic programming ‘that regulates the level of protection against stochastic damage, and therefore the length of time an organism remains healthy’. Finally, so-called aging-clock theory, which also falls within the programmed theories, stipulates that ‘Aging is programmed into our bodies, like a clock ticking away from the moment of conception’ (Moody and Sasser, 2014). The two classes of theories are not mutually exclusive; and there is in fact wide recognition that aging exhibits genetic programming or predetermined, and accumulated deficits aspects, with disagreement about their relative importance. We therefore choose to remain agnostic about the aging process, using a specification $d_t=d_t^{\ast }{H}_t^v$ that is flexible enough to encompass both deficits as well as calendar age aspects of aging. In essence, we ask the data which aspects of aging are important in our model for a good fit. We find that both calendar age and deficits features are needed.

Fourth, we fix a large number of model parameters by taking values from the literature (see Table 1 in section C). In particular, we set α = 0.75 in line with Hugonnier et al. (2013, 2016) who use values of 0.69 and 0.77, respectively. We follow Scholz and Seshadri (2016), setting A₀ = A_T = 0, ρ = 3, ζ = 0.7 and γ = 1.7.¹⁸ We follow Blau (2008) and DeNardi et al. (2016), setting the time preference rate β = 0.03, and the interest rate r equal to β. We further normalise prices of consumption and health investment and the efficiency of consumption to 1. The remaining parameters to be calibrated are ν, μ_I, μ_U, and the parameters a and b of the deterioration rate $d_t^{\ast }$.

Given the data moments and our model solutions, we calibrate the parameters ν, μ_I, μ_U, a and b using a Method of Simulated Moments (MSM) approach (see Appendix C for details). Admittedly, this parameter space leaves many degrees of freedom. We do not claim our parametrization is unique. See for example Dalgaard and Strulik (2014) for an alternative framework using health deficits that is also able to reproduce the life-cycle profiles for health and health investment. Our aim is more modest: to illustrate that for a realistic set of parameter values the model can reproduce the empirical stylised facts. Table 1 in Appendix C provides the fixed and calibrated parameter values, and Figure 1 shows the resulting simulated profiles (solid lines) alongside the empirical moments (dots). For this realistic set of parameter values, the fit of our simulated profiles is fairly accurate. The model can generate empirically plausible trajectories.¹⁹

The calibrated simulations provide three additional pieces of information. First, the calibrated simulations suggest an optimal length of life of T = 76.8 years.

Second, our calibration establishes a benchmark for the sign of relationships we require to obtain comparative dynamic results. The parameter value ν = 0.3 in equation (40) is consistent with ∂d/∂H ≥ 0 and ∂²d/∂H² ≤ 0. Further, in counterfactual simulations where we increase A₀ and H₀ by a small amount, we obtain ∂q_A(0)/∂A₀ < 0 and ∂q_A(0)/∂H₀ < 0 (see Table 2 in Appendix C).

Third, the calibrated model demonstrates that while health declines, the relative marginal value of health increases, with age. We will use these life-cycle patterns to derive from theory the implied life-cycle profiles for healthy and unhealthy consumption and job-related health stress in the general model.

3.3 Health Behaviour Over the Life-Cycle

As illustrated by the calibrated simulations, for plausible parameter values, the relative marginal value of health q_h/a(t) increases with age. This would suggest that the health cost of unhealthy consumption and of job-related health stress and the health benefit of healthy consumption increase with age.²⁰ Smoking rates are 8.9% among the 65+ compared to 21.6% among the 25–44 (US DHHS, 2014), and intake of fruit and vegetables increases with age (Serdula et al., 2004; Pearson et al., 2005). These patterns are consistent with the notion that the health benefit of healthy behaviour and the health cost of unhealthy behaviour increase with age: individuals start caring more about their health when they get older.

With declining health H(t) and an increasing marginal value of health q_h/a(t) with age we obtain the following life-cycle patterns for health behaviours. Early in life, individuals are generally healthy and therefore plausibly value health less (see Table 2 in Appendix C and propositions 5 and 7, section 4.3). As a result, they invest less in their health (equation 15), engage more in unhealthy consumption (see 24), and less in healthy consumption (see 21). As individuals age, declining health becomes a burden as poor health reduces utility and increased sick time reduces earnings. As a result, the benefits of health increase and individuals invest more in health, shift toward healthier consumption, and reduce the level of job-related health stress. This general trend of improved health behaviour may be partially reversed in mid life, as wages peak, leading to a higher opportunity cost of time. This may result in a reduction in health investment and healthy consumption in mid life, relative to a general trend of improved health behaviours with age.

The pattern for job stress is distinct. Early in life the health cost of job stress q_h/a(t) [∂d/∂z] is low, but so is the marginal benefit of job stress ∂Y/∂z (see 27). As wages increase, the benefit of job-stress increases. After mid age, declining health reduces the marginal benefit of job-stress, as sick time reduces the time available for work and wages plateau or even decrease. This suggests a pattern in which job stress initially increases as the marginal benefit of job-stress increases due to wage growth, followed by a decline in job stress due to plateauing or declining wages, increasing sick time, and an increasing health cost of job stress with age.

Prediction 1

Individuals in mid life plausibly accept unhealthy working conditions as they value the associated wage premium, but as they age they seek to engage in healthier work.

4 Variation in Health behaviour by SES and Health

Comparative dynamic analyses allow exploration of the effect of SES and health on the life-cycle trajectories of the control and state variables. We investigate the change in the optimal trajectory in response to variation in initial conditions or other model parameters, by comparing the “perturbed” optimal trajectory with respect to the “unperturbed” (or original) trajectory. Comparative dynamic analysis is an alternative to numerical simulation that has the benefit of being less restrictive by allowing for quite general functional forms (i.e. that utility be concave rather than, e.g., CRRA). Moreover, as Dalgaard and Strulik (2015, p.2) put it: ‘A purely numerical analysis entails a danger of neglecting general properties and implications of the model’.

Our emphasis is on exploring differences in constraints related to SES and health.²¹ Common measures of SES employed in empirical research are wealth, earnings (income), and education. Here we provide an intuitive discussion of the comparative dynamic results, supported by a number of propositions, whose formal proof we relegate to the Appendix.

The effect of variation in an initial condition or other model parameter δZ, where we are particulary interested in Z = {A₀, w_E, E, H₀}, on any control or state variable g(t) can be separated into two components²²

$$\frac{\partial g(t)}{\partial Z}={\frac{\partial g(t)}{\partial Z}|}_T+{\frac{\partial g(t)}{\partial T}|}_Z\frac{\partial T}{\partial Z},$$ (41)

where the first term on the right-hand side (RHS) represents the response to variation in Z for constant T and the second term on the RHS represents the additional response due to the associated variation in T.

4.1 Variation in Initial Wealth, δA₀

Let us focus first on the hypothetical case where length of life T is fixed. Contrasting the fixed T case with the general case where T is free provides us with useful insights regarding the properties of the model. This scenario may represent a developing nation with a high disease burden (where there may be lack of access to medical or public health technology, and competing risks from many diseases), the developed world, if it were faced with diminishing ability to further extend life, or individuals with a disease that severely limits longevity, such as Huntington’s disease (Oster, Shoulson and Dorsey, 2013).

• ◦PROPOSITION 1: Absent ability to extend life, wealthy individuals, ceteris paribus, value health only marginally more than less wealthy individuals. For proof see Appendix D.1.

For fixed length of life T, additional wealth δA₀ increases the relative marginal value of health initially, ${\partial q_{h/a}(t)/\partial A_0|}_T>0$, but eventually the relative marginal value of wealth decreases with respect to the unperturbed path, ${\partial q_{h/a}(t)/\partial A_0|}_T<0$. This result is illustrated in Figure 2, where the thick solid line labelled “Unperturbed” represents the unperturbed trajectory of the relative marginal value of health q_h/a(t) versus age t, and the dotted line labelled “T fixed” represents the perturbed path for fixed T. Note that both curves end at t = T. The intuition is that the relative marginal value of health cannot be higher at all times, as this would be associated with higher health investment, improved health behaviour (see the first-order conditions in section 2.2), and a longer life, violating the condition that end of life occurs at t = T (fixed) at the minimum health level H(T) = H_min. Indeed, simulations confirm this pattern: in the calibrated model, for individuals with higher initial wealth, the marginal value of health is higher up to age 70 and lower thereafter.²³ The response to additional wealth is thus muted as the individual is forced to invest less later in life in order not to extend life. Hence, the first term on the RHS of equation (41) is small for variation in wealth A₀.

Figure 2.

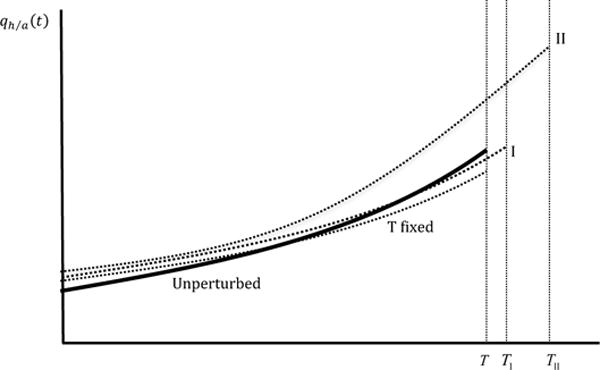
Evolution of the relative marginal value of health q_h/a(t) with age due to variation in A₀. The solid thick line, labelled “Unperturbed”, represents the unperturbed path. The perturbed paths are shown for the T fixed case (dotted line, labelled “T fixed”), scenario I, associated with small life extension T_I (dotted line, labelled “I”), and scenario II, associated with large life extension T_II (dotted line labelled “II”).

Let us now turn to the more interesting case where individuals can optimally choose T; they not only invest in the quality of life but also in the quantity of life.

Individuals optimally choose longevity T such that the marginal value of life extension is zero at this age, $\mathfrak{J}(T)=0$ (see 14),

$$\frac{\mathfrak{J}(T)}{q_A(T)}=\frac{1}{q_A(0)}U(T)e^{-(\beta -r)T}+q_{h/a}(T){\frac{\partial H}{\partial t}|}_{t=T}+{\frac{\partial A}{\partial t}|}_{t=T}=0,$$ (42)

where for reasons of exposition we have divided by q_A(T). As (42) shows, the marginal benefit of extending life consists of the additional utility from consumption and health. The marginal costs consist of the increasingly binding wealth and health constraints, due to declining wealth and declining health near the end of life.²⁴ With declining health, the utility U(t) gained over the extra years decreases, and thereby the marginal benefit of life extension. The calibrated simulation shows that q_h/a(t) increases rapidly with age as health declines, suggesting that the marginal cost of life extension does too. Eventually, the depreciation of health and decumulation of assets render additional life extension non-optimal.

As we will see, ability to extend life changes the picture dramatically as life extension increases the return to health investment by increasing the period over which a multitude of benefits of health can be accrued. The results can be summarised by propositions 2 and 3.

• ◦PROPOSITION 2: Wealthy individuals live longer: ∂T/∂A₀ > 0. For proof see Appendix D.2.
• ◦PROPOSITION 3: Wealthy individuals value health more and are healthier at all ages. The more life can be extended, the stronger is the increase in the value of health in response to additional wealth. For proof see Appendix D.3.

Intuitively, at high values of wealth (and hence consumption), individuals prefer investing in health over consuming, since health extends life, the period over which they can enjoy the benefits of health, leisure and consumption, whereas additional consumption per period would yield only limited marginal utility due to diminishing utility of consumption (see also Becker, 2007; Hall and Jones, 2007). With sufficient wealth one starts caring more about other goods, in particular health. Wealthier individuals value health more relative to wealth, invest more, are healthier, and live longer (propositions 2 and 3).

The second part of proposition 3 is best understood by its visual representation in Figure 2. The extent to which individuals are able to extend life, ∂T/∂A₀, depends on the model’s parameters r, α, μ_I, etc. These parameters are in turn determined by biology, medical technology, and environmental factors. If these factors are unfavorable to life extension (scenario I; small life extension), then individuals value health more early in life, but value health less later in life (the perturbed path starts higher, but eventually crosses the unperturbed path). This is the case we observe in our calibrated simulations. The pattern of initially higher investment, and subsequently lower investment, closely resembles that of the fixed T case (see proposition 1).

In contrast, if additional wealth affords considerable life extension (scenario II), the relative marginal value of health is higher at all times. Life extension raises the return to health investment and healthy behaviours. Further, utility from leisure and consumption can be enjoyed with additional years of life. Health also generates additional wealth from work, reinforcing the effect of the initial endowment of wealth δA₀. Together, these various benefits substantially raise the value of health, leading to improved health behaviours, better health throughout life, and greater longevity. This leads to the following prediction.

Prediction 2

Health disparities are larger in environments where the wealthy can effectively use their resources to extend life.

Propositions 2 and 3 also allow gauging the predicted response of an increase in wealth on health behaviours. A higher relative marginal value of health directly increases the health benefit of healthy behaviour, and the health cost of unhealthy behaviour. Plausibly, this represents the dominant effect,²⁵ consistent with wealthy individuals behaving healthier (e.g., Cutler and Lleras-Muney, 2010; Cutler, Lleras-Muney and Vogl, 2011; Cawley and Ruhm, 2012), and consistent with less affluent individuals responding more strongly to an unanticipated wealth shock (Van Kippersluis and Galama, 2014).

Prediction 3

Wealthy individuals shift consumption toward healthy consumption: they consume more healthy and moderately unhealthy consumption goods and services, but fewer severely unhealthy consumption goods and services.

The comparative dynamic effect of wealth on healthy consumption can be decomposed into a “direct” and an “indirect” wealth effect. The direct wealth effect is positive: an increase in wealth affords more healthy consumption (see Table 2 in Appendix C). Yet, wealth also has an indirect effect: an increase in wealth leads to a higher relative marginal value of health q_h/a(t) (proposition 3), which increases the health benefit of healthy consumption [−q_h/a(t)∂d/∂C_h]. Both the direct and indirect effects operate in the same direction, and wealthy individuals engage more in healthy consumption: ∂C_h(t)/∂A₀ > 0, at least initially.²⁶

Similar to healthy consumption, additional wealth enables purchases of more unhealthy consumption goods – the direct wealth effect is positive. Yet, additional wealth also increases the marginal health cost of unhealthy consumption q_h/a(t)∂d/∂C_u (the indirect wealth effect), through a higher relative marginal value of health q_h/a(t). The indirect wealth effect competes with the direct wealth effect.

While we cannot a priori sign the relation between unhealthy consumption and wealth, the two competing effects predict an interesting pattern of behaviour. The health cost increases in the severity of its impact on health, ${\pi }_{d{C}_u(t)}\propto \partial d/\partial C_u$ (the degree of “unhealthiness” of the consumption good). This suggests that for moderately unhealthy goods the direct wealth effect would dominate, while for severely unhealthy goods the indirect wealth effect would dominate.

4.2 Variation in Wages, δw_E, and education δE

• ◦PROPOSITION 4: Permanently higher wages and education operate in a similar manner to an increase in wealth δA₀ (propositions 1 through 3), with some differences: (i) the wealth effect is muted by the increased opportunity cost of time, (ii) permanent wages w_E and education E also raise the production benefit of health, and (iii) education raises the efficiency of health investment. For proof see Appendix D.4.

It is important to distinguish between an evolutionary wage change and permanent differences in the wage rate w(t), i.e. permanent income. In our model of perfect certainty and perfect capital markets, an evolutionary increase in the wage rate w(t) raises the opportunity cost of time but does not affect the marginal value of wealth q_A(t) (i.e. the life-cycle trajectory is unchanged). In contrast, if wages are permanently higher, i.e. larger w_E in (10), earnings are higher over the entire life cycle,²⁷ and in addition to the opportunity cost of time effect, there is also a wealth effect (operating by decreasing the marginal value of wealth q_A(t); see Table 2 in Appendix C). Further, the production benefit of health is higher as higher wages increase the value of health in reducing sick time.

There are reasons to believe that the wealth effect and the effect of a higher production benefit of health dominate the opportunity cost of time effect. First, this is consistent with the result by Dustmann and Windmeijer (2000) and Contoyannis, Jones and Rice (2004) that a permanent wage change affects health positively, while a transitory wage increase affects health negatively. Second, it is consistent with the rich literature on SES and health that consistently finds that high-income individuals are generally in better health than low-income individuals.

Permanently higher wages due to education E (see equation 10) are also associated with an increased opportunity cost of time effect, a wealth effect, and higher production benefits. But, education also increases the efficiency μ_I(t; E) of health investment, as the educated are assumed to be more efficient consumers and producers of health. The efficiency effect of education has two implications. First, it increases total health investment I[m(t), τ_m(t); E]. However, improved efficiency implies that fewer inputs are required to obtain a certain level of investment, potentially reducing the market m(t) and time inputs τ_m(t) devoted to health investment (e.g., Grossman, 1972a;b). Second, it could potentially explain the stronger evidence for an effect of education on health and the weaker evidence for effects of income and wealth on health, since the efficiency effect does not operate for income and wealth (see section 1). Thus, among the socioeconomic indicators, education improves health behaviours and health potentially the most.

4.3 Variation in Initial Health, δH₀

• ◦PROPOSITION 5: Absent ability to extend life, healthy individuals, ceteris paribus, value health cumulatively less, ${\displaystyle {\int }_0^T[{\partial q_{h/a}(t)/\partial H_0|}_T]dt<0}$. For proof see Appendix D.5.

For fixed length of life T, when starting off with a higher level of health, cumulatively the relative marginal value of health has to be lower over the life cycle, leading to cumulatively unhealthier behaviour and lower health investment, in order to arrive at H_min over the same duration of life T. The calibrated model simulations confirm this pattern and Figure 3 illustrates it: the perturbed fixed T path (dotted line) lies below the unperturbed curve, and both end at t = T.²⁸

Figure 3.

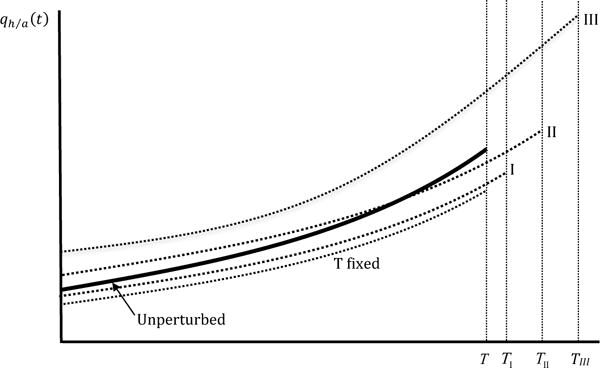
Evolution of the relative marginal value of health q_h/a(t) with age due to variation in H₀. The solid thick line, labelled “Unperturbed”, represents the unperturbed path. The perturbed paths are shown for the T fixed case (dotted line, labelled “T fixed”), scenario I, associated with small life extension T_I (dotted line, labelled “I”), scenario II, associated with intermediate life extension T_II (dotted line labelled “II”), and scenario III, associated with large life extension (dotted line labelled “III”).

• ◦PROPOSITION 6: Healthy individuals live longer ∂T/∂H₀ ≥ 0. For proof see Appendix D.6.
• ◦PROPOSITION 7: Individuals with greater endowed health are healthier at all ages, ∂H(t)/∂H₀ > 0, ∀t. For small life extension, they cumulatively value health less ${\displaystyle {\int }_0^T[\partial q_{h/a}(t)/\partial H_0]dt<0}$, for intermediate life extension they value health cumulatively more ${\displaystyle {\int }_0^T[\partial q_{h/a}(t)/\partial H_0]dt>0}$, and for large life extension they value health more at all ages, ∂q_h/a(t)/∂H₀ > 0, ∀t. For proof see Appendix D.7.

When T can be optimally chosen, individuals with greater endowed health are healthier throughout life, and live longer (proposition 6 and 7).²⁹ We distinguish between three scenarios: “small”, “intermediate”, and “large” life extension, as illustrated in Figure 3 (see Appendix section D.7 and Figure 10 for more detail). For small life extension, healthier individuals value health more than in the fixed T case, but cumulatively still less than for the unperturbed path, and life is extended to T_I. For intermediate life extension, the relative marginal value of health is cumulatively higher compared with the unperturbed path, but health is still valued less in old age. Life is extended to T_II. For large life extension, the relative marginal value of health is higher at all ages, and life is extended to T_III. In such a scenario, healthy individuals care more about their health as for them investment pays off in terms of a longer lifespan over which the benefits of health, consumption, and leisure may be enjoyed. Since health investment increases in the value of health (see 15 and 17) it follows similar patterns in these three scenarios.

Which scenario is more plausible depends on the extent to which medical technology, institutional, and environmental factors, allow for endowed health to extend life (∂T/∂H₀): in developed countries with few competing risks from diseases, universal access to health care, and cutting-edge medical technology, or in developing nations where large gains in longevity can potentially be achieved with relatively low cost interventions such as provision of clean water and improving sanitation. In our calibrated simulations for an average U.S. college graduate, we find ∂q_h/a(t)/∂H(t) < 0 for all ages (see Table 2 in section C), which would be consistent with the “small” life extension scenario T_I (see Figure 3 and for more detail Figure 10 in Appendix section D.7), and is consistent with the empirical regularity that healthy individuals consume less medical care (Van de Ven and Van der Gaag, 1982; Wagstaff, 1986a; Erbsland, Ried and Ulrich, 2002).³⁰

4.4 Variation in Work, Leisure, and Retirement by SES and Health

Important variation exists across individuals both in the type of work and in the amount of time spent working, during a day and over the life cycle. We first discuss variation in the type of work, then turn to time spent working.

Work and job-related health stress

A higher relative marginal value of health q_h/a(t) induced by wealth (proposition 3) increases the health cost of job-related health stress (see 29). Eventually, however, wealth leads to better health (proposition 3) and better health increases the marginal benefit ∂Y/∂z of job-related health stress through reduced sick time. Permanently higher wages, e.g., through better education, are also associated with the above competing wealth and health effects. In addition, the marginal benefit of job-related health stress ∂Y/∂z increases directly with the wage rate. Empirical evidence suggests that high SES individuals on average work in less demanding occupations (e.g., Ravesteijn, van Kippersluis and van Doorslaer, 2013). This suggests that higher SES increases the marginal costs of job-related health stress more than it increases its marginal benefits.

The effect of health on job-related health stress is plausibly positive. Better health reduces sick time, which increases the marginal benefit of job-related health stress. Further, if the relative marginal value of health decreases in health (proposition 5 and 7), then healthier individuals will have lower marginal costs of engaging in job-related health stress. With higher benefits and lower costs, we expect the healthy to engage in unhealthy jobs, consistent with empirical evidence (Kemna, 1987).

Leisure and retirement

To analyze retirement, we informally treat a small amount of time devoted to work τ_w(t), i.e. below a certain threshold, say τ_R, as a retirement phase. With declining health, time spent working τ_w(t) (see 6) gradually decreases, as a result of increasing sick time and the increasing demand for time devoted to health investment. Hence, the model produces a phase of life in old age that naturally qualifies as retirement. During working life, individuals divide their time between work, leisure, and time inputs into consumption and health investment (see 6). Therefore, we can infer the effect on the time spent working by investigating effects on leisure and time inputs.

Wealth increases the demand for leisure, for (time inputs into) healthy and unhealthy consumption, and for (time devoted to) health investment, through a “direct” wealth effect, reducing the marginal value of wealth q_A(t), and an “indirect” value of health effect, increasing the relative marginal value of health (proposition 3). This leads wealthier individuals, ceteris paribus, to work less (see 6), and hence retire earlier, in line with empirical evidence (Imbens, Rubin and Sacerdote, 2001; Brown, Coile and Weisbenner, 2010).³¹ Permanently higher wages, e.g., through education, are also associated with the above wealth and value of health effects, but higher wages also increase the cost of time inputs, i.e. of leisure, of healthy and unhealthy consumption, and of health investment (see sections D.8.2 and D.8.3 in the Appendix). The higher opportunity cost of not working encourages higher educated individuals to retire later. Thus, the wealthy retire earlier, but the higher educated and those with higher permanent wages may retire later.

Healthier individuals spend more time working, as good health reduces sick time and reduces the demand for (time inputs into) health investment (proposition 5 and 7). This encourages healthier individuals to work more and retire later (see 6). However, health is also associated with a wealth effect, reducing the marginal value of wealth q_A(t) (see Table 2 in Appendix C), which increases the demand for leisure, and for (time inputs into) healthy and unhealthy consumption, and thereby encourages early retirement.³² While the net effect is therefore ambiguous, it seems plausible that the direct effect of health on reducing sick time, and reducing time inputs into health investment, outweighs the indirect effect of health on leisure by relaxing the wealth constraint. This is consistent with an extensive literature showing quantitatively large effects of health on labour force participaton, with unhealthier individuals retiring earlier (e.g., Currie and Madrian, 1999; Smith, 2007).

Prediction 4

Under plausible assumptions, healthier individuals retire later. This, combined with an effect of health on earnings, leads to reverse causality as healthier individuals accumulate more wealth by earning more and retiring later.

5 Discussion and Conclusions

We have developed a theory of the relation between health and SES over the life-cycle. Our life-cycle model incorporates health, longevity, wealth, earnings, education, work, job-related physical and psychosocial health stressors, leisure, health investment (e.g., exercise, medical care), and healthy and unhealthy consumption (including housing, neighborhood social environment). Our review of the literature identifies these as essential mechanisms in the formation and evolution of disparities in health.

The theory is capable of reproducing stylised facts regarding the life-cycle profiles of health and health investment, as illustrated by calibrated simulations of the model. The theory is further able to reproduce stylised facts characteristic of the SES-health gradient. We find that greater SES, as measured by wealth, earnings, and education, induces a healthy lifestyle: it encourages investment in health, encourages healthy consumption, discourages unhealthy consumption, and protects individuals from the health risks of physically and psychosocially demanding working conditions. The healthier lifestyle of high SES individuals causes the health trajectories of high and low SES individuals to diverge. As a result they are healthier and live longer (propositions 2 to 4). In addition, health generates earnings and the worsening health of low SES individuals potentially leads to early withdrawal from the labour force (prediction 4). This reverse causality from health to financial measures of SES potentially reinforces the widening of the SES-health gradient, as documented in empirical studies (e.g., Smith, 2007).

In middle to late life the divergence of health trajectories potentially slows as lower levels of health encourages low SES individuals to invest more in health and engage in healthier behaviour in order to slow down their health deterioration (propositions 3 and 4). Also, mortality selection, i.e. the least healthy among lower SES individuals die sooner, results in an apparently healthier surviving disadvantaged population, potentially narrowing the gradient in late age.³³ Thus, the theory is capable of reproducing the characteristic life cycle patterns of the SES-health gradient.

Apart from providing a framework to interpret stylised facts, the theory also makes novel testable predictions and provides new intuition. In particular, we emphasise the importance of our concept of a health cost (benefit) of unhealthy (healthy) behaviours, in explaining health behaviour. Individuals make decisions regarding health by taking into account not just monetary prices and preferences, but additionally the life-time health consequences of their choices, as embodied by the health cost (benefit). Variation in the health cost over the life cycle and across SES potentially explains several empirical phenomena.

For example, we predict that individuals in mid life, particularly the healthy and poor, engage in work associated with unhealthy working conditions as they value the associated wage premium. However, as individuals age they engage in healthier work, as the health cost of unhealthy working conditions increase with declining health (prediction 1). Another implication of our concept of a health cost is a pattern in which high SES individuals consume more of moderately unhealthy consumption goods (e.g., moderate alcohol consumption) and less of severely unhealthy consumption goods (e.g., cigarettes, high alcohol consumption, illicit drugs) than do lower SES individuals (prediction 3). Greater wealth permits more consumption but also increases the health cost. This could provide an explanation for the observation that high SES individuals are less likely to smoke cigarettes (bad for health) but are more likely to be moderate drinkers (moderately bad) than low SES individuals (e.g., Cutler and Lleras-Muney, 2008).

Another insight is that (endogenous) longevity is crucial in explaining observed associations between SES and health (cf. propositions 1, 3, and 4, and prediction 2). Absent ability to extend life (fixed horizon), the association between SES and health is small (proposition 1). If, however, life can be extended, SES and health are positively associated and the greater the degree of life extension afforded by SES, the greater is their association (propositions 3 and 4). Thus, health disparities are larger in environments where higher SES individuals can effectively use their resources to extend life (prediction 2). For example, if the latest medical technology is more easily accessible to higher SES individuals, health disparities across SES groups may be larger.

In deriving predictions from the comparative dynamic analyses we have made a number of assumptions, most of which are conventional, such as diminishing marginal utility and Cobb-Douglas production functions. Our calibrated model corroborated other necessary relations. However, one assumption we had to make is that first-order effects dominate second-order effects (assumption 4 in section 2.4). Future work could investigate the sensitivity of results to this assumption, although it is less restrictive than the fairly conventional assumption of functions being additively separable in their arguments, and other (potentially stronger) assumptions are likely needed to derive unambiguous predictions from the comparative dynamic analyses.

Future work may also extend the model to incorporate the joint determination of SES and health (e.g., Chiteji, 2010; Conti et al., 2010), the evolution of child health (e.g., Case, Lubotsky and Paxson, 2002; Currie and Stabile, 2003; Heckman, 2007), and the impact of fetal and early-childhood conditions on health in adulthood (e.g., Barker et al., 1993; Case, Fertig and Paxson, 2005).³⁴ Early childhood could be included modelling the production of health by the family, similar to, e.g., Jacobson (2000) and Bolin, Jacobson and Lindgren (2001). We do not explicitly take into account the influence of the wider social context and social relationships of the family or neighborhood on health (e.g., Kawachi and Berkman, 2003), or of social capital on health (e.g., Bolin et al., 2003). Insights from the behavioural-economic and psychological literature regarding myopia and lack of self-control (e.g., Blanchflower, Oswald, and van Landeghem, 2009) might be incorporated following Laibson (1998). Uncertainty (e.g., health shocks) could be included similar to, e.g., Cropper (1977), Dardanoni and Wagstaff (1990), Liljas (1998), and Ehrlich (2000).

A First-Order Conditions

Associated with the Hamiltonian (equation 11) we have the following conditions:

$$\begin{gathered} \frac{\partial q_A(t)}{\partial t}=-\frac{\partial \mathfrak{J}}{\partial A}\Rightarrow \\ \frac{\partial q_A(t)}{\partial t}=-r{q}_A(t)\iff \\ {q}_A(t)=q_A(0)e^{-rt}, \end{gathered}$$ (43)

$$\begin{gathered} \frac{\partial q_H(t)}{\partial t}=-\frac{\partial \mathfrak{J}}{\partial H}\Rightarrow \\ \frac{\partial q_H(t)}{\partial t}=q_H(t)\frac{\partial d}{\partial H}-\frac{\partial U}{\partial H}{e}^{-\beta t}-q_A(0)\frac{\partial Y}{\partial H}{e}^{-rt}, \end{gathered}$$ (44)

$$\begin{gathered} \frac{\partial \mathfrak{J}}{\partial L}=0\Rightarrow \\ \frac{\partial U}{\partial L}=q_A(0)w(t)e^{(\beta -r)t}, \end{gathered}$$ (45)

$$\begin{gathered} \frac{\partial \mathfrak{J}}{\partial X_h}=0\Rightarrow \\ \frac{\partial U}{\partial C_h}=q_A(0)\frac{p_{X_h}}{\partial C_h/\partial X_h}{e}^{(\beta -r)t}+q_H(t)\frac{\partial d}{\partial C_h}{e}^{\beta t}, \end{gathered}$$ (46)

$$\begin{gathered} \frac{\partial \mathfrak{J}}{\partial {\tau }_{C_h}}=0\Rightarrow \\ \frac{\partial U}{\partial C_h}=q_A(0)\frac{w(t)}{\partial C_h/\partial {\tau }_{C_h}}{e}^{(\beta -r)t}+q_H(t)\frac{\partial d}{\partial C_h}{e}^{\beta t}, \end{gathered}$$ (47)

$$\begin{gathered} \frac{\partial \mathfrak{J}}{\partial X_u}=0\Rightarrow \\ \frac{\partial U}{\partial C_u}=q_A(0)\frac{p_{X_u}(t)}{\partial C_u/\partial X_u}{e}^{(\beta -r)t}+q_H(t)\frac{\partial d}{\partial C_u}{e}^{\beta t}, \end{gathered}$$ (48)

$$\begin{gathered} \frac{\partial \mathfrak{J}}{\partial {\tau }_{C_u}}=0\Rightarrow \\ \frac{\partial U}{\partial C_u}=q_A(0)\frac{w(t)}{\partial C_u/\partial {\tau }_{C_u}}{e}^{(\beta -r)t}+q_H(t)\frac{\partial d}{\partial C_u}{e}^{\beta t}, \end{gathered}$$ (49)

$$\begin{gathered} \frac{\partial \mathfrak{J}}{\partial m}=0\Rightarrow \\ {q}_H=q_A(0)\frac{p_m(t)}{\partial I/\partial m}{e}^{-rt}, \end{gathered}$$ (50)

$$\begin{gathered} \frac{\partial \mathfrak{J}}{\partial {\tau }_m}=0\Rightarrow \\ {q}_H(t)=q_A(0)\frac{w(t)}{\partial I/\partial {\tau }_m}{e}^{-rt}, \end{gathered}$$ (51)

$$\begin{gathered} \frac{\partial \mathfrak{J}}{\partial z}=0\Rightarrow \\ 0=q_H(t)\frac{\partial d}{\partial z}-q_A(0)\frac{\partial Y}{\partial z}{e}^{-rt}. \end{gathered}$$ (52)

Equation (50) and (51) provide the first-order condition for health investment (15). Equation (45) provides the first-order condition for leisure (20). Equations (46) and (47) provide the first-order condition for healthy consumption (21). Equations (48) and (49) provide the first-order condition for unhealthy consumption (24). Last, equation (52) provides the first-order condition for job-related health stress (equation 27).

B Functional Relations

From (5) and (17) we obtain

$${\pi }_I(t)=\frac{p_m(t)m(t)}{{\alpha }_{I}I[m(t),{\tau }_m(t);E]}=\frac{w(t){\tau }_m(t)}{{\beta }_{I}I[m(t),{\tau }_m(t);E]},$$ (53)

and hence

$$\frac{m(t)}{{\tau }_m(t)}=\frac{{\alpha }_{I}w(t)}{{\beta }_I{p}_m(t)}.$$ (54)

Use (54) to substitute τ_m(t) into (5) to obtain

$$I[m(t),{\tau }_m(t);E]={\mu }_I(t;E){\left[\frac{{\alpha }_{I}w(t)}{{\beta }_I{p}_m(t)}\right]}^{-{\beta }_I}m{(t)}^{{\alpha }_I+{\beta }_I},$$ (55)

and, likewise, use (54) to substitute m(t) into (5) to obtain

$$I[m(t),{\tau }_m(t);E]={\mu }_I(t;E){\left[\frac{{\alpha }_{I}w(t)}{{\beta }_I{p}_m(t)}\right]}^{{\alpha }_I}{\tau }_m{(t)}^{{\alpha }_I+{\beta }_I}.$$ (56)

Use (55) to substitute I[m(t), τ_m(t); E] into (53) to obtain (18). Likewise, use (56) to substitute I[m(t), τ_m(t); E] into (53) to obtain (19). Use (55) to substitute m(t) into (53), or alternatively, use (56) to substitute τ_m(t) into (53), to obtain

$$I[m(t),{\tau }_m(t);E]={\varphi }^{\ast }(t)q_{h/a}{(t)}^{\frac{{\alpha }_I+{\beta }_I}{1-{\alpha }_I-{\beta }_I}},$$ (57)

where we have used (15), and where

$${\varphi }^{\ast }(t)={\left[\frac{{\mu }_I(t;E){\alpha }_I^{{\alpha }_I}{\beta }_I^{{\beta }_I}}{p_m{(t)}^{{\alpha }_I}w{(t)}^{{\beta }_I}}\right]}^{\frac{1}{1-{\alpha }_I-{\beta }_I}}.$$ (58)

C Calibrated Simulations

For the calibrated simulations, we resort to discrete time. In the simplified version of our model discussed in section 3.2, individuals maximise the life-time utility function

$${\displaystyle \sum _{t=0}^{T-1}\frac{U(C_t,H_t)}{{(1+\beta )}^t}},$$ (59)

where individuals live for T (endogenous) periods, β is a subjective discount factor and individuals derive utility U(C_t, H_t) from consumption C_t and from health H_t.

The objective function (59) is maximised subject to the dynamic constraints:

$$H_{t+1}-H_t={\mu }_I{m}_t^{\alpha }-d_t^{\ast }{H}_t^v,$$ (60)

$$A_{t+1}-A_t=r{A}_t+w_t[\Omega -s_t]-p_{X_t}{X}_t-p_{m_t}{m}_t,$$ (61)

with $d_t^{\ast }=e^{a+bt}$, wages w_t are given by (38), $s_t=H_t^{-\gamma }$, and initial and end conditions: H₀, H_T, A₀ and A_T are given. Individuals live for T periods and die at the end of period T − 1. Life cannot be sustained below a minimum health level H_min, and the individual dies when H_T = H_min.

The Lagrangian of this problem is:

$${\mathfrak{J}}_t=\frac{U(C_t,H_t)}{{(1+\beta )}^t}+q_t^H[H_{t+1}-H_t]+q_t^A[A_{t+1}-A_t],t=0,\dots ,T-1,$$ (62)

where $q_t^H$ is the adjoint variable associated with the dynamic equation (60) for the state variable health H_t, and $q_t^A$ is the adjoint variable associated with the dynamic equation (61) for the state variable assets A_t.

Associated with the Lagrangian we have the following conditions:

$$\begin{gathered} q_t^A-q_{t-1}^A=-\frac{\partial {\mathfrak{J}}_t}{\partial A_t}\Rightarrow \\ {q}_{t-1}^A=(1+r)q_t^A\iff \\ {q}_t^A=\frac{q_0^A}{(1+r)t}, \end{gathered}$$ (63)

$$\begin{gathered} q_t^H-q_{t-1}^H=\frac{\partial {\mathfrak{J}}_t}{\partial H_t}\Rightarrow \\ {q}_{t-1}^H=q_t^H(1-d_t^{\ast }v{H}_t^{v-1})+\frac{\partial U/\partial H_t}{{(1+\beta )}^t}-q_t^A{w}_t\frac{\partial s}{\partial H_t} \end{gathered}$$ (64)

$$\begin{gathered} \frac{\partial {\mathfrak{J}}_t}{\partial C_t}=0\Rightarrow \\ \frac{\partial U}{\partial C_t}=q_0^A\frac{p_C}{{\mu }_C}{\left(\frac{1+\beta }{1+r}\right)}^t \end{gathered}$$ (65)

$$\begin{gathered} \frac{\partial {\mathfrak{J}}_t}{\partial m_t}=0\Rightarrow \\ {q}_t^H=q_t^A\left\{\frac{p_m}{\alpha {\mu }_I}\right\}{m}_t^{1-\alpha } \\ \equiv q_t^A{\pi }_{I_t}. \end{gathered}$$ (66)

We start with the initial condition for health, H₀. Initial consumption C₀ then follows from the first-order condition for consumption (65), which, for the assumed utility function (39) in section 3.2, can be written as

$$C_t={\left[\frac{q_0^A}{\zeta {\mu }_U}\frac{p_C}{{\mu }_C}{\left(\frac{1+\beta }{1+r}\right)}^t\right]}^{-1/\rho \chi }{H}_t^{\frac{\chi -1}{\chi }},$$ (67)

where χ ≡ (1 + ρζ − ζ)/ρ. Initial consumption C₀ is a function of initial health H₀, the utility share of consumption ζ, the price of goods and services p_C, the efficiency of the consumption production process μ_C, and the marginal value of initial wealth $q_0^A$.

Next, the initial level of health investment m₀ follows from the initial relative marginal value of health $q_0^{h/a}$ (see 66). In particular,

$$m_t={\left[q_t^{h/a}\frac{\alpha {\mu }_I}{p_m}\right]}^{\frac{1}{1-\alpha }}.$$ (68)

The initial level of health investment m₀ is a function of the price of goods and services p_m, the effectiveness and efficiency of health investment, α and μ_I, and the initial marginal value of wealth $q_0^A$ and of health $q_0^H$.

Health in the next period H₁ is determined by the dynamic equation (60). Assets in the next period A₁ follow from the initial condition for assets A₀ and the dynamic equation for assets (61).

Using the functional form for the utility function, sick time, and the deterioration rate in section 3.2, the relative marginal value of health is updated according to

$$q_{t+1}^{h/a}=\frac{1}{1-d_t^{\ast }v{H}_t^{v-1}}\left[q_t^{h/a}(1+r)-\frac{(1-\zeta ){\mu }_U}{q_0^A}{C}_t^{1-\rho \chi }{H}_t^{\rho (\chi -1)-1}{\left(\frac{1+r}{1+\beta }\right)}^t-w_t\gamma H_t^{-(1+\gamma )}\right]$$ (69)

The solutions for consumption C_t, health investment m_t, health H_t, and wealth A_t, for every period t are functions of the initial marginal values of wealth $q_0^A$ and health $q_0^H$. In the final period, the end conditions for health H_T = H_min and for assets A_T determine $q_0^A$ and $q_0^H$

We employ the downhill simplex method (Nelder and Mead, 1965) to iteratively determine the initial marginal value of wealth $q_0^A$ and of health $q_0^H$ that satisfy the end conditions A_T and H_T. We use the usual values α_NM = 1, γ_NM = 2, ρ_NM = 0.5 and σ_NM = 0.5 for the reflection, expansion, contraction and shrink coefficients, respectively. We use a period step size of one fifth of a year.

The optimal control problem presented so far is formulated for a fixed length of life T. To allow for differential longevity one needs to optimise over all possible lengths of life T. We achieve this by first solving the problem conditional on length of life T, inserting the optimal solutions $C_t^{\ast }$, $H_t^{\ast }$ into the “indirect utility function”

$$V_T\equiv {\displaystyle \sum _{t=0}^{T-1}\frac{U\left(C_t^{\ast },H_t^{\ast }\right)}{{\left(1+\beta \right)}^t}},$$ (70)

and maximizing V_T with respect to T by evaluating V_T for different values of T.³⁵

The parameters used in the calibration are presented in Table 1, and are motivated in section 3.2. The parameters to be calibrated are μ_I, μ_U, ν, the health deterioration parameters a and b, and optimal length of life T. In the calibration, to minimise the curse of dimensionality in calibrating six parameters, we first choose six values that produce a reasonable fit. We then define a six-dimensional discrete grid between 0.75 and 1.25 of the initial parameter values (i.e. 3 to 5 parameter values between 25% smaller and 25% larger than the original value).³⁶ For each value in this six-dimensional grid, we compute the sum of the absolute deviation between the simulated moments and the data moments consisting of the 5-year averages of health and health investment shown in Figure 1, where the deviations are scaled by the value of each observed moment so that the deviations from health and health investment receive equal weight. The parameter values that jointly produce the lowest deviation are presented in Table 1, and the corresponding life-cycle profiles for health and health investment are shown in Figure 1.

Next we use our calibrated simulations to perform several counterfactual experiments regarding the signs of ∂q_A(0)/∂x, and ∂q_h/a(0)/∂x for x = A₀, w, E, H₀, where we increase x by a small amount and observe the change in the optimal co-state variable. The resulting signs are presented in Table 2. All relations are valid for fixed T and free T. To get a feel for the magnitude of these effects in the calibrated model, we also compute elasticities. However, since A₀ is zero at baseline, it is not possible to compute an elasticity for A₀. For the remaining initial conditions, we compute elasticities by increasing the value of the relevant initial condition by 1%. Increasing wages by 1%, the observed elasticity for q_A(0) is −1.82, and the elasticity for q_h/a(0) is 0.45. For education, it is not straightforward to compute elasticities, since education influences both wages and the efficiency of health investment. First, we solely increase the efficiency of health investment μ_I by 1%, and obtain very small elasticities of 0.005 and −0.005 for q_A(0) and q_h/a(0), respectively. When we make the restrictive assumption that a 1% increase in education increases both wages as well as the efficiency of health investment by 1%, the resulting elasticities are −2.18 and 0.13 for q_A(0) and q_h/a(0) respectively. Finally, the elasticity with respect to initial health H₀ of q_A(0) is −0.91 and of q_h/a(0) is −0.44. Reassuringly (not shown in the Table), we also find ∂H(t)/∂x > 0, and ∂T/∂x > 0 for all parameters x = A₀, w_E, E, and H₀.

Table 1.

Parameter Values for the Calibrated Simulations

Parameter	Description	Value
Parameters taken from the literature
α	Effectiveness of health investment	0.75
r	Interest rate	0.03
β	Time preference rate	0.03
γ	Power law relation sick time and health	1.7
ρ	Coefficient of relative risk aversion	3
ζ	Utility share of consumption vs health	0.7
μC	Efficiency of consumption	1
pm	Price of medical care	1
pc	Price of consumption	1
A0, AT	Assets	0
Calibrated parameters
μI	Efficiency of health investment	0.25
μU	Scale parameter utility	0.00001
ν	Dependency of depreciation on health	0.3
a	Deterioration rate intercept	−3.6
b	Deterioration rate slope	1/17 ≈ 0.059
T	Length of life	76.8

Table 2.

Sign of the Effect on Co-states q_A(0) and q_h/a(0) of Perturbations in Initial Conditions

Initial condition x	∂qA(0)/∂x	∂qh/a(0)/∂x
A0	−	+
wE	−	+
E	−	+
H0	−	−

Note: All signs are valid for both fixed T and free T.

D Proofs of Propositions

D.1 Proof of Proposition 1

Absent ability to extend life, wealthy individuals, ceteris paribus, value health only marginally more than less wealthy individuals.

The dynamic equation for the relative marginal value of health is given by (37). The dynamic equation for health can be rewritten (see 57) as

$$\begin{gathered} \frac{\partial H(t)}{\partial t}=I\left[m(t),{\tau }_m(t);E\right]-d(t) \\ ={\varphi }^{\ast }(t)q_{h/a}{(t)}^{\frac{{\alpha }_I+{\beta }_I}{1-{\alpha }_I-{\beta }_I}}-d(t). \end{gathered}$$ (71)

The comparative dynamic effect of initial wealth on the relative marginal value of health, keeping length of life T fixed, is obtained by taking the derivate of (37) with respect to intial wealth A₀

$$\begin{gathered} \frac{\partial }{\partial t}{\frac{\partial q_{h/a}(t)}{\partial A_0}|}_T=\left[\frac{1}{q_A{(0)}^2}\frac{\partial U}{\partial H}{e}^{-(\beta -r)t}\right]\times {\frac{\partial q_A(0)}{\partial A_0}|}_T \\ +\left[\frac{\partial d}{\partial H}+r\right]\times {\frac{\partial q_{h/a}(t)}{\partial A_0}|}_T \\ +\left[q_{h/a}(t)\frac{{\partial }^{2}d}{\partial C_h\partial H}-\frac{1}{q_A(0)}\frac{{\partial }^{2}d}{\partial C_h\partial H}{e}^{-(\beta -r)t}\right]\times {\frac{\partial C_h(t)}{\partial A_0}|}_T \\ +\left[q_{h/a}(t)\frac{{\partial }^{2}d}{\partial C_u\partial H}-\frac{1}{q_A(0)}\frac{{\partial }^{2}d}{\partial C_u\partial H}{e}^{-(\beta -r)t}\right]\times {\frac{\partial C_u(t)}{\partial A_0}|}_T \\ -\left[\frac{1}{q_A(0)}\frac{{\partial }^{2}U}{\partial L\partial H}{e}^{-(\beta -r)t}\right]\times {\frac{\partial L(t)}{\partial A_0}|}_T \\ +\left[q_{h/a}(t)\frac{{\partial }^{2}d}{\partial z\partial H}-\frac{{\partial }^{2}Y}{\partial z\partial H}\right]\times {\frac{\partial z(t)}{\partial A_0}|}_T \\ -\left[\frac{1}{q_A(0)}\frac{{\partial }^{2}U}{\partial H^2}{e}^{-(\beta -r)t}+\frac{{\partial }^{2}Y}{\partial H^2}-q_{h/a}(t)\frac{{\partial }^{2}d}{\partial H^2}\right]\times {\frac{\partial H(t)}{\partial A_0}|}_T. \end{gathered}$$ (72)

Likewise, for the health stock, the comparative dynamic effect of A₀, keeping length of life T fixed, is obtained by taking the derivative of equation (71) with respect to A₀

$$\begin{gathered} \frac{\partial }{\partial t}{\frac{\partial H(t)}{\partial A_0}|}_T=\left[\frac{{\alpha }_I+{\beta }_I}{1-{\alpha }_I-{\beta }_I}\frac{I\left[m(t),{\tau }_m(t);E\right]}{q_{h/a}(t)}\right]\times {\frac{\partial q_{h/a}(t)}{\partial A_0}|}_T \\ -\left[\frac{\partial d}{\partial C_h}\right]\times {\frac{\partial C_h(t)}{\partial A_0}|}_T \\ -\left[\frac{\partial d}{\partial C_u}\right]\times {\frac{\partial C_u(t)}{\partial A_0}|}_T \\ -\left[\frac{{\gamma }_w(1-{\kappa }_I)}{1-{\alpha }_I-{\beta }_I}\frac{I\left[m(t),{\tau }_m(t);E\right]}{1+z(t)}+\frac{\partial d}{\partial z}\right]\times {\frac{\partial z(t)}{\partial A_0}|}_T \\ -\left[\frac{\partial d}{\partial H}\right]\times {\frac{\partial H(t)}{\partial A_0}|}_T. \end{gathered}$$ (73)

One can develop similar relations for the comparative dynamic effect of initial wealth on the controls: L(t), C_h(t), C_u(t), and z(t) (see section D.8). These too are expressed in terms of variation in controls, in health, in the marginal value of initial wealth and in the relative marginal value of health.

Pontryagin’s maximum principle (e.g., Caputo 2005) informs us that the solution of the optimal control problem is no longer a function of the controls and can be fully expressed in the state and co-state functions. Indeed, one can substitute the expressions for variation in the control variables, ${\partial L\left(t\right)/\partial A_0|}_T$, $\partial C_h(t)/\partial A_0{|}_T$, $\partial C_u(t)/\partial A_0{|}_T$, and $\partial z(t)/\partial A_0{|}_T$, into one another such that the final result (not shown) are comparative dynamic expressions in terms of the variation in state and co-state functions but no longer contain variation in control functions. These expressions however are unwieldy with a cumbersome mix of opposite-sign coefficients from which it is hard to draw firm conclusions. Therefore, we assume that first-order (direct) effects dominate higher-order (indirect) effects (assumption 4 in section 2.4).

As an example, wealth affects the rate of change of variation in the relative marginal value of health $(\partial /\partial t)({\partial q_{h/a}(t)/\partial A_0|}_T)$ directly (first term on the right-hand side [RHS] of 72), but also indirectly through, for example, the effect that wealth has on healthy consumption, and healthy consumption in turn has on $(\partial /\partial t)({\partial q_{h/a}(t)/\partial A_0|}_T)$ (third term on the RHS of 72). The comparative dynamic effect of wealth on healthy consumption is given by (94). Combining (94) with (72), we obtain the combined wealth effect

$$\left[\frac{1}{q_A{(0)}^2}\frac{\partial U}{\partial H}{e}^{-(\beta -r)t}\right]\left[1+\frac{\frac{1}{q_A{(0)}^2}\frac{\partial U}{\partial C_h}}{\frac{1}{q_A(0)}\frac{{\partial }^{2}U}{\partial C_h^2}-q_{h/a}(t)\frac{{\partial }^{2}U}{\partial C_h^2}{e}^{-(\beta -r)t}}\right]\times {\frac{\partial q_A(0)}{\partial A_0}|}_T,$$

where the first term, 1, in the large term in brackets represents the first-order (direct) effect of wealth, and the second term represents the second-order (indirect) effect operating through healthy consumption. The assumption is that the direct effect of wealth dominates any indirect wealth effect that operates through healthy consumption or through any other control variable. This simplifies the expressions considerably. We have:

$$\begin{gathered} \frac{\partial }{\partial t}{\frac{\partial q_{h/a}(t)}{\partial A_0}|}_T\approx \left[\frac{1}{q_A{(0)}^2}\frac{\partial U}{\partial H}{e}^{-(\beta -r)t}\right]\times {\frac{\partial q_A(0)}{\partial A_0}|}_T \\ +\left[\frac{\partial d}{\partial H}+r\right]\times {\frac{\partial q_{h/a}(t)}{\partial A_0}|}_T \\ -\left[\frac{1}{q_A(0)}\frac{{\partial }^{2}U}{\partial H^2}{e}^{-(\beta -r)t}+\frac{{\partial }^{2}Y}{\partial H^2}-q_{h/a}(t)\frac{{\partial }^{2}d}{\partial H^2}\right]\times {\frac{\partial H(t)}{\partial A_0}|}_T, \end{gathered}$$ (74)

and

$$\frac{\partial }{\partial t}{\frac{\partial H(t)}{\partial A_0}|}_T\approx \left[\frac{{\alpha }_I+{\beta }_I}{1-{\alpha }_I-{\beta }_I}\frac{I\left[m(t),{\tau }_m(t);E\right]}{q_{h/a}(t)}\right]\times {\frac{\partial q_{h/a}(t)}{\partial A_0}|}_T-\frac{\partial d(t)}{\partial H(t)}\times {\frac{\partial H(t)}{\partial A_0}|}_T.$$ (75)

Figure 4 shows the phase diagram for the motion paths of the variation of the relative marginal value of health with respect to initial wealth ${\partial q_{h/a}(t)/\partial A_0|}_T$ (y-axis) versus the variation of health with respect to initial wealth ${\partial H(t)/\partial A_0|}_T$ (x-axis). Conditional on our assumptions in section 3.4 and the signs for relations (a), (b), and (c) obtained from the calibrated model, we obtain a two-dimensional phase diagram. The boundaries between regimes, the so-called null-clines, are shown by the thick lines in the figure and are obtained by setting the derivatives $(\partial /\partial t){(\partial q_{h/a}(t)/\partial A_0)|}_T$ and $(\partial /\partial t){(\partial H(t)/\partial A_0)|}_T$ to zero. While the null-clines may vary over time, the properties of the comparative dynamic phase diagrams do not change: the null-cline (∂/∂t)(∂H/∂A₀) will always slope upward and cross the origin, and the null-cline (∂/∂t)(∂q_h/a/∂A₀) will always slope downward and cross the y-axis above the origin. Hence, the “steady state” is always above and to the right of the origin. Note that the unperturbed path corresponds with the origin (where variations are equal to zero at all ages). The phase diagram allows us to explore how changes in model parameters dynamically shift the optimal path with respect to the unperturbed life-cycle trajectory (represented by the origin).

We know the signs of most of the coefficients in (74) and (75), for example ∂²U/∂H² < 0, ∂²Y/∂H² < 0 (assumption 1). However, two relationships are a priori unknown: ${\partial q_A(0)/\partial A_0|}_T$ and ∂d/∂H. We proceed as follows. We obtain our preferred sign for these relationships from the calibrated simulations in section 3.2. We estimated the parameter ν in equation (40) at 0.3, which implies ∂d/∂H > 0. Further, we varied initial wealth by a small amount δA₀ to obtain the sign of the change in the marginal value of initial wealth in response to variation in initial wealth for fixed T and find that ${\partial q_A(0)/\partial A_0|}_T<0$ (see Table 2 in Appendix C). These coefficients, based on the calibrated model, represent our benchmark case in the comparative dynamics below. Next, we investigate the robustness of these results to the opposite sign of these two relationships. We find the results to be robust.

Benchmark case

With all coefficients known, we can predict the sign of $(\partial /\partial t){(\partial q_{h/a}(t)/\partial A_0)|}_T$ and $(\partial /\partial t){(\partial H(t)/\partial A_0)|}_T$ in the four dynamic regions of the phase diagram, defined by the null-clines. The block arrows indicate the direction of motion in each of the four dynamic regions and the dotted lines provide example trajectories.³⁷

Since both initial health H(0) = H₀ and end-of-life health H(T) = H_min are fixed, it follows that ${\partial H(0)/\partial A_0|}_T={\partial H(T)/\partial A_0|}_T=0$. Thus, in the phase diagram all admissible paths start and end at the vertical axis.

Consider a path that starts at the vertical axis, but below the horizontal axis $(\text{corresponding to}{\partial q_{h/a}(0)/\partial A_0|}_T)$. Such a path will move toward the South-West, and stay there indefinitely, as illustrated by the dotted line (c). Similarly, a path starting at the vertical axis, but above the $(\partial /\partial t){(\partial q_{h/a}(t)/\partial A_0)|}_T$ null-cline, will move toward the North-East and stay there indefinitely, never returning to the vertical axis in finite time, as illustrated by trajectory (a).

Now consider a path starting at the vertical axis, between the $(\partial /\partial t){(\partial q_{h/a}(t)/\partial A_0)|}_T=0$ null-cline and the origin. This path is associated with ${\partial q_{h/a}(0)/\partial A_0|}_T>0$, and returns to the vertical axis in finite time if it crosses the horizontal axis and enters dynamic region IV at some point over the life cycle. This path satisfies all conditions, and an example trajectory (b) is shown for illustrative purposes.³⁸

We conclude from this (see trajectory b) that wealth increases the relative marginal value of health ${\partial q_{h/a}(t)/\partial A_0|}_T>0$ initially, but decreases it ${\partial q_{h/a}(t)/\partial A_0|}_T<0$ eventually. In a model with a fixed life span T, health is higher at all ages, ${\partial H(t)/\partial A_0|}_T>0$ ∀t (trajectory a lies to the right of the vertical axis), except for t = 0 and t = T. Q.E.D.

Figure 4.

Phase diagram of the deviation from the unperturbed path, resulting from variation in initial wealth δA₀, of the relative marginal value of health ${\partial q_{h/a}(t)/\partial A_0|}_T$ and of the health stock ${\partial H(t)/\partial A_0|}_T$, for fixed T.

Sensitivity to the sign of ∂d/∂H

Consider the case where ∂d/∂H < 0, consistent with the health-deficit approach of Dalgaard and Strulik (2014). Further, r + ∂d/∂H > 0, since a negative sign would necessarily imply an ever decreasing relative marginal value of health and therefore ever decreasing health investment over the life cycle (see equation 37). This is inconsistent with empirical evidence and with our calibrated simulations. The null-cline for (∂/∂t)(∂q_h/a/∂A₀) still slopes downward, but the null-cline for (∂/∂t)(∂H/∂A₀) now also slopes downward. Depending on which slope is steeper we have two scenarios, as shown in Figure 5. Recall that for fixed T all trajectories start and end at the vertical axis, since initial and terminal health are fixed, and so ${\partial H(0)/\partial A_0|}_T={\partial H(T)/\partial A_0|}_T=0$. In both figures the only feasible trajectory b is identical to the case where ∂d/∂H > 0. That is, ∂q_h/a(0)/∂A₀ > 0 and ∂q_h/a(T)/∂A₀ < 0, and ∂H(t)/∂A₀ ≥ 0 for 0 < t < T. Therefore, reassuringly, our main predictions regarding the effect of wealth on health investment and health are insensitive to the sign of ∂d/∂H.

Sensitivity to the sign of ${\partial q_A(0)/\partial A_0|}_T$

Figure 6 shows the phase diagram for the case where ${\partial q_A(0)/\partial A_0|}_T>0$.

Here, once more trajectory b is the only path that satisfies all conditions. However, in this case, health is lower at all ages ${\partial H(t)/\partial A_0|}_T<0$ ∀t, except for t = 0 and t = T. Moreover, the path is associated with ${\partial q_{h/a}(t)/\partial A_0|}_T>0$, which implies that length of life is reduced (as we explore in the next section D.2). Finally, (healthy) consumption is reduced (see equation 94). Hence, for ${\partial q_A(0)/\partial A_0|}_T>0$ the model predicts that increases in wealth lead to worse health, less consumption, and a shorter life, which is inconsistent with optimizing behaviour (see Ehrlich and Chuma, 1990, for a similar argument), with our calibrated model and with empirical stylised facts. Therefore, we dismiss the case where ${\partial q_A(0)/\partial A_0|}_T>0$.

Figure 5.

Phase diagram of the deviation from the unperturbed path, resulting from variation in initial wealth δA₀, of the relative marginal value of health ${\partial q_{h/a}(t)/\partial A_0|}_T$ and of the health stock ${\partial H(t)/\partial A_0|}_T$, for fixed T. The left panel represents the situation where the ${(\partial /\partial t)[\partial H(t)/\partial A_0|}_T$ nullcline is steeper than the ${(\partial /\partial t)[\partial q_{h/a}(t)/\partial A_0|}_T$ nullcline and the right panel represents the opposite case.

D.2 Proof of Proposition 2: Wealthy individuals live longer: ∂T/∂A₀ > 0

Taking into account that in the optimum the condition $\mathfrak{J}(T)=0$ has to be satisfied (see 14), we have

$${\frac{\partial \mathfrak{J}(T)}{\partial A_0}|}_T+{\frac{\partial \mathfrak{J}(T)}{\partial T}|}_{A_0}\frac{\partial T}{\partial A_0}=0,$$ (76)

where ${\partial g(t)/\partial A_0|}_T$ denotes variation in an endogenous function g(t) with respect to initial wealth A₀, keeping length of life T fixed, and ${\partial g(t)/\partial T|}_{A_0}$ denotes variation in an endogenous function g(t) with respect to T, keeping A₀ fixed $\left(\text{in this case the notation is used for}\mathfrak{J}\left(T\right)\right).$

The change in life expectancy due to an increase in initial wealth ∂T/∂A₀ can then be identified from the identity

$$\frac{\partial T}{\partial A_0}=-\frac{{\frac{\partial \mathfrak{J}(T)}{\partial A_0}|}_T}{{\frac{\partial \mathfrak{J}(T)}{\partial T}|}_T}.$$ (77)

Using the expression for the Hamiltonian (11) we obtain

$$\begin{gathered} {\frac{\partial \mathfrak{J}(T)}{\partial A_0}|}_T=\frac{\partial \mathfrak{J}(T)}{\partial ℂ(T)}{\frac{\partial ℂ(T)}{\partial A_0}|}_T+\frac{\partial \mathfrak{J}(T)}{\partial A(T)}{\frac{\partial A(T)}{\partial A_0}|}_T+\frac{\partial \mathfrak{J}(T)}{\partial H(T)}{\frac{\partial H(T)}{\partial A_0}|}_T \\ +\frac{\partial \mathfrak{J}(T)}{\partial q_A(T)}{\frac{\partial q_A(T)}{\partial A_0}|}_T+\frac{\partial \mathfrak{J}(T)}{\partial q_H(T)}{\frac{\partial q_H(T)}{\partial A_0}|}_T \\ ={\frac{\partial q_A(T)}{\partial A_0}|}_T{\frac{\partial A(t)}{\partial t}|}_{t=T}+{\frac{\partial q_H(T)}{\partial A_0}|}_T{\frac{\partial H(t)}{\partial t}|}_{t=T} \\ ={\frac{\partial q_A(0)}{\partial A_0}|}_T{e}^{-rT}{\frac{\partial A(t)}{\partial t}|}_{t=T} \\ +\left\{{\frac{\partial q_A(0)}{\partial A_0}|}_T{e}^{-rT}{q}_{h/a}(T)+q_A(0)e^{-rT}{\frac{\partial q_{h/a}(T)}{\partial A_0}|}_T\right\}{\frac{\partial H(t)}{\partial t}|}_{t=T}. \end{gathered}$$ (78)

where ℂ(t) denotes the vector of control variables, ℂ(t) = [C_h(t), C_u(t), L(t), m(t), τ_m(t), z(t)]. In the derivations we have used $\partial \mathfrak{J}(T)/\partial \mathrm{ℂ}(T)=0$, which follows from the first-order conditions, and ${\partial A(T)/\partial A_0|}_T={\partial H(T)/\partial A_0|}_T=0$, since A(T) and H(T) are fixed.

Note that we distinguish in notation between ${\partial g(t)/\partial t|}_{t=T}$, which represents the derivative with respect to time t at time t = T, and ${\partial g(t)/\partial T|}_{t=T}$, which represents variation with respect to the parameter T at time t = T.

Using (77) and (78), and assuming diminishing returns to life extension ${\partial \mathfrak{J}(T)/\partial (T)|}_{A_0}<0$ (cf. assumption 1 in section 2.4), wealth increases longevity ∂T/∂A₀ > 0 if ${\partial \mathfrak{J}(T)/\partial A_0|}_T<0$. In (78), both ${\partial A(t)/\partial t|}_{t=T}$ and ${\partial H(t)/\partial t|}_{t=T}$ are negative since health declines near the end of life as it approaches H_min from above, and assets decline near the end of life in absence of a strong bequest motive. For diminishing returns to wealth ${\partial q_A(0)/\partial A_0|}_T<0$ (see the proof of proposition 1 in section D.1), a sufficient requirement for length of life to increase in response to positive variation in wealth is ${\partial q_{h/a}(T)/\partial A_0|}_T\le 0$. As one can see from Figure 4, indeed ${\partial q_{h/a}(T)/\partial A_0|}_T\le 0$, and thus ∂T/∂A₀ > 0. Q.E.D.

Figure 6.

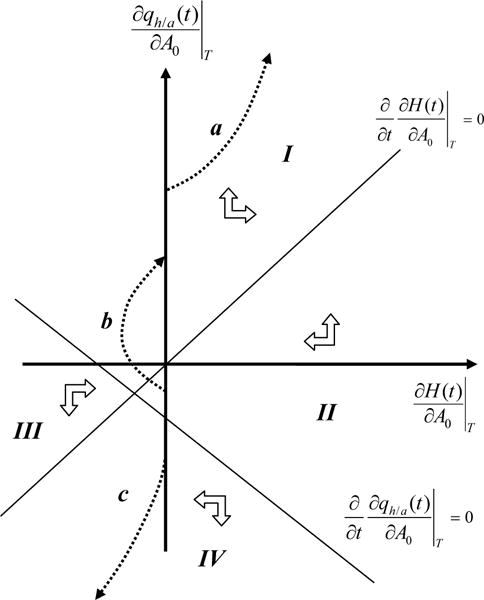
Phase diagram of the deviation from the unperturbed path, resulting from variation in initial wealth δA₀, of the relative marginal value of health ${\partial q_{h/a}(t)/\partial A_0|}_T$ and of the health stock ${\partial H(t)/\partial A_0|}_T$, for fixed T with ${\partial q_A(0)/\partial A_0>0|}_T$.

D.3 Proof of Proposition 3

Wealthy individuals value health more and are healthier at all ages. The more life can be extended, the stronger is the increase in the value of health in response to additional wealth.

In the previous section D.2, we showed that wealthy individuals live longer. We are now interested in understanding the full comparative dynamic response of the relative marginal value of health q_h/a(t) and the health stock H(t) to an increase in initial wealth, employing the full model with optimally chosen T. The total differentials

$$\frac{\partial q_{h/a}(t)}{\partial A_0}={\frac{\partial q_{h/a}(t)}{\partial A_0}|}_T+{\frac{\partial q_{h/a}(t)}{\partial T}|}_{A_0}\frac{\partial T}{\partial A_0},$$ (79)

$$\frac{\partial H(t)}{\partial A_0}={\frac{\partial H(t)}{\partial A_0}|}_T+{\frac{\partial H(t)}{\partial T}|}_{A_0}\frac{\partial T}{\partial A_0},$$ (80)

consist of the effect of variation in wealth keeping T fixed (first term on the RHS in 79 and in 80), which we explored in section D.1, and the effect that operates through responses in the optimal length of life T, keeping initial wealth A₀ fixed (second term on the RHS in 79 and in 80).

The coefficients in the comparative dynamic expressions for the response in the relative marginal value of health and the health stock to variation in length of life T, holding initial wealth A₀ constant, are identical to the coefficients derived for the response to variation in initial wealth A₀, holding length of life T fixed, shown in (74) and (75). That is, we simply have to replace the partial differentials with their total differentials, i.e. ${\partial q_A(0)/\partial A_0|}_T$with ∂q_A(0)/∂T, ${\partial q_{h/a}(t)/\partial A_0|}_T$ with ∂q_h/a(t)/∂T, and ${\partial H(t)/\partial A_0|}_T$ with ∂H(t)/∂T, in (74) and (75) to obtain the total comparative dynamic effect.

There is, however, one important difference compared to the previous case in which we explored variation with respect to A₀ for fixed T: the terminal value of the variation in health with respect to T, for fixed A₀, is positive, ${\partial H(t)/\partial T|}_{A_0,t=T}>0$. Thus the total differential with respect to wealth A₀ is too, ∂H(T)/∂A₀ > 0, implying that all admissible paths end to the right of the vertical axis in the phase diagram (and not on the vertical axis as is the case for fixed T in section D.1). This can be seen as follows. First, solve the state equation for health (4):

$$H(t)=H(0)+{\displaystyle {\int }_0^t[f(s)-d(s)]ds.}$$ (81)

Then take the derivative of (81) with respect to T to obtain

$${\frac{\partial H(t)}{\partial T}|}_{A_0}={\displaystyle {\int }_0^t\left\{{\frac{\partial I(s)}{\partial T}|}_{A_0}-{\frac{\partial d(s)}{\partial T}|}_{A_0}\right\}}ds.$$ (82)

Now take the derivative of (81) with respect to T for t = T

$$\begin{gathered} {\frac{\partial H(T)}{\partial T}|}_{A_0}={\frac{\partial H_{min}}{\partial T}|}_{A_0}=0 \\ =I[m(T),{\tau }_m(T);E]-d(T)+{\frac{\partial H(t)}{\partial T}|}_{A_0,t=T} \\ ={\frac{\partial H(t)}{\partial t}|}_{A_0,t=T}+{\frac{\partial H(t)}{\partial T}|}_{A_0,t=T}, \end{gathered}$$ (83)

The derivative of health with respect to time at t = T is negative since we approach H_min from above. Thus we have

$${\frac{\partial H}{\partial T}|}_{A_0,t=T}=-{\frac{\partial H(t)}{\partial t}|}_{A_0,t=T}>0.$$

Intuitively, if length of life is extended to T + δT the health stock has to be higher at the previous point of death T, and it is higher by exactly the change in health over a small period of time. Thus, $\partial H(T)/\partial A_0={\partial H(T)/\partial A_0|}_T+({\partial H(t)/\partial T|}_{A_0,t=T})(\partial T/\partial A_0)=({\partial H(t)/\partial T|}_{A_0,t=T})(\partial T/\partial A_0)>0$.

Figure 7 presents the comparative dynamic results. The initial condition ∂H(0)/∂A₀ = 0, implies that all admissible paths start on the vertical axis, and the end-condition ∂H(T)/∂A₀ > 0, implies that all admissible paths end to the right of the vertical axis, at ∂H(T)/∂A₀ (indicated by the four dotted vertical lines in the figure). As the phase diagram shows, trajectories a, b, c and d, corresponding to four different levels of ∂H(T)/∂A₀, are feasible. This implies that ∂H(t)/∂A₀ > 0 ∀t (except for t = 0), ∂q_h/a(t)/∂A₀ > 0 initially, and while potentially the relative marginal value is lower ∂q_h/a(t)/∂A₀ < 0 after some t = t^† (as for trajectory d, but not for a, b or c), cumulatively it is higher ${\displaystyle {\int }_0^T[\partial q_{h/a}(t)/\partial A_0]}dt>0$, which proves the first part op proposition 3.

Consider equation (80) for t = T. In proposition 1, section D.1, we established that for fixed T, ${\partial H(T)/\partial A_0|}_T=0$. Thus the value of the total differential ∂H(T)/∂A₀ is determined by the second term on the RHS of (80). Since ${\partial H(T)/\partial T|}_{A_0,t=T}={-\partial H(t)/\partial t|}_{A_0,t=T}=-\{I[m(t),{\tau }_m(t);E-d(T)]\}$ (compare with 83), it is the same for all four scenarios as it re presents the negative of the derivate with respect to time t at t = T of the unperturbed (unchanged) path. Thus the end point ∂H(T)/∂A₀ is proportional to the degree of life extension afforded by additional wealth ∂T/∂A₀: it thus lies further to the right in the phase diagram (vertical dotted lines) for greater ∂T/∂A₀.

In scenario d (see Figure 7), if life extension due to additional wealth is small, wealthier individuals will value health more cumulatively, but not necessarily at all times, the relative marginal value of health increases less rapidly over the life cycle, compared to the unperturbed path (less steep increase), and the trajectory eventually crosses the unperturbed path. Moving from scenario d to c to b and finally to a, the marginal value of health increases progressively and so does life extension. This proves the second part of proposition 3. In all four scenarios individuals value health more cumulatively ${\displaystyle {\int }_0^T[\partial q_{h/a}(t)/\partial A_0]}dt>0$ but they may value health less at certain ages (for example in scenario d individuals value health less late in life, compared to the unperturbed path). Q.E.D.

Figure 7.

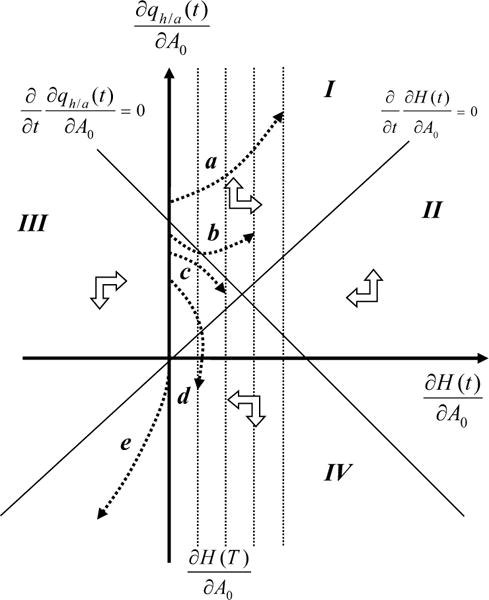
Phase diagram of the deviation from the unperturbed path, resulting from variation in initial wealth δA₀, of the relative marginal value of health ∂q_h/a(t)/∂A₀ and of the health stock ∂H(t)/∂A₀, allowing length of life T to be optimally chosen. The four vertical dotted lines represent different potential values for the end point ∂H(T)/∂A₀.

D.4 Proof of Proposition 4

Permanently higher wages and education operate in a similar manner to an increase in wealth δA₀ (propositions 1 through 3), with some differences: (i) the wealth effect is muted by the increased opportunity cost of time, (ii) permanent wages w_E and education E also raise the production benefit of health, and (iii) education raises the efficiency of health investment.

Permanent wages w_E

The comparative dynamic effect of a permanent increase in the wage rate w(t), through, e.g., an increase in the parameter w_E in (10), on the relative marginal value of health q_h/a(t) can be obtained by taking the derivate of (37) with respect to w_E and keeping first-order terms (total differentials, free T):

$$\begin{gathered} \frac{\partial }{\partial t}\frac{\partial q_{h/a}(t)}{\partial w_E}\approx \frac{w_{\ast }(t)}{w_E}{[1+z(t)]}^{{\gamma }_w}\frac{\partial s}{\partial H} \\ +\left[\frac{1}{q_A{(0)}^2}\frac{\partial U}{\partial H}{e}^{-(\beta -r)t}\right]\times \frac{\partial q_A(0)}{\partial w_E} \\ +\left[\frac{\partial d}{\partial H}+r\right]\times \frac{\partial q_{h/a}(t)}{\partial w_E} \\ -\left[\frac{1}{q_A(0)}\frac{{\partial }^{2}U}{\partial H^2}{e}^{-(\beta -r)t}+\frac{{\partial }^{2}Y}{\partial H^2}-q_{h/a}(t)\frac{{\partial }^{2}d}{\partial H^2}\right]\times \frac{\partial H(t)}{\partial w_E}. \end{gathered}$$ (84)

The first term on the RHS of (84) represents a wealth effect. Permanently higher wages raise the production benefit of health, as health is more valuable in reducing sick time (freeing time for work) when wages are higher. In addition there is the usual wealth effect (second term on the RHS). Both wealth terms are negative since sick time decreases with health ∂s/∂H < 0, and ${\partial q_A(0)/\partial w_E|}_T<0$ because w_E raises lifetime earnings (permanent income) and relaxes the budget constraint (7), see also Table 2 in section C. Variation in permanent wages δw_E is thus distinct from variation in wealth δA₀ in that it not only raises the consumption benefit of health (as is the case for variation in δA₀) but also the production benefit of health (which is not the case for variation in δA₀).

Likewise, the comparative dynamic effect of a permanent increase in the wage rate on health H(t) is obtained by taking the derivative of (71) with respect to w_E and keeping first-order terms:

$$\begin{gathered} \frac{\partial }{\partial t}\frac{\partial H(t)}{\partial w_E}\approx -\frac{{\alpha }_I+{\beta }_I}{1-{\alpha }_I-{\beta }_I}\frac{(1-{\kappa }_I)}{w_E(t)}I[m(t),{\tau }_m(t);E] \\ +\left[\frac{{\alpha }_I+{\beta }_I}{1-{\alpha }_I-{\beta }_I}\frac{I[m(t),{\tau }_m(t);E]}{q_{h/a}(t)}\right]\times \frac{\partial q_{h/a}(t)}{\partial w_E} \\ -\frac{\partial d}{\partial H}\times \frac{\partial H}{\partial w_E}, \end{gathered}$$ (85)

where the first term on the RHS of equation (85) represents the negative effect of the opportunity cost of time on health investment, and in turn on health.

The corresponding phase diagram is shown in Figure 8. It is nearly identical to the phase diagram for variation in initial wealth δA₀ (Figure 7), except that the (∂/∂t)(∂H(t)/∂w_E) null cline crosses the vertical ∂q_h/a(t)/∂w_E axis at q_h/a(t)(1 −κ_I)/w_E and not at the origin. This term represents the effect of a permanent increase in wages w_E on the opportunity cost of investing time in health. The (∂/∂t)(∂q_h/a(t)/∂w_E) null cline crosses the vertical ∂q_h/a(t)/∂w_E axis at $(-{\partial }_s/\partial H)(w_{\ast }(t)/w_E){[1+z(t)]}^{{\gamma }_w}/[\partial d/\partial H+r]-[q_A{(0)}^{-2}\partial U/\partial H{e}^{-(\beta -r)t}]\partial q_A(0)/\partial w_E$. This expression represents a wealth, or permanent income, effect: permanently higher wages increase the production benefit of health (first term) and increases wealth, thereby raising the consumption benefit of health (second term; operating through ∂q_A(0)/∂w_E < 0). In the scenario depicted in Figure 8, it is assumed that the opportunity cost of time effect is small compared to the wealth / permanent income effect.

Following similar steps as in sections D.1 and D.3 for variation in wealth, we first need to establish whether length of life is extended as a result of a permanent increase in income. This can be accomplished by considering the fixed T case. The comparative dynamic effect of a permanent increase in the wage rate w_E on longevity can be obtained by replacing A₀ with w_E in (76), (77), and (78). Since ${\partial q_A(0)/\partial w_E|}_T<0$ (see Table 2 in section C), it follows that, similar to the case for variation in initial wealth δA₀ (see section D.2), a sufficient condition for life extension in response to positive variation in permanent wages is ${\partial q_{h/a}(T)/\partial w_E|}_T\le 0$.

For fixed T all admissible paths in the phase diagram have to start and end at the vertical axis, since H(0) and H(T) are fixed. Trajectory e in the phase diagram of Figure 8 is consistent with these conditions and the trajectory is characterised by ${\partial q_{h/a}(T)/\partial w_E|}_T<0$. Thus length of life is extended ∂T/∂w_E > 0.

Considering the T free case, the reasoning is identical to the discussions for propositions 3 and 4 in sections D.2 and D.3. Following the logic outlined there, we find that trajectories a, b, c, and d are consistent with life extension. The greater life is extended as a result of greater permanent income, the further to the right is the trajectory’s end point ∂H(T)/∂w_E. Example trajectory a is associated with a large increase in the marginal value of health ∂q_h/a(t)/∂w_E and in health ∂H(t)/∂w_E, compared to the unperturbed trajectory, and this trajectory is associated with the greatest gain in longevity ∂T/∂w_E. Trajectory b and c represent an intermediary case and trajectory d a case of limited response, the latter most closely resembles the fixed T case, represented by trajectory e. Trajectory f is incompatible with live extension and ruled out. Q.E.D.

These results rely on our assumption that the opportunity cost effect is smaller than the wealth / permanent income effect. If, however, the opportunity cost effect is substantial, the ∂H(t)/∂w_E null cline is shifted further upward in the phase diagram of Figure 8 than shown. A trajectory similar to e might then end up above the ∂H(t)/∂w_E axis with a positive end value of ${\partial q_{h/a}(T)/\partial w_E|}_T$, in which case we cannot unambiguously establish that length of life increases.³⁹

If the opportunity cost is very high, outweighing the wealth / permanent income effect, the ∂H(t)/∂w_E null cline could even cross the vertical ∂q_h/a(t)/∂w_E axis above the location where the ∂q_h/a(t)/∂w_E null cline crosses the vertical ∂q_h/a(t)/∂w_E axis. In such a scenario (not shown), for fixed T, any admissible trajectory is characterised by ${\partial q_{h/a}(T)/\partial w_E|}_T>0$, and we cannot unambiguously establish that length of life increases. While theoretically we cannot rule out the scenario where the opportunity cost effect outweighs the wealth effect, empirical evidence suggests that a permanent wage change affects health positively, while a transitory wage increase affects health negatively (e.g., Contoyannis, Jones and Rice 2004), and that high-income individuals are generally in better health than low-income individuals. Thus, in practice it appears the opportunity cost effect is not large.

Education E

The comparative dynamic effect of an increase in education E (see 9 and 10), on the relative marginal value of health q_h/a(t) is obtained by taking the derivate of (37) with respect to E and keeping first-order terms (total differentials, free T):

$$\begin{gathered} \frac{\partial }{\partial t}\frac{\partial q_{h/a}(t)}{\partial E}\approx {\rho }_E{w}_{\ast }(t){[1+z(t)]}^{{\gamma }_w}\frac{\partial s}{\partial H} \\ +\left[\frac{1}{q_A{(0)}^2}\frac{\partial U}{\partial H}{e}^{-(\beta -r)t}\right]\times \frac{\partial q_A(0)}{\partial E} \\ +\left[\frac{\partial d}{\partial H}+r\right]\times \frac{\partial q_{h/a}(t)}{\partial E} \\ -\left[\frac{1}{q_A(0)}\frac{{\partial }^{2}U}{\partial H^2}{e}^{-(\beta -r)t}+\frac{{\partial }^{2}Y}{\partial H^2}-q_{h/a}(t)\frac{{\partial }^{2}d}{\partial H^2}\right]\times \frac{\partial H(t)}{\partial E}. \end{gathered}$$ (87)

Likewise, the comparative dynamic effect of an increase in education on health H(t) is obtained by taking the derivative of (71) with respect to E and keeping first-order terms:

$$\begin{gathered} \frac{\partial }{\partial t}\frac{\partial H(t)}{\partial E}\approx \frac{{\alpha }_I-{\beta }_I}{1-{\alpha }_I-{\beta }_I}I[m(t),{\tau }_m(t);E]\left[\frac{1}{{\mu }_I}\frac{\partial {\mu }_I}{\partial E}-(1-{\kappa }_I){\rho }_E\right] \\ +\left[\frac{{\alpha }_I+{\beta }_I}{1-{\alpha }_I-{\beta }_I}\frac{I[m(t),{\tau }_m(t);E]}{q_{h/a}(t)}\right]\times \frac{\partial q_{h/a}(t)}{\partial E} \\ -\frac{\partial d}{\partial H}\times \frac{\partial H}{\partial E}, \end{gathered}$$ (88)

where we have used (58). Contrasting the results of the comparative dynamics for education E (equations 87 and 88) with those obtained for permanent income w_E (equations 84 and 85) we observe that permanent wages w_E and education E operate in the same way. This should come as no surprise, as they both operate by increasing permanent wages. There is however one important difference: the first term on the RHS of (88) represents both the effect of education on the efficiency of health investment ∂μ_I/∂E (the educated are assumed to be more efficient producers and consumers of health) and the effect of education on the opportunity cost of time ρ_E(1 − κ_I). The efficiency effect of education reduces the opportunity cost of time effect. The phase diagram for the effect of variation in education δE is essentially the same as for variation in permanent income w_E, shown in Figure 8, and replacing w_E by E (for this reason we do not provide a separate phase diagram). Given strong empirical support for a positive association between education and health, it could be that the efficiency effect dominates, in which case the (∂/∂t)(∂H(t)/∂E) null cline would cross the vertical ∂q_h/a(t)/∂E axis below instead of above the origin. This would make the case for variation in education δE stronger (compared to the case for variation in permanent wages w_E) in ensuring that the condition ${\partial q_{h/a}(t)/\partial E|}_T\le 0$ is obtained and hence length of life is extended.

Figure 8.

Phase diagram of the deviation from the unperturbed path, resulting from variation in permanent wages δw_E, of the relative marginal value of health ∂q_h/a(t)/∂w_E and of the health stock ∂H(t)/∂w_E, allowing length of life T to be optimally chosen. The four vertical dotted lines represent different potential values for the end point ∂H(T)/∂w_E.

D.5 Proof of Proposition 5

Absent ability to extend life, healthy individuals, ceteris paribus, value health cumulatively less, ${\displaystyle {\int }_0^T({\partial q_{h/a}(t)/\partial H_0|}_T)dt<0}$

The comparative dynamic effect of variation in initial health δH₀ on the relative marginal value of health, keeping length of life T fixed, is obtained by taking the derivative of (37) with respect to initial health H₀ and keeping first-order terms. Likewise, the comparative dynamic effect of initial health on health, keeping length of life T fixed, is obtained by taking the derivate of (71) with respect to intial health H₀ and keeping first-order terms:

$$\begin{gathered} {\frac{\partial }{\partial t}\frac{\partial q_{h/a}(t)}{\partial H_0}|}_T\approx \left[\frac{1}{q_A{(0)}^2}\frac{\partial U}{\partial H}{e}^{-(\beta -r)t}\right]\times {\frac{\partial q_A(0)}{\partial H_0}|}_T \\ +\left[\frac{\partial d}{\partial H}+r\right]\times {\frac{\partial q_{h/a}(t)}{\partial H_0}|}_T \\ -{\left[\frac{1}{q_A(0)}\frac{{\partial }^{2}U}{\partial H^2}{e}^{-(\beta -r)t}+\frac{{\partial }^{2}Y}{\partial H^2}-q_{h/a}(t)\frac{{\partial }^{2}d}{\partial H^2}\right]\times \frac{\partial H(t)}{\partial H_0}|}_T, \end{gathered}$$ (89)

and

$$\begin{gathered} \frac{\partial }{\partial t}{\frac{\partial H(t)}{\partial H_0}|}_T\approx {\left[\frac{{\alpha }_I+{\beta }_I}{1-{\alpha }_I-{\beta }_I}\frac{I[m(t),{\tau }_m(t);E]}{q_{h/a}(t)}\times \frac{\partial q_{h\times a}(t)}{\partial H_0}\right]}_T \\ -{\frac{\partial d}{\partial H}\times \frac{\partial H}{\partial H_0}|}_T. \end{gathered}$$ (90)

Thus, the coefficients in (89) and (90) are identical to the coefficients in the comparative dynamic relations (74) and (75) for variation with respect to wealth δA₀.

A-priori we don’t know the sign of ${\partial q_A(0)/\partial H_0|}_T$. First, consider the scenario where health reduces the marginal value of wealth, ${\partial q_A(0)/\partial H_0|}_T<0$, consistent with results obtained for our calibrated model (see Table 2 in section C). In this case the phase diagram for variation in initial health δH₀, shown in Figure 9, is similar to the phase diagram for variation in initial wealth δA₀, shown in Figure 4. Importantly, the ${(\partial /\partial t)(\partial q_{h/a}(t)/\partial H_0)|}_T$ null-cline crosses the vertical ${\partial q_{h/a}(t)/\partial H_0|}_T$ axis above the origin. While any admissible path has to end on the vertical ${\partial q_{h/a}(t)/\partial H_0|}_T$ axis, an important difference with wealth is that any admissible path has to start at ${\partial H(t)/\partial H_0|}_{T,t}=0$, which for t = 0 is identical to 1. We don’t know a-priori where ${\partial H(t)/\partial H_0|}_T=1$ is located with respect to the steady state (where the two null-clines cross) and we show one case where the initial point lies to the left (vertical dashed line to the left) and another case where it lies to the right (vertical dashed line to the right) of the steady state (Figure 9).

In case ${\partial H(t)/\partial H_0|}_T=1$ is located to the left of the steady state, we can rule out trajectory a as it does not end on the vertical axis. For the same reason we can also eliminate trajectory e in case ${\partial H(t)/\partial H_0|}_T=1$ is located to the right of the steady state.

Trajectories b, c and f represent an initial increase, followed by a subsequent decrease, in the marginal value of health q_h/a(t), with respect to the unperturbed path. Trajectories d and g represent solutions where the relative marginal value of health is lower at all times. Also for these solutions health is higher at all times (except t = T) and the individual uses the additional health δH₀ to shift resources from health to other uses. For these solutions better health reduces the demand for health investment and healthy behaviour at all times.

Those trajectories that are feasible (that are consistent with the begin and end conditions), i.e. b, c, d, f and g, all involve a cumulatively lower marginal value of health as initially higher health δH₀ requires lower health investment and less healthy behaviour over the life cycle in order for health to reach the minimum health level H_min within the same length of life T.⁴⁰ Q.E.D.

Figure 9.

Phase diagram of the deviation from the unperturbed path, resulting from variation in initial wealth δH₀, of the relative marginal value of health ${\partial q_{h/a}(t)/\partial H_0|}_T$ and of the health stock ${\partial H(t)/\partial H_0|}_T$, for fixed T.

Sensitivity to the sign of ∂d/∂H

Using similar reasoning and procedures as in Appendix section D.1 we find that the results remain valid for the opposite sign of ∂d/∂H.

Sensitivity to the sign of ${\partial q_A(0)/\partial H_0|}_T$

Now consider the scenario where health raises the marginal value of wealth, ${\partial q_A(0)/\partial H_0|}_T>0$. In this scenario the $(\partial /\partial t)({\partial q_{h/a}(t)/\partial H_0)|}_T$ null-cline shifts downward, crossing the $(\partial /\partial t)({\partial H(t)/\partial H_0)|}_T$ null cline to the left of and below the origin. In this case (not shown), all admissible trajectories start with a lower relative marginal value of health ${\partial q_{h/a}(0)/\partial H_0|}_T<0$ and either end with a higher relative marginal value of health ${\partial q_{h/a}(T)/\partial H_0|}_T>0$, in which case life is not extended but reduced ∂T/∂H₀ < 0 as a result of greater health (see 91), or end with a lower relative marginal value of health ${\partial q_{h/a}(T)/\partial H_0|}_T<0$, in which case we cannot unambiguously establish that life is extended. While we cannot rule out this scenario in the general case, our calibrated simulations show that a small increase in initial health δH₀ leads to a reduction in the marginal value of wealth, which is consistent with ∂q_A(0)/∂H₀ < 0 (see Table 2 in section C). Therefore, we favor the scenario where health reduces the marginal value of wealth, which is consistent with empirical evidence that worse childhood health is associated with shorter lives (Currie, 2009), and it has a natural intuitive interpretation that health and wealth are to some extent substitutable in financing consumption (e.g., Muurinen, 1982; Case and Deaton, 2005).

D.6 Proof of Proposition 6: Healthy individuals live longer ∂T/∂H₀ ≥ 0

The comparative dynamic effect of variation in initial health δH₀ on length of life T can be obtained by following the same steps as in section D.2. The result is identical to replacing A₀ with H₀ in conditions (76), (77) and (78). Assuming diminishing returns to life extension ${\partial \mathfrak{J}(T)/\partial T|}_{H_0}<0$ (cf. assumption 1 in section 2.4), length of life is extended ∂T/∂H₀ > 0, if:

$$\begin{gathered} {\frac{\partial \mathfrak{J}(T)}{\partial H_0}|}_T={\frac{\partial q_A(0)}{\partial H_0}|}_T{e}^{-rT}{\frac{\partial A(t)}{\partial t}|}_{t=T} \\ +\left\{{\frac{\partial q_A(0)}{\partial H_0}|}_T{e}^{-rT}{q}_{h/a}(T)+{q_A(0)e^{-rT}\frac{\partial q_{h/a}(T)}{\partial H_0}|}_T\right\}{\frac{\partial H(t)}{\partial t}|}_{t=T}>0. \end{gathered}$$ (91)

As argued before in section D.2, in (91), both ${\partial A(t)/\partial t|}_{t=T}$ and ${\partial H(t)/\partial t|}_{t=T}$ are negative since health declines near the end of life as it approaches H_min from above, and assets decline near the end of life in absence of a very strong bequest motive. Further, we have ${\partial q_A(0)/\partial H_0|}_T<0$. Note that all admissible scenarios b, c, d, f and g, end with negative values for variation in the relative marginal value of health with respect to initial health ${\partial q_{h/a}(T)/\partial H_0|}_T<0$. Thus, length of life is extended ∂T/∂H₀ > 0. Q.E.D.

D.7 Proof of Proposition 7

Individuals with greater endowed health are healthier at all ages, ∂H(t)/∂H₀ > 0, ∀t. For small life extension healthy individuals cumulatively value health less ${\displaystyle {\int }_0^T[\partial q_{h/a}(t)/\partial H_0]dt<0}$, for intermediate life extension they value health cumulatively more ${\displaystyle {\int }_0^T[\partial q_{h/a}(t)/\partial H_0]dt>0}$, and for large life extension they value health more at all ages, $\partial q_{h/a}(t)/\partial H_0>0$, ∀t.

Having established that length of life is extended, ∂T/∂H₀ > 0, now consider the more interesting case where T is free. Analogous to the discussion in section D.3 we have

$${\frac{\partial H}{\partial T}|}_{H_0,t=T}=-{\frac{\partial H(t)}{\partial t}|}_{H_0,t=T}>0.$$

Thus, $\partial H(T)/\partial H_0=({\partial H(t)/\partial T|}_{H_0,t=T})(\partial T/\partial H_0)>0$.

Figure 10 presents the comparative dynamic results for free T. The phase diagram on the left shows feasible trajectories a through g for the case where the starting point ∂H(t)/∂H₀ = 1 is located to the left of the steady state, and the phase diagram on the right shows feasible trajectories a through f for the case where the starting point ∂H(t)/∂H₀ = 1 is located to the right of the steady state (the starting values are indicated by the dashed vertical lines in both phase diagrams). The initial condition ∂H(t)/∂H₀ = 1 for t = 0, and the end-condition ∂H(T)/∂H₀ > 0, imply that all admissible paths start and end to the right of the vertical axis. Three example end values ∂H(T)/∂H₀ are indicated by the three dotted vertical lines in both figures.

All feasible trajectories for health lie to the right of the vertical axis. Thus individuals with greater endowed health are healthier at all ages, ∂H(t)/∂H₀ > 0, ∀t. Further, as the result $\partial H(T)/\partial H_0=({\partial H(t)/\partial T|}_{H_0,t=T})(\partial T/\partial H_0)>0$ shows, also for health the greater life is extended, the further is the end point ∂H(T)/∂H₀ located to the right in the phase diagram. While both phase diagrams are quite complicated, they clearly show that for end points ∂H(T)/∂H₀ (the vertical dotted lines) that lie further to the right (i.e. those associated with a greater degree of life extension), the variation in the value of health ∂q_h/a(t)/∂H₀ becomes more and more positive, with some scenarios even allowing for the possibility that healthy individuals value health more at every age. Whereas for end points ∂H(T)/∂H₀ that lie more to the left (i.e. those associated with a smaller degree of life extension), the variation in the value of health ∂q_h/a(t)/∂H₀ becomes more and more negative. These latter cases more closely resemble the fixed T case (proposition 7). Q.E.D.

Figure 10.

Phase diagram of the deviation from the unperturbed path, resulting from variation in initial health δH₀, of the relative marginal value of health ∂q_h/a(t)/∂H₀ and of the health stock ∂H(t)/∂H₀, for free T. The left shows feasible trajectories a through g for the case where the starting point ∂H(t)/∂H₀ = 1 is located to the left of the steady state, and the phase diagram on the right shows feasible trajectories a through f for the case where the starting point ∂H(t)/∂H₀ = 1 is located to the right of the steady state (the starting values are indicated by the dashed vertical lines in both phase diagrams).

D.8 Comparative Dynamics of the Controls

D.8.1 Variation in initial wealth, δA₀

In signing the following comparative dynamic results we rely on assumptions 1 to 4 and propositions 1 to 7.

Health investment

For the control variable health investment the comparative dynamic effect of initial wealth A₀ is obtained from (15), 18 and (19)

$$\frac{1-{\alpha }_I-{\beta }_I}{m(t)}\times \frac{\partial m(t)}{\partial A_0}\approx \frac{1}{q_{h/a}(t)}\times \frac{\partial q_{h/a}(t)}{\partial A_0},$$ (92)

$$\frac{1-{\alpha }_I-{\beta }_I}{{\tau }_m(t)}\times \frac{\partial {\tau }_m(t)}{\partial A_0}\approx \frac{1}{q_{h/a}(t)}\times \frac{\partial q_{h/a}(t)}{\partial A_0},$$ (93)

where we assume that first-order effects dominate and we focus on the total differential (full model with free T). Since ∂m(t)/∂A₀ and ∂τ_m(t)/∂A₀ are proportional to ∂q_h/a(t)/∂A₀, they will mimic the pattern of the variation in the response to wealth of the relative marginal value of health (see propositions 1 and 3).

Healthy and unhealthy consumption

For the control variable healthy consumption the comparative dynamic effect of initial wealth A₀ is obtained from (21):

$$\begin{gathered} \left[\frac{1}{q_A(0)}\frac{{\partial }^{2}U}{\partial C_h^2}-q_{h/a}(t)\frac{{\partial }^{2}d}{\partial C_h^2}{e}^{(\beta -r)t}\right]\times \frac{\partial C_h(t)}{\partial A_0} \\ \approx \left[\frac{1}{q_A{(0)}^2}\frac{\partial U}{\partial C_h}\right]\times \frac{\partial q_A(0)}{\partial A_0} \\ +\left[\frac{\partial d}{\partial C_h}{e}^{(\beta -r)t}\right]\times \frac{\partial q_{h/a}(t)}{\partial A_0} \\ +\left[q_{h/a}(t)\frac{{\partial }^{2}d}{\partial C_h\partial H}{e}^{(\beta -r)t}\right]\times \frac{\partial H(t)}{\partial A_0}. \end{gathered}$$ (94)

The direct wealth effect (first term on the RHS of 94) as well as the effect of an increase in the relative marginal value of health (second term on the RHS) is positive.⁴¹ The sign of the third term is undetermined, since the sign of ∂²d/∂H∂C_h is not known. One could imagine that healthier individuals benefit less from healthy consumption, but one could also imagine the opposite scenario. Since the effect of wealth on health ∂H(t)/∂A₀ is gradual and not immediate, the third term is initially small compared to the first two terms. As a result, an increase in endowed wealth increases the demand for healthy consumption, ∂C_h(t)/∂A₀ > 0, initially.

Likewise, for unhealthy consumption the comparative dynamic effect of initial wealth is obtained from (24):

$$\begin{gathered} \left[\frac{1}{q_A(0)}\frac{{\partial }^{2}U}{\partial C_u^2}-q_{h/a}(t)\frac{{\partial }^{2}d}{\partial C_u^2}{e}^{(\beta -r)t}\right]\times \frac{\partial C_u(t)}{\partial A_0} \\ \approx \left[\frac{1}{q_A{(0)}^2}\frac{\partial U}{\partial C_u}\right]\times \frac{\partial q_A(0)}{\partial A_0} \\ +\left[\frac{\partial d}{\partial C_u}{e}^{(\beta -r)t}\right]\times \frac{\partial q_{h/a}(t)}{\partial A_0} \\ +\left[q_{h/a}(t)\frac{{\partial }^{2}d}{\partial C_u\partial H}{e}^{(\beta -r)t}\right]\times \frac{\partial H(t)}{\partial A_0}. \end{gathered}$$ (95)

For unhealthy consumption, the effect is ambiguous. While the direct wealth effect is positive (first term on the RHS of 95), the effect of an increase in the marginal health cost (last two terms on the RHS) is negative.

Job-related health stress

The comparative dynamic effect of initial wealth A₀ on job-related health stress is obtained from (27):

$$\begin{gathered} \left[q_{h/a}(t)\frac{{\partial }^{2}d}{\partial z^2}-\frac{{\partial }^{2}Y}{\partial z^2}\right]\times \frac{\partial z(t)}{\partial A_0} \\ =-\frac{\partial d}{\partial z}\times \frac{\partial q_{h/a}(t)}{\partial A_0} \\ -\left[q_{h/a}(t)\frac{{\partial }^{2}d}{\partial z\partial H}+\frac{\partial w}{\partial z}\frac{\partial s}{\partial H}\right]\times \frac{\partial H(t)}{\partial A_0}. \end{gathered}$$ (96)

where the coefficient of ∂z(t)/∂A₀ is positive under assumptions 1 and 2, but the coefficient of ∂H(t)/∂A₀ cannot be signed. Initially, the term in ∂H(t)/∂A₀ is small as the effect of wealth on health is gradual.

Leisure

The comparative dynamic effect of variation in initial wealth A₀ on leisure is obtained from (20):

$$\frac{{\partial }^{2}U}{\partial L^2}\frac{\partial L(t)}{\partial A_0}\approx \frac{1}{q_A(0)}\frac{\partial U}{\partial L}\times \frac{\partial q_A(0)}{\partial A_0}-\frac{{\partial }^{2}U}{\partial L\partial H}\frac{\partial H(t)}{\partial A_0}.$$ (97)

For diminishing utility of leisure ∂²U/∂L² < 0, diminishing returns to wealth ∂q_A(0)/∂A(0) < 0 (see Table 2 in section C), the demand for leisure is initially higher as a result of greater wealth. But wealth eventually leads to better health, and if leisure and health are complements in utility ∂²U/∂H∂L > 0, we have ∂L(t)/∂A₀ > 0, ∀t. If, however, health and leisure are substitutes in utility, then the demand for leisure is initially higher but could be reduced eventually with improved health.

D.8.2 Variation in the permanent wage rate, δw_E

Health investment

For the control variable health investment the comparative dynamic effect of the wage rate w_E is obtained from (92) replacing A₀ by w_E, and adding the term −(1 −κ_I)/w_E on the RHS.

Healthy and unhealthy consumption

For the control variable healthy consumption the comparative dynamic effect of the wage rate w_E is obtained from (94) replacing A₀ by w_E and adding the term $\{(1-{\kappa }_{C_h})/w_E\}{\pi }_{C_h}(t)e^{(\beta -r)t}$ on the RHS.

Likewise, for unhealthy consumption the comparative dynamic effect of the wage rate w_E is obtained from (95) replacing A₀ by w_E and adding the term $\{(1-{\kappa }_{C_u})/w_E\}{\pi }_{C_u}(t)e^{(\beta -r)t}$ on the RHS.

Job-related health stress

The comparative dynamic effect of w_E on job-related health stress is obtained from (96) replacing A₀ by w_E and adding the term {(∂w/∂z)/w_E}τ_w(t) on the RHS.

Leisure

The comparative dynamic effect of the wage rate on leisure is obtained from (97) by replacing A₀ by w_E and adding the term q_A(0)(w(t)/w_E)e^(β−r)t on the RHS.

D.8.3 Variation in education, δE

Health investment

For the control variable health investment the comparative dynamic effect of education E is obtained from (92) replacing A₀ by E, and adding the term {−ρ_E(1 −κ_I) + (1/μ_I(E)) (∂μ_I/∂E)} on the RHS.

Healthy and unhealthy consumption

For the control variable healthy consumption the comparative dynamic effect of education E is obtained from (94) replacing A₀ by E, and adding the term

$$\left({\rho }_E(1-{\kappa }_{C_h})-\frac{1}{{\mu }_{C_h}(E)}\frac{\partial {\mu }_{C_h}}{\partial E}\right){\pi }_{C_h}(t)e^{(\beta -r)t}$$

on the RHS. Likewise, for unhealthy consumption the comparative dynamic effect of education is obtained from (95) replacing A₀ by E and adding the term

$$\left({\rho }_E\left(1-{\kappa }_{C_u}\right)-\frac{1}{\mu C_u(E)}\frac{\partial {\mu }_{C_u}}{\partial E}\right){\pi }_{C_u}(t)e^{(\beta -r)t}$$

on the RHS.

Job-related health stress

The comparative dynamic effect of education E on job-related health stress is obtained from (96) replacing A₀ by E, and adding the term ρ_E (∂Y/∂z) on the RHS.

Leisure

The comparative dynamic effect of education on leisure is obtained from (97) by replacing A₀ by E and adding the term ρ_Eq_A(0)w(t)e^(β−r)t on the RHS.

D.8.4 Variation in initial health, δH₀

The comparative dynamics of the control variables with respect to H₀ can be directly obtained by using the comparative dynamics for initial wealth in (92) to (97), replacing A₀ by H₀.