Broken adaptive ridge regression and its asymptotic properties

Abstract

This paper studies the asymptotic properties of a sparse linear regression estimator, referred to as broken adaptive ridge (BAR) estimator, resulting from an L₀-based iteratively reweighted L₂ penalization algorithm using the ridge estimator as its initial value. We show that the BAR estimator is consistent for variable selection and has an oracle property for parameter estimation. Moreover, we show that the BAR estimator possesses a grouping effect: highly correlated covariates are naturally grouped together, which is a desirable property not known for other oracle variable selection methods. Lastly, we combine BAR with a sparsity-restricted least squares estimator and give conditions under which the resulting two-stage sparse regression method is selection and estimation consistent in addition to having the grouping property in high- or ultrahigh-dimensional settings. Numerical studies are conducted to investigate and illustrate the operating characteristics of the BAR method in comparison with other methods.

1. Introduction

Simultaneous variable selection and parameter estimation is an essential task in statistics and its applications. A natural approach to variable selection is L₀-penalized regression, which directly penalizes the cardinality of a model through well-known information criteria such as Mallow’s C_p [35], Akaike’s information criterion (AIC) [1], the Bayesian information criterion (BIC) [9, 38], and risk inflation criteria (RIC) [17]. It has also been shown to have an optimality property for variable selection and parameter estimation [40]. However, the L₀-penalization problem is nonconvex and finding its global optima requires exhaustive combinatorial best subset search, which is NP-hard and computationally infeasible even for data in moderate dimension. Moreover, it can be unstable for variable selection [6]. A popular alternative is L₁-penalized regression, or Lasso [43], which is known to be consistent for variable selection [36, 48] although not consistent for parameter estimation [13, 51]. During the past two decades, much e orts have been devoted to improving Lasso using various variants of the L₁ penalty, which are not only consistent for variable selection, but also consistent for parameter estimation [13, 15, 24, 27, 47, 51]. Yet another approach is to approximate the L₀ penalty using a surrogate L₀ penalty function, which could lead to a more sparse model with favorable numerical properties [11, 25, 40, 41].

This paper concerns a different L₀-based approach to variable selection and parameter estimation which performs iteratively reweighted L₂ penalized regressions in order to approximate an L₀ penalized regression [19, 33]. Unlike a surrogate L₀ penalization method such as the truncated Lasso penalization (TLP) method [41], the L₀-based iteratively reweighted L₂ penalization method can be viewed as performing a sequence of surrogate L₀ penalizations, where each reweighted L₂ penalty serves as an adaptive surrogate L₀ penalty and the approximation of L₀ penalization improves with each iteration. It is also computationally appealing since each iteration only involves a reweighted L₂ penalization. The idea of iteratively reweighted penalization has its roots in the well-known Lawson algorithm [29] in classical approximation theory, which later found applications in L_d minimization for values of d ∈ (0, 1) [37], sparse signal reconstruction [21], compressive sensing [7, 8, 10, 20, 45], and variable selection [19, 33]. However, despite its increasing popularity in applications and favorable numerical performance, theoretical studies of the iteratively reweighted L₂ penalization method have so far focused on its non-asymptotic numerical convergence properties [10, 19, 33]. Its statistical properties such as selection consistency and estimation consistency remain unexplored.

The primary purpose of this paper is to study rigorously the asymptotic properties of a specific version of the L₀-based iteratively reweighted L2-penalization method for the linear model. We will refer to the resulting estimator as the broken adaptive ridge (BAR) estimator to reflect the fact that it is obtained by fitting adaptively reweighted ridge regression which eventually breaks part of the ridge with the corresponding weights diverging to infinity to produce sparsity. The BAR algorithm uses an L2-penalized (or ridge) estimator as its initial estimator and updates the estimator iteratively using reweighted L2 penalizations where the weight for each coe cient at each iteration step is the inverse of its squared estimate from the previous iteration as defined later in Eqs. (2)–(3) of Section 2.

Our key theoretical contribution is to establish two large-sample properties for the BAR estimator. First, we will show that the BAR estimator possesses an oracle property: when the true model is sparse, with probability tending to 1, it estimates the zero coefficients as zeros and estimates the non-zero coefficients as well as the scenario when the true sub-model is known in advance. To this end, we stress that because the BAR estimator is the limit of an iterative penalization algorithm, commonly used techniques for deriving oracle properties of a single-step penalized regression method do not apply directly. As pointed out by a reviewer, the common strategies used in analyzing approximate solutions to nonconvex penalized method such as SCAD and MCP usually rely on an initial estimator that is close to the optimal, and then show that some kind of iterative refinement of the initial estimator would lead to a good local estimator [15, 34]. Our derivations of the asymptotic oracle properties for BAR are inspired by this idea, but the technical details are substantially different from those for other variable selection methods in the literature. A unique feature of the BAR algorithm is that at each reweighted L₂ iteration, the resulting estimator is not sparse. We show that with a good initial ridge estimator, each BAR iteration shrinks the estimates of the zero coefficients towards zero and drives the estimates of the nonzero coefficients towards an oracle ridge estimator. Consequently, sparsity and selection consistency are achieved only in the limit of the BAR algorithm and the estimation consistency of the ridge estimator for the nonzero coefficients is preserved. Second, we will show that the BAR estimator has a grouping effect that highly correlated variables are naturally grouped together with similar coefficients, which is a desirable property inherited from the ridge estimator. Therefore, our results show that the BAR estimator enjoys the best of the L₀ and L₂ penalized regressions, while avoiding some of their limitations. Lastly, we consider high- or ultrahigh-dimensional settings when the dimension is larger or much larger than the sample size. Frommlet and Nuel [19] suggested to use the mBIC penalty for the BAR method in high-dimensional settings, but its asymptotic consistency has yet to be studied rigorously. We propose a different extension of the BAR method to ultrahigh-dimensional settings by combining it with a sparsity-restricted least squares estimation method and show rigorously that the resulting two-stage estimator is asymptotically consistent for variable selection and parameter estimation, and that it retains the grouping property.

In Section 2, we review the BAR estimator. In Section 3, we state our main results on its oracle property and grouping property for the general non-orthogonal case; we also develop rigorously a two-stage BAR method for high-or ultrahigh-dimensional settings. Section 4 illustrates the finite-sample operating characteristics of BAR in comparison with some popular methods for variable selection, parameter estimation, prediction, and grouping. Section 5 presents illustrations involving a prostate cancer data and a gut microbiota data. Concluding remarks are given in Section 6. Proofs of the theoretical results are deferred to the Appendix.

2. Broken adaptive ridge estimator

Consider the linear regression model

$$\mathbf{y}={\displaystyle \sum _{j=1}^{p_n}{x}_j{\beta }_j+\mathit{\epsilon }},$$

where $\mathbf{y}\in {ℝ}^n$ is a response vector, ${\mathbf{x}}_1,\dots ,{\mathbf{x}}_{p_n}\in {ℝ}^n$ are predictors, and $\mathit{\beta }={\left({\beta }_1,\dots ,{\beta }_{p_n}\right)}^{\top }$ is the vector of regression coefficients. Assume that β₀ is the true parameter. Without loss of generality, we suppose X = (x₁,…,x_p) = (w₁,…,w_n)^⊤ and y are centralized. In this paper, || ‧ || represents the Euclidean norm for a vector and spectral norm for a matrix. Let

$${\widehat{\mathit{\beta }}}^{\left(0\right)}=\arg \underset{\mathit{\beta }}{\min }\left\{{\Vert \mathbf{y}-X\mathit{\beta }\Vert }^2+{\xi }_n{\displaystyle \sum _{j=1}^{p_n}{\beta }_j^2}\right\}={\left(X^{\top }X+{\xi }_{n}I\right)}^{-1}{X}^{\top }y$$ (1)

be the ridge estimator, where ξ_n ≥ 0 is a tuning parameter. For any integer k ≥ 1, define

$${\widehat{\mathit{\beta }}}^{\left(k\right)}=g\left\{{\widehat{\mathit{\beta }}}^{\left(k-1\right)}\right\},$$ (2)

where

$$g\left(\tilde{\mathit{\beta }}\right)=\arg \underset{\mathit{\beta }}{\min }\left\{{\Vert \mathbf{y}-X\mathit{\beta }\Vert }^2+{\lambda }_n{\displaystyle \sum _{j=1}^{p_n}{\beta }_j^2/{\tilde{\beta }}_j^2}\right\}={\left\{X^{\top }X+{\lambda }_{n}D\left(\tilde{\mathit{\beta }}\right)\right\}}^{-1}{X}^{\top }y,$$ (3)

and $\mathbf{D}\left(\tilde{\mathit{\beta }}\right)=\mathrm{diag}\left({\tilde{\beta }}_1^{-2},\dots ,{\tilde{\beta }}_{p_n}^{-2}\right)$. The broken adaptive ridge (BAR) estimator is defined as

$${\widehat{\mathit{\beta }}}^{*}=\underset{k\to \infty }{\lim }{\widehat{\mathit{\beta }}}^{\left(k\right)}.$$

Remark 1. [Weight selection and arithmetic overflow] The initial ridge estimator ${\widehat{\mathit{\beta }}}^{\left(0\right)}$ and its subsequent updates ${\widehat{\mathit{\beta }}}^{\left(k\right)}$ do not yield any zero coefficient. Thus, the weights ${\tilde{\beta }}_i^{-2}s$ in each iteration are well defined. However, as the iterated values converge to its limit, the weight matrix $\mathbf{D}\left\{{\widehat{\mathit{\beta }}}^{\left(k-1\right)}\right\}$ will inevitably run into division by a very small nonzero value, which could cause an arithmetic overflow. A commonly used solution to this problem is to introduce a small perturbation, or more specifically, replace $\mathbf{D}\left(\tilde{\mathit{\beta }}\right)=\mathrm{diag}\left({\tilde{\beta }}_1^{-2},\dots ,{\tilde{\beta }}_{p_n}^{-2}\right)$ by $\mathrm{diag}\left\{1/\left({\tilde{\beta }}_1^2+{\delta }^2\right),\dots ,1/\left({\tilde{\beta }}_{p_n}^2+{\delta }^2\right)\right\}$ for some δ > 0 to avoid numerical instability [10, 19]. Here we provide a different solution by rewriting formula (3) as

$$g\left(\tilde{\mathit{\beta }}\right)=\Gamma \left(\tilde{\mathit{\beta }}\right){\left\{{\tilde{X}}^{\top }\left(\tilde{\mathit{\beta }}\right)\tilde{X}\left(\tilde{\mathit{\beta }}\right)+{\lambda }_n{I}_{p_n}\right\}}^{-1}{\tilde{X}}^{\top }\left(\tilde{\mathit{\beta }}\right)y,$$ (4)

where $\mathbf{\Gamma }\left(\tilde{\mathit{\beta }}\right)=\mathrm{diag}\left({\tilde{\beta }}_1,\dots ,{\tilde{\beta }}_{p_n}\right)$, and $\tilde{\mathbf{X}}\left(\tilde{\mathit{\beta }}\right)=\mathbf{X}\mathbf{\Gamma }\left(\tilde{\mathit{\beta }}\right)$. Because the right-hand side of (4) involves only multiplication, instead of division, by the ${\tilde{\beta }}_{j}s$., numerical stability is achieved without having to introduce a perturbation δ. We also note that the BAR algorithm based on (4) is equivalent to the algorithm of Liu and Li [33].

Remark 2. [Orthogonal case] To appreciate how the BAR method works, it is helpful to examine the orthogonal case which admits a closed form for the BAR estimator and which has been previously studied in [19]. Assume that ${\mathbf{X}}^{\top }\mathbf{X}/n={\mathbf{I}}_{p_n}$. Then, for each j ∈ {1, …, p_n}, the jth component of $g\left(\tilde{\mathit{\beta }}\right)$ defined by (3) is equal to

$$g_j\left({\tilde{\beta }}_j\right)=\frac{{\tilde{\beta }}_j^2}{{\tilde{\beta }}_j^2+{\lambda }_n/n}{\tilde{\beta }}_j\left(\text{OLS}\right),$$

where $\widehat{\mathit{\beta }}\left(\mathrm{OLS}\right)=n^{-1}{\mathbf{X}}^{\top }\mathbf{y}$ is the ordinary least squares (OLS) estimate. Hence the BAR algorithm can be implemented component by component. First, we show the existence and uniqueness of the BAR estimator ${\widehat{\beta }}^{\ast }$. Without loss of generality, assume ${\widehat{\beta }}_j\left(\mathrm{OLS}\right)>0$ and then $0\le {\widehat{\beta }}_j^{\left(k\right)}\le {\widehat{\beta }}_j\left(\mathrm{OLS}\right)$ for every integer k. Also note that the map $x\mapsto g\left(x\right)=x^2{\widehat{\beta }}_j\left(\mathrm{OLS}\right)/\left(x^2+{\lambda }_n/n\right)$ is increasing in x on (0, ∞). Set ϕ(x) = g(x) − x. For fixed n and λ_n, the following facts can be verified easily.

• (i)If ${\widehat{\beta }}_j^2\left(\mathrm{OLS}\right)<4{\lambda }_n/n$, then ϕ (x) < 0. Therefore, ${\widehat{\beta }}_j^{\left(k+1\right)}<{\widehat{\beta }}_j^{\left(k\right)}$ for all k and ${\widehat{\beta }}_j^{\ast }=0$.
• (ii)
  If ${\widehat{\beta }}_j^2\left(\mathrm{OLS}\right)=4{\lambda }_n/n$, then ϕ (x) ≤ 0. This leads to ${\widehat{\beta }}_j^{\left(k+1\right)}\le {\widehat{\beta }}_j^{\left(k\right)}$ for all k. Then,

  $${\widehat{\beta }}_j^{*}=\{\begin{array}{ll}0\hfill & \text{if }{\widehat{\beta }}_j^{\left(0\right)}<{\widehat{\beta }}_j\left(\text{OLS}\right)/2,\hfill \\ {\widehat{\beta }}_j\left(\text{OLS}\right)/2\hfill & \text{otherwise}.\hfill \end{array}$$
• (iii)
  If ${\widehat{\beta }}_j^2\left(\mathrm{OLS}\right)\ge 4{\lambda }_n/n$, then (x) ≥ 0 when x ∈ [x₁, x], where $x_1={\widehat{\beta }}_j\left(\mathrm{OLS}\right)/2-{\left\{{\widehat{\beta }}_J^2\left(\mathrm{OLS}\right)/4-{\lambda }_n/n\right\}}^{1/2}$ and $x_2={\widehat{\beta }}_j\left(\mathrm{OLS}\right)/2+{\left\{{\widehat{\beta }}_J^2\left(\mathrm{OLS}\right)/4-{\lambda }_n/n\right\}}^{1/2}$ and ϕ(x) < 0 otherwise. As a result,

  $${\widehat{\beta }}_j^{*}=\{\begin{array}{ll}0\hfill & \text{if }{\widehat{\beta }}_j^{\left(0\right)}<x_1,\hfill \\ {\widehat{\beta }}_j\left(\text{OLS}\right)/2+\sqrt{{\widehat{\beta }}_j^2\left(\text{OLS}\right)/4-{\lambda }_n/n},\hfill & \text{otherwise}.\hfill \end{array}$$

In conclusion, the BAR estimator always converges to a unique solution depending on the settings of the initial value. Since we choose the ridge estimator as the initial value, which would be close to the OLS estimator under mild conditions, the BAR algorithm for the jth component converges to the following limit:

$${\widehat{\beta }}_j^{*}=\{\begin{array}{ll}0\hfill & \text{if }{\widehat{\beta }}_j\left(\text{OLS}\right)\in \left(-2\sqrt{{\lambda }_n/n},2\sqrt{{\lambda }_n/n}\right),\hfill \\ {\widehat{\beta }}_j\left(\text{OLS}\right)/2+\sqrt{{\widehat{\beta }}_j^2\left(\text{OLS}\right)/4-{\lambda }_n/n}\hfill & \text{if }{\widehat{\beta }}_j\left(\text{OLS}\right)\notin \left(-2\sqrt{{\lambda }_n/n},2\sqrt{{\lambda }_n/n}\right).\hfill \end{array}$$ (5)

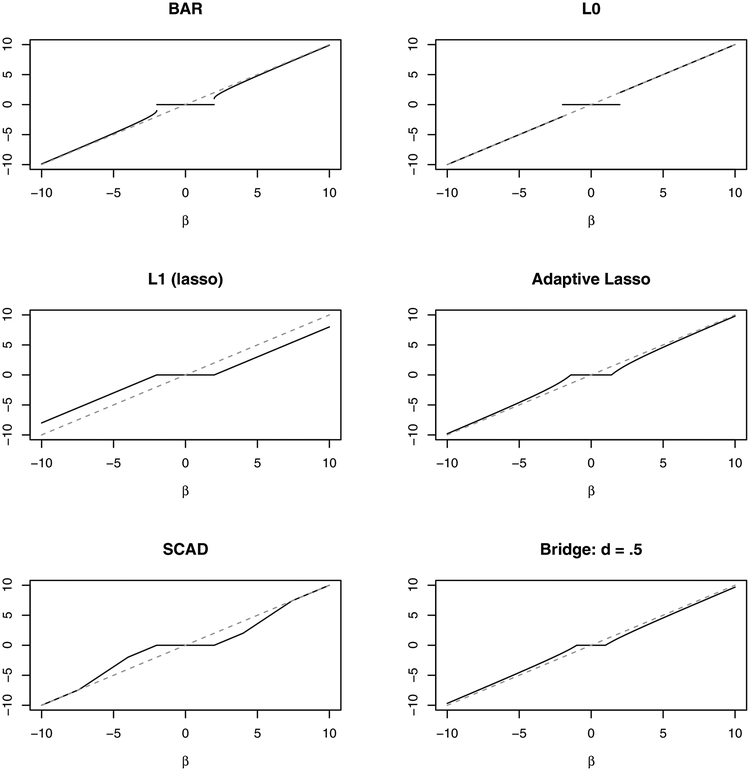
Hence, the BAR estimator ${\widehat{\mathit{\beta }}}^{\ast }$ shrinks the small values of $\widehat{\mathit{\beta }}\left(\mathrm{OLS}\right)$ to 0 and keeps its large values essentially unchanged provided that λ_n/n is small. Figure 1 depicts the BAR thresholding function (5), along with some well-known thresholding functions (L₀, Lasso, Adaptive Lasso, and SCAD), suggesting that BAR gives a good approximation to an L₀ penalized regression. The existence and uniqueness of the BAR estimator for X in a general form are nontrivial, although they have been verified empirically in our extensive numerical studies. A slightly weaker theoretical result is provided in Theorem 1(i) of Section 3. Therefore, BAR is expected to behave like an L₀-penalized regression, but is more stable and easily scalable to high-dimensional settings.

Figure 1:

Thresholding functions of BAR, L₀, Lasso, Adaptive Lasso, SCAD, and L_0.5.

3. Large-sample properties of BAR

3.1. Oracle property

We next develop the oracle properties of the BAR estimator for the general case without requiring the design matrix to be orthogonal.

Let ${\mathit{\beta }}_0={\left({\beta }_{01},\dots ,{\beta }_{0p_n}\right)}^{\top }$ be the true parameter value with dimension p_n diverging to infinity but p_n < n. For simplicity, write ${\mathit{\beta }}_0={\left({\mathit{\beta }}_{01}^{\top },{\mathit{\beta }}_{02}^{\top }\right)}^{\top }$ where ${\mathit{\beta }}_{01}\in {ℝ}_n^q$ and ${\mathit{\beta }}_{02}\in {ℝ}^{p_n-q_n}$. Assume β₀₁ ≠ 0 and β₀₂ = 0. Let ${\widehat{\mathit{\beta }}}^{\ast }={\left({\widehat{\mathit{\beta }}}_{01}^{\ast }{}^{\top },{\widehat{\mathit{\beta }}}_{02}^{\ast }{}^{\top }\right)}^{\top }$ denote the BAR estimator of β₀. Set ${\mathbf{X}}_1=\left({\mathbf{x}}_1,\dots ,{\mathbf{x}}_{q_n}\right)$, ${\sum }_{n1}={\mathbf{X}}_1^{\top }{\mathbf{X}}_1/n$ and ${\sum }_n={\mathbf{X}}^{\top }\mathbf{X}/n$.

The following conditions are needed to derive the asymptotic properties of the BAR estimator.

• (C1)The errors ε₁, …, ε_n are independent and identically distributed random variables with mean zero and variance 0 < σ² < ∞.
• (C2)There exists a constant C > 1 such that 0 < 1/C < λ_min (Σ_n) ≤ λ_max (Σ_n) < C < ∞ for every integer n.
• (C3)Let $a_{0n}={\min }_{1\le j\le q_n}\left|{\beta }_{0j}\right|$ and $a_{1n}={\min }_{1\le j\le q_n}\left|{\beta }_{0j}\right|$. As $n\to \infty ,p_n{q}_n/\sqrt{n}\to 0,{\xi }_n{a}_{1n}/\sqrt{n}\to 0,{\left(p_n/n\right)}^{1/2}/a_{0n}\to 0$, and ${\lambda }_n{a}_{1n}{\left(q_n/n\right)}^{1/2}/a_{0n}^2\to 0$

Theorem 1 (Oracle property). Assume the conditions (C1)–(C3)| are satisfied. For any q_n-vector b_n satisfying ||b_n|| ≤ 1, define $s_n^2={\sigma }^2{\mathbf{b}}_n^{\top }{\sum }_{n1}^{-1}{\mathbf{b}}_n$ Then, the fixed point of $f\left(\mathit{\alpha }\right)={\left\{{\mathbf{X}}_1^{\top }{\mathbf{X}}_1+{\lambda }_n{\mathbf{D}}_1\left(\mathit{\alpha }\right)\right\}}^{-1}{\mathbf{X}}_1^{\top }\mathbf{y}$ exists and is unique, where ${\mathbf{D}}_1\left(\mathit{\alpha }\right)=\mathrm{diag}\left({\alpha }_1^{-2},\dots ,{\alpha }_{p_n}^{-2}\right)$ Moreover, with probability tending to 1,

• (i)the BAR estimator ${\widehat{\mathit{\beta }}}^{\ast }={\left({\widehat{\mathit{\beta }}}_1^{\ast }{}^{\top },{\widehat{\mathit{\beta }}}_2^{\ast }{}^{\top }\right)}^{\top }$ exists and is unique, where ${\widehat{\mathit{\beta }}}_2^{\ast }=0$ and ${\widehat{\mathit{\beta }}}_1^{\ast }$ is the unique fixed point of f (α);
• (ii)$\sqrt{n}{s}_n^{-1}{\mathbf{b}}_1^{\top }\left({\widehat{\mathit{\beta }}}_1^{\ast }-{\mathit{\beta }}_{01}\right)⇝\mathcal{N}\left(0,1\right)$.

3.2. Grouping effect

When the true model has a natural group structure, it is desirable to have all coefficients within a group clustered together. For example, by virtue of gene network relationships, some of the genes will strongly correlate and are referred to as grouped genes [39]. The next theorem shows that the BAR method has a grouping property.

Theorem 2. Assume that the columns of matrix X are standardized such that x_1j + ⋯ + x_nj = 0 and ${\Vert {\mathbf{x}}_j\Vert }_2^2=1$ for all j ∈ {1, …, p_n}. Let ${\widehat{\mathit{\beta }}}^{\ast }$ be the BAR estimator. Then, with probability tending to 1, for any i < j,

$$\left|{\widehat{\beta }}_i^{*-1}-{\widehat{\beta }}_j^{*-1}\right|\le \frac{1}{{\lambda }_n}\Vert y\Vert \sqrt{2\left(1-{\rho }_{ij}\right)},$$

provided that ${\widehat{\beta }}_i^{\ast }{\widehat{\beta }}_j^{\ast }\ne 0$, where ${\rho }_{ij}={\mathbf{x}}_i^{\top }{\mathbf{x}}_j$ is the sample correlation of x_i and x_j.

The above grouping property of BAR is similar to that of Elastic Net. In particular, Zou and Hastie [52] showed that if ${\widehat{\beta }}_i\left(\mathrm{EN}\right){\widehat{\beta }}_j\left(\mathrm{EN}\right)>0$, then

$$\left|{\widehat{\beta }}_i\left(\text{EN}\right)-{\widehat{\beta }}_j\left(\text{EN}\right)\right|\le \frac{1}{\lambda }\Vert y\Vert \sqrt{2\left(1-{\rho }_{ij}\right)},$$

where ${\widehat{\beta }}_i\left(\mathrm{EN}\right)$ is the Elastic Net estimate of β_i and λ is a tuning parameter. As seen in the proof of Theorem 2, the reason for stating the grouping effect of the BAR estimator in terms of ${\widehat{\beta }}_i^{-1}$ is the weight ${\widehat{\beta }}_i^{-2}$ used in the reweighted L₂ penalization.

3.3. High-dimensional setting

Like most oracle variable selection methods, the oracle property of the BAR estimator in Theorem 1 is derived for p_n < n. In high- or ultrahigh-dimensional problems where the number of variables p_n can be much larger than the sample size n, it is not clear if BAR would still enjoy the oracle property under the similar conditions. A commonly used strategy for ultrahigh-dimensional problems is to add a screening step to reduce the dimension before performing variable selection and parameter estimation [14]. During the past decades, many variable screening procedures have been developed with the sure screening property that with probability tending to 1, the screened model retains all important variables; see, e.g., [12, 14, 15, 22, 28, 30–32, 44, 46, 49, 50] and the references therein. Our results in Theorems 3 and 4 guarantee that when combined with a sure screening procedure, the BAR estimator has the oracle and grouping property in ultrahigh-dimensional settings.

Inspired by Xu and Chen [46], who studied a sparse maximum likelihood estimation method for generalized linear models, we introduce below a sparsity-restricted least squares estimate for screening joint effects for the linear model with unspecified error distribution and establish its sure screening property. Specifically, for a given k, define the following sparsity-restricted least squares estimate (sLSE):

$${\tilde{\mathit{\beta }}}_{\text{sLSE}}=\arg \underset{\mathit{\beta }}{\min }\left\{\mathcal{l}\left(\mathit{\beta }\right):{\Vert \mathit{\beta }\Vert }_0\le k\right\},$$ (6)

where $\mathcal{l}\left(\mathit{\beta }\right)={\left(\mathbf{y}-\mathbf{X}\mathit{\beta }\right)}^{\top }\left(\mathbf{y}-\mathbf{X}\beta \right)$ Solving for ${\widehat{\mathit{\beta }}}_{sLSE}$ can be computationally demanding even for moderately large k since it is equivalent to the best subset search. Here we adopt the iterative hard-thresholding (IHT) algorithm of Blumensath and Davies [4] to approximately solve the optimization problem (6). Define a local quadratic approximation of ℓ(β) by

$$h\left(\mathit{\gamma },\mathit{\beta }\right)=\mathcal{l}\left(\mathit{\beta }\right)+{\left(\mathit{\gamma }-\mathit{\beta }\right)}^{\top }S\left(\mathit{\beta }\right)+\frac{u}{2}{\Vert \mathit{\gamma }-\mathit{\beta }\Vert }_2^2,$$

where $S\left(\mathit{\beta }\right)={\mathcal{l}}^{\prime }\left(\mathit{\beta }\right)=-2{\mathbf{X}}^{\top }\left(\mathbf{y}-\mathbf{X}\mathit{\beta }\right)$ and u > 0 is a scaling parameter. The IHT algorithm solves (6) via the following iterative algorithm

$${\mathit{\beta }}^{\left(t+1\right)}=\arg \underset{\mathit{\gamma }}{\min }\left\{h\left(\mathit{\gamma },{\mathit{\beta }}^{\left(t\right)}\right):{\Vert \mathit{\gamma }\Vert }_0\le k\right\}$$ (7)

where β⁽⁰⁾ = 0. Note that without the sparsity constraint, (7) has an explicit solution

$$\mathit{\gamma }={\mathit{\beta }}^{\left(t\right)}+u^{-1}2X^{\top }\left(y-X{\mathit{\beta }}^{\left(t\right)}\right).$$

Adding the sparsity constraint, the solution of (7) is then given by

$${\mathit{\beta }}^{\left(t+1\right)}={\left({\gamma }_{1}1\left\{\left|{\gamma }_1\right|\ge r\right\},\dots ,{\gamma }_{p_n}1\left\{\left|{\gamma }_{p_n}\right|\ge r\right\}\right)}^{\top },$$

with r being the kth largest component of $\left|\mathit{\gamma }\right|={\left(\left|{\gamma }_1\right|,\dots ,\left|{\gamma }_{p_n}\right|\right)}^{\top }$ Therefore the update at each iteration of the IHT algorithm is straightforward and The following theorem shows that with an appropriate scaling parameter u, the sequence {β^(t)}obtained from the above IHT algorithm decreases the objective function ℓ at every iteration and converges to a local solution of (6).

Theorem 3. Let {β^(t)} be the sequence defined by (7). Assume that $u\ge 2{\lambda }_{\max }\left({\mathbf{X}}^{\top }\mathbf{X}\right)$ where ${\lambda }_{\max }\left({\mathbf{X}}^{\top }\mathbf{X}\right)$ denotes the largest eigenvalue of ${\mathbf{X}}^{\top }\mathbf{X}$ Then

• (a)ℓ{β^(t)} ≥ {β^(t+1)} for every integer t.
• (b)Assume that the parameter space $\mathcal{B}$ Assumeis a compact subset of ${ℝ}^p$ Assumeand contains the true parameter value β₀. If ${\sum }_S{\mathbf{w}}_S{\mathbf{w}}_{{}_S}^{\top }\succ 0$ for all submodels s such that ||s||₀ ≤ k, then {β^(t)} converges to a local solution to (6).

Let $s_0=\left\{j:{\beta }_{0j}\ne 0\right\}$ denote the true model and ${\widehat{s}}_{\mathrm{sLSE}}=\left\{j:{\widehat{\beta }}_{\mathrm{sLSE},j}\ne 0\right\}$ the screened model via the sparsity-restricted least squares estimate ${\widehat{\mathit{\beta }}}_{\mathrm{sLSE}}$ The following conditions are needed to establish the sure screening property of ŝ_sLSE.

• (D1)There exist ω₁, ω₂ > 0 and some nonnegative constants τ₁, τ₂ such that τ₁ + τ₂ < 1/2, ${\min }_{j\in s_0}\left|{\beta }_{0j}\right|\ge {\omega }_1{n}^{-{\tau }_1}$ and q_n < k ≤ ω₂n^τ2.
• (D2)ln(p_n) = O(n^d) for some d ∈ [0, 1 − 2τ₁ − 2τ₂).
• (D3)There exist constants c₁ > 0, δ₁ > 0 such that for sufficiently large n, ${\lambda }_{\min }\left(n^{-1}{\mathbf{X}}_s^{\top }{\mathbf{X}}_s\right)\ge c_1$ for ${\mathit{\beta }}_s\in \left\{{\mathit{\beta }}_s:{\Vert {\mathit{\beta }}_s-{\mathit{\beta }}_{s0}\Vert }_2\le {\delta }_1\right\}$ and $s\in S_{+}^{2k}=\left\{s:s_0\subset s,{\Vert s\Vert }_0\le 2k\right\}$ where λ_min denotes the smallest eigenvalue of a matrix.
• (D4)Let ${\sigma }_i^2=\mathrm{var}\left(y_i\right)$ There exist positive constants c₂, c₃, c₄, σ such that $\left|x_{ij}\right|\le c_2,\left|{\mathbf{w}}_i^{\top }{\mathit{\beta }}_0\right|\le c_3,\left|{\sigma }_i\right|\le \sigma$ and for sufficiently large n,

$$\underset{1\le j\le p}{\max }\underset{1\le i\le n}{\max }\left\{\frac{x_{ij}^2}{{\displaystyle {\sum }_{i=1}^n{x}_{ij}^2{\sigma }_i^2}}\right\}\le c_4{n}^{-1}.$$

Theorem 4. (Sure Joint Screening Property) Under conditions (D1)–(D4), $\mathrm{Pr}\left(s_0\subset {\widehat{s}}_{\mathrm{sLSE}}\right)\to 1asn\to \infty$.

Finally, let ${\widehat{\mathit{\beta }}}_{\mathrm{sLSE}-\mathrm{BAR}}$ be BAR estimator for the screened submodel

$$\mathbf{y}={\displaystyle \sum _{j\in {\widehat{s}}_{\text{sLSE}}}{x}_j{\beta }_j+\mathit{\epsilon }}.$$ (8)

It then follows immediately from Theorems 1, 2 and 4 that under conditions (D1)–(D4), ${\widehat{\mathit{\beta }}}_{\mathrm{sLSE}-\mathrm{BAR}}$ has the oracle properties for variable selection and parameter estimation and the grouping property for highly correlated covariates, provided that Model (8) satisfies conditions (C1)–(C3).

4. Simulation study

4.1. Variable selection, estimation, and prediction

We first present a simulation to illustrate the performance of BAR for variable selection, parameter estimation, and prediction in comparison with some L₁-based variable selection methods (Lasso, adaptive Lasso, SCAD and MCP) and a surrogate L₀ method (TLP) [40] under some low-dimensional settings when p ≤ n. Here we consider two linear models, viz.

$$\mathrm{Model}1:\mathrm{True}\mathrm{parameter}{\mathit{\beta }}_0={\left(2,-3,0,0,4,0,\dots ,0\right)}^{\top },$$

$$\mathrm{Model}2:\mathrm{True}\mathrm{parameter}{\mathit{\beta }}_0={\left(2,-3,0,0,4,0.2,–0.3,0,0,0.4,0,\dots ,0\right)}^{\top },$$

where in both models, the p-dimensional covariate vector X is generated from a multivariate Gaussian distribution with mean 0 and variance-covariance matrix Σ = (r^|i−j|), and the error ε is Gaussian and independent of the covariates. Model 1 has sparse strong signals and Model 2 contains a mix of both strong and weak signals. Five-fold CV was used to select tuning parameters for each method. For BAR, we used ten grid points evenly spaced on the interval [10⁻⁴, 100] for ξ_n and ten equally spaced grid points on [1, 10] for λ_n. We observed from our limited experience that BAR is insensitive to the choice of ξ_n and its solution path is essentially flat over a broad range of ξ_n. So the selection of λ_n is more relevant. In this simulation, we used only ten grid points to reduce the computational burden. In practice, however, a more refined grid for λ_n would generally be preferred. We used the R package glmnet [18] for Lasso, adaptive Lasso and ncvreg [5] for SCAD and MCP in our simulations. The TLP method [40] requires to specify a resolution tuning parameter τ. To illustrate the impact of τ, we considered two τ values (0.15 and 0.5), although a data-driven τ would be used in practice as demonstrated in [40]. We considered a variety of scenarios by varying n, p, and r for each of the above two models, but only present partial results in Tablel 1 due to space limitation.

Table 1:

(Low-dimensional settings: n = 100, p ∈ {10, 50, 100} Comparison of BAR, Lasso, SCAD, MCP, and Adaptive Lasso (ALasso) and TLP based on 100 Monte-Carlo samples. (Misclassification = mean number of misclassified non-zeros and zeros; FP = mean number of false positives (non-zeros); FN = mean number of false negatives (zeros); TM = probability that the selected model is exactly the true model; MAB = mean absolute bias; MSPE = mean squared prediction error from five-fold CV.)

Model	p	Method	Misclassification	FP	FN	TM	MAB	MSPE
1	10	BAR	0.08	0.08	0	93%	0.26	1.02
		Lasso	3.28	3.28	0	6%	0.56	1.08
		SCAD	0.90	0.90	0	62%	0.34	1.03
		MCP	0.72	0.72	0	68%	0.33	1.03
		ALasso	0.26	0.26	0	89%	0.29	1.03
		TLP(0.15)	0.54	0.54	0	63%	0.34	1.04
		TLP(0.5)	0.64	0.64	0	77%	0.31	1.04
	50	BAR	0.26	0.26	0	86%	0.32	1.04
		Lasso	7.75	7.75	0	2%	0.95	1.18
		SCAD	1.81	1.81	0	65%	0.37	1.05
		MCP	0.97	0.97	0	73%	0.34	1.05
		ALasso	3.99	3.99	0	40%	0.68	1.03
		TLP(0.15)	0.98	0.98	0	60%	0.45	1.05
		TLP(0.5)	1.51	1.51	0	77%	0.36	1.08
	100	BAR	0.44	0.44	0	80%	0.35	1.02
		Lasso	10.38	10.38	0	2%	1.08	1.2
		SCAD	1.41	1.41	0	65%	0.31	1.03
		MCP	1.04	1.04	0	66%	0.32	1.03
		ALasso	1.51	1.51	0	32%	0.42	1.08
		TLP(0.15)	1.31	1.31	0	55%	0.46	1.02
		TLP(0.5)	2.21	2.21	0	70%	0.38	1.05
2	10	BAR	1.14	0.12	1.02	30%	0.67	1.11
		Lasso	2.70	2.61	0.09	5%	0.76	1.11
		SCAD	1.87	1.58	0.29	14%	0.74	1.1
		MCP	1.69	1.27	0.42	19%	0.74	1.1
		ALasso	1.55	1.11	0.44	18%	0.69	1.07
		TLP(0.15)	1.02	0.40	0.62	33%	0.66	1.07
		TLP(0.5)	2.27	1.87	0.4	9%	0.74	1.09
	50	BAR	2.18	0.68	1.5	4%	0.94	1.17
		Lasso	10.56	10.09	0.47	0%	1.51	1.29
		SCAD	5.36	4.32	1.04	1%	1.06	1.19
		MCP	3.33	2.1	1.23	4%	0.99	1.19
		ALasso	8.22	7.38	0.84	0%	1.41	1.1
		TLP(0.15)	2.25	1.36	1.19	7%	1.03	1.1
		TLP(0.5)	6.07	5.13	0.94	3%	1.09	1.2
	100	BAR	2.67	0.94	1.73	2%	1.05	1.17
		Lasso	14.63	14.02	0.61	0%	1.79	1.34
		SCAD	4.24	3.08	1.16	1%	1.01	1.21
		MCP	3.34	1.99	1.35	3%	0.96	1.2
		ALasso	4.42	2.27	2.15	1%	1.26	1.32
		TLP(0.15)	3.14	1.88	1.26	2%	1.03	1.08
		TLP(0.5)	7.67	6.71	0.96	1%	1.17	1.19

From Table 1, it appears that the BAR and TLP methods generally produce more sparse models than the L₁-based methods, with BAR having the lowest number of false positives (nonzeros). When the signals are strong (Model 1), BAR demonstrates better performance in most categories with (i) better variable selection performance (the lowest number of misclassifications (non-zeros and zeros), lowest false positives, highest probability of selecting the true model (TM), and equally low false rate (close to 0)); (ii) better estimation performance (the smallest estimation bias, MAB); and (iii) for equally good prediction performance (similar mean squared prediction error (MSPE)).

Similar trends are observed for Model 2, in which there are both strong and weak signals. BAR still produces the sparsest model with the lowest positive false positive rate and lowest number of misclassifications, but it tends to miss the small effects with more false negatives. For estimation, BAR has comparable or smaller bias, but no method dominates others across all scenarios. For prediction, all methods had comparable performance with similar MSPE.

Because some signals are weak and the sample size n = 100 is relatively small, it is challenging for all methods to select the exact correct model (TM close to zero), but for different reasons: BAR tends to miss some small signals with more false negatives (zeros) whereas the other methods tend to include some zeros as signals with more false positives. Moreover, as a surrogate L₀ method, the TLP method generally produces a more sparse model than an L₁-based method. In principle, the TLP method with a smaller τ value gives a closer approximation to L₀ penalization and thus leads to a more sparse model as shown in Table A.1. In practice, however, τ cannot be too small since the TLP estimate obtained from Algorithm 1 in [40] would be no more sparse than its initial Lasso estimator.

In summary, BAR shows an advantage of more accurately selecting and estimating strong signals. On the other hand, if weak signals are also of interest and the sample size is relatively small, then an L₁-based method with smaller false negatives might be preferred.

4.2. Grouping effect

We now present a simulation to illustrate the grouping effect of BAR for highly correlated covariates. Assume y = Xβ₀ + ε with p_n = 9 and β₀ = (2, 2, 2, 0.4, 0.4, 0.4, 0, 0, 0), where $\mathit{\epsilon }~\mathcal{N}\left(\mathbf{0},0.2^2{\mathbf{I}}_n\right)$ and

$$\{\begin{array}{ll}{x}_i=z_1+e_i,z_1~\mathcal{N}\left(0,{30}^2{I}_n\right)\hfill & \text{for }i\in \left\{1,2,3\right\},\hfill \\ x_i=z_2+e_i,z_2~\mathcal{N}\left(0,{30}^2{I}_n\right)\hfill & \text{for }i\in \left\{4,5,6\right\},\hfill \\ x_i~\mathcal{N}\left(0,{30}^2{I}_n\right)\hfill & \text{for }i\in \left\{7,8,9\right\},\hfill \end{array}$$

where e_i are independent $\mathcal{N}\left(\mathbf{0},0.1^2{\mathbf{I}}_n\right)$. In this setting, x₁, x₂, and x₃ form a group with latent factor z₁, and x₅, x₆, and x₇ form another group with latent factor z₂. The with-in group correlations are almost 1 and the between-group correlations are almost 0. Figure 2 plots the solution paths of BAR, Elastic Net, Lasso, Adaptive Lasso, SCAD, and MCP for a random sample of size n = 200. The estimated coefficients and cross-validation errors together with the corresponding optimal tuning parameters are provided in Table 2.

Figure 2:

Path plots of BAR, Elastic Net, Lasso, SCAD, Adaptive Lasso, and MCP for a linear model with two groups of highly correlated covariates with true coefficients β_j = 2 for j =1,2, and 3; β_j = 0.5 for j = 4, 5, and 6; and β_j = 0 for j ≥ 7, as described in Section 3.2. For BAR, we fixed ξ_n = 100. For Elastic Net, the fixed tuning parameter is λ₂ = 0.001 and SCAD with γ = 3.7, Adaptive Lasso with ξ = 18.68, MCP with γ = 3. The dashed vertical lines are the optimal tuning parameters obtained by 5-fold CV with lowest CV error and the corresponding estimated coefficients are provided in Table 2.

Table 2:

(Grouping effects) Estimated coefficients of BAR, Elastic Net, Lasso, SCAD, Adaptive Lasso, and MCP for a linear model with optimal tuning parameters selected by five-fold CV. The full solution paths are depicted in Figure 2.

Parameter	BAR	Elastic Net	Lasso	SCAD	Adaptive Lasso	MCP
(Intercept)	−0.008	−0.004	−0.005	0.031	−0.009	0.029
β1	1.902	2.000	2.137	6.001	1.585	6.001
β2	2.016	1.998	1.441		1.908
β3	2.081	1.999	2.421		2.506
β4	0.499	0.406	0.894	1.200	1.153	1.200
β5	0.469	0.401	0.292		0.047
β6	0.233	0.392	0.013
β7				−0.001
β8
β9
Tuning	ξn = 100	λ1 = 0.017	λ = 0.017	γ = 3.7,	ξ = 18.68	γ = 3,
parameters	λn = 0.043	λ2 = 0.001		λ = 0.044	λ = 0.001	λ = 10.861
CV Error	0.038	0.045	0.331	0.048	0.043	0.330

It is seen from Figure 2 and Table 2 that both BAR and Elastic Net selected all three variables in each of the two non-zero groups with almost evenly distributed coefficients within each group, whereas Lasso, adaptive Lasso, SCAD, and MCP failed to reveal any grouping information with disorganized paths and erratic coefficient estimates.

4.3. High-dimensional settings (p ≫ n)

We finally present a simulation to illustrate the performance of BAR in comparison with some other variable selection methods when combined with the sparsity-restricted least squares estimate-based screening method in a high-dimensional setting. Specifically, we consider Models 1 and 2 in Section 3.1, but increase p to 2000. The simulation results for the two-stage estimators with n = 100 are presented in Table 3.

Table 3:

(High-dimensional settings: n = 100, p = 2000) Comparison of BAR, Lasso, SCAD, MCP, Adaptive Lasso (ALasso), and TLP Following the Sparsity-Restricted Least Squares Estimate (sLSE). (Misclassification = Mean Number of Misclassified Non-zeros and Zeros; FP = Mean Number of False Positives (Non-zeros); FN = Mean Number of False Negatives (Zeros); TM = Probability that the Selected Model is Exactly the True Model; MAB = Mean Absolute Bias; MSPE = Mean Squared Prediction Error from Five-Fold CV.)

Model	Method	Misclassification	FP	FN	TM	MAB	MSPE
1	sLSE-BAR	0.32	0.18	0.14	75.72%	0.55	1.04
	sLSE-Lasso	5.10	4.96	0.14	3.8%	0.97	1.13
	sLSE-SCAD	0.94	0.80	0.14	64.60%	0.57	1.05
	sLSE-MCP	0.67	0.53	0.14	68.32%	0.57	1.05
	sLSE-ALasso	0.92	0.78	0.14	63.88%	0.61	1.05
	sLSE-TLP(0.15)	0.74	0.60	0.14	56.56%	0.64	1.06
	sLSE-TLP(0.5)	0.89	0.75	0.14	67.72%	0.57	1.06
2	sLSE-BAR	0.30	0.18	0.12	0%	1.45	1.04
	sLSE-Lasso	5.09	4.98	0.11	0%	1.87	1.13
	sLSE-SCAD	0.95	0.83	0.12	0%	1.47	1.05
	sLSE-MCP	0.66	0.54	0.12	0%	1.47	1.05
	sLSE-ALasso	0.93	0.81	0.12	0%	1.51	1.05
	sLSE-TLP(0.15)	0.72	0.60	0.12	0%	1.53	1.06
	sLSE-TLP(0.5)	0.91	0.79	0.12	0%	1.47	1.07

It is seen that for both Models 1 and 2, sLSE-BAR outperformed other methods for variable selection and parameter estimation with a lower number of misclassifications, fewer false positives, and a smaller estimation bias (MAB). Consistent with the low-dimensional settings, BAR shows similar prediction performance to the other methods. Again it is challenging for all methods to select exactly the true model under Model 2 when there are both strong and weak signals, but our limited simulations (not presented here) showed that TM (the probability of selecting the correct model) will improve, especially for BAR, as n increases.

5. Data examples

5.1. Prostate cancer data

As an illustration, we analyze the prostate cancer data described in [42]. There are eight clinical predictors, namely ln(cancer volume) (lcavol), ln(prostate weight) (lweight), age, ln(amount of benign prostatic hyperplasia) (lpbh), seminal vesicle invasion (svi), ln(capsular penetration) (lcp), Gleason score (gleason) and percentage Gleason scores 4 or 5 (pgg45). We consider the problem of selecting important predictors for the logarithm of prostate-specific antigen (lpsa). We randomly split the data set into a training set of size 67 and a test set of size 30, and compare the results of six variable selection methods: BAR, lasso, adaptive lasso, SCAD, MCP and Elastic Net by selecting nonzero features based on the training data set and test error as the mean squared prediction error on the test data set. We performed an analysis with p = 36 features consisting of all the main effects and two-way interactions. The five-fold CV method was used to select the optimal ξ_n and λ_n values for BAR, with 100 evenly-spaced grid points on the interval [10⁻⁴, 100] for ξ_n, and 100 equally-spaced grid points on [1, 100] for λ_n. The estimated coefficients are given in Table 4, together with a summary of the number of selected features and test errors for each method.

Table 4:

Coefficients of selected features and test mean squared prediction error for a prostate data (with p = 36 main effects and two-way interactions)

Variable	BAR	Lasso	SCAD	MCP	Adaptive Lasso	Elastic Net
lcavol	0.573	0.560	0.637	0.627	0.594	0.264
lweight					0.020	0.056
Age		−0.028	−0.073	−0.149	−0.077	−0.053
lbph						0.070
svi		0.125	0.422	0.440	0.141	0.090
lcp						0.001
gleason						0.013
(lcavol)×(lweight)						0.068
(lcavol)×(age)						0.036
(lcavol)×(svi)	0.341	0.216			0.233	0.150
(lcavol)×(gleason)						0.196
(lweight)×(gleason)	0.315	0.238	0.243	0.305	0.259	0.171
(age)×(lbph)		0.184	0.277	0.282	0.194	0.098
(age)×(svi)						0.045
(lbph)×(gleason)						0.021
(svi)×(gleason)		0.030				0.090
(lcp)×(pgg45)			−0.019	−0.067
Tuning	ξn = 44.45	λ = 0.08	γ = 3.7	γ = 3	ξ = 1.16	λ1 = 0.06
Parameters	λn = 0.1		λ = 0.08	λ = 0.07	λ = 0.21	λ2 = 0.1
Number of Selected Features	3	7	6	6	7	16
Test Error	0.461	0.484	0.587	0.583	0.513	0.498

It is seen that BAR produces the sparsest model with three nonzero features as compared with at least six nonzero features by the other methods. Its prediction performance is comparable to other methods with a slightly lower test error. This is consistent with the simulation results in Section 4.1.

5.2. Gut microbiota data

In this example, we illustrate our method on a metagenomic dataset on gut microbiota that was downloaded from dbGaP under study ID phs000258 [53]. After aligning the 16S rRNA sequences of gut microbiota to reference sequences and taxonomy databases, we had a total of 240 taxa at the genus level. Here we are interested in identifying BMI associated taxa. Because taxa with small reads are not reliable and subject to noise and measurement error, we first dropped the taxa with average reads below 2, resulting in 62 features. For each taxon, we created a dummy variable 1(value of taxon > 25th quantile of the taxon). We used 304 patients after removing missing values. As in the previous example, we randomly split the data set into a training set of size 228 to select nonzero features and a test set of size 76 to compute the mean squared prediction error (MSPE). Table 5 gives the selected taxa, together with a summary of the number of selected features and test errors for each of six methods: BAR, lasso, adaptive lasso, SCAD, MCP and Elastic Net.

Table 5:

Coefficients of selected BMI-related features and test mean squared prediction error for a gut microbiota metagenomic data

Taxon	BAR	Lasso	SCAD	MCP	Adaptive Lasso	Elastic Net
Acetanaerobacterium						−0.064
Acidaminococcus						−0.014
Akkermansia						0.233
Anaerotruncus						−0.105
Asteroleplasma						−0.058
Bacteroides						−0.110
Barnesiella						0.195
Butyricicoccus						−0.046
Butyrivibrio						0.205
Catenibacterium						0.198
Clostridium						−0.259
Collinsella	1.066	0.669	0.689	0.867	0.908	0.708
Coprobacillus		−0.165	−0.133	−0.064	−0.216	−0.295
Coprococcus						0.014
Desulfovibrio		−0.082	−0.049		−0.122	−0.308
Escherichia Shigella						0.081
Eubacterium						0.021
Faecalibacterium	−0.610	−0.389	−0.352	−0.352	−0.584	−0.591
Hydrogenoanaerobacterium		0.099	0.044		0.223	0.409
Lachnobacterium						0.294
Lactobacillus						0.115
Megasphaera	0.761	0.458	0.410	0.470	0.716	0.639
Odoribacter						−0.024
Parabacteroides						−0.043
Prevotella						0.335
Rikenella						−0.065
Robinsoniella		−0.113	−0.088	−0.050	−0.124	−0.344
Sporobacter						−0.102
Streptococcus						0.050
Subdoligranulum						−0.018
Succiniclasticum		0.119	0.080		0.211	0.344
Succinivibrio						0.238
Sutterella		−0.001				−0.224
Treponema					−0.115
Turicibacter	−0.996	−0.622	−0.615	−0.807	−0.846	−0.611
Xylanibacter						0.160
Tuning	ξn = 77.78	λ = 0.54	γ = 3.7	γ=3	ξ = 14.19	λ1 = 0.19
Parameters	λn = 38		λ = 0.57	λ = 0.66	λ = 3.67	λ2 = 0.26
Number of Selected Taxa	4	10	9	6	9	36
Test Error	28.630	28.189	28.311	28.230	27.926	27.062

Consistent with the simulation results in Section 3, BAR yields the sparsest model (four nonzero features as compared to at least six nonzero features by the other methods) with similar test errors to other methods. Among the four identified taxa by BAR, Faecalibacterium is well known to be associated with obesity. For example, some recent studies showed that Faecalibacterium increases significantly in lean people and has a negative association with BMI [2, 23]. The other three taxa (Collinsella, Megasphaera, and Turicibacter) have also been shown to be correlated with obesity and BMI in animal models and clinical trials [3, 16, 26].

6. Discussion

We have established an oracle property and a grouping property for the BAR estimator, a sparse regression estimator resulted from an L₀-based iteratively reweighted L₂-penalized regressions using a ridge estimator as the initial value. Hence, BAR enjoys the best of both L₀ and L₂ penalized regressions while avoiding their pitfalls. For example, BAR shares the consistency properties of L₀-penalized regression for variable selection and parameter estimation, avoids its instability, and is computationally more scalable to high-dimensional settings. BAR can also be viewed as a sparse version of the ridge estimator obtained by shrinking the small ridge coefficients to zeros via an approximate L₀-penalized regression and consequently inherits the stability and grouping effect of the ridge estimator. In addition to the low-dimensional setting (p < n), we have extended the BAR method to high- or ultrahigh-dimensional settings when p is larger and potentially much larger than n, by combining it with a sparsity-restricted least squares estimate and provided conditions under which the two-stage estimator possesses the oracle property and grouping property.

We have conducted extensive simulations to study the operating characteristics of the L₀-based BAR method in comparison with some popular L₁-based variable selection methods. It was observed that as an L₀-based method, BAR tends to produce a more sparse model with lower false positive rate and comparable prediction performance, and generally can select and estimate strong signals more accurately with a lower misclassification rate and a smaller estimation bias. In contrast, it is more likely to shrink weak signals to null when the sample size is not very large. Therefore, in practice, one may choose between an L₁-based method and an L₀-based method such as BAR based on whether or not weak signals are of interest.

Our theoretical developments for the asymptotic properties of the L₀-based BAR estimator can be easily modified to analyze large sample properties of an L_d-based BAR estimator obtained by replacing ${\tilde{\beta }}_j^{-2}$ with ${\left|{\tilde{\beta }}_j\right|}^{d-2}$ in Eq. (3) for any d ∈ [0, 1]. Our simulations (not reported in this version of the paper) suggests that there is a trade-off between the false positive rate and false negative rate as d varies. Specifically, as d increases from 0 to 1, the L_d-based BAR estimator becomes less sparse with an increased false positive rate but decreased false negative rate.

Finally, this paper focuses on the linear model. Extensions to more complex models and applications such as generalized linear models and survival data are currently under investigation by our team.

Appendix A. Proofs of the theorems

To prove Theorems 1–4, we need to introduce some notations and lemmas. Write $\mathit{\beta }={\left({\mathit{\alpha }}^{\top },{\mathit{\gamma }}^{\top }\right)}^{\top }$ where α is a q_n × 1 vector and γ is a (p_n − q_n) × 1 vector. Analogously, write ${\widehat{\mathit{\beta }}}^{\left(k\right)}={\left({\widehat{\mathit{\alpha }}}^{\left(k\right)\mathrm{T}},{\widehat{\mathit{\gamma }}}^{\left(k\right)\mathrm{T}}\right)}^{\top }$ and

$$g\left(\mathit{\beta }\right)={\left\{X^{\top }X+{\lambda }_{n}D\left(\mathit{\beta }\right)\right\}}^{-1}{X}^{\top }y={\left\{{\mathit{\alpha }}^{*}{\left(\mathit{\beta }\right)}^{\top },{\mathit{\gamma }}^{*}{\left(\mathit{\beta }\right)}^{\top }\right\}}^{\top }.$$ (A.1)

For simplicity, we write α*(β) and γ* (β) as α* and γ* hereafter. We further partition ${\sum }_n^{-1}$ as

$${\Sigma }_n^{-1}=\left(\begin{array}{ll}{A}_{11}\hfill & A_{12}\hfill \\ A_{12}^{\top }\hfill & A_{22}\hfill \end{array}\right)$$

where the A₁₁ is a q_n × q_n matrix. Then, multiplying ${\left({\mathbf{X}}^{\top }\mathbf{X}\right)}^{-1}\left\{{\mathbf{X}}^{\top }\mathbf{X}+{\lambda }_n\mathbf{D}\left(\mathit{\beta }\right)\right\}$ to Eq. (A.1) gives

$$\left(\begin{array}{c}{\mathit{\alpha }}^{*}-{\mathit{\beta }}_{01}\\ {\mathit{\gamma }}^{*}\end{array}\right)+\frac{{\lambda }_n}{n}\left(\begin{array}{l}{A}_{11}{D}_1\left(\mathit{\alpha }\right){\mathit{\alpha }}^{*}+A_{12}{D}_2\left(\mathit{\gamma }\right){\mathit{\gamma }}^{*}\hfill \\ A_{12}^{\text{T}}{D}_1\left(\mathit{\alpha }\right){\mathit{\alpha }}^{*}+A_{22}{D}_2\left(\mathit{\gamma }\right){\mathit{\gamma }}^{*}\hfill \end{array}\right)={\left(X^{\top }X\right)}^{-1}{X}^{\top }\mathit{\epsilon },$$ (A.2)

where ${\mathbf{D}}_1\left(\mathit{\alpha }\right)=\mathrm{diag}\left({\alpha }_1^{-2},\dots ,{\alpha }_{q_n}^{-2}\right)$ and ${\mathbf{D}}_2\left(\mathit{\gamma }\right)=\mathrm{diag}\left({\gamma }_1^{-2},\dots ,{\gamma }_{p_n-q_n}^{-2}\right)$.

Lemma 1. Let δ_n be a sequence of positive real numbers satisfying δ_n → ∞ and $p_n{\delta }_n^2/{\lambda }_n\to 0$ Define ${\mathbf{H}}_n=\left\{\mathit{\beta }\in {ℝ}^{p_n}:\Vert \mathit{\beta }-{\mathit{\beta }}_0\Vert \le {\delta }_n\sqrt{p_n/n}\right\}$ and ${\mathbf{H}}_{n1}\equiv \left\{\mathit{\alpha }\in {ℝ}^{q_n}:\Vert \mathit{\alpha }-{\mathit{\beta }}_{01}\Vert \le {\delta }_n\sqrt{p_n/n}\right\}$. Assume conditions (C1)−(C3) hold. Then, with probability tending to 1, we have

• (a)${\sup }_{\mathit{\beta }\in {\mathbf{H}}_n}\Vert {\mathit{\gamma }}^{\ast }\Vert /\Vert \mathit{\gamma }\Vert <1/C_0$ for some constant C₀ > 1;
• b)g is a mapping from H_n to itself.

Proof. We first prove part (a). Because ${\lambda }_n/\sqrt{n}\to 0$ and $p_n{\delta }_n^2/{\lambda }_n\to 0$, we have ${\delta }_n\sqrt{p_n/n}\to 0$. By (C2), $n\mathrm{E}\left({\Vert \widehat{\mathit{\beta }}\left(\mathit{OLS}\right)-{\mathit{\beta }}_0\Vert }^2\right)=n\mathrm{E}\left({\Vert {\left({\mathbf{X}}^{\top }\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\top }\mathit{\epsilon }\Vert }^2\right)={\sigma }^2\mathrm{trace}\left({\sum }_n^{-1}\right)=O\left(p_n\right)$ Hence, ${\Vert \widehat{\mathit{\beta }}\left(\mathrm{OLS}\right)-{\mathit{\beta }}_0\Vert }^2=O_p\left(p_n/n\right)$. It then follows from (A.2) that

$$\underset{\beta \in H_n}{\sup }\Vert {\mathit{\gamma }}^{*}+{\lambda }_n{A}_{12}^{\top }{D}_1\left(\mathit{\alpha }\right){\mathit{\alpha }}^{*}/n+{\lambda }_n{A}_{22}{D}_2\left(\mathit{\gamma }\right){\mathit{\gamma }}^{*}/n\Vert =O_p\left(\sqrt{p_n/n}\right).$$ (A.3)

Note that $\Vert \mathit{\alpha }-{\mathit{\beta }}_{01}\Vert \le {\delta }_n{\left(p_n/n\right)}^{1/2}$ and $\Vert {\mathit{\alpha }}^{\ast }\Vert \le \Vert g\left(\mathit{\beta }\right)\Vert \le \Vert \widehat{\mathit{\beta }}\left(\mathrm{OLS}\right)\Vert =O_p\left(a_{1n}\sqrt{p_n}\right)$ By assumptions (C2) and (C3), we have

$$\underset{\mathit{\beta }\in H_n}{\sup }\Vert {\lambda }_n{A}_{12}^{\top }{D}_1\left(\mathit{\alpha }\right){\mathit{\alpha }}^{*}/n\Vert \le \frac{{\lambda }_n}{n}\Vert A_{12}^{\top }\Vert \underset{\mathit{\beta }\in H_n}{\sup }\Vert D_1\left(\mathit{\alpha }\right){\mathit{\alpha }}^{*}\Vert \le \sqrt{2}C\frac{{\lambda }_n}{n}\frac{a_{1n}}{a_{0n}^2}\underset{\mathit{\beta }\in H_n}{\sup }\Vert {\mathit{\alpha }}^{*}\Vert =o_p(\sqrt{p_n/n}),$$ (A.4)

where the second inequality uses the fact $\Vert {\mathbf{A}}_{12}^{\top }\Vert \le \sqrt{2}C$, which follows from the inequality $\Vert {\mathbf{A}}_{12}{\mathbf{A}}_{12}^{\top }\Vert -\Vert {\mathbf{A}}_{11}^2\Vert \le \Vert {\mathbf{A}}_{11}^2+{\mathbf{A}}_{12}{\mathbf{A}}_{21}\Vert \le \Vert {\sum }_n^{-2}\Vert <C^2$. Combining (A.3) and (A.4) gives

$$\underset{\mathit{\beta }\in H_n}{\sup }\Vert {\mathit{\gamma }}^{*}+{\lambda }_n{A}_{22}{D}_2\left(\mathit{\gamma }\right){\mathit{\gamma }}^{*}/n\Vert =O_p(\sqrt{p_n/n}).$$ (A.5)

Note that A₂₂ is positive definite and by the singular value decomposition, ${\mathbf{A}}_{22}={\displaystyle {\sum }_{i=1}^{p_n-q_n}{\tau }_{2i}{\mathbf{u}}_{2i}{\mathbf{u}}_{2i}^{\top }}$, where τ_2i and u_2i are eigenvalues and eigenvectors of A₂₂. Then, since 1/C < τ_2i < C, we have

$$\begin{gathered} \frac{{\lambda }_n}{n}\Vert A_{22}{D}_2\left(\mathit{\gamma }\right){\mathit{\gamma }}^{*}\Vert =\frac{{\lambda }_n}{n}\Vert {\displaystyle \sum _{i=1}^{p_n-q_n}{\tau }_{2i}{u}_{2i}{u}_{2i}^{\text{T}}{D}_2\left(\mathit{\gamma }\right){\mathit{\gamma }}^{*}}\Vert =\frac{{\lambda }_n}{n}{\left\{{\displaystyle \sum _{i=1}^{p_n-q_n}{\tau }_{2i}^2{\Vert u_{2i}^{\text{T}}{D}_2\left(\mathit{\gamma }\right){\mathit{\gamma }}^{*}\Vert }^2}\right\}}^{1/2} \\ \ge \frac{{\lambda }_n}{n}\frac{1}{C}{\left\{{\displaystyle \sum _{i=1}^{p_n-q_n}{\Vert u_{2i}^{\text{T}}{D}_2\left(\mathit{\gamma }\right){\mathit{\gamma }}^{*}\Vert }^2}\right\}}^{1/2}=\frac{1}{C}\Vert {\lambda }_n{D}_2\left(\mathit{\gamma }\right){\mathit{\gamma }}^{*}/n\Vert . \end{gathered}$$

This, together with (A.5) and (C2), implies that with probability tending to 1,

$$\frac{1}{C}\Vert {\lambda }_n{D}_2\left(\mathit{\gamma }\right){\mathit{\gamma }}^{*}/n\Vert -\Vert {\mathit{\gamma }}^{*}\Vert \le {\delta }_n\sqrt{p_n/n}.$$ (A.6)

Let ${\mathbf{d}}_{{\gamma }^{*}/\gamma }={\left({\gamma }_1^{\ast }/{\gamma }_1,\dots ,{\gamma }_{p_n-qn}^{\ast }/{\gamma }_{p_n-qn}\right)}^{\top }$. Because $\Vert \mathit{\gamma }\Vert \le {\delta }_n\sqrt{p_n/n}$ we have

$$\frac{1}{C}\Vert \frac{{\lambda }_n}{n}{D}_2\left(\mathit{\gamma }\right){\mathit{\gamma }}^{*}\Vert =\frac{1}{C}\frac{{\lambda }_n}{n}\Vert {\left\{D_2\left(\mathit{\gamma }\right)\right\}}^{1/2}{d}_{{\mathit{\gamma }}^{*}/\mathit{\gamma }}\Vert \ge \frac{1}{C}\frac{{\lambda }_n}{n}\frac{\sqrt{n}}{{\delta }_n\sqrt{p_n}}\Vert d_{{\mathit{\gamma }}^{*}/\mathit{\gamma }}\Vert$$ (A.7)

and

$$\Vert {\mathit{\gamma }}^{*}\Vert =\Vert D_2{\left(\mathit{\gamma }\right)}^{-1/2}{d}_{{\mathit{\gamma }}^{*}/\mathit{\gamma }}\Vert \le \frac{{\delta }_n\sqrt{p_n}}{\sqrt{n}}\Vert d_{{\mathit{\gamma }}^{*}/\mathit{\gamma }}\Vert .$$ (A.8)

Combining (A.6), (A.7) and (A.8), we have that with probability tending to 1,

$$\Vert d_{{\mathit{\gamma }}^{*}/\mathit{\gamma }}\Vert \le \frac{1}{{\lambda }_n/\left(p_n{\delta }_n^{2}C\right)-1}<1/C_0$$ (A.9)

for some constant C₀ > 1 provided that ${\lambda }_n/\left(p_n{\delta }_n^2\right)\to \infty$ It is worth noting that $\mathrm{Pr}\left(\Vert {\mathbf{d}}_{\mathit{\gamma }\ast /\mathit{\gamma }}\Vert \to 0\right)\to 1$, as n → ∞.

Furthermore, with probability tending to 1,

$$\Vert {\mathit{\gamma }}^{*}\Vert \le \Vert d_{{\mathit{\gamma }}^{*}/\mathit{\gamma }}\Vert \underset{1\le j\le \left(p_n-q_n\right)}{\max }\left|{\mathit{\gamma }}_j\right|\le \Vert d_{{\mathit{\gamma }}^{*}/\mathit{\gamma }}\Vert \times \Vert \mathit{\gamma }\Vert \le \Vert \mathit{\gamma }\Vert /C_0.$$

This proves part (a).

Next we prove part (b). First, it is easy to see from (A.8) and (A.9) that, as n → ∞,

$$\mathrm{Pr}\left(\Vert {\mathit{\gamma }}^{*}\Vert \le {\delta }_n\sqrt{p_n/n}\right)\to 1.$$ (A.10)

Then, by (A.2), we have

$$\underset{\mathit{\beta }\in H_n}{\sup }\Vert {\mathit{\alpha }}^{*}-{\mathit{\beta }}_{01}+{\lambda }_n{A}_{11}{D}_1\left(\mathit{\alpha }\right){\mathit{\alpha }}^{*}/n+{\lambda }_n{A}_{12}{D}_2\left(\mathit{\gamma }\right){\mathit{\gamma }}^{*}/n\Vert =O_p\left(\sqrt{p_n/n}\right).$$ (A.11)

Similar to (A.4), it is easily to verify that

$$\underset{\mathit{\beta }\in H_n}{\sup }\Vert {\lambda }_n{A}_{11}{D}_1\left(\mathit{\alpha }\right){\mathit{\alpha }}^{*}/n\Vert =o_p\left(\sqrt{p_n/n}\right).$$ (A.12)

Moreover, with probability tending to 1,

$$\underset{\mathit{\beta }\in H_n}{\sup }\Vert {\lambda }_n{A}_{12}{D}_2\left(\mathit{\gamma }\right){\mathit{\gamma }}^{*}/n\Vert \le \frac{{\lambda }_n}{n}\underset{\beta \in H_n}{\sup }\Vert D_2\left(\mathit{\gamma }\right){\mathit{\gamma }}^{*}\Vert \times \Vert A_{12}\Vert \le 2\sqrt{2}{C}^2{\delta }_n\sqrt{p_n/n},$$ (A.13)

where the last step follows from (A.6), (A.10), and the fact that $\Vert {\mathbf{A}}_{12}\Vert \le \sqrt{2}C$ It follows from (A.11), (A.12) and (A.13) that with probability tending to 1,

$$\underset{\mathit{\beta }\in H_n}{\sup }\Vert {\mathit{\alpha }}^{*}-{\mathit{\beta }}_{01}\Vert \le \left(2\sqrt{2}{C}^2+1\right){\delta }_n{n}^{-1/2}\sqrt{p_n}.$$ (A.14)

Because ${\delta }_n\sqrt{p_n}/\sqrt{n}\to 0$ we have, as n → ∞,

$$\mathrm{Pr}\left({\mathit{\alpha }}^{*}\in H_{n1}\right)\to 1.$$ (A.15)

Combining (A.10) and (A.15) completes the proof of part (b).

Lemma 2. Assume that (C1)–(C3) hold. For any q_n-vector b_n satisfying ||b_n|| ≤ 1, define $s_n^2={\sigma }^2{\mathbf{b}}_n^{\top }{\mathbf{\sum }}_{n1}^{-1}{\mathbf{b}}_n$ as in Theorem 1. Define

$$f\left(\mathit{\alpha }\right)={\left\{X_1^{\top }{X}_1+{\lambda }_n{D}_1\left(\alpha \right)\right\}}^{-1}{X}_1^{\top }y.$$ (A.16)

Then, with probability tending to 1,

• (a)f(α) is a contraction mapping from ${\mathbf{B}}_n\equiv \left\{\mathit{\alpha }\in {ℝ}^{q_n}:\Vert \mathit{\alpha }-{\mathit{\beta }}_{01}\Vert \le {\delta }_n\sqrt{p_n/n}\right\}$ to itself;
• (b)$\sqrt{n}{s}_n^{-1}{\mathbf{b}}_n^{\top }\left({\widehat{\mathit{\alpha }}}^{\circ }-{\mathit{\beta }}_{01}\right)⇝\mathcal{N}\left(0,1\right)$ where ${\widehat{\mathit{\alpha }}}^{\circ }$ is the unique fixed point of f (α) defined by

$${\widehat{\mathit{\alpha }}}^{\circ }={\left\{X_1^{\top }{X}_1+{\lambda }_n{D}_1\left({\widehat{\mathit{\alpha }}}^{\circ }\right)\right\}}^{-1}{X}_1^{\top }y.$$

Proof. We first prove part (a). Note that (A.16) can be rewritten as

$$f\left(\mathit{\alpha }\right)-{\mathit{\beta }}_{01}+{\lambda }_n{\displaystyle {\mathbf{\Sigma }}_{n1}^{-1}{D}_1\left(\mathit{\alpha }\right)}f\left(\mathit{\alpha }\right)/n={\left(X_1^{\top }{X}_1\right)}^{-1}{X}_1^{\top }\mathit{\epsilon }.$$

Thus,

$$\underset{\mathit{\alpha }\in B_n}{\sup }\Vert f\left(\mathit{\alpha }\right)-{\mathit{\beta }}_{01}+{\lambda }_n{\displaystyle {\mathbf{\Sigma }}_{n1}^{-1}{D}_1\left(\mathit{\alpha }\right)}f\left(\mathit{\alpha }\right)/n\Vert =O_p\left(\sqrt{q_n/n}\right).$$ (A.17)

Similar to (A.4), it can be shown that

$$\underset{\mathit{\alpha }\in B_n}{\sup }\Vert {\lambda }_n{\displaystyle {\mathbf{\Sigma }}_{n1}^{-1}{D}_1\left(\mathit{\alpha }\right)}f\left(\mathit{\alpha }\right)/n\Vert =o_p\left(\sqrt{q_n/n}\right).$$ (A.18)

It follows from (A.17) and (A.18) that

$$\underset{\mathit{\alpha }\in B_n}{\sup }\Vert f\left(\mathit{\alpha }\right)-{\mathit{\beta }}_{01}\Vert \le {\delta }_n\sqrt{q_n/n},$$

where δ_n is a sequence of real numbers satisfying δ_n → ∞ and ${\delta }_n\sqrt{q_n/n}\to 0$. This implies that, as n → ∞,

$$\mathrm{Pr}\left\{f\left(\mathit{\alpha }\right)\in {\mathbf{B}}_n\right\}\to 1.$$ (A.19)

In other words, f is a mapping from the region B_n to itself.

Rewrite (A.16) as $\left\{{\mathbf{X}}_1^{\top }{\mathbf{X}}_1+{\lambda }_n{\mathbf{D}}_1\left(\mathit{\alpha }\right)\right\}f\left(\mathit{\alpha }\right)={\mathbf{X}}_1^{\top }\mathbf{y}$ and then differentiate it with respect to α, we have

$$\left\{{\Sigma }_{n1}+{\lambda }_n{D}_1\left(\mathit{\alpha }\right)/n\right\}\dot{f}\left(\mathit{\alpha }\right)+\left({\lambda }_n/n\right)\times \text{diag}\left\{-2f_j\left(\mathit{\alpha }\right)/{\alpha }_j^3\right\}=0,$$

where $\dot{f}\left(\mathit{\alpha }\right)=\partial f\left(\mathit{\alpha }\right)/\partial {\mathit{\alpha }}^{\top }$ and $\mathrm{diag}\left\{-2f_j\left(\mathit{\alpha }\right)/{\alpha }_j^3\right\}=\mathrm{diag}\left\{-2f_1\left(\mathit{\alpha }\right)/{\alpha }_1^3,\dots ,-2f_{q_n}\left(\mathit{\alpha }\right)/{\alpha }_{q_n}^3\right\}$ This, together with the assumption ${\lambda }_n/\sqrt{n}\to 0$, implies that

$$\underset{\mathit{\alpha }\in B_n}{\sup }\Vert \left\{{\Sigma }_{n1}+{\lambda }_n{D}_1\left(\mathit{\alpha }\right)/n\right\}\dot{f}\left(\mathit{\alpha }\right)\Vert =\underset{\mathit{\alpha }\in B_n}{\sup }\frac{2{\lambda }_n}{n}\Vert \text{diag}\left\{f_j\left(\mathit{\alpha }\right)/{\alpha }_j^3\right\}\Vert =o_p\left(1\right).$$ (A.20)

Note that Σ_n1 is positive definite. Write ${\sum }_{n1}={\displaystyle {\sum }_{i=1}^{q_n}{\tau }_{1i}{\mathbf{u}}_{1i}{\mathbf{u}}_{1i}^{\top }}$, where τ_1i and u_1i are eigenvalues and eigenvectors of Σ_{n1. Then,} by (C2), τ_1i ∈ (1/C,C) for all i and

$$\begin{gathered} \Vert {\Sigma }_{n1}\dot{f}\left(\mathit{\alpha }\right)\Vert =\underset{\Vert x\Vert =1,x\in {ℝ}^{q_n}}{\sup }\Vert {\Sigma }_{n1}\dot{f}\left(\mathit{\alpha }\right)x\Vert =\underset{\Vert x\Vert =1,x\in R^{q_n}}{\sup }\Vert {\displaystyle \sum _{i=1}^{q_n}{\lambda }_{1i}{u}_{1i}{u}_{1i}^{\top }\dot{f}\left(\mathit{\alpha }\right)x}\Vert \\ =\underset{\Vert x\Vert =1,x\in {ℝ}^{q_n}}{\sup }{\left\{{\displaystyle \sum _{i=1}^{q_n}{\lambda }_{1i}^2{\Vert u_{1i}^{\top }\dot{f}\left(\mathit{\alpha }\right)x\Vert }^2}\right\}}^{1/2}\ge \underset{\Vert x\Vert =1,x\in {ℝ}^{q_n}}{\sup }\frac{1}{C}{\left\{{\displaystyle \sum _{i=1}^{q_n}{\Vert u_{1i}^{\top }\dot{f}\left(\mathit{\alpha }\right)x\Vert }^2}\right\}}^{1/2} \\ =\underset{\Vert x\Vert =1,x\in {ℝ}^{q_n}}{\sup }\frac{1}{C}\Vert \dot{f}\left(\mathit{\alpha }\right)x\Vert =\frac{1}{C}\Vert \dot{f}\left(\mathit{\alpha }\right)\Vert . \end{gathered}$$ (A.21)

Therefore, it follows from α ∈ B_n, (A.21) and (C2) that

$$\Vert \left\{{\Sigma }_{n1}+{\lambda }_n{D}_1\left(\mathit{\alpha }\right)/n\right\}\dot{f}\left(\mathit{\alpha }\right)\Vert \ge \Vert {\Sigma }_{n1}\dot{f}\left(\mathit{\alpha }\right)\Vert -\Vert {\lambda }_n{D}_1\left(\mathit{\alpha }\right)\dot{f}\left(\mathit{\alpha }\right)/n\Vert \ge \frac{1}{C}\Vert \dot{f}\left(\mathit{\alpha }\right)\Vert -\frac{{\lambda }_n}{n}{a}_{0n}^{-2}\Vert \dot{f}\left(\mathit{\alpha }\right)\Vert ,$$

This, together with (A.20) and (C2), implies that

$$\underset{\mathit{\alpha }\in B_n}{\sup }\Vert \dot{f}\left(\mathit{\alpha }\right)\Vert =o_p\left(1\right).$$ (A.22)

Finally, the conclusion in part (a) follows from (A.19) and (A.22).

Next we prove part (b). Write

$$\begin{gathered} n^{1/2}{s}_n^{-1}{b}_n^{\top }\left({\widehat{\mathit{\alpha }}}^{\circ }-{\mathit{\beta }}_{01}\right)=n^{1/2}{s}_n^{-1}{b}_n^{\top }\left[{\left\{{\Sigma }_{n1}+{\lambda }_n{D}_1\left({\widehat{\mathit{\alpha }}}^{\circ }\right)/n\right\}}^{-1}{\Sigma }_{n1}-I_{q_n}{\mathit{\beta }}_{01}\right] \\ +n^{1/2}{s}_n^{-1}{b}_n^{\top }{\left\{{\Sigma }_{n1}+{\lambda }_n{D}_1\left({\widehat{\mathit{\alpha }}}^{\circ }\right)/n\right\}}^{-1}{X}_1^{\top }\mathit{\epsilon }\equiv I_1+I_2. \end{gathered}$$ (A.23)

By the first order resolvent expansion formula, viz. (H + Δ)⁻¹ = H⁻¹ − H⁻¹ Δ (H + Δ)⁻¹, the first term on the right-hand side of Eq. (A.23) can be written as

$$I_1=-s_n^{-1}{b}_n^{\top }{\Sigma }_{n1}^{-1}\frac{{\lambda }_n}{\sqrt{n}}{D}_1\left({\widehat{\mathit{\alpha }}}^{\circ }\right){\left\{{\Sigma }_{n1}+{\lambda }_n{D}_1\left({\widehat{\mathit{\alpha }}}^{\circ }\right)/n\right\}}^{-1}{\Sigma }_{n1}{\mathit{\beta }}_{01}.$$

Hence, by the assumptions (C2) and (C3), we have

$$\Vert I_1\Vert \le \frac{{\lambda }_n}{\sqrt{n}}{s}_n^{-1}{a}_{0n}^{-2}\Vert {\Sigma }_{n1}^{-1}{\mathit{\beta }}_{01}\Vert =O_p\left({\lambda }_n\frac{a_{1n}}{a_{0n}^2}\sqrt{\frac{q_n}{n}}\right)\to 0.$$ (A.24)

Furthermore, by writing $X_1^{\top }=\left({\tilde{w}}_1,\dots ,{\tilde{w}}_n\right)$ and applying the first order resolvent expansion formula, it can be shown that

$$I_2=\frac{s_n^{-1}}{\sqrt{n}}{\displaystyle \sum _{i=1}^n{b}_n^{\top }{\Sigma }_{n1}^{-1}{\tilde{w}}_i{\epsilon }_i+o_p\left(1\right)},$$ (A.25)

which converges in distribution to N(0, 1) by the Lindeberg–Feller Central Limit Theorem. Finally, combining (A.23), (A.24), and (A.25), we can conclude the proof of part (b).

Proof of Theorem 1. Note that for the initial ridge estimator ${\widehat{\mathit{\beta }}}^{\left(0\right)}$ defined by (1), we have

$${\widehat{\mathit{\beta }}}^{\left(0\right)}-{\mathit{\beta }}_0\left\{{\left({\Sigma }_n+{\xi }_n{I}_{p_n}/n\right)}^{-1}{\Sigma }_n-I_{p_n}\right\}{\mathit{\beta }}_0+{\left({\Sigma }_n+{\xi }_n{I}_{p_n}/n\right)}^{-1}{X}^{\top }\mathit{\epsilon }/n\equiv T_1+T_2.$$

By the first order resolvent expansion formula and ${\xi }_n/\sqrt{n}\to 0$,

$$\Vert T_1\Vert =\Vert -{\Sigma }_n^{-1}{\xi }_n{\left({\Sigma }_n+{\xi }_n{I}_{p_n}/n\right)}^{-1}{\Sigma }_n{\mathit{\beta }}_0/n\Vert \le C^3{\xi }_n{a}_{1n}\sqrt{p_n}/n=o_p\left(\sqrt{p_n/n}\right).$$

It is easy to see that $\Vert T_2\Vert =O_p\left(\sqrt{p_n/n}\right)$.Thus $\Vert {\widehat{\mathit{\beta }}}^{\left(0\right)}-{\mathit{\beta }}_0\Vert =O_p\left\{{\left(p_n/n\right)}^{1/2}\right\}$. This, combined with part (a) of Lemma 1, implies that

$$\mathrm{Pr}\left(\underset{k\to \infty }{\lim }{\widehat{\mathit{\gamma }}}^{\left(k\right)}=0\right)\to 1.$$ (A.26)

Hence, to prove part (i) of Theorem 1, it is su cient to show that

$$\mathrm{Pr}\left(\underset{k\to \infty }{\lim }\Vert {\widehat{\mathit{\alpha }}}^{\left(k\right)}-{\widehat{\mathit{\alpha }}}^{\circ }\Vert =0\right)\to 1,$$ (A.27)

where ${\widehat{\mathit{\alpha }}}^{\circ }$ is the fixed point of f(α) defined in part (b) of Lemma 2.

Define γ* = 0 if γ= 0. It is easy to see from (A.2) that for any α ∈ Bn,

$$\underset{\mathit{\gamma }\to 0}{\lim }{\mathit{\gamma }}^{*}\left(\mathit{\alpha },\mathit{\gamma }\right)=0.$$ (A.28)

Combining (A.28) with the fact

$$\left(\begin{array}{cc}{X}_1^{\top }{X}_1+{\lambda }_n{D}_1\left(\mathit{\alpha }\right)& X_1^{\top }{X}_2\\ X_2^{\top }{X}_1& X_2^{\top }{X}_2+{\lambda }_n{D}_2\left(\mathit{\gamma }\right)\end{array}\right)\left(\begin{array}{l}\mathit{\alpha }*\hfill \\ {\mathit{\gamma }}^{*}\hfill \end{array}\right)=\left(\begin{array}{l}{X}_1^{\top }y\hfill \\ X_2^{\top }y\hfill \end{array}\right),$$

we find that, for any α ∈ B_n,

$$\underset{\mathit{\gamma }\to 0}{\lim }\mathit{\alpha }*\left(\mathit{\alpha },\mathit{\gamma }\right)={\left\{X_1^{\top }{X}_1+{\lambda }_n{D}_1\left(\mathit{\alpha }\right)\right\}}^{-1}{X}_{1}y=f\left(\mathit{\alpha }\right).$$ (A.29)

Therefore, g is continuous and thus uniformly continuous on the compact set β ∈ H_n. This, together with (A.26) and (A.29), implies that, as k → ∞,

$${\eta }_k\equiv \underset{\mathit{\alpha }\in B_n}{\sup }\Vert f\left(\mathit{\alpha }\right)-{\mathit{\alpha }}^{*}\left(\mathit{\alpha },{\widehat{\mathit{\gamma }}}^{\left(k\right)}\right)\Vert \to 0$$ (A.30)

with probability tending to 1. Note that

$$\Vert {\widehat{\mathit{\alpha }}}^{\left(k+1\right)}-{\widehat{\mathit{\alpha }}}^{\circ }\Vert =\Vert {\mathit{\alpha }}^{*}\left({\widehat{\mathit{\beta }}}^{\left(k\right)}\right)-{\widehat{\mathit{\alpha }}}^{\circ }\Vert \le \Vert {\mathit{\alpha }}^{*}\left({\widehat{\mathit{\beta }}}^{\left(k\right)}\right)-f\left({\widehat{\mathit{\alpha }}}^{\left(k\right)}\right)\Vert +\Vert f\left({\widehat{\mathit{\alpha }}}^{\left(k\right)}\right)-{\widehat{\mathit{\alpha }}}^{\circ }\Vert \le {\eta }_k+\frac{1}{C}\Vert {\widehat{\mathit{\alpha }}}^{\left(k\right)}-{\widehat{\mathit{\alpha }}}^{\circ }\Vert ,$$

where the last step follows from $\Vert f\left({\widehat{\mathit{\alpha }}}^{\left(k\right)}\right)-{\widehat{\mathit{\alpha }}}^{\circ }\Vert =\Vert f\left({\widehat{\mathit{\alpha }}}^{\left(k\right)}\right)-f\left({\widehat{\mathit{\alpha }}}^{\circ }\right)\Vert \le \Vert {\widehat{\mathit{\alpha }}}^{\left(k\right)}-{\widehat{\mathit{\alpha }}}^{\circ }\Vert /C$. Let $a_k=\Vert {\widehat{\mathit{\alpha }}}^{\left(k\right)}-{\widehat{\mathit{\alpha }}}^{\circ }\Vert$, for every integer k ≥ 0. From (A.30), we can induce that with probability tending to 1, for any ∊ > 0, there exists a positive integer N such that for every integer k > N, |η_k| < ∊ and

$$\begin{array}{lll}{a}_{k+1}\le \frac{a_{k-1}}{C^2}+\frac{{\eta }_{k-1}}{C}+{\eta }_k\hfill & \le \hfill & \frac{a_1}{C^k}+\frac{{\eta }_1}{C^{k-1}}+\cdots +\frac{{\eta }_N}{C^{k-N}}+\left(\frac{{\eta }_{N+1}}{C^{k-N-1}}+\cdots +\frac{{\eta }_{k-1}}{C}+{\eta }_k\right)\hfill \\ \hfill & \le \hfill & \left(a_1+{\eta }_1+\cdots +{\eta }_N\right)\frac{1}{C^{k-N}}+\frac{1-{\left(1/C\right)}^{k-N}}{1-1/C}\in \hfill \end{array}$$

and the right-hand term tends to 0 as k → ∞. This proves (A.27).

Therefore, it follows immediately from (A.26) and (A.27) that with probability tending to 1, ${\lim }_{k\to \infty }{\mathit{\beta }}^{\left(k\right)}={\lim }_{k\to \infty }{\left({\widehat{\mathit{\alpha }}}^{\left(k\right)\text{T}},{\widehat{\mathit{\gamma }}}^{\left(k\right)\text{T}}\right)}^{\top }={\left({\widehat{\mathit{\alpha }}}^{\circ \text{T}},0\right)}^{\top }$, which completes the proof of part (i). This, in addition to part (b) of Lemma 2, proves part (ii) of Theorem 1

Proof of Theorem 2. Recall that ${\widehat{\mathit{\beta }}}^{\ast }={\lim }_{k\to \infty }{\widehat{\mathit{\beta }}}^{\left(k+1\right)}$ and ${\widehat{\mathit{\beta }}}^{\left(k+1\right)}=\arg {\min }_{\mathit{\beta }}\left\{Q\left(\mathit{\beta }|{\widehat{\mathit{\beta }}}^{\left(k\right)}\right)\right\}$, where

$$Q\left(\mathit{\beta }|{\widehat{\mathit{\beta }}}^{\left(k\right)}\right)={\Vert y-X\mathit{\beta }\Vert }^2+{\lambda }_n{\displaystyle \sum _{\mathcal{l}=1}^{p_n}{\beta }_{\mathcal{l}}^2/{\left\{{\widehat{\beta }}_{\mathcal{l}}^{\left(k\right)}\right\}}^2}.$$

If ${\beta }_{\mathcal{l}}^{\ast }\ne 0$ for ℓ ∈ {i, j}, then ${\widehat{\mathit{\beta }}}^{\ast }$ must satisfy the following normal equations for ℓ ∈ {i, j}

$$-2x_{\mathcal{l}}^{\top }\left\{y-X{\widehat{\mathit{\beta }}}^{\left(k+1\right)}\right\}+2{\lambda }_n{\widehat{\beta }}_{\mathcal{l}}^{\left(k+1\right)}/{\left\{{\widehat{\beta }}_{\mathcal{l}}^{\left(k\right)}\right\}}^2=0.$$

Thus, for ℓ ∈ {i, j},

$${\widehat{\beta }}_{\mathcal{l}}^{\left(k+1\right)}/{\left\{{\widehat{\beta }}_{\mathcal{l}}^{\left(k\right)}\right\}}^2=x_{\mathcal{l}}^{\top }{\widehat{\mathit{\epsilon }}}^{\left(k+1\right)}/{\lambda }_n,$$ (A.31)

where ${\widehat{\mathit{\epsilon }}}^{\left(k+1\right)}=\mathit{y}-\mathbf{X}{\widehat{\mathit{\beta }}}^{\left(k+1\right)}$. Moreover, because

$${\Vert {\widehat{\mathit{\epsilon }}}^{\left(k+1\right)}\Vert }^2+{\lambda }_n{\displaystyle \sum _{i=1}^{p_n}\frac{{\widehat{\beta }}_i^2}{{\tilde{\beta }}_i^2}}=Q\left({\widehat{\mathit{\beta }}}^{\left(k+1\right)}|{\widehat{\mathit{\beta }}}^{\left(k\right)}\right)\le Q\left(0|{\widehat{\mathit{\beta }}}^{\left(k\right)}\right)={\Vert y\Vert }^2,$$

we have

$$\Vert {\widehat{\mathit{\epsilon }}}^{\left(k+1\right)}\Vert \le \Vert y\Vert$$ (A.32)

Letting k → ∞ in (A.31) and (A.32), we have, for ℓ ∈ {i, j}, and $\Vert \widehat{\mathit{ϵ}}\Vert \le \Vert \mathit{y}\Vert ,{\beta }_{\mathcal{l}}^{\ast -1}={\mathbf{x}}_{\mathcal{l}}^{\top }\widehat{\mathit{ϵ}}{\lambda }_n$ where $\widehat{\mathit{ϵ}}=\mathbf{y}-\mathbf{X}{\widehat{\mathit{\beta }}}^{\ast }$.

Therefore,

$$\left|{\widehat{\beta }}_i^{*-1}-{\widehat{\beta }}_j^{*-1}\right|\le \frac{1}{{\lambda }_n}\Vert y\Vert \times \Vert x_i-x_j\Vert \frac{1}{{\lambda }_n}\Vert y\Vert \sqrt{2\left(1-{\rho }_{ij}\right)}.$$

and the proof is complete.

Proof of Theorem 3. (a) It is easy to check that

$$\begin{gathered} \mathcal{l}\left\{{\mathit{\beta }}^{\left(t\right)}\right\}=h\left\{{\mathit{\beta }}^{\left(t\right)},{\mathit{\beta }}^{\left(t\right)}\right\}\ge h\left\{{\mathit{\beta }}^{\left(t+1\right)},{\mathit{\beta }}^{\left(t\right)}\right\}=\mathcal{l}\left\{{\mathit{\beta }}^{\left(t\right)}\right\}+{\left\{{\mathit{\beta }}^{\left(t+1\right)}-{\mathit{\beta }}^{\left(t\right)}\right\}}^{\top }S\left\{{\mathit{\beta }}^{\left(t\right)}\right\}+\frac{u}{2}{\Vert {\mathit{\beta }}^{\left(t+1\right)}-{\mathit{\beta }}^{\left(t\right)}\Vert }_2^2 \\ =\mathcal{l}\left\{{\mathit{\beta }}^{\left(t+1\right)}\right\}+\frac{u}{2}{\Vert {\mathit{\beta }}^{\left(t+1\right)}-{\mathit{\beta }}^{\left(t\right)}\Vert }_2^2+\left[-\mathcal{l}\left\{{\mathit{\beta }}^{\left(t+1\right)}\right\}+\mathcal{l}\left\{{\mathit{\beta }}^{\left(t\right)}\right\}+{\left\{{\mathit{\beta }}^{\left(t+1\right)}-{\mathit{\beta }}^{\left(t\right)}\right\}}^{\top }S\left\{{\mathit{\beta }}^{\left(t\right)}\right\}\right] \\ =\mathcal{l}\left\{{\mathit{\beta }}^{\left(t+1\right)}\right\}+\frac{u}{2}{\Vert {\mathit{\beta }}^{\left(t+1\right)}-{\mathit{\beta }}^{\left(t\right)}\Vert }_2^2-{\Vert X\left({\mathit{\beta }}^{\left(t+1\right)}-{\mathit{\beta }}^{\left(t\right)}\right)\Vert }_2^2 \\ \ge \mathcal{l}\left\{{\mathit{\beta }}^{\left(t+1\right)}\right\}+\frac{u}{2}{\Vert {\mathit{\beta }}^{\left(t+1\right)}-{\mathit{\beta }}^{\left(t\right)}\Vert }_2^2-{\lambda }_{\max }\left(X^{\top }X\right){\Vert \left({\mathit{\beta }}^{\left(t+1\right)}-{\mathit{\beta }}^{\left(t\right)}\right)\Vert }_2^2\ge \mathcal{l}\left\{{\mathit{\beta }}^{\left(t+1\right)}\right\}, \end{gathered}$$ (A.33)

where the last step follows from the assumption that $u\ge 2{\lambda }_{\max }\left({\mathbf{X}}^{\top }\mathbf{X}\right)$.

(b) The proof for the convergence of{β^(t)} to a local solution of (6) essentially mimicks the proof of Theorem 1 of Xu and Chen (2014) and thus is omitted here.

Proof of Theorem 4. Define $S_{+}^k=\left\{s:s_0\subset s;{\Vert s\Vert }_0\le k\right\}$ and $S_{-}^k=\left\{s:s_0\not\subset s;{\Vert s\Vert }_0\le k\right\}$ to be the collections the over-fitted models and the under-fitted models. Let ${\widehat{\mathit{\beta }}}_s$ be the estimate of β based on the model s Clearly the result holds if $\mathrm{Pr}\left({\widehat{s}}_{\mathrm{sLSE}}\in S_{+}^k\right)\to 1$. Thus, it suffices to show that as n → ∞,

$$\mathrm{Pr}\left\{\underset{s\in S_{-}^k}{\min }\mathcal{l}\left({\widehat{\mathit{\beta }}}_s\right)\le \underset{s\in S_{+}^k}{\max }\mathcal{l}\left({\widehat{\mathit{\beta }}}_s\right)\right\}\to 0.$$

For any $s\in S_{-}^k,s^{\prime }=s\cup s_0\in S_{+}^{2k}$. Consider ${\Vert {\mathit{\beta }}_{s^{\prime }}-{\mathit{\beta }}_{s^{\prime }0}\Vert }_2{\omega }_1{n}^{-{\tau }_1}$, and by the Taylor expansion and conditions (D1) and (D3), we have

$$\begin{gathered} \mathcal{l}\left({\mathit{\beta }}_{s^{\prime }0}\right)-\mathcal{l}\left({\mathit{\beta }}_{s^{\prime }}\right)={\left({\mathit{\beta }}_{s^{\prime }0}-{\mathit{\beta }}_{s^{\prime }}\right)}^{\top }S\left({\mathit{\beta }}_{s^{\prime }0}\right)-\frac{1}{2}{\left({\mathit{\beta }}_{s^{\prime }}-{\mathit{\beta }}_{s^{\prime }0}\right)}^{\top }2X_{s^{\prime }}^{\top }{X}_{s^{\prime }}\left({\mathit{\beta }}_{s^{\prime }}-{\mathit{\beta }}_{s^{\prime }0}\right) \\ \le {\left({\mathit{\beta }}_{s^{\prime }0}-{\mathit{\beta }}_{s^{\prime }}\right)}^{\top }S\left({\mathit{\beta }}_{s^{\prime }0}\right)-c_{1}n{\Vert {\mathit{\beta }}_{s^{\prime }}-{\mathit{\beta }}_{s^{\prime }0}\Vert }_2^2\le {\omega }_1{n}^{-{\tau }_1}{\Vert S\left({\mathit{\beta }}_{s^{\prime }0}\right)\Vert }_2-c_1{\omega }_1^2{n}^{1-2{\tau }_1}. \end{gathered}$$

Thus, upon setting $c={\omega }_2^{-1/2}{c}_1{\omega }_1/\sqrt{2}$, we have

$$\begin{array}{lll}\mathrm{Pr}\left\{\mathcal{l}\left({\mathit{\beta }}_{s^{\prime }0}\right)-\mathcal{l}\left({\mathit{\beta }}_{s^{\prime }}\right)\ge 0\right\}\hfill & \le \hfill & \mathrm{Pr}\left\{{\Vert S\left({\mathit{\beta }}_{s^{\prime }0}\right)\Vert }_2\ge c_1{\omega }_1{n}^{1-{\tau }_1}\right\}\hfill \\ \hfill & \le \hfill & {\displaystyle \sum _{j\in s^{\prime }}\mathrm{Pr}\left\{S_j^2\left({\mathit{\beta }}_{s^{\prime }0}\right)\ge \frac{1}{2k}{\left(c_1{\omega }_1\right)}^2{n}^{2-2{\tau }_1}\right\}}={\displaystyle \sum _{j\in s^{\prime }}\mathrm{Pr}\left\{\left|S_j\left({\mathit{\beta }}_{s^{\prime }0}\right)\right|\ge \frac{1}{{\left(2k\right)}^{1/2}}{c}_1{\omega }_1{n}^{1-{\tau }_1}\right\}}\hfill \\ \hfill & \le \hfill & {\displaystyle \sum _{j\in s^{\prime }}\mathrm{Pr}\left\{\left|S_j\left({\mathit{\beta }}_{s^{\prime }0}\right)\right|\ge c{n}^{1-{\tau }_1-{\tau }_2/2}\right\}}.\hfill \end{array}$$ (A.34)

Let $t_{ni}=x_{ij}{\left({\sum }_{i=1}^n{x}_{ij}^2{\sigma }_i^2\right)}^{-1/2}$ Such that ${\sum }_{i=1}^n{t}_{ni}^2{\sigma }_i^2=1$ Under condition (D4), we have ${\max }_i\left(t_{ni}^2\right)\le c_4/n$ and ${\sum }_{i=1}^n{x}_{ij}^2{\sigma }_i^2\le c_2^{2}n{\sigma }^2$ for some positive constant σ. Then,

$$\begin{gathered} \mathrm{Pr}\left\{S_j\left({\mathit{\beta }}_{s^{\prime }0}\right)\le -c{n}^{1-{\tau }_1-{\tau }_2/2}/2\right\}=\mathrm{Pr}\left\{2{\displaystyle \sum _{i=1}^n{x}_{ij}\left(y_i-w_{i{s}^{\prime }}^{\top }{\mathit{\beta }}_{s^{\prime }0}\right)\ge c{n}^{1-{\tau }_1-{\tau }_2/2}/2}\right\} \\ \le \mathrm{Pr}\left\{2{\displaystyle \sum _{i=1}^n{t}_{ni}\left(y_i-w_{i{s}^{\prime }}^{\top }{\mathit{\beta }}_{s^{\prime }0}\right)\ge \frac{c}{2c_2\sigma }{n}^{1/2-{\tau }_1-{\tau }_2/2}}\right\}\le \exp \left(-c^{\prime }{n}^{1-2{\tau }_1-{\tau }_2}\right), \end{gathered}$$

where the last step uses Lemma A.1 in [46] and c^’ is a positive constant. Similarly,

$$\mathrm{Pr}\left\{S_j\left({\mathit{\beta }}_{s^{\prime }0}\right)\ge c{n}^{1-{\tau }_1-{\tau }_2/2}\right\}\le \exp \left(-c^{\prime }{n}^{1-2{\tau }_1-{\tau }_2}\right).$$ (A.35)

Combining (A.34)–(A.35), we have $\mathrm{Pr}\left\{\mathcal{l}\left({\mathit{\beta }}_{s^{\prime }0}\right)-\mathcal{l}\left({\mathit{\beta }}_{s^{\prime }}\right)\ge 0\right\}\le 4k\exp \left(-c^{\prime }{n}^{1-2{\tau }_1-{\tau }_2}\right)$. Hence,

$$\begin{array}{lll}\mathrm{Pr}\left\{\underset{s\in S_{-}^k}{\min }\mathcal{l}\left({\mathit{\beta }}_{s^{\prime }}\right)\le \mathcal{l}\left({\mathit{\beta }}_{s^{\prime }0}\right)\right\}\hfill & \le \hfill & {\displaystyle \sum _{s\in S_{-}^k}\mathrm{Pr}\left\{\mathcal{l}\left({\mathit{\beta }}_{s^{\prime }}\right)\le \mathcal{l}\left({\mathit{\beta }}_{s^{\prime }0}\right)\right\}}\hfill \\ \hfill & \le \hfill & 4k{p}_n^k\exp \left(-c^{\prime }{n}^{1-2{\tau }_1-{\tau }_2}\right)=4\exp \left(\ln k+k\ln p_n-c^{\prime }{n}^{1-2{\tau }_1-{\tau }_2}\right)\hfill \\ \hfill & \le \hfill & 4w_2\exp \left\{{\tau }_2\ln n+O\left(n^{{\tau }_2+d}\right)-c^{\prime }{n}^{1-2{\tau }_1-{\tau }_2}\right\}=o\left(1\right),\hfill \end{array}$$

where the last two steps follow from conditions (D1)–(D2). Because $\mathcal{l}\left({\mathit{\beta }}_{s^{\prime }}\right)$ is convex ${\mathit{\beta }}_{s^{\prime }}$, the above result holds for any ${\mathit{\beta }}_{s^{\prime }}$ such that ${\Vert {\mathit{\beta }}_{s^{\prime }}-{\mathit{\beta }}_{s^{\prime }0}\Vert }_2\ge {\omega }_1{n}^{-{\tau }_1}$.

For any $s\in S_{-}^k$, let ${\check{\mathit{\beta }}}_{s^{\prime }}$ be ${\widehat{\mathit{\beta }}}_s$ augmented with zeros corresponding to the elements in $s^{\prime }/s_0$ By condition (D1), we have ${\Vert {\check{\mathit{\beta }}}_{{\mathit{s}}^{\prime }}-{\mathit{\beta }}_{s^{\prime }0}\Vert }_2\ge {\omega }_1{n}^{-{\tau }_1}$. Thus

$$\mathrm{Pr}\left\{\underset{s\in S_{-}^k}{\min }\mathcal{l}\left({\widehat{\mathit{\beta }}}_s\right)\le \underset{s\in S_{+}^k}{\max }\mathcal{l}\left({\widehat{\mathit{\beta }}}_s\right)\right\}\le \mathrm{Pr}\left\{\underset{s\in S_{-}^k}{\min }\mathcal{l}\left({\check{\mathit{\beta }}}_{s^{\prime }}\right)\le \mathcal{l}\left({\mathit{\beta }}_{s^{\prime }0}\right)\right\}=o\left(1\right).$$

This concludes the argument.