Conditional moving linear regression: modeling the recruitment process for ALLHAT

Abstract

Effective recruitment is a prerequisite for successful execution of a clinical trial. ALLHAT, a large hypertension treatment trial (N = 42, 418), provided an opportunity to evaluate adaptive modeling of recruitment processes using conditional moving linear regression. Our statistical modeling of recruitment, comparing Brownian and fractional Brownian motion, indicates that fractional Brownian motion combined with moving linear regression is better than classic Brownian motion in terms of higher conditional probability of achieving a global recruitment goal in four week ahead projections. Further research is needed to evaluate how recruitment modeling can assist clinical trialists in planning and executing clinical trials.

Clinical Trial Registration: www.clinicaltrials.gov NCT00000542

Introduction:

For a clinical trial to be viable, investigators need to recruit the required number of participants to meet the target sample size within a given period of time. Statistical methods for sample size determination in clinical trials are well established (Silagy et al., 1991; Stibolt, Manske, Zavela, Youtsey & Buist, 1991; Vierron & Giraudeau, 2007). Recruiting the estimated number of patients is critical in conducting a successful clinical trial. Statistical methods to model recruitment processes are less well understood, yet essential, for efficiently planning and conducting clinical trials (Lai, Moyé, Davis, Brown, & Sacks, 2001; Anisimov 2011, Zhang & Long, 2012).

The cumulative number of participants recruited for a clinical trial forms a stochastic process. Two fundamental types of processes have been used to model recruitment. For discrete processes, Poisson processes and their variants such as Poisson processes with random gamma distributed rates are popular and established methods for modeling recruitment (Lee, 1983; Williford et al., 1987; Anisimov, 2009; Anisimov & Fedorov, 2007). When a clinical trial is relatively large, recruitment process may be approximated by continuous process such as a classic Brownian motion process or fractional Brownian motion. For example, the recruitment process of the Cholesterol and Recurrent Events (CARE) Trial was modelled with a Brownian motion process and fractional Brownian motion with a deterministic linear regression trend over the entire recruitment period (Lai et al., 2001; Zhang & Lai, 2011). The applications of Poisson process and its variants in modeling recruitment of clinical trials have been extensively reviewed (Anisimov, 2011; Senn, 1996; Bakhshi, Senn & Phillips, 2013; Barnard, Dent & Cook, 2010).

In both classic Poisson and Brownian motion processes, the independent increment property for non-overlapping time intervals is assumed. However, in many situations, the number of participants recruited may be a function of enhancements adopted midstream, such as broadening of eligibility criteria; implementing incentives; adding clinical sites; extending the recruitment period; and increasing publicity through radio, TV, or internet advertisements (Pressel et al., 2001). These methods may have lasting effects on future recruitment and may result in non-independent arrivals of participants. Therefore, the recruitment process may not have the independent increment structure that is usually assumed in many modeling strategies.

Fractional Brownian motion, with classic Brownian motion as a special case, relaxes the independent increment assumption. We have previously applied fractional Brownian motion, using a global regression trend to model recruitment, in the CARE trial (Zhang & Lai, 2012). (Zhang & Lai, 2012). Similarly, the full Poisson-Gamma model with center modeling also relaxes the independent increment assumption of the recruitment process since the sum of several processes that individually have the independent increment property may not itself have independent increment property.

The Antihypertensive and Lipid-Lowering Treatment to Prevent Heart Attack Trial (ALLHAT), the largest ever antihypertensive clinical trial, recruited 42,418 participants from 623 centers across many regions from the United States, Puerto Rico, Canada, and the US Virgin Islands (Pressel et al., 2001). All recruited patients provided written informed consent to participate in the trial, which had been approved by the institutional review board at the University of Texas Health Science Center at Houston and each clinic site.

Because of the complex recruitment process, a fractional Brownian motion process with a fixed regression trend to model recruitment may not be flexible enough to capture the recruitment dynamics of participating clinical centers and their patients. Therefore, a more flexible model may be warranted for this type of trial.

In this analysis, we propose an adaptive conditional linear moving regression as the deterministic trend, comparing both Brownian motion and fractional Brownian motion, to model the recruitment process of ALLHAT. The large number of participants and the diversity of the ALLHAT population provide an excellent dataset to compare these methods. The same method can be used to investigate recruitment of subgroups, such as treatment arm in cluster-randomized trials, region, gender, or age; other social, demographic, or clinical characteristics; or time period. It is noteworthy that our proposed method was applied directly to aggregate process of multi-center trials without investigating the detailed dynamics of the recruitment process of individual clinical centers. Our approach avoided estimating a large number of parameters and can explicitly model the possible dependent increment structure of the recruitment process.

Methods

In modeling the recruitment process, let X(t) be the cumulative number of participants recruited from the start of the clinical trial until time t. Hence X (0) = 0. Further assume the expected number of participants of X(t) to be f(t). In modeling the recruitment process of the CARE study, the deviation B(t) = X(t) - f(t) was assumed to be a Brownian motion (Lai et al., 2001). That is, B(t) is a continuous function of t. For t₂ >, t₁ the increment B(t₂)-B(t₁) has the following properties:

• (i)$B\left(t_1\right)\text{ and }B\left(t_2\right)-B\left(t_1\right)$ are normal and independent;
• (ii)$E\left(B\left(t_1\right)\right)=0$ and$E\left(B\left(t_2\right)-B\left(t_1\right)\right)$ =0;
• (iii)$Var\left(B\left(t_1\right)\right)={\sigma }^2{t}_1$ and $Var\left(B\left(t_2\right)-B\left(t_1\right)\right)={\sigma }^2\left(t_2-t_1\right)$.

Zhang and Lai (2011) extended Brownian motion modeling of clinical trial recruitment processes to fractional Brownian motion to provide more flexibility in modeling recruitment. Fractional Brownian motion, B_H(t) with increment B_H(t₂)-B_H(t₁) has the following properties:

• (i)$B_H\left(t_2\right)-B_H\left(t_1\right)$ is normal;
• (ii)$E\left[B_H\left(t_2\right)-B_H\left(t_1\right)\right]=0$;
• (iii)$E{\left[B_H\left(t_2\right)-B_H\left(t_1\right)\right]}^2={\sigma }^2{\left|t_2-t_1\right|}^{2H}$,

where H is the Hurst constant with range 0 < H < 1 (Beran, 1994). The covariance between $B_H\left(t_2\right)$ and $B_H\left(t_1\right)$ is. $Cov\left(B_H\left(t_2\right),B_H\left(t_1\right)\right)=\left({\sigma }^2/2\right)\left(t_2^{2H}+t_1^{2H}-{\left|t_2-t_1\right|}^{2H}\right)$ Classic Brownian motion is a special case of fractional Brownian motion, with a Hurst parameter of H = 0.5.

The conditional probability$P\left(X\left(t_k\right)>a|X\left(t_n\right)=r_{t_n},\dots ,X\left(t_1\right)=r_{t_1}\right)$ with $t_1<t_2<\dots <t_n<t_k$ for $\text{k > n}$ under fractional Brownian motion is derived as follows:

$$P\left(X\left(t_k\right)>a|X\left(t_n\right),\dots ,X\left(t_1\right)\right)=P\left(X\left(t_k\right)-f\left(t_k\right)>a-f\left(t_k\right)|X\left(t_n\right),\dots ,X\left(t_1\right)\right)=P\left(B\left(t_k\right)\right)>a-f\left(t_k\right)|X{\left(t_n\right)}_{z\cdots ,}X\left(t_1\right))=1-\Phi \left(\frac{a-f\left(t_k\right)-{\mu }_{H_n}}{{\sigma }_{H_{\kappa }}}\right)$$

where, ${\mu }_{H_n}={\Sigma }_{12}{\Sigma }_{22}^{-1}{\mu }_n$ and ${\mu }_n=\left(B_H\left(t_n\right),B_H\left(t_{n-1}\right),\dots ,B_H\left(t_1\right)\right)$. ${\Sigma }_{12}={\Sigma }_{21}$ are the covariance matrices between $B_H\left(t_k\right)$ and $B_H\left(t_n\right),B_H\left(t_{n-1}\right),\dots ,B_H\left(t_1\right)$. The variance of the conditional distribution of $B_H\left(t_k\right)$ is ${\sigma }_{H_n}^2=\left({\Sigma }_{11}-{\Sigma }_{12}{\sum }_{22}^{-1}{\sum }_{21}\right)$ and ${\Sigma }_{22}$ is the variance covariance matrix of$B_H\left(t_n\right),B_H\left(t_{n-1}\right),\dots ,B_H\left(t_1\right)$. We can use the method of moments to estimate ${\sigma }^2$ based on the lag 1 differences of $B_H\left(t_k\right)$. That is, ${\widehat{\sigma }}^2=\frac{1}{n-1}{\displaystyle \sum _{i=2}^n{\left(B_H\left(t_i\right)-B_H\left(t_{i-1}\right)\right)}^2}$ . In the current application, we modeled the weekly recruitment process of ALLHAT with ${\text{t}}_{\text{i}}{\text{ - t}}_{\text{i - 1}}\text{= 1}$, to reflect the weekly management meeting of the trial.

The predictive conditional 95% confidence interval $[a_t,b_t]$of the future expected recruitment path of X(t) given existing observations$X(t_n),X(t_{n-1}),\mathrm{...},X(t_1)$, is

$$a_t=f(t)+{\mu }_{H_n}-1.96{\sigma }_{H_n}$$

$$b_t=f(t)+{\mu }_{H_n}+1.96{\sigma }_{H_n}$$

Several methods have been proposed to estimate the Hurst coefficient based on partial observation of a process. These methods include the maximum likelihood estimation and rescaled adjusted range analysis (Beran, 1994; Davies & Harte, 1987; Mandelbrot & Wallis, 1969). We estimated the Hurst exponent using the periodogram (with a perFit procedure in the fArma package in R). In the finite variance case a periodogram is an estimator of the spectral density of a time series. A series with long-range dependence will show a spectral density with a lower law behavior in the frequency domain. Thus, we expect that a log-log plot of the periodogram versus frequency will display a straight line, and the slope can be computed as 1–2H (Geweke & Porter-Hudak, 1983).

In ALLHAT, there were 623 clinical centers and their participation in the study was staged over time. To better reflect this, we used an adaptive approach by fitting a conditional moving regression line with the intercept being the observed cumulative number of participants who had been recruited at the beginning of the fitting. We started our estimation of the linear regression line f(t) = a_t + b_t t after the first year (n = 52 weeks), where a_t = cumulative participants observed before time t and b_t is the average rate of change during the previous 52 weeks. Then we performed the regressions moving along time with one more data point (week). We kept the total number of 52 weeks for the model and treated the residuals as a realization of fractional Brownian motion. The conditional probabilities of reaching given recruitment goals were calculated for projections in periods of 1 to 4 weeks. In addition, we also applied both models to compare long-term predictions over subsequent months. As Figure 2 shows, long term projections of recruitments without further conditional moving adjustment were not accurate.

Figure 2.

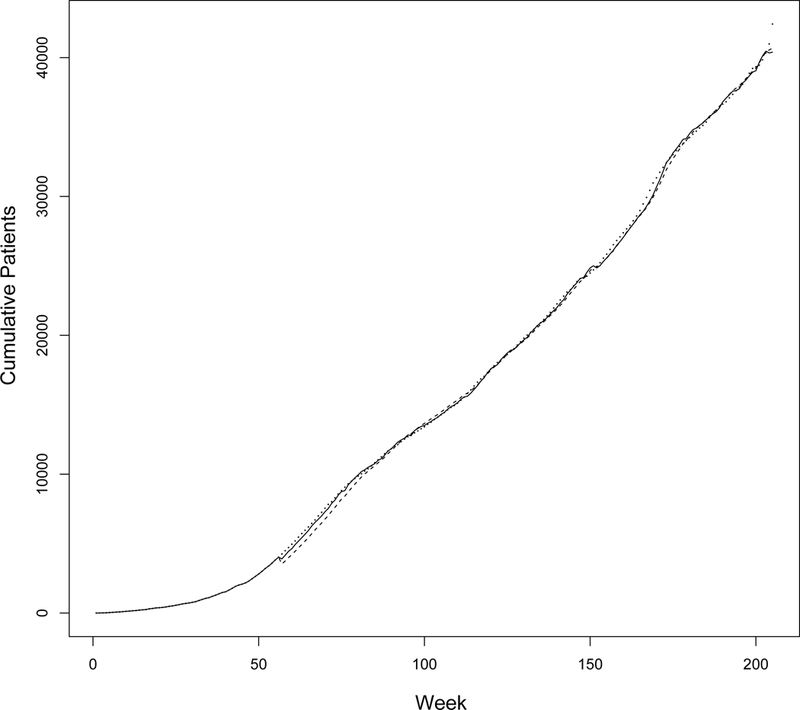
Comparisons of the conditional predicted 95% confidence intervals based on classic and fractional Brownian motion at week 105. The dotted line denotes the actual observed number of recruited participants. The upper and lower dashed lines represent the predicted confidence interval computed at week 105. The solid lines denote the conditional expectations.

In multicenter clinical trials, weekly staff meetings are usually held to review the trial’s progress. Recruitment is a major issue on meeting agendas at the beginning of trials. Reasonable projections of patient recruitment during subsequent 1–4 week periods would give investigators information to better chart the course ahead. In our illustration of the methods, we focused on the results for 4-week projections of recruitment.

The extra parameter H in fractional Brownian motion can measure this long-term dependence. For example, if H > 0.5, the correlation is positive; if H = 0.5, then the fractional Brownian motion becomes a classic Brownian motion; and if H < 0.5, the correlation is negative. In this article, we compared the effect of estimating the Hurst parameter in modeling the recruitment process of ALLHAT.

Results

We modeled the recruitment process of the ALLHAT study using conditional moving linear regression with classic and fractional Brownian motion for the residual process. Each moving window in our model used observations from 52 weeks (one year). Using the least squares method, we estimated the weekly rate of recruitment conditioned on recruitment observed prior to the moving window. Figure 1 shows the actual number of participants recruited (dotted line), the predictions of subsequent 4-week recruitment based on classic Brownian motion (dashed line), and based on fractional Brownian motion (solid line).

Figure 1.

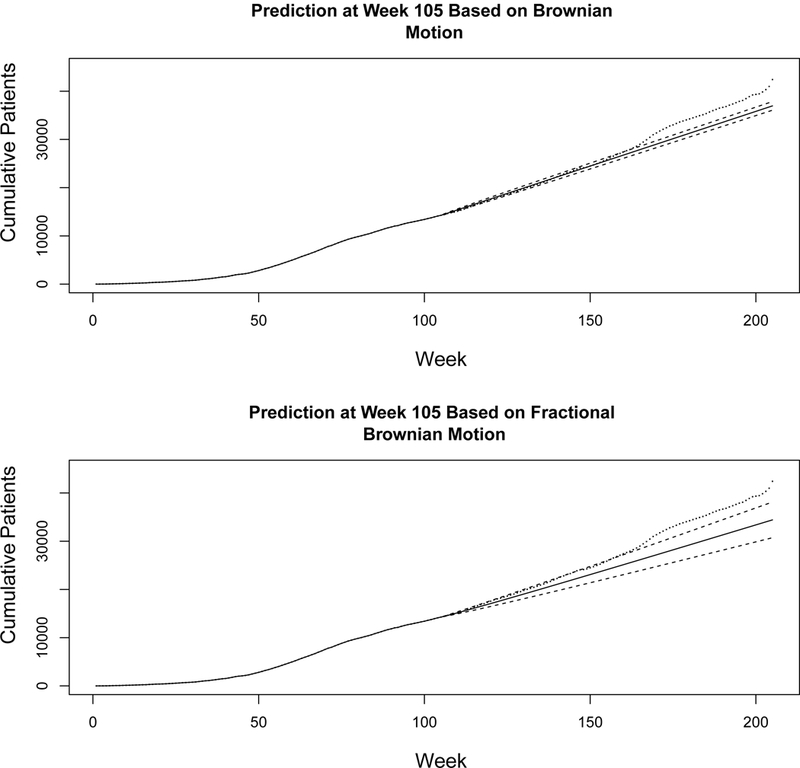
The predictions of subsequent 4-week recruitment, starting week 53, based on the conditional moving linear model with Brownian motion (dashed line) and fractional Brownian motion (solid line). The actual number of participants recruited is denoted by the dotted line.

At week 105, 14,269 participants had been recruited. The average weekly rate of recruitment for the previous period of 52 weeks was 227 participants. Under classic Brownian motion, the expected number of participants to be recruited during the subsequent 4 week period would be 14,269 + 4*227 = 15,177. The actual number of participants who had been recruited at week 109 was 14,939. The estimated standard deviation was 46. Conditional on the number of participants recruited at week 105 and the estimated weekly rate, the lower and upper bounds of the conditional predicted 95% confidence interval were 14,997 and 15,357, respectively. The width of the predicted confidence interval for the subsequent 4-week period under Brownian motion was 2*1.96 * (2*46) = 360 participants. The actual number of participants, 14,939, who had been recruited at week 109 was slightly outside the predicted confidence interval. Under fractional Brownian motion, the expected number of participants recruited at week 109 would be 14,978. The estimated Hurst coefficient was 0.9263 and it differed significantly from 0.5. The lower and upper bounds of the conditional predicted 95% confidence interval were 14,803 and 15,153, respectively. The actual number of participants recruited was 14,939, which was within the predicted 95% confidence interval. The predicted confidence interval length was 2*1.96*89.3 = 350, which was slightly narrower than that calculated based on classic Brownian motion. However, as Figure 2 shows, for a relatively long-term prediction derived from the conditional moving linear model between weeks 53 and 105, the confidence interval based on fractional Brownian motion was wider than that based on classic Brownian motion.

Based on classic Brownian motion, the conditional expectation for subject recruitment at week 150 was 24,478, with a 95% confidence interval of 23,875 and 25,080, whereas based on fractional Brownian motion, the conditional expectation was 23,080 participants recruited with a 95% confidence interval of 21,382 and 24,779. The estimated Hurst coefficient at week 150 was 0.7734. The actual number of participants recruited was 24,483, which was within the 95% confidence intervals for both classic and fractional Brownian motion predictions. When the projection was extended to week 200, the number of participants actually recruited was outside the 95% confidence intervals for both classic and fractional Brownian motion predictions.

In addition to providing point estimates and confidence intervals for monitoring the recruitment process, one can also compute the probability of achieving a given recruitment goal within a set time period. For example, we can compute the conditional probability of achieving 30,000 participants recruited at week 169, given what we observed at week 165. ALLHAT had recruited 28,988 participants at week 165, and the estimated Hurst coefficient based on the previous 52 weeks of recruitment process was 0.7290. Based on fractional Brownian motion, we can compute the conditional probability as$\text{P ( X ( 169 ) > 30,000 | X ( 165 ) = 28,988 ) = 0}.\text{7981}$. However, based on classic Brownian motion, the conditional probability was 0.3385 and the number of recruited participants was predicted to be 30,974 at week 169. In other words, at week 165 with the same probability of 0.7981 of achieving the target of 30,000 participants, classic Brownian motion predicted that it would take about 5 weeks (4.62 weeks) to reach goal. At week 172, the estimated H coefficient was 0.8508 from the previous 52 weeks. The conditional probability of reaching more than 33,000 participants recruited at week 176 was 0.6644 and 0.9760 based on classic Brownian motion and fractional Brownian motion, respectively.

Discussion

In this article we used conditional moving linear regression to model the recruitment process in ALLHAT and compared statistical inferences based on classic Brownian motion and fractional Brownian motion. The detailed participant recruitment history of ALLHAT was documented and reported previously (Pressel et al., 2001) The recruitment occurred over a period of 205 weeks (4 years) and the actual management of the recruitment process was adaptive. During the first 100 weeks of recruitment, there were too few clinical centers to recruit an adequate number of participants within a reasonable time frame (Pressel et al., 2001), so the ALLHAT Steering Committee expanded the number of clinical centers adaptively. Our proposed moving linear regression is consistent with that practice. Midway through the recruitment process, in order to increase the number of recruited participants, the ALLHAT Steering Committee revised the eligibility criteria to include cigarette smoking as a risk factor; lowered the age of eligibility to 55 from 65 years; increased reimbursements for clinical sites with more than 25 participants; expanded the number of clinical sites from 270 to 623, with clinic sites in Puerto Rico and Canada; increased publicity through radio, TV, and internet advertisements; and provided a field personnel program to assist selected clinics (Pressel et al., 2001). Those efforts altered the rate of subject recruitment over time. A moving linear model can refit the data each week and adjust the estimate of the rate of recruitment accordingly.

There were 623 clinic sites. The cumulative recruitment for each clinic site depended strongly on the site’s previous recruitment rate. Therefore, there was a strong autocorrelation of the cumulative recruitment for each site. Granger showed that an aggregate time series of large numbers of autoregressive processes lead to long-range dependence that can be taken into account by fractional Brownian motion (Granger, 1980).

In comparing aggregate approaches (Brownian motion and fractional Brownian motion) with approaches that account for center level accrual information (Poisson-Gamma) for modeling recruitment in large clinical trials (e.g., ALLHAT), researchers were more concerned with total number recruited rather than numbers recruited from subgroups (clinical centers) (Heitjan, Ge & Ying 2015). Further discussions on the properties of the Poisson-Gamma model are given by Anisimov (2016).

To attract and recruit potential participants, ALLHAT spent close to $2 million on radio, direct mail, and newspaper advertisements. ALLHAT also increased the number of clinical sites to include, in addition to the US, both Canada and Puerto Rico. Rewards given to clinical sites for successful recruitment encouraged both the sites that were recruiting well and those that were lagging behind. Those interventions may have had delayed effects on different clinic sites. As a component of the aggregated time series, each cumulative number of participants recruited at a given clinic site reflected the effects those efforts had on recruitment, and the fractional Brownian motion took into account those effects, whereas the classic Brownian motion ignored those lasting impacts. In fact, many test statistics computed sequentially may have a dependent increment structure (Slud & Wei, 1982).

In our study, we calculated the conditional probabilities of achieving the recruitment goal. In our example, where ALLHAT recruited 28,988 participants at week 165, the conditional probability of recruiting 30,000 participants at week 169 was more than doubled by fractional Brownian motion (0.7981) compared with classic Brownian motion (0.3385) processes. Fractional Brownian motion is a class of continuous stochastic processes that includes classic Brownian motion with a Hurst coefficient H = 0.5. In general, fractional Brownian motion modeling provided higher conditional probability of recruiting a given goal of participants over the subsequent 4-week period. That is, given the same probability, classic Brownian motion processes would predict a longer period to achieve the recruitment target.

If classic Brownian motion is assumed, we do not need to estimate the Hurst coefficient. However, if fractional Brownian motion is used, we need to estimate the Hurst coefficient, based on previously observed number of participants recruited. In our application, we used the differences of the residuals from the conditional moving linear regression with 52 weeks (one year). The range of the estimated Hurst coefficients was from 0.42 to 0.97. We used a conditional moving linear model to capture the deterministic trend of the recruitment process of ALLHAT, which resulted in a relatively short time series of residuals in estimating Hurst coefficients. Therefore, variability in estimates of the Hurst coefficients was quite high and led to wider confidence intervals of the predicted conditional expectation of the recruitment process than those based on Brownian motion. A comparison of the confidence intervals of the predictions and the probabilities of achieving stated recruitment goals led us to believe that fractional Brownian motion, with an extra parameter of measuring the Hurst effect, was better than classic Brownian motion in modeling the ALLHAT recruitment process.

We performed conditional analyses on subsequent 1-week, 2-week, and 3-week forecasts. The results were very similar to those based on predictions for subsequent 4-week periods, although predictions for subsequent 4-weekperiods had a large average of absolute deviations. From Figure 2, we can see, for long term projection, the actual observation at the end would be out of the confidence interval if there were no further adjustment of the regression. Therefore, frequent conditional moving adjustment is necessary to provide accurate projection of recruitment as Figure 1 shows. We also noticed that the model under-predicted actual recruitment during the closing weeks, as many clinical centers made special efforts to recruit available participants during the final weeks. This phenomenon was anticipated, without using analytical models.