Knowledge infrastructure and safe operating spaces in social–ecological systems

Abstract

Maintaining safe operating spaces for exploited natural systems in the face of uncertainty is a key sustainability challenge. This challenge can be viewed as a problem in which human society must navigate in a limited space of acceptable futures in which humans enjoy sufficient well-being and avoid crossing planetary boundaries. A critical obstacle is the nature of society as a controller with endogenous dynamics affected by knowledge, values, and decision-making fallacies. We outline an approach for analyzing the role of knowledge infrastructure in maintaining safe operating spaces. Using a classic natural resource problem as an illustration, we find that a small safe operating space exists that is insensitive to the type of policy implementation, while in general, a larger safe operating space exists which is dependent on the implementation of the “right” policy. Our analysis suggests the importance of considering societal response dynamics to varying policy instruments in defining the shape of safe operating spaces.

As the impact of human activities continues to increase in scale and intensity, so does the need for effective environmental policy. Effective policy in this context of dynamically evolving systems must rely on iterative feedback processes that guide a collection of system characteristics (e.g., human well-being, atmospheric CO₂ concentration, or fish biomass) toward desirable levels. At a minimum, effective policies require (i) the capacity to measure system characteristics, (ii) mechanisms to translate such measurements into actions, and (iii) knowledge of how such actions affect the target system. Ideally, any social objective can be achieved within the constraints of a given biophysical system if these three conditions are met. For most environmental problems, however, measurement is imperfect and costly; knowledge of how actions impact nonlinear, open ecological and environmental systems is limited; and the translation of information to action in decentralized decision-making systems is difficult to predict.

There are many approaches to policy design and analysis for such less-than-ideal situations that make varying assumptions regarding how deviations from the ideal are characterized. Stochastic optimization approaches common in resource economics focus on finding the best policy (element ii) given probabilistic characterizations of imperfect measurement and system knowledge (elements i and iii) and do not typically address practical challenges of implementing the best policy. Approaches in control systems engineering typically make less restrictive assumptions and focus not on the “best” policy, but on the design of robust policies to manage systems under a wide range of uncertain circumstances and place more emphasis on the practical challenges of policy implementation. Interestingly, neither of these approaches provides theoretical treatments of the question of how political systems and complex organizations translate information into action, a critical issue in the context of real-world environmental policy, the former because it tends not to treat such practical issues, and the latter because, for the kinds of problems it addresses, element ii is, in fact, nearly ideal: Information is translated into action through a control unit (e.g., an algorithm executed by a device such as the cruise control unit in one’s car) designed with a clear goal and whose performance is limited only by well-understood physical constraints. This is a far cry from environmental policy contexts where the goal is contested and the performance of the “controller” is poorly understood.

This combination of disciplinary interests, methods, and problem focus leaves a research gap between theory and practice for environmental policy design problems, which motivates our work and our use of the term “knowledge infrastructure.” We intend the term to convey both a sense of the many ways that imperfect measurement and information get reflected in practical decision making and that information is processed through complex “knowledge infrastructure systems” that produce, curate, and communicate information. Knowledge infrastructure includes universities, government agencies, communities, media, and their associated assets composed of people, knowledge itself, organizational skill, and a host of shared infrastructure (e.g., transportation and communication) that undergrids their function. We suggest that the implications of the size, complexity, and operation of knowledge infrastructure for environmental policy deserve more careful consideration. Specifically, knowledge infrastructure is costly to maintain and can be improved through investment. Decisions must be made regarding managing these costs and investments.

Our aim here is to contribute to building some analytical capacity for the design of knowledge infrastructure systems for environmental policy with the goal of moving thinking beyond the narrow interpretation of “policy” as merely a decision-making recipe toward consideration of the full process of mobilizing knowledge in practice. To set the stage, we briefly review treatments of knowledge and information in environmental policy, tracing them through increasing nuance regarding how knowledge is characterized and how it is applied in practice. Based on this foundation, we propose a method that merges ideas from mathematical bioeconomics, control theory, and institutional analysis. We then present the results of a dynamic mathematical model of resource management that explicitly includes key aspects of knowledge infrastructure. We propose a typology of knowledge and use it in concert with the model to analyze the performance of various strategies for actualizing these knowledge types to manage the safe operating space of an exploited natural resource system.

A Brief History of Environmental Policy and Knowledge Infrastructure

To structure our review of the literature, we use concepts from control systems theory. Specifically, various streams of environmental policy research address different aspects of general feedback systems such as in Figs. 1 and 2. Arrows depict information flows. The blue block represents decision-making processes, i.e., the transformation of information into instructions for action, and can represent anything from a simple physical device such as a thermostat to a social entity such as a harbor gang, a ministry of fisheries and agriculture, or the United Nations. The orange block represents the biophysical system that translates incoming instructions (e.g., how many fish to extract, how much ${\mathrm{C}\mathrm{O}}_2$ to emit, or how much effort to invest in canal maintenance) into desired material and information flows. Examples range from simple physical devices (an air-conditioning unit) to the entire Earth system. Information about desired flows (output from the orange block on the right) is compared with (indicated by the circle and the minus sign) incoming information about a goal (the desired temperature in your house or concentration of ${\mathrm{C}\mathrm{O}}_2$ in the atmosphere) entering from the left. The difference (indicated by the minus sign) between information about actual and desired outcomes (the “error” signal) is fed back into the decision-making entity. Such information feedback loops, created by periodic measurement, iterative decision making, and instruction updating, are essential for generating any persistent structure within dynamically evolving systems, e.g., an ecosystem, a society, or any combination of the two.

Fig. 1.

General structure of the natural resource management problem.

Fig. 2.

The real-world policy problem. Rather than a single (or relatively simple) goal or “set point” in typical feedback control problems, the goal is to keep the planetary system in the multidimensional SOS inside the outer boundary of the octagon and outside of the space in which society does not meet minimum welfare goals.

Scholars unpack these blocks and arrows in different ways. Social scientists may focus on the politics of goal setting or decentralized decision making in the blue block in Figs. 1 and 2. Ecologists, Earth scientists, and engineers may focus on built and natural systems in the orange block. The term “policy,” narrowly defined, refers to instructions used to translate data into action. In control theory, environmental policy is equivalent to a feedback control law for a system involving natural and/or ecological processes. Various approaches to policy design and analysis make very different assumptions about these boxes and information flows. In the remainder of this section, we summarize key insights from some dominant approaches that focus on this narrow definition of policy to provide a departure point for a more general design process that considers the knowledge infrastructure required to develop, adapt, and deploy the policy over time in its various aspects throughout the entire system. This view recognizes aspects of the broader notion of “environmental governance,” i.e., the complex of interacting infrastructures that actualize policy.

Natural Resource Management Under Uncertainty.

Seminal studies in this area focused on fisheries (1, 2) but the basic problem setup places any resource composed of a single stock (e.g., fish, trees, water) in the biophysical systems block and a benevolent social planner in the decision-making block (Fig. 1). The basic intuition for all such studies is that the social planner, based on perfect understanding of the internal dynamics of the natural system being managed and how society values the resource flows, determines a set of instructions for how much effort should be directed at extracting resources at each point in time to maximize the benefit of the resource to society.

Arrows $d_i$, $d_o$, and $d_m$ in Figs. 1 and 2 depict exogenous drivers that may affect input to, output from, and measurement of the managed system, respectively. Seminal treatments (1–4) and many subsequent variations set $d_i=d_o=d_m=0$ and analyze general aspects of managing common-pool resources (CPRs) composed of a single harvestable stock. This analysis has generated high-level guiding principles for policy design but they are less valuable in practice. Many subsequent studies have explored the implications of $d_i=d_o=d_m\hspace{0.17em}\ne \hspace{0.17em}0$. For example, ref. 5 explores the value of stock assessment in light of imperfect knowledge of the stock size ($d_m\hspace{0.17em}\ne \hspace{0.17em}0$). Others have considered measurement uncertainty in both stock and recruitment (6) and its effects on optimal harvest strategies (7). Yet others have focused on uncertainty regarding how fishers determine where and when to fish (8–10). Others have explored policy under multiple sources of uncertainty (11) and yet others have derived general principles for policy choice, e.g., landing fees vs. quotas, for a specific uncertain dynamic resource (12). Note that this same basic model setup can and has been easily extended to address climate policy questions by choosing the atmosphere as the single-stock CPR of interest (13).

A key feature of these studies and their many variations is the rather restrictive probabilistic characterization of uncertainty upon which they rely. As an alternative, some have suggested the “precautionary principle” (14) which shifts attention away from optimal path-based management given specific uncertainties to what we might call “structural” management where policy intervention focuses on modification of the internal dynamics of the system being managed. Marine reserves are prominent examples of this approach.

Sensitivity-Based Perspectives.

In the absence of probabilistic knowledge of $d_i$, $d_o$, and $d_m$, policy design may take the form of reducing the sensitivity of the system to variation in unknown quantities. From this approach, based on mathematical analysis of feedback control systems, comes a guiding principle akin to the precautionary principle mentioned above: “fragility” is conserved (15, 16). Policy designs that reduce sensitivity to a particular class of disturbances (e.g., high frequency) will necessarily increase sensitivity (fragility) to others (e.g., low frequency). This is the so-called waterbed effect: Suppressing one class of disturbances causes new vulnerabilities to pop up somewhere else. These so-called robustness–fragility trade-offs (RFTOs) must be addressed in the design of feedback control systems. Application of the RFTO perspective to the standard natural resource management model (17, 18) where the structure of the system is assumed known but none of the six relevant parameters (see Materials and Methods for details) are known illustrates a RFTO between “economic” and “biophysical” parameters. For example, policies that reduce sensitivity to uncertainty about the resource growth rate and carrying capacity increase sensitivity to variation in price, harvestability, and cost.

The notion of knowledge infrastructure is more natural in this view of policy design. Navigating RFTOs involves (i) deciding which uncertainties to address with a feedback policy, (ii) identifying potential fragilities thus created, and (iii) allocating resources to manage i and ii such as to reduce uncertainties (directly addressed, associated with emergent fragilities, or both) or managing emergent fragilities directly. That is, knowledge infrastructure is deployed on a number of interrelated fronts involving measuring, learning, deciding, and acting. In fact, even though it treats multiple uncertainties, the RFTO analysis just discussed captures very little of the full uncertainty associated with actual human–environment systems such as how individual cognition and decision making feed into collective decision-making contexts (e.g., how people respond to policy interventions) and uncertainty about ecological/environmental dynamics. We now turn our attention to work that unpacks these two sources of uncertainty as support for the knowledge and actor typologies we propose.

Empirical Perspectives.

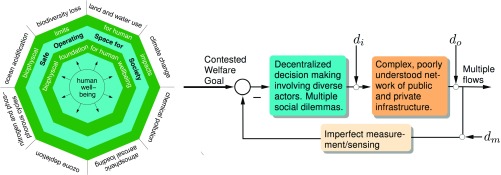
The view of environmental policy in Fig. 1 involves relatively restrictive representations of human behavior and ecology. Real-world environmental policy feedback systems are more accurately depicted in Fig. 2. Here, the management objective is complex, represented as an annulus between minimum biophysical needs and maximum biophysical limits. Generating human welfare within a set of technological constraints requires a minimum biophysical foundation (inner green octagon, Fig. 2). Planetary system function puts a limit on tolerable impacts (outer green octagon, Fig. 2). The safe operating space (SOS) is the annulus between the outer planetary boundary (19) and the inner social boundary (20). Increasing population and per capita demands puts outward pressure on the social boundary. Complex, poorly understood feedbacks between planetary boundary elements decrease the size of the planetary boundary. Together, these processes shrink the size of the SOS. The global-level governance objective is then to keep the coupled social–planetary system within the SOS.

Fig. 2 illustrates this complex welfare goal acting as the set point for the policy control loop. Other new challenges follow: The size and definition (i.e., the goal) of the SOS are contested, creating delays in the feedback system; the omniscient social planner is replaced by decentralized decision makers; and the simple resource system is replaced with an extraordinarily complex one. This diagram highlights how empirical realities from studies of ecological systems and human behavior play into environmental policy, shifting the narrative from resource management under uncertainty to managing for resilience in social–ecological systems. This narrative highlights at least two challenges. First, translating measurements to action requires an internal model of how the target system functions. Human behavior deeply complicates this translation because the basis (beliefs, values, epistemologies) of internal models varies across actors (21). Conflicts between these internal models can slow or completely stop action in deliberative democratic decision-making systems (22). Variation in human behavior prevents convergence to a single “rationality” required for effective feedback control. Second, nonlinearity and complexity of ecological systems give rise to the potential for multiple regimes, difficult to measure tipping points, and rapid movement between regimes. These factors make the policy problem much more difficult.

Deviations from the homo economicus representation of human behavior in policy design have been the subject of intense investigation in recent decades. This work ranges from Kahneman and Tversky’s (23) work on the inconsistency between human decision making and the expected utility model to experimental work revealing altruistic behavior and conditional cooperation in social dilemmas (24) to very recent calls to treat humans as enculturated actors whose behavior is, at least in part, socially determined (25). If humans behaved as atomistic information-processing algorithms, design of robust feedback policies would be much easier. The fact that this is not the case has major implications for policy design. Again, we have mentioned only a few of a very large number of studies, but the main implication for our discussion is that the control unit has its own endogenous dynamics that cause its function to change over time! Not having a fixed, predictable control unit makes policy design extremely difficult.

Similarly, work on regime shifts in ecological systems has significantly impacted thinking in environmental policy. If the ecological system is well understood, regime shifts do not present fundamentally new problems for policy design. In practice, system understanding is limited so the location of tipping points between regimes is typically not known. Under these circumstances, ref. 26 showed that the possibility of regime shifts induces maintenance of higher resource stock levels for optimal management (more precautionary). Subsequent work building on ref. 26 that generalizes the utility and resource growth functions shows that potential regime shifts may make the optimal policy more precautionary (risk avoidance of lost future harvest) or more aggressive (low postregime shift harvest reduces the resource asset value, suggesting liquidation of the resource and investment elsewhere) (27). This is a generalization of Clark’s (2) analysis of the economics of overexploitation showing that resource growth rate determines optimality of conservation or liquidation of the resource. Potential regime shifts increase or decrease the “effective” growth rate. Several other studies analyze the optimal management of natural resources in the presence of thresholds, e.g., refs. 28 and 29. Optimality, however, often depends on subtle details of the model. Thus, although we get some general insights, the policy prescriptions that flow from this work are of limited practical value.

This last point is the point of departure for our analysis. Rather than seek optimal policy prescriptions for narrowly defined feedback systems that do not consider practical implementation challenges, we ask how we might invest in knowledge infrastructure systems for the messy world of Fig. 2. Our work builds on ref. 30, which integrates notions of RFTOs (18, 31) and the SOS (19) to explore how a particular management strategy (short-term variance reduction) affects the SOS of several different exploited ecosystems. Here we focus on one ecosystem type, but explore a range of strategies involving different uses of knowledge infrastructure.

Modeling Knowledge Infrastructure Mobilization in Environmental Management

To ground the mathematical model, consider riding a bicycle—so familiar that we lose sight of the ubiquity and complexity of feedback control problems. The coupled rider–bicycle unit is the biophysical system (orange block, Fig. 2). The rider (controller) senses (tan block, Fig. 2) tilt, direction, and forces and translates these measurements into action (blue block, Fig. 2) through the handlebar (relative orientation of front and rear wheels) and body position relative to the bicycle. Based on experience (an informal time-series analysis), the rider has developed an internal model of how the relative angles of front and rear wheels and body position change tilt, direction, and forces which is used to keep the bicycle in the SOS (upright). Once in the SOS, the rider can implement a goal such as traversing a distance as quickly as possible or leisurely reaching a destination. Increasing performance for speed (e.g., very narrow tires, frame geometry for quick response) may decreases the SOS. Even though humans can handle this task quite easily once learned, building a robotic controller for this task is nontrivial. Imagine now the difficulty of riding a tandem bicycle while blindfolded over a very bumpy road where both riders can steer. This is much closer to the actual environmental management problems we aim to solve.

Building on refs. 30 and 32, we present a modeling framework that provides an initial step toward thinking systematically about knowledge infrastructure and managing the SOS with different types of knowledge gaps. To connect the framework with the existing literature, we extend the standard bioeconomic model. Fig. 3 shows our extension mapped onto the standard control system diagram in which $x\left(t\right)$ is the biomass of a single stock and $e\left(t\right)$, the policy variable, is appropriation effort. The biophysical system dynamics are a simple mass balance between natural growth and harvest as determined by $x\left(t\right)$ and $e\left(t\right)$. The function $U\left(t\right)$ is a stochastic process (e.g., white noise) that exogenously drives the system. We incorporate the potential for regime shifts through a feature of the standard model referred to as critical depensation, the existence of a minimum population level below which the population cannot recover, which we call $\alpha$. We assume that the harvest increases linearly with effort and stock biomass as in the standard model.

Fig. 3.

Extension of the standard bioeconomic model of a renewable resource. See Materials and Methods for full mathematical details.

We extend this standard model in two ways. First, we replace the idealized decision making of a social planner with one that makes explicit the multiple ways knowledge plays into decision making shown in Fig. 5. Second, we replace maximizing a weighted sum of welfare over a time path with keeping $x\left(t\right)$ and $e\left(t\right)$ in a SOS. In the following sections, we define the SOS, formalize the notion of knowledge infrastructure as elements in the space of combinations of strategies (manager types) and knowledge types, and analyze the model to sketch out a more systematic approach to studying practical environmental policy design.

Fig. 5.

The role of different knowledge types in the decision-making process.

Defining the SOS.

The notion of “SOS” prioritizes finding regions in state space which allow safe negotiation of welfare goals. The management problem can also be viewed with these priorities reversed, focusing on finding the welfare-maximizing path while remaining in the SOS. While the mathematics for both views are similar in many respects, the narrative produced by the analyses is subtly different. The latter requires a clear rationale for picking a single time path in the SOS that forces assumptions about the particular structure of the system. Further, optimal paths are often close to the SOS boundary, a fact that may be lost in the narrative. The focus on SOSs is more appealing when there is so much uncertainty about system structure and measurement that optimization results have little value. For instance, consider the cycling example again. Cyclists aim at staying on the right side of the road (SOS) to avoid oncoming traffic. Casual cyclists may stay far from the boundary between lanes. Cyclists in the Tour de France may come very close to the boundary to gain time. For a single rider with a single goal, this may not be a problem. But if a single rider getting close to the SOS boundary may cause problems for others, the group may want to negotiate where they all wish to be within the SOS. This example shows how SOS and optimization views may be complementary. Here we focus on the SOS view as it is a more realistic goal in the context of environmental management.

Our state space is defined by combinations of biomass and effort levels and the SOS is based on an economic and a socio-political constraint. The economic constraint is defined by a minimum subsistence level. For clarity, we assume $N$ identical appropriators so that individual effort is simply $e\left(t\right)/N$. This allows us to define the SOS based on aggregate effort and avoid difficult distributional issues beyond the scope of this paper. Following the standard model (4) we assume constant market price $p$ and cost per unit effort, $c$, so that profit, $\pi$, is $\pi =pH\left(x,e\right)-ce$. Defining minimum per unit effort profit as ${\pi }_{min}$, then the economic constraint is $px-c\ge {\pi }_{min}$ from which we can define the corresponding $x_{min}$ as $x_{min}=\left(c+{\pi }_{min}\right)/p$ (Fig. 4). Setting ${\pi }_{min}=0$ corresponds to open access. Typically managers will set ${\pi }_{min}>0$.

Fig. 4.

The SOS for the natural resource management problem under constant exploitation (long-run biomass will converge to the thick black curve within the SOS). Note that when effort is dynamic, the SOS is typically considerably smaller (compare with Fig. 6).

The socio-political constraint is defined by the appropriators’ perception of having fair access to the resource (to meet subsistence needs, traditional or spiritual access, etc.). If this minimum fair effort, $e_{min}$, is not realized, social and political unrest may ensue. The values of $x_{min}$ and $e_{min}$ set the lower boundary for the SOS analogous to the inner octagonal boundary in Fig. 2. The upper boundary is determined by the interaction between endogenous resource regeneration and appropriation pressure which gives rise to a series of (regulated) bioeconomic equilibria. If $\alpha >0$, there are two sets of interior equilibria, one stable and the other unstable (thick and thin black curves in Fig. 4, respectively). Part of the latter (highlighted in red in Fig. 4) defines the most challenging portion of the SOS boundary to navigate.

Defining Knowledge Infrastructure.

We conceptualize knowledge infrastructure in terms of combinations of knowledge types and knowledge mobilization strategies managers use. We identify two broad manager types: incentive-based and regulatory. The former influences the system by manipulating benefit flows to appropriators via the cost of effort (e.g., a landing tax or annual license fee) by which $c$ is replaced with $c+a\left(t\right)$, where $a\left(t\right)$ is controlled by the manager. The latter focuses on controlling $H\left(x,e\right)$ directly [e.g., setting a quota (e.g., total allowable catch) under a catch share system]. Each strategy involves different configurations of knowledge types and, as a result, different costs. Within these two broad types, there are then different rules for choosing $a\left(t\right)$ or $H\left(x,e\right)$, depending on management goals and available infrastructure. For example, imposing a fixed license fee may require less infrastructure than a landing tax which, in turn, requires less infrastructure than variance management (cf. ref. 30). Four key knowledge types are as follows:

• •Knowledge of the past based on time series ($x\left(t\right),x\left(t-1\right),x\left(t-2\right),\dots$) ($K_1$, Fig. 5). This requires investment and maintenance of monitoring infrastructure (sensors, people, etc.) and is subject to measurement errors (33) that may cause substantial difficulties in understanding ecosystem dynamics (34). Methods exist to limit measurement error in time series (34) but such errors inevitably persist.
• •Knowledge of social and ecological dynamics $F\left(x\right)$, $H\left(x,e\right)$ ($K_2$, Fig. 5). The structure of the interactions between ecosystem dynamics, decision makers, and exogenous drivers is known. Building and maintaining such knowledge requires many experts, e.g., climate scientists, economists, biologists. Representing social–ecological systems and their complexity (so-called model representativeness) remains a critical issue (35) that can be a significant barrier to producing useful models (36). Measurement errors (calibration errors), biases, beliefs, and values may affect how the system is perceived (37). In what follows, we test the influence of poor representativeness of the system (e.g., under/overestimation of $K$).
• •Knowledge of future events based on the properties of $U$ ($K_3$, Fig. 5). Events are characterized from data and/or from expertise (from climate scientists to mathematicians). $K_3$ is sensitive to the likelihood of extreme events because such hazards (especially tail distributions) are difficult to model due to nonlinearities and multiple interactions. By virtue of the fact that they are rare, knowledge associated with extreme events necessarily remains limited (38), leading to a natural tendency to underestimate their frequency. Underestimating the likelihood of extreme events can be catastrophic, while overestimating the likelihood of extreme events may yield needless precaution. As with representativeness, mental representation of likelihoods may evolve over time based on experience and learning.
• •Knowledge of appropriation levels based on self-reporting or observed harvest (denoted $K_4$). The latter requires significant investment in monitoring. The former generates errors due to inaccurate reporting.

Fig. 5 shows the “internal model” that policy actors use to determine $e\left(t\right)$. Red arrows indicate how each knowledge type and its associated information flow enter into the iterative decision-making process. The blue arrows indicate actual actions: the effort level, $e\left(t\right)$ and exogenous driver $U\left(t\right)$ act on the dynamics which, in turn, act on the present state $x\left(t\right)$ to generate an actual future system state, e.g., $x\left(t+1\right)$. In each iteration of the policy process, decision makers may use any combination of knowledge types $K_1-K_4$ to choose their target $e\left(t\right)$. This iterative policy process produces a sequence of biomass and effort values through time which, in turn, generates welfare for society. Because each knowledge type involves significant infrastructure investment, the cost of its use must be weighed against the benefits it brings through welfare-improving choices of $e\left(t\right)$. This consideration, central in control systems engineering but seldom considered in environmental policy contexts, may even suggest that it is best to deploy no knowledge infrastructure. Alternatively, decision makers may deploy $K_4$ to ensure that their target $e\left(t\right)$ is actually realized. They may deploy $K_2$ to study social–ecological dynamics to improve their ability to predict $x\left(t+1\right)$ given a measurement for $x\left(t\right)$. Of course, the quality of this prediction depends on the deployment of $K_1$ to get good measurements for $x\left(t\right)$ and of $K_3$ to gain understanding of $U\left(t\right)$.

Analysis: From Knowledge to Action

The most general insight that emerges from our analysis is that for incentive-based strategies, imperfect knowledge shrinks the SOS. While this is consistent with our intuition, there are counterintuitive cases in which particular combinations of imperfect knowledge and management strategy may enlarge the SOS. For a variance reduction manager as in ref. 30, overestimation of the stock (errors in $K_1$) artificially increases the variance-based indicator, exaggerating early warnings. For a maximum sustainable yield (MSY) manager, overestimation of carrying capacity artificially increases the biomass target, resulting in more cautious strategies. In the case of management based on a proportional tax, overestimation of $e\left(t\right)$ leads to overestimation of the tax which leads to a stronger reduction of $e\left(t\right)$ than conditions actually dictate. This enlarges the SOS. Finally, more adaptive strategies are not always better than less adaptive strategies (32). The moral of this story is that the interaction between how and what knowledge is applied is quite complex.

To sharpen this point, consider the concrete case of the managed fishery. Management seeks to keep biomass near MSY (still a common management objective, e.g., the European Union Common Fisheries Policy), denoted $x^{MSY}$, while remaining in the SOS. This requires maintaining $x\left(t\right)>x_{min}$ and $e\left(t\right)>e_{min}$ and avoiding crossing tipping points. We compare three strategies:

• i)An economic incentives (EI) manager who adapts the level of a landing tax over time according to $x^{MSY}$. Below $x^{MSY}$, there is no tax ($a\left(t\right)=0$), and above $x^{MSY}$ the tax is maximum ($a\left(t\right)=a_{max}$). This strategy is an integral-like controller because tax changes effort through an integral (Materials and Methods) which generates a delay.
• ii)An optimal economic (OE) manager who has full access to perfect knowledge to maximize the probability of sustaining the fishery over a predefined time interval (i.e., meet social–ecological constraints) through setting $a\left(t\right)$. This is also an integral-like controller which suffers from delays. The OE manager’s job is much more demanding than the EI manager’s is.
• iii)A catch share (CS) manager who sets total harvest rather than a tax to drive the system to $x^{MSY}$. The CS manager can change harvest directly from year to year. As such, the controller is called proportional because $H\left(t\right)$ at time $t$ is based directly on the proportional difference between $x\left(t\right)$ and $x^{MSY}$ in contrast to the OE and EI strategies where the change in $e\left(t\right)$ is based on this difference. This subtle difference between integral and proportional controls is important in what follows.

We compare these strategies in terms of the size of their SOS based on a 0.9 probability of complying with the social–ecological constraints given exogenous driver $U\left(t\right)$ in two different knowledge situations. Fig. 6 compares these management strategies in the case of perfect knowledge. The CS manager has the largest SOS because her strategy behaves like a proportional controller with more immediate impact over harvest levels with little delay. This is in sharp contrast to the integral-like OE and EI managers. The OE SOS is obviously bigger than the EI SOS in this case because the OE uses more sophisticated knowledge infrastructure. Note that the CS manager uses simpler knowledge infrastructure (much simpler rules and less information). Note that although the CS SOS is largest, it does not contain the others. It cannot handle cases of low biomass that the others can. This is due to the fact that when biomass gets low, the CS manager reacts strongly and stops exploitation, causing the system to cross the social constraint. The fact that no SOS contains all others shows there is no panacea: There is no policy that works in all cases.

Fig. 6.

SOSs for different managers with perfect knowledge.

The existence of an “unerring operating space” (UOS) is interesting. The UOS corresponds to the intersection of all SOSs: Whatever the policy, the system is unerringly safe. In our case, it corresponds to an area around an attractor. The dead operating space (DOS), on the other hand, corresponds to the case where there is no safe policy: Whatever the policy, the system will not be safe. For example, a person aiming to lose weight may use different strategies such as diet change, exercise, liposuction, or gastric surgery that require very different knowledge infrastructures and have very different impacts on other health factors. Each one may enable a person to reach and maintain a target weight interval (SOS) given sufficient time (UOS). However, reaching the SOS in a shorter time may not be possible for any strategy (DOS).

In Fig. 6, there are two DOSs: the right DOS corresponds to an ecological DOS whereas the left DOS corresponds to a social DOS. It is important to identify UOSs and DOSs: The type of management does not influence the final results and it is not necessary to invest in mobilizing additional knowledge. On the other hand, there are critical zones—where SOSs do not overlap—for which it is necessary either to invest in more knowledge (e.g., move within the SOS of an OE manager) or to switch from EIs to direct regulation.

The imperfect knowledge case (Table 1 and Materials and Methods) assumes decisions are based on 50% over/underestimation of carrying capacity $K$. For the OE manager, $K$ changes the shape of equilibrium curves and the locations of tipping points, shrinking the OE SOS. The impact of $K$ is quite different for the MSY-based manager. The EI manager bases policy on $x^{MSY}$ whereas the CS manager bases his policy on $x^{MSY}$ and MSY. In the case of underestimation, both managers aim at having a lower biomass, yielding a higher probability of crossing tipping points. On the other hand, overestimation of $K$ yields a cautious strategy for the EI manager (he aims at having a higher biomass) whereas an overestimation of $K$ yields strategies based on higher MSY for the CS manager, which is catastrophic in terms of SOS. In summary, the largest SOS is produced by the CS manager in the cases with perfect knowledge and underestimation of $K$ while the EI SOS is largest in the case of overestimation of $K$. Table 1 shows the ranking of SOS size for different managers. However, as mentioned above, it would not be wise to select a management strategy based on the size of the SOS alone.

Table 1.

Robustness ranking of the SOS for different managers with imperfect knowledge

Manager	Mobilized knowledge	Ranking with PK	Ranking with UE	Ranking with OE
EI manager	K1, K2	3	3	1
OE manager	K1, K2, K3, K4	2	2	2
CS manager	K1, K2	1	1	3

PK, perfect knowledge; UE/OE, under/overestimation.

Implications for Policy in the Anthropocene

Our objective in this article has been to explore the challenges of mobilizing knowledge to manage exploited ecosystems. As human impact on ecosystems increases, linkages between various exploited ecosystems will become more important and the need for management at the planetary scale will intensify. Management at the planetary scale will necessarily involve a very diverse set of actors, aspirations, and beliefs. Such biophysical, social, and economic complexity requires us to move from the simple conceptualization of policy design in Fig. 1 to the one in Fig. 2. We traced the literature on policy design with uncertainty across these conceptualizations to set the stage for an approach based on analyzing the impact of knowledge infrastructure mobilization on SOSs rather than on more restrictive, probabilistic, trajectory-based approaches. In a similar spirit to ref. 39, our approach focuses on how knowledge (what kind and in what way) is used.

Our analysis shows that the role of knowledge mobilization on the sustainability of a resource system (i.e., the size of the SOS) is quite subtle. Whether imperfect knowledge is problematic or helpful depends on the context, so there are few general principles that emerge. The few that do include the following:

• •The importance of identifying UOSs and DOSs. In the UOS and the DOS, what knowledge is mobilized and how it is applied do not matter. There is no value in investing in generating additional knowledge or in implementing other policy tools.
• •The need to navigate a portfolio of SOSs. In the absence of a SOS that contains all others, management should focus not on staying within a particular SOS, but on navigating a portfolio of SOSs based on available knowledge and policy tools.
• •The need for infrastructure to deploy multiple combinations of knowledge and policy types. Navigating from one SOS to another may require investing in knowledge infrastructure and/or changing policy tools on the fly. It is thus not a question of “prices vs. quantities” but, rather, of how to dynamically navigate among policy instruments as changing context dictates. This navigation will require not only economic investment, but also socio-political investment. Changing policy instruments has nonmonetary cognitive costs that may be barriers to social acceptance.

Although our analysis represents a small step, it highlights a critical need for research on how knowledge infrastructure, composed of systems of beliefs, perceptions, models, data, and practical mechanisms to actualize this knowledge, interacts with ecological dynamics to create SOSs. Such research will be critical for policy design, at scale, in the Anthropocene.

Materials and Methods

Managing Exploited Populations.

The standard bioeconomic model is $x\prime \left(t\right)=F\left(x\right)-H\left(x,e\right)$. $F\left(x\right)$ represents the stock-dependent regenerative capacity of the resource. The typical minimal biologically representative choice is logistic growth: $F\left(x\right)=rx\left(K-x\right)$. We add critical depensation and an exogenous driver by defining $F\left(x\right)=r\left(x-\alpha \right)\left(K-x\right)+U\left(t\right)$. The harvest, $H\left(x,e\right)$, depends on the stock $x\left(t\right)$ (e.g., tons) and effort $e\left(t\right)$ (e.g., vessel days per year) according to the standard model, $H\left(x,e\right)=qex$. The biomass dynamics follow

$$\frac{dx}{dt}=r\left(K-x\right)\left(x-\alpha \right)-qex+U\left(t\right).$$ (1)

The parameters are intrinsic growth, $r=0.25$; carrying capacity, $K=4$; sigmoid predation consumption coefficient, $\alpha =0.25$; and “catchability” (technology), $q$, which we normalize to 1. $U\left(t\right)$ is a white noise process with a SD equal to 0.075.

Incentive-Based Management.

Effort dynamics.

We consider EI management based on an adaptive tax. The effort dynamics are

$$\frac{de}{dt}=\beta e\left(px-c-a\left(t\right)\right)\left(1-e\right)$$ (2)

with $\beta =0.05$, $c=1.5$, $p=4.5$. The term $a\left(t\right)\in \left[0,a_{max}\right]$ is the control with $a_{max}=4.5$. The term $\left(1-e\right)$ is used to set an upper limit on the effort equal to 1. We set the minimum effort $e_{min}$ to 0.05 and ${\pi }_{min}$ to 0.2. In what follows, 1,000 simulations were used for assessing the probability of complying with the socio-ecological constraints. The time horizon $T$ is equal to 100 time steps.

The EI manager.

The EI manager adapts regulation $a\left(t\right)$ according to biomass and the MSY,

• •if $x\left(t\right)$ $<$ $x^{MSY}$, $a\left(t\right)=a_{max}$; and
• •if $x\left(t\right)$ $>$ $x^{MSY}$, $a\left(t\right)=0$.

Here, $x^{MSY}$ = 2.125.

The OE manager.

The OE manager adapts the control $a\left(t\right)$ based on time series to maximize the probability of sustainability. This problem can be solved using dynamic programming. Consider a time horizon of $T$ and define ${\mathbb{P}}^s\left(T,X\right)$ as the probability of complying with the social–ecological constraints at $T$, with $X$ being the state vector of the ecosystem (i.e., $x$ and $e$). This initial probability is equal to 1 if state $X$ complies with the socio-ecological constraints and is equal to 0 elsewhere. This means that if $x<x_{min}$ or $e<e_{min}$, the system is considered failed. Then we use the following backward technique (dynamic programming) from $t=T-1$ to $t=0$:

$$\forall t\in \left[0,T-1\right],{\mathbb{P}}^s\left(t,X\right)=\underset{a\left(t\right)}{max}\sum _y\mathbb{P}\left(g\left(X,a\left(t\right)\right)=Y\right){\mathbb{P}}^s\left(t+1,Y\right).$$ (3)

The $g$ function corresponds to the right term of Eqs. 1 and 2 (transition from one state to another). Finally we arrive at the strategy $a\left(0\right),a\left(1\right),\dots ,a\left(T\right)$ that maximizes the probability ${\mathbb{P}}^s\left(0,X\right)$.

Regulatory Management.

We consider a CS manager who, instead of controlling effort through a tax, controls total allowable catch by fixing the yield $H\left(t\right)$ with the goal of driving $H\left(t\right)$ to the MSY. $H\left(t\right)$ is set based a on proportional controller:

$$H\left(t\right)=MSY+\gamma \frac{x\left(t-1\right)-x^{MSY}}{x^{MSY}}.$$ (4)

In terms of “proportional” controller,

• •“MSY” corresponds to the “controller output with zero error”;
• •$\frac{x\left(t-1\right)-x^{MSY}}{x^{MSY}}$ corresponds to the instantaneous process error at time t; and
• •$\gamma$ corresponds to the proportional gain and is equal to 1.5 here.

Effort $e\left(t\right)$ is then estimated with this yield objective and the estimation of the biomass $x\left(t\right)$ via the equation $e\left(t\right)=H\left(t\right)/x\left(t\right)$.

Imperfect Knowledge.

We explore how biases in knowledge assessment impact the system when managers under- and overestimate $K$ by 50%. The SOSs are shown in Fig. 7 in support of Table 1.

Fig. 7.

SOS of the different managers (during 100 time steps). The SOS is described by the probability of sustainability higher than 0.9.