Abstract
Cuffless technique holds great promise to measure blood pressure (BP) in an unobtrusive way, improving diagnostics and monitoring of hypertension and its related cardiovascular diseases, and maximizing the independence and participation of individual. Pulse transit time (PTT) has been the most commonly employed techniques for cuffless BP estimation. Many studies have been conducted to explore its feasibility and validate its performance in the clinical settings. However, there is still issues and challenges ahead before its wide application. This review will investigate the understanding and development of the PTT technique in depth, with a focus on the physiological regulation of arterial BP, the relationship between PTT and BP, and the summaries of the PTT-based models for BP estimation.
Keywords: Pulse transit time, Cuffless blood pressure, Physiological regulation, Relationship, Models
Introduction
Cardiovascular diseases (CVDs) are the world’s biggest killer, and hypertension is the major modifiable contributory risk factor for the CVDs [1]. Hypertension is the most common and potentially lethal condition that may result in heart attack, stroke, myocardial infarction, cerebrovascular accident, congestive heart failure, myocardial ischemia, etc., if it is not detected early and treated appropriately [2]. Hypertension is highly prevalent, affecting more than 40% (1.5 billion) of adults worldwide, and this number is expected to rise dramatically due to a rapidly ageing population and increasing prevalence of obesity [3]. Worse still, hypertension is a “silent killer” that it rarely causes symptoms in the early stages, leading to its low awareness rate thus high prevalence, as well as very low control and treatment rate. A multinational study reported in 2013 shows that only around 46% hypertensive patients are actually aware of their disease and measure BP regularly, with BP controlled among 32.5% of those being treated [3]. Early detection of hypertension to reduce cardiovascular risk in people with hypertension is therefore vital to reduce the prevalence of hypertension, thereby preventing the development of CVDs and its associated morbidity and mortality [4].
Early, accurate and regular monitoring of BP is essential for diagnosis of hypertension, to evaluate BP-related risk, to predict acute cardiovascular events, and to meet treatment targets. BP measured in the physician’s office using the auscultatory mercury sphygmomanometer has been considered the standard method for over 100 years [5]. Nevertheless, it becomes increasingly evident that the office BP is inadequate to reveal a patient’s true BP status, particularly for those with the masked hypertension—the hypertension that cannot be detected by the routine methods. Masked hypertension is associated with subclinical damages and treatable form of hypertension; it is very common and prognostically important, but insufficiently recognized [6]. On the other hand, the office BP may be misleading because of the white-coat effect, a phenomenon in which patient exhibits a BP level above the normal range in a clinical setting. As a result, the ambulatory BP and self-measured BP at home have shown to be superior to the office BP in predicting mortality [7], and have been recommended for routine BP measurement for the majority of patients with known or masked hypertension [8]. The major advantage of the ambulatory BP monitoring is to provide information about BP during daily activities and sleep. The self-measured BP monitoring at home may benefit individuals by affording information to assess lifestyle and identify risk factors in hypertension, monitoring the response to antihypertensive treatment with lifestyle modifications or drugs, improving patient adherence with therapy, as well as evaluating white-coat hypertension.
Devices for the ambulatory BP measurement and home BP monitoring are usually developed based upon the oscillometric approach, which requires an inflatable cuff and may cause discomfort and pain to the user, in particular the individual with high BP and who need frequent repeated readings. Moreover, the conventional cuff-based techniques can only provide a snapshot of dynamic BP readings, but not the continuous BP throughout the day and night. The long-term longitudinal changes in BP is well-recognized as a more accurate determinant of cardiovascular risk as the changes in systolic or diastolic BP over a period reflect the evolution of arterial and arteriolar alterations. Also, BP variability (BPV) has been reported to be a valuable prognostic indicator for hypertension [9]. Moreover, targeting a lower BP value than the hypertension threshold expects to achieve better outcomes. A recent study by the Systolic Blood Pressure Intervention Trial suggests that targeting a systolic BP of less than 120 mmHg, as compared with less than 140 mmHg, would result in lower rates of fatal and nonfatal major cardiovascular events and death among patients at high risk for cardiovascular events [10]. All these evidences reveal the importance of continuous BP monitoring for diagnosing hypertension and evaluating hypertension control [11]. Continuous BP monitoring is therefore imperative for early prevention, detection, management, and treatment of hypertension to reduce the morbidity and mortality of the CVDs.
Compared with intermittent BP, unobtrusive and continuous BP in a long-term period, such as day by day, would offer a deeper insight into the profile of BP fluctuations and allows better understanding of the mechanisms responsible for the marked variations of BP that occur throughout the day and night [12]. Intra-arterial BP monitoring by inserting a cannula needle in a suitable artery can directly detect continuous BP in real-time. It is commonly used in the Intensive Care Unit and considered the gold standard for arterial pressure measurement. However, the invasive manner may have adverse effects such as bleeding, infection and ischemia, and is only limited to clinical settings. Arterial tonometry, arterial volume clamp and pulse wave velocity (PWV) method are three primary techniques to obtain continuous BP in a noninvasive way. The former two kinds of methods can monitor the continuous BP through compressing the artery to the optimal ‘applanation position’ and keeping the arterial wall in an unloaded state, respectively. Both methods cannot yet fundamentally get rid of the use of the occlusive cuff and are restricted to use in research and specific situation of clinical setting due to the large physical size, uncomfortable user experience and cumbersome operation. The method that can measure continuous or beat-to-beat BP without user interruption is highly desirable for ubiquitous application.
Method based on PWV recording is a promising alternative for continuous cuffless BP measurement. This technique relies on the fact that, the velocity of the arterial pressure pulse propagating along the arterial system intrinsically varies with the underlying physiological variation, of which BP is an important element. PWV can be measured from pulse transit time (PTT) via PWV = L/PTT, where PTT refers to the time it takes a pulse wave to travel between two places in the cardiovascular system, and L is the distance between the two places of the propagation. PTT can be easily obtained from two cardiac pulse signals, such as electrocardiogram (ECG) and photoplethysmogram (PPG), and it can be translated into BP with a calibration procedure. The PTT method has received much attention over the recent decades because of its capability to track BP change, as well as its advantages as a noninvasive, continuous and most importantly unobtrusive tool for BP measurement [13–15].
The aims of this paper are: to describe the cardiovascular physiology that relates to BP regulations; to provide comprehensive review of the PTT-based method for cuffless BP estimation; and to indicate the challenges and opportunities for future study. This article will focus on the review of the PTT-based methods for the cuffless continuous BP. In section II, we present the physiological mechanism for the pulse wave velocity recording. Section III provides a critical review of the relationship between the PTT and the BP, and section IV summaries the PTT-based algorithms for BP estimation. In Section V, we address the challenges and future directions to further develop the field of cuffless BP measurement.
Physiological regulation of arterial blood pressure and arterial pulse wave propagation
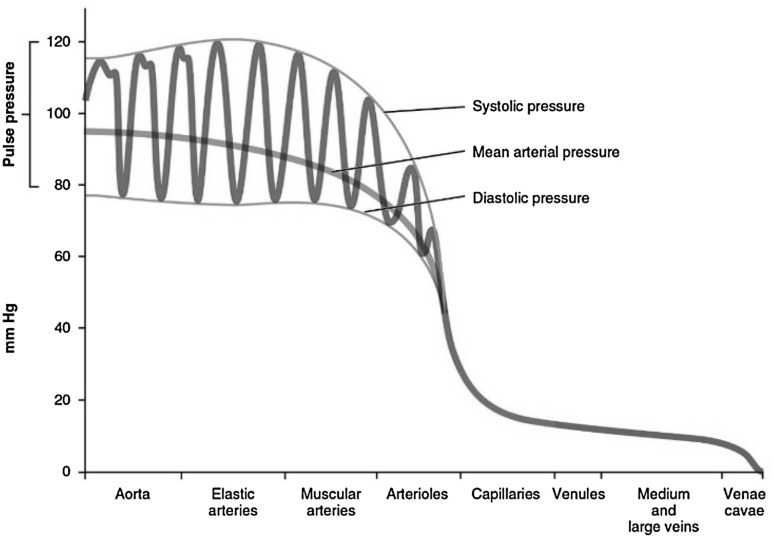
The arterial BP is the pressure that exerted on the vessel walls when the blood streams through the blood vessels. Each heart beat causes the arterial BP to vary between systolic BP (SBP), an increase of pressure induced by the systolic contraction of the left ventricle, and diastolic BP (DBP), a drop of arterial pressure occurring during the diastolic arrest of the heart between two contractions. BP varies in different types of blood vessels, as can be seen in Fig. 1. SBP is primarily dependent on the characteristics of the stroke volume, whereas DBP is shaped largely by the conditions of the arteries and arterioles and their abilities to accept the runoff of blood from the aorta [16].
Fig. 1.
The components of blood pressure (BP) throughout different types of blood vessels, including systolic, diastolic, pulse and mean arterial pressures [17]
Physiological regulation of arterial blood pressure
BP is a hemodynamic parameter that fluctuates throughout the day. It can be affected by various factors including physiological factor (e.g., breathing), psychological factor (e.g., mental stress), behavioral factor (e.g., exercise, sleeping), and even environmental factor (e.g., temperature change), etc. The regulation of BP is conventionally portrayed as homeostasis. The word “homeostasis” is derived from the Greek “homeo” (similar) and “stasis” (steady), indicating that BP, although being continuously perturbed by external stimulations, always tends to get back toward a reference set point [18].
Regulation of arterial BP is a very complex physiological function, involving a continuum of interactions among cardiovascular system, autonomic nervous system, and endocrine systems. Investigating the indirect continuous BP measurement methods thus needs a good understanding of the factors that are responsible for the normal BP control, on the one hand to explore the potential noninvasive physiological indicators, and to develop appropriate models that represent the relationship between the indicators and the variations of BP.
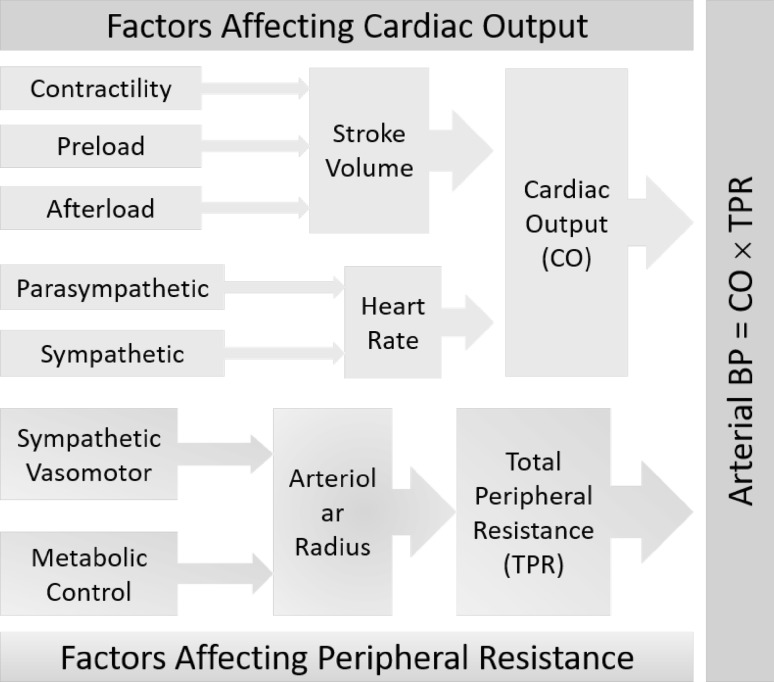
Different components of arterial pressure are determined by different factors [19]. The main contributing factors of SBP are the cardiac output, the circulating blood volume, the blood viscosity, the elasticity of large arteries, and the peripheral vascular resistance. DBP is essentially determined by the peripheral vascular resistance and the elastic contraction of the large arteries during the cardiac diastole. And the major determining factors of pulse pressure (PP) are cardiac performance and aortic stiffness [20]. The mean BP (MBP) is mainly determined by the cardiac output and systemic vascular resistance. Therefore, changes in either factor will affect BP. To a large extent, BP is related to the product of the cardiac output and the total peripheral resistance [21]. The circulating blood volume, the viscosity of the blood, and the elasticity of the large arteries are comparatively stable factors, and thus, under normal conditions, influence the arterial pressure only to a minor degree. Therefore, the regulation of arterial pressure basically relies upon the changes of cardiac output and the peripheral vascular resistance.
Cardiac Output is the amount of blood pumped by the heart per minute. As described by Guyton, cardiac output per se is regulated by two functions: cardiac function and the return function, which are determined by cardiac performance and the return of blood to the heart, respectively [22]. It is also usually evaluated as a product of heart rate (HR) and stroke volume, and thereby being regulated under the interaction of HR and stroke volume. HR is controlled by sympathetic and parasympathetic input to the sinoatrial node, since the heart rhythm is regulated thoroughly by the sinoatrial node under normal conditions [23]. Stoke volume is the volume of blood ejected by the left ventricle per heartbeat. It can be calculated from ventricle volumes measured by an echocardiogram, as the difference between the volume of the blood in the ventricle at the end of a beat (end-systolic volume) and the volume of blood just prior to the beat (end-diastolic volume). It is therefore mainly dependent on the heart contractility, preload (end-diastolic volume), and afterload.
Peripheral Resistance Peripheral resistance refers to the resistance of the circulatory system to blood flow. The resistance generated by the peripheral circulation is the systemic vascular resistance, which is also known as the total peripheral resistance (TPR). The peripheral resistance is produced and controlled mainly by the variably contractile arterioles and probably also the capillaries. Other factors such as viscosity also induce a resistance to the peripheral flow of blood. The degree of contraction or tone of the arterioles and the capillaries is maintained and controlled by several aspects, which of prime importance are the nervous impulses that arise in the vasomotor center and keep the normal degree of contraction of the peripheral blood vessels.
The resistance is inversely proportional to the fourth power of radius of blood vessels, which can be evaluated by Poiseuille’s Law [24] through the formula:
| 1 |
where η is the viscosity of the fluid, L the length of the blood vessel, and R the radius of the blood vessel. It can be seen that the peripheral resistance is predominantly determined by the large changes in diameter of small arteries and arterioles, which are dependent on the degree of constriction of vascular smooth muscle surrounding the arterioles. Vascular smooth muscle is subject to the simultaneous influence of vasodilator factors and vasoconstrictor factors. Regulation of the peripheral vascular resistance is achieved by sympathetically mediated vasoconstriction of any tissue that is not producing vasodilting metabolic byproducts. For example, when environmental changes occur (e.g. exercise), neuronal and hormonal signals, including binding of norepinephrine and epinephrine to the α1 receptor on vascular smooth muscles, cause either vasoconstriction or vasodilation, further leading to the arterial diameter change.
BP Variability The main contributor of the short-term BPV in healthy subjects is the sympathovagal balance [25]. BP is also regulated by baroreflex, a buffering mechanism that opposes increases or decreases of BP by changes in HR, myocardial contractility, and peripheral resistance. In this respect, baroreflex has been thought to be the link between BPV and HR variability. On the other hand, there is some evidence that changes HR that is related to respiration may contribute to BPV, suggesting fundamental relationship between BPV and HR variability. With spectral analysis, the rhythmic oscillations of BPV can be identified with the appearance of individual peaks, which reflect: (1) the oscillations at HF range typically between 0.2 and 0.35 Hz, a frequency like that of normal respiratory activity; (2) oscillations with low frequency range of approximately 0.1–0.15 Hz, suggesting the sympathetic modulation of vasomotor tone.
To put it simple, determinants of arterial BP are approximated by Ohm’s law modified for fluid dynamics, i.e., pressure = flow × resistance. Blood flow depends on cardiac output and blood volume, whereas resistance is primarily determined by the contractile state of small arteries and arterioles throughout the body. The overall factors that affect BP is thus summarized in Fig. 2.
Fig. 2.
Summary of factors that affect arterial pressure
Arterial pulse wave propagation
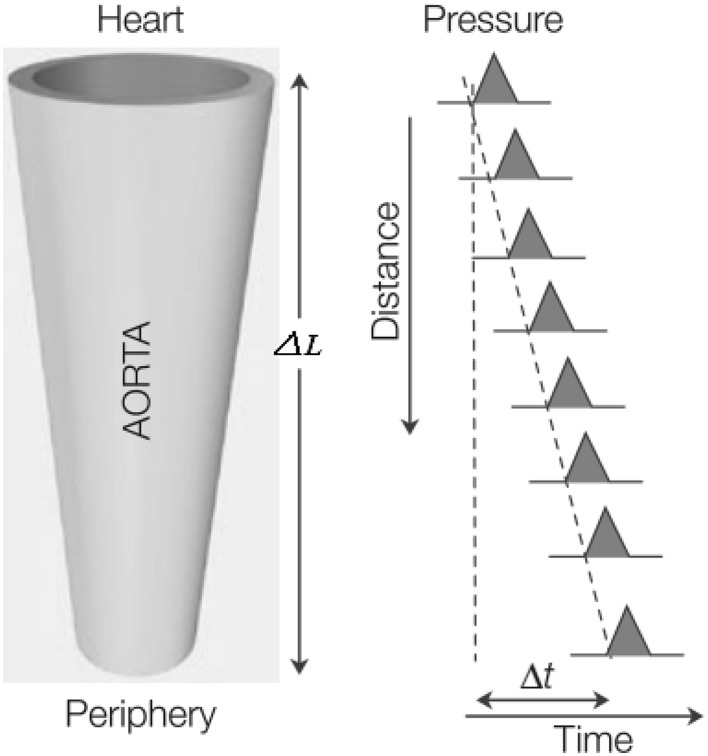
The pulsatile nature of blood flow generates a pressure pulse wave that is propagated from the heart down the arterial tree through the artery walls, with a certain speed that is called pulse wave velocity (PWV). The distance ∆L traveled by the wave over the time delay ∆t between two sites in the arterial system gives the PWV, as schematically shown in Fig. 3.
Fig. 3.
Schematic diagram of the pressure pulse wave velocity (PWV = ∆L/∆t) [24]
To understand the relationship between PWV and arterial BP, it is necessary to analyze the transmission of the pulse wave in the arterial system. PWV can be quantitatively evaluated by the well-known Moens and Korteweg (M–K) equation [26] as given by (2).
| 2 |
The M–K equation correlates PWV with the modulus of elasticity of the artery E, the thickness of the arterial wall h, the diameter of the artery D and the density of the blood ρ. If ρ is assumed to be constant, among the other three variables (i.e., E, h, and D), E is the major factor that PWV depends upon. Further, elasticity of arterial wall is significant to the circulatory mechanism, owing to the theory that the arteries can transform an intermittent cardiac output into a continuous capillary flow. Therefore, the more elastic the artery, the greater will be the blood volume changes, with which the artery can accommodate for a given rise of pressure. The elastic conditions of the arterial wall may be affected by various factors in healthy and diseased population, which would further alter PWV. Taking age for example, the older the subject the more stiff or less elastic are the arteries, and the higher the velocity of the pulse wave [27].
Since the parameters in M–K equation may differ from artery to artery, and they are difficult to be measured, an alternative formula has been transformed from M–K equation by Bramwell and Hill [28]:
| 3 |
which is the Bramwell and Hill (B–H) equation, with V and P being the blood volume and pressure, respectively, and (dV/dP)/V is the relative increase in the volume of the artery per mmHg increase of pressure. The B–H equation is more convenient to use, since only the observable increase of volume with pressure may give PWV, when there is no knowledge about the arterial elasticity and the arterial dimensions.
Pulse transit time (PTT) and its relationship with BP
Definition and calculation of PTT
PTT refers to the time it takes a pulse wave to travel between two places in the cardiovascular system [29]. Because of its noninvasive, reliable, low-cost and ease of use properties, PTT is a powerful physiological parameter that has been widely used for various clinical applications, for example, as a measure of respiratory effort [30], evaluation of arterial stiffness, estimation of BP, etc. [31]. Particularly, PTT has been extensively studied for unobtrusive and continuous BP measurement. Although the usage of PTT has been growing in science and engineering in the past 50 years, there is still a lack of common terminology for PTT. There are also distinct differences between research groups in terms of the PTT definition, and PTT has been usually mixed up with pulse arrival time (PAT). This section will elucidate the definition and terminology of PTT to resolve the difficulties and confusion within the scientific community.
The usage of PTT can be dated back to 1964, when Weltman et al. [32] devised the PWV computer by “utilizing the EKG complex and a downstream pulse signal to define pulse transit time over a known arterial length”. To the best of our knowledge, this is the first time the word “pulse transit time” being used and defined. In 1976, Steptoe [33] reported the “transit time”—the interval between R wave of the ECG and the proximal pulse, as a modification of the interval between pulse arrivals at two sites on the same major artery for the sake of convenience. Later in 1978, Obrist et al. [34] measured PTT as the time between the initiation of the pre-ejection period (PEP) and the peak of the pulse wave. Formally PEP is defined as the time span between the Q wave of the ECG and the onset of the opening of the aortic valve. In practice, the R wave of the ECG is usually used as the reference point since its determination is easier and precise. In 1980, Weiss et al. [35] defined PTT as the interval between ventricular electrical activity and the peripheral appearance of the pulse. In the same year, Marie et al. [36] mentioned the time interval between R wave of ECG and peripheral pulse as absolute PTT measures, while that between two peripheral pulses as a measure of PTT differences, which were referred as ECG-initiated transit time (ECG-TT) and arterial PTT respectively by Redman et al. [37] in 1983. Thus, PTT contains the intra-cardiac and arterial components of pulse transmission time, and we express it with PEP and the vascular transit time (VTT) as given in (4).
| 4 |
It is evident that the PTT calculating from ECG and peripheral pulse includes PEP [34]. Ever since 1981, there have been some studies taking PTT as the interval between pulse arrivals between two arterial sites. For example, in the studies [38, 39], PTT was measured as the interval between pulses collected at two arterial sites, meanwhile the time difference between the R wave of ECG and the peripheral pulse was called ECG-pulse interval or PAT.
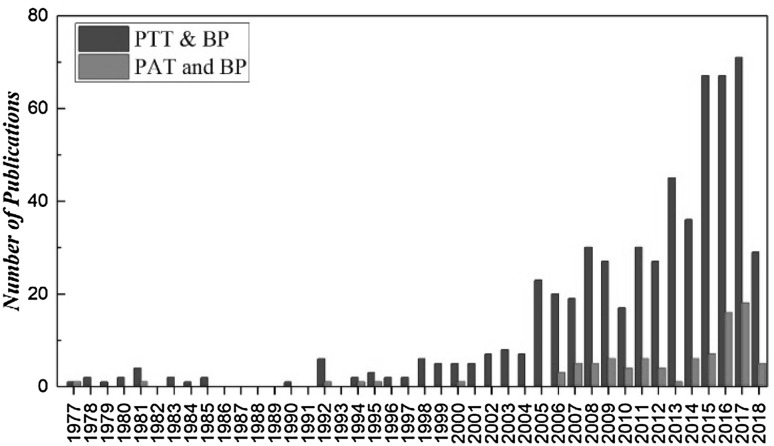
We have conducted a survey with the usage of terminology of “pulse transit time” and “pulse arrival time”. According to Thomson Reuters Web of Science, the total number of publications with topics of “pulse transit time” and “blood pressure” was 583, with the sum of times cited was 7903, among which PTT was commonly used not only as the time difference from R wave of ECG to peripheral pulse but also as the time intervals between two peripheral pulses; while the total number of publications of “pulse arrival time” and “blood pressure” was 92 with the sum of times cited was 761. As shown in Fig. 4, the number of publications in the recent four decades for “PTT” is increasing with years more than that for “PAT”. Our recent survey of the PTT studies during 1977–2018 demonstrates that among 129 publications with title including “pulse transit time” and “blood pressure”, PTT that defined and calculated as the time interval between R wave of ECG and peripheral pulse is dominant.
Fig. 4.
Number of publications of pulse transit time (PTT) and pulse arrival time (PAT) for the recent three decades
Thus, use of longer-established, more plausible and recognizable term—PTT, would replace the need to use the term—PAT to avoid any confusion in the research community.
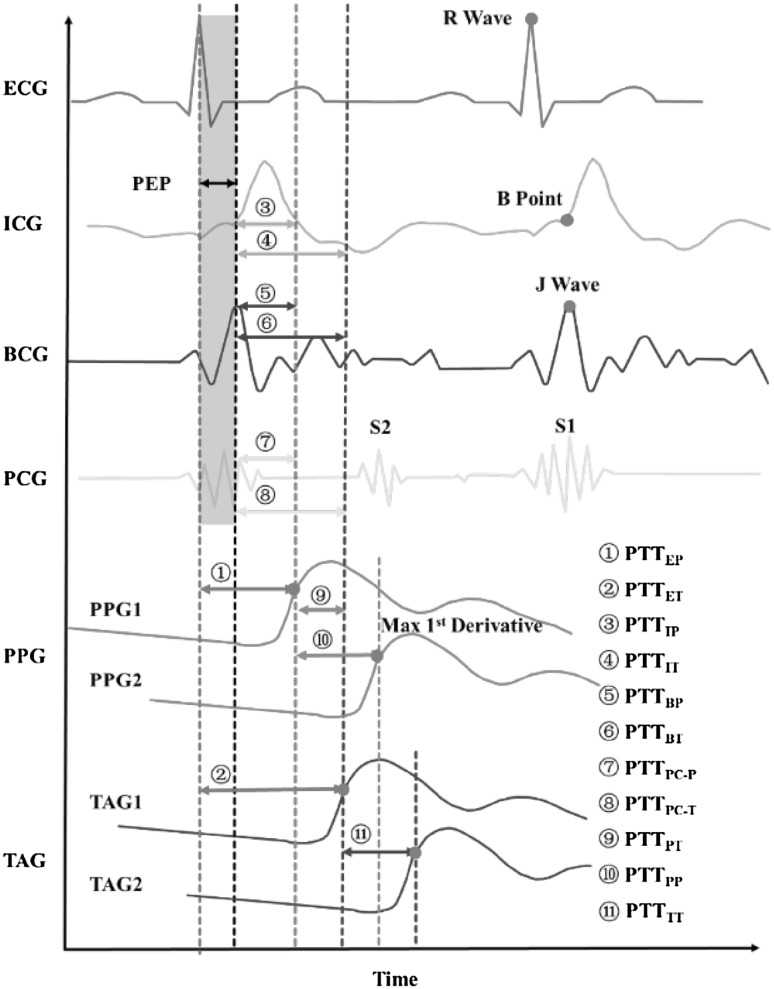
Definition of PTT The word “transit” is defined as “carrying of people or things from one place to another” according to Oxford Dictionaries. Accordingly, the definition of PTT—“The time for the carrying of pulse wave information by pulse signal from one location to another in the cardiovascular system”—is a more broad definition which covers the transit times determined by different approaches, such as the time intervals between R wave of the ECG and the PPG/tonoarteriogram (TAG) [40] which includes the PEP, impedance cardiogram (ICG)/ballistocardiogram (BCG)/phonocardiogram (PCG) to PPG/TAG, PPG to TAG, or by two PPGs/TAGs at different arterial sites, etc. However, “arrival” should be referred to the pulse in the same form of energy from the starting point to the arrival point, suggesting that PAT is not equivalent of PTT.
Terminologies of PTT To clarify the ambiguity on the usage of PTT, we propose to label PTT calculated from different methods, with the indexes consisting of the first one/two letter(s) of the starting signal and the arrival signal. Most of the current PTT calculation methods are illustrated in Fig. 5.
Fig. 5.
Diagram of PTT calculation with different technologies [29]
In the review, we will use PTT calculated from ECG and PPG, i.e. PTTEP, and we call it PTT for simple of use. Here we chose the maximal upstroke of the peripheral pulse because it is generally accepted that the time delay should be calculated from the foot or the early upslope of the wave rather than the systolic part, since the peak of the pulse wave would underestimate PTT due to the wave reflections that contribute to peak systole [24], and the maximal upslope is easier to be detected than the foot [41].
Principle of PTT-based BP measurement
Most PTT-based cuffless BP measurement approaches are based on the principle of PWV recording through the M–K equation (2). Further according to Hughes et al. [42], the elastic modulus is exponentially correlated with mean distending pressure as given by (5)
| 5 |
where is the zero-pressure modulus, and is a constant typically between 0.016 and 0.018. Both and are site and individual dependent. The combination of Eqs. (2) and (5) thus gives the relationship between PWV and arterial BP as given by (6).
| 6 |
PWV is reciprocally related with PTT as given by (7).
| 7 |
It is immediate that the arterial pressure P can be derived from (6) with (7) substituted in, as given by (8).
| 8 |
Therefore, with initial calibration of PTT to BP, beat-to-beat BP can be estimated from beat-to-beat PTT that calculated from each cardiac cycle.
Relationship between PTT and BP
Since Weltman’s seminal work on PTT in 1964 [32], a considerable number of studies have focused on the use of PTT in psychophysiological research in 1970s. Because PTT has a reciprocal relationship with PWV, and it is an indirect continuous measure of BP variation. The continuous recording of arterial BP at that period was not yet available due to many unsolved physiological and technical problems [34]. During 1970s–1980s, there have been active research efforts on the relationship between PTT and BP, with the aim to investigate whether PTT is sufficient to evaluate BP changes [32–34, 38, 39, 43–57]. With the research progress achieved on the potential of PTT to track BP changes, PTT has been used for inspiratory effort evaluation during 1980s–1990s [30], since dynamic BP contains respiratory-related variations. Since 2000, the study on PTT for BP estimation has attracted more and more attention [14]. The fundamental of the applications of PTT for respiratory evaluation and BP measurement is its relationship with BP. The methods and results of the studies about PTT-BP relationship are briefly summarized in Table 1.
Table 1.
Summary of studies about the correlation between PTT and BP
| References | PTT/PWV calculation | Subjects | Condition | BP measurement | Correlation Coefficient | ||
|---|---|---|---|---|---|---|---|
| SBP | DBP | MBP | |||||
| [44] | PWV: PTTTT | 26 | Externally applied pressures | Intra-arterial | – | – | 0.92–0.99 |
| [33] | PTTETf | 5 | Valsalva, Amyl nitriteinhalation, mental arithmetic, isometric exercise | Intra-arterial | – | – | − 0.91 to − 0.98 |
| [45] | PTTETp | 14 | Rest, cold pressor, pornographic movie, unsignaled shock | Noninvasive | − 0.85 | − 0.30 | – |
| 7 | Inter-arterial | − 0.76 | − 0.44 | – | |||
| [38] | PWV: PTTTT | 6 | Injection of epinephrine, vagal stimulation | Inter-arterial | – | 0.76–0.86 | – |
| [47] | PTTEPu | 94 | Unsignaled shock, Stroop Color-Word Interference Test, isometric handgrip | Sphygmomanometer | − 0.49 | − 0.03 | – |
| PEP | − 0.44 | − 0.03 | – | ||||
| VTT | − 0.09 | − 0.04 | – | ||||
| [39] | PTTEPf | 8 | Rest, mental arithmetic, cold pressor, inhalation of amyl nitrite | Intra-arterial | − 0.49 to − 0.90 | − 0.33 to − 0.69 | – |
| PEP | − 0.33 to − 0.67 | − 0.33 to − 0.47 | – | ||||
| VTT | − 0.03 to − 0.77 | − 0.08 to − 0.62 | – | ||||
| [49] | PTTEPu | 5 | Rest and physical exercise | Intra-arterial | − 0.66 to − 0.77 | − 0.19 to − 0.37 | – |
| VTT | − 0.38 to − 0.75 | − 0.60 to − 0.76 | – | ||||
| [52] | PTTEPf | 44 | Rest | Sphygmomanometer | − 0.95 | 0.09 | – |
| VTT | − 0.32 | 0.21 | – | ||||
| [53] | PTTEPf | 14 | Lower body negative pressure | Intra-arterial | 0.80 | – | – |
| PEP | 0.72 | – | – | ||||
| VTT | 0.48 | – | – | ||||
| [54] | PTTEPf | 18 | Bicycle test | Sphygmomanometer | > 0.80 | – | – |
| PEP | > 0.80 | – | – | ||||
| VTT | < 0.80 | – | – | ||||
| [55] | PTTEPf | 20 | Drug administration (glyceryl trinitrate, angiotensin II, etc.) | Intra-arterial | − 0.62 | − 0.14 | − 0.28 |
| VTT | − 0.57 | − 0.64 | − 0.67 | ||||
| [57] | PTTEPu | 41 | Exercise | Sphygmomanometer | − 0.92 | − 0.38 | – |
PTTABc: where A represents the signal collected at the proximal site to calculate PTT, e.g. E for ECG; B represents the signals collected from the distal site, e.g. P for PPG, T for TAG [40], “c” represents the feature point of the distal signal, e.g. “f” for foot, “u” for maximal upslope, and “p” for peak
Most of those studies have been from the perspective of the relationship between PTT and BP with experimental stressors or clinical interventions to elicit changes in BP. The interventions include pharmacological administration (e.g., epinephrine, amyl nitrite), maneuvers (e.g., Valsalva maneuver, paced respiration, and isometric exercise), various stressors (e.g., mental arithmetic, cold pressor), etc. At early stage of PTT study in 1980s, some investigators pointed out to use arterial PWV as a continuous measure of BP changes, and they carried out experiment to assess the relationship between PTT and MBP. Gribbin et al. [44] measured brachial-to-radial PWV in humans and correlated it with MBP changes. The variation of BP was induced by externally applied positive and negative pressures to alter the transmural pressure. The PWV was found to change linearly with mean pressure. Similar study by Steptoe et al. [33] reported that the changes in PTT was dependent on arterial pressure changes which were caused by maneuvers including mental arithmetic and isometric exercise. The PTT that calculated from ECG and peripheral pulse, was linearly correlated with mean arterial pressure, with correlation coefficients varying between − 0.91 and − 0.98 on five subjects. After that, there have been studies investigating the correlation of PTT with SBP and DBP. As listed in the Table 1, it is clear that PTT had stronger correlation with SBP than DBP for almost all the studies [39, 45–48, 52]. Several studies have also examined the effect of PEP on BP change [39, 47, 53, 54], and confirmed the prominent role of PEP on PTT.
As shown in Table 1, although the correlations between PTT and BP depend upon, how PTT and BP were measured, the method of recording and inducing BP changes, and whether the subjects displayed differences in BP reactivity, the results of those studies reveal that:
Most of the studies report the changes in PTT reliably track the changes in BP, which support the usage of PTT as an indirect measure of BP change;
PTT correlates with SBP significantly better than with DBP. However, VTT has better correlation with DBP than PTT;
PTT that encompasses PEP correlates with SBP better than that without PEP included, and PEP accounted for a substantial and variable proportion of PTT [55]. This finding indicates that the association of PTT with SBP is by virtue of the fact that PTT encompasses PEP rather than the arterial components [47], and an inclusion of PEP in the measurement of PTT is necessary to have an accurate PTT-based SBP estimation [58].
Though VTT correlates with DBP better than with SBP, the correlation is still not strong enough to demonstrate the ability of VTT to track DBP. This suggests that PTT or VTT is not a good indicator for evaluating DBP changes.
Majority of the studies show that the correlation coefficients between PTT and BP vary from individual to individual, which means that in any one subject an absolute change in arterial pressure is not exclusively due to change in PTT.
PTT-based BP estimation models
Modeling method
Based on the theoretical relationship between PTT and BP as mentioned in part B in section III, and their phenomenological relationship as discussed in the part C, a wide variety of studies have been conducted involving the development of analytical model of the relationship between PTT and BP to achieve BP estimation. Table 2 summarizes the studies about PTT-based cuffless BP measurement in the last couple of decades.
Table 2.
Summary of studies about pulse transit time (PTT) based cuffless blood pressure (BP) measurement
| First Author (year, country) | Indicator | Method (model) | Calibration (method/interval)/reference method | Subjects | Accuracy (mmHg) | |
|---|---|---|---|---|---|---|
| SBP | DBP | |||||
| Young (1995, US) [71] | PTTPP | SBP = a1/PTT + b1 DBP = a2/PTT + b2 |
Oscillometric BP (5 min)/Invasive radial BP | 35 patients | − 0.37 (− 29.0 to 28.2) | − 0.01 (− 14.9 to 14.8) |
| Chen (2000, Japan) [59] | PTTEPf | Intermittent BP from Invasive BP (5 min)/Invasive radial arterial BP | 20 patients | RMSE: 3.70 ± 1.85 | ||
| Fung (2004, Canada) [70] | PTTEPu | Cuff Sphygmomanometer (10 min)/Cuff Sphygmomanometer | 22 patients | − 0.08 ± 11.32 | ||
| Poon (2005, China) [60] | PTTEPu |
|
Cuff BP (Initial calibration)/Average of auscultatory and oscillometric BP | 85 (39 hypertensive) | 0.6 ± 9.8 | 0.9 ± 5.6 |
| Muehlsteff (2006, Germany) [54] | PTTEPf | SBP = a * lnPTT + b | Cuff BP (Physical test)/Cuff BP | 18 healthy | RMSE: 7.5 | |
| SBP = a * L/PTT + b | RMSE: 6.9 | |||||
| SBP = a*(L/PTT)2 + b | RMSE: 7.3 | |||||
| Wong (2009, China) [57] | PTTEPu | SBP = a1*PTT + b1 DBP = a2*PTT + b2 |
Oscillometric BP (exercise, half year)/Oscillometric BP | 41 healthy (14 for 0.5 year) | 0.0 ± 5.3 Half year: 1.4 ± 10.2 | 0.0 ± 2.9 Half year: 2.1 ± 7.3 |
| Cattivelli (2009, US) [68] | PTTEPu | SBP = a1*PTT + b1*HR + c1 DBP = a2*PTT + b2*HR + c2 |
MIMIC Database (invasive BP, 1 h)/Invasive BP | 25 ICU patients | − 0.41 ± 7.77 | − 0.07 ± 4.96 |
| Gesche (2011, Germany) [78] | PTTEPu | Sphygmomanometer (13 subjects, exercise)/Sphygmomanometer | 63 | SD: 10.10 95% CI: − 19.8 to 19.8 |
||
| Chen (2012, Singapore) [79] | PTTPP |
|
Intra-arterial BP (9 subjects)/Intra-arterial BP | 35 healthy | 1.49 ± 6.51 | 2.16 ± 6.23 |
| Choi (2013, Canada) [64] | PTTEPu | BP = a * PTT + b Recursive least square algorithm for recalibration |
Cuff-based BP | 25 patients | − 0.44 ± 3.85 | − 0.93 ± 1.84 |
| Kachuee (2015, Iran) [80] | PTTEP and PPG features | Support Vector Machine regression | Intra-arterial BP | – | MAE: 12.38 | MAE: 6.34 |
| Ding (2016, China) [81] | PTTEPu and PIR |
|
Finapres BP | 27 healthy | − 0.37 ± 5.21 | − 0.08 ± 4.06 |
| Kachuee (2017) [82] | PTTEP and PPG features | Calibration free: Adaptive Boosting | Intra-arterial BP | 942 | MAE: 11.17 | MAE: 5.35 |
| Calibration based | 57 | MAE: 8.21 | MAE: 4.31 | |||
| Buxi (2017) [83] | PTTEI | SBP = a1 * PTTEI + b1 | Oscillometric BP | 6 healthy | r (PTTEI − SBP) = 0.66 | r (PTTIR − DBP) = 0.48 |
| PTTIR | DBP = a2 * PTTIR + b2 | |||||
| Huynh (2018) [84] | PTTIP and ICG indicator |
|
Oscillometric BP | 15 healthy | RMSE: 8.47 ± 0.91 | RMSE: 5.02 ± 0.73 |
| Liu (2018) [85] | PTTPP | MBP = HR*(K1*DRPPG TD + b1) PP = MBP*(k2*t/HP + b2) SBP = MBP + 2/3PP; DBP = MBP-1/3PP |
Finapres BP | 20 healthy | SD: 2.85 | SD: 1.75 |
| Ma (2018) [86] | PWV | BP = αPWV2 + β | – | – | – | – |
Among those studies, two of the most cited works are by Chen et al. [59] and Poon et al. [60]. Chen’s method relies on the fact that SBP estimates can be obtained from PTT variations by combing the high frequency component of PTT and low frequency component of the calibrated BP measured by the oscillometric device. The derivation of Chen’s method will be elaborated as follows. With the logarithm relationship between PTT and arterial BP as given in (8) as well as the assumption that the second term of the right side is constant and the parameters , , , , and being unchanged, (9) can be obtained after taking derivative of (10) in terms of PTT.
| 9 |
Therefore, the change of arterial BP can be indicated by the PTT change via (10).
| 10 |
Through calibration, the absolute BP can be estimated through (11).
| 11 |
where and are the calibrated values of BP and PTT, respectively. The BP estimate consists of two components: (1) the baseline BP that can be obtained by frequent intermittent calibration at a regular interval of 5 min to track the slow changes of BP, and (2) the BP variations that can be addressed by the PTT fluctuations. The validation of this method with 20 patients that were under cardiovascular surgery showed that the correlation coefficients between the SBP estimate and the reference intra-arterial SBP was 0.97 ± 0.02. Although this method is potential, it requires frequent calibration which to some extent would limit its application.
Another algorithm developed by Poon et al. [60] is also based on the M–K formula, and can provide promising accuracy for both SBP and DBP estimate. With the definition of the Young’s Modulus E = σ/ε applicable to the arterial system, the changes in PP (the difference between SBP and DBP) can be considered as the stress σ, while ε is the extensional strain. The elastic modulus of the artery can therefore be expressed as:
| 12 |
Substituting (7) and (12) into the M–K equation (2), we have:
| 13 |
Equation (13) indicates that PP is inversely proportional to PTT, if the changes in the arterial dimensions and other factors are negligible. With initial calibration, we have:
| 14 |
Taking the ratio of (13) and (14), PP can be obtained from measured PTT with calibrated PP0 and PTT0 as given in (15).
| 15 |
Based on above assumption that , , , , and would keep constant, MBP can be deduced from (8) as given in (16).
| 16 |
Thereupon, the calibrated MBP0 is related to the calibrated PTT0 through (17):
| 17 |
With (16) and (17), MBP estimates can be derived with calibrated MBP0 and PTT0 with equation as given in (18).
| 18 |
Further with the empirical equation MBP = DBP + PP/3, and the derived PP as given in (15), the DBP and SBP can be reached as given in (19) and (20).
| 19 |
| 20 |
The evaluation of this method on 85 subjects over an average period of 6.4 weeks found that the estimation error of SBP and DBP were 0.6 ± 9.8 mmHg and 0.9 ± 5.6 mmHg respectively against the reference BP, which suggests the method holds great potential following the AAMI standard. The advantages of Poon’s algorithm are that both SBP and DBP could be estimated with satisfactory accuracy. In addition, the accuracy could keep a longer period compared with Chen’s method [61].
McCarthy et al. [61] have compared Chen’s and Poon’s algorithms on 15 healthy subjects and found that neither of these two algorithms could provide reliable BP estimations over a long period. The possible reason for Chen’s method with acceptable accuracy is probably due to the combination of the slow variation of cuff-based BP with the fast variation of PTT. Without the intermittent calibration, the error of the SBP estimate was reported to deteriorate from 0.64 ± 1.55 mmHg to − 3.42 ± 29.22 mmHg within 10 min. As for Poon’s method, the accuracy remained relatively stable, from 1.79 ± 10.50 mmHg to 1.24 ± 9.74 mmHg within the same period.
Except for the abovementioned two representative PTT-BP algorithms, most other algorithms are based on linear or nonlinear regression models. Simple linear regression model as given in (21) is the most common one.
| 21 |
In the linear model, the regression coefficients a and b are obtained through two-point calibration. There have been a number of studies using the linear model to investigate the BP measurement with sole PTT [41, 55, 62–65]. For example, Wong et al. [57] have investigated the linear relationship between PTT and BP and evaluated the accuracy of PTT-based BP estimation with linear regression method on 41 normotensive subjects. The findings show that PTT was strongly correlated with SBP (r = − 0.92), with an error of 0.0 ± 4.0 mmHg for SBP estimate. However, PTT was found to be weakly correlated with DBP (r = − 0.38) with an estimation error of 0.0 ± 3.5 mmHg. Fourteen of the subjects were followed for half a year, and the corresponding correlation and estimation error with PTT for SBP were − 0.84 and 1.4 ± 10.2 mmHg, respectively. Like SBP, the degree of association and the estimation accuracy also significantly reduced for DBP, demonstrating that the relationship between PTT and BP varies with the increase of the calibration interval. It is especially noteworthy that the studies by Deb et al. [66] and Wong et al. [58] further confirm that PTT with the inclusion of PEP can achieve BP estimates with better accuracy than that without PEP.
The abovementioned studies with linear models have three points in common: (1) sole PTT is used as BP indicator; (2) the regression coefficients a, b, are assumed to be constant, and obtained with two calibrations; (3) since DBP is poorly correlated with PTT as mentioned in part C of section III, usually only SBP is derived with the linear model. Although multivariate regression model by introducing extra parameter other than PTT, such as HR [67–69], or PTT calculated by different methods [70], have been attempted to improve the estimation accuracy, the accuracy has not significantly improved. The very limited accuracy of the liner model can be explained with serval reasons: (1) PTT alone might not be able to track all kinds of BP variations. Most importantly, the relationship between PTT and BP is far more complicated than a simple linear regression model; (2) the regression coefficients a and b, would vary with time and different situations. The frequent intermittent calibration is thus necessary to maintain the estimation accuracy; (3) only SBP can be estimated with reasonable accuracy, whereas the DBP and MBP cannot be derived with same accuracy.
Likewise, the reciprocal model, as given in (22) has been substantially studied [54, 70–73].
| 22 |
In addition, by linearizing the exponential of the Eq. (5) as E ~ E0(1 + γP), the quadratic model can be derived with (23).
| 23 |
Except for the different formulas, these models given in (22) and (23) are comparable with the linear model in terms of calibration and estimation accuracy. Early in 2000, Heard et al. [74] have simplified the pressure–volume distensibility given by Eq. (3) to the form as given by (24).
| 24 |
SBP and DBP can be derived respectively through (25) and (26) under the assumption that the measured PTT is able to represent PWV as well as the relative volume change.
| 25 |
| 26 |
The validation of this model with data collected from 28 intensive care unit patients reveals that the estimation precision with intra-arterial BP being used for calibration and reference for all SBP, DBP and MBP, was 10.1 mmHg, 6.0 mmHg and 6.7 mmHg, respectively. Another study by Muehlsteff et al. [54], has reported the estimation of SBP by using heuristic algorithms given by (22) and (23). The validation on 18 healthy subjects showed that these two models had comparable estimation errors, with the quadratic one achieving the better results with an intra-subjects RSME of 3.6 mmHg.
Further with (8) under the assumption that the parameters such as , , , , , and keep unchanged, BP can be expressed with PTT with constant coefficients, a and b, as given by (27).
| 27 |
Other nonlinear models, similar with (27) by using novel calibration method to achieve the coefficients involved without a cuff, has been studied [75]. One variant of this logarithm model has been proposed by Ochiai et al. [76] based on the B–H model (3) with the dV/dP being approximated as [77]:
| 28 |
which indicates that Dv/Dp would approximate zero when P is large enough, where k and Vm are the artery compliance and the maximum blood volume, respectively. By solving (28), V can be expressed as:
| 29 |
where , usually . By substituting (7), (28) and (29) into (3), P can be attained as:
| 30 |
Other empirical models with exponential relationship between PTT and BP have been studied with calibration at population level rather than individual. Gesche et al. [78] have proposed the function of PWV for the estimate of BP:
| 31 |
where the coefficients P1 ~ P4 were estimated by least square fitting of the function to the data collected from 13 subjects; BPPTT, cal was the BP value calculated from PTT, and BPcal was the calibrated BP value at the beginning of the experiment. The validation of the method on 50 subjects achieved an estimation error of SBP with bias around zero and SD of 10.10 mmHg. The other similar study by Chen et al. [79] used the empirical model as given by (32) and (33) to estimate SBP and DBP.
| 32 |
| 33 |
where the bi,j and ki,j were obtained with curve fitting of the measured PWV and BP with data collected from a specific population. With the calibrated model, BP can be estimated from the measured PWV. In this study, a family of BP-PWV functions for specific age and gender groups were identified using statistical methods based on data collected from 9 subjects. Then the calibration models were verified on 26 subjects without cardiovascular history. The estimation error of SBP and DBP were 2.16 ± 6.23 mmHg and 1.49 ± 6.51 mmHg, respectively, against the intra-arterial BP. However, one of the major limitations of this study is that a certain population is required to obtain the empirical model, which is not flexible for application.
In summary, these studies about PTT-based BP estimation as listed in Table 2 indicate that:
Over 90% of the studies calculated PTT with ECG as the reference signal. It means that BP was estimated with PTT that includes PEP for these studies.
The PTT-BP models can be roughly classified into three major categories: (1) physiological model based on the M–K equation or B–H equation, (2) linear or nonlinear regression model, and (3) empirical model with parameters identified from a population. Among all the studies, category (2) accounts for more than 70%.
Regarding the sample size of the subjects, a very few studies have met the requirement of standards. For example, both AAMI and BHS require 85 subjects, while ESH and IEEE 1708 require 33 and 45 subjects, respectively.
The performance of these methods was evaluated with different metrics, e.g., mean ± SD, mean absolute difference (MAD), root mean square error (RMSE), percentage of error, limits of agreement, correlation coefficients between the estimation and the reference, etc.
Performance evaluation of cuffless BP measurement
Accurate measurement of BP is essential to diagnose hypertension, evaluate BP-related risks, predict acute cardiovascular events, monitor the treatment response, and guide the management of diseases. The standard for evaluating BP measurement accuracy is thus significant for device validation before it is recommended for clinical use. With the development of techniques for BP measurement, standards have evolved and there are different types of standards for different kinds of devices in different countries. There are currently mainly four standards for assessment of the accuracy of BP monitoring devices. They have different criteria for evaluation of the accuracy in term of reference method to measure BP, the sample size, validation protocol, the accuracy evaluation metrics and criteria for clinical use. Differences of those standards are briefly summarized in Table 3.
Table 3.
Summary of the international standards for BP measurement grading criteria and accuracy requirement
| Standards | Reference device | Sample Size | Difference between standard and test device (mmHg) | Recommendation for clinical use | |||
|---|---|---|---|---|---|---|---|
| Mean | Standard deviation (SD) | ||||||
| American National Standard: ANSI/AAMI/ISO 81060-2:2013 | Mercury sphygmomanometer | ≥ 85 | ≤ 5 | ≤ 8 | Yes | ||
| British Hypertension Society (BHS) | Mercury sphygmomanometer | ≥ 85 | Grade | Absolute difference | |||
| ≤ 5 | ≤ 10 | ≤ 15 | |||||
| A | 60% | 85% | 95% | Yes | |||
| B | 50% | 75% | 90% | Yes | |||
| C | 40% | 65% | 85% | No | |||
| D | Worse than C | No | |||||
| European Society of Hypertension International Protocol (ESH-IP) | Mercury sphygmomanometer | 33 | Grade | Absolute difference | |||
| ≤ 5 | ≤ 10 | ≤ 15 | |||||
| 1 | 73% | 87% | 96% | Yes | |||
| 2/3 ≤ 5 | 0/3 ≤ 5 | – | |||||
| 2 | ≥ 24% | ≤ 3% | Yes | ||||
| 3 | – | – | – | No | |||
| IEEE Standard for Wearable Cuffless Blood Pressure Measuring Devices (IEEE Std 1708-2014) | All types of wearable BP measurement devices | 45 | Grade | Mean absolute difference (MAD) | |||
| A | ≤ 5 | Yes | |||||
| B | 5–6 | Yes | |||||
| C | 6–7 | Yes | |||||
| D | ≥ 7 | No | |||||
These four standards are the standard for manual, electronic, or automated sphygmomanometers from the Association for the Advancement of Medical Instrumentation (AAMI) [87], the British Hypertension Society (BHS) standard [88], the European Society of Hypertension (ESH) evaluation standard [89], and the IEEE standard for Wearable, Cuffless Blood Pressure Measuring Devices [90]. The first three standards mainly focus on cuff-based manual/automated auscultatory/oscillometric BP devices for office examination or ambulatory monitoring, whereas the IEEE Std 1708TM-2014 is applicable to all types of wearable BP measurement devices including unobtrusive BP devices that have different modes of operation (e.g., to measure short-term, long-term, snapshot, continuous, beat-to-beat BP, or BPV). The accuracy of the device is evaluated by the difference between test value and reference value in terms of bias and SD of the bias, absolute difference, and MAD.
Challenges and future directions
Challenges
Although PTT method for cuffless BP monitoring has already shown remarkable advancement, there are still numerous issues and challenges that lie ahead for the pervasive and ubiquitous health monitoring. In particular, the cuffless continuous noninvasive monitoring technique is not of sufficient accuracy to replace direct invasive measurement of arterial BP. The major issues and challenges of the PTT-based BP measurement is summed up as follows.
First, most research has attempted to use PTT for SBP estimation rather than DBP or MBP. Although PTT correlates better with SBP than with DBP, PTT-based DBP estimation usually has lower error than that of SBP. This might be due to different physiological mechanisms of SBP and DBP. DBP varies quite slowly under the regulation of peripheral arteries, compared with SBP that includes both slow and fast variations.
Second, most studies use PTT as the only variable targeting for BP with linear or nonlinear regression models. However, on the one hand, sole PTT cannot fully represent dynamic BP, as PTT is determined by factors other than just the arterial BP, and vice versa. On the other hand, PWV is a function of the elasticity of the vessel, where the function would vary among individuals and even within the same individual at different situations. Because the PWV changes in a given segment of artery should be determined almost entirely by changes in the local BP and/or the activity of the smooth musculature of the segment.
Third, frequent calibration is required for most of the studies to remain the accuracy acceptable. The reason lies in the assumption and simplification of the M–K equation or the B–H model, since the arterial dimensions such as the arterial diameter is not a constant but a variable changing with the arterial pressure cycle by cycle under the regulation of vascular vasomotion. Although calibration method by using adaptive algorithms (e.g. adaptive Kalman filter algorithm, recursive least square algorithm) has been explored for the improvement, the fundamental issue is still there.
Future directions
Further study should therefore aim to address the issues of accuracy and calibration of PTT-based BP measurement. Considering the major limitations of current studies, it will be helpful to explore new indicators or new modality of signals that are able to reflect BP changes from different perspective complementing PTT, to establish appropriate models to illustrate the relationship between the indicators and arterial BP, and to verify the cuffless methods following with international standard.
In summary, we reviewed the regulation of BP and the factors that would affect arterial BP, which is a prerequisite understanding for noninvasive indirect methods to derive continuous BP. Simply speaking, the cardiac output and peripheral arterial resistance are two dominant determinants of arterial BP. Furthermore, PTT with its definition, calculation, and relationship with BP are discussed. Most importantly, current studies about PTT-based BP methods have been reviewed, with the existed issues and challenges being addressed.
Conflict of interest
All authors declare to have no conflict of interests.
Human and animals rights
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent
Not applicable.
References
- 1.The top 10 causes of death. http://www.who.int/en/news-room/fact-sheets/detail/the-top-10-causes-of-death. Accessed 6 Sep 2018.
- 2.James PA, Oparil S, Carter BL, Cushman WC, Dennison-Himmelfarb C, Handler J, Lackland DT, LeFevre ML, MacKenzie TD, Ogedegbe O. 2014 Evidence-based guideline for the management of high blood pressure in adults: report from the panel members appointed to the Eighth Joint National Committee (JNC 8) JAMA. 2014;311(5):507–520. doi: 10.1001/jama.2013.284427. [DOI] [PubMed] [Google Scholar]
- 3.Chow CK, Teo KK, Rangarajan S, Islam S, Gupta R, Avezum A, Bahonar A, Chifamba J, Dagenais G, Diaz R, Kazmi K, Lanas F, Wei L, Lopez-Jaramillo P, Lu FH, Ismail NH, Puoane T, Rosengren A, Szuba A, Temizhan A, Wielgosz A, Yusuf R, Yusufali A, Mckee M, Liu LS, Mony P, Yusuf S, Rural PPU. Prevalence, awareness, treatment, and control of hypertension in rural and urban communities in high-, middle-, and low-income countries. JAMA. 2013;310(9):959–968. doi: 10.1001/jama.2013.184182. [DOI] [PubMed] [Google Scholar]
- 4.Global atlas on cardiovascular disease prevention and control. https://www.who.int/cardiovascular_diseases/publications/atlas_cvd/en/. Accessed: 6 Sep 2018. [DOI] [PubMed]
- 5.Pickering TG, Hall JE, Appel LJ, Falkner BE, Graves J, Hill MN, Jones DW, Kurtz T, Sheps SG, Roccella EJ. Recommendations for blood pressure measurement in humans and experimental animals—part 1: blood pressure measurement in humans—a statement for professionals from the Subcommittee of Professional and Public Education of the American Heart Association Council on High Blood Pressure Research. Circulation. 2005;111(5):697–716. doi: 10.1161/01.CIR.0000154900.76284.F6. [DOI] [PubMed] [Google Scholar]
- 6.Pickering TG, Davidson K, Gerin W, Schwartz JE. Masked hypertension. Hypertension. 2002;40(6):795–796. doi: 10.1161/01.hyp.0000038733.08436.98. [DOI] [PubMed] [Google Scholar]
- 7.Dolan E, Stanton A, Thijs L, Hinedi K, Atkins N, McClory S, Den Hond E, McCormack P, Staessen JA, O’Brien E. Superiority of ambulatory over clinic blood pressure measurement in predicting mortality the Dublin outcome study. Hypertension. 2005;46(1):156–161. doi: 10.1161/01.HYP.0000170138.56903.7a. [DOI] [PubMed] [Google Scholar]
- 8.Pickering TG, Miller NH, Ogedegbe G, Krakoff LR, Artinian NT, Goff D. Call to action on use and reimbursement for home bood pressure monitoring a joint scientific statement from the American Heart Association, American Society of Hypertension, and Preventive Cardiovascular Nurses Association. Hypertension. 2008;52(1):10–29. doi: 10.1161/HYPERTENSIONAHA.107.189010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Parati G, Ochoa JE, Lombardi C, Bilo G. Assessment and management of blood-pressure variability. Nat Rev Cardiol. 2013;10(3):143–155. doi: 10.1038/nrcardio.2013.1. [DOI] [PubMed] [Google Scholar]
- 10.Wright JT, Williamson JD, Whelton PK, Snyder JK, Sink KM, Rocco MV, Reboussin DM, Rahman M, Oparil S, Lewis CE, Kimmel PL, Johnson KC, Goff DC, Fine LJ, Cutler JA, Cushman WC, Cheung AK, Ambrosius WT, Grp SR. A randomized trial of intensive versus standard blood pressure control. N Engl J Med. 2015;373(22):2103–2116. doi: 10.1056/NEJMoa1511939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gorostidi M, Vinyoles E, Banegas JR, de la Sierra A. Prevalence of white-coat and masked hypertension in national and international registries. Hypertens Res. 2015;38(1):1–7. doi: 10.1038/hr.2014.149. [DOI] [PubMed] [Google Scholar]
- 12.Kikuya M, Hozawa A, Ohokubo T, Tsuji I, Michimata M, Matsubara M, Ota M, Nagai K, Araki T, Satoh H. Prognostic significance of blood pressure and heart rate variabilities the Ohasama study. Hypertension. 2000;36(5):901–906. doi: 10.1161/01.hyp.36.5.901. [DOI] [PubMed] [Google Scholar]
- 13.Buxi D, Redouté JM, Yuce MR. A survey on signals and systems in ambulatory blood pressure monitoring using pulse transit time. Physiol Meas. 2015;36(3):R1–R26. doi: 10.1088/0967-3334/36/3/R1. [DOI] [PubMed] [Google Scholar]
- 14.Zheng YL, Ding XR, Poon CCY, Lo B, Zhang H, Zhou XL, Yang GZ, Zhao N, Zhang YT. Unobtrusive sensing and wearable devices for health informatics. IEEE Trans Biomed Eng. 2014;61(5):1538–1554. doi: 10.1109/TBME.2014.2309951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Peter L, Noury N, Cerny M. A review of methods for non-invasive and continuous blood pressure monitoring: Pulse transit time method is promising? IRBM. 2014;35:271–282. [Google Scholar]
- 16.Porth CM. Disorders of blood pressure regulation. In: Grossman S, Porth CM, editors. Porth’s pathophysiology. Philadelphia: Lippincott Williams Wilkins; 2009. [Google Scholar]
- 17.Blood flow, blood pressure, and resistance. https://cnx.org/contents/A4QcTJ6a@3/Blood-Flow-Blood-Pressure-and-Resistance. Accessed Oct 2018.
- 18.Hall JE. Guyton and hall textbook of medical physiology. Amsterdam: Elsevier; 2015. [Google Scholar]
- 19.Heymans CJF. Introduction to the regulation of blood pressure and heart rate. New York: CC Thomas; 1950. [Google Scholar]
- 20.Ackermann U. Regulation of arterial blood pressure. Surgery (Oxford) 2004;22(5):120a–120f. [Google Scholar]
- 21.Cannesson M, Pearse R. Perioperative hemodynamic monitoring and goal directed therapy: from theory to practice. Cambridge: Cambridge University Press; 2014. [Google Scholar]
- 22.Magder S. Bench-to-bedside review: an approach to hemodynamic monitoring-Guyton at the bedside. Crit Care. 2012;16(5):236. doi: 10.1186/cc11395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Akselrod S, Gordon D, Ubel FA, Shannon DC, Barger AC, Cohen RJ. Power spectrum analysis of heart rate fluctuation—a quantitative probe of beat-to-beat cardiovascular control. Science. 1981;213(4504):220–222. doi: 10.1126/science.6166045. [DOI] [PubMed] [Google Scholar]
- 24.Westerhof N, Stergiopulos N, Noble MI. Snapshots of hemodynamics: an aid for clinical research and graduate education. New York: Springer; 2010. [Google Scholar]
- 25.Laitinen T, Hartikainen J, Niskanen L, Geelen G, Lansimies E. Sympathovagal balance is major determinant of short-term blood pressure variability in healthy subjects. Am J Physiol Heart Circ Physiol. 1999;276(4):H1245–H1252. doi: 10.1152/ajpheart.1999.276.4.H1245. [DOI] [PubMed] [Google Scholar]
- 26.Nichols W, O’Rourke M, Vlachopoulos C. McDonald’s blood flow in arteries: theoretical, experimental and clinical principles. Boca Raton: CRC Press; 2011. [Google Scholar]
- 27.Laurent S, Cockcroft J, Van Bortel L, Boutouyrie P, Giannattasio C, Hayoz D, Pannier B, Vlachopoulos C, Wilkinson I, Struijker-Boudier H. Expert consensus document on arterial stiffness: methodological issues and clinical applications. Eur Heart J. 2006;27(21):2588–2605. doi: 10.1093/eurheartj/ehl254. [DOI] [PubMed] [Google Scholar]
- 28.Bramwell JC. The velocity of the pulse wave in man. Proc R Soc Lond Ser B Contain Pap Biol Charact. 1922;93(652):298–306. [Google Scholar]
- 29.Ding XR, Liu J, Dai WX, Carvalho P, Magjarevic R, Zhang YT. An attempt to define the pulse transit time. In: Conf Proc IFMBE international conference on biomedical and health informatics (ICBHI 2015); 2015.
- 30.Smith RP, Argod J, Pepin JL, Levy PA. Pulse transit time: an appraisal of potential clinical applications. Thorax. 1999;54(5):452–457. doi: 10.1136/thx.54.5.452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Naschitz JE, Bezobchuk S, Mussafia-Priselac R, Sundick S, Dreyfuss D, Khorshidi I, Karidis A, Manor H, Nagar M, Peck ER, Peck S, Storch S, Rosner I, Gaitini L. Pulse transit time by R-wave-gated infrared photoplethysmography: review of the literature and personal experience. J Clin Monit Comput. 2004;18(5–6):333–342. doi: 10.1007/s10877-005-4300-z. [DOI] [PubMed] [Google Scholar]
- 32.Weltman G, Sullivan G, Bredon D. The continuous measurement of arterial pulse wave velocity. Med Biol Eng Comput. 1964;2(2):145–154. doi: 10.1007/BF02484213. [DOI] [PubMed] [Google Scholar]
- 33.Steptoe A, Smulyan H, Gribbin B. Pulse wave velocity and blood pressure change—calibration and applications. Psychophysiology. 1976;13(5):488–493. doi: 10.1111/j.1469-8986.1976.tb00866.x. [DOI] [PubMed] [Google Scholar]
- 34.Obrist PA, Light KC, McCubbin JA, Hutcheson JS, Hoffer JL. Pulse transit time: relationship to blood pressure. Behav Res Methods Instrum. 1978;10(5):623–626. doi: 10.1111/j.1469-8986.1979.tb02993.x. [DOI] [PubMed] [Google Scholar]
- 35.Weiss T, Del Bo A, Reichek N, Engelman K. Pulse transit time in the analysis of autonomic nervous system effects on the cardiovascular system. Psychophysiology. 1980;17(2):202–207. doi: 10.1111/j.1469-8986.1980.tb00136.x. [DOI] [PubMed] [Google Scholar]
- 36.Marie GV, Lo CR, Johnston DW. The relationship between pulse transit time and blood pressure. Biol Psychol. 1980;11(3–4):298–298. [Google Scholar]
- 37.Redman S, Dutch J. Classical conditioning of arterial pulse transit time and ECG-initiated transit time with the cold pressor as unconditioned stimulus. Physiol Psychol. 1983;11(1):87–90. [Google Scholar]
- 38.Geddes LA, Voelz MH, Babbs CF, Bourland JD, Tacker WA. Pulse transit time as an indicator of arterial blood pressure. Psychophysiology. 1981;18(1):71–74. doi: 10.1111/j.1469-8986.1981.tb01545.x. [DOI] [PubMed] [Google Scholar]
- 39.Pollak MH, Obrist PA. Aortic radial pulse transit time and ECG Q-wave to radial pulse wave interval as indexes of beat-by-beat blood pressure change. Psychophysiology. 1983;20(1):21–28. doi: 10.1111/j.1469-8986.1983.tb00895.x. [DOI] [PubMed] [Google Scholar]
- 40.Ding X-R, Dai W-X, Luo N, Liu J, Zhao N, Zhang Y-T. A flexible tonoarteriography-based body sensor network for the cuffless measurement of arterial blood pressure. In: Proceedings of the 2015 IEEE international conference on body sensor networks (BSN).
- 41.Yoon Y, Cho JH, Yoon G. Non-constrained blood pressure monitoring using ECG and PPG for personal healthcare. J Med Syst. 2009;33(4):261–266. doi: 10.1007/s10916-008-9186-0. [DOI] [PubMed] [Google Scholar]
- 42.Hughes DJ, Babbs CF, Geddes LA, Bourland JD. Measurements of Young’s modulus of elasticity of the canine aorta with ultrasound. Ultrason Imaging. 1979;1(4):356–367. doi: 10.1177/016173467900100406. [DOI] [PubMed] [Google Scholar]
- 43.Williams JGL, Williams B. Arterial pulse wave velocity as a psychophysiological measure. Psychosom Med. 1965;27(5):408–414. doi: 10.1097/00006842-196509000-00002. [DOI] [PubMed] [Google Scholar]
- 44.Gribbin B, Steptoe A, Sleight P. Pulse wave velocity as a measure of blood pressure change. Psychophysiology. 1976;13(1):86–90. doi: 10.1111/j.1469-8986.1976.tb03344.x. [DOI] [PubMed] [Google Scholar]
- 45.Obrist PA, Light KC, McCubbin JA, Hutcheson J, Hoffer JL. Pulse transit time: relationship to blood pressure and myocardial performance. Psychophysiology. 1979;16(3):292–301. doi: 10.1111/j.1469-8986.1979.tb02993.x. [DOI] [PubMed] [Google Scholar]
- 46.Allen RA, Schneider JA, Davidson DM, Winchester MA, Taylor CB. The covariation of blood pressure and pulse transit time in hypertensive patients. Psychophysiology. 1981;18(3):301–306. doi: 10.1111/j.1469-8986.1981.tb03038.x. [DOI] [PubMed] [Google Scholar]
- 47.Newlin DB. Relationships ol pulse transmission times to pre-ejection period and blood pressure. Psychophysiology. 1981;18(3):316–321. doi: 10.1111/j.1469-8986.1981.tb03042.x. [DOI] [PubMed] [Google Scholar]
- 48.Lane JD, Greenstadt L, Shapiro D, Rubinstein E. Pulse transit time and blood pressure—an intensive analysis. Psychophysiology. 1983;20(1):45–49. doi: 10.1111/j.1469-8986.1983.tb00899.x. [DOI] [PubMed] [Google Scholar]
- 49.Marie GV, Lo CR, Vanjones J, Johnston DW. The relationship between arterial blood pressure and pulse transit time during dynamic and static exercise. Psychophysiology. 1984;21(5):521–527. doi: 10.1111/j.1469-8986.1984.tb00235.x. [DOI] [PubMed] [Google Scholar]
- 50.Sawada Y, Yamakoshi K. A correlation analysis between pulse transit time and instantaneous blood pressure measured indirectly by the vascular unloading method. Biol Psychol. 1985;21(1):1–9. doi: 10.1016/0301-0511(85)90049-3. [DOI] [PubMed] [Google Scholar]
- 51.Zong W, Moody G, Mark R. Effects of vasoactive drugs on the relationship between ECG-pulse wave delay time and arterial blood pressure in ICU patients. Comput Cardiol. 1998;25:673–676. [Google Scholar]
- 52.Nitzan M, Khanokh B, Slovik Y. The difference in pulse transit time to the toe and finger measured by photoplethysmography. Physiol Meas. 2002;23(1):85–93. doi: 10.1088/0967-3334/23/1/308. [DOI] [PubMed] [Google Scholar]
- 53.Ahlstrom C, Johansson A, Uhlin F, Länne T, Ask P. Noninvasive investigation of blood pressure changes using the pulse wave transit time: a novel approach in the monitoring of hemodialysis patients. J Artif Organs. 2005;8(3):192–197. doi: 10.1007/s10047-005-0301-4. [DOI] [PubMed] [Google Scholar]
- 54.Muehlsteff J, Aubert X, Schuett M. Cuffless estimation of systolic blood pressure for short effort bicycle tests: the prominent role of the pre-ejection period. Conf Proc IEEE Eng Med Biol Soc. 2006;1:5088–5092. doi: 10.1109/IEMBS.2006.260275. [DOI] [PubMed] [Google Scholar]
- 55.Payne RA, Symeonides CN, Webb DJ, Maxwell SRJ. Pulse transit time measured from the ECG: an unreliable marker of beat-to-beat blood pressure. J Appl Physiol. 2006;100(1):136–141. doi: 10.1152/japplphysiol.00657.2005. [DOI] [PubMed] [Google Scholar]
- 56.Marcinkevics Z, Greve M, Aivars JI, Erts R, Zehtabi AH. Relationship between arterial pressure and pulse wave velocity using photoplethysmography during the post-exercise recovery period. Acta Univ Latv Biol. 2009;753:59–68. [Google Scholar]
- 57.Wong MYM, Poon CCY, Zhang Y-T. An evaluation of the cuffless blood pressure estimation based on pulse transit time technique: a half year study on normotensive subjects. Cardiovasc Eng. 2009;9(1):32–38. doi: 10.1007/s10558-009-9070-7. [DOI] [PubMed] [Google Scholar]
- 58.Wong MYM, Zhang YT. The effects of pre-ejection period on the blood pressure estimation using pulse transit time. In: 2008 5th International summer school and symposium on medical devices and biosensors; 2008. p. 301–302.
- 59.Chen W, Kobayashi T, Ichikawa S, Takeuchi Y, Togawa T. Continuous estimation of systolic blood pressure using the pulse arrival time and intermittent calibration. Med Biol Eng Comput. 2000;38(5):569–574. doi: 10.1007/BF02345755. [DOI] [PubMed] [Google Scholar]
- 60.Poon CCY, Zhang YT. Cuff-less and noninvasive measurements of arterial blood pressure by pulse transit time. Conf Proc IEEE Eng Med Biol Soc. 2005;6:5877–5880. doi: 10.1109/IEMBS.2005.1615827. [DOI] [PubMed] [Google Scholar]
- 61.McCarthy B, Vaughan C, O’Flynn B, Mathewson A, Mathúna CÓ. An examination of calibration intervals required for accurately tracking blood pressure using pulse transit time algorithms. J Hum Hypertens. 2013;27:744–750. doi: 10.1038/jhh.2013.41. [DOI] [PubMed] [Google Scholar]
- 62.Douniama C, Sauter CU, Couronne R. Blood pressure tracking capabilities of pulse transit times in different arterial segments: a clinical evaluation. Comput Cardiol. 2009;201–204.
- 63.Cheol Jeong I, Wood J, Finkelstein J. Using individualized pulse transit time calibration to monitor blood pressure during exercise. Inf Manag Technol Healthc. 2013;190:39. [PubMed] [Google Scholar]
- 64.Choi Y, Zhang Q, Ko S. Noninvasive cuffless blood pressure estimation using pulse transit time and Hilbert–Huang transform. Comput Electr Eng. 2013;39(1):103–111. [Google Scholar]
- 65.Heravi MY, Khalilzadeh M, Joharinia S. Continuous and cuffless blood pressure monitoring based on ECG and SpO2 signals by using microsoft visual C sharp. J Biomed Phys Eng. 2014;4(1):27. [PMC free article] [PubMed] [Google Scholar]
- 66.Deb S, Nanda C, Goswami D, Mukhopadhyay J, Chakrabarti S. Cuff-less estimation of blood pressure using pulse transit time and pre-ejection period. In: 2007 International conference on convergence information technology; p. 941–944.
- 67.Kim JS, Kim KK, Baek HJ, Park KS. Effect of confounding factors on blood pressure estimation using pulse arrival time. Physiol Meas. 2008;29(5):615. doi: 10.1088/0967-3334/29/5/007. [DOI] [PubMed] [Google Scholar]
- 68.Cattivelli FS, Garudadri H. Noninvasive cuffless estimation of blood pressure from pulse arrival time and heart rate with adaptive calibration. In: Sixth international workshop on wearable and implantable body sensor networks (BSN 2009); p. 114–119.
- 69.Jadooei A, Zaderykhin O, Shulgin V. Adaptive algorithm for continuous monitoring of blood pressure using a pulse transit time. In: 2013 IEEE XXXIII international scientific conference electronics and nanotechnology (ELNANO); p. 297–301.
- 70.Fung P, Dumont G, Ries C, Mott C, Ansermino M. Continuous noninvasive blood pressure measurement by pulse transit time. Conf Proc IEEE Eng Med Biol Soc. 2004;1:738–741. doi: 10.1109/IEMBS.2004.1403264. [DOI] [PubMed] [Google Scholar]
- 71.Young CC, Mark JB, White W, DeBree A, Vender JS, Fleming A. Clinical evaluation of continuous noninvasive blood pressure monitoring: accuracy and tracking capabilities. J Clin Monit. 1995;11(4):245–252. doi: 10.1007/BF01617519. [DOI] [PubMed] [Google Scholar]
- 72.Masè M, Mattei W, Cucino R, Faes L, Nollo G. Feasibility of cuff-free measurement of systolic and diastolic arterial blood pressure. J Electrocardiol. 2011;44(2):201–207. doi: 10.1016/j.jelectrocard.2010.11.019. [DOI] [PubMed] [Google Scholar]
- 73.Wibmer T, Denner C, Fischer C, Schildge B, Rudiger S, Kropf-Sanchen C, Rottbauer W, Schumann C. Blood pressure monitoring during exercise: comparison of pulse transit time and volume clamp methods. Blood Press. 2015;24(6):353–360. doi: 10.3109/08037051.2015.1053253. [DOI] [PubMed] [Google Scholar]
- 74.Heard SO, Lisbon A, Toth I, Ramasubramanian R. An evaluation of a new continuous blood pressure monitoring system in critically ill patients. J Clin Anesth. 2000;12(7):509–518. doi: 10.1016/s0952-8180(00)00201-4. [DOI] [PubMed] [Google Scholar]
- 75.McCombie DB, Reisner AT, Asada HH. Adaptive blood pressure estimation from wearable PPG sensors using peripheral artery pulse wave velocity measurements and multi-channel blind identification of local arterial dynamics. Conf Proc IEEE Eng Med Biol Soc. 2006;1:3521–3524. doi: 10.1109/IEMBS.2006.260590. [DOI] [PubMed] [Google Scholar]
- 76.Ochiai R, Takeda J, Hosaka H, Sugo Y, Tanaka R, Soma T. The relationship between modified pulse wave transit time and cardiovascular changes in isoflurane anesthetized dogs. J Clin Monit Comput. 1999;15(7–8):493–501. doi: 10.1023/a:1009950731297. [DOI] [PubMed] [Google Scholar]
- 77.Hardy H, Collins R. On the pressure-volume relationship in circulatory elements. Med Biol Eng Comput. 1982;20(5):565–570. doi: 10.1007/BF02443403. [DOI] [PubMed] [Google Scholar]
- 78.Gesche H, Grosskurth D, Küchler G, Patzak A. Continuous blood pressure measurement by using the pulse transit time: comparison to a cuff-based method. Eur J Appl Physiol. 2012;112(1):309–315. doi: 10.1007/s00421-011-1983-3. [DOI] [PubMed] [Google Scholar]
- 79.Chen Y, Wen C, Tao G, Bi M. Continuous and noninvasive measurement of systolic and diastolic blood pressure by one mathematical model with the same model parameters and two separate pulse wave velocities. Ann Biomed Eng. 2012;40(4):871–882. doi: 10.1007/s10439-011-0467-2. [DOI] [PubMed] [Google Scholar]
- 80.Kachuee M, Kiani MM, Mohammadzade H, Shabany M. Cuff-less high-accuracy calibration-free blood pressure estimation using pulse transit time. In: 2015 IEEE international symposium on circuits and systems (ISCAS); p. 1006–1009.
- 81.Ding XR, Zhang YT, Liu J, Dai WX, Tsang HK. Continuous cuffless blood pressure estimation using pulse transit time and photoplethysmogram intensity ratio. IEEE Trans Biomed Eng. 2016;63(5):964–972. doi: 10.1109/TBME.2015.2480679. [DOI] [PubMed] [Google Scholar]
- 82.Kachuee M, Kiani MM, Mohammadzade H, Shabany M. Cuffless blood pressure estimation algorithms for continuous health-care monitoring. IEEE Trans Biomed Eng. 2017;64(4):859–869. doi: 10.1109/TBME.2016.2580904. [DOI] [PubMed] [Google Scholar]
- 83.Buxi D, Redouté J-M, Yuce MR. Blood pressure estimation using pulse transit time from bioimpedance and continuous wave radar. IEEE Trans Biomed Eng. 2017;64(4):917–927. doi: 10.1109/TBME.2016.2582472. [DOI] [PubMed] [Google Scholar]
- 84.Huynh TH, Jafari R, Chung W-Y. Noninvasive cuffless blood pressure estimation using pulse transit time and impedance plethysmography. IEEE Trans Biomed Eng 2018. [DOI] [PubMed]
- 85.Liu J, Yan B, Zhang Y, Ding X-R, Peng S, Zhao N. Multi-wavelength photoplethysmography enabling continuous blood pressure measurement with compact wearable electronics. IEEE Trans Biomed Eng. 2018. [DOI] [PubMed]
- 86.Ma Y, Choi J, Hourlier-Fargette A, Xue Y, Chung HU, Lee JY, Wang X, Xie Z, Kang D, Wang H. Relation between blood pressure and pulse wave velocity for human arteries. Proc Natl Acad Sci. 2018;115(44):11144–11149. doi: 10.1073/pnas.1814392115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.ANSI/AAMI SP10:2002 & ANSI/AAMI SP10:2002/A1:2003. American National Standard. Manual, electronic, or automated sphygmomanometers; 2002.
- 88.O’Brien E, Petrie J, Little W, de Swiet M, Padfield PL, Altma DG, Bland M, Coats A, Atkins N. Short report: an outline of the revised British Hypertension Society protocol for the evaluation of blood pressure measuring devices. J Hypertens. 1993;11(6):677–679. doi: 10.1097/00004872-199306000-00013. [DOI] [PubMed] [Google Scholar]
- 89.O’Brien E, Atkins N, Stergiou G, Karpettas N, Parati G, Asmar R. European Society of Hypertension International Protocol revision 2010 for the validation of blood pressure measuring devices in adults. Blood Press Monit. 2010;15(3):171–172. doi: 10.1097/MBP.0b013e3283360e98. [DOI] [PubMed] [Google Scholar]
- 90.IEEE Standard for Wearable, Cuffless blood pressure measuring devices; 2014. [PubMed]