Abstract
Objective:
to both qualitatively and quantitatively investigate corneal biomechanical properties through an ultrasonic micro-elastography imaging system, which is potentially useful in diagnosis of diseases such as keratoconus, post-refractive keratectasia and tracking treatment such as cross-linking surgery.
Methods:
our imaging system has a dual frequency configuration, including a 4.5 MHz ring transducer to push the tissue and a confocally aligned 40 MHz needle transducer to track micron-level displacement. 2D/3D acoustic radiation force impulse (ARFI) imaging and the Young’s modulus in the region of interest were performed on ex vivo porcine corneas that were either cross-linked using formalin solution or preloaded with IOPs from 5 mmHg to 30 mmHg.
Results:
the increase of corneal stiffness and the change in cross-linked volume following formalin crosslinking could be precisely observed in the ARFI images and reflected by the reconstructed Young’s modulus while the B-mode structural images remained almost unchanged. In addition, the relationship between the stiffness of the cornea and IOPs was investigated among twelve porcine corneas. The corneal stiffness is significantly different at various IOPs and has a tendency to become stiffer with increasing IOP.
Conclusion:
Our results demonstrate the principle of using ultrasonic micro-elastography techniques to image the biomechanical properties of the cornea. Integrating high-resolution ARFI imaging labelled with reconstructed Young’s modulus and structural imaging of the cornea can potentially lead to a routinely performed imaging modality in the field of ophthalmology.
Keywords: high frequency ultrasound elastography, acoustic radiation force, shear wave propagation, cornea
I. INTRODUCTION
The cornea is the transparent, anterior tissue of the eye that provides approximately two-thirds of the eye’s total refractive power [1]. Its unique structure exhibits both transparency to allow light to pass through and high tensile strength to maintain shape while subject to intraocular pressure (IOP) variations with exercise, posture, and diurnal, as well as cardiac cycles. Many factors such as ageing, disease, trauma or surgery affect the physiological function of the cornea. Current quantitative assessments of the cornea based on corneal morphologic features including thickness and curvature measurements are all secondary signs of diagnostic value for corneal disease such as keratoconus and post-refractive surgery ectasia (a serious condition that can cause permanent loss of vision if not treated) [2, 3]. It has been proposed that the primary abnormalities of importance for diagnosis of corneal disease are the biomechanical properties. This has become increasingly evident as knowledge of the significant implications on current ocular treatments and diagnosis has garnered increasing interest in many potential clinical applications [4].
Many interventions such as photorefractive keratectomy (PRK) and laser-assisted in situ keratomileusis (LASIK) are effective in modifying corneal structural properties and have become popular corneal treatment tools [5, 6]. It is widely accepted that the postoperative residual corneal thickness should be at least 250 µm to reduce the risk of post-refractive corneal ectasia (abnormal bulging). However, corneal stiffness may vary among different individuals, and there have been reported cases of post-refractive corneal ectasia occurring in individuals with residual bed thickness greater than 250 µm [7]. The incidence of keratoconus has been reported to be as high as 1 in 2000, and there is a need for early identification of these patients because there now is a treatment that can halt the progression of the disease. UV-induced collagen cross-linking (CXL), which was recently approved by the Food and Drug Administration (FDA) for the treatment of keratoconus [8], strengthens the cornea by introducing covalent links between collagen lamellae and halts the progression of ectasia. Given the fact that the standard CXL treatment is not customized for individual cases, the additional information provided by preexisting biomechanical properties as well as the changes in elasticity during the CXL treatment itself would contribute to an optimal CXL treatment. Therefore, it would be beneficial to precisely track the stiffness distribution or changes of the cornea in multiple applications such as diagnosis, tracking and treatment.
The progress in relating biomechanical properties to clinical diagnosis or treatment is currently limited by the lack of tools that have the ability to precisely determine corneal biomechanical properties. Goldmann applanation tonometry (GAT) is the gold standard for measuring IOP in clinical settings. GAT makes assumptions regarding corneal stiffness and its measurement is significantly associated with central corneal thickness (CCT). It was shown that corneal biomechanics across individuals may have a greater impact on tonometry IOP readings than CCT or curvature [9]. Because corneal biomechanical properties can influence the IOP reading with standard GAT, the Ocular Response Analyzer (ORA) was first developed to measure corneal biomechanics in vivo and provides IOP measurements taking its biomechanical properties into consideration. To be specific, the system uses a transient air-pulse to calculate cornea hysteresis based on the difference in air pressures between force-in and force-out applanation at the surface of the cornea. Later, a similar clinically available device called a Corvis ST, utilizing a high speed Scheimpflug-camera to record the air pulse induced reaction of the cornea, was released to measure biomechanically corrected IOP. However, the sensitivity of both ORA and Corvis ST remains questionable [10]. Moreover, ORA or Corvis ST only provide the average stiffness of the entire cornea instead of a point-to-point stiffness mapping, which increases the possibility of missing focal abnormalities.
Elastography, an imaging modality capable of mapping the biomechanical properties of soft tissues, provides additional insight into diagnosis of various diseases such as fibrosis, atherosclerosis and cancer. However, the current clinically available elastography techniques, including conventional ultrasonic elastography [11] and magnetic resonance elastography (MRE) [12], do not fulfill the micro-scale resolution requirement for ophthalmologic applications. Recently developed optical coherence elastography (OCE) techniques, utilizing optical coherence tomography (OCT) to detect the propagation of induced mechanical waves, have gained momentum in characterizing subtle stiffness changes in corneal tissue with high spatial resolution. However, some OCE systems using either a tilted air-pulse [13, 14] or a tilted air-coupled ultrasound transducer [15] as the “pushing source” might generate complex waves mixed with Love waves, and shear/Lamb waves, resulting in bias or error estimation [16]. It is notable that Ultrasound Biomicroscopy (UBM) has become an indispensable technique for ophthalmic imaging owing to its natural advantage of visualizing some ocular structures such as ciliary bodies and zonules through the use of high frequency ultrasound [17–19]. Inspired by UBM techniques and as an alternative to OCE, high frequency ultrasound-based elastography has been developed toward the goal of characterizing the biomechanical properties of corneal tissue. To be specific, Tanter et al. developed a novel method called supersonic shear imaging (SSI) to measure the quantitative shear modulus of the porcine cornea using a 15-MHz array transducer [20], but the relative low frequency limited the spatial resolution of the obtained images. To improve the spatial resolution, Shih et al. [21, 22] (using a confocally aligned dual-element transducer) and Urs et al. [23] (using a single element high frequency transducer) implemented acoustic radiation force impulse imaging (ARFI) to characterize the biomechanical properties of the cross-linked cornea. However, both the fixed structure of the confocal transducer and the single-element transducer lack the ability to quantify the Young’s modulus of the cornea.
In this study, we implemented a multi-functional ultrasonic micro-elastography technique that has the capability to provide a qualitative corneal stiffness distribution at micrometer resolution via ARFI, and reconstruct the Young’s modulus at region of interest (ROI) via shear wave elasticity imaging (SWEI) technology [24]. Our dual-frequency ultrasonic imaging system consists of a 4.5 MHz focused ring shape transducer for inducing tissue deformation, and a 40 MHz unfocused needle transducer for precise detection of tissue deformation. Using the high resolution stiffness map labelled with the reconstructed Young’s modulus at the ROI, we can evaluate direct delineation of the local deformations of the cornea in response to either cross-linking intervention or IOP elevations which is clinically important.
II. MATERIALS AND METHODS
A. Experimental Setup
The ring-shaped pushing transducer has a 10 mm inner diameter and 30 mm outer diameter, and its focal distance is 30 mm. The aperture size of the tracking transducer is around 300 µm. A schematic diagram of the experimental setup consisting of dual-frequency transducers and synchronized timing sequence is shown in Figure 1. The 40 MHz needle tracking transducer was first inserted inside the hole of the 4.5 MHz ring-shaped pushing transducer, then the two transducers were carefully aligned along both axial and lateral direction under the guidance of hydrophone measurements to eliminate any offset.
Fig. 1.
Schematic diagram of the ultrasonic micro-elastography system and the synchronized timing sequence for the pushing and tracking transducers. Two transducer are confocally aligned to ensure that the pushing force is applied orthogonally to the cornea. In this study, a commercial artificial anterior chamber was used to hold the cornea tissue.
To obtain point-by-point ARFI imaging, the confocally aligned transducers were mounted on a 3-axis translation motorized linear stage (SGSP33–200, OptoSigma Corporation, Santa Ana, CA, USA) for 1D/2D mechanical scanning. With this system, 24 µm increments and a total 4.8 mm scanning distance were employed in ARFI acquisition. Owing to the precise alignment, the acoustic radiation force (ARF) generated by the pushing transducer is applied orthogonally to the imaging subject, meaning only shear waves are generated [16]. In order to track the shear wave propagation, the pushing transducer was fixed at the target position while the tracking transducer was controlled by a linear stage which was moved based on the designed distance between the central positions of the pushing and tracking transducers. In detail, the step size and scanning distance are 39 µm and 3.9 mm, respectively. In addition, to avoid any issues with vibration of the needle during movement, the time delay between successive positions was set to 200 ms, including the data acquisition time and extra wait time.
During the experiment, an arbitrary function generator (AFG 3252C, Tektronix, Beaverton, OR, USA) generating a 4.5 MHz sinusoidal tone bursts signal was connected to a radio-frequency (RF) power amplifier (100A250A, Amplifier Research, Souderton, PA, USA) which was itself coupled to transmit an amplified sinusoidal signal to the 4.5 MHz pushing transducer to induce tissue deformation. The 40 MHz needle transducer was set in conventional pulse-echo mode and was driven by a pulser/receiver (JSR500, Ultrasonics, NY, USA) with a pulse repetition frequency (PRF) of 10 kHz. After 20–80 MHz analog band-pass filtering (Mini-Circuits, Brooklyn, NY, USA) to remove signal contamination from the pushing beam, the RF ultrasonic data was captured using a 12-bit digitizer (ATS9360, Alazartech, Montreal, QC, Canada) at a sampling rate of 1.8 GHz and stored for off-line analysis. To reduce system jitter, the same clock was used to synchronize the digitizer, pulser/receiver, and arbitrary function generator.
To record the initial tissue position at each scanning position, the first tracking A-line acquired by the tracking transducer served as the reference point and the pushing transducer was excited 100 µs after the tracking transducer started to acquire data. Based on our previous calibration studies and potential issues caused by obvious increased stiffness at high IOP [25, 26], the voltage applied on the pushing transducer was set to 140V peak to peak in amplitude corresponding to 2 MPa acoustic pressure, and the excitation duration of the pushing transducer was fixed at 200 µs. All parameter settings were kept constant for all measurements.
B. Viscoelastic model
Available literature clearly suggests that the cornea is a viscoelastic material. The shear wave speed (SWS) for viscoelastic material increases monotonically with frequency instead of maintaining a constant value in a pure elastic medium [27]. It has been well established that the Kelvin-Voigt and Maxwell models are linear descriptions of a viscoelastic medium. They consist of an elastic spring and a viscous dashpot, either in parallel (Kelvin-Voigt) or in series (Maxwell). In the elasticity imaging community, the Kelvin-Voigt model is preferred to quantify both tissue elasticity and viscosity by evaluating dispersion of shear wave propagation speed versus its frequency [28]. For a homogeneous medium, the shear wave propagation speed cs is related to its angular frequency ωc by the equation (1).
| (1) |
where ρ is the corneal density – around 1062 kg/m3 [29]. µ1 and µ2 are shear elasticity, and shear viscosity of the cornea, respectively. Once the experimental dispersion curves are obtained, µ1 and µ2 can be determined by fitting this Kelvin-Voigt equation to the phase velocity curve (described in the next Section) using the linear least square algorithm. The fitting relation is cs = cp(ω) where the frequency selected in the model ranges from 200 Hz to 800 Hz with a step size of 50 Hz.
Under the assumption of a homogenous, isotropic medium, the Young’s modulus ( E) can be further derived from the Poisson’s ration (υ) and the shear elasticity (µ1) using equation (2).
| (2) |
Where Poisson’s ratio is assumed to be 0.49 due to the near incompressibility of the corneal tissue [30].
C. Post-processing and data analysis
Data analysis was performed using MATLAB 2017a software (The MathWorks, Natick, MA, USA). The dynamic tissue displacements were calculated using the 1-D normalized cross-correlation algorithm with a symmetric search region and 1.5λ window size (λ is the wavelength of the tracking transducer) [31]. The peak deformation of each dynamic displacement curve at each axial and lateral position was used to construct the point-to-point ARFI displacement map [32]. The final reconstructed 2D/3D images were generated after applying a median filter so as to increase the signal-to-noise-ratio (SNR). Equation (3) shows the relationship between Young’s modulus and peak tissue displacement.
| (3) |
where E is Young’s modulus, F is force, A is the sample surface area, L is the sample thickness, and 6L is the peak tissue displacement.
To reconstruct shear wave speed, the axial displacement map was first obtained by averaging axial displacements over the depth direction so as to improve the SNR of the displacement map (the averaging depths were determined by the region that has relative uniform distributed displacements in the ARFI image). For example, the center position of the cornea ± 0.5 mm was selected in the IOP experiment. Then the propagation distance versus time shifts curve was obtained from the axial displacement map where the wave propagation distance was measured by the moving step size of the tracking transducer and the time shift was defined as the time to reach the peak displacement at each dynamic displacement.
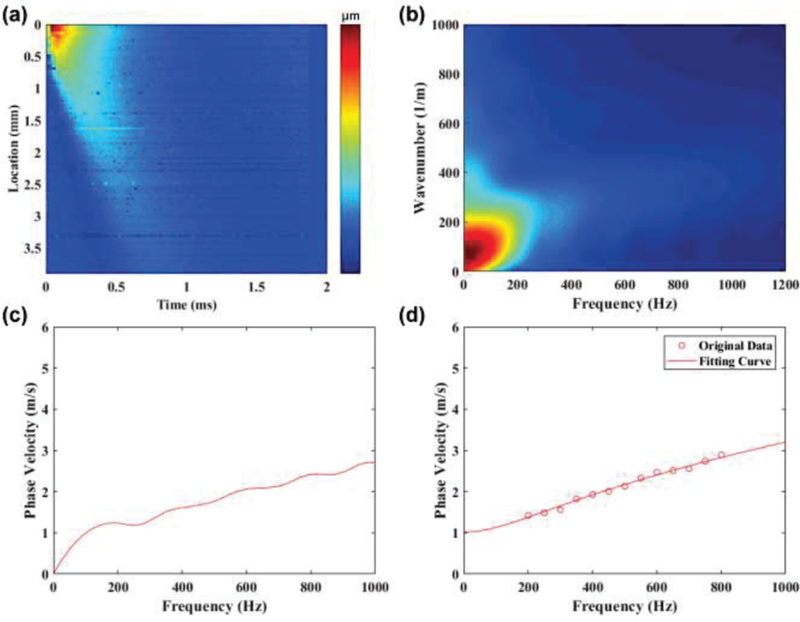
As opposed to group velocity (cg), which is estimated by applying a linear regression to the time shifts versus the distance between each lateral position of the axial displacement map [33], phase velocity (cp) as a function of frequency can be obtained using the Fourier transform. Figure 2 shows the post-processing steps used to obtain the phase velocity curve for one of the control corneas at 5 mmHg IOP. The axial displacement map was first transformed from the spatial-temporal domain into the wavenumber-frequency domain (also denoted as k-space) by using the 2D discrete Fast Fourier Transform to obtain an initial k-space map. To avoid low frequency noise, the initial k-space map with frequency below 5 Hz was masked. The masked k-space map was then interpolated to obtain the final k-space map. The wave number (kL) for each frequency (ƒ) in the first quadrant of k-space was found by identifying the intensity maximum at that frequency. The phase velocity curve (cp) was calculated by the ratio of ƒ and kL through equation (4):
| (4) |
With ƒ being the frequency at each specific position in the phase velocity –frequency map.
Fig. 2.
The post-processing procedures to emphasis how to get the phase velocity curve from the experimental collected axial displacement maps. (a) axial displacement map, (b) k-space, (c) phase velocity curve, and (d) fitting curve with selected frequency range from 200 Hz to 800 Hz with a 50 Hz interval.
D. Biologic tissue preparation
In some slaughterhouses, porcine eyes are scalded with hot water before harvest. Thus, fourteen fresh, unscalded porcine eyes were obtained from a local service-oriented company (Sierra Medical Science, Inc., Whittier, CA, USA) within 24 hours of death in this study. The corneas were carefully removed and stored in 10% dextran solution (Dextran 40, Sigma-Aldrich Inc, MO, USA) for approximately one hour at 5°C prior to imaging [34]. Before the experiments, each cornea was mounted on an artificial anterior chamber (K20–2125, Katena Products Inc, Denville, NJ, USA) with two ports of silicone tubing to control and read the true IOP inside. During the experiment, the sample was submerged in a tank with balanced salt solution (Life Technologies Co, CA, USA) to minimize cornea edema.
The first task was to observe small elasticity changes with respect to different crosslinking time. The second task was to monitor the effect of elevated IOP on corneal elasticity, and in the meantime to investigate the relationship between the corneal elasticity and different IOP levels. The detailed operating procedures for each task are described below.
To artificially induce local corneal cross-linking, 0.05 cc of formalin solution (F79–1 Formaldehyde, Fisher Scientific, Waltham, MA, USA) was applied to a small spot of the corneal surface via a 1-cc disposable syringe with a 30-gauge needle. The 30-gauge needle was bundled at a fixed position of the top surface of a home-made mold that is well fitted with the artificial anterior chamber to ensure the formalin drop location at each time. At the end of each formalin drop time, the cornea was washed and then submerged for scanning. After each scanning, the cornea was removed from the water tank and a new formalin drop was applied at the same spot between each time-point. In this task, one fresh cornea was used to observe the time-dependent crosslinking effect though cross-sectional view. To be specific, the control group had no formalin drops while experimental groups had formalin drops administered at 2, 5, and 10 minutes, respectively (All times in this study are cumulative exposure times. For example, ‘5 minutes’ here means that there is an addition 3 minutes added to the ‘2 minutes’ from the first exposure). To obtain a 3D view of the cornea with or without crosslinking, another fresh cornea was first scanned as a control group (no formalin drop), then was dropped with a single formalin at 20 minutes only, and finally imaged as an experimental group. IOP was controlled at 5 mmHg for all crosslinking experiments.
For the second task, all corneas were not formalin-treated and the only variable was the IOP. As mentioned above, the artificial anterior chamber has two ports. One port was connected to the balanced saline solution bag set at various heights to manipulate IOP. The other port was connected to a pressure sensor (Model SPR-524, Millar Inc, TX, USA) to read the true IOP inside the chamber. Because the normal physiological IOP range is 12–22 mmHg, thus, six IOP levels −5, 10, 15, 20, 25 and 30 mmHg were investigated in this study.
III. RESULTS
A. Calibration of the Imaging System
The acoustic output of the 4.5 MHz pushing transducer was measured using a needle hydrophone (HGL-0085, ONDA Co, Sunnyvale, CA, USA). To avoid damaging the hydrophone, 10-cycle sinusoidal bursts were used instead of 900-cycle bursts used in the porcine cornea experiment. At the focal point, the measured spatial peak temporal average intensity (Ispta.3) was 44.5 mW/cm2 in water. The actual spatial resolution of the ARFI image was determined in our previous study [25] by using bi-layer gelatin based tissue-mimicking phantoms. The full width half maximum (FWHM) resolution of ARFI imaging was 109.8±6.9 µm axially and 223.7±20.1 µm laterally. The FOV determined by the maximum overlap of depth of focus (DOF) of the pushing and tracking transducer was beyond 1.5 mm. Therefore, the effective FOV of our micro-elastography imaging system covers the imaging subjects where normal human corneal thickness averages about 500–600 microns and normal porcine corneal thickness averages about 800–1000 microns. With respect to the accuracy of the reconstructed Young’s modulus, the SWS based method was compared with the gold standard – uniaxial mechanical testing (Instron 5942). In our previous study [25], the Young’s modulus of the 2% gelatin phantom was 1.13 ± 0.07 kPa in SWE, and 1.26 ± 0.1 kPa in mechanical testing. Moreover, the Young’s modulus of the 5% gelatin phantom was 12.18 ± 0.42 kPa in SWE, and 12 ± 0.5 kPa in mechanical testing. All these results demonstrated that our imaging methods have a good agreement with the gold standard.
B. Corneal cross-linking intervention
Figure 3 (a, e) show a 2D cross-sectional B-mode image and corresponding ARFI image of an ex vivo porcine cornea in the control group. The differences in the appearance of the B-mode images obtained at each time point are barely discernable. The CCT is around 1 mm which is reasonable compared with literature studies [35–37]. The color-coded ARFI image shows a regional stiffness map with softer areas in red and stiffer areas in blue. ARFI image results indicated that the stiffness is relatively uniform in the control cornea.
Fig. 3.
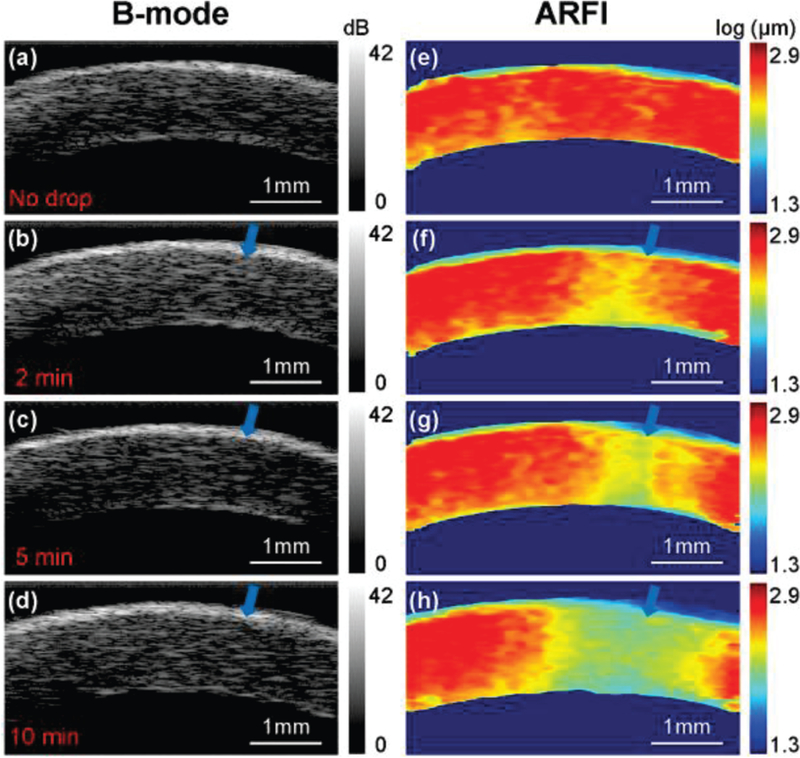
A time series of B-mode and ARFI images for one cornea sample. The blue arrow indicates the small spot of formalin drop between each time-point. (a,e) control group with no formalin drop; experimental groups with (b,f) 2 minutes, (c,g) 5 minutes and (d,h) 10 minutes formalin drop. In the cross-linking experiments, the intraocular pressure was set at 5 mmHg so as to maintain normal corneal curvature.
Figure 3 (b-d) show the B-mode images obtained at three experimental conditions −2, 5, and 10 minutes after artificially induced cross-linking where the blue arrow indicates the site of the small cross-linking spot. For each experimental group, B-mode images show almost identical structures except that the cornea thickness has a slight increase from 1 mm (control group) to 1.2 mm (10 minutes experimental group). At the cross-linking site, the high resolution ARFI images in Fig. 3 (f-h) show an increasing stiffness relative to post-drop time with a corresponding color change from red to yellow to green. In addition, the volume of the stiffening became greater because of the diffusion of formalin solution.
The reconstructed Young’s modulus values at the small cross-linked spot are 4.39 kPa for the control group, 4.56 kPa in the experimental group with 2 minutes formalin drop, 4.81 kPa in the experimental group with 5 minutes formalin drop, and 5.03 kPa in the experimental group with 10 minutes formalin drop. The apparent increasing trend of the Young’s modulus is consistent with ARFI observations.
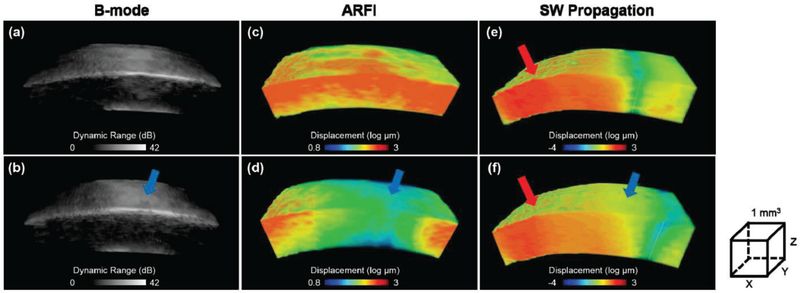
Figure 4 (a-d) shows 3D maps of morphological structure and relative stiffness distribution of the cornea in the control group, and the experimental group (20 minutes). The volume dimensions (xyz) of the reconstructed 3D images are 4.8×1.5×1 mm. With the high resolution capability of the B-mode and ARFI images, it is straight-forward to locate the ROI which is the site of formalin drop in this study. By moving the pushing transducer 2mm away from the central cornea (opposite direction of the site of formalin drop), shear wave propagation at the ROI can be observed. The Young’s modulus at the ROI before and after the formalin drop were then reconstructed which is 4.4 kPa and 6.55 kPa, respectively. Figure 4 (e,f) show the shear wave fronts after 1.5 ms ARF pushing. From the gray dash line, it can clearly be seen that the shear wave front propagated faster in the experimental group than that in the control group.
Fig. 4.
The reconstructed 3D B-mode and ARFI maps of another cornea. (a,c) control group, (b,d) experimental group with 20 minutes formalin drop, (e,f) one moment (1.5 ms after ARF pushing) of the shear wave propagation where gray dash lines represent current wave fronts position. The red arrow indicates the ARF pushing location which is 2 mm away from the central cornea. The blue arrow indicates the site of small spot formalin drop. Volume dimensions (xyz) are 4.8 mm ×1.5 mm ×1 mm for (a-d) and 6 mm ×1.5 mm ×1 mm for (e-f), respectively.
C. Corneal response to intraocular pressure
The biomechanical response to elevated IOP was also investigated in this study. In Figure 5 (a-f), it was observed that it is difficult to observe changes in the B-mode images caused by elevated IOP. Although there may be subtle changes in thickness or curvature, it is difficult to provide quantitative measurements by relying solely on the B-mode images. However, in examining Figure 5 (g-l), it is readily apparent that ARFI imaging is far more sensitive to changes in IOP than gray-scale B-mode. To be specific, the cornea has a tendency to become stiffer with the increasing IOP. This change in elasticity was noted to be more prominent in the central cornea than in the peripheral cornea. From high resolution ARFI images, the ROI defined by +/−0.5 mm of the central cornea is relatively uniform under different IOPs, which satisfied the prerequisite tracking conditions of the shear wave. Figure 6 shows three timing intervals (0.1 ms, 0.3 ms, 0.5 ms) of shear wave propagation under elevated IOP. The color bar in Fig. 6 was normalized based on the maximum and minimum displacement at t=0 which can help us to directly visualize the shear wave speed at different IOPs.
Fig. 5.
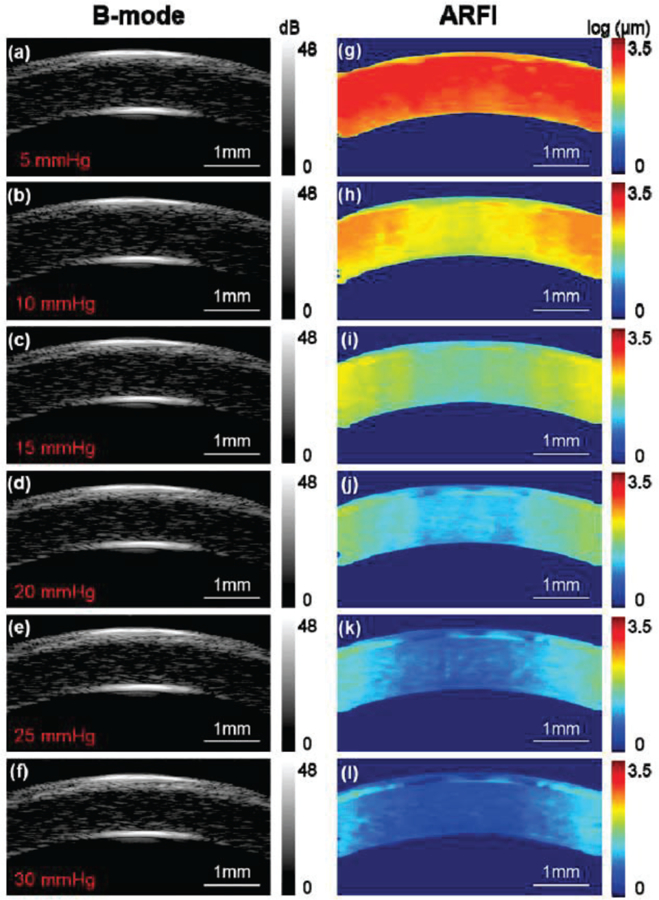
B-mode and ARFI images of the cornea under various intraocular pressures. (a,g) – 5 mmHg, (b,h) – 10 mmHg, (c,i) – 15 mmHg, (d,j) – 20 mmHg, (e,k) – 25 mmHg and (f,l) – 30 mmHg. The ROI is +/− 0.5 mm of the central cornea which was relative uniformly distributed demonstrated by high resolution ARFI images. Note: the cornea here is not formalin-treated.
Fig. 6.
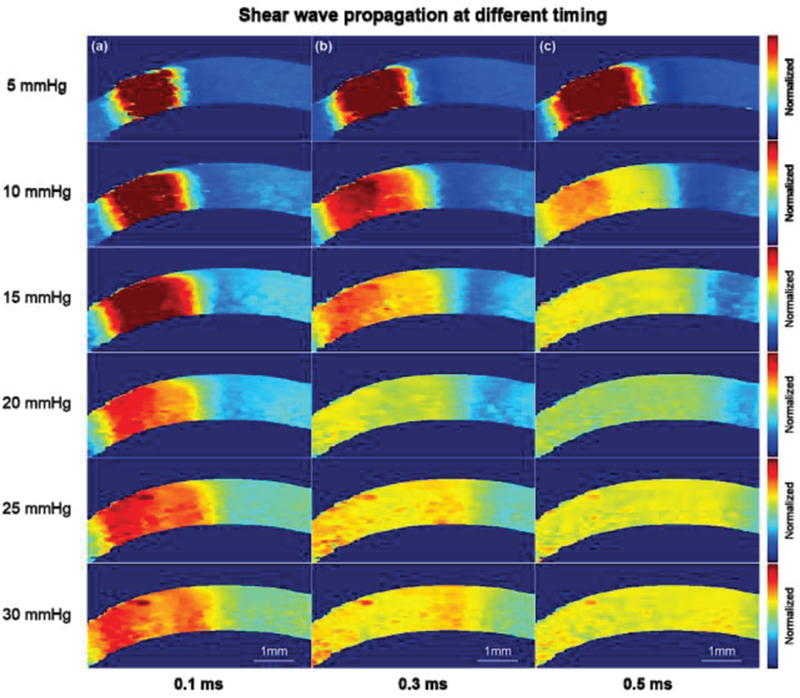
Shear wave propagation after (a) 0.1 ms, (b) 0.3 ms and (c) 0.5 ms ARF pushing. It was observed that the shear wave propagates faster at a higher IOP. The Young’s modulus of the cornea at elevated IOPs were reconstructed within +/−0.5 mm uniform region which is confirmed from ARFI. Note: the cornea here is not formalin-treated.
In this experiment, to determine the relationship between Young’s modulus of the cornea and elevated IOP, twelve porcine corneas were used. The reconstructed Young’s modulus are all expressed as mean ± standard deviation. In detail, the reconstructed values were 3.6 ± 0.71 kPa at 5 mmHg, 7.94 ± 1.86 kPa at 10 mmHg, 15.03 ± 3.78 kPa at 15 mmHg, 22.11 ± 5.69 kPa at 20 mmHg, 32.29 ± 6.84 kPa at 25 mmHg, and 43.05 ± 5.01 kPa at 30 mmHg, respectively. The differences between the various IOP values were evaluated by one-way ANOVA. The statistical analysis showed that changes in Young’s modulus were statistically significant at different IOP values where P < 0.01 was considered to be significant. In Figure 7, the averaged Young’s modulus at elevated IOP level were plotted, and then fitted by a linear equation (5) using a standard linear least squares fitting algorithm. In this case, R2, a parameter which reflects the goodness of fit, is greater than 0.95.
Fig. 7.
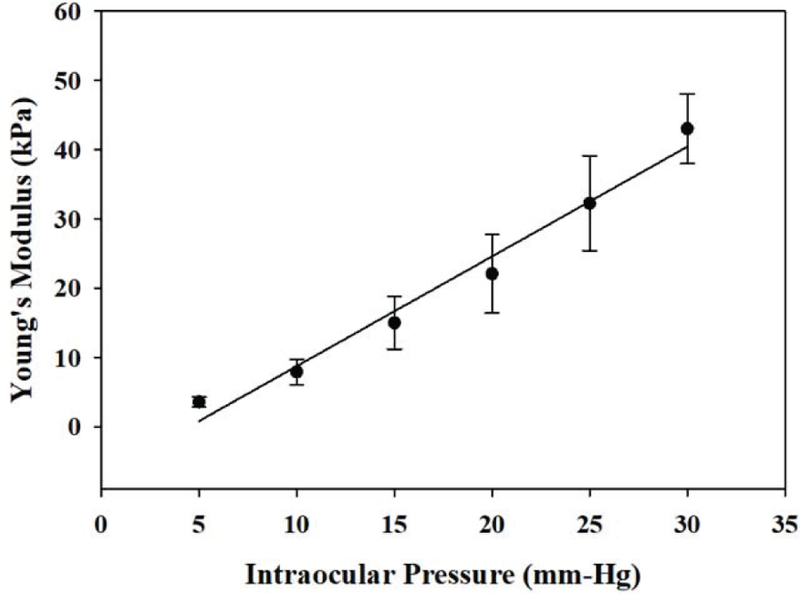
The averaged Young’s modulus of the cornea at elevated IOPs. And it expressed as a linear relationship within the normal physiological IOP range (12–22 mmHg).
| (5) |
E is Young’s modulus, IOP is the intraocular pressure, A is the slope of linear trend.
IV. DISCUSSION
High frequency transducers provide excellent resolution for both B-mode and elasticity imaging. However, previously, it has been difficult to induce significant deformation of tissue using high frequency transducers due to their low power output. In this study, a dual frequency configuration was implemented to push/track tissue utilizing the high power capability of the 4.5 MHz transducer and high resolution of the 40 MHz transducer. Also, a hollow shaped pushing transducer coaxially aligned with a needle tracking transducer eliminate dual-frequency transducer offset and ensure that the pushing force is applied orthogonally to the imaging subject in order to provide shear wave propagation only. According to the previous study by Palmeri et. al., the frequency bandwidth of phase velocity depends on the excitation duration and spatial beamwidth used to generate the shear wave [38]. Widman further used different excitation durations from 100 to 700 µs to induce shear wave propagation in porcine arteries. The results demonstrated that shorter excitation duration can obtain wider bandwidth and more accurate estimation of elasticity [39]. However, shorter excitation duration leads to a smaller intensity to push the tissue. Usage of excitation duration below 200 µs would not induce enough detectable displacement in our system, especially when the shear wave propagates far away from the region of excitation of the pushing transducer. Therefore, the pushing duration of ARF was set to 200 µs as a balance in this study. Since both formalin cross-linking and various IOP levels were tested here, the tissue deformation under these conditions has a large dynamic range. To better highlight disparities and help with comparison, a log10 scale was used in all axial displacement maps.
Corneal biomechanical behavior is primarily a function of the stroma consisting primarily of water and collagen fibrils that confer its strength and form. Specifically, the orientation and spacing of the collagen fibrils provide the cohesive forces to confer most of the structural stability. Corneal cross-linking intervention induces covalent bonds between collagen lamellae to halt the progression of corneal ectasia and was recently approved by the US FDA for the treatment of keratoconus. Figure 3 shows a time-series of the corneal cross-linking effect where the blue arrow indicates a small spot where a formalin drop was applied. A slight increase in CCT caused by swelling of the tissue after inducement was observed in the B-mode images. This is because two confounding variables are unavoidable under ex vivo conditions: the lack of aqueous humor production/ outflow, and corneal desiccation. Previous findings on porcine corneas indicate that cross-linking might enhance corneal swelling which can explain these phenomena [40]. Moreover, there was an increase in stiffness with a longer formalin drop time, and the increased stiffness extended both horizontally and vertically as shown by ARFI images in Figs. 3 (e-h). This likely represented the diffusion of formalin within the corneal stroma. Through high resolution stiffness distribution, the Young’s modulus was reconstructed by tracking the shear wave propagation within the ROI. Figure 4 (e,f) showed that the shear wave front in the experimental group is further away from the pushing point than that in the control group. The increasing stiffness from 4.4 kPa in the control group to 6.55 kPa in the experimental group is consistent with our ARFI observations. Our imaging system demonstrated the capability to precisely track small changes in local stiffness and provide the quantified Young’s modulus of the cross-linked region which is potentially useful in cornea-like microstructure tissue characterization. Moreover, 3D volume imaging capability achieves some valuable information such as the exact formalin drop position, volume of the target of interest and stereo tissue anisotropy which may be useful for physicians performing refractive surgery or observing changes after CXL treatment.
Any imbalance between aqueous humor production and outflow leads to abnormal IOPs associated with eye diseases such as glaucoma. Therefore, the relationship between central cornea stiffness and IOPs is important. Figure 5 (a-f) show the B-mode images under six different IOP conditions. The thickness and curvature changes in B-mode at elevated IOP are not obvious while ARFI images in Fig. 5 (g-l) show a better contrast than B-mode images. In addition, the ARFI images, clearly show that corneal elasticity is IOP dependent, and corneal structure appears to provide the central cornea with a greater stiffness than that in the peripheral cornea (associated with greater tolerance to elevation in IOP). This finding is consistent with previous studies [41]. Another possible influence factor here is the boundary effect. In this study, the corneal tissue was mounted on a tissue pedestal and its peripheral region was locked using a tissue retainer and locking ring which were part of the artificial anterior chamber. This structure created additional boundary conditions to affect the estimation accuracy of the peripheral cornea. In the present study, we focused mainly on the central region of the cornea which appeared to be uniformly distributed. The increasing stiffness of the central cornea at elevated IOP is based on the fact that collagen fibers become taut at high IOP [42]. Figure. 6 depicts a visualization of shear wave propagation for different IOP levels, it’s obvious that shear wave propagates further at higher IOPs under the same traveling time through tracking the shear wavefront. Twelve cornea tissues were used to statistically investigate the relationship between Young’s modulus and IOP as shown in Fig. 7. It has been previously reported that under increasing IOP, collagen fibrils give rise to a non-linear mechanical behavior of the cornea with a stiffening effect at IOP greater than 60 mmHg [43]. It has also been shown both by finite element modeling as well as experimental data analysis, that it is reasonable to model the cornea as a linear viscoelastic material around the normal IOP range (12–22 mmHg) [44, 45]. In this study, the stiffness of the cornea increased linearly as a function of IOP which is consistent with previous literature studies.
The elasticity range of the cornea in the literature is very large, spanning a few orders of magnitude from 1 kPa to greater than 1 MPa depending on many parameters such as test conditions, species, and most importantly, measurement technique [8, 46–48]. Some studies also indicated that the thickness, curvature and fluid structure interface between the corneal posterior surface and aqueous humor all must be considered for accurate biomechanical assessment of the cornea [14]. In this study, the corneal tissue was mounted at the artificial anterior chamber instead of using a whole eye globe. As a result, the boundary conditions may also affect the measured corneal elasticity. According to the previous literature, the Young’s modulus of the porcine cornea at 20 mmHg was reported to be 1–10 kPa using ultrasound [43] and around 60 kPa using OCE [14, 49]. Since there is no gold standard to follow and compared with results above, our results are in a reasonable range. The cross-linked corneal elasticity is influenced by many factors such as the amount and concentration of the formalin solution, and the treatment time. It is therefore difficult to obtain quantitative comparison of our observed cross-linked corneal elasticity measurements with those in the literature. Nevertheless, the achievement of observing the small cross-linked region helps us to demonstrate the high resolution capability of our system. Viscosity is another parameter that is crucial for biomechanical characterization of tissues but is not easily measured in cornea-like solids. To the best of our knowledge, viscosity of the cornea has not been well measured experimentally.
Herein, we successfully demonstrate the capability of our imaging system to characterize the biomechanical properties of the cornea through a high resolution ARFI imaging and a quantitative Young’s modulus estimation at the ROI. However, there are still some limiting factors that hinder the technology’s translational potential for clinical diagnosis. First of all, the measured Ispta.3 (44.5 mW/cm2) of our imaging system is above the FDA approved value (17 mW/cm2 for ocular tissue). Given the fact that the minimum displacement in the normal physiological IOP range (12–22 mmHg) in the current experiments is ten times higher than our system’s minimum detectable ultrasonically induced displacement (± 0.1 µm), the acoustic output power can be expected to decrease by at least a factor of 10 to meet the FDA standard without sacrificing too much image contrast.
Second, the imaging frame rate is limited by the moving speed of the translation motorized linear stage used in this study. In our current setup, the time to reconstruct one group of images including the B-mode image, ARFI image, and the reconstructed Young’s modulus map is on the order of tens of seconds which is still relatively slow. Integrating a high-speed sector scanning motor would potentially achieve a much higher frame rate without compromising the current image quality. Moreover, the future implementation of advanced plane wave image processing algorithms using high frequency array-based ultrasonic systems will further drive the practice of ultrasonic micro-elastography imaging into in vivo study [50].
Third, formalin solution was used in this proof-of-concept study for artificially induced corneal cross-linking because it is easier to use and more readily available than a commercial FDA approved ultraviolet-activated riboflavin (UV-A) crosslinking machine. Formalin crosslinking has been previously used by groups performing both ultrasound [21] and OCT [51] studies. In addition, therapeutic corneal cross-linking using formaldehyde releasing agents is an open research topic [52]. However, it is recognized that in clinical practice and in vivo studies formalin is not a current acceptable solution for general practice. In the future, UV-A crosslinking procedures such as the UV-A dose time, intensity and spot size of the commercial UV-A CXL system, would be comprehensively evaluated for human cornea or clinical translation study.
Finally, the simple Kelvin-Voigt model for corneal elasticity assessment in this study is known to be inaccurate and may lead to some bias because of boundary conditions and the ratio of corneal thickness to shear wavelength. Derived from the Kelvin-Voigt model, guided Lamb wave models have been proposed to further enhance estimation accuracy by considering the confined structure of the cornea. For example, Nenadic et al. inferred the Lamb wave model by considering corneal tissue bounded on both two fluids sides [53, 54]; Han et al. calculated a modified Lamb wave model which has no stress on the anterior surface and fluid on the posterior surface [14]. In other words, Lamb wave model based results are highly influenced by the structural definition and coupling medium conditions. In addition, Couade et al. suggested that the experimental Lamb wave velocities are different from the measured values [16]. The possible reason is the ratio between A1 and A0 modes in water. These results indicate that the guided Lamb wave model is still under investigation and a detailed analysis of mechanical mode propagation in a bounded medium is complicated, requiring a careful theoretical analysis to account for the spherical geometry of the eye. This is beyond the scope of this manuscript, but we will be addressed it in future studies.
V. CONCLUSIONS
In summary, investigating the link between corneal microstructure and biomechanics of the cornea may provide additional information that could be valuable in corneal disease diagnosis and refractive surgery planning. We show proof of principle of using ultrasonic micro-elastography to characterize biomechanical properties of the cornea qualitatively and quantitatively. Achieving micro-level resolution, this technique can also be employed to image the entire anterior segment of the eye where the UBM is currently used. Therefore, the proposed ultrasonic micro-elastography method can provide clinicians with a powerful tool to assess both morphological and biomechanical properties of ocular tissue, potentially leading to a new, routinely performed imaging modality in the field of ophthalmology.
Acknowledgments
This work was supported by the National Institutes of Health (NIH) NEI under grant R01EY026091, R01EY028662 and P41-EB002182. Unrestricted departmental grant from research to prevent blindness.
Contributor Information
Xuejun Qian, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA, and also with the Roski Eye Institute, Department of Ophthalmology, University of Southern California, Los Angeles, CA 90033, USA. (xuejunqi@usc.edu)..
Teng Ma, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA, and with the Roski Eye Institute, Department of Ophthalmology, University of Southern California, Los Angeles, CA 90033, USA, and also with the Institute of Biomedical and Health Engineering, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China..
Cho-Chiang Shih, Institute of Biomedical Engineering, National Cheng Kung University, Tainan City 701, Taiwan and also with Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA. (garyshihx@gmail.com)..
Martin Heur, Roski Eye Institute, Department of Ophthalmology, University of Southern California, Los Angeles, CA 90033, USA. (heur@med.usc.edu)..
Jun Zhang, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA (zhangjun2010@whu.edu.cn)..
K. Kirk Shung, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA (kkshung@usc.edu)..
Rohit Varma, Roski Eye Institute, Department of Ophthalmology, University of Southern California, Los Angeles, CA 90033, USA. (rvarma@usc.edu)..
Mark S. Humayun, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA, and also with the Roski Eye Institute, Department of Ophthalmology, University of Southern California, Los Angeles, CA 90033, USA. (humayun@usc.edu).
Qifa Zhou, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA, and also with the Roski Eye Institute, Department of Ophthalmology, University of Southern California, Los Angeles, CA 90033, USA..
VI. REFERENCE
- [1].Ruberti JW, Sinha Roy A, and Roberts CJ, “Corneal biomechanics and biomaterials,” Annual review of biomedical engineering, vol. 13, pp. 269–295, 2011. [DOI] [PubMed] [Google Scholar]
- [2].Andreassen TT, Simonsen AH, and Oxlund H, “Biomechanical properties of keratoconus and normal corneas,” Experimental eye research, vol. 31, no. 4, pp. 435–441, 1980. [DOI] [PubMed] [Google Scholar]
- [3].Binder PS, “Analysis of ectasia after laser in situ keratomileusis: risk factors,” Journal of Cataract & Refractive Surgery, vol. 33, no. 9, pp. 1530–1538, 2007. [DOI] [PubMed] [Google Scholar]
- [4].Roberts CJ, and Dupps WJ, “Biomechanics of corneal ectasia and biomechanical treatments,” Journal of Cataract & Refractive Surgery, vol. 40, no. 6, pp. 991–998, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Munnerlyn CR, Koons SJ, and Marshall J, “Photorefractive keratectomy: a technique for laser refractive surgery,” Journal of Cataract & Refractive Surgery, vol. 14, no. 1, pp. 46–52, 1988. [DOI] [PubMed] [Google Scholar]
- [6].Pallikaris LG, Papatzanaki ME, Stathi EZ, Frenschock O, and Georgiadis A, “Laser in situ keratomileusis,” Lasers in surgery and medicine, vol. 10, no. 5, pp. 463–468, 1990. [DOI] [PubMed] [Google Scholar]
- [7].Ou RJ, Shaw EL, and Glasgow BJ, “Keratectasia after laser in situ keratomileusis (LASIK): evaluation of the calculated residual stromal bed thickness,” American journal of ophthalmology, vol. 134, no. 5, pp. 771–773, 2002. [DOI] [PubMed] [Google Scholar]
- [8].Wollensak G, Spoerl E, and Seiler T, “Stress-strain measurements of human and porcine corneas after riboflavin– ultraviolet-A-induced cross-linking,” Journal of Cataract & Refractive Surgery, vol. 29, no. 9, pp. 1780–1785, 2003. [DOI] [PubMed] [Google Scholar]
- [9].Liu J, and Roberts CJ, “Influence of corneal biomechanical properties on intraocular pressure measurement: quantitative analysis,” Journal of Cataract & Refractive Surgery, vol. 31, no. 1, pp. 146–155, 2005. [DOI] [PubMed] [Google Scholar]
- [10].Singh M, Li J, Vantipalli S, Wang S, Han Z, Nair A, Aglyamov SR, Twa MD, and Larin KV, “Noncontact elastic wave imaging optical coherence elastography for evaluating changes in corneal elasticity due to crosslinking,” IEEE Journal of Selected Topics in Quantum Electronics, vol. 22, no. 3, pp. 266–276, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Ophir J, Cespedes I, Ponnekanti H, Yazdi Y, and Li X, “Elastography: a quantitative method for imaging the elasticity of biological tissues,” Ultrasonic imaging, vol. 13, no. 2, pp. 111–134, 1991. [DOI] [PubMed] [Google Scholar]
- [12].Muthupillai R, Lomas D, Rossman P, Greenleaf JF, Manduca A, and Ehman RL, “Magnetic resonance elastography by direct visualization of propagating acoustic strain waves,” science, vol. 269, no. 5232, pp. 1854–1857, 1995. [DOI] [PubMed] [Google Scholar]
- [13].Han Z, Li J, Singh M, Wu C, Liu C.-h., Wang S, Idugboe R, Raghunathan R, Sudheendran N, and Aglyamov SR, “Quantitative methods for reconstructing tissue biomechanical properties in optical coherence elastography: a comparison study,” Physics in Medicine & Biology, vol. 60, no. 9, pp. 3531, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Han Z, Li J, Singh M, Wu C, Liu C.-h., Raghunathan R, Aglyamov SR, Vantipalli S, Twa MD, and Larin KV, “Optical coherence elastography assessment of corneal viscoelasticity with a modified Rayleigh-Lamb wave model,” Journal of the mechanical behavior of biomedical materials, vol. 66, pp. 87–94, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Ambrozinski Ł, Song S, Yoon SJ, Pelivanov I, Li D, Gao L, Shen TT, Wang RK, and O’Donnell M, “Acoustic micro-tapping for non-contact 4D imaging of tissue elasticity,” Scientific reports, vol. 6, pp. 38967, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Couade M, Pernot M, Prada C, Messas E, Emmerich J, Bruneval P, Criton A, Fink M, and Tanter M, “Quantitative assessment of arterial wall biomechanical properties using shear wave imaging,” Ultrasound in medicine and biology, vol. 36, no. 10, pp. 1662–1676, 2010. [DOI] [PubMed] [Google Scholar]
- [17].Silverman RH, “High-resolution ultrasound imaging of the eye–a review,” Clinical & experimental ophthalmology, vol. 37, no. 1, pp. 54–67, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Ishikawa H, and Schuman JS, “Anterior segment imaging: ultrasound biomicroscopy,” Ophthalmology Clinics of North America, vol. 17, no. 1, pp. 7, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Hollman KW, Emelianov SY, Neiss JH, Jotyan G, Spooner GJ, Juhasz T, Kurtz RM, and O’Donnell M, “Strain imaging of corneal tissue with an ultrasound elasticity microscope,” Cornea, vol. 21, no. 1, pp. 68–73, 2002. [DOI] [PubMed] [Google Scholar]
- [20].Tanter M, Touboul D, Gennisson J-L, Bercoff J, and Fink M, “High-resolution quantitative imaging of cornea elasticity using supersonic shear imaging,” IEEE transactions on medical imaging, vol. 28, no. 12, pp. 1881–1893, 2009. [DOI] [PubMed] [Google Scholar]
- [21].Shih C-C, Huang C-C, Zhou Q, and Shung KK, “High-resolution acoustic-radiation-force-impulse imaging for assessing corneal sclerosis,” IEEE transactions on medical imaging, vol. 32, no. 7, pp. 1316–1324, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Shih C-C, Lai T-Y, and Huang C-C, “Evaluating the intensity of the acoustic radiation force impulse (ARFI) in intravascular ultrasound (IVUS) imaging: Preliminary in vitro results,” Ultrasonics, vol. 70, pp. 64–74, 2016. [DOI] [PubMed] [Google Scholar]
- [23].Urs R, Lloyd HO, and Silverman RH, “Acoustic Radiation Force for Noninvasive Evaluation of Corneal Biomechanical Changes Induced by Cross-linking Therapy,” Journal of Ultrasound in Medicine, vol. 33, no. 8, pp. 1417–1426, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Sarvazyan AP, Rudenko OV, Swanson SD, Fowlkes JB, and Emelianov SY, “Shear wave elasticity imaging: a new ultrasonic technology of medical diagnostics,” Ultrasound in medicine & biology, vol. 24, no. 9, pp. 1419–1435, 1998. [DOI] [PubMed] [Google Scholar]
- [25].Qian X, Ma T, Yu M, Chen X, Shung KK, and Zhou Q, “Multi-functional Ultrasonic Micro-elastography Imaging System,” Scientific Reports, vol. 7, no. 1, pp. 1230, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Ma T, Qian X, Chiu CT, Yu M, Jung H, Tung Y-S, Shung KK, and Zhou Q, “High-resolution harmonic motion imaging (HR-HMI) for tissue biomechanical property characterization,” Quantitative imaging in medicine and surgery, vol. 5, no. 1, pp. 108, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Chen S, Fatemi M, and Greenleaf JF, “Quantifying elasticity and viscosity from measurement of shear wave speed dispersion,” The Journal of the Acoustical Society of America, vol. 115, no. 6, pp. 2781–2785, 2004. [DOI] [PubMed] [Google Scholar]
- [28].W Urban M, Chen S, and Fatemi M, “A review of shearwave dispersion ultrasound vibrometry (SDUV) and its applications,” Current medical imaging reviews, vol. 8, no. 1, pp. 27–36, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Kampmeier J, Radt B, Birngruber R, and Brinkmann R, “Thermal and biomechanical parameters of porcine cornea,” Cornea, vol. 19, no. 3, pp. 355–363, 2000. [DOI] [PubMed] [Google Scholar]
- [30].Cartwright NEK, Tyrer JR, and Marshall J, “Age-related differences in the elasticity of the human cornea,” Investigative ophthalmology & visual science, vol. 52, no. 7, pp. 4324–4329, 2011. [DOI] [PubMed] [Google Scholar]
- [31].Pinton GF, Dahl JJ, and Trahey GE, “Rapid tracking of small displacements with ultrasound,” IEEE transactions on ultrasonics, ferroelectrics, and frequency control, vol. 53, no. 6, pp. 1103–1117, 2006. [DOI] [PubMed] [Google Scholar]
- [32].Nightingale K, Soo MS, Nightingale R, and Trahey G, “Acoustic radiation force impulse imaging: in vivo demonstration of clinical feasibility,” Ultrasound in medicine & biology, vol. 28, no. 2, pp. 227–235, 2002. [DOI] [PubMed] [Google Scholar]
- [33].Palmeri ML, Wang MH, Dahl JJ, Frinkley KD, and Nightingale KR, “Quantifying hepatic shear modulus in vivo using acoustic radiation force,” Ultrasound in medicine & biology, vol. 34, no. 4, pp. 546–558, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Hamaoui M, Tahi H, Chapon P, Duchesne B, Fantes F, Feuer W, and Parel J-M, “Corneal preparation of eye bank eyes for experimental surgery,” Cornea, vol. 20, no. 3, pp. 317–320, 2001. [DOI] [PubMed] [Google Scholar]
- [35].Bartholomew L, Pang D, Sam D, and Cavender J, “Ultrasound biomicroscopy of globes from young adult pigs,” American journal of veterinary research, vol. 58, no. 9, pp. 942–948, 1997. [PubMed] [Google Scholar]
- [36].Hayes S, Boote C, Lewis J, Sheppard J, Abahussin M, Quantock AJ, Purslow C, Votruba M, and Meek KM, “Comparative study of fibrillar collagen arrangement in the corneas of primates and other mammals,” The Anatomical Record, vol. 290, no. 12, pp. 1542–1550, 2007. [DOI] [PubMed] [Google Scholar]
- [37].Jay L, Brocas A, Singh K, Kieffer J-C, Brunette I, and Ozaki T, “Determination of porcine corneal layers with high spatial resolution by simultaneous second and third harmonic generation microscopy,” Optics express, vol. 16, no. 21, pp. 16284–16293, 2008. [DOI] [PubMed] [Google Scholar]
- [38].Palmeri ML, Deng Y, Rouze NC, and Nightingale KR, “Dependence of shear wave spectral content on acoustic radiation force excitation duration and spatial beamwidth” pp. 1105–1108.
- [39].Widman E, Maksuti E, Amador C, Urban MW, Caidahl K, and Larsson M, “Shear wave elastography quantifies stiffness in ex vivo porcine artery with stiffened arterial region,” Ultrasound in Medicine and Biology, vol. 42, no. 10, pp. 2423–2435, 2016. [DOI] [PubMed] [Google Scholar]
- [40].Wollensak G, Aurich H, Pham D-T, and Wirbelauer C, “Hydration behavior of porcine cornea crosslinked with riboflavin and ultraviolet A,” Journal of Cataract & Refractive Surgery, vol. 33, no. 3, pp. 516–521, 2007. [DOI] [PubMed] [Google Scholar]
- [41].Elsheikh A, McMonnies CW, Whitford C, and Boneham GC, “In vivo study of corneal responses to increased intraocular pressure loading,” Eye and Vision, vol. 2, no. 1, pp. 20, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Kling S, Remon L, Pérez-Escudero A, Merayo-Lloves J, and Marcos S, “Corneal biomechanical changes after collagen cross-linking from porcine eye inflation experiments,” Investigative ophthalmology & visual science, vol. 51, no. 8, pp. 3961–3968, 2010. [DOI] [PubMed] [Google Scholar]
- [43].Zhou B, Sit AJ, and Zhang X, “Noninvasive measurement of wave speed of porcine cornea in ex vivo porcine eyes for various intraocular pressures,” Ultrasonics, vol. 81, pp. 86–92, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Elsheikh A, Wang D, and Pye D, “Determination of the modulus of elasticity of the human cornea,” Journal of refractive surgery, vol. 23, no. 8, pp. 808–818, 2007. [DOI] [PubMed] [Google Scholar]
- [45].Elsheikh A, Geraghty B, Rama P, Campanelli M, and Meek KM, “Characterization of age-related variation in corneal biomechanical properties,” Journal of the Royal Society Interface, pp. rsif20100108, 2010. [DOI] [PMC free article] [PubMed]
- [46].Dias J, Diakonis VF, Lorenzo M, Gonzalez F, Porras K, Douglas S, Avila M, Yoo SH, and Ziebarth NM, “Corneal stromal elasticity and viscoelasticity assessed by atomic force microscopy after different cross linking protocols,” Experimental eye research, vol. 138, pp. 1–5, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Elsheikh A, Alhasso D, and Rama P, “Biomechanical properties of human and porcine corneas,” Experimental eye research, vol. 86, no. 5, pp. 783–790, 2008. [DOI] [PubMed] [Google Scholar]
- [48].Mikula E, Hollman K, Chai D, Jester JV, and Juhasz T, “Measurement of corneal elasticity with an acoustic radiation force elasticity microscope,” Ultrasound in Medicine and Biology, vol. 40, no. 7, pp. 1671–1679, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Han Z, Aglyamov SR, Li J, Singh M, Wang S, Vantipalli S, Wu C, Liu C.-h., Twa MD, and Larin KV, “Quantitative assessment of corneal viscoelasticity using optical coherence elastography and a modified Rayleigh–Lamb equation,” Journal of biomedical optics, vol. 20, no. 2, pp. 020501–020501, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Huang CC, Chen PY, Peng PH, and Lee PY, “40 MHz high-frequency ultrafast ultrasound imaging,” Medical Physics, vol. 44, no. 6, pp. 2185–2195, 2017. [DOI] [PubMed] [Google Scholar]
- [51].Qu Y, Ma T, He Y, Zhu J, Dai C, Yu M, Huang S, Lu F, Shung KK, Zhou Q, and Chen Z, “Acoustic radiation force optical coherence elastography of corneal tissue,” IEEE Journal of Selected Topics in Quantum Electronics, vol. 22, no. 3, pp. 288–294, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Babar N, Kim M, Cao K, Shimizu Y, Kim S-Y, Takaoka A, Trokel SL, and Paik DC, “Cosmetic preservatives as therapeutic corneal and scleral tissue cross-linking agents,” Investigative ophthalmology & visual science, vol. 56, no. 2, pp. 1274–1282, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Nenadic IZ, Urban MW, Aristizabal S, Mitchell SA, Humphrey TC, and Greenleaf JF, “On Lamb and Rayleigh wave convergence in viscoelastic tissues,” Physics in Medicine & Biology, vol. 56, no. 20, pp. 6723, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Nenadic IZ, Urban MW, Mitchell SA, and Greenleaf JF, “Lamb wave dispersion ultrasound vibrometry (LDUV) method for quantifying mechanical properties of viscoelastic solids,” Physics in Medicine & Biology, vol. 56, no. 7, pp. 2245, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]