Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Feb 14;15(3):2101–2109. doi: 10.1021/acs.jctc.9b00040

Open-Boundary Molecular Mechanics/Coarse-Grained Framework for Simulations of Low-Resolution G-Protein-Coupled Receptor–Ligand Complexes

Thomas Tarenzi †,‡,§, Vania Calandrini §,*, Raffaello Potestio ||,#,*, Paolo Carloni ‡,§,
PMCID: PMC6433333  PMID: 30763087

Abstract

graphic file with name ct-2019-00040c_0009.jpg

G-protein-coupled receptors (GPCRs) constitute as much as 30% of the overall proteins targeted by FDA-approved drugs. However, paucity of structural experimental information and low sequence identity between members of the family impair the reliability of traditional docking approaches and atomistic molecular dynamics simulations for in silico pharmacological applications. We present here a dual-resolution approach tailored for such low-resolution models. It couples a hybrid molecular mechanics/coarse-grained (MM/CG) scheme, previously developed by us for GPCR–ligand complexes, with a Hamiltonian-based adaptive resolution scheme (H-AdResS) for the solvent. This dual-resolution approach removes potentially inaccurate atomistic details from the model while building a rigorous statistical ensemble—the grand canonical one—in the high-resolution region. We validate the method on a well-studied GPCR–ligand complex, for which the 3D structure is known, against atomistic simulations. This implementation paves the way for future accurate in silico studies of low-resolution ligand/GPCRs models.

Introduction

Membrane proteins constitute as much as 60% of the overall proteins targeted by FDA-approved drugs.1 Among them, G-protein-coupled receptors (hGPCRs)2,3 are the largest family, comprising more than 800 members,4 and the most important one from a pharmaceutical perspective.5−7 Unfortunately, the lack of experimental structural information for most (more than 90%) hGPCRs8,9 along with low sequence identity (SI) across these proteins (often below 30%10,11) has hampered rational design efforts for many highly promising hGPCR drug targets. For instance, 99% hGPCRs have an SI < 30% with bovine rhodopsin,12 the first solved GPCR structure.13 This condition strongly limits the predictive power of computer-aided structural predictions because traditional homology modeling techniques applied to proteins with low SI with their template may lead to rather inaccurate models.14,15 All-atoms molecular dynamics (MD) simulations, very successful in refining high-quality homology-based models,16,17 may fail to improve the predictions and even lead to partial unfolding18−21 if one starts from structures with highly inaccurate side-chain orientations as encountered in very low resolution protein models. An alternative strategy to address this issue consists of including the minimum number of degrees of freedom of the system for the specific problem that one has in mind, leaving out unreliable information that could bias the simulation results.18,22,23 In this context, hybrid multiscale simulation methods, transcending a single, uniform resolution, represent a highly optimized approach to predict ligands poses;24−27 on one hand, a high-resolution, atomistic description of the region of interest (which includes the binding site) allows unveiling of the interactions between the receptor and the ligand; on the other hand, the surrounding environment can be described in a coarse-grained, less computationally intensive way.

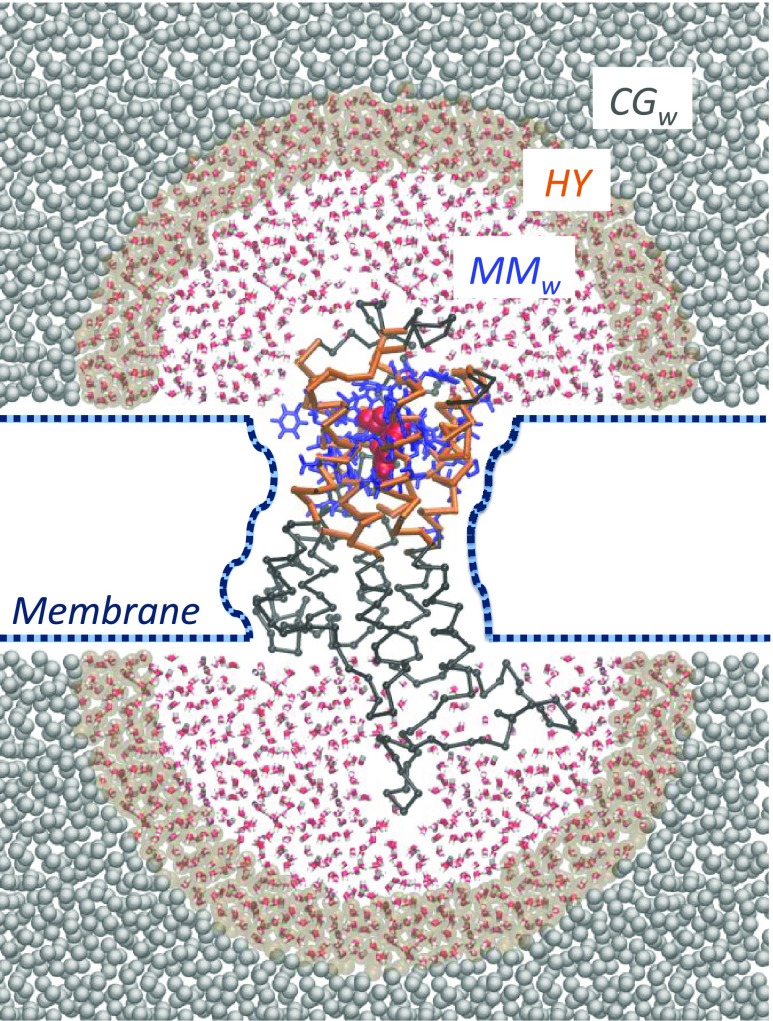
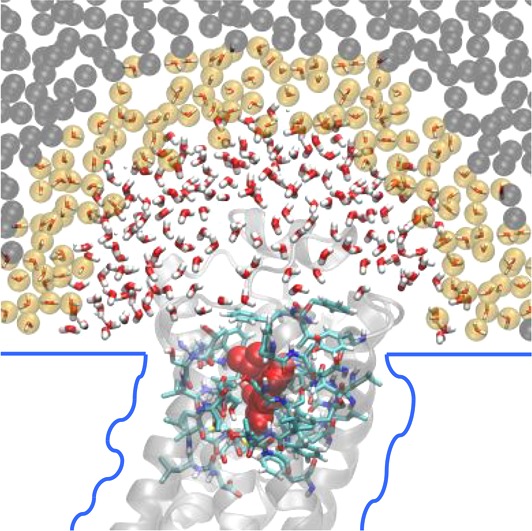
Here, we describe and validate a novel hybrid multiscale approach, the open-boundary molecular mechanics/coarse-grained (OB-MM/CG) scheme, tailored for the study of low-resolution GPCR–ligand complexes. It involves a concurrent multiscale simulation of both the protein and the water molecules (Figure 1).

Figure 1.

Figure 1

Open in a new tab

Scheme of the OB-MM/CG setup for hGPCR–ligand complexes. Protein residues belonging to the MM, I, and CG regions are represented in blue, orange, and black, respectively. The ligand is represented in red in the binding site and is modeled at the MM level. The two atomistic MMw hemispheres are coupled to the coarse-grained reservoir CGw through the hybrid region HY.

(i) The dual-resolution representation of the protein28 is based on a scheme previously developed in our team,22,28−30 successfully applied to predict binding poses in several low-resolution GPCR–ligand complexes.18,19,23,31 It aims at preserving an atomistic description of the binding pocket and of the neighboring residues (MM region, described with the Gromos force field32) while leaving to a coarse-grained description the rest of the protein22 (CG region, where each residue is modeled through a CG bead centered on the Cα and interacting with the other beads through a Go̅-type potential33). An intermediate region (I) between the MM and the CG domains ensures the coupling between the two levels of description and the protein backbone integrity. I residues are described atomistically, and their Cα and Cβ atoms interact with CG beads according to the CG potential. The selection of the atoms in the MM, I, or CG regions does not require updates during the simulation. The presence of the membrane is implicitly modeled as a series of boundary potentials (Figure 1): two repulsive potentials placed at the level of the lipids’ heads prevent penetration of water molecules in the membrane space, while a softened Lennard-Jones-like potential (2-1) acting on transmembrane residues’ Cα mimics the interactions between the protein and the membrane.

(ii) As opposed to the original MM/CG scheme, where hydration around the binding site is taken into account by introducing a droplet of atomistic water molecules confined through a repulsive potential preventing water evaporation (Figure SI 1), in the new implementation we adopt a multiscale representation of the solvent, based on an adaptive resolution scheme34−37 in the Hamiltonian formulation (H-AdResS).38 This allows water molecules to freely diffuse between fully atomistic (MMw) and coarse-grained (CGw) domains, maintaining a uniform density between the two while changing on-the-fly their resolution. The MMw regions, where atomistic water is described by the SPC/E potential39 (VwMM), are shaped as hemispheres capping the extracellular and intracellular domains of the protein, whereas coarse-grained water is present outside of these boundaries in a bigger box (CGw). Coarse-grained water is modeled by beads coinciding with the center of mass (CoM) of each molecule, interacting through a potential, VwCG, derived from fully atomistic simulation of pure water at the same state point through iterative Boltzmann inversion.40 The smooth coupling between the two domains is achieved by introducing an intermediate hybrid region (HY), where the potentials describing the MMw and CGw models are linearly combined through a switching function λα = λ(Rα), which depends on the instantaneous position Rα of the CoM of the α water molecule. Specifically, λα smoothly changes from 1 to 0 when moving from MMw to CGw boundaries. A correction term is added to water molecules in the HY region to ensure uniform density across the MMw, HY and CGw domains. This term preserves a constant chemical potential,41 leading to the simulation of a grand canonical ensemble in the high-resolution region. In this respect, the CGw region can be regarded as a reservoir of coarse-grained water molecules, and we call the overall setup open-boundary (OB)-MM/CG (see the Theory section for a more complete description of the method).

Compared to the previous MM/CG method, the new OB-MM/CG enables thus a priori rigorous ligand binding free energy calculations.41 Moreover, by ensuring the free diffusion of water between the binding cavity and the CGW reservoir, it prevents possible artifacts due to the solvent confinement in the hemisphere while keeping the number of the additional degrees of freedom smaller than a fully atomistic simulation. Given the recognized role of water for ligand binding in membrane receptors42−47 and the overall interplay between water dynamics and protein properties,48 this is likely to improve the description of interactions between the ligand and the protein. In this paper, we tackle in particular this point.

It is worth noticing that the applicability of H-AdResS for the simulation of water solvating biomolecules has been recently assessed49 using as test systems fully atomistic cytoplasmic proteins in the center of a spherical MMw region (OB-MM). However, it has never been applied in the presence of a dual-resolution protein and, importantly, never in the presence of a discontinuity, here represented by the repulsive walls mimicking the membrane, which break the spherical symmetry of the MMw region of H-AdResS tested in the previous OB-MM implementation.49 The higher pressure attained by the CGw model with respect to the atomistic one requires a correction of the repulsive membrane potential in order to impose the correct virial pressure on the CGw domain50−52 and guarantee a uniform density profile in the vicinity of the membrane planes. Details on the derivation of this correction term are given in the Theory section.

The paper is organized as follows. After the Theory section, where the OB-MM/CG method is presented in detail, and a Methods section with the simulation details, we validate the approach by comparing structural and dynamical properties computed with the OB-MM/CG scheme with those from all-atom MD simulations of a GPCR–ligand complex, namely, the β2-adrenergic receptor in complex with its inverse agonist S-carazolol.53 This validation represents the necessary preliminary step toward future usage of the method for the calculation of binding free energies, on which we are currently working. For comparison, we present results obtained from simulations performed using the original MM/CG scheme as well.

Theory

The total Hamiltonian of the system reads

graphic file with name ct-2019-00040c_m001.jpg 1

K represents the total kinetic energy. We now describe the terms associated with the potential energy of the system.

Vp is the protein’s potential energy22

graphic file with name ct-2019-00040c_m002.jpg 2

The first term on the right-hand side of eq 2 describes the MM and interface (I) regions of the protein, along with the ligand. The function of the I region is to mechanically couple the MM and CG domains of the protein. MM and I regions are described by the Gromos43a1 force field,32 widely validated for protein simulations in the MM/CG framework.19,22,31 The same potential is used for the coupling between the MM and I regions (VpMM/I). Vp represents the CG protein potential energy. The mapping employed for the coarse-graining procedure reduces each residue to a singe CG bead, centered on the Cα. VpCG is a Go̅-type potential.33 It integrates out the degrees of freedom defining the chemical nature of the CG residues while preserving the folded structure of the protein and its characteristic fluctuations by stabilizing the native contacts. It includes both bonded and nonbonded interactions between CG protein beads; the former are modeled as a quartic potential and the second as a Morse-type potential.22 The same scheme is applied to model the interactions between the CG and I regions. In particular, the nonbonded potential is applied here not only between Cα’s but also between Cα belonging to CG residues and Cβ belonging to I residues.

According to the H-AdResS38 scheme, water is described by the potential energy term Vw, which includes the contributions from the atomistic water molecules in the MMw region (VwMM), and those from the coarse-grained water molecules in the CGw region (Vw). Vw reads38

graphic file with name ct-2019-00040c_m003.jpg 3

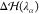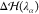As pointed out in the introduction, VwMM is described by the SPC/E water potential energy,39 while Vw is obtained through iterative Boltzmann inversion.40 The switching function λα = λ(Rα) depends on the position Rα of the CoM of the α water molecule.38 Its value is 1 in the MMw region, 0 in the CGw region, and smoothly changes from 1 to 0 in the HY region. The term Inline graphic represents a correction that is applied independently on each water molecule in the HY region. It has the double purpose of (1) removing on average the effect of the spurious force that emerges as a consequence of the linear combination between VwMM and Vw(38,41) and (2) correcting for the density imbalance across the MMw and CGw regions.54 Specifically, Inline graphic reads

graphic file with name ct-2019-00040c_m006.jpg 4

Here ΔF(λα) and Δp(λα) represent, respectively, the Helmholtz free energy difference and the pressure difference between a system at hybrid resolution λα and the CGw system at resolution λα = 0. N is the number of water molecules, and ρ0 is the reference density of water. Correspondingly, in each subdomain, the pressure attains the value at which that model (either atomistic or coarse-grained) gets the target density.54

The term Vp/w describes protein/water interactions. Only MMw water molecules are in contact with the protein. The interactions between atomistic water and the atomistic region of the protein are described by the standard atomistic force field, while the interactions between atomistic water and CG residues are modeled with a Lennard-Jones potential so as to reproduce the excluded volume around the Cα of the CG residues.55

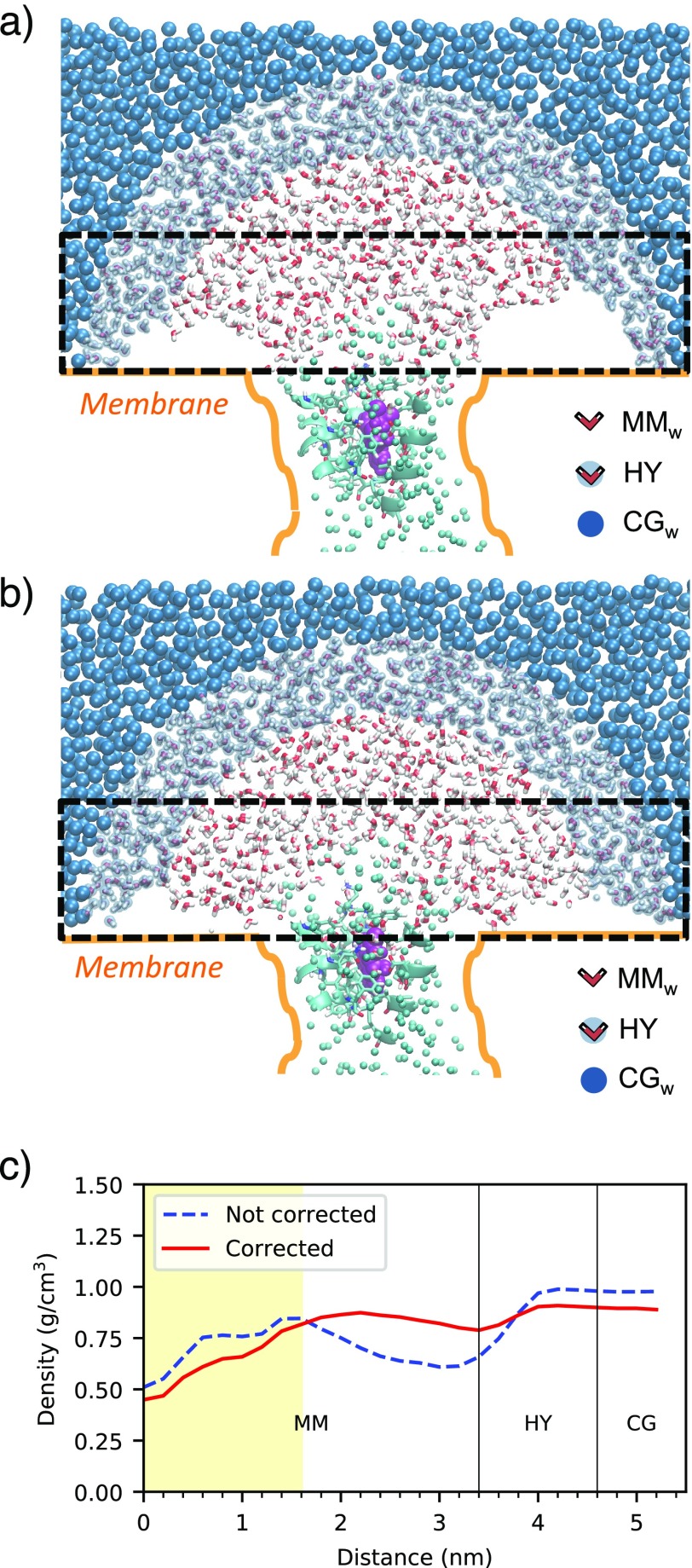
The last term in eq 1, Vsurf, is the potential mimicking the membrane effects. Specifically, it contains a term aiming at reproducing the interactions between the protein and the membrane and a term preventing water penetration in the transmembrane space. The first is represented by a softened Lennard-Jones-like potential (2-1), with the minimum at a distance rp from a virtual surface enveloping the transmembrane portion of the protein, acting on the Cα of the transmembrane protein residues and on each atom of TRP and TYR residues.22 This term constrains the shape of the protein while providing a good degree of flexibility. The second one is a repulsive term proportional to 1/r, where r is the distance from virtual planar walls coinciding with the heads of the lipid bilayer.22 These virtual walls represent boundaries that introduce spatial inhomogeneity in the solvent. Because of the higher pressures attained in the CGw region with respect to the atomistic one, the water confinement achieved by applying the repulsive force mimicking the membrane is less effective in the CGw region than that in the MMw one. Therefore, closer to the repulsive membrane surface, CGw water expands more than MMw water, leading to density fluctuations in the vicinity of the membrane upon passing from CGw to MMw regions (Figure 2a,c). This requires the introduction of a correction of the repulsive boundary potential in order to impose the correct virial pressure on the CGw domain.50−52 The correction of the repulsive force is proportional to the gradient of the difference between the target density profile (resulting from an atomistic simulation) in the direction perpendicular to the membrane, ρt(r), and the current CGw density profile, ρCG(r)56

graphic file with name ct-2019-00040c_m007.jpg 5

where r is the distance to the planar wall. In this way, a uniform depletion layer in proximity of the repulsive planes of the membrane is guaranteed (Figure 2b,c), and the uniform bulk density across MMw, HY, and CGw is preserved (Figure SI 2). In the latter, only small fluctuations in the HY regions, smaller than 5%, are observed.

Figure 2.

Figure 2

Open in a new tab

Snapshots with the uncorrected (a) and corrected (b) membrane potentials in OB-MM/CG simulations. The regions parallel to the membrane considered for the calculation of the planar radial density are highlighted with a dashed line. (c) Planar radial density computed from the center of the upper MMw region in a disk of height 2.0 nm just above the membrane planes, before and after the correction to the membrane potential. The yellow-shaded area corresponds to the presence of the protein. The density value lower than 1 g/cm3 computed in the corrected simulation is attributable to the natural depletion layer in proximity of the membrane plane.

Here we stress that the differences between the new OB-MM/CG scheme and the previous MM/CG lie in the boundary conditions and in the solvent representation, while the hybrid scheme used for the protein–ligand system is identical. Comparing term by term the MM/CG Hamiltonian with the OB-MM/CG one (eq 1), the potential energy internal to the protein, Vp, is identical; the potential term for water, Vw, reduces to the MMw term, Vw,αMM, with λα = 1 (no coarse-grained water is present in the MM/CG); the Vsurf term contains an additional boundary potential, proportional to 1/r, to confine water in the hemispherical domain (placed above the binding cavity) and prevent its evaporation. Moreover, the repulsive potential from the membrane planes is uniform in the xy-plane, as opposed to the analogous term in the OB-MM/CG scheme.

Methods

System Setups

The system simulated is the human β2-adrenergic receptor (β2-AR) in complex with its inverse agonist S-carazolol (PDB code: 2RH1).53 The third intracellular loop (ICL3, between residues 231 and 262), lacking in the PDB file, was modeled using the Web server HHPred57 in conjunction with MODELLER,58 as in ref (22). The system was first equilibrated by all-atoms MD. To this aim, the protein was inserted into a bilayer of 1-palmitoyl-2-oleoyl-phosphatidylcholine (POPC), which represents the most abundant phospholipid in animal cell membranes.59 After having solvated the box with SPC/E water molecules,39 the total size of the system amounted to ∼232000 atoms. The protein is described using the Gromos43a1 force field,60 while the parameters for the POPC are those by Berger, Edholm, and Jähnig.61 The fully atomistic setup differs from a previous atomistic simulation of the same system62 (employed in the validation of the MM/CG approach22) in the choice of the protein force field and in the composition of the membrane. The atomic charges for the ligand have been derived by RESP fitting63−65 using the Gaussian03 package,66 as in ref (62). Details on the simulation parameters for the equilibration step are reported in the next section.

In the OB-MMCG setup, performed using the equilibrated structure, the radius of each MMw hemisphere, rMM, is set to 3.4 nm, while the width of the HY region, rHY, is 1.2 nm. The former is chosen so that the distance between the atomistic protein and the boundary of the MMw region is at least 1.6 nm, as suggested in ref (49); the latter, instead, corresponds to the cutoff used for the nonbonded interactions, so that water molecules at the border of the MMw region do not interact directly with CG water molecules. The x,y-coordinates of the center of the MMw hemisphere correspond to the x,y-coordinates of the CoM of the protein. The distance between the membrane-mimicking planes is 52 Å. As in previous MM/CG works,22,31 the MM region in the OB-MM/CG simulation includes all of the residues at a maximum distance of 5 Å from the ligand. Specifically, they consist of residues 79–82, 86, 109–118, 164, 165, 193–195, 199–208, 282, 286, 289, 290, 293, 308, and 311–316. The total number of particles in the OB-MM/CG system is ∼163000 (including the fourth site on each water molecule, which plays a role only in the CG interactions).

Comparisons are made both with an all-atoms MD, in order to validate the OB-MM/CG simulation, and with the original version of the MM/CG in order to assess possible differences in structural and dynamical properties. The setup for the all-atoms production runs is the same as that for the fully atomistic equilibration. In the MM/CG simulation, the protein is coarse-grained in the same way as in the OB-MM/CG case. The radius of the hemisphere, rhemi, is slightly bigger than rMM; in this way, a similar number of atomistic water molecules (∼2200) can be accommodated with the right density when the potential preventing evaporation is switched on. The planar walls are placed as in the OB-MM/CG system. The total number of particles in the MM/CG system is ∼8100.

Equilibration and Production Simulations

The equilibration simulation, fully atomistic, has been performed with Gromacs 5.1.2.67 First, the all-atoms system underwent 1661 steps of minimization using the steepest descent integrator. Subsequently, the temperature was slowly raised to 300 K using the Nosé–Hoover thermostat;68 once the final temperature was reached, we ran a 300 ns simulation in the NPT ensemble, fixing the pressure at 1 bar by means of the Parrinello–Rahman barostat,69 with a time constant of 5.0 ps. The pressure coupling was isotropic in the x,y-directions and independent in the z-direction. In the NPT simulation, a temperature of 300 K was controlled through a leapfrog stochastic dynamics integrator,70 with an inverse friction constant of 0.5 ps. For all of the simulations, a 2 fs integration time step was used, constraining the hydrogen-containing bonds with the LINCS algorithm.71 A cutoff of 1.2 nm was used for electrostatics and van der Waals interactions. Periodic boundary conditions were used with the minimum image convention. The equilibrated system was used as a starting structure for the OB-MM/CG, MM/CG, and fully atomistic production runs. All of these simulations were performed with the same parameters as the equilibration but in the NVT ensemble. The OB-MM/CG and MM/CG simulations were performed using customized versions of Gromacs 4.72 For the calculation of structural properties, two 10 ns replicas of the production run were performed on each system with a sampling time of 10 ps. For calculation of dynamical properties, two replicas, each 2 ns long, were performed with a sampling time of 0.05 ps.

Postprocessing Analyses

Visual inspection of the trajectories was made using VMD 1.9.2.73 Data analyses were performed with GROMACS utilities, VMD, and in-house scripts. The 10 ns replicas were used for the calculation of structural properties and the 2 ns replicas for dynamical properties. Water properties were calculated on the MMw regions of the OB-MM/CG and MM/CG simulations and on the corresponding, hemispherical volume of the all-atom system (with an approach similar to that in refs (22), (49), and (74)). The probability distribution of the water tetrahedral order parameter was calculated as in ref (75). The reorientation time correlation function (tcf) of the water OH bonds was defined as ⟨P2[u(0) · u(t)]⟩, where P2 is the second-order Legendre polynomial and u is the vector along the OH bond. The characteristic reorientation times were computed as the integral of the corresponding tcfs. Receptor ligand hydrogen bonds were identified assuming that an H-bond is formed when the distance is less than 3.5 Å and the angle is less than 30°. Hydration of the binding site has been assessed by monitoring the number of water molecules at a maximum distance of 5 Å from the ligand. The reorientational tcf of the ligand in the binding pocket was computed with respect to the angle between the vector crossing the carbazole ring of the ligand and the z-axis (defined as the axis perpendicular to the membrane plane).

Results and Discussion

Our approach is validated by comparing structural and dynamical properties computed with the OB-MM/CG scheme with those from all-atoms MD simulations of the human β2-adrenergic receptor76 (β2-AR) rhodopsin-like (or “Class A”) hGPCR. β2-AR is an important target for a variety of drugs, including the FDA-approved antiasthma agonist salbutamol.77 We focus on the complex with the inverse agonist S-carazolol [4-(2-hydroxy-3-isopropylamino-propoxy)-carbazole]78−80 (Chart 1), for which experimental structural information (PDB code 2RH1(53)) and MD studies62,81 have been reported. The same analyses have been carried out using the original MM/CG scheme as well in order to assess possible differences. In the following analysis, hydration water refers to the water molecules in the hemispherical MMw region of MM/CG and OB-MM/CG simulations and to those in an equivalent hemispherical region in the case of all-atoms MD (Figure SI 3).

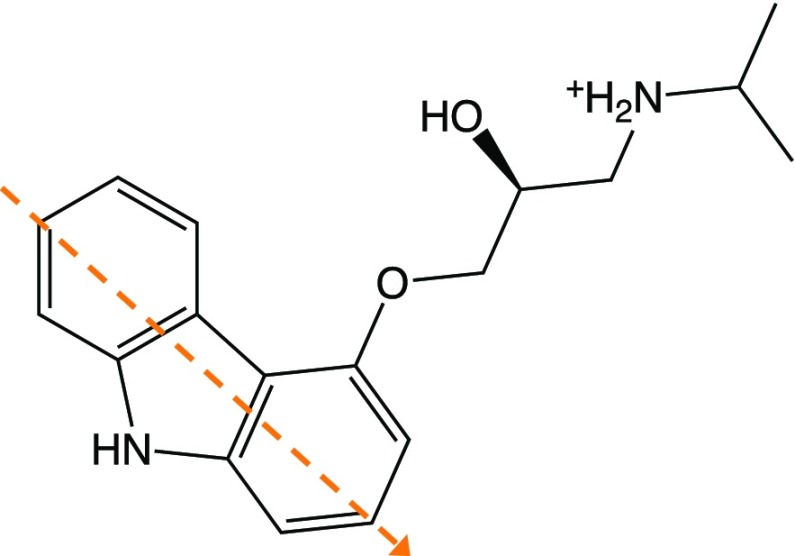
Chart 1. Chemical Structure of the Inverse Agonist S-Carazolola.

Chart 1

Open in a new tab

a The orange dashed line represents the vector coplanar to the carbazole ring that is used for calculation of the reorientational tcf ⟨P2(cos θ)⟩.

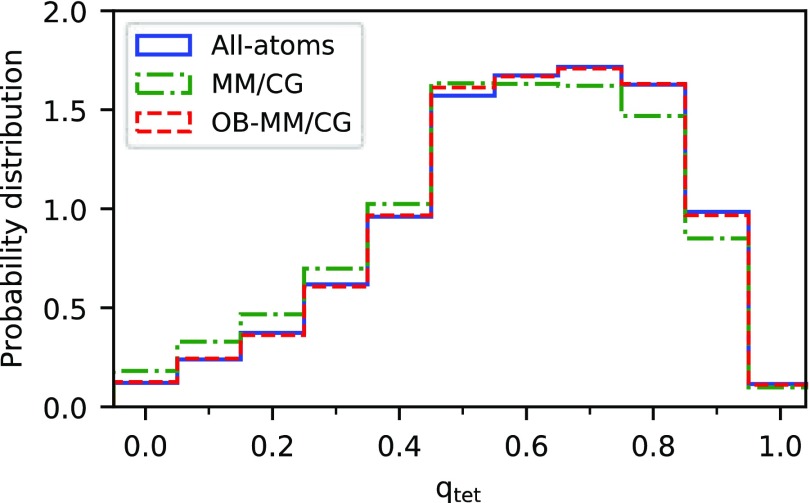
Structural properties of the hydration water, such as the oxygen–oxygen and oxygen–hydrogen pair radial distribution functions (Figure SI 4) and the tetrahedral order parameter75 (Figure 3), show that the OB-MM/CG is in closer agreement with fully atomistic simulations than the MM/CG. We observe here that also the average orientation times of hydration water molecules are similar (1.88 ± 0.10 and 1.82 ± 0.03 ps for OB-MM/CG and all-atoms MD, respectively, as opposed to 2.07 ± 0.03 ps for MM/CG). These are slightly higher values than that for all-atoms MD of pure water using the same force field as the one used here (SPC/E)39 (1.7 ps82). This can be related to the presence of the protein, which is known to slow down the dynamics of water molecules in its first hydration shells.83

Figure 3.

Figure 3

Open in a new tab

Histograms of the tetrahedral order parameter qtet for the water molecules above the binding site, calculated using all-atoms, MM/CG, and OB-MM/CG approaches.

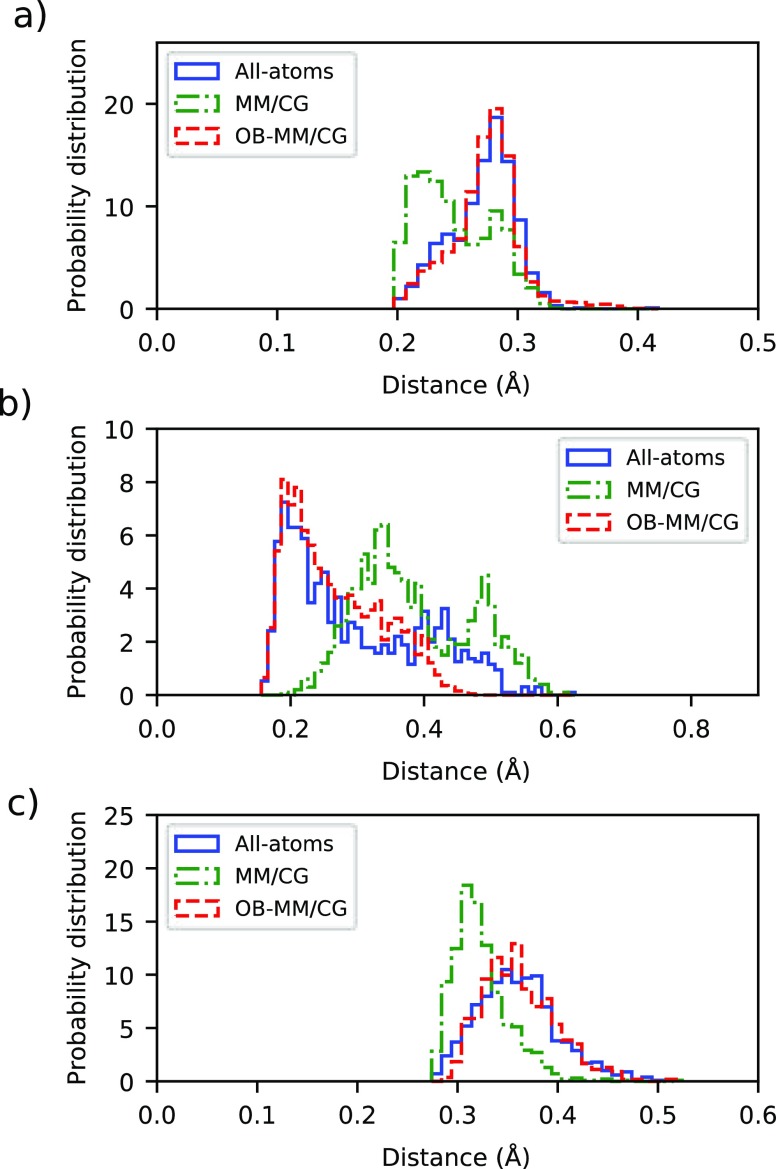
In accordance with the experimental structural study53 and the reported all-atoms MD simulations,62,81 the carbazole ring of the ligand forms, in our simulations, hydrophobic interactions with the side chains of residues Trp286 (6.48 according to Ballesteros–Weinstein numbering84), Phe289 (6.51), and Phe290 (6.52) (Figure SI 5a,c), as well as directed H-bonds with Asp113 (3.32), Ser203 (5.42), and Asn312 (7.39) (Figure SI 5b,d). The ligand–Asn312 interaction is at times mediated by a water molecule, as in previous MD studies.62 Another water molecule bridges the ligand and residue Tyr316 (7.43). In the MM/CG simulation, in addition to the mentioned interactions, Ser204 (5.43) competes with Ser203 for binding to the ligand. Histograms of the H-bond distances involving residues Asp113, Ser203, and Asn312 as obtained from OB-MM/CG, all-atom MD, and MM/CG are displayed in Figure 4. The OB-MM/CG scheme reproduces fairly well the atomistic case, both in terms of the average and variance of the distances, which are instead slightly underestimated by the original MM/CG in the case of Asp113 and Asn312. In the case of Ser203, the overall distribution obtained from MM/CG is shifted to larger distances than that in fully atomistic or OB-MM/CG, very likely because of the competitive interaction with Ser204.

Figure 4.

Figure 4

Open in a new tab

Histograms of the distances of hydrogen bonds between the receptor and the ligand. (a) Distance Asp113(3.32) CCOO–S-car HOH. (b) Distance Ser203(5.42) OCO–S-car HNH. (c) Distance Asn312(7.39) OCO–S-car NNH2+.

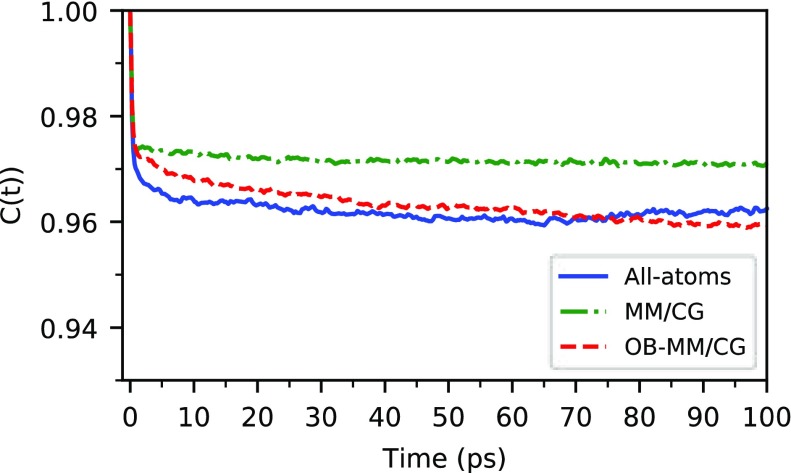
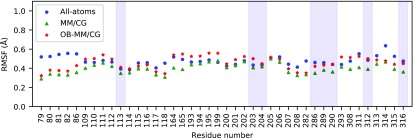
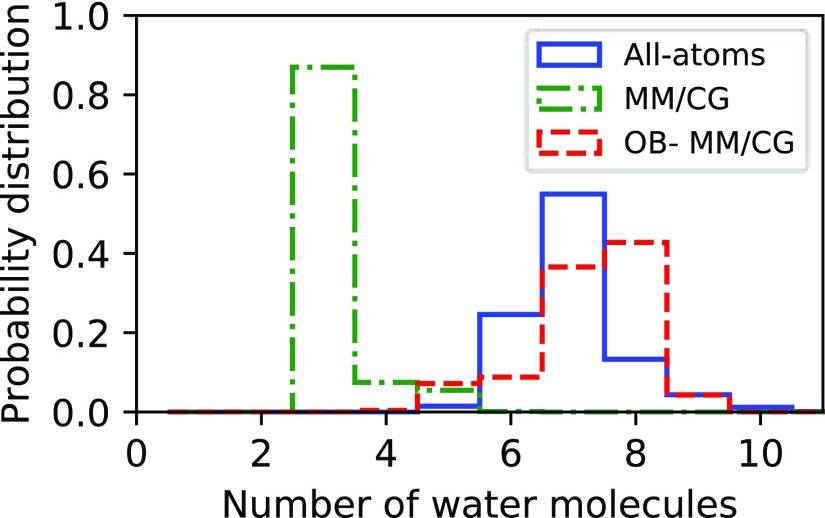
We also investigate ligand dynamics through the tcfs relevant to the reorientational dynamics of the vector crossing its carbazole ring (Figure 5). In the system under study, we observe that the reorientational time scales estimated by atomistic MD and OB-MM/CG are consistent among them, while MM/CG produces faster relaxation dynamics. The plateau values of the tcf, related to the degree of restriction of the reorientational dynamics, show that both atomistic MD and OB-MM/CG lead to less restricted dynamics compared to MM/CG. These differences are consistent with the root-mean-square fluctuation (RMSF) values of Cα atoms of the residues stabilizing the ligand through hydrophobic interactions or hydrogen bonds (Figure 6). They show that indeed these residues can in general undergo smaller fluctuation in MM/CG simulations, indicating more rigid binding compared to atomistic MD or OB-MM/CG. The spreading of ϕ and ψ Ramachandran angles estimated through the PADω parameter85 (Figure SI 6), on the other hand, shows that these residues maintain comparable torsional plasticity in the three simulation schemes. Regarding hydration properties, Figure 7, illustrating the number of water molecules in the binding cavity, clearly proves that the binding pocket hydration in the OB-MM/CG simulation is more representative of the fully atomistic case with respect to the MM/CG simulation. Therefore, although the original MM/CG scheme reproduces ligand poses fairly well, as proved here and for a plethora of protein–ligand complexes including GPCRs,18,19,22,23,30,31 the more realistic hydration achieved in our system through OB-MM/CG can explain the observed improvements in the description of the binding configurations explored by the ligand–protein complex and of the binding site flexibility in particular.

Figure 5.

Figure 5

Open in a new tab

Reorientational tcfs of the ligand in the binding pocket. When the tcfs are fitted with a “model-free” function of the form C(t) = S2 + (1 – S2)e–t/τ, the generalized order parameter S2 takes the values 0.963, 0.972, and 0.963 for the all-atom MD, MM/CG, and OB-MM/CG case, respectively.

Figure 6.

Figure 6

Open in a new tab

RMSFs of the Cα atoms in the MM region. The overall protein backbone flexibility is in line with that of previously published atomistic and MM/CG models of β2-AR,22 with differences typically smaller than 0.3 Å. The shaded areas correspond to the residues stabilizing the ligand through hydrophobic interactions or hydrogen bonds.

Figure 7.

Figure 7

Open in a new tab

Histograms of the number of water molecules at a maximum distance of 5 Å from the ligand in the binding cavity.

Conclusions

This paper introduced a novel hybrid multiscale approach, named OB-MM/CG, for the simulation of membrane protein–ligand complexes. The method couples concomitant atomistic/coarse-grained representations of the protein and the solvent, while the cell membrane is represented implicitly through a series of confining potentials. Specifically, the representation of the protein–ligand complex (based on the MM/CG scheme) aims at reducing the number of degrees of freedom of residues far from the binding site, making the approach tailored for low-resolution protein models where the inaccurate orientations of side chains would introduce artifacts in all-atoms simulations. On the other side, the implementation of H-AdResS for the representation of hydration water leads to the simulation of a rigorous statistical ensemble—the grand canonical one—in the region at atomistic resolution, allowing a more accurate description of hydration and ligand–protein interactions and, in principle, opening the possibility of binding free energy calculations.

In this paper, we validated the OB-MM/CG method on a well-studied GPCR, the β2-adrenergic receptor, in complex with its inverse agonist S-carazolol. Structural and dynamical properties of both the solvent and the complex in the OB-MM/CG simulations are in good agreement with results from fully atomistic simulations. Moreover, some analyses (namely, hydration properties and binding site flexibility) show appreciable improvement with respect to the previous MM/CG implementation. These results provide solid ground for the use of the OB-MM/CG scheme for drug design applications and binding free energy calculations in GPCR–ligand complexes, where a fully atomistic description of the receptor is still impaired by the lack of experiment-based structural information.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.9b00040.

  • MM/CG scheme; radial density from the center of the MMw region; hydration water in the all-atoms simulation; radial distribution function of hydration water; snapshots of the ligand in the binding site; and PADω of MM residues (PDF)

Author Contributions

T.T., V.C., R.P., and P.C. designed the study; T.T. performed the simulations; T.T. and V.C. conceived the analyses; and T.T. wrote the manuscript with contributions from all coauthors. All authors have given approval to the final version of the manuscript.

This research is supported by the European Union’s Horizon 2020-MSCA-ITN program under Grant Agreement No. 642069 (HPC-LEAP project). Simulations were performed with computing resources granted by JARA-HPC from RWTH Aachen University. This project has received funding also from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant Agreement No. 758588).

The authors declare no competing financial interest.

Supplementary Material

ct9b00040_si_001.pdf (14.6MB, pdf)

References

  1. Santos R.; Ursu O.; Gaulton A.; Bento A. P.; Donadi R. S.; Bologa C. G.; Karlsson A.; Al-Lazikani B.; Hersey A.; Oprea T. I.; Overington J. P. A comprehensive map of molecular drug targets. Nat. Rev. Drug Discovery 2017, 16 (1), 19–34. 10.1038/nrd.2016.230. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Katritch V.; Cherezov V.; Stevens R. C. Structure-Function of the G Protein-Coupled Receptor Superfamily. Annu. Rev. Pharmacol. Toxicol. 2013, 53, 531–556. 10.1146/annurev-pharmtox-032112-135923. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Hilger D.; Masureel M.; Kobilka B. K. Structure and dynamics of GPCR signaling complexes. Nat. Struct. Mol. Biol. 2018, 25 (1), 4–12. 10.1038/s41594-017-0011-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Schoneberg T.; Schulz A.; Biebermann H.; Hermsdorf T.; Rompler H.; Sangkuhl K. Mutant G-protein-coupled receptors as a cause of human diseases. Pharmacol. Ther. 2004, 104 (3), 173–206. 10.1016/j.pharmthera.2004.08.008. [DOI] [PubMed] [Google Scholar]
  5. Sriram K.; Insel P. A. G Protein-Coupled Receptors as Targets for Approved Drugs: How Many Targets and How Many Drugs?. Mol. Pharmacol. 2018, 93 (4), 251–258. 10.1124/mol.117.111062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Hauser A. S.; Attwood M. M.; Rask-Andersen M.; Schioth H. B.; Gloriam D. E. Trends in GPCR drug discovery: new agents, targets and indications. Nat. Rev. Drug Discovery 2017, 16 (12), 829–842. 10.1038/nrd.2017.178. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Hauser A. S.; Chavali S.; Masuho I.; Jahn L. J.; Martemyanov K. A.; Gloriam D. E.; Babu M. M. Pharmacogenomics of GPCR Drug Targets. Cell 2018, 172 (1–2), 41. 10.1016/j.cell.2017.11.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Isberg V.; Mordalski S.; Munk C.; Rataj K.; Harpsoe K.; Hauser A. S.; Vroling B.; Bojarski A. J.; Vriend G.; Gloriam D. E. GPCRdb: an information system for G protein-coupled receptors. Nucleic Acids Res. 2016, 44 (D1), D356–D364. 10.1093/nar/gkv1178. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Pandy-Szekeres G.; Munk C.; Tsonkov T. M.; Mordalski S.; Harpsoe K.; Hauser A. S.; Bojarski A. J.; Gloriam D. E. GPCRdb in 2018: adding GPCR structure models and ligands. Nucleic Acids Res. 2018, 46 (D1), D440–D446. 10.1093/nar/gkx1109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Mobarec J. C.; Sanchez R.; Filizola M. Modern Homology Modeling of G-Protein Coupled Receptors: Which Structural Template to Use?. J. Med. Chem. 2009, 52 (16), 5207–5216. 10.1021/jm9005252. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Esguerra M.; Siretskiy A.; Bello X.; Sallander J.; Gutierrez-de-Teran H. GPCR-ModSim: A comprehensive web based solution for modeling G-protein coupled receptors. Nucleic Acids Res. 2016, 44 (W1), W455–W462. 10.1093/nar/gkw403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Zhang Y.; DeVries M. E.; Skolnick J. Structure modeling of all identified G protein-coupled receptors in the human genome. PLoS Comput. Biol. 2006, 2 (2), 88–99. 10.1371/journal.pcbi.0020013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Palczewski K.; Kumasaka T.; Hori T.; Behnke C. A.; Motoshima H.; Fox B. A.; Le Trong I.; Teller D. C.; Okada T.; Stenkamp R. E.; Yamamoto M.; Miyano M. Crystal structure of rhodopsin: A G protein-coupled receptor. Science 2000, 289 (5480), 739–745. 10.1126/science.289.5480.739. [DOI] [PubMed] [Google Scholar]
  14. Chung S. Y.; Subbiah S. A structural explanation for the twilight zone of protein sequence homology. Structure 1996, 4 (10), 1123–1127. 10.1016/S0969-2126(96)00119-0. [DOI] [PubMed] [Google Scholar]
  15. Chothia C.; Lesk A. M. The Relation between the Divergence of Sequence and Structure in Proteins. EMBO J. 1986, 5 (4), 823–826. 10.1002/j.1460-2075.1986.tb04288.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Fan H.; Mark A. E. Refinement of homology-based protein structures by molecular dynamics simulation techniques. Protein Sci. 2004, 13 (1), 211–220. 10.1110/ps.03381404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Feig M.; Heo L. Protein Structure Refinement via Molecular Dynamics Simulations. Biophys. J. 2018, 114 (3), 575a. 10.1016/j.bpj.2017.11.3143. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Fierro F.; Suku E.; Alfonso-Prieto M.; Giorgetti A.; Cichon S.; Carloni P. Agonist Binding to Chemosensory Receptors: A Systematic Bioinformatics Analysis. Front Mol. Biosci 2017, 4, 63. 10.3389/fmolb.2017.00063. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Sandal M.; Behrens M.; Brockhoff A.; Musiani F.; Giorgetti A.; Carloni P.; Meyerhof W. Evidence for a Transient Additional Ligand Binding Site in the TAS2R46 Bitter Taste Receptor. J. Chem. Theory Comput. 2015, 11 (9), 4439–4449. 10.1021/acs.jctc.5b00472. [DOI] [PubMed] [Google Scholar]
  20. Raval A.; Piana S.; Eastwood M. P.; Dror R. O.; Shaw D. E. Refinement of protein structure homology models via long, all-atom molecular dynamics simulations. Proteins: Struct., Funct., Genet. 2012, 80 (8), 2071–2079. 10.1002/prot.24098. [DOI] [PubMed] [Google Scholar]
  21. Heo L.; Feig M. What makes it difficult to refine protein models further via molecular dynamics simulations?. Proteins: Struct., Funct., Genet. 2018, 86, 177–188. 10.1002/prot.25393. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Leguebe M.; Nguyen C.; Capece L.; Hoang Z.; Giorgetti A.; Carloni P. Hybrid Molecular Mechanics/Coarse-Grained Simulations for Structural Prediction of G-Protein Coupled Receptor/Ligand Complexes. PLoS One 2012, 7 (10), e47332. 10.1371/journal.pone.0047332. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Schneider J.; Korshunova K.; Musiani F.; Alfonso-Prieto M.; Giorgetti A.; Carloni P. Predicting ligand binding poses for low-resolution membrane protein models: Perspectives from multiscale simulations. Biochem. Biophys. Res. Commun. 2018, 498 (2), 366–374. 10.1016/j.bbrc.2018.01.160. [DOI] [PubMed] [Google Scholar]
  24. Zhou H. X. Theoretical frameworks for multiscale modeling and simulation. Curr. Opin. Struct. Biol. 2014, 25, 67–76. 10.1016/j.sbi.2014.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Ayton G. S.; Noid W. G.; Voth G. A. Multiscale modeling of biomolecular systems: in serial and in parallel. Curr. Opin. Struct. Biol. 2007, 17 (2), 192–198. 10.1016/j.sbi.2007.03.004. [DOI] [PubMed] [Google Scholar]
  26. Kmiecik S.; Gront D.; Kolinski M.; Wieteska L.; Dawid A. E.; Kolinski A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116 (14), 7898–7936. 10.1021/acs.chemrev.6b00163. [DOI] [PubMed] [Google Scholar]
  27. Noid W. G. Perspective: Coarse-grained models for biomolecular systems. J. Chem. Phys. 2013, 139 (9), 090901. 10.1063/1.4818908. [DOI] [PubMed] [Google Scholar]
  28. Neri M.; Anselmi C.; Cascella M.; Maritan A.; Carloni P. Coarse-grained model of proteins incorporating atomistic detail of the active site. Phys. Rev. Lett. 2005, 10.1103/PhysRevLett.95.218102. [DOI] [PubMed] [Google Scholar]
  29. Neri M.; Baaden M.; Carnevale V.; Anselmi C.; Maritan A.; Carloni P. Microseconds dynamics simulations of the outer-membrane protease T. Biophys. J. 2008, 94 (1), 71–78. 10.1529/biophysj.107.116301. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Neri M.; Anselmi C.; Carnevale V.; Vargiu A. V.; Carloni P. Molecular dynamics simulations of outer-membrane protease T from E-coli based on a hybrid coarse-grained/atomistic potential. J. Phys.: Condens. Matter 2006, 18 (14), S347–S355. 10.1088/0953-8984/18/14/S16. [DOI] [Google Scholar]
  31. Marchiori A.; Capece L.; Giorgetti A.; Gasparini P.; Behrens M.; Carloni P.; Meyerhof W. Coarse-Grained/Molecular Mechanics of the TAS2R38 Bitter Taste Receptor: Experimentally-Validated Detailed Structural Prediction of Agonist Binding. PLoS One 2013, 8 (5), e64675. 10.1371/journal.pone.0064675. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Daura X.; Mark A. E.; van Gunsteren W. F. Parametrization of aliphatic CHn united atoms of GROMOS96 force field. J. Comput. Chem. 1998, 19 (5), 535–547. . [DOI] [Google Scholar]
  33. Noguti T.; Go N. Collective Variable Description of Small-Amplitude Conformational Fluctuations in a Globular Protein. Nature 1982, 296 (5859), 776–778. 10.1038/296776a0. [DOI] [PubMed] [Google Scholar]
  34. Zavadlav J.; Bevc S.; Praprotnik M. Adaptive resolution simulations of biomolecular systems. Eur. Biophys. J. 2017, 46 (8), 821–835. 10.1007/s00249-017-1248-0. [DOI] [PubMed] [Google Scholar]
  35. Praprotnik M.; Cortes-Huerto R.; Potestio R.; Delle Site L.. Adaptive Resolution Molecular Dynamics Technique. In Handbook of Materials Modeling: Methods: Theory and Modeling; Andreoni W., Yip S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp 1–15. [Google Scholar]
  36. Zavadlav J.; Sablic J.; Podgornik R.; Praprotnik M. Open-Boundary Molecular Dynamics of a DNA Molecule in a Hybrid Explicit/Implicit Salt Solution. Biophys. J. 2018, 114, 2352. 10.1016/j.bpj.2018.02.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Zavadlav J.; Marrink S. J.; Praprotnik M. Multiscale Simulation of Protein Hydration Using the SWINGER Dynamical Clustering Algorithm. J. Chem. Theory Comput. 2018, 14 (3), 1754–1761. 10.1021/acs.jctc.7b01129. [DOI] [PubMed] [Google Scholar]
  38. Potestio R.; Fritsch S.; Espanol P.; Delgado-Buscalioni R.; Kremer K.; Everaers R.; Donadio D. Hamiltonian Adaptive Resolution Simulation for Molecular Liquids. Phys. Rev. Lett. 2013, 10.1103/PhysRevLett.110.108301. [DOI] [PubMed] [Google Scholar]
  39. Berendsen H. J. C.; Grigera J. R.; Straatsma T. P. The Missing Term in Effective Pair Potentials. J. Phys. Chem. 1987, 91 (24), 6269–6271. 10.1021/j100308a038. [DOI] [Google Scholar]
  40. Reith D.; Putz M.; Muller-Plathe F. Deriving effective mesoscale potentials from atomistic simulations. J. Comput. Chem. 2003, 24 (13), 1624–36. 10.1002/jcc.10307. [DOI] [PubMed] [Google Scholar]
  41. Espanol P.; Delgado-Buscalioni R.; Everaers R.; Potestio R.; Donadio D.; Kremer K. Statistical mechanics of Hamiltonian adaptive resolution simulations. J. Chem. Phys. 2015, 142 (6), 064115. 10.1063/1.4907006. [DOI] [PubMed] [Google Scholar]
  42. Yuan S. G.; Filipek S.; Palczewski K.; Vogel H. Activation of G-protein-coupled receptors correlates with the formation of a continuous internal water pathway. Nat. Commun. 2014, 10.1038/ncomms5733. [DOI] [PubMed] [Google Scholar]
  43. Yuan S. G.; Palczewski K.; Peng Q.; Kolinski M.; Vogel H.; Filipek S. The Mechanism of Ligand-Induced Activation or Inhibition of - and -Opioid Receptors. Angew. Chem., Int. Ed. 2015, 54 (26), 7560–7563. 10.1002/anie.201501742. [DOI] [PubMed] [Google Scholar]
  44. Angel T. E.; Chance M. R.; Palczewski K. Conserved waters mediate structural and functional activation of family A (rhodopsin-like) G protein-coupled receptors. Proc. Natl. Acad. Sci. U. S. A. 2009, 106 (21), 8555–8560. 10.1073/pnas.0903545106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Granier S.; Manglik A.; Kruse A. C.; Kobilka T. S.; Thian F. S.; Weis W. I.; Kobilka B. K. Structure of the delta-opioid receptor bound to naltrindole. Nature 2012, 485 (7398), 400–U171. 10.1038/nature11111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Manglik A.; Kruse A. C.; Kobilka T. S.; Thian F. S.; Mathiesen J. M.; Sunahara R. K.; Pardo L.; Weis W. I.; Kobilka B. K.; Granier S. Crystal structure of the mu-opioid receptor bound to a morphinan antagonist. Nature 2012, 485 (7398), 321–U170. 10.1038/nature10954. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Zia S. R.; Gaspari R.; Decherchi S.; Rocchia W. Probing Hydration Patterns in Class-A GPCRs via Biased MD: The A(2A) Receptor. J. Chem. Theory Comput. 2016, 12 (12), 6049–6061. 10.1021/acs.jctc.6b00475. [DOI] [PubMed] [Google Scholar]
  48. Bellissent-Funel M. C.; Hassanali A.; Havenith M.; Henchman R.; Pohl P.; Sterpone F.; van der Spoel D.; Xu Y.; Garcia A. E. Water Determines the Structure and Dynamics of Proteins. Chem. Rev. 2016, 116 (13), 7673–7697. 10.1021/acs.chemrev.5b00664. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Tarenzi T.; Calandrini V.; Potestio R.; Giorgetti A.; Carloni P. Open Boundary Simulations of Proteins and Their Hydration Shells by Hamiltonian Adaptive Resolution Scheme. J. Chem. Theory Comput. 2017, 13 (11), 5647–5657. 10.1021/acs.jctc.7b00508. [DOI] [PubMed] [Google Scholar]
  50. O’Connell S. T.; Thompson P. A. Molecular dynamics-continuum hybrid computations: A tool for studying complex fluid flows. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1995, 52 (6), R5792–R5795. 10.1103/PhysRevE.52.R5792. [DOI] [PubMed] [Google Scholar]
  51. Werder T.; Walther J. H.; Koumoutsakos P. Hybrid atomistic-continuum method for the simulation of dense fluid flows. J. Comput. Phys. 2005, 205 (1), 373–390. 10.1016/j.jcp.2004.11.019. [DOI] [Google Scholar]
  52. Kotsalis E. M.; Walther J. H.; Kaxiras E.; Koumoutsakos P. Control algorithm for multiscale flow simulations of water. Phys. Rev. E 2009, 10.1103/PhysRevE.79.045701. [DOI] [PubMed] [Google Scholar]
  53. Cherezov V.; Rosenbaum D. M.; Hanson M. A.; Rasmussen S. G. F.; Thian F. S.; Kobilka T. S.; Choi H. J.; Kuhn P.; Weis W. I.; Kobilka B. K.; Stevens R. C. High-resolution crystal structure of an engineered human beta(2)-adrenergic G protein-coupled receptor. Science 2007, 318 (5854), 1258–1265. 10.1126/science.1150577. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Fritsch S.; Poblete S.; Junghans C.; Ciccotti G.; Delle Site L.; Kremer K. Adaptive resolution molecular dynamics simulation through coupling to an internal particle reservoir. Phys. Rev. Lett. 2012, 10.1103/PhysRevLett.108.170602. [DOI] [PubMed] [Google Scholar]
  55. Fogarty A. C.; Potestio R.; Kremer K. A multi-resolution model to capture both global fluctuations of an enzyme and molecular recognition in the ligand-binding site. Proteins: Struct., Funct., Genet. 2016, 84 (12), 1902–1913. 10.1002/prot.25173. [DOI] [PubMed] [Google Scholar]
  56. Kotsalis E. M.; Walther J. H.; Koumoutsakos P. Control of density fluctuations in atomistic-continuum simulations of dense liquids. Phys. Rev. E 2007, 10.1103/PhysRevE.76.016709. [DOI] [PubMed] [Google Scholar]
  57. Soding J.; Biegert A.; Lupas A. N. The HHpred interactive server for protein homology detection and structure prediction. Nucleic Acids Res. 2005, 33, W244–W248. 10.1093/nar/gki408. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Fiser A.; Do R. K. G.; Sali A. Modeling of loops in protein structures. Protein Sci. 2000, 9 (9), 1753–1773. 10.1110/ps.9.9.1753. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. van Meer G.; Voelker D. R.; Feigenson G. W. Membrane lipids: where they are and how they behave. Nat. Rev. Mol. Cell Biol. 2008, 9 (2), 112–124. 10.1038/nrm2330. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Scott W. R. P.; Hunenberger P. H.; Tironi I. G.; Mark A. E.; Billeter S. R.; Fennen J.; Torda A. E.; Huber T.; Kruger P.; van Gunsteren W. F. The GROMOS biomolecular simulation program package. J. Phys. Chem. A 1999, 103 (19), 3596–3607. 10.1021/jp984217f. [DOI] [Google Scholar]
  61. Berger O.; Edholm O.; Jahnig F. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 1997, 72 (5), 2002–2013. 10.1016/S0006-3495(97)78845-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Vanni S.; Neri M.; Tavernelli I.; Rothlisberger U. Predicting Novel Binding Modes of Agonists to beta Adrenergic Receptors Using All-Atom Molecular Dynamics Simulations. PLoS Comput. Biol. 2011, 7 (1), e1001053. 10.1371/journal.pcbi.1001053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Cornell W. D.; Cieplak P.; Bayly C. I.; Gould I. R.; Merz K. M.; Ferguson D. M.; Spellmeyer D. C.; Fox T.; Caldwell J. W.; Kollman P. A. A 2nd Generation Force-Field for the Simulation of Proteins, Nucleic-Acids, and Organic-Molecules. J. Am. Chem. Soc. 1995, 117 (19), 5179–5197. 10.1021/ja00124a002. [DOI] [Google Scholar]
  64. Bayly C. I.; Cieplak P.; Cornell W. D.; Kollman P. A. A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges - the Resp Model. J. Phys. Chem. 1993, 97 (40), 10269–10280. 10.1021/j100142a004. [DOI] [Google Scholar]
  65. Wang J. M.; Cieplak P.; Kollman P. A. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules?. J. Comput. Chem. 2000, 21 (12), 1049–1074. . [DOI] [Google Scholar]
  66. Frisch M. J.; Trucks G.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; et al. Gaussian 03; Gaussian, Inc.: Wallingford, CT, 2004.
  67. Pall S.; Abraham M. J.; Kutzner C.; Hess B.; Lindahl E. Tackling Exascale Software Challenges in Molecular Dynamics Simulations with GROMACS. Lect Notes Comput. Sc 2015, 8759, 3–27. 10.1007/978-3-319-15976-8_1. [DOI] [Google Scholar]
  68. Hoover W. G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A: At., Mol., Opt. Phys. 1985, 31 (3), 1695–1697. 10.1103/PhysRevA.31.1695. [DOI] [PubMed] [Google Scholar]
  69. Parrinello M.; Rahman A. Polymorphic Transitions in Single-Crystals - a New Molecular-Dynamics Method. J. Appl. Phys. 1981, 52 (12), 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
  70. Van Gunsteren W. F.; Berendsen H. J. C. A Leap-Frog Algorithm for Stochastic Dynamics. Mol. Simul. 1988, 1 (3), 173–185. 10.1080/08927028808080941. [DOI] [Google Scholar]
  71. Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18 (12), 1463–1472. . [DOI] [Google Scholar]
  72. Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4 (3), 435–447. 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
  73. Humphrey W.; Dalke A.; Schulten K. VMD: visual molecular dynamics. J. Mol. Graphics 1996, 14 (1), 27–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  74. Fogarty A. C.; Potestio R.; Kremer K. Adaptive resolution simulation of a biomolecule and its hydration shell: Structural and dynamical properties. J. Chem. Phys. 2015, 142 (19), 195101. 10.1063/1.4921347. [DOI] [PubMed] [Google Scholar]
  75. Errington J. R.; Debenedetti P. G. Relationship between structural order and the anomalies of liquid water. Nature 2001, 409 (6818), 318–321. 10.1038/35053024. [DOI] [PubMed] [Google Scholar]
  76. Johnson M. Molecular mechanisms of beta(2)-adrenergic receptor function, response, and regulation. J. Allergy Clin. Immunol. 2006, 117 (1), 18–24. 10.1016/j.jaci.2005.11.012. [DOI] [PubMed] [Google Scholar]
  77. Jack D. A Way of Looking at Agonism and Antagonism - Lessons from Salbutamol, Salmeterol and Other Beta-Adrenoceptor Agonists. Br. J. Clin. Pharmacol. 1991, 31 (5), 501–514. 10.1111/j.1365-2125.1991.tb05571.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  78. Keul J.; Schmid P.; Neiss A. Treatment of Arterial-Hypertension - Efficiency and Tolerance of the Beta-Receptor Blocker Carazolol in the Framework of a Field-Study. Munchen Med. Wochen 1985, 127 (25), 664–668. [Google Scholar]
  79. Main B. G.; Tucker H. Recent advances in beta-adrenergic blocking agents. Prog. Med. Chem. 1985, 22, 121. 10.1016/S0079-6468(08)70230-3. [DOI] [PubMed] [Google Scholar]
  80. Mejean A.; Guillaume J. L.; Strosberg A. D. Carazolol: A potent, selective beta(3)-adrenoceptor agonist. Eur. J. Pharmacol., Mol. Pharmacol. Sect. 1995, 291 (3), 359–366. 10.1016/0922-4106(95)90077-2. [DOI] [PubMed] [Google Scholar]
  81. Chan H. C. S.; Filipek S.; Yuan S. G. The Principles of Ligand Specificity on beta-2-adrenergic receptor. Sci. Rep. 2016, 10.1038/srep34736. [DOI] [PMC free article] [PubMed] [Google Scholar]
  82. Laage D.; Hynes J. T. On the Molecular Mechanism of Water Reorientation. J. Phys. Chem. B 2008, 112 (45), 14230–14242. 10.1021/jp805217u. [DOI] [PubMed] [Google Scholar]
  83. Bizzarri A. R.; Cannistraro S. Molecular dynamics simulation evidence of anomalous diffusion of protein hydration water. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1996, 53 (4), R3040–R3043. 10.1103/PhysRevE.53.R3040. [DOI] [PubMed] [Google Scholar]
  84. Ballesteros J. A.; Weinstein H. Integrated methods for the construction of three-dimensional models and computational probing of structure-function relations in G protein-coupled receptors. Methods Neurosci. 1995, 25, 366–428. 10.1016/S1043-9471(05)80049-7. [DOI] [Google Scholar]
  85. Caliandro R.; Rossetti G.; Carloni P. Local Fluctuations and Conformational Transitions in Proteins. J. Chem. Theory Comput. 2012, 8 (11), 4775–4785. 10.1021/ct300610y. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct9b00040_si_001.pdf (14.6MB, pdf)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES