Uncovering general, shared, and unique temporal patterns in ambulatory assessment data

Abstract

Intensive longitudinal data provide psychological researchers with the potential to better understand individual-level temporal processes. While the collection of such data has become increasingly common, there are a comparatively small number of methods well-suited for analyzing these data, and many methods assume homogeneity across individuals. A recent development rooted in structural equation and vector autoregressive modeling, Subgrouping Group Iterative Multiple Model Estimation (S-GIMME), provides one method for arriving at individual-level models composed of processes shared by the sample, processes shared by a subset of the sample, and processes unique to a given individual. As this algorithm was motivated and validated for use with neuroimaging data, its performance and utility is less understood in the context of ambulatory assessment data collected by psychologists. Here, we evaluate the performance of the S-GIMME algorithm across various conditions frequently encountered with daily diary (compared to neuroimaging) data; namely, a smaller number of variables, a lower number of time points, and smaller autoregressive effects. Importantly, we demonstrate for the first time the importance of the autoregressive effects in recovering data-generating connections and directions, and the ability to use S-GIMME with lengths of data commonly seen in daily diary studies. We demonstrate the use of the S-GIMME algorithm with an empirical example evaluating the general, shared, and unique temporal processes associated with a sample of individuals with borderline personality disorder (BPD). Finally, we underscore the need for methods such as S-GIMME moving forward given the increasing use of intensive longitudinal data in psychological research, and the potential for these data to provide novel insights into human behavior and mental health.

It is now well recognized that the individuals comprising a priori categories, such as gender, age, or psychiatric diagnosis, are remarkably heterogeneous in their characteristic manners of mood, behavior, or cognition. Presumably, this rich variability within a given category reveals individual differences (perhaps unrelated to category) that undermine the validity of the categorization. Indeed, this heterogeneity poses challenges to psychological and behavioral classification systems, including those used in high stakes settings (e.g., psychiatric diagnosis and treatment). Additionally, these categories have problematically nebulous boundaries, and supposedly discrete groups may overlap substantially. A prime example of these issues can be found in psychiatric diagnoses, which are paradoxically both too specific (i.e., high rates of co-variation or “co-morbidity”; Lilienfeld et al., 1994) and too general (i.e., high heterogeneity within diagnosis; Hyman, 2010). These challenges have generated a broad and growing literature on quantitative modeling approaches to uncover the symptomatic patterns of psychopathology (see e.g., Kotov et al., 2017 for review). The present paper evaluates one analytic approach for ambulatory data analysis, Subgrouping Group Iterative Multiple Model Estimation (S-GIMME; Gates, Lane, Varangis, Giovanello, & Guskiewicz, 2017), for the modeling of emotional, behavioral, and cognitive processes. S-GIMME arrives at general patterns of relations that exist for the entire sample, patterns that are shared by only a subset of individuals, and patterns that are unique to a given individual. Originally developed for use on functional brain imaging data, we evaluate the utility of this approach for data qualities that are sometimes seen in analysis on ecological momentary assessments.

To date, efforts to generate quantitatively derived taxonomies have largely relied on assessment approaches that are temporally distal from the putative mechanisms of interest. That is, indicators are assessed in cross-section or at a temporal scale (e.g., years) that miss the target underlying dynamic processes in real time that serve to define and maintain the constructs of interest (e.g., psychopathology). However, over the past two decades, there has been a surge in method development and implementation to study mood, behavior, and cognition as they unfold in the naturalistic settings of daily life. Referred to variously as experience sampling, ecological momentary assessment, or ambulatory assessment (Shiffman, Stone, & Hufford, 2008; Trull & Ebner-Primer, 2013), these approaches generally use intensive longitudinal data collection designs to sample behavior on a time-scale closer to the dynamic processes they intend to measure. Research in psychopathology increasingly relies on these methods to understand the nuanced and complex dynamic processes of mental illness (e.g., Ebner-Priemer et al., 2007; Hamaker & Wichers, 2017; Muehlenkamp et al., 2009; Myin-Germeys, van Os, Schwartz, Stone, & Delespaul, 2001; Pe et al., 2015; Sadikaj et al., 2013; Shiffman et al., 2002; Silk, Steinberg, & Morris, 2003; Smyth et al., 2007; Trull et al., 2008; Wright & Simms, 2016; see also Myin-Germeys et al., 2009 and Trull & Ebner-Priemer, 2013 for reviews). This work has almost exclusively relied on the aforementioned diagnostic classification schemes by placing individuals in predefined groups and conducting analysis under the assumption of within-group homogeneity. However, if the assumption of within-group homogeneity does not hold for a given sample, then results do not reflect the symptomatology present for individuals seeking treatment. To understand individual-level symptoms and experiences, temporal processes must be examined. Further, it has now been demonstrated that heterogeneity in temporal processes also exists in normative samples, such as the structure of personality (e.g., Borkenau & Ostendorf, 1998; Ram et al., 2005; Ram & Grimm, 2009; Molenaar & Campbell, 2009).

Even though diagnostic categories may not accurately reflect the symptoms or experiences of individuals, there may exist groups of individuals who share similar behavioral or cognitive profiles. Thus, research on the temporal processes of individuals would ideally be extended to parsing individuals into subgroups based on similarity in the dynamic processes underlying their behavior. Identifying these subgroups first requires quantitative methods for arriving at individual-level models that accurately and reliably capture the unique patterns of effects among variables across time (Molenaar, 2004), a goal that has gained much traction in human brain neuroimaging literature (Smith et al., 2011). From this work, Bayes net approaches, a class of algorithms for model selection, have been identified as the most promising analytic methods for arriving at data-driven models of temporal processes (Mumford & Ramsey, 2014; Ramsey, Hanson, & Glymour, 2011; Ramsey, Sanchez-Romero, & Glymour, 2014). Among those, Group Iterative Multiple Model Estimation (GIMME; Gates & Molenaar, 2012) has surfaced as a highly reliable model building procedure for arriving at individual-level patterns of effects underlying dynamic processes. One recent extension to the original GIMME algorithm is the ability to cluster individuals into subgroups based on similarities in their dynamic processes. Termed, “Subgrouping GIMME” (S-GIMME; Gates, Lane, Varangis, Giovanello, & Guskiewicz, 2017), this method provides an unsupervised classification approach to arrive at data-driven subgroups. S-GIMME thus identifies dynamic relations that exist at the group- (i.e., sample), subgroup-, and individual-levels, providing estimates for these relations separately for each individual.

Previous work involving GIMME and S-GIMME has been rooted in modeling functional magnetic resonance imaging (fMRI) brain data. That is, computer simulations have focused on data generated to mimic characteristics of fMRI data, and empirical applications have focused on modeling relationships among brain regions of interest (ROIs) from fMRI data (e.g., Beltz et al., 2013; Karunanayaka et al., 2014; Nichols, Gates, Molenaar, & Wilson, 2014; Price et al., 2017; Yang, Gates, Molenaar, & Li, 2015). The present paper provides evidence that with some consideration, S-GIMME can be applied to ambulatory assessment data, of which daily diary data is a specific type. Here, daily diaries were specifically chosen because (a) they are an oft used variant of ambulatory assessment both historically (e.g., Borkenau & Orstendorf, 1998; Lebo & Nesselroade, 1978; Searles, Perrine, Mundt, & Helzer, 1995; Zevon & Tellegen, 1982) and at present (e.g., Bachrach & Read, 2017; Castro-Schilo & Ferrer, 2016; Gadassi et al., 2016; Hamaker, Grasman, & Kamphuis, 2016; Lee et al., 2017; Zimmermann et al., in press), and (b) the sampling rate is sometimes conducted at relatively equal spacing, an advantageous feature for time-series data in the current modeling context¹. Nevertheless, application to daily diary data presents novel analytic concerns which may be absent in neuroimaging data.

Motivation for Simulation Study

One important difference in the qualities of the data results from the psychophysiological nature of fMRI data. In fMRI data, the extent to which a variable predicts itself at subsequent time points, also known as the autoregressive (AR) effect (Chatfield, 2003), is sizable. The magnitude of these autoregressive effects stems from the slowness of the biological process under study relative to the temporal resolution of data collection, such that values at a given time are highly predictive of values at the same brain region at the next time point. In contrast to fMRI data, where an AR effect concerns an ROI predicting itself at the next time point (often two seconds later), there may be little reason to expect a construct examined in a daily diary study, such as affect, to strongly predict itself at the next time point since changes may occur on the order of hours (or minutes) rather than days. Even when data are obtained multiple times within a day, the AR effects have been shown to vary across individuals and constructs (see e.g., Fernandez & Fisher, 2017; Fisher & Boswell, 2016), suggesting that the assumption of strong AR effects may not hold in these types of data.

When the rate of measurement is slow relative to the process being studied, time-lagged effects surface as contemporaneous (Granger, 1969). As describe in detail below, strong contemporaneous relations can prevent the estimation of AR effects in the GIMME process, thus changing the search space from what is seen in brain imaging situations where the AR effects are often (but not always) high. In these cases, multiple solutions may surface from within a GIMME framework that describe the data approximately equally well (Beltz & Molenaar, 2016). Accordingly, one issue the present paper seeks to investigate is whether the inclusion of AR relations in the base model circumvents this problem and provides reliable results even in the presence of relatively low AR estimates. By estimating AR effects (even if small), one can directly examine whether a given variable statistically predicts another variable – at a lag or contemporaneously – more so than the reverse (Granger, 1969). It has previously been shown in simulations emulating fMRI data that failure to include both contemporaneous and lagged effects leads to spurious results when both types of effects exist in the true generative model (Gates et al., 2010). However, it remains unknown whether the inclusion of small, potentially nonsignificant, autoregressive effects perhaps seen in daily diary data will allow for the reliable recovery of directed effects among variables.

A second difference is that daily diary data may possess fewer group-level relationships compared to fMRI data. This notion again stems directly from fMRI being a biological process and as such, having known properties that exist for all individuals. For example, a strong connection is typically found between left and right hemispheres of the same region; further, this connection is often found across all individuals (e.g., Zelle, Gates, Fiez, Sayette, & Wilson, 2016). Thus, for data containing multiple bilateral ROIs, there will be a larger number of group-level relationships. While daily diary data may also contain relationships common to all individuals (e.g., stress and negative affect), there may be fewer in general since there are no biological constraints underlying group-level relations.

A third difference is that daily diary studies likely will have far fewer observations per person than fMRI studies. As with any time series analysis, the power to detect effects increases with greater numbers of observations across the time. For instance, it is rare for an fMRI study to have fewer than 150 observations, but daily dairy studies rarely collect that number of observations.

A related and final difference is the number of variables (or ROIs). Given the decrease in sample size, researchers may opt for fewer variables to model in order to ensure model convergence and to facilitate interpretation. For these reasons, the present paper investigates the performance of S-GIMME on simulated behavioral data, which are expected to differ from fMRI data in the following ways: (1) different parameters governing temporal effects; (2) shorter time series (3) fewer group-level relationships and (4) a smaller number of variables.

Empirical Study

Following examination of simulated data, we provide evidence of heterogeneity in the temporal processes of symptoms across days in a sample of individuals diagnosed with borderline personality disorder (BPD). That is, we investigate if patterns of relations among symptoms vary across individuals within a sample of individuals diagnosed with BPD. BPD, in particular, is a psychiatric diagnosis plagued by heterogeneity in clinical presentation (Hallquist & Pilkonis, 2012; Wright, Hallquist, Morse, et al., 2013). As defined by the Diagnostic and Statistical Manual of Mental Disorders – Fifth Edition (DSM-5; American Psychiatric Association, 2013), BPD is a syndrome composed of interpersonal (e.g., unstable and intense relationships), affective (e.g., marked reactivity of mood; difficulty controlling anger), behavioral (e.g., impulsivity; recurrent suicidal behavior), and cognitive (e.g., identity disturbance; transient psychosis) features. Thus, there is diversity in the component features of the syndrome. Further, like many DSM-5 diagnoses, BPD is a polythetic category, such that only five out of the nine criteria are necessary for diagnosis. As such, there are 256 possible combinations of features that would satisfy the threshold for BPD diagnosis. This fact, along with seminal clinical theory (Kernberg, 1975), has motivated the search for meaningful subgroupings to parse this observed heterogeneity. In turn, parsing this heterogeneity may inform more personalized treatment.

Previous efforts have enlisted cluster analysis or finite mixture modeling of various concurrently assessed diagnostic, personality, and behavioral features to empirically establish more homogeneous groups (Bradley, Conklin, & Westen, 2005; Critchfield, Clarkin, Levy, & Kernberg, 2008; Lenzenweger, Clarkin, Yeomans, Kernberg, & Levy, 2008; Hallquist & Pilkonis, 2012; Wright, Hallquist, Morse, et al., 2013). These studies have largely used other dispositional scales to derive more homogenous subgroups, but not direct assessments of processes as they might unfold over time and across contexts. However, in both the DSM-5 and the broader clinical literature, the cardinal impairments of BPD are dynamic and contextualized. For instance, the symptoms of BPD involve not only merely elevated negative affect, but also “reactivity of mood,” as well as frantic efforts to avoid abandonment, unstable relationships, transient psychosis, difficulty controlling anger, and impulsivity. These features are generally understood to have important dynamic relationships to each other (e.g., self-harm may serve to regulate negative emotions; Miskewicz et al., 2015); further, the individual variability present in these relations likely gives rise to the observed heterogeneity in the presentation of symptoms. To date, there has been scant investigation into the potential between-person heterogeneity in within-person couplings of BPD features over time.

Methods

Definition of unified structural equation modeling (uSEM) implemented in S-GIMME

The current paper uses the S-GIMME algorithm (Gates & Molenaar, 2012; Gates et al., 2017), which reliably recovers data-generating group-, subgroup-, and individual-level relations at the level of the person. This algorithm is rooted in the uSEM framework (Kim, Zhu, Chang, Bentler, & Ernst, 2007), a variant of structural vector autoregressive modeling that simultaneously estimates both contemporaneous and lagged relations. The uSEM capitalizes on the known ability to conduct time-series analysis from within an SEM framework, which allows one to draw on the many strengths of SEM to arrive at individual-level models with directed (not correlational) relationships among variables of interest. The inclusion of the lagged effects, including the autoregressive (AR) effects, allows specification of the direction of a relationship from within a Granger causality framework. That is, a variable X is said to “Granger-cause” variable Y if it explains variance in variable Y above and beyond the variance explained by the autoregressive term of Y (Granger, 1969). This is typically evaluated by looking at the error variance; as a proxy, we examine whether the candidate variable (X in our example) would significantly improve model fit if it were added as a predictor to variable Y after considering the AR effect for variable Y. Note that this definition centers on the improvement of prediction in variable Y when using information from variable X; it does not represent causality in an absolute sense. Importantly, making stronger claims of causality rests in part on the assumption that all relevant variables are in the model, a known limitation of drawing claims of causality in SEM (see omitted variable problem: Bollen, 1989). Results must be interpreted as causal with the caveat that the only putative third-variable influences were those contained in the set used and not the universe of variables.

Including the AR relations during the path search procedure in S-GIMME automatically tests for Granger causality in each step². Each additional path added provides a significant improvement upon the reduced model (which in this case includes the AR effect for the target variable) as well as any other predictors that have been added. The interpretation of lagged relations that are added is quite straightforward: deviation from the mean at the prior time point relates to deviation from the mean at the next time point. Directed contemporaneous relations can emerge because (1) the time delay for cause and effect is small (or unmeasurable) relative to the time interval of data collection or (2) both variables are caused by a different unmeasured variable at a prior time point (Granger, 1988). The latter reason provides further motivation for researchers to carefully consider variables to include in the model to avoid the absence of necessary third-variable influences. In many cases it is reasonable to expect contemporaneous relations due to the temporal resolution of data collection being too large to capture the effect as lagged. In functional MRI for instance, the biological process is slow (on the order of seconds) relative to the underlying neuronal activity it aims to capture (which occurs on the order of milliseconds). Thus it is expected that effects are larger for contemporaneous relations. The same may occur when measurements are taken daily but the process changes hourly, or any other such situation where the measurement rate is slower than the rate under which the process evolves.

The general uSEM may be formally defined as:

$${\eta }_t=A{\eta }_t+\mathrm{ }\varphi {\eta }_{t-1}+\mathrm{ }{\zeta }_t$$

where A is a p × p matrix containing the contemporaneous relations among p variables (with a zero diagonal to prevent contemporaneous self-prediction), ϕ is a p × p matrix containing the lagged relations among p variables with AR effects on the diagonal, η is the observed time series, and ζ contains residuals with a mean of zero and diagonal covariance matrix, assumed to be white noise processes and therefore contain no temporal dependencies.

These relations can be further decomposed for each individual into group-, subgroup-, and individual-level relations. That is, certain relations exist for the entire sample; certain relations exist within a given subgroup k; and certain relations exist for a given individual i. This decomposition can be expressed as:

$${\eta }_{i,t}=\left(A_i+A_{i,k}^s+A_i^g\right){\eta }_{i,t}+\left({\varphi }_i+\mathrm{ }{\varphi }_{i,k}^s+{\varphi }_i^g\right){\eta }_{i,t-1\mathrm{ }}+{\zeta }_{i,t}$$

Here, A, ϕ, and ζ are defined as before, where the superscripts s and g indicate that these paths exist at the subgroup- and group-level, respectively. Importantly, should no subgroup division exist (i.e., all individuals are in one “subgroup”), these relations will be contained in the group-level matrix. Parameter matrices A and ϕ that lack a superscript denote matrices containing only the individual-level relations. Finally, the subscript i on all matrices indicates that each relation is estimated at the individual-level, even in the cases where there are group- and subgroup-level patterns of relations.

Assumptions of S-GIMME

S-GIMME requires that the assumption of stationarity be met but does not require the assumption of ergodicity be met. We first define stationarity since it is part of an ergodicity assumption. Stationary (formally, “weakly stationary”) multivariate time series data has statistical properties, such as mean, variance, and covariance, that are constant over time and only depend on the lag. Data that has a trend violates this assumptions since the mean level changes across time. This issue can be accommodated prior to analysis using preprocessing steps described in Beltz & Gates (2017). In a similar vein, data where the autocovariance value (at a given lag) changes across time violates the stationarity assumption, as do data where the covariance among variables changes across time. For these instances the researcher may want to consider approaches that allow for these estimates to vary across time (e.g., Molenaar, Beltz, Gates, & Wilson, 2016). To be ergodic, a process (1) must be stationary and (2) each unit (here, person) must have the same dynamic processes (Molenaar, 2008). While S-GIMME requires that each unit of data (however defined) be stationary, it does not require that all individuals have the same process: individuals can vary in their processes. The rate of recovery of data-generating relations is improved when some relations are consistently found across individuals since this helps to detect signal from noise, but the entire process does not have to be the same either in terms of the pattern of relations or the estimates of those relations. Two other noteworthy assumptions related to any SEM analysis also exist for the S-GIMME framework: that the data are normally distributed and have equal intervals between them.

Model Selection Procedure

Group-level search.

The ultimate goal of GIMME (and S-GIMME) is to allow for individual-level estimates and relations in order to attend to heterogeneity in dynamic processes. However, GIMME begins with a group-level search for two related reasons. First, when using model selection procedures for SEM, the recovery of individual-level relationships is greatly improved when the starting model is closer to the data-generating model (MacCallum, 1986). This follows from suggestions that model search procedures work best when starting from a point in the model formation that is as close as possible to the final model (MacCallum, Roznowski, & Necowitz, 1992). Second, there likely is noise in any process being studied, and looking for similarities in relations across individuals aids in detecting signal from noise. Taken together, by looking for consistencies across individuals GIMME detects signal from noise to arrive at group-level paths which then greatly aid in accurately recovering individual-level relations. Full details of the model selection procedure can be found in Gates et al. (2017) and Gates & Molenaar (2012). Here, we briefly describe the relevant steps. The model selection procedure is implemented in the freely distributed R package, gimme (Lane, Gates, & Molenaar, 2014; Lane & Gates, 2017), which allows for both traditional GIMME and S-GIMME to be implemented. For each individual, the model search procedure begins with a null model; that is, all values in the A matrix and ϕ matrix are zero. Optionally, a researcher may choose to have this null model estimate the diagonal of the ϕ matrix (i.e., the AR effects) rather than initially constrain them to be zero. While it is standard (and the default in gimme) to have the AR elements freely estimated in the null model, it is ultimately the decision of the researcher. For this reason, investigation into best practices is warranted here.

Upon estimation of the null model for each individual, S-GIMME examines the modification index (MI) associated with each fixed parameter. Modification indices are Lagrange Multiplier equivalents tests that indicate the anticipated improvement in model fit should that parameter be freely estimated (Jöreskog & Sörbom, 1986). There are unique MI estimates for all of the elements in the ϕ matrix (when AR effects are not included initially) and for the estimates in the A matrix (excluding the diagonal). For each of these estimates, GIMME counts the number of individuals for whom it is significant after a Bonferroni correction of α= .05/N. From these counts, the MI that is significant for the largest proportion of individuals is selected for inclusion in each individual’s model (i.e., considered a “group-level” relation). The selection of group-level paths terminates when no path is significant for a prespecified proportion of individuals. Informed by prior research and simulations, the default cutoff is 75% (Gates & Molenaar, 2012; Smith et al., 2011). Although 75% is a strict cutoff for what constitutes a majority, this cutoff aids in the subsequent search for paths which may exist at a subgroup level. The researcher can adjust this value if a more or less strict criterion is desired. A group-level pruning procedure is conducted following the group-level search, where paths are removed sequentially which are no longer significant for 75% of individuals at a Bonferroni-corrected α = .05/N.

Subgroup-level search.

Following the identification of the group-level model, S-GIMME searches for the existence of subgroups. These subgroups are defined based on shared characteristics of individuals’ temporal processes. Specifically, an adjacency matrix is created which counts the number of similar effects shared by each dyad of two individuals, i and j. Here, similarity is defined using the correspondence between individuals’ already-estimated values contained in the A and ϕ matrices (collectively referred to here as β), as well as the correspondence of the expected parameter change (EPC) associated with each potential path that could be added to the model. The EPC for a given parameter is preferred to the MI since the EPC also provides an indication of the direction of the effect (should it be freely estimated). If both the significance and sign of individuals i and j match for a given β or EPC value, the similarity count increases by 1. In this way, the adjacency matrix which forms the basis for subgrouping is constructed. This matrix is adjusted by the lowest similarity count to increase the sparseness of the matrix. Generation of an appropriate similarity matrix is highly critical for accurate clustering of time series data (Liao, 2005), and prior work indicated that the count matrix constructed here is optimal when compared to other feature-selection techniques, such as label propagation, Infomap, and fast modularity (Gates et al., 2017).

The community detection procedure known as Walktrap is then applied to this adjacency matrix (Pons & Latapy, 2006). Briefly, as a random walk approach, Walktrap performs short random walks, generally with three to five steps, and merges communities in a bottom-up fashion using traditional Ward’s clustering (Ward, 1963). Then, a quality function called modularity (Newman, 2004) is used to identify the optimal cut point in the dendrogram. In this way, the researcher does not need to specify a priori the number of subgroups or subjectively decide given the options for cluster solutions. Full details of this procedure can be found in Pons and Latapy (2006). A benefit of Walktrap is that it is one of the few approaches that reliably recovers cluster (i.e., subgroup or community) assignments on data that are in the form of a dense correlation matrix or a count matrix as used in S-GIMME (Gates, Henry, Steinley, & Fair, 2016). Once subgroup membership is established, a search is conducted within each subgroup using the same procedure as the group-level search. Here, the starting model is now the previously-established group-level model. This search terminates when no path is significant for the majority of individuals (here, 51%) in that subgroup. This cutoff can also be adjusted by the researcher. As before, a subgroup-level pruning procedure is conducted, where paths are removed sequentially which are no longer significant for 51% of individuals at a Bonferroni-corrected α = .05/N, where N represents the number of individuals in the sample.

Individual-level search.

By this point in the search procedure, all individuals enter the individual-level search with a model composed of (potentially) group- and (potentially) subgroup-level paths. The individual-level search adds paths which are significant for an individual at α = .01 until an “excellent” model is obtained. Here, an excellent fit is obtained when two of four fit indices are excellent (RMSEA < .05, SRMR < .05, CFI > .95, NNFI > .95; Brown, 2006). An individual’s final model is composed of (potentially) group-, (potentially) subgroup-, and individual-level paths, all of which are estimated at the individual level. Importantly, if a sample is so heterogeneous that no paths exist at the group- or subgroup-level, then the final model for an individual will be entirely composed of paths unique to that individual.

Estimation.

In order to represent the lagged and contemporaneous relationships, a block Toeplitz structure is used, enabling estimates which can be considered quasi-maximum likelihood estimates. The block Toeplitz covariance matrix is structured to represent the covariance among lag-0 variables, the covariance among lag-1 variables, and the covariance among lag-0 and lag-1 variables. Importantly, assuming normality, these parameters approximate true ML estimates (Hamaker, Dolan, & Molenaar, 2002). Finally, the default estimation method is full information maximum likelihood (Enders & Bandalos, 2001), which allows for the presence of missing data under the assumption that they are missing at random (MAR).

Stimulation Study: Monte Carlo Simulation and Evaluation Criteria

Data generation.

We designed a Monte Carlo simulation consistent with empirical daily diary data. The intentions of this simulation were to evaluate the reliability of the recovery of paths with and without the autoregressive effects across common conditions. Here, in the data-generating process, we varied: (1) the number of time points, T, to be 30, 60, 90, and 120; (2) the number of variables, p, to be 5 and 10; (3) the number of individuals, N, to be 25, 75, and 150. When applying S-GIMME to these data, two conditions were tested – (4) AR fixed and AR freed. This yielded a fully factorial design, with 4 × 2 × 3 × 2 conditions. These conditions were evaluated across R = 100 replications. The data were generated using an algebraic manipulation of the formula depicted in Equation 2:

$${\eta }_{i,t,k}={\left(I_p-\left(A_i+A_{i,k}^s+A_i^g\right)\right)}^{-1}\left({\varphi }_i+\mathrm{ }{\varphi }_{i,k}^s+{\varphi }_i^g\right){\eta }_{i,t-1}+{\left(I_p-\left(A_i+A_{i,k}^s+A_i^g\right)\right)}^{-1}{\zeta }_{i,t}$$

The values for the autoregressive paths were set to 0.2 (SD = .1); this value reflects that autoregressive processes may not be as strong in daily diary data as in fMRI data, with prior simulation work placing them at 0.6 (Gates & Molenaar, 2012). Therefore, for ambulatory data that has higher AR estimates (perhaps due to shorter time intervals as seen in Fisher & Boswell, 2016), prior work supports that accurate model recovery should be high. The path weights for the off-diagonal elements in ϕ were set to −0.4 (SD = 0.1), and the path weights for the off-diagonal elements in A were set to 0.4 (SD = 0.1). The errors were generated to be Gaussian white noise errors; that is, normally distributed for all variables and all individuals. All individual time series were checked for stability over time, such that the mean and variance of the time series remained relatively constant.

To prevent the results from being driven by a specific network structure (e.g., one that is particularly easy or difficult to recover), we generated each set of paths for each replication randomly, holding constant the overall density of the network structure at approximately 20%. Of the paths generated for each individual, 25% percent were generated to exist at the group level (not including AR effects), 50% were generated to exist at the subgroup level, and 25% were generated to exist at the individual level. Group- and subgroup-level paths were varied across replications but not within replications; individual-level paths were varied randomly both across and within replication. For each simulated time series, a series of T + 50 observations were generated, where the first 50 observations were discarded to remove deviations due to initialization of the time series.

Hubert-Arabie Adjusted Rand Index.

In order to evaluate the accuracy of subgroup recovery, we computed the Hubert-Arabie Adjusted Rand Index (ARI_HA; Hubert & Arabie, 1985). It is considered an adjusted index because it corrects for the grouping of elements by chance. This index compares the vector of recovered subgroup assignment with the vector of true subgroup assignment, where values closer to 1 indicate better recovery of the true subgroup structure. The ARI_HA can be formally expressed as:

$$AR{I}_{HA}=\frac{\left({}_2^N\right)(a+d)-[(a+b)(a+c)+(c+d)(b+d)]}{{\left({}_2^N\right)}^2-[(a+b)(a+c)+(c+d)(b+d)]}$$

where N indicates the number of individuals, α indicates the number of pairs assigned to the same community who truly belonged in the same community, b indicates the number of pairs assigned to the different communities but truly belonged to the same community, c indicates the number of pairs assigned to the same community but truly belonged in different communities, and d indicates the number of pairs assigned to different communities which truly belonged in different communities. Perfect recovery results in an ARI_HA of 1, where excellent recovery is >.90, good recovery is >.8, moderate recovery is >.65, and poor recovery is <.65 (Steinley, 2004).

Recovery Indices.

To evaluate the accuracy of the path recovery, we compute four indices popularized by Ramsey, Hanson, & Glymour (2011), which evaluate both the presence and the direction of the paths in the true and recovered individual-level models: path recall, path precision, direction recall, and direction precision. Here, recall pertains to the proportion of true paths (or directions) in the recovered model relative to the paths (or directions) in the data-generating model. Thus, recall evaluates S-GIMME’s power to find relations that existed in the data-generating model. Direction recall takes into account both the detection of the presence of a path as well as the directionality, and as such is always lower than path recall. Neither the path recall nor the direction recall takes into account recovered paths which did not exist in the data-generating model (false positives). Therefore, we also evaluate precision, which is a proportion of the true paths (or directions) in the recovered model relative to the total paths (or directions) in the recovered model. Using these pieces of information, we are able to evaluate the algorithm’s ability to accurately recover an individual’s data-generating model (i.e., sensitivity), while balancing both false positives and false negatives (specificity).

Meta-models.

We estimated a series of four-factor general linear models to examine mean differences in the path recovery using the aforementioned measures of recall and precision. Each GLM was estimated using all main effects (i.e., AR open or closed, number of variables, sample size, and length of observations) and two-, three-, and four-way interactions. Any effects with a partial η² exceeding .01 were examined further. Full results for each meta-model can be found in the appendix.

Empirical Study

As a final step, we applied S-GIMME to an available clinical dataset to demonstrate its performance in real-world empirical daily diary data. Our goal was to examine potential group, subgroup, and individual-specific paths among cardinal BPD manifestations at the daily level. BPD was selected as a target for these investigations because it is a highly heterogeneous diagnosis by definition, and this heterogeneity has been studied using traditional dispositional assessments in cross-section (e.g., Hallquist & Pilkonis, 2012; Wright, Hallquist, Morse, et al., 2013). For the current example, we drew the data from a study of the processes involved in the daily manifestation of personality disorder (see e.g., Wright, Beltz, Gates, Molenaar, & Simms, 2015; Wright, Hopwood, & Simms, 2015; Wright & Simms, 2016). For a detailed description of the method and procedure involved in data collection, see Wright & Simms (2016). In brief, a large group of participants (N = 628) were recruited from outpatient psychiatric treatment settings and received diagnostic clinical interviews. Subsequently, a subset of those participants (n = 116) who met the criterion for any personality disorder were enrolled in the daily diary study, provided they also had daily access to the Internet. Written informed consent was obtained prior to participation. The relevant institutional review board approved all study procedures. Participants attended an in-person training and assessment session during which study procedures were explained, and self-report measures were completed via computer. Starting the evening of the in-person assessment, participants began completing daily diaries via secure website every evening for 100 consecutive days. Surveys were to be completed at (roughly) the same time each day, between 8pm and 12am. However, participants were allowed to deviate from this schedule if necessary (e.g., working nightshift) provided (a) they completed diaries at the end of their day, and (b) the diaries were completed at roughly the same time each day. Participants received daily email reminders and were also provided several paper diaries they could use in the event of technological difficulties. Compensation was provided for daily participation at the rate of $100 for ≥ 80% participation, and prorated at $1/day for < 80%. Participation also was incentivized though recurring raffles ($10 drawing every 5 days for those providing at least 4 diaries) and drawings for additional money and tablet computers at the end of the study, with the odds of winning proportionally tied to participation. Of the total number of participants in the daily diary study, we selected 36 who met the threshold for a BPD diagnosis and had ≥ 60 days worth of daily diary responses.

Daily Personality Disorder Manifestations.

Daily expression of PD was measured using 30 items created for this project. Details related to full item set and scale development can be found in Wright and Simms (2016) supplementary material. Daily items included the stem, “Over the past 24 hours…” and were rated on an 8-point response scale for each item anchored with Not at All (0) and Very Much So (7). Of the 30 items, seven were selected for being (a) core features of the BPD construct, and (b) exhibiting enough variability across the majority of participants to be suitable for S-GIMME analyses. These items included measures of mood lability (“My mood was up and down”), anxiousness (“I felt anxious”), depression (“I felt depressed”), anger (“I lost my temper”), impulsivity (“I did something on impulse”), emptiness (“My relationships felt empty”), and urgency (“I acted on my emotions”). One participant was removed due to no variability on the urgency item. Thus, the final analyses used a total of n = 35 participants.

MANOVA.

We conducted a one-way multivariate analysis of variance (MANOVA) to evaluate if the average level of symptoms across the days used in the present study differed across the subgroups obtained from S-GIMME. We wished to examine if the subgroups based on temporal processes differed in terms of symptom severity. As such, we conducted a MANOVA to examine potential between-subgroup differences in symptom severity using the same variables used in the analysis of temporal processes (described below): participant’s mood lability, impulsivity, anger, anxiousness, depression, emptiness, and urgency.

Results

Convergence

Across all simulation conditions, there was noticeable variability in the percentage of converged cases. The lowest convergence was seen in the 5 variable condition with 30 time points and AR effects closed at the beginning of estimation, with approximately 48% of individual-level models terminating normally. The models that did not terminate normally either (1) halted at a model one path prior to nonconvergence or (2) failed to converge at all. However, if AR effects were open at the beginning of estimation, more than 99% of cases converged normally, meaning that the final model experienced no convergence issues and at least two of four fit indices met the criteria to be considered “excellent.”

Meta-Model Results

As seen previously (Gates & Molenaar, 2012), the performance of S-GIMME did not fluctuate across varying levels of sample size in the present study. For this reason, Figure 1 collapses across sample size to display the path recovery of S-GIMME for the conditions when the AR effects are fixed (closed) and freed (open) across varying lengths of time and number of variables. As can clearly be seen, S-GIMME conducted with AR effects freely estimated greatly improves the accurate and reliable recovery of paths. Further, a larger number of time points greatly improves the recovery of data-generating relationships. Finally, though we find promising results in both the 5 and 10 variable conditions, performance is better in the 5 variable condition. Specifics regarding precision and direction as well as performance across the specific conditions are discussed below.

Figure 1.

All outcomes by number of variables, time, and autoregressive estimation.

Path and direction recall.

We statistically evaluated the recovery of data-generating paths across four simulation factors corresponding to conditions frequently encountered in daily diary data: the estimation of autoregressive effects, sample size, number of time points, and number of variables. The outcome measures relating to path recovery were evaluated using an ANOVA which included main effects and interactive effects among the simulation factors. For the recall of true paths, main effects were present for opening the AR effects in estimation$\mathrm{ }({\eta }_p^2=\mathrm{ }.34)$, the number of time points$\mathrm{ }({\eta }_p^2=\mathrm{ }.19)$, and the number of variables$\mathrm{ }({\eta }_p^2=\mathrm{ }.02)$. Thus, the recovery of true paths was improved in the presence of freely estimated autoregressive effects, a larger number of time points, and a smaller number of variables.

A three-way interaction between AR, number of time points, and number of variables clarified these main effects; this interaction explained 6% of the variance $({\eta }_p^2=\mathrm{ }.06)$ in true path recovery. The same interaction effect was present for the recall of true directions$\mathrm{ }({\eta }_p^2=\mathrm{ }.04)$. Increased rates of path and direction recovery was observed in cells where the AR paths were open, the number of time points was greater (see Figure 2 for path recall), and the number of variables was lower. The total number of individuals, or sample size, did not meaningfully impact the path recovery. There was a large amount of variability present depending on simulation condition. For example, collapsing over sample size, the average path recovery in the condition with T = 120, AR effects open, and 5 variables was 93.3% compared to 45.9% in the condition with T = 30, AR effects closed, and 10 variables.

Figure 2.

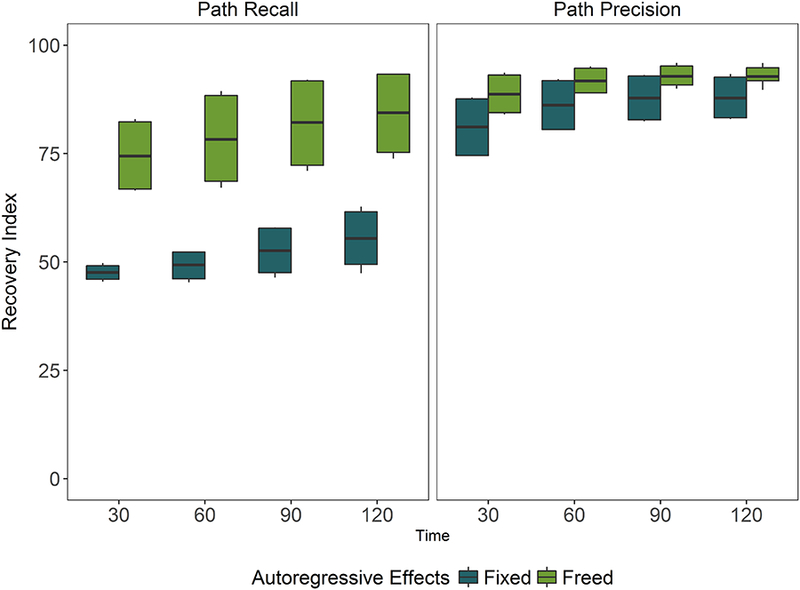
Path recall and precision by time and autoregressive estimation.

Path and direction precision.

Whereas our two measures of recall provide information regarding our ability to recover paths that existed in the true model, our two measures of precision provide information regarding the quality of the paths we recovered in terms of false positives. That is, precision addresses the number of true paths in the recovered model relative to the number of total paths in the recovered model. Here, the number of individuals again was not influential. The interaction of AR estimation with the number of variables was the most important determination of precision, where precision was highest when AR effects were freed for estimation and the number of variables was smaller. There was also an interaction between the number of time points and the number of variables $({\eta }_p^2=\mathrm{ }.02)$, such that the greatest precision of paths is obtained when the number of variables is low and the number of time points is high. If the number of variables is large relative to the number of time points (e.g., in the condition with 10 variables and 30 time points), then the precision of paths is low. Figure 1 summarizes the findings across all four measures of path recovery. Table 1 contains comprehensive results for path recall by simulation condition.

Table 1.

Path recall across all simulation conditions.

AR Effects	Number of Time Points	Sample Size	Path Recall: 5 variables	Path Recall: 10 variables
Fixed	30	25	46.30	48.86
		75	45.90	49.19
		150	45.45	49.75
	60	25	52.28	45.27
		75	52.21	46.04
		150	52.38	46.40
	90	25	57.64	46.37
		75	57.97	47.49
		150	57.81	47.60
	120	25	62.78	47.40
		75	61.72	49.77
		150	61.14	49.33
Freed	30	25	82.93	67.06
		75	82.47	66.73
		150	81.82	66.46
	60	25	89.43	68.87
		75	88.62	68.53
		150	87.73	67.11
	90	25	92.05	72.70
		75	91.75	72.12
		150	91.72	70.98
	120	25	93.43	75.77
		75	93.38	75.07
		150	93.08	73.86

Performance by level.

All results discussed thus far focus on recall and precision of all paths, regardless of the data-generating level (e.g., group-, subgroup-, individual-level). Figure 3 displays the path recovery of group, subgroup, and individual-level paths across the number of time points with estimated AR paths. We observe that the recovery of group-level relationships is most robust within S-GIMME. The recovery of subgroup-level relationships is next, followed by the recovery of individual-level relationships. Importantly, the recovery of subgroup-level paths will be in part determined by the quality of the data-driven subgrouping. If a path is not added in the subgroup-level search, it may be recovered at the individual level. The high recovery of subgroup-level paths points to the benefits of searching for consistencies across individuals in order to arrive at reliable models. The recovery of individual-level paths was lowest averaging around 60% recall, suggesting that S-GIMME may achieve a model characterized by “excellent” fit before all individual-level paths have been added. The trade-off of the use of a fit index as a stopping criterion is that while not all paths may be recovered, favoring parsimony prevents false positives.

Figure 3.

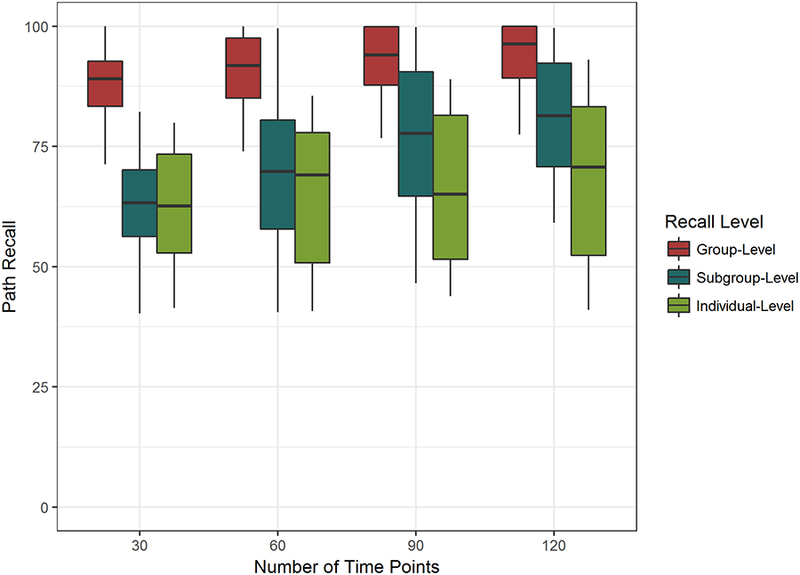
Recall by level.

Relative bias.

Finally, we assessed the relative bias of the recovered path estimates by condition. There existed variability across conditions, though no individual effect exceeded a partial η² value of .01. A graphic depiction (see Figure 4) shows the amount of bias present across the number of time points, split by AR condition. For the conditions in which the AR effects are freed at the start of estimation, the relative bias stays within +/− 10% across the number of time points, where bias is lowest when T = 120. These findings are consistent with prior work evaluating bias when using the block-Toeplitz method to implement SEM-based time series models.

Figure 4.

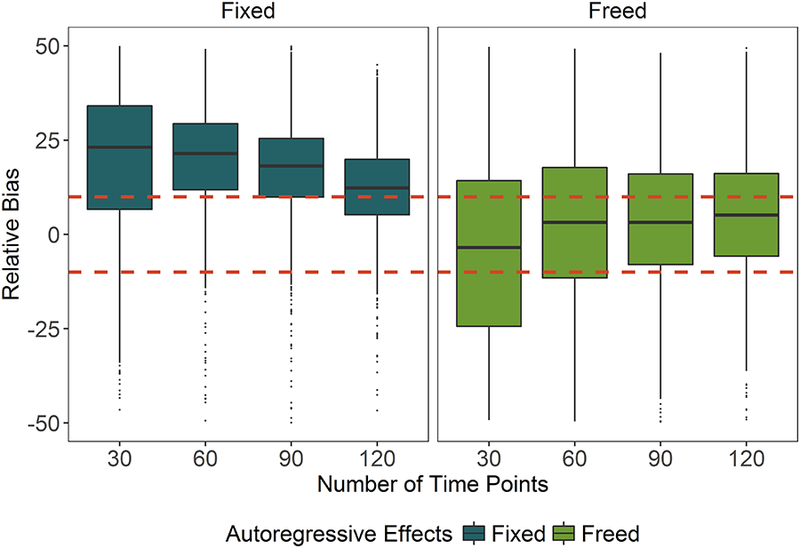
Relative bias by time and autoregressive estimation.

Subgroup recovery.

Finally, we examined the ARI_HA as a measure of subgroup recovery. Subgroup results generally follow those seen for recall and precision because the algorithm uses path information to cluster individuals. Therefore, the most accurate recovery of subgroups was present in conditions with AR effects freed, and 120 time points. For the ten variable condition, the Adjusted Rand index exceeded .8 provided that T ≥ 90 and AR effects were freely estimated. The subgroup recovery of the five variable condition was poorer, though it too increased with an increasing number of time points (range = .09-.47 between T = 30 and T = 120, respectively). A graphical examination of the results revealed that freeing the estimation of the AR effects was the most important determination of subgroup recovery; however, no simulation factor exceeded the cutoff for partial η². Table 2 shows comprehensive results for subgroup recovery by simulation condition.

Table 2.

Subgroup recovery across all simulation conditions.

AR Effects	Number of Time Points	Sample Size	ARIHA: 5 variables	ARIHA: 10 variables
Fixed	30	25	0.00	0.00
		75	0.00	0.00
		150	0.00	0.00
	60	25	0.01	0.00
		75	0.01	0.00
		150	0.00	0.00
	90	25	0.08	0.01
		75	0.05	0.01
		150	0.04	0.01
	120	25	0.15	0.04
		75	0.11	0.04
		150	0.09	0.03
Freed	30	25	0.12	0.37
		75	0.10	0.42
		150	0.06	0.37
	60	25	0.35	0.71
		75	0.31	0.68
		150	0.30	0.66
	90	25	0.39	0.81
		75	0.45	0.85
		150	0.44	0.82
	120	25	0.42	0.85
		75	0.50	0.91
		150	0.48	0.89

Empirical Study

S-GIMME discovered three subgroups from the 35 individuals. These subgroups are labeled “A”, “B”, and “C”, in order of size, for descriptive purposes. Subgroup A comprised the largest proportion of the sample with n = 24; subgroup B was the second largest (n = 10). Subgroup C contained only one individual; this singleton group demonstrates the strength of the Walktrap approach for clustering individuals. Rather than combining individuals who do not share temporal processes into a “super” subgroup, it allows the existence of subgroups with very low numbers. This individual can thus be considered an outlier with respect to the multivariate pattern of temporal relations. Thus, it is not included in subsequent analysis.

Figure 5 depicts the patterns of effects found for the group, subgroups A and B, and individuals. Only one group-level path was found – after controlling for other individual-level lagged and contemporaneous effects, feelings of depression within the last 24 hours can be statistically predicted by reports of mood lability at that same time period. The small number of group-level paths suggests a very high degree of heterogeneity in this sample, supporting the decision to conduct subgroup- and individual-level searches for temporal patterns rather than treating individuals as the same (as is frequently done within diagnostic categories). In contrast to the relatively sparse group-level structure, each subgroup was typified by 5–6 subgroup-level paths. The network of paths that defined Subgroup A included contemporaneous prediction of Anxiety by Depression and Mood Lability, Depression also predicted Emptiness, Anxiety predicted Anger, Anger predicted Urgency, and Urgency predicted Impulsivity. Interestingly, Subgroup B included a path that linked two of the same daily BPD manifestations as in Subgroup A, but in the opposite direction: Anxiety predicted Mood Lability, Anxiety also predicted Impulsivity, Mood Lability predicted Urgency and Anger, and Urgency predicted Emptiness. Each of these groups is suggestive of potentially important clinical differences that are given greater treatment in the Discussion section.

Figure 5.

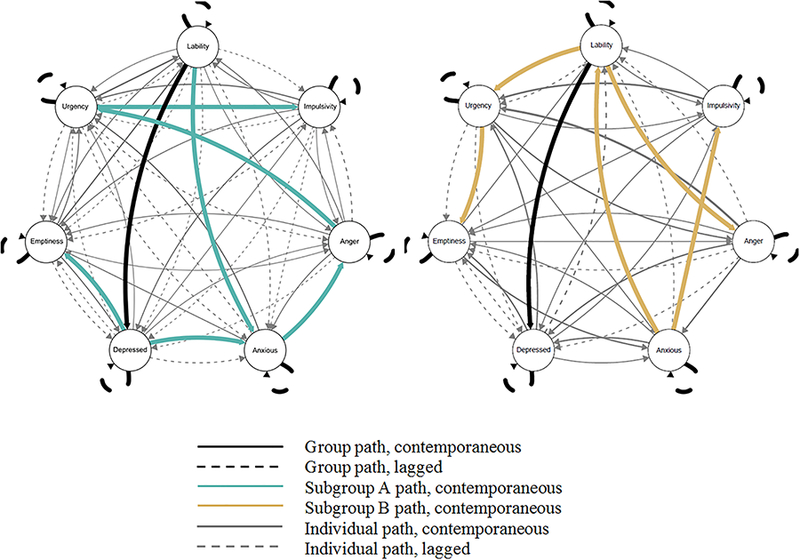
Depiction of relationships for Subgroups A and B.

Although the sample is small and any group comparison is likely to be low powered to detect anything but sizeable effects, we conducted a one-way MANOVA with the seven indicators of daily BPD symptomology as independent variables and subgroup assignment as dependent variables, similar to a discriminant analysis. Results yielded a nonsignificant main effect for BPD symptomology, Pillai’s Trace = 0.35, F(7, 26) = 1.98, p > .05, suggesting no differences in the average daily symptom endorsement based on subgroup allocation. Thus, these subgroups are not typified by symptom level but rather by similarities in their symptom dynamics. This demonstration illustrates that the relations of symptoms across time reveals information above and beyond simply averaging the data.

Discussion

The analytic method evaluated here enables researchers to reliably parse individuals into clusters based on similarities in their emotional, behavioral, and cognitive processes. From the S-GIMME results, researchers can make inferences regarding dynamic processes that are generalizable to the population from which individuals are drawn. Additionally, the results reveal patterns of effects that exist for a subset of individuals and finally, individual-level effects. Originally developed for use on brain imaging data, we found that with minor adaptation (specifically, forcing autoregressive effects to be freed at the start of model building), S-GIMME can be used for data with the same qualities as those seen in daily diary studies. Specifically, these results provide evidence that including the AR effects greatly improves recovery of the contemporaneous and lagged temporal effects among variables when conducting S-GIMME for model selection. This information may be particularly useful for ambulatory assessment, such as daily self-report, that may be collected at a low temporal resolution relative to the process of interest. In this case, as seen here in the empirical example, the majority of effects may surface contemporaneously, particularly if the relations among variables occur faster than the data collection (as described in Granger, 1988). Further, we find our results to be robust to the formation of the data-generating network structure, as a strength of the current study is our use of randomly generated network structures. The results from the simulation study suggest that S-GIMME is a viable option, assuming certain data features, for studying heterogeneity in multivariate processes assessed using daily diary studies. Namely, data characterized by moderate to strong autoregressive effects, a longer time series (e.g., T > 60), a relatively small number of variables (e.g., 5–10), and equally spaced time intervals are best suited for use with S-GIMME.

The present project found lower rates of recovery than what has been seen previously in data generated to emulate brain imaging data. A few factors decrease the utility of S-GIMME in the context of daily diary studies. First, many effects may be missed for studies that only have 30 data points (e.g., daily measures for one month). Here, we saw that having a higher number of variables (10) when there were under 60 time points decreased accurate model recovery. However, there were also relatively few false positives, indicating that the effects that were recovered, although potentially more sparse, were accurate and reliable. Second, the AR effect sizes were much smaller than had been previously tested. The present paper provides evidence that S-GIMME has satisfactory rates of recovery of the data-generating relations even when AR effects are small. Still, the rate of recovery was worse than seen in data generated to have higher AR effect sizes. S-GIMME favors parsimony by using fit indices as a stopping criteria rather than adding all paths that might be significant. While this keeps false positives at a minimum, we see that it might have an unintended effect of stopping too early in the search and not adding paths that were in the data-generating model. More work needs to be done to identify the best fit indices for this context.

The model search procedure that began with AR effects estimated greatly improved recovery of the presence and direction of effects from within an S-GIMME framework. This finding aligns with statistical theory and prior research that demonstrate the utility of examining how variables relate after controlling for the influence each variable has on itself at a later time (Gates et al., 2010; Granger, 1969). However, other noteworthy options exist for accurately detecting the direction of prediction between variables. One option, GIMME for Multiple Solutions (GIMME-MS; Beltz & Molenaar, 2016) generates a set of possible connectivity maps from which the optimal solution can be selected using decision criteria (e.g., based on information criteria or residuals). Other Bayesian network approaches perform well in terms of accurate model recovery in the absence of autoregressive effects. One such approach, independent multisample greedy equivalence search (iMaGES; Ramsey et al., 2011) uses information across all individuals in a manner that does not produce false paths. A second approach in the Bayesian network class of algorithms originally designed for cross-sectional studies, Linear Non-Gaussian Acyclical Model (LiNGAM; Shimizu et al., 2006; Hyvärinen, Zhang, Shimizu, & Hoyer, 2010), performs well for non-Gaussian data but likely requires a greater number of observations than typical in daily diary studies. These latter two approaches, like the original GIMME, performed well on a canonical set of benchmark fMRI data (Gates & Molenaar, 2012; Mumford & Ramsey, 2014; Smith et al., 2011). Much like including ARs for all individuals with S-GIMME, GIMME-MS, iMaGES, and LiNGAM appear to be useful when contemporaneous effects are large compared to lagged effects and when AR effects are low or inconsistent (i.e., present for some variables but not for others).

Other areas of growth for model selection pertain specifically to qualities of daily diary data. As noted above, multiple items were removed from the empirical demonstration due to there being no variability for some individuals. Analysis from within a general linear modeling framework (including time series) cannot immediately utilize variables that are constant across the measurement period. Additionally, it is highly likely that these processes may change across time, reflecting non-stationarity (and a violation of the assumptions of S-GIMME). This is particularly true if the participants are measured during an intervention. In these cases, trends may be addressed through preprocessing or other approaches (e.g., splitting of time series) prior to S-GIMME analysis. Another option is to increase the lag order to account for periodic effects (e.g., a lag of 7 for weekly effects), but this may only be tenable when a small number of variables is used. Adding an exogenous basis vector that contains the shape of the trend is another option that will be shortly available. Non-normality in the distribution of the data presents another issue. At present, it is unknown the influence that this will have on S-GIMME’s recovery rate. A more pressing issue is that of measurement error. Within the SEM framework it is rather straightforward to arrive at latent variables in an effort to obtain more precise measurements of underlying constructs. Extension of GIMME to manage latent variables is currently underway by integrating the gimme package with MIIVsem (Fisher, Bollen, Gates, & Rönkkö, 2017).

Further, given the data-driven nature of the GIMME approach, the role of measurement error should be investigated in future work, particularly when considering how different modalities of data collection may affect the precision of our instrument, and therefore, our error in measurement. Finally, some designs will encounter unequal spacing between observations. This unequal spacing may occur in ecological momentary assessments where the measurement is taken only when the participant indicates a life event occurred (as described in the review by Laurenceau & Bolger, 2005) or when there are no measurements obtained while the participants are at sleep (eg., the publicly available data described in Fisher, 2015) or in burst designs. Furthermore, in the case of designs that use multiple intra-day assessments, the matter of the lack of assessments during the overnight further imposes large periods without assessment, and it is difficult to make the argument that the final and first assessments going between days are equivalent to other successive periods. These sorts of irregular time-series pose methodological and conceptual problems for contemporary time-series methods, not just GIMME. A number of approaches have been proposed and implemented to generate series with equal spacing from these types of data, such as continuous time modeling or rescaling continuous time to integer time (see, e.g., Asparouhov, Hamaker, & Muthén, in press). Users interested in implementing GIMME with irregularly spaced data may wish to create equally spaced time-series in advance by using interpolation and resampling methods (Beltz & Gates, 2017; Fisher & Biswal, 2016). However, the effect of these approaches on parameter estimates for ambulatory assessment data and recovery of the correct model remains unstudied in GIMME, and poorly understood across all analytic approaches. These issues warrant much more attention for time series analysis for intensively gathered longitudinal data collected for psychological studies.

Empirical Study

To illustrate the utility of using S-GIMME method, we examined group, subgroup, and individual-level temporal models in a sample of 35 patients diagnosed with BPD who completed daily diaries of various clinical features over 60 days or more. We found that only a single group-level path existed tying together all of these participants with the same diagnosis. This path suggests that the common feature in this group is the within-day prediction of depression from mood lability. At the same time, we found rich individual heterogeneity in contemporaneous and lagged paths. Moreover, we found that two subgroups emerged which were markedly distinct in the daily associations among several variables. We also found that the subgroups could not be differentiated using the average daily endorsement of the symptom variables examined in their temporal processes, though we note that this was a low powered comparison for all but large effects. Nevertheless, this demonstrates that the information regarding how the symptoms relate across time differed from what can be reaped by looking at average scores alone. Although necessarily speculative given the limitations of the data (e.g., modest sample size), interpreting the subgroup specific models offers compelling results and beckon further analyses in larger samples. The processes that differentiate the Subgroup A from Subgroup B may best be understood as internalizing vs. externalizing processes. That is, the majority of relationships within Subgroup A were between the predominantly affective variables (e.g., Depression, Anxiety, Mood Lability, Anger, and Emptiness); the disinhibitory behaviors (Urgency, Impulsivity) are linked, but are largely separate from these processes.

Conclusion

The present paper introduces one approach for analyzing daily diary data for heterogeneous populations that satisfies a few issues seen in the analysis of temporal processes across individuals. Namely, S-GIMME arrives at individual-level models that are accurate and reliable even when parameters mimic those seen in daily diary studies. Additionally, S-GIMME provides robust results for as few as 60 time points, which is far fewer than the number that has been tested in neuroimaging research. Finally, S-GIMME performs well even with a relatively low number of participants. Ultimately, our demonstration underscores the need for methods such as S-GIMME moving forward given the increasing use of intensive longitudinal data in psychological research, and the potential for these data to provide novel insights into human behavior and mental health.