Abstract.
We propose to characterize the bias and variability of quantitative morphology features of lung lesions across a range of computed tomography (CT) imaging conditions. A total of 15 lung lesions were simulated (five in each of three spiculation classes: low, medium, and high). For each lesion, a series of simulated CT images representing different imaging conditions were synthesized by applying three-dimensional blur and adding correlated noise based on the measured noise and resolution properties of five commercial multislice CT systems, representing three dose levels ( of 1.90, 3.75, 7.50 mGy), three slice thicknesses (0.625, 1.25, 2.5 mm), and 33 clinical reconstruction kernels from five clinical scanners. The images were segmented using three segmentation algorithms and each algorithm was evaluated by computing a Sørensen–Dice coefficient between the ground truth and the segmentation. A series of 21 shape-based morphology features were extracted from both “ground truth” (i.e., preblur without noise) and “image rendered” lesions (i.e., postblur and with noise). For each morphology feature, the bias was quantified by comparing the percentage relative error in the morphology metric between the imaged lesions and the ground-truth lesions. The variability was characterized by calculating the average coefficient of variation averaged across repeats and imaging conditions. The active contour segmentation had the highest average Dice coefficient of 0.80 followed by 0.63 for threshold, and 0.39 for fuzzy c-means. The bias of the features was segmentation algorithm and feature-dependent, with sharper kernels being less biased and smoother kernels being more biased in general. The feature variability from simulated images ranged from 0.30% to 10% for repeats of the same condition and from 0.74% to 25.3% for different lesions in the same spiculation class. In conclusion, the bias of morphology features is dependent on the acquisition protocol in combination with the segmentation algorithm used and the variability is primarily dependent on the segmentation algorithm.
Keywords: morphology, lung lesions, quantitative imaging, computed tomography, imaging conditions
1. Introduction
Computed tomography (CT) scanners were initially designed for anatomical imaging purposes. However, due to their relatively high ability to render spatial details, CT images have increasingly been used to extract quantitative data with the aim of more accurately and precisely diagnosing disease and assessing treatment response.1–3 For example, quantitative morphological features describing a lesion’s size, shape, radiodensity, and heterogeneity have been proposed as radiomics-based biomarkers that could, in theory, be used in conjunction with machine learning tools to help better identify a patient’s disease state and predict outcomes.4
Although many radiomics studies have demonstrated significant utility in oncologic quantification, including some in lung cancer,5–7 the application of data-driven techniques has been limited by a lack of scientific knowledge about repeatability of feature measurements within a given imaging condition (i.e., protocol) and by the variability of feature measurements across imaging conditions. CT scanners have many “knobs” that can be turned to change the imaging acquisition, including reconstruction method—iterative versus filtered backprojection (FBP), the reconstruction kernel, the slice thickness, and the dose level.8 These knobs can affect the resolution and noise properties of an image in several ways. For example, using sharp reconstruction kernels improve edge representation but amplify image noise, and increasing the slice thickness lowers image noise for a given dose but degrades -dimensional resolution, obscuring subtle features of lung lesions.8 Further, due to the scheduling limitations in a clinical workflow, patients are rarely imaged on the same scanner and their images are not always reconstructed using the same method. In longitudinal imaging studies, this lack of consistent protocol makes it difficult to know if a change in a measured radiomics feature is truly representative of the physical state of the patient, or if the apparent feature change is induced by a change in the imaging condition. If specific radiomics features are identified as biomarkers of lung cancer that should be utilized in the clinic, then it will be necessary to characterize how they change with different CT imaging protocols.
Several studies have previously brought attention to the need to characterize the impact of the imaging system on the measurement of radiomics features. Aerts et al.7 used the publicly available RIDER database to test the repeatability of radiomics feature measurement within a given imaging protocol and used feature measurement repeatability as a criterion for feature selection in models relating radiomics features to patient outcomes. Zhao et al.9 used the same patient dataset and reconstructed the images using three slice thicknesses and two reconstruction kernels to show how the radiomics features varied across these imaging settings. These studies highlight the importance of assessing the variability of features within a given protocol and across several reconstruction parameters. However, patients can change over time and it is not possible to image the same patient multiple times on multiple scanners. This can be remedied with the use of phantoms. Mackin et al.10 highlighted the need to use a physical textured model to assess the variability of radiomics features, both within a given scanning condition and between different CT scanner manufacturers. They also demonstrated the utility of physical phantoms, which can be scanned many times repeatedly without concern for dose. Shafiq‐ul‐Hassan et al.11 further characterized variability by studying the effect of voxel size and number of gray levels using a similar physical textured model that can be imaged many times.
The studies by Mackin et al.10 and Shafiq‐ul‐Hassan et al.11 focused on features reflective of internal heterogeneities. Chen et al.12 used a physical phantom to ascertain the influence of tens of CT protocols of varying reconstruction and slice thickness on the quantification of lung nodules. The study by Chen et al. focused primarily on volume, however, there is a need to characterize other morphologic features. To our knowledge, no study to date has specifically examined the bias and variability of a large cohort of morphological (size- and shape-related) radiomics features across a wide range of protocols and CT scanner manufactures. The purpose of this study was to explicitly address this gap. The study was performed using a simulation of CT resolution and noise properties and computational models of lung lesions. Given the extensive number of protocols tested (297), the study used a simulation platform. The computational lung lesion models were “imaged” across the protocols and then each segmented and quantified. Multiple segmentation algorithms were used for assessing the effects of the imaging system on an array of morphological features in the context of multiple segmentation algorithms.
2. Materials and Methods
2.1. Computational Lesion Models
Fifteen ground-truth computational lung lesion models were developed for their use in creating simulated images.13 Lung lesion models were simulated in a uniform background for three distinct classes of lung lesions, with low, medium, and high spiculation, five lesions per class. The low spiculation lesions were created using a prior method to simulate realistic lung lesions,14 10 mm in nominal diameter and 400 in Hounsfield unit (HU). This low spiculation class was used as the basis to create the two additional classes of lesions with increasing spiculation levels following Sisternes et al.15 (Fig. 1). The lesions were voxelized to 0.25-mm isotropic resolution.
Fig. 1.
Example of low, medium, and high spiculation lesions.
2.2. Computed Tomography Imaging Protocols
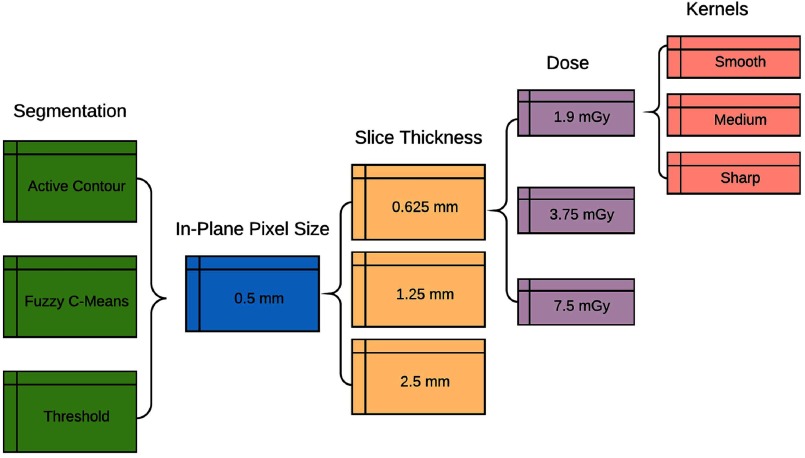
Imaging conditions were simulated for 3 dose levels ( of 1.90, 3.75, and 7.50 mGy), 3 slice thicknesses (0.625, 1.25, and 2.5 mm), and 33 reconstruction kernels from a combination of FBP and iterative kernels from 5 clinical CT scanners (Siemens Somatom Flash, Siemens Somatom Force, GE Lightspeed VCT, GE Discovery 750 HD, and GE Revolution). The reconstruction kernels (Table 1) were chosen to represent the diversity of possible clinical reconstructions, ranging from soft to sharp, including common kernels used for chest imaging. The dose level of 7.5 mGy was chosen to represent a typical standard chest imaging protocol at our institution and the dose levels of 1.9 and 3.75 mGy were chosen as 25% and 50% of that value, respectively.
Table 1.
The five scanners and associated reconstruction method and kernels are shown.
| Scanner | Reconstruction | Kernel |
|---|---|---|
| Discovery 750 HD | ASiR-50% | Soft, standard, lung, bone |
| FBP | Soft, standard, bone | |
| Lightspeed VCT | ASiR-50% | Soft, standard, bone |
| FBP | Soft, standard, bone | |
| Revolution | ASiR-V-50% | Soft, standard, bone |
| FBP | Soft, standard, bone | |
| Somatom definition flash | SAFIRE-1 | I26f, I31f, I50f |
| SAFIRE-3 | I70f | |
| FBP | B20f, B31f, B50f | |
| Somatom force | ADMIRE-1 | Br36d, Br40d, Br59d, Br64d |
| FBP | Br36d, Br40d, Br59d |
2.3. Computed Tomography Image Simulation
CT images corresponding to a small region of interest around the lesion were simulated for this study by degrading the idealized lesion images with correlated noise and blur, according to the noise and resolution properties of each imaging condition. The correlated noise was generated based on an empirically measured noise power spectrum (NPS) specific to each imaging condition and the resolution properties were simulated based on the empirically measured task-transfer functions (TTFs) (nonlinear analog to the modulation transfer function).16 For each imaging condition, the NPS and TTFs were measured from the images of the ACR phantom using a method described by Solomon et al.17 The TTFs used in this study were measured from the phantom’s bone insert.
The empirical TTF curves, which included those from a combination of edge-enhancing and nonedge-enhancing reconstruction kernels, were fit to a theoretical mathematical function to reduce the effects of the measurement uncertainty. The nonedge-enhancing TTF curves were fit using a theoretical model, as described by Ott et al.:18
| (1) |
where is the spatial frequency and is a parameter that describes the steepness of the TTF. The in-plane edge-enhancing curves () were modeled using the same non-edge-enhancing model as Eq. (1) except shifted by the location of the edge enhancement peak, , and normalized by a factor so that at zero frequency:
| (2) |
The -dimension TTF was approximated using a theoretical model, as described by Boyce et al.:19
| (3) |
where is the magnification, is the full width at half maximum (FWHM) of the focal spot, is the spatial frequency, and is the slice thickness. The magnification for the study was assumed to be 1.82, the FWHM of the focal spot was assumed to be 0.5 mm, and the slice thickness was changed depending on the specific imaging protocol.
The measured NPS curves were likewise fit to a theoretical function to reduce the effects of the measurement uncertainty. The functional form used can be given as
| (4) |
where describes the maximum height of the NPS, and and describe the ramp up and fall of the NPS curve. The simulations were based on an axial imaging acquisition, and so the z-dimensional noise correlation was assumed negligible.
After acquiring functional forms of the NPS and TTF, the voxelized lesion images were blurred by filtering the images (in the Fourier domain) with the TTF. Correlated noise was synthesized by first generating a zero-mean white Gaussian noise image using a pseudorandom number generator. This noise image was then filtered by the square root of the NPS to achieve the desired correlations and scaled to achieve the targeted pixel standard deviation (i.e., noise magnitude) according to each imaging condition. The noise image was then added to the blurred lesion images to achieve the final degraded image. The noise magnitude for each dose level was determined using
| (5) |
where is the standard deviation of the noise, is the slice thickness (mm), and are the parameters calculated for a given scanning condition, and Dose () is the dose in terms of CTDI in milligray. The and parameters had been previously characterized for each of the 33 reconstruction kernels at a slice thickness of 5 mm, which is why the factor was needed in the equation.
In total, 297 unique protocols were tested and were each repeated five times for a total of 1485 images per lesion. The repeated images were generated by repeating the random noise generation process. Figure 2 shows some examples of the process and how the same lesion can be altered by the noise and resolution properties of the CT system.
Fig. 2.
Example slices from simulated FBP images of a medium spiculation lesion with a dose of 7.5 mGy and a slice thickness of 1.25 mm. The top row shows different kernels of the GE LightSpeed scanner including (a) soft, (b) standard, and (c) bone. The bottom row shows different kernels of the Siemens Flash scanner including from (d) B20f, (e) B31f, and (f) B50f.
2.4. Segmentation Algorithms
After the images were simulated, it was necessary to segment the lesions from the background. As there were a total of 22,275 images that needed to be segmented, it was necessary to use an automated segmentation method. However, each segmentation algorithm performs differently depending on the nature of the segmentation task (e.g., lesion contrast, image noise, and anatomical complexity) and the intrinsic characteristics of the segmentation method.20 Therefore, the effects of the imaging system and the effects of the segmentation algorithm cannot be fully decoupled. To account for possible segmentation-induced bias, three different segmentation algorithms were used for determining the bias and variability of radiomics morphology features as a function of the segmentation algorithm.
The three segmentations used for this study were active contour (MATLAB 2017b), fuzzy c-means (MATLAB 2017b), and thresholding. The active contour algorithm was a built-in MATLAB function based on Whitaker.21 The active contour algorithm required a starting seed, which for this study was chosen to be all pixels of the maximum contrast of the lesion in the central slice of the lesion. The fuzzy c-means algorithm (FastCMeans, Anton Semechko, MATLAB) worked by using c-means clustering of the data. For this study, the algorithm was performed to find two clusters, lesion and background. The thresholding segmentation was created in MATLAB by first applying a threshold of 20% of the maximum contrast of the lesion to exclude all pixels less than the threshold from the lesion. Second, the lesion segmentation was processed by removing all pixels not connected to the central core of the lesion and filling in any holes in the central core segmentation. Each segmentation was evaluated for each imaging condition by calculating a Dice coefficient between the segmented lesion and the ground-truth lesion.
2.5. Morphology Feature Definitions
Zwanenburg et al.22 were used as a common morphology feature set based on the work by Aerts et al.7 and Hatt et al.23 Three additional features (discrete compactness, radius, and spiculation) were added from Huang et al.24 A complete list of features with associated definitions has been included in Table 2.
Table 2.
Feature definitions used in this study.
| Feature | Description |
|---|---|
| Volume () | : Fit an isosurface mesh to the binarized lesion segmentation mask (lesion = 1, background = 0), with 0.5 as the threshold for the isosurface function, and calculate the volume from the mesh |
| Approximate volume ()) | : Added up all the voxels in the segmentation mask multiplied by the voxel volume |
| Surface area () | : Fit an isosurface mesh to the binarized lesion segmentation mask (lesion = 1, background = 0), with 0.5 as the threshold for the isosurface function, and calculate the surface area from the mesh |
| Surface area-to-volume ratio | |
| Compactness 1 () | |
| Compactness 2 () | |
| Spherical disproportion () | |
| Sphericity () | |
| Asphericity () | |
| Radius () | , where is the number of boundary voxels and are the indices of boundary voxels and and are the center of mass coordinates of the lesion |
| Spiculation () | , where is the radius at each boundary point |
| Discrete compactness () | , where is the number of voxels in the tumor, is the total surface area of external facing voxels, and is the area of a single voxel face |
| Major () | , where is the largest eigenvalue of the region-based 3-D ellipsoid fitting |
| Minor () | , where is the second-largest eigenvalue of the region-based 3-D ellipsoid fitting |
| Least () | , where is the smallest eigenvalue of the region-based 3-D ellipsoid fitting |
| Elongation () | |
| Flatness () | |
| Ellipsoid surface area () | , where , , , |
| Ellipsoid volume () | , where , , |
| Surface area-to-ellipsoid surface area ratio () | |
| Volume-to-ellipsoid volume ratio () |
2.6. Bias Analysis
The morphology features were calculated for both the ground-truth lesions () and the image-simulated lesions () for each ’th lesion model and ’th spiculation level. The image-simulated feature measurements were denoted by for each ’th lesion model, ’th spiculation level, ’th reconstruction algorithm, ’th dose level, ’th slice thickness, ’th repeat (number of times the imaging condition was repeated), and ’th segmentation algorithm.
To characterize the bias, the percent relative bias in each morphology feature was calculated between the imaged lesions and the ground-truth lesions as
| (6) |
The bias was averaged within each protocol, by averaging over repeats and lesions within a spiculation category , to give an average percent relative bias . Given that is an average value, an associated variability related to the data points that went into the average bias was also reported as
| (7) |
The and results were then structured into heatmaps for each morphology feature (-axis) and each imaging protocol (-axis). Each segmentation algorithm and each spiculation level was put into a separate heatmap. Within each heatmap, the data were arranged in order by increasing slice thickness, followed by increasing dose, and last by increasing kernel sharpness. The overall organization of the protocol data has been shown in Fig. 3. The data were analyzed quantitatively by comparing the absolute value of the percent relative bias of sharp reconstruction kernels compared with medium and smooth reconstruction kernels.
Fig. 3.
The flow chart describes the organization of the simulated feature data into heatmap tables. Each segmentation is separated into a separate set of heatmaps. For the 0.5 mm in-plane pixel size, the data are organized first by increasing slice thickness, next by increasing dose, and finally by increasing kernel sharpness.
2.7. Variability Analysis
The feature variability of the lesions was studied at three different levels: (i) the variability of the ground-truth features for each spiculation class, (ii) the variability of features measured from simulated images and averaged across all protocols for each spiculation class, and (iii) the variability of the measured features due to repeats of the same imaging condition for a specific lesion averaged across all lesions and protocols for each spiculation class. The variability was calculated as a coefficient of variation for each level of variability studied. The coefficient of variation for the ground-truth features () was calculated as
| (8) |
where the mean and standard deviation are calculated across all lesions models () within a given spiculation level (). The average intraprotocol coefficient of variation for the image-simulated features () was calculated as
| (9) |
where the inner mean and standard deviation are calculated across all lesion models () and repeats (), and the outer mean is calculated across all reconstruction algorithms (), dose levels (), and slice thicknesses (). The coefficient of variation due to repeats of the same imaging condition () was calculated as
| (10) |
where the inner mean and standard deviation are calculated across all repeats (), and the outer mean is calculated across all lesion models (), reconstruction algorithms (), dose levels (), and slice thicknesses (). The results of the three variability levels have been presented in bar graphs with a bar for each spiculation level () and for each feature.
2.8. Comparison with Commercial Segmentation
A subset of the bias and variability results generated from the automatic segmentation methods were compared with a semiautomatic commercial segmentation tool (Siemens Radiomics Prototype) designed for lesion segmentation. The commercial segmentation tool required a user to place a seed point by clicking a point in the lesion and then used the seed point to perform a segmentation of the lesion. The commercial segmentation was not studied for every imaging condition previously tested with the automatic segmentations due to the time and logistical constraints of having a user interact with the software to place the seed point 22,275 times. However, a representative subset of the data was compared in a smaller scale study to determine how the active contour automatic segmentation used previously compares with the commercial software.
The subset of the data chosen for the comparison study is highlighted in Table 3. The study was structured to focus on a single medium spiculation lesion model and a single low spiculation model. The imaging conditions were chosen such that all imaging acquisition and reconstruction parameters were held constant at average values while a single acquisition or reconstruction parameter was changed. In the case of the medium spiculation lesion, all imaging conditions were held constant except for the reconstruction kernel, which was studied for three different kernels ranging from smooth (B20f) to sharp (B50f). Similarly, in the case of the low spiculation lesion, all imaging conditions were held constant except the slice thickness, which was studied for three different values ranging from 0.625 to 2.5 mm.
Table 3.
A subset of the lesion and imaging condition combinations are chosen for a comparison study between the automatic segmentation method and a commercial semiautomatic segmentation tool.
| Low spiculation lesion | Medium spiculation lesion | |
|---|---|---|
| Number of lesion models | 1 | 1 |
| Slice thicknesses (mm) | 0.625, 1.25, 2.5 | 1.25 |
| Scanner models | Siemens Flash | Siemens Flash |
| Reconstruction method | FBP | FBP |
| Reconstruction kernels | B31f | B20f, B31f, B50f |
| (mGy) | 3.75 | 3.75 |
| Number of noise repeats | 5 | 5 |
The commercial segmentation tool required that the data be formatted in the DICOM file format of commercial CT images; however, the simulated image data for the study were not formatted as a DICOM. The previously simulated data were converted to DICOM format by using the DICOM header from a real CT dataset and by modifying the relevant DICOM tags to match the desired scan protocol for each simulated imaging condition. The simulated images, which were created to contain the lesions and a small region of interest around the lesion, were placed in the middle of a CT image dataset with each lesion repeat placed consecutively next to each other (Fig. 4 shows a slice from one example CT). In total, six CT datasets were created with five different lesions placed in each dataset leading to 30 semiautomatic segmentations, which were performed by the commercial software. The segmentations were exported from the commercial software as an STL file, which was loaded into MATLAB and converted to a three-dimensional (3-D) voxelized dataset. The voxelized dataset was used for calculating the 21 morphology features.
Fig. 4.
Repeated simulated images of one medium spiculation lesion model, which is imaged with a Siemens Flash scanner model using FBP reconstruction, B31f reconstruction kernel, 1.25-mm slice thickness, and 3.75 mGy .
The morphology features were compared with the ground truth by calculating an average bias . The morphology features were also used for calculating a coefficient of variation due to repeats . The bias and variability were compared between the active contour segmentation method and the commercial segmentation method by calculating the median value of the variability and of the median absolute value of the bias across all features and imaging conditions tested. The median value was chosen as the comparison metric because it is less sensitive to outlying variability and bias values for specific features and imaging conditions. The results were further analyzed by comparing the magnitude and trends of the average bias and the variability due to repeats for different features for different combinations of lesion spiculation class, morphology feature, and imaging condition.
3. Results
3.1. Feature Assessment
Table 4 shows the ground truth () for 21 morphology features across the 15 lesions that were used in this simulation study. Of the 21 morphology feature studies, most showed a trend of increasing feature value with increasing spiculation level, whereas 5 studies showed a trend of decreasing feature value with increasing spiculation level. Those included discrete compactness, sphericity, compactness 1, compactness 2, and volume-to-ellipsoid volume ratio. As a reminder, these ground-truth feature measurements () were used for calculating the percent relative bias of image-simulated lesions.
Table 4.
Ground-truth lesion morphology features for 15 lesions with three categories of low, medium, and high spiculations. The ground-truth feature values are displayed for each category as mean ± standard deviation. The values in this table are used for calculating the percent relative bias.
| Low spiculation | Medium spiculation | High spiculation | |
|---|---|---|---|
| Radius | |||
| Spiculation | |||
| Discrete compactness | |||
| Volume | |||
| Approximate volume | |||
| Surface area | |||
| Surface area-to-volume ratio | |||
| Sphericity | |||
| Spherical disproportion | |||
| Asphericity | |||
| Compactness1 | |||
| Compactness2 | |||
| MajorLength | |||
| MinorLength | |||
| LeastLength | |||
| Elongation | |||
| Flatness | |||
| Ellipsoid surface area | |||
| Ellipsoid volume | |||
| Surface area-to-ellipsoid surface area ratio | |||
| Volume-to-ellipsoid volume ratio |
3.2. Sørensen–Dice Coefficient Assessment
The Dice coefficient results exhibit the combined effects of both segmentation algorithm performance and imaging system degradation. Figure 5(a) shows a box and whisker plot for the Dice coefficients of each segmentation algorithm across all 22,275 data points for each segmentation algorithm and Fig. 5(b) shows how the same Dice coefficients change as a function of increasing image noise. Out of a maximum possibility of unity, the average Dice coefficient across all imaging conditions is 0.80 for active contour, 0.63 for thresholding, and 0.39 for fuzzy c-means. Of the three algorithms, the active contour algorithm performs best in discerning between the lesion and its background, and it is the least susceptible to image noise. The thresholding segmentation algorithm performs well when image noise is ; however, consistently, it did not perform well with noise . The fuzzy c-means algorithm has the lowest average Dice coefficient and has low performance on images with high noise and is unable to perform well on some images with noise .
Fig. 5.
(a) The mean and interquartile range of the Dice coefficient of simulated images and three segmentation algorithms (active contour, threshold, and fuzzy c-means). (b) The Dice coefficient of simulated images changes as a function of image noise (HU) depending on which segmentation algorithm is used.
3.3. Bias Assessment
The results demonstrate varied bias across features and protocols, with image noise, affected by the dose level and slice thickness, exhibiting segmentation dependence. Among all results from all segmentation algorithms tested, the morphology features’ discrete compactness, elongation, and flatness are consistently the least biased features. This could mean that these features are robust, or it could mean that they are not sensitive to changes in morphology. To ascertain the bias in detail, the best-performing segmentation algorithm, active contour, is studied in more detail to understand the percent relative bias relationship with imaging protocol. Figure 6 shows the average percent relative bias () for active contour. Figures 6(a)–6(c) shows spiculation low, medium, and high, respectively. The imaging protocols are arranged on the -axis of Fig. 6 first by increasing slice thickness, then by increasing dose, and last by increasing kernel sharpness. The morphology features are arranged on the -axis based on how the feature is calculated.
Fig. 6.
The average percent relative bias () for active contour and for low spiculation (a), medium spiculation (b), and high spiculation (c), for 297 common CT imaging protocols, including 33 reconstruction kernels from five clinical CT scanners including both iterative and FBP kernels ranging from smooth to sharp, three slice thicknesses (0.625, 1.25, and 2.5 mm), and three dose values (1.9, 3.75, and 7.5 mGy ). The low spiculation results (a) show that sharper kernels at 7.5 mGy and 0.625 mm slice thickness have the lowest bias with an average absolute value of bias with a value of . The medium (b) and high (c) spiculation results show the main trend that sharper reconstruction kernels are less biased with an average absolute value of compared with , and an average absolute value of of compared with .
The low spiculation active contour results [Fig. 6(a)] showed that sharper kernels at 7.5 mGy and 0.625 mm slice thickness had the lowest bias, which was , when the absolute value of the relative bias was averaged across all features. The low spiculation results [Fig. 6(a)] also showed a general trend that the bias increased with increasing slice thickness. It could be that the increasing slice thickness led to partial volume effects that caused the features to become more biased with increasing slice thickness. However, it could also be the case that the larger slice thickness, and therefore lower image noise, yielded the bias that would result mainly from the image blur. Alternatively, the smaller slice thicknesses yielded less bias because the segmentation included more image noise, artificially exhibiting less bias. The low spiculation results [Fig. 6(a)] also showed that the bias of most features was positive (magenta), which means that the imaging system led to an overestimation of the feature values.
The medium and high spiculation results [Figs. 6(b) and 6(c)] for the active contour segmentation showed the main trend that sharper reconstruction kernels were less biased with an average absolute value of compared with and an average absolute value of compared with . Interestingly, some features that tended to be positively biased (pink) for low spiculation [Fig. 6(a)] tended to be negatively biased for both medium and high spiculations [Figs. 6(b) and 6(c)] and vice versa for features that tended to be negatively biased (blue) for low spiculations.
The variability associated with the bias () is shown in Fig. 7. The low spiculation results [Fig. 7(a)] showed that asphericity had the highest variability with an average value of 35.4%. The medium [Fig. 7(b)] and high [Fig. 7(c)] spiculation results showed that the features in the middle, which are features derived from ratios of volume and surface area, had the highest variability, with compactness 2 being the most variable with an average value of 108.4% for medium spiculation and an average value of 70.6% for high spiculation.
Fig. 7.
The variability of bias () for active contour and for (a) low spiculation, (b) medium spiculation, and (c) high spiculation, for 297 common CT imaging protocols, including 33 reconstruction kernels from five clinical CT scanners including both iterative and FBP kernels ranging from smooth to sharp, three slice thicknesses (0.625, 1.25, and 2.5 mm), and three dose values (1.9, 3.75, and 7.5 mGy ). The low spiculation results (a) show that asphericity had the highest variability with an average value of 35.4%. The medium (b) and high (c) spiculation results show features in the middle have the highest variability, with compactness 2 being the most variable with an average value of 108.4% for medium spiculation and an average value of 70.6% for high spiculation.
3.4. Variability Assessment
The three levels of variability showed that, in general, the ground-truth variability was either similar or higher than the intra-protocol variability (Fig. 8). The ground-truth variability was found to be higher than the intraprotocol variability for features where the ground-truth variability was relatively high compared to other features. The repeat variability was the smallest variability in most cases with a minimum value of 0.30% and a maximum value of 10% (Fig. 8). The intra-protocol variability had a minimum value of 0.74% and a maximum value of 25.3% (Fig. 8). The magnitude of the variability was relatively consistent across spiculation levels except for the ground-truth variability of compactness 2 for the medium spiculation lesions, which was the highest variability with a value of 64%.
Fig. 8.
The coefficient of variation (%) for repeat variability (gray), intraprotocol variability (blue striped), and ground-truth variability (black) for active contour and for low spiculation (a), medium spiculation (b), and high spiculation (c). In all cases, the repeat variability (gray) is the smallest value of the three variabilities with a maximum value of 10% and a minimum value of 0.30%. The intraprotocol variability and ground-truth variability are usually comparable, although in the cases where the ground-truth variability is comparatively large, the intraprotocol variability is smaller than , particularly for the case of the medium spiculation compactness 2 feature.
3.5. Commercial Segmentation Assessment
The median bias and variability results are summarized in Table 5. Results of the medium spiculation lesion show that the commercial segmentation tool is less variable and is more biased as compared with the active contour segmentation. Results of the low spiculation tool also show the same trend that the commercial segmentation is less variable and more biased; however, the trend is not as pronounced with the bias and variability median being more similar in magnitude.
Table 5.
The median absolute value of bias (%) and median repeat variability (%) are shown for both the medium and low spiculation lesion classes for two different segmentation algorithms (active contour and commercial).
| Spiculation | Segmentation | Median absolute value of bias (%) | Median repeat variability (%) |
|---|---|---|---|
| Medium | Active contour | 24.9 | 1.4 |
| Commercial | 42.0 | 0.6 | |
| Low | Active contour | 5.7 | 2.2 |
| Commercial | 9.4 | 1.6 |
The coefficient of variation was studied in more detail across the different imaging conditions for specific lesion models and morphology features. For the low spiculation lesion model [Figs. 9(a) and 9(b)], the coefficient of variation had similar magnitude between active contour and the commercial tool; however, the specific magnitudes varied depending on the combination of slice thickness and segmentation. For example, the 0.625-mm slice thickness images led to a higher coefficient of variation for active contour and a lower coefficient of variation for the commercial tool. The low spiculation lesions also showed differences in variability magnitude, depending on the combination of specific feature and segmentation. For example, the active contour led to a more variable estimation of asphericity, compactness 1, and compactness 2; however, the commercial segmentation led to a more variable estimation of volume, approximate volume, and ellipsoid volume.
Fig. 9.
The coefficient of variation (%) due to repeated scans is shown for (a) the low spiculation lesion model and the active contour segmentation, (b) the low spiculation lesion model with commercial segmentation, (c) the medium spiculation lesion model and the active contour segmentation, and (d) the medium spiculation lesion model and the commercial segmentation. Note that the scales of (a) and (b) are the same allowing for comparison between the two graphs, while the scale of (c) and (d) are intentionally different to highlight the similar trends in rank ordering of features from most to least variable.
For medium spiculation lesion model [Figs. 9(c) and 9(d)], the magnitude of the variability was different between the active contour and the commercial tool, with the active contour having a higher variability overall as compared with the commercial tool. However, it was interesting to see that if the magnitude was disregarded, the rank ordering of the features from most to least variable was similar for both segmentation algorithms. In addition, the trends in variability as a function of kernel sharpness were also similar in terms of rank ordering of variability from most to least variable for specific features.
The average bias was also studied in more detail across the different imaging conditions for the two specific lesion models. For both the low and the medium spiculation models, the active contour segmentation tended to lead to an overestimation of the morphology features (positive bias), whereas the commercial segmentation tended to lead to an underestimation of the morphology features (negative bias). For the low spiculation lesion model [Figs. 10(a) and 10(b)], the bias was similar to the variability in that it also strongly depended on the combination of segmentation algorithm and slice thickness used. For the 0.625-mm slice thickness, the active contour segmentation had a smaller bias compared with the commercial segmentation. However, for the 2.5-mm slice thickness, the active contour had a greater bias compared with the commercial segmentation. The medium spiculation lesion bias analysis [Figs. 10(c) and 10(d)] showed an interesting relationship between segmentation algorithm and kernel sharpness. For example, the commercial segmentation tool did not show much difference between different kernel sharpness; however, the active contour segmentation tool showed that for most features the sharpest kernel was more biased. The medium spiculation lesion also showed the overall trend that the commercial segmentation bias was greater than the active contour bias.
Fig. 10.
(a) The average bias (%) across repeat scans is shown for (a) the low spiculation lesion model and the active contour segmentation, (b) the low spiculation lesion model with commercial segmentation, (c) the medium spiculation lesion model and the active contour segmentation, and (d) the medium spiculation lesion model and the commercial segmentation. Note that in (a) the asphericity feature for the B50f kernel has an average bias of 266%; however, the result shown here is truncated to better see the bias trends for the remaining 20 features. Also note that in (d) the compactness 2 feature had an average bias of 1038% across all three kernels; however, the result shown here is truncated to better see the bias trends for the remaining 20 features.
4. Discussion
This study quantified the intra-protocol percent relative bias and coefficient of variation for 297 imaging protocols and 21 morphology features using computational models of lung lesions and a simulation of CT image resolution and noise properties. This study included 3 dose levels, 3 slice thicknesses, and 33 kernels from 5 clinical CT scanners. In analyzing the results, 4 segmentation algorithms were used for quantifying the interplay between imaging protocol properties and segmentation algorithm performance. The results showed that the percent relative bias has a complex relationship with imaging protocols that is influenced by the underlying morphology used for the quantification and the segmentation algorithm used for analysis.
The results of this study highlight that there is a differential in morphology feature measurements between different CT imaging protocols, which should be factored in when comparing morphology feature measurements extracted from inconsistently acquired retrospective data. The results of this study can be used prospectively to determine which protocols and segmentation algorithms would be most effective for quantitative feature extraction and radiomics studies. The results of this study could potentially also be used retrospectively to inform a model that translates radiomics feature values between imaging protocols so that images acquired with different protocols can be compared with each other on the same scale.
The active contour volume bias results for the low spiculation lesions compare well with previous work,12,25 which show for physical phantoms scanned with a clinical CT scanner that lesion volume was significantly more biased for slice thickness of 2.5 mm compared with 1.25 and 0.625 mm slice thickness. Although the results compared well for low spiculation lesions, the trend did not hold for the medium and high spiculation lesions; they show no noticeable changes in bias with increased slice thickness, but rather showed increased bias for less sharp kernels. These low and medium spiculation results highlight the need to account for morphological complexity in feature measurements. The similarity of trends in bias for low spiculation lesions between two different segmentation algorithms and between a clinical CT system and a CT image simulation platform validates the methods used in this study. Further, the absolute value of the low spiculation volume bias has a magnitude similar to that of a previous physical phantom study,12 with an average absolute value of volume bias of for the low spiculation lesions in this study and bias ranging from 3.5% to 10% for one segmentation algorithm with similar sized lesions in the previous work.12,25 This comparison suggests limited generalizability of our results for low spiculation lesions. The active contour bias results show an interesting trend where for low spiculation lesions, the CT system introduces positive bias that leads to an overestimation of most size-based morphology features. However, the medium and high spiculation lesions show the opposite results where size-based morphology features tend to be underestimated. This phenomenon could possibly be a result of the interplay between the system blur of the object and the segmentation performance on the complicated morphology at the boundary of the lesion. For example, the low spiculation lesions are likely to be mainly affected by the system blur and the morphology is likely to not be difficult to segment. Because the blur leads to a spreading out of the ground-truth lesion, these lesions are likely to be overestimated in size. However, the medium and high spiculation lesions have complicated edge morphology, which when combined with image blur and noise, might be much more challenging for the segmentation algorithm to segment correctly. The segmentation algorithm might assume that the complicated spiculation distorted by blur and noise is more likely to be a part of the background noise, and therefore the segmentation algorithm might not include complicated spiculations leading to an underestimation of the lesion size.
This study purposefully chose to highlight the effects of different segmentation algorithms to underscore the importance of characterizing the bias and variability for each specific segmentation algorithm. It is important to note that to make the large number of protocols studied possible, the segmentation algorithms used are automatic segmentations, which are not developed exclusively for clinical use. Although these segmentation tools are not optimized specifically for lesion segmentation, the segmentations rely on segmentation techniques, which are commonly incorporated in aspects of clinical lesion segmentation software. The comparison between the active contour and a commercial segmentation tool (specifically designed for lesion segmentation) reveals that, in general, the commercial system is less variable and more biased. However, the specific trends of bias and variability continue to depend on the specific features of interest, imaging conditions, and underlying lesion spiculation category. Therefore, given the complicated interplay of imaging conditions, lesion spiculation and segmentation algorithm, it is not possible to say which of the two segmentation algorithms would be better for segmenting lesions overall. The most important aspect of using multiple algorithms is to demonstrate the influence of the different algorithm on the results. The results of the study indeed highlight that segmentation methods can greatly influence the bias and variability of these features and therefore it would be important to characterize bias and variability for any segmentation algorithm that is used for extracting radiomics morphology features.
The results of this study are limited in a few ways. Although the lesions used in this study had reasonable anatomical complexity as validated by observer studies in hybrid datasets,14 the morphological spiculation model can be further improved. In addition, it is possible in future studies to test a vastly larger number of different lesions with varying morphology, size, contrast, and other features. Second, the pre-blurred, pre-noised lesion models are given distinct borders for clearly identifying the ground truth, but in real patients, the lesion truth may be more ambiguous. This is an issue that requires input from the science of tumor progression and microbiology. Third, the simulations are done with a single constant background rather than an anatomically complex background like lungs. Future studies should include a textured anatomical lung background to ensure that the segmentation results are relevant to textured backgrounds. Fourth, results of this study are generated using a CT image simulation platform, which is somewhat oversimplified compared to an actual clinical CT system. Despite these limitations, we believe that the results are informative as they describe the lower limit on the bias and variability across a wide range of CT protocols, not practically approachable experimentally, and serve as a strong basis for further study.
5. Conclusion
This study quantified bias and variability for a subset of morphological radiomics features under a wide range of possible clinical CT imaging protocols. The results demonstrated that the feature bias has a nuanced relationship between imaging protocol factors and segmentation algorithm. The methods of this study can be applied prospectively to inform the best practices for deciding imaging protocols for quantitative imaging and can be used retrospectively to develop a model that corrects morphology feature measurements while accounting for the imaging protocol used to image the patient.
Biography
Biographies of the authors are not available.
Disclosures
Jocelyn Hoye, Justin Solomon, Thomas J. Sauer, and Marthony Robins have no conflicts of interest and nothing to disclose. Ehsan Samei lists relationships with the following entities unrelated to the present publication: GE, Siemens, Bracco, Imalogix, 12Sigma, Sun Nuclear, and Metis Health Analytics.
References
- 1.Lambin P., et al. , “Radiomics: extracting more information from medical images using advanced feature analysis,” Eur. J. Cancer 48, 441–446 (2012). 10.1016/j.ejca.2011.11.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gillies R. J., Kinahan P. E., Hricak H., “Radiomics: images are more than pictures, they are data,” Radiology 278, 563–577 (2016). 10.1148/radiol.2015151169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Clarke L. P., et al. , “Quantitative imaging for evaluation of response to cancer therapy,” Transl. Oncol. 2, 195–197 (2009). 10.1593/tlo.09217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kumar V., et al. , “Radiomics: the process and the challenges,” Magn. Reson. Imaging 30, 1234–1248 (2012). 10.1016/j.mri.2012.06.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cunliffe A., et al. , “Lung texture in serial thoracic computed tomography scans: correlation of radiomics-based features with radiation therapy dose and radiation pneumonitis development,” Int. J. Radiat. Oncol. Biol. Phys. 91, 1048–1056 (2015). 10.1016/j.ijrobp.2014.11.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Coroller T. P., et al. , “CT-based radiomic signature predicts distant metastasis in lung adenocarcinoma,” Radiother. Oncol. 114, 345–350 (2015). 10.1016/j.radonc.2015.02.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Aerts H. J., et al. , “Decoding tumour phenotype by noninvasive imaging using a quantitative radiomics approach,” Nat. Commun. 5, 4006 (2014). 10.1038/ncomms5006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bushberg J. T., Boone J. M., The Essential Physics of Medical Imaging, Lippincott Williams & Wilkins, Philadelphia: (2011). [Google Scholar]
- 9.Zhao B., et al. , “Reproducibility of radiomics for deciphering tumor phenotype with imaging,” Sci. Rep. 6, 23428 (2016). 10.1038/srep23428 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mackin D., et al. , “Measuring CT scanner variability of radiomics features,” Invest. Radiol. 50, 757–765 (2015). 10.1097/RLI.0000000000000180 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shafiq-ul-Hassan M., et al. , “Intrinsic dependencies of CT radiomic features on voxel size and number of gray levels,” Med. Phys. 44, 1050–1062 (2017). 10.1002/mp.12123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chen B., et al. , “Volumetric quantification of lung nodules in CT with iterative reconstruction (ASiR and MBIR),” Med. Phys. 40, 111902 (2013). 10.1118/1.4823463 [DOI] [PubMed] [Google Scholar]
- 13.Hoye J., et al. , “Bias and variability in morphology features of lung lesions across CT imaging conditions,” Proc. SPIE 10573, 105731Z (2018). 10.1117/12.2293545 [DOI] [Google Scholar]
- 14.Solomon J., Samei E., “A generic framework to simulate realistic lung, liver and renal pathologies in CT imaging,” Phys. Med. Biol. 59, 6637–6657 (2014). 10.1088/0031-9155/59/21/6637 [DOI] [PubMed] [Google Scholar]
- 15.Sisternes L., et al. , “A computational model to generate simulated three‐dimensional breast masses,” Med. Phys. 42, 1098–1118 (2015). 10.1118/1.4905232 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Richard S., et al. , “Towards task‐based assessment of CT performance: system and object MTF across different reconstruction algorithms,” Med. Phys. 39, 4115–4122 (2012). 10.1118/1.4725171 [DOI] [PubMed] [Google Scholar]
- 17.Solomon J., Wilson J., Samei E., “Characteristic image quality of a third generation dual-source MDCT scanner: noise, resolution, and detectability,” Med. Phys. 42, 4941–4953 (2015). 10.1118/1.4923172 [DOI] [PubMed] [Google Scholar]
- 18.Ott J. G., et al. , “Update on the non-prewhitening model observer in computed tomography for the assessment of the adaptive statistical and model-based iterative reconstruction algorithms,” Phys. Med. Biol. 59, 4047–4064 (2014). 10.1088/0031-9155/59/4/4047 [DOI] [PubMed] [Google Scholar]
- 19.Boyce S. J., Samei E., “Imaging properties of digital magnification radiography,” Med. Phys. 33, 984–996 (2006). 10.1118/1.2174133 [DOI] [PubMed] [Google Scholar]
- 20.Ma Z., Tavares J. M. R., Jorge R. N., “A review on the current segmentation algorithms for medical images,” in Proc. 1st Int. Conf. Imaging Theory and Appl. (IMAGAPP) (2009). [Google Scholar]
- 21.Whitaker R. T., “A level-set approach to 3D reconstruction from range data,” Int. J. Comput. Vision 29, 203–231 (1998). 10.1023/A:1008036829907 [DOI] [Google Scholar]
- 22.Zwanenburg A., et al. , “Image biomarker standardisation initiative,” arXiv:1612.07003 [cs.CV] (2016).
- 23.Hatt M., et al. , “Characterization of PET/CT images using texture analysis: the past, the present… any future?” Eur. J. Nucl. Med. Mol. Imaging 44, 151–165 (2017). 10.1007/s00259-016-3427-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Huang Y.-H., et al. , “Computer-aided diagnosis of mass-like lesion in breast MRI: differential analysis of the 3-D morphology between benign and malignant tumors,” Comput. Methods Prog. Biomed. 112, 508–517 (2013). 10.1016/j.cmpb.2013.08.016 [DOI] [PubMed] [Google Scholar]
- 25.Chen B., et al. , “Quantitative CT: technique dependence of volume estimation on pulmonary nodules,” Phys. Med. Biol. 57, 1335–1348 (2012). 10.1088/0031-9155/57/5/1335 [DOI] [PubMed] [Google Scholar]