IMPLEMENTATION OF ICRP 116 DOSE CONVERSION COEFFICIENTS FOR RECONSTRUCTING ORGAN DOSE IN A RADIATION COMPENSATION PROGRAM

Abstract

Since 2000, National Institute for Occupational Safety and Health (NIOSH) has used dose conversion coefficients published by the International Commission on Radiation Protection in report 74 (ICRP 74) to determine organ dose from external radiation sources. In 2010, the ICRP issued publication 116 using more realistic phantoms than ICRP 74. NIOSH has developed a Monte Carlo method to sample the energy-organ-specific distribution of the ICRP 116 conversion coefficients to determine the organ dose and the associated uncertainty. Using Monte Carlo methods, irradiation geometry factors (IGFs) were developed to convert the measured dosemeter dose on the front of the body to values that are compatible with ICRP 116 organ dose conversion coefficients. Specific IGFs were developed for (1) both neutrons and photon exposures, (2) to male and female workers and (3) for rotational and isotropic exposure geometries. The computed mean organ dose and the associated uncertainty are used in the probability of causation calculation for compensation.

INTRODUCTION

Under the US Energy Employee’s Occupational Illness Compensation Program Act (EEOICPA) of 2000⁽¹⁾, the National Institute for Occupational Safety and Health (NIOSH), part of the Centers for Disease Control and Prevention (CDC), is responsible for reconstructing worker radiation doses that are subsequently used to determine the probability that a worker’s exposure caused a specified cancer. Since 2000, NIOSH has used dose conversion coefficients, published in ICRP 74⁽²⁾, to determine organ dose from external sources of radiation. In 2010, the ICRP issued publication 116⁽³⁾ that used more realistic models than ICRP 74. This publication included separate values for both males and females, and provided conversion coefficients for 14 additional organs. These new conversion coeffi-cients were developed based on extensive Monte Carlo modeling conducted since the publication of ICRP 74 in 1996. This paper discusses the implementation of these new conversion coefficients in the EEOICPA dose reconstruction process, with a focus on how the various components are incorporated into a probabilis-tic sampling methodology. Throughout this paper, the term ‘conversion coefficients’ refer to ICRP-published values. The term factor (conversion factor, irradiation geometry factor (IGF)) refers to computed values developed in this work or referenced in other works.

METHOD

The ICRP 116⁽³⁾ conversion coefficients convert from either photon fluence or photon air kerma (kinetic energy released per unit mass in air) to absorbed organ dose. Measured radiation doses, however, using either film badges or thermoluminescent dosemeters (TLDs), conventionally are reported as H_p(10)—personal dose equivalent at 10 mm in tissue, H*(10)—ambient dose equivalent at 10 mm in tissue, or historically as the Roentgen (R) in air. Further complicating the conversion from measured dose to organ dose is that the ICRP reports the conversion coefficients for mono-energetic photons. However, due to variability in radiation source emissions, shielding and subsequent scatter, the photon energy spectrum in the workplace can vary significantly. In addition, the probability of causation methodology used to evaluate cases under EEOICPA requires that uncertainty in the organ dose be included in the cal-culation. To allow for this, NIOSH has developed a Monte Carlo method to sample the energy-specific distribution of the ICRP 116 organ dose conversion coefficients. The end result of this calculation produces a central estimate of the organ dose along with its associated uncertainty.

Another complicating factor associated with the use of the ICRP 116 conversion coefficients is the choice of irradiation geometry that should be used for a particular exposure scenario. Generally, occupational exposures occur in an anterior–posterior (AP) direction. Some occupations, such as construction trades workers, may receive most of their exposure in a rotational (ROT) geometry, with the external sources being fixed with the worker’s movements creating an ROT exposure effect. The ICRP 116 conversion coefficients for an ROT geometry assume that the radiation is uniform in a circular pattern about the central vertical axis of the body. When converting from a measured dose, the measurement device (film badge or TLD) is typically worn in a single point location on the center mass of the body, pocket or collar. Thus, when the body is rotating about a fixed source, the measurement device can be shielded by the body while at other times the measurement device is facing the fixed source. To account for this scenario, IGFs were developed to convert a dosemeter dose measured at various wear positions (center chest, pocket and collar) on the front of the body to values that are compatible with ICRP 116 organ dose conversion coefficients. Using Monte Carlo N-Particle (MCNP) methods, IGFs as a function of energy were developed for both neutrons and photon exposures to male and female workers for ROT and isotropic (ISO) exposure geometries.

Operational measured quantity conversion

For radiation protection purposes, the effective dose is commonly utilized to establish exposure limits and to control radiation hazards. These effective dose limits are compared against measured radiation exposures (occupational quantities), whether they be personal dose equivalent (H_p(10)), ambient dose equivalent (H*(10) or the Roentgen (R)), to ensure protection or compliance with guidance, rules or regulations. To convert from a measured dose (e.g. H_p(10)) to an organ dose (colon) using ICRP 116, the measured quantity must be converted to either fluence or air kerma before the application of the ICRP 116 conversion coefficients (Table 1). The basic equation for energy-dependent personal dose equivalent conversion factor for the AP geometry is described in equation (1).

Table 1.

Operationally measured photon fluence conversion factors.

Photon energy (MeV)	Hp(10)/ϕ (pSv cm2)(4)	H*(10)/ϕ (Sv cm2)(5)	Exposure/ϕ
			(Sv cm2)(5)	(Sv/R)(6)
0.010	0.065	8.33E−14	8.33E−14	1.00E−03
0.015	0.825	8.52E−13	8.52E−13	0.002858
0.020	1.056	1.05E−12	1.05E−12	0.005663
0.030	0.828	8.00E−13	8.00E−13	0.009762
0.040	0.669	6.20E−13	6.20E−13	0.012762
0.050	0.574	5.20E−13	5.20E−13	0.014609
0.060	0.552	5.10E−13	5.10E−13	0.015369
0.080	0.585	5.60E−13	5.60E−13	0.015154
0.100	0.670	6.20E−13	6.20E−13	0.014370
0.150	0.943	8.70E−13	8.70E−13	0.012884
0.200	1.247	1.23E−12	1.23E−12	0.012064
0.300	1.846	1.81E−12	1.81E−12	0.011213
0.400	2.429	2.36E−12	2.36E−12	0.010771
0.500	2.989	2.78E−12	2.78E−12	0.010499
0.600	3.451	3.46E−12	3.46E−12	0.010314
0.800	4.464	4.29E−12	4.29E−12	0.010081
1.000	5.274	5.18E−12	5.18E−12	0.009942
1.500	7.200	6.92E−12	6.92E−12	0.009763
2.000	8.675	8.25E−12	8.25E−12	0.009680
3.000	10.950	1.04E−11	1.04E−11	0.009609

$$\begin{array}{l}{\text{CF}}_{H_P\left(10\right),\text{Organ}}\left(E\right)\left(\frac{\text{pGy}}{\text{pSv}}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\text{ICRP}\hspace{0.17em}\text{116}\hspace{0.17em}\text{photon}\hspace{0.17em}\text{fluence}\hspace{0.17em}\text{conversion}\\ \hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\frac{{\text{coefficient}}_{\text{organ}}\left(E\right)\left(\text{pGy}-{\text{cm}}^2\right)}{\begin{array}{c}\text{photon}\hspace{0.17em}\text{fluence}\hspace{0.17em}\text{conversion}\\ \text{factor}{\hspace{0.17em}}_{H_p\left(10\right)}\left(E\right)\left(\text{pSv}-{\text{cm}}^2\right)\end{array}}\end{array}$$ (1)

Table 1 only provides conversion coefficients from operational measured quantities up to 3 MeV. Around 3 MeV charged particle equilibrium can begin to significantly influence photon fluence conversion factors. While ICRP 116 conversion coefficients consider charge particle equilibrium, the operational measured quantity to fluence conversion factors also need to consider charge particle equilibrium. In the special case of the Roentgen, the calibration of the film badge dosemeter or the TLD needs to be carefully considered to correctly account for the effect. Since the vast majority of the occupational photon exposures are below 3 MeV at Department of Energy sites, the current analysis to photons <3 MeV is limited such that charged particle equilibrium can be assumed.

ICRP 116 conversion coefficients

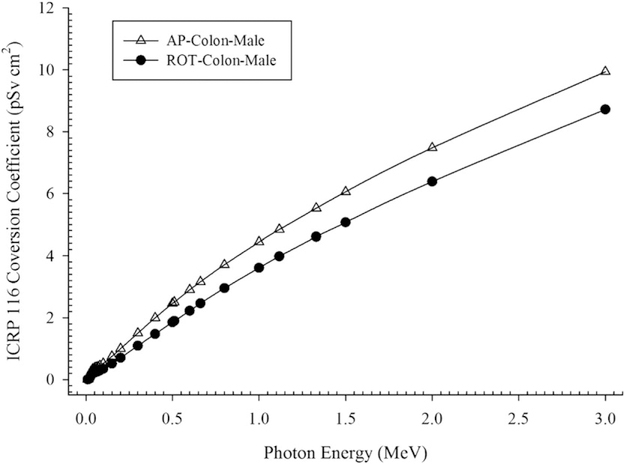
Both the operationally measured quantity conversion factors (Table 1) and the ICRP 116 conversion coefficients vary with emission energy (Figure 1). In the case where the source of the exposure is mono-energetic, the calculation of the conversion factor is straightforward. For example, consider an exposure to 100 keV photons (E) in the AP geometry (G). The resulting conversion factor from the measured personal dose equivalent (H_p(10)) to the colon dose for a male would be 0.778 (equation 2)

$$\begin{gathered} {\text{CF}}_{H_P\left(10\right),\text{Colon,Male}}\left(100\hspace{0.17em}\text{keV}\right)=\frac{0.521}{0.670} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}=0.778\left(\frac{\text{pGy}}{\text{pSv}}\right) \end{gathered}$$ (2)

Figure 1.

AP and ROT ICRP 116 conversion coefficients for the male colon.

This value is multiplied by the operationally measured dosemeter dose (H_p(10)). A reported H_p(10) dose of 1.00 mSv would thus result in a colon dose of 0.778 mGy.

Under the EEOICPA, the NIOSH Interactive RadioEpidemiological Program (NIOSH-IREP) uses energy-dependent radiation effectiveness factors in the calculation of probability of cancer causation. These factors have previously been published by Kocher et al.⁽⁷⁾. For photons, three energy intervals have been defined: <30, 30–250 and >250 keV. As noted above, the upper energy range for occupational photon exposures has been set to 3 MeV.

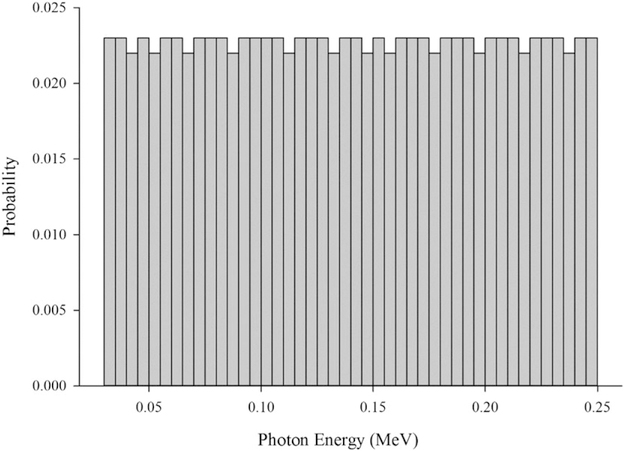
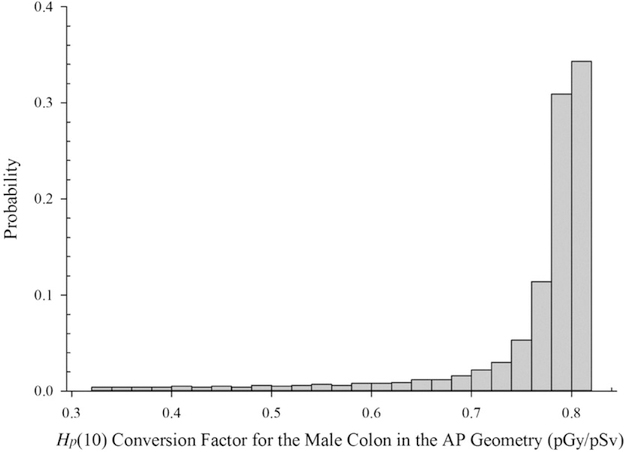
Some averaging is necessary to convert from the operationally measured dose to the organ dose of interest within these photon energy intervals. This averaging is accomplished using Monte Carlo techniques by assuming a uniform photon energy distribution within the energy region of interest or energy bin. Ideally, the workplace photon energy spectra could be used to more accurately estimate the true organ dose, but this information is rarely available and when available consists of discrete measurements or a mocked-up configuration. The true integrated photon energy spectra during the exposure period are not known. Assuming a uniform photon energy distribution is considered to be claimant neutral (i.e. neither beneficial nor detrimental to the case being evaluated). The advantage of assuming a uniform distribution is that the uncertainty of the dose estimate is maximized. That is, the variability in the ICRP 116 conversion coefficients is fully represented by sampling each photon energy equally. Figure 2 illustrates the energy sampling frequency based on 1000 iterations (n = 1000) for 30–250 keV photons. The results of the photon energy sampling and subsequent combination of the ICRP 116 conversion coefficients and the operational photon fluence conversion factors result in a distribution of conversion factors within a defined energy interval (Figure 3).

Figure 2.

Uniform distribution sampling for 30–250 keV photons.

Figure 3.

Operational H_p(10) conversion factor distribution for the male colon in the AP geometry for 30–250 keV photons.

Irradiation geometry factors

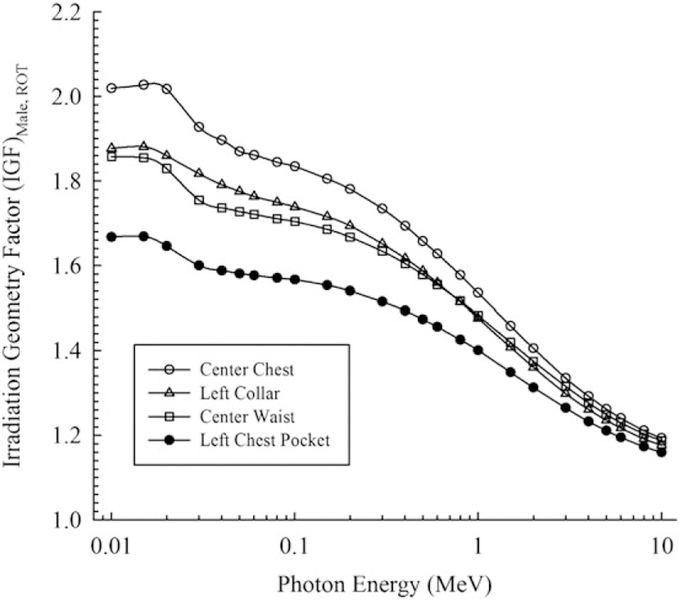
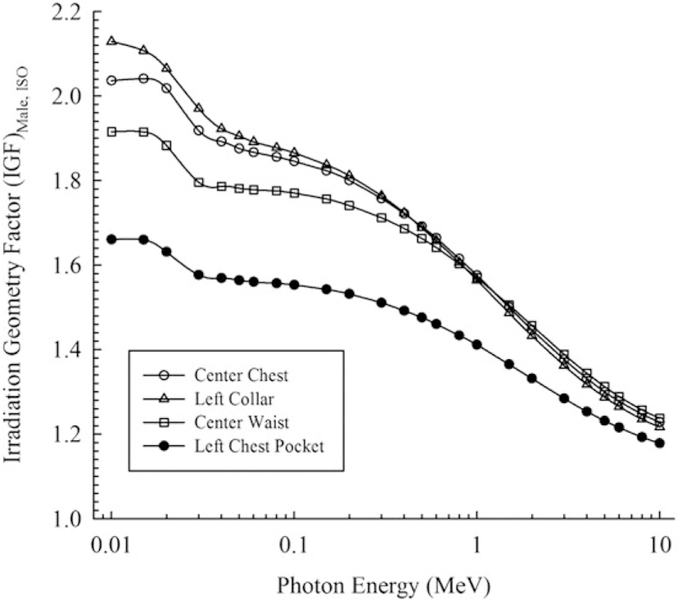
Another issue to be addressed in the implementation of ICRP 116 conversion coefficients is the effect of exposure geometry (G). In some instances, the radiation exposure was not received in an AP geometry, but in an ROT or ISO manner. The operationally measured dosemeter dose (D_m), however, is located at a fixed point on the individual worker. When the exposure is received in an ROT manner, the dosemeter is only measuring a portion of the actual exposure. If the exposure is truly rotational, then the photons from the back and sides are shielded or attenuated due to the body. If the exposure is from a fixed location, but the worker is moving around in an ROT manner, then the dosemeter is again only measuring a portion of the integrated exposure. During another portion of the integrated exposure, the body is again shielding or attenuating the photons, thus reducing the measured dosemeter dose. To correctly account for this reduced measurement effect, energy-specific IGFs were developed using MCNP. The H_p(10) IGFs as a function of photon energy for ROT and ISO geometries for a male are provided in Figures 4 and 5, respectively.

Figure 4.

Male—Photon ROT irradiation geometry factor for H_p(10).

Figure 5.

Male—Photon ISO irradiation geometry factor for H_p(10).

When considered independently, the IGFs range from 1.2 to 2.1 for photons in the ROT geometry depending on gender, dosemeter location and photon energy. The IGFs range from 1.2 to 2.2 for photons in the ISO geometry again depending on gender, dosemeter location and photon energy.

As with the ICRP 116 conversion coefficients and the photon fluence conversion coefficients, the IGFs are energy dependent and can also be sampled based on photon energy instead of using a single average value. The total organ dose conversion factor is the product of the conversion factor from equation (1) and the IGF. Simplistically, this total organ dose conversion factor is then multiplied by the operational measured dosemeter dose (D_m) to obtain the organ dose (equation 3).

$$\begin{gathered} \text{Organ}\hspace{0.17em}\text{dose}\left(\text{pGy}\right)=D_{\text{m}}\left(\text{pSv}\right)\times {\text{CF}}_{H_p\left(10\right),\text{Organ}}\left(E\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\times \text{IGF}\left(E\right)\left(\frac{\text{pGy}}{\text{pSv}}\right) \end{gathered}$$ (3)

Measured dose uncertainty

The operational measured dosemeter dose (D_m) contains uncertainty and is also a distribution of possible values. For example, an operational measured personal dose equivalent might be within ±10%. Thus, the operational measured dosemeter dose of 1.00 mSv is actually (1.00 ± 0.10 mSv). For this uncertainty distribution, it is assumed that the operational measured dosemeter dose is normally (N) distributed (equation 4).

$$D_{\text{m}}=N\left(D_{\text{reported}},{\sigma }^2\right)$$ (4)

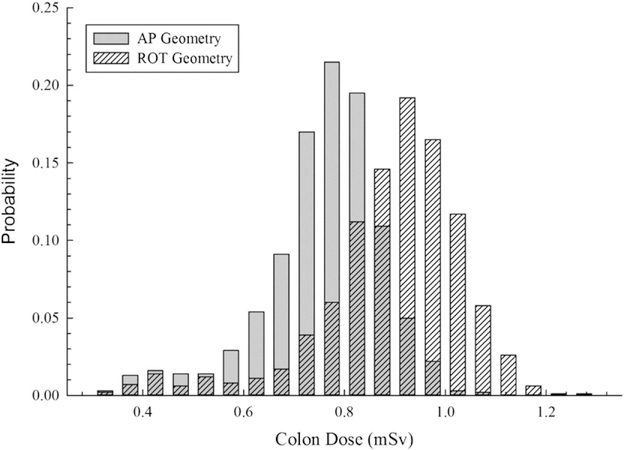
To fully consider all of the uncertainty in the organ dose (photon energy and measurement uncertainty), Monte Carlo sampling is also conducted on the measured dosemeter dose (D_m) as well as the photon energy discussed above. Sampling from these two distributions 1000 times and tallying the potential organ doses develops the final organ dose distribution. Figure 6 depicts both the AP geometry and the ROT geometry colon dose for a male from an operationally measured dosemeter dose of 1.00 ± 0.10 mSv. These organ dose distributions are subsequently fitted for direct input into the NIOSH-IREP for probability of causation determination.

Figure 6.

Colon dose distribution for an adult male with a measured personal dose equivalent (H_p(10)) of 1.00 ± 0.10 mSv in assuming an AP and an ROT exposure geometry.

DISCUSSION

The implementation of the ICRP 116 conversion coefficients into external dose reconstruction is a complex process that must consider the types of particles (photons, neutrons and electrons), the energy of each type of particle in conjunction with the occupationally measured dose in the workplace, the effect of exposure geometry and the organ for which doses must be reconstructed. In this paper, a method for taking into account all of the above factors and incorporating them into the organ dose uncertainty for probability of causation calculations is presented.

In the examples presented, the ICRP 116 ROT geometry conversion coefficients for the male colon were considerably smaller than the AP geometry conversion coefficients (Figure 1). This may lead one to conclude that the AP geometry will always result in a higher organ dose. However, when the IGF was incorporated, the resulting total dose conversion factor for the ROT geometry was greater thus resulting in a larger organ dose. There are offsetting effects with regard to the total dose conversion factor between the ICRP 116 conversion coefficients and the IGFs that depend on photon energy. Lower energy photons are more easily attenuated and therefore result in lower ICRP 116 conversion coefficients. However, due to this ease of attenuation lower energy photons result in a higher IGF. The dominance of these competing effects can vary greatly depending on the organ of interest (i.e. organs closer to the surface vs. deep organs), the photon or particle energy and the exposure geometry. As the photon energy spectra shift toward higher energy photons (1 MeV), these effects become much less pronounced.

All of the examples presented were specific to the male phantom as defined in ICRP 110⁽⁸⁾. The same methodology can be used for the adult female, however, virtually all of the ICRP 116 conversion coefficients and the IGFs are different. This effectively doubles the number of factors and distributions that need to be developed. There are many other aspects that need to be considered when modeling other particle types, as well as the operationally measured dose. A few of the additional considerations are mentioned below.

Additional photon considerations

The examples in Method section were for simple photon exposure measured using the modern personal dose equivalent. When using ambient dose equivalent, the IGFs are not needed as the measurement is not shielded or attenuated due to the body. The same, may or, may not be true for exposures measured in Roentgen. The true definition of the Roentgen is only defined in free air. However, historically film badge dosemeters were calibrated in free air in units of Roentgen. These dosemeters were then worn by workers on their body resulting in a shielded or attenuated measurement. These effects can be corrected using MCNP modeling, however, in some cases a few simple favorable assumptions can also be made that give the benefit of the uncertainty toward the claimant.

Neutrons

The examples in Method section were for simple photon exposures. For neutron irradiations, radiation weighting factors such as those published in ICRP 103⁽⁹⁾ need to be considered. In the EEOICPA program, era-dependent quality factors or radiation weighting factors from the recorded dose are removed. Then, the Monte Carlo computations are performed on the original measurement with a preference to use neutron fluence when available. Within the NIOSH-IREP, there are five neutron energy intervals for radiation effectiveness considerations. Thus, the number of conversion coefficients and result combinations nearly doubles compared with photons.

Special exposure geometry (near field exposures)

Near field exposures (e.g. glovebox work) should also be carefully considered when using ICRP 116 conversion coefficients and the methods described above. The operationally measured dose could be significantly different from the dose at the point of entry to the body. For example, a dosemeter worn on the collar can be further away than the abdomen from a radiation source being handled in a glovebox. Thus, the measured dose is artificially lower than the dose if the dosemeter was worn on the abdomen. While the collar worn dosemeter result would be a good value for estimating the thyroid dose, it would not be a good measure for the dose to the colon.

CONCLUSION

This paper presents a Monte Carlo method for implementing ICRP 116 [3] conversion coefficients into dose reconstructions that incorporate various sources of uncertainty in the underlying workplace exposure. Organ-specific conversion factors considering the particle energy in the workplace, the measured quantity (H_p(10), H*(10) or Roentgen) and the exposure geometry were combined using Monte Carlo methods that are based on the particle energy. The total organ dose conversion factor can then be applied to the operationally measured dosemeter dose in order to determine the dose to the organ of interest and the associated uncertainty.