The evolution of practical radiobiological modelling

Abstract

A summary of the key aspects of radiobiological modelling is provided, based on the theoretical and practical concepts of the linear quadratic model, which gradually replaced other numerical approaches. The closely related biological effective dose concept is useful in many clinical applications. Biological effective dose formulations in conventional photon-based radiotherapy continue to be developed, and can be extended to the now increasingly used proton and ion-beam therapy, to very low or high dose ranges, the dose rate effect, hypoxia and repopulation. Such established and new research developments will be of interest to clinicians, physicists and biologists to better understand the processes underlying radiotherapy and assist their collaborative efforts to make radiotherapy safer and more effective.

Introduction

The linear quadratic (LQ) model is presently the standard method for modelling the influence of radiation dose on cell survival and tissue responses: its advantages and limitations are given in further detail below. Oliver Scott and Jack Fowler both considered how best to model radiation effects in a simple and effective way, using fewer yet more biologically realistic parameters. They helped to guide the acceptance of the LQ model as the best method for clinical application when earlier methods, based on either target theory^1,2 or using crude power laws, which were inflexible and relied on a greater number of unrealistic bioparameters, had been shown to fail.^3,4

The representation of radiosensitivity and repair within the LQ model, and its modification by fractionation and dose protraction (see paper by Dale in same Special Feature), is now well-known. Further advances were the inclusion of a repopulation correction factor,^5–7 methods for inclusion of “sensitising” drugs, and for different qualities of radiation such as positively charge particles. The guidance provided by the LQ model in radiotherapy dose adjustments, has included applications in unintended treatment interruptions, errors in treatment delivery, dose-rate changes, technique comparisons, mixed modalities, dose-fractionation optimisation, retreatments and clinical trial design, some of which are discussed below. These techniques can provide rational information to help improve medical decision-making in situations when standard clinical trials cannot. Both authors have experience in the development and application of such models in clinical practice, and received considerable encouragement from Dr Scott and Dr Fowler. Medical graduates should not be daunted by the mathematics, but take a reasonable interest and use these modelling “tools” to enhance their expertise.

First, it is necessary to provide a brief account of the LQ model before considering its applications.

The Linear Quadratic model

Douglas Lea⁸ fitted the average yield of severe (or lethal) chromosomal aberrations per cell (E), in the form of a linear–quadratic relationship with single dose (d), and radiosensitivity parameters α and β:

$${\displaystyle E=\alpha d+\beta d^2}$$

Although initially neglected, this finding later became increasingly important. It is remarkable that theoretical approaches at different physical and biological scales such as microdosimetry, molecular damage reparability and lethal chromosomal aberration yields, all approximate to the LQ formulation.^9–12

Table 1 provides a brief summary of the basic aspects of the LQ model. Figure 1a illustrates the separate contributions of the linear and quadratic cell survival components to the full model, and in Figure 1b the recovery of the survival fraction effect seen by splitting a 4 Gy single dose into two fractions is shown. By increasing the number of fractions, more recovery can take place, the amount depending on the α and β radiosensitivity parameter values. Figure 1b also shows how a sufficient time interval is required between fractions to ensure full repair of sublethal damage. Failure to do this results in reduced recovery and increased net damage, a point which is of particular clinical concern in normal tissues.

Table 1. .

Summary of LQ model: Contrary to common misconceptions, α and β are not dose specific coefficients for SSB and DSB DNA breaks. Many SSB and DSB, existing in close proximity, and before repair, are required to produce a lethal event (normally accompanied by the appearance of a lethal chromosomal aberration to cause cell death due to asymmetric segregation of genetic information at mitosis). Consequently, SSB and DSB are necessary precursors, but not sufficient requirements, for lethality. In cell survival experiments, α and β must reflect the probability of lethality with increasing dose and are best defined as: αis the coefficient of lethal events per cell per unit dose (units Gy−1) βis the coefficient of lethal events per cell per unit dose squared (units Gy−2) In this way, α and β probably reflect the number of lethal chromosomal events with dose and dose squared respectively. It follows that the probability of cell survival (where there are no lethal events), referred to as the Survival Fraction (SF), is obtained using Poisson statistics: ${\displaystyle SF=e^{-\left(expectednumberoflethalevents\right)}=e^{-d-b{d}^2}}$ For n fractions of dose d, then ${\displaystyle SF=e^{-n\left(d+b{d}^2\right)}}$. The LQ model can alternatively be expressed as: α = Σ (localised unrepaired DNA damage ⇒ lethal chromosomal injury events per cell)/dose β= Σ (localised unrepaired DNA damage ⇒ lethal chromosomal injury events per cell)/dose2 The predominant mode of cell killing at low dose is via α-mediated damage, but β-mediated damage dominates at high dose (Figure 1).

DSB, doublestrand; SSB, singlestrand.

Figure 1.

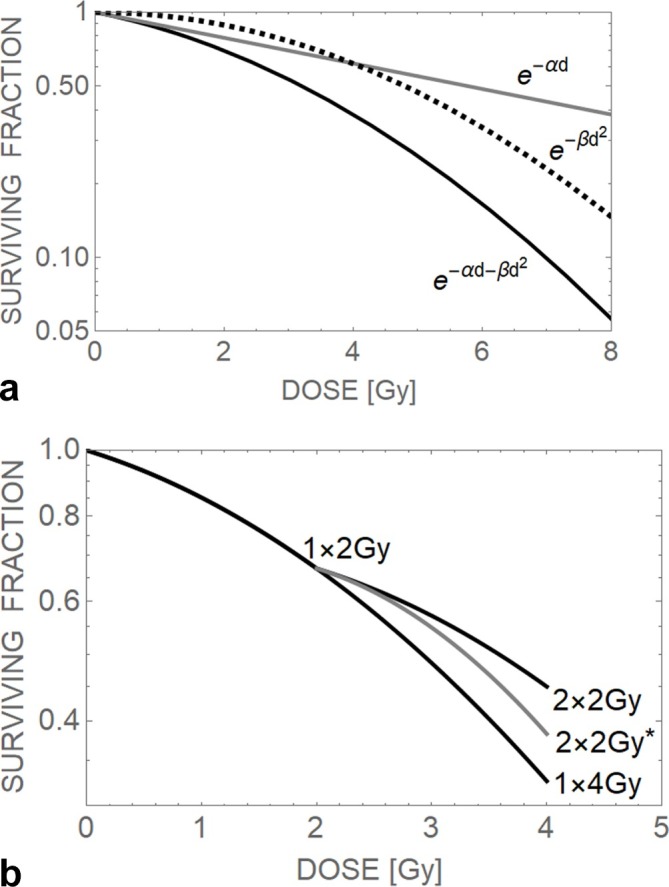
Theoretical cell survival curves, (a) showing the linearity of the exponential -αd  relationship and the curvature provided by the -βd2 relationship, and their summation as -αd-βd2, which shows only initial linearity followed by increasing curvature, (b) the survival curves for a single dose of 2 Gy, 4 Gy and a ‘split’ dose of 2 × 2 Gy after an interval of time that has allowed near complete repair of sub-lethal damage. An example of incomplete repair is shown by the grey 2 × 2 Gy* plot where the second dose of 2 Gy has been delivered after a shorter interval of time that allows substantial amounts of incompletely repaired damage to form more lethal events during the second 2 Gy fraction, resulting in a higher survival fraction than in the other 2 × 2 Gy case.

Animal and human fractionation data could be fitted by transformations of the LQ model. Douglas and Fowler¹³ showed that the reciprocal of total dose, when plotted against dose per fraction, produced reasonably good linear fits of isoeffective fractionation data, where the same biological endpoint was obtained using different dose fractionation schedules. These fractionation-effect, or Fe, plots were used to estimate α/β ratios. Thames et al¹⁴ used many isoeffective data sets to show the important dissociation between classes of tissues with different α/β ratios: acute reacting systems (such as rapidly growing tissues and normal epithelial tissues) had high α/β ratios (typically 7–15 Gy), but late reacting systems (slowly growing tumours or low turnover normal tissues) had low α/β ratios (typically 2–3 Gy). In comparison to the non-biologically based power law models, which failed at high and low dose limits and were initially believed to apply to all tissues and tumours, the LQ approach, although not without its shortcomings, was in fact more flexible and produced more realistic predictions over a wide range of doses.

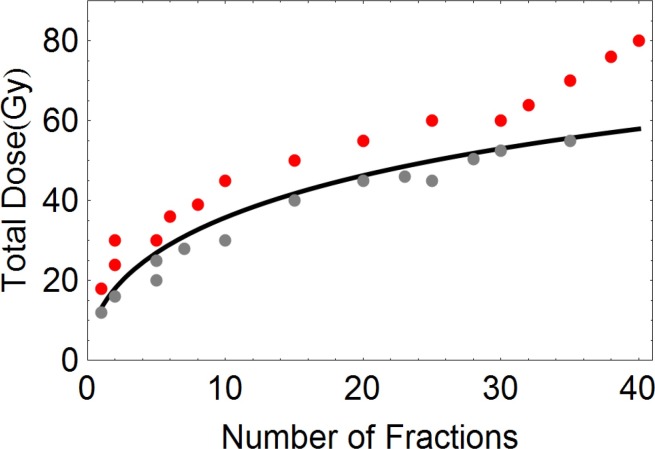
An example of the clinical utility of the LQ model is given in Figure 2. The LQ based curve is isoeffective to a low-risk “tolerance” dose for spinal cord myelitis (taken to be 50 Gy in 25 fractions). The data points correspond to clinical fractionation schedules used by the first author and are considered to be safe (provided these doses are not exceeded in the spinal cord). The theoretical curve provides an effective practical spinal cord dose limit and separates the safe fractionation schedules from those used for radical tumour treatments.

Figure 2.

The relationship between total dose and number of fractions which result in the same low risk (iso-effect) of spinal cord paralysis, obtained using the LQ model with αβ = 2 Gy. Thegrey points correspond to safe treatment schedules, all of which are below theiso-effect curve. The red points are the doses often used to treat squamous cell cancers and which exceed the iso-effect curve. Clinical radiotherapy may utilise the grey dose-fractionation points to palliate cancer close to the spinal cord, but when the red point curative doses are given, great care is taken to ensure that the spinal cord doses are either on or below the curve (reproduced with permission from Jones).

Model classes

As can be seen in Table 1, the LQ model is a multiscaled concept, since the general form of the equation can represent response at many levels (DNA strands, chromosomes, repair enzymes, cells, tissues and individuals). In general terms, there are two classes of models, namely:

1. Bottom-up models: examples include the microdosimetry models mentioned above, the developing GEANT4-DNA project, and the linear energy transfer (LET) based local effect model,¹³ which assumes many subcellular and cellular parameters, which allow relative biological effect (RBE) prediction, although imperfectly.

2. B. Top-Down models: these use high level parameters (at the clinical level) such as the BED, tissue or tumour α/β ratios, or α and β. They are essentially phenomenological, but with an inherent real radiobiological basis.

Obtaining a totally comprehensive model that contains all contributions that govern outcomes may not be fully obtainable, because it is not possible to define the event probabilities down to individual cells, with heterogeneity of cell sensitivities which vary with position in the cell reproductive cycle, the biochemical redox state, the nuclear and cell volumes, repair proficiency etc. However, the LQ model does possess features of both of the above categories, although for many clinical applications incorporation of further refinements are necessary and are described below, commencing with the transformation of the LQ model into the biological effective dose (BED).

Biological Effective Dose

Many authors^15–18 have contributed to the development and application of the BED concept to experimental and clinical data sets. Essentially, the BED is obtained by taking the natural logarithm of the Surviving Fraction (see equation in Table 1), multiplying by −1 and dividing throughout by α and rearranging the terms. Earlier publications used the term Extrapolated Response Dose, but this is synonymous with BED.

For standard megavoltage radiation the basic expression for BED is:

$${\displaystyle BED=nd\left(1+\frac{d}{\frac{\alpha }{\beta }}\right)}$$

For any specified BED, the equivalent dose in 2 Gy fractions (the EQD-2) is simply:

$${\displaystyle EQ{D}_2=BED/(1+2/(\alpha /\beta )).}$$

BED is an end point specific concept and individual values is, therefore, usually written in the form Gy _[x], where x is the α/β ratio used in the BED calculation. Many BED applications with worked examples are given elsewhere.¹⁹

In the case of no-homogenous irradiation BEDs can, in principle, be expressed as equivalent uniform BED just as in the case of equivalent uniform dose,²⁰ but in such cases there is loss of information on the extreme values which can influence outcomes; also information on the anatomical positioning of the dose distribution is lost. It is arguably better to use a BED display superimposed on three-dimensional anatomy or using representative points where possible.

Repopulation effects

Since tumour cells grow exponentially in good growth conditions, it is now standard to express this process as a reduction of BED by using a BED-dose equivalent of repopulation.²¹ The surviving fraction (S) following radiotherapy expresses the surviving clonogenic cells and must be increased by a factor which accounts for the cellular repopulation during the treatment time (t). This is normally represented as N_t = N ₀ e^{–t/T eff}, where T _eff is the effective doubling time of the repopulating cells, from N ₀ cells at time zero to N_t at time t. T _eff may initially correspond to the pre-treatment tumour volume doubling time, but in some tumours may shorten during treatment, approaching the pre-treatment potential doubling time.

For late-responding normal tissues, no allowance for repopulation should normally be necessary. Inclusion of normal tissue repopulation, or “recovery”, following treatment may be required when considering retreatment after an interval of many months or years.²² Some guidance on repopulation allowances for acute mucosal tissue effects exist,²³ although the situation is made more complex by the fact that α/β ratios appear to increase during treatment, which probably reflects the process of accelerated repopulation in normal epithelial tissues and in some tumour types. Hopewell and colleagues found averaged α/β ratio values of 4, 12 and 35 Gy in the first 2, 2–4 and 4–6 weeks of treatment in the case of acute skin reactions, which are inversely related to the cellular proliferation rates.²⁴

Biological Effective Dose and Repopulation

To allow for the effect of repopulation during treatment, the standard BED equation requires a subtractive repopulation factor. Assuming a constant rate of BED compensation during treatment:

$${\displaystyle BED=D\left[1+\frac{d}{⟮\alpha /\beta ⟯}\right]-KT}$$

where K, (units of Gy per day), is the daily BED equivalent of repopulation (rather than the physical dose per day) required to offset repopulation,²¹ and T is the overall treatment duration. Since K_ is defined as 0.693/(α.T _eff), even tumours with low values of α (due to slow proliferation rates, with a high proportion of cells being non-cycling in G ₀ phase) may have significant K values.

Typical values of K used for rapidly growing squamous cell cancers are 0.5–1.0 Gy₁₀ per day. With slower growth kinetics, e.g. in breast and prostate cancers, there is little evidence for repopulation until durations of greater than 6 weeks or more have elapsed, when the K value may be close to 0.3 Gy per day or higher in prostate cancer^25,26 and up to 0.6 Gy per day for breast cancer.²⁷ In very poorly differentiated tumours with total lack of growth control mechanisms, it is possible that repopulation will be continuous without a lag-time.

Alternative patterns of repopulation

Equation (4) assumes continuous repopulation (i.e. the repopulation rate is continuous, at the same rate during the entire treatment time). For tumours where steady-state repopulation begins after an apparent time lag of T_K days, the repopulation termed is modified to be K(T-T_K). The BED is then:

$${\displaystyle BED=nd(1+d/(\alpha /\beta ))-K(T-T_K)}$$

This pattern of repopulation can be described as being discontinuous. For head and neck cancers, T_K is between 21 and 28 days, but it would be incorrect to assume that all tumour behave like most differentiated squamous cell cancers. Also, and in all cases, the approach adopted in Equation (5) is only valid if T > T_K. For ultrashort fractionation schedules with overall times shorter than 21 days, the repopulation correction can either be omitted or a longer T _eff can be assumed, e.g. 5–10 times larger than T _pot values. An alternative formulation, based on a progressive or delayed reduction in the cell loss factor during treatment can also be used.²¹

It was Oliver Scott that originally suggested shortening of overall treatment times to overcome rapid repopulation, specifically in the case of childhood Burkitt’s Lymphoma (OCA Scott, personal communication, 1982). This suggestion also led to other “accelerated schedules” whichshould include the effect,²⁸ but including the effect of incomplete radiation repair, which occurs in some critical normal tissue such as the central nervous system when interfraction intervals are shortened (Figure 1 which shows how there is less than full recovery of surviving fraction between closely-spaced fractions). This topic needs to be reinvestigated using optimisation techniques for dose per fraction²⁹ and the best available mathematical models, while also introducing the acute normal tissue reaction constraint of not permitting greater than 10 Gy per week in more than 1–2 weeks of treatment.²³ The propensity for enhanced normal tissue effects to cause consequential late effects in some tissues must also be included, while the prospect for selecting tumours where repopulation during treatment (including the accelerated variety) can be identified not only from histological grading and conventional proliferation indices, but also from genetic and proteomic characterisation. Thus, the optimum treatment for such tumours might be the greatest number of fractions within 28 days that obeys all the above constraints including a limited number of 8–12 hours interfraction intervals and also allows use of some weekend treatments.

Another important consideration is the relationship between cellular proliferation rates and the α/β ratio.³⁰ Slower growing tumour such as most breast and prostate cancers and brain meningiomas have lower α/β ratios and are more “fraction sensitive” than more rapidly proliferating tumours. The cell kill per unit change in dose is greater in tumours with low α/β. This is an inevitable consequence of the in-parenthesis terms in Equation (2) (often referred to as the relative effectiveness factor). This ensures that shorter treatment schedules of hypofractionated treatment, using 5–6 fractions in 1–2 weeks can be effective for such tumours,^31–35 regardless of there being no advantage of overall treatment time reductions in such tumours. In such cases, the dose per fraction is the critical determinant, rather more than overall time considerations.

BED expression for high LET radiation

For high-LET radiations, it is necessary to allow for the separate increments in α and β due to increasing LET, and to distinguish between the radiosensitivity values of α_L and β_L (of the low LET reference radiation), and α_H and β_H (their respective values at higher LET). The increase in alpha normally exceeds that for β by a considerable margin.^36–38 Some authors ignore the smaller β increments for low dose treatments, but the β contribution to effectiveness inevitably increases with dose per fraction.

Dale and Jones³⁹ analytically derived a fractionated high-LET BED equation using the concept of RBEmax, the maximum RBE occurring at zero dose and equal in value to the ratio α_H/α_L

$${\displaystyle BED=D_H.(RB{E}_{max}+d_H/(\alpha /\beta ))}$$

where D _H and d _H are respectively the high-LET total and fraction doses and α/β is that of the low-LET reference radiation.

Equation (6) assumes that beta remains unaltered by changes in LET, such that RBE tends to unity at high fractional doses. However, as β is LET-dependent, then the expected lower limit of RBE at high fraction dose (RBEmin) must exceed 1 and is given by √(β_H/β_L).^37,38 The complete BED equation is then:

$${\displaystyle BED=D_H\left(RB{E}_{max}+\frac{RB{E}_{min}{}^2{d}_H}{(\frac{\alpha }{\beta }{)}_L}\right)}$$

Equivalent high-LET dose fractionation schedules can be determined by solving the isoeffect defined by Equating equations 4 and 7:

$${\displaystyle D_L\left(1+\frac{d_L}{{\left(\frac{\alpha }{\beta }\right)}_L}\right)=D_H\left(RBEmax+\frac{RBEmi{n}^2{d}_H}{{\left(\frac{\alpha }{\beta }\right)}_L}\right)}$$

Many applications of these equations in particle therapy, along with the linkage of the RBE parameters with LET are given elsewhere.^40,41

Dose rate effects, incomplete repair and closely spaced fractions.

This topic is covered elsewhere in this Special Feature. Protraction of radiation exposure occurs with large single fractions using external beam techniques, and can be as long as 2 h or more in some instances, which allows considerable sub-lethal damage repair and hence loss of biological effect. These issues are also considered in the context if radiosurgery by Jones and Hopewell (given elsewhere in Special Feature).

Unlike the dose-rate effect where biological effect is reduced with increasing irradiation time, closely spaced fractions incur increased effects by virtue of the compounding of any unrepaired damage across subsequent dose fractions. This is allowed for in BED calculations by introducing an additional factor (1 + h), so that

$${\displaystyle BED=nd\left(1+\frac{d\left(1+h\right)}{\frac{\alpha }{\beta }}\right)}$$

Tables of h-factors are available.^16,19 At high-LET, the increments in α will diminish the magnitude of the fractionation effect and hence that of closer fraction spacing, but even small changes can be important.

Using the earlier terminology, the high LET BED equation for incomplete repair becomes

$${\displaystyle BED=nd\left(RB{E}_{max}+\frac{d\left(1+h\right).RB{E}_{min}^2}{\frac{\alpha }{\beta }}\right)}$$

Hypoxia and Drug Radiosensitisation

For modelling studies that assess the contribution of hypoxic radioresistance, the separate oxygen enhancement ratios for α_L and β_L terms can be incorporated as respective dose multipliers OER_α and OER_β, as multipliers of the dose, so that, with low-LET radiations:

${\displaystyle BED=nd.\left(OE{R}_{\alpha }+\frac{d.OE{R}_{\beta }}{\frac{\alpha }{\beta }}\right)}$ (11)

The same replacements can be used within the high LET BED equation, as

$${\displaystyle BED=nd.\left(RB{E}_{max}.OE{R}_{\alpha }+\frac{d.OE{R}_{\beta }.RB{E}_{min}^2}{\frac{\alpha }{\beta }}\right)}$$

Care must be taken to use the appropriate OER which will itself diminish with LET. This aspect has been explored by several authors.^42–44

Similar expressions, using drug sensitisation factors A and B for α and β respectively, modifies BED as:

$${\displaystyle BED=nd.\left(A+\frac{d.B}{\frac{\alpha }{\beta }}\right)}$$

The implications for dose fractionation are potentially important since if A > B, sensitisation is largest at low d, but if B > A it is largest at high d, with the condition of pure dose modification and no dependency on d if A = B.

Low dose hypersensitivity

Fast growing cells can show “low dose hypersensitivity”, a biphasic cell survival response found in detailed experiments, and thought to be caused by induced repair.⁴⁵ This phenomenon has been modelled mechanistically using the well-established Michaelis–Menten enzyme kinetics, where the rate of reaction depends on substrate concentration, but modified by additional induction of enzyme capacity.⁴⁶ The low LET formulations are:

$$\begin{gathered} {\displaystyle SF[overall]=f.e-\frac{\alpha d}{{\rho }_{res}}-\frac{\beta d^2}{{\rho }_{res}}+(1-f).e^{(-\alpha d-\beta d^2)},where \\ {\rho }_{res}=x+\rho (1-x)\mathrm{a}\mathrm{n}\mathrm{d}\frac{\nu }{V_{max}}=\frac{\alpha d+\beta d^2}{K_M+\alpha d+\beta d^2}=\rho } \end{gathered}$$

where f is the fraction of cells in G2 phase, and x is the fraction of DNA repair that is active at zero dose. The saturation of repair rate (ρ) is described by v/V _max, where v is the rate at dose d.

The change in effective K _M from a minimum to maximum value is described by

$${\displaystyle K_{Meff}=K_{Mmax}+e^{-jd}(K_{Mmin}-K_{Mmax})}$$

Suitable parameter values can be obtained elsewhere.⁴⁶

The more pragmatic equation developed by Joiner,⁴⁷ simulates changes in α with dose as:

$${\displaystyle SF=\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\alpha }_{r}d\left(1+\left(\frac{{\alpha }_s}{{\alpha }_r}-1\right)\right).\exp \left(-\frac{d}{d_C}\right)-\beta d^2\right]}$$

where α_r is the “normal” LQ parameter, and α_s the more sensitive parameter initial slope.

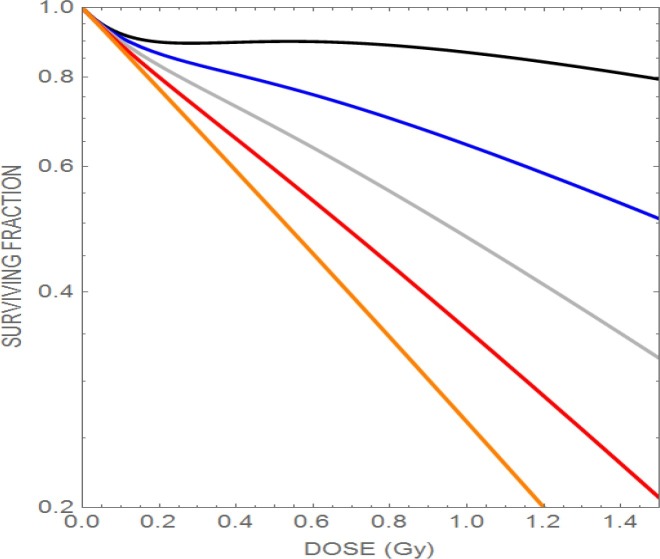
This phenomenon may have relevance to high LET radiations, since the α_s probably reflects high LET conditions. Figure 3 shows the effect of increasing the α radiosensitivity parameter with increasing LET, and the associated loss of the phenomenon. By increasing the LET delivered to the tumour but keeping normal tissue LET values as low as possible should confer a considerable advantage in reduction of normal tissue reactions regardless of any change in dose, as might be the case in some parts of the target volume.

Figure 3.

Plot of the effect of increasing the radiosensitivity (assumed here due to the LET-RBE effect) causing progressive loss of low dose hyper-radiosensitivity. The upper curve has α=0.1 Gy^{− 1}, followed downwards by α=0.4 Gy^{− 1}, α=0.7 Gy^{− 1}, and α=1.0 Gy^{− 1}. The lowest line represents the maximum possible radiosensitivity for the cell line (1.3 Gy^{− 1}). (reproduced with permission from Jones).

“Straightening-out”of the LQ relationship at higher doses per fraction

With increasing use of extreme hypofractionation (sometimes involving only one fraction) in radiosurgical techniques, the shape of the survival curve must be considered. The LQ model may in some instances overestimate biological effect at doses above 6–10 Gy, since some cell-survival curves, unlike the increasingly-bending LQ curves, tend to linearity above such doses. To allow for this, two methods are considered.

Method 1

According to Lea,⁸ αd+βd² is the yield of lethal chromosome breaks per cell at low dose. With increasing dose, some breaks will be second- or third-breaks on the same chromosomes, which will not increase overall lethality and so represent wasted dose. Such an effect would require modification of the yield of lethal chromosomal events on individual chromosomes. By considering Poisson statistics (Table 2), a function that becomes increasingly linear with dose can be deduced.

Table 2.

Statistical influence of chromosomal number in apparent straightening of the cell survival curve with increasing dose

The total chromosome number is M Number of lethal chromosome breaks (E) per cell caused by radiation, E= α d+ β d 2 Average number of lethal breaks per chromosome at dose d = ( α d+ β d 2 )/M Probability of NO breaks on an individual chromosome = Exp [- ( α d+ β d 2 )/M] Probability of any number of lethal breaks on an individual chromosome = 1 -Exp[- ( α d+ β d 2 )/M] The expected average number of lethally damaged chromosomes per cell is M(1-Exp[-( α d+ β d 2 )/M]) = E M So, at higher doses, the relationship for surviving fraction (S) becomes: S = Exp [-E M ]

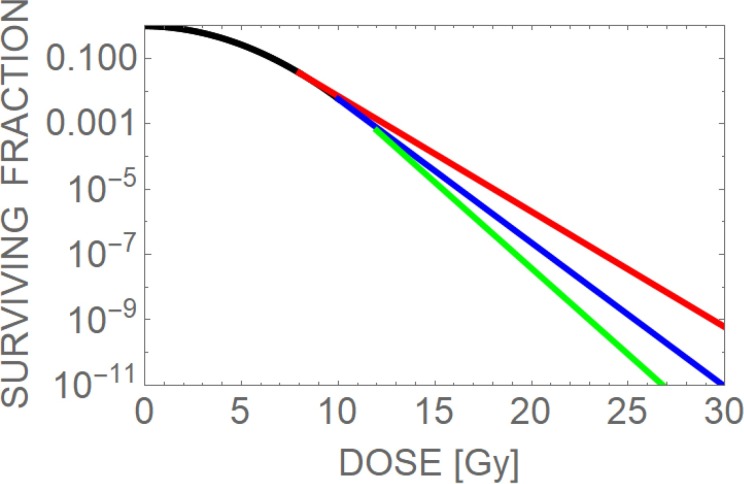
This model may be appropriate for normal tissue, where M = 46. Rapidly dividing cells have the added complexity of chromatids, and tumour cells may possess greater than 46 chromosomes per cell. Individual chromosomal volumes are variable, so some chromosomes will be more susceptible than others to random radiation damage. Because of this, the effective number of chromosomes may be less than 46, e.g. 40. Some unpublished work showed that a greater number of cell survival curves were better fitted by this model than the standard LQ model, despite inclusion of very linear neutron irradiated cell lines, but the difference was not statistically significant. However, the model presented above is attractive for normal tissue modelling purposes and may be biologically more realistic than the assumption of an arbitrary dose beyond linearity is assumed (Method 2). Figure 4 shows how a survival curve may change for each of the two proposed models.

Figure 4.

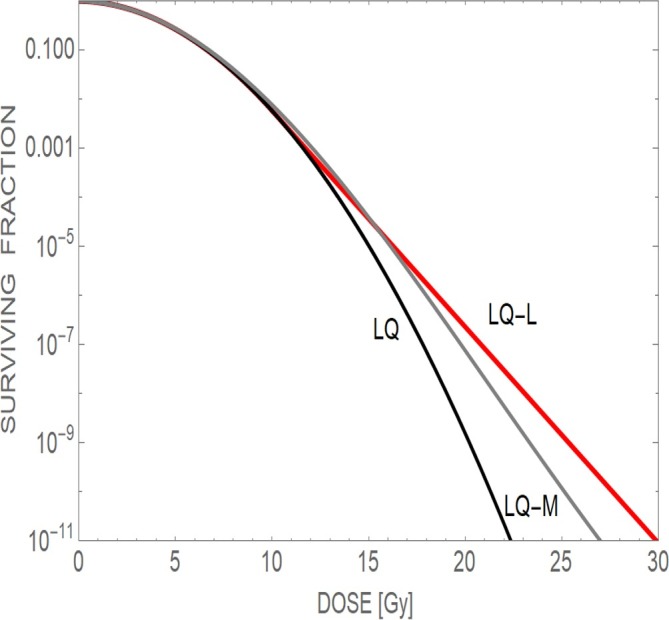
Three theoretical survival curves taken to high doses capable of causing tumour sterilisation. The curves appear to deviate around 10 Gy. The standard LQ model shows progressive curvature, the LQ-M (chromosomal) model 1 gradually straightens and the LQ-L (or LQ-Linear) model 2 follows a constant slope after a dose of 10 Gy has been achieved. (reproduced with permission from Jones).

A disadvantage of Model 1 is that it is not possible to use the BED concept with accuracy, because series expansion of the exponential term does not converge well on the pure function, but graphical methods to determine the reduction of effectiveness or isoeffective dose and then apply BED equations.

Method 2

An alternative BED method assumes that the transition from curvature to linearity is abrupt, rather than gradual, occurring at a specific fractional dose (c) followed by a constant slope at higher doses.⁴⁸

At low fraction doses (<c): E = αd + βd ² to a limit of E=αc+βc². At a dose of c, the gradient is α +2βc, given by the first differential coefficient of the latter equation, so that for doses which exceed c (i.e. d-c):

$${\displaystyle E=\alpha c+\beta c^2+(\alpha +2\beta c)(d-c)}$$

providing a constant slope for doses greater than c.

The BED for N fraction treatments, for fractional doses greater than c is:

$${\displaystyle BE{D}_N=N\left(c+\frac{c^2}{(\alpha /\beta )}+\left(1+\frac{2c}{(\alpha /\beta )}\right)(d-c)\right)}$$

Which simplifies to:

$${\displaystyle BE{D}_N=N_d\left(1+\frac{c}{(\alpha /\beta )}\left(2-\frac{c}{d}\right)\right)}$$

For example, in the case of a late reacting normal tissue with α/β = 3 Gy (for 60 Gy in 30 fractions, BED = 100Gy₃): then solve ${\displaystyle 1\times d\times \left(1+\frac{10}{3}\left(2-\frac{10}{d}\right)\right)=100}$.

Then, d = 17.4 Gy (compared with d = 15.9 Gy for the “pure-LQ” model).

The effect of changing the transitional dose c is shown in Figure 5.

Figure 5.

Changing the LQ model transition points at doses of 8 Gy (red), 10Gy (blue) and 12 Gy (green). (reproduced with permission from Jones).

High LET formulations for each method

1. Chromosomal M model: use the BED formulation containing RBEmax and RBEmax instead of the standard BED`s.

$$\begin{gathered} {\displaystyle E_M=M\left(1-Exp[-({\alpha }_{Hd}+{\beta }_{H{d}^2})/M]\right), \\ or{E}_M=M(1-Exp[-({\alpha }_L.R_{max}D+{\beta }_L.RB{E}_{min}{}^2{d}^2)/M])} \end{gathered}$$

2. For Model 2, it can be shown that

$${\displaystyle BE{D}_N=Nd⟮RB{E}_{\mathrm{m}\mathrm{a}\mathrm{x}}+\frac{RB{E}_{min}^{2}c}{\left(\alpha /\beta \right)}\left(2-\frac{c}{d}\right)⟯}$$

Since the dose-response curves “straighten out”, these methods provide higher tolerance or isoeffective dose estimates compared with the standard LQ approach. In comparison, the standard BED calculations tend to “fail-safe” for normal tissues, since the isoeffective dose may be underestimated and consequently, be safer. This needs to be understood within the treatment planning process.

Alternative approaches include a gradual transition from the LQ to increasing linearity at higher doses.⁴⁹ Such models should be used cautiously,^18,50 but they could allow better correlations with clinical data outcomes to be obtained.

A note about the α/β ratio

Radiobiological models can only aid clinical decision-making, if their input parameters are reasonably accurate. This being not always the case, it is sometimes prudent to use worst case parameter assumptions to better ensure a “fail safe” result. Unfortunately, good predictive assays are not available for α/β, although it is clear that correlations between concepts like repair capacity will correlate with radiosensitivity and that α and β will reflect the fidelity and capacity of the limiting repair processes such as non-homologous end-joining and recombination repair. Much work is needed to establish firm links between molecular based assays and the modelling parameters.

Tumour α/β ratios should reflect tumour pathology: a choice of a larger value within the accepted range should be considered for poorly differentiated tumours and lower values for the well differentiated state. Slow growing tumours require low α/β ratios. The α/β ratios of late-reacting normal tissues are considered to be more stable: 2 Gy for the central nervous system, 3 Gy for all other tissues.

The α/β ratios for various tumours have been published elsewhere.^51,52 The variation in α/β will normally be greater for tumours than for normal tissues, since the former contain greater genetic and phenotypic heterogeneity. Another issue is that α/β may vary with age and be lower in younger individuals, consequently making them more fractionation sensitive; alternatively an equivalent BED for age can be used.⁵³ Ideally, a range of solutions to any clinical problem should be obtained using a reasonable range of α/β values. It should also be noted that, due to their slower growth rates, human tumour α/β values may be lower than those obtained from animal experiments (e.g. 5–8 Gy may be more reasonable than 10 Gy). Fowler often stated that the fractionation effects were far less substantial for tumour α/β greater than 7–8 Gy when compared with normal tissue values of 2–4 Gy.

Some normal tissues probably exhibit dual response characteristics where the combined effects of severe acute reactions can make a significant contribution to the late effects; these are termed consequential late reactions. They may be the weighted product of the acute and late reacting α/β ratios and so can be greater than 3 Gy. An example is rectal damage, where α/β is often quoted as 4 Gy, but in practical (and conservative) terms assumed to be 3 Gy. The duration of radiation exposure may also be relevant. For the extreme example, the acute exposure of a large single fraction, we should assume the lowest α/β value since irradiation takes place in the situation of (relatively) low proliferation. But in the case of a more protracted irradiation, the acute reacting epithelial tissue α/β ratios increase significantly with time, from 5 to 35 Gy in five weeks.²⁴

Where an α/β value is not reported, it can be estimated³⁰ from a potential doubling time as α/β = 48.8/T _pot. This formulation was derived from the equation K = 0.693/(α.T _eff ), since it can be divided throughout by β and rearranged to give α/β = C/T _pot, where C is a replacement constant and assumes T _pot is the operative effective doubling time (T _eff ) during accelerated repopulation in radiotherapy schedules.

Applications of BED equations

There are some important rules and caveats concerning BED equations, summarised as:

1. BED`s can be added for different components of an overall treatment given by different types of radiation (e.g. for a treatment combining X-rays and electrons, the overall BED = electron BED+ X ray BED, or for a treatment comprising X-rays and an ion beam boost, then the overall BED = X ray BED + ion beam BED).This rule strictly only applies to the volume of tissue irradiated by the combined modalities and also assumes a relatively high degree of dose uniformity throughout that volume. Within treatment planning systems, the addition of BEDs within individual voxels is not so constrained.

2. Additional risk factors such as chemotherapy, age or other medical conditions can be included as overall BED = radiation BED + risk factor BED. The latter is determined from clinical studies which contain multiple radiation dose levels with and without the risk factor, where an isoeffect can be identified.^19,54

3. Calculations which involve a specified bioeffect in a given tissue or tumour type should be done only using the same α/β ratio; it follows that different α/β ratios cannot be used to describe the same bioeffect.

4. It is assumed that the α/β ratio reflects an average value during treatment. During a course of radiotherapy lasting 4–8 weeks, the ratio is probably stable only in the case of slow growing tumours and slow cell turnover tissues.

5. In acute reacting tissues, fast growing tumours or normal tissues that exhibit real or apparent acceleration of their proliferation rates during treatment, the α/β ratio may itself increase.²⁴

6. In situations where under- or overdose has occurred or in calculation of X-ray equivalent schedules, general advice for such calculations in the case of X-rays has been published elsewhere,⁵⁵ but the additional effect of RBE must be included, if there is any attempt to use (low LET) X-ray tissue tolerances or X-ray tumour control data. This becomes complicated, since a change in dose or dose placement may be accompanied by a change in LET, so changing the RBE.⁵⁶

7. Methods for solving interrupted treatments are available for conventional^57–59 and high LET radiotherapy.^37,60

Conclusions

The major contributions of Oliver Scott and Jack Fowler to radiation biology⁶¹ have encouraged research in basic and applied radiobiology. Both would be delighted to see that modelling approaches continue to support and help guide safer and more effective radiotherapy, including newer developments in particle therapy, although they would probably express concerns as to whether the present momentum will continue in the future. They also fostered multidisciplinary teams to solve difficult problems, with active participation by medically qualified radiobiologists⁶² (as was Oliver Scott) and those from physics backgrounds (as was Jack Fowler).