Abstract
This study analyzes the core energy consumption among countries’ specific variables by Environmental Kuznets Curve hypothesis (EKC), for a panel data of 29 (14 developed and 15 developing) countries during the period of 1977–2014. By assessing Generalized Method of Moments (GMM) regressions with first generation tests such as common root, individual Augmented Dickey-Fuller (ADF), and individual root-Fisher-PP which have been computed individually, the results confirm the EKC hypothesis in the case of emissions of solid, liquid, gases, manufacturing industries and also construction. Hence, we computed the cointegration test by Pedroni Kao from Engle-Granger based and Fisher. Since the variables are co-integrated, a panel vector error correction model is estimated in GDP per capita, emission from manufacturing industries, arms import, commercial service export, and coal rent, in order to perform Pairwise Granger Causality test and indicate Vector Error Correction (VEC), with co-integration restrictions. Moreover, the statistical finding from VEC short-run unidirectional causality from GDP per capita growth to manufacturing industries and coal rent, as well as the causal link with manufacturing industries and commercial service export. Additionally, there occurred no causal link among economic growth, arm import and coal rent.
1. Introduction
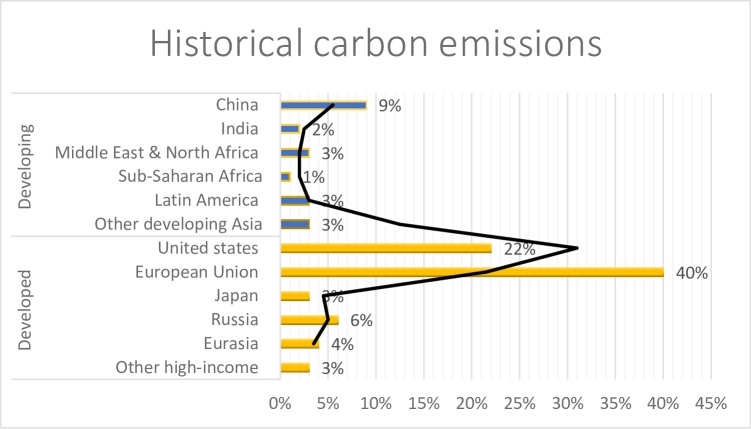
Developing countries, with the rapid development of economy, are leading the growth of energy consumption globally. The energy consumption of developing countries was 7.64×109 (ton) oil equivalent (toe), accounting for 58.1% in 2005 all over the world, also in 2015 the consumption of energy increase in developing countries by 2.38×109 (toe). The level of energy intensity in China (8.34), Russia (9.49) and Germany (3.88), indicate a big gap between developing and developed countries. Another side the developing countries decrease energy intensity slowly and try to achieve the bottleneck problems with well-developed technology [1,2]. Furthermore, 79% of developed countries are responsible for historical carbon emission, in which the USA is 22%, the European Union is 40% and China is 9% Fig 1. There are 60% of CO2 emission responsible countries are China and USA, it’s is two-fifth and these top polluters do about the heat-trapping gases liable for global warming and their infections. Also in 2013 CO2 emission is 11 billion tons with 1.36 billion population. The 62% coal consumption cap has been announced by 2020 in China. The China and USA deal on greenhouse gas emission growth by 2030, while its significant and also little effected on the global thermostat. The USA government estimates China doubling it emission by 2040 cause of major changes and reliant on fossil fuels for steel and electricity production. There was 2.6 billion tons CO2 emission in India with 1.2 billion population, 2 billion tons in Russia with 143.5 million population, 1.4 billion tons in Japan with 127 million population, 836 million tons in Germany with 80.6 million population in 2013.
Fig 1. Historical carbon emission.
Source: LUCEF, 1850-2011(CAIT v2.0).
The solid fuel consumption varies in different countries regarding with magnitude of indicators, the darker shade, and higher the value. The China highest value in all over the world is 7,431,146.00. Bolivia is the lowest value with 0.00. CO2 is naturally occurred with gas fixed by photosynthesis into organic matter, also biomass burning and the byproduct of fuel consumption of fossil emitted from land use to changes along with industrial processes. The industrial revolution has rapidly increased global warming and atmospheric carbon dioxide [3]. Burning wood, oil, coal and waste material, such as in the industrial process of cement has been increased CO2 emission.
The USA is one of a top developed country by CO2 emission from gaseous fuel consumption in all over the world and 1.43 million kt that account for 21.72% of world’s CO2 emission from gaseous fuel consumption in 2014. Other five top countries (China, Russian Federation, Iran, and Japan), 48.97% account of it. In 2014, estimated emission of CO2. from fuel gaseous was at 6.6 million. Furthermore, it’s injected into the melting zone, auto-ignited (Solid combustion zone) and the methane concentrations of 0 to 5% vol, also the total calorific heat input unchanged. The pattern of heat in the melting zone was recorded by non-contact thermal infrared imager and thermocouples. Significantly, the result indicated that extend the melting zone from the upstream and it higher than from coke sintering, without increasing the energy consumption. Therefore, the saving potential was evaluated by reducing the heat 4 to 8%. [4,5]. The continue modification and well-developed technology have been directly affected by solid combustion zone, like 15% energy consumption in the iron and steel industry in China and 26% consumption in the pre-treatment process. The CH4 emission was approximately 5.1million tones, equivalent to 10.78 million of CO2, it indicated the third largest source of CH4 emission.
Municipal solid waste (MSW) landfills 69% of the solid waste which received from USA (94% of total landfills emission). Furthermore, the waste of energy emission was accounted 12.1 million metric tonnes of CO2 emission competitively 1745 million emitted in the field of transportation.
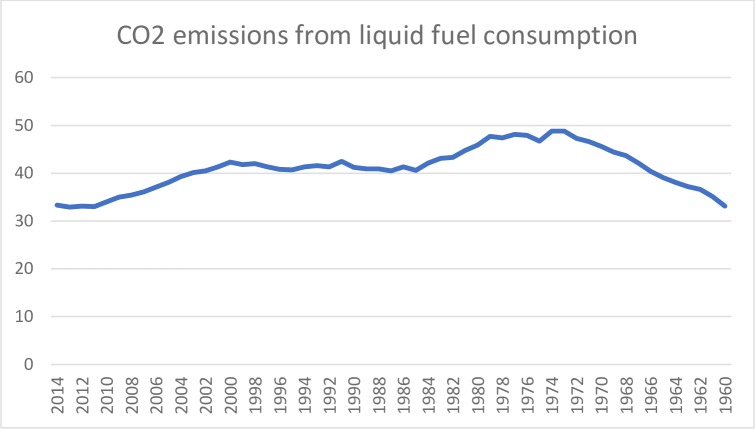
While 26.5 million tonnes incineration is used to treat waste in the USA, or approx. 7 to 19 percent of solid waste generated. Meanwhile, 3.2% CO2. emission have been increased in 2010 and total greenhouse gases were equivalent to 6.82% billion metric tonnes of CO2. While CO2 is found in our environment but the problem is that the industrial revolution has increased the quantity of it in the 19th century by industrial modification Fig 2, because it’s most prominent greenhouse gases climate change and most of the scientists agree on that is not only for Chinese hoax. The Carbon dioxide information analysis center (CDIAC), realized more than 400 billion metric tonnes in atmosphere from fossil consumption and especially production of cements since 1751. Also, the combustion of solid and liquid fossil fuel causes of 4th of all CO2 which is 9.9 billion tones in 2014.
Fig 2. CO2 emission from liquid fuel consumption.
Source: Authors’ amplification.
Environmental Kuznets Curve (EKC) has been already explored different ideas in CO2 emission. The EKC growth strategy is to grow now and clean later is the too much intensive resource and huge environmental cost and developing countries should follow the growth path than that of EKC.[6–8] In the emerging economies a substantial fraction of the production satisfies the consumption in developed countries cause of the notorious carbon leakage problem and embodied of carbon emission in exports not contacted in the production-based emission accounting (PBA) [9]. The U-shaped of EKC is the relationship between income and environmental degradation and it increases as income increases and declines after income exceeds, suggest that growth is the cause and cure of air pollution [10]. However, the consequence of economic growth and trade policies should the align with energy sector [11]. The economic growth is not suitable and for environmental protection so, therefore, we should lower the economic growth. [12–14].
Such EKC tested for historical perspective along with fuel prices and growth in Sweden in the period of 1870–1997[15]. Explored the energy consumption and study of the electricity in Saudi Arabia with Time-Varying parameters vector autoregressive (TVP-VAR) in the period of 1970–2010. [16]. Study the dynamic impact and economic output and Carbon emission from 1991–2012[17]. Tested the EKC hypothesis for the solid waste generation with panel data from 1997–2010 in 32 European states [18]. Studied the technological progress and EKC, associated with economic growth and CO2 emission in panel data in 24 European nations from 1990–2013 [19]. Explored the transport energy by using EKC with the hypothesis in EU-27 countries from 1995–2009 [20].
The main feature of this paper is to distinguish from others on the bases on research samples, as well as several part of emission apart from CO2, namely CEMIC (CO2 emission from manufacturing industries and construction), AET (Arms export trend indicator), AIT (Arms import trend indicator), CSE (Commercial service export), IF (Insurance and financial service), CR (Coal rents (GDP)) and MIE (Military expenditure). Also, this study is unique on the bases of economic growth, Likewise, in decoupling of economic growth and CO2 emission in developing and developed on seven state, industrialization of CO2, renewable and non-renewable energy of 42 developing economy, three groups of renewable energy and southwest economic zone CO2 emission in China [21–25] has not indicated the 29 (14 developed and 15 developing) countries. Furthermore, how developing countries are creating effects on CO2 emission on other developed countries and how the manufacturing industries and military expenditure effects on the CO2 emission. The following logical structure and literature highlighted the EKC hypothesis along with the relationship between CO2 emission and economic growth. Section 3 is presented the data analysis with the econometric framework. Section 4 are shown empirical result and discussion, while the final section of the paper concludes and provides implication policies with recommendations.
2. Literature review
Catholic part of specific literature explores the association between EKC and the national income of the countries, and greater environmental quality and their effects on developed and developing countries Table 1. According to Kuznets’ inverted U-hypothesis, initial stage as per capita national income of countries rise, inequality in income distribution rises after reaching the highest degree, where the country develops and it is per capita income automatically rises in maximum level, and it falls as GDP per capita increases further [26]. Explored the study of 1955, and calculated the Kuznets’ ratio and found that, whereas developed countries tend to have a lower degree of inequality, the developing countries tend to have a higher degree of inequality [27]. That the evidence of inverted U-hypothesis, regarding the relationship between economic growth and inequality. It means those income inequalities where higher in developing countries compared to developed countries, but after that in particular stage, increase in economic growth will reduce the environmental pressure.
Table 1. Literature review of economic growth and CO2 emission.
| Study | Datasets | Econometric techniques | Period | Outcomes |
|---|---|---|---|---|
| [28] | 12 Western European countries | linear cointegration model | 1861–2015 | Elasticity of income of CO2 emission in all countries. The cointegration method of CO2 emission and GDP of countries. The study important for developing countries. |
| [29] | Tunisian | Vector Autoregressive (VAR) model. | 1980–2014 | Determined the influence factor of CO2 emission. Explored, the EKC with inverted U-shaped pattern in CO2 emission. |
| [30] | 21 industrial countries | Unit root test | 1960–1997 | The test result was consistent with narrow and wide application in different industrial countries. |
| [31] | 21 OECD countries | Univariate unit root tests | 1950–2014 | The per capita CO2 emission is less explosive at each quantile without smooth break in 21 OECD Countries. |
| [32] | Pakistan | ARDL approach | 2014 | Dynamic causality between energy consumption, economic growth and CO2 emission. |
| [33] | South African | ARDL approach, Engel Granger method. | 1960–2009 | Per capita has significant long positively effect in level of CO2. Find bidirectional causality between in income per capita and foreign trade. |
| [34] | 116 Countries | Panel vector autoregressive (PVAR), Generalized method of moment (GMM) | 1990–2014 | Energy consumption does not cause of regional level, Economic growth has negative casual impact on carbon emission, energy consumption positively causes of economic growth in sub-Saharan Africa. |
| [35] | 28 subsectors | Generalized Method of Moments (GMM) | 2002–2015 | FDI is positive predictor of environmental quality and reduce CO2 emission level. |
| [23] | 42 developing countries | Granger causality modeling, error correction model (ECM), Generalized Method of Moments (GMM) | 2002–2011 | In long the energy consumption positively contribute to economic growth. |
| [36] | India, Indonesia, China and Brazil | Autoregressive Distributed Lag (ARDL) | 1970–2012 | EKC finding that Brazil, China and Indonesia impact on income and reduce their CO2 emission. |
| [37] | 24 sub-Saharan African countries | Panel cointegration | 1980–2010 | Inverted U-Shaped EKC is not supported for these countries in long-run estimation; export have a positive and import have a negative impact on CO2 emission. |
| [38] | China and India | ARDL | 1965–2013 | EKC result supported by long-run positive impact on emission |
| 20 countries in Middle East and North Africa (MENA) | Regression | 1980–2014 | EKC impact by regression on population, affluence and technology framework. | |
| [19] | 5 economies of South Asia | FMOLS | 1971–2013 | Consumption of energy and population density will increase in long run. |
| [39] | 14 Asian countries | GMM | 1990–2011 | To support EKC by emissions and income per capita and results are statistically significant. |
| Middle East, North Africa, Sub-Saharan Africa | DOLS and VEC | 1980–2010 | The results of EKC indicate significance of renewable energy consumption. | |
| [40] | 25 OECD countries | FMOLS | 1980–2010 | EKC verified that non-renewable energy CO2 emissions renewable. |
Sources: Authors’ compiling by the literature review
The EKC point starting from [41] showed that there is an inverted U-Shaped and relationship between per capita income and energy intensity in 173 countries and found CO2 emission by error correction model [42]. Explored the EKC hypothesis for a panel of 20 countries with traditional inverted U-shaped relationship. [43] That study empirically related to economic and population growth and CO2 emission from 1990 to 2014. The cross-sectional study results dependent on slop homogeneity and heterogeneity. The common correlated effect means a group (CCEMG), indicated the population size, economic growth and the significant influence on the level of CO2 emission.
3. Data and methodology
3.1 Sample and variables
The data sample covers the period of 1977–2014 for a panel consisting of the 29 (14 developed and 15 developing) countries. Table 2 indicate the variables, used for analysis, as well as their definitions and the sources of data, are presented with different abbreviations. A part of preceding studies the EKC have already treated with different variables, like consumption of energy and economic growth. [23,28,32,42,44], while the other new variables such as corruption, electricity consumption, population urbanization, industrial revolution provides more consideration [30,45]. In CESFC, CEGFC, CELFC, CE, CEMIC control the trend of explanatory variables of AIT, CSE, IGD, CR, IF, ME and AL as well, high technology manufacturing sector includes high skill labor contribution in development and creating the significant effects on the economy. Furthermore, Table 3 summarized the turning points to identify the earlier studies.
Table 2. Variables description for the analysis.
| Variables | Definition | Unit measurement | Time frame availability | Data sources |
|---|---|---|---|---|
| GDP | GDP per capita | Constant 2010 US dollars | 1977–2017 | World Bank (NY.GDP.MKTP. KD) |
| GDPC | GDP Per capita growth | Annual % | 1977–2017 | World Bank (NY.GDP.PCAP.KD. ZG) |
| CESFC | Co emissions from solid fuel consumption | kt | 1977–2014 | World Bank (EN.ATM.CO2E.SF.KT) |
| CEGFC | Co emissions from gaseous fuel consumption | kt | 1977–2014 | World Bank (EN.ATM.CO2E.GF.KT) |
| CELFC | Co emissions from liquid fuel consumption | kt | 1977–2014 | World Bank (EN.ATM.CO2E.LF.KT) |
| CE | Co emissions | kt | 1977–2014 | World Bank (EN.ATM.CO2E. KT) |
| CEMIC | Co emissions from manufacturing industries and construction | % of total fuel combustion | 1977–2014 | World Bank (EN.CO2.MANF. ZS) |
| ME | Merchandise Export | % of total merchandise exports | 1977–2016 | World Bank (TX.VAL.MRCH. R2. ZS) |
| AET | Arms export trend indicator | Value | 1977–2017 | World Bank (MS.MIL.XPRT. KD) |
| MI | Merchandise Import | % of total merchandise imports | 1977–2016 | World Bank (TM.VAL.MRCH. R2. ZS) |
| AIT | Arms import trend indicator | Value | 1977–2017 | World Bank (MS.MIL.MPRT. KD) |
| CSE | Commercial service export | Current US dollar | 1977–2017 | World Bank (TX.VAL.SERV.CD.WT) |
| IGD | inflation GDP deflator | Annual % | 1977–2017 | World Bank (NY.GDP.DEFL.KD. ZG) |
| CR | Coal rents (GDP) | % of GDP | 1977–2016 | World Bank (NY.GDP.COAL. RT. ZS) |
| IF | Insurance and financial service | % of commercial service exports | 1977–2017 | World Bank (TX.VAL.INSF.ZS. WT) |
| MIE | Military expenditure | % of GDP | 1977–2017 | World Bank (MS.MIL.XPND.GD.ZS) |
| AL | Agriculture land | % of land area | 1977–2015 | World Bank (AG.LND. AGRI. ZS) |
Sources: Selection based on databases’ availability
Table 3. Turning points reached earlier studies by pollutant type.
| Pollutant types | Study | Datasets | Period | Econometric techniques | Turning points |
|---|---|---|---|---|---|
| CO2 emission | 173 countries | 1990–2014 | Error correction model | (402,125.361 US$) | |
| CO2 emission | 20 countries | 1870–2014 | Bivariate model | $18,955 and $89,540 (in 1990 US$) | |
| CO2 emission | 128 countries | 1990–2014 | cross-sectional dependence and slope homogeneity tests | Significant | |
| CO2 emission | 141 countries | 1970–2014 | Spatial Green Solow model | Statistically significant | |
| CO2 emission | India | 1970–2015 | autoregressive distributed lag (ARDL) | USD 2937.77 | |
| Renewable energy | Pakistan | 1970–2014 | autoregressive distributed lag (ARDL) | Significant | |
| CO2 emission | 27 Chinese cities | 2001–2005 | Panel data parameter estimation | 34,328 CNY and 47,669 CNY | |
| Industrial CO2 emission | USA | 1973–2015 | multilevel mixed-effect | Significant | |
| CO2 emission | China | 1995–2011 | Input-output analysis | Significant | |
| Fuel energy consumption | East Asian and Pacific countries | 1990–2014 | Generalized Method of Moment (GMM) | $5112.65 |
Sources: Authors’ compiling by the literature review
While MI and AET control the GDP, high manufacturing and export development creating negative aspects. Initially per capita increase the wealth also increases the CO2 emission. However, arms import has created also significant effects on CESFC, CEGFC, and CEMIC but not creating effects on CE Table 4. In empirical methodology, in what we follow, we start by testing unit roots all explanatory variables individually in panel data. If the variables have found non-stationary, we investigate the prevailing long run cointegration relationship and investigate their magnitude for long-run stationary. We employ a class of panel unit root test and panel cointegration test individually on all explanatory variables, which allow the serial correlation among the cross-section, i.e. the so-called second-generation test. Augmented IPS used by cross sectional [46] panel unit root test by Pesaran (2007) and as for panel cointegration used error-correction by Westerlund (2007), which both account for possible cross-sectional dependencies for individual explanatory variables. The key variables- CO2 emission of GDP (Constant 2010 US dollars) and per capita GDP (Annual %) growth along with other explanatory variables—in for both level and first difference. In the level case, we are unable to reject the null hypothesis, except for the GDP per capita growth, CO2 emission, arm import trend, commercial service export, and inflation GDP deflator.
Table 4. GMM regression with AB in n-Step.
| Dependent variables | |||||
|---|---|---|---|---|---|
| IDV | CESFC (1) |
CEGFC (2) |
CELFC (3) |
CE (4) |
CEMIC (5) |
| GDP | 13.417*** | 16.319*** | 2.557*** | -0.429*** | 6.731*** |
| GDPSQ | -7.539*** | -1.868* | -1.266* | -0.535* | -4.481*** |
| ME | -1.565* | 0.238* | -0.468* | 0.115* | -3.367*** |
| AET | 45.327*** | 15.195*** | 2.804*** | 0.446* | 11.343*** |
| MI | 2.772*** | -0.602* | -0.123* | -0.286* | 0.017* |
| AIT | 12.944*** | 2.188*** | 1.809** | -0.857* | 3.257*** |
| CSE | -5.080*** | 2.945*** | -4.878*** | -0.436* | -1.963*** |
| IGD | -0.739* | 0.368* | -0.776* | -0.532* | 0.274* |
| CR | 27.038*** | -0.809* | -0.276* | 1.053* | 3.970*** |
| IF | 16.766*** | -6.582*** | 2.311*** | -0.833* | 0.291* |
| MIE | -3.117*** | -3.044*** | -1.069* | -0.854* | -1.099* |
| AL | 0.652* | 0.465* | -0.756* | -0.429* | -1.755** |
| Sargan statistic | 0.384 | 0.102 | 0.827 | 0.212 | 0.185 |
| J-statistic | 8.520 | 17.220 | 5.080 | 12.021 | 17.319 |
| Obs | 480 | 480 | 480 | 480 | 480 |
| N Countries | 29 | 29 | 29 | 29 | 29 |
Sources: Computation by authors. Note: Please see, Table 2 for the variable’s definition.
*** specifies the statistically significant at 1% levels.
** specifies the statistically significant at 5% levels.
* specifies the statistically significant at 10% levels.
3.2 Econometric methods
EKC hypothesis, we followed the approach of [23,34,41,42,47–50]. The long-run relationship between polluted emission, GDP per capita, merchandise export, arms export, merchandise import, commercial service export, inflation GDP, coal rent, insurance, and financial service, military expenditure and agriculture land, is given as follows:
| (1) |
Where PE shows the polluted emission and i = 1,….,29 and t = 1977,….,2014 reveal the country and time, respectively whereas emission, which we take from solid, gases, and liquid fuel, CO2 emission and CO2 emission from manufacturing industries and construction. ait indicates the country fixed effect. The δ1i−δ13i are parameters of long-run elasticities, which are related to each explanatory variable of the panel εit, indicate estimated residuals, characterized for long-run equilibrium. Since the inverted U-shaped EKC hypothesis, ε2t is expected to be positive and ε3t is expected to be negative, also the monitoring value representing the turning points which is computed by τ = exp[−β1/(2β2)] [42,47,49]. Additionally, the research aims to establish the causal link between manufacturing industries and construction, economic growth, arms export, commercial service export and coal rent (GDP). Additionally, the Generalized Method of Moments (GMM) yields a steady and efficient parameter estimate in a regression, the explanatory variables are not strictly exogenous, heteroscedasticity and autocorrelation within existing [51]. The GMM is more efficient and effectual with an additional assumption that is the first difference in explanatory variables, which in turn allows the inclusion of more instruments. The GMM applied on 29 countries over 1977–2014 in order to analyze the impact of different explanatory variables on CO2 emissions. [52]. Thus, according to [53–55] first generation test such as common root-Levin, Lin (LLC), Chu and Breitung, individual (lm), Pesaran, shin (IPS), Augmented Dickey-Fuller (ADF), and individual root-Fisher-PP, and Hadri have been computed individually from all explanatory variables. Afterward, we computed the cointegration test by Pedroni, Kao from Engle-Granger based and Fisher (combined Johansen).
| (2) |
Where i = 1,….,29 and t = 1977,….,2014 for each country in panel data. Besides, the parameters ai and δi indicate the fixed effect and deterministic trend. It is computing by Engle-Granger, long term model, specified in Eq (2) is estimated in which one period lagged and residual as an error correction term.
The dynamic error correction model is represented below:
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
Where the first-difference operator indicates by Δ, the lag of length specified by q at one according to likelihood ratio test, and Ʋ specify serial uncorrelated error term.
4. Results
4.1 Descriptive statistics, correlation and unit root examination
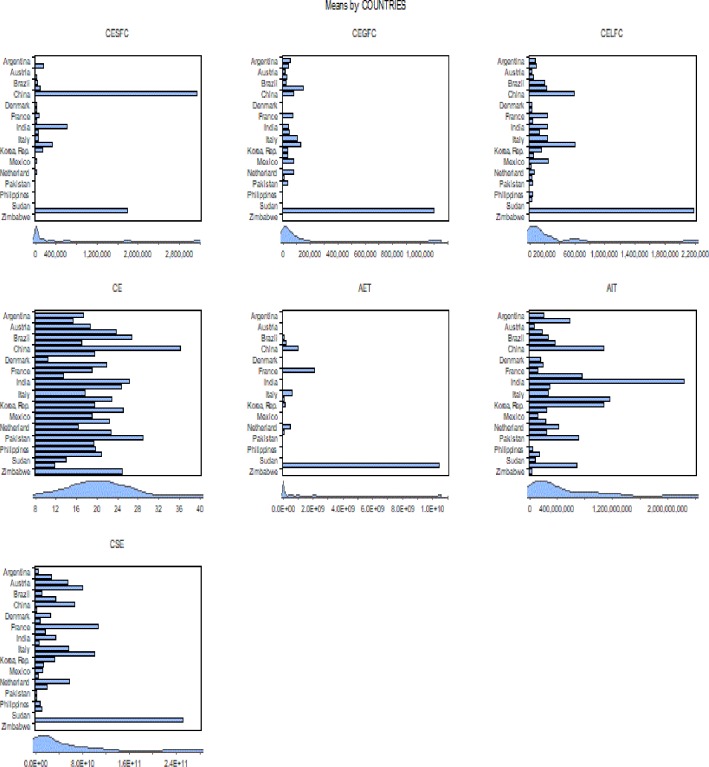
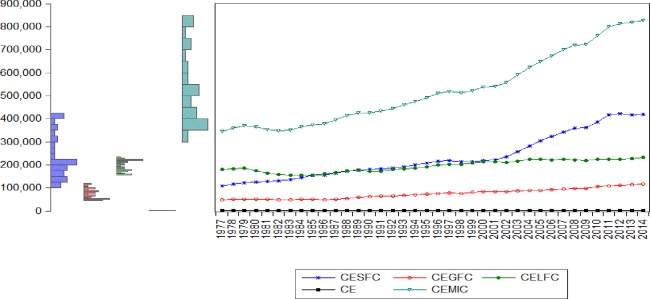
Table 5 shows the descriptive statistics of the particular variables of high mean value over the period of 1977–2014, countries by the type of pollutant emissions, China (CESFC, CE), USA (CEGFC, CELFC, AET, CSE) and India (AIT) show the highest mean value Fig 3 Although, Morocco (CR), Mexico (MI, ME), Philippine and Canada (ME), Mexico and Panama (MIE), Costa Rica and Argentina (IF) register the lowest mean value. Table 6 indicate the term of matrix correlation, relationships between energy consumption and selected instrumental variables, emissions such as CESFC, CEGFC, CELFC, CE, and CEMIC were noticed. Fig 4 explored the value of the mean, the manufacturing industries, and construction increase continuously comparatively solid, liquid and gaseous fuel consumption. The result computed by GMM method and in order to remove inconvenience, consider stationary test according to cross-section independence in first generation Table 7 unit root test in common root and individual intercept in level and 1st generation and Table 8 with first deference.
Table 5. Descriptive statistics (raw data).
| Variables | Mean | Median | Max | Min | Sta.Dev. | Skewness | Kurtosis | Jarque-Bera | Prob | Obs |
|---|---|---|---|---|---|---|---|---|---|---|
| GDP | 1,080,000 m | 309,000, m | 16,200,000, m | 6,750, m | 2,250,000m | 4.11 | 22.03 | 19,728.63 | 0.00 | 1,102 |
| GDPC | 2.209713 | 2.26 | 13.64 | -15.32 | 3.73 | -0.73 | 6.46 | 646.47 | 0.00 | 1,102 |
| CESFC | 231,943.80 | 21,536.29 | 7,499,587.00 | -113.68 | 752,749.80 | 5.98 | 47.32 | 96,758.81 | 0.00 | 1,102 |
| CEGFC | 74,688.62 | 17,552.10 | 1,432,767.00 | 0.00 | 202,645.60 | 4.84 | 26.34 | 29,322.15 | 0.00 | 1,102 |
| CELFC | 195,177.90 | 56,612.98 | 2,494,601.00 | 1,452.13 | 411,692.50 | 4.04 | 19.65 | 15,727.17 | 0.00 | 1,102 |
| CE | 525,318.10 | 114,734.90 | 10,291,927.00 | 2,002.18 | 1,276,136.00 | 4.23 | 22.95 | 21,557.75 | 0.00 | 1,102 |
| CEMIC | 20.54 | 19.53 | 49.15 | 0.00 | 7.29 | 0.69 | 3.77 | 115.22 | 0.00 | 1,102 |
| ME | 2.15 | 1.08 | 28.83 | 0.00 | 3.55 | 4.25 | 24.91 | 24,815.98 | 0.00 | 1,079 |
| AET | 943 m | 76 m | 15,700 m | 0.00 | 2,610 m | 3.79 | 17.03 | 6,592.15 | 0.00 | 622 |
| MI | 2.13 | 0.96 | 27.10 | 0.00 | 3.23 | 3.31 | 17.06 | 10,832.16 | 0.00 | 1,077 |
| AIT | 444 m | 200 m | 5,320, m | 0.00 | 638 m | 2.88 | 13.85 | 6,421.31 | 0.00 | 1,022 |
| CSE | 34,300 m | 10,100 m | 721,000 m | 13.5 m | 70,000 m | 5.13 | 38.34 | 55,969.20 | 0.00 | 992 |
| IGD | 25.76 | 4.61 | 3,057.63 | -27.05 | 176.35 | 13.00 | 186.77 | 1,581,752.00 | 0.00 | 1,102 |
| CR | 0.22 | 0.00 | 8.71 | 0.00 | 0.66 | 6.18 | 58.31 | 147,507.50 | 0.00 | 1,102 |
| IF | 3.56 | 2.30 | 22.08 | -2.28 | 3.66 | 1.36 | 4.88 | 439.85 | 0.00 | 964 |
| MIE | 2.39 | 2.12 | 10.67 | 0.00 | 1.47 | 1.04 | 4.67 | 316.74 | 0.00 | 1,071 |
| AL | 40.62 | 44.82 | 71.54 | 2.46 | 18.69 | -0.43 | 2.17 | 64.52 | 0.00 | 1,079 |
Note: m indicates million. Sources: Definition of variable available in Table 2.
Fig 3. Highest mean valuation of pollutant emission by 29 countries.
Source: Authors’ amplification.
Table 6. Matrix correlation.
| Prob | GDP | GDPC | CESFC | CEGFC | CELFC | CE | CEMIC | ME | AET | MI | CR | CSE | IGD | CR | IF | MIE | AL |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GDP | 1.00 | ||||||||||||||||
| GDPC | 0.022*** | 1.00 | |||||||||||||||
| CESFC | 0.571*** | 0.403*** | 1.00 | ||||||||||||||
| CEGFC | 0.945*** | -0.043* | 0.433*** | 1.00 | |||||||||||||
| CELFC | 0.941*** | 0.093*** | 0.606*** | 0.956*** | 1.00 | ||||||||||||
| CE | -0.280*** | 0.367*** | 0.220*** | -0.361*** | -0.203*** | 1.00 | |||||||||||
| CEMIC | 0.814*** | 0.294*** | 0.929*** | 0.731*** | 0.855*** | 0.034* | 1.00 | ||||||||||
| ME | -0.061*** | -0.092*** | -0.034* | -0.097** | -0.118*** | -0.299*** | -0.074** | 1.00 | |||||||||
| AET | 0.799*** | -0.021* | 0.374*** | 0.893*** | 0.897*** | -0.274*** | 0.657*** | -0.126*** | 1.00 | ||||||||
| MI | -0.096*** | -0.094*** | -0.028* | -0.134*** | -0.153*** | -0.215*** | -0.085*** | 0.086*** | -0.147*** | 1.00 | |||||||
| AIT | 0.121*** | 0.380*** | 0.413*** | 0.064*** | 0.183*** | 0.215*** | 0.343*** | -0.002* | 0.016* | -0.100*** | 1.00 | ||||||
| CSE | 0.837*** | -0.056* | 0.414*** | 0.733*** | 0.659*** | -0.378*** | 0.591*** | 0.040* | 0.520*** | 0.082** | 0.092*** | 1.00 | |||||
| IGD | -0.040* | -0.113*** | -0.052* | -0.061* | -0.046* | 0.087*** | -0.057* | -0.059* | -0.052* | -0.091*** | -0.06* | -0.088*** | 1.00 | ||||
| CR | 0.155*** | 0.298*** | 0.553*** | 0.078** | 0.201*** | 0.221*** | 0.446*** | 0.236*** | 0.034* | -0.096*** | 0.451*** | 0.111*** | -0.052* | 1.00 | |||
| IF | 0.443*** | -0.170*** | 0.049* | 0.386*** | 0.320*** | -0.250*** | 0.188*** | 0.092*** | 0.226*** | -0.036* | -0.133*** | 0.503*** | -0.021** | -0.029* | 1.00 | ||
| MIE | 0.350*** | 0.118*** | 0.146*** | 0.414*** | 0.444*** | 0.069* | 0.292*** | -0.216*** | 0.518*** | -0.283*** | 0.265*** | 0.144*** | -0.037*** | 0.015* | -0.093*** | 1.00 | |
| AL | 0.137*** | 0.061* | 0.211*** | 0.088*** | 0.143*** | -0.099*** | 0.198*** | 0.275*** | 0.151*** | -0.051* | 0.215*** | 0.162*** | -0.04* | 0.2*** | -0.005* | 0.205*** | 1.00 |
Sources: Computation by authors. Note: Please see, Table 2 for the variable’s definition
*** specifies the statistically significant at 1% levels.
** specifies the statistically significant at 5% levels.
* specifies the statistically significant at 10% levels
Fig 4. Mean value of pollutant emissions by years.
Source: Authors’ amplification.
Table 7. Unit root of individual variables (level).
| Level | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Individual intercept | Individual intercept and trend | ||||||||||
| Variables | CR | Individual root | Hadri | CR | Individual root | Hadri | |||||
| LLC | IPS | ADF | PP | LLC | Breitung | IPS | ADF | PP | |||
| GDP | 8.739 | 13.65 | 16.039 | 17.32 | 19.797*** | 3.537** | 6.503 | 5.835 | 31.959** | 40.602** | 15.174*** |
| GDPC | -13.66*** | -12.975*** | 280.248*** | 380.343*** | 4.285*** | -13.69*** | -14.14*** | -12.784*** | 263.21*** | 425.104*** | 2.308*** |
| CESFC | 3.314** | 3.172** | 49.643** | 51.126** | 17.197*** | 1.202** | 6.941 | 2.330** | 60.639** | 64.380** | 13.552*** |
| CEGFC | 3.025** | 6.834 | 18.342 | 25.46** | 16.917*** | 4.958 | 7.018 | 5.049 | 41.332** | 44.202** | 7.476*** |
| CELFC | 2.695** | 3.300** | 59.771** | 55.412** | 16.591*** | -1.041** | 2.297** | 1.086** | 59.143** | 36.310** | 9.302*** |
| CE | -4.601*** | -1.436** | 74.517** | 89.044*** | 16.995*** | -0.633** | -0.7237*** | -0.783** | 67.931** | 83.414*** | 11.111*** |
| CEMIC | 3.992*** | 6.072 | 26.559** | 28.959** | 17.839*** | 2.607*** | 6.2 | 3.839** | 36.388** | 39.174** | 14.375*** |
| ME | 1.475** | 2.156** | 42.353** | 68.413** | 18.215*** | -1.518** | -1.482** | -2.352** | 81.068** | 102.354*** | 7.125*** |
| AET | -2.149*** | -3.04*** | 79.523 | 110.819 | 11.871*** | .717** | -5.135*** | -1.167*** | 61.545 | 87.606 | 3.010*** |
| MI | 3.707** | 5.879 | 37.712** | 52.798** | 18.826*** | -2.416** | 2.854** | -2.118** | 88.14** | 113.464*** | 13.400*** |
| AIT | -6.969*** | -8.674*** | 185.301*** | 248.052*** | 6.569*** | -6.696*** | -5.215*** | -6.628*** | 139.403*** | 203.930*** | 7.207*** |
| CSE | 11.033 | 14.16 | 3.186 | 1.533 | 19.175 | 2.628** | 6.902 | 5.625 | 19.432 | 15.76 | 14.747*** |
| IGD | -5.321*** | -6.227*** | 147.989*** | 202.607*** | 2.050** | -6.39*** | -5.44*** | -6.066*** | 144.463*** | 204.946*** | 7.540*** |
| CR | -3.471*** | -3.471*** | 72.654*** | 117.598*** | 4.397*** | -3.677*** | -3.956*** | -2.407 | 61.733** | 81.987*** | 9.117*** |
| IF | -2.095*** | -2.917*** | 96.901*** | 113.746*** | 11.374*** | -6.89*** | -3.299*** | -4.257*** | 107.359*** | 127.867*** | 127.867*** |
| MIE | -3.048** | -0.505** | 62.802** | 60.849** | 15.849*** | -1.574*** | -1.968*** | -0.695 | 60.823 | 68.363 | 8.344*** |
| AL | -1.654** | 3.599** | 39.238** | 53.892** | 14.337*** | -0.876** | 1.459** | 1.960** | 38.680** | 45.758** | 12.985** |
Source: Computation by authors. Note: Please see, Table 2 for the variable’s definition
*** specifies the statistically significant at 1% levels.
** specifies the statistically significant at 5% levels.
* specifies the statistically significant at 10% levels.
Table 8. Unit root of individual variables (first difference).
| First difference | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Individual intercept | Individual intercept and trend | ||||||||||
| Variables | CR | Individual root | Hadri | CR | Individual root | Hadri | |||||
| LLC | IPS | ADF | PP | LLC | Breitung | IPS | ADF | PP | |||
| GDP | -6.892*** | -9.509*** | 217.311*** | 321.655*** | 14.3024*** | -11.7028*** | -7.733*** | -11.631*** | 229.986*** | 379.76*** | 9.978*** |
| GDPC | -26.19*** | -29.252*** | 692.647*** | 771.738*** | -5.267** | -23.208*** | -15.864*** | -26.604*** | 686.887*** | 5352.97*** | 9.362*** |
| CESFC | -12.81*** | -18.857*** | 430.863*** | 650.227*** | 7.574*** | -11.713*** | -6.668*** | -18.948*** | 431.265*** | 970.338*** | 2.286** |
| CEGFC | -8.981*** | -11.885*** | 293.098*** | 593.465*** | 4.065*** | -10.029*** | -2.635*** | -11.885*** | 243.819*** | 1059.95*** | 3.771*** |
| CELFC | -11.43*** | -14.09*** | 311.425*** | 584.042*** | 2.304*** | -10.102** | -7.062*** | -12.884*** | 269.772*** | 1016.83*** | 7.214*** |
| CE | -15.56*** | -20.566*** | 474.701*** | 779.588*** | .8016** | -13.235** | -13.79*** | -19.213*** | 429.375*** | 1259.51*** | 4.450*** |
| CEMIC | -9.513*** | -14.738*** | 334.107*** | 65.894*** | 10.289*** | -8.196*** | -5.221*** | -13.383*** | 281.423*** | 688.814*** | 3.978*** |
| ME | -14.77** | -20.001** | 462.271*** | 793.076*** | -0.17** | -12.353*** | -10.094** | -18.622*** | 389.420*** | 1483.56*** | 4.355*** |
| AET | -6.224*** | -11.817*** | 226.406*** | 488.133*** | 5.059*** | -1.429** | -4.816*** | -7.762*** | 175.094*** | 906.84*** | 25.403*** |
| MI | -11.5*** | -20.324*** | 468.653*** | 745.406*** | 2.193** | -7.822*** | -4.919*** | -18.521*** | 410.287*** | 2596.82*** | 5.858*** |
| AIT | -19.22*** | -22.654*** | 520.978*** | 782.556*** | -1.269*** | -15.856*** | -8.849*** | -17.968*** | 426.592*** | 3790.04*** | 4.138*** |
| CSE | -10.58*** | -14.029*** | 318.835*** | 551.193*** | 12.867*** | -11.013*** | -8.543*** | -13.078*** | 330.713*** | 863.553*** | 5.204*** |
| IGD | -22*** | -24.622*** | 589.251*** | 790.052*** | 3.526*** | -19.072*** | -14.156*** | -22.111*** | 486.624*** | 3147.26*** | 23.308*** |
| CR | -21.31*** | -25.57*** | 552.546*** | 653.620*** | -2.768*** | -18.106*** | -15.786*** | -23.328*** | 468.263*** | 656.767*** | 1.455** |
| IF | -22.4*** | -19.626*** | 442.645*** | 740.570*** | .0.187** | -29.65*** | -11.275*** | -16.375*** | 361.590*** | 1509.40*** | 6.791*** |
| MIE | -12.71*** | -14.969*** | 326.141*** | 635.900*** | 3.653*** | -10.897*** | -11.559*** | -12.816*** | 262.854*** | 1462.23*** | 16.187*** |
| AL | -8.498*** | -12.687*** | 291.138*** | 559.093*** | 5.3833*** | -7.563*** | -5.376*** | -10.829*** | 238.115*** | 796.856*** | 7.260*** |
Source: Computation by authors. Note: Please see, Table 2 for the variable’s definition
*** specifies the statistically significant at 1% levels.
** specifies the statistically significant at 5% levels.
* specifies the statistically significant at 10% levels.
As we notice the variables are non-stationary in their level and become stationary after 1st difference. [56–58]
4.2 Panel regression analysis
Panel regression indicate the GMM a regression method with AB in n-step. In the GMM estimation, the explanatory variable individually estimated regression with dependent variables. The panel data study by providing the solution of common problems in different developed and developing countries; the heterogeneity of behavior of the individual explanatory variable, the endogenous and simultaneity by bidirectional causality problem. This research paper will estimate a dynamic model (where the endogenous variables are included as explanatory variables along with more than one lag). The white period method applies for the coefficient covariance method individually for computation of CESFC, CEGFC, CELFC, CE, and CEMIC with other explanatory variables. The difference cross-sectional period was used for cross section in none period, the GMM iterations was computing in 2-step, that varies by cross-section in the white period.
According to Sargan statistic, all estimated models are statistically highly significant, and the value of J-Statistic, that could be explained between 5.08 and 17.31 of the variability in pollutant emission. Hence in the model, where the same number in instrument as a parameter, the optimized value of the objective function is zero. If the number of the instruments increased than parameters, the optimized value will be greater than zero, and the J-statistic used as the test of over-identifying moment condition. The J-statistics and instrumental rank, reported by Sargan statistics, where the instrumental rank greater in the individual model, than the number of estimated coefficients, we may use to construct Sargan test over the identifying restrictions. While in the null hypothesis over-identifying restriction is valid, the J-statistic in panel equation is different from the ordinary equation, where the Sargan statistics are distributed as a χ(ρ−k). Where the estimated coefficient is k and instrumental rank is ρ individual in each model. The Sargan test was computed in CESFC by scalar pval = @chisq (8.50,9.0) individually. The related coefficient of GDP per capita and squared GDP per capita are statistically significant in all estimated model, except model 4, the EKC hypothesis is confirmed in case of CE negatively impact. Furthermore, estimated regression appears to fit the data by the value of the Sargan test, they can explain all most 10% to 82% of the pollutant emission. The inverted U-Shaped curve emerges in all cases of harming secretions, except CE, with regard of GDPSQ, MI, AIT, CSE, IGD, IF, ME and AL; knowledge that expectation ecological damage reduction is not supported positively in estimated models, show a negative influence on pollutant emission. Also, we notice with some exceptional the renewable energies consumption reduces the pollution emission, like the higher GDP implies higher production and more insurance and financial services acquired [59]. In the term of merchandise export (ME) like [60]. The results of the variables employed to control for the scale effect and pollution conditions.
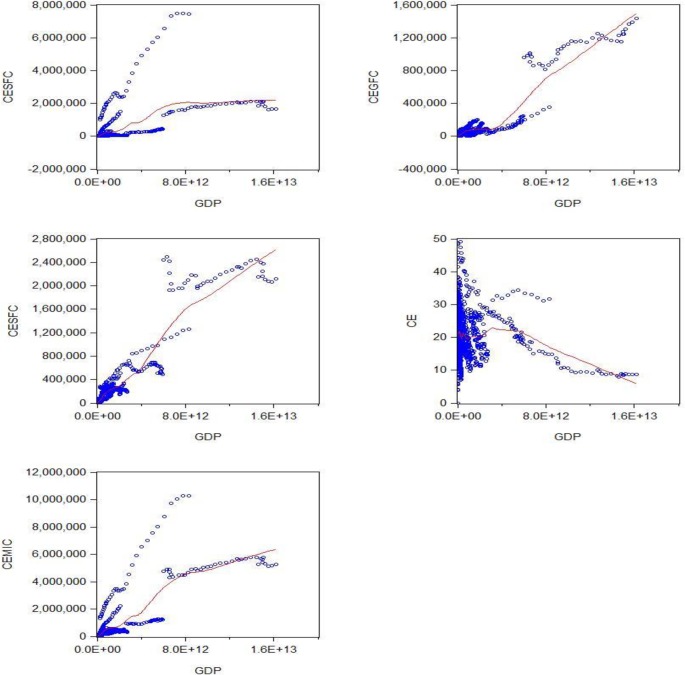
Fig 5 reveals the plotted graphs between GDP and pollutant emission. The EKC hypothesis appaired to be sustained since the inverted U-shaped curve tends to be fit properly in CESFC, and also indicated the sequence of U-shaped, in the term of CEGFC and CESFC, curve straightly going upward and we notice that the turning points are not in line. Hence in carbon emission the EKC curve coming down and notice that after high technology in industries and export reduce the level of EKC. In the last CEMIC the intensity of emission continuously in developing countries. Furthermore, [61] specified a higher likelihood of identifying turning points in the case of developed to developing countries.
Fig 5. Plotted graph between GDP per capita and CESFC, CEGFC, CESFC, CE and CEMIC.
Source: Authors’ amplification.
4.3 Co-integration and causal investigation
In the co-integration, the Padroni panel test is explored in Table 9. The dimensional approach of statistics, the autoregressive coefficient in the different developed and developing countries [53,62] for the unit root test on the estimated residual consideration for heterogeneity across the country and time factor. And the analysis of long-run cointegration relationships has been taken from developed and developing countries in the modern series analysis.
Table 9. Pedroni (Engle-Granger based) test.
| Panel A: Wintin-dimension | ||||||
| Panel co-integration test | Individual intercept | Individual intercept and trend | No intercept or trend | |||
| Statistic | Weighted Statistic | Statistic | Weighted Statistic | Statistic | Weighted Statistic | |
| Panel v-Statistic | 2.737*** | -3.115* | 22.167*** | -0.938* | -1.480* | -3.404* |
| Panel rho-Statistic | 0.658* | 1.524* | -1.226* | 2.162* | -0.248* | 1.393* |
| Panel PP-Statistic | -0.388* | 2.749* | -3.865*** | 0.195* | -0.144* | 1.822* |
| Panel ADF-Statistic | -0.242* | 2.993* | -3.652*** | 4.061 | -0.235* | 1.105* |
| Panel B: Between- dimension | ||||||
| Panel co-integration test | Individual intercept | Individual intercept and trend | No intercept or trend | |||
| Statistic | Statistic | Statistic | ||||
| Group rho-Statistic | 3.275* | 4.086 | 2.660* | |||
| Group PP-Statistic | 1.776* | 0.617* | 1.635* | |||
| Group ADF-Statistic | 2.981* | 0.236* | 2.977* | |||
Source: Computation by authors. The lag length was selected by Schwarz Info criterion.
Note: Please see, Table 2 for the variable’s definition
*** specifies the statistically significant at 1% levels.
** specifies the statistically significant at 5% levels.
* specifies the statistically significant at 10% levels.
The Padroni panel test in panel A, ADF statistically reject the null hypothesis of no co-integration with individual intercept, trend and No intercept or trend. The statistically mean value of individual autoregressive coefficient related with unit root test of individual each developed and developing the state. In the panel B, the co-integration employed with rho, PP and ADF statistics, and explored by the Kao Table 10 in Engle-Granger based test, the ADF (t-statistics) is 2.490 (sig) with residual variance. Where the vector of co-integration is homogenous in different states. The result provides the hypothesis of co-integration of developing and developed states variables.
Table 10. Kao (Engle Granger based) test.
| ADF (t-Statistic) | Residual variance | HAC variance |
|---|---|---|
| 2.490*** | 8.24E+21 | 2.64E+22 |
Source: Computation by authors. The lag length was selected by Schwarz Info criterion.
*** specifies the statistically significant at 1% levels.
** specifies the statistically significant at 5% levels.
* specifies the statistically significant at 10% levels.
The third test is a Fisher, that approach is used to underlying Johansen methodology by panel co-integration test [63], showed in Table 11. This panel co-integration test aggregates with the p-value of individual Johansen trace statistics and eigenvalue [64]; also reject the null hypothesis of no cointegration.
Table 11. Fisher (Combined Johansen) test.
| Hypothesized No. of CE(s) | Fisher Stat.* (from trace test) | Fisher Stat.* (from max-eigen test) |
|---|---|---|
| None | 135.8*** | 102.0*** |
| At most 1 | 64.86*** | 61.32*** |
| At most 2 | 32.51* | 32.51* |
Source: Computation by authors. The lag length was selected by Schwarz Info criterion and Probabilities are computed using asymptotic Chi-square distribution
*** specifies the statistically significant at 1% levels.
** specifies the statistically significant at 5% levels.
* specifies the statistically significant at 10% levels.
Onward, since the variables are co-integrated, a panel vector error correction model is estimated in order to perform Pairwise Granger Causality test Table 12, we reject the null that GDPC does not Granger cause CEMIC, and also in the opposite direction.
Table 12. Pairwise Granger causality tests.
| Null Hypothesis: | Obs | F-Statistic |
|---|---|---|
| CEMIC does not Granger Cause GDPC | 1073 |
13.732*** |
| GDPC does not Granger Cause CEMIC | 47.520*** | |
| AIT does not Granger Cause GDPC | 965 |
16.161*** |
| GDPC does not Granger Cause AIT | 4.293*** | |
| CSE does not Granger Cause GDPC | 961 |
1.510 |
| GDPC does not Granger Cause CSE | 11.346*** | |
| CR does not Granger Cause GDPC | 1073 |
21.069*** |
| GDPC does not Granger Cause CR | 5.530*** | |
| AIT does not Granger Cause CEMIC | 965 |
56.007*** |
| CEMIC does not Granger Cause AIT | 6.348*** | |
| CSE does not Granger Cause CEMIC | 961 |
133.750*** |
| CEMIC does not Granger Cause CSE | 22.872*** | |
| CR does not Granger Cause CEMIC | 1073 |
51.272*** |
| CEMIC does not Granger Cause CR | 3.889*** | |
| CSE does not Granger Cause AIT | 863 |
0.498 |
| AIT does not Granger Cause CSE | 3.675*** | |
| CR does not Granger Cause AIT | 965 |
4.190*** |
| AIT does not Granger Cause CR | 3.319** | |
| CR does not Granger Cause CSE | 961 |
0.009 |
| CSE does not Granger Cause CR | 0.929 |
Source: Computation by authors. The lag length was selected by Schwarz Info criterion.
Note: Please see, Table 2 for the variable’s definition
*** specifies the statistically significant at 1% levels.
** specifies the statistically significant at 5% levels.
* specifies the statistically significant at 10% levels.
Table 13. Indicate Vector Error Correction (VEC), with cointegration restrictions B (1,1) = 1 and the convergence attained after 1 iteration with t-statistics and Standard error Fig 6. The specification of VEC has five (k = 5) endogenous variables, GDPC, CEMIC, AIT, CSE and CR, the exogenous intercept C(d = 1) and lags include 1 to 2 (p = 1). Thus, there is (kp+d = 6) regression of each of the three-equation in the VEC individually.
Table 13. Vector error correction model.
| Error Correction: | Cointegration | Standard error | t-statistics | R-squared | F-statistic |
|---|---|---|---|---|---|
| D(GDPC) | -0.033 | -0.01641 | -2.04368 | 0.162128 | 26.05806 |
| D(CEMIC) | 2034.459 | -209.35 | 9.71799 | 0.690684 | 300.7023 |
| D(AIT) | 1093653 | -1525124 | 0.71709 | 0.049723 | 7.046426 |
| D(CSE) | 4.62E+08 | -3.20E+07 | 14.2740 | 0.291235 | 55.33518 |
| D(CR) | -0.002747 | -0.00132 | -2.08210 | 0.069086 | 9.994087 |
Source: Computation by authors. The lag length was selected by Schwarz Info criterion in cointegration restriction. Note: Please see, Table 2 for the variable’s definition
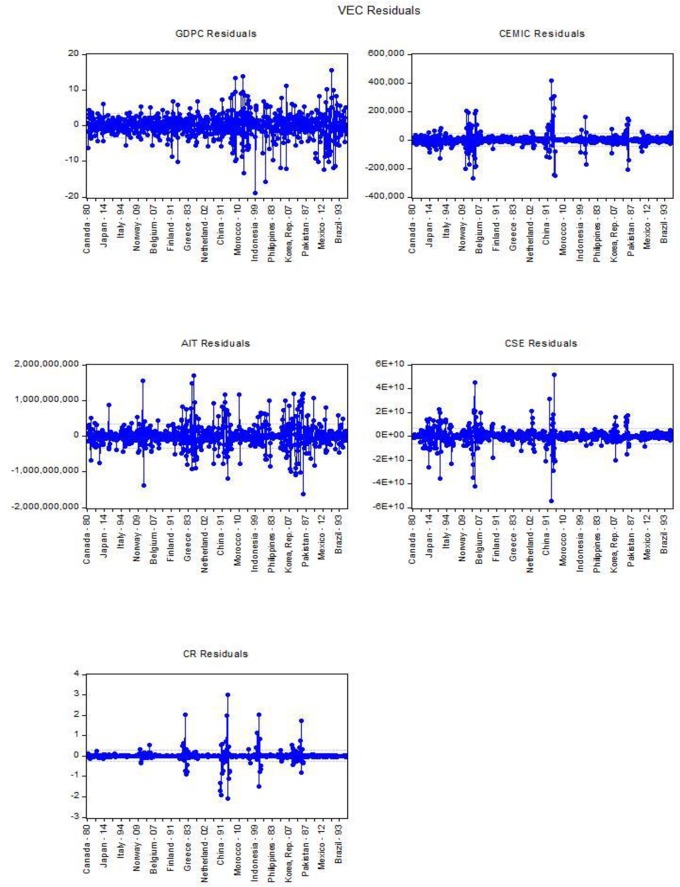
Fig 6. VEC residuals by states.
Source: Authors’ amplification.
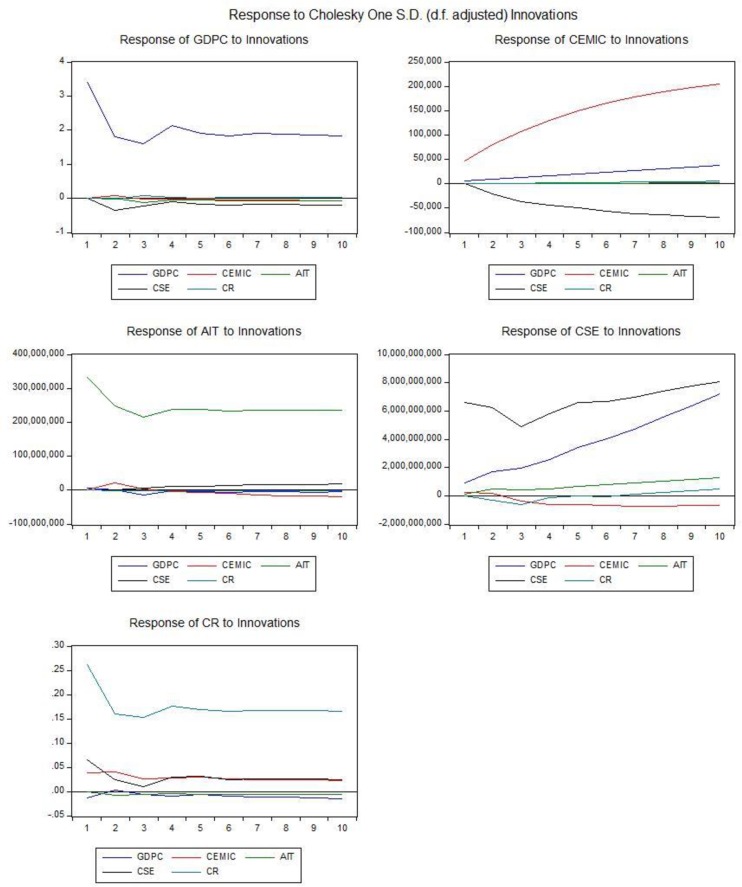
The effect of CEMIC has also been investigated by using impulse response by Cholesky one S. D (d.f. adjusted) innovation in decomposition method Fig 7, the impulse response of emission shock to Eqs 3–4 individually. The level of significance impulse function has been investigated at 95%. The result from variance decomposition indicate the individual variables effects. In order to measure the deviation method, which impulses to GDPC are explained by CEMIC, AIT, CSE, and CR. Eq 4 according to VAR lag order selection criteria the endogenous variables indicated significant relationship in lag-2 at Schwarz information criteria (SC) and lag-17 at Hannan-Quinn information criteria, the CO2 emission is not too much efficient in lag-17, therefore the Johansen Fisher Panel Cointegration Test is applied in lag (2–1 = 1), it indicates the significant p-value (0.000) in model Table 13 are cointegrated in that case we use Vector Error Correction Estimates (VECM) in lag-1 with cointegration restrictions. The t-test in error correction model indicate significant relationship among GDP per capita and manufacturing industries and construction (CEMIC) with 9.718 which is more than 1.96, concerning Eq 4 identify that 69.0% manufacturing industries and construction have the influence on the level of GDP per capita with F-statistics (300.702) comparatively others. In Eq 5 noticed the statistically insignificant influence on arms import (AIT) with 4.9% by GDP per capita. Hence, the commercial service export (CSE) also indicate the significant relationship with GDP per capita in Eq 6, 29.123% has the influence on the level of GDP per capita with F-statistics (55.335). Eq 7 indicates the coal rent (CR) has not too influence on GDP per capita with 6.90%. Moreover, the vector error correction term statistically significant in two endogenous variables, the analysis suggests that the above explanatory variables Table 13. are the main sources of volatility in different states by GDP per capita.
Fig 7. Impulse response.
Source: Authors’ amplification.
5. Conclusion
The objective of this research study was to determine the EKC hypothesis and afterward the causal relationships between carbon emission solid, liquid and gases fuel, merchandise export, economic growth, arms export trend, coal rents, and military expenditure, for a panel consisting of 29 countries the period 1977–2014.
In the panel data, we noticed cross-sectional dependence in each of the variables, we employed the Generalized Method of Movement/Dynamic Panel data, the transformation of first deference with white period instrumental weighted mix. The results of GMM regression confirmed the acquired hypothesis for emission of CO2 emission from liquid fuel consumption, CO2 emission from manufacturing industries, where the outcome of GMM estimation corroborated, furthermore the EKC approach for solid, liquid and fuel consumption emission and CO2 emission.
Moreover, the estimation of GDP per capita with a panel vector error correction model in order to performed Pairwise Granger Causality test. The model shows a short run unidirectional causality from GDP per capita growth to CO2 emission from manufacturing industries and construction, arms import, commercial service export, and coal rents, as well as a causal link between manufacturing industries, arms import, commercial service export and coal rent.
Likewise, the neoclassical view was endorsed in developing and developed countries, respectively the hypothesis impartiality. The main implication instigating from this research can be followed: 29 developed and developing countries should promote the use of renewable vitalities that are constantly restocked and which will not directly be diminished. Hence, the use of renewable vitalities will contribute to the decrease in GHGs emission.
Besides, 29 developed and developing countries may benefit from enhanced social stability, job opportunity by modernized technologies. Finally, as endeavors of future research, our aim to outspread the empirical analysis in order to verify and test the EKC hypothesis employing the environmental performance and encourage to developed countries to secure the environment especially for arms and huge manufacturing industries.
Acknowledgments
The authors admiringly acknowledge the financial support of the National Natural Science Foundation of China No: 71371087 of Jiangsu University, as well as thanks to my supervisor Dr. YuSheng Kong about review and editing. Hina (Rawaa) is thankful for the excellence idea also appreciates for the study support in the Republic of China (Zhenjiang). I would like to thanks to my parents and co-author who support me in different conceptual ideas and techniques.
Data Availability
All the relevant data are within the paper.
Funding Statement
Rabnawaz Khan and Dr. Yusheng Kong were supported by The National Natural Science Foundation of China No: 71371087 of Jiangsu University. Dr. Yusheng Kong was supported by The School of Finance and Economics, Jiangsu University, Zhenjiang 212013, People’s Republic of China, http://oec.ujs.edu.cn/en/index.
References
- 1.Wang B, Sun Y, Wang Z (2018) Agglomeration effect of CO2 emissions and emissions reduction effect of technology: A spatial econometric perspective based on China's province-level data. Journal of Cleaner Production 204: 96–106. [Google Scholar]
- 2.Xu B, Lin B (2018) Investigating the differences in CO2 emissions in the transport sector across Chinese provinces: Evidence from a quantile regression model. Journal of Cleaner Production 175: 109–122. [Google Scholar]
- 3.Luzzati T, Orsini M, Gucciardi G (2018) A multiscale reassessment of the Environmental Kuznets Curve for energy and CO2 emissions. Energy Policy 122: 612–621. [Google Scholar]
- 4.Cheng Z, Wang J, Wei S, Guo Z, Yang J, et al. (2017) Optimization of gaseous fuel injection for saving energy consumption and improving imbalance of heat distribution in iron ore sintering. Applied Energy 207: 230–242. [Google Scholar]
- 5.Mikayilov JI, Galeotti M, Hasanov FJ (2018) The impact of economic growth on CO2 emissions in Azerbaijan. Journal of Cleaner Production 197: 1558–1572. [Google Scholar]
- 6.Rashid Gill A, Viswanathan KK, Hassan S (2018) The Environmental Kuznets Curve (EKC) and the environmental problem of the day. Renewable and Sustainable Energy Reviews 81: 1636–1642. [Google Scholar]
- 7.Selden T SD (1994) Environmental quality and development: is there a Kuznets Curve for air pollution emissions. Journal of Environmental Economics and management: 409–423. [Google Scholar]
- 8.Al-mulali U, Tang CF, Ozturk I (2015) Estimating the Environment Kuznets Curve hypothesis: Evidence from Latin America and the Caribbean countries. Renewable and Sustainable Energy Reviews 50: 918–924. [Google Scholar]
- 9.Dong B, Wang F, Guo Y (2016) The global EKCs. International Review of Economics & Finance 43: 210–221. 10.1007/s12232-017-0277-4 [DOI] [Google Scholar]
- 10.Keho Y (2017) Revisiting the Income, Energy Consumption and Carbon Emissions Nexus: New Evidence from Quantile Regression for Different Country Groups. International Journal of Energy Economics and Policy 7: 356–363. [Google Scholar]
- 11.Ahmed K, Bhattacharya M, Shaikh Z, Ramzan M, Ozturk I (2017) Emission intensive growth and trade in the era of the Association of Southeast Asian Nations (ASEAN) integration: An empirical investigation from ASEAN-8. Journal of Cleaner Production 154: 530–540. [Google Scholar]
- 12.Dasgupta P HG (1979) Economic theory and exhaustible resources Cambridge Cambridge University; p. [Google Scholar]
- 13.Grossman G KA (1995) Economic growth and the environment. Quarterly Journal of Economics 100: 353–377. [Google Scholar]
- 14.W B (1992) Economic growth and the environment: whose growth? whose environment. World Development: 481–496. [Google Scholar]
- 15.Lindmark M (2002) An EKC-pattern in historical perspective: carbon dioxide emissions, technology, fuel prices and growth in Sweden 1870–1997. Ecological Economics 42: 333–347. [Google Scholar]
- 16.Mezghani I, Ben Haddad H (2017) Energy consumption and economic growth: An empirical study of the electricity consumption in Saudi Arabia. Renewable and Sustainable Energy Reviews 75: 145–156. [Google Scholar]
- 17.Bhattacharya M, Awaworyi Churchill S, Paramati SR (2017) The dynamic impact of renewable energy and institutions on economic output and CO2 emissions across regions. Renewable Energy 111: 157–167. [Google Scholar]
- 18.Arbulú I, Lozano J, Rey-Maquieira J (2015) Tourism and solid waste generation in Europe: A panel data assessment of the Environmental Kuznets Curve. Waste Management 46: 628–636. 10.1016/j.wasman.2015.04.014 [DOI] [PubMed] [Google Scholar]
- 19.Ahmed A, Uddin GS, Sohag K (2016) Biomass energy, technological progress and the environmental Kuznets curve: Evidence from selected European countries. Biomass and Bioenergy 90: 202–208. [Google Scholar]
- 20.Pablo-Romero MP, Cruz L, Barata E (2017) Testing the transport energy-environmental Kuznets curve hypothesis in the EU27 countries. Energy Economics 62: 257–269. [Google Scholar]
- 21.Wu Y, Zhu Q, Zhu B (2018) Decoupling analysis of world economic growth and CO2 emissions: A study comparing developed and developing countries. Journal of Cleaner Production 190: 94–103. [Google Scholar]
- 22.Dong F, Wang Y, Su B, Hua Y, Zhang Y (2019) The process of peak CO2 emissions in developed economies: A perspective of industrialization and urbanization. Resources, Conservation and Recycling 141: 61–75. [Google Scholar]
- 23.Ito K (2017) CO2 emissions, renewable and non-renewable energy consumption, and economic growth: Evidence from panel data for developing countries. International Economics 151: 1–6. [Google Scholar]
- 24.Amri F (2017) Intercourse across economic growth, trade and renewable energy consumption in developing and developed countries. Renewable and Sustainable Energy Reviews 69: 527–534. [Google Scholar]
- 25.Tian X, Bai F, Jia J, Liu Y, Shi F (2019) Realizing low-carbon development in a developing and industrializing region: Impacts of industrial structure change on CO2 emissions in southwest China. Journal of Environmental Management 233: 728–738. 10.1016/j.jenvman.2018.11.078 [DOI] [PubMed] [Google Scholar]
- 26.J A Kuznet’s Inverted U-Hypothesis on Income Inequality | Economics. Economics discussion.
- 27.Ahmed KR, Mujeeb Ur & Ozturk Ilhan(2017) What drives carbon dioxide emissions in the long-run? Evidence from selected South Asian Countries. Renewable and Sustainable Energy Reviews 70: 1142–1153. [Google Scholar]
- 28.Mikayilov JI, Hasanov FJ, Galeotti M (2018) Decoupling of CO2 emissions and GDP: A time-varying cointegration approach. Ecological Indicators 95: 615–628. [Google Scholar]
- 29.Talbi B (2017) CO2 emissions reduction in road transport sector in Tunisia. Renewable and Sustainable Energy Reviews 69: 232–238. [Google Scholar]
- 30.Karakaya E, Alataş S, Yılmaz B (2017) Replication of Strazicich and List (2003): Are CO2 emission levels converging among industrial countries? Energy Economics. [Google Scholar]
- 31.Cai Y, Chang T, Inglesi-Lotz R (2018) Asymmetric persistence in convergence for carbon dioxide emissions based on quantile unit root test with Fourier function. Energy 161: 470–481. [Google Scholar]
- 32.Mirza FM, Kanwal A (2017) Energy consumption, carbon emissions and economic growth in Pakistan: Dynamic causality analysis. Renewable and Sustainable Energy Reviews 72: 1233–1240. [Google Scholar]
- 33.Kohler M (2013) CO2 emissions, energy consumption, income and foreign trade: A South African perspective. Energy Policy 63: 1042–1050. [Google Scholar]
- 34.Acheampong AO (2018) Economic growth, CO2 emissions and energy consumption: What causes what and where? Energy Economics 74: 677–692. [Google Scholar]
- 35.Sung B, Song W-Y, Park S-D (2018) How foreign direct investment affects CO2 emission levels in the Chinese manufacturing industry: Evidence from panel data. Economic Systems 42: 320–331. [Google Scholar]
- 36.Alam MM, Murad M, Noman A, Ozturk I (2016) Relationships among Carbon Emissions, Economic Growth, Energy Consumption and Population Growth: Testing Environmental Kuznets Curve Hypothesis for Brazil, China, India and Indonesia. 477–479 p. [Google Scholar]
- 37.Ben Jebli M, Ben Youssef S, Ozturk I (2015) The Role of Renewable Energy Consumption and Trade: Environmental Kuznets Curve Analysis for Sub-Saharan Africa Countries. African Development Review 27: 288–300. [Google Scholar]
- 38.Adebola Solarin S, Al-Mulali U, Ozturk I (2017) Validating the environmental Kuznets curve hypothesis in India and China: The role of hydroelectricity consumption. Renewable and Sustainable Energy Reviews 80: 1578–1587. [Google Scholar]
- 39.Apergis N, Ozturk I (2015) Testing Environmental Kuznets Curve hypothesis in Asian countries. Ecological Indicators 52: 16–22. [Google Scholar]
- 40.Ben Jebli M, Ben Youssef S, Ozturk I (2016) Testing environmental Kuznets curve hypothesis: The role of renewable and non-renewable energy consumption and trade in OECD countries. Ecological Indicators 60: 824–831. [Google Scholar]
- 41.Bimonte S, Stabile A (2017) Land consumption and income in Italy: a case of inverted EKC. Ecological Economics 131: 36–43. [Google Scholar]
- 42.Awaworyi Churchill S, Inekwe J, Ivanovski K, Smyth R (2018) The Environmental Kuznets Curve in the OECD: 1870–2014. Energy Economics 75: 389–399. [Google Scholar]
- 43.Dong K, Hochman G, Zhang Y, Sun R, Li H, et al. (2018) CO2 emissions, economic and population growth, and renewable energy: Empirical evidence across regions. Energy Economics 75: 180–192. [Google Scholar]
- 44.Armeanu D VG, Andrei JV,Gherghina ŞC, Drăgoi MC, Teodor C (2018) Exploring the link between environmental pollution and economic growth in EU-28 countries: Is there an environmental Kuznets curve? PloS one 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Aslan A, Destek MA, Okumus I (2018) Sectoral carbon emissions and economic growth in the US: Further evidence from rolling window estimation method. Journal of Cleaner Production 200: 402–411. [Google Scholar]
- 46.Im KS, Pesaran M.H, Shin Y(2003) Testing for unit roots in heterogenous panels Journal of Econometrics,: 53–74. [Google Scholar]
- 47.Balado-Naves R, Baños-Pino JF, Mayor M (2018) Do countries influence neighbouring pollution? A spatial analysis of the EKC for CO2 emissions. Energy Policy 123: 266–279. [Google Scholar]
- 48.Danish, Zhang B, Wang B, Wang Z (2017) Role of renewable energy and non-renewable energy consumption on EKC: Evidence from Pakistan. Journal of Cleaner Production 156: 855–864. [Google Scholar]
- 49.Sinha A, Shahbaz M (2018) Estimation of Environmental Kuznets Curve for CO2 emission: Role of renewable energy generation in India. Renewable Energy 119: 703–711. [Google Scholar]
- 50.Du G, Liu S, Lei N, Huang Y (2018) A test of environmental Kuznets curve for haze pollution in China: Evidence from the penal data of 27 capital cities. Journal of Cleaner Production 205: 821–827. [Google Scholar]
- 51.Berk I, Kasman A, Kılınç D (2018) Towards a common renewable future: The System-GMM approach to assess the convergence in renewable energy consumption of EU countries. Energy Economics. [Google Scholar]
- 52.Hasanov FJ, Liddle B, Mikayilov JI (2018) The impact of international trade on CO2 emissions in oil exporting countries: Territory vs consumption emissions accounting. Energy Economics 74: 343–350. [Google Scholar]
- 53.Apergis N, Payne JE (2010) The emissions, energy consumption, and growth nexus: Evidence from the commonwealth of independent states. Energy Policy 38: 650–655. [Google Scholar]
- 54.Ozcan B (2013) The nexus between carbon emissions, energy consumption and economic growth in Middle East countries: A panel data analysis. Energy Policy 62: 1138–1147. [Google Scholar]
- 55.Pao H-T, Yu H-C, Yang Y-H (2011) Modeling the CO2 emissions, energy use, and economic growth in Russia. Energy 36: 5094–5100. [Google Scholar]
- 56.Hadri K (2000) Testing for stationarity in heterogeneous panel data. Econometric Journal 3: 148–161. [Google Scholar]
- 57.Perron P (1988) Testing for a Unit Root in Time Series Regression. Biometrika 75: 335–346. [Google Scholar]
- 58.Banerjee JJD A., Galbraith J. W., and Hendry D. F. (1993) Cointegration, Error Correction, and the Econometric Analysis of Non-Stationary Data Oxford: Oxford University Press. [Google Scholar]
- 59.Xu H, Li Y, Huang H (2017) Spatial Research on the Effect of Financial Structure on CO2 Emission. Energy Procedia 118: 179–183. [Google Scholar]
- 60.Tang X, Jin Y, Wang X, Wang J, McLellan BC (2017) Will China’s trade restructuring reduce CO2 emissions embodied in international exports? Journal of Cleaner Production 161: 1094–1103. [Google Scholar]
- 61.Iwata H, Okada K, Samreth S (2010) Empirical study on the environmental Kuznets curve for CO2 in France: The role of nuclear energy. Energy Policy 38: 4057–4063. [Google Scholar]
- 62.Apergis N, Payne JE (2009) Energy consumption and economic growth in Central America: Evidence from a panel cointegration and error correction model. Energy Economics 31: 211–216. [Google Scholar]
- 63.Johansen S, xf, ren (1991) Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models. Econometrica 59: 1551–1580. [Google Scholar]
- 64.Lean HH, Smyth R (2010) CO2 emissions, electricity consumption and output in ASEAN. Applied Energy 87: 1858–1864. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All the relevant data are within the paper.