A non-dimensional parameter for classification of the flow in intracranial aneurysms. I. Simplified geometries

Abstract

Non-dimensional parameters are routinely used to classify different flow regimes. We propose a non-dimensional parameter, called Aneurysm number (An), which depends on both geometric and flow characteristics, to classify the flow inside aneurysm-like geometries (sidewalls and bifurcations). The flow inside aneurysm-like geometries can be widely classified into (i) the vortex mode in which a vortex ring is formed and (ii) the cavity mode in which a stationary shear layer acts similar to a moving lid of a lid-driven cavity. In these modes, two competing time scales exist: (a) a transport time scale, T_t, which is the time scale to develop a shear layer by transporting a fluid particle across the expansion region, and (b) the vortex formation time scale, $T_v$. Consequently, a relevant non-dimensional parameter is the ratio of these two time scales, which is called Aneurysm number: An = T_t/$T_v$. It is hypothesized, based on this definition, that the flow is in the vortex mode if the time required for vortex ring formation $T_v$ is less than the transport time T_t (An ≳ 1). Otherwise, the flow is in the cavity mode (An ≲ 1). This hypothesis is systematically tested through numerical simulations on simplified geometries and shown to be true through flow visualizations and identification of the main vortex and shear layer. The main vortex is shown to evolve when An ≳ 1 but stationary when An ≲ 1. In fact, it is shown that the flows with An ≲ 1 (cavity mode) are characterized by much smaller fluctuations of wall shear stress and oscillatory shear index relative to flows with An ≳ 1 (vortex mode) because of their quasi-stationary flow pattern (cavity mode) compared to the evolution and breakdown of the formed vortex ring (vortex mode).

I. INTRODUCTION

Non-dimensional parameters have been used to characterize the flow since the early nineteenth century; e.g., the Reynolds number, the ratio of inertia to viscous forces, has been used to classify the flow into laminar and turbulence regimes,¹ or the Mach number, the ratio of fluid velocity to the speed of sound, has been used to classify the flow into compressible and incompressible regimes. Here we investigate the ability of a non-dimensional parameter to classify the flow in aneurysm-like geometries, which are localized enlargements or ballooning on an artery (pipe); e.g., see Fig. 1. Such flow classification with a simple parameter can provide insight into the flow even before any detailed flow measurement or simulation. The local flow is known to affect the initiation, growth, and rupture of an aneurysm.^2,3

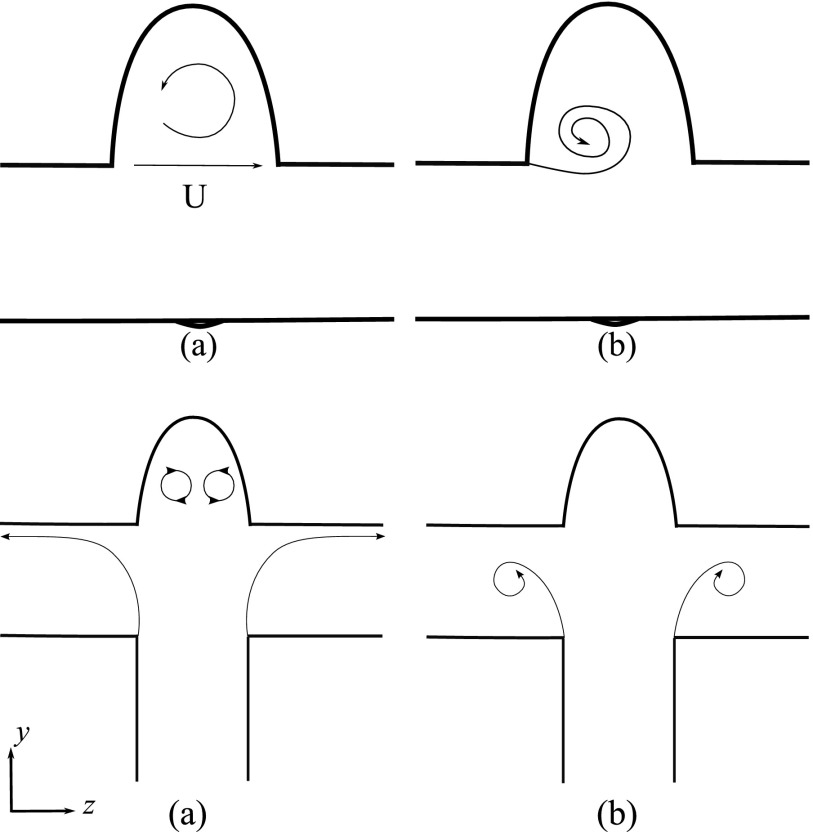
FIG. 1.

Schematic illustration of (a) the cavity mode with a stationary shear layer and (b) the vortex mode with an evolving ring-like vortex in sidewall (upper row) and bifurcation (lower row) geometries.

The hemodynamics in aneurysms depends on the geometry and flow conditions in the parent artery. Le et al. classified the main features of the flow in sidewall aneurysms into (upper row of Fig. 1) (1) the cavity mode and (2) the vortex mode. In the cavity mode, the jet in the parent artery transports fluid across the neck and acts as the equivalent of a moving rigid-lid driving a cavity-like flow inside the aneurysm dome [upper row of Fig. 1(a)]. The slowly circulating flow in the dome is separated from the jet flow in the artery by a quasi-steady shear layer across the entire neck [upper row of Fig. 1(a)]. The shear layer extends from the proximal to the distal wall, where it may exhibit flapping instabilities.⁴ In the vortex mode, however, the shear layer originates at the intersection of the parent artery and the proximal neck, becomes unstable, and rolls up to form a vortex ring that grows as it moves across the neck and breaks down when it hits the distal wall [upper row of Fig. 1(b)]. These flow modes can be observed in flow visualizations reported in the literature as well; e.g., see Fig. 4 of Le et al.,⁴ Fig. 3 of Hope et al.,⁵ Fig. 7 of Sheard et al.,⁶ Fig. 8 of Asgharzadeh et al.,⁷ and Fig. 10 of Le et al.⁸—see Sec. IV D for more details.

Le et al.⁴ observed a vortex ring in an intracranial aneurysm (IA) when flow in the parent artery had a high pulsatility but a cavity mode at low pulsatility. They,⁴ through simulations with different inlet waveforms on a single geometry, found that the only parameter in the waveform that affects the flow mode is the pulsatility index⁹ (defined as $\frac{△U}{U}$, where U is the bulk velocity and △U is the difference between the inlet peak systole and minimum diastole velocities during the cardiac cycle). The other parameters of the waveform such as the shape of the waveform (acceleration and deceleration rates), maximum and minimum velocities, i.e., Reynolds number, and the frequency, i.e., Womersley number, did not affect the main features of the flow and the flow mode.⁴ Similarly, Yu¹⁰ stated that Reynolds and Womersley numbers only affect the strength of the vortex in abdominal aortic aneurysm. In addition, Gopalakrishnan et al.¹¹ reported that the Reynolds and Womersley numbers impact the strength of the primary vortex structure, while the flow mode, which was the vortex mode in their simulations, remained unchanged in abdominal aortic aneurysms. Finol et al.¹² observed that the Reynolds number influenced the peak wall shear stress (WSS), but it did not change the flow mode. Furthermore, the effect of Reynolds and Womersley numbers was investigated in our previous work.⁷ We observed that the flow mode was not changed by the variation of Reynolds and Womersley numbers. However, the propagation of the vortex ring was controlled by both Reynolds and Womersley numbers.

Le et al.,⁴ based on their observation, hypothesized that the flow mode is the result of two competing time scales: (a) a transport time scale, which is the time that takes a fluid particle to be transported across the neck which tends to generate a quasi-steady shear layer at the neck [Fig. 1(a)], and (b) the vortex formation time scale, which is the time that takes a vortex ring to form [Fig. 1(b)]. Therefore, a relevant non-dimensional parameter is the ratio of these two time scales, called Aneurysm number, $An=\frac{T_t}{T_v}$. Based on this definition, the flow mode is in vortex mode if the time required for vortex ring formation is less than the time required to transport a fluid particle across the IA neck (An > 1). Otherwise, the flow is in the cavity mode (An < 1).

For sidewall aneurysms, the transport time scale was approximated by $T_t=\frac{W}{U}$, where W is the width of the aneurysm neck and U is the average flow velocity in the parent artery. Furthermore, the vortex time scale was approximated by $T_v=\frac{D}{△U}$, where D is the diameter of the parent artery and △U is the flow pulse,⁴ similar to the vortex formation time of a vortex ring generated in a tank using a piston-cylinder setup.¹³ Note that, in the piston-cylinder setup,¹³ there is no steady flow out of the pipe, i.e., the piston velocity is equal to the flow pulse. However, the flow waveforms of aneurysms are better represented by a steady flow plus a flow pulse ΔU (Sec. III). Because the flow pulse (not the steady flow) generates the vortex ring, the flow pulse ΔU is used as the characteristic velocity for the formation time.⁴ Substituting the definition of $T_v$ and T_t into An, we reach to the following equation, which incorporates both geometric and flow characteristics:

$$An=\frac{T_t}{T_v}=\frac{W}{D}PI,$$ (1)

where $PI=\frac{△U}{U}$ is Gosling’s pulsatility index⁹ of the flow waveform. The hypothesis of Le et al.,^4,8 i.e., the flow mode depends on An, agreed with their simulations on a single sidewall aneurysm. However, it was not tested on different geometries with a variety of W/D. Furthermore, this hypothesis was not tested on bifurcation geometries, which may show different hemodynamics than sidewalls.¹⁴ Our goal here is to test this hypothesis on both bifurcation and sidewall types and on different geometries (W/D). Simplified geometries enable us to systematically vary W/D when all the other parameters are kept constant, which is not possible with anatomic geometries.

In this work, therefore, numerical simulations (Sec. II) are performed in sidewall and bifurcation geometries—see details of geometries in Sec. III—and the results are presented in Secs. IV A and IV B. We show that the specific An definition by Le et al. [Eq. (1)] cannot classify the flow mode in bifurcation cases (Appendix A). Therefore, we modify the definition of the transport time scale in An to classify the flow structure in bifurcation geometries (Sec. IV B) and test it on different simplified models (Secs. IV B 1 and IV B 2). We investigate the effect of flow mode on the near wall flow indicators such as wall shear stress and oscillatory shear index (OSI) in Sec. IV C. Finally, we compare our results with previous work in Sec. IV D and summarize the conclusions in Sec. V.

II. THE NUMERICAL METHOD

The governing equations are the three-dimensional (3D), unsteady incompressible Navier-Stokes equations for a Newtonian fluid in curvilinear coordinates. The curvilinear formulation is based on the hybrid staggered/non-staggered approach,¹⁵ which has all the advantages of a pure staggered grid formulation (i.e., satisfies the discrete continuity exactly) and eliminates the need for computing the Christoffel symbols. These governing equations are solved using a fractional step method.¹⁵ The momentum equations are solved implicitly using an efficient Newton-Krylov method (NKM), in which the Jacobian is formed analytically.¹⁶ The Poisson equation for the pressure is solved using a flexible generalized minimal residual method (FGMRES) with a multigrid as a preconditioner.¹⁵

A sharp-interface immersed boundary method is used to handle the 3D, arbitrary complex boundaries inside the domain.¹⁷ The method blanks out the nodes that are outside the flow domain and do not affect the solution. These nodes are identified using an efficient ray-tracing algorithm.¹⁸ The boundary conditions are reconstructed on the fluid nodes in the immediate vicinity of the immersed boundary along the normal to the boundary.¹⁷ The equations are solved on the rest of the grid nodes (fluid nodes). The method has been shown to be second-order accurate for a variety of flows.^16,17,19 In order to reduce wasted nodes in a domain, which are blanked out by the immersed boundary method, we use the overset grid approach. In this approach, several sub-grids are arbitrarily overlapped to discretize a complex, multi-connected flow domain. To solve the governing equations at each sub-grid, boundary conditions at the interfaces are constructed by interpolation from host sub-grids (i.e., sub-grids that contain the interface). The interpolation between the sub-girds has been shown to be 2nd order accurate.²⁰ The details of the overset-CURVIB method can be found in the work of Borazjani et al.²⁰ The immersed boundary method has been validated against experimental and benchmark solutions^16,18,21 and has been applied to a variety of problems such as cardiovascular flows,^7,22–26 aquatic swimming,^19,27–32 and rheology,^33,34 among others.

III. SIMULATED TEST CASES AND COMPUTATIONAL DETAILS

All numerical simulations have been carried out on simplified, aneurysm-like geometries to test the effects of An on the flow mode under controlled conditions. Using simplified geometries (Fig. 2) enables us to isolate the effect of different parameters by changing only one geometric parameter at a time, which is not possible in patient-specific simulations as different patient-specific aneurysms have completely different geometries. Table I presents the geometrical specifications of the simulated models along with their type, pulsatility index (PI), and denoted names. We have systematically varied An by varying the neck ratio, W/D (subsequently diameter of outlets in the direction of the inlet flow to inlet diameter, WO/D, in bifurcation geometries), and the pulsatility index PI. W/Ds and PIs in Table I are selected to produce a wide range of An (0.57–2.86) to systematically test our hypothesis. For bifurcations, WO/Ds are varied instead of W/D because the specific definition of Eq. (1) is only valid for sidewall geometries (see Appendix A) and the transport time scale in bifurcations depends on WO/D as will be discussed in Sec. IV B.

FIG. 2.

Schematic illustration of simplified aneurysm-like models: (a) sidewall and (b) bifurcation. The radii of the elliptical cross sections of the dome are $a=\frac{W}{2}$, b = D, and c = 0.6D, and the radii of the elliptical cross section of bifurcation outlets are $O1=\frac{W}{2}$ and $O2=\frac{WO}{2}$.

TABLE I.

Specification of simplified models, where D = 0.005 m and W are the parent artery diameter and aneurysm neck, respectively, and WO is the minor diameter of the elliptical cross section of the outlet. Lx, Ly, and Lz are dimensions of the uniform grid (see Fig. 3). An is the aneurysm number [Eq. (2)], and α = 1 or 2 for sidewall and bifurcation geometries, respectively. Nomenclature: m = meter, S = sidewall, B = bifurcation, T = T-junction, H = high pulsatility (PI = 1.43), and L = low pulsatility (PI = 0.57).

Simulation	Type	W/D	WO/D	PI	α	An	Lx/D	Ly/D	Lz/D
S1H	Sidewall	0.5	1	1.43	1	0.715	1.4	1 + WO/D	2 + W/D
S2H	Sidewall	1	1	1.43	1	1.43	1.4	1 + WO/D	2 + W/D
S2L	Sidewall	1	1	0.57	1	0.57	1.4	1 + WO/D	2 + W/D
S3H	Sidewall	2	1	1.43	1	2.86	1.4	1 + WO/D	2 + W/D
S3L	Sidewall	2	1	0.57	1	1.14	1.4	1 + WO/D	2 + W/D
S4L	Sidewall	4	1	0.57	1	2.28	1.4	1 + WO/D	2 + W/D
B1H	Bifurcation	1	1	1.43	2	2.86	1.4	2 + WO/D	2 + W/D
B1L	Bifurcation	1	1	0.57	2	1.14	1.4	2 + WO/D	2 + W/D
B2H	Bifurcation	2	1	1.43	2	2.86	1.4	2 + WO/D	2 + W/D
B2L	Bifurcation	2	1	0.57	2	1.14	1.4	2 + WO/D	2 + W/D
B3H	Bifurcation	1	0.5	1.43	2	1.43	1.4	2 + WO/D	2 + W/D
B3L	Bifurcation	1	0.5	0.57	2	0.57	1.4	2 + WO/D	2 + W/D
B4H	Bifurcation	1	0.25	1.43	2	0.715	1.4	2 + WO/D	2 + W/D
TH	T-junction	…	1	1.43	2	2.86	1.4	3	2

Figure 2 shows the configuration of simplified models for (a) sidewall and (b) bifurcation geometries. The inlet and outlet of the sidewall geometries are constructed by using two pipes, each with a diameter D and a length of 5D [Fig. 2(a)]. The inlet of the bifurcation geometries is constructed by using a pipe with diameter D and a length of 5D, whereas their outlets are constructed by using a 5D-long pipe with an elliptical cross section whose minor and major diameters are WO and D, respectively [Fig. 2(b)]. The dome is modeled by a cone-like shape with an elliptical base and locus, whose radii are $a=\frac{W}{2}$, b = D, and c = 0.6D. These dimensions are within the range of intracranial aneurysm shapes from 119 patient-specific IAs,³⁵ e.g., the aspect ratios in patient-specific IAs and our simplified geometries are AR = 1.16 ± 0.52 and 0.94 ± 0.42, respectively, and nonsphericity indices are NSI = 0.16 ± 0.07 and 0.12 ± 0.08, respectively (values are presented as the mean ± standard deviations). It should be noted that NSI is the deviation of a geometry from the spherical shape and $AR=\frac{b}{W_h}$, where $W_h=\frac{4Area}{Perimeter}\approx \frac{4\pi ac}{2\pi {\left(\left(a^2+c^2\right)/2\right)}^{0.5}}$ is the hydraulic diameter of the cross section of an aneurysm neck.^35,36

Figure 3 shows the immersed body and the overset grid layout for bifurcation geometries. The inlet and outlet(s) are meshed by body-fitted curvilinear grids; the base (circular or elliptical) is meshed by 41 × 41 grid nodes and the axial (flow) direction is meshed by 81 grid nodes. The geometry of the aneurysm is placed as an immersed boundary in the uniform grid and all subdomains are solved simultaneously.²⁰ The uniform domain size is Lx, Ly, Lz in each direction, as shown in Fig. 3 and given in Table I, and it is meshed by 50 grids/D in each direction. Such a grid resolution is found to be sufficient to provide grid-independent results, as shown in Appendix B.

FIG. 3.

The immersed body and overset grid layouts for bifurcation type simplified models. The immersed body is meshed with triangular elements.

Neumann boundary conditions are applied at the outlets, and a uniform (plug) flow is used at the inlet. Note that the profile of the inlet boundary has negligible influence on the IA flow pattern if the inlet is sufficiently far from the dome (here 5D).³⁷ The inlet velocity varies in time according to one of the waveforms shown in Fig. 4 with PI = 0.57 and 1.43 from the internal carotid artery of a normal subject³⁸ and a patient with a cerebral aneurysm,³⁹ respectively. The period of the waveform is determined based on the 75 beats/min heart rate (T = 0.8 s). The bulk velocity of the waveform is U = 0.25 m/s which is within the physiologically relevant range.⁴⁰ The non-dimensional time step is set to $△\overline{t}=0.0125$ (3200 time steps/cycle), which is small enough according to the sensitivity study in Appendix B. The Reynolds number is 378.8 ($Re=\frac{UD}{𝜗}$, where D = 0.005 m is the inlet pipe diameter and ϑ = 3.3 × 10⁻⁶ m² s⁻¹ is the blood kinematic viscosity) in all simulations. The Womersley number is 3.855 ($=\left(D/2\right)\sqrt{\frac{2\pi }{T𝜗}}$) for all simulated cases. The numerical simulations are carried for three cycles to obtain quasi-steady state, and all the reported results are from the third cycle. Based on our tests, the results are identical after the third cycle; i.e., the velocity field and flow features, such as the vortex structure (identified by Burgers’ model) and its circulation/axis, remain the same at comparable time instants in a cycle during the quasi-steady state.

FIG. 4.

The velocity at the inlet varies in time according to one of the waveforms. PI is the pulsatility index of the waveform.

IV. RESULTS AND DISCUSSIONS

The results are discussed in two subsections for sidewall (Sec. IV A) and bifurcation (Sec. IV B) geometries. To systematically investigate if the flow mode is classified by An, both W/D and PI, on which An depends on [Eq. (1)], are independently varied for each type of aneurysm-like geometries. The results are visualized using non-dimensional out-of-plane vorticity on the mid-plane of models (z-y plane). The three-dimensional vortex structures are visualized using q-criteria⁴¹ to study the phenomena that cannot be observed in the two-dimensional visualizations. Burgers’ vortex model is used to capture the bounds of the main vortex structure. Burgers’ vortex model is described in Appendix C, and it is shown that this model can be used to capture the vortex structures in our simulations (Appendix C). The effect of An on hemodynamic parameters such as wall shear stress and oscillatory shear index is investigated in Subsection IV C. Finally, the results are discussed and compared with previous work in Subsection IV D.

A. Sidewall simplified models

The ability of An to classify the flow mode in sidewall geometries is systematically studied by varying An (1) through geometry when the flow waveform PI is fixed in Sec. IV A 1 and (2) through flow waveform PI when the geometry is the same in Sec. IV A 2.

1. The effect of geometry (W/D) in sidewalls

The effect of W/D, and consequently An, on the flow mode is investigated at both high and low PI. Figure 5 shows the evolution of the non-dimensional out-of-plane vorticity at high PI(=1.43) for different W/D at various time instants during a cycle. Dashed lines and the cross sign depict the vortex structure and its axis in the dome, respectively, determined based on Burgers’ model. At the widest W/D (An = 2.86), vortex structure starts to roll up to form a vortex ring in the early acceleration phase [Figs. 5(a, S3H) and 5(b, S3H)]. During the acceleration of the inlet velocity, the vortex ring moves toward the distal wall [Fig. 5(c, S3H)] as it grows in size and swirls. Thereafter, the vortex ring hits the distal wall in the late acceleration phase and breaks down into two segments [Fig. 5(d, S3H)]. The upper segment is convected into the dome and diffuses [becomes weaker, see the rectangle in Fig. 5(e, S3H)], and the lower segment forms a shear layer that extends from the proximal to the distal wall after the peak systole [Fig. 5(e, S3H)]. The shear layer starts to roll up and becomes thicker at the distal end later in the cycle, as observed in Fig. 5(f, S3H).

FIG. 5.

Evolution of the non-dimensional out-of-plane vorticity for S3H, S2H, and S1H with W/D = 2 (An = 2.86), W/D = 1 (An = 1.43), and W/D = 0.5 (An = 0.715), respectively, at PI = 1.43 during different time instants in a cycle. The red dot shows the time instant on the flow curve for rows (a)-(f). Dashed lines and the cross sign depict the vortex structure and its axis in the dome, respectively, determined based on Burgers’ model. The vortex structure (dashed line) expands across the neck at all time instants in case S1H but rolls up, dynamically evolves, and moves across the neck in cases S3H and S2H. The rectangle points out weaker vortices in S3H.

S2H (An = 1.43) shows a similar behavior to S3H (An = 2.86) [Fig. 5(S2H)]. Nevertheless, the vortex ring breaks down earlier in S2H than S3H because of its smaller W/D, i.e., hits the distal wall earlier [Fig. 5(c, S2H)]. Notwithstanding, the vortex dynamics, i.e., rolling up of the vorticity to form a ring and its breakdown, clearly shows that S2H (An = 1.43) and S3H (An = 2.86) are in the vortex mode. By contrast, the shear layer (denoted by the dashed line) spans across the neck from the distal to the proximal wall quickly in the early acceleration phase [Figs. 5(a, S1H) and 5(b, S1H)] before a vortex ring can form at An = 0.715 [Fig. 5(S1H)]. Thereafter, the shear layer separates the recirculation zone from the continuous high-speed jet in the parent artery [Figs. 5(b, S1H)–5(f, S1H)]. Therefore, the flow mode at An < 1 for S1H (An = 0.715) is in the cavity mode while at An > 1 for S2H and S3H is in the vortex mode.

The effect of W/D on the flow mode shows the same trend at low PI = 0.57, as shown in Fig. 6. In fact, S4L and S3L cases with An > 1 (An = 2.28 and 1.14, respectively) are in the vortex mode since the vortex structure rolls up as a ring and breaks down [Figs. 6(S4L) and 6(S3L)], while S2L with An < 1 (An = 0.57) is in the cavity mode because a strong shear layer is observed across the neck at all time instants [Fig. 6(S2L)], i.e., the dashed line is present at the neck at all time instants. Some small instabilities are observed in the shear layer at the distal wall [Fig. 6(S2L)], but such small instabilities are very different than the evolution of the main vortex in the vortex mode [Figs. 6(S4L) and 6(S3L)].

FIG. 6.

Evolution of the non-dimensional out-of-plane vorticity for S4L, S3L, and S2L with W/D = 4 (An = 2.28), W/D = 2 (An = 1.14), and W/D = 1 (An = 0.57), respectively, at PI = 0.57 during different time instants in a cycle. The red dot shows the time instant on the flow curve for rows (a)-(f). Dashed lines and the cross sign depict the vortex structure and its axis in the dome, respectively, determined based on Burgers’ model. The vortex structure (dashed line) expands across the neck at all time instants in case S2L but rolls up, dynamically evolves, and moves across the neck in cases S4L and S3L. The rectangle points out weaker vortices in S4L.

2. The effect of PI in sidewalls

The effect of PI, and consequently An, on the flow mode is investigated by the three-dimensional (3D) vortical structures (VS) visualized by the iso-surfaces of q-criteria.⁴¹ The 3D structures complement the 2D vorticity figures in Subsection IV A 1 and provide the 3D shape of the main vortical structures in space which cannot be observed through the 2D ones. The value of q-criteria (q-value) was selected in a way that all dominant structures can be observed, and the selected value (q-value = 30) was kept the same at all time instants and all geometries for consistency. In addition, the selected q-value is in a range where the structures are not that sensitive to its value. Figure 7 presents the evolution and topology of the three-dimensional vortical structures at various time instants during a cycle for S2 (W/D = 1) with PI = 0.57 and 1.43. Thus, An is 0.57 and 1.43 for S2L and S2H, respectively, in Fig. 7. In S2L [Fig. 7(S2L)], an almost stationary vortical structure (VS), denoted as VS2, can be observed at all time instants, i.e., the flow at An = 0.57 is in the cavity mode.

FIG. 7.

Evolution and topology of the three-dimensional vortical structures (q-value = 30) for S2 (W/D = 1) at different PIs (S2L and S2H). Two left columns correspond for PI = 0.57 (An = 0.57), and two right columns correspond for PI = 1.43 (An = 1.43) during different time instants in a cycle. The red dot shows the time instant on the flow curve for (a)-(f). R1 and VS1 depict the vortex ring and recirculation vortex structures, respectively, and VS2 depicts a stationary vortical structure.

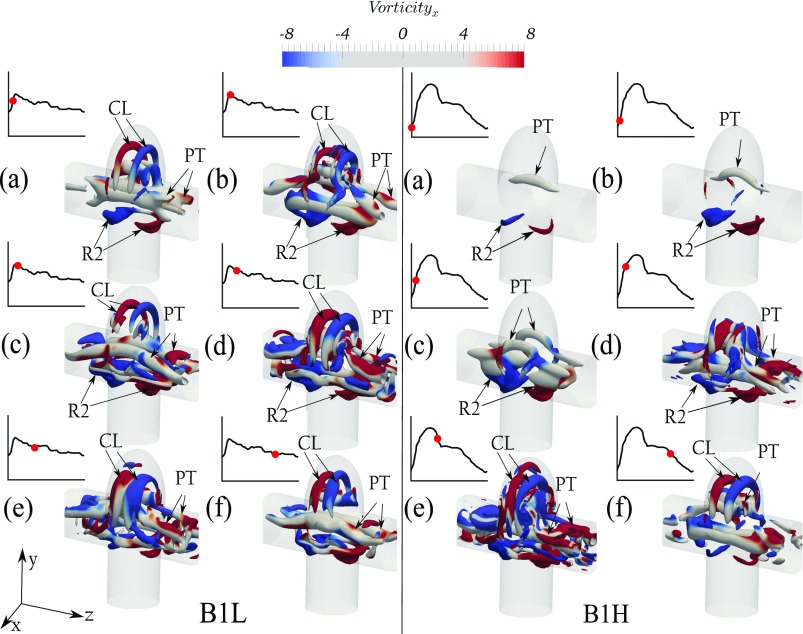
The vortical structures in S2H are quite different from S2L. In fact, there are two main vortical structures in S2H [Fig. 7(S2H)]: the vortex ring structure denoted as R1 and the recirculation vortex structure denoted as VS1. The vortex ring (R1) starts to form asymmetrically as an inclined vortex,⁴² while it is attached to the proximal wall in the early acceleration phase [Fig. 7(a, S2H)]. R1 detaches from the proximal wall [Fig. 7(b, S2H)] and moves toward the distal wall across the neck [Fig. 7(c, S2H)]. Thereafter, R1 hits the distal wall [Fig. 7(d, S2H)] and rolls up to form VS1 [Figs. 7(e, S2H) and 7(f, S2H)] which remains into the next cycle, i.e., the early acceleration phase [Fig. 7(a, S2H)]. When R1 moves from the proximal wall toward the distal wall, it interacts with VS1 as VS1 becomes weaker and diffuses away [Fig. 7(b, S2H)]. Because of such dynamic evolution of vortical structures [Fig. 7(S2H)], the flow at An = 1.43 for S2H is in the vortex mode.

To show that the main parameter determining the evolution of the vortex ring is An and not just PI, cases S3L and S3H are chosen because An > 1 for both cases (An = 1.14 and 2.86, respectively) when PI is varied. Although the stationary vortical structure VS1 is present throughout most of the cycle in S3L (Fig. 8), the ring vortex R1 is observed in both S3L and S3H (see R1 in Fig. 8). The evolution of the vortex for S3L is more clear on the midplane (Fig. 6). The presence of VS1 is probably due to the fact that An (=1.14) is close to one, i.e., in the transition range, which will be discussed further in Sec. IV D. Nevertheless, this shows that the development of the vortex structure R1 is also possible at low PI, i.e., the governing parameter is An and not the PI.

FIG. 8.

Evolution and topology of the three-dimensional vortical structures (q-value = 30) for S3 (W/D = 2) with different PIs (S3L and S3H). Two left columns correspond for PI = 0.57 (An = 1.14), and two right columns correspond for PI = 1.43 (An = 2.86) during different time instants in a cycle. The red dot shows the time instant on the flow curve for (a)-(f). R1 and VS1 depict the vortex ring and recirculation vortex structures, respectively.

B. Bifurcation simplified models

Generally, to form a vortex ring, the shear layer should roll up in an expansion area. The shear layer is generated by the flow from the parent artery streaming into the expansion area. Figure 1 (lower row) shows a schematic of cavity and vortex modes in bifurcation geometries. The flow mode in a bifurcation geometry is in the vortex mode if the shear layer rolls up [Fig. 1(b)], while it is in the cavity mode if the steady shear layer extends from the parent artery into the outlets [Fig. 1(a)]. These shear layer evolutions will affect the flow inside the dome. In fact, the steady shear layer creates cavity-like structures in the dome of bifurcation geometries [Fig. 1(a)] but ideally not in the vortex mode [Fig. 1(b)]. The effect of these flow modes with different evolution of shear layer on the near wall flow is further discussed in Sec. IV C.

By comparing the sidewall and bifurcation geometries in Fig. 1, it is observed that the primary difference between bifurcation and sidewall geometries is the expansion area: the dome for sidewalls [Fig. 9(a)] but the inlet/outlet intersection for bifurcations [Fig. 9(b)]. Therefore, we expect different geometric factors to be important in bifurcations compared to sidewalls. As a consequence, the specific definition of Eq. (1) might not work for bifurcations. In fact, in Appendix A, we show that the specific definition of An [Eq. (1)] cannot predict the vortex formation in bifurcation geometries. Therefore, we need to modify the definition of An for bifurcation geometries.

FIG. 9.

Schematic of the expansion area in (a) bifurcation and (b) sidewall simplified geometries. The transport time scale is approximated for a fluid particle to move from A to B. The distance between points A and B is WO in (a) and W in (b) in the inlet flow direction. The velocities at A and B are depicted by vectors.

In An definition for sidewalls [Eq. (1)], $T_v$ ($=\frac{D}{PSV-EDV}$, where PSV and EDV are the peak systole velocity and the end diastole velocity, respectively) is the time required for the formation of the vortex ring and T_t ($=\frac{W}{U}$) is the time that it takes for a fluid particle to be transported by the parent artery flow across the neck, i.e., the expansion area. The definition of $T_v$ in bifurcation geometries is similar to that in sidewall geometries because the vortex formation process, which depends on the parent artery diameter (D), PSV, and EDV, is similar. However, T_t needs to be modified for bifurcation geometries because the expansion area, in which the transport phenomena compete with the vortex formation, is different.

To generalize, we approximate $T_t=\frac{L}{U_{expansion}}$ as the time required for a fluid particle to be transported across the expansion area, i.e., from point A to point B (Fig. 9). Consequently, the length scale L is along the flow direction into the expansion area from point A to point B, i.e., the width of aneurysm neck [W in Fig. 9(b)] and the outlet [WO in Fig. 9(a)] in sidewall and bifurcation geometries, respectively. U_expansion is the average velocity in the direction of the flow into the expansion area. We approximate U_expansion by taking average of the bulk velocity at points A and B in the flow direction, i.e., U_expansion = (U^A + U^B)/2. We approximate the velocities along the direction L by U^B = 0 and U^A = U in bifurcations, and U^A = U^B = U in sidewalls. Therefore, U_expansion will be U/2 (half of the average inlet bulk velocity) for bifurcation geometries and U for sidewall geometries. Substituting the modified definition of T_t into An = T_t/$T_v$, the general form of the aneurysm number is written as follows:

$$An=\frac{T_t}{T_v}=\alpha \frac{L}{D}PI,$$ (2)

where L is the aneurysm neck (W) and the outlet diameter (WO) in sidewall and bifurcation IAs. U_expansion = U/α is applied to obtain Eq. (2); hence, α = 1 and 2 for sidewalls and bifurcations, respectively. We explore the ability of the above An definition [Eq. (2)] for classifying the flow mode in bifurcations by investigating the effect of geometry and PI in Secs. IV B 1 and IV B 2, respectively.

1. The effect of geometry (WO/D) in bifurcations

The effect of WO/D, and consequently An, on the flow mode is investigated when PI is kept constant. Figure 10 shows evolution of the non-dimensional out-of-plane vorticity for bifurcation cases B1H, B3H, and B4H with $\frac{WO}{D}=1.0$ (left column), $\frac{WO}{D}=0.5$ (middle column), and $\frac{WO}{D}=0.25$ (right column), respectively, at high PI (=1.43) during various time instants in a cycle. Dashed lines and the cross sign depict the vortex structure and its axis in the right outlet, respectively, determined based on Burgers’ model. The vortex structure is shown only in one of the outlets due to the symmetry with respect to the y-plane.

FIG. 10.

Evolution of the non-dimensional out-of-plane vorticity for B1H, B3H, and B4H with WO/D = 1 (An = 2.86), W0/D = 0.5 (An = 1.43), and W0/D = 0.25 (An = 0.715), respectively, at PI = 1.43 during different time instants in a cycle. The red dot shows the time instant on the flow curve for rows (a)-(f). Dashed lines and the cross sign depict the vortex structure and its axis in the right outlet, respectively, determined based on Burgers’ model. The shear layer at inlet/outlet intersection is stable at all time instants in case B4H but rolls up, dynamically evolves, and breaks down in cases B1H and B3H.

In B1H and B3H cases with An = 2.86 and 1.43, respectively, the formation of a vortex ring and its evolution are observed, i.e., vortex ring mode. For example, in B1H, the vortex structure (delineated by the dashed lines) rolls up in the early acceleration phase [Figs. 10(a, B1H) and 10(b, B1H)], and it moves in the direction of the inlet flow [Fig. 10(c, B1H)] as it grows in size. The vortex ring is convected toward outlets before the peak systole [Fig. 10(d, B1H)]. Thereafter, the vortex ring becomes unstable and breaks down [Figs. 10(e, B1H) and 10(f, B1H)]. A similar evolution of vortical structures can be observed in Fig. 10(B3H). By contrast, the shear layer (delineated by the dashed lines) at inlet/outlet intersection is stable at all time instants in the flow with WO/D = 0.25 [Fig. 10(B4H)]. Therefore, the B4H case with An = 0.715 is in the cavity mode.

A similar trend is observed at low PI (=0.57) for B1L and B3L with $\frac{WO}{D}=1.0$ (left column) and $\frac{WO}{D}=0.5$ (right column) in Fig. 11; i.e., at a given PI by decreasing WO/D in bifurcations, the shear layer becomes stable when An < 1. In fact, the B1L case with An = 1.14 [Fig. 11(BlL)] shows a similar evolution of vortical structures with B1H [Fig. 10(B1H)], i.e., in the vortex mode. However, the B3L case with An = 0.57 is in the cavity mode because the shear layer (denoted by the dashed lines) at inlet/outlet intersection [Fig. 11(B3L)] is stable at all time instants similar to B4H [Fig. 10(B4H)]. In summary, the cases with An < 1 (B4H and B3L) have a stable shear layer (cavity mode), whereas the cases with An > 1 (B1H, B1L, and B3H) have a dynamically evolving vortex (vortex mode).

FIG. 11.

Evolution of the non-dimensional out-of-plane vorticity for B1L and B3L with WO/D = 1 (An = 1.14) and WO/D = 0.5 (An = 0.57), respectively, at PI = 0.57 during different time instants in a cycle. The red dot shows the time instant on the flow curve for rows (a)-(f). Dashed lines and the cross sign depict the vortex structure and its axis in the right outlet, respectively, determined based on Burgers’ model. The shear layer at inlet/outlet intersection is stable at all time instants in case B3L but rolls up, dynamically evolves, and breaks down in case B1L.

2. The effect of PI in bifurcations

The effect of PI, and consequently An, on the flow mode is investigated by three-dimensional vortical structures visualized by the iso-surfaces of q-criteria colored by helicity. The 3D structures complement the 2D vorticity figures in Subsection IV B 1 and even enable us to visualize some of the structures which cannot be observed by the out-of-plane vorticity. Helicity emphasizes the three-dimensionality of the flow, and it can discriminate different vortical structures based on their rotations.

To ease the discussion on the vortical structures in bifurcation geometries, first, the main structures in a pipe T-junction, which is a bifurcation model without an aneurysm dome, are discussed (Fig. 12). Two main structures are observed in T-junctions (note that other structures are excluded in Fig. 12): the particle trapping^43,44 and vortex ring structures, as shown in Figs. 12(a) and 12(b), respectively. Particle trapping structures are vortical structures stretched in the direction of the outlets, which are reported to trap particles and bubbles for a long time.^43,44 They are distinguished from other structures by the vorticity magnitude in the normal direction to the mid-plane of models (x direction) because these structures have almost zero vorticity in the normal direction to the mid-plane of the models. The vortex rings in Fig. 12(b) are colored by helicity to emphasize their three-dimensionality and better differentiate the vortex ring from the other vortical structures.

FIG. 12.

Topology of the three-dimensional vortical structures at t/T = 0.06 for a T-junction with PI = 1.43: (a) the particle trapping structures colored by vorticity-x magnitude, (b) the ring vortical structures (q-value = 30) colored by helicity (dot product of vorticity and velocity vectors), and (c) schematic skeleton of vortex lines illustrating the vorticity fields. The red dot shows the time instant on the flow curve. The arrow indicates the direction of the vorticity vector, and dotted lines depict that they may not be visible or formed properly. R2 and VS depict the vortex ring and vortical structure, respectively.

The vortex ring in Fig. 12(b) shows two vortical structures: The Wall VS, which is attached to the inlet/outlet pipe intersection, and the vortex ring R2, which evolves from the Wall VS. Walls VS and R2 are connected through twisted sheet-like vortical structures denoted as sheet-like VS. The schematic skeleton of vortex lines of the ring vortices is presented in Fig. 12(c). Walls VS and R2 are broken into two segments because of the shape of inlet/outlet intersection. The dotted lines depict the vortex lines that are not visible (because of the chosen iso-surface’s value for q-criteria). The arrows indicate the direction of the vorticity vector.

The vortical structures in bifurcations include the structures observed in the T-junction (Fig. 12) as well as cavity-like structures that are driven by the shear layer (see the schematic footprints of these structures in the lower row of Fig. 1). Figure 13 presents the evolution and topology of the three-dimensional vortical structures colored by vorticity-x magnitude at various time instants during a cycle for B3 at PI = 0.57 and 1.43. It can be observed in Fig. 13 that particle trapping structures [similar to vortical structures in Fig. 12(a)], denoted as PT, form at all time instants regardless of the pulsatility index similar to previous work which observed these structures in both steady and pulsatile flows.⁴³ The particle trapping structures in bifurcations are deformed in comparison with the T-junction, i.e., the middle of the PT is curved into the dome.

FIG. 13.

Evolution and topology of the three-dimensional vortical structures (q-value = 30) for B3 (WO/D = 0.5) with different PIs (B3L and B3H). Two left columns correspond for PI = 0.57 (An = 0.57), and two right columns correspond for PI = 1.43 (An = 1.43) during different time instants in a cycle. The red dot shows the time instant on the flow curve for (a)-(f). R2, PT, and CL depict a vortex ring, particle trapping, and cavity like structures, respectively.

A vortex ring [similar to R2 in Fig. 12(b)] is observed only in the B3H case at An = 1.43 [Fig. 13(B3H)], whereas the shear layer is stable at all time instants in B3L at An = 0.57 and does not roll up to form a vortex ring [Fig. 13(B3L)]. The stable shear layer is associated with cavity like structures, denoted as CL, which are observed at all time instants in B3L [Fig. 13(B3L)]. In B3H, however, CL does not form during the vortex ring formation and evolution [Figs. 13(a, B3H)–13(d, B3H)], while it is observed after vortex ring break down and the formation of the shear layer [Figs. 13(e, B3H) and 13(f, B3H)]. In B3H, the vortex ring structure R2 rolls up in the early acceleration phase [Figs. 13(a, B3H) and 13(b, B3H)]. It moves in the direction of the inlet jet [Fig. 13(c, B3H)] and interacts with PT [Fig. 13(d, B3H)]. Thereafter, the vortex ring breaks down because of its interaction with particle trapping structures [Fig. 13(e, B3H)] and does not form until the next cycle [Fig. 13(f, B3H)].

One may argue that the above difference in vortex R2 in B3L and B3H is due to the PI and not necessarily An. A counter example would be B1H and B1L with the same geometry and different PI such that for both An > 1 (An = 2.86 and An = 1.14, respectively), in which both show a similar evolution of the vortex ring structure (denoted by R2)—see Fig. 14. However, CL forms during all time instants in B1L, whereas CL does not form during vortex ring evolution in B3H [Fig. 13(B3H)]. This might be the consequence of An (=1.14) being close to one in B1L, i.e., in the transition range, which will be discussed further in Sec. IV D.

FIG. 14.

Evolution and topology of the three-dimensional vortical structures (q-value = 30) for B1 (WO/D = 1.0) with different PIs (B1L and B1H). Two left columns correspond for PI = 0.57 (An = 1.14), and two right columns correspond for PI = 1.43 (An = 2.86) during different time instants in a cycle. The red dot shows the time instant on the flow curve for (a)-(f). R2, PT, and CL depict a vortex ring, particle trapping, and cavity like structures, respectively.

C. The effect of An on wall shear stress and oscillatory shear index in simplified models

In this section, we investigate how the flow mode (An) affects the fluid in the near wall region quantified by wall shear stress and oscillatory shear index.⁴⁵ The fluid forces on the endothelial cells regulate the aneurysm initiation and growth.^46,47 These forces are quantified by wall shear stress and oscillatory shear index, which depend on the flow inside the dome. Figures 15 and 16 present the contours of oscillatory shear index (OSI) and wall shear stress (WSS) for all sidewall and bifurcation geometries, respectively. WSS is the cycle averaged wall shear stress. Consistent with previous work,^7,35,38,48 we normalize all WSS values in the dome with the WSS at the inlet of the parent artery to produce comparable magnitude of WSS between sidewall and bifurcation geometries. The inlet WSS (nondimensionalized by ρU²) was similar among similar types of geometries, i.e., 0.0199 ± 0.0001 and 0.0224 ± 0.0002 for sidewall and bifurcation geometries, respectively.

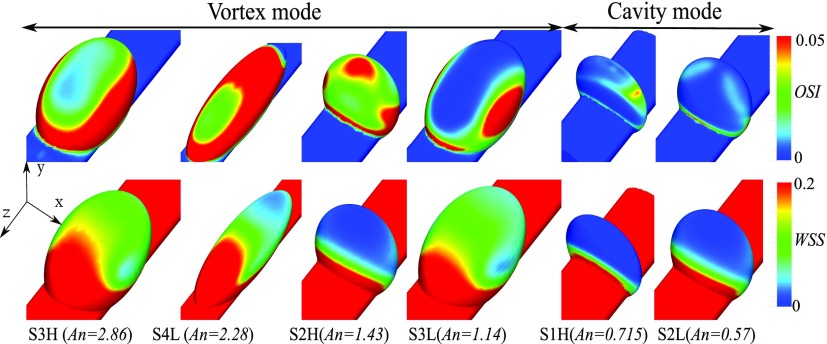
FIG. 15.

Contours of OSI (upper row) and cycle averaged wall shear stress (lower row), denoted by WSS, are shown for all sidewall geometries. The flow mode affects the flow in the near wall region of the dome. The vortex mode has larger regions of high OSI in the dome than the cavity mode. WSS in the dome depends on the dome geometry, and it correlates with W/D.

FIG. 16.

Contours of OSI (upper row) and cycle averaged wall shear stress (lower row), denoted by WSS, are shown for all bifurcation geometries. The vortex mode has larger regions of high OSI in the dome than the cavity mode. WSS of all geometries are similar as their domes are the same.

The flow mode affects the fluctuations of velocity in time, quantified by OSI, in the near wall region of the dome (upper rows of Figs. 15 and 16). High OSI areas in the dome are remarkably increased when the flow mode switches from cavity to vortex in both sidewalls and bifurcations (upper rows of Figs. 15 and 16). Note that we are not stating that the OSI is directly correlated with An, i.e., OSI does not necessarily increase if An is increased, but we are stating that OSI of flows with An > 1 is higher than those with An < 1. Here, we focus on the reasons behind the relation of OSI and the flow mode.

In sidewalls, OSI of flows in the vortex mode is higher than the cavity mode because the vortex ring evolution and breakdown in the dome creates fluctuations in the velocity field. In bifurcations, although the vortex ring forms in the inlet/outlet intersection (Figs. 14 and 13), it affects the near wall behavior in the dome (upper row of Fig. 16). In fact, the vortex ring evolution and breakdown interact with particle trapping structures (PT in Figs. 13 and 14) in the dome and consequently affect the near wall vortical structures. Furthermore, the cavity-like structures stay longer in the dome (CL in Figs. 13 and 14) which results in a lower OSI as it resembles a steady like flow. For example, B3H and B1H have a higher OSI than B3L and B1L (upper row of Fig. 16) as CL is formed later in the cycle in B3H and B1H [instants (e) and (f) in Figs. 13 and 14] compared to B3L and B1L in which CL exists at all time instants.

In contrast to OSI, the flow mode (An) does not affect WSS in both sidewalls and bifurcations (lower rows of Figs. 15 and 16). In fact, the contours of WSS for all bifurcation geometries are quite similar (lower row of Fig. 16) probably because of similar dome geometries. In sidewalls (lower row of Fig. 15), WSS does not seem to be related to the flow mode but more related to the dome geometry as well, e.g., contours of WSS for S2L (cavity mode) are quite similar to those for S2H (vortex mode). Contours of WSS for S3L and S3H, which have the same dome geometry, are similar as well (lower row of Fig. 15). Therefore, PI or the flow mode (An) does not affect the cycle averaged wall shear stress. However, contours of WSS for different geometries are quite different, i.e., the cycle averaged wall shear stress is a function of the dome geometry.

In summary, regardless of the location of vortex ring formation (neck area in sidewall and inlet/outlet intersection in bifurcation geometries), sidewall and bifurcation geometries show similar behavior: (1) higher OSI is observed in geometries with the vortex mode (An > 1) in comparison with the cavity mode (An < 1) and (2) the cycle averaged wall shear stress is a function of dome; e.g., contours of WSS for simplified geometries with the same dome geometry (all bifurcations, S2L vs S2H, or S3L vs S3H) are similar. By comparing Figs. 15 and 16, a higher range of WSS and OSI are observed in the dome of bifurcation geometries in comparison with sidewall geometries.

D. Discussion and comparison with previous work

Based on our results, the evolving vortex turns into a stable shear layer as L/D is decreased for a given waveform PI (Figs. 5, 6, 10, and 11). Similarly, the evolving vortex turns into a stable shear layer as PI is decreased for a given geometry (L/D), as seen in Figs. 7 and 13. In fact, the determining parameter is their multiplication, i.e., An [Eq. (2)]. The critical An at which the flow mode transition from cavity to vortex is equal to one according to its definition [Eq. (2)]; e.g., a shorter vortex time scale (An > 1) indicates the presence of a vortex and vice versa. In our simulations, An could discriminate the evolving vortex (vortex mode) when An > 1 (cases S2H, S3H, S3L, S4L, B1L, B2H, B2L, and B3H) and the stable shear layer (cavity mode) when An < 1 (cases S1H, S2L, B3L, and B4H) based on the evolution of the main vortex structure using Burgers’ model (delineated by dashed lines in Figs. 5, 6, 10, and 11). In fact, the shear layer was stable when An < 1 but evolving when An > 1 (dashed lines in Figs. 5, 6, 10, and 11).

Based on the above, it might be thought that there is a sharp transition between the cavity and vortex modes at An = 1. This is not the case, however, as the flows with An close to one show some properties of both modes. To investigate this further, the test cases S3L and B1L are examined more closely. In these two cases, An is close to one (An = 1.14 for both), and the dynamic vortex evolution is clearly observed in Figs. 6 and 11 for S3L and B1L, respectively. Nevertheless, the 3D structures in these cases show the features of both modes. In S3L, the stationary vortical structure VS1 (a feature of the cavity mode) is present throughout most of the cycle (Fig. 8). In B1L, similarly, the cavity-like structure CL is present throughout the cycle (Fig. 14). Consequently, at An ≈ 1, both features of the flow modes, i.e., the vortex and cavity structures, might be observed and there is no sharp transition between the flow modes. This is typical for most classifying parameters as most show a transition range; e.g., a sharp transition between laminar and turbulent regimes, identified by the Reynolds number, is not observed as there is a transition range in which the flow intermittently flips between the two regimes. To emphasize this transition range, we use An ≳ 1 or An ≲ 1.

To see if our observed trend can be seen on previously reported data, we calculated An for some of the previous numerical and experimental studies in the literature. The vortex mode is observed and reported by the numerical simulations of Gopalakrishnan et al.¹¹ on an aortic sidewall aneurysm with An ≈ 3.2, the numerical simulations of Sheard⁶ in a fusiform sidewall aneurysm with An > 10, the experimental and numerical results of Le et al.⁸ on a sidewall rabbit aneurysm with An ≈ 2.9, and the numerical results of Asgharzadeh and Borazjani⁷ on a patient-specific aneurysm with An = 2.4. The cavity mode is observed and reported by the experimental results of Hope et al.⁵ on a human sidewall aneurysm located at the left middle cerebral artery with An ≈ 0.95 and the numerical simulation of Le et al.⁴ on a sidewall rabbit aneurysm with An ≈ 0.89. Although we calculated An approximately based on the reported schematics of aneurysms and their inlet waveforms, still An can distinguish the flow mode: the vortex ring and cavity mode occur for An > 1 and An < 1, respectively; i.e., the reported results in the literature agree with the observed trend here.

The vortex ring in sidewall geometries (Figs. 8 and 7) is similar to that of inclined nozzles.^42,49 Nevertheless, the expansion area in these two is somewhat different. The expansion area is one-sided in sidewall geometries (the dome), but it can be considered infinite and not confined by any walls in inclined nozzle experiments. Therefore, the shape of the inclined vortex ring in an aneurysm is different than that in those experiments.⁴² The vortex structure in our pipe T-junction [Fig. 12(a)] is similar to the particle trapping structures observed by Vigolo et al.⁴³ in both steady and pulsatile flows. In bifurcation cases, we also observe particle trapping structures (PT in Figs. 13 and 14) similar to the previous work on T-junctions by Vigolo et al.⁴³ and Chen et al.⁴⁴ However, the shape of particle trapping structures is curved into dome in bifurcation geometries compared to T-junctions. A vortex ring (R2) is observed in bifurcation geometries when An > 1 [Fig. 13(B3H)], which is connected to the wall vortical structure through twisted sheet-like vortical structures [Figs. 12(b) and 13(B3H)]. The twisted sheet-like VS, which connects the vortex ring to the Wall VS, is consistent with the observations of Le et al.⁴⁹ in vortex rings from inclined nozzles.

It is observed in Fig. 13 that the vortical structures are asymmetric, in spite of the fact that the bifurcation geometries are symmetric. This behavior was also reported in experimental and numerical studies of Durst et al.⁵⁰ and Battaglia et al.,⁵¹ respectively, for a sudden expansion in a duct in a similar range of Re to our simulations. Durst et al.⁵⁰ observed strongly three-dimensional and asymmetric flow for an expansion ratio of 3 to 1 (ratio of the duct diameter to its inlet diameter) for Re > 114. These asymmetric vortical structures are the consequence of the highly disturbed fluid motion in the separation zones,⁵⁰ i.e., at inlet/outlet intersection.

The vorticity magnitude in the shear layer of the parent artery remains high throughout the cycle, as observed in Figs. 5, 6, 10, and 11. The vorticity magnitude in the shear layer is higher than the dome as it drives the flow in the dome. In addition, the waveforms of aneurysm (Fig. 4) are better represented by a constant flow plus a flow pulse, i.e., the flow rate does not go to zero. The constant part of the waveform will generate a steady shear layer, while the pulsatile part follows a Womersley-like solution. Consequently, the constant flow part creates an almost constant vorticity, which remains high throughout the cycle. Note that the identified vortex or the shear layer (dashed lines in Figs. 5, 6, 10, and 11) is independent of the vorticity magnitude because Burgers’ method (Appendix C) identifies the maximum vorticity for the axis location and then the boundaries are the locations with magnitude e⁻¹ relative to this magnitude, i.e., the vortex boundaries are relative to the maximum vorticity and do not depend on the maximum magnitude.

V. SUMMARY AND CONCLUSION

We modified the An definition [Eq. (2)] to work for both sidewall and bifurcation type geometries. The modification is applied on the transport time scale of bifurcation geometries, while the vortex formation time scale of bifurcations is similar to that in sidewalls. Based on our numerical simulations, An [Eq. (2)] can clearly discriminate the flow mode in sidewall and bifurcation geometries; i.e., a stable shear layer (cavity mode) is observed when An ≲ 1, and a dynamically evolving vortex (vortex mode) is observed when An ≳ 1. It should be noted that a sharp transition of the flow mode across An = 1 does not exist. In fact, An has a transition range in which the flow mode changes from cavity to vortex modes. This behavior can be seen in other classifying non-dimensional parameters; e.g., there is no critical Re at which the flow sharply transitions from laminar to turbulence. In fact, there is a transitional regime in which the flow is partly laminar and partly turbulent.¹

Three dominant vortical structures are observed in the sidewall geometries (Figs. 7 and 8): (1) vortex ring, (2) recirculating, and (3) stationary cavity structures. Vortex ring and recirculating vortical structures form when An > 1, and stationary cavity vortical structure forms when An < 1. The vortex ring in sidewall geometries is similar to that in inclined nozzles⁴⁹ because of the similarity between inlet/dome intersection in sidewall geometries and inclined nozzle exit. Three dominant vortical structures are observed in the bifurcation geometries (Figs. 13 and 14): (1) “particle trapping” [Fig. 12(a)], (2) vortex ring [Fig. 12(b)], and (3) cavity-like structures. The particle trapping structure is similar to that observed by Vigolo et al.⁴³ in a T-junction. The vortex ring in bifurcation geometries is attached to the wall vortical structure through a twisted sheet-like vortical structure [Figs. 12(b) and 12(c)]. The twisted sheet-like vortical structure which connects the vortex ring to the Wall VS is observed in inclined nozzles⁴⁹ as well. The vortex ring in bifurcation geometries is broken into two segments [Fig. 12(c)] because of the configuration of the inlet/outlet intersection in bifurcation geometries [Fig. 12(b)]. The cavity-like structures form inside the dome and are associated with the stable shear layer.

The flow mode, i.e., how the shear layer evolves in the expansion region, affects the near wall flow, to which endothelial cells respond to, in the dome of both sidewall and bifurcation geometries as shown in Figs. 15 and 16. A geometry in the vortex mode has higher oscillatory shear index in comparison with the cavity mode because of the dynamic evolution of the vortex and the shear layer, as discussed in Sec. IV C. The time averaged wall shear stress is only a function of the dome geometry and does not change significantly by the inlet flow or the flow mode.

The results and conclusions of this study are based on simplified geometries, which helped to systematically investigate the effect of different parameters without changing the others to come up with the approximations for An [Eq. (2)]. Note that systematically changing a parameter is not possible with anatomical geometries. Nevertheless, it is not clear if the results of such simplified geometries are applicable to real aneurysms with more complex geometries. In our future work, we test if the results of simplified geometries are applicable to the patient-specific ones.

In summary, the vortex mode (An > 1) is associated with the highly dynamic and the complex flow with high OSI because of the vortex formation in aneurysms. By contrast, the cavity mode (An < 1) is associated with the quasi-stationary shear layer, slow recirculation, and simple flow with low OSI in aneurysms. Aforementioned classification, i.e., complex vs. simple or unstable vs. stable, plays an important role in discrimination of ruptured from unruptured aneurysms.⁵² In fact, the study of Cebral et al.⁵² on a database containing 210 intracranial aneurysms reported that complex and unstable flow patterns are correlated with the clinical history of aneurysm rupture. Furthermore, the classification of flow in aneurysms into vortex and cavity might be helpful to assess the thrombogenic potential of an aneurysm. It was shown that regions of slow recirculation in aneurysms (cavity mode) are prone to thrombus deposition.^53,54 The correlation of An and such clinical issues will be pursued as part of the future work.

APPENDIX A: THE ABILITY OF An IN CLASSIFYING FLOW MODE IN BIFURCATION GEOMETRIES

Here, we show that the specific definition of An [Eq. (1)], originally developed for sidewall aneurysms by Le et al.,⁴ does not correctly predict the vortex formation in bifurcation geometries. To show this, two bifurcations geometries B1 and B2 with W/D = 1 and 2, respectively, are reconstructed and simulated at low PI = 0.57, i.e., An = 1.14 and 0.57 based on the specific definition of An by Le et al.⁴ [Eq. (1)].

Figure 17 shows the evolution of the non-dimensional out-of-plane vorticity at various time instants during a cycle. The vortex ring structure (denoted as R2 and delineated by the dashed lines using Burgers’ model) rolls up in the acceleration phase [Figs. 17(a) and 17(b)] and grows in size [Fig. 17(c)] and eventually breaks down [Figs. 17(d)–17(f)] in both geometries; i.e., both are in the vortex mode. Although W/D affects the size and breakdown of vortices, the vortex formation process and the flow mode (vortex formation vs. steady shear layer) are independent of the W/D in bifurcations as the vortex is observed in both An > 1 (B2L) and An < 1 (B1L). The steady shear layer is not observed in B1L, in which An < 1 based on the definition involving W/D. This suggests that the specific definition of An [Eq. (1)],⁴ which involves W/D, needs to be modified for bifurcations.

FIG. 17.

Evolution of the non-dimensional out-of-plane vorticity for B1L and B2L with W/D = 1 (An = 0.57) and W/D = 2 (An = 1.14), respectively, at PI = 0.57 during different time instants in a cycle. The red dot shows the time instant on the flow curve for rows (a)-(f). Dashed lines and the cross sign depict the vortex structure and its axis in the right outlet, respectively, determined based on Burgers’ model. R2 depicts the vortex ring, which is observed in both cases, i.e., even at An < 1 defined based on the specific definition of An by Le et al.⁴

APPENDIX B: GRID AND TIME STEP SENSITIVITY INVESTIGATION

Grid and time step sensitivity investigation is carried out by simulating the case S2H (Table I). Simulations are carried out for a grid size of (1) 73 × 109 × 153 with $△\overline{t}=0.0125$, (2) 108 × 164 × 228 with $△\overline{t}=0.008$, and (3) 73 × 109 × 153 with $△\overline{t}=0.00625$. Simulation (2) is carried out to investigate the grid sensitivity of results. It is noted that the time step for simulation (2) is chosen such that the Courant-Friedrichs-Lewy (CFL) number ($CFL=\frac{U△t}{h_{min}}$, where U is the inlet average velocity, △t is the time step, and h_min is the minimum grid size of all directions) is the same as simulation (1). Simulation (3) is carried out to investigate the time-step sensitivity of results. The stated grid sizes are for uniform mesh which contains an immersed body, while the grid sizes for the inlet/outlet are similar (41 × 41 × 81) for all simulations. The magnitude of the non-dimensional velocity at the intersection of the mid-surface (x = 0) and z = 0 surface at t/T = 0.06 is plotted in Fig. 18. The magnitudes of the non-dimensional velocities at the intersection of the mid-surface and z = 0 surface are almost identical (Fig. 18). Therefore, the grid size of 73 × 109 × 153, which was used in all the simulations for case S2 and reported in Sec. III, is enough to obtain grid independent results. Furthermore, as it is evident from Fig. 18, the non-dimensional velocities at the intersection of the mid-surface and z = 0 surface for similar grid size (73 × 109 × 153) and different time-steps ($△\overline{t}=0.0125$ and 0.00625) are identical. Therefore, the results obtained using $△\overline{t}=0.0125$ are independent from the time step size. The flow visualizations of these simulations were also identical showing the results are grid and time step independent.

FIG. 18.

The magnitude of the non-dimensional velocity [$u_{mag}={\left(u_x^2+u_y^2+u_z^2\right)}^{1/2}$] at the intersection of the mid-surface (x = 0) and z = 0 surface at t/T = 0.06 for 73 × 109 × 153 with $△\overline{t}=0.0125$, 108 × 164 × 228 with $△\overline{t}=0.008$, and 73 × 109 × 153 with $△\overline{t}=0.00625$ (the grid resolutions are for uniform mesh which contains an immersed body).

APPENDIX C: BURGERS’ VORTEX MODEL

Burgers’ vortex^55–57 is the exact solution of the Navier-Stokes equation for a steady viscous vortex for which the stretching and viscous effects are in balance;⁵⁸ consequently, the total variation of enstrophy (Ω) is equal to zero [Eq. (C1)].⁵⁹ It is noted that Eq. (C1) is written based on the incompressible and constant viscosity assumptions,

$$\frac{D\mathrm{\Omega }}{Dt}=2{\omega }_i{\omega }_j\frac{\partial u_i}{\partial x_j}+\frac{1}{\mathrm{R}\mathrm{e}}\frac{{\partial }^2\mathrm{\Omega }}{\partial x_j\partial x_j}-\frac{2}{\mathrm{R}\mathrm{e}}\frac{\partial {\omega }_i}{\partial x_j}\frac{\partial {\omega }_i}{\partial x_j},$$ (C1)

where ω is the vorticity. The radius of the vortex structure defined as the distance from the vortex axis to the location at which the ratio of vorticity magnitude to the vorticity on the axis of the vortex is equal to e⁻¹.⁵⁹ In Burgers’ model, the axis of the vortex structure is determined by the maximum vorticity.^55–57 Figure 19 shows the probability density function (PDF) of the absolute value of the total variation of enstrophy normalized by its own standard deviation for case S2H at t/T = 0.3. As it can be seen in Fig. 19, the PDF has a peak at a value of 0, which shows that the stretching and viscous effects are in balance. Therefore, the Burgers’ model can be used for finding the vortex structures. It is noted that the similar trend can be observed for other test cases at different time instants.

FIG. 19.

PDFs of the absolute value of the total variation of enstrophy normalized by its own standard deviation for the case S2H at t/T = 0.3 in the dome.