Echo Planar Time-resolved Imaging (EPTI)

Abstract

Purpose:

To develop an efficient distortion- and blurring-free multi-shot EPI technique for time-resolved multiple-contrast/quantitative imaging.

Methods:

EPI is a commonly used sequence but suffers from geometric distortions and blurring. Here, we introduce a new multi-shot EPI technique termed Echo Planar Time-resolved Imaging (EPTI), which has the ability to rapidly acquire distortion- and blurring-free multi-contrast dataset. The EPTI approach performs encoding in k_y-t space and utilizes a new highly-accelerated spatio-temporal CAIPI sampling trajectory to take advantage of signal correlation along these dimensions. Through this acquisition and a B₀-informed parallel imaging reconstruction, hundreds of ‘time-resolved’ distortion- and blurring-free images at different TEs across the EPI readout window can be created at sub-millisecond temporal increments using a small number of EPTI-shots. Moreover, a method for self-estimation and correction of shot-to-shot B₀-variations was developed. Simultaneous-multislice acquisition was also incorporated to further improve the acquisition efficiency.

Results:

We evaluated EPTI under varying simulated acceleration factors, B₀-inhomogeneity and shot-to-shot B₀-variations to demonstrate its ability to provide distortion- and blurring-free images at multiple TEs. Two variants of EPTI were demonstrated in vivo at 3T: i) A combined gradient- and spin-echo EPTI for quantitative mapping of T₂, T₂*, proton density, and susceptibility at 1.1×1.1×3 mm³ whole-brain in 28 s (0.8 s/slice); and ii) a gradient-echo EPTI, for multi-echo and quantitative T₂* fMRI at 2×2×3 mm³ whole-brain at a 3.3 s temporal resolution.

Conclusion:

EPTI is a new approach for multi-contrast/quantitative imaging that can provide fast acquisition of distortion- and blurring-free images at multiple TEs.

Introduction

Echo planar imaging (EPI) is a rapid MRI acquisition technique capable of producing a 2D image in a single shot using a readout of a few tens of milliseconds (1,2). Due to its ability to achieve high temporal resolution, single-shot EPI (ss-EPI) has been widely used in diffusion imaging (3,4), functional imaging (5,6) and perfusion imaging (7,8). Multi-echo EPI can also be used to increase the functional sensitivity in functional MRI (fMRI) (9–11) or to measure T₂* time courses in BOLD experiments (12,13). Combined spin and gradient multi-echo EPI sequence has also been developed to extract BOLD signal that is more confined to microvasculature (14), to achieve fast quantification of T₂ and T₂* (15) or to assess vascular properties in perfusion imaging (16–18).

Despite EPI’s advantage of rapid k-space coverage, the prolonged readout time for high-resolution image leads to several major problems: i) severe geometric distortion due to B₀-inhomogeneity disrupting the encoding along the low bandwidth phase-encoding (PE) direction, ii) spatial filtering from the time dependent T₂/T₂* decay across the EPI readout, and iii) typically only a single-contrast image (with blurring and distortion effects) at the effective echo time is produced. If multi-TE acquisitions are applied, the minimum temporal spacing of the multiple TEs is set by the readout length, and this long readout duration makes it difficult to acquire multiple image echoes prior to significant T₂/T₂* decay. The first two problems significantly compromise the quality of high-resolution EPI images and limit its application to high-quality structural imaging. The third issue precludes multi-echo EPI from common use for quantitative multi-contrast imaging.

A number of distortion mitigation approaches have been developed for ss-EPI. The most popular post-processing approaches include field-map based corrections (19,20), and image-based corrections through a modified acquisition, such as reversed phase encoding (21). These methods correct for distortion by using estimated local pixel shifts in the image. Parallel imaging techniques (22,23) with in-plane acceleration have also been applied to ss-EPI to reduce distortion/blurring by decreasing the effective echo spacing. However, all of these methods have limited capability in correcting severe distortions in regions with strong susceptibility, leading to inaccurate anatomical information and loss of effective resolution. Multi-shot EPI techniques, including interleaved multi-shot EPI (ms-EPI) (4,24–27) and readout-segmented EPI (rs-EPI) (28,29), have been developed as alternatives to ss-EPI to further increase the sampling bandwidth in the PE direction and thus provide less distortion and blurring. These approaches, however, come a cost of longer scan time and a need for phase navigation/estimation for shot-to-shot B₀-variations.

The distortion and blurring in EPI is caused by the nuisance signal evolution from susceptibility-induced phase accumulation and magnitude signal decay during prolonged echo train acquisition. If this nuisance signal evolution can be sampled, that is, with each echo time-point along the EPI train, all of the k-space lines composing an image can be acquired with the same susceptibility-induced phase and T₂/T₂* decay, then hundreds of distortion- and blurring-free multi-contrast images can be created along the readout train at a temporal resolution in the order of a millisecond (equal to that of the echo-spacing). This can be achieved by Echo Planar Spectroscopic Imaging (EPSI) (30) in which different phase encodings are acquired in a multi-shot manner to obtain a full image at each echo time. Another multi-shot technique, Point-Spread Function mapping EPI (PSF-EPI) (31–33), which has currently been used to acquire distortion-free images, is also able to sample and extract such information. However, both PSF-EPI and EPSI require hundreds of acquisition shots to fully-sample the k_y-t space, leading to an extremely long acquisition (e.g., ~200 times longer when compared to ss-EPI for brain imaging at 1 mm resolution). Even after parallel imaging acceleration (and reduced FOV approach in the case of PSF-EPI), more than 30 shots are still needed to achieve acceptable image quality (33–35), limiting their routine usage in high-resolution quantitative imaging or dynamic imaging. Significant improvements of EPSI have been made recently in fast spectroscopic imaging through exploring spatiospectral correlation and subspace model-based reconstruction (36–38).

In this study, we proposed a new imaging technique termed Echo Planar Time-resolved Imaging (EPTI), to achieve fast, distortion- and blurring-free multi-contrast imaging with resolved signal evolution for EPI, first described in (39). With this approach, a novel spatio-temporal CAIPI sampling trajectory was developed to efficiently cover the desired k_y-t space using several EPI readouts. The undersampled k_y-t space is then recovered by exploring the signal correlation across the time and coil dimensions in a B₀-informed parallel imaging reconstruction. To provide robustness to shot-to-shot B₀-variations, a self-B₀-variation estimation and correction method was also developed that takes advantage of the unique k_y-t sampling of EPTI. To further accelerate the acquisition, simultaneous multislice (SMS) (40,41) was incorporated into EPTI, with an optimized k_y-k_z-t trajectory and reconstruction.

EPTI provides hundreds of distortion- and blurring-free T₂&T₂*-weighted images across the EPI readout, spaced at a time interval equal to an EPI echo-spacing (~1 ms), providing new signal evolution information. An acceleration factor up to 20–40× can be achieved along the PE direction, which allows high-resolution time-resolved brain imaging to be performed in less than 10 EPI-shots. Here, EPTI was demonstrated for two in vivo applications: i) fast quantitative mapping via Gradient-Echo and Spin-Echo EPTI (GESE-EPTI) to provide, simultaneously, maps of proton-density, T₂, T₂*, B₀, tissue-phase, and susceptibility weighted imaging (SWI) at 1.1×1.1×3 mm³ resolution whole-brain in ~28 s, and ii) dynamic imaging via GE-EPTI to acquire whole-brain BOLD fMRI and T₂* maps at 2×2×3 mm³ resolution with a temporal resolution of 3.3 s. The high efficiency of EPTI should also make it useful for a number of other applications where high-SNR undistorted images, multiple-contrast images or quantitative mapping are desired.

Theory

Phase Encoding-Time (k_y-t) space

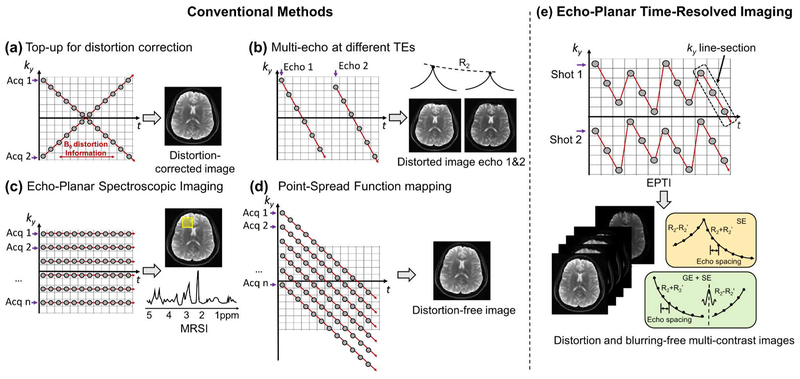
Figure 1 demonstrates the k_y-t space sampling strategy of EPTI. In contrast to the usual signal space used in conventional k-t based methods (42,43), the time dimension here represents the echo time of each k_y-line within an EPI readout train as in (30,44,45). Each gray circle in the figure represents an EPI readout line. For traditional ss-EPI, the sampling is expressed in the k_y-t space as a diagonal line. Magnitude T₂* decay and susceptibility-induced phase accumulates over time, leading to blurring and distortion. To correct for distortion, a pair of datasets with reversed phase-encoding can be acquired (21), shown as a pair of reversed diagonal lines in the k_y-t space (Fig. 1a). To obtain multiple-contrast images, multi-echo EPI methods (9,15) can be used as shown in Figure 1b to help fill the k_y-t space.

FIG. 1.

The ky-t trajectories of (a) ‘top-up’ distortion correction using reversed phase encoding acquisition, (b) multi-echo EPI combined with parallel imaging for multi-contrast imaging, (c) EPSI for spectroscopic imaging, (d) PSF-EPI for distortion- and blurring-free imaging, and (e) the proposed EPTI using an efficient spatial and temporal CAIPI sampling trajectory for distortion- and blurring-free multi-contrast imaging, which is able to provide signal evolution information across EPI readout as shown in the bottom yellow and green boxes. Here, each dot represents an EPI readout line.

If the k_y-t space is fully-sampled, a 2D k-space (k_x-k_y) without any phase accumulation or signal decay along the PE direction, can be obtained at each echo time point. Therefore, a series of images with different contrasts, spaced at a time interval of just an echo-spacing, can be generated without any distortions and blurring. Such fully-sampled k_y-t data can be acquired via EPSI (30), using a multi-shot acquisition with step-wise increase of PE gradient after each shot (Fig. 1c). On the other hand, the PSF mapping approach (31–33) uses acquisitions with additional PE gradients before a conventional EPI readout, which creates diagonal lines in the k_y-t space as shown in Figure 1d.

Echo Planar Time-resolved Imaging (EPTI)

The key assumption underlying the EPTI concept is that one can highly undersample the k_y-t space, and recover the missing data points by exploiting the correlation across the time and PE directions. Here, we demonstrate that this is possible through an optimized k_y-t sampling and a B₀-informed reconstruction.

Optimized k_y-t space sampling

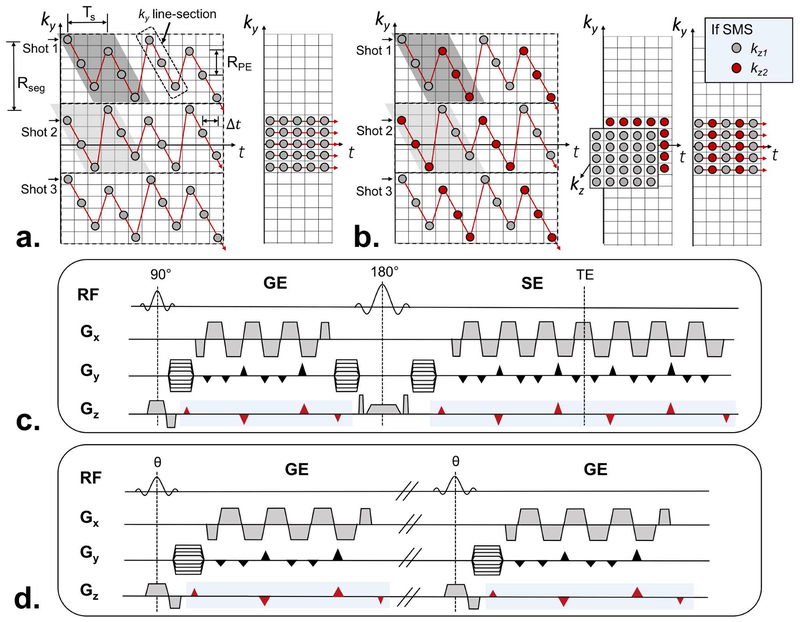
Instead of acquiring one or all of the k_y lines with each EPI shot, each EPTI shot covers a k_y segment in k_y-t space using a spatio-temporal CAIPI trajectory as shown in Figure 1e. This k_y-t trajectory ensures that the neighboring diagonal k_y line-sections within each EPTI-shot are acquired only a few milliseconds apart, and thus contain only a small amount of B₀-inhomogeneity induced phase accumulation and T₂* decay that can be well approximated by parallel imaging and B₀-informed reconstruction (46).

Figure 2a provides a detailed description of EPTI using a 3-shot EPTI acquisition as an example. Each EPTI-shot includes several diagonal k_y line-sections that contain a plurality of temporally adjacent readout lines acquired in a temporally sequential manner. These readout lines are spaced apart in time by an EPI echo-spacing (Δt) and in PE direction by R_PE. Within each EPTI-shot, two temporally adjacent k_y line-sections are interleaved in the PE direction with complementary k_y sampling, and repeated multiple times across the readout. An example of such interleaved pair of k_y line-sections for shot 1 is highlighted in dark-gray in Figure 2a. This complementary undersampling is designed to better utilize the coil sensitivity in the B₀-informed reconstruction. Here, the two adjacent k_y line-sections are separated by another temporal spacing T_s, equal to the product of the echo spacing (Δt) and the number of data samples in each k_y line-section (N_s). As such, the number of k_y lines covered by each EPTI shot, R_seg, is R_PE×N_s. For a typical brain acquisition at 3T (1 mm resolution with 200 k_y lines, FOV_y = 20 cm), R_seg will usually be set to 20–40, resulting in 5–11 EPTI-shots. N_s is usually selected to keep T_s to be in the order of 5–10 ms, to ensure that the phase accumulation and signal decay are small between adjacent k_y line-sections. The different EPTI-shots are acquired in consecutive TRs, with a modified starting k_y line-section pattern for even-numbered EPTI-shots (light-gray highlight in Fig. 2a) to ensure a uniform undersampling across the shots along the k_y line-sections. With this strategy, only a small number of GRAPPA-like (23) kernel patterns are needed in the shot-combined reconstruction (see below).

FIG. 2.

Detailed description of EPTI sampling pattern and sequence diagram. (a) Multiple shots are used to cover the k_y-t space, each with a spatial and temporal CAIPI trajectory that contains multiple diagonal k_y line-sections. Each of these k_y line-sections includes a number of temporally adjacent readout lines (dot) spacing apart in time by an EPI echo spacing Δt and in PE direction by R_PE. The two adjacent k_y line-sections are interleaved in the PE direction (highlighted in gray), and separated in time by a spacing of T_s, equal to the product of the echo spacing (Δt) and the number of data samples in each k_y line-section (N_s). The segment size along PE direction of each shot (R_seg) can be determined by the product of R_PE and N_s. A low-resolution calibration scan can be acquired by 20–30 EPI readouts without any phase encoding blips as shown on the right. (b) The red and gray color illustrate the sampling pattern when SMS is applied into EPTI acquisition at MB=2. The fully-sampled low resolution calibration data (k_x-k_y-k_z-t) can be acquired as shown in the middle. This fully-sampled acquisition can be further accelerated using blipped-CAIPI SMS as shown on the right, in which case additional short SMS calibration data is acquired and used to reconstruct the EPTI calibration data first. The sequence diagrams of (c) GESE-EPTI, and (d) GE-EPTI are also shown, where EPTI readout can be continuously played out in the sequence to achieve high efficiency. The marked blue region indicates the G_z gradients that should be applied when SMS is employed.

B₀-informed parallel imaging reconstruction

The EPTI reconstruction uses GRAPPA-like (23) compact kernels to interpolate the undersampled k_x-k_y-t data, similar to the approach that has previously been employed for accelerated PSF-EPI data (46). For each horizontal line in k_y-t space, the signal differences of the neighboring k-space points would be i) B₀-inhomogeneity-induced phase, and ii) T₂* decay/T₂’ recovery. Since the neighboring points along time are close together, the signal differences should be small. The small and spatially-smooth phase accumulation can be considered as an additional encoding information that can be estimated by a convolutional kernel in k-space, while the small T₂* decay/T₂’ recovery can be approximated by a linear interpolation within the kernel. Here, each reconstruction kernel is designed to cover two adjacent k_y line-sections, spanning several milliseconds. The missing data points are recovered by a weighted combination of their neighboring points in a multi-channel dataset as follows (46),

$${\mathrm{s}}_i\left(k_x,k_y,t\right)={\sum }_{j=1}^{N_c}{\sum }_{(k_x^{\prime },k_y^{\prime },t^{\prime })\in K}{w}_i\left(j,k_x^{\prime }-k_x,k_y^{\prime }-k_y,t^{\prime }-t\right)\mathrm{*}{s}_j(k_x^{\prime },k_y^{\prime },t^{\prime })$$ (1)

Where s_i(k_x, k_y, t) is the missing data point of the i-th channel at position (k_x, k_y, t) to be reconstructed, ${\mathrm{s}}_j\left(k_x^{\prime },k_y^{\prime },t^{\prime }\right)$ is the acquired data point inside the kernel denoted by K, j is the index of channels counting from 1 to the total number of channels N_c, and w_i is the weights of the kernel containing coil sensitivity and B₀-inhomogeneity information.

After this k_y-t reconstruction, inverse Fourier transforms are applied along the phase- and frequency-encoding directions at each time point to obtain a series of images with different T₂/T₂*-weighted contrasts. The reconstruction kernels are trained using a low-resolution k_x-k_y-t calibration data as shown on the right panel of Figure 2a. Typically, 20–30 phase encodings are acquired in the training dataset, using an EPSI-like acquisition.

SMS-EPTI

To further accelerate EPTI, SMS is incorporated into the sequence using multiband RF excitation and an optimized k_y-k_z-t sampling trajectory (Fig. 2b). The blipped-CAIPI acquisition technique (41) is used here to improve the reconstruction quality by better utilizing the coil sensitivity. For SMS acquisition with a multiband (MB) acceleration of 2, a partition-encoding blip is applied after each k_y line-section in an EPTI-shot. The polarity of this G_z blip alternates as the acquisition moves from one k_y line-section to the next as shown in Figure 2c&d. This moves the k_z sampling positions from +dk_z to −dk_z, and then from −dk_z to +dk_z for subsequent k_y line-section to achieve good sampling coverage in k_y-k_z-t space. Note that other suitable G_z blip schemes can also be employed for different acquisition protocols and MB accelerations. For B₀-informed reconstruction, the reconstruction kernel is extended by one more dimension along slice direction to jointly reconstruct the k-space for simultaneously acquired slices.

The fully-sampled low resolution calibration data (k_x-k_y-k_z-t) should be acquired as shown in Figure 2b (middle). To minimize the time needed for calibration, this fully-sampled acquisition can also be accelerated using the blipped-CAIPI SMS as shown in Figure 2b (right), in which case additional short SMS calibration data is acquired and used to reconstruct the EPTI calibration data first using slice-GRAPPA (41).

Sequence diagram

The EPTI acquisition can be incorporated into different sequences to acquire different contrasts and signal evolution information. As a proof of concept, two types of EPTI sequences were created: i) GESE-EPTI as shown in Figure 2c, and ii) GE-EPTI as shown in Figure 2d. In GESE-EPTI, a 90° and a 180° pulse are played out, while the EPTI readout is employed to fill any dead time in the sequence to obtain the signal evolution of an FID followed by a SE. The resulting multi-contrast data enables the calculation of a number of quantitative maps including T₂, T₂*, proton density, B₀, and SWI/quantitative susceptibility mapping (QSM). In GE-EPTI, no 180° pulse is added to the sequence, allowing for a shorter TR for fast multi-contrast dynamic imaging such as in dynamic T₂* imaging, multi-echo BOLD fMRI and functional QSM (fQSM).

Navigator-free estimation and correction of shot-to-shot B₀-variations

The B₀-inhomogeneity can vary across different EPTI-shots due to respiration and/or physiological noises. As such, each reconstructed k_y segment from a given EPTI-shot is contaminated with an added image phase from B₀-variation specific to that shot, causing artifacts in the segment-combined images. This issue is analogous to that in rs-EPI for diffusion imaging (29,47), with phase corruption being much smaller than in diffusion. In rs-EPI, the phase contaminations are estimated and corrected using additional navigators and an image-based phase-correction for each segment (29). Unlike diffusion rs-EPI, in EPTI, the amount of phase contamination will increase linearly during each readout at multiple TEs, causing images at the later time-points to contain larger phase contaminations (with GESE-EPTI, it will also decrease linearly between the 180^o and the spin-echo as B₀ phase unwinds). If the shot-to-shot B₀-variations (sB₀) can be estimated, the amount of phase contamination at each time-point along the EPTI readout can be corrected for.

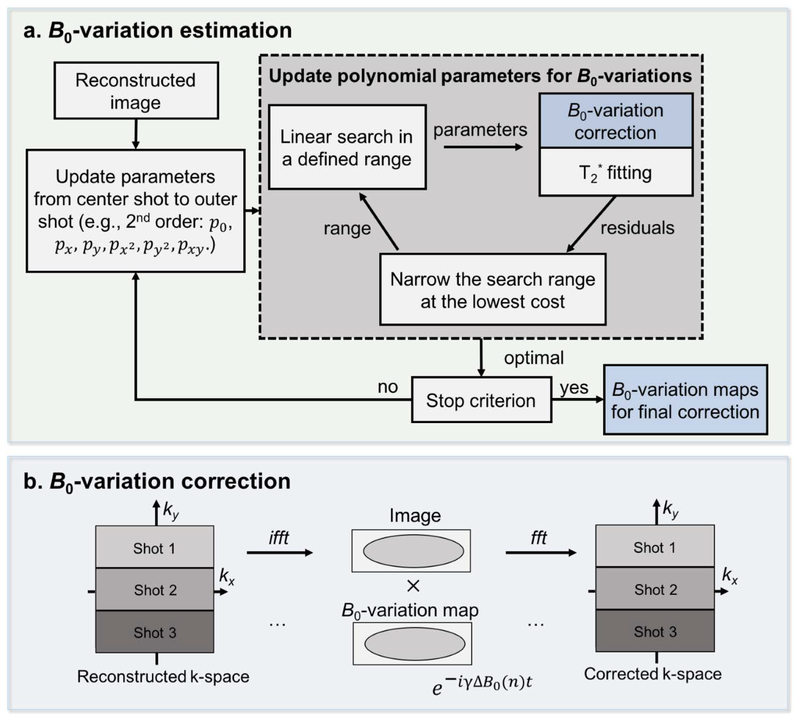
With our current acquisition, we expect sB₀ to be small and spatially smooth, such that they can be approximated well using a low order polynomial. With this assumption, a navigator-free B₀-variation estimation and correction method was developed (Fig. 3). This method is a data driven approach which relies on a greedy search algorithm (48,49) to find polynomial coefficients that can best approximate sB₀ using the acquired EPTI data. The goodness of fit is chosen to be the root mean square error of the T₂* fitting from the reconstructed GE EPTI image-series, as reducing phase corruptions should reduce image artifacts and fitting errors. The estimated B₀-variation maps are then used to correct the phase for each segment in the image domain as shown in Figure 3b, similar to the phase correction in rs-EPI (29).

FIG. 3.

An illustration of the proposed self-B₀ variation estimation (a) and correction (b). After reconstruction, fully-sampled EPTI-shots can be obtained but with different B₀-variations. Polynomial maps are used to estimate these B₀-variations assuming they are of sufficient low spatial frequency. To estimate the variation maps, the polynomial parameters are updated iteratively from the center to the outer segments. A linear greedy search algorithm within a selected range is performed for each parameter by selecting the value that gives the minimal residual errors of T₂* fitting, assuming that the clean images without artifacts will have minimized residual errors. The estimated B₀-variation maps are then used to correct the phase for each segment in the image domain as shown in (b). The corrected segments are combined to obtain the final image series.

Methods

All data were acquired with a consented institutionally approved protocol on a Siemens Prisma 3T scanner with a 32-channel head coil (Siemens Healthineers, Erlangen, Germany). Both the simulated and in vivo EPTI data (GE and SE) were reconstructed using low-resolution calibration GE data with 29 PE lines and 23 echotimes, using the same echo spacing as in the imaging data.

Simulation experiments

There are several factors that will affect the performance of EPTI, including the undersampling rates along the time (T_s) and the PE (R_PE) directions, the level of B₀-inhomogeneity (dB₀), and the shot-to-shot B₀-variations. Since the effect of R_PE is mostly determined by coil sensitivity, an R_PE of 4 was selected in our experiments for 32-channel acquisition, which is considered to be at the limit of what this coil can achieve when accelerating across one direction (note that the ‘effective’ acceleration along the phase-encoding in EPTI here is somewhat smaller than 4, as data from adjacent k_y line-sections that contain complementary k_y undersamplings will be jointly reconstructed). With R_PE fixed at 4, simulation experiments were performed to investigate the effect of T_s, dB_0, and sB₀. Since the gradient-echo and spin-echo EPTI data should behave similarly in terms of these three factors, only the gradient-echo EPTI data were examined in this section.

Acceleration factors

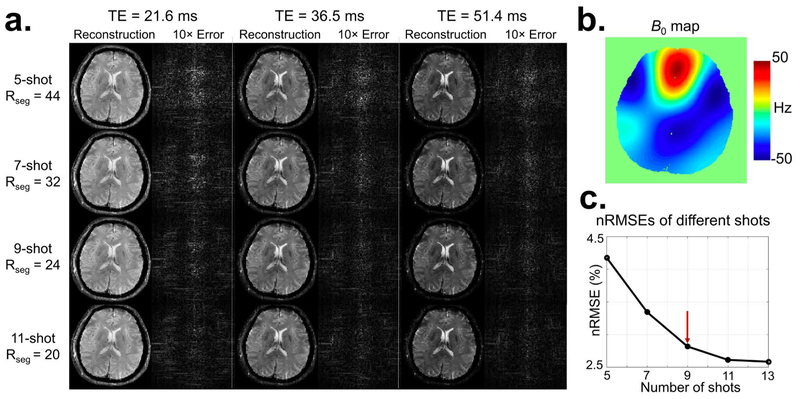
Bloch simulations were used to simulate k_y-t EPTI data at different acceleration factors. In order to perform this simulation, proton density, T₂, T₂*, B₀ and coil sensitivity maps were obtained from multiple-TE acquisitions of the single-echo SE sequence and the multi-echo 2D GRE sequence on a healthy subject at a 1×1×3 mm² resolution. With these parameter maps, a fully-sampled k_y-t EPTI data was simulated with a realistic T₂/T₂* decay and B₀-inhomogeneity induced phase. An echo spacing of 0.93 ms was used, which corresponds to the minimum echo spacing achievable for this 1-mm EPTI protocol on the Prisma scanner. Four EPTI acquisitions that utilize different total numbers of acquisition shots (5, 7, 9, 11 shots) and hence different R_seg sizes (44, 32, 24, 20 lines) were created by undersampling the simulated fully-sampled data. The R_PE was kept at 4 for all of the four cases, resulting in time intervals between adjacent k_y line-sections (T_s) of 10.23 ms, 7.44 ms, 5.58 ms, and 4.65 ms, respectively. Note that the data matrix sizes (k_x×k_y×t) of the different EPTI cases will be slightly different, since the number of total k_y-lines is the product of the number of shots and R_seg, and t should be a multiple of N_s. Nonetheless, its effect on the image resolution is negligible and should not affect the comparison between acquisitions. The matrix sizes used were (k_x=224) × (k_y=220, 224, 216, 220) × (t=88, 96, 96, 100). Spatially uncorrelated Gaussian noise was also added to the k-space data to mimic the in vivo conditions, with the signal-to-noise ratio (SNR) set to 40. Reconstruction was performed for the four EPTI cases, and the normalized Root Mean Squared Error (nRMSE) between the reference images and the reconstructed images were calculated for evaluation.

Levels of B₀-inhomogeneity (dB₀)

In order to investigate the performance of EPTI under different B₀-inhomogeneity levels, fully-sampled reference data and 9-shot EPTI data with B₀-inhomogeneity with ranges of ±25 Hz, ±50 Hz, ±75 Hz, ±100 Hz were simulated. The B₀-inhomogeneity maps used in these simulations are scaled versions of the acquired in vivo map shown in Figure 4b that has a range of ±50 Hz.

FIG. 4.

The results of simulation experiments investigating varying acceleration factors. A larger size of each EPTI shot (R_seg), and thus higher undersampling along PE and time, leads to reduced shot numbers for a given resolution. (a) Reconstructed images of different EPTI shots and their corresponding 10× error maps at 3 selected TEs. All EPTI datasets were simulated using a B₀ map with a range of ±50 Hz (b). Figure 4c shows a plot of the average nRMSEs across all TEs vs. the number of EPTI shots. EPTI performed well at all shot numbers with relatively small errors, and the error decreases as the shot number increases due to the reduced undersampling rate. In addition, 9-shot EPTI provides a good tradeoff between image quality and acquisition time.

Shot-to-shot B₀-variations (sB₀)

To evaluate the effect of shot-to-shot B₀-variations, EPTI data were simulated with added sB₀ using a time-series of B₀ maps obtained from an in vivo scan with a 5-echo spin and gradient echo EPI (SAGE-EPI) sequence (15). A time series of data was acquired with the following parameters: FOV = 224×224 mm²; in-plane resolution = 2×2 mm²; slice thickness = 4 mm, R_inplane = 3, TEs = 25, 68, 111, 154, 197 ms (with the first two TEs acquired prior to the 180^o), TR = 2.2 s. The T₂ and T₂* maps were measured by fitting the images to the signal equation (50), and the B₀ map for each TR was calculated using the phase difference. The SAGE-EPI data were interpolated to match with another 1-mm single-echo ss-EPI data (for proton density estimation). This high-resolution image and the interpolated T₂, T₂* and 9-dynamic B₀ maps were used to simulate a 9-shot EPTI data with sB₀ corruption. Here, the magnitude of sB₀ was scaled by 1.5× to slightly exaggerate the level of shot-to-shot phase variations. Other imaging parameters for this simulation were kept the same as in previous simulations. An additional 9-shot EPTI data without B₀-variations was also simulated for comparison.

The proposed self-B₀-variation estimation and correction was applied to the reconstructed EPTI data using: a 3^rd order polynomial, 2 iterations, a searching range of ±3 Hz. Both the uncorrected and the corrected EPTI data were evaluated against the reconstruction from the EPTI data without shot-to-shot variations. Additionally, resolution and artifact characterizations using PSF analysis was conducted for EPTI, which was then compared against the conventional 3-shot ms-EPI at the same resolution and echo spacing.

In-vivo experiments

Acceleration factors

The first in vivo dataset of prospectively accelerated EPTI was designed to evaluate the performance of EPTI at four different acceleration levels. GESE EPTI data were acquired using the following parameters: FOV = 240 × 240 mm²; in-plane resolution = 1.1×1.1 mm²; slice thickness = 3 mm; number of slices = 19; number of shots = 5, 7, 9, 11; segment size R_seg = 44, 32, 24, 20; R_PE = 4; number of echotimes (GE/SE) = 44/88, 48/96, 48/96, 40/80; echo time range of GE/SE = 6.9–48.2 ms/65.8–149.3 ms, 6.7–50.4 ms/68.4–156.7 ms, 6.7–50.4 ms/69.4–157.7 ms, 6.4–42.7 ms/61.8–135.3 ms; TR per shot, TR_shot = 3.8 s. The echo-spacing used for the 5-shot acquisition is slightly larger (0.96 ms) than the other acquisitions (0.93 ms) due to the enlarged G_y phase-encoding blips to achieve a large R_seg. After EPTI reconstruction, the self-B₀-variation correction was applied to both spin- and gradient-echo data using the B₀-variation parameters estimated from gradient-echo data. The final image-series at multiple TEs was then used to calculate T₂, T₂* and tissue phase.

For comparison, spin-echo ss-EPI and gradient-echo ss-EPI data were also acquired on the same subject with matching resolution, using the following parameters: R_inplane = 3; echo spacing = 0.93 ms; TE/TR for SE = 95/3000 ms and TE/TR was 27/3000 ms for GE. To match the SNR level of the EPTI data, 9 averages of this data were acquired and averaged for comparison. Additionally, standard single-echo SE and multi-echo 2D GRE were acquired to obtain the reference T₂, T₂* and tissue phase maps, using the following parameters: TEs for SE = 25, 50, 75, 100, 125, 150, 175 ms; TEs for multi-echo 2D GRE = 10, 20, 30, 40, 50, 60 ms.

GESE SMS-EPTI for fast whole brain quantitative imaging

In this experiment, SMS acceleration was incorporated into EPTI to provide faster, whole-brain multi-contrast and quantitative imaging. Whole-brain data were acquired using GESE SMS-EPTI on a healthy volunteer. A 9-shot EPTI acquisition was used with a multiband (MB) acceleration of 2 and a TR_shot of 3.1 s for 34 slices, while the other imaging parameters were kept the same as before. The total acquisition time for this whole-brain 1.1×1.1×3 mm³ quantitative imaging acquisition is 27.9 s (3.1 s × 9 shots). Three averages were acquired to boost the SNR of the quantitative maps. A low-resolution calibration data was also acquired with MB = 2 (total ~23 s).

GE SMS-EPTI for fMRI

The feasibility of EPTI for dynamic quantitative imaging was tested using a time-series of GE SMS-EPTI acquisition to provide dynamic T₂* quantification in a blood oxygenation level dependent (BOLD) fMRI experiment. Imaging parameters were: FOV = 240×240×102 mm³; in-plane resolution = 2×2 mm²; slice thickness = 3 mm; number of shots = 3; R_seg = 40; R_PE×MB = 4×2; echo spacing = 0.66 ms; number of GE echotimes = 60; echo time range = 6.2–45.1 ms; flip angle = 64°; TR_shot = 1.1 s (providing a temporal resolution to the fMRI experiment of 3.3 s). Data were acquired for a total of 6 minutes, with visual stimulus presentation following a standard block-design paradigm consisting of a 25-second full-field black-and-white “checkerboard” pattern contrast-reversing at 12 Hz followed by a 30-second uniform gray field. An initial 20-second fixation period was performed. To assist with fixation, a red dot with time-varying brightness was positioned at the center of the screen, and the subjects were asked to press a button as soon as they detected a change in brightness. Data were reconstructed using EPTI reconstruction with self-B₀-variation correction. For each TR, T₂* was estimated through a mono-exponential fit of the multi-contrast images, and a weighted-average based combination of images acquired at different TEs was also generated by using the method in (9,51). Statistical analysis was then performed on both the weighted-average magnitude data and the T₂* time course using a General Linear Model (GLM) as implemented in FSL (52–55). The data were motion corrected and smoothed with a Gaussian kernel with 5-mm FWHM, and activation was identified with a standard GLM using the stimulus timing convolved with a canonical double-gamma hemodynamic response function (HRF) that included a temporal derivative term to account for slight temporal offsets in the response timing. Clusters were determined by Z>2.3 and a cluster significance threshold of p=0.05 was used to threshold the statistical maps.

Results

Figure 4 shows the results from the simulation experiments investigating the effects of R_seg acceleration. Figure 4a shows reconstructed images of the different acceleration cases and their corresponding 10× error maps at 3 selected TEs, with the corresponding B₀ map (range ±50 Hz) shown in Figure 4b. The reconstructed images at all R_seg acceleration levels are of high quality and low errors. The error decreases with decreasing R_seg and hence increasing number of EPTI-shots as expected. Figure 4c shows the plot of the average nRMSE across all TEs vs. the number of EPTI shots, where 9-shot EPTI provides a good tradeoff between image quality and scan time for this acquisition at 1 mm in-plane resolution, and therefore 9-shot EPTI was used in all subsequent tests. The effect of the level of B₀ inhomogeneity on EPTI reconstruction was also investigated in the Supporting Information (Fig. S1), which shows the ability of EPTI to provide high quality images even in presence of large B₀ inhomogeneity (±100 Hz).

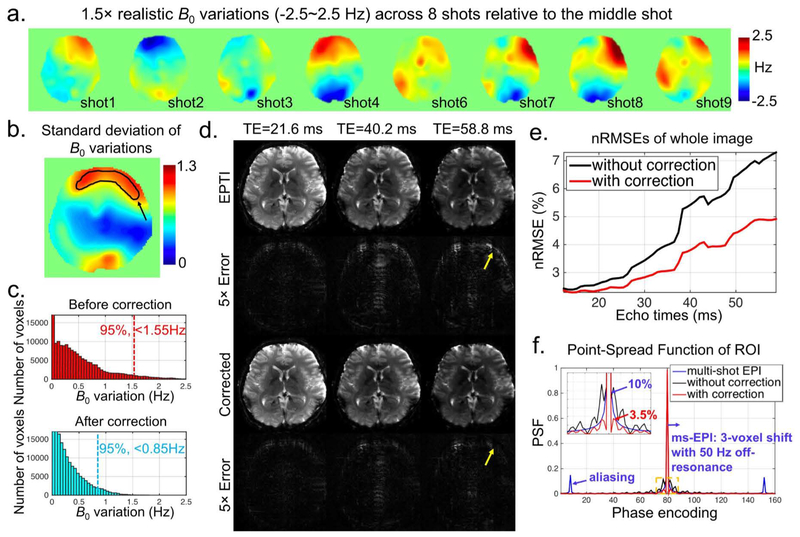
Figure 5 examines the effects of B₀ shot-to-shot variations on EPTI and the effectiveness of the proposed self-B₀-variation correction. Figure 5a shows the B₀-variations (±2.5 Hz) across 8 EPTI-shots relative to the middle 5^th EPTI-shot in a simulated 9-shot EPTI acquisition. A standard deviation map of sB₀ across the 9 EPTI-shots is also shown in Figure 5b. Figure 5c depicts the histograms of the original simulated B₀-variations and the residual effective B₀-variations after correcting B₀-variation induced phase. The residual effective B₀-variations are the equivalent field variations corresponding to the corrected phase values. The proposed correction reduces the maximum B₀-variation component from 2.5 Hz to 1.5 Hz, and the upper bound of the B₀-variation components in 95% of the voxels from 1.55 Hz to 0.85 Hz. Figure 5d shows the reconstructed images with and without self-B₀-variation correction, as well as their corresponding 5× error maps at 3 selected TEs. Overall, the errors from B₀-variations in EPTI are relatively mild, and are reduced by the proposed correction method. The yellow arrows mark the region where the B₀ field varies the most (indicated by a black arrow in Fig. 5b) and where the signal intensity is high. As expected, large image errors and artifacts are observed in this region, and they increase with TE as the shot-to-shot phase variation accumulates along the EPTI readout. Figure 5e shows that the nRMSE increases with echo time as expected, with the proposed correction providing markedly lower errors at all echo points.

FIG. 5.

The effects of shot-to-shot B₀-variations on EPTI. (a) 1.5× realistic B₀-variations with a range of ±2.5 Hz were used to simulate a 9-shot EPTI dataset with phase variations. Eight maps are shown here relative to the middle shot. (b) Spatial distribution of standard deviation of B₀-variations across 9 time points, with a marked ROI showing the region with the most-varied B₀. (c) The histograms of the original simulated B₀-variations and the residual effective B₀-variations after correcting B₀-variation induced phase. The maximum B₀-variation component was reduced from 2.5 Hz to 1.5 Hz, and the upper bound of the B₀-variation components in 95% of the voxels from 1.55 Hz to 0.85 Hz. (d) The reconstructed images and their corresponding 5× error maps at three selected TEs, with yellow arrows indicating the regions with the most varied B₀ field as shown in (b). (e) The nRMSEs of the whole image as a function of echo times with and without correction. (f) PSFs of the conventional interleaved multi-shot EPI, and EPTI with and without correction. Note that only the middle part of the PE direction is shown here (the actual size is 224).

Results from the voxel’s PSF analysis of the shot-to-shot B₀-variations are shown in Figure 5f. Here, the EPTI data without (black) and with (red) correction were compared against conventional 3-shot ms-EPI (blue). Noted that in all three cases, the PSF was generated at a long TE of 58.8 ms with large shot-to-shot phase variations. In all simulations, B₀ off-resonance of 50 Hz was used, along with shot-to-shot B₀-variation profiles taken from representative voxels in the high-variation area of the image (Fig. 5b black region) to represent a worst-case scenario. As shown in the figure, PSF of the conventional ms-EPI has been broadened across multiple voxels (with ~10% sidelobe) by T₂* blurring along the PE direction (assuming T₂*=35 ms). Moreover, it also has ~15% ghosting artifacts at ±FOV/3 positions from the shot-to-shot phase variations, as well as an approximately 3-voxel shift along the PE direction due to the imposed 50 Hz off-resonance (not shown). In comparison, the PSF of EPTI does not contain any ghosting artifacts, shifting, or T₂* blurring, but only contains local blurring due to shot-to-shot phase variations (black curve). This blurring effect was well mitigated through the proposed correction method, as indicated by the red curve, where the PSF sidelobes are reduced to only ~3.5%.

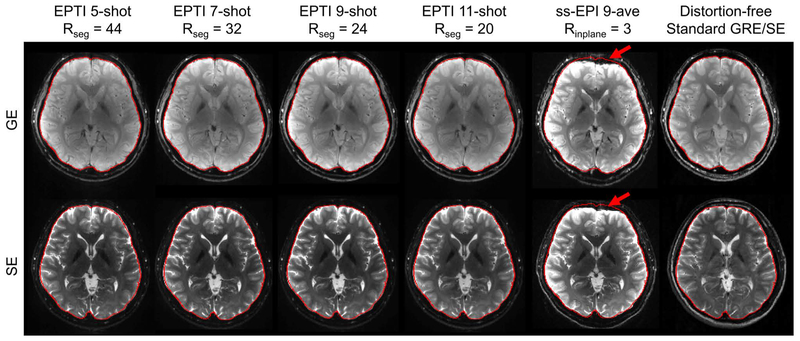
Figure 6 shows the reconstruction results of in vivo GESE-EPTI at different prospective acceleration levels. For each acquisition, gradient-echo and spin-echo images were averaged respectively to obtain a combined GE and a combined SE image. These combined EPTI images show high-SNR and good image quality without any noticeable artifacts, even at a large R_seg undersampling rate of 44. In addition, these images are free from geometric distortion as their brain boundaries are identical to those extracted from distortion-free standard GRE/SE images shown on the right. Here, a ss-EPI image at R_inplane=3, averaged across 9 repetitions is included for comparison where severe distortions can be seen on both GE and SE images (red arrows). Note the contrast differences in the GE and SE images from EPTI vs. ss-EPI or standard GRE/SE, which can be attributed to differences in the effective TEs, slightly different TRs, and the fact that the GE data in EPTI was acquired as part of a 90^o-180^o GESE acquisition, with the additional 180^o causing changes in spin-history/contrast.

FIG. 6.

Results of in-vivo experiments with different EPTI shots at 1.1×1.1×3 mm³ resolution. Combined GE and SE EPTI images eliminated the severe distortion appeared in ss-EPI (red arrows), and achieved high-SNR artifact-free images under all acceleration factors. The brain boundaries were extracted from distortion-free standard GRE/SE acquisition as shown on the right and overlaid on the EPTI and ss-EPI images for comparison.

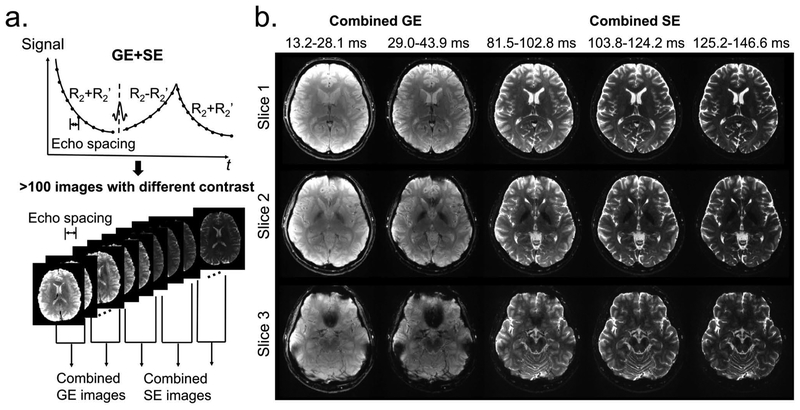
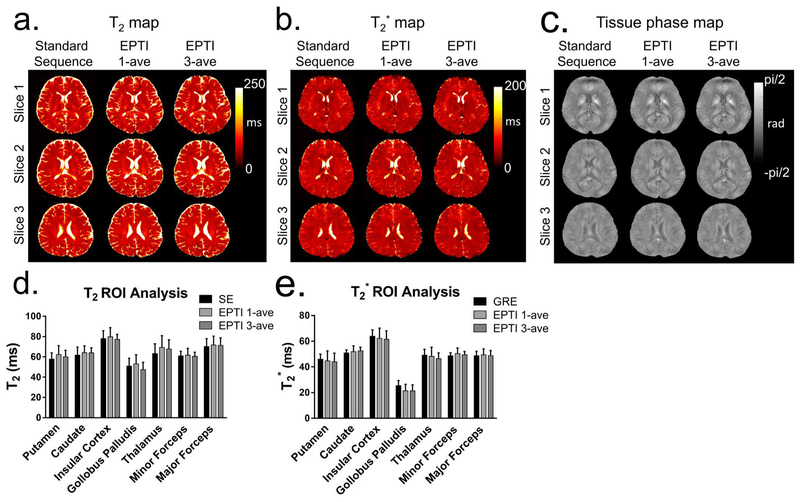
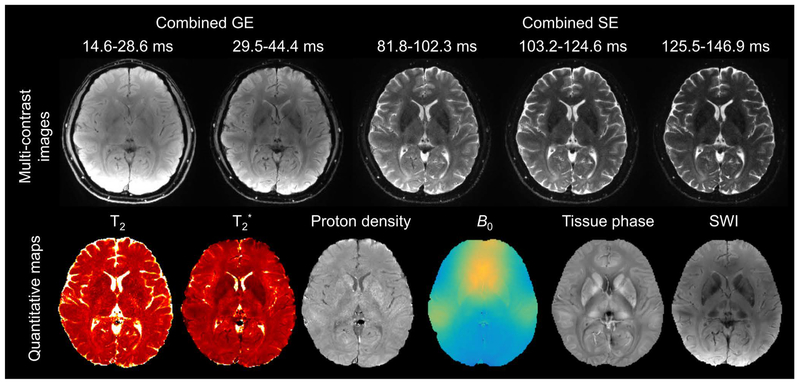
Multi-contrast images obtained from the 9-shot GESE-EPTI acquisition are shown in Figure 7, where a series of images were created at different time points on the signal evolution curve (Fig. 7a), and averaged across several TE ranges to generate combined multi-contrast images with enhanced SNR (Fig. 7b). It can be seen that the resulting multi-contrast images are of high-quality and are distortion-free. Signal and contrast variations across TEs are well captured, with the amount of signal dropout in strong B₀ through-slice dephasing regions increasing with TE and then refocusing back as expected at the center SE image. T₂, T₂* and tissue phase were also calculated and shown in Figure 8 using 1-average 9-shot EPTI, 3-average 9-shot EPTI, and standard GRE/SE method, respectively. It can be seen that EPTI can be used to acquire high-resolution quantitative maps with image quality close to that of the conventional standard methods. The 3-average acquisition further increases image SNR especially in regions in the middle of the brain that inherently have relatively poor coil sensitivity. A ROI analysis of different tissues is shown (Fig. 8e&f) for quantitative comparison. The quantitative values of EPTI in different ROIs are relatively consistent with the standard sequence. The sources of small differences between these acquisitions could be i) subject movements during and between the scans, especially for the long standard acquisitions; ii) different fitting methods and different sampled echo times; and iii) reconstruction errors and noise. To provide further quantification, fully-sampled k_y-t data was acquired on a phantom containing a number of T₂ and T₂* compartments, and retrospectively undersampled to EPTI pattern. Details of the acquisition and evaluations are included in Supporting Information (Fig. S2).

FIG. 7.

Multi-contrast images obtained by 9-shot EPTI acquisition at 1.1×1.1×3 mm³ resolution. (a) The signal evolution curve acquired by GESE-EPTI consists of more than 100 images with a time interval of an echo spacing. These images are averaged in several TE ranges to generate combined multi-contrast images with enhanced SNR as shown in (b). Multi-contrast images at 3 slices and 5 TE ranges are shown without distortion/blurring.

FIG. 8.

(a, b and c) T₂, T₂* and tissue phase maps calculated from the single-average and 3-average 9-shot EPTI, as well as standard GRE/SE. EPTI acquired high-resolution quantitative maps with image quality close to that of the standard GRE/SE, but with dramatically reduced scan time: EPTI obtained these maps simultaneously within 34.2 s (19 slices, up to 21 slices), which was much faster than the conventional SE (~28 min, 10 slices) and GRE (~7 min, 10 slices). The 3-average acquisition further increases image SNR for more accurate quantification. (e and f) An ROI analysis of T₂ and T₂* for different tissues is shown for quantitative comparison.

Figure 9 shows the in vivo results from GESE SMS-EPTI, where whole-brain scan at 1.1×1.1×3 mm³ can be performed in only 27.9 s. This rapid scan provides distortion- and blurring-free multi-contrast images that can be used to extract multiple quantitative maps as shown in Figure 9. Here, 3 averages were used to boost the SNR, and with a calibration scan of 23 s, the total scan time of this dataset is 107 s. As shown in the figure, the selected multi-contrast images, T₂, T₂*, proton density, B₀ maps, as well as tissue phase and SWI show high SNR and good image quality.

FIG. 9.

Multi-contrast images and quantitative maps acquired by GESE SMS-EPTI at 1.1×1.1×3 mm³ resolution with whole-brain coverage (34 slices) using 9-shot EPTI. The acquisition time for a single average was 27.9 s, and 3 averages were used to boost the SNR. The calibration scan was about 23 s. The combined multi-contrast images, T₂, T₂*, proton density, B₀ map, as well as tissue phase and SWI were obtained simultaneously, demonstrating the high efficiency of EPTI to obtain high-resolution high-quality multi-contrast and quantitative images without distortion/blurring.

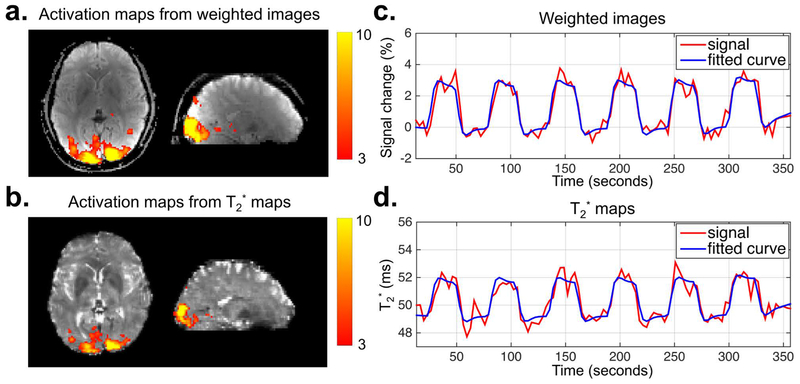
The results of the fMRI response to visual stimulation calculated from time-series of the weighted images and T₂* maps acquired using GE-EPTI are shown in Figure 10, including the z-score activation maps, the percent signal change for weighted images and the T₂* signal values of a voxel with the peak z-score. In this experiment, 3-shot GE-EPTI was used to provide a temporal resolution of 3.3 s for a whole-brain acquisition at 2×2×3 mm³ resolution, where distortion-free images at 34 echotimes were obtained for each TR. Strong activation was observed within the occipital cortex in both of the activation maps calculated by the weighted images and T₂* maps, and there is a strong correspondence between the signal and the visual stimulus timing as shown in Figure 10c&d. Moreover, the result from T₂* maps shows a smaller activation region compared to that of the weighted images, probably due to the higher contrast-to-noise ratio of the weighted images (11). Overall, these results demonstrate the potential in using EPTI for multi-echo fMRI to enhance functional sensitivity and to provide a means of detecting BOLD activation from quantitative imaging data.

FIG. 10.

The results of the fMRI experiment acquired by GE SMS-EPTI with visual stimuli from a single subject. The z-score activation maps (a and b), the percentage signal change curve of the weighted images (c) and the T₂* value curve (d) (from the maximum z statistic voxel) are shown. A temporal resolution of 3.3 s per volume was provided by 3-shot GE SMS-EPTI with a whole-brain coverage at a 2×2×3 mm³ resolution. The multi-contrast images acquired at 34 TEs for each TR were used to generate a time series of weighted images and T₂* maps for activation analysis as shown in the top and bottom row respectively. Both results show strong activation in the occipital cortex, and strong correspondence between the signal changes (red) and the task contrast (blue).

Discussion and Conclusion

In this work, EPTI was proposed as a new rapid imaging technique for distortion- and blurring-free multi-contrast imaging and quantitative imaging. A new spatial-temporal sampling trajectory was developed to achieve high accelerations, and to ensure the robustness to artifacts from shot-to-shot B₀-variations, that have plagued many existing ms-EPI approaches. The approach was demonstrated in vivo for brain imaging, both in retrospectively and prospectively accelerated acquisitions, where EPTI was shown to be robust to both B₀ inhomogeneity and shot-to-shot B₀-variations. The efficacy of EPTI for fast, high-resolution ‘time-resolved’ imaging was then demonstrated through a GESE SMS-EPTI acquisition. This acquisition provides hundreds of multi-contrast images that can be used to estimate T₂, T₂*, proton density, B₀ and SWI maps at about 1.1 mm in-plane resolution in a timeframe of 0.8 s per imaging slice. The application of EPTI for dynamic imaging was also demonstrated through a GE SMS-EPTI acquisition for whole-brain multi-echo and quantitative T₂* fMRI at a 2-mm in-plane resolution and a 3.3 s temporal resolution. This preliminary results show the feasibility of EPTI for multi-echo fMRI, which has been demonstrated in the past to provide enhanced functional sensitivity (9,51), and to reduce vulnerability to physiological noise and motion/spin-history artifacts by measuring BOLD activation from quantitative T₂* (12,56). EPTI should also prove useful to a number of other current and new applications that could benefit from fast quantitative and dynamic imaging, and the adaption of the EPTI acquisition concept into other sequences/contrasts is readily feasible.

The spatio-temporal CAIPI undersampling in EPTI allows for an efficient coverage of a large section of k_y-t space with each EPTI-shot, and the B₀-informed parallel imaging reconstruction allows this highly undersampled data to be reconstructed using compact k-space kernels that can effectively interpolate data in k_y-t space (For SMS-EPTI, the acquisition and reconstruction are done jointly in k_x-k_y-k_z-t space). The proposed k_y-t acquisition not only enables image formation from all k_y lines at the same echo time, thus achieving distortion- and blurring-free imaging, but also provides a ‘time-resolved’ imaging series with a rapid temporal sampling rate equal to that of the echo-spacing (~1 ms). With this time-resolved approach, the EPTI readout can be applied continuously within the sequence to fill any dead time, leading to a very high acquisition efficiency. Compared to a multi-echo EPI approach which can also fill out sequence dead time, the spatial resolution specification in EPTI does not dictate the desired number of image TEs acquired, but rather depends on the number of EPTI-shots and the k_y coverage of each shot (R_seg).

The selection of the undersampling rate along k_y (R_PE), k_z (MB) and time (T_s) will affect the performance of EPTI. The use of larger R_PE and T_s factors will help increase k_y coverage of each EPTI-shot (R_seg), which will reduce the number of acquisition shots and provide faster scan. The key factors that determine the achievable R_PE, MB and T_s are i) the ability of coil sensitivities of the receiver array to approximate spatial harmonics to interpolate along k_y and k_z (57); and ii) the ability of B₀-informed interpolation to approximate the image phase evolution along t_. The spatio-temporal CAIPI undersampling pattern and joint k_x-k_y-k_z-t reconstruction should also play key roles in helping push the achievable R_PE, MB and T_s. According to the simulation experiment, 9-shot EPTI with 32 channels was able to achieve high-quality images at about 1 mm resolution even in the presence of exaggerated B₀-inhomogeneity with a range up to ±100 Hz, using R_PE = 4, T_s ~5.6 ms, and R_seg = 24. Note that since coil sensitivities should also contribute to approximate B₀-inhomogeneity induced image phase, not only the level but also the spatial frequency content of the B₀-inhomogeneity are important in determining T_s. In brain imaging, areas of high B₀-inhomogeneity with strong spatial variabilities are typically located at the air-tissue interface in the periphery of the brain, where the coil sensitivities are also varying rapidly in space and thus providing good encoding ability. This likely helped contribute to the ability of EPTI to achieve very high accelerations. The use of shared information among neighboring echoes in the spatio-temporal interpolation enables high acceleration, but also results in temporal noise correlation along echo-time domain. The degree to which this happens is analyzed in the supplementary figure (Fig. S3). This spatio-temporal reconstruction also complicates the g-factor calculation. Hence, empirical g-factor (58,59) was calculated based on the reduction factor along PE and noise correlation along echo-time direction (Fig. S4).

The effect of shot-to-shot B₀-variations on the EPTI acquisition and reconstruction was characterized. Instead of inducing strong ghosting artifacts along y as in conventional ms-EPI, B₀-variations only lead to a small local spatial smoothing in the EPTI PSF. The self-B₀-variation estimation and correction method was developed to mitigate this smoothing, and was demonstrated to provide ~70% reduction in the PSF sidelobes, resulting in sidelobes level of only 3.5% even in an area with strong B₀-variations. Our current approach utilizes a polynomial fitting to estimate B₀-variations and the use of more complex fittings or approaches that exploit data structures or priors similar to (27,60) could allow for further mitigation.

The proposed EPTI reconstruction utilizes coil and B₀ information to recover k-t data, and approximates signal decay by linear interpolation in local kernels. However, such interpolation might lead to temporal smoothing or local errors in the signal curve if decay rates are different for calibration data and target undersampled data. Therefore, the T_s and hence the temporal kernel width in this work is in the range of several milliseconds, which causes only local signal smoothing or small errors for the T₂ and T₂* range of interest in the brain (see Fig. S2 for supporting evidence). The effect of the different decay rates of calibration and target data on reconstruction was also proved minor in Figure S5. Future work will explore the use of a model based reconstruction that can directly account for the signal decay information, and the partial separability and sparsity constraints similar to ones in (61,62). Such an approach could allow further accelerations and more accurate signal-evolution reconstruction for short T₂* species. Moreover, to allow for motion robustness, motion-corrected reconstruction approaches could also be integrated into EPTI, either using the image domain (63,64) or k-space (65) approach.

EPTI utilizes a continuous readout that helps it achieve high SNR acquisition efficiency. Nonetheless, owing to its fast encoding and short scan, the reconstructed images at high spatial resolution can still be noisy and multiple data averages might still be required. In this work, SMS has been incorporated to boost the SNR efficiency of EPTI, and the development of 3D-EPTI to further boost SNR will be explored in future work. In addition, including inversion preparation or a variable flip angle train could sensitize EPTI to more contrast (e.g. T₁) (66) and also achieve further acceleration. The ability of EPTI to provide rapid time-resolved imaging opens up new possibilities in a number of directions, including multicompartment tissue fitting, numerous dynamic imaging applications, and the development of new techniques to fully-harness the rich information that the EPTI acquisition can provide.

Supplementary Material

Supp figS1-5

FIG. S1. Simulation for different levels of B₀-inhomogeneity using 9-shot EPTI acquisition. The reconstructed images and the corresponding 10× error maps under four levels of B₀-imhomogeneity (±25 Hz, ±50 Hz, ±75 Hz, ±100 Hz) are shown. A higher level of inhomogeneity leads to larger image errors, and nRMSE increases with echo time due to signal decay. However, the error is still relatively low at ±100 Hz without any obvious image artifacts.

FIG. S2. A fully-sampled k_y-t data was acquired on a phantom at 1×1×3 mm³ resolution using 216 shots. The fully-sampled data was then retrospectively undersampled to generate a 9-shot GESE-EPTI dataset with R_seg = 24 to evaluate the performance of EPTI for quantitative T₂/T₂* mapping. The imaging parameters were: FOV = 216×216 mm², echo spacing = 0.95 ms, TR_shot = 2.5 s, echo time range of GE/SE = 16.3–53.4 ms / 84.3–161.3 ms. The T₂ and T₂* maps calculated from fully-sampled data and EPTI are shown in (a, b) and (d, e), and the corresponding ROI analysis of T₂ and T₂* are shown in (c) and (f) respectively. The estimated T₂ and T₂* values of EPTI are similar to the fully-sampled data even at a reduction factor of 24 along PE direction, which demonstrates the ability of EPTI for quantitative mapping under high accelerations. Figure S2 (g) and (h) present the signal curves (GE and SE) of a single image pixel using fully-sampled and EPTI-reconstructed data. The zoomed-in GE signal evolution of EPTI data is also shown in (i).

FIG. S3. A Monte Carlo based simulation was performed on a 9-shot EPTI dataset with 45 echoes. The voxel-wise noise correlation (a) of the 45 echoes relative to the middle 23^rd echo was calculated using 128 replicas. The high noise correlation of the adjacent echoes results from the use of shared information among neighboring echoes in the EPTI reconstruction, which then drops quickly after 3–4 echoes. The full width at half maximum (FWHM) of the mean noise correlation of all voxels is 7.6 echoes (~ 7 ms). The noise covariance matrix of all 45 echoes is also shown in (b). As can be seen, the temporal correlation exists as expected, but there is still sufficient amount of independency for linear regression, considering EPTI is able to provide more than 100 echoes in a single scan.

FIG. S4. (a) The empirical g-factor of 9-shot EPTI was calculated using 128 replicas according to the reduction factor along phase-encoding direction (R_seg = 24) and the effective width of neighboring data along echo-time domain that is used to reconstruct a single echo image. Here, the effective data width is characterized by the correlation along echo-time dimension (FWHM_corr), and is specified by the FWHM of the noise correlation as shown in Fig. S3. SD represents standard deviation of the real part for each voxel location through the stack of replicas. The maximum g-factor is 2.01, and the mean g-factor is 1.30. (b) In addition, empirical SNR maps of fully-sampled single-echo, EPTI single-echo and EPTI echo-combined are shown.

FIG. S5. The T₂ (a) and T₂* (b) maps obtained from the reconstructed 9-shot EPTI images using GE and SE calibration data with different signal decay rates. (c, d, and e) The signal evolution curves of three selected voxels reconstructed using GE and SE calibration data were compared with the signal evolution of a fully-sampled data. As shown in the plots, the signal evolutions of the data reconstructed from GE and SE calibration both agree well with the fully-sampled data, and the difference between their corresponding quantitative maps are small, indicating the minor effects of using calibration data with different decay rates for local interpolation.