Abstract
Purpose:
To enable parameter-free, accelerated cardiovascular magnetic resonance (CMR).
Methods:
Regularized reconstruction methods, such as compressed sensing (CS), can significantly accelerate MRI data acquisition but require tuning of regularization weights. In this work, a technique, called Sparsity adaptive Composite Recovery (SCoRe), that exploits sparsity in multiple, disparate sparsifying transforms is presented. A data-driven adjustment of the relative contributions of different transforms yields a parameter-free CS recovery process. SCoRe is validated in a dynamic digital phantom as well as in retrospectively and prospectively undersampled cine CMR data.
Results:
The results from simulation and six retrospectively undersampled datasets indicate that SCoRe with auto-tuned regularization weights yields lower root-mean-square error (RMSE) and higher structural similarity index (SSIM) compared to state-of-the-art CS methods. In 45 prospectively undersampled datasets acquired from 15 volunteers, the image quality was scored by two expert reviewers, with SCoRe receiving a higher average score (p<0.01) compared to other CS methods.
Conclusion:
SCoRe enables accelerated cine CMR from highly undersampled data. In contrast to other acceleration techniques, SCoRe adapts regularization weights based on noise power and level of sparsity in each transform, yielding superior performance without admitting any free parameters.
Keywords: cardiac MRI, cine, image reconstruction, adaptive, compressed sensing
Introduction
Aided by advances in hardware and software, MRI has evolved rapidly in the last two decades. The availability of high-field scanners and high-performance gradients as well as the development of parallel MRI (1, 2) and optimized pulse sequences have led to new applications. Parallel MRI alone has enabled 2 to 3 fold acceleration for a variety of MRI applications. In the last decade, significant developments have been made in the field of compressed sensing (CS), which exploits underlying sparsity in the signal to enable recovery from highly undersampled data (3, 4). Dynamic applications of MRI such as cardiovascular magnetic resonance (CMR) have especially benefited from CS recovery because of the inherent redundancies in spatiotemporal images (5). Using the combination of CS recovery and parallel MRI, several studies have demonstrated the feasibility of dynamic MRI with improved resolution (6), reduced acquisition time (7), and in higher spatial dimensions (8).
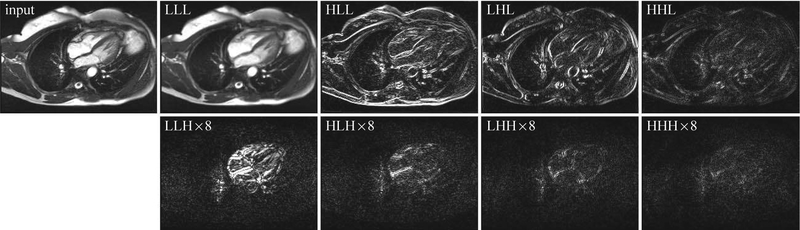
The success of CS is predicated on identifying a sparse representation of the signal being recovered. Since the true image content is not known a priori, it is difficult to select a single, optimal transform. Dictionary learning methods provide a promising avenue for data-driven learning of an optimal sparsifying transform (9). Such methods, however, are computationally slow and their performance is sensitive to the values assigned to several tuning parameters, including patch size, dictionary size, fraction of the patches used for training, required sparsity level, extent of patch overlap, and data consistency weight (10). A more common remedy is to use composite regularization with two or three disparate sparsifying transforms (4, 11) or use sparsity averaging where a composite sparsifying transform is constructed by concatenating multiple individual sparsifying transforms (12, 13). These approaches expose the rich structure in MR images that is not revealed by a single transform. However, the level of sparsity may differ widely across different transforms. For example, Figure 1 shows the decomposition of a typical cine image series into nondecimated wavelet subbands. The disparity in the level of sparsity across different wavelet subbands is obvious. This vast disparity in sparsity shows both the opportunity and challenge of using a composite regularization. On one hand, multiple transforms exploit rich structure in the data, but on the other hand, such approaches suggest the use of multiple tuning parameters (regularization weights).
Figure 1:
Decomposition of a typical GRAPPA-reconstructed segmented cardiac cine dataset (input) using 3D nondecimated wavelet transform (NWT) with single-level Haar wavelet filter. LLL, HLL, LHL, HHL, LLH, HLH, LHH, and HHH represent eight NWT subbands in the (x, y, t) domain, with x, y, and t representing vertical axis, horizontal axis, and time, respectively. Only one representative temporal frame is shown. Compared to the first four subbands (LLL, HLL, LHL, and HHL), the intensity of the last four subbands (LLH, HLH, LHH, and HHH) was amplified by a factor of 8 for better visualization. The fraction of coefficients in each subband that is larger than 1% of the maximum value across all subbands is 0.96, 0.37, 0.29, 0.16, 0.13, 0.09, 0.05, and 0.04 for LLL, HLL, LHL, HHL, LLH, HLH, LHH, and HHH, respectively. This disparity in the level of sparsity across different subbands is also visually evident.
The performance of any regularized reconstruction is sensitive to the selection of regularization weight, and methods to adjust these weights have a long history (14, 15). Current practices in MRI include: (i) finding an “appropriate” weight based on visual assessment of the resulting image quality, (ii) learning the weights from high-quality, independent datasets and applying those values to the datasets of interest, and (iii) using some heuristic weights based on a specific normalization of the data. Classical methods, such as L-curve, discrepancy principle, and generalized cross-validation (16) are often listed as plausible options to adjust regularization weight but are seldom used due to a significant computation burden or a nontrivial extension to CS-based nonlinear methods. More recently, Weller et al. extended Stein’s Unbiased Risk Estimate for parameter tuning in MRI (17). Such methods, however, either require an explicit computation of the Jacobian matrix of the nonlinear reconstruction function or a Monte Carlo approximation to the trace of the Jacobian, leading to increased computation time. More importantly, all the above mentioned approaches are typically described in the context of single-parameter tuning and their use in the multiple-parameter context is significantly more difficult.
In this work, we present and validate a versatile CS recovery method, called Sparsity adaptive Composite Recovery (SCoRe), that provides high acceleration by exploiting sparsity across multiple, disparate transforms and provides a data-driven tuning of regularization weights. The theoretical basis for SCoRe has been provided here (18), where the algorithm was referred to as the “composite L1 (Co-L1).” For validation, we have applied SCoRe to simulated cine data, retrospectively downsampled segmented cine, and prospectively downsampled real-time, free-breathing cine data.
Theory
For a spatiotemporal image sequence, the most commonly employed SENSE-based CS-recovery can be expressed as the following ℓ2-ℓ1 optimization problem
| [1] |
where is a vectorized spatiotemporal image, is measured noisy data, σ2 is noise variance in the measured data, is a spatiotemporal sparsifying transform with L ≥ N, λ is the regularization weight, and is the measurement operator for parallel MRI that includes multiplication with sensitivity maps, discrete Fourier transform, and undersampling. Commonly employed choices for Ψ include Discrete Wavelet Transform (DWT) (19), Nondecimated Wavelet Transform (NWT) (20), Temporal Fourier Transform (TFT) (21), and Total Variation (TV) operator (22).
To exploit sparsity in multiple transforms, one could build by vertically concatenating D > 1 sparsifying transforms (12), each with Ld rows. For example, Ψ can be constructed by concatenating spatial and temporal TV operators or different subbands of NWT. This formulation, however, ignores disparity in the level of sparsity among individual transforms. For example, in CMR, the temporal TV representation is typically more sparse than the spatial TV representation. Likewise, the lowpass (approximation) subband of NWT is rarely sparse for most CMR applications. For this reason, composite regularization is often utilized for MRI or CMR image recovery, leading to the following optimization problem
| [2] |
where Ψd represents the dth sparsifying transform with Ld rows, and λd represents the corresponding regularization weight. The following SCoRe algorithm attempts to recover x while auto-tuning the λd values.
| Algorithm 1 The SCoRe Algorithm |
| 1: input: A, y, normalized |
| 2: initialization: |
| 3: for |
| 4: |
| 5: |
| 6: end |
| 7: output: |
In Algorithm 1, represents the level of redundancy, i.e., the ratio of the total number of coefficients to the total number of pixels or voxels, and ensures that regularizing effects of multiple transforms are averaged and not accumulated. As described in Line 5 of Algorithm 1, regularization weight, λd, of sparse representation, Ψdx, is inversely related to its normalized ℓ1-norm, i.e., mean of the absolute values of the coefficients in that representation. As a result, SCoRe preferentially emphasizes the influence of sparse representations with small normalized ℓ1-norm. To avoid nonuniform scaling among different Ψd, the ℓ2-norm of the rows of Ψd is set to a constant value. For typical choices of Ψd and realistic x, the vector Ψdx will almost never be exactly zero; however, a small constant can be optionally added to prevent denominator from reaching zero. For MRI, σ2 can be readily calculated from a pre-scan. The main computational burden of Algorithm 1 is the convex ℓ2-ℓ1 optimization given in Line 4, which can be solved using any of several algorithms (23, 24, 25, 26).
Methods
For validation, we performed a simulation and two in vivo studies, one with retrospective undersampling (RU) and one with prospective undersampling (PU). For both in vivo studies, the protocol involving human subjects was approved by the institutional review board, and a written consent was obtained from each volunteer. For each study, results from SCoRe are compared with three other state-of-the-art CS methods: low-rank and sparse (L+S) (27), spatiotemporal 3D total variation (3DTV) (28) and spatiotemporal 3D NWT (3DNW) (26).
Simulation Study
The simulation study is based on the MRXCAT digital phantom for free-breathing cardiac cine (29). In its default setting, the phantom has 408 × 408 pixels, 1 mm isotropic spatial resolution, twelve receive coils, and 96 frames that span four cardiac cycles. To mimic the variations in the MRI acquisition process, the image recovery process was repeated for these 150 combinations of simulation parameters: three spatial resolutions (3.20 × 3.20 mm2, 2.25 × 2.25 mm2, and 1.60 × 1.60 mm2), two temporal resolutions (24 frames per cardiac cycle and 12 frames per cardiac cycle), five pre-downsampling SNR values (18 dB, 21 dB, 24 dB, 27 dB, and 30 dB), and five acceleration rates (R = 4, 8, 12, 16, and 20). The spatial resolution was adjusted by cropping the k-space, while the temporal resolution was lowered from its default value of 24 frames per cardiac cycle to 12 frames per cardiac cycle by discarding even-numbered frames. The sampling pattern used for undersampling was generated using VISTA (30). Supporting Information Figure S1 shows an example VISTA pattern. The reconstruction was performed using SCoRe, L+S, 3DTV, and 3DNW.
In Vivo Study with RU
Two healthy volunteers were imaged on a 1.5 T scanner (MAGNETOM, Avanto, Siemens Healthcare, Erlangen, Germany) with an 18-channel cardiac array, where anterior 6-channel body array was combined with 12 channels in the posterior spine array coil. Three fully sampled slices were collected from each subject, resulting in six datasets. Each slice was collected under a separate breathhold using balanced SSFP. For the first volunteer, three parallel short-axis slices were collected, with a gap of 15 mm between the neighboring slices. To enhance data diversity, one short-axis and two long-axis slices were collected from the second volunteer. Other imaging parameters included: 8 to 10 mm slice thickness, 50° to 55° flip angle, 1.8 to 2.5 mm isotropic spatial resolution, 360 to 400 mm FOV in the readout direction, 280 to 400 mm FOV in the phase-encode direction, 33 to 36 ms temporal resolution, 1.4 to 1.7 ms TE, 2.8 to 3.2 ms TR, and 11 to 15 heartbeats per breathhold. The datasets were retrospectively undersampled at rates R = 2, 4, 6, 12, 15, 18 using VISTA. To calculate root-mean-square error (RMSE) and structural similarity index (SSIM), reference images were reconstructed from the fully sampled datasets using the 3DNW algorithm with the regularization turned off, which generated the least squares solution.
In Vivo Study with PU
Fifteen volunteers were imaged on a 1.5 T scanner (MAGNETOM, Avanto, Siemens Healthcare, Erlangen, Germany) with an 18-channel cardiac array. Three views (short-axis, 2-chamber, and 4-chamber) were collected from each volunteer, resulting in 45 datasets. Each slice was collected during free-breathing using balanced SSFP with VISTA undersampling. Other imaging parameters included: 8 to 10 mm slice thickness, 60° to 80° flip angle, 1.8 to 2.2 mm spatial resolution in the readout direction and 2.2 to 2.5 mm spatial resolution in the phase-encode direction, 350 to 450 mm FOV in the readout direction, 250 to 380 mm FOV in the phase encoding direction, 9 to 12 acceleration rate, 38 to 50 ms temporal resolution, 1.3 to 1.4 ms TE, 2.5 to 3.1 ms TR, and 4 heartbeats per scan.
Image Reconstruction
All the images were reconstructed in 64-bit Matlab (Mathworks, Natick, MA). Sensitivity maps were estimated from time-averaged data using ESPIRiT (31). To reduce computation burden, coil compression was employed to generate 12 virtual coils. To solve the ℓ2-ℓ1 optimization for 3DNW (Eq. 1 without the factor and with Ψ defining the vertical concatenation of eight subbands of single-level 3D NWT with Haar filter), the bFISTA algorithm (26) was used. For SCoRe, the subbands of 3D NWT were treated as eight separate sparsifying transforms, with their regularization weights adjusted via Line 5 of Algorithm 1. To solve Line 4 in Algorithm 1, the bFISTA algorithm was employed. For 3DTV (Eq. 1 without the factor and with Ψ defining the vertical concatenation of two spatial and one temporal finite difference operators), where Ψ does not yield a tight frame, i.e., a more general algorithm, called mFISTA (25), was used. For L+S, Matlab code was downloaded from here (32).
All the reconstructions were performed off-line using an Ubuntu 14.04 workstation with 12-core Intel Core i7–5820K CPU running at 3.3 GHz with 64 GB system memory. For SCoRe, the number of inner iterations (to solve Line 4 in Algorithm 1 using bFISTA) was set at 10. The number of outer iterations for SCoRe and the total number of iterations for 3DNW, 3DTV, and L+S were selected by qualitatively observing the RMSE convergence curves () in a small number of training datasets selected from the simulation study. Based on the RMSE convergence curves (not shown), 100 bFISTA iterations for 3DNW, 160 mFISTA iterations for 3DTV, 250 iterations for L+S, and 16 outer iterations (the for loop in Algorithm 1) for SCoRe were adequate to reach convergence. In addition, the value of the normalized image update was recorded during the training phase, with the minimum value observed to be 3 × 10−5 across all reconstruction methods. Based on this information, the early termination threshold, δ, (i.e., terminate if ) was conservatively set at 2 × 10−6 for all methods. For SCoRe, the early termination criterion was set for the inner loop. The maximum number of iterations and the value of δ were not changed across different studies. For the in vivo study with PU, average reconstruction time, including preprocessing steps, was 123 s, 251 s, 347 s, and 173 s for 3DNW, L+S, 3DTV, and SCoRe, respectively. A Matlab implementation of SCoRe is provided on Github: https://github.com/MRIOSU/SCoRe_demo.
For every in vivo dataset, a 250 ms pre-scan was used to pre-whiten noise across receive channels and to estimate the σ2 used in Line 4 of Algorithm 1. To avoid convergence to bad minima in SCoRe, extremely large values of λd, which can set all coefficients in the dth representation to zero, were discouraged in the earlier iterations of SCoRe. To this end, the maximum value of λd, across different subbands, was capped at 20 times the minimum value of λd during the first 50% of the outer iterations, i.e., . This restriction was removed during the last 50% of the outer iterations. The value of ϵ was set at 0.01% of the maximum absolute value from all coefficients. The SCoRe-based tuning of regularization weights was not influenced by a particular choice of ϵ because . For 3DNW, L+S, and 3DTV, the data were similarly pre-whitened but the resulting value of σ2 was not used to scale the ℓ2 term in Eq. 1. Instead, as per common practice for regularized MRI reconstruction, the data were normalized such that the maximum absolute value in the measured k-space was set to a positive constant (33).
The regularization weights for 3DNW (λNW), L+S (λL and λS), and 3DTV (λTV) were manually tuned using one dataset from each study. To avoid artifacts associated with thresholding the non-sparse LLL subband (34) and thus to improve RMSE, λLLL was set at one fourth of the value, λNW, used for other seven subbands in 3DNW. For simulation, the values were adjusted using the dataset with medium spatial resolution, high temporal resolution, R = 12, and SNR = 24 dB. For the in vivo study with RU, Dataset #6 at R = 9 was used to tune those parameters. For these two studies, the values of λNW, λL, λS, and λTV were adjusted to minimize RMSE. For the in vivo study with PU, one dataset (out of 45) was randomly selected for parameter tuning; the images were reconstructed for a number of different regularization weights, and the image quality, assessed by an expert (OPS) with over twenty-five years of experience in CMR, was used to select the optimal values.
Quality Comparison
For the simulation study and the in vivo study with RU, the comparison was based on RMSE and SSIM. For the in vivo study with PU, the comparison was based on visual assessment of images by two experts (JC and NJ) each with over ten years of experience in CMR. For each of the 45 datasets, the movies originating from four reconstruction methods were placed next to one another on a PowerPoint slide. The order of the movies was randomly varied from slide to slide. The reviewers were instructed to assign a score (scale 1 to 5) to each movie, with a score of 5 (excellent) indicating images that are equivalent to or better than a typical segmented cine at 1.5 T, score of 4 (good) indicating images with visible but insignificant degradation, score of 3 (acceptable) indicating images that are of diagnostic quality but have significant degradation, score of 2 (poor) indicating images that may not be of diagnostic quality and have severe degradation, and the score of 1 (very poor) indicating images that are unusable. For datasets where two or more reconstruction methods received the highest score, the reviewers were instructed to select the results that they thought had the highest image quality.
Results
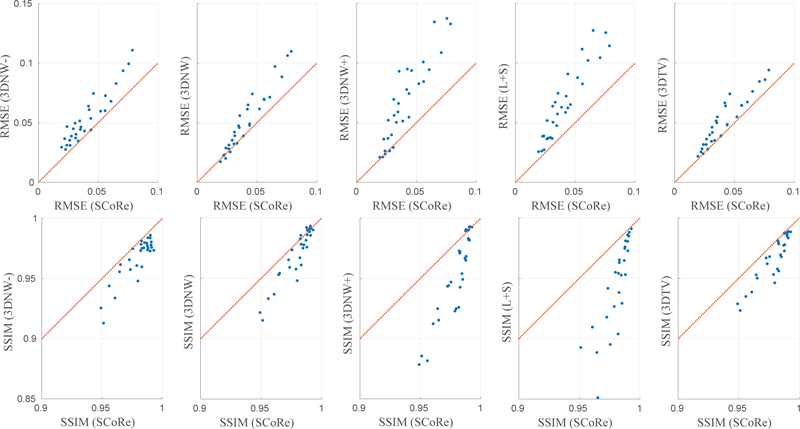
The results from the simulation study are summarized in Figure 2. SCoRe was compared, in terms of RMSE and SSIM, with 3DNW, L+S, and 3DTV for 150 different combinations of simulation parameters. For 3DNW, the comparison was also drawn after the regularization weight was increased or decreased from its manually tuned value by a factor of 3. Overall, SCoRe outperformed the other three reconstruction methods with lower RMSE and higher SSIM. To demonstrate that the superior performance of SCoRe was not merely due to the inclusion of term, the results with only one SNR (24 dB) are plotted separately in Figure 3. Representative results for one of the 150 simulated datasets are shown in Figure 4; a single frame is shown along with the corresponding error map.
Figure 2:
RMSE (top row) and SSIM (bottom row) comparison of various image reconstruction methods for the simulation study. SCoRe is compared to 3DNW with three different values of regularization weight, L+S, and 3DTV. The regularization weights for 3DNW, L+S, and 3DTV were manually optimized for one specific simulation setting. Compared to 3DNW, the regularization weight was decreased and increased by a factor of 3 for 3DNW- and 3DNW +, respectively. The identity line is represented in red, and each dot corresponds to a unique combination of simulation parameters, i.e., spatial resolution, temporal resolution, SNR, and acceleration.
Figure 3:
A subset of the data shown in Figure 2. Results from only one SNR value (24 dB) are shown.
Figure 4:
Reconstructed images from the simulation study. Representative frames from noiseless, fully sampled (FS) data and four different reconstruction methods are shown in the first row. Corresponding error maps after five-fold amplification are shown in the second row. This particular dataset was simulated with high temporal resolution, medium spatial resolution, R = 16, and SNR = 27 dB.
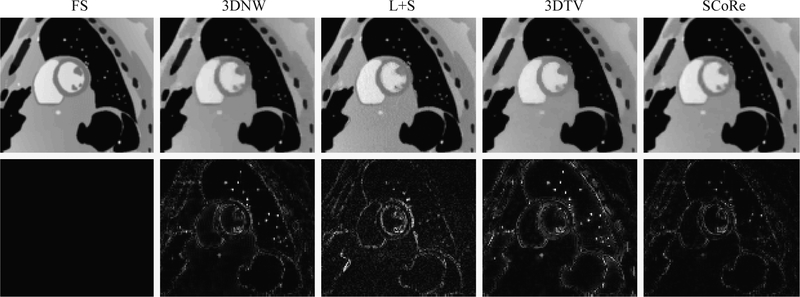
The results from the in vivo study with RU are summarized in Figure 5 and Supporting Information Figure S2; SCoRe was compared, in terms of RMSE and SSIM, with 3DNW, L+S, and 3DTV for seven different acceleration rates (R = 2, 4, 6, 9, 12, 15, 18). SCoRe consistently outperformed the other reconstruction methods, with more pronounced advantage at higher acceleration rates. For this study, the performance of L+S was only slightly inferior to SCoRe. Figure 6 provides an example showing different reconstruction methods, with SCoRe showing the least signal in the error map.
Figure 5:
RMSE comparison of various image reconstruction methods for the in vivo study with RU. The identity line is shown in red, and the seven dots in each panel represent different acceleration rates (R = 2, 4, 6, 9, 12, 15, 18). In all cases, the values of RMSE for SCoRe monotonically increased with R.
Figure 6:
Reconstructed images from the in vivo study with RU. A representative frame from (Dataset #1) is shown. Results from fully sampled (FS) reference and four different reconstruction methods are shown in the first row. Corresponding error maps after three-fold amplification are shown in the second row. For the images shown, the data were retrospectively undersampled at R = 12.
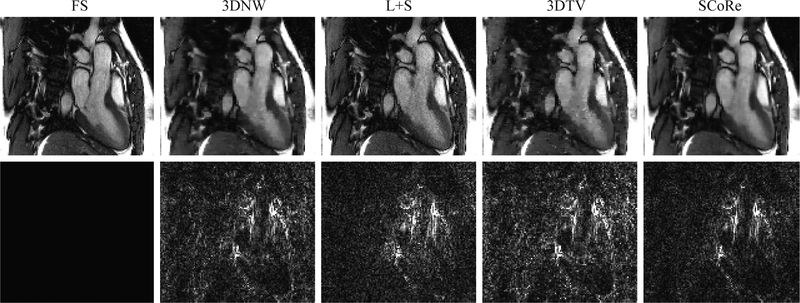
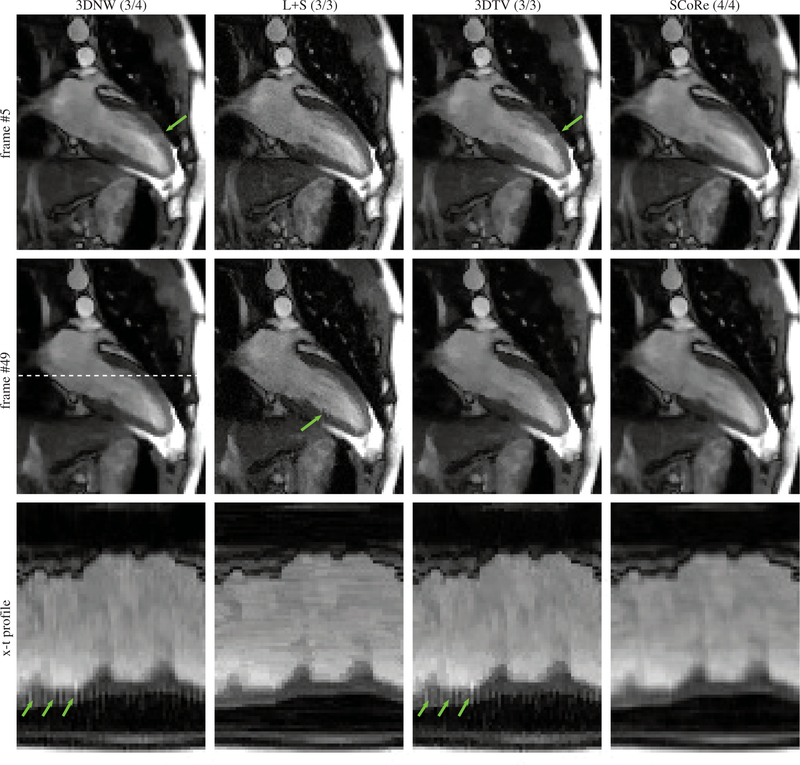
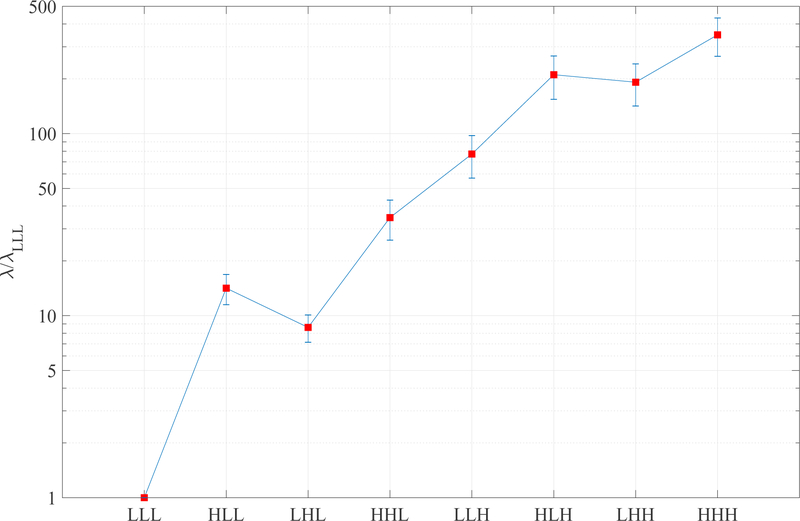
The results from the in vivo study with PU are summarized in Table 1. Paired t-tests were used to compare the image quality score of SCoRe with other CS methods, with SCoRe receiving significantly (p<0.01) higher score than each of the other three methods. The SCoRe was also the most frequent choice (62.2%) by the reviewers in terms of overall image quality. Figure 7 shows two different frames from one of the datasets, with 3DNW, L+S, and 3DTV showing visible artifacts in or around the myocardium. The figure also shows x-t profile, with SCoRe showing minimal artifacts while preserving pertinent details. Related time-resolved images comparing different reconstruction methods are included as Supporting Information Video S1 (2-chamber view, R = 11.1). Two additional time resolved images, Supporting Information Video S2 (short-axis view, R = 10.2) and Supporting Information Video S3 (4-chamber view, R = 11.1) are also included. In these videos, 3DNW, L+S, 3DTV, and SCoRe are arranged from left to right. Figure 8 provides an example where SCoRe was not deemed the best by the reviewers perhaps due to softer appearance of the endocardium edges. The relative values of the SCoRe-tuned regularization weights for eight different sparse representations are captured in Figure 9.
Table 1:
Scores (mean±std.) assigned to the four reconstruction methods by the two reviewers. The numbers in parenthesis indicate the relative frequency of being considered the “best” out of the four image series. The pooled score of SCoRe was significantly higher (p<0.01) than the other three CS methods.
| 3DNW | L+S | 3DTV | SCoRe | |
|---|---|---|---|---|
| Reviewer #1 | 3.31±0.47 (31.1%) |
3.02±0.34 (4.4%) |
3.13±0.41 (6.7%) |
3.51±0.55 (57.8%) |
| Reviewer #2 | 3.73±0.44 (26.7%) |
3.27±0.50 2.2%) |
3.35±0.48 (4.4%) |
3.93±0.45 (66.7%) |
| Pooled | 3.52±0.50 (28.9%) |
3.14±0.44 (3.3%) |
3.24±0.46 (5.6%) |
3.72±0.54 (62.2%) |
Figure 7:
Representative results from a real-time cine dataset collected under free-breathing. The data were prospectively undersampled at R = 11.1. The numbers in parenthesis are the scores given by the two reviewers. Two different frames are shown. The x-t profiles (third row) are plotted for the location shown with dashed line in the second row. The green arrows highlight artifacts on the myocardium.
Figure 8:
Representative results from a real-time cine dataset where SCoRe was not considered the best by the reviewers. The data were prospectively undersampled at R = 11.6. The numbers in parenthesis are the scores given by the two reviewers. Two different frames are shown. The x-t profiles (third row) are plotted for the location shown with dashed line in the second row. The green arrows highlight endocardium edges.
Figure 9:
The final values of SCoRe-tuned regularization weights of 3D (x-y-t) NWT subbands. Only the relative values are shown, with the value of λLLL normalized to one for each dataset. The error bars represent the standard deviation across 45 real-time cine datasets with PU.
To demonstrate the application of SCoRe for other sparsifying transforms, the simulation study was repeated with NWT replaced with TV. For TV, two spatial and one temporal finite difference operators were used to create three distinct sparse representations. Supporting Information Figure S3 shows results from the combination of SCoRe and TV. To further illustrate that the benefit of SCoRe is tied to not just optimal but also independent tuning of the regularization weights, we compared SCoRe with a reduced version of SCoRe, called SCoRe-Red; see Supporting Information Figure S4. For SCoRe, the regularization weights for all eight subbands (λLLL, λHLL, λLHL, λHHL, λLLH, λHLH, λLHH, and λHHH) were auto-tuned independently. In contrast, for SCoRe-Red, the NWT coefficients were divided into only two groups, i.e., LLL and non-LLL, and the resulting regularization weights ( and .) were auto-tuned following the procedure similar to that for SCoRe.
Discussion
Regularized MRI reconstruction methods enable higher acceleration than possible with unregularized methods. In particular, CS-inspired reconstruction methods that exploit sparsity and/or low-rank property have become increasingly popular and have demonstrated great promise for a variety of MRI applications (35, 22, 36). Application of CS often involves selecting a sparsifying transform and related regularization weight. To exploit rich data structure, especially for spatiotemporal applications, it is a common practice to utilize multiple sparsifying representations. Since the level of sparsity can vary significantly across different sparse representations, a single regularization weight, even when carefully tuned, may yield suboptimal results. The level of disparity among different sparse representations can be particularly evident for dynamic applications, where temporal sparsity is typically more pronounced than spatial sparsity, as demonstrated in Figure 1. In addition, considering that bandwidth, slice thickness, coil array, flip angle, spatial and temporal resolutions, acceleration rate, and patient habitus can vary significantly from one scan to another and also from subject to subject, optimizing multiple parameters for such a diversity of acquisition settings may not be practical. The proposed method, SCoRe, not only provides unmatched acceleration by exploiting sparsity across multiple representations but it also provides a data-driven tuning of all free parameters and thus eliminates the need to hand-tune regularization weights. Also, SCoRe is amenable to fast algorithms, such as bFISTA (26).
We have validated SCoRe using three different CMR studies. In the simulation study, to mimic the diversity encountered in CMR acquisition, the data were simulated with 150 different combinations of spatial and temporal resolution, acceleration rate, and SNR. The performance of the four tested reconstruction methods was similar under low acceleration rates, where accurate recovery was possible even without regularization. For more challenging scenarios, e.g., high acceleration or low SNR, the advantage of SCoRe over the other method was more pronounced. In addition to highlighting the benefits of SCoRe, Figure 2 also highlights the impact of suboptimally selecting the regularization weight. A factor of 3 variation in λNW showed a tangible degradation in the performance of 3DNW.
SCoRe is equally applicable when sparse representations are merged into a smaller number of representations. For example, one could treat all NWT subbands as one representation or divide them into two (LLL and non-LLL) representations. However, the full benefit of SCoRe is realized only when the regularization weights for disparate representations are adjusted independently. In Supporting Information Figure S4, we compare RMSE of SCoRe with a reduced version of SCoRe, called SCoRe-Red. Since the only difference between SCoRe and SCoRe-Red is the number of distinct sparse representations, the superior performance of SCoRe highlights the benefit of treating disparate representations individually.
To comply with existing practice, the factor was not included in 3DNW, L+S, and 3DTV reconstructions. However, the superior performance of SCoRe should not be solely attributed to this factor. As shown in Figure 3, SCoRe also maintained its advantage over other methods when SNR was restricted to the value (24 dB) used to optimize parameters for 3DNW, L+S, and 3DTV. An example comparing different reconstruction methods is shown in Figure 4, with SCoRe exhibiting the smallest error signal. Compared to 3DNW, the reconstruction using 3DTV showed more error around the edges. This is because 3DTV prefers perfect edges while the underlying true phantom has more realistic, soft edges. In comparison to other methods, L+S results look visually noisy with the error more pronounced in the moving parts of the phantom, which do not comply with the low rank constraint.
The in vivo study with RU agrees with the simulation study. SCoRe is consistently superior to other methods in terms of RMSE and SSIM, especially at high acceleration rates. Compared to the simulation study, the performance of L+S is only marginally inferior to SCoRe. We conjecture that relative improvement in the performance of L+S is due to lack of respiratory motion for the in vivo data, which makes the low rank constraint more effective. Figure 6 shows a representative frame from Dataset #1 reconstructed at R = 12. All reconstruction methods present some level of blurring, which is expected at the high acceleration rate of 12. Both 3DNW and 3DTV show blocky artifacts in the ventricular blood pool, while L+S exhibits more noise across the image. In contrast, SCoRe is devoid of major artifacts.
For the in vivo study with PU, since the ground truth was not available, the images were subjectively evaluated by two experts. As summarized in Table 1, SCoRe received the highest score from both the reviewers and was the most frequent choice (in 62.2% of cases) in terms of “best” overall quality. In contrast, 3DNW, on average, was selected in 28.9% of cases and 3DTV and L+S were selected in less than 10% of cases. Also, SCoRe and 3DNW were the only methods that did not receive a score below 3 (acceptable). Typical results from the different reconstruction methods are shown in Figure 7 and Supporting Information Videos S1, S2, and S3. The poor performance of 3DTV can be attributed to blocky artifacts that are easily noticeable in dynamic images. The relatively poor performance of L+S can be attributed to a noisy appearance due to lack of explicit spatial regularization or perhaps poor generalization of λS and λL tuning that was performed using a single dataset in each study. SCoRe results, however, were not deemed superior in all instances. Figure 8 shows an example where both reviewers preferred 3DNW over SCoRe. Although SCoRe images have the least amount of blocky artifact compared to other reconstructions, a slightly softer appearance of endocardium edges in SCoRe may have led to lower scores.
For the in vivo datasets with PU, relative regularization weights for eight subbands are reported in Figure 9. A large difference among the regularization weights points to widely varying levels of sparsity for different subbands. The last four subbbands have higher regularization weights due to stronger redundancies along the temporal (third) dimension, leading to more sparse representations in LLH, HLH, LHH, and HHH. The value of λLHL is slightly lower than that of λHLL. This difference can be attributed to slightly worse spatial resolution along the phase encoding dimension, which, in most cases, was the second spatial dimension.
It is worth mentioning that the performances of 3DNW, L+S, and 3DTV could be further improved. For 3DNW, separately adjusting different wavelet subbands should improve the performance. In fact, this is what separates 3DNW from SCoRe, where the regularization weight of each subband is auto-tuned. However, for 3DNW, manually tuning the regularization weights of all eight subbands may not be practical, especially considering the variations in MRI setup and in underlying sparsity. For 3DTV, performance could be improved by separately adjusting the regularization weights of two spatial and one temporal dimensions (37). Also, 3DTV may benefit from employing higher order derivatives, which can combat the blocky appearance associated with the first derivative (38). These remedies, however, would introduce additional tuning parameters. Likewise, L+S could also be improved by incorporating spatial regularization, e.g., spatial TV. Again, including additional regularization terms will make manual adjustment more challenging.
We recognize that SCoRe has several limitations. First, the optimality of SCoRe’s parameter tuning can be justified using variational expectation maximization under the Laplacian prior or fully Bayesian estimation under a hierarchical Laplace-Gamma prior (18), but the images generated by SCoRe may not be subjectively viewed as optimal. As shown in Figure 8, a viewer may find a SCoRe reconstruction too soft or too noisy. Also, since the estimation of regularization weights in SCoRe is data-driven, low SNR for a specific sparse representation can lead to imprecise estimation of its regularization weight, which, in turn, can impact the image quality. However, in the studies presented in this work, we did not encounter an instance where SCoRe images were overwhelmingly under- or overregularized. Also, if needed, the overall regularization can be manually adjusted by scaling all λd values generated by SCoRe, for example, using discrepancy principle (39). This remedy preserves the relative ratios between different λd and thus introduces only one tuning parameter. Second, SCoRe is nonconvex and thus its performance may depend on the initialization. To evaluate the impact of initialization on the final SCoRe reconstruction, we reconstructed six in vivo datasets (R = 12) with RU from two different initializations, i.e., and the time-averaged image replicated across all frames. In all cases, the impact of initialization on RMSE was less than 0.2%, with no discernible differences between the reconstructed images. In addition to the initialization of the image, SCoRe is also sensitive to the initialization of λd. If the value of λd ∀ d becomes comparable to or larger than the maximum value of the coefficients in the dth sparse representation, it can threshold the entire representation to zero, which, in turn, will further increase λd (Line 5 of Algorithm 1), ensuring that the dth representation stays zero. To reduce the possibility of extremely large λd values, we forced the maximum value of λd, during earlier iterations of SCoRe, to be capped at 20 times the minimum value of λd, as explained in the previous section. In addition, the value of ϵ was set to 0.01% of the maximum absolute value rather than the machine precision to further discourage extreme values of λd. Although not included in the presented implementation of SCoRe, the value of ϵ can be lowered to machine precision in the later iterations of SCoRe. Third, the computation times of SCoRe was comparable to that of non-adaptive CS methods, making it a practical choice for clinical implementation.
In this work, we limited the different sparse representations to be subbands of NWT or spatial and temporal finite differences, but SCoRe is equally applicable for other sparsifying transforms or patch-based processing, where the regularization weight of each patch is adjusted independently. Another potential extension of SCoRe is to expand the number of sparse representations to include both NWT subbands and TFT, with NWT exploiting spatially and temporally local structures and TFT exploiting semiperiodic physiological motions. Yet another potential application of SCoRe is to auto-tune the parameters for XD-GRASP (40). With two temporal and three spatial dimensions, XD-GRASP can benefit from the data-driven auto-tuning provided by SCoRe. Also, SCoRe can be applied to non-cardiac MRI applications and can be readily extended to 3D.
Conclusions
We have presented a reconstruction method, SCoRe, that can employ a large number of sparse representations and provides data-driven auto-tuning of regularization weights. SCoRe is amenable to fast algorithms and is parameter free, making it an attractive candidate for clinical use. Based on the preliminary results, SCoRe outperforms other state-of-the-art CS method in terms of RMSE, SSIM and subjective evaluation.
Supplementary Material
Supporting Information Video S1: Time resolved 2-chamber image series, corresponding to Figure 7, reconstructed from a prospectively undersampled (R = 11.6) dataset.
Supporting Information Video S2: Time resolved short-axis image series reconstructed from a prospectively undersampled (R = 10.2) dataset.
Supporting Information Video S3: Time resolved 4-chamber image series reconstructed from a prospectively undersampled (R = 11.1) dataset.
Acknowledgments
This work was funded by NIH-R01HL135489.
References
- [1].Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P, et al. SENSE: Sensitivity encoding for fast MRI. Magnetic Resonance in Medicine 1999;42(5):952–962. [PubMed] [Google Scholar]
- [2].Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magnetic Resonance in Medicine 2002;47(6):1202–1210. [DOI] [PubMed] [Google Scholar]
- [3].Donoho DL. Compressed sensing. IEEE Transactions on Information Theory 2006;52(4):1289–1306. [Google Scholar]
- [4].Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine 2007;58(6):1182–1195. MRI cosparse in wavelet and TV. [DOI] [PubMed] [Google Scholar]
- [5].Gamper U, Boesiger P, Kozerke S. Compressed sensing in dynamic MRI. Magnetic Resonance in Medicine 2008;59(2):365–373. [DOI] [PubMed] [Google Scholar]
- [6].Jung H, Sung K, Nayak KS, Kim EY, Ye JC. k-t FOCUSS: a general compressed sensing framework for high resolution dynamic MRI. Magnetic Resonance in Medicine 2009;61(1):103–116. [DOI] [PubMed] [Google Scholar]
- [7].Liang D, Liu B, Wang J, Ying L. Accelerating SENSE using compressed sensing. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2009;62(6):1574–1584. [DOI] [PubMed] [Google Scholar]
- [8].Tariq U, Hsiao A, Alley M, Zhang T, Lustig M, Vasanawala SS. Venous and arterial flow quantification are equally accurate and precise with parallel imaging compressed sensing 4D phase contrast MRI. Journal of Magnetic Resonance Imaging 2013;37(6):1419–1426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Wang Y, Ying L. Compressed sensing dynamic cardiac cine MRI using learned spatiotemporal dictionary. IEEE Transactions on Biomedical Engineering 2014;61(4):1109–1120. [DOI] [PubMed] [Google Scholar]
- [10].Ravishankar S, Bresler Y. MR image reconstruction from highly undersampled k-space data by dictionary learning. IEEE Transactions on Medical Imaging 2011;30(5):1028–1041. [DOI] [PubMed] [Google Scholar]
- [11].Qu X, Cao X, Guo D, Hu C, Chen Z. Combined sparsifying transforms for compressed sensing MRI. Electronics letters 2010;46(2):121–123. [Google Scholar]
- [12].Carrillo RE, McEwen JD, Van De Ville D, Thiran JP, Wiaux Y. Sparsity averaging for compressive imaging. IEEE Signal Processing Letters 2013;20(6):591–594. [Google Scholar]
- [13].Jp Huang, Lk Zhu, Lh Wang, Wl Song. Compressed Sensing MRI Using Sparsity Averaging and FISTA. Applied Magnetic Resonance 2017. August;48(8):749–760. [Google Scholar]
- [14].Mitsuhata Y Adjustment of regularization in ill-posed linear inverse problems by the empirical Bayes approach. Geophysical Prospecting 2004;52(3):213–239. [Google Scholar]
- [15].Zhang Y, Li R, Tsai CL. Regularization parameter selections via generalized information criterion. Journal of the American Statistical Association 2010;105(489):312–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Shen Y, Xu G. Regularization and adjustment In: Sciences of Geodesy-II Springer; 2013. p. 293–337. [Google Scholar]
- [17].Weller DS, Ramani S, Nielsen JF, Fessler JA. Monte Carlo SURE-based parameter selection for parallel magnetic resonance imaging reconstruction. Magnetic Resonance in Medicine 2014;71(5):1760–1770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Ahmad R, Schniter P. Iteratively Reweighted ℓ1 Approaches to Sparse Composite Regularization. IEEE Transactions on Computational Imaging 2015;1(4):220–235. [Google Scholar]
- [19].Lustig M, Donoho DL, Santos JM, Pauly JM. Compressed sensing MRI. IEEE Signal Processing Magazine 2008;25(2):72–82. [Google Scholar]
- [20].Kayvanrad MH, McLeod AJ, Baxter JS, McKenzie CA, Peters TM. Stationary wavelet transform for under-sampled MRI reconstruction. Magnetic Resonance Imaging 2014;32(10):1353–1364. [DOI] [PubMed] [Google Scholar]
- [21].Otazo R, Kim D, Axel L, Sodickson DK. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magnetic Resonance in Medicine 2010;64(3):767–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Feng L, Grimm R, Block KT, Chandarana H, Kim S, Xu J, et al. Golden-angle radial sparse parallel MRI: Combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magnetic Resonance in Medicine 2014;72(3):707–717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Becker S, Bobin J, Candès EJ. NESTA: A fast and accurate first-order method for sparse recovery. SIAM Journal on Imaging Sciences 2011;4(1):1–39. [Google Scholar]
- [24].Afonso MV, Bioucas-Dias JM, Figueiredo MA. Fast image recovery using variable splitting and constrained optimization. IEEE Transactions on Image Processing 2010;19(9):2345–2356. [DOI] [PubMed] [Google Scholar]
- [25].Tan Z, Eldar YC, Beck A, Nehorai A. Smoothing and decomposition for analysis sparse recovery. IEEE Transactions on Signal Processing 2014;62(7):1762–1774. [Google Scholar]
- [26].Ting ST, Ahmad R, Jin N, Craft J, Serafim da Silveira J, Xue H, et al. Fast implementation for compressive recovery of highly accelerated cardiac cine MRI using the balanced sparse model. Magnetic Resonance in Medicine 2017;77(4):1505–1515. [DOI] [PubMed] [Google Scholar]
- [27].Otazo R, Candès E, Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magnetic Resonance in Medicine 2015;73(3):1125–1136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Chen L, Adluru G, Schabel MC, McGann CJ, DiBella EV. Myocardial perfusion MRI with an undersampled 3D stack-of-stars sequence. Medical Physics 2012;39(8):5204–5211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Wissmann L, Santelli C, Segars WP, Kozerke S. MRXCAT: Realistic numerical phantoms for cardiovascular magnetic resonance. Journal of Cardiovascular Magnetic Resonance 2014;16(1):63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Ahmad R, Xue H, Giri S, Ding Y, Craft J, Simonetti OP. Variable density incoherent spatiotemporal acquisition (VISTA) for highly accelerated cardiac MRI. Magnetic Resonance in Medicine 2015;74(5):1266–1278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magnetic Resonance in Medicine 2014;71(3):990–1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].http://cai2r.net/resources/software/ls-reconstruction-matlab-code;.
- [33].Kim D, Dyvorne HA, Otazo R, Feng L, Sodickson DK, Lee VS. Accelerated phase-contrast cine MRI using k-t SPARSE-SENSE. Magnetic Resonance in Medicine 2012;67(4):1054–1064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Selesnick IW, Figueiredo MA. Signal restoration with overcomplete wavelet transforms: Comparison of analysis and synthesis priors In: Wavelets XIII, vol. 7446 International Society for Optics and Photonics; 2009. p. 74460D. [Google Scholar]
- [35].Vasanawala S, Murphy M, Alley MT, Lai P, Keutzer K, Pauly JM, et al. Practical parallel imaging compressed sensing MRI: Summary of two years of experience in accelerating body MRI of pediatric patients. In: Biomedical Imaging: From Nano to Macro, 2011 IEEE International Symposium on IEEE; 2011. p. 1039–1043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Jaspan ON, Fleysher R, Lipton ML. Compressed sensing MRI: a review of the clinical literature. The British Journal of Radiology 2015;88(1056):20150487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Abascal JF, Montesinos P, Marinetto E, Pascau J, Desco M. Comparison of total variation with a motion estimation based compressed sensing approach for self-gated cardiac cine MRI in small animal studies. PloS one 2014;9(10):e110594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Knoll F, Bredies K, Pock T, Stollberger R. Second order total generalized variation (TGV) for MRI. Magnetic Resonance in Medicine 2011;65(2):480–491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Morozov VA. On the solution of functional equations by the method of regularization In: Doklady Akademii Nauk, vol. 167 Russian Academy of Sciences; 1966. p. 510–512. [Google Scholar]
- [40].Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R. XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magnetic Resonance in Medicine 2016;75(2):775–788. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information Video S1: Time resolved 2-chamber image series, corresponding to Figure 7, reconstructed from a prospectively undersampled (R = 11.6) dataset.
Supporting Information Video S2: Time resolved short-axis image series reconstructed from a prospectively undersampled (R = 10.2) dataset.
Supporting Information Video S3: Time resolved 4-chamber image series reconstructed from a prospectively undersampled (R = 11.1) dataset.