A non-dimensional parameter for classification of the flow in intracranial aneurysms. II. Patient-specific geometries

Abstract

A simple parameter, called the Aneurysm number (An) which is defined as the ratio of transport to vortex time scales, has been shown to classify the flow mode in simplified aneurysm geometries. Our objective is to test the hypothesis that An can classify the flow in patient-specific intracranial aneurysms (IA). Therefore, the definition of this parameter is extended to anatomic geometries by using hydraulic diameter and the length of expansion area in the approximate direction of the flow. The hypothesis is tested using image-based flow simulations in five sidewall and four bifurcation geometries, i.e., if An ≲ 1 (shorter transport time scale), then the fluid is transported across the neck before the vortex could be formed, creating a quasi-stationary shear layer (cavity mode). By contrast, if An ≳ 1 (shorter vortex time scale), a vortex is formed. The results show that if An switches from An ≲ 1 to An ≳ 1, then the flow mode switches from the cavity mode to the vortex mode. However, if An does not switch, then the IAs stay in the same mode. It is also shown that IAs in the cavity mode have significantly lower An, temporal fluctuations of wall shear stress and oscillatory shear index (OSI) compared to the vortex mode (p < 0.01). In addition, OSI correlates with An in each flow mode and with pulsatility index in each IA. This suggests An to be a viable hemodynamic parameter which can be easily calculated without the need for detailed flow measurements/ simulations.

I. INTRODUCTION

Hemodynamic factors play an essential role in the initiation, growth, and rupture of an intracranial aneurysm (IA),^1–5 e.g., wall shear stress (WSS) and its spatial and temporal gradient, and oscillatory shear index (OSI) have been shown to initiate vascular remodeling^6–8 and to be correlated with IA rupture status.^3,4,9,10 WSS, OSI, and frequency-based parameters have been used to quantify flow instabilities observed in aneurysms.¹¹ To better understand the behavior of WSS, gradients of WSS, and OSI, the basic flow physics of aneurysms needs to be investigated.¹ In addition, the flow physics in aneurysms, such as flows involving complex vortical structures (high flow instabilities),¹² complex and unstable core lines,¹³ or higher fraction of vortex structures near the wall,¹⁴ can be helpful in identifying the main factors in aneurysm rupture.¹² All of the above hemodynamic parameters require simulations or experiments to be computed. To date, there is no simple parameter that can predict the flow features/instabilities in IAs without time consuming simulations or flow measurements.

Le et al.¹⁵ hypothesized that a dimensionless parameter, denoted as the Aneurysm number (An), can broadly classify the flow in aneurysms. Based on numerical experiments of Le et al.¹⁵ on a single sidewall IA of a rabbit, An was defined as the ratio of the time required for the flow to be transported across the neck ($T_t=\frac{W}{U}$, where W is the width of the aneurysm neck and U is the inlet’s average (bulk) velocity, i.e., the cycle-averaged velocity of the inlet’s flow waveform) to the time required for vortex ring formation ($T_v=\frac{D}{△U}$, where D is the diameter of the parent artery and △U is the difference between the flow waveform’s maximum and minimum velocities at the peak systole and diastole during a cardiac cycle,¹⁵ similar to the vortex formation time of a vortex ring generated in a tank using a piston-cylinder setup¹⁶). Therefore, $An=\frac{T_t}{T_v}$ can be written as

$$An=\frac{T_t}{T_v}=\frac{W}{D}PI,$$ (1)

where $PI=\frac{△U}{U}$ is Gosling’s pulsatility index¹⁷ of the flow waveform. Based on this definition,¹⁵ the flow is in the vortex mode if the time required for vortex ring formation T_$v$ is less than the transport time T_t (An ≳ 1). Otherwise, the flow is in the cavity mode (An ≲ 1).

The An definition of Le et al.¹⁵ [(Eq. (1)] was specifically developed for sidewall aneurysms. Real IAs in patients may involve more complex geometries and can be either sidewall or bifurcation type, e.g., in the database of Xiang et al.,⁴ 41% of IAs are bifurcations. Therefore, it was necessary to extend the An definition to bifurcations for this parameter to be applicable clinically. Toward this end, the specific definition of An for sidewall IAs¹⁵ was generalized by modifying the transport time scale as $T_t=\frac{W}{U_{expansion}}$, where W is along the flow direction in expansion area (width of aneurysm neck and outlet diameter in sidewall and bifurcation IAs, respectively) and U_expansion is the average velocity in that direction, as shown in Fig. 1. Because the velocity at the beginning and end of expansion area for bifurcation IAs is approximated as U and 0, respectively, along W; therefore, $T_t=\frac{W}{U/2}$—see Paper I¹⁸ for details. Combining the definition of T_t for bifurcations and sidewalls, An can be written as¹⁸

$$An=\frac{T_t}{T_v}=\alpha \frac{W}{D}PI,$$ (2)

where α = 1 and 2 for sidewall and bifurcation IAs, respectively. The definition of D and W is clear in simplified geometries but not for anatomic ones. The definition of these factors is clarified for patient-specific geometries in Sec. II A. Note that complex simulations or flow measurements are not required to compute An [Eq. (2)]. It can be computed based on an IA’s geometry from any medical imaging modality and flow pulsatility in the parent artery.

FIG. 1.

Schematic illustration of (a) the cavity mode with a stationary shear layer and (b) the vortex mode with an evolving ring-like vortex for sidewall (upper row) and bifurcation (lower row) IAs. The directions of the rotation of the vortices for patient-specific geometries are subject to change during the cycle due to complexity of the flow inside the dome.

Figure 1 shows schematics of the cavity and vortex modes in sidewall and bifurcation aneurysms. The vortex mode is identified by the formation of a vortex ring, while the cavity mode is identified by the formation of a quasi-stationary shear layer which is stretched from the inlet to the outlet.^15,18 Although the vortex and shear layer evolution is in the parent artery, the evolution of the vortex structure affects the flow fluctuations in the dome, as shown in Paper I¹⁸ as well as in the results in Sec. III. These modes can also be observed in visualizations reported in the literature even though they were not necessarily described as cavity or vortex modes. The cavity mode, i.e., a simple cavity-like flow, is observed in simulations; e.g., see Fig. 4 of Le et al.¹⁵ or Fig. 9 of Poelma et al.,¹⁹ and experiments (see Fig. 3 of Hope et al.²⁰). The vortex mode, i.e., a complex and unstable flow, is observed in simulations; e.g., see Fig. 4 of Le et al.,¹⁵ Fig. 10 of Salsac et al.,²¹ Fig. 7 of Sheard et al.,²² Fig. 4 of Poelma et al.,¹⁹ or Fig. 8 of Asgharzadeh and Borazjani,²³ and experiments (see Fig. 10 of Le et al.²⁴).

An [Eq. (2)] is formed based on two main parameters: the flow waveform and neck/diameter morphology. These two parameters individually have been reported to affect the hemodynamics in aneurysms. Jansen et al.²⁵ showed that altering inflow resulted in statistically significant differences for WSS values in aneurysms. Xiang et al.²⁶ observed high correlation between inflow pulsatility index and OSI in IAs. Nair et al.²⁷ found dome-to-neck ratio to have the greatest impact on hemodynamics of cerebral aneurysm in comparison with other morphological parameters. Schneiders et al.²⁸ claimed that the neck size has non-negligible effect on numerical results obtained from twenty IAs. Baek et al.²⁹ observed lower instability in a narrow-necked saccular aneurysms in comparison with wide-necked ones.

In Paper I,¹⁸ the An definition [Eq. (2)] was derived and systematically investigated on simplified geometries. It was shown that An can classify the flow mode in simplified geometries. It is unclear if An can detect the flow mode in realistic geometries. Therefore, the main goal of Paper II is to investigate if An can classify the flow mode in patient-specific IAs. The definition of An for patient-specific geometries is described in Sec. II A. The numerical method is presented in Sec. II B. The description of test cases, boundary conditions, and other computational details are presented in Sec. II C. The results of the simulations are presented and discussed in Sec. III. The effect of the flow mode and An on hemodynamic indicators that are frequently implicated in IA pathology, e.g., wall shear stress and oscillatory shear index, is also investigated (Secs. III B and III C) as the vortex and cavity modes leave different imprints on the aneurysm wall. At the end, the findings of this study are summarized in Sec. IV.

II. METHODS

A. $\mathit{A}\mathit{n}$ definition for patient-specific geometries

The definition of An [Eq. (2)] for sidewall and bifurcation geometries was developed based on simplified geometries in Paper I.¹⁸ In simplified geometries (sidewalls and bifurcations), the inlet and outlets had circular or elliptical cross sections.¹⁸ Therefore, the definition of W and D in Eq. (2) was clear. However, W and D need to be approximated in patient-specific geometries because of their complex shapes; e.g., see Fig. 2. The diameter D is approximated by the hydraulic diameter of the cross section of the parent artery similar to previous work which investigated geometric parameters such as the size ratio or the neck ratio.³⁰ In previous work, e.g., Dhar et al.,³⁰ the diameter is measured about 1.5 diameters away from the aneurysm. However, here, the diameter is measured at the plane which is the closest to the expansion area (neck plane) because the vortex time T_$v$ in the definition of An depends on the diameter at the expansion area. The expansion length W in Eq. (2) is approximated by the distance between the start and end of the expansion area in the direction of the parent artery flow because W is related to the transport time scale T_t of a fluid particle by the flow in the parent artery along the expansion length—see Paper I¹⁸ for details of An definition.¹⁸ The flow direction is approximated by the normal vector to the cross section of the parent artery, which is used to compute D. Note that typically two outlets (two W, i.e., two An) exist in bifurcation IAs (Fig. 2). We consider the maximum An since it determines the existence of the vortex ring.

FIG. 2.

Nine patient-specific IAs for current study: (a) a bifurcation IA located in Anterior Communicating Artery–unruptured, (b) a bifurcation IA located in Basilar Artery–unruptured, (c) a bifurcation IA located in Anterior Communicating Artery–unruptured, (d) a sidewall IA located in Internal Carotid Artery–ruptured, (e) a sidewall IA located in Posterior Communicating Artery–unruptured, (f) a sidewall IA located in Internal Carotid Artery–unruptured, (g) a bifurcation IA located in Anterior Cerebral Artery–unruptured, (h) a sidewall IA located in Anterior Cerebral Artery–ruptured, and (i) a sidewall IA located in Posterior Inferior Cerebellar Artery–unruptured. D is the diameter of the inlet parent artery, and W is the aneurysm neck and the outlet diameter in the direction of the inlet flow in sidewall and bifurcation IAs, respectively. Subscripts are used when more than one inlet parent artery (e.g., D₁) or outlet (e.g., W₁) exists. The immersed body (IB) is meshed with triangular elements and put inside the computational domain. The slice indicates the plane selected to visualize the vortical structures.

B. The numerical method

The flow in patient-specific geometries is simulated using the curvilinear-immersed boundary (CURVIB), which is extensively validated and described in previous publications.^31–34 In this method, the governing equations are the 3D, unsteady incompressible Navier-Stokes equations for a Newtonian fluid in curvilinear coordinates.³¹ These equations are solved using a fractional step method.³¹ The momentum equations are solved implicitly using an efficient Newton-Krylov method (NKM), in which the Jacobian is formed analytically.³⁴ The convergence criterion for momentum equations is to reduce the relative residual at least two orders of magnitude.³⁴ The Poisson equation for the pressure is solved using the flexible generalized minimal residual (GMRES) method with a multigrid as a preconditioner.³¹ The correction step drives the divergence of velocity to machine zero (<10⁻¹⁰).^31,33

A sharp-interface immersed boundary method³⁵ is used to handle the 3D, arbitrary complex anatomic geometries of patient-specific IAs. In this method, the grid is not fitted to the boundaries of the anatomic geometries, and the complex geometries are placed over the fixed background grid. The grid nodes that are outside the flow domain (outside the immersed boundary) are blanked out and do not affect the solution. These nodes are identified using an efficient ray-tracing algorithm.³² The boundary conditions are reconstructed on the fluid nodes in the immediate vicinity of the immersed boundary along the normal direction to the boundary.³⁵ This method has been shown to be second-order accurate for a variety of flows.^34–36

This method has been validated against experimental and benchmark solutions^33,34,37 and has been applied to a variety of problems such as cardiovascular flows,^{15,23,38–41} aquatic swimming,^36,42 rheology,⁴³ among others. More specifically, the NKM method with immersed boundaries has been validated for different flows by Asgharzadeh and Borazjani.³⁴ In addition, the method is validated for flows inside an immersed body by comparing the results against the measurements of pulsatile flow through a 90° bend⁴⁴ by Asgharzadeh and Borazjani.²³ More recently, the method is validated by comparing the propagation of vortex rings in a tank against experimental measurements⁴⁵ by Asadi et al.⁴⁶

Aneurysm walls are assumed rigid in this study as frequently assumed in such simulations^4,15,19,47 since the distensibility of aneurysm’s wall is typically small and it was shown that the flow patterns of small distensible and rigid models in the carotid region are very similar.⁴⁸ The fluid is assumed to be Newtonian in our simulations because the non-Newtonian effects are negligible in larger (>500 μm) arteries⁴⁹ and previous simulations of both non-Newtonian and Newtonian fluids in IAs have shown similar flow patterns.⁴⁷

C. Test cases, boundary conditions, and other computational details

To test if An calculated as above can detect the flow mode in patient-specific geometries, nine of these geometries (five sidewalls and four bifurcations) with two inflow waveforms (total of 18 cases) have been selected—see Xiang et al.⁴ for details regarding image acquisition, segmentation, and reconstitution of geometries. The patient-specific geometries are selected from both sidewall and bifurcation types such that they produce: (1) a wide range of An (0.38–3) to systematically investigate the effect of An on the flow mode; (2) a few An close to one (0.91, 0.96, 1.07, 1.08) to capture approximate corresponding An for transition from cavity to vortex mode; and (3) An that stays below 1 by increasing PI from 0.57 to 1.43 and stays above 1 by increasing PI from 0.57 to 1.43. The patient-specific geometries are shown in Fig. 2 along with their corresponding computational domains and the morphological parameters (W and D) required to calculate An.

For all of the simulated cases, the Reynolds number is set to 378.8 (Re = UD_in/ϑ, where U is the average bulk inlet velocity, D_in is the inlet diameter, and ϑ is the blood kinematic viscosity) and the Womersley number is set to 3.855 [$Wo=\left(D_{in}/2\right)\sqrt{2\pi /T𝜗}$, where T is the time period of one heart beat], which is within the physiologically relevant range.^50,51 Re and Wo were kept constant for all of the simulations to isolate the effect of An on the flow mode. Note that Re and Wo (heart rate), as discussed in the introduction of Paper I,¹⁸ did not correlate with the flow mode based on the systematic study of Le et al.¹⁵ as well as other work.^23,52–54 Furthermore, the variation of Re and Wo did not affect the flow mode but changed the propagation of the main vortex according to Asgharzadeh and Borazjani.²³ In all of the above studies, the waveform was kept the same when frequency (Womersley) was changed. Clinically, however, a statistically significant inverse correlation between heart rate and PI has been observed,⁵⁵ i.e., the flow curve and PI change as the heart rate changes. Consequently, An, which correlates with PI based on Eq. (2), might inversely correlate with heart rate. This correlation does not indicate that heart rate may independently change the flow mode but indicates its secondary effect through PI.

The computational domains (Fig. 2) are meshed with the grid resolution of 50 grid nodes per inlet diameter, which was found to be enough to obtain grid independent solutions based on our grid refinement studies. A plane to visualize the flow, shown by slice in Fig. 2, is selected such that it passes through the middle of the inlet and the largest expansion region of the aneurysm. As discussed in Paper I¹⁸ and based on the definition of An, the flow mode is determined by the evolution of the shear layer from the inlet into the expansion region, i.e., a stationary shear layer is extended from the inlet into the outlet in the cavity mode, whereas the shear layer rolls up and evolves in the vortex mode. Therefore, the selected planes (Fig. 2) are the best planes to show the evolution of the shear layer and the flow mode.

The Neumann boundary condition is applied at the outlet boundaries with a correction for mass flow. The mass flow rate through each outlet artery is determined based on the principle of optimal work.^4,56 A uniform (plug) flow in space is applied at the inlet boundary. The inlet velocity is changed in time according to two waveforms shown in Fig. 3. Waveform 1 is based on the flow measurements at the internal carotid artery of a normal subject with PI = 0.57,²⁶ and waveform 2 is taken from a patient with a cerebral aneurysm with PI = 1.43.⁵⁷ The period T of the waveforms is determined based on the 75 beats per minute heart rate (T = 0.8 s). The non-dimensional time step is obtained based on 3200 time steps per cycle. The numerical simulations were carried out for three cycles to obtain quasi-steady state. Based on our tests, the results are identical after the third cycle, i.e., the velocity field and flow features, such as the vorticity, WSS, and OSI, remain the same at comparable time instants in a cycle during the quasi-steady state. All of the reported results are from the third cycle. The details of the simulations are summarized in Table I.

FIG. 3.

The two inflow velocity waveforms used as inlet boundary condition of the simulations. PI refers to the pulsatility index of the waveforms.

TABLE I.

Specifications of the simulated IAs in this study, where D and W are the parent artery diameter and aneurysm neck (sidewall IAs)/outlet diameter in the direction of the inlet flow (bifurcations IAs), respectively. α is equal to 1 in sidewall IAs, while it is 2 in bifurcation IAs.

Aneurysm	Type	Waveform	PI	α	W/D	An
A	Bifurcation	1	0.57	2	0.95	1.08
A	Bifurcation	2	1.43	2	0.95	2.72
B	Bifurcation	1	0.57	2	0.8	0.91
B	Bifurcation	2	1.43	2	0.8	2.29
C	Bifurcation	1	0.57	2	1.05	1.2
C	Bifurcation	2	1.43	2	1.05	3
D	Sidewall	1	0.57	1	1.68	0.96
D	Sidewall	2	1.43	1	1.68	2.4
E	Sidewall	1	0.57	1	1.3	0.74
E	Sidewall	2	1.43	1	1.3	1.86
F	Sidewall	1	0.57	1	0.67	0.38
F	Sidewall	2	1.43	1	0.67	0.96
G	Bifurcation	1	0.57	2	0.94	1.07
G	Bifurcation	2	1.43	2	0.94	2.69
H	Sidewall	1	0.57	1	1.42	0.81
H	Sidewall	2	1.43	1	1.42	2.03
I	Sidewall	1	0.57	1	1.09	0.62
I	Sidewall	2	1.43	1	1.09	1.56

III. RESULTS AND DISCUSSION

To investigate if the flow mode is classified by An in anatomic geometries, both bifurcation and sidewall IAs are simulated, the flow is visualized using non-dimensional out-of-plane vorticity, and the Burgers vortex model^58–60 is used to capture the bounds of the main vortex structure in Sec. III A—see the Appendix in Paper I¹⁸ for the details of Burgers’ vortex model. The effects of An on hemodynamic parameters such as wall shear stress and oscillatory shear index are investigated in Secs. III B and III C, respectively.

A. Vortical structures and the flow mode

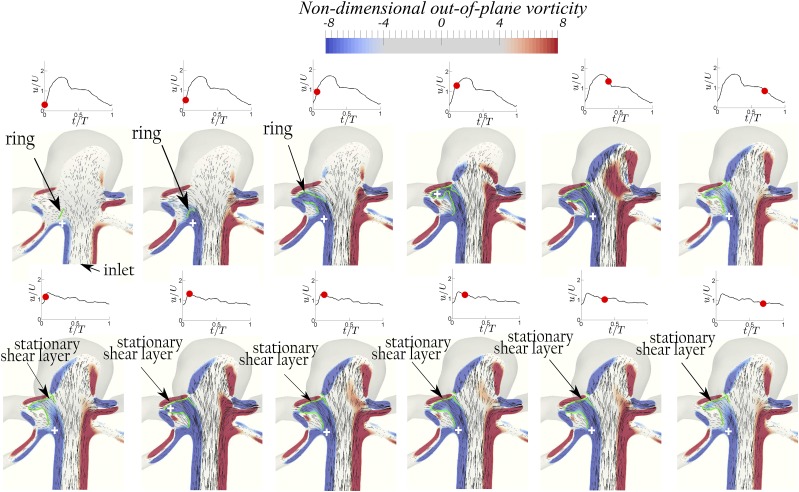
The vortical structures are visualized in Figs. 4 (Multimedia view), 6–8, 10, and 11 using contours of non-dimensional out-of-plane vorticity and in-plane velocity vectors on the planes shown by the slices in Fig. 2. Green lines and the cross signs depict the vortex structures and their axis in the dome, respectively, determined based on Burgers’ model. The out-of-plane vorticity is normalized by U/D, which was defined in Sec. II A, to obtain the non-dimensional out-of-plane vorticity. In order to better illustrate the dynamics of vortical structures for both bifurcation and sidewall aneurysms, 3D iso-surfaces of q-criterion with magnitudes of 10 and 12 are shown in Figs. 5 and 9 for geometries A and D, respectively. The upper and lower rows of Figs. 4 (Multimedia view) and 5–11 correspond to simulations with waveform 2 (PI = 1.43) and 1 (PI = 0.57) of Fig. 3, respectively. Max(a, b) indicates the maximum of a and b. Note that in bifurcation IAs, two An numbers can be calculated since they have two outlets. We consider the maximum An, calculated based on the maximum W/D, as the effective An since it determines the existence of the vortex ring.

FIG. 4.

Geometry A ($Max\left(\frac{W_1}{D_1},\frac{W_2}{D_2}\right)=0.95$ and α = 2): The evolution of the non-dimensional out-of-plane vorticity and in-plane velocity vectors shows the development of a vortex ring with waveform 2 (PI = 1.43) at An = 2.72 (upper row) and a stationary shear layer with waveform 1 (PI = 0.57) at An = 1.08 (lower row) at various time instants during the cycle. The red dot on the waveform shows the time instant in the cycle. The green lines and the white cross signs depict the vortex structure and its axis, respectively, determined based on Burgers’ model.⁶⁰ Multimedia views: https://doi.org/10.1063/1.5081451.1Download video file ^{(2.1MB, avi)} DOI: 10.1063/1.5081451.1; https://doi.org/10.1063/1.5081451.2Download video file ^{(2MB, avi)} DOI: 10.1063/1.5081451.2

FIG. 6.

Geometry B [$Max\left(\frac{W_1}{D},\frac{W_2}{D}\right)=0.8$ and α = 2]: The evolution of the non-dimensional out-of-plane vorticity and in-plane velocity vectors shows the development of a vortex ring with waveform 2 (PI = 1.43) at An = 2.29 (upper row) and a quasi-stationary shear layer with waveform 1 (PI = 0.57) at An = 0.91 (lower row) at various time instants during the cycle. The red dot on the waveform shows the time instant in the cycle. The green lines and the white cross signs depict the vortex structure and its axis, respectively, determined based on Burgers’ model.⁶⁰

FIG. 7.

Geometry C [$Max\left(\frac{W_1}{D},\frac{W_2}{D}\right)=1.05$ and α = 2]: The evolution of the non-dimensional out-of-plane vorticity and in-plane velocity vectors shows the development of a vortex ring with both waveforms when An ≳ 1 (An = 3 with waveform 2 at PI = 1.43 in the upper row and An = 1.2 with waveform 1 at PI = 0.57 in the lower row) at various time instants during the cycle. The red dot on the waveform shows the time instant in the cycle. The green lines and the cross signs depict the vortex structures and their axes, respectively, determined based on Burgers’ model.⁶⁰

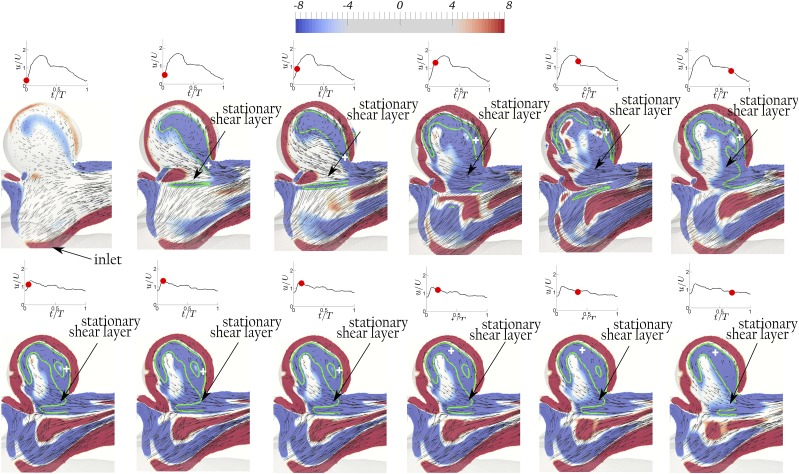
FIG. 8.

Geometry D (W/D = 1.68 and α = 1): The evolution of the non-dimensional out-of-plane vorticity and in-plane velocity vectors shows the development of a vortex ring with waveform 2 (PI = 1.43) at An = 2.4 (upper row) and a stationary shear layer with waveform 1 (PI = 0.57) at An = 0.96 (lower row) at various time instants during the cycle. The red dot on the waveform shows the time instant in the cycle. The green lines and the white cross signs depict the vortex structure and its axis, respectively, determined based on Burgers’ model.⁶⁰

FIG. 10.

Geometry E (W/D = 1.3 and α = 1): The evolution of the non-dimensional out-of-plane vorticity and in-plane velocity vectors shows the development of a vortex ring with waveform 2 (PI = 1.43) at An = 1.86 (upper row) and a stationary shear layer with waveform 1 (PI = 0.57) at An = 0.74 (lower row) at various time instants during the cycle. The red dot on the waveform shows the time instant in the cycle. The green lines and the white cross signs depict the vortex structure and its axis, respectively, determined based on Burgers’ model.⁶⁰

FIG. 11.

Geometry F (W/D = 0.67 and α = 1): The evolution of the non-dimensional out-of-plane vorticity and in-plane velocity vectors shows a stationary shear layer with both waveforms when An ≲ 1 (An = 0.96 with waveform 2 at PI = 1.43 in the upper row and An = 0.38 with waveform 1 PI = 0.57 in the lower row) at various time instants during the cycle. The red dot on the waveform shows the time instant in the cycle. The green lines and the white cross signs depict the vortex structure and its axis, respectively, determined based on Burgers’ model.⁶⁰

FIG. 5.

Iso-surfaces of q-criterion (q = 10) for geometry A [$Max\left(\frac{W_1}{D_1},\frac{W_2}{D_2}\right)=0.95$ and α = 2]: the development of a vortex ring with waveform 2 (PI = 1.43) at An = 2.72 (upper row) and a stationary shear layer with waveform 1 (PI = 0.57) at An = 1.08 (lower row) at various time instants during the cycle. The red dot on the waveform shows the time instant in the cycle. Note that this geometry has two inlets.

FIG. 9.

Geometry D (W/D = 1.68 and α = 1): the evolution of iso-surfaces of q-criterion (q = 12) shows the development of a vortex ring with waveform 2 (PI = 1.43) at An = 2.4 (upper row) and a stationary shear layer with waveform 1 (PI = 0.57) at An = 0.96 (lower row) at various time instants during the cycle. The red dot on the waveform shows the time instant in the cycle.

The vortical structures for bifurcation geometries A and B with waveform 2 at An = 2.72 and 2.29, respectively, clearly show the evolution of ring structure [the upper row of Figs. 4 (Multimedia view), 5, and 6]. It is observed that the vortex ring structure [delineated by the green lines in Fig. 4 (Multimedia view) and denoted as ring in Figs. 4 (Multimedia view) and 5] in geometry A moves in the direction of the inlet jet flow in the early acceleration phase [the upper row of Figs. 4(a), 4(b) (Multimedia view), and 5(a)] in the left inlet/outlet intersection. The ring structure rolls up [the upper row of Figs. 4(c) (Multimedia view), 5(b), and 5(c)] and stretches toward the outlet [the upper row of Figs. 4(d) (Multimedia view) and 5(d)] in the late acceleration phase. Thereafter, the vortex ring becomes unstable and breaks into several vortical structures, which can be observed inside the dome [the upper row of Fig. 4(e) (Multimedia view)]. In the deceleration phase, the segments of the vortical structures diffuse away [the upper row of Fig. 4(f) (Multimedia view)]. Such a dynamic vortex structure, i.e., rolling up of the vorticity structure to a vortex ring and its breakdown, clearly shows that the flow at An = 2.72 is in the vortex mode. A similar dynamic vortex evolution is observed at An = 2.29 for geometry B in the upper row of Fig. 6 on the left (the larger) inlet/outlet intersection. By contrast, the same geometries A and B with waveform 1 (PI = 0.57) at lower An = 1.08 and 0.91, respectively, show a shear layer (denoted by the green lines) that spans across the neck from the inlet to the outlet quickly in the early acceleration phase [the lower row of Figs. 4(a), 4(b) (Multimedia view), 5(a)–5(c), 6(a), and 6(b)] before a vortex ring can form, i.e., they are in the cavity mode. Some instabilities of the shear layer can be observed in the left outlet/dome intersection, similar to the instabilities reported on the distal wall of a sidewall aneurysm in the cavity mode.^15,19,61 Even a shear layer in an aneurysm generated by a steady flow can lose its stability which leads to a self-sustained flow oscillation, called the cavity-tone.⁶¹ Nevertheless, the quasi-stationary shear layer (denoted by the green lines) that spans across the neck during the whole cycle in the lower row of Figs. 4 (Multimedia view), 5, and 6 indicates that the flow is in the cavity mode. Note that the evolution of the vortex structure (ring) versus the stationary shear layer affects the flow inside the dome [Figs. 4 (Multimedia view), 5, and 6]. In fact, the flow in the dome is highly dynamic in the vortex mode while the vortical structures remain stationary in the dome for the cavity mode [Figs. 4 (Multimedia view), 5, and 6].

Geometry G, which is another bifurcation IA, shows a similar mode transition from vortex to cavity (not shown here to avoid repetition) as geometries A and B when An decreases from 2.69 to 1.07 by changing the waveform. One might argue that this transition is just the effect of waveform and pulsatility PI and not An. To show that this transition is due to An and not just PI, geometry C is selected in which An only drops from 3 to 1.2 when using different waveforms. A dynamic vortex evolution is observed in the upper row of Fig. 7 at both right and left inlet/outlet intersections for geometry C (An = 3, PI = 1.43). Similarly, the dynamic vortex evolution is observed in the lower row of Fig. 7 but only at right inlet/outlet intersections for geometry C (An = 1.2, PI = 0.57). In fact, the shear layer only becomes unsteady in the larger outlet at low PI (Fig. 7 lower row) and the smaller outlet shows a steady shear layer as computing An based on the smaller outlet falls below one. Notwithstanding, the vortex evolution is observed in the right outlet in geometry C, in contrast to geometries A and B, at low PI = 0.57. This shows that the vortex mode can also be observed at low PI (=0.57) if the transport time scale is larger than vortex formation time scale (An > 1), i.e., the main parameter is An and not PI. The larger ratio of the outlet to the inlet diameter at low PIs leads to a larger transport time scale and smaller vortex formation time scale, which provides enough time for vortex to evolve before passing the inlet/outlet intersection. In summary, bifurcation geometries A, B, and G which have lower An (1.08, 0.91, and 1.07, respectively) at PI = 0.57 are in the cavity mode, but geometry C at PI = 0.57, which has a higher An (=1.2) at the same PI, is in the vortex mode.

Sidewall geometries D and E with waveform 2 (high PI) at An = 2.4 and 1.86, respectively, are in the vortex mode (the upper row of Figs. 8–10), whereas they are in the cavity mode with waveform 1 (low PI) at An = 0.96 and 0.74, respectively (the lower row of Figs. 8–10). In fact, the vortex ring structure (denoted on Figs. 8 and 9) for geometry D at An = 2.4 can be observed in the early acceleration phase [the upper row of Figs. 8(a) and 9(a)] in the proximal wall. The vortex moves in the direction of the inlet jet flow [the upper row of Figs. 8(b) and 9(b)], until it hits the distal wall and extracts an opposite sign vorticity near the distal wall, as shown in the upper row of Fig. 8(c). The vortex ring rolls up as it moves into the dome when the inlet velocity reaches peak systole [the upper row of Figs. 8(d), 9(c), and 9(d)]. Thereafter, the vortex ring becomes unstable inside the dome [the upper row of Fig. 8(e)] and it diffuses in the deceleration phase (the upper row of Fig. 8(f)]. A similar dynamic vortex evolution can be observed in the upper row of Fig. 10 for geometry E. By contrast, geometries D and E at lower An = 0.96 and 0.74 with waveform 1 show a stationary flow structure (the lower row of Figs. 8–10), i.e., cavity mode, as the shear layer remains stationary during the whole cycle. Some small instabilities are observed at the distal wall (the lower row of Figs. 8–10), which have also been observed previously,^15,19 but such small instabilities does not destabilize the strong shear layer stretching from the proximal to the distal wall.

Sidewall geometries H and I show a similar mode transition from cavity to vortex (not shown here to avoid repetition) as in geometries D (Figs. 8 and 9) and E (Fig. 10), i.e., when An increases for H and I from 0.81 to 2.03 and 0.62 to 1.56, respectively, by increasing PI from 0.57 to 1.43, the flow mode switch from the cavity mode to the vortex mode. Note that the higher size ratio⁴ of geometries H and I does not affect the flow mode transition. Again, to show that the main parameter determining this transition is An and not PI, geometry F is selected such that An remains below one, i.e., 0.96 and 0.38, for waveform 2 and 1, respectively. Geometry F with both waveforms is in the cavity mode since the stationary shear layers are observed in both upper and lower rows of Fig. 11. Neither a ring vortex nor a stable shear layer is observed at t/T = 0 [Fig. 11(a)] because of the low vorticity in the shear layer at the low flow rate at t/T = 0. However, the stable shear layer is promptly visible in early acceleration phase at t/T = 0.03 [Fig. 11(b)]. This behavior shows that the cavity mode can be observed at high PI and the determining parameter is An (combination of PI and W/D) and not PI by itself.

Based on vortical structures (quasi-stationary shear layer vs vortex evolution) in all of the above patient-specific IAs, An can classify the flow into cavity and vortex modes, i.e., An = 0.38, 0.62, 0.74, 0.81, 0.91, 0.96, 1.07, and 1.08 are in the cavity mode and IAs with An = 1.2, 1.56, 1.86, 2.03, 2.29, 2.4, 2.69, 2.72, and 3 are in the vortex mode. To determine if An numbers in cavity and vortex modes are significantly different from each other, a t-test analysis was performed. Figure 12(a) shows the box plot of An for all simulations in this study and their average for each flow mode. Based on the t-test analysis, the flows in the cavity mode have significantly lower An (mean 0.84) than those in the vortex mode (mean 2.19, p < 0.01). Note that as An increases, the vortex ring strength increases, while as An goes to zero, the shear layer becomes more stationary (lower perturbations).

FIG. 12.

Box plots show (a) An, (b) standard deviation of WSS (S), (c) <WSS>, and (d) OSI of all simulations in this study (see Table I for details) categorized by their flow mode, i.e., cavity or vortex. The central mark, the bottom, and top edges of each box indicate the median, the 25th, and 75th percentiles, respectively. The whiskers extend to the most extreme data points which are not considered outliers, and the outliers are plotted individually using the “+” symbol. Dotted-dashed lines indicate averages of An, S, <WSS>, and OSI for each mode in corresponding figures. The flows in the cavity mode have significantly lower An, S, and OSI than those in the vortex mode (p < 0.01), whereas <WSS> does not significantly change between flow modes.

We (based on the discussion in Paper I¹⁸ and similar to the work of Le et al.¹⁵) expected that the critical An (at which the flow transitions from the cavity mode to the vortex mode) to be equal to one, i.e., An < 1 for the cavity mode and An > 1 for the vortex mode. Based on our results, however, An = 1.08 and 1.07 for geometries A and I, respectively, are also in the cavity mode. This might be because of the approximate calculation of An due to the geometrical complexities of patient-specific IAs. Furthermore, An might have a transition range (from the cavity mode to the vortex mode) similar to other classifying non-dimensional parameters as discussed in Paper I,¹⁸ e.g., Re, which separates laminar from turbulent regimes, has a transition range in which the flow might intermittently transition between laminar and turbulent states.⁶² To stress this approximation and the transition range, therefore, we use the approximate sign, e.g., IAs with An ≲ 1 are in the cavity mode and with An ≳ 1 are in the vortex mode.

Cebral et al.⁶³ considered complex and unstable flows, i.e., flows with high instabilities, as a single category. In addition, Valen-Sendstad et al.¹² showed that complex vortical structures were associated with high flow instabilities in aneurysms. Consequently, the vortex mode should be associated with high instabilities because of their complex vortical structures, i.e., vortex ring formation, evolution, and break down [the upper row of Figs. 4 (Multimedia view), 5–10]. By contrast, the stationary shear layer generates stationary vortical structures in the dome which are visible throughout the cycle [the lower row of Figs. 4 (Multimedia view) and 5–11]. Note that the shear layer evolution in the parent artery directly affects the flow fluctuations in the dome. The flow fluctuations are quantified using the standard deviation of WSS and OSI in Secs. III B and III C. Baek et al.²⁹ stated that low and high flow instabilities were observed for narrow and wide-necked IAs, respectively. This is consistent with our observation only when increasing neck size under similar PI switches An from An ≲ 1 to An ≳ 1 (the upper row of Figs. 8 and 11) because the flow transition from the cavity mode to the vortex mode results in the increase in flow instabilities.

B. Wall shear stress

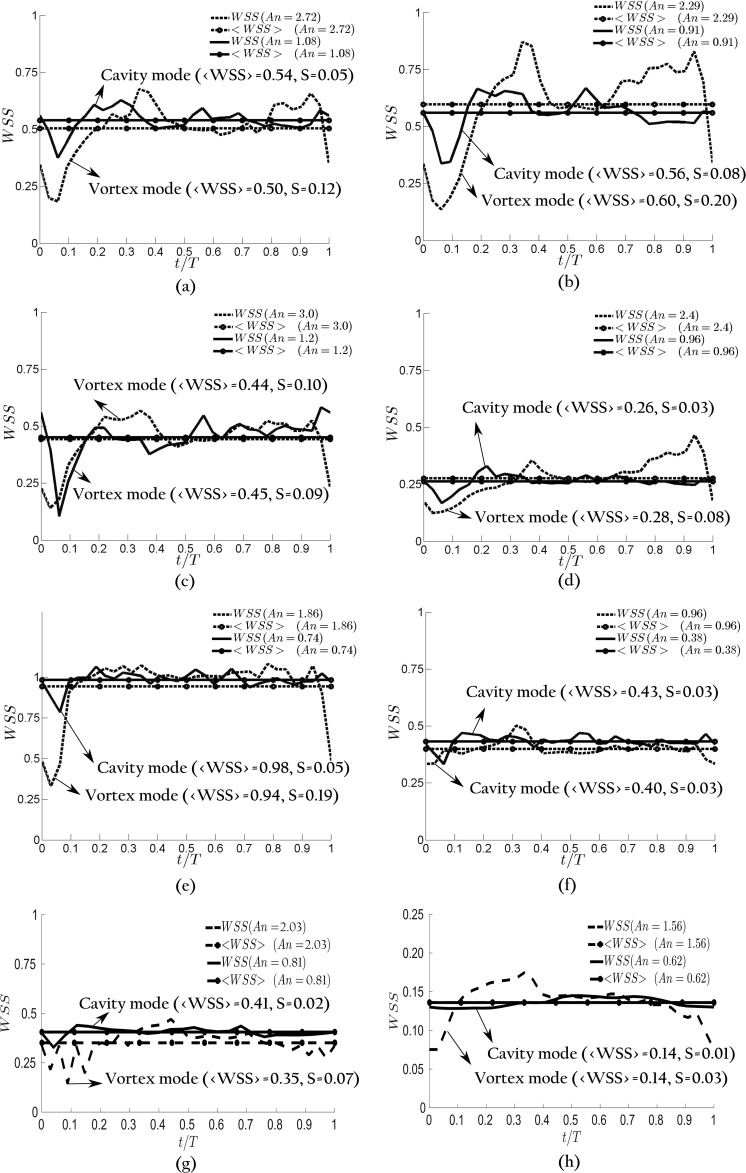
WSS, a hemodynamic factor which is the tangential friction force on the wall, is known to correlate with tissue remodeling, aneurysm initiation, and growth.^6–8 The effect of An on WSS is investigated in this section. Consistent with previous work,^4,23,26,64 WSS values in the IA are normalized with that at the inlet parent artery. Figure 13 shows the instantaneous wall shear stress averaged over the dome area as a function of time during a cycle for geometries A, B, C, D, E, F, H, and I at PI = 0.57 and 1.43. Note that instantaneous wall shear stress of G IA is not shown in Fig. 13 as it presents a similar trend to A, B, D, and E IAs. As can be observed in Fig. 13, IAs in the vortex mode (An = 1.56, 1.86, 2.03, 2.29, 2.4, and 2.72) have considerably higher temporal fluctuations of WSS in comparison with IAs in the cavity mode (An = 0.62, 0.74, 0.81, 0.91, 0.96, and 1.08) for each of A, B, D, E, H, and I geometries in which the flow mode changes form cavity to vortex by increasing PI. By contrast, the temporal fluctuations of WSS for geometry F [Fig. 13(f)], in which the flow mode remains cavity by increasing PI, remains similarly low for both waveforms (An = 0.38, 0.96). Similarly, the temporal fluctuations of WSS for geometry C [Fig. 13(c)], in which the flow remains in the vortex mode for both low and high PIs, are close to each other (An = 1.2 and 3.).

FIG. 13.

Wall shear stress (WSS) at PI = 1.43 (dashed lines) and PI = 0.57 (solid lines) for different IA geometries: (a) A, (b) B, (c) C, (d) D, (e) E, (f) F, (g) H, and (h) I. <WSS> is the cycle average of WSS. S is the standard deviations of WSS for each geometry and PI. In A, B, D, E, H, and I geometries, the vortex mode (larger PI) gives rise to larger temporal fluctuations of WSS and hence large S value than the cavity mode. In C and F geometries, the temporal fluctuations of larger PI is close to the smaller one because both flows are in the vortex and cavity modes, respectively, <WSS> does not present any significant differences between flow modes, but <WSS> for different IA geometries are quite different from each other.

The temporal fluctuations of WSS can be quantified by standard deviation (S in Fig. 13). S for IAs at high PI (dashed lines) are 2.38–3.88 times larger than that of a similar IA at low PI (solid lines) for geometries in which the flow mode changes from cavity to vortex (A, B, D, E, H, and I). By contrast, for geometries C and F, in which the flow modes does not change, S of high PIs (dashed lines) are only slightly (about 10% and 28%, respectively) higher than that at low PIs (solid lines).

Considering all nine IA geometries with different An, it is observed that IAs in the vortex mode have 3.16 times larger standard deviation of WSS in comparison with IAs in cavity modes in cycle-averaged sense. To investigate the significance of difference between the cavity and vortex modes for S, a t-test analysis was performed [Fig. 12(b)]. Based on this analysis, the flows in the cavity mode have significantly lower S (mean 0.05) than those in the vortex mode (mean 0.13, p < 0.01). This is probably due to the fact that the flow of IAs in the vortex mode involves evolution of a vortex ring, which results in significant temporal variation of velocity field, and thus of the WSS, during a cycle [the upper row of Figs. 4 (Multimedia view), 6, 8, and 10]. By contrast, the flow of IAs in the cavity mode [the lower row of Figs. 4 (Multimedia view), 6, 8, and 10] involves a quasi-stationary shear layer, which results in smaller variation of velocity field, and consequently the WSS. The clinical importance of the temporal fluctuation of WSS has been suggested by Shimogonya et al.,⁶⁵ in which they defined an index based on the temporal fluctuations of WSS, and showed that it significantly correlates with the location of cerebral aneurysm formation.

The cycle-averaged WSS ($<WSS>$) is shown in Fig. 13 by constant lines. $<WSS>$ slightly changes between flow modes in each geometry. However, $<WSS>$ values for different geometries are quite different from one another. It seems that the flow mode (or An) has little influence on $<WSS>$, while it has a significant effect on WSS fluctuations, i.e., the difference between the vortex and cavity modes in terms of temporal fluctuation of WSS disappears in cycle-averaged sense as WSS fluctuates around almost similar WSS in each IA. $<WSS>$ changes up to 73.3% among nine IA geometries at a similar PI (occurred at PI = 0.57 between geometry D and E), while it changes at most by 7.8% by altering PI for each of geometries (occurred in geometry F). Based on the t-test analysis, $<WSS>$ does not significantly change between flow modes [Fig. 12(c)]. Therefore, $<WSS>$ is not associated with the pulsatility or the flow mode. This behavior is consistent with previous observations,^26,66,67 in which PI was found to negligibly influence the cycle-averaged WSS. However, it is in contrast to the conclusion obtained by Le et al.,¹⁵ in which the cycle-averaged WSS of IA in the cavity mode is higher than that of the vortex mode. This might be due to the fact that conclusion of Le et al.¹⁵ was based on a single geometry. Here, our results suggest that $<WSS>$ is mainly determined by the IA geometry and does not change appreciably with pulsatility. Note that some studies indicate low $<WSS>$^4,68 whereas some others indicate high $<WSS>$^3,69 to be related to the aneurysm rupture, probably due to the different pathological pathways for aneurysmal remodeling.⁵

C. Oscillatory shear index

OSI, which measures the change in the magnitude and direction of WSS,⁷⁰ is believed to promote inflammation and thrombosis^71,72 and is an important hemodynamic parameter for rupture risk.⁴ The effect of An on OSI is shown in Fig. 14 by plotting OSI for different geometries at PI = 0.57 and 1.43 as a function of An. Subscripts 1 and 2 denote PI = 0.57 and PI = 1.43 for all IAs in Fig. 14, respectively. As can be observed in Fig. 14, OSI of each geometry increases by increasing PI, which is similar to the findings of Xiang et al.²⁶ This behavior mainly is observed since higher PI conveys higher change of the inlet velocity. Moreover, Fig. 14 shows that OSI generally correlates with An of different geometries in each mode: OSI is higher for IAs with higher An if the flow mode does not change. This might be the consequence of the fact that IAs in each mode shares a similar behavior of flow structures, i.e., a vortex ring evolution and quasi stationary shear layer in vortex and cavity modes, respectively. At each flow mode, higher An corresponds to higher expansion length and/or PI, which indicates more instantaneous flow structures and subsequently higher OSI. We do not observe a general trend among all IA geometries with different PIs for OSI because fundamental differences exist in the flow structure of IAs in the cavity mode versus those in the vortex mode, as explained in Sec. III A.

FIG. 14.

Oscillatory shear index for different geometries (Table I) at PI = 0.57 and 1.43 as a function of An represented by circles with corresponding geometry. The lines are the linear fits for cavity and vortex modes. Circles are labeled by their IA names with subscripts 1 and 2 for PI = 0.57 and PI = 1.43, respectively.

Note that the general correlation between the flow mode and An is not that significant. The Pearsons correlation coefficient and p-value between OSI data points and their linear-fit for the cavity mode are 0.638 and 0.0639, respectively. Similar behavior is observed for the vortex mode with 0.612 and 0.0798 Pearsons correlation coefficient and p-value, respectively. Since the p-value is larger than 0.05, the correlation coefficients are not statistically significant. Nevertheless, the OSI in cavity and vortex modes still might be significantly different. To quantify the significance of difference between the cavity and vortex modes for OSI, a t-test analysis was performed [Fig. 12(d)]. Based on this analysis, the flows in the vortex mode have a significantly higher OSI (mean 0.019) than those in the cavity mode (mean 0.005, p < 0.01).

IV. SUMMARY AND CONCLUSION

In this work, we show that the flow mode is determined by both the pulsatility index and the geometry. By increasing pulsatility index from PI = 0.57 to 1.43, flow modes of IAs switch from cavity to vortex modes for geometries A, B, D, E, G, H, and I. Furthermore, by increasing the determining geometric parameter (αW/D) from 0.67 (in geometry F) to 2.1 (in geometry C), at constant PI (0.57 and 1.43), flow modes switch from cavity to vortex modes for geometries C and F. In fact, we show that An, which combines the IA geometry features with the pulsatility index, classifies the dominant flow mode (cavity or vortex ring) inside patient-specific IAs. Based on our results, An = 0.38, 0.62, 0.74, 0.81, 0.91, 0.96, 1.07, and 1.08 are in the cavity mode and IAs with An = 1.2, 1.56, 1.86, 2.03, 2.29, 2.4, 2.69, 2.72, and 3 are in the vortex mode. An can detect the flow mode in IAs [Fig. 12(a)]; the flows in the cavity mode have significantly lower An than those in the vortex mode (p < 0.01), i.e., the classifying parameter is An and not just PI or W/D.

It should be emphasized that there is not a sharp transition at An = 1. In fact, as discussed previously in Paper I¹⁸ and at the end of Sec. III A, the critical An at which transition occurs might be slightly above or below one due to either approximations in calculating An or the transition range of An. Nevertheless, flows in the vortex mode with higher An show a stronger vortex (Fig. 7), whereas flows in the cavity mode with lower An show a more stable shear layer (Fig. 11).

We also showed that the flow mode, and consequently An, affect the hemodynamic factors such as WSS and OSI. IAs in the vortex mode have significantly higher temporal fluctuations of WSS in comparison with a similar IA in the cavity mode [Fig. 12(b)]. However, cycle-averaged WSS mainly depends on the IA geometry because cycle averaging smooths out the temporal fluctuations [Fig. 12(c)]. OSI correlates with An in each flow mode and also correlates with PI in each geometry. IAs in the vortex mode have significantly higher OSI in comparison with a similar IA in the cavity mode [Fig. 12(d)].

High OSI and temporal fluctuations of WSS in the vortex mode (An ≳ 1) are the consequence of vortex ring formation which evolves and generates a highly dynamic flow and higher fluctuations of velocity in the dome [the upper row of Figs. 4 (Multimedia view) and 5–10]. In short, the evolution of the vortex ring in the parent artery creates higher velocity fluctuations in the dome. By contrast, low OSI and temporal fluctuations of WSS in the cavity mode (An ≲ 1) is because of the existence of a quasi-stationary shear layer which generates stationary vortical structures in the dome throughout the cycle [the lower row of Figs. 4 (Multimedia view) and 5–11]. Unstable flows, high OSI, and fluctuations of WSS are known factors that predispose aneurysms to rupture.^1–4,13,73 The temporal fluctuations of WSS is shown to significantly correlate with the location of cerebral aneurysm formation,⁶⁵ and OSI promotes inflammation and thrombosis.^71,72 Therefore, we hypothesize that IAs with An ≳ 1 (vortex mode) have a higher risk of rupture in comparison with IAs with An ≲ 1 (cavity mode), which will be tested in our future studies. This can have a significant clinical impact because An is a simple parameter, which in contrast with other hemodynamic parameters that require simulations or flow measurements, can easily be calculated from the geometry obtained through any medical imaging modality and local flow pulsatility (location) of an IA.