Breaking crosstalk limits to dynamic holography using orthogonality of high-dimensional random vectors

Abstract

Holography is the most promising route to true-to-life 3D projections, but the incorporation of complex images with full depth control remains elusive. Digitally synthesised holograms^1–7, which do not require real objects to create a hologram, offer the possibility of dynamic projection of 3D video^8,9. Extensive efforts aimed 3D holographic projection^10–17, however available methods remain limited to creating images on a few planes^10–12, over a narrow depth-of-field^13,14 or with low resolution^15–17. Truly 3D holography also requires full depth control and dynamic projection capabilities, which are hampered by high crosstalk^9,18. The fundamental difficulty is in storing all the information necessary to depict a complex 3D image in the 2D form of a hologram without letting projections at different depths contaminate each other. Here, we solve this problem by preshaping the wavefronts to locally reduce Fresnel diffraction to Fourier holography, which allows inclusion of random phase for each depth without altering image projection at that particular depth, but eliminates crosstalk due to near-orthogonality of large-dimensional random vectors. We demonstrate Fresnel holograms that form on-axis with full depth control without any crosstalk, producing large-volume, high-density, dynamic 3D projections with 1000 image planes simultaneously, improving the state-of-the-art^12,17 for number of simultaneously created planes by two orders of magnitude. While our proof-of-principle experiments use spatial light modulators, our solution is applicable to all types of holographic media.

Holography was originally invented to bypass limitations of lens aberrations to electron microscopy^19,20, but it was its optical implementation that captured the imagination of the general public as means for true-to-life recreation of 3D objects^21,22. Interest in this hitherto elusive goal is rapidly intensifying with the advent of virtual and augmented reality^23,24. A hologram comprises a holographic field and a physical medium to store it. There is steady progress in improving the physical medium, using metamaterials^2–4, graphene²⁵, photorefractives²⁶, stretchable materials¹², silicon⁶, improving metrics such as viewing angle¹⁷, pixel size²⁵, spectral response²⁵, and reconfigurability¹², while deformable mirrors¹⁷ and spatial light modulators (SLMs)²² are still the most commonly used. The key to creating realistic-looking projections, independent of the media, is the hologram field itself, which is often digitally synthesised: Computer generated holograms (CGHs)^1–7 do not require real objects to create the hologram, which is essential for dynamic holography²⁴. Both Fourier and Fresnel holography have been used to create CGHs. Fourier holograms based on established methods^27–28 such as the Kinoform technique²⁷ can project only around the focal plane of a lens, limiting them primarily to microscopy applications¹¹. In contrast, Fresnel holography can project arbitrarily large images with 3D depth²⁹. The first 3D Fresnel CGHs were based on the ping-pong algorithm¹⁰, which works only for two-plane projection. Alternative methods have been proposed³⁰, but they are computationally heavy, do not project deep 3D scenes and cannot be implemented on common holographic media. A popular approach is to use look-up tables^15,22, which is limited to reconstructing simple, low-resolution images. Projection quality can be improved with cascaded diffractive elements³¹, which is a costly and overly complicated method. While projections of up to several tens of planes have been demonstrated¹⁷, it was only for a single dot in each plane and could not be obtained simultaneously, but had to be created sequentially. For anything more complex than a single dot, earlier demonstrations have been limited to a few image planes, such as that of 3 letters in ref. 11. In all of these approaches, simultaneous multiplane image projection remains extremely limited by high crosstalk, resulting in projections that are too flat, too blurry or too low resolution and can only be viewed from within a tiny angular range.

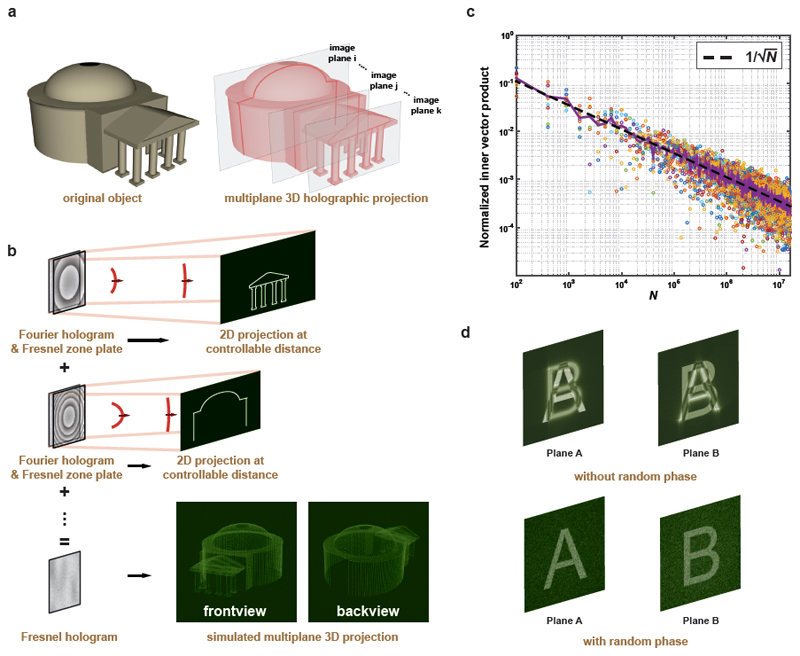
To approximate a genuinely 3D object, a large number of images must be projected to successive planes (Fig 1a) and all these images must be embedded into the hologram. We use a succession of lenses, implemented as Fresnel zone plates (FZPs), to focus each image to a particular plane. The first key step is to shape the wavefronts to reduce the Fresnel diffraction to Fourier transform locally at each image plane, so that construction of a single Fresnel hologram comprising an arbitrary number of planes is reduced to a trivial superposition operation (Fig. 1b). The second step is to add random phase at each image plane to suppress crosstalk: An image can be regarded as an N-dimensional vector, where N is the number of pixels (order of 10⁶). Random vectors become asymptotically orthogonal in the limit of N → ∞ (Fig. 1c). This property, which is due to the central limit theorem and the law of large numbers, leads to the elimination of any coherent trace of the images on each other during hologram reconstruction, virtually eliminating crosstalk from the reconstructed images (Fig. 1d).

Figure 1.

(a) Computer-generated holograms need to comprise large numbers of individual holograms of 2D images projected to different foci to serve as realistic representations of 3D objects, requiring excellent depth control, separation and elimination of crosstalk. (b) We simultaneously project multiplane images with controllable separation, while remaining in the Fresnel regime. To achieve this, we add a phase Fresnel Zone Plane (FZP) to a phase Fourier hologram to shift its image to the focal plane of the FZP. This corresponds to projecting a Fourier image in the Fresnel regime. Multiple holograms can be generated this way, each is designed to project a slice of a 3D object, then superposed to create a single Fresnel hologram. (c) Normalised inner product of two complementary checkerboard images is calculated as a function of total pixel size (N). The phase of each source image is random, uniformly distributed over 0 – 2π. (d) Adding random phase to each image suppresses unwanted crosstalk.

We preshape the wavefront at each foci not only to allow for superposition of many holograms to form a single one, but also to prevent the random phase that we add from distorting the images to which they are added. This would be nearly automatic if the reconstructed image would have a flat wavefront at its focal plane, as would be for Fourier holography, but Fourier holography is limited to the far field. Fresnel holograms can operate at virtually any distance but the propagation kernel is parabolic. We preshape the wavefront of the source hologram with a parabolic phase such that it becomes locally flat at each foci, much like prechirping of an ultrashort laser pulse entering a dispersive medium, where it accumulates a parabolic phase shift, only to be chirp free at a specific propagation distance. Consider a Fresnel hologram that projects a complex field distribution,

$$W\left(x,y,z\right)=\frac{e^{j\frac{2\pi z}{\lambda }}}{j\lambda z}{e}^{j\frac{\pi }{\lambda z}\left(x^2+y^2\right)}{\displaystyle {\iint }_{-\infty }^{\infty }\left\{H\left(\xi ,\eta \right)e^{j\frac{\pi }{\lambda z}\left({\xi }^2+{\eta }^2\right)}\right\}{e}^{-j\frac{2\pi }{\lambda z}\left(x\xi +y\eta \right)}d\xi d\eta ,}$$ (1)

where z is the distance between the image and hologram, (x, y) and (ξ, η) are the spatial coordinates at the image and hologram planes, respectively, H(ξ, η) is the complex field distribution of the hologram, and λ is the wavelength¹. The main difference from a Fourier hologram is the presence of the term, $e^{j\frac{\pi }{\lambda z}\left({\xi }^2+{\eta }^2\right)}.$ If this term can be cancelled at a specific plane z = z₀, this would correspond to reducing Fresnel diffraction to a Fourier transform at that plane. To this end, we construct the hologram, H(ξ, η), in the form of $H\left(\xi ,\eta \right)=F\left(\xi ,\eta \right)e^{-j\frac{\pi }{\lambda z_0}\left({\xi }^2+{\eta }^2\right)},$ where F(ξ, η) is the Fourier hologram of the product of the desired image, U(x, y), and a random phase, e^{−jϕ(x, y)}, which is added to suppress crosstalk (see Methods for details). The appended quadratic term counteracts the effect of the propagation kernel, such that, at the particular position of z₀, the projected field is

$$W\left(x,y,z_0\right)=\frac{e^{j\frac{2\pi }{\lambda }{z}_0}}{j\lambda z_0}{e}^{j\frac{\pi }{\lambda z_0}\left(x^2+y^2\right)}{\displaystyle {\iint }_{-\infty }^{\infty }F\left(\xi ,\eta \right)e^{-j\frac{2\pi }{\lambda z_0}\left(x\xi +y\eta \right)}d\xi d\eta ,}$$ (2)

which is similar, in form, to a Fourier hologram. For maximum generality and best results, F(ξ, η) should be complex. However, we restrict ourselves to using phase-only holograms, so a single SLM is sufficient for experimental realisation. The points with phase of nπ for $e^{-j\frac{k}{2f}\left({\xi }^2+{\eta }^2\right)}$ correspond to concentric circles with radii, $r_n=\sqrt{nf\lambda },$ which closely approximate a FZP of focal length f, for integer n. Direct superposition of a phase-type FZP on a phase-type Fourier hologram will generate a single-plane, phase-type Fresnel hologram, where the focal length of the FZP can be used to controllably translate the image to any distance z beyond the Talbot length (Fig. 1b). Then, construction of a single Fresnel hologram with M multiplane projections is straightforward: $H_M\left(\xi ,\eta \right)={\displaystyle \sum _{s=1}^M{F}_s\left(\xi ,\eta \right)e^{-j\frac{\pi }{\lambda z_s}\left({\xi }^2+{\eta }^2\right)},}$ where F_s(ξ, η) are the Fourier holograms of the images to be projected at z = z_k. This way, the otherwise extremely complicated procedure of packing many images into a single Fresnel hologram becomes a trivial superposition operation. The final Fresnel hologram is

$$\underset{\text{multiplane}\text{hologram}}{\underbrace{H_M\left(\xi ,\eta \right)}}={\displaystyle \sum _{s=1}^M\{\frac{e^{-j\frac{2\pi }{\lambda }{z}_f}}{j\lambda z_f}}{\displaystyle {\iint }_{-\infty }^{\infty }\underset{\text{intended}\text{image}}{\underbrace{U_s\left(x,y\right)}}\underset{\text{random}\text{phase}}{\underbrace{e^{-j{\varphi }_s(x,y)}}}}{e}^{j\frac{2\pi }{\lambda z_f}\left(x\xi +y\eta \right)}dxdy\}\underset{\text{Fresnel}\text{zone}\text{plate}}{\underbrace{e^{-j\frac{\pi }{\lambda z_s}\left({\xi }^2+{\eta }^2\right)}}}.$$ (3)

After lengthy, but straightforward calculations, the image projected by this hologram at each of the image planes reduces to

$$W^{\prime }\left(x^{\prime },y^{\prime },z_i\right)=k(U_i^{\prime }\left(x^{\prime },y^{\prime }\right)e^{-j{\varphi }_i^{\prime }(x^{\prime },y^{\prime })}+\frac{j}{\pi }{\displaystyle \sum _{\begin{array}{l}s=1\\ s\ne i\end{array}}^M{Y}_s\left(x^{\prime },y^{\prime }\right)}),$$ (4)

where k is a constant, $Y_s\left(x^{\prime },y^{\prime }\right)\equiv U_s^{\prime }\left(x^{\prime },y^{\prime }\right)e^{j{\varphi }_s^{\prime }(x^{\prime },y^{\prime })}⊛e^{j({x^{\prime }}^2+{y^{\prime }}^2)},$ the sign ⊛ denotes convolution, and x′ and y′ are normalised versions of x and y. The primed terms, $U_i^{\prime }\left(x^{\prime },y^{\prime }\right),$ ϕ′(x′, y′) and W′(x′, y′, z_i), are functions of the normalised coordinates, but remain otherwise identical in form and amplitude. The 3D image formed on any conventional detector is given by the light intensity, which is proportional to,

$${\left|W^{\prime }\left(x^{\prime },y^{\prime },z_i\right)\right|}^2={\left|k\right|}^2(\underset{\text{intended}\text{image}}{\underbrace{{\left|U_i^{\prime }\left(x^{\prime },y^{\prime }\right)\right|}^2}}+\frac{1}{{\pi }^2}{\displaystyle \sum _{\begin{array}{l}s=1\\ s\ne i\end{array}}^M{\left|Y_s\left(x^{\prime },y^{\prime }\right)\right|}^2}+\frac{j}{\pi }{\displaystyle \sum _{\begin{array}{l}s=1\\ s\ne i\end{array}}^M\left(U_i^{\prime }\left(x^{\prime },y^{\prime }\right)*e^{j{\varphi }_i^{\prime }(x^{\prime },y^{\prime })}{Y}_s\left(x^{\prime },y^{\prime }\right)-U_i^{\prime }\left(x^{\prime },y^{\prime }\right)e^{-j{\varphi }_i^{\prime }(x^{\prime },y^{\prime })}{Y}_s\left(x^{\prime },y^{\prime }\right)*\right)}+\frac{1}{{\pi }^2}{\displaystyle \sum _{\begin{array}{l}s=1\\ s>m\end{array}}^M{\displaystyle \sum _{m=1}^M\left(Y_s\left(x^{\prime },y^{\prime }\right)*Y_m\left(x^{\prime },y^{\prime }\right)+Y_s\left(x^{\prime },y^{\prime }\right)Y_m\left(x^{\prime },y^{\prime }\right)*\right)}}).$$ (5)

Here, the first term, ${\left|U_i^{\prime }\left(x^{\prime },y^{\prime }\right)\right|}^2,$ corresponds to perfect projection of the intended image. The second term is a sum of M − 1 individually as well as mutually random images due to the convolution of the random phases and parabolic wavefronts; in practice, they add white noise to the ideal image and with increasing M, their contribution, already suppressed by the factor of π², regresses further to the mean by the central limit theorem. The third and fourth terms are sums over order of M and M² terms, respectively, and each is in a form such that their average contribution over the image is in similar form as the orthogonality of two images. This contribution is ensured to be almost surely zero in the limit of N → ∞ by the orthogonality of high dimensional mutually random vectors. Furthermore, these terms are all mutually independent and of zero expected values, and their summations get closer to zero by the central limit theorem for large M. Overall, the final result for any image plane, i, is the ideal image, |U_i(x, y)|² and a small amount of white noise. Practically (in all examples considered, N is 10⁵ – 10⁷), crosstalk is completely eliminated.

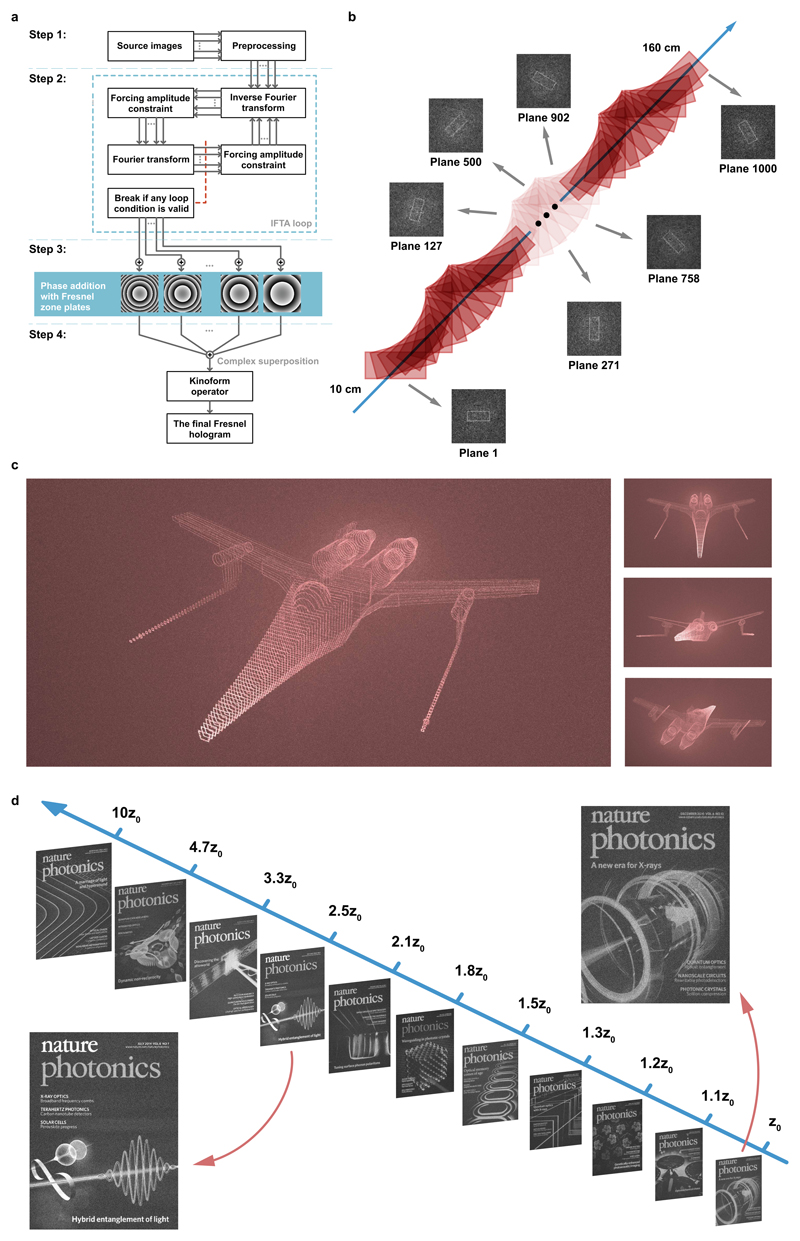
The algorithmic implementation of our method is shown in Fig. 2a. In step 1, we start with a stack of target images that form the desired 3D projection. Each image is passed through a preprocessing stage, where random phase is added. In step 2, each image goes through a number of iterations to generate its Fourier CGH (kinoform). We use an iterative Fourier transform algorithm (IFTA) to generate a set of kinoforms, F_i(ξ, η), each to be used for projecting an image plane of the targeted 3D projection. We use the adaptive additive IFTA³², which fast enough for real time applications. In step 3, each Fourier CGH is superposed with a phase FZP, to shift its projection to the focal plane of the corresponding FZP. In step 4, the translated holograms are added in complex form to create a single complex Fresnel hologram. After the complex superposition, the phase of the resulting sum is used as the final hologram.

Figure 2.

(a) Outline of the 3D Fresnel algorithm. (b) Representative schematic and simulations corresponding to a large-volume high-density 3D Fresnel hologram extending 150 cm in depth. The simultaneously projected 1000 on-axis images are simulated using a 4000 × 4000 hologram. (c) Simulation of a complex projected object when from various angles. 100 planes are simultaneously projected from a single 4000 × 4000 pixel hologram to distances spanning 10 cm to 20 cm from the hologram. (d) Simulation of 11 high-definition (1435 × 1080 pixels) images projected simultaneously from a single 16K hologram. The projection extends over 90 cm.

We first show a set of simulation results for simultaneous projection of 1000 images to their respective planes from a single 4000 × 4000-pixel 3D hologram. Light is able to focus/defocus repeatedly along the propagation axis to form high-fidelity images with minimal crosstalk (Fig. 2b and Supplementary Video 1). Next, as a demonstration of how the front, back and many in-between layers of a complex 3D object can be represented through simultaneous projection of multiple planes, we show a 3D spacecraft that can be viewed with the correct perspective from any direction over the full 4π solid angle (Fig. 2c and Supplementary Video 2). The simulation assumes a medium that emits or scatters light only at foci (for instance, ref. 33 or Supplementary Fig. 1). We also demonstrate the possibility of projecting much more complex images from a single Fresnel hologram (Fig. 2d and Supplementary Video 3). As expected, we find that larger hologram sizes in terms of geometry and pixel-count lead to lower crosstalk between adjacent planes, increasing the number of separable planes. This increased axial resolution is enabled by FZPs, each acting like an imaging lens, extending over the entire hologram. Larger hologram sizes enable higher numerical aperture lenses, leading to a smaller depth-of-field at each plane, which allows for projecting at a higher number of planes. The performance of 3D holograms in terms of the number of projected planes and image quality is further discussed in Methods. Multiplane projection achieved with our method is applicable at any distance beyond the Talbot zone, and no physical lens is required to project the images. Thus, the method can be used to project over a large depth of field at nearly arbitrarily separated planes, e.g., to depict a closed-surface 3D object using a single hologram (Fig. 1b, Fig. 2c and Supplementary Video 2).

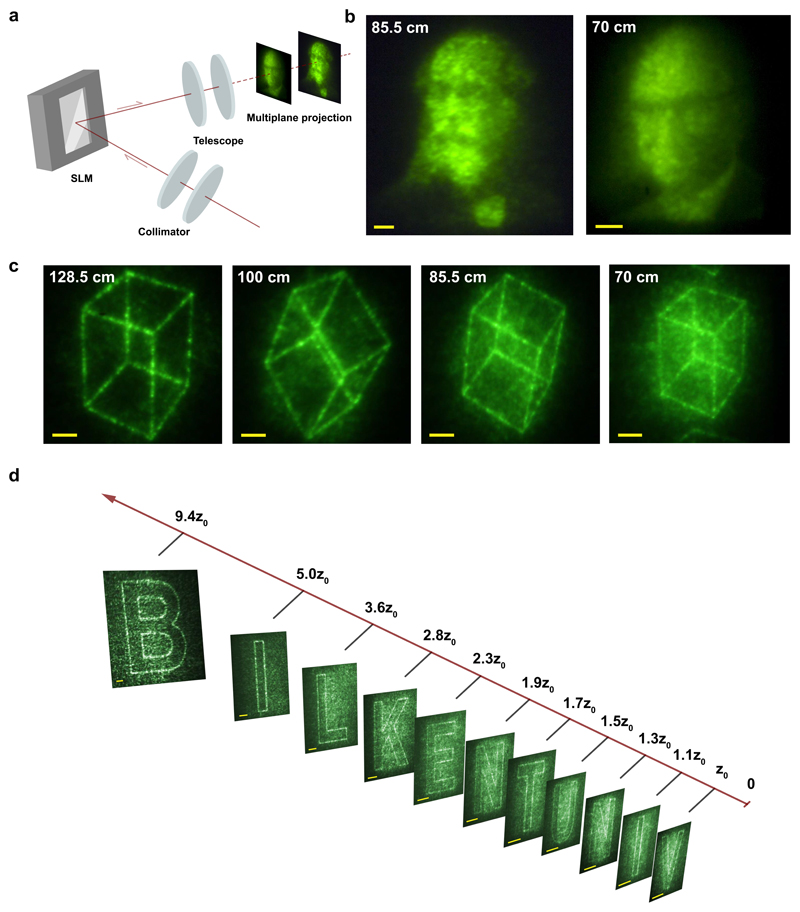
We performed a set of experiments to prove the concept using different laser wavelengths and SLMs (Fig. 3a and Methods). The SLM used in the experiments limited the holograms to 512 × 512 pixels. We first demonstrate two-plane reconstruction from a single Fresnel hologram, projecting grayscale images that are high resolution in terms of the number of active (non-black) pixels (Fig. 3b). Next, we show a four-plane projection from a single Fresnel hologram (Fig. 3c). Finally, we demonstrate the ability to project images over a large number of planes (Fig. 3d). This projection, encompassing 11 images of on-axis letters, constitutes the highest number of planes experimentally imaged from a single Fresnel CGH. Altogether, these results highlight the exceptional flexibility achieved in the design of 3D Fresnel CGHs. A second group of experiments demonstrate the applicability of our method to low-cost 3D projection. We used a green laser and a liquid crystal on silicon (LCoS) SLM that we extracted from a very low-cost consumer-grade projector. The results of the 3D display prototype demonstrating large-volume projection are shown in Supplementary Fig. 1. The hologram was designed to project 3 back-to-back images at different depths. We also implemented a dynamic display by animating 3 videos simultaneously, which were projected on-axis, without lateral shift (Supplementary Video 4).

Figure 3.

(a) Optical setup used in the experiments. (b) Two-plane, high-resolution simultaneous projection (portraits of Maxwell and Gabor). The distances from the hologram are, 85.5 and 70 cm. (c) Four-plane simultaneous projection of a rotating cube. The distances from the hologram are 128.5, 100, 85.5 and 70 cm. (d) Eleven-plane simultaneous projection of the letters spelling BILKENT UNIV, where z₀ = 18 cm. Scale bars are 2 mm. Each image set is projected without lateral shift from a single hologram.

The results reported here are far from fundamental limits imposed by physical optics; the quality and number of image planes scale up linearly with the number of the pixels available from the holographic media, accompanied by a merely linear increase in required computation time. These two favourable scaling properties are direct consequences of elimination of crosstalk and our wavefront engineering trick that reduces Fresnel diffraction locally to Fourier transforms respectively. SLMs with much higher numbers of pixels than those we have used in our experiments have been available since 2009³⁴, which suggests that more dramatic demonstrations are already possible. Our method can be used for realtime, video-rate dynamic holography even with current computer technology (see Methods). Such realtime capability can conceivably be used to incorporate occlusion effects (Supplementary Information). While our proof-of-concept results are targeted towards various 3D display applications, including volumetric displays³⁵, in diverse scenarios, such as medical visualisation or air traffic control, our method can find use in a wide range of applications, including modern electro-optical devices³⁶, microscopy¹¹ and laser-material interactions. Just as holography was invented for electron microscopy, but made impact to optics, given the rich history of judicious use of random fields in optics³⁷ and the generality of the mathematical result that our approach is based on, there may be exciting applications to near-zero epsilon optics³⁸ and imaging with flat optics².

Methods

Experimental setup

The experimental setup (Fig. 3a), in the case of IR illumination, includes a laser source (Yb-fibre laser operating at 1035 nm, 300 mW), a collimator to nullify the divergence of laser beam and enlarges the beam spot size to fill the hologram displayed on SLM completely (~1 cm diameter), a reflective liquid-crystal-on-silicon spatial light modulator (Hamamatsu, X10468-03) with 800 × 600 pixels, 20 μm pixel size, and a digital camera (Canon, 60D). The SLM reflects the collimated, linearly polarised laser beam after modulating it with the Fresnel CGH. The beam is then optionally (used only in Fig. 3b-c) expanded with a 3× telescope to block the zero-order diffraction, and then impinges on a screen. The hologram size is chosen to be 512 × 512 pixels, and the phase quantisation is set to 202 levels. In case of visible illumination (Supplementary Fig. 1 and Supplementary Video 4), the setup remains the same except for two changes. First, the wavelength of the laser is converted to green (517 nm) second harmonic generation in a BBO crystal. Second, the SLM is replaced with a visible one taken from a very inexpensive LCoS projector (LG, PH150G). A 3× telescope is used (Supplementary Fig. 1 and Supplementary Video 4). The distances at which images can be projected and their sizes depend on the SLM size and its pixel dimensions, both of which can be scaled up with larger SLMs and smaller pixels, respectively.

Simulations of 3D Fresnel holograms

The simulations of Fresnel hologram are carried out with the Fresnel diffraction equation. In order to achieve clear images, the zero order was filtered with a simulated 4f lens system. This corresponds to masking a small central section of the image spectrum, and then calculating the final image with the inverse Fourier transform of the spectrum.

Performance characterisation of 3D Fresnel holograms

Performance of 3D Fresnel CGHs depends on pixel size and pixel density of the hologram, modulation type, illumination wavelength, and the amplitude and phase distributions at all image planes. In addition, practical limitations can effect performance, such as experimental limitations in forming images in the vicinity of a reflection-type hologram. Therefore, finding an exact analytical expression involving all relevant parameters would be extremely complicated. Instead, we choose two metrics, which we believe still provide a good insight into the performance of 3D Fresnel holograms. The first is the root-mean-square error (RMSE), and the second is depth-of-field (DoF). The former is based on image quality, and is a measure of similarity between the source images and projected images at each plane. The latter is based on axial resolution, and is related to the maximum number of separable planes for a given image quality.

The RMSE is first calculated for each image at its corresponding plane, and the results from all planes are then averaged to provide a collective quality metric for a 3D hologram. This value is used to evaluate how the projection quality changes as a function of the number of separate planes. For instance, the RMSE of a set of rotating back-to-back cubes is given in Supplementary Fig. 2, showing that error rises linearly with increasing projection planes. For a given error tolerance expressed in RMSE, the number of image planes can be truncated.

In parallel, DoF is used for evaluating the axial resolution. DoF is a metric used widely in photography in identifying the maximum distance between two separated objects at which the objects still appear acceptably sharp. Thus, crosstalk between images can be evaluated with DoF_i at each plane (Supplementary Fig. 3). Minimising crosstalk in multiplane projection is critical, since an image suffering significant crosstalk from neighbouring planes can not accurately perform as a slice of a 3D projection.

We derive a DoF equation using two expressions, one for Rayleigh range of a FZP, and the other for spatial relationships between the sizes of the hologram and its image. We arrive at the following expression for depth-of-field at plane i, DoF_i (Supplementary Fig. 3)

$$Do{F}_i\propto \lambda {[\frac{1}{n_h}\frac{z_i}{d\xi }]}^2,$$

where z_i is the focal length for image plane i, λ is the illuminating wavelength, dξ is pixel size of the hologram, and n_h × n_h is the resolution of Fresnel hologram. This expression provides a reasonably accurate estimation of the effect of parameters included in it. For instance, we would expect that for two similar 3-plane projections, each with a different focal distance for the central plane, then the crosstalk suffered by the side images should be similar, given that the ratio of consecutive image separations is equal to the square of the ratio of central image locations. Supplementary Fig. 4 shows a simulation confirming this estimate.

We further see that increasing the hologram size (n_h × n_h) would enable projecting to a higher number of image planes. This can also be understood from the following perspective: A FZP act like a lens, thus larger FZP sizes allow larger numerical apertures (NA). A larger NA leads to tighter focus, and similar to the case in optical lenses, we expect the depth-of-field for each projection plane to be reduced. In parallel, one expects reduced crosstalk, since the images defocus faster when removed from the focal plane of FZPs. Thus the axial resolution (i.e., the number of separable planes) can be increased simply by increasing the hologram pixel number. We note that one should not confuse the depth-of-field of a slice of the 3D projection, discussed above in analogy to photography, with the depth-of-field of the entire projection. The latter is meant to describe the depth of the entire 3D projection. In this sense, it is analogous to the depth-of-field term described for the holo-video camera in ref. 29.

Holograms used in the experiments were of 512 × 512 pixels. If a higher resolution SLM was available, for instance, an 8k SLM over which 4000 × 4000 pixel holograms are useable, then we expect the DoF_i values to be reduced by a factor of 60. This would allow significantly higher axial resolutions and many more image layers. We demonstrate this prediction by propagating such a high-resolution 3D Fresnel hologram (4000 × 4000 pixels) using the Fresnel equation. The simulation results shown in Supplementary Fig. 5 show the odd-numbered images from among the 200 images that are projected directly back-to-back using a single 3D Fresnel CGH.

The 3D projections in simulations are in good agreement with the experimental results. For instance, a set of representative simulations are compared with experiments in Supplementary Fig. 6. Simulations of a single 3D hologram which projects 2 high-resolution portraits to directly back-to-back planes are given in Supplementary Fig. 6a. In comparison, the corresponding experiments shown in fig. Supplementary Fig. 6b are in good agreement with the simulations. The hologram is of 512 × 512 pixels and uses 20-μm pixels in both experiments and simulations.

Scaling of the number of planes with number of SLM pixels

We observed a linear scaling between the number of planes and number of pixels of the SLM. In order to see this, we assumed a distance between consecutive images as, z_i+1 = z_i + γ(DoF_i + DoF_i+1), where γ is an empirical parameter chosen to minimise crosstalk. This recursive relation can be directly used to calculate the image positions. The number of projected planes for given constants of γ, z₁, and dξ is calculated, resulting in linear scaling of maximum number of planes with the total number of pixels (Supplementary Fig. 7), preserving the image quality (RMSE ~ 0.24).

Computation time and possibility of realtime calculations for video-rate holography

The most time consuming step in our calculations is Fourier transform, which is well optimised for parallel computation, including for graphics processor unit (GPU) based computation. Furthermore, in case of video-rate holographic projections, it will rarely be the case that every part of the holographic image will change from one frame to the next. Much more commonly, changes will be limited to parts of the hologram. In that case, thanks to its superposition-based multiplane construction, large parts of our calculation would remain unchanged and would not need to be recalculated. For instance, if the canopy of the spacecraft in Fig. 2c opens up with the rest of craft remaining unchanged, only parts of the hologram describing the canopy will have to be recalculated. This unique property of our algorithm is similar to a technique commonly used in most compression algorithms and further eases requirements on realtime calculations. The typical calculation time for the experimentally demonstrated 3D holograms presented here is about 22 seconds using a single-CPU computer (Intel Core i7 4790K). A speed-up of 275 fold is achieved using a modern GPU, resulting in a 80 ms calculation time for experimental projection (Nvidia GeForce GTX980). We note that already available advanced GPUs, such as Nvidia Tesla v100 will allow another 10-fold speed-up. Further, these calculations were performed using Matlab for its convenience. Implementation of our algorithm in a low-level programming language, such as C, would likely result in at least 2-fold improvement. The projected calculation time with these improvements is likely to allow video rates of 20 Hz. More specialised hardware, such as field-programmable gate-array platform can improve calculation times further. Given the past rate of development of computational hardware, calculation time and cost appears unlikely to pose a limitation to realtime generation of 3D dynamic holograms at video rates using our approach.

Orthogonality of large random vectors

The orthogonality of large random vectors can be proved through several different approaches, including the waist concentration theory³⁹. Here, we follow a simple approach based on the law of large numbers⁴⁰, and the central limit theorem.

Assume X and Y to be non-equal large uniformly random vectors with equal size of N, which is large. After normalisation the vectors become X / ‖ X ‖ and Y / ‖ Y ‖, where ‖ X ‖ and ‖ Y ‖ are the lengths of X and Y respectively. The inner vector product of the two vectors is given as,

$$IP=\frac{<X,Y>}{\Vert X\Vert .\Vert Y\Vert }.$$

By the law of large numbers, $\Vert X\Vert /\sqrt{N}\to 1$ and $\Vert Y\Vert /\sqrt{N}\to 1$ with high probability for large N. Large N also yields $<X,Y>/\sqrt{N}\to 1$ according to the central limit theorem. The inner product scales with $1/\sqrt{N},$ showing that large random vectors rapidly converge to zero, rendering these vectors orthogonal. Similarly in multi-plane Fresnel holography, we see that adding random phase to source images renders them orthogonal, and reduces the crosstalk between their corresponding projected images (Supplementary Fig. 8).

Orthogonality of two images

We begin by cautioning the reader that use of a single quantity to characterise the cumulative amount of crosstalk between two images, each comprising of large numbers of elements, would, inevitably, prove insufficient for the most general use. Nevertheless, orthogonality, defined through the inner product, works as an excellent measure for a wide range of images, from the simple, complementary geometric patterns to human portraits (Supplementary Fig. 8). We calculate this quantity as follows: The images, together with their phase, are represented in complex form and are treated as vectors. The baseline of each vector is corrected by its average value, and each is normalised by its length. Then we simply calculate the inner product as,

$$IP=\frac{|x_1{e}^{j{\alpha }_1}{y}_1{e}^{-j{\beta }_1}+x_2{e}^{j{\alpha }_2}{y}_2{e}^{-j{\beta }_2}+\dots +x_N{e}^{j{\alpha }_N}{y}_N{e}^{-j{\beta }_N}|}{\Vert X\Vert \Vert Y\Vert },$$

where the vectors are X = (x₁e^jα₁, x₂e^jα₂, .. , x_Ne^jα_N), and Y = (y₁e^jβ₁, y₂e^jβ₂, .. ,y_Ne^jβ_N). N is the total number of pixels in each image.

Theoretical calculations

The first step is to configure the hologram so as to produce a flat “propagation kernel” even though we are in the Fresnel regime, such that the projected field magnitude will correspond to the desired 2D image at a given z. This opens the door to adding a pure phase term to each plane in a way that it does not alter the image formed at that plane. This is possible because an image will be formed by detecting the light intensity, which is proportional to the absolute square of the field, an operation, which drops any pure phase contributions. If the projection W(x, y, z) is of the form W(x, y, z) = W_A(x, y, z)e^jΦ(x,y,z), then the image formed will be proportional to |W_A(x, y, z)|².

We start by recalling the Fresnel and Fourier hologram equations (ref. ¹). We consider the Fourier hologram, F(ξ, η), of an image U(x, y), which is additionally multiplied by a random phase, e^−jϕ(x,y), to suppress crosstalk, as will be shown below. The physical significance of being in the Fourier (Fraunhofer) regime is that U(x, y)e^−jϕ(x,y) is the field that would be formed in the far field, at the plane z = z_f,

$$F\left(\xi ,n\right)=-\frac{e^{-j\frac{2\pi }{\lambda }{z}_f}}{j\lambda z_f}{\displaystyle {\iint }_{-\infty }^{\infty }U\left(x,y\right)e^{-j\varphi \left(x,y\right)}{e}^{j\frac{2\pi }{\lambda z_f}\left(x\xi +y\eta \right)}dxdy.}$$ (6)

Here, z_f ≫ π(ξ² + η²)/λ, which is the Fraunhofer condition. Similarly, the image formed by such a Fourier hologram in the far field is given by

$$U\left(x,y\right)e^{-j\varphi \left(x,y\right)}=\frac{e^{j\frac{2\pi }{\lambda }{z}_f}}{j\lambda z_f}{\displaystyle {\iint }_{-\infty }^{\infty }F\left(\xi ,\eta \right)e^{-j\frac{2\pi }{\lambda z_f}\left(x\xi +y\eta \right)}d\xi d\eta .}$$ (7)

The Fresnel hologram is more flexible in that it can project an image, W(x, y, z_i), at some arbitrary plane, z = z₀, and is given by

$$H_0\left(\xi ,\eta \right)=-\frac{e^{-j\frac{2\pi }{\lambda }{z}_0}}{j\lambda z_0}{e}^{-j\frac{\pi }{\lambda z_0}\left({\xi }^2+{\eta }^2\right)}{\displaystyle {\iint }_{-\infty }^{\infty }W\left(x,y,z_0\right)e^{-j\frac{\pi }{\lambda z_0}\left(x^2+y^2\right)}{e}^{j\frac{2\pi }{\lambda z_0}\left(x\xi +y\eta \right)}dxdy.}$$ (8)

Similarly, the image to be projected at a plane z = z₀, W(x, y, z₀), by a Fresnel hologram, H(ξ, η), is given by

$$W\left(x,y,z_0\right)=\frac{e^{j\frac{2\pi }{\lambda }{z}_0}}{j\lambda z_0}{e}^{j\frac{\pi }{\lambda z_0}\left(x^2+y^2\right)}{\displaystyle {\iint }_{-\infty }^{\infty }H\left(\xi ,\eta \right)e^{j\frac{\pi }{\lambda z_0}\left({\xi }^2+{\eta }^2\right)}{e}^{-j\frac{2\pi }{\lambda z_0}\left(x\xi +y\eta \right)}d\xi d\eta .}$$ (9)

The main difference of the Fresnel hologram (equation (8)) from a Fourier hologram (equation (6)) is the presence of a parabolic wavefront, which can be cancelled, albeit only for a specific plane, if we construct the hologram in the form,

$$H\left(\xi ,\eta \right)=F\left(\xi ,\eta \right)e^{-j\frac{\pi }{\lambda z_0}\left({\xi }^2+{\eta }^2\right)},$$ (10)

which projects an image, W(x, y, z_i), at a plane z = z₀. As explained in the main text, with this arrangement, a simple superposition operation is sufficient to construct a multiplane Fresnel hologram that projects a different image to each plane,

$$H_M\left(\xi ,\eta \right)={\displaystyle \sum _{s=1}^M{F}_s\left(\xi ,\eta \right)e^{-j\frac{\pi }{\lambda z_s}\left({\xi }^2+{\lambda }^2\right)}.}$$ (11)

Here, M is the total number of image planes, F_s(ξ, η) is the Fourier hologram of the image to be projected to a plane at z = z_s. The final Fresnel hologram is

$$\underset{\text{multiplane}\text{hologram}}{\underbrace{H_M\left(\xi ,\eta \right)}}=-{\displaystyle \sum _{s=1}^M\{\frac{e^{-j\frac{2\pi }{\lambda }{z}_f}}{j\lambda z_f}{\displaystyle {\iint }_{-\infty }^{\infty }\underset{\text{intended}\text{image}}{\underbrace{U_s\left(x,y\right)}}\underset{\text{random}\text{phase}}{\underbrace{e^{-j{\varphi }_s\left(x,y\right)}}}{e}^{j\frac{2\pi }{\lambda z_f}\left(x\xi +y\eta \right)}dxdy}\}\underset{\text{Fresnel}\text{zone}\text{plate}}{\underbrace{e^{-j\frac{\pi }{\lambda z_s}\left({\xi }^2+{\eta }^2\right)}}}}.$$ (12)

We emphasise that the random phase, e^{−jϕ_s(x, y)}, is different and mutually independent for each plane, s. Next, we want to calculate the image projected by this hologram at an arbitrary plane, i, and demonstrate how the addition of the random phase does not distort the image it is added to, but that the random phase added to the other images suppress their crosstalk.

The image formed by this hologram at an arbitrary plane, z_i, is given by

$$W(x,y,z_i)=\frac{e^{j\frac{2\pi }{\lambda }{z}_i}}{j\lambda z_i}{e}^{j\frac{\pi }{\lambda z_i}(x^2+y^2)}{\displaystyle {\iint }_{-\infty }^{\infty }{H}_M(\xi ,\eta )e^{j\frac{\pi }{\lambda z_i}({\xi }^2+{\eta }^2)}{e}^{-j\frac{2\pi }{\lambda z_i}(x\xi +y\eta )}d\xi d\eta ,}$$ (13)

or using equation (11),

$$W(x,y,z_i)=\frac{e^{j\frac{2\pi }{\lambda }{z}_i}}{j\lambda z_i}{e}^{j\frac{\pi }{\lambda z_i}(x^2+y^2)}{\displaystyle {\iint }_{-\infty }^{\infty }{\displaystyle \sum _{s=1}^M{F}_s(\xi ,\eta )}{e}^{-j\frac{\pi }{\lambda z_s}({\xi }^2+{\eta }^2)}{e}^{j\frac{\pi }{\lambda z_i}({\xi }^2+{\eta }^2)}{e}^{-j\frac{2\pi }{\lambda z_i}(x\xi +y\eta )}d\xi d\eta .}$$ (14)

We now separate the sum into terms s = i and s ≠ i, and evaluating $e^{j\frac{\pi (z_s-z_i)}{\lambda z_i{z}_s}({\xi }^2+{\eta }^2)}$ in the limit of z_s → z_i,

$$\begin{array}{l}W\left(x,y,z_i\right)=\frac{e^{j\frac{2\pi }{\lambda }{z}_i}}{j\lambda z_i}{e}^{j\frac{\pi }{\lambda z_i}\left(x^2+y^2\right)}{\displaystyle {\iint }_{-\infty }^{\infty }{F}_i\left(\xi ,\eta \right)}{e}^{-j\frac{2\pi }{\lambda z_i}\left(x\xi +y\eta \right)}d\xi d\eta +\frac{e^{j\frac{2\pi }{\lambda }{z}_i}}{j\lambda z_i}{e}^{j\frac{\pi }{\lambda z_i}\left(x^2+y^2\right)}{\displaystyle {\iint }_{-\infty }^{\infty }{\displaystyle \sum _{\begin{array}{l}s=1\\ s\ne i\end{array}}^M{F}_s\left(\xi ,\eta \right)}}{e}^{j\frac{\pi \left(z_s-z_i\right)}{\lambda z_i{z}_s}\left({\xi }^2+{\eta }^2\right)}{e}^{-j\frac{2\pi }{\lambda z_i}\left(x\xi +y\eta \right)}d\xi d\eta .\end{array}$$ (15)

Using the relation ${\displaystyle {\iint }_{-\infty }^{\infty }{F}_i\left(\xi ,\eta \right)}{e}^{-j\frac{2\pi }{\lambda z_f}\left(x\xi +x\eta \right)}d\xi d\eta =j\lambda z_f{e}^{-j\frac{2\pi }{\lambda }{z}_f}{U}_i\left(x,y\right)e^{-j{\varphi }_i\left(x,y\right)}$ (from equation (6)) to simplify the first term, interchanging the order of the summation and the integral transform for the second term, and making the transformations, $f_x=\frac{\xi }{\lambda z_f},f_y=\frac{\eta }{\lambda z_f},$ to cast the integral transform into an inverse Fourier transform (see ref. 1), we obtain,

$$W\left(x,y,z_i\right)=\frac{z_f}{z_i}{e}^{j\frac{2\pi }{\lambda }\left(z_i-z_f\right)}{e}^{j\frac{\pi }{\lambda z_i}\left(x^2+y^2\right)}{U}_i\left(x,y\right)e^{-j{\varphi }_i\left(x,y\right)}+\frac{\lambda z_f^2}{j{z}_i}{e}^{j\frac{2\pi }{\lambda }{z}_i}{e}^{j\frac{\pi }{\lambda z_i}\left(x^2+y^2\right)}{\displaystyle \sum _{\begin{array}{l}s=1\\ s\ne i\end{array}}^M{\displaystyle {\displaystyle {\iint }_{-\infty }^{\infty }{F}_s\left(\lambda z_f{f}_x,\lambda z_f{f}_y\right)e^{j\frac{\pi \lambda z_f^2}{z_i{z}_s}\left(z_s-z_i\right)\left(f_x^2+f_y^2\right)}{e}^{-j2\pi \left(x{f}_x+y{f}_y\right)}d{f}_{x}d{f}_y}}}.$$ (16)

Now, let’s use the following relations, where ℱ denotes Fourier transform,

$$F_s\left(\lambda z_f{f}_x,\lambda z_f{f}_y\right)=\frac{-e^{-j\frac{2\pi }{\lambda }{z}_f}}{j\lambda z_f}{\displaystyle {\displaystyle {\iint }_{-\infty }^{\infty }U\left(x,y\right)e^{-j\varphi \left(x,y\right)}{e}^{j2\pi \left(x{f}_x+y{f}_y\right)}dxdy=\frac{-e^{-j\frac{2\pi }{\lambda }{z}_f}}{j\lambda z_f}ℱ\{U_s\left(x,y\right)e^{-j{\varphi }_s\left(x,y\right)}\}}},$$ (17)

which is obtained by applying the same transformation above on equation (6) and using

$$e^{j\frac{\pi \lambda z_f^2}{z_i{z}_s}\left(z_s-z_i\right)\left(f_x^2+f_y^2\right)}=-\frac{j{z}_i{z}_s}{\lambda z_f^2\left|z_s-z_i\right|}ℱ\{e^{-j\frac{\pi z_i{z}_s\left(x^2+y^2\right)}{\lambda z_f^2{z}_s-z_i}}\},$$ (18)

we rewrite the terms above as Fourier transforms themselves.

$$W\left(x,y,z_i\right)=\frac{z_f}{z_i}{e}^{j\frac{2\pi }{\lambda }\left(z_i-z_f\right)}{e}^{j\frac{\pi }{\lambda z_i}\left(x^2+y^2\right)}{U}_i\left(x,y\right)e^{-j{\varphi }_i\left(x,y\right)}+\frac{\lambda z_f^2}{j{z}_i}{e}^{j\frac{2\pi }{\lambda }{z}_i}{e}^{j\frac{\pi }{\lambda z_i}\left(x^2+y^2\right)}\times {\displaystyle \sum _{\begin{array}{l}s=1\\ s\ne i\end{array}}^M{\displaystyle {\displaystyle {\iint }_{-\infty }^{\infty }(\frac{e^{-j\frac{2\pi }{\lambda }{z}_f}}{j\lambda z_f}ℱ\{U_s\left(x,y\right)e^{-j{\varphi }_s\left(x,y\right)}\})}(\frac{-j{z}_i{z}_s}{\lambda z_f^2\left|z_s-z_i\right|}ℱ\{e^{-j\frac{\pi z_i{z}_s\left(x^2+y^2\right)}{\lambda z_f^2\left|z_s-z_i\right|}}\})}}{e}^{-j2\pi \left(x{f}_x+y{f}_y\right)}d{f}_{x}d{f}_y$$ (19)

$$\begin{array}{l}W\left(x,y,z_i\right)=\frac{z_f}{z_i}{e}^{j\frac{2\pi }{\lambda }\left(z_{i-}{z}_f\right)}{e}^{j\frac{\pi }{\lambda z_i}\left(x^2+y^2\right)}{U}_i\left(x,y\right)e^{-j{\varphi }_i\left(x,y\right)}+\frac{j}{\lambda }{\displaystyle \sum _{\begin{array}{l}s=1\\ s\ne i\end{array}}^M\frac{z_s}{z_f\left|z_s-z_i\right|}{e}^{j\frac{2\pi }{\lambda }\left(z_{i-}{z}_f\right)}{e}^{j\frac{\pi }{\lambda z_i}\left(x^2+y^2\right)}}\times {\displaystyle {\iint }_{-\infty }^{\infty }ℱ\left\{U_s\left(x,y\right)e^{-j{\varphi }_s\left(x,y\right)}\right\}ℱ\{e^{-j\frac{\pi z_i{z}_s\left(x^2+y^2\right)}{\lambda z_f^2{z}_s-z_i}}\}{e}^{-j2\pi \left(x{f}_x+y{f}_y\right)d{f}_{x}d{f}_y.}}\end{array}$$ (20)

Thus, each element of the second term is in the form of the inverse Fourier transform of the product of Fourier transforms of two functions. Using the convolution property, they can be replaced by the Fourier transform of their convolution, which cancels the inverse Fourier transform,

$$\begin{array}{l}W\left(x,y,z_i\right)=\frac{z_f}{z_i}{e}^{j\frac{2\pi }{\lambda }\left(z_{i-}{z}_f\right)}{e}^{j\frac{\pi }{\lambda z_i}\left(x^2+y^2\right)}{U}_i\left(x,y\right)e^{-j{\varphi }_i\left(x,y\right)}+j{\displaystyle \sum _{\begin{array}{l}s=1\\ s\ne i\end{array}}^M\frac{z_s}{\lambda z_f\left(z_s-z_i\right)}{e}^{j\frac{2\pi }{\lambda }\left|z_{i-}{z}_f\right|}{e}^{j\frac{\pi }{\lambda z_i}\left(x^2+y^2\right)}(U_s\left(x,y\right)e^{-j{\varphi }_s\left(x,y\right)}⊛e^{-j\frac{\pi z_i{z}_s\left(x^2+y^2\right)}{\lambda z_f^2{z}_s-z_i}})}.\end{array}$$ (21)

Next, we simplify the notation by introducing ${\alpha }^2=\frac{\lambda z_f^2}{\pi z_i{z}_s}(z_s-z_i),k=\frac{z_f}{z_i}{e}^{j\frac{2\pi }{\lambda }(z_i-z_j)}{e}^{j\frac{\pi }{\lambda z_i}(x^2+y^2)},$ and $k^{\prime }=\frac{z_s}{\lambda z_f|z_s-z_f|}{e}^{j\frac{2\pi }{\lambda }(z_i-z_f)}{e}^{j\frac{\pi }{\lambda z_i}(x^2+y^2)}=\frac{z_i{z}_s}{\lambda z_f^2|z_s-z_f|}k,$

$$W\left(x,y,z_i\right)=k\underset{desiredimage}{\underbrace{U_i\left(x,y\right)}}\underset{randomphase}{\underbrace{e^{-j{\varphi }_i\left(x,y\right)}}}+j{\displaystyle \sum _{\begin{array}{l}s=1\\ s\ne i\end{array}}^M{k}^{\prime }(U_s\left(x,y\right)e^{-j{\varphi }_s\left(x,y\right)}⊛e^{-j\left(x^2+y^2\right)/{\alpha }^2}).}$$ (22)

The series term contains the convolution of the product of the other images and their random phases with a parabolic phase (wavefront). The convolution with a parabolic phase plays a very important role, because it mixes the random phase with the amplitude, rendering both the amplitude and phase of the resulting field random. This effect is illustrated in Supplementary Fig 9.

We want to compare the magnitude of the first term with the magnitudes of the terms within the series. Before we can do so, we should arrange for the integration due to the convolution to be over dimensionless coordinates. To achieve this, we transform the entire equation into normalised (dimensionless) lateral coordinates through the transformation x → αx′ and y → αy′. By its definition, the convolution term is

$$U_s\left(x,y\right)e^{-j{\varphi }_s\left(x,y\right)}⊛e^{-j\left(x^2+y^2\right)/{\alpha }^2}={\displaystyle {\iint }_{-\infty }^{\infty }{U}_s\left(x-u,y-v\right)e^{-j{\varphi }_s\left(x-u,y-v\right)}{e}^{j\frac{(u^2+v^2)}{{\alpha }^2}}dudv,}$$ (23)

Introducing the normalised coordinates, u = αu′, v = αv′, x = αx′ and y = αy′,

$$U_s(x,y)e^{-j{\varphi }_s(x,y)}⊛e^{-j(x^2+y^2)/{\alpha }^2}={\alpha }^2{\displaystyle {\iint }_{-\infty }^{\infty }{U}_s(\alpha x^{\prime }-\alpha u^{\prime },\alpha y^{\prime }-\alpha v^{\prime })e^{-j{\varphi }_s(\alpha x^{\prime }-\alpha u^{\prime },\alpha y^{\prime }-\alpha v^{\prime })}{e}^{j(u^{\prime 2}+v^{\prime 2})}d{u}^{\prime }d{v}^{\prime }}$$ (24)

Now, we introduce the new functions, $U_i^{\prime }(x^{\prime },y^{\prime })$ and ϕ′ (x′, y′), taking the normalised coordinates as their parameters, but otherwise identical in form, amplitude and unit, as U_i(x, y) and ϕ(x, y). To give a concrete example, for $U_i(x,y)=U_0{e}^{-{(x+y)}^2/r_0^2},$ the new function would become $U_i^{\prime }(x^{\prime },y^{\prime })=U_0{e}^{-{(x^{\prime }+y^{\prime })}^2}.$ The convolution takes the form,

$$\begin{array}{l}{U}_s\left(x,y\right)e^{-j{\varphi }_s\left(x,y\right)}⊛e^{-j\left(x^2+y^2\right)/{\alpha }^2}={\alpha }^2{\displaystyle {\iint }_{-\infty }^{\infty }{U}_s^{\prime }}\left(x^{\prime }-u^{\prime },y^{\prime }-v^{\prime }\right)e^{-j{\varphi }_s^{\prime }\left(x^{\prime }-u^{\prime },y^{\prime }-v^{\prime }\right)}{e}^{j\left(u^{\prime 2}+v^{\prime 2}\right)}d{u}^{\prime }d{v}^{\prime }\\ ={\alpha }^2{U}_s^{\prime }\left(x^{\prime },y^{\prime }\right)e^{-j{\varphi }_s^{\prime }\left(x^{\prime },y^{\prime }\right)}⊛e^{-j\left(x^{\prime 2}+y^{\prime 2}\right).}\end{array}$$ (25)

Similarly, W(x, y) gets mapped to W′(x′, y′) and using the relation, α²k′ = k/π, to simplify, W′(x′, y′) is given by,

$$W^{\prime }\left(x^{\prime },y^{\prime },z_i\right)=k(U_i^{\prime }\left(x^{\prime },y^{\prime }\right)e^{-j{\varphi }_i^{\prime }\left(x^{\prime },y^{\prime }\right)}+\frac{j}{\pi }{\displaystyle \sum _{\begin{array}{l}s=1\\ s\ne i\end{array}}^M{U}_s^{\prime }\left(x^{\prime },y^{\prime }\right)e^{-j{\varphi }_s^{\prime }\left(x^{\prime },y^{\prime }\right)}⊛e^{-j{\left(x^{\prime }+y^{\prime }\right)}^2}}).$$ (26)

This expression can be analysed to clearly reveal how the random phase suppresses crosstalk. As mentioned at the beginning of this section, the 3D image formed on any conventional detector or an image viewed through a scattering process is given by |W′(x′,y′,z_i)|². To simplify further, we introduce $Y_s(x^{\prime },y^{\prime })\equiv U_s^{\prime }(x^{\prime },y^{\prime })e^{j{\varphi }_s^{\prime }(x^{\prime },y^{\prime })}⊛e^{j(x^{\prime 2}+y^{\prime 2})}.$ We note that all Y_s(x′, y′) are random, because they are all convolutions of $U_s^{\prime }(x^{\prime },y^{\prime })e^{j{\varphi }_s^{\prime }(x^{\prime },y^{\prime })}$ the product of the coherent amplitude defining the image, $U_s^{\prime }(x^{\prime },y^{\prime })$ and the random phase corresponding to that image, $e^{j{\varphi }_s^{\prime }(x^{\prime },y^{\prime })},$ with a parabolic wavefront, e^{−j(x′+y′)2}. This operation is sufficient to thoroughly mix the non-random amplitude information defining the image with the random phase information. The end result is virtually completely random valued (see Supplementary Fig. 9), except in the limiting case of α → 0, in which case e^{−j(x′+y′)2} → δ(x′+y′) and the convolution operation yields U′_s(x′+y′)e^{jϕ′_s(x′+y′)} unaltered. However, α → 0 implies z_i → z_s, which would mean that the two images are already in the same plane. Thus, this limit is not relevant in practice.

Next, we calculate the value of |W′(x′,y′,z_i)|²:

$${\left|W^{\prime }(x^{\prime },y^{\prime },z_i)\right|}^2={\left|k\right|}^2({\left|U_i^{\prime }(x^{\prime },y^{\prime })\right|}^2+\frac{1}{{\pi }^2}{\displaystyle \sum _{\begin{array}{l}s=1\\ s\ne i\end{array}}^M{\left|Y_s(x^{\prime },y^{\prime })\right|}^2}+\frac{j}{\pi }{\displaystyle \sum _{\begin{array}{l}s=1\\ s\ne i\end{array}}^M(U_i^{\prime }(x^{\prime },y^{\prime })*e^{j{\varphi }_i^{\prime }(x^{\prime },y^{\prime })}{Y}_s(x^{\prime },y^{\prime })-U_i^{\prime }(x^{\prime },y^{\prime })e^{-j{\varphi }_i^{\prime }(x^{\prime },y^{\prime })}{Y}_s(x^{\prime },y^{\prime })*)}+\frac{1}{{\pi }^2}{\displaystyle \sum _{\begin{array}{l}s=1\\ s>m\end{array}}^M{\displaystyle \sum _{m=1}^M(Y_s(x^{\prime },y^{\prime })*Y_m(x^{\prime },y^{\prime })+Y_s(x^{\prime },y^{\prime })Y_m(x^{\prime },y^{\prime })*)}}).$$ (27)

We now discuss each of the terms of the result above. The first term, ${\left|U_i^{\prime }\left(x\prime ,y\prime \right)\right|}^2,$ corresponds to the production of the desired image in perfect form, apart from an overall multiplicative constant, which is not important. The second term is a sum of M − 1 random images, as discussed above. They are also mutually independent, so their summation is further closer to a constant value by the central limit theorem for large M. In practice, their role is to add certain amount of white noise to the ideal image. Furthermore, their contribution is strongly suppressed by the prefactor of π² ~ 10, as well as the summation of M − 1 of them. The third term is a sum over M − 1 terms, each of which are in a form such that their contribution, averaged over the image (in all the examples considered here, N, the number of hologram pixels, varies between 10⁵ − 10⁷), is similar to inner products of very high dimensional (equivalent to N) mutually random vectors. Furthermore, unlike the second term, they do not involve absolute squares, so their random values are allowed to converge to zero. Together with the near-complete orthogonality of mutually random vectors in high dimensions, their contribution vanishes in the limit of large dimensions, i.e., large number of pixels in the images and large number of planes. The fourth term involves in the order of M² terms, which vanish for the same reasons, but even faster due to their large numbers for large M.

Overall, we see that the final result for any image plane, i, is that we obtain the ideal image, |U_i(x, y)|², only with the addition of some amount of white noise. There remains absolutely no trace of any coherent manifestation of any of the other images. We declare crosstalk to have been suppressed (see Supplementary Fig. 10 for a simple demonstration for the case of M = 2). Finally, we note that the demonstrations here were restricted to the use of pure phase holograms, F_i (x, y), due to practical reasons. This limitation causes additional deterioration of the image reproduction, which can be avoided at the cost of increased complexity of the experimental implementation, if so desired.

Supplementary Material

Video 1. Simultaneous 1000-plane projection from a 3D Fresnel hologram.

The simulated on-axis projection of a single Fresnel hologram (4000 × 4000, 20-µm pixels) create rotating rectangles at different planes, realising 3D projection. The images form at 10 - 160 cm from the SLM.

Video 2. Full solid angle projection.

Simulated projection of a spaceship from a Fresnel hologram (4000 × 4000 pixels), where the camera is rotating around the object over the 4π viewing angle.

Video 3. Simultaneous 21-plane projection from a 3D Fresnel hologram.

The simulated on-axis projection of a single Fresnel hologram (8000 × 8000, 20-µm pixels) create step-by-step angular rotation of a 3D scene depicting the final state of the chessboard from a historic chess match. The images form at 10 - 60 cm from the SLM. The video is not meant to indicate occlusion.

Video 4. 3D dynamic display prototype.

Optically reconstructed images form at 70 - 120 cm relative to the hologram (512 × 512 pixels). The CGH is implemented on a visible-light SLM, illuminated with 520 nm.