Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2020 Mar 1.
Published in final edited form as: Exp Brain Res. 2019 Jan 11;237(3):865–871. doi: 10.1007/s00221-019-05470-w

Beyond rambling and trembling: Effects of visual feedback on slow postural drift

Momoko Yamagata 1,2, Marta Popow 1, Mark L Latash 1
PMCID: PMC6436822  NIHMSID: NIHMS1524755  PMID: 30635703

Abstract

We explored one of the unusual predictions of the concept of back-coupling within the theoretical scheme of the control of posture and movement with setting referent coordinates for the effectors. This concept implies slow drifts of referent coordinates toward actual coordinates leading to unintentional drift in performance. During standing, such slow drifts may lead to a protective step or even a fall and, therefore, corrections are expected leading to body sway at frequencies under 0.1 Hz. Young healthy subjects stood on the force platform quietly for 60 s under two single-task conditions, with eyes open and closed, and two double-task conditions, matching an irrelevant muscle activation signal to a target (MATCH) and performing a subtraction task. The latter was performed with eyes open and closed. The rambling-trembling decomposition was applied to the displacements of the center of pressure in the anterior-posterior direction. Spectral analysis was used to quantify power within typical ranges for Tr and Rm, as well as for a slow Rm component (under 0.1 Hz) addressed as Drift. Closing eyes led to a significant increase in Rm and Tr, but no effects on Drift. Drift increased significantly in the MATCH task with no changes in Rm and a drop in Tr. No effects of the subtraction task were seen on Drift. Overall, our findings suggest that unintentional slow drift of referent body orientation towards the actual body orientation leads to Drift, a specific example of back-coupling reflected in postural sway. This observation can be also seen as an example of physiological minimization of activity of motoneurons. Natural visual feedback is used to avoid the COP drift and/or correct it quickly and effectively; this ability is compromised when vision is used for an unrelated task.

Keywords: Posture, Referent coordinate, Sway, Rambling, Trembling, Drift, Visual feedback

Introduction

Quiet standing is associated with continuous changes in a variety of mechanical variables addressed as body sway (reviewed in Winter et al. 2006). Analysis of forces applied to the supporting surface has resulted in a hypothesis that body sway is associated with two processes termed rambling (Rm) and trembling (Tr) (Zatsiorsky and Duarte 1999, 2000). Rm represents a trajectory of the center of pressure (COP, the point of application of the resultant vertical force acting on the body), computed as an interpolation of instantaneous equilibrium points, i.e., the points when the resultant force in the selected direction, anterior-posterior or medio-lateral, is zero. Tr is the difference between the COP trajectory and Rm. Rm has been viewed as predominantly a consequence of supraspinal control, while Tr has been considered a reflection of peripheral mechanics and action of spinal reflex loops.

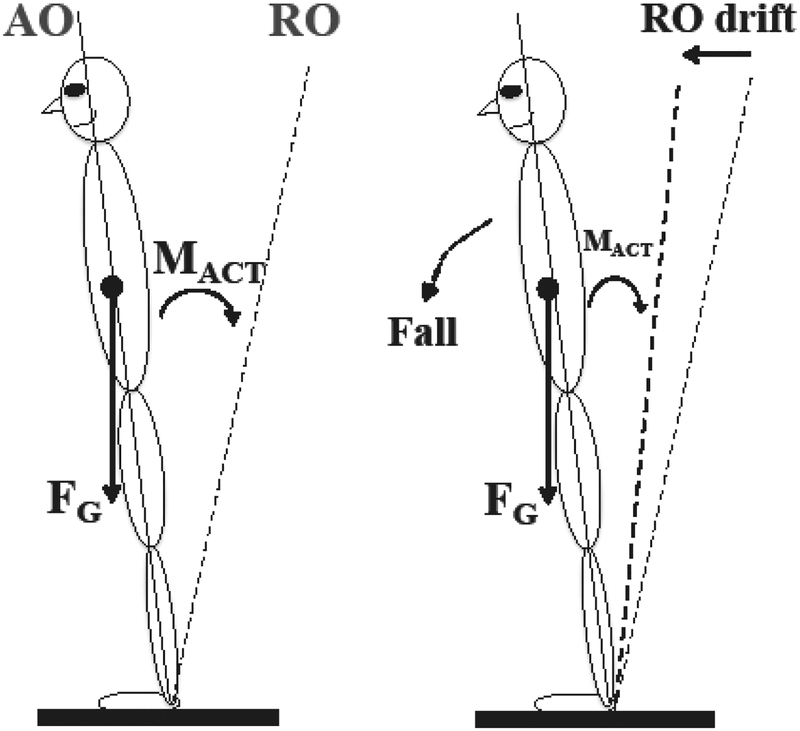
The Rm-Tr decomposition fits the theory of the neural control of posture and movement with setting referent coordinates (RCs) for the involved effectors (Feldman 2015; Latash and Zatsiorsky 2016; Mullick et al. 2018). According to this theory, the controller specifies RC time profiles for effectors at the task-specific level (e.g., for the whole body) and then a sequence of few-to-many (abundant, Latash 2012) transformations leads to RCs at the levels of extremities, joints, and muscles. At the single-muscle level, RC is equivalent to threshold of the stretch reflex (λ) as postulated by the classical equilibrium-point hypothesis (Feldman 1966, 1986). During quiet standing with the body center of gravity projecting in front of the ankle joints, the trunk referent orientation (RO, a specific case of RC) has to be behind the actual trunk orientation, which allows generating the moment of force acting against the moment produced by gravity (Fig. 1).

Figure 1.

Figure 1

Open in a new tab

An illustration of the control of vertical posture with setting referent orientation (RO) of the body. Left: When RO deviates from actual body orientation (AO), active moment of force (MACT) counteracts the moment produced by the gravity force (FG). Right: A drift of RO toward AO leads to a drop in MACT, and the body is expected to fall.

A number of recent studies have shown that, when a person performs a task, which requires the RC and the actual coordinate of the effector to differ (e.g., during pressing with a finger against a stop), a slow drift of RC toward the actual coordinate is observed with characteristic times on the order of 10–20 s (Vaillancourt and Russell 2002; Wilhelm et al. 2013; Reschechtko et al. 2014, 2017; Ambike et al. 2015, 2016). Slow drifts have also been reported for whole-body voluntary rhythmical sway performed by standing persons (Rasouli et al. 2017). These phenomena have been interpreted as consequences of RC-back-coupling (cf. Martin et al. 2009; Zhou et al. 2015), a natural process moving the system toward states with lower potential energy.

The idea of RC-back-coupling suggests that, during quiet standing, a RO drift can be observed towards the actual body orientation. A direct consequence of this prediction is that there should be a drop in the actively produced moment of force and – unless these effects are corrected – a protective step or even a fall when the COP projects outside the support area (see Fig. 1). Naturally, the system of postural control does not allow this to happen and acts to correct such RO drifts when they reach a certain threshold or even over-compensates leading to a COP drift in the opposite direction (Rasouli et al. 2017). Given the reported time constants of RC drift, COP deviations in the anterior-posterior direction (COPAP) over periods of 10–20 s can be expected with a large signal power in the frequency range about 0.05 – 0.1 Hz, below the typical values of peak power for Rm and Tr (cf. Zatsiorsky and Duarte 2000). Note that, in an earlier study, Duarte and Zatsiorsky (1999) reported very slow COP shifts (addressed by the authors as “drifting”), but during standing over much longer time intervals.

In this study, we explored this prediction. To facilitate the natural RO drift, we used two manipulations to reduce potential COP-stabilizing effects of the natural visual cues. In the first, we asked the subjects to perform the task of quiet standing while matching a visual target on the monitor with a signal reflecting an irrelevant variable, the level of activation of a finger flexor muscle (see Methods). In the second, the subjects stood with eyes closed. Control conditions involved standing with eyes open and a typical dual-task condition, standing while counting backwards, which is known to affect sway characteristics (Andersson et al. 2002; Wollesen et al. 2016). Our main hypothesis was that the slow COPAP drifts would be large during standing with eyes closed and with vision focused on producing a required level of the wrist flexor muscle activation, and the drift would be reduced during standing with open eyes, with no additional effects of counting backwards.

Methods

Subjects

Three women and six men (22.7 ± 3.3 years old, body mass 66.1 ± 8.5 kg, height 1.7 ± 0.1 m; mean ± SD) participated in this study. All subjects were free of neurological and musculo-skeletal disorders. They were right-leg dominant as defined by the test of kicking a ball. Prior to the testing, the participants gave informed consent approved by the Office for Research Protections of the Pennsylvania State University.

Apparatus

A force platform (AMTI, OR-6, Watertown, MA, USA), was used to record three force (FX, FY, and FZ) and three moment components (MX, MY, and MZ) along the anterior-posterior (X), medio-lateral (Y) and vertical (Z) directions with respect to the subject’s body. A 21-inch monitor located at the eye level about 1 m away from the subject displayed real-time visual feedback in some conditions. The feedback on the flexor digitorum superficialis (FDS) activation level (FDS EMG) was showed as a bar moved upwards by an increase in muscle activation (see later). A customized LabView program was used to collect the data at 1 kHz with the 16-bit resolution (PCI-6225, National Instruments Corp., Austin, TX, USA).

Procedures

In each trial, the subject was asked to stand quietly for 65 s with the arms crossed over the chest and the fingertips placed on the shoulders. The feet were parallel to each other at the hip width, and the foot position was marked on top of the platform for consistency across trials. The following single-task conditions were used: Standing with eyes open (EO) and closed (EC), There were also two dual-task conditions: standing while performing a mental subtraction task (MATH) and while matching the FDS EMG signal to the target (MATCH). In the MATH task, the subjects started from a random three-digit number between 400 and 500 and counted backwards by subtracting seven at each step (speaking up the numbers); this task was performed with eyes open (MATH_EO) and eyes closed (MATH_EC).

In the MATCH condition, visual feedback on the rectified FDS activation level was provided after filtering with a moving average 250-ms window. The subjects were asked to press with their right hand on the left shoulder to match the target corresponding to twice the FDS activation level seen during quiet standing. The single-task conditions (EO and EC) were performed both at the beginning and at the end of the experiment. The dual-task conditions (MATH_EO, MATH_EC, and MATCH) were performed three times each. There were three blocks of conditions: single-task, dual-task, and single-task. Within each block, the order of the conditions was randomized. Three practice trials were performed prior to each of the dual-task conditions. To minimize fatigue, 30-s and 1-min rest periods were provided between trials and conditions, respectively.

Data processing

All calculations were done using a customized MATLAB R2016a program (Mathworks Corp., Natick, MA, USA). The force platform signals were low-pass filtered at 10 Hz with a 4-th order, zero-lag Butterworth filter. The first 5 s of the data in each trial were removed, and the rest of the data over 60 s were used for further analysis.

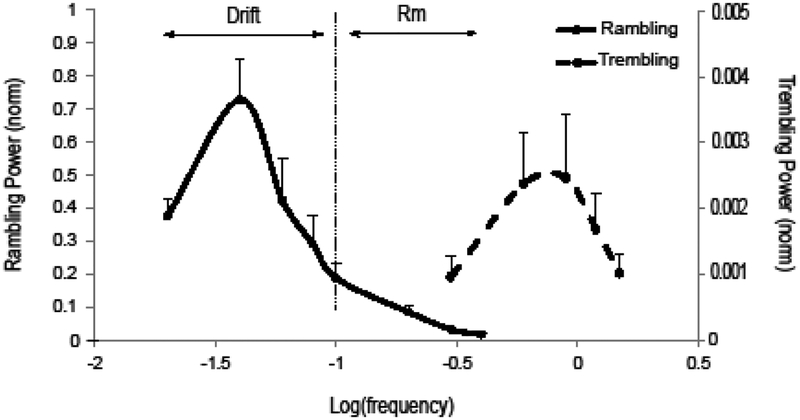
Decomposition of the COPAP signal into Rm and Tr was done following the procedures described by Zatsiorsky and Duarte (1999, 2000). In brief, we identified instantaneous equilibrium points (IEPs), defined as COPAP coordinates when FAP was zero. Rm was estimated as the interpolation of the IEP coordinates with a cubic spline, whereas Tr was estimated as the difference between the COP and Rm trajectories. The first and last one-second intervals of Rm and Tr were removed to avoid edge effects. The power spectrum analysis of COPAP, Rm and Tr was done for each trial. Further, each power signal was normalized by the COPAP peak power. We defined Drift as the Rm within the {0; 0.1 Hz} interval, Rm within the {0.1; 0.4 Hz} interval, and Tr within the {0.2; 1.5 Hz} interval (see Fig. 3 in Results).

Figure 3.

Figure 3

Open in a new tab

The power of the sway components (averaged across subjects data with standard error bars) for the rambling (Rm) and Trembling (Tr). The low-frequency Rm (< 0.1 Hz) has been designated as Drift. The values were normalized by the peak COP power for each individual subject. Note the different scales for the Rm and Tr signals.

Statistics

The following statistical tests were performed using SPSS (IBM Corp., Armonk, NY, USA): (1) To test the effects of closing eyes on the sway components, two-way repeated-measure ANOVA over single-task conditions was used, Vision (EO and EC) × Component (Drift, Rm, and Tr); (2) To test the effects of dual-tasking on the sway components, we used a three-way repeated-measure ANOVA: Task (EO and MATH) × Vision × Component, (3) To test the effects of FDS EMG matching (MATCH) on the sway components a two-way repeated-measure ANOVA was used, Condition (EO and MATCH) × Component, and (4) To compare the two dual-task conditions (MATH and MATCH) on the sway components, we used a two-way repeated-measure ANOVA, Task (MATH_EO and MATCH) × Component.

We checked the assumptions of normality and sphericity before applying parametric statistics. Log-transformation were used to satisfy the normality assumptions in cases of violations of normality, and the Greenhouse-Geisser procedure was used in case of violations of sphericity. When necessary, pairwise contrasts with Bonferroni corrections were carried out. The significance level was set at 0.05 and adjusted as needed when Bonferroni corrections were used.

Results

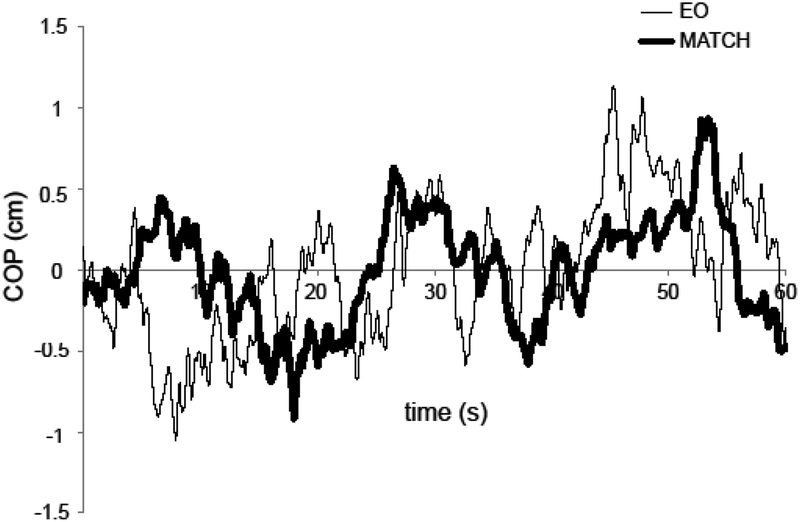
Typical COPAP time series during standing with eyes open (EO, thin trace) and during matching the target with the FDS EMG signal (MATCH) are illustrated in Figure 2. Note that there is a large-amplitude, slow COP change in the MATCH condition, but not in the EO condition. Averaged across subjects power spectra of Rm and Tr are shown in Figure 3 for the EO condition. Note the different scales for Rm and Tr in Figures 2 and 3. Based on earlier studies, reporting typical Rm frequency characteristics (Zatsiorsky and Duarte 2000), we considered Rm within the very slow range (under 0.1 Hz) as a separate component, Drift.

Figure 2.

Figure 2

Open in a new tab

Examples of the center of pressure (COP) time series for a representative subject performing the task of quiet standing with eyes open (thin line, EO) and while matching the EMG of the finger flexors to a target (thick line, MATCH). Note the low-frequency cycles obvious in MATCH, not in EO.

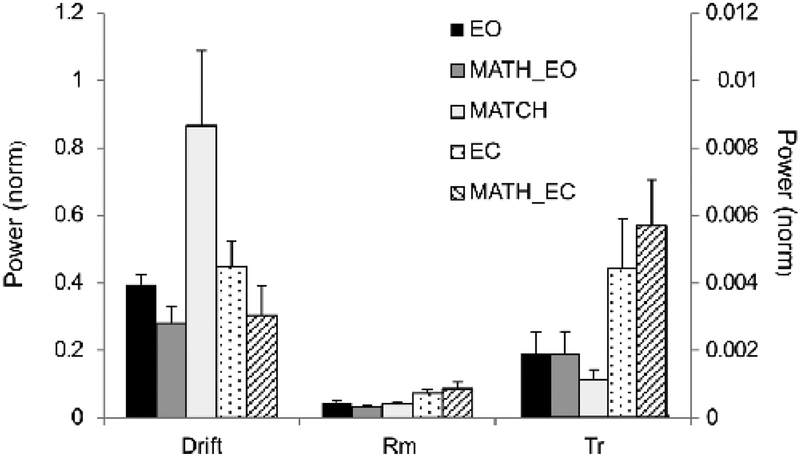
Averaged across subjects power of each of the three sway components for each of the five conditions is shown in Figure 4. Note the very large Drift component in the MATCH condition (the white bar) with no similar effect for the EC condition (the dotted bar).

Figure 4.

Figure 4

Open in a new tab

The power magnitudes for the three sway components across the five conditions. Note the large Drift value for the MATCH condition without similar effects on Rm and Tr. Note also the effects of closing eyes, particularly obvious for Rm and Tr and modest, if any, for Drift. The scales for the Rm and Tr signals are different. Averaged across subjects data with standard error bars are shown.

Standing with eyes closed resulted in larger signal power for all three sway components: Drift, Rm, and Tr, although the effect on Drift was relatively small. A two-way ANOVA showed main effects of both Vision: F[1, 8] = 13.5; p < 0.01 and Component: F[2, 16] = 27.4; p < 0.01). The effect of component reflected Drift > Rm > Tr confirmed by pairwise contrasts (p < 0.05). There was also a close to significant interaction effect (p = 0.068).

The dual-task MATH condition led to a decrease in Drift with no consistent effects on Rm and Tr. Effects of Vision (F[1, 8] = 15.8; p < 0.01) and Component (F[2, 16] = 66.9; p < 0.01) were confirmed in ANOVA involving the MATH condition. Also, there were significant interactions Vision × Component (F[2, 16] = 11.5; p < 0.01) and Task × Component (F[2, 16] = 4.7; p < 0.05). The latter reflected smaller Drift for MATH compared to single-task conditions (EO and EC) without such effects on Rm and Tr.

When the subjects matched the FDS EMG signal to the target on the screen (MATCH), they showed an increase in Drift and a drop in Tr, without a change in Rm. Two-way ANOVA confirmed the main effect of Component (F[2, 16] = 105.4; p < 0.01) and a significant Condition × Component interaction (F[2, 16] = 15.4; p < 0.01). The interaction reflected the larger Drift and smaller Tr in the MATCH condition compared to the EO condition.

Direct comparison between the two dual-task conditions, MATH_EO and MATCH, showed a main effect of Component (F[2, 16] = 98.3; p < 0.01) and a Task × Component interaction (F[2, 16] = 12.4; p < 0.01), reflecting larger Drift in the MATCH condition compared to that in the MATH_EO condition.

Discussion

Our main hypothesis formulated in the Introduction has been supported for one of the conditions (MATCH) and falsified for the other one (EC). Indeed, we expected the largest slow COP drift magnitudes during standing with eyes closed and with visual feedback on FDS EMG. The experiment showed no significant effects of closing the eyes on the COP drift characteristics, and an increase in the drift component under visual feedback on FDS EMG. This effect was not due to dual-tasking, because another typical dual-task condition involving quiet standing while counting backwards (cf. Andersson et al. 2002; Wollesen et al. 2016) led to an opposite effect, namely a drop in the drift compared to the single-task conditions. Further, we consider these results within the theory of control of posture and movement with referent coordinates for the effectors (Feldman 2015).

Control of vertical posture with changes in body referent coordinates

Several recent studies have produced results compatible with the idea of control of vertical posture with changes in referent body orientation (RO) (Mullick et al. 2018; Yamagata et al. 2018; Zhang et al. 2018). This idea is a particular example of a more general theory, which considers the neural control of posture and movement as the process of setting time profiles of referent coordinates (RC) for the involved effectors (Latash 2010; Feldman 2015). RC(t) functions are used by the CNS as tools leading to desired motor effects based on memory and sensory feedback. This is done without computations that would link neural variables to peripheral variables such as muscle activations, forces, and displacements. RC can be expressed in spatial Cartesian coordinates as well as in angular coordinates; then, it is addressed as referent orientation (RO) (Latash et al. 2010; Mullick et al. 2018).

Within this general framework, shifts in the body RO lead to changes in the equilibrium states of the body in the field of gravity reflected in the Rm component of the sway (Zatsiorsky and Duarte 2000). In contrast, Tr is affected by the neural control process only indirectly, e.g., as a result of associated changes in the apparent stiffness of the body joints (cf. Latash and Zatsiorsky 1993; Latash 2018) following changes in muscle activation patterns. A number of studies have corroborated different origins of Rm and Tr by showing differential effects on these two sway components of such factors as visual feedback (Danna-dos-Santos et al. 2008), aging (Sarabon et al. 2013; Degani et al. 2017), typical and atypical development (Monteiro Ferronato and Barela 2011; Speedtsberg et al. 2017), neurological disorders (Shin et al. 2011; Shin and Sosnoff 2017), postural instability (Mochizuki et al. 2006), bedrest (Sarabon and Rosker 2012), ballet dancing (Michalska et al. 2018), and cannabis use (Bolbecker et al. 2018). Rm is a non-stationary process (Bottaro et al. 2005), and the original studies had used de-trending or high-pass filtering before the Rm-Tr decomposition process (e.g., Zatsiorsky and Duarte 2000; Sarabon et al. 2013). Some of these procedures could effectively remove the very slow COPAP drift observed in our experiment. We view this drift as a third sway component with the origin different from those of both Rm and Tr.

RC-back-coupling as a potential mechanism leading to postural drift

One of the unusual predictions of the scheme of control with RC is unintentional drift in performance when RC is kept away from the actual coordinate of the effector by external forces. Such drifts in performance have been interpreted as consequences of RC drifts reflecting the natural tendency of all physical systems to move toward states with lower potential energy (Latash 2017). Performance drifts have been documented across a variety of tasks including accurate force production by fingers (Vaillancourt and Russell 2002; Wilhelm et al. 2014; Ambike et al. 2015) and accurate positioning of the hand (Zhou et al. 2014, 2015). A few recent studies have confirmed and quantified RC drifts during finger force production in the absence of visual feedback (Reschechtko and Latash 2017; Ambike et al. 2018), thus providing direct support for the RC-back-coupling concept. So far, only one study reported findings interpreted as consequences of RO drift during whole-body voluntary sway tasks (Rasouli et al. 2017).

The idea of RC-back-coupling may be seen as a particular realization of the principle of minimization of activity of motoneurons as suggested recently by Feldman (2018). Indeed, the generalization of the idea of control of movements with shifts in threshold of the stretch reflex (Feldman 1986, 2015) defines a condition for muscle activation as the one when referent body configuration (RO for the example of standing, see Fig. 1) differs from its actual configuration. Commonly, when this happens, the body moves toward RC thus minimizing the difference between the two and, as a result, minimizing muscle activation. In certain conditions, when external forces do not allow body to move toward RC, RC starts to move toward the actual body orientation also contributing to minimization of muscle activation. Note that, unlike other applications of optimization principles in motor control (Prilutsky and Zatsiorsky 2002; Todorov 2004; Diedrichsen et al. 2010), in this example, muscle activation is minimized by physical (including physiological) processes, without assuming any computations within the central nervous system.

We interpret the Drift component in our study as a consequence of an unintentional slow RO drift towards the actual body orientation, a specific example of RC-back-coupling. When the COPAP drift reached a threshold magnitude detected by the subject with the help of available sensory signals, a postural correction was introduced. The drift continued until reaching the threshold magnitude again, followed by another postural correction, and so on (see Figure 2).

When the subjects in our experiment looked at external objects, many vertical and horizontal cues were available, likely helping to avoid the COP drift and/or correct it quickly and effectively. This ability was unaffected by dual-tasking since the MATH condition showed lower Drift compared to the similar single-task conditions. When vision was used for an irrelevant task (MATCH), Drift was corrected only after reaching a relatively large magnitude. Note that the exponential nature of the drift (cf. Zhou et al. 2014; Ambike et al. 2015) resulted the relatively high overall power of the signal as a consequence of the drift being corrected at discrete time moments and reset.

It seems counter-intuitive that Drift was relatively small during standing with eyes closed (see Fig. 4, EC). In the EC condition, the subjects had to rely on non-visual sensory signals, which are less effective in preventing large COP deviations (in our study Rm and Tr were significantly larger in the EC condition compared to the EO one, see Fig. 4). This could lead to longer COP drifts and fewer corrections leading to the relatively modest Drift power.

Concluding comments

We demonstrate very slow COPAP drift (at frequencies below 0.1 Hz), which showed particularly large power in conditions with visual feedback on an irrelevant variable. This third component of sway (in addition to Rm and Tr) is interpreted as a consequence of an unintentional drift of body RO toward its actual orientation. This study represents a step toward understanding postural sway and its components within a physical theory on the control of posture and movement.

ACKNOWLEDGMENTS

The study was in part supported by NIH grant NS095873.

REFERENCES

  1. Ambike S, Mattos D, Zatsiorsky VM, Latash ML (2016) Unsteady steady-states: Central causes of unintentional force drift. Exp Brain Res 234: 3597–3611. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ambike S, Mattos D, Zatsiorsky VM, Latash ML (2018) Systematic, unintended drifts in the cyclic force produced with the fingertips. Motor Control 22: 82–99. [DOI] [PubMed] [Google Scholar]
  3. Ambike S, Zatsiorsky VM, Latash ML (2015) Processes underlying unintentional finger force changes in the absence of visual feedback. Exp Brain Res 233: 711–721. [DOI] [PubMed] [Google Scholar]
  4. Andersson G, Hagman J, Talianzadeh R, Svedberg A, Larsen HC (2002) Effect of cognitive load on postural control. Brain Res Bull 58: 135–139. [DOI] [PubMed] [Google Scholar]
  5. Bolbecker AR, Apthorp D, Martin AS, Tahayori B, Moravec L, Gomez KL, O’Donnell BF, Newman SD, Hetrick WP (2018) Disturbances of postural sway components in cannabis users. Drug Alcohol Depend 190: 54–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bottaro A, Casadio M, Morasso PG, Sanguineti V (2005) Body sway during quiet standing: is it the residual chattering of an intermittent stabilization process? Hum Mov Sci 24: 588–615 [DOI] [PubMed] [Google Scholar]
  7. Danna-Dos-Santos A, Degani AM, Zatsiorsky VM, Latash ML (2008) Is voluntary control of natural postural sway possible? J Mot Behav 40: 179–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Degani AM, Leonard CT, Danna-Dos-Santos A (2017) The effects of early stages of aging on postural sway: A multiple domain balance assessment using a force platform. J Biomech. 64: 8–15. [DOI] [PubMed] [Google Scholar]
  9. Diedrichsen J, Shadmehr R, Ivry RB (2010) The coordination of movement: optimal feedback control and beyond. Trends Cogn Sci 14: 31–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Duarte M, Zatsiorsky VM (1999) Patterns of center of pressure migration during prolonged unconstrained standing. Motor Control 3: 12–27. [DOI] [PubMed] [Google Scholar]
  11. Feldman AG (1966) Functional tuning of the nervous system with control of movement or maintenance of a steady posture. II. Controllable parameters of the muscle. Biophysics 11: 565–578 [Google Scholar]
  12. Feldman AG (1986) Once more on the equilibrium-point hypothesis (λ-model) for motor control. J Mot Behav 18: 17–54. [DOI] [PubMed] [Google Scholar]
  13. Feldman AG (2015) Referent control of action and perception: Challenging conventional theories in behavioral science. Springer, NY. [Google Scholar]
  14. Feldman AG (2018) Indirect, referent control of motor actions underlies directional tuning of neurons. J Neurophysiol (in press) doi: 10.1152/jn.00575.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Latash ML (2010) Motor synergies and the equilibrium-point hypothesis. Motor Control 14: 294–322. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Latash ML (2012) The bliss (not the problem) of motor abundance (not redundancy). Exp Brain Res 217: 1–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Latash ML (2017) Biological movement and laws of physics. Motor Control 21: 327–344. [DOI] [PubMed] [Google Scholar]
  18. Latash ML, Friedman J, Kim SW, Feldman AG, Zatsiorsky VM (2010) Prehension synergies and control with referent hand configurations. Exp Brain Res 202: 213–229. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Latash ML, Zatsiorsky VM (1993) Joint stiffness: Myth or reality? Hum Move Sci 12: 653–692. [Google Scholar]
  20. Latash ML, Zatsiorsky VM (2016) Biomechanics and Motor Control: Defining Central Concepts. Academic Press: New York, NY. [Google Scholar]
  21. Martin V, Scholz JP, Schöner G (2009) Redundancy, self-motion, and motor control. Neural Comput 21:1371–1414 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Michalska J, Kamieniarz A, Fredyk A, Bacik B, Juras G, Słomka KJ (2018) Effect of expertise in ballet dance on static and functional balance. Gait Posture 64: 68–74. [DOI] [PubMed] [Google Scholar]
  23. Mochizuki L, Duarte M, Amadio AC, Zatsiorsky VM, Latash ML (2006) Changes in postural sway and its fractions in conditions of postural instability. J Appl Biomech 22: 51–66. [DOI] [PubMed] [Google Scholar]
  24. Monteiro Ferronato PA, Barela JA (2011) Age-related changes in postural control: rambling and trembling trajectories. Motor Control. 15: 481–93. [DOI] [PubMed] [Google Scholar]
  25. Mullick AA, Turpin NA, Hsu SC, Subramanian SK, Feldman AG, Levin MF (2018) Referent control of the orientation of posture and movement in the gravitational field. Exp Brain Res. 236: 381–398. [DOI] [PubMed] [Google Scholar]
  26. Prilutsky BI, Zatsiorsky VM (2002) Optimization-based models of muscle coordination. Exer Sport Sci Rev 30: 32–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Rasouli O, Solnik S, Furmanek MP, Piscitelli D, Falaki A, Latash ML (2017) Unintentional drifts during quiet stance and voluntary body sway. Exp Brain Res 235: 2301–2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Reschechtko S, Zatsiorsky VM, Latash ML (2014) Stability of multi-finger action in different spaces. J Neurophysiol 112: 3209–3218. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Reschechtko S, Latash ML (2017) Stability of hand force production: I. Hand level control variables and multi-finger synergies. J Neurophysiol 118: 3152–3164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Sarabon N, Rosker J (2013) Effect of 14 days of bed rest in older adults on parameters of the body sway and on the local ankle function. J Electromyogr Kinesiol. 23: 1505–1511. [DOI] [PubMed] [Google Scholar]
  31. Sarabon N, Panjan A, Latash ML (2013) The effects of aging on the rambling and trembling components of postural sway: Effects of motor and sensory challenges. Gait Posture 38: 637–642. [DOI] [PubMed] [Google Scholar]
  32. Shin S, Motl RW, Sosnoff JJ (2011) A test of the rambling and trembling hypothesis: multiple sclerosis and postural control. Motor Control 15: 568–579. [DOI] [PubMed] [Google Scholar]
  33. Shin S, Sosnoff JJ (2017) Spinal cord injury and seated postural control: A test of the rambling and trembling hypothesis. Motor Control 21: 443–456. [DOI] [PubMed] [Google Scholar]
  34. Speedtsberg MB, Christensen SB, Andersen KK, Bencke J, Jensen BR, Curtis DJ (2017) Impaired postural control in children with developmental coordination disorder is related to less efficient central as well as peripheral control. Gait Posture 51: 1–6. [DOI] [PubMed] [Google Scholar]
  35. Todorov E (2004). Optimality principles in sensorimotor control. Nature Neurosci 7: 907–915. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Vaillancourt DE, Russell DM (2002) Temporal capacity of short-term visuomotor memory in continuous force production. Exp Brain Res 145:275–285 [DOI] [PubMed] [Google Scholar]
  37. Wilhelm L, Zatsiorsky VM, Latash ML (2013) Equifinality and its violations in a redundant system: Multi-finger accurate force production. Journal of Neurophysiology 110: 1965–1973. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Winter DA, Prince F, Frank JS, Powell C, Zabjek KF (1996) Unified theory regarding A/P and M/L balance in quiet stance. J Neurophysiol 75: 2334–2343. [DOI] [PubMed] [Google Scholar]
  39. Wollesen B, Voelcker-Rehage C, Regenbrecht T, Mattes K (2016) Influence of a visual-verbal Stroop test on standing and walking performance of older adults. Neuroscience 318:166–77. [DOI] [PubMed] [Google Scholar]
  40. Yamagata M, Falaki A, Latash ML (2018) Effects of voluntary agonist-antagonist co-activation on stability of vertical posture. Motor Control (in press). [DOI] [PubMed] [Google Scholar]
  41. Zatsiorsky VM, Duarte M (1999) Instant equilibrium point and its migration in standing tasks: rambling and trembling components of the stabilogram. Motor Control 1999 3: 28–38. [DOI] [PubMed] [Google Scholar]
  42. Zatsiorsky VM, Duarte M (2000) Rambling and trembling in quiet standing. Motor Control 4: 185–200. [DOI] [PubMed] [Google Scholar]
  43. Zhang L, Feldman AG, Levin MF (2018) Vestibular and corticospinal control of human body orientation in the gravitational field. J Neurophysiol 2018 September 12. doi: 10.1152/jn.00483.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Zhou T, Solnik S, Wu Y-H, Latash ML (2014) Unintentional movements produced by back-coupling between the actual and referent body configurations: Violations of equifinality in multi-joint positional tasks. Exp Brain Res 232: 3847–3859. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Zhou T, Zhang L, Latash ML (2015) Intentional and unintentional multi-joint movements: Their nature and structure of variance. Neurosci 289: 181–193. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES