Optimized dual-time-window protocols for quantitative [¹⁸F]flutemetamol and [¹⁸F]florbetaben PET studies

Abstract

Background

A long dynamic scanning protocol may be required to accurately measure longitudinal changes in amyloid load. However, such a protocol results in a lower patient comfort and scanning efficiency compared to static scans. A compromise can be achieved by implementing dual-time-window protocols. This study aimed to optimize these protocols for quantitative [¹⁸F]flutemetamol and [¹⁸F]florbetaben studies.

Methods

Rate constants for subjects across the Alzheimer’s disease spectrum (i.e., non-displaceable binding potential (BP_ND) in the range 0.02–0.77 and 0.02–1.04 for [¹⁸F]flutemetamol and [¹⁸F]florbetaben, respectively) were established based on clinical [¹⁸F]flutemetamol (N = 6) and [¹⁸F]florbetaben (N = 20) data, and used to simulate tissue time-activity curves (TACs) of 110 min using a reference tissue and plasma input model. Next, noise was added (N = 50) and data points corresponding to different intervals were removed from the TACs, ranging from 0 (i.e., 90–90 = full-kinetic curve) to 80 (i.e., 10–90) minutes, creating a dual-time-window. Resulting TACs were fitted using the simplified reference tissue method (SRTM) to estimate the BP_ND, outliers (≥ 1.5 × BP_ND max) were removed and the bias was assessed using the distribution volume ratio (DVR = BP_ND + 1). To this end, acceptability curves, which display the fraction of data below a certain bias threshold, were generated and the area under those curves were calculated.

Results

[¹⁸F]Flutemetamol and [¹⁸F]florbetaben data demonstrated an increased bias in amyloid estimate for larger intervals and higher noise levels. An acceptable bias (≤ 3.1%) in DVR could be obtained with all except the 10–90 and 20–90-min intervals. Furthermore, a reduced fraction of acceptable data and most outliers were present for these two largest intervals (maximum percentage outliers 48 and 32 for [¹⁸F]flutemetamol and [¹⁸F]florbetaben, respectively).

Conclusions

The length of the interval inversely correlates with the accuracy of the BP_ND estimates. Consequently, a dual-time-window protocol of 0–30 and 90–110 min (=maximum of 60 min interval) allows for accurate estimation of BP_ND values for both tracers.

[¹⁸F]flutemetamol: EudraCT 2007-000784-19, registered 8 February 2007, [¹⁸F]florbetaben: EudraCT 2006-003882-15, registered 2006.

Electronic supplementary material

The online version of this article (10.1186/s13550-019-0499-4) contains supplementary material, which is available to authorized users.

Background

Deposition of amyloid-beta (Aβ) plaques in the brain is the earliest in vivo measurable hallmark in the development of Alzheimer’s disease (AD), which is the most common type of dementia [1–3]. Therefore, visualization of Aβ deposits in vivo is essential for improving early diagnosis and monitoring treatment effects [4]. To this end, various positron emission tomography (PET) amyloid tracers have been developed [5]. Among those, fluorine-18 (18F)-labeled tracers approved by the European Medicines Agency (EMA)/Food and Drug Administration (FDA) are of special interest for clinical trials due to their relatively long half-life t_1/2 = 109.8 min compared to [¹¹C]PiB (Carbon-11 Pittsburgh Compound B) and commercial availability [5, 6].

In addition to visualization, amyloid PET allows for quantification of underlying physiological processes, such as the level of Aβ plaque burden [7–10]. For diagnostic purposes, a static scan acquired at pseudo-equilibrium, using a tracer-specific approved method, has been deemed sufficient in combination with visual assessment of the images. In research settings, this simplified protocol is commonly used to calculate the standardized uptake value ratio (SUVR) [5]. SUVR, however, is only a semi-quantitative parameter that is known to be affected by both scanning time window and (changes in) blood flow [11, 12]. Given this dependency, full quantification using pharmacokinetic modeling may be required to obtain higher overall sensitivity for measuring longitudinal changes (e.g., for monitoring disease progression or treatment response), especially during the early stages of the disease when amyloid is still accumulating. Pharmacokinetic modeling, however, requires a dynamic scanning protocol, which can last for up to 2 h depending on the actual tracer. These long acquisition protocols result in lower patient comfort and lesser efficient use of both scanner and tracer batch, in addition to an increased risk of motion artifacts. Dynamic data acquisition in a dual-time-window protocol (also called “coffee-break” protocol), however, can be used to reduce overall scanning time, in which data are acquired separately for early and late phases. Such a protocol provides a resting period for the patient and, when long enough, may also allow for interleaved scanning protocols, thereby optimizing tracer batch and scanner usage (i.e., costs), while maintaining a high quantitative accuracy.

So far, some studies have used a dual-time-window protocol using static acquisition of amyloid-PET data. An early scan (i.e., 0–10 min p.i.) was proposed in addition to the (standard) late static scan, as it has been reported that the early scan may provide information on metabolism and neuronal injury, possibly circumventing the need for additional [¹⁸F]FDG imaging [12–16]. Recently, Bullich and colleagues demonstrated that the non-displaceable binding potential (BP_ND) obtained using a dual-time-window acquisition protocol (0–30 and 120–140 min p.i.) correlated well with BP_ND obtained using a full dynamic acquisition protocol of 140 min [17]. This [¹⁸F]florbetaben study, however, did not report details about different resting periods, nor did it assess the robustness of the dual-time-window protocol for subjects across the AD spectrum and for different noise levels (e.g., for regions of different sizes).

The purpose of the present simulation study was to define optimal dual-time-window acquisition protocols for [¹⁸F]florbetaben and [¹⁸F]flutemetamol, both in terms of patient comfort and throughput, while maintaining high quantitative accuracy. These simulations were focused on early stages of the disease, given the potential value of amyloid imaging to guide interventions aimed at secondary prevention of AD dementia.

Methods

Subjects and PET data

[¹⁸F]flutemetamol whole blood input curves, metabolite-corrected arterial plasma input curves, and time-activity curves (TACs) from 12 volumes of interest (VOIs) of three healthy controls and three probable AD subjects were obtained from Heurling et al. and Nelissen et al. [7, 18]. [¹⁸F]florbetaben metabolite-corrected and metabolite-uncorrected plasma input curves together with whole blood samples and TAC data from 13 VOIs of 10 healthy controls and 10 AD subjects were obtained from Becker et al. [8].

Kinetic models for BP_ND estimation

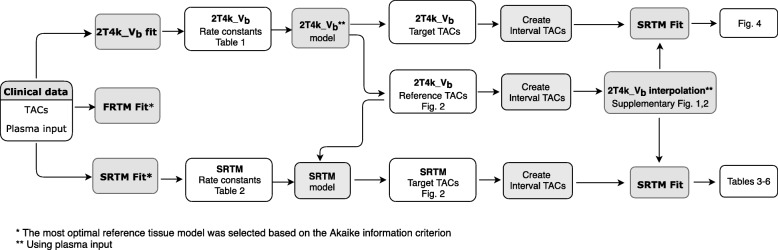
It has been shown that the reversible two-tissue compartment model (4 rate constants) with additional blood volume fraction parameter (2T4k_V_b) is the optimal plasma input model for describing both [¹⁸F]flutemetamol and [¹⁸F]florbetaben kinetics [8, 18]. In addition, several non-invasive reference tissue-based approaches have also been used: the simplified reference tissue model (SRTM) and its basis function approach (receptor parametric mapping, RPM), the multilinear reference tissue method (MRTM), and reference Logan [19–22]. In the present study, the 2T4k_V_b, SRTM and the full reference tissue model (FRTM [23]) were examined (Fig. 1 provides an overview of the kinetic models used during each step of the analysis). The main aim, however, was to verify the applicability of a reference tissue model approach given its applicability for large clinical trials.

Fig. 1.

Overview of the kinetic models used during each step of the analysis

Kinetic parameters for TAC simulations

Both reported whole blood and metabolite-corrected arterial plasma input curves were used for [¹⁸F]flutemetamol analysis [24]. For [¹⁸F]florbetaben, continuous whole blood curves were generated by scaling the continuous (non-metabolite-corrected) plasma curves using discrete whole blood samples. Subsequently, all cortical and cerebellar TACs of all subjects were analyzed using the 2T4k_V_b model, SRTM, and FRTM [19, 23, 25]. The Akaike information ciriterion was used to determine which reference tissue method best described the kinetics of the tracer [26]. Both the optimal reference tissue model and the 2T4k_V_b model were then used for estimating rate constants.

Finally, from the rate constants of the cortical regions (target tissue consisting of anterior and posterior cingulate, frontal, parietal, and lateral and medialtemporal cortex) and cerebellum gray matter (reference tissue), mean and standard deviations were calculated and used to establish the range of rate constants for composite cortical and reference tissue regions. The resulting rate constants for the 2T4k_V_b and reference tissue model can be found in Tables 1 and 2, respectively.

Table 1.

Pharmacokinetic parameters for simulating TACs using 2T4k_V_b

	[18F]flutemetamol		[18F]florbetaben
Level	BPND	k 3	BPND	k 3
BPND I	0.380	0.008	1.000	0.010
BPND II	0.635	0.013	1.500	0.015
BPND III	0.890	0.018	2.000	0.020
BPND IV	1.145	0.023	2.500	0.025
BPND V	1.400	0.028	3.000	0.030
	${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{NS}}$	k3	${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{NS}}$	k 3
Reference	0.350	0.018	0.950	0.007

BP_ND binding potential of target tissue, V_b had a constant value of 0.05. [¹⁸F]flutemetamol target tissue: K₁ = 0.248, k₂ = 0.08, reference tissue: K₁ = 0.32, k₂ = 0.103. [¹⁸F]florbetaben target tissue: K₁ = 0.226, k₂ = 0.069, reference tissue: K₁ = 0.25, k₂ = 0.076

Table 2.

Pharmacokinetic parameters for simulating TACs using SRTM

	[18F]flutemetamol	[18F]florbetaben
Level	BPND	BPND
BPND I	0.020	0.021
BPND II	0.208	0.277
BPND III	0.397	0.532
BPND IV	0.585	0.787
BPND V	0.774	1.042

BP_ND binding potential of target tissue, [¹⁸F]flutemetamol: R₁ = 0.775, k₂ = 0.02, [¹⁸F]florbetaben: R₁ = 0.904, k₂ = 0.03

TAC simulations

Plasma input-generated TACs

Noiseless target and reference tissue TACs of 110 min duration were simulated (see Table 1 for kinetic parameters used) using the 2T4k_V_b model to assess the bias in BP_ND estimates when fitting these TACs with SRTM. The 2T4k_V_b model was also used to generate a reference tissue TAC for the SRTM simulations described in the next section.

SRTM-generated TACs

Using SRTM, tissue target TACs of 110 min duration were simulated for the range of BP_ND values observed clinically (50 TACs per BP_ND, see Table 2 for kinetic parameters used), along the AD continuum. Various levels of typical PET noise were added to these target TACs only (coefficient of variation (COV) of 1, 2, and 5%, respectively) according to the variance model used by Yaqub et al., creating 50 TACs per noise level for each BP_ND [27]:

$${\sigma }_1^2=\alpha \bullet \mathrm{dcf}\bullet \mathrm{dcf}\frac{T}{L^2}$$ 1

where ${\sigma }_1^2$ is the variance for each frame, calculated using the whole scanner true counts T, dcf is the decay correction factor, L is the frame length, and α is a proportionality constant signifying the variance level. In practice, most clinical TACs corresponded best with simulated TACs with 1 or 2% noise added, while TACs with 5% noise only corresponded with very small regions with a low BP_ND [7, 8].

Dual-time-window protocols

The “late frame” acquisition window of 90–110 min (used within Europe) was left intact, given that it constitutes the approved acquisition protocol for clinical use with visual analysis. Next, data points corresponding to the intervals in the dual-time-window protocols were removed from both the target and reference tissue TACs (creating “interval TACs”), ranging from 0 min (no interval) to 80 min (i.e., interval 10–90 min: a 0–10-min p.i. acquisition followed by a 90–110-min p.i. acquisition) in steps of 10 min. This resulted in a total of nine different protocols.

Estimating parameters of interest

Missing data points in the reference tissue TACs, resulting from the introduction of the interval, were interpolated using the 2T4k_V_b model, which was used to fit the interval TACs together with a typical, tracer-specific input function, since a well-defined complete reference tissue input curve is required for SRTM to estimate the kinetic parameters of interest (R_1, BP_ND, k₂) [19]. A typical input function could be used for this purpose, based on the observed negligible between-subject variation in the tail of the curve. In future applications of this protocol, either an equivalent approach or an existing population-derived input function could be used, provided that a similar injection protocol is used. In addition, boundary values were set for all kinetic parameters (Additional file 1: Tables S1a and b) and for k₃ of the 2T4k_V_b interpolation of the interval (lower boundary k₃ = 0.005).

All TACs were fitted with SRTM, and DVR values were calculated as DVR = BP_ND + 1. This additional parameter was introduced as it is frequently used to express amyloid burden in other studies [28], and it better allows for expressing any bias in percentages due to its larger values.

Evaluation of outcome parameters

Results of 2T4k_V_b and SRTM-generated TACs fitted with SRTM were checked for values that were physiologically not expected, here called outliers (≥ 1.5∙max simulated BP_ND). These outliers were registered and removed from the overall dataset before further analysis. Subsequently, bias as induced by the interval was assessed for all simulated dual-time-window protocols, by calculating the bias between simulated BP_ND $({\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$) and corresponding mean fitted BP_ND (${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{fit}})$:

$$\text{Bias}{\mathrm{BP}}_{\mathrm{ND}}={\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{fit}}-{\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$$ 2

Next, for each set of 50 simulated TACs at a given ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$ and noise level, an acceptability curve was computed by plotting the fraction of data versus a span of bias values ranging from 0 to 1 called the “absolute bias threshold.” These curves were generated for all ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$ values across all protocols, and the area under the curve (AUC) was calculated for all dual-time-window protocols, as a global measure of reliability. Finally, the percentage bias in the interval TAC-derived DVR was assessed by comparing it to DVR derived from the full-kinetic curve:

$$\text{Bias}{\mathrm{DVR}}_{\mathrm{ND}}\left(\%\right)=\frac{{\mathrm{DVR}}_{\text{dual}-\text{time window protocol}}-{\mathrm{DVR}}_{\text{full dataset}}}{{\mathrm{DVR}}_{\text{full dataset}}}\bullet 100\%$$ 3

Finally, also the percentage bias in R₁ was assessed by comparing R₁ derived from the various dual-time-window protocols with R₁ obtained from the full-kinetic curve (in a similar way as for DVR, see Eq. 3).

Results

Kinetic parameters for TAC simulation

The Akaike information criterion showed that for [¹⁸F]flutemetamol (62.7%) and [¹⁸F]florbetaben (79.2%) SRTM was the preferred reference tissue method. Pharmacokinetic parameters derived from existing clinical data and used for simulating TACs based on the 2T4k_V_b model and SRTM are presented in Tables 1 and 2. The range of BP_ND values is equally spaced and corresponds to the BP_ND range present in the data, with BP_ND I being the lowest and BP_ND V the highest value. Of note, as described previously, BP_ND estimates are always different between 2T4k_V_b and SRTM. In the present study, additional differences are present, since the first corresponds to the sum of specific binding and a slow component of non-specific binding (in the target tissue), while in the latter a correction for all non-specific binding is made, provided that it is the same in target and reference tissues [18, 28, 29].

TAC simulation

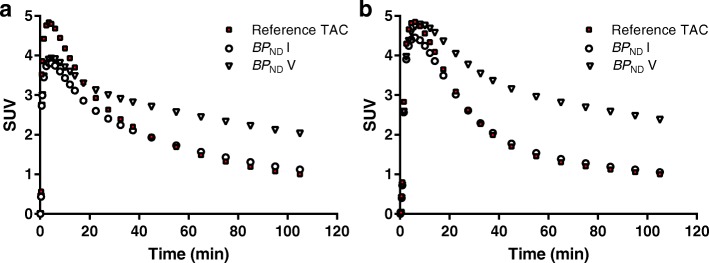
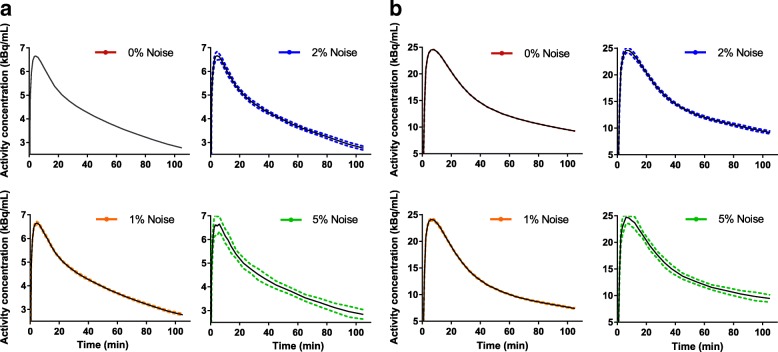
Full reference and target tissue TACs, the latter covering the range of ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$ values, are shown in Fig. 2. Figure 3 shows the pattern in which the different noise levels were simulated for a target tissue TAC (global cortical region), resembling the shape of clinical TACs published previously [7, 8].

Fig. 2.

SRTM simulated target tissue TACs for the range of ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$ values and 2T4k_V_b-generated reference tissue TACs for a [¹⁸F]flutemetamol and b [¹⁸F]florbetaben

Fig. 3.

SRTM simulated TACs from a global cortical region (mean TAC value ± SD, shown solid and dashed lines, respectively) for all noise levels (COV 0–5%) for a [¹⁸F]flutemetamol and b [¹⁸F]florbetaben. All TACs were simulated using a ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$ III (Table 2)

Estimating parameters of interest

Plasma input-generated TACs

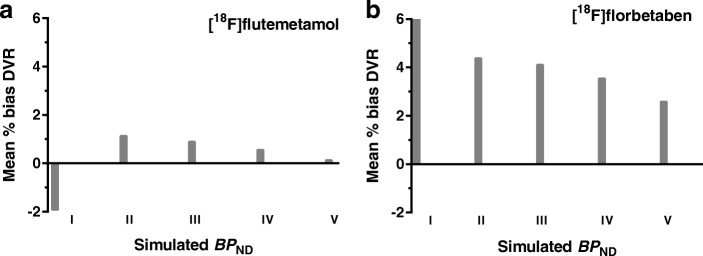
As can be seen in Fig. 4, SRTM-derived DVR resulted in a systematic bias when fitting the noiseless, full-kinetic curve (90–90) 2T4k_V_b-generated TACs for both tracers. For [¹⁸F]flutemetamol, this bias ranged between the 0.17 and 1.95% and for [¹⁸F]florbetaben between the 2.62 and 6.04%. Compared to the full-kinetic curves, 2T4k_V_b interval TACs showed a greater bias in SRTM-derived DVR only for the 10–90 and 20–90 interval TACs (maximum bias of 3.10 and 2.25%, respectively for [¹⁸F]flutemetamol and maximum bias of 8.73 and 10.10%, respectively for [¹⁸F]florbetaben) and comparable or smaller bias for the other interval TACs.

Fig. 4.

Percentage bias in SRTM-derived DVR of 2T4k_V_b-generated TACs. a Bias in DVR for [¹⁸F]flutemetamol. b Bias in DVR for [¹⁸F]florbetaben

Evaluation of outcome parameter

Outliers

No outliers were present when no noise was added to the TACs, and the largest number of outliers occurred at the highest noise level for both tracers (Tables 3 and 4), full colour version see Additional file 1: Tables S2 and S3. More specifically, a positive correlation was observed between percentage of outliers and interval (R² = 0.47, p = 0.04) and between percentage outliers and noise levels (R² = 0.91, p < 0.05) for [¹⁸F]flutemetamol. For [¹⁸F]florbetaben, outliers were mostly present at a noise level of 5% and the number increased for higher ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$ values (R² = 0.85, p = 0.03). The percentage of [¹⁸F]flutemetamol outliers exceeded the 20% for the two largest intervals, while for [¹⁸F]florbetaben it exceeded the 20% only for the 10–90 interval.

Table 3.

Bias in DVR and outliers as a result of noise and the dual-time-window protocol for SRTM-generated [¹⁸F]flutemetamol TACs

FLUT		% bias DVR			% outlier
	Interval	1%	2%	5%	1%	2%	5%
BPND I	10–90	0.0	1.9	2.0	0.0	0.0	0.0
	20–90	6.4	6.1	2.4	0.0	0.0	0.0
	30–90	0.5	0.5	3.1	0.0	0.0	0.0
	40–90	1.5	1.6	1.6	0.0	0.0	0.0
	50–90	1.5	1.5	1.7	0.0	0.0	0.0
	60–90	1.5	1.6	1.9	0.0	0.0	0.0
	70–90	1.8	2.1	0.3	0.0	0.0	0.0
	80–90	0.8	1.3	1.3	0.0	0.0	0.0
	90–90	0.0	0.0	0.0	0.0	0.0	0.0
BPND II	10–90	1.0	6.2	8.2	0.0	2.0	12.0
	20–90	1.5	0.2	4.0	0.0	0.0	2.0
	30–90	0.1	0.2	1.3	0.0	0.0	0.0
	40–90	0.0	0.3	0.1	0.0	0.0	0.0
	50–90	0.0	0.3	0.4	0.0	0.0	0.0
	60–90	0.0	0.2	0.6	0.0	0.0	0.0
	70–90	0.0	0.1	0.6	0.0	0.0	0.0
	80–90	0.1	0.0	0.3	0.0	0.0	0.0
	90–90	0.0	0.0	0.0	0.0	0.0	0.0
BPND III	10–90	0.9	1.4	2.0	0.0	10.0	34.0
	20–90	0.1	0.5	0.6	0.0	0.0	10.0
	30–90	0.1	0.3	0.3	0.0	0.0	4.0
	40–90	0.1	0.5	0.0	0.0	0.0	4.0
	50–90	0.1	0.5	0.2	0.0	0.0	4.0
	60–90	0.1	0.5	0.1	0.0	0.0	4.0
	70–90	0.1	0.4	0.3	0.0	0.0	4.0
	80–90	0.0	0.1	0.5	0.0	0.0	2.0
	90–90	0.0	0.0	0.0	0.0	0.0	2.0
BPND IV	10–90	1.6	2.7	1.8	0.0	2.0	32.0
	20–90	0.2	0.3	0.8	0.0	0.0	12.0
	30–90	0.0	0.0	1.3	0.0	0.0	6.0
	40–90	0.0	0.1	0.6	0.0	0.0	0.0
	50–90	0.0	0.1	0.7	0.0	0.0	0.0
	60–90	0.0	0.1	0.7	0.0	0.0	0.0
	70–90	0.1	0.2	0.7	0.0	0.0	0.0
	80–90	0.0	0.1	0.9	0.0	0.0	0.0
	90–90	0.0	0.0	0.0	0.0	0.0	0.0
BPND V	10–90	1.2	0.1	6.5	2.0	14.0	48.0
	20–90	0.1	0.0	0.5	0.0	0.0	22.0
	30–90	0.0	0.6	0.8	0.0	0.0	18.0
	40–90	0.0	0.5	1.0	0.0	0.0	16.0
	50–90	0.0	0.6	0.9	0.0	0.0	14.0
	60–90	0.0	0.6	0.3	0.0	0.0	12.0
	70–90	0.0	0.4	0.5	0.0	0.0	14.0
	80–90	0.0	0.2	0.4	0.0	0.0	12.0
	90–90	0.0	0.0	0.0	0.0	0.0	12.0

Bias in simulated DVR compared to full-kinetic curve DVR and % outliers across noise levels (1–5%) for [¹⁸F]flutemetamol

Table 4.

Bias in DVR and outliers as a result of noise and the dual-time-window protocol for SRTM-generated [¹⁸F]florbetaben TACs

FBB		% bias DVR			% outlier
	Interval	1%	2%	5%	1%	2%	5%
BPND I	10–90	2.1	0.9	3.3	0.0	0.0	0.0
	20–90	0.9	0.2	2.3	0.0	0.0	0.0
	30–90	1.0	1.2	1.8	0.0	0.0	0.0
	40–90	0.6	1.9	0.3	0.0	0.0	0.0
	50–90	0.1	1.1	1.2	0.0	0.0	0.0
	60–90	1.0	1.0	0.4	0.0	0.0	0.0
	70–90	1.0	1.1	0.7	0.0	0.0	0.0
	80–90	0.5	0.4	0.4	0.0	0.0	0.0
	90–90	0.0	0.0	0.0	0.0	0.0	0.0
BPND II	10–90	0.1	3.4	9.1	0.0	0.0	0.0
	20–90	0.1	0.1	5.0	0.0	0.0	0.0
	30–90	0.1	0.4	0.2	0.0	0.0	0.0
	40–90	0.0	0.2	0.1	0.0	0.0	0.0
	50–90	0.0	0.2	0.3	0.0	0.0	0.0
	60–90	0.1	0.1	0.3	0.0	0.0	0.0
	70–90	0.0	0.1	0.3	0.0	0.0	0.0
	80–90	0.0	0.0	0.2	0.0	0.0	0.0
	90–90	0.0	0.0	0.0	0.0	0.0	0.0
BPND III	10–90	0.2	0.7	3.5	0.0	2.0	16
	20–90	0.2	0.2	1.8	0.0	0.0	0.0
	30–90	0.3	0.5	0.6	0.0	0.0	0.0
	40–90	0.2	0.4	0.7	0.0	0.0	0.0
	50–90	0.1	0.4	0.7	0.0	0.0	0.0
	60–90	0.1	0.4	0.8	0.0	0.0	0.0
	70–90	0.0	0.3	0.5	0.0	0.0	0.0
	80–90	0.0	0.1	0.3	0.0	0.0	0.0
	90–90	0.0	0.0	0.0	0.0	0.0	0.0
BPND IV	10–90	0.5	0.8	4.0	0.0	0.0	20.0
	20–90	0.0	0.2	1.3	0.0	0.0	0.0
	30–90	0.2	0.3	0.1	0.0	0.0	0.0
	40–90	0.0	0.2	0.2	0.0	0.0	0.0
	50–90	0.0	0.1	0.3	0.0	0.0	0.0
	60–90	0.0	0.1	0.3	0.0	0.0	0.0
	70–90	0.1	0.1	0.3	0.0	0.0	0.0
	80–90	0.0	0.0	0.5	0.0	0.0	0.0
	90–90	0.0	0.0	0.0	0.0	0.0	0.0
BPND V	10–90	0.4	1.4	2.7	0.0	0.0	32
	20–90	0.3	0.5	0.9	0.0	0.0	10
	30–90	0.3	0.8	0.7	0.0	0.0	2.0
	40–90	0.0	0.6	0.4	0.0	0.0	0.0
	50–90	0.0	0.6	0.8	0.0	0.0	2.0
	60–90	0.0	0.6	0.6	0.0	0.0	2.0
	70–90	0.0	0.4	0.2	0.0	0.0	2.0
	80–90	0.0	0.2	0.0	0.0	0.0	2.0
	90–90	0.0	0.0	0.0	0.0	0.0	0.0

Bias in simulated DVR compared to full-kinetic curve DVR and % outliers across noise levels (1–5%) for [¹⁸F]florbetaben

SRTM-generated [¹⁸F]flutemetamol interval TACs

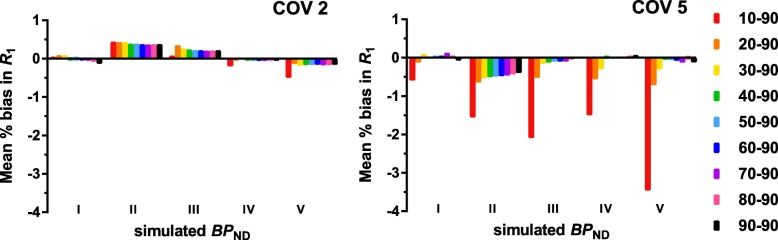
The interpolated TACs can be found in Additional file 1: Figure S1. Table 5 (full color version, see Additional file 1: Table S4) shows, as expected, increasing absolute bias in ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{fit}}$,with increasing noise levels (R² = 0.98, p = 0.01) and longer intervals (R² = 0.51, p = 0.03) (maximum bias of 0.128 for the 10–90 ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$ II interval, at 5% noise). In addition, there was a trend towards a negative correlation between absolute bias and ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$ (R² = 0.74, p = 0.06). The AUC values calculated from the acceptability curves show a trend of smaller (poorer) AUC values at higher noise levels (R² = 1.00, p < 0.001) and larger intervals (R² = 0.64, p = 0.01). As expected, the full-kinetic curve provided the highest AUC except for the lowest ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$. Furthermore, the 10–90 and 20–90-min intervals result in a bias in DVR of maximal 6.4%, while all other intervals showed a bias in DVR of maximum 1.6% for noise levels of up to 2%. For higher noise levels corresponding to very small regions (5%), bias in DVR was a maximum of 8.2 and 3.1%, for the 10–90 and 20–90 intervals (Table 3). Finally, Fig. 5 shows the percentage bias in R₁, which was only larger than 1% for the largest interval. The bias in R₁ estimates also increased with increasing noise level (R² = 0.99, p = 0.004, COV2 ranging from 0.04 to − 0.497 and COV5 0.034 to − 3.462).

Table 5.

Absolute bias in BP_ND and AUC as a result of noise and the dual-time-window protocol for SRTM-generated [¹⁸F]flutemetamol TACs

FLUT		Absolute mean bias BPND (SD)				AUC
	Interval	0%	1%	2%	5%	0%	1%	2%	5%
BPND I	10–90	0.001 (0.000)	0.017 (0.058)	0.042 (0.079)	0.093 (0.154)	0.993	0.971	0.943	0.894
	20–90	0.001 (0.000)	0.084 (0.283)	0.086 (0.276)	0.098 (0.211)	0.993	0.908	0.902	0.887
	30–90	0.001 (0.000)	0.012 (0.079)	0.017 (0.074)	0.105 (0.222)	0.993	0.969	0.961	0.878
	40–90	0.001 (0.000)	0.002 (0.011)	0.006 (0.022)	0.055 (0.113)	0.993	0.986	0.977	0.929
	50–90	0.000 (0.000)	0.002 (0.011)	0.007 (0.025)	0.053 (0.116)	0.993	0.986	0.976	0.929
	60–90	0.000 (0.000)	0.002 (0.029)	0.006 (0.045)	0.051 (0.115)	0.993	0.981	0.974	0.932
	70–90	0.000 (0.000)	0.036 (0.119)	0.000 (0.020)	0.075 (0.147)	0.993	0.948	0.978	0.909
	80–90	0.000 (0.000)	0.026 (0.174)	0.035 (0.181)	0.058 (0.133)	1.000	0.955	0.946	0.923
	90–90	0.000 (0.000)	0.018 (0.162)	0.022 (0.162)	0.072 (0.202)	1.000	0.962	0.958	0.910
BPND II	10–90	0.002 (0.000)	0.014 (0.046)	0.081 (0.217)	0.128 (0.271)	0.993	0.970	0.895	0.838
	20–90	0.001 (0.000)	0.021 (0.135)	0.009 (0.040)	0.076 (0.200)	0.993	0.963	0.965	0.881
	30–90	0.001 (0.000)	0.002 (0.015)	0.003 (0.030)	0.043 (0.159)	0.993	0.982	0.971	0.906
	40–90	0.000 (0.000)	0.002 (0.015)	0.003 (0.029)	0.029 (0.112)	0.993	0.982	0.971	0.919
	50–90	0.000 (0.000)	0.002 (0.015)	0.002 (0.029)	0.022 (0.097)	0.993	0.982	0.972	0.923
	60–90	0.000 (0.000)	0.003 (0.014)	0.004 (0.029)	0.020 (0.095)	0.993	0.983	0.972	0.922
	70–90	0.000 (0.000)	0.002 (0.014)	0.005 (0.029)	0.020 (0.096)	0.993	0.984	0.972	0.924
	80–90	0.000 (0.000)	0.002 (0.013)	0.007 (0.027)	0.023 (0.098)	1.000	0.985	0.973	0.924
	90–90	0.000 (0.000)	0.003 (0.013)	0.006 (0.024)	0.027 (0.098)	1.000	0.985	0.975	0.925
BPND III	10–90	0.003 (0.000)	0.014 (0.063)	0.031 (0.099)	0.023 (0.128)	0.993	0.956	0.924	0.898
	20–90	0.002 (0.000)	0.001 (0.026)	0.019 (0.080)	0.060 (0.145)	0.993	0.975	0.946	0.876
	30–90	0.001 (0.000)	0.001 (0.023)	0.007 (0.054)	0.056 (0.158)	0.993	0.977	0.956	0.881
	40–90	0.001 (0.000)	0.001 (0.023)	0.004 (0.049)	0.051 (0.146)	0.993	0.978	0.958	0.885
	50–90	0.001 (0.000)	0.001 (0.023)	0.005 (0.048)	0.049 (0.147)	0.993	0.978	0.959	0.886
	60–90	0.001 (0.000)	0.001 (0.022)	0.005 (0.048)	0.050 (0.147)	0.993	0.978	0.959	0.887
	70–90	0.001 (0.000)	0.000 (0.021)	0.006 (0.047)	0.047 (0.144)	0.993	0.979	0.960	0.888
	80–90	0.000 (0.000)	0.001 (0.022)	0.010 (0.046)	0.059 (0.164)	1.000	0.979	0.961	0.883
	90–90	0.000 (0.000)	0.001 (0.021)	0.012 (0.043)	0.051 (0.142)	1.000	0.979	0.963	0.894
BPND IV	10–90	0.005 (0.000)	0.034 (0.082)	0.041 (0.147)	0.027 (0.192)	0.993	0.932	0.892	0.854
	20–90	0.003 (0.000)	0.012 (0.038)	0.004 (0.067)	0.043 (0.183)	0.993	0.963	0.942	0.859
	30–90	0.002 (0.000)	0.008 (0.032)	0.002 (0.055)	0.036 (0.168)	0.993	0.968	0.949	0.866
	40–90	0.001 (0.000)	0.008 (0.030)	0.003 (0.054)	0.048 (0.173)	0.993	0.970	0.950	0.858
	50–90	0.001 (0.000)	0.007 (0.031)	0.003 (0.054)	0.045 (0.174)	0.993	0.970	0.949	0.858
	60–90	0.001 (0.000)	0.008 (0.030)	0.003 (0.053)	0.046 (0.169)	0.993	0.969	0.951	0.863
	70–90	0.001 (0.000)	0.007 (0.031)	0.004 (0.051)	0.045 (0.165)	0.993	0.969	0.953	0.868
	80–90	0.000 (0.000)	0.008 (0.030)	0.000 (0.050)	0.043 (0.163)	1.000	0.969	0.954	0.867
	90–90	0.000 (0.000)	0.008 (0.028)	0.001 (0.045)	0.057 (0.179)	1.000	0.970	0.959	0.861
BPND V	10–90	0.006 (0.000)	0.023 (0.082)	0.005 (0.145)	0.117 (0.111)	0.988	0.929	0.885	0.852
	20–90	0.004 (0.000)	0.001 (0.042)	0.004 (0.090)	0.011 (0.179)	0.993	0.960	0.925	0.850
	30–90	0.002 (0.000)	0.000 (0.037)	0.014 (0.074)	0.015 (0.179)	0.993	0.965	0.938	0.851
	40–90	0.001 (0.000)	0.001 (0.034)	0.014 (0.072)	0.019 (0.168)	0.993	0.968	0.940	0.853
	50–90	0.001 (0.000)	0.001 (0.034)	0.015 (0.071)	0.018 (0.164)	0.993	0.968	0.940	0.855
	60–90	0.001 (0.000)	0.001 (0.034)	0.015 (0.071)	0.008 (0.173)	0.993	0.968	0.940	0.849
	70–90	0.001 (0.000)	0.001 (0.033)	0.012 (0.072)	0.010 (0.163)	0.993	0.968	0.939	0.856
	80–90	0.000 (0.000)	0.001 (0.031)	0.008 (0.067)	0.006 (0.172)	1.000	0.969	0.943	0.849
	90–90	0.000 (0.000)	0.001 (0.029)	0.004 (0.061)	0.002 (0.150)	1.000	0.971	0.949	0.867

Absolute bias in ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$ and the area under the curve (AUC) for the acceptability curves across all noise levels (0–5%) for [¹⁸F]flutemetamol

Fig. 5.

[¹⁸F]flutemetamol: percentage bias in SRTM-derived R₁ across the range of ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$ values for two noise levels

SRTM-generated [¹⁸F]florbetaben interval TACs

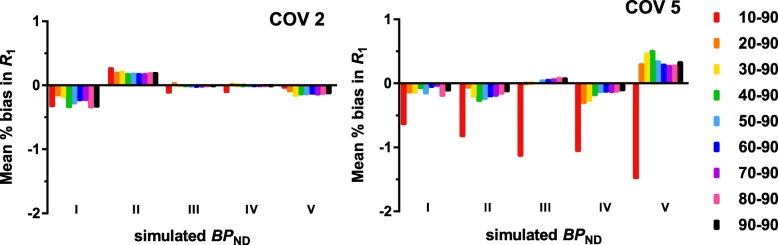
The interpolated TACs can be found in Additional file 1: Figure S2. Table 6 (full color version, see Additional file 1: Table S5) shows an increasing absolute bias for longer intervals (R² = 0.48, p = 0.04) as well as for higher noise levels (R² = 0.96, p = 0.02, maximum bias 1.31 for the 10–90 ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$ II interval, at 5%). This positive correlation was also supported by the AUC values, where lower (poorer) values were correlated with larger intervals (R² = 0.74, p = 0.002), higher ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$ values (R² = 0.98, p = 0.001), and higher levels of noise (R² = 1.0, p < 0.001). As expected, the full-kinetic curve provided the highest AUC except for the lowest ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$. Furthermore, the 10–90 interval showed a bias in DVR of 3.4%, all other intervals showed a bias of ≤ 1.9% for noise levels up to 2%. For higher noise levels corresponding to very small regions (5%), bias in DVR was a maximum of 9.1% for the 10–90 interval, 5.0% for the 20–90 interval, and 1.8% for all others (Table 4). The R₁ bias plots (Fig. 6) show an increase in bias at higher noise levels (R² = 0.99, p = 0.005, COV2 ranging from 0.001 to − 0.359 and COV5 0.003 to − 1.497).

Table 6.

Absolute bias in BP_ND and AUC as a result of noise and the dual-time-window protocol for SRTM-generated [¹⁸F]florbetaben TACs

FBB		Absolute mean bias BPND (SD)				AUC
	Interval	0%	1%	2%	5%	0%	1%	2%	5%
BPND I	10–90	0.000 (0.000)	0.012 (0.026)	0.021 (0.043)	0.059 (0.080)	0.993	0.979	0.966	0.929
	20–90	0.000 (0.000)	0.000 (0.011)	0.013 (0.040)	0.048 (0.076)	0.993	0.986	0.971	0.937
	30–90	0.000 (0.000)	0.000 (0.008)	0.001 (0.028)	0.006 (0.046)	0.993	0.988	0.979	0.968
	40–90	0.000 (0.000)	0.003 (0.032)	0.008 (0.014)	0.021 (0.063)	0.993	0.978	0.981	0.956
	50–90	0.000 (0.000)	0.009 (0.012)	0.000 (0.037)	0.012 (0.056)	0.993	0.983	0.978	0.962
	60–90	0.000 (0.000)	0.000 (0.007)	0.001 (0.015)	0.029 (0.063)	0.993	0.989	0.983	0.956
	70–90	0.000 (0.000)	0.001 (0.006)	0.000 (0.013)	0.032 (0.069)	0.993	0.990	0.984	0.953
	80–90	0.000 (0.000)	0.005 (0.036)	0.007 (0.066)	0.029 (0.081)	1.000	0.978	0.963	0.948
	90–90	0.000 (0.000)	0.010 (0.011)	0.011 (0.064)	0.024 (0.067)	1.000	0.983	0.962	0.956
BPND II	10–90	0.001 (0.000)	0.003 (0.013)	0.045 (0.167)	0.131 (0.307)	0.993	0.984	0.935	0.861
	20–90	0.001 (0.000)	0.000 (0.012)	0.000 (0.023)	0.079 (0.207)	0.993	0.985	0.976	0.891
	30–90	0.002 (0.000)	0.000 (0.012)	0.003 (0.023)	0.016 (0.063)	0.993	0.985	0.975	0.946
	40–90	0.000 (0.000)	0.001 (0.012)	0.001 (0.023)	0.012 (0.062)	0.993	0.985	0.976	0.946
	50–90	0.000 (0.000)	0.001 (0.011)	0.001 (0.022)	0.010 (0.060)	0.993	0.986	0.977	0.948
	60–90	0.000 (0.000)	0.002 (0.010)	0.000 (0.021)	0.009 (0.056)	0.993	0.987	0.978	0.948
	70–90	0.000 (0.000)	0.001 (0.009)	0.001 (0.020)	0.010 (0.055)	0.993	0.988	0.979	0.950
	80–90	0.000 (0.000)	0.001 (0.007)	0.002 (0.017)	0.011 (0.053)	1.000	0.989	0.981	0.954
	90–90	0.000 (0.000)	0.001 (0.008)	0.002 (0.015)	0.014 (0.053)	1.000	0.989	0.983	0.954
BPND III	10–90	0.002 (0.000)	0.002 (0.022)	0.014 (0.066)	0.084 (0.159)	0.993	0.978	0.955	0.875
	20–90	0.002 (0.000)	0.003 (0.016)	0.000 (0.041)	0.058 (0.117)	0.993	0.982	0.964	0.898
	30–90	0.003 (0.000)	0.004 (0.016)	0.004 (0.035)	0.038 (0.112)	0.993	0.982	0.966	0.910
	40–90	0.001 (0.000)	0.002 (0.016)	0.003 (0.036)	0.041 (0.116)	0.993	0.982	0.966	0.909
	50–90	0.001 (0.000)	0.002 (0.016)	0.002 (0.035)	0.041 (0.117)	0.993	0.982	0.967	0.908
	60–90	0.001 (0.000)	0.001 (0.015)	0.002 (0.034)	0.041 (0.114)	0.993	0.983	0.968	0.909
	70–90	0.001 (0.000)	0.001 (0.014)	0.001 (0.031)	0.037 (0.108)	0.993	0.984	0.971	0.911
	80–90	0.000 (0.000)	0.000 (0.014)	0.002 (0.030)	0.033 (0.092)	1.000	0.985	0.972	0.926
	90–90	0.000 (0.000)	0.000 (0.013)	0.003 (0.027)	0.029 (0.083)	1.000	0.985	0.974	0.933
BPND IV	10–90	0.003 (0.000)	0.014 (0.035)	0.014 (0.074)	0.085 (0.184)	0.993	0.964	0.943	0.848
	20–90	0.004 (0.000)	0.004 (0.024)	0.003 (0.047)	0.036 (0.148)	0.993	0.975	0.956	0.891
	30–90	0.005 (0.000)	0.001 (0.023)	0.006 (0.046)	0.011 (0.115)	0.993	0.976	0.958	0.904
	40–90	0.001 (0.000)	0.004 (0.023)	0.003 (0.046)	0.008 (0.108)	0.993	0.976	0.958	0.907
	50–90	0.001 (0.000)	0.004 (0.024)	0.002 (0.045)	0.006 (0.107)	0.993	0.975	0.959	0.909
	60–90	0.001 (0.000)	0.005 (0.022)	0.002 (0.043)	0.007 (0.099)	0.993	0.976	0.961	0.917
	70–90	0.001 (0.000)	0.004 (0.022)	0.003 (0.040)	0.006 (0.092)	0.993	0.977	0.964	0.924
	80–90	0.000 (0.000)	0.005 (0.021)	0.000 (0.037)	0.003 (0.089)	1.000	0.977	0.966	0.926
	90–90	0.000 (0.000)	0.005 (0.019)	0.000 (0.034)	0.012 (0.091)	1.000	0.978	0.970	0.925
BPND V	10–90	0.005 (0.000)	0.005 (0.044)	0.024 (0.122)	0.029 (0.111)	0.993	0.960	0.911	0.903
	20–90	0.006 (0.000)	0.008 (0.027)	0.015 (0.056)	0.008 (0.147)	0.988	0.971	0.950	0.882
	30–90	0.007 (0.000)	0.008 (0.027)	0.021 (0.051)	0.011 (0.165)	0.988	0.972	0.954	0.870
	40–90	0.002 (0.000)	0.002 (0.026)	0.016 (0.052)	0.018 (0.172)	0.993	0.973	0.955	0.868
	50–90	0.002 (0.000)	0.002 (0.026)	0.016 (0.052)	0.010 (0.156)	0.993	0.973	0.955	0.878
	60–90	0.001 (0.000)	0.002 (0.025)	0.016 (0.051)	0.015 (0.156)	0.993	0.974	0.955	0.875
	70–90	0.001 (0.000)	0.002 (0.024)	0.012 (0.050)	0.022 (0.153)	0.993	0.976	0.955	0.876
	80–90	0.000 (0.000)	0.002 (0.022)	0.008 (0.045)	0.027 (0.147)	0.993	0.978	0.959	0.876
	90–90	0.000 (0.000)	0.002 (0.020)	0.005 (0.041)	0.026 (0.135)	0.993	0.979	0.963	0.888

Absolute bias in ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$ and the area under the curve (AUC) for the acceptability curves across all noise levels (0–5%) for [¹⁸F]florbetaben

Fig. 6.

[¹⁸F]florbetaben: percentage bias in SRTM-derived R₁ across the range of ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{sim}}$ values for two noise levels

Discussion

The present pharmacokinetic simulation study demonstrated that, for [¹⁸F]flutemetamol and [¹⁸F]florbetaben, the introduction of a break with a maximum of 60 min in a dual-time-window acquisition protocol (early interval of 0–30 min followed by a late interval of 90–110 min) results in a minimal loss in quantitative accuracy while presenting major logistic advantages as compared with full dynamic acquisitions. Therefore, this protocol could serve as suitable alternative in research or clinical trial settings where accurate and fully quantitative measurements might be required.

Analysis of the 2T4k_V_b noiseless full TACs showed a systematic bias (0.17–1.95% for [¹⁸F]flutemetamol and 2.62–6.04% for [¹⁸F]florbetaben) in SRTM-derived DVR values compared with simulated DVR values. These findings are in line with previous studies reporting that kinetics of [¹⁸F]flutemetamol and [¹⁸F]florbetaben are better described by a two-tissue compartment model in target as well as reference tissues [8, 18]. In addition, Nelissen et al. showed that there were similar levels of binding in the second reference tissue compartment for both healthy control and AD subjects and therefore concluded that this binding is likely due to (relatively slow) non-specific retention [18]. As this violates one of the assumptions of SRTM, a slight bias in DVR estimates can be expected [19, 30]. Given the aim of validating a dual-time-window protocol for a reference tissue-based approach, TACs were both generated and fitted according to the SRTM model to prevent a systematic bias in the results.

A first examination of SRTM-derived ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{fit}}$ values revealed that most outliers were observed for fits of the 10–90-min interval, and, to a lesser extent, also for fits of the 20–90-min interval. In addition, compared with the full-kinetic curve, the bias in DVR only exceeded previously reported [¹¹C]PIB TRT values, of which [¹⁸F]flutemetamol is an analog, for the 10–90 and 20–90-min intervals for [¹⁸F]flutemetamol [9, 10]. For the other dual-time-window protocols, the bias remained ≤ 3.1%. Analysis of [¹⁸F]florbetaben data showed a bias of ≤ 9.1% for the 10–90-min interval and ≤ 5.0% for the 20–90 interval for the highest noise levels, while for all intervals it was ≤ 1.9%. The latter well within previously reported TRT values for [¹⁸F]florbetaben SUVR data (ranging between 2.9% HC and 6.2% AD) [31]. Reported AUC values also showed a general trend of worse values for longer breaks and higher noise level, with the exception of some extremely low BP_ND cases, where the performance of SRTM is known to be suboptimal [10].

Finally, the bias plots of SRTM-generated TACs demonstrated that bias in SRTM-derived R₁ increased as a function of noise and interval for both tracers. More specifically, a larger error in R₁ (> 3% for [¹⁸F]flutemetamol and > 1% for [¹⁸F]florbetaben) was observed for the 10–90-min intervals compared with the other intervals. For practical applications, this error would be negligible since the TRT of flow is known to be approximately 9% [32]. As expected, the results showed that the length of the interval is related to bias in ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{fit}}$ or DVR and the number of outliers. More specifically, results suggest that it is not advisable to use the 10–90 and 20–90-min intervals for full quantification, especially due to the relatively large percentage of outliers and larger bias in DVR compared with other intervals. Moreover, the observed larger amount of unusable data would result in smaller power to detect changes in clinical trials.

Shorter scan durations are better for the patient and, as such, longer breaks would be preferred. Since the 10–90 and 20–90-min intervals result in a large number of outliers and larger bias, the 30–90-min interval would be a good compromise. This interval would have the additional advantage of a 60-min break, which may allow for interleaved scanning protocols. Consequently, the 30–90-min interval is recommended as the optimal trade-off between patient comfort and quantitative accuracy (bias in DVR < 2% and a maximum of 18% outliers for highest noise level and ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{fit}}$). This conclusion is in agreement with recent work of Bullich et al. regarding the optimal [¹⁸F]florbetaben dual-time-window protocol [17]. Based on their analysis of clinical data, which did not include the 90–110-min diagnostic window, a dual-time-window protocol of 0–30 and 120–140 min was described as optimal. However, their simulations also supported that 0–30 and 90–110-min scanning times would maintain the best compromise between quantitative accuracy and patient comfort. The present simulation study, including TACs representing the AD spectrum and different noise levels, further validated their findings.

A major advantage of a 60-min gap in the scanning protocol is that it allows for interleaved scanning protocols, in which the first scan of the second patient can be acquired within the resting period (interval) of the first patient. An interleaved scanning protocol would increase both patient throughput and efficient use of tracer batches, thereby decreasing costs. An assessment of the practical feasibility of such an interleaved scanning protocol is beyond the scope of the present study and needs to be addressed in future studies. Main limitations of the current study include the use of fixed K₁ and k₂ parameters for simulations, the limited sample size of the available clinical dataset, and the extrapolation of TRT variability from other radiotracers to this work. The first limits the possibility of assessing the impact of changes in cerebral blood flow on dual-time-window protocol-based quantification, but it can be expected to introduce only small additional bias over and above the one introduced by the protocol itself [11]. Regarding the second, additional clinical data would have allowed the verification of the simulation results, which remains a goal for future work once larger cohorts are available. With respect to extrapolating TRT variability, although values from other tracers might not directly translate to our data, they are expected to be in comparable ranges [24]. In addition, although outside of the scope of this study, the evaluation of parametric methods for quantification of dual-time-window-derived data is warranted, which would require imaging data in order to optimize image contrast and reduce noise and artifacts. Finally, it must be noted that the goal of this study was not to compare these two tracers, but to identify the optimal dynamic dual-time-window scanning protocol for both of them. In order to make a head-to-head comparison between tracers, PET imaging data from both tracers within the same patient would be required.

Conclusion

Accurate estimates of ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{fit}}$ can be obtained for both [¹⁸F]flutemetamol and [¹⁸F]florbetaben using a 60-min dual-time-window protocol, with dynamic scanning from 0 to 30 and again from 90 to 110 min. This protocol results in a limited number of outliers, and an acceptable bias in ${\mathrm{BP}}_{\mathrm{ND}}^{\mathrm{fit}}$ and DVR estimates. Moreover, it enables interleaved scanning protocols, optimizing tracer batch usage and patient throughput, thereby reducing costs and improving patient comfort.

Abbreviations

[¹¹C]PiB

Carbon-11 Pittsburgh Compound B

18F

Fluorine-18

2T4k_V_b

Reversible two tissue compartment model (4 rate constants) with additional blood volume fraction parameter

AD

Alzheimer’s disease

AUC

Area under the curve

Aβ

Amyloid-beta

BP_ND

Non-displaceable binding potential

COV

Coefficient of variation

DVR

Distribution volume ratio

FDG

Fluorodeoxyglucose

FRTM

Full reference tissue model

MRTM

Multilinear reference tissue method

PET

Positron emission tomography

RPM

Receptor parametric mapping

SRTM

Simplified reference tissue method

SUVR

Standardized uptake value ratio

TAC

Time activity curve

TRT

Test-retest

VOI

Volume of interest

Authors’ contributions

FH, MY, ILA, JDG, and AAL contributed to the concept and design of the study. FH, MY, ILA, and AAL drafted the article. SB, CF, and KH provided the data. FH, MY, ILA, HB, and AAL contributed to the data analysis. FH, MY, ILA, KH, HB, JDG, SB, CF, and AAL contributed to the interpretation of the data. Technical or material support was provided by MY, SB, CF, and KH. FH, MY, ILA, KH, HB, JDG, SB, CF, and AAL read, critically reviewed, and approved the manuscript.

Ethics approval and consent to participate

All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards. Informed consent was obtained from all individual participants included in the study[7, 8]. The Ethical Committee of the University Hospitals Leuven approved the study protocol for the [¹⁸F]flutemetamol study [7, 8]. Local Institutional Review Board of University of Leipzig, the National Radiation Safety Committee, and the German Federal Institute for Drugs and Medical Devices approved the study protocol for the [¹⁸F]florbetaben study [7, 8].

Consent for publication

All participants included in this study provided consent for publication.

Competing interests

CF is employed by GE Healthcare and SB by Life Molecular Imaging GmbH. All other authors declare that they have no conflict of interest.

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.