Abstract
Aims
Machine learning (ML) is widely believed to be able to learn complex hidden interactions from the data and has the potential in predicting events such as heart failure (HF) readmission and death. Recent studies have revealed conflicting results likely due to failure to take into account the class imbalance problem commonly seen with medical data. We developed a new ML approach to predict 30 day HF readmission or death and compared the performance of this model with other commonly used prediction models.
Methods and results
We identified all Western Australian patients aged above 65 years admitted for HF between 2003 and 2008 in the linked Hospital Morbidity Data Collection. Taking into consideration the class imbalance problem, we developed a multi‐layer perceptron (MLP)‐based approach to predict 30 day HF readmission or death and compared the predictive performances using the performance metrics, that is, area under the receiver operating characteristic curve (AUC), area under the precision–recall curve (AUPRC), sensitivity and specificity with other ML and regression models. Out of the 10 757 patients with HF, 23.6% were readmitted or died within 30 days of hospital discharge. We observed an AUC of 0.55, 0.53, 0.58, and 0.54 while an AUPRC of 0.39, 0.38, 0.46, and 0.38 for weighted random forest, weighted decision trees, logistic regression, and weighted support vector machines models, respectively. The MLP‐based approach produced the highest AUC (0.62) and AUPRC (0.46) with 48% sensitivity and 70% specificity.
Conclusions
We show that for the medical data with class imbalance, the proposed MLP‐based approach is superior to other ML and regression techniques for the prediction of 30 day HF readmission or death.
Keywords: Heart failure, Machine learning, Prediction, Readmission
Introduction
Heart failure (HF) is a global public health problem affecting millions of people and has high hospital readmission rates and a growing prevalence.1, 2 The cost of in‐hospital treatment of HF absorbs a big portion of healthcare budgets.3, 4 Some HF readmissions result from an early discharge from hospital, bad discharge planning, and poor in‐hospital care.5 Some of these may be considered as avoidable readmissions. There is now motivation to identify, at the time of discharge, patients who are at risk of readmission.6 Models that predict readmission can stratify high‐risk patients leading to increase in the research in predicting HF readmissions.
Healthcare business models are gradually shifting towards data‐driven systems.7 This is because the availability of large amounts of medical data has the potential to be used in new ways to gain insights on how to improve healthcare outcomes. Machine learning (ML) techniques have already been applied for various diseases.8 Previous studies have complemented administrative data with clinical information to develop predictive models. However, clinical data are not always integrated electronically in health databases in many jurisdictions, making it problematic to apply predictive models derived from clinical data. Moreover, medical data often are limited by class imbalance where the majority of the data belong to one outcome event resulting in poor performance of prediction models and incongruent results questioning the utility of ML techniques.9, 10, 11, 12, 13, 14, 15 Lastly, most ML studies have used area under the receiver operating characteristic curve (AUC) as the only performance metric to assess the model performance. It was reported in Davis and Goadrich16 that precision–recall curves are better for highly imbalanced datasets.
In our study, we evaluated different ML models for the prediction of 30 day HF readmission or death using a linked administrative health dataset with the aim to address the class imbalance problem seen in medical datasets. We hypothesized that with the right choice of ML algorithm, a better prediction can be achieved than with the standard regression methods.
Methods
Cohort and data sources
We obtained extracts of linked data from two core datasets [Hospital Morbidity Data Collection (HMDC) and mortality database] of the Western Australian Data Linkage System.17 This is a whole‐of‐population record linkage system with dynamic linkages based on probabilistic matching algorithms between multiple core datasets. Data are maintained by the Western Australian Department of Health and supplied by hospitals under mandatory reporting rules and laws. A detailed description of the datasets and cohorts that supplied this study has been reported previously.18
We identified patients in the HMDC extract above 65 years who were residents of Western Australia and were admitted to any hospital in Western Australia with a principal discharge diagnosis of HF (International Classification of Diseases, 10th Revision, Australian Modification Code I50) in 2003–2008 (Figure 1 ). The age limit was applied to capture complete medication history data (deemed necessary). As our patients aged 65 years or more own a concession card, the use of a concession card for the purchase of medicine gets recorded automatically into the Pharmaceutical Benefits Scheme (PBS) data, ensuring robust capture of medicine data in this age group. Patient characteristics were obtained from these admissions. Co‐morbidities and HF history were identified by looking back 20 years from the 2003–2008 HF admissions, while the outcome of death or 30 day readmissions for HF were identified by looking forward from the initial HF admissions. Data on history of medication use and out‐of‐hospital services were obtained from linked records from the PBS and Medicare Benefits Schedule, respectively. As the ejection fraction of HF patients is not routinely collected in the administrative data, we were unable to subclassify the subtypes of HF. The PBS dataset contains the dispatch of medications such as beta‐blockers [Anatomical Therapeutic Chemical (ATC) Code C07AB], angiotensin‐converting enzyme inhibitors (ATC Code C09AA), and angiotensin receptor blockers (ATC Code C09CA)].
Figure 1.
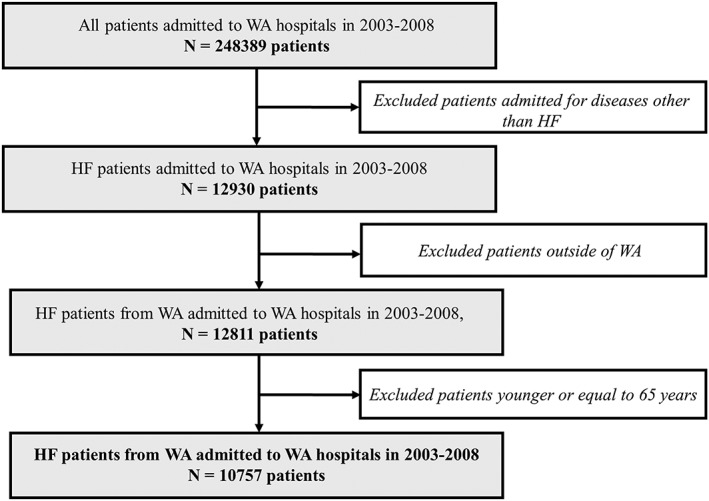
Cohort identification flow chart. The final cohort contains 10 757 HF patients admitted to WA hospitals in 2003–2008. HF, Heart failure; WA, Western Australia.
Data preprocessing
The preprocessing of HMDC admission records involved the following steps (Figure 1 ):
First, we separated the admissions during the period of interest (2003 to 2008) from historic data and follow‐up records.
Admissions may contain multiple records for each patient. Some of these records are transfer admissions (patient transferred from one hospital to another). Two consecutive admission records were defined as a transfer if the admission and separation (discharge) dates were within 1 day of each other. If so, these were merged into a single hospital admission. This left us with 248 389 patients.
Next, we identified and extracted only the HF admissions (index HF admissions). We also excluded patients who were not residents of Western Australia and were left with 12 811 patients.
We then applied an age limit and excluded patients aged less than 65 years. This reduced the number of patients to 10 757.
Finally, we linked the cohort from Step 4 with matching records of emergency department visits, death records, medications, and out‐of‐hospital care (e.g. general practitioner visits) to create the linked study database.
Extraction of features (variables)
We extracted all relevant available features for our HF cohort, from the linked study database (Table 1). There was a total of 47 variables, which included patient demographics, admission characteristics, medical history (co‐morbidities), visits to emergency departments, history of medication use, healthcare services out of hospital, and death. The continuous variables such as age and length of stay were normalized to zero mean and unit variance, and the categorical variables were encoded as one‐hot‐encoding vectors before using as inputs to the prediction models.
Table 1.
Characteristics of HF patients in the study cohort
| Characteristic | Count (percentage) | |
|---|---|---|
| Alive and non‐readmitted within 30 days | Readmitted or dead within 30 days | |
| Total number of HF patients | 8211 (76.3) | 2546 (23.7) |
| Age (years), mean (SD) | 81.1 (7.6) | 83.1 (7.6) |
| Male (%) | 4028 (49.0) | 1247 (49.0) |
| Indigenous status: Aboriginal or Torres Strait Islander (%) | 141 (1.7) | 35(1.4) |
| History of heart failure | 3642 (44.3) | 1422 (55.8) |
| Length of stay (days), mean (SD) | 10.39 (15.9) | 16.22 (46.8) |
| Co‐morbidities (%) | ||
| Ischaemic heart disease | 4506 (54.9) | 1457 (57.2) |
| Hypertension | 5497 (66.9) | 1751 (68.8) |
| Atrial fibrillation | 3398 (41.4) | 1102 (43.3) |
| Diabetes | 2458 (29.9) | 806 (31.6) |
| Chronic obstructive pulmonary disease | 2240 (27.3) | 783 (30.7) |
| Peripheral vascular disease | 1547 (18.8) | 549 (21.5) |
| Stroke | 1014 (12.3) | 366 (14.4) |
| Dementia | 545 (6.6) | 270 (10.6) |
| Depression | 691 (8.4) | 272 (10.7) |
| Cancer | 2811 (34.2) | 934 (36.7) |
| Chronic kidney disease | 2027 (24.7) | 795 (31.2) |
| Cardiogenic shock | 68 (0.8) | 30 (1.1) |
| Cardiomyopathy | 344 (4.2) | 115 (4.5) |
| SEIFA (%) | ||
| 5th quintile (least disadvantage) | 552 (6.7) | 182 (7.1) |
| 4th quintile | 1398 (17.0) | 439 (17.2) |
| 3rd quintile | 1450 (17.6) | 474 (18.6) |
| 2nd quintile | 1810 (22.0) | 555 (21.8) |
| 1st quintile (highest disadvantage) | 3001 (36.5) | 896 (35.2) |
| ARIA (%) | ||
| Major cities of Australia | 4247 (51.7) | 1334 (52.4) |
| Inner regional Australia | 2514 (30.6) | 692 (27.1) |
| Outer regional Australia | 897 (10.9) | 327 (12.8) |
| Remote Australia | 330 (4.0) | 118 (4.6) |
| Very remote Australia | 223 (2.7) | 75 (2.9) |
| History of drugs in the last 6 months (%) | ||
| No supply of BB or RAASi | 2298 (28.0) | 731 (28.7) |
| 1 or more supplies of RAASi only | 3249 (39.6) | 1097 (43.1) |
| 1 or more supplies of BB only | 741 (9.0) | 205 (8.0) |
| 1 or more supplies of both BB and RAASi | 1518 (18.5) | 411 (16.1) |
| At least one visit to health professionals in the last 6 months | ||
| GP | 6929 (84.4) | 2131 (83.7) |
| Specialist | 3980 (48.8) | 1079 (42.4) |
| Diagnostic | 6556 (79.8) | 2028 (79.6) |
| Allied Health | 1384 (16.8) | 353 (13.9) |
| At least one emergency admission in the last 6 months | 3591 (43.7) | 1303 (51.1) |
| Charlson Comorbidity Index score, mean (SD) | 4.2 (3.0) | 4.8 (3.1) |
| At least two supplies of ATC drugs in the last 6 months | ||
| Alimentary tract and metabolism | 4868 (59.3) | 1660 (65.2) |
| Blood and blood forming organs | 3835 (46.7) | 1183 (46.5) |
| Cardiovascular system | 7190 (87.6) | 2251 (88.4) |
| Dermatologicals | 730 (8.9) | 253 (9.9) |
| Genito urinary system and sex hormones | 388 (4.7) | 123 (4.8) |
| Systemic hormonal preparations, excluding sex hormones and insulins | 974 (11.9) | 356 (14.0) |
| Antiinfectives for systemic use | 3101 (37.8) | 1071 (42.1) |
| Antineoplastic and immunomodulating agents | 276 (3.4) | 111 (4.3) |
| Musculo‐skeletal system | 2390 (29.1) | 770 (30.2) |
| Nervous system | 4883 (59.5) | 1674 (65.7) |
| Antiparasitic products, insecticides, and repellents | 243 (2.9) | 79 (3.1) |
| Respiratory system | 1977 (24.0) | 616 (24.2) |
| Sensory organs | 1950 (23.7) | 656 (25.8) |
| Readmission or death within 30 days | 2546 (23.6) | |
| Readmission within 30 days (emergency only) | 1121 (10.4) | |
| Death within 30 days | 1574 (14.6) | |
ARIA, Accessibility/Remoteness Index of Australia; ATC, Anatomical Therapeutic Chemical Index; BB, beta‐blocker; GP, general practitioner; HF, heart failure; RAASi, renin–angiotensin–aldosterone system index; SD, standard deviation; SEIFA, Socio‐Economic Indexes for Areas.
Model description
Multi‐layer perceptron
In short, a multi‐layer perceptron (MLP) is a feedforward artificial neural network with an input layer, at least one hidden layer, and an output layer.19 Every node in the input layer is fully connected to all the nodes of the hidden layer. Similarly, all the nodes of the hidden layer are fully connected to the nodes of the output layer as shown in Figure 2 . The information flows from the input layer, through the hidden layers, towards the output layer. The network uses nonlinear transformations to learn high‐level abstractions in the data to build the predictive model. The number of hidden layers, number of nodes in the hidden layers, the type of activation function, and the loss function are among the hyper‐parameters, which need to be adjusted for every problem. We used grid search approach to tune the hyper‐parameters of the MLP network. We used the traditional grid search for hyperparameter optimization, where stepwise exhaustive searching through a range of parameter values was considered. For the number of layers, we used a range from 5 to 50, and for the number of neurons, we used a range from 5 to 100 with the step size being 5 in both cases. The number of training epochs was selected by observing the minimum validation error. For our study, we modelled an MLP network containing an input layer with the number of nodes equal to the total number of features available, one hidden layer of 50 nodes, and an output layer of one node. All the hyper‐parameters were chosen by a trial and test method. We chose a rectified linear unit as the non‐linear transformation for the hidden layer and a sigmoid for the output layer. The number of nodes (n = 50) in the hidden layer were also empirically chosen to yield the best performance.
Figure 2.
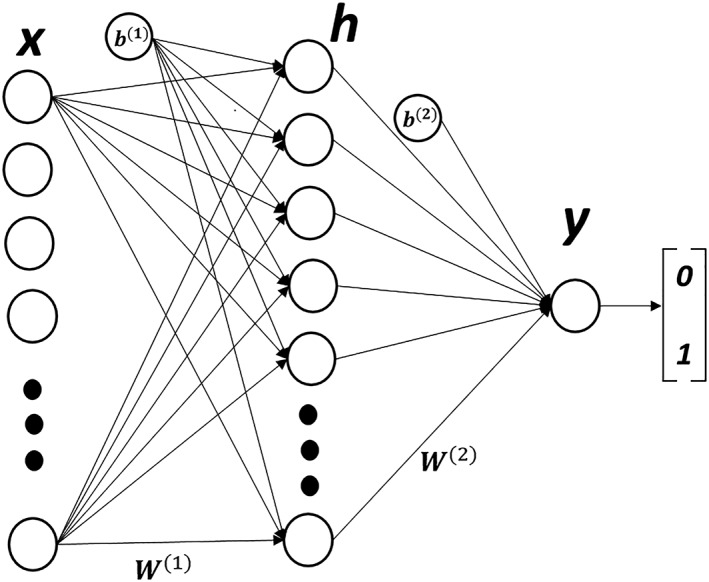
Our three‐layer multi‐layer perceptron network with one hidden layer ‘h’ containing 50 hidden nodes. ‘W’ represents the node weights, ‘b’ denotes the node biases, ‘x’ is the input feature vector, and ‘y’ represents the binary output.
The class imbalance problem
Only 24% of the HF patients were readmitted or died within 30 days of the index HF hospital discharge in our study confirming the highly imbalanced data (i.e. a low proportion of outcome events compared with patients who did not experience the outcome) often seen with medical data. To address the class imbalance seen with our dataset, we set the minority class weight to three times the weight of the majority class (based on the imbalance in our data) to produce a model with better generalization. These class weights are used during the training of MLP model to increase the misclassification cost of minority class samples. This makes the training process pay more attention towards the minority class samples, thus increasing the sensitivity of the prediction model.
Splitting of study cohort
We divided our cohort into three random sets of data to build a generalized model for 30 day HF readmission or death. We kept 70% of the data for the training of the prediction model, 15% of the data were used for the validation of the model during the development phase, and the remaining 15% of the data were used to test the performance of the model (over unseen data). The proportion of minority class samples in the training, validation, and testing datasets was kept similar to that in the original dataset. The performance of the model was tested using four performance measures, that is, AUC, area under the precision–recall curve (AUPRC), sensitivity, and specificity. We report sensitivity and specificity because the prediction of readmission/death is as important as the prediction of no readmission or death.
We compared our MLP‐based approach with a clinical score called LACE, the standard statistical method (logistic regression), and other ML algorithms such as decision tree, random forest (RF), and support‐vector machine (SVM) techniques for predicting 30 day HF readmission or death in our cohort.10 The LACE score uses length of hospital stay (L), acuity of admission [A (emergency or not)], Charlson Comorbidity Index score (C), and number of emergency visits in the last 6 months (E) of the patient to predict the risk of 30 day readmission or death.20 The machine learning approaches predicted the distinct classes in classification mode. The quantitative output of the regression approaches was dichotomized into distinct classes by applying the most commonly used threshold of 0.5 to the output probabilities. We also developed the weighted versions of the decision tree, RF, and SVM models, which deal with the class imbalance by assigning more weight to the minority class samples. We tested a wide range of hyper‐parameters such as depth of the tree, minimum number of samples to split a node, and number of trees in the RF algorithm using grid search. The validation set was evaluated using the validation error during the training process. We present the results of the hyper‐parameter configuration, which gives the best performance for each algorithm. Lastly, we compared the reported performance of three of the best four models used by the Frizzell et al., that is, logistic regression with backward stepwise selection, logistic regression with least absolute shrinkage and selection operator (LASSO), and RF model with their performance on our data.
Software packages
All the programming codes used in this work were written in Python programming environment v3.6. The MLP‐based approach was implemented using the Keras Library v2.1.5 with Tensor Flow backend v1.8.0. We used the scikit‐learn library v0.19.1 for developing all other prediction models including the logistic regression. To create the models, we set the corresponding parameter, namely, class_weights in the scikit library implementation.
Results
We had access to the patients' demographics and socio‐economic indicators, medical history, out‐of‐hospital services, medication history, and deaths. Table 1 presents the characteristics of the patients in our cohort. Of the 10 757 patients with HF, 2546 (23.6%) were readmitted or died within 30 days of the index HF hospital discharge. The mean age of HF patients was 82 (SD: 7.6) years with approximately an equal proportion of men and women (i.e. 49 vs. 51%). More than half of patients (55%) had ischaemic heart disease. Other common co‐morbidities included hypertension (67%), atrial fibrillation (42%), diabetes (30%), chronic obstructive pulmonary disease (28%), and chronic kidney disease (26%). The average length of hospital stay during the index HF admission was 11.7 (SD: 26.7) days. The out‐of‐hospital services included visits to general practitioners (84%), pathologists (80%), specialists (47%), and allied health professionals (16%). About half of the patients (46%) had at least one emergency admission within the past 6 months of the index admission. The mean Charlson Comorbidity Index score was 4.3 (SD: 3.0). The socio‐economic (Socio‐Economic Indexes for Areas) and remoteness (Accessibility/Remoteness Index of Australia) variables, provided by the Australian Bureau of Statistics, show that 3897 (36%) HF patients belonged to the most disadvantageous quintile of the cohort and 5581 (52%) HF patients were from the major cities of Western Australia. The Socio‐Economic Indexes for Areas values are based on education, occupation, and economic resources of the residents of an area using information from the five yearly census.21 The accessibility/remoteness index divides Australia into categories of remoteness based on the relative access to services.22
The performance of different models for the prediction of 30 day HF readmission or death on our dataset is provided in Table 2. While the standard logistic regression model produced an AUC of 0.57 and an AUPRC of 0.45 with 62.26% accuracy, 48.37% sensitivity, and 66.85% specificity, the ML models produced AUC in the range 0.50–0.63, AUPRC in the range 0.31–0.46, accuracy ranging from 64.93 to 76.39%, and specificity in the range 70.01 to 99.75%. The weighted versions of the prediction models consistently outperformed their non‐weighted counterparts on our data. Of note, the MLP‐based approach outperformed the standard logistic regression model for all predictive performance measures. In Table 3, we present the results reported by Frizzell et al.10 and compare with the performance of the reproduced statistical and ML models used in their study using our data. The AUCs of RF, logistic regression, and LASSO regression‐based models reported by Frizzell et al. were 0.61, 0.62, and 0.62, respectively. With our data, these models yielded AUCs of 0.50, 0.56, and 0.64, respectively. Note the difference in the results of the LR and RF models between Tables 2 and 3. Table 3 provides the results, which are based on the specifications provided by Frizzell et al.10 (page 2 of the supplementary appendix), while the results in Table 2 are based on our own models. This difference appears as an AUC of 0.576 and 0.501 for LR and RF, accordingly, in Table 2 where we used our own models and an AUC of 0.56 and 0.50 for LR and RF models, accordingly, in Table 3 based on the LR and RF parameters provided by Frizzell et al.10 Of note, our newly built MLP‐based approach yielded the best AUC of 0.62 with 48.42% sensitivity and 70.01% specificity on our data.
Table 2.
Performance measure of our prediction models developed for the HF cohort
| Model | AUC | AUPRC | Accuracy (%) | Sensitivity (%) | Specificity (%) |
|---|---|---|---|---|---|
| LACE | 0.551 | 0.448 | 59.85 | 45.54 | 64.80 |
| Logistic regression | 0.576 | 0.455 | 62.26 | 48.37 | 66.85 |
| Random forests | 0.501 | 0.319 | 76.39 | 0.52 | 99.75 |
| Weighted random forests | 0.548 | 0.386 | 76.22 | 21.71 | 88.07 |
| Decision trees | 0.520 | 0.367 | 66.97 | 22.84 | 81.22 |
| Weighted decision trees | 0.528 | 0.379 | 64.18 | 31.44 | 74.16 |
| Support‐vector machines | 0.528 | 0.367 | 71.80 | 16.03 | 89.76 |
| Weighted support‐vector machines | 0.535 | 0.377 | 65.36 | 31.39 | 75.78 |
| Multilayer perceptron | 0.628 | 0.461 | 64.93 | 48.42 | 70.01 |
AUC, area under the receiver operating characteristic curve; AUPRC: area under the precision–recall curve; LACE, length of stay (L), acuity of admission (A), Charlson Comorbidity Index score (C), and number of emergency visits in the last 6 months (E).
Table 3.
The performance of our reproduced prediction models from Frizzell et al.10 on our HF cohort compared with the prediction models of Frizzell et al.10 based on their data (results extracted from the paper)
| Model | Frizzell et al.10 dataset | Our cohort | ||
|---|---|---|---|---|
| AUC | AUC | Sensitivity (%) | Specificity (%) | |
| Logistic regression | 0.62 | 0.56 | 33.18 | 79.92 |
| Random forests | 0.61 | 0.50 | 1.71 | 99.00 |
| LASSO regression | 0.62 | 0.64 | 0.51 | 100 |
| Multilayer perceptron | — | 0.62 | 48.42 | 70.01 |
AUC, area under the receiver operating characteristic curve; HF, heart failure; LASSO, least absolute shrinkage and selection operator; LR, logistic regression; RF, random forest.
Discussion
In our study, we investigated different ML‐based models to predict 30 day HF readmission or death using the linked administrative health data. We report improved performance by using the MLP approach compared with the standard regression model and other ML‐based predictive models. In addition, in our study, we have also taken into consideration the class imbalance issue, which is commonly encountered with medical data.
Several attempts have been made previously to build readmission models for HF taking into account the common limitations seen with this type of datasets. Koulaouzidis et al.23 used the naive Bayes classifier on telemonitored data, such as left ventricular systolic dysfunction, New York Health Association score, co‐morbidities, blood pressure, and medications, to predict HF readmissions. They concluded that weight and diastolic blood pressure are the most useful factors to predict HF readmissions. Mortazavi et al.13 used more sophisticated ML algorithms, such as RF, boosting, and RF combined with SVM to predict 30 and 180 day readmissions (all cause and HF specific). While their boosting model (AUC of 0.68) outperformed the standard logistic regression model (AUC of 0.54) for 30 day HF readmission, the sensitivity of the model was only 0.45, meaning it was only 45% accurate in identifying true HF readmissions. Taking cue from the commonly used two‐stage screening processes in the medical field, Turgeman and May14 presented a hybrid of a C5.0 tree and SVM classifier for predicting HF readmissions, but their model also showed a low sensitivity of 25.8%. Zheng et al.15 used a hybrid of swarm intelligence heuristic and SVM to model readmissions and achieved 78.4% accuracy and 97.3% sensitivity. As their dataset had a class imbalance ratio of 1 to 5, the authors used replication‐based random oversampling technique, which may have limited their study results due to an overfitting problem.24 Futoma et al. used neural network to predict HF readmissions with an imbalanced dataset composing of the diagnosis and procedures assigned for each hospital admission but only presented their models' performance in terms of AUC (0.67), which is not considered to be an adequate performance metric for imbalanced datasets.11, 16
Recently, Frizzell et al.10 compared the effectiveness of ML algorithms and standard regression methods to predict 30 day all‐cause readmissions in HF patients. For regression analysis, they used the logistic regression with backward stepwise selection and logistic regression with LASSO, while for ML analyses, the tree‐augmented naive Bayes network, gradient‐boosted model, and an RF model were used. All the models produced AUCs in the range 0.59–0.62 in their study (Table 3). The authors concluded that ML techniques are unable to outperform the standard regression models to predict HF readmissions. However, the dataset used in their work was imbalanced, and performance metrics other than AUC were not provided. Furthermore, no attempt was made to address the class imbalance problem in their study. We report that our MLP‐based approach has shown ability to outperform the standard regression and other ML algorithms used by Frizzell et al. for the prediction of 30 day HF readmission or death on our data. We first developed prediction models using algorithms used by Frizzell et al. and trained and tested these models on our data. We also developed the weighted versions of the techniques used by Frizzell et al. and trained and tested on our data. The weighted versions improved the predictive performance. We then developed, trained, and tested the new MLP‐based approach, which was not investigated by Frizzell et al. in their work. This MLP‐based approach outperformed all the other approaches based on our data. Furthermore, AUC alone is not the most appropriate measure for an imbalanced dataset. For example, the AUC for the LASSO technique applied to our data yielded an AUC of 0.64, but the sensitivity of this model was only 0.51%. This means that the model can predict an actual readmission or death as a readmission or death with only 0.51% accuracy, which is poor. The LASSO model only learnt to predict the majority group in the data (no readmission or death), thus yielding high specificity close to 100%, but the MLP‐based approach developed in our study is trained to identify both outcomes (classes) and produced better sensitivity than the other models. Therefore, other performance measures such as sensitivity and specificity, when working on datasets with high class imbalance, should be provided. Considering these performance metrics, our MLP‐based approach holistically outperforms the other prediction models.
Lastly, some of the previous studies have reported slightly higher AUCs than ours.9, 11, 13 However, our MLP‐based approach produces a comparable AUC of 0.63 with only 47 variables (vs. hundreds in other studies); signifying more variables may not necessarily lead to better prediction, and basic variables from the core hospitalization and death datasets are sufficient. Of note, the prediction models developed in the previous studies performed poorly on our dataset, highlighting the utility of our MLP approach (Table 3).
Limitations and future work
This work is based on retrospective data that portends some limitations. Because of policy restrictions, some of the clinical data (e.g. heart rate or laboratory values) were missing that could have potentially further improved the model performance. Another limitation of this study was the exclusion of patients younger than 65 years, which allows us to capture complete medication history data of our HF cohort. This study does not deal with the types of HF such as HF with preserved ejection fraction and HF with reduced ejection fraction due to the unavailability of ejection fraction in our administrative data.
Apart from these, for hyperparameter optimization for the grid search, we only considered traditional stepwise range values for the parameters (i.e. the number of layers and the number of neurons). However, the consideration of a performance measure that takes class imbalance problem for parameter tuning can be further investigated.
Conclusions
We show in our study that for Western Australian‐linked administrative medical data with class imbalance, the proposed MLP‐based approach with the right class weight settings is superior to other ML and statistical techniques for the prediction of 30 day HF readmission or death. In our study, we also demonstrate the importance of other performance measures, in addition to the AUC, for medical datasets with a high‐class imbalance while predicting HF readmissions and deaths.
Conflict of interest
None declared.
Funding
This work was supported by the Scholarships for International Research Fees (SIRF) scholarship awarded by the University of Western Australia and funding from a project grant from the National Health and Medical Research Council of Australia (NHMRC Project Grant 1066242).
Ethics
This study complies with the Declaration of Helsinki. Human Research Ethics Committee approvals were received from the Western Australian Department of Health (#2011/62); the Australian Department of Health (XJ‐16); and the University of Western Australia (RA/4/1/1130).
Awan S. E., Bennamoun M., Sohel F., Sanfilippo F. M., and Dwivedi G. (2019) Machine learning‐based prediction of heart failure readmission or death: implications of choosing the right model and the right metrics, ESC Heart Failure, 6: 428–435. 10.1002/ehf2.12419.
This work was performed at the School of Population and Global Health, The University of Western Australia, and Harry Perkins Institute of Medical Research, The University of Western Australia, Australia.
References
- 1. Desai AS, Stevenson LW. Rehospitalization for heart failure: predict or prevent? Circulation 2012; 126: 501–506. [DOI] [PubMed] [Google Scholar]
- 2. Savarese G, Lund LH. Global public health burden of heart failure. Card Fail Rev 2017; 3: 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Dharmarajan K, Hsieh AF, Lin Z, Bueno H, Ross JS, Horwitz LI, Barreto‐Filho JA, Kim N, Bernheim SM, Suter LG, Drye EE, Krumholz HM. Diagnoses and timing of 30‐day readmissions after hospitalization for heart failure, acute myocardial infarction, or pneumonia. JAMA 2013; 309: 355–363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Kocher RP, Adashi EY. Hospital readmissions and the Affordable Care Act: paying for coordinated quality care. JAMA 2011; 306: 1794–1795. [DOI] [PubMed] [Google Scholar]
- 5. Annema C, Luttik M‐L, Jaarsma T. Reasons for readmission in heart failure: perspectives of patients, caregivers, cardiologists, and heart failure nurses. Heart Lung J Acute Crit Care 2009; 38: 427–434. [DOI] [PubMed] [Google Scholar]
- 6. Verhaegh KJ, MacNeil‐Vroomen JL, Eslami S, Geerlings SE, de Rooij SE, Buurman BM. Transitional care interventions prevent hospital readmissions for adults with chronic illnesses. Health Aff 2014; 33: 1531–1539. [DOI] [PubMed] [Google Scholar]
- 7. Auffray C, Balling R, Barroso I, Bencze L, Benson M, Bergeron J, Bernal‐Delgado E, Blomberg N, Bock C, Conesa A, Del Signore S, Delogne C, Devilee P, Di Meglio A, Eijkemans M, Flicek P, Graf N, Grimm V, Guchelaar HJ, Guo YK, Gut IG, Hanbury A, Hanif S, Hilgers RD, Honrado Á, Hose DR, Houwing‐Duistermaat J, Hubbard T, Janacek SH, Karanikas H, Kievits T, Kohler M, Kremer A, Lanfear J, Lengauer T, Maes E, Meert T, Müller W, Nickel D, Oledzki P, Pedersen B, Petkovic M, Pliakos K, Rattray M, I Màs JR, Schneider R, Sengstag T, Serra‐Picamal X, Spek W, Vaas LAI, Van Batenburg O, Vandelaer M, Varnai P, Villoslada P, Vizcaíno JA, Wubbe JPM, Zanetti G. Making sense of big data in health research: towards an EU action plan. Genome Med 2016; 8: 71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Fatima M, Pasha M. Survey of machine learning algorithms for disease diagnostic. J Intell Learn Syst Appl 2017; 9: 1–16. [Google Scholar]
- 9. Bayati M, Braverman M, Gillam M, Mack KM, Ruiz G, Smith MS, Horvitz E. Data‐driven decisions for reducing readmissions for heart failure: general methodology and case study. PloS One 2014; 9: e109264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Frizzell JD, Liang L, Schulte PJ, Yancy CW, Heidenreich PA, Hernandez AF, Bhatt DL, Fonarow GC, Laskey WK. Prediction of 30‐day all‐cause readmissions in patients hospitalized for heart failure: comparison of machine learning and other statistical approaches. JAMA Cardiol 2017; 2: 204–209. [DOI] [PubMed] [Google Scholar]
- 11. Futoma J, Morris J, Lucas J. A comparison of models for predicting early hospital readmissions. J Biomed Inform 2015; 56: 229–238. [DOI] [PubMed] [Google Scholar]
- 12. Jamei M, Nisnevich A, Wetchler E, Sudat S, Liu E. Predicting all‐cause risk of 30‐day hospital readmission using artificial neural networks. PloS One 2017; 12: e0181173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Mortazavi BJ, Downing NS, Bucholz EM, Dharmarajan K, Manhapra A, Li S‐X, Negahban SN, Krumholz HM. Analysis of machine learning techniques for heart failure readmissions. Circ Cardiovasc Qual Outcomes 2016:CIRCOUTCOMES. 116.003039; 9: 629–640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Turgeman L, May JH. A mixed‐ensemble model for hospital readmission. Artif Intell Med 2016; 72: 72–82. [DOI] [PubMed] [Google Scholar]
- 15. Zheng B, Zhang J, Yoon SW, Lam SS, Khasawneh M, Poranki S. Predictive modeling of hospital readmissions using metaheuristics and data mining. Expert Syst Appl 2015; 42: 7110–7120. [Google Scholar]
- 16. Davis J, Goadrich M, editors. The Relationship between Precision–Recall and ROC Curves. Proceedings of the 23rd International Conference on Machine Learning; 2006: ACM: New York, NY, USA. [Google Scholar]
- 17. Holman CAJ, Bass AJ, Rouse IL, Hobbs MST. Population‐based linkage of health records in Western Australia: development of a health services research linked database. Aust N Z J Public Health 1999; 23: 453–459. [DOI] [PubMed] [Google Scholar]
- 18. Gunnell AS, Knuiman MW, Geelhoed E, Hobbs MST, Katzenellenbogen JM, Hung J, Rankin JM, Nedkoff L, Briffa TG, Ortiz M, Gillies M, Cordingley A, Messer M, Gardner C, Lopez D, Atkins E, Mai Q, Sanfilippo FM. Long‐term use and cost‐effectiveness of secondary prevention drugs for heart disease in Western Australian seniors (WAMACH): a study protocol. BMJ Open 2014; 4: e006258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Khan S, Rahmani H, Shah SAA, Bennamoun M, Medioni G, Dickinson S. A Guide to Convolutional Neural Networks for Computer Vision. 2018: Morgan & Claypool Publishers: San Rafael, California (USA). [Google Scholar]
- 20. van Walraven C, Dhalla IA, Bell C, Etchells E, Stiell IG, Zarnke K, Austin PC, Forster AJ. Derivation and validation of an index to predict early death or unplanned readmission after discharge from hospital to the community. Can Med Assoc J 2010; 182: 551–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. The Australian Bureau of Statistics . Socio‐economic indexes for areas. http://www.abs.gov.au/websitedbs/censushome.nsf/home/seifa (27 March 2018).
- 22. The Australian Bureau of Statistics . The Australian Statistical Geography Standard (ASGS) remoteness structure. http://www.abs.gov.au/websitedbs/d3310114.nsf/home/remoteness+structure (15 March 2018).
- 23. Koulaouzidis G, Iakovidis DK, Clark AL. Telemonitoring predicts in advance heart failure admissions. Int J Cardiol 2016; 216: 78–84. [DOI] [PubMed] [Google Scholar]
- 24. Hawkins DM. The problem of overfitting. J Chem Inf Comput Sci 2004; 44: 1–12. [DOI] [PubMed] [Google Scholar]


