Outcome-Weighted Learning for Personalized Medicine with Multiple Treatment Options

Abstract

To achieve personalized medicine, an individualized treatment strategy assigning treatment based on an individual’s characteristics that leads to the largest benefit can be considered. Recently, a machine learning approach, O-learning, has been proposed to estimate an optimal individualized treatment rule (ITR), but it is developed to make binary decisions and thus limited to compare two treatments. When many treatment options are available, existing methods need to be adapted by transforming a multiple treatment selection problem into multiple binary treatment selections, for example, via one-vs-one or one-vs-all comparisons. However, combining multiple binary treatment selection rules into a single decision rule requires careful consideration, because it is known in the multicategory learning literature that some approaches may lead to ambiguous decision rules. In this work, we propose a novel and efficient method to generalize outcome-weighted learning for binary treatment to multi-treatment settings. We solve a multiple treatment selection problem via sequential weighted support vector machines. We prove that the resulting ITR is Fisher consistent and obtain the convergence rate of the estimated value function to the true optimal value, i.e., the estimated treatment rule leads to the maximal benefit when the data size goes to infinity. We conduct simulations to demonstrate that the proposed method has superior performance in terms of lower mis-allocation rates and improved expected values. An application to a three-arm randomized trial of major depressive disorder shows that an ITR tailored to individual patient’s expectancy of treatment efficacy, their baseline depression severity and other characteristics reduces depressive symptoms more than non-personalized treatment strategies (e.g., treating all patients with combined pharmacotherapy and psychotherapy).

I. Introduction

For many chronic diseases including major depressive disorder, substantial treatment heterogeneity has been documented where a treatment with a larger average effect in the overall sample may be ineffective in a subgroup of patients with specific characteristics [1]. On the other hand, a newly developed intervention may not be more efficacious compared to an existing active treatment in the overall population, but may reveal a large benefit in a subgroup of patients [2]. Henceforth, there has been a growing interest in understanding treatment heterogeneity and discovering individualized treatment strategies tailored to patient-specific characteristics to maximize efficacy and achieve personalized medicine [3]. The tailored treatment strategy recommends optimal treatment decision for an individual patient using information collected on patient-specific characteristics which may include genomic features, medical history and health status.

Recently, there has been a surge of machine learning methods on estimating optimal treatment regimes involving a single decision point or multiple decision points using data collected from clinical trials or observational studies [4], [5], [6], [7], [8], [9]. A class of popular methods is regression based Q-learning [10], [11], [6], which relies on some postulated models to predict mean outcome given treatment-by-covariate interactions and then compares these means to select the best treatment. Alternatively, machine learning algorithms, referred to as outcome-weighted learning (O-learning) [8], was proposed to estimate the optimal treatment rule by directly optimizing the expected clinical outcome when assigning treatments using the rule (i.e., value function). O-learning converts the optimal treatment selection to a classification problem. These existing methods are designed to estimate decision rules with two treatment options. However, in many real world applications it is common that more than two treatments are being compared. For example, in our motivating study, Research Evaluating the Value of Augmenting Medication with Psychotherapy (REVAMP) trial [12], non-responders or partial responders to a first-line antidepressant were randomized to three second-line treatment strategies.

When it comes to multiple-armed trials where treatment options are more than two, Q-learning is more prone to model misspecification than for two-armed trials because it relies heavily on the correctness of the postulated models. To extend the O-learning methods in [8], [9], an ad hoc approach is to estimate treatment decision rules via combining one-vs-one (OVO) or one-vs-all (OVA) comparisons. However, it is well known in multicategory learning literature that the resulting classification rules may lead to ambiguous classification for some input space [13], [14], [15], [16], [17]. Therefore, we focus on extending O-learning for binary treatment to learn an optimal individualized treatment rules (ITRs) for multiple treatment options.

In this paper, we propose a new multi-category learning approach to estimate the optimal ITR from multiple treatment options. Specifically, we transform the value maximization problem into a sequence of binary weighted classifications, and refer our method as sequential outcome-weighed multicategory (SOM) learning. At each step, we use a weighted binary support vector machine (SVM) to determine patients for whom a target treatment is optimal compared to the remaining options. The weights in SOM are proportional to the clinical outcome values and reflect the fact that a single treatment category is being compared to one or more categories. We first estimate the optimal rule for a designated treatment option by excluding the possibility of declaring any other treatment as optimal via sequential SVMs; next, we exclude the treatments that have been already screened for optimality and repeat the same learning approach for the remaining options. Theoretically, we show that the derived treatment rule is Fisher consistent, i.e., the derived rule gives the maximal benefit among all treatment rules when the data size is infinite. We demonstrate through extensive simulations that SOM learning has superior performance in comparison to Q-learning, OVA and OVO. Finally, an application of SOM to REVAMP shows that an ITR tailored to individual characteristics such as patients’ expectancy of treatment efficacy and baseline depression severity reduces depressive symptoms more than a non-personalized treatment strategy.

II. Methodology

A. Optimal ITR with multiple treatments

Assume data are collected from a randomized trial of patients affected by a chronic disorder (e.g., depression) with n patients and k different treatment options. For each patient i, we observe a d-dimensional vector of feature variables, denoted by $X_i\in \mathcal{X}$, the treatment assignment $A_i\in \mathcal{A}=\{1,2,\dots ,k\}$, i = 1, …, n, and the clinical outcome after treatment denoted by R_i, also referred as the “reward” (thus the patient’s health outcome is quantified by a scalar). Assume a large value of R_i is desirable (e.g., improvement of patient functioning). A multicategory ITR, denoted by $\mathcal{D}$, is a mapping from the space of feature variables, $\mathcal{X}$, to the domain of treatments, $\mathcal{A}$. An optimal ITR is a treatment assignment rule that maximizes the mean clinical outcome $E[R(\mathcal{D}(X))|X]$, where _R(a) is the potential outcome had treatment a been given. For randomized trials and assuming consistency of the potential outcomes, the optimal ITR maximizes the following value function [6]:

$$E\left[\frac{I\{A=\mathcal{D}(X)\}}{{\pi }_A(X)}R\right],$$ (1)

where π_a(x) = pr(A = a|X = x) is the randomization probability for treatment a as designed in the trial a = 1, …, k, assumed to be bounded by a positive constant from below, and ${\sum }_{a=1}^k{\pi }_a(x)=1$. The goal is to learn the optimal ITR using empirical observations (R_i, A_i, X_i), i = 1, …, n.

Theoretically, it can be shown that the optimal ITR is

$${\mathcal{D}}^{*}(x)={\mathrm{argmax}}_{a}E[R|A=a,X=x].$$ (2)

Therefore, one approach to estimate the optimal ITR is using a regression model to estimate the conditional means on the right-hand side. However, this approach heavily relies on the correctness of the postulated model, and model misspecification can lead to substantially non-optimal ITR even for a binary treatment situation [8]. Alternatively, O-learning [8] was proposed to maximize the empirical version of the value function in (1) but replaced $I(A=\mathcal{D}(x))$ by 1 − max(0, 1 − Af(x)) where f(x) is the decision function such that $\mathcal{D}(x)=\mathrm{sign}(f(x))$. The latter corresponds to a weighted support vector machine where the weight for each observation is proportional to R_i. Because of this connection, the method is referred as outcome-weighted learning (abbreviated as O-learning). They demonstrated that O-learning outperformed the regression model based method in small samples, but this approach can only be applied to estimate binary treatment decisions, and thus not directly applicable when more than two treatment options are of interest. Here, we develop a robust method that builds on binary O-learning to learn multicategory treatment decision rules.

B. Main idea

The main idea of the proposed method, sequential outcome-weighted multicategory (SOM) learning, is to perform a sequence of binary treatment decision learning. The key result is that by applying appropriate subject-specific weights in a binary classification algorithm, each step compares E[R|A = a, X] for a given treatment a with E[R|A = a′,X] for the remaining treatment categories a′ ≠ a. Hence, through a novel arrangement of such comparisons, we can eventually determine the optimal treatment for a patient to be category a* for which E[R|A = a*,X] achieves the maximum among all categories. This coincides with the theoretical optimal treatment rule for this patient as in (2).

To illustrate SOM learning, we order the candidate treatment categories based on the descending order of its prevalence in the observed data. Without loss of generality, we assume that the order of the labels of treatment options are k, k − 1, …, 1. We first learn an optimal treatment rule that will determine whether a patient affected by a chronic disorder (e.g., major depression) should be treated with the kth option. We partition the domain of X into ${\mathcal{X}}_k$ and ${\mathcal{X}}_k^c$ such that for subjects with features $X\in {\mathcal{X}}_k$, the optimal treatment is the kth option; and for subjects with $X\in {\mathcal{X}}_k^c$, the optimal treatment is not the kth option. For the remaining k – 1 options, we consider any ordered sequence of {1, …, k − 1}, denoted by {j₁, …, j_k−1}, and let j_k = k. A sequential ITR learning is then constructed as follows.

In the first step, starting with j₁ versus {j₂, …, j_k}, we determine whether a subject should be treated optimally with the j₁th option or some other option. Since this is a binary decision problem, we can use existing methods for learning a binary treatment decision rule, for example, O-learning, with additional modifications as explained in a later section. Applying this binary rule to a future patient with feature variables X, if he or she is assigned to treatment j₁ ≠ k, then clearly, $X\in {\mathcal{X}}_k^c$. Otherwise, we cannot determine whether X should be in ${\mathcal{X}}_k$ or ${\mathcal{X}}_k^c$, since his/her optimal treatment can be one of j₂, …, j_k.

In the second step of this sequential learning, we only consider patients whose optimal treatments are not determined as j₁ in the previous step. We then learn a binary treatment rule to decide whether this subject should be optimally treated with j₂ or the remaining treatment choices, {j₃, …, j_k}. Again, this is a binary treatment decision problem so we can perform estimation similar to the first step. With the second decision rule, we can check whether the patient should be treated with j₂ or some treatment among the remaining options. If j₂ ≠ k is selected, we conclude $X\in {\mathcal{X}}_k^c$; otherwise, we are still uncertain whether $X\in {\mathcal{X}}_k$.

Continue this process sequentially in the third step till the kth step when there is only treatment category k in consideration. Consequently, for this given sequence, {j₁, …, j_k−1} the optimal treatment for this patient is k, i.e., $X\in {\mathcal{X}}_k$, if and only if at each step, the binary decision learning concludes that the patient should not be treated by j₁, j₂, …, j_k−1, in turn. The choice of the ordered sequence {j₁, …, j_k−1} is arbitrary, so we propose to consider all possible permutations of {1, …, k−1}. Then a patient with X should be treated with treatment k once he/she is determined to have the kth option as the optimal treatment in at least one permuted sequence.

The above procedure only provides a treatment rule that decides whether a subject has the optimal treatment as $k\left(X\in {\mathcal{X}}_k\right)$ or some other option $\left(X\in {\mathcal{X}}_k^c\right)$. Thus, for a subject with features $X\in {\mathcal{X}}_k^c$, we need to determine which of the remaining {1, …, k − 1} options is optimal. This can be carried out as follows. We only consider patients whose optimal treatment is not k based the previous procedure and whose actual treatments received are not k. For these patients, the optimal treatment options can only be one of {1, …, k−1}, so the goal reduces to finding the optimal treatment decision within (k−1) categories. Therefore, we can repeat the previous procedure but consider treatment (k − 1) as the target in treatment optimization. At the end, we obtain a treatment rule that determines whether a subject should be optimally treated with (k−1). Finally, the same procedure can be carried out sequentially to decide which patients have the optimal treatment as (k − 2), …, 1, in turn.

An advantage of SOM learning is that at every step of the sequential learning, one only needs to learn a binary decision rule, and thus many learning algorithms for binary decision are applicable. In particular, in our subsequent algorithm and implementation, we adopt the method from O-learning [8] to use a binary weighted SVM. However, one significant difference is that due to the multicategory nature, weights in SOM learning should not only be proportional to the outcome R as in O-learning, but should also reflect the imbalanced comparison between one treatment category and the combination of multiple treatment categories. The latter ensures that the derived optimal treatment rule is Fisher consistent, i.e., it is the same as the best rule that maximizes the outcome/reward when the data size is infinite, as will be shown in Section 3.

C. Method and algorithm

Start from estimating the optimal rule for a target treatment category k. Consider the jth permutation {j₁, …, j_k−1}, and let j_k = k. The main SOM algorithm is:

Step 1. Learn a binary rule to decide whether a future patient should be treated by option j₁. Intuitively, we shall estimate the optimal decision function $f_{j_1}^{*}(X)$ such that the corresponding value for this decision, i.e.,

$$E\left[RI\left\{Z_{j_1}{f}_{j_1}(X)>0\right\}/{\pi }_A(X)\right],$$

is maximized with Z_j1 = 2I(A = j₁)−1. According to [18], even if R may be negative, this maximization is equivalent to minimize

$$E\left[\left|R\right|I\left\{Z_{j_1}\mathrm{sign}(R)f_{j_1}(X)\le 0\right\}/{\pi }_A(X)\right].$$

Thus, using the empirical data, we may consider minimizing the empirical loss of the above expectation. However, there are two important issues to be considered. First, since solving the above problem is NP-hard, we can use a weighted SVM which essentially replaces the 0–1 loss with a continuous and convex hinge-loss function. Second, since this learning is comparing one treatment category versus (k−1) categories, it is necessary to weight observations with treatment j₁ by (k−1)/k and the others by 1/k in order to balance the comparison.

Therefore, our algorithm is as follows. Define π_jl (x) = pr(A = j_l|X = x), where l = 1, …, k, and let Z_ijl = 2I(A_i = j_l) – 1. Estimate the optimal decision rule as $\mathrm{sign}\left({\widehat{f}}_{j_1}(x)\right)$, where ${\widehat{f}}_{j_1}(x)$ minimizes the following empirical risk of a weighted hinge loss:

$$\begin{gathered} V_{n{j}_1}(f)=n^{-1}\sum _{i=1}^n[\frac{\left|R_i\right|}{{\pi }_{j_1}\left(X_i\right)}I\left\{Z_{i{j}_1}\mathrm{sign}\left(R_i\right)=1\right\}{\left\{1-f\left(X_i\right)\right\}}_{+} \\ \times \left\{\frac{k-1}{k}I\left(R_i>0\right)+\frac{1}{k}I\left(R_i\le 0\right)\right\} \\ +\frac{\left|R_i\right|}{{\pi }_{j_1}^{*}\left(X_i\right)}I\left\{Z_{i{j}_1}\mathrm{sign}\left(R_i\right)=-1\right\}{\left\{1+f\left(X_i\right)\right\}}_{+} \\ \times \left\{\frac{1}{k}I\left(R_i>0\right)+\frac{k-1}{k}I\left(R_i\le 0\right)\right\}] \\ +{\lambda }_{n{j}_1}\Vert f{\Vert }^2, \end{gathered}$$

where ${\pi }_{j_1}^{*}\left(X_i\right)={\sum }_{l=2}^{k}I\left\{A_i=j_l\right\}{\pi }_{j_l}\left(X_i\right)$ is the hinge loss, ∥ · ∥ denotes a semi-norm for f and ${\mathrm{\lambda }}_{n{j}_1}$ is a tuning parameter. Particularly, consider a linear decision rule, i.e., f(x) = β^T x + β₀, ∥f∥ is chosen as the Euclidean norm of β; if a nonlinear decision rule is desired, f will be chosen from a reproducing kernel Hilbert space (RKHS) and ∥f∥ is the corresponding norm in that space.

Step 2. Determine the optimal decision to be either treatment j₂ or one of {j₃, …, j_k} among those patients whose optimal treatments are not determined as j₁ from step 1. Thus, restrict the data to those subjects who do not receive the j₁th treatment and whose optimal treatments are not j₁ as from the previous step. We then estimate a decision rule as $\mathrm{sign}\left({\widehat{f}}_{j_2}(x)\right)$ using a weighted SVM by minimizing

$$\begin{gathered} V_{n{j}_2}(f)=n^{-1}\sum _{i=1}^{n}I\left\{A_i\ne j_1,{\widehat{f}}_{j_1}\left(X_i\right)<0\right\} \\ \times [\frac{\left|R_i\right|}{{\pi }_{j_2}\left(X_i\right)}I\left\{Z_{i{j}_2}\mathrm{sign}\left(R_i\right)=1\right\}{\left\{1-f\left(X_i\right)\right\}}_{+} \\ \times \left\{\frac{k-2}{k-1}I\left(R_i>0\right)+\frac{1}{k-1}I\left(R_i\le 0\right)\right\} \\ +\frac{\left|R_i\right|}{{\pi }_{j_2}^{*}\left(X_i\right)}I\left(Z_{i{j}_2}\mathrm{sign}\left(R_i\right)=-1\right){\left\{1+f\left(X_i\right)\right\}}_{+} \\ \times \left\{\frac{1}{k-1}I\left(R_i>0\right)+\frac{k-2}{k-1}I\left(R_i\le 0\right)\right\}] \\ +{\lambda }_{n{j}_2}\Vert f{\Vert }^2, \end{gathered}$$

where ${\pi }_{j_2}^{*}\left(X_i\right)={\sum }_{l=3}^{k}I\left\{A_i=j_l\right\}{\pi }_{j_l}\left(X_i\right),Z_{i{j}_l},{\pi }_{j_l}\left(X_i\right)$ are defined as same as in step 1, and λ_nj2 is a tuning parameter. Note that in addition to weights based on the outcome values, we also weigh the observations from treatment j₂ by (k − 2)/(k − 1) and the others by 1/(k − 1) in order to account for the fact that the decision rule is based on comparing one category versus (k − 2) categories.

Step 3. In turn, at step h = 3, …, k − 1, we obtain the rule as $\mathrm{sign}\left({\widehat{f}}_{jh}(x)\right)$ by minimizing

$$\begin{gathered} V_{n{j}_h}(f)= \\ \frac{1}{n}\sum _{i=1}^{n}I\left\{A_i\ne j_1,\dots ,\ne j_{h-1},{\widehat{f}}_{j_1}\left(X_i\right)<0,\dots ,{\widehat{f}}_{j_{h-1}}\left(X_i\right)<0\right\} \\ \times [\frac{\left|R_i\right|}{{\pi }_{j_h}\left(X_i\right)}I\left\{Z_{i{j}_h}\mathrm{sign}\left(R_i\right)=1\right\}{\left\{1-f\left(X_i\right)\right\}}_{+} \\ \times \left\{\frac{k-h}{k-h+1}I\left(R_i>0\right)+\frac{1}{k-h+1}I\left(R_i\le 0\right)\right\} \\ +\frac{\left|R_i\right|}{{\pi }_{j_h}^{*}\left(X_i\right)}I\left\{Z_{i{j}_h}\mathrm{sign}\left(R_i\right)=-1\right\}{\left\{1+f\left(X_i\right)\right\}}_{+} \\ \times \left\{\frac{1}{k-h+1}I\left(R_i>0\right)+\frac{k-h}{k-h+1}I\left(R_i\le 0\right)\right\}] \\ +{\lambda }_{n{j}_h}\Vert f{\Vert }^2, \end{gathered}$$

where ${\pi }_{j_h}^{*}\left(X_i\right)={\sum }_{l=h+1}^{k}I\left\{A_i=j_l\right\}{\pi }_{j_l}\left(X_i\right),Z_{i{j}_l},{\pi }_{j_l}\left(X_i\right)$ are defined as same as above steps. Again, we use weight (k − h)/(k − h+1) for treatment j_h versus 1/(k − h+1) for the others to balance comparison. At the end of this sequence, we conclude that if

$${\widehat{f}}_{j_1}(x)<0,{\widehat{f}}_{j_2}(x)<0,\dots {\widehat{f}}_{j_{k-1}}(x)<0,$$

then the optimal treatment for a patient with features x will be the kth option. To simplify notation, we denote ${\widehat{\mathcal{D}}}_{\left(j_1,\dots ,j_{k-1}\right)}^k(x)=1$ if the above conditions hold, and let ${\widehat{\mathcal{D}}}_{\left(j_1,\dots ,j_{k-1}\right)}^k(x)=-1$ otherwise.

The choice of this sequential decision rule is based on the permutation (j₁, …, j_k−1), and thus may not exhaust the correct optimal treatment assignment for the kth option due to a specific choice. We thus repeat the above sequential learning for any possible permutations to obtain ${\widehat{\mathcal{D}}}_{\left(j_1,\dots ,j_{k-1}\right)}^k(x)$. Consequently, our final decision rule is to assign a patient with treatment k if and only if ${\widehat{\mathcal{D}}}_{\left(j_1,\dots ,j_{k-1}\right)}^k(x)=1$ for at least one permutation (j₁, …, j_k−1). Let Π_s denote all permutations of (1, …, s). If we define

$${\widehat{\mathcal{D}}}^k(x)=\underset{\left(j_1,\dots ,j_{k-1}\right)\in {\Pi }_{k-1}}{\max }{\widehat{\mathcal{D}}}_{\left(j_1,\dots ,j_{k-1}\right)}^k(x),$$

then the optimal treatment for patient with x is treatment k if and only if ${\widehat{\mathcal{D}}}^k(x)=1$.

Step 4. To determine whether a patient’s optimal treatment is the (k − 1)th option, we adopt a backward elimination procedure. We exclude the patients who receive treatment option k or whose optimal treatments are determined as k in the previous step. In other words, we restrict the data to subjects with A_i ≠ k and ${\widehat{\mathcal{D}}}^k\left(x_i\right)=-1.$. Because the data consist of only (k − 1) treatment options, we use the same SOM learning procedure as before but now set option (k − 1) as the target treatment, i.e., the last category in consideration. By this procedure, we obtain a decision rule at each step for each permutation of {1,.., k – 2}, denoted by ${\widehat{\mathcal{D}}}_{\left(j_1,\dots ,j_{k-2}\right)}^{(k-1)}(x)$ for permutation (j₁, …, j_k−2). Let

$${\widehat{\mathcal{D}}}^{(k-1)}(x)=\underset{{}_{\left(j_1,\dots ,j_{k-2}\right)\in {\Pi }_{k-2}}}{\max }{\widehat{\mathcal{D}}}_{\left(j_1,\dots ,j_{k-2}\right)}^{(k-1)}(x).$$

Consequently, the optimal treatment for a patient with x is (k − 1) if and only if ${\widehat{\mathcal{D}}}^{(k-1)}(x)=1$ and ${\widehat{\mathcal{D}}}^{(k)}(x)=-1$.

Step 5. Continue this backward elimination and sequential learning in turn for treatment (k − 2), …, 1 so as to obtain ${\widehat{\mathcal{D}}}^{(k-2)}(x),\dots ,{\widehat{\mathcal{D}}}^1(x)$. Our final estimated optimal ITR is

$$\widehat{\mathcal{D}}(x)=\{\begin{array}{ll}k\hfill & {\widehat{\mathcal{D}}}^{(k)}(x)=1\hfill \\ k-1\hfill & {\widehat{\mathcal{D}}}^{(k)}(x)=-1,{\widehat{\mathcal{D}}}^{(k-1)}(x)=1\hfill \\ ⋮\hfill & ⋮\hfill \\ 2\hfill & {\widehat{\mathcal{D}}}^{(k)}(x)=-1,\dots ,{\widehat{\mathcal{D}}}^{(3)}(x)=-1,{\widehat{\mathcal{D}}}^{(2)}(x)=1\hfill \\ 1\hfill & {\widehat{\mathcal{D}}}^{(k)}(x)=-1,\dots ,{\widehat{\mathcal{D}}}^{(3)}(x)=-1,{\widehat{\mathcal{D}}}^{(2)}(x)=-1.\hfill \end{array}$$

We summarize the algorithm for k-category SOM learning in Algorithm 1. We note that because of the sequential exclusion of subjects, the size of the input data decreases in a proportional fashion in each step of SOM. Therefore, SOM can be computationally efficient due to the fast implementation of SVM and reduced data sizes in each step. In our numeric examples, SVM at each step is implemented using quadratic programming tools in MATLAB. MATLAB codes to implement SOM are available at http://www.columbia.edu/~yw2016/code_SOM.zip.

We note that SOM learning requires a total of ${\sum }_{l=1}^k(l-1)\times (l-1)!=k!-1$ weighted binary SVM classifications. Thus, the computational cost increases exponentially with the number of treatment categories. However, because of the sequential exclusion of subjects, the size of the input data decreases in a proportional fashion so that computation is faster at each step.

III. Theoretical Justification

In this section, we first establish the Fisher consistency of the optimal ITR estimated using SOM learning. Next, we obtain a risk bound for the estimated ITR and show how the bound can be improved in certain situations.

Algorithm 1: Sketch of SOM Learning Algorithm

Backward loop: for a target treatment category s ∈ {k, …, 1}, do

Inner loop: for each permutation of the remaining treatment assignments except the previously classified ones and target treatment label s, perform a sequence

of weighted O-learning to learn $\widehat{\mathcal{D}}\left(j_1,\dots ,j_{s-1}\right)(x)$for each permutation (j1, …, js) of {1, …, s}.

Collect all rules to obtain $${\widehat{\mathcal{D}}}^s(x)=\underset{\left(j_1,\dots ,j_{s-1}\right)\in {\Pi }_{s-1}}{\max }{\widehat{\mathcal{D}}}_{\left(j_1,\dots ,j_{s-1}\right)}^s(x).$$

After eliminating all samples with observed treatment labels as previously considered treatment or whose optimal treatments are within any of the previous categories, go to

the backward loop step.

A. Fisher consistency

We provide the Fisher consistency for the proposed SOM learning. That is, when the sample size is infinity, we show that the derived ITR is the same as the true optimal ITR

$${\mathrm{argmax}}_{l=1}^{k}E(R|X=x,A=l).$$

Let $f_{j_l}^{*}(x)$ be the counterpart of ${\widehat{f}}_{j_l}(x)$ in the SOM learning procedure when n = ∞ and the tuning parameters vanish. Let ${\mathcal{D}}_{\left(j_1,\dots ,j_s\right)}^{*l}(x)$ and ${\mathcal{D}}^{*l}(x)$ be the corresponding limits of ${\widehat{\mathcal{D}}}_{\left(j_1,\dots ,j_s\right)}^l(x)$ and ${\widehat{\mathcal{D}}}^l(x)$, respectively, when n = ∞. Then the limit of the ITR from SOM learning is

$${\mathcal{D}}^{*}(x)=\{\begin{array}{cc}k& {\mathcal{D}}^{*(k)}(x)=1\\ k-1& \left\{{\mathcal{D}}^{*(k)}(x)=-1,{\mathcal{D}}^{*(k-1)}(x)=1\right\}\\ ⋮& ⋮\\ 2& \{{\mathcal{D}}^{*(k)}(x)=-1,\dots ,{\mathcal{D}}^{*(3)}(x)=-1\\ & {\mathcal{D}}^{*(2)}(x)=1\}\\ 1& \{{\mathcal{D}}^{*(k)}(x)=-1,\dots ,{\mathcal{D}}^{*(3)}(x)=-1\\ & {\mathcal{D}}^{*(2)}(x)=-1\}.\end{array}$$

The following result holds.

Theorem 1: SOM learning rule ${\mathcal{D}}^{*}(X)$ is Fisher consistent. That is, ${\mathcal{D}}^{*}(x)=l$ if and only if $E\left(R\right|X=x,A=l)={\max }_{h=1}^{k}E(R|X=x,A=h)$ for l = 1, …, k.

Theorem 1 provides a theoretical justification that SOM yields the true optimal ITR asymptotically. The proof of Theorem 1 is given in the appendix. The key result is to show that at each step of SOM learning, we compare the conditional mean E[R|X, A = j₁] with the average value of E[R|X, A = j₂], where j₁ is the target treatment category in consideration at this step and j₂ is any treatment category among the remaining options.

B. Risk bounds

For any ITR $\mathcal{D}(x)$ associated with decision function $\mathcal{D}(x)$, define

$$\mathcal{R}(\mathcal{D})=E\left[\frac{R}{{\pi }_A(X)}I\{A\ne \mathcal{D}(X)\}\right]$$

where $j=1,\dots ,k,{\pi }_A(x)={\sum }_{j=1}^{k}I(A=j)pr(A=j|x)$; and let ${\mathcal{R}}^{*}=\mathcal{R}\left({\mathcal{D}}^{*}\right)$. Clearly, $\mathcal{R}(\mathcal{D})$ and ${\mathcal{R}}^{*}$ correspond to E[R] subtracting the value function for $\mathcal{D}$ and ${\mathcal{D}}^{*}$, respectively. In the section, we will derive the convergence rate of the estimated value function from the optimal value, which is equivalent to $\mathcal{R}(\widehat{\mathcal{D}})-{\mathcal{R}}^{*}$, under some regularity conditions and assuming that the functional spaces for f_jl in SOM learning are from a RKHS with Gaussian kernel and bandwidth 1/σ_n.

For any l and subset S in {1, …, k} where $l\notin \mathcal{S}$, we define

$${\eta }_{l,\mathcal{S}}(x)=\frac{E(R|X=x,A=l)}{|\mathcal{S}{|}^{-1}{\sum }_{h\in \mathcal{S}}E(R|X=x,A=h)},$$

where $|\mathcal{S}|$ denotes the cardinality of S. That is, η_l,S(x) is the ratio between the mean outcome of the treatment arm _l and the average mean outcome of the treatment options from S. We assume that the following conditions hold:

Condition 1: (Geometric noise conditions) There exist q, β > 0, and a constant c such that for any l and set $\mathcal{S}$ with $l\notin \mathcal{S}$, it holds that

$$r\left\{\left|{\eta }_{l,\mathcal{S}}(X)-1\right|<t\right\}\le {(ct)}^q,$$

and moreover,

$$E\left\{\exp \left(-\frac{\Delta {(X)}^2}{t}\right)\left|{\eta }_{l,S}(X)-1\right|\right\}\le c{t}^{\beta },$$

where Δ(X) denotes the distance from X to the boundary defined as {x : η_l,S(x) = 1}.

Condition 2: The distribution of X satisfies tail component condition pr(|X| ≥ r) ≤ cr^−τ for some τ ∈ (0, ∞] and E(|R||A = a, X = x) is uniformly bounded away from zero and infinity.

Condition 3: There exists λ_n such that λ _n → 0 and nλ_n → ∞. Moreover, all tuning parameters λ_nj ’s in SOM satisfy M⁻¹λ_n ≤ λ_nj ≤ Mλ_n for a positive constant M. We further assume σ_n → ∞.

Remark 1: In condition 1, the constants q and β are called noise exponent and marginal noise exponent, respectively. They are used to characterize the data distribution near the decision boundary at each step of SOM where we compare treatment j_l versus any subset of {j_l+1, …, j_k}. In particular, when the boundary is fully separable, that is, |η_l,S − 1| > δ₀ for a constant δ₀, these conditions hold for q = β = ∞. In condition 2, τ describes the decay of the distribution of X. When X is bounded, τ = ∞. Condition 3 characterizes the choice of tuning parameter and bandwidth in RKHS. We choose this simplification for convenience, although we can allow the tuning parameter and bandwidth to be different for each treatment decision in the proposed method. Note that these conditions are similar to the ones used to establish the convergence rate for the two treatment decision probem in [8]. When R = 1, these conditions reduce to the conditions for deriving the convergence rate in support vector machine given in [19]. Under conditions 1–3, the following theorem holds.

Theorem 2: Under conditions 1–3, for any ϵ₀ > 0, d/(d + τ) < p ≤ 2, there exists a constant C such that for any ϵ > 1 and ${\sigma }_n={\lambda }_n^{-q/(2\beta (1+q))}$, with probability at least 1 − e^−ϵ,

$$\mathcal{R}(\widehat{\mathcal{D}})\le {\mathcal{R}}^{*}+C{\left\{{\lambda }_n^{-\frac{2}{2+p}+\frac{(2-p)\left(1+{ϵ}_0\right)}{(2+p)(1+q)}}{n}^{-\frac{2}{2+p}}+\frac{ϵ}{n{\lambda }_n}+{\lambda }_n^{\frac{q}{1+q}}\right\}}^{\frac{q}{1+q}}$$

Remark 2: Suppose that X is bounded such that τ = ∞ in condition 2. By choosing the optimal λ_n for the last two terms on the right-hand side, i.e., λ_n = n^{−(1+q)/(1+2q)}, we find that the convergence rate is n^−q/(1+2q). Furthermore, if the separating boundaries are all completely separable such that q = ∞, then the convergence rate is close to the square-root-n rate.

IV. Related Work

When setting R = 1 and letting (A|X) be a constant, maximizing (1) is equivalent to solving a multi-classification problem where A is the class label and X is the vector of feature variables. Therefore, SOM also provides a sequential procedure to extend binary SVM to multicategory classification. This is different from existing multicatory classification methods that convert the multicategory classification into sequential binary problems such as OVA and OVO [13], [14], [15]. The latter methods are relatively simple to implement by using existing off-the-shelf techniques for binary classifications, although OVO requires significantly more computational time than OVA [20], [21]. However, for both OVA and OVO, an input sample may be assigned to multiple classes, so ad hoc procedures are required to resolve the inconsistency. It is not guaranteed that OVO and OVA will achieve the optimal Bayesian error rate. Another line of work carries out multicategory learning by optimizing a single loss function so as to obtain a simultaneous multicategory objective function [22], [23], [16]. The computational challenge of such approaches is to learn multiple decision boundaries at the same time and all existing algorithms no longer enjoy the flexibility and simplicity of many binary classifiers. Finally, we note that for SOM, the weights related to classification, 1/(k − h+1), can be replaced by any weights w_j that satisfies ${\sum }_{j=1}^{k-h+1}{w}_j=1$. In particular, by taking w_j = 1 for the hth target category and 0 for other categories, the computation of SOM reduces to OVO. However, the construction of the final decision rule for SOM and OVO is completely different.

V. Experiments

A. Simulated Data

We conduct extensive simulation studies from two settings to examine the small-sample performance of SOM. In the first simulation setting, 20 feature variables are simulated from a multivariate normal distribution, where the first 10 variables X₁, X₂, …, X₁₀ have a pairwise correlation of 0.8, the remaining 10 variables are uncorrelated, and the marginal distribution for each variable is N(0, 1). We generate 3-category random treatment assignments with equal probability, i.e. pr(A = 1|X) = pr(A = 2|X) = pr(A = 3|X) = 1/3. The clinical outcomes are generated as: $R=X_4+\left(X_2^2-X_1^2\right)I(A=2)+X_3^{3}I(A=3)+0.5\times N(0,1)$.

In the second simulation setting, we simulate data to imitate patient heterogeneity as observed in real world studies under a latent class model similar to [18] and [9]. The patient population consists of a finite number of latent subgroups for which the optimal treatment rule is the same within each subgroup. Specifically, we consider 10 latent groups and the true optimal treatment category of each group is, in turn, A* = 3, 3, 1, 2, 2, 1, 2, 3, 3, 1. To generate data mimicking a three-arm randomized trial, for each subject, the observed treatment assignment A is randomly generated with an equal probability. The clinical outcome is generated as R = 4×I(A = A*)−1+ 0.5 × N(0, 1). Furthermore, we imitate a common real world scenario where the treatment mechanism may not be known and thus the latent subgroup labels are not observed: instead of directly using group labels as observed feature variables, we generate feature variables that are informative of the latent group membership as observed data. We simulate 30 feature variables from a multivariate normal distribution, where the first 10 variables X₁, X₂, …, X₁₀ have a pairwise correlation of 0.8, the remaining 20 variables are uncorrelated, and the variance for each variable is 1. Moreover, X₁, X₂, …, X₁₀ have mean values of μ_l for the latent group l, which are generated from N(0, 5), while the means of X₁₁, …, X₃₀ are all zeros. Therefore, only X₁, X₂, …, X₁₀ are informative of the optimal treatment labels due to different μ_l. The observed data for each subject consist of the treatment assignment A, the feature variables X₁, …, X₃₀, and the clinical outcome R.

For each simulated data, we apply SOM learning to estimate the optimal ITR. At each step, we fit a weighted SVM with a linear kernel. The tuning parameter is chosen using cross-validation. Furthermore, we compare SOM regression-based Q-learning, OVA and OVO based on the value function (reward) of the estimated optimal treatment rules. Q-learning is obtained by fitting a linear model, regressing R on X, A and their interactions, in which A is replaced by dummy variables created for each category of A. For OVA and OVO, to ensure the rewards are positive, we use the absolute value of rewards as weights, and at each binary step, new labels are created by multiplying the original labels with the sign of reward. This approach is extracted from our SOM learning. Because both OVO and OVA algorithms break multi-treatment problem down to binary ones, the main drawback is that if a subject is assigned to different treatments in the binary classifications, the final assignment will be the one with the smallest label value. For each setting, we compare the four methods with different sample sizes: n =300, 600, and 900.

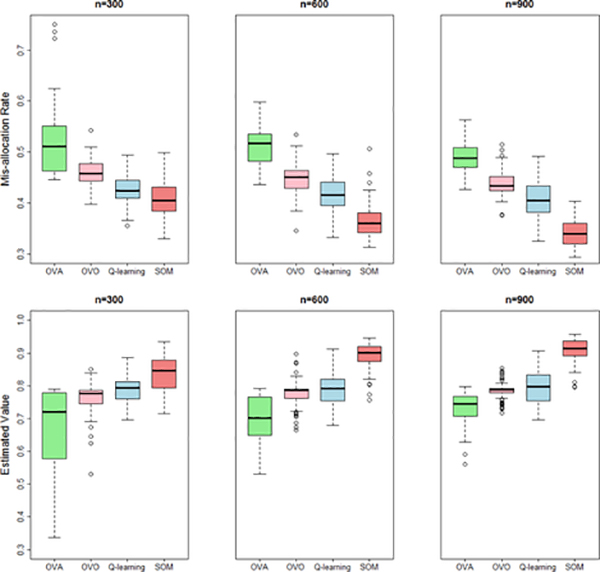
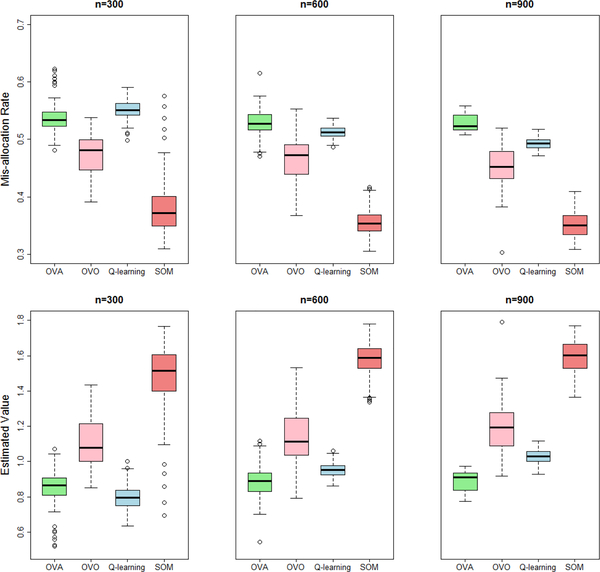
Figures 1 and 2 present the results of the optimal treatment mis-allocation rates and the estimated value functions from 100 replicates and difference sample sizes, which are computed in an independently generated test data of size 3 million. In both settings, the regression model in Q-learning is misspecified, so it performs worse under all sample sizes. Instead, SOM learning outperforms the competitors including OVA and OVO in all the simulation settings. For SOM learning, we also used Gaussian kernel when training binary weighted SVMs and found negligible differences from using linear kernel. However, since computational burden using the former is much more intensive, we recommend to use linear kernel in practice.

Fig. 1:

Simulation setting 1 (clinical outcome simulated from a regression model). Box plots of the optimal treatment mis-allocation rates and value functions (higher better) on independent testing data of ITR constructed by SOM, Q-learning, OVA and OVO (with sample size of 300, 600, and 900).

Fig. 2:

Simulation setting 2 (clinical outcome simulated from a latent class model). Box plots of the optimal treatment mis-allocation rates and value functions (higher better) on independent testing data of ITR constructed by SOM, Q-learning, OVA and OVO (with sample size of 300, 600, and 900).

To compare the running time of different methods, we performed a simulation study under the same setting as [16] with 3 categories (Figure 1 in [16]). The reward weights were set as a constant of one. On a Linux-based computing system with 2-core, 2.40 GHz Intel processor, the average CPU running time for SOM (without subject-specific weights), OVA, [23] and [16] are: 0.4, 1, 14, 26 seconds, respectively. The average test errors are 29.4%, 41.7%, 32.0%, 34.0% on independent testing data (Bayes error 28.5%). SOM not only achieves the lowest testing error but also runs the fastest.

B. Real World Data: REVAMP Study

We obtained data from a real world study of major depression, REVAMP trial [12], to evaluate the performance of various methods (data access information available at https://ndar.nih.gov/edit_collection.html?id=2153). The study aimed to evaluate the efficacy of adjunctive psychotherapy to treat patients with chronic depression who have failed to fully respond to the initial treatment with an antidepressant medication. Among 808 participants in phase I of REVAMP, 491 were nonresponders or partial responders and entered phase II of the study. At phase II, these 491 participants were then randomized to receive continued pharmacotherapy and augmentation with brief supportive psychotherapy (MEDS+BSP), continued pharmacotherapy and augmentation with cognitive behavioral analysis system of psychotherapy (MEDS+CBASP), or continued pharmacotherapy (MEDS) alone. Patients were followed for 12 weeks. The primary outcome was the Hamilton Scale for Depression (HAM-D) scores at the end of 12-week follow-up. There were 17 baseline feature variables including participants’ demographics, patient’s expectation of treatment efficacy, social adjustment scale, mood and anxiety symptoms, and depression experience, as well as phase I depressive symptom measures such as rate of change in HAM-D score over phase I, HAM-D score at the end of phase I, rate of change of Quick Inventory of Depression Symptoms (QIDS) scores during phase I, and QIDS at the end of phase I.

After excluding participants with missing data (assuming missing completely at random), the final analysis consists of 318 participants, among whom 134, 123, and 61 were assigned to MEDS+BSP, MEDS+CBASP, and MEDS, respectively. The mean HAM-D at the end of phase II for the non-personalized treatment rule assigning all patients to each of the three treatments is summarized in Table I. Treating all patients by MEDS+CBASP has the lowest post-treatment HAM-D score, but there is no statistically significant differences in the changes of HAM-D scores during phase II between the 3 treatment rules [12].

Table I:

Mean (standard deviation) of the HAM-D under non-personalized treatment assignment and value function of ITR (2-fold cross-validation with 500 repetitions)

Treatment†	MEDS+ BSP	MEDS+ CBSP	MEDS ONLY
Value*	13.51(0.05)	10.75(0.05)	12.66(0.13)
Method	SOM	Q-learning	OVA	OVO
Value*	8.91(2.91)	16.16(2.64)	12.18(1.67)	10.85(2.24)

^†Treatment arm under the designed non-personalized, random assignment rule.

^*Value function is the average HAM-D score at the end of phase II for patients following an estimated optimal treatment (smaller HAM-D indicates a better outcome) in the testing samples.

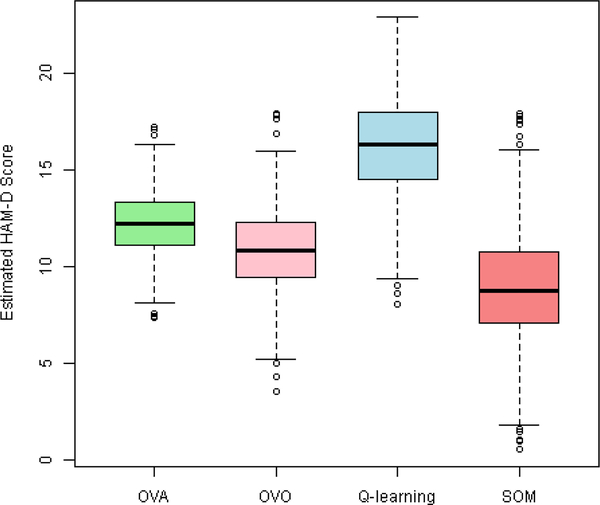
Our analysis goal is to estimate the optimal ITR among three different options depending on 17 baseline feature variables, so that the value function (average HAM-D scores) under the ITR can be as low as possible. All feature variables are standardized before the analyses. We apply SOM learning and compare with Q-learning that uses (1, X, A, X A) in the regression model, where X represents feature variables and A is the randomized treatment assignments, as well as OVA and OVO. The expected HAM-D for an ITR is calculated from 2-fold cross-validation with 500 replicates: at each replicate, we randomly split the data into a training sample and a testing sample; we then apply SOM to learn the optimal ITR using the training data and compute the expected value in the testing sample under this estimated rule. The averages of the cross-validated value functions from four methods are presented in Table I, and their distributions over cross-validations are plotted in Figure 3. With a value function of 8.91, the SOM learning achieves the lowest HAM-D compared to Q-learning, OVA, OVO, and any of the non-personalized rules. For example, treating patients using the SOM estimated ITR according to their individual characteristics will reduce HAM-D by 17% compared to treating all patients by MEDS+CBASP (8.91 points versus 10.75 points), and the reduction is also substantial compared to OVA and OVO (27% and 18%).

Fig. 3:

Box plot of the value function for the optimal ITR estimated by various methods from 2-fold cross-validation with 500 repetitions using REVAMP data: HAM-D score after phase II treatment (a smaller score indicates a better outcome).

There are 99, 103, and 116 patients predicted to have MEDS+BSP, MEDS+CBASP, and MEDS alone as the optimal treatment, respectively. Table II presents the coefficients of the 5 submodels derived from SOM learning rule in the REVAMP study. Model 1 and model 2 correspond to the 2 permutations of the inner loop, determining whether a subject should be optimally assigned to MEDS only or not. After eliminating the possibility of being assigned to MEDS only, model 3 assigns a subject into MEDS+BSP or MEDS+CBASP treatment. Let ${\widehat{\beta }}_{11}$, ${\widehat{\beta }}_{12}$, ${\widehat{\beta }}_{21}$, ${\widehat{\beta }}_{22}$, ${\widehat{\beta }}_3$ be the estimated coefficients of model 1(1), 1(2), 2(1), 2(2) and 3, respectively. A patient will be assigned with: MEDS if $\left\{X^T{\widehat{\beta }}_{11}<0,X^T{\widehat{\beta }}_{12}<0\right\}$, or $\left\{X^T{\widehat{\beta }}_{21}<0,X^T{\widehat{\beta }}_{22}<0\right\}$; MEDS+CBASP if not assigned to MEDS and $X^T{\widehat{\beta }}_3<0$; MEDS+BSP if not assigned to MEDS and $X^T{\widehat{\beta }}_3>0$.

Table II:

Coefficients of decision rules from SOM in REVAMP (ranked by the overall effect of a feature variable).

Feature Variable	Model 1(1)	Model 1(2)	Model 2(1)	Model 2(2)	Model 3	Norm*
QISD phase I change	− 0.1281	0.0765	0.1200	2.2308	− 0.1338	2.2430
HAM-D phase I change	− 0.0063	0.0050	0.0285	1.7769	− 0.0252	1.7773
Gender (Male)	− 0.2726	− 0.0565	− 0.0880	− 1.0370	0.0753	1.0800
Phase I response	− 0.2269	− 0.0147	0.0166	− 0.7567	− 0.0382	0.7913
Tx efficacy expectation	0.4010	0.1026	0.1232	0.5791	0.0268	0.7229
CBASP expectation	− 0.2767	− 0.0153	0.0093	− 0.6371	− 0.1444	0.7097
History of drug abuse	0.3187	0.0199	0.0017	0.5644	0.0648	0.6517
Current alcohol use	0.3159	0.0100	− 0.0801	0.0877	0.2214	0.4038
Social adjustment	0.0813	0.0481	0.1075	− 0.3202	− 0.0207	0.3513
BSP expectation	0.1498	− 0.0349	− 0.0542	0.2703	0.1087	0.3338
Freq of side effects	− 0.0189	0.1816	0.1394	0.0909	− 0.1199	0.2746
QISD end of phase I	0.1999	− 0.0216	− 0.0796	0.1259	0.1005	0.2697
Anxious Arousal	0.0957	0.1316	0.1227	0.0850	− 0.0069	0.2209
General Distress	− 0.0975	− 0.0900	− 0.0954	− 0.0844	− 0.0085	0.1842
HAMD end of phase I	− 0.0449	− 0.0101	0.0108	− 0.0798	− 0.0520	0.1063
Dysfunctional Attitudes	− 0.0099	0.0041	0.0058	− 0.0108	− 0.0049	0.0170
Age	0.0017	− 0.0001	− 0.0009	0.0011	0.0018	0.0029

^*“Norm” measures the overall effect of a variable on the optimal treatment assignment rule as the L₂ norm of all coefficients for predicting each model.

The column “Norm” in Table II reports the overall effect of feature variables on the optimal treatment decision rule as the L₂-norm of all coefficients for predicting each model. The overall most predictive variable in estimating the optimal ITR as determined by the norm is phase I QISD rate of change, followed by phase I HAM-D rate of change. Both variables are most predictive of patients with MEDS alone as the optimal choice compared to two other combined pharmacotherapy and psychotherapy. Gender, response at phase I, patients expectancy of treatment efficacy, and CBASP expectation are also informative with an overall effect size greater than 0.7. Gender is also most predictive of MEDS alone versus two combined therapies with females favoring the latter. Other predictive variables include history of drug abuse and current alcohol use. No feature variable has a substantially large effect in model 3, implies that potentially many variables are in play to distinguish MEDS only versus the other two combined therapies. In a recent analysis of another randomized trial on major depressive disorder comparing Nefazodone, CBASP, and the combination of the two treatments, obsessive compulsive and past history of alcohol dependence [24], race, and education level [25] are identified as predictive by Q-learning, which partially corroborates our findings. Our analyses identify several additional feature variables as informative.

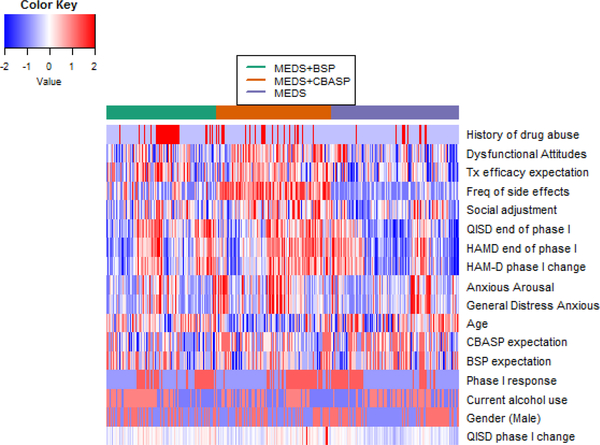
To further visualize the relationship between feature variables and the optimal treatment for each individual, in Figure 4 we present the heatmap of 17 standardized feature variables by predicted optimal treatment on all subjects. The history of drug abuse has a different pattern between patients with MEDS+BSP as the optimal choice and patients in the other two groups (more prevalent in the former versus the latter groups), and thus may be informative of distinguishing MEDS+BSP versus others; dysfunctional attitudes, and patient’s treatment efficacy expectation, frequency of sides effects, HAM-D rate of change during phase I, QIDS and HAM-D end of phase I score are informative for distinguishing all three treatments. It is clear that no single variable has a dominating effect on estimating the optimal ITR, and combining all feature variables is more effective.

Fig. 4:

Heatmap of 17 standardized feature variables on all patients grouped by predicted optimal treatment. Row corresponds to feature variables and column corresponds to patients stratified by predicted optimal treatment.

VI. Conclusions

We propose a sequential outcome-weighted learning, SOM learning, to estimate the optimal ITRs with multicategory treatment studies, where each step solves a weighted binary classification problem via SVMs. By carefully choosing weights in each SVM step and combining the treatment decision functions from all steps, we showed that the derived treatment rule is Fisher consistent. This consistency is not guaranteed by other simpler mutli-category learning algorithms (e.g., OVA). In comparison to consistent learning algorithm [17], SOM does not require non-convex optimization and thus is more reliable. In both numeric simulations and data application, SOM learning yields a better value function as compared to the method based on standard regression model or other straightforward methods such as OVO and OVA. Computationally, the running time of SOM is comparable to existing multicateogry learning methods. An application to REVAMP study demonstrates that treating patients with major depression by an individualized rule estimated by SOM reduces their depressive symptoms more than the best non-personalized treatment rule (e.g., treating all patients by the combined therapy of medication and CBASP), and more than ITRs estimated by all alternative methods (Q-learning, OVA and OVO).

A major computational cost for SOM learning is to screen all possible permutations of the treatment categories. Since the sequential learning for each permutation can be carried out independent of one another, an improvement in implementation is to incorporate distributed computing to leverage this natural parallel computing structure especially when there is a large number of treatment categories.

SOM learning can be extended in several directions. First, for some chronic diseases with multi-stage therapy, dynamic treatment regimens (DTRs) can be more powerful in obtaining favorable outcomes than a simple combination of single-stage treatment rules. Various approaches have been developed to estimate optimal DTR, such as [4], [26], [5], [7], [27], [18]. While our method has focused on single-stage studies only, the proposed procedure can be easily generalized to handle multicategory DTR for multiple stage trials. Second, although the proposed method was only applied to a finite number of categories, it can be naturally extended to find optimal personalized dose, where treatment is on a continuous scale, after discretizing the dosage into categories. However, one challenge is to determine the number of the categories and the threshold of discretization. A possibility is to include these uncertainties as parameters to be estimated in SOM learning.

Finally, although we suggest to treat the most prevalent treatment as the first target optimal treatment in SOM, this may result in few cases for later treatments in consideration and cause a high mis-allocation rate for patients whose optimal treatments are less prevalent. In practice, when different treatments have different importance, for instance, due to the need to balance efficacy and risk, the order of the targeted treatments should take into account the practical importance.