Abstract
Background
Patient-centred care requires evidence of treatment effects across many outcomes. Outcomes can be beneficial (e.g. increased survival or cure rates) or detrimental (e.g. adverse events, pain associated with treatment, treatment costs, time required for treatment). Treatment effects may also be heterogeneous across outcomes and across patients. Randomized controlled trials are usually insufficient to supply evidence across outcomes. Observational data analysis is an alternative, with the caveat that the treatments observed are choices. Real-world treatment choice often involves complex assessment of expected effects across the array of outcomes. Failure to account for this complexity when interpreting treatment effect estimates could lead to clinical and policy mistakes.
Objective
Our objective was to assess the properties of treatment effect estimates based on choice when treatments have heterogeneous effects on both beneficial and detrimental outcomes across patients.
Methods
Simulation methods were used to highlight the sensitivity of treatment effect estimates to the distributions of treatment effects across patients across outcomes. Scenarios with alternative correlations between benefit and detriment treatment effects across patients were used. Regression and instrumental variable estimators were applied to the simulated data for both outcomes.
Results
True treatment effect parameters are sensitive to the relationships of treatment effectiveness across outcomes in each study population. In each simulation scenario, treatment effect estimate interpretations for each outcome are aligned with results shown previously in single outcome models, but these estimates vary across simulated populations with the correlations of treatment effects across patients across outcomes.
Conclusions
If estimator assumptions are valid, estimates across outcomes can be used to assess the optimality of treatment rates in a study population. However, because true treatment effect parameters are sensitive to correlations of treatment effects across outcomes, decision makers should be cautious about generalizing estimates to other populations.
1. Background
The healthcare literature is beginning to appreciate the importance of variation in treatment effectiveness across patients, or ‘treatment effect heterogeneity’, when evaluating the potential effects of policies designed to modify healthcare decisions in practice [1–7]. If treatment effects are heterogeneous across patients it may not be valid to use the single effect estimate from a randomized controlled trial (RCT) as the basis for these evaluations [1]. In addition, an existing methods literature focuses on treatment effect estimate interpretation using observational databases when the effect of treatment on a single study outcome or the ‘outcome of interest’ is heterogeneous across patients [8–12]. This literature describes the conditions under which various estimators can produce estimates of treatment effect parameters, such as the average treatment effect across a population (ATE), the average treatment effect on the patients in a population who were treated (ATT), the average treatment effect on the untreated in a population (ATU), and the local average treatment effect (LATE), which is the average treatment effect for patients in a population whose treatment choices are sensitive to the value of a specific instrumental variable. This literature stresses the importance in estimate interpretation of ‘sorting on the gain’ or ‘essential heterogeneity’ in which treatment choice reflects the expected treatment effectiveness on the single outcome of interest for each patient [9, 13–16]. It has been shown that regression and instrumental variable estimators yield estimates of distinct treatment effect parameters [9, 13–15, 17]. As a result, with essential heterogeneity, treatment effect estimates for the outcome of interest can differ across estimators for the same study population and all be correct [9, 13–15]. In addition, it has been shown that alternative instruments in an instrumental variable analysis with the same population can yield different and correct estimates of LATE for the outcome of interest [18–21].
This is not the end of the parameter variation story. With essential heterogeneity, the true values of ATT, ATU, and LATE in study populations reflect the distribution of other factors affecting treatment choice within each population [22, 23]. In consequence, treatment effect estimates for the outcome of interest can differ across study populations and be correct for each study population. We demonstrate this result here using scenarios in which a treatment has heterogeneous effects across more than one outcome [24, 25]. Theoretical models of essential heterogeneity over a single outcome of interest are insufficient to describe observed behaviours such as ‘treatment-risk paradox’ [26–33]. Treatment-risk paradox is the label applied to clinical situations in which patients thought to have the most to gain from treatment in the outcome of interest are observed to be the least likely treated in real-world practice. For example, research showed higher-risk coronary patients were less likely to receive guideline-supported care [34].
A possible explanation for treatment-risk paradox is that patients with the most to gain from treatment in the outcome of interest may have higher expected losses from treatment in other outcomes. Instead of sorting on the gain from a single outcome, observed treatment variation may result from ‘sorting on the mix’ of expected benefits and detriments across outcomes. The implications of treatment effect heterogeneity across outcomes on treatment choice and the inferences that can be made from treatment effect estimates using observational data have not been investigated. If treatment choice affects an array of outcomes differentially across patients, the true treatment effect parameters on the outcome of interest can vary across study populations or within stratified subsets of the same study population. For example, research assessing the treatment effects of statins after acute myocardial infarction (AMI) in the Medicare population found similar absolute survival benefits from statins for both complex and non-complex patients, yet treatment rates for complex statin patients were much lower than for the non-complex patients [35]. Stratified analysis by patient complexity revealed that complex AMI patients had liver, kidney, and muscular adverse effect risks that were not observed in the non-complex patients. It is possible that lower statin prescribing rates for complex AMI patients in practice reflected consideration of both the benefits and the detriments of statin use in complex patients. Modifying statin prescribing rates for the complex AMI patients to match the rates in the non-complex patients could result in intolerable increases in side effect rates for complex patients.
Therefore, interpreting treatment effect estimates on a single outcome of interest without considering the effects of treatment on other outcomes can lead to improper conclusions and misguided clinical and policy recommendations. This study uses simulation modelling to demonstrate this point. We assessed the sensitivity of treatment effect estimates from regression and instrumental variable (IV) estimators when treatment effects are heterogeneous for both benefit and detriment outcomes, and treatment choice reflects this heterogeneity. In each simulation scenario, the assumptions required for the consistency of regression and IV estimates are met so that the estimates in each scenario are not affected by unmeasured confounding. The distributions of the treatment effects across populations for the benefit outcome was consistent across simulation scenarios. The distribution of treatment effects across the detriment outcome was varied across the simulated populations.
It was our objective to show in these simulations that, even in the best of circumstances for both regression estimators (no correlation between treatment and the error term) and IV estimators (no correlation between the instrument and the error term and an instrument with a strong effect on treatment choice), the resulting unbiased estimates are sensitive to the distinct circumstances related to treatment choice within each sample population. In empirical work with observational data, researchers still need theory to justify these assumptions [13, 36, 37], and IV analysis requires the existence of instruments with strong relationships with treatment choice [38, 39].
2. Methods
2.1. Interpretive Framework
Assume the research goal is to assess the comparative effectiveness of a treatment (T) relative to an alternative (A) on the outcome of interest (Y#) across a population of patients with a given health condition. However, for each patient, the decision of T versus A affects K distinct outcomes (Yk), which include Y# [24, 25]. The Yks can represent benefits such as increased cure or survival probabilities or detriments such as direct treatment costs, time costs, or adverse event risks [24]. Equations (1)–(3) describe the true effect of T relative to A on each outcome Yk for patient ‘i’ with a counterfactual model:
| (1) |
| (2) |
Yk1i equals outcome ‘k’ for patient ‘i’ if treated with T, and Yk0i equals the value of outcome ‘k’ for patient ‘i’ if treated with A. The treatment effect (TE) of T relative to A on outcome ‘k’ is specific to each patient:
| (3) |
The parameters δk1i can be positive or negative across the ‘k’ outcomes depending on how each outcome is measured. For example, relative to A, for patient ‘i’, T may increase cure probability, lower costs, and increase risk of an adverse event. The treatment effect for the outcome of interest for patient ‘i’ is designated δ#1i
Research to obtain evidence about the distribution of δ#1i across patients requires a dataset in which Ti varies across patients. In observational healthcare databases, this variation results from different patient–provider dyads making different treatment choices. Following suggested approaches [11, 40], treatment choice is modelled here on the beliefs or expectations each dyad ‘i’ has over how treatments will affect each Yk outcome for patient ‘i’ and the values ‘i’ places on each of the K expected outcome changes:
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
Equations (4) and (5) are patterned after (1) and (2), except the αk0i and αk1i parameters reflect the effectiveness beliefs of ‘i’ with respect to each outcome ‘k’. and are the expected results of ‘i’ for outcome ‘k’ if treated with T and A, respectively and is the expected treatment effect. NVi is the expected net value of T relative to A for dyad ‘i’ at treatment decision time. The parameters Vki (k = 1–K) reflect the value ‘i’ places on each unit of expected outcome change. The Vkis are positive for outcome changes that benefit the patient and negative for outcome changes detrimental to the patient. A dyad chooses Ti if NVi> 0. Variation in Ti across patients with the same condition in an observational healthcare database stems from differences in the belief and value parameters in equation (7) across the patient–provider dyads.
The specification of the K outcomes important to patients in equation (7) makes their role explicit when interpreting and generalizing treatment effect estimates across study populations. In prior discussions of essential heterogeneity, only variation in α#1i across patients provided the basis for ‘sorting on the gain’. It was acknowledged that treatment choice can affect other outcomes (e.g. costs), but it was also assumed implicitly that no relationships existed between α#1i and treatment effects on the other outcomes [8, 10]. In real-world practice, it is possible that correlations in treatment effects across outcomes exist across patients and these correlations differ across study populations. For example, in complex elderly populations, patients with the highest expected benefit from treatment in the outcome of interest may also have the highest expected risk of detriment from treatment. This positive relationship between benefit and detriment may not exist for younger non-complex patients.
2.2. Simulation Approach
We expanded the simulation model of treatment choice and outcome used in other research [22, 41] to include two outcomes representing the benefit (B) and detriment (D) associated with treatment choice. For this exercise, B and D are modelled as discrete events. Relative to alternative (A), for patient ‘i’ treatment (T) increases the probability of both the benefit P(Bi) and detriment P(Di) occurring. These probabilities are heterogeneous across patients based on a factor (Xi) that is observed by the decision dyad but is unobserved by the researcher. These relationships are represented by the following equations for patient ‘i’:
| (9) |
| (10) |
Ti = 1 if patient ‘i’ receives treatment and 0 if patient ‘i’ receives A. Xi affects the effect of Ti on both P(Bi) and P(Di) but does not have a direct effect on either P(Bi) or P(Di). The true treatment effects of T relative to A for patient ‘i’ are represented by equations (11) and (12):
| (11) |
| (12) |
Because Xi is in both equations, varying the parameters in equations (11) and (12) leads to different relationships in treatment effects across outcomes in the simulated populations. We label B as the outcome of interest and fixed the parameters in equation (11) across simulations. The parameters in equation (12) were varied across simulations to reflect distinct treatment effect relationships between TEBi and TEDi in each population. A ‘noise’ term vi is specified in equation (12) to portray real-world conditions in which the correlations in treatment effects across outcomes are not perfect.
Xi affects net treatment value through its influence on expected treatment effects as seen in the following relationship:
| (13) |
where NVi is the expected net value of T relative to A for patient ‘i’; VB is the value each patient gains if the benefit occurs, and VD is each value a patient loses if the detriment occurs. These value parameters can be patient specific, as in equation (7). In our simulations, we specified them as constants across patients to focus on the implications of correlations of treatment effects across outcomes. The parameters in equations (11) and (12) reflect the true treatment effect relationships conditional on Xi, whereas the parameters in equation (13) reflect the expected treatment effects conditional on Xi when the treatment decision is made. This distinction enabled us to simulate the consequences when expectations do not match the true treatment effects for each patient. VB·(αB10 + αB11·Xi) represents the value decision dyad ‘i’ places on the expected change in benefit probability associated with treatment. VD-((αD10 + αD11·Xi) + vi) represents the value decision dyad ‘i’ places on the expected change in the probability of the detriment associated with treatment. Zi and μi represent factors affecting net treatment value that have no effect on either P(Bi) or P(Di). Zi is measured by the researcher and μi is not. Zi will serve as our instrument and is specified as a binary variable. VZ is specified as a negative value if Zi = 1 and a positive value if Zi = 0.
Five simulation scenarios were generated by varying the parameters in equations (11), (12) and (13). These scenarios are summarized in Table 1. Simulated patients were randomly assigned values of Xi, Zi, vi, and μi using distributions detailed in Table 1. NVi was then computed for each patient. Following standard discrete choice theory [42], simulated patients chose treatment (Ti) if NVi was >0. Equations (11) and (12) were used to estimate the ‘true’ benefit and detriment treatment effects for each patient, respectively, conditional on treatment choice. Using the outcome probabilities from equations (9) and (10), respectively, benefit/non-benefit (Bi) and detriment/non-detriment (Di) binary outcomes were simulated for each patient using the ‘Bernoulli’ option within the RAND function in SAS 9.1. The Bernoulli option simulates a binary outcome (1 if the outcome occurs, 0 otherwise) based on the probability of an outcome occurring.
Table 1.
Parameters for five simulation scenarios with varying relationships of treatment effect heterogeneity across two outcomes
| Parameters | Scenarios | ||||
|---|---|---|---|---|---|
| I | II | III | IV | V | |
| αB10 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 |
| αB11 | −0.25 | −0.25 | −0.25 | −0.25 | −0.25 |
| δB0 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 |
| δB10 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 |
| δB11 | −0.25 | −0.25 | −0.25 | −0.25 | −0.25 |
| αD10 | 0.05 | 0.10 | 0.35 | 0.05 | 0.05 |
| αD11 | 0.10 | 0.20 | −0.35 | 0.10 | 0.10 |
| δD0 | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 |
| δD10 | 0.05 | 0.10 | 0.35 | 0.10 | 0.35 |
| δD11 | 0.10 | 0.20 | −0.35 | 0.20 | −0.35 |
| VB | 2000 | 2000 | 2000 | 2000 | 2000 |
| VD | 1800 | 1800 | 1800 | 1800 | 1800 |
| VZ | −50 if Zi = 1; 50 if Zi = 0 |
−50 if Zi = 1; 50 if Zi = 0 |
−50 if Zi = 1; 50 if Zi = 0 |
−50 if Zi = 1; 50 if Zi = 0 |
−50 if Zi = 1; 50 if Zi = 0 |
| Xi | Uniform (0,1) | Uniform (0,1) | Uniform (0,1) | Uniform (0,1) | Uniform (0,1) |
| vi | Normal (0,0.01) | Normal (0,0.01) | Normal (0,0.01) | Normal (0,0.01) | Normal (0,0.01) |
| Zi | Bernoulli P(Zi = 1) = 0.5 |
Bernoulli P(Zi = 1) = 0.5 |
Bernoulli P(Zi = 1) = 0.5 |
Bernoulli P(Zi = 1) = 0.5 |
Bernoulli P(Zi = 1) = 0.5 |
In all five scenarios, the true distribution of TEBi conditional on Xi was distributed uniformly across patients between 0 and 0.25, with an average treatment effect on the benefit in each simulated population of 0.125. For the benefit outcome, the expected treatment effect used in treatment choice equalled the true treatment effect (δB10 = δB10 and δB11 = δB11) in all scenarios. The δD10, δD11, αD10, αD11 parameters were modified across scenarios to reflect different correlations between benefit and detriment treatment effects and distinct relationships between expected and true treatment effects on the detriment. In scenario I, a negative correlation existed between TEBi and TEDi. Patients with low values of Xi had the highest probability of benefit from treatment and the lowest probability of detriment. RCTs often use exclusion rules to try to isolate patients like those in scenario I. Scenario II was also characterized by a negative correlation between TEBi and TEDi, but relative to scenario I, patients in scenario II had a higher probability of detriment at every Xi level. Scenario III displays treatment–risk paradox with a positive correlation between TEBi and TEDi. Patients with low values of Xi had the highest probability of both benefit and detriment from treatment. In addition, in scenario III, the probability of detriment was high enough so that for most patients with low Xi values NVi<0. In scenario IV, patients have the true detriment relationship in scenario II, but the decision dyads have expectations of detriment risk as in scenario I. Scenario IV occurs if providers accept claims of external validity of RCT results for a new treatment without experiencing how the treatment works in patients unlike those in the trial. Scenario V is like scenario IV except that the true detriment relationship matches the treatment–risk paradox case of scenario III.
In all five scenarios, 1000 simulations were run, each containing 5000 patients. Within each simulated population we calculated the true ATT, ATU, and LATE for both the benefit (Bi) and the detriment (Di). We identified the simulated patients whose treatment choices were responsive to their instrument values in each simulation run—the marginal patients [43, 44]. These patients were used to estimate the true LATE. Marginal patients were those with (a) Zi = 1 who did not choose treatment but would have chosen treatment had Zi = 0, or (b) Zi = 0 who chose treatment but would not have chosen treatment had Zi = 1. Using the Ti, Bi, Di, and Zi values in each simulation run, we estimated equations (9) and (10) using regression and IV estimators and compared the estimates to the true ATE, ATT, ATU, and LATE values.
3. Results
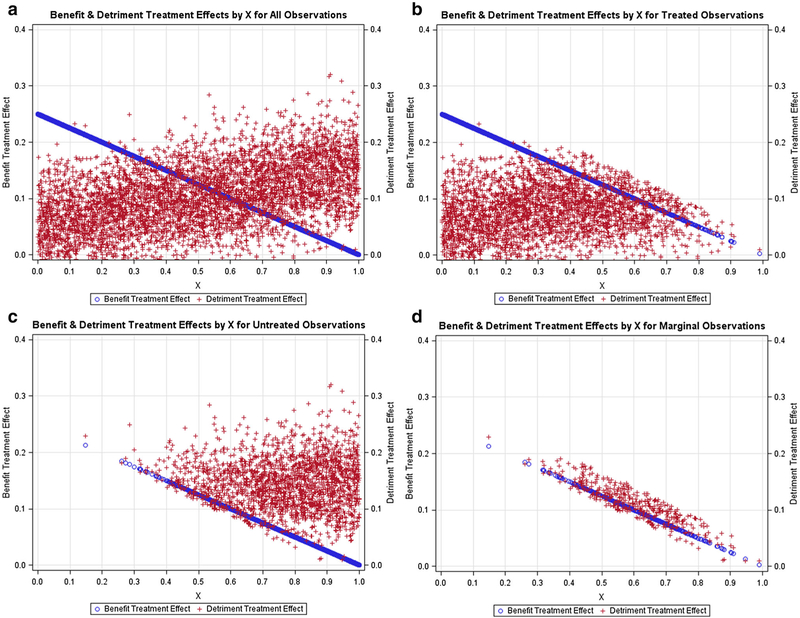
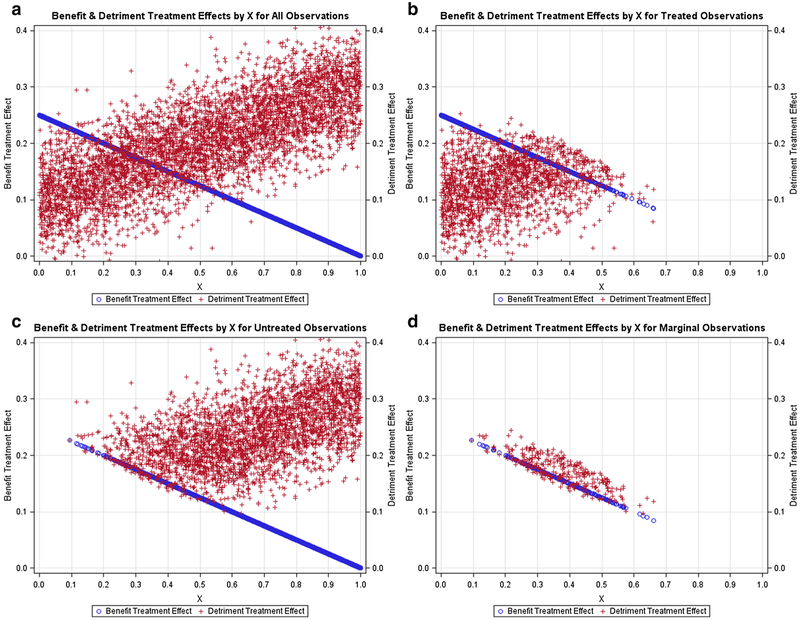
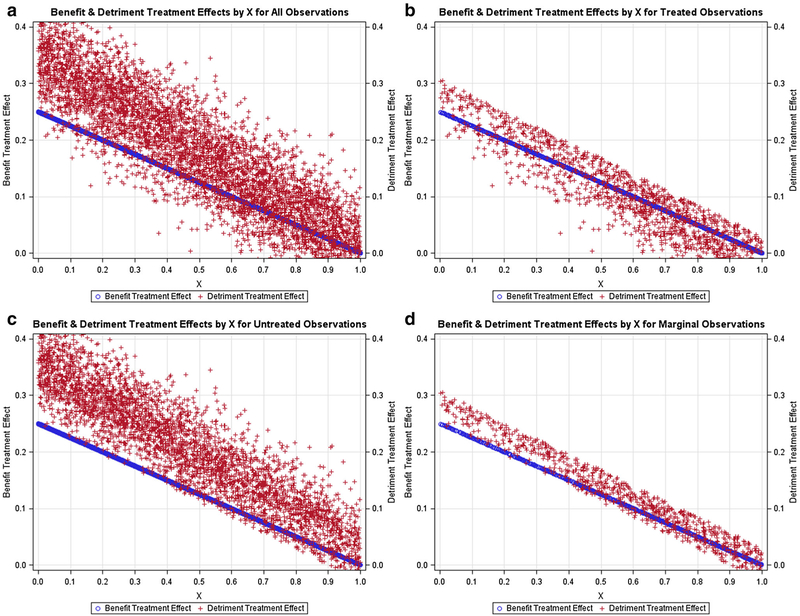
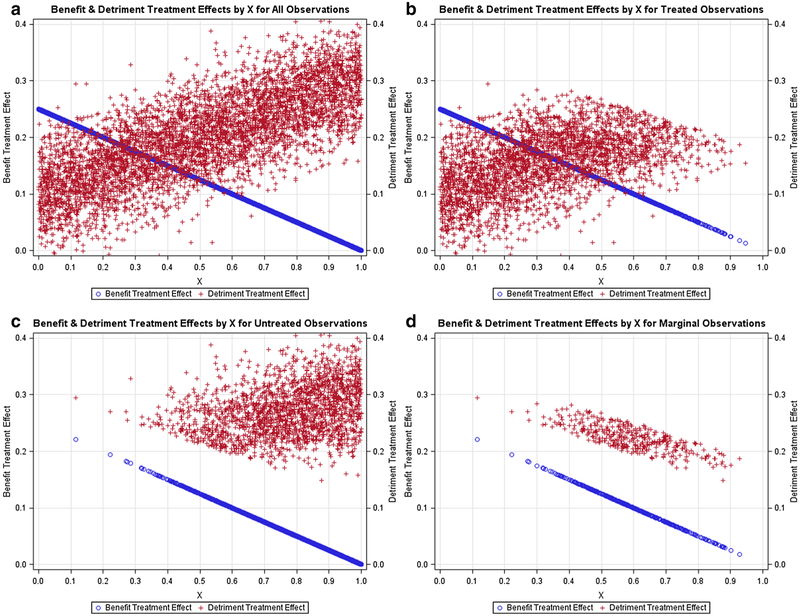
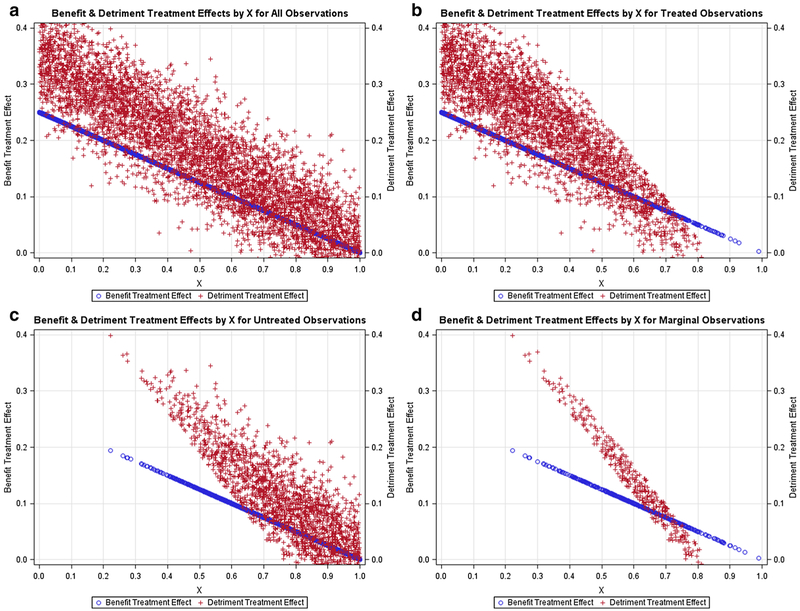
Figures 1, 2, 3, 4, 5 contain scatter plots of the true TEBi (blue) and true TEDi (red) distributions for scenarios I–V, respectively. The horizontal axis displays the Xi value for each simulated patient. For clarity, only the 1000 observations from the first simulation in each scenario are displayed. In the simulations, each patient chose treatment if the expected benefit from treatment was greater than the expected detriment. Each figure contains a frame for (a) all simulated patients, (b) all simulated patients who chose treatment, (c) all simulated patients who did not choose treatment, and (d) the marginal simulated patients—those whose treatment choice would have changed if their discrete instrument value switched. The left and right vertical axes are in terms of the true benefit treatment effect and (TEBi) detriment treatment effect (TEDi) for each simulated patient, respectively. Frame (b) in each figure shows several patients with TEBi<TEDi who were treated, and frame (c) shows several patients with TEBi>TEDi who were not treated. This occurs because the net value of treatment (NVi) also varies with the value associated with the instrument (Zi) and the random error term (μi). In addition, in scenarios IV and V, NVi is calculated with expected detriment treatment effects that do not match the true effects.
Fig. 1.
Negative relationship between benefit and detriment treatment effects: Scatter plots containing the benefit probabilities and detriment probabilities for subsets of the simulated population in scenario I. a All simulated patients, b simulated patients who chose treatment T, c simulated patients who chose the alternative treatment, d marginal simulated patients, or those whose treatment choice would have changed if their instrument value switched
Fig. 2.
Negative relationship between benefit and detriment treatment effects with detriment effects larger than scenario I: Scatter plots containing the benefit probabilities and detriment probabilities for subsets of the simulated population in scenario II. a All simulated patients, b simulated patients who chose treatment T, c simulated patients who chose the alternative treatment, d marginal simulated patients, or those whose treatment choice would have changed if their instrument value switched
Fig. 3.
Positive relationship between benefit and detriment treatment effects: Scatter plots containing the benefit probabilities and detriment probabilities for subsets of the simulated population in scenario III. a All simulated patients, b simulated patients who chose treatment T, c simulated patients who chose the alternative treatment, d marginal simulated patients, or those whose treatment choice would have changed if their instrument value switched
Fig. 4.
Negative relationship between benefit and detriment treatment effects and expected detriment effects as in scenario I and true detriment effects as in scenario II: Scatter plots containing the benefit probabilities and detriment probabilities for subsets of the simulated population in scenario IV. a All simulated patients, b simulated patients who chose treatment T, c simulated patients who chose the alternative treatment, d marginal simulated patients, or those whose treatment choice would have changed if their instrument value switched
Fig. 5.
Expected negative relationship between benefit and detriment treatment effects in scenario I and but true positive relationship between benefit and detriment treatment effects in scenario III: Lots containing the benefit probabilities and detriment probabilities for subsets of the simulated population in scenario IV. a All simulated patients, b simulated patients who chose treatment T, c simulated patients who chose the alternative treatment, d marginal simulated patients, or those whose treatment choice would have changed if their instrument value switched
Figures 1, 2, 3 contain scenarios in which treatment effect expectations match the truth. In scenario I (Fig. 1b), treated patients are more likely those with lower Xi values and higher expected benefit treatment effects but are found nearly across the range of the Xi axis. In contrast, in scenario II (Fig. 2b), no treated patients have an X value > 0.65 and, in scenario III (Fig. 3b), treated patients are found mostly at higher levels of Xi. With respect to marginal patients, in scenario I (Fig. 1d), the majority are distributed at levels of Xi between 0.25 and 0.75. In scenario II (Fig. 2d), the majority of marginal patients are distributed at levels of Xi between 0.05 and 0.55. In scenario III, marginal patients are found across the Xi distribution but mostly at higher levels of Xi. In scenarios IV (Fig. 4) and V (Fig. 5), treatment choice is based on the treatment effect distribution found in scenario I so that the distributions Xi for the treated and marginal patients in these scenarios match scenario I.
3.1. Variation in True Treatment Effect Parameters
Table 2 contains the true average treatment effects for both the benefit and detriment in each simulation scenario and the regression and IV parameter estimates for the treatment effect on both the benefit and the detriment. All values in Table 2 are averages over the 1000 simulations for each scenario. The average treatment effect on the benefit in the population (ATEB) is the same by design (0.125) across scenarios. The average treatment effect on the detriment in the population (ATED) varies across scenarios and was lowest in scenario I. Despite a consistent distribution of benefit treatment effects across scenarios, the true average treatment effects on the benefit for the treated (ATTB), untreated (ATUB), and marginal patients (LATEB) in scenarios 1–3 varied significantly. In scenario II, true ATTB, ATUB, and LATEB are all higher than in scenario I. This occurs because ATED is higher in scenario II than in scenario I and, like scenario I, benefit treatment effects in scenario II are negatively correlated with detriment treatment effects across patients. Higher expected benefits from treatment are required for patients to choose treatment in scenario II than scenario I, and fewer patients chose treatment. In scenario III, ATED was also greater than the ATED in scenario I, yet ATTB and LATEB were lower in scenario III than in scenario I. These differences are attributable to the positive correlation between benefit and detriment treatment effects in scenario III. Few patients with high probabilities of obtaining the benefit from treatment in scenario III chose treatment because they also had high detriment risk. In scenarios IV and V, the expectations of benefit and detriment treatment effects used to calculate NVi were identical to scenario I, so each patient in scenarios IV and V made the same treatment choices as in scenario I. The true values of ATTB, ATUB, and LATEB match scenario I. However, the true values of ATTD, ATUD, and LATED are considerably higher than in scenario I because the true detriment treatment effects in scenarios IV and V were higher than the detriment effect expectations used to calculate NVi.
Table 2.
True benefit and detriment average values in each simulation scenario and regression and instrumental variable treatment effect estimates
| Parametersa | Simulation scenarios | ||||
|---|---|---|---|---|---|
| I | II | III | IV | V | |
| Percent of patients treated | 60.7 | 37.2 | 28.7 | 60.6 | 60.6 |
| True benefit average treatment parameters | |||||
| Average treatment effect in population | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 |
| Average treatment effect on the treated | 0.169 | 0.199 | 0.096 | 0.170 | 0.170 |
| Average treatment effect on the untreated | 0.056 | 0.081 | 0.137 | 0.056 | 0.056 |
| Average treatment effect on marginal patients | 0.098 | 0.157 | 0.108 | 0.099 | 0.099 |
| True detriment average treatment parameters | |||||
| Average treatment effect in population | 0.100 | 0.200 | 0.175 | 0.200 | 0.175 |
| Average treatment effect on the treated | 0.071 | 0.127 | 0.085 | 0.154 | 0.226 |
| Average treatment effect on the untreated | 0.144 | 0.243 | 0.211 | 0.272 | 0.096 |
| Average treatment effect on marginal patients | 0.111 | 0.174 | 0.124 | 0.221 | 0.138 |
| Estimates | |||||
| Treatment effect on the benefit—regressionb | 0.169 | 0.198 | 0.096 | 0.170 | 0.170 |
| Treatment effect on the benefit—instrumental variablec | 0.100 | 0.157 | 0.108 | 0.101 | 0.100 |
| Treatment effect on the detriment—regressionb | 0.071 | 0.126 | 0.085 | 0.153 | 0.226 |
| Treatment effect on the detriment—instrumental variablec | 0.110 | 0.171 | 0.124 | 0.221 | 0.136 |
| Instrumental variable first-stage F-statistic | 115.7 | 74.1 | 738.0 | 115.1 | 114.9 |
Averages over 1000 simulations
Linear probability model
Linear two-stage least squares
Correlations of expected treatment effects across outcomes also affected the relationships among the treatment effect parameters in each scenario. In scenarios I and II, true ATTB>LATEB. Treated patients had a higher average treatment effect on the benefit than the patients whose treatment choices were responsive to the instrument. This result is universal under essential heterogeneity with respect to a benefit if the treatment effects on benefit are uncorrelated or negatively correlated with the treatment effects on the detriment across patients. The set of treated patients contains both marginal and non-marginal patients. Under the conditions listed above, all non-marginal treated patients will have benefit treatment effects greater than those of the marginal patients. This can be seen by comparing Figs. 1b, d, as no treated patients with Xi values between 0 and 0.1 are in the marginal group. Under the same conditions, the opposite is true for detriments, ATTD<LATED. Alternatively, if the treatment effects on the benefit are positively correlated with the treatment effects on the detriment across patients, it is possible for true ATTB<LATEB, as shown in scenario III.
Evaluating the true LATEB and LATED parameters in each scenario with the outcome valuation parameters VB and VD in Table 1 provides insight into the treatment allocation process within a population. In scenarios I–III, the average value of the expected benefit from treatment for marginal patients approximately equalled the average expected losses from treatment. For example, in scenario I, the average value of the benefit gained by treatment for marginal patients equalled (0.098 × 9 2000 = 196.0). The average value of detriment lost by treatment for marginal patients equalled (0.111 × 1800 = 199.8). If treatment effect expectations match the truth, as in scenarios I–III, this result is expected under essential heterogeneity. If treatments are correctly sorted across patients, the marginal patients would be those whose expected benefit and detriment values from treatment are sufficiently similar that their treatment choices are sensitive to their instrument values. In contrast, in scenarios IV and V, treatment effect expectations for the detriment were lower than the true detriment treatment effects. In these scenarios, the true average value of the loss associated with treatment for the marginal patients was greater than the average value of the benefit for these patients. These results are borne out when evaluating the true LATE values for the marginal patients. For example, in scenario V for marginal patients, the average value of the true benefit gained by treatment equalled (0.099 × 2000 = 198), whereas the average value of the true detriment lost by treatment equalled (0.221 × 1800 = 397.8). These results show that decision dyads used incorrect information when making treatment choices and that treatment was overused in scenario V. Similar results can be found for scenario IV.
3.2. Regression and Instrumental Variable Treatment Effect Estimates
Comparisons of the treatment effect estimates in Table 2 to the true underlying parameter values demonstrate that the methodological findings that focused on a single outcome of interest [8, 10, 22] generalize to clinical scenarios in which a treatment has heterogeneous effects on more than one outcome. Regression estimators yield estimates of the ATT for each outcome, and IV estimators yield the average treatment effect over the marginal patients—the LATE for each outcome. In addition, the estimates in Table 2 show the sensitivity of these estimates to the relationships of expected treatment effects across outcomes in each population. Despite the identical distribution of benefit treatment effects across the simulated populations in scenarios I–III, estimates of ATTB and LATEB varied substantially across scenarios. Regression estimates and IV estimates from scenario I provide unbiased estimates of ATTB, ATTD, LATEB and LATED, respectively, for scenario I. Yet, these estimates provide a poor representation of the true values of these parameters in scenarios II and III.
3.3. Assessing Whether the Treatment Rate is ‘Right’ in a Study Population
The usefulness of estimates of ATTB, ATTD, LATEB and LATED for policy making can be seen in scenarios IV and V. When coupled with outcome valuations, estimates of these parameters from each scenario can assess whether treatment rate changes in a study population would be advantageous. In scenario IV, the estimated value of the treatment benefit for marginal patients (2000 × 0.101 = 202) is substantially less than the estimated treatment costs associated with the detriment (1800 × 0.221 = 397.8). In addition, in scenario IV, estimates of ATTB are greater than estimates of LATEB, and estimates of ATTD are less than estimates of LATED. This combination of estimates suggests that decision dyads were unaware of the higher detriment costs associated with treatment across this population. These estimates coupled with outcome valuations could be used to develop policies to lower treatment rates. These policies would be centred on informing decision dyads about the higher detriment risks associated with treatment for the patients in scenario IV to shift expectations toward the true detriment treatment effects. In scenario V, the value of the treatment benefit for marginal patients (2000 × 0.100 = 200) is also substantially less than the treatment costs associated with the detriment (1800 × 0.1 = 244.8), also indicating treatment overuse. However, in contrast to scenario IV, estimates of ATTD are greater than estimates of ATTB, which suggests a more complicated misalignment between expected and true treatment effect distributions in this population. Policies would have to realign the expected relationships between Xi and detriment risk across the decision dyads in this population.
4. Discussion
Estimates from treatment effect studies using observational data have often been interpreted in a ubiquitous manner without discussions of context and addressing to whom the estimates apply [45–48]. For example, a study reviewed 56 treatment effect studies using observational data that used a functional relationship between treatment and outcome that ensured treatment effect heterogeneity [49]. Each of these studies used an IV estimator that yields average treatment effect estimates for marginal patients. Under these circumstances, extra assumptions are required to properly generalize IV estimates beyond the marginal patients. Yet, few of these studies discussed any limits in their ability to generalize estimates to either non-marginal patients within their study population or to other populations. This problem also occurs when interpreting results from RCTs [50].
Researchers need to be more aware of the consequences of treatment effect heterogeneity across outcomes when interpreting and generalizing treatment effect estimates using observational healthcare data. Previous methodological research that focused on making inferences about a single outcome of interest laid the groundwork for this stipulation. This prior research showed that regression estimators yield the ATT, and IV estimators yield LATEs for the outcome of interest [9, 13–15, 17]. Proper generalization of estimates of ATT or LATE for the outcome of interest to the untreated patients in a study population requires the assumption that treatments were not chosen based on expected treatment benefit, i.e. no ‘sorting on the gain’ or essential heterogeneity [18, 51]. It has also been shown that different IVs affect the treatment choices of a different subset of patients in the same study, producing different but valid estimates of LATE [18–21]. Other studies have shown that treatment effect estimates can vary across study populations with factors affecting outcome valuations [22, 23].
This study expanded on this earlier work to assess the implications on treatment effect estimates when treatments have heterogeneous effects on more than one outcome. We use simulation modelling to assess an expanded version of essential heterogeneity, which we coin as ‘sorting on the mix’. Decision dyads make treatment choices considering the effects of treatment on more than one outcome with treatment effects that vary across patients. Our simulation models showed that, under such conditions, the interpretation of estimates when using regression and IV estimators remains consistent for each outcome. Regression estimators yield ATT, and IV estimators yield LATE, for each outcome. Estimates of ATT and LATE across outcomes can be used to help address whether a treatment has been under or overused in the given study population. However, we also showed that the true values of ATT and LATE for each outcome are sensitive to the relationships in treatment effects across outcomes in each study population. Therefore, researchers and policy makers should be very cautious about assuming that estimates of ATT and LATE from a single study population can be generalized to other populations of patients. External validity must be based on arguments that the relationships of treatment effect distributions across outcomes are consistent across populations.
5. Conclusions
Analysis of observational data has been suggested as an approach to finding treatment effect estimates across patient circumstances and across outcomes. Observed treatments found in these databases are not the result of randomization but rather of choice. Real-world treatment choices often involve complex assessments of the expected effects of treatments across outcomes. This study demonstrates that failing to consider this complexity when interpreting treatment effect estimates using observational data could lead to clinical and policy mistakes. If treatment choices reflect expected effects over more than one outcome, our simulation results showed that treatment effect estimates can provide evidence as to whether treatments were over or underused in the study population. We also showed that these estimates are very sensitive to the distributions of treatment effects across outcomes in each study population. As a result, researchers and policy makers should be extremely cautious of generalizing estimates from a single study population to other patient populations.
Supplementary Material
Key Points for Decision Makers.
In clinical scenarios in which treatment effects are heterogeneous across patients for more than one outcome, treatment effect estimates for each outcome share properties previously demonstrated in single outcome models.
Treatment effect estimates can properly vary across study populations with differences in the correlations in treatment effects across outcomes in each population.
Treatment effect estimates across multiple outcomes can be used to assess whether treatments rates are ‘right’ in the study population, but decision makers should be very careful in generalizing treatment effect estimates to other patient populations.
Funding
This project was funded by the Patient-Centered Outcomes Research Institute (PCORI) under project number (ME-1303–6011).
Footnotes
Electronic supplementary material The online version of this article (https://doi.org/10.1007/s40258-018-0380-z) contains supplementary material, which is available to authorized users.
Conflict of interest John Brooks, Cole Chapman, and Mary Schroeder have no conflicts of interest that are directly relevant to the content of this study.
Data Availability Statement The data from the five simulation scenarios presented are available as ZIP SAS datasets in supplementary material for this paper.
References
- 1.Kravitz RL, Duan N, Braslow J. Evidence-based medicine, heterogeneity of treatment effects, and the trouble with averages. Milbank Q. 2004;82(4):661–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lohr KN, Eleazer K, Mauskopf J. health policy issues and applications for evidence-medicine and clinical practice guidelines. Health Policy. 1998;46:1–19. [DOI] [PubMed] [Google Scholar]
- 3.Rothwell PM. Subgroup analysis in randomized controlled trials: importance, indications, and interpretation. Lancet. 2005;365:176–86. [DOI] [PubMed] [Google Scholar]
- 4.Threads Starfield B. and yarns: weaving the tapestry of comorbidity. Ann Family Med. 2006;4(2):101–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Steinberg EP, Luce BR. Evidence based? Caveat emptor! Health Aff. 2005;24(1):80–92. [DOI] [PubMed] [Google Scholar]
- 6.Upshur REG. Looking for rules in a world of exceptions. Perspect Biol Med. 2005;48(4):477–89. [DOI] [PubMed] [Google Scholar]
- 7.Dubois RW. From methods to policy: a ‘one-size-fits-all’ policy ignores patient heterogeneity. J Comp Eff Res. 2012;1(2):119–20. [DOI] [PubMed] [Google Scholar]
- 8.Heckman JJ, Urzua S, Vytlacil E. Understanding instrumental variables in models with essential heterogeneity. Rev Econ Stat. 2006;88(3):389–432. [Google Scholar]
- 9.Angrist JD. Treatment effect heterogeneity in theory and practice. Econ J. 2004;114:C52–83. [Google Scholar]
- 10.Heckman JJ, Vytlacil E. Structural equations, treatment effects, and econometric policy evaluation. Econometrica. 2005;73(3):669–738. [Google Scholar]
- 11.Heckman JJ, The scientific model of causality. Sociol Methodol 35, 2005. 35: p. 1–97. [Google Scholar]
- 12.Heckman J, Navarro-Lozano S. Using matching, instrumental variables, and control functions to estimate economic choice models. Rev Econ Stat. 2004;86(1):30–57. [Google Scholar]
- 13.Heckman JJ. Econometric causality. Int Stat Rev. 2008;76(1):1–27. [Google Scholar]
- 14.Brooks JM, Gang F. Interpreting treatment effect estimates with heterogeneity and choice: simulation model results. Clin Ther. 2009;31(4):902–19. [DOI] [PubMed] [Google Scholar]
- 15.Brooks JM, Chrischilles EA. Heterogeneity and the interpretation of treatment effect estimates from risk-adjustment and instrumental variable methods. Med Care. 2007;45(10 supplement):S123–30. [DOI] [PubMed] [Google Scholar]
- 16.Basu A, et al. Use of instrumental variables in the presence of heterogeneity and self-selection: an application to treatments of breast cancer patients. Health Econ. 2007;16(11):1133–57. [DOI] [PubMed] [Google Scholar]
- 17.Heckman JJ, Robb R. Alternative Methods for Evaluating the Impact of Interventions, in Longitudinal Analysis of Labor Market Data. In: Heckman JJ, Singer B (eds). 1985, Cambridge University Press: New York: p. 156–245. [Google Scholar]
- 18.Angrist JD, Ferandez-Val I. ExtrapoLATE-ing: external validity and overidentification in the LATE framework. Advances in Economics and Econometrics, Vol Iii: Econometrics, ed. Acemoglu D, Arellano M, Dekel E. 2013. 401–433. [Google Scholar]
- 19.Angrist JD, Pischke J-S. Mostly harmless econometrics: an empiricist’s companion. New Jersey: Princeton University Press; 2009. [Google Scholar]
- 20.Heckman JJ, Schmierer D, Urzua S. Testing the correlated random coefficient model. J Econ. 2010;158(2):177–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Brooks JM, Chrischilles EA. Heterogeneity and the interpretation of treatment effect estimates from risk adjustment and instrumental variable methods. Med Care. 2007;45(10):S123–30. [DOI] [PubMed] [Google Scholar]
- 22.Brooks JM, Fang G. Interpreting treatment-effect estimates with heterogeneity and choice: simulation model results. Clin Ther. 2009;31(4):902–19. [DOI] [PubMed] [Google Scholar]
- 23.Brooks JM, McClellan M, Wong HS. The marginal benefits of invasive treatments for acute myocardial infarction: Does insurance coverage matter? Inquiry-the J Health Care Organ Provis Financ. 2000;37(1):75–90. [PubMed] [Google Scholar]
- 24.Greenfield S, Kaplan SH. Building useful evidence: changing the clinical research paradigm to account for comparative effectiveness research. J Comp Eff Res. 2012;1(3):263–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Heckman JJ, Urzua S. Comparing IV with structural models: what simple IV can and cannot identify. J Econ. 2010;156(1):27–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Spertus JA, Furman MI. Translating evidence into practice: are we neglecting the neediest? Arch Intern Med. 2007;167(10):987–8. [DOI] [PubMed] [Google Scholar]
- 27.Yan AT, et al. Management patterns in relation to risk stratification among patients with non-ST elevation acute coronary syndromes. Arch Intern Med. 2007;167(10):1009–16. [DOI] [PubMed] [Google Scholar]
- 28.Ko DT, Mamdani M, Alter DA. Lipid-lowering therapy with statins in high-risk elderly patients—the treatment-risk paradox. J Am Med Assoc. 2004;291(15):1864–70. [DOI] [PubMed] [Google Scholar]
- 29.Sandhu RK, et al. Risk stratification schemes, anticoagulation use and outcomes: the risk-treatment paradox in patients with newly diagnosed non-valvular atrial fibrillation. Heart. 2011;97(24):2046–50. [DOI] [PubMed] [Google Scholar]
- 30.Wimmer NJ, et al. Risk-treatment paradox in the selection of transradial access for percutaneous coronary intervention. J Am Heart Assoc. 2013;2(3):e000174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.McAlister FA. The end of the risk-treatment paradox? A rising tide lifts all boats. J Am Coll Cardiol. 2011;58(17):1766–7. [DOI] [PubMed] [Google Scholar]
- 32.McGlynn E, et al. The quality of health care delivered to adults in the United States. N Engl J Med. 2003;348(26):2635–45. [DOI] [PubMed] [Google Scholar]
- 33.Levine DM, Linder JA, Landon BE. The quality of outpatient care delivered to adults in the United States, 2002 to 2013. JAMA Intern Med. 2016;176(12):1778–90. [DOI] [PubMed] [Google Scholar]
- 34.Yan AT, et al. Management patterns in relation to risk stratification among patients with non-ST elevation acute coronary syndromes. Arch Intern Med. 2007;167(10):1009–16. [DOI] [PubMed] [Google Scholar]
- 35.Brooks JM, et al. Statin use after acute myocardial infarction by patient complexity: are the rates right? Med Care. 2015;53(4):324–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cozad MJ, Chapman CG, Brooks JM. Specifying a conceptual treatment choice relationship before analysis is necessary for comparative effectiveness research. Med Care. 2017;55(2):94–6. [DOI] [PubMed] [Google Scholar]
- 37.Heckman JJ. Causal parameters and policy analysis in economics: a twentieth century retrospective. Quart J Econ. 2000;115(1):45–97. [Google Scholar]
- 38.Crown WH, Henk HJ, Vanness DJ. Some cautions on the use of instrumental variables estimators in outcomes research: how bias in instrumental variables estimators is affected by instrument strength, instrument contamination, and sample size. Value Health. 2011;14(8):1078–84. [DOI] [PubMed] [Google Scholar]
- 39.Bound J, Jaeger DA, Baker RM. Problems with instrumental variables estimation when the correlation between the instruments and the endogenous explanatory variable is weak. J Am Stat Assoc. 1995;90(430):443–50. [Google Scholar]
- 40.Heckman JJ. Rejoinder: response to Sobel. Sociol Methodol. 2005;35:135–62. [Google Scholar]
- 41.Brooks JM, Ohsfeldt RL. Squeezing the balloon: propensity scores and unmeasured covariate balance. Health Serv Res. 2013;48(4):1487–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ben-Akiva M, Lerman SR, Analysis Discrete choice. Cambridge Massachusetts: The MIT Press; 1985. [Google Scholar]
- 43.Harris KM, Remler DK. Who Is the marginal patient? Understanding instrumental variables estimates of treatment effects. Health Serv Res. 1998;33(5):1337–60. [PMC free article] [PubMed] [Google Scholar]
- 44.McClellan M, McNeil BJ, Newhouse JP. Does more intensive treatment of acute myocardial infarction in the elderly reduce mortality? Analysis using instrumental variables. JAMA. 1994;272(11):859–66. [PubMed] [Google Scholar]
- 45.Knol MJ, et al. Potential misinterpretation of treatment effects due to use of odds ratios and logistic regression in randomized controlled trials. Plos One. 2011;6(6):e21248 10.1371/journal.pone.0021248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Knol MJ, et al. What do case-control studies estimate? Survey of methods and assumptions in published case-control research. Am J Epidemiol. 2008;168(9):1073–81. [DOI] [PubMed] [Google Scholar]
- 47.Pocock SJ, et al. Issues in the reporting of epidemiological studies: a survey of recent practice. BMJ. 2004;329(7471):883–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Tooth L, et al. Quality of reporting of observational longitudinal research. Am J Epidemiol. 2005;161(3):280–8. [DOI] [PubMed] [Google Scholar]
- 49.Brooks JM, Chapman CG, Cozad MJ. The identification process using choice theory is needed to match design with objectives in CER. Med Care. 2017;55(2):91–3. [DOI] [PubMed] [Google Scholar]
- 50.Stuart EA, Rhodes A. Generalizing treatment effect estimates from sample to population: a case study in the difficulties of finding sufficient data. Eval Rev. 2017;41(4):357–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Chapman CG, Brooks JM. Treatment effect estimation using nonlinear two-stage instrumental variable estimators: another cautionary note. Health Serv Res. 2016;51(6):2375–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.