Abstract
Object:
We describe measurement of skeletal muscle kinetics with multiple echo diffusion tensor imaging (MEDITI). This approach allows characterization of the microstructural dynamics in healthy and pathologic muscle.
Materials and Methods:
In a Siemens 3 T Skyra scanner, MEDITI was used to collect dynamic DTI with a combination of rapid diffusion encoding, radial imaging, and compressed sensing reconstruction, in a multi-compartment agarose gel rotation phantom and within in vivo calf muscle. An MR-compatible ergometer (Ergospect Trispect) was employed to enable in-scanner plantarflexion exercise. In a HIPAA-compliant study with written informed consent, post-exercise recovery of DTI metrics were quantified in 8 volunteers. Exercise response of DTI metrics was compared with that of T2-weighted imaging and characterized by a gamma variate model.
Results:
Phantom results show quantification of diffusivities in each compartment over its full dynamic rotation. In vivo calf imaging results indicate larger radial than axial exercise response and recovery in the plantarflexion-challenged gastrocnemius medialis (fractional response: nT2w = 0.385 ± 0.244, nMD = 0.163 ± 0.130, nλ1 = 0.110 ± 0.093, nλrad = 0.303 ± 0.185). Diffusion and T2-weighted response magnitudes were correlated (e.g. r = 0.792, p =0.019 for nMD vs. nT2w).
Conclusion:
We have demonstrated feasibility of MEDITI for capturing spatially resolved diffusion tensor data in dynamic systems including post-exercise skeletal muscle recovery following in-scanner plantar flexion.
Keywords: diffusion tensor imaging, multiple echo diffusion tensor acquisition technique (MEDITATE), compressed sensing, dynamic imaging
Introduction
Diffusion-weighted imaging (DWI) probes tissue microstructure in a variety of neurologic, oncologic, and musculoskeletal applications. Furthermore, tissue types with local orientational order (white matter axons, renal medulla, skeletal muscle) are well characterized by diffusion tensor imaging (DTI) [1], which provides measures of the degree and directional dependence of microstructural restriction. Different apparent diffusion along different directions, such as faster ‘axial’ transport (along muscle fibers) than ‘radial’ transport (perpendicular to fiber axes) is termed anisotropy and is quantified in DTI. DTI has been extensively applied to skeletal muscle to probe myofiber architecture [2-5]. However, the majority of this work is performed for static muscle, due in large part to the time requirements of directional diffusion-weighted sampling of the diffusion tensor fit. This type of acquisition thus precludes characterization of key aspects of skeletal muscle function: contraction, exertion, and recovery (collectively referred to here as exercise effects). Imaging studies with other MR contrast mechanisms (e.g. T2 relaxometry, BOLD, phosphorous spectroscopy) have been performed with and without load, before and after exertion, or even during muscle flexion to study in situ biomechanics [6-15]. Elevated muscle signal intensity on T2-weighted imaging following exercise is well-documented [15-17]. Exercise response of diffusion-weighted contrast has also been observed, but often with coarse temporal sampling [18-20]. Static DTI studies performed before and after exercise have revealed anisotropic increases in diffusion metrics (specifically radial diffusion increasing more than axial diffusion), motivating more rapid and comprehensive sampling of this transient behavior [21,22]. Thus a detailed understanding of post-exercise transients in MR contrast has potential clinical value. Recently, post-exercise dynamic diffusion MRI has gained more attention [20,23] but conventional single-encoding sequences can limit temporal resolution, particularly in the case of DTI.
Recently, a new approach for compressing the required directional encodings has been demonstrated [24], titled “multiple echo diffusion tensor acquisition technique (MEDITATE)” and based on prior work in preclinical scanners [25,26], A single-voxel variant (SV-MEDITATE) has been applied to measure dynamic anisotropic diffusion exercise response in normal calf muscle [27] and thigh muscles in controls and dermatomyositis patients [28]. However, to produce a spatially-resolved variant of MEDITATE, k-space acquisition and reconstruction must be chosen to (a) include self-navigation of phase errors and (b) achieve sufficient temporal resolution to capture post-exercise recovery. In the present work, we describe such a spatially-resolved technique (Multiple Echo Diffusion Tensor Imaging, or MEDITI) with a multi-spoke radial k-space trajectory and compressed sensing reconstruction. The full workflow including self-navigation, diffusion tensor fitting, and response analysis is detailed in the Methods section. This approach allows migration of diffusion tensor mapping into a ‘fast imaging’ regime and enables a broad range of kinetic muscle investigations.
Materials and Methods
In this study, the MEDITI approach was applied in two contexts (see Figure 1): (a) 4-chamber rotatable phantom and (b) in vivo imaging of calf muscles before and after in-scanner exercise in healthy subjects. The phantom (Fig. 1a) was a custom-designed cylinder with four chambers containing agarose gel mixtures of different concentration as prescribed in a recent study [29] to generate a targeted range of diffusion coefficients between 1 and 2 μm2 / ms while minimizing convective flow effects of free fluids. This design presents a space- and time-varying system, with physiologically ranged diffusivities, on which to test the MEDITI workflow. The phantom was placed in the center of a 15-channel knee coil (QED, Mayfield Village, OH, USA) in a Siemens Skyra 3 T scanner (Siemens Healthineers, Erlangen, Germany) with its axis oriented along the z-axis of the scanner bore. Details on sequences used are given in Image Acquisition (below).
Figure 1:
(a) Photograph of cylindrical 4 chamber rotation phantom employed in this study. (b) Setup for in vivo dynamic MEDITI acquisition before and following in-scanner plantarflexion using an Ergospect Trispect ergometer with pneumatic resistance.
In a HIPAA-compliant, IRB-approved study, 10 volunteers provided written informed consent for a unilateral calf MRI scan in a Siemens Skyra 3 T scanner with a 15-channel knee coil (QED, Mayfield Village, OH, USA). Data from 2 subjects was excluded for poor image quality (see below), leaving 8 subjects (4 M, 4 F; ages 23 to 54 (33 ±10); BMI 20–31 (26 ±4)). Subjects were positioned (dominant leg if known; 2 left, 6 right) in a MR-compatible piantarflexion ergometer (non-FDA approved device for investigational research). The ergometer (Ergospect Trispect, Figure 1b) used pneumatic resistance set by an external controller connected to a laptop computer with the manufacturer’s software. This system allows manual setting of resistance in units of pressure (bar); the manufacturer provided a calibration allowing conversion of resistance to force units (N). Real time monitoring and recording of applied force and pedal displacement timecourses was performed. Once subjects were positioned, an immovable resistance was set and subjects isometrically exerted for ~10 s to measure maximum voluntary contraction (MVC). Resistance was then set to approximately 25% of MVC for that subject. Subjects performed repeated plantarflexion at approximately 40 Hz frequency for 3 minutes. A continuous MEDITI acquisition was performed throughout pre-exercise (5.1 ± 0.4 minutes), exercise (2.7± 0.6 minutes), and post-exercise (13.9± 1.9 minutes) periods.
Image acquisition
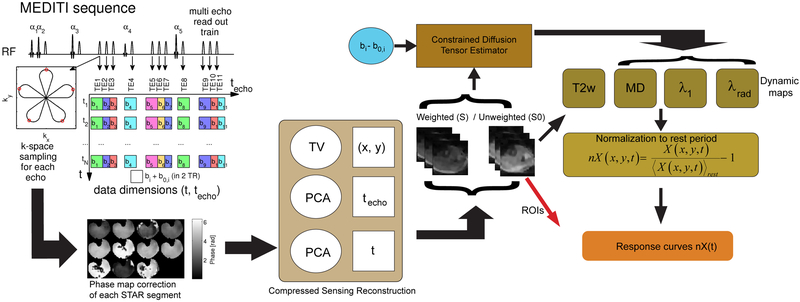
The structure of the MEDITI pulse sequence and processing workflow is indicated in Figure 2; it was built on prior implementations of the MEDITATE approach [24,27], Multiple slice selective RF pulses (flip angles 61°/73°/85°/45°/85°) generated a train of 11 echoes (time to echo formation 90 to 245 ms; transverse relaxation encoding 18 to 108 ms; longitudinal relaxation encoding 0 to 183 ms) that was acquired alternately with low and high diffusion gradients that provided diffusion weighting from 145 to 718 (145, 225, 252, 337, 361, 389, 401, 521, 590, 633, 718) s/mm2 over 11 different directions [24], Repetition time for each echo train was TR = 2 s. The sequence was prefaced by a spectrally adiabatic inversion recovery (SPAIR) fat suppression preparation. Prior work has explored the diffusion-weighting pattern’s capturing of dynamic diffusion tensor behavior [24,27]; the current study focused upon spatially-resolved dynamic imaging. In this implementation, each of the 11 echoes in each MEDITI echo train was measured with a 5-petal Single TrAjectory radial (STAR) k-space acquisition [30]. In order to complete the required k-space sampling for full image encoding, multiple shots were required. To provide efficient k-space coverage and maximal image reconstruction flexibility, the angle between consecutive STAR trajectories within each echo train was chosen according to the GRASP (Golden Radio Angle Radial Sparse Parallel) [31] scheme.
Figure 2:
MEDITI workflow. The MEDITI-sequence acquires a STAR-trajectory for each of 11 diffusion-weighted echoes in each TR, alternating between b and b0-sets in subsequent TRs. Phase correction is performed for each STAR segment via low resolution phase map. The reconstruction algorithm exploits similarities between diffusion-weighted images along techo- and t-dimensions. Weighted and unweighted images are submitted to a constrained diffusion tensor estimator based on the diffusion weighting pattern of the MEDITI sequence. Resulting mean, axial, and radial diffusion maps (as well as T2-weighted series) are normalized to the average over the pre-exercise resting period. Finally, normalized maps are averaged over muscle compartment regions of interest drawn on T2-weighted images to generate response curves nX(t) for each parameter for further analysis.
For the rotation phantom study, first, a conventional static EPI-DTI acquisition (TR/TE = 7400 / 59 ms, 64 × 64 matrix, 8 slices, 3.3 × 3.3 × 10 mm resolution, 6 diffusion directions, 3 averages) was performed for quantitative comparison with MEDITI. Next, during a continuous MEDITI acquisition a 90 degree rotation was manually performed every 24 seconds. 2 shots of 5-spoke STARS for both weighted and unweighted images were acquired to generate images of 2.2 mm inplane resolution and 20 mm slice thickness with a matrix of 64 × 64 and a field of view of 140 mm. For TR = 2 s, this gave a temporal resolution of 8 s and amounted to a factor of 10 undersampling compared to a conventional reconstruction. For the in vivo imaging, 4 shots of 5-spoke STARS were combined to generate images that were reconstructed to a 64 × 64 matrix. Field of view varied slightly to accommodate leg size (FOV = 226 ±58 mm, resolution 3.5 ± 0.9 mm). For TR = 2 s, this gave a temporal resolution of 16 s.
Image reconstruction and processing
The following processing pipeline was used for the in vivo imaging data. Following the collection of a full dynamic series, each shot for each echo was separately self-navigated since each STAR shot samples the center of k-space. To estimate the motion-induced phase errors, phase images were reconstructed from the central quarter of k-space for each shot. The resulting low-resolution phase image was unwrapped and linearly interpolated to the image resolution. Complex images were reconstructed for each shot from its full respective k-space segment, the corresponding phase errors were subtracted, and the corrected k-space segments were submitted to reconstruction. This procedure is similar to other self-navigated multi-shot diffusion approaches [32,33]. Next, the number of shots required for full image generation was determined, taking into account the desired resolution and data compressibility. Then, a conventional non-uniform fast Fourier transform (NUFFT) reconstruction was performed at the desired spatiotemporal resolution for (a) initial data inspection and (b) identification of time points during plantarflexion exercise if present. Exercise points (typically showing very low SNR due to motion during diffusion gradients) were removed from subsequent reconstructions to minimize noise propagation.
A dynamic series reconstruction with compressed sensing was performed as follows. Sparsifying transforms exploited the similarity between diffusion-weighted images along the echo (techo)- and the time (t)-dimensions to avoid undersampling artifacts, as part of the following reconstruction:
| (1) |
with X the time-series of images to be reconstructed, Y its k-space, E the multicoil encoding matrix, including coil sensitivities [34] and NUFFT according to the sampling pattern, PCA the Principal Component Analysis transform applied to the echo-train (PCAtecho) and to the time dimension (PCAt), TVxy the in plane total variation transform and λPCA, λPCAt and λTV regularization parameters. Operationally, a separate space-time matrix for each temporal dimension was formed for the corresponding PCA, and minimization of the L1-norm of each PCA was done by minimizing the rank of the space-time matrix that it is represented by the main singular vectors. Reconstructions were performed with heuristically-chosen parameters of λPCA=2.5*10−5, λPCAt =2.5*10−5 and λTV =5*10−5 multiplied by the norm of X. Solutions were found using a non-linear conjugate gradient method [35].
From the logarithmic ratio of unweighted (S0) and weighted (S) dynamic series and the known diffusion weighting factors of the MEDITI sequence bij, the diffusion tensor was estimated with a cylindrical tensor model [36], from which mean diffusivity (MD), axial (λ1), and radial (λrad) diffusion maps were generated. For these maps, as well as one of the unweighted echo series with T2-weighting encoding time of 90 ms to reflect dynamic T2-weighted imaging, the following procedure was used to generate exercise response curves. For each variable X(t) (MD, λ1, λrad, T2w), a pre-exercise map ⟨X(t)⟩rest was generated from the average of the middle of the resting period (sampled duration 2.0 ± 0.2 min). Normalizing the post-exercise period by the average pre-exercise map generated exercise response maps nX(t), which were subjected to post-hoc temporal binomial smoothing (5 frame width). Muscle compartments (anterior tibialis (AT), peroneus longus (PL), soleus (SOL), and gastrocnemius (GM)) were segmented on one of the low-diffusion-weighted images and response curves were derived. Based on feature observations and prior literature, each post-exercise period was fitted to a gamma variate function with 1st and 2nd order baseline terms:
| (2) |
This semi-empirical form captures the characteristics of muscle biomarker’s exercise change and return to equilibrium, and has some precedent in muscle characterization [37]. As a quality control measure, fit residual was measured for each metric’s post-exercise response curve and if it exceeded an empirical threshold of 0.10, that subject was excluded from analysis. Total response R0X+l0X+ l1XTTPX, time to peak (TTP), and exponent α were compared between diffusion/T2w metrics. Pearson’s correlation coefficients r were measured comparing parameters between DTI metrics (nMD, nλ1, nλrad) and nT2w metrics, only for the activated gastrocnemius medialis (GM) compartments. Independent sample t-tests assuming unequal variance were used to compare response magnitudes, times to peak (TTP), and α values between each parameter, and Pearson Correlation coefficients between DTI and T2w kinetic metrics, were determined using SPSS v23 (IBM, USA). Slopes S for linear fits between these metrics were computed in Igor Pro (Wavemetrics, USA).
Custom software, executed in Matlab (Mathworks, USA) on a high performance computing cluster (see Acknowledgments), was used for the dynamic image reconstruction and diffusion tensor fitting analysis. ROI sampling of the dynamic MEDITI DTI maps from the rotation phantom study was performed in Matlab as follows. Mean diffusion (MD) values for the same compartment as it underwent rotation were collected using regions of interest drawn on the initial time point (t=0) and propagated spatially through to the whole time series; three timepoints at each of 10 rotations were collected for a total of 30 samples for each compartment. To illustrate repeatability, intraposition and inter-position coefficient of variation (CV) were computed in Igor Pro by the mean value-normalized standard deviation among 3 adjacent samples or that among all mean position values, respectively. Custom software in Igor Pro was used for normalization of post-exercise metrics to rest values, ROI sampling, temporal smoothing and post-exercise recovery fitting of the in vivo calf muscle imaging results. DTI tensor fitting and ROI sampling of static phantom EPI-DTI data was performed in Igor Pro.
Results
Phantom study
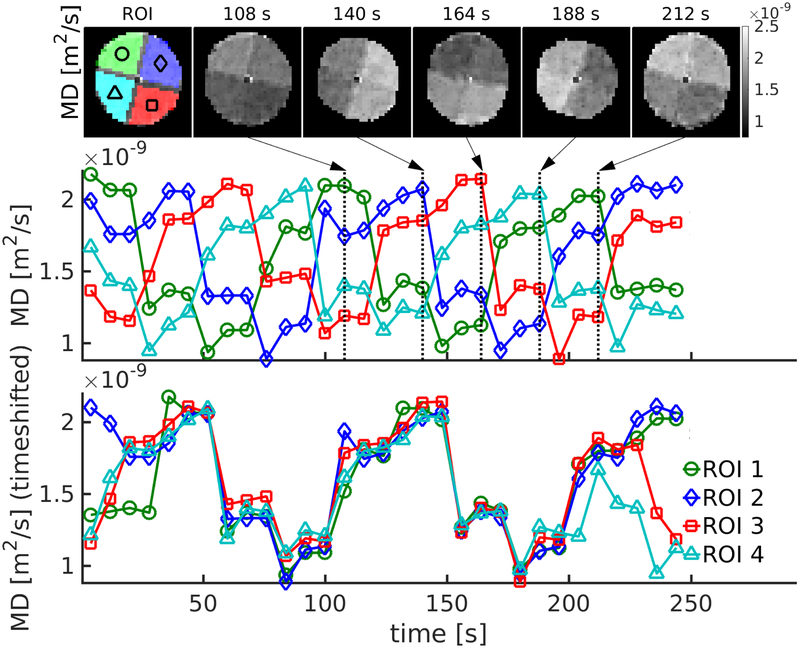
Figure 3 shows results of the dynamic MEDITI acquisition in the rotation phantom. MD maps are shown at several time points in the reconstruction showing the successful depiction of the time-varying location of each gel compartment. As indicated in Figure 3, the MD values in these fixed ROIs took on 4 separate values as each chamber of the phantom was progressively rotated through each position. For illustration purposes, the resulting time curves from each ROI were time-shifted to coincide, confirming the quantitative accuracy of ADC measurement in each chamber for each point in the rotation. Table 1 shows a comparison of MD values from conventional EPI-DTI acquisition and an average of values from the same chamber observed in the MEDITI acquisition (3 timepoints for each of 10 phantom positions, giving 30 values for each compartment). Good correlation (r=0.998, p<0.001) between MD values from each sequence is observed. Intra-position and inter-position coefficients of variation (CV) both show reasonable reproducibility (average of 5% for both metrics).
Figure 3:
Dynamic MEDITI in a phantom with manual rotation of 90 degrees every 24 seconds. (a) MD maps at several different time points (chambers and ROIs indicated in first panel). (b) Time-dependence of MD values sampled in each ROI. (c) Shifted time-dependences from each chamber ROI.
Table 1.
Mean diffusivity values in rotation phantom chamber as measured by EPI-DTI and MEDITI. EPI-DTI MD values reflect compartment ROI averages over one static acquisition, and MEDITI MD values reflect averages over 30 timepoints for each compartment ROI. Intra- and inter-position coefficient of variation (CV) values are explained in text.
| Chamber | MD (μm2/ms) EPI |
MD (μm2/ms) MEDITI |
Intra-position CV (%) MEDITI |
Inter-position CV (%) MEDITI |
|---|---|---|---|---|
| A | 1.62 ± 0.06 | 1.82 ± 0.10 | 5.0 ± 2.9 | 4.4 |
| B | 1.91 ± 0.03 | 2.07 ± 0.07 | 2.8 ± 1.4 | 4.3 |
| C | 1.07 ± 0.04 | 1.21 ± 0.10 | 8.3 ± 3.4 | 5.6 |
| D | 1.28 ± 0.03 | 1.44 ± 0.08 | 3.9 ± 2.6 | 5.6 |
| Average | 5.0 | 5.0 | ||
In vivo Study
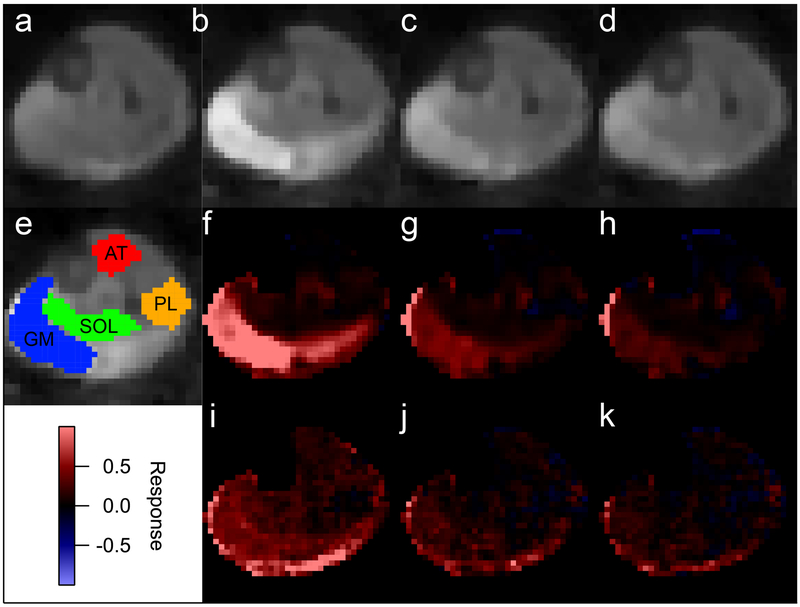
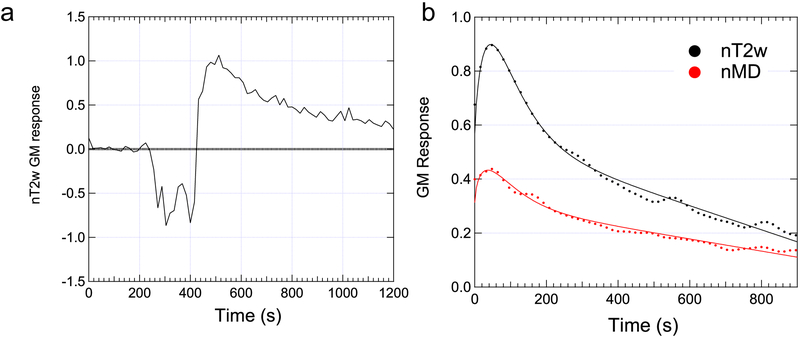
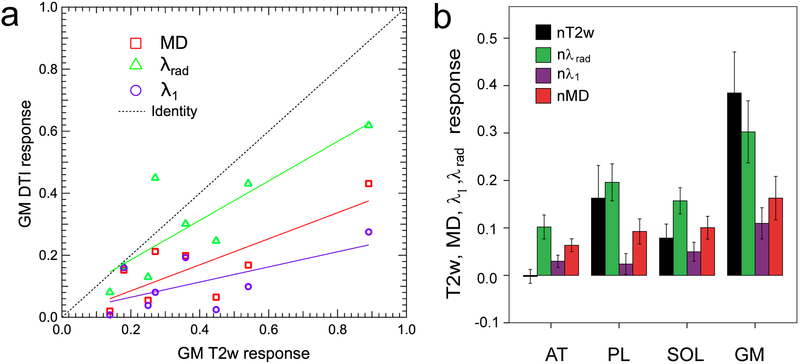
Two volunteers’ data were excluded due to high residual levels for at least one metric. In the remaining cohort of 8 volunteers, maximum voluntary contraction levels ranged from 550 to 900 N (739 ± 109 N) and resistance levels for the exercise bouts were ranged from 16% to 39% (26 ± 7 %) of MVC. Figure 4 (and supplementary animation material) shows example MEDITI data in a volunteer with in-scanner piantarflexion. Figure 4e shows example segmentation of muscle compartments on a T2-weighted image for this subject. Both raw T2w images and T2w response maps clearly indicate post-exercise activation in the gastrocnemius muscles, which resolves over the monitored resting period. Similarly, MD response maps show activation in the same compartment. This temporal behavior is more fully illustrated in ROI-sampled response curves from the gastrocnemius muscle in Figure 5, in which T2w response is larger (90% vs. 45%) than MD response. Figure 6 and Table 2 show group total responses and kinetic parameters for T2w and DTI metrics, stratified by parameter, for the activated gastrocnemius medialis (GM) compartments. Pairwise compartment comparisons showed significant differences between total responses of GM compartments for nT2w vs. nλ1 (p=0.006), nT2w vs. nMD (p=0.006), and nλ1 vs. nλrad (p=0.024). Table 3 shows Pearson correlation coefficients between T2w and DTI metrics from gamma variate fits for all gastrocnemius medialis (GM) compartments. There are significant correlations between nT2w response and nMD (r=0.792, p=0.019) and nλrad (r=0.840, p=0.009). Also, the linear slopes S between diffusion and T2w metrics are not unity and are larger for radial than for axial diffusion. Conversely, less correlation exists between times to peak (TTP) and exponent α of T2w and DTI metric responses, with the exception of TTP for nT2w vs. nλ1. Group responses of imaging metrics are also shown stratified by compartment in Figure 6b. Positive responses were observed in soleus, peroneus, and gastrocnemius compartments. Conversely, anterior tibialis responses were minimal.
Figure 4:
Example MEDITI images and normalized response maps (nT2w and nMD) of the post-exercise recovery in a volunteer. (a) Pre-exercise T2w image. (b-d) Post exercise T2w images (times 0.8 minutes, 6.7 minutes, and 12.5 minutes). (e) Compartment ROI segmentation. (f-h) Post-exercise nT2w images. (i-k) Post-exercise nMD images. Both T2-weighted (nT2w) and mean diffusivity (nMD) normalized response maps show activation of gastrocnemius medialis (GM) muscle compartment.
Figure 5:
(a) Raw ROI-averaged response curve in the GM of subject shown in Figure 4 before, during, and after exercise show clear activation with plantarflexion. (b) Gamma variate fitting of post exercise response curves from final reconstruction shows recovery of nT2w and nMD.
Figure 6:
(a) Crossplot of exercise responses on T2w and diffusion metrics in GM compartment, stratified by DTI metric. Gastrocnemius (GM) compartments generally showed large and correlated T2w and DTI responses. (b) Group response magnitudes for T2w and DTI metrics as a function of compartment. Response levels were higher in PL, SOL, and GM than AT muscles.
Table 2:
Mean, median, and standard deviation of total response levels R, times to peak TTP, and exponents α of all dynamic imaging metrics (nT2w, nMD, nλ1, nλrad) measured in the gastrocnemius medialis (GM) compartment from all 8 subjects in this study.
| Total Response R | Time to Peak TTP (s) | Exponent α | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Median | St. dev. | Mean | Median | St. dev. | Mean | Median | St. dev. | |
| nT2w | .385 | .315 | .244 | 48.3 | 41.9 | 39.1 | 1.01 | .72 | .69 |
| nMD | .163* | .160 | .130 | 123.1 | 43.8 | 224.2 | 1.02 | .69 | 1.02 |
| nλ1 | .110* | .090 | .093 | 111.7 | 66.0 | 158.1 | 45.5 | .96 | 126.3 |
| nλrad | .303† | .274 | .185 | 78.1 | 37.0 | 76.1 | 1.71 | .58 | 2.94 |
significant difference from nT2w;
significant difference from nλ1.
Table 3.
Pearson correlation coefficients r, significance values p, and linear slopes S between nT2w and DTI metrics (nMD, nλ1, nλrad) for all GM compartments in this study (N = 8).
| nMD vs. nT2w | nλ1 vs. nT2w | nλrad vs. nT2w | nλ1 vs. nλrad | |
|---|---|---|---|---|
| Total Response r | 0.792 | 0.642 | 0.840 | 0.660 |
| Total Response p | 0.019 | 0.086 | 0.009 | 0.075 |
| Total Response S | 0.42 ± 0.13 | 0.24 ± 0.12 | 0.64 ± 0.17 | 0.33 ± 0.15 |
| TTP r | −0.291 | 0.821 | 0.480 | 0.176 |
| TTP p | 0.484 | 0.012 | 0.229 | 0.677 |
| TTP S | −1.67 ± 2.24 | 3.32 ± 0.94 | 0.93 ± 0.70 | 0.37 ± 0.84 |
| α r | 0.460 | −0.140 | −0.019 | −0.159 |
| α p | 0.251 | 0.740 | 0.965 | 0.708 |
| α S | 0.68 ± 0.54 | −25.8 ± 74.1 | −0.080 ± 1.74 | −6.8 ± 17.3 |
Discussion
This work shows feasibility of a radically new quantitative imaging approach (MEDITI) for dynamic DTI in a synthetic phantom as well as calf muscles of healthy subjects with exercise. The approach is a blend of rapid multidirectional diffusion encoding, radial imaging trajectories and phase error corrections, and compressed sensing reconstruction that together enable a robust scheme for sensitizing the spatiotemporal dynamics of anisotropic diffusion in skeletal muscle recovery from exercise.
The rotation phantom results successfully demonstrate the MEDITI workflow in capturing spatiotemporal variation of diffusion, though some systematic difference from EPI-DTI exists. One contributing factor to this discrepancy may be in effective diffusion time, which varies in the MEDITI echo train as opposed to the singular EPI-DTI value. We have previously noted this systematic error and studied it with simulations [27], finding the pre-exercise normalization, as employed in the present study, to dramatically reduce its influence on the signal kinetics. Also, the repeatability indicated by the ~5% coefficient of variation estimates over the dynamic series, which include multiple sources of variability (coil sensitivity, rotation artifact) in addition to the diffusion processing, is quite reasonable given the levels of activation in muscle shown in Figs 4-6.
The temporal characteristics of the exercise response in calf muscle in this study are reasonably captured by the gamma variate form we have employed, including transient increase in T2 or diffusion signal following exercise cessation that has been noted in other studies [38], but displays some additional features. Namely, some periodicity appears in the timecourses that may be a combination of temporal regularization and post-hoc smoothing. This merits further scrutiny to refine the exercise response contrast.
Response to exercise for in vivo imaging was observed primarily in GM compartments, consistent with plantarflexion exercise, as seen in previous studies [37,22,38,39]. The anterior muscle compartment showed minimal response. Different and even competing changes in exercising and non-exercising muscles have been previously observed, and interpreted in terms of fluid redistribution from circulatory and hydration demands, in both diffusion metrics [40] and cross-sectional area [41]. As previously observed, correlation exists between exercise response of relaxation (T2) and diffusion contrast (e.g. Figure 6a); this is consistent with a temporary increase in the less restricted and more slowly relaxing extracellular space. However, the anisotropic character of the diffusion response measured in this study may provide more detailed insight. GM compartments showed higher radial than axial diffusion response, consistent with a recent dynamic DTI study in muscle [23]. The mechanisms for these changes likely involve sarcolemma dilation and muscular edema (affecting radial diffusion) and perfusion changes (affecting axial diffusion), as is suggested by radiotracer [42] and MR relaxometry [43] studies. These effects occur in varying amounts due to the level of exertion performed by each subject relative to their own capacity. Thus, this pilot study was sufficient to indicate that the kinetics of the post-plantarflexion diffusion response display subject-dependent delayed maxima, different radial and axial responses, and distinct behavior from T2-weighted imaging. The behavior of the second order features of the gamma-variate characterization (time to peak and α-exponent) are less statistically definitive, possibly due to limited sample size and data precision. The exercise response of this pilot cohort as a whole empirically merited use of a model including latency such the gamma variate form. There are trends that suggest axial diffusion response to have larger latency (higher TTP) and less stretching (higher α) than radial diffusion, possibly consistent with post-exercise reperfusion; however, a far larger cohort study would be required to establish this conclusively.
This study had some limitations and areas for future development. Our rotation phantom allowed dynamic diffusion behavior but did not include anisotropy. The sample size of subjects for this feasibility study was small and not sufficient to conclusively establish mechanisms of relaxation / diffusion exercise response. The subjects were not trained in the exercise regimen prior to scanning, and there was some variability in the same exercise duration and flexion rate between subjects. The spatial resolution of MEDITI may not have been sufficient to recognize and avoid all blood vessels or muscle fascia on ROI compartment sampling, which may have limited assessment of muscle changes alone. Use of a separate co-registered imaging standard for segmentation may provide a degree of stability. SPAIR fat suppression may not have been equally effective on all echoes which may have affected the tensor quantification. An analytical motivation for the choice of regularization parameters (λPCA, λPCAt, λTV) based on signal to noise ratio, spatial resolution, and temporal features has not yet been performed. The current workflow involves a combination of compressed sensing reconstruction and direct post-hoc temporal smoothing to mitigate random variance. A future iteration will involve a systematic evaluation of regularization space as well as elimination of post-hoc smoothing. Prior studies in the literature can help guide choice of regularization parameters [44,34]. While we did not incorporate the diffusion tensor solution itself into the compressed sensing reconstruction process, prescriptions exist in the literature for performing such an integration and potentially benefitting from higher dimensional sparsity [45]. The novelty of the present workflow lies in achieving a novel combination of accelerated diffusion encoding and compressed sensing image reconstruction. While imaging fields of view allowing successful calf imaging have been demonstrated, larger fields of view involve weaker imaging encoding gradients that might be correspondingly more sensitive to off-resonance effects. Incorporation of magnetic field (B0) mapping into the radial reconstruction might allow larger fields of view and a more general application of the MEDITI approach to different skeletal muscles or other organs. Finally, the diffusion-weighting gradients of the multiple echo train, configured to sensitize multiple directions in the present study, could be reconfigured for other contrast schemes (such as intravoxel incoherent motion or diffusion kurtosis imaging) that could then be captured in a dynamic fashion.
Conclusion
We have demonstrated the feasibility on clinical scanners of MEDITI for capturing spatially and temporally resolved diffusion tensor data in post-exercise skeletal muscle recovery. MEDITI leverages rapid diffusion encoding and compressed sensing spatial reconstruction to enable a new paradigm of kinetic monitoring. Ongoing work is directed to optimize the image quality and fully characterize dynamic physiologic signatures of diffusion anisotropy to maximize their clinical benefit.
Supplementary Material
Acknowledgements
This work was supported by the NIH (R21EB009435, S10OD021702). This work has also utilized computing resources at the High Performance Computing Facility of the Center for Health Informatics and Bioinformatics at the NYU Langone Medical Center, see http://www.med.nyu.edu/chibi/services/hpcf/acknowledgement-statement.
Footnotes
Conflict of Interest: The authors declare that they have no conflict of interest.
Ethical approval: All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.
Informed consent: Informed consent was obtained from all individual participants included in the study.
References:
- 1.Basser PJ, Mattiello J, LeBihan D (1994) Estimation of the effective self-diffusion tensor from the NMR spin echo. Journal of Magnetic Resonance Series B 103 (3):247–254. [DOI] [PubMed] [Google Scholar]
- 2.Heemskerk AM, Damon BM (2007) Diffusion Tensor MRI Assessment of Skeletal Muscle Architecture. Curr Med Imaging Rev 3 (3):152–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sinha S, Sinha U, Edgerton VR (2006) In vivo diffusion tensor imaging of the human calf muscle. Journal of Magnetic Resonance Imaging 24 (1):182–190. [DOI] [PubMed] [Google Scholar]
- 4.Noseworthy MD, Davis AD, Elzibak AH (2010) Advanced MR Imaging Techniques for Skeletal Muscle Evaluation. Semin Musculoskel R 14 (2):257–268. [DOI] [PubMed] [Google Scholar]
- 5.Froeling M, Nederveen AJ, Nicolay K, Strijkers GJ (2013) DTI of human skeletal muscle: the effects of diffusion encoding parameters, signal-to-noise ratio and T2 on tensor indices and fiber tracts. NMR Biomed 26 (11):1339–1352. [DOI] [PubMed] [Google Scholar]
- 6.Zhong X, Epstein FH, Spottiswoode BS, Helm PA, Blemker SS (2008) Imaging two-dimensional displacements and strains in skeletal muscle during joint motion by cine DENSE MR. Journal of Biomechanics 41 (3):532–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhou H, Novotny JE (2007) Cine phase contrast MRI to measure continuum Lagrangian finite strain fields in contracting skeletal muscle. Journal of Magnetic Resonance Imaging 25 (1):175–184. [DOI] [PubMed] [Google Scholar]
- 8.Litwiller D, Amrami K, Dahm D, Smith J, Laskowski E, Stuart M, Felmlee J (2007) Chronic exertional compartment syndrome of the lower extremities: improved screening using a novel dual birdcage coil and in-scanner exercise protocol. Skeletal Radiology 36 (11): 1067–1075. [DOI] [PubMed] [Google Scholar]
- 9.Ward SR, Terk MR, Powers CM (2005) Influence of patella alta on knee extensor mechanics. Journal of Biomechanics 38 (12):2415–2422. [DOI] [PubMed] [Google Scholar]
- 10.Sinha S, Hodgson JA, Finni T, Lai AM, Grinstead J, Edgerton VR (2004) Muscle kinematics during isometric contraction: Development of phase contrast and spin tag techniques to study healthy and atrophied muscles. Journal of Magnetic Resonance Imaging 20 (6):1008–1019. [DOI] [PubMed] [Google Scholar]
- 11.Asakawa DS, Nayak KS, Blemker SS, Delp SL, Pauly JM, Nishimura DG, Gold GE (2003) Real-time imaging of skeletal muscle velocity. Journal of Magnetic Resonance Imaging 18 (6):734–739. [DOI] [PubMed] [Google Scholar]
- 12.Bendahan D, Giannesini B, Cozzone PJ (2004) Functional investigations of exercising muscle: a noninvasive magnetic resonance spectroscopy-magnetic resonance imaging approach. Cellular and Molecular Life Sciences (CMLS) 61 (9):1001–1015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Price TB, Gore JC (1998) Effect of muscle glycogen content on exercise-induced changes in muscle T2 times. J Appl Physiol 84 (4):1178–1184. [DOI] [PubMed] [Google Scholar]
- 14.Parasoglou P, Xia D, Chang G, Regatte RR (2013) Dynamic three-dimensional imaging of phosphocreatine recovery kinetics in the human lower leg muscles at 3T and 7T: a preliminary study. NMR Biomed 26 (3):348–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Andreisek G, White LM, Sussman MS, Langer DL, Patel C, Su JWS, Haider MA, Stainsby JA (2009) T2*-Weighted and Arterial Spin Labeling MRI of Calf Muscles in Healthy Volunteers and Patients With Chronic Exertional Compartment Syndrome: Preliminary Experience. Am J Roentgenol 193 (4):W327–W333. [DOI] [PubMed] [Google Scholar]
- 16.Saab G, Thompson RT, Marsh GD (1999) Multicomponent T2 relaxation of in vivo skeletal muscle. Magn Reson Med 42 (1):150–157. [DOI] [PubMed] [Google Scholar]
- 17.Ababneh Z, Beloeil H, Berde CB, Gambarota G, Maier SE, Mulkern RV (2005) Biexponential parameterization of diffusion and T2 relaxation decay curves in a rat muscle edema model: decay curve components and water compartments. Magn Reson Med 54 (3):524–531. [DOI] [PubMed] [Google Scholar]
- 18.Ababneh ZQ, Ababneh R, Maier SE, Winalski CS, Oshio K, Ababneh AM, Mulkern RV (2008) On the correlation between T(2) and tissue diffusion coefficients in exercised muscle: quantitative measurements at 3T within the tibialis anterior. MAGMA 21 (4):273–278. [DOI] [PubMed] [Google Scholar]
- 19.Morvan D, Leroy-Willig A, Malgouyres A, Cuenod CA, Jehenson P, Syrota A (1993) Simultaneous temperature and regional blood volume measurements in human muscle using an MRI fast diffusion technique. Magn Reson Med 29 (3):371–377. [DOI] [PubMed] [Google Scholar]
- 20.Filli L, Boss A, Wurnig MC, Kenkel D, Andreisek G, Guggenberger R (2015) Dynamic intravoxel incoherent motion imaging of skeletal muscle at rest and after exercise. NMR Biomed 28 (2):240–246. [DOI] [PubMed] [Google Scholar]
- 21.Sigmund EE, Novikov DS, Sui D, Ukpebor O, Baete S, Babb JS, Liu K, Feiweier T, Kwon J, McGorty K, Bencardino J, Fieremans E (2014) Time-dependent diffusion in skeletal muscle with the random permeable barrier model (RPBM): application to normal controls and chronic exertional compartment syndrome patients. NMR Biomed 27 (5):519–528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sigmund EE, Sui D, Ukpebor O, Baete S, Fieremans E, Babb JS, Mechlin M, Liu K, Kwon J, McGorty K, Hodnett PA, Bencardino J (2013) Stimulated echo diffusion tensor imaging and SPAIR T2 -weighted imaging in chronic exertional compartment syndrome of the lower leg muscles. J Magn Reson Imaging 38 (5):1073–1082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rockel C, Akbari A, Kumbhare DA, Noseworthy MD (2017) Dynamic DTI (dDTI) shows differing temporal activation patterns in post-exercise skeletal muscles. MAGMA 30 (2):127–138. [DOI] [PubMed] [Google Scholar]
- 24.Baete SH, Cho G, Sigmund EE (2013) Multiple-echo diffusion tensor acquisition technique (MEDITATE) on a 3T clinical scanner. NMR Biomed 26 (11):1471–1483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tang X-P, Sigmund EE, Song Y-Q (2004) Simultaneous measurement of diffusion along multiple directions. Journal of the American Chemical Society 126 (50):16336–16337. [DOI] [PubMed] [Google Scholar]
- 26.Sigmund EE, Song YQ (2006) Multiple echo diffusion tensor acquisition technique. Magnetic Resonance Imaging 24 (1):7–18. [DOI] [PubMed] [Google Scholar]
- 27.Baete SH, Cho GY, Sigmund EE (2015) Dynamic diffusion-tensor measurements in muscle tissue using the single-line multiple-echo diffusion-tensor acquisition technique at 3T. NMR Biomed 28 (6):667–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sigmund EE, Baete SH, Luo T, Patel K, Wang D, Rossi I, Duarte A, Bruno M, Mossa D, Femia A, Ramachandran S, Stoffel D, Babb JS, Franks A, Bencardino J (2018) MRI assessment of the thigh musculature in dermatomyositis and healthy subjects using diffusion tensor imaging, intravoxel incoherent motion, and dynamic DTI. European Radiology (in press). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lavdas I, Behan KC, Papadaki A, McRobbie DW, Aboagye EO (2013) A phantom for diffusion-weighted MRI (DW-MRI). J Magn Reson Imaging 38 (1):173–179. [DOI] [PubMed] [Google Scholar]
- 30.Sarty GE (2004) Single TrAjectory radial (STAR) imaging. Magn Reson Med 51 (3):445–451. [DOI] [PubMed] [Google Scholar]
- 31.Feng L, Grimm R, Block KT, Chandarana H, Kim S, Xu J, Axel L, Sodickson DK, Otazo R (2014) Golden-angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn Reson Med 72 (3):707–717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Truong TK, Chen NK, Song AW (2012) Inherent correction of motion-induced phase errors in multishot spiral diffusion-weighted imaging. Magn Reson Med 68 (4):1255–1261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Liu C, Moseley M, Bammer R (2005) Simultaneous phase correction and SENSE reconstruction for navigated multi-shot DWI with non-cartesian k-space sampling. Magn Reson Med 54 (6):1412–1422. [DOI] [PubMed] [Google Scholar]
- 34.Otazo R, Kim D, Axel L, Sodickson DK (2010) Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magn Reson Med 64 (3):767–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lustig M, Donoho D, Pauly JM (2007) Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 58 (6):1182–1195. [DOI] [PubMed] [Google Scholar]
- 36.Hsu EW, Mori S (1995) Analytical expressions for the NMR apparent diffusion coefficients in an anisotropic system and a simplified method for determining fiber orientation. Magn Reson Med 34 (2):194–200. [DOI] [PubMed] [Google Scholar]
- 37.Schmid AI, Meyerspeer M, Robinson SD, Goluch S, Wolzt M, Fiedler GB, Bogner W, Laistler E, Krssak M, Moser E, Trattnig S, Valkovic L (2016) Dynamic PCr and pH imaging of human calf muscles during exercise and recovery using (31) P gradient-Echo MRI at 7 Tesla. Magn Reson Med 75 (6):2324–2331. [DOI] [PubMed] [Google Scholar]
- 38.Schewzow K, Fiedler GB, Meyerspeer M, Goluch S, Laistler E, Wolzt M, Moser E, Schmid AI (2015) Dynamic ASL and T2-weighted MRI in exercising calf muscle at 7 T: a feasibility study. Magn Reson Med 73 (3):1190–1195. [DOI] [PubMed] [Google Scholar]
- 39.Yanagisawa O, Kurihara T, Kobayashi N, Fukubayashi T (2011) Strenuous resistance exercise effects on magnetic resonance diffusion parameters and muscle-tendon function in human skeletal muscle. J Magn Reson Imaging 34 (4):887–894. [DOI] [PubMed] [Google Scholar]
- 40.Nygren AT, Kaijser L (2002) Water exchange induced by unilateral exercise in active and inactive skeletal muscles. J Appl Physiol (1985) 93 (5):1716–1722. [DOI] [PubMed] [Google Scholar]
- 41.Nygren AT, Greitz D, Kaijser L (2000) Changes in cross-sectional area in human exercising and non-exercising skeletal muscles. Eur J Appl Physiol 81 (3):210–213. [DOI] [PubMed] [Google Scholar]
- 42.Sjogaard G, Saltin B (1982) Extra- and intracellular water spaces in muscles of man at rest and with dynamic exercise. Am J Physiol 243 (3):R271–280. [DOI] [PubMed] [Google Scholar]
- 43.Saab G, Thompson RT, Marsh GD (2000) Effects of exercise on muscle transverse relaxation determined by MR imaging and in vivo relaxometry. J Appl Physiol (1985) 88 (1):226–233. [DOI] [PubMed] [Google Scholar]
- 44.Otazo R, Candes E, Sodickson DK (2015) Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn Reson Med 73 (3):1125–1136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Knoll F, Raya JG, Halloran RO, Baete S, Sigmund E, Bammer R, Block T, Otazo R, Sodickson DK (2015) A model-based reconstruction for undersampled radial spin-echo DTI with variational penalties on the diffusion tensor. NMR Biomed 28 (3):353–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.