HYBRID MODELS OF CELL AND TISSUE DYNAMICS IN TUMOR GROWTH

Abstract

Hybrid models of tumor growth, in which some regions are described at the cell level and others at the continuum level, provide a flexible description that allows alterations of cell-level properties and detailed descriptions of the interaction with the tumor environment, yet retain the computational advantages of continuum models where appropriate. We review aspects of the general approach and discuss applications to breast cancer and glioblastoma.

1. Introduction.

Tumor growth is a complex evolutionary process driven by dynamic feedback between a heterogeneous cell population and selection pressures from the tumor microenvironment (TME). The TME comprises the extracellular matrix (ECM), growth promoting and inhibiting factors, nutrients such as oxygen and glucose, chemokines, and other cell types in the stromal tissue, including tumor-associated fibroblasts (TAFs), immune cells, and normal endothelial and epithelial cells [32]. Alterations in gene regulation and signaling networks involved in cell proliferation and survival have been studied by many, but there is little understanding of how the chemical and mechanical signals from the TME interact to affect tumor progression. Here we review the multiscale nature of the tumor growth process and its interaction with the TME in the context of breast cancer and glioblastoma.

Growth of malignant cells often leads to a microenvironment (ME) of limited oxygen and nutrient availability, and cells in such environments can adapt by stimulating angiogenesis and altering their metabolism [41, 19]. In addition, tumor cells may produce chemoattractants to attract stromal cells such as macrophages and TAFs, which can also supply the signals and substrates required for growth. Cells are also subject to external forces that arise from cell-cell adhesion, cell growth, and cell-substrate (fluid or ECM) interactions during movement. It is widely recognized that forces within a cell and between a cell and its ME, whether the ME is other cells in an epithelial sheet, or the ECM in the tissue, give rise to an additional mode of signaling that can influence cell growth, differentiation, and the morphology of a tissue. Experimental studies have shown that the mechanical properties of the TME can significantly affect the growth of a tumor [15], and that these forces can affect the packing density of cells in a tumor, and thereby, the penetrability and distribution of drugs in a tumor [13].

Tumor progression involves a hierarchy of time and space scales, the former ranging from seconds for individual reactions, to months or years for the emergence of mutations and tumor growth, and the latter ranging from the molecular level at one end, to the tissue level for description of tumors, metastasis, and the evolution of nutrients at the other end. A brief outline of the main processes is as follows.

• Nutrient and drug transport – A key factor that affects tumor growth is the spatial distribution of nutrients, growth factors and drugs, which is determined by transport into the tumor by diffusion or convection. The transport processes determine length scales over which these factors vary and impact the spatial organization and evolution of tumor cell populations by inducing intratumoral heterogeneity in cell division/death rates, signaling processes, motility and intercellular forces. Many models of tumor growth incorporate nutrient transport at various scales using continuum or cell-based models [28, 6], but further work is needed on the effect of cell packing and cell-cell interactions on cell- and population-level phenomena [27].

• Mechanics and cell movement – Understanding how the mechanical properties of the ECM affect tumor growth and how to model movement of single cells and small groups of cells through a tumor or the ECM is important for understanding how mechanics at the cell and tissue levels affect tumor evolution. Work cited above treats some of the effects of the TME on growth, but a cell’s morphology and the interaction with the ME can be very different in 3D than in 2D [8]. Detailed models of single cell motility have been developed in 2D [12, 38], and less detailed cell-based models have been used to predict movement of cellular aggregates [34, 33] and to understand force transmission within a moving aggregate [4]. Detailed models of single-cell movement in 3D that account for local mechanical interactions with the ECM remain a challenge.

• Signaling – Many mutations affect signaling pathways involving growth factors or cytokines, and cell-cell signaling frequently involves indirect interactions between spatially-separated cell populations within the ME, eg., between tumor and stromal cells [27], or between normoxic and hypoxic cells within a tumor. Factors such as cell packing density and anisotropy of transport through the tissue affect the signaling process, but despite its importance, experimental data on signaling within tumors is sparse. Thus computational studies and sensitivity analysis on the effects of these interactions on tumor progression can provide valuable insights.

2. The hybrid model for tumor growth.

Most models treat a tumor either as a spatially-averaged continuum or as discrete individual cells, and both approaches have advantages and drawbacks. The former is easier to analyze analytically and computationally, but suffers from the fact that one cannot vary properties on the scale of single cells. One can incorporate much more detail in a cell-based model, but this limits the number of cells that can be treated computationally. For instance, a spheroid 2 mm in diameter contains ~ 2×10⁶ cells of 15 μm in diameter, and new parallel algorithms are needed to treat this many cells if both internal variables and cell-cell interactions are incorporated. However, it may be unnecessary to describe the entire tumor with such detail, since quiescent or necrotic regions only affect the mechanical and rheological properties of the tumor. Furthermore, the ECM can invariably be treated as a continuum, which makes it feasible to use a cell-based model in some regions of space and continuum models in others [22, 27].

For these reasons we developed a hybrid model that uses a cell-based description in rapidly-proliferating regions, and describes the remainder of a tumor and the ECM or surrounding gel as continua, possibly with variable properties [22, 38, 25, 27]. This allows for changes in properties at the individual cell level in regions where it is likely to be most important, while retaining the computational advantage of a continuum description for both the interior of the tumor and the exterior tissue. In the hybrid model only a few hundred actively-proliferating cells on the outer layer of larger spheroids are treated individually, and therefore one can allow variations in cell adhesion, the cell cycle time, the metabolic state, cell size, and intra- and intercellular mechanics. As a result, one can study the effect of changes in the balances between adhesion, chemotaxis and other effects on the rate of detachment of individual cells or small groups of cells from the tumor. This has been useful for predicting the spread of highly invasive tumors such as gliomas, for which the leading edge is diffuse and difficult to define precisely in a continuum description. In addition, the model can shed light on the question of whether there must be significant phenotypic differences between these invasive cells and other proliferating cells not at the leading edge, and whether cell-cycle-specific changes are involved. Other hybrid models are discussed in [29, 6].

The model treats the mechanics and growth of individual cells, but models the nutrients and the mechanics of the ECM and stromal tissue as continuua. Three properties are used to describe individual cells: (i) their mechanical interaction with the surroundings and how an individual cell reacts to forces on it, (ii) their growth and division rates, which depend on stress and other factors, and (iii) metabolic and signaling networks. The mechanical behavior of individual cells is based on an earlier model [34, 4, 22]. The forces on a cell are (i) active forces exerted on neighboring cells or the substrate, (ii) reactive forces exerted by other cells on it, (iii) drag forces that arise as a moving cell forms or breaks adhesive bonds with neighboring cells, and (iv) a static force that exists when cells are rigidly attached to each other or to the substrate. The cells are treated as oriented ellipsoids (ellipses in 2D) whose cytoplasm is an incompressible viscoelastic solid [4]. To describe growth and division, let V₀ be the cell volume immediately after division. In the absence of nutrient or stress limitations cells grow to the volume 2V₀ and then immediately divide into two equal daughter cells. In the presence of extracellular forces the orientation of cell division is determined by the direction of the net force exerted on the cell, as others have assumed [9]. Complete statements of the governing equations are given in [22].

A major advantage of cell-based models is the ability to track lineages of individual cells as they grow and divide. In Fig. 1 we show the evolution of cells in a monolayer in the presence of sufficient nutrients, and the absence of drugs and forces other than those due to growth and attachment to the substrate. One sees that even though all cells have access to the same nutrient levels (the specific forms of uptake are described later) the internally-generated forces due to growth and attachment to the substrate reduces the growth rate of the black cells in the interior of the aggregate. This illustrates the importance of understanding the individual effects of different factors on patterns of cell growth in an aggregate.

Figure 1:

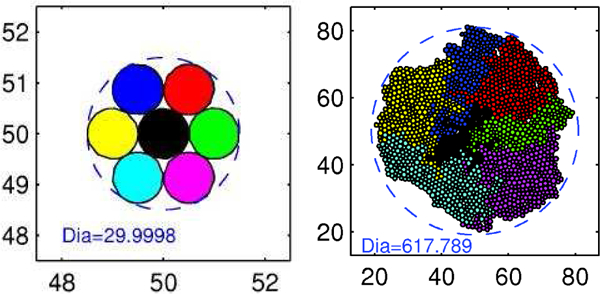
The pattern of growth in a monolayer. Left: t = 0, Right: T= 276 hr (Dia = diameter in microns). (From [38], with permission.)

2.1. Tumor growth in the ECM.

The hybrid model comprises up to four distinct spatial regions: stromal tissue or matrigel surrounding the tumor, a shell of actively-proliferating cells at the outer edge of the tumor, a quiescent zone bordering the actively-proliferating region, and possibly a necrotic core, which we denote as $\mathcal{G},\mathcal{P},\mathcal{Q},\text{and}\mathcal{N}$ respectively (cf. Fig. 2). For small tumors only $\mathcal{G},\mathcal{P},\mathcal{Q}$ are present. When nutrient penetration into the tumor is inadequate, the actively proliferating region comprises a layer 3–5 cells thick in the radial direction, and therefore contains a few hundred cells. When there are multiple cell types in the tumor the respective regions may differ for each type - i.e., one type may be able to proliferate under conditions that drive another type into quiescence. Furthermore, when the force is spatially nonuniform, as can occur as a result of nonuniform cell densities and different mechanical properties of different cell types, the balance between the effects of force and administered drugs on the growth rate may be quite subtle. In fact, the proliferating regions may be distributed in non-intuitive ways due to spatially-varying balances between nutrient availability, drug level, and intra-tumor forces.

Figure 2:

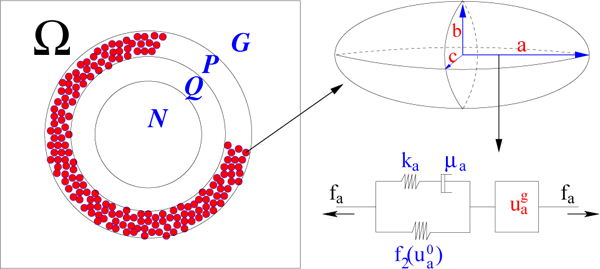
A schematic showing the notation used for the subdomains, the representation of cells in the proliferating zone as ellipsoids, and the representation of the standard solid and growth elements that characterize the internal rheology of each cell in P. (From [22], with permission.)

The mathematical description of the composite system is based on the assumption that the outer gel or ECM, the quiescent region, and the necrotic region are homogeneous materials, but different material parameters are used in $\mathcal{G},\mathcal{Q}\text{and}\mathcal{N}$ and a spatially non-uniform description of the ECM is feasible ([22] - hereafter the model and paper are referred to as KSO). The cell-based KSO component of the model facilitates a variety of computational experiments that probe the effects of variations in cell parameters and allows the tracking of lineages of specific cells. We first examine various behaviors of cells in a two-dimensional layer supplied with adequate nutrients. In Fig. 3(a-f) we show how clones evolve and how their spatial localization changes with time. One sees there how the competition for space affects the size of clones: cells in the interior of an aggregate grow slowly compared to those on the outer boundary because they are compressed by surrounding cells (see also Fig. 3(g)) even in the absence of constraints at the edge of the tissue. The simulation reveals an asymmetric pattern of clones and irregular boundaries between them, which are dictated in part by the initial conditions. The dramatic effect of different levels of the compression parameter σ_ on the total number of cells is shown in Fig. 3(h), where one sees that cells grow faster for smaller (more negative) values of σ_.

Figure 3:

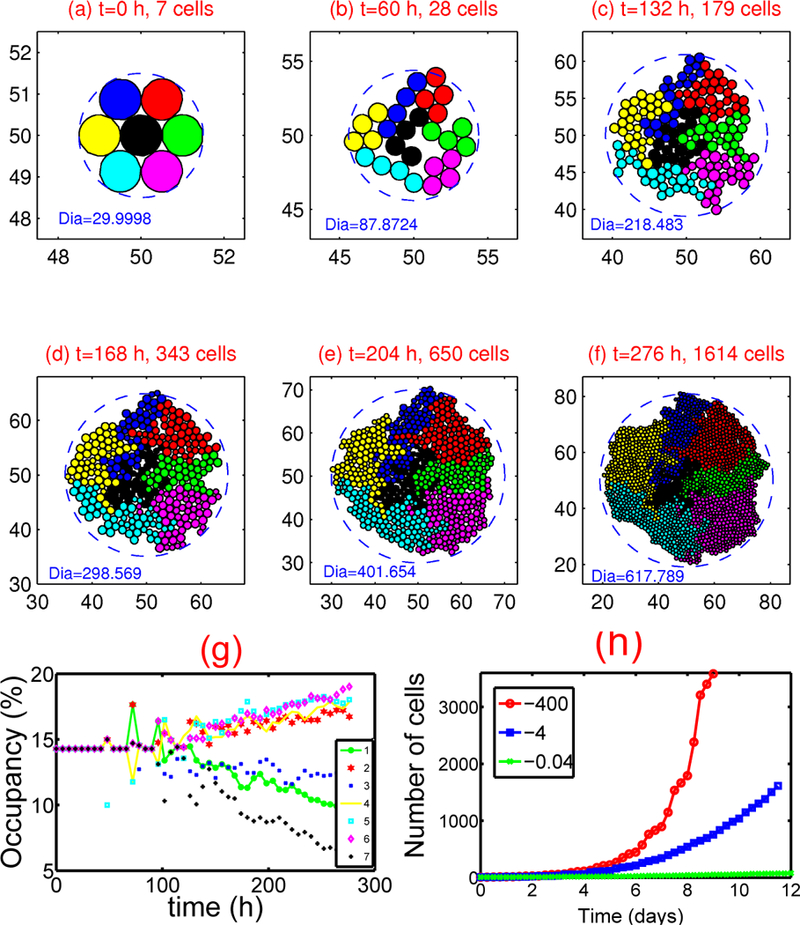
Tumor growth in the presence of adequate nutrients. (a)-(f) : Tumor growth. Parameters used: σ_- =−4.0nN, σ₊=800.0nN, c⁺ = 5.16089 × 10⁻⁹ mm/(min nN) - Dia = diameter in microns. (g) : The occupancy (%) for each clone corresponding to (a)-(f). Notice that the occupancy by cells in the central clone (black cells) decreases significantly compared to other types due to the stress effect on growth. (h) : Growth kinetics for different levels of the compression parameter σ_- = −400, −4, −0.04 nN. From [38], with permission.

The next step is to incorporate the mechanical interaction of a growing tumor with its ME in vitro, to study the effect of external stresses on growth. The actively proliferating region comprises a layer 3–5 cells thick in the radial direction that is described with the cell-based model, whereas the outer gel, the quiescent region, and the necrotic region are homogeneous materials that we represent as continua. These regions have the same rheological properties, but different material parameters are used in $\mathcal{G},\mathcal{Q}\text{and}\mathcal{N}.$ The irregular boundaries between the cell-based region $\mathcal{P}$ and the continuum regions $\mathcal{G}\text{and}\mathcal{Q}$ are represented by two artificial boundaries across which the forces are transmitted.

The proliferating zone $\mathcal{P}$ comprises a few hundred cells that grow and divide as dictated by nutrient conditions, and whose shape changes are governed by their internal rheology and the forces acting on them. We assume that cells grow as long as $\sigma \in \left[{\sigma }^{-},{\sigma }^{+}\right]$ and they have adequate nutrients. Some of the cells in may $\mathcal{P}$ become quiescent when the level of nutrients drops below the threshold, and since the quiescent region $\mathcal{Q}$ is represented as a continuum, those cells must be transformed into the continuum region $\mathcal{Q}$ The displacements of these transformed cells and the forces acting on them are converted into displacements and stress fields in this newly-formed continuum material in $\mathcal{Q},$ as described in KSO. To preserve mass during the transformation, it is also assumed that the ECM between cells that are converted into continuum is converted as well.

The outer gel $\left({\Omega }_0\right)$ and the inner region $\left({\Omega }_m,m=1,2\right)$ are treated as linear viscoelastic materials with different material properties ${\mathcal{C}}^m,{\mathcal{D}}^m,$ m = 0,1, and therefore the constitutive equations and the momentum equation, neglecting inertial effects, are

$$\sigma =\mathcal{C}\text{e}+\mathcal{D}\stackrel{.}{\text{e}}on\Omega \times (0,T),$$ (1)

$$\nabla \cdot \sigma =0on\Omega \times (0,T),$$ (2)

with boundary conditions $u^0=0\text{on}{\Gamma }_0\times (0,T),{\sigma }^0\cdot n=q_0\text{on}{\Gamma }_{c0}\times (0,T),$ and ${\sigma }^1\cdot n=q_1\text{on}{\Gamma }_{c1}\times (0,T).$ Here C and D are second-order tensors with entries described in KSO, e is the strain, Г₀ is the fixed outer boundary, Г_c0 is the interface between $\mathcal{G}$ and $\mathcal{P},{\Gamma }_{c1}\text{is}\text{the}\text{interface}\text{between}\mathcal{P}$ and $\mathcal{Q},u^0$ is the displacement field on $\mathcal{G},{\sigma }^0$ and ${\sigma }^1$ are the stress fields on ${\Omega }_0$ and ${\Omega }_1,$ resp. $q_{\text{0}}$ and $q_1$ are boundary forces acting on ${\Gamma }_{c0}$ and ${\Gamma }_{c1}$ resp. These equations are solved using first- or second-order elements in a finite-element discretization. The parameters used in the computations are given in Table 2 in KSO.

The nutrients considered here are oxygen and glucose, and we assume that their consumption is described by Michaelis-Menten kinetics. The governing equations for the evolution of the nutrients, assuming Dirichlet boundary conditions, are

$$\begin{array}{l}\frac{\partial c_{O_2}}{\partial t}=D_o{\nabla }^2{c}_{O_2}-{\varphi }_{O_2}\left(c_{O_2}\right)\left(A_{O_2}+\frac{B_{O_2}}{c_{\text{gl}}+n_{O_2}}\right)\left(\frac{c_{O_2}}{c_{O_2}+k_{O_2}}\right)\text{in}\Omega \\ \frac{\partial c_{\text{gl}}}{\partial t}=D_g{\nabla }^2{c}_{\text{gl}}-{\varphi }_{gl}\left(c_{\text{gl}}\right)\left(A_{gl}+\frac{B_{gl}}{c_{O_2}+n_{gl}}\right)\left(\frac{c_{\text{gl}}}{c_{\text{gl}}+k_{gl}}\right)\text{in}\Omega \\ c_{O_2}={\overline{c}}_{O_2},c_{\text{gl}}={\overline{c}}_{gl}\text{on}\partial \Omega .\end{array}$$ (3)

Here c₀₂and c_g1 are the molar concentrations of oxygen and glucose, resp., and ${\overline{c}}_{O_2}\text{and}{\overline{c}}_{gl}$ are fixed values of these quantities on the boundary. The second term of each equation is a function describing the consumption of oxygen (glucose) by the tumor, $D_o\left(D_g\right)$ is the space-dependent $(\mathcal{G},\mathcal{P},\mathcal{Q},\mathcal{N})$ diffusion coefficient of oxygen (glucose), $A_{O\text{2}},A_{gl},B_{O2},B_{gl}{k}_{O\text{2}},k_g,n_{O2},$ and $n_{gl}$ are empirically determined parameters, and ${\varphi }_{O_2}\left(c_{O_2}\right),{\varphi }_{gl}\left(c_{\text{gl}}\right)$ are the cell consumption indicator functions which give 1 in $\mathcal{P},\mathcal{Q}$ and 0 otherwise. The parameter values for the reaction-diffusion equations are given in Table 3 in KSO. The reaction-diffusion equations (3) are solved on a regular grid using an alternating-direction implicit (ADI) scheme and the package nksol (which has been superseded by nitsol) for nonlinear algebraic systems. Details of the computational algorithm can be found in KSO.

2.2. The mechanical effects of the surrounding medium.

It was shown in KSO that (i) the shape of a tumor spheroid embedded in a sufficiently dense agarose gel is relatively symmetric and smoother than the shape of a tumor growing in free suspension, and that (ii) tumors maintain a viable rim of relatively constant thickness regardless of the stiffness of the surrounding gel. In [38] it was shown that a stiffer gel inhibits tumor growth more effectively, as shown in Figure 4(a). The gel stiffness also affects the packing density of cells in the proliferating region, as found experimentally [15]. The packing density is determined from the total area P_A of region P and the area Ca covered by cells in P. Since the force required to deform a stiffer outer gel is larger, the cells in region P tend to rearrange themselves to fill a more constrained area, which leads to a larger packing density. The cells can deform a more compliant outer gel more easily, which leads to a lower packing density and more irregular interfaces at the gel and quiescent zone interfaces. Furthermore, the average cell area converges to a limiting value after an initial fluctuation due to initial massive growth of tumor before transformation happens (cf. Figure 4(c)). In the KSO model, the cell area indicates the cells’ phase at a given time and the distribution of area of cells shows that more cells remain in an early phase of cell cycle (cf. Fig. 4(d)).

Figure 4:

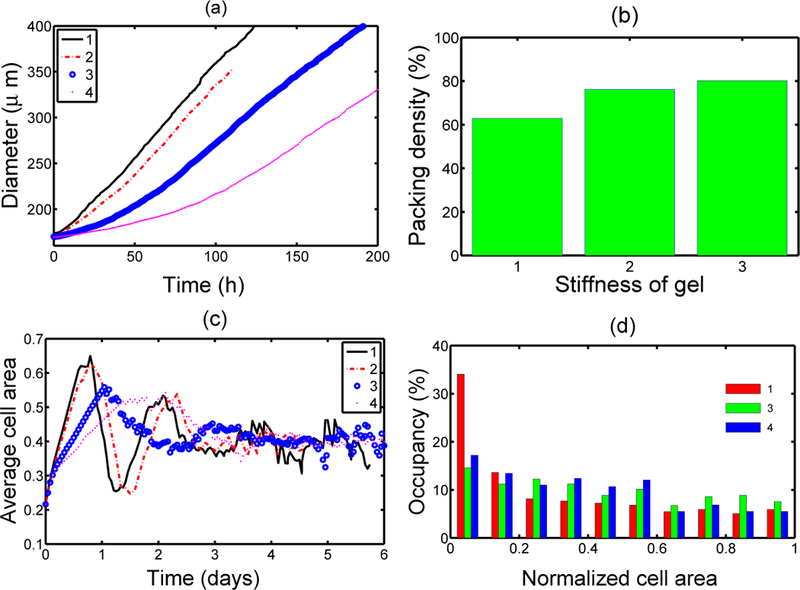
(a) The effect of gel stiffness on tumor growth. 1–4 correspond to different Young’s moduli E^a (10, 20, 80, 200 MPa, resp. ) of the agarose gel. The diameter of the tumor is defined as $\left({\displaystyle {\sum }_i{d}_i^c}\right)/N_{bd}^G$ where $d_i^c$ is the distance from the i-th node point on the $\mathcal{P}-\mathcal{G}$ interface to the tumor center and $N_{bd}^G$ is the number of nodes on the $\mathcal{P}-\mathcal{G}$ interface, (b) The effect of gel stiffness on packing density: Packing density at 137 h. (c) The average cell area A_c(t) (normalized) in the $\mathcal{P}$ region for each case. $A_c(t)={\displaystyle {\sum }_i{A}_n^i}(t)/N_c(t)\text{ where }{A}_n^i(t)$ is the normalized cell area and $N_c\text{ ( }t\text{) }$ is the number of cells at time t. (d) Area distribution of proliferating cells corresponds to cases 1,3, and 4 in (c) at 137 h. From [38], with permission.

3. Applications of the hybrid model to breast cancer.

The KSO model has also been applied to breast cancer, in particular ductal carcinoma in situ (DCIS), that originates in milk ducts. The ducts are comprised of a layer of ECs, a layer of myo-epithelial cells, and a layer of basement membrane, surrounded by the ECM. The ECM usually contains fibroblasts, myofibroblasts, and macrophages that can secrete growth factors and cytokines, which leads to autocrine and paracrine signaling that produces a complex biochemical landscape in the TME. Fibroblasts can also secrete ECM, which modulates the mechanical environment of a duct. Homeostasis in a duct involves a number of growth factors, including TGF-β, which inhibits division, that determine whether a cell remains in G₁ or goes on to divide. Changes in TGF-β, signaling usually arise from changes in the balances between the TGF-β, pathways and other growth factor pathways, primarily the EGF pathway. A model based on the interaction between these pathways, which includes both paracrine and autocrine signaling in the ECM, was developed in [27].

In a homeostatic state the fibroblasts in the TME divide infrequently and secrete only just enough EGF and other factors needed to maintain homeostasis. In this state the rates of TGF-β, and EGF production are balanced, and growth and proliferation are controlled. However when the populations of transformed epithelial cells (TECs) is sufficiently large, proliferation and secretion of TGF-β, increases [30, 31], and the increased secretion of TGF-β, into the surrounding ECM stimulates differentiation of fibroblasts into myofibroblasts and up-regulates their secretion of EGF. This increase in EGF may in turn lead to up-regulation of EGF receptors such as Her2/Neu on ECs, which enhances signaling via the EGF pathway [3]. This creates a positive feedback loop that enhances proliferation (see Fig. 5).

Figure 5:

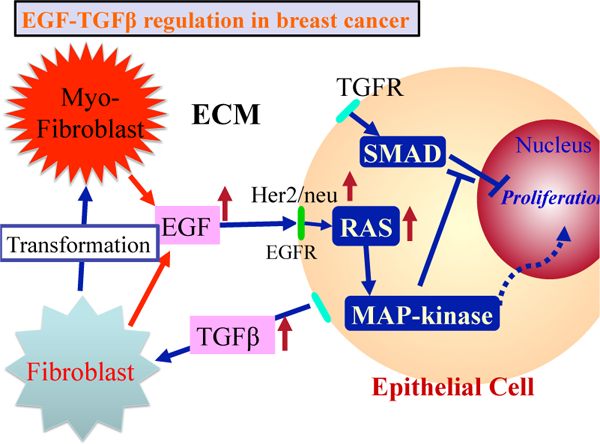
The interaction of the EG F and TGF-β pathways in the control of proliferation in breast cancer. In normal ECs these pathways are balanced so as to control growth, but in TECs increased secretion of TGF-β induces fibroblasts and myofibroblasts to secrete more EGF. This disrupts the prolifération-inhibition mechanism by partially blocking the TGF-β-Smad pathway and triggers proliferation. From [27], with permission.

In the early stages of DCIS the tumor remains in the duct because the basement membrane is intact, and at this stage the surrounding ECM has little effect. Later, ‘tumor-associated-fibroblasts’ (TAFs) secrete paracrine factors detected by tumor cells, and stimulate alterations to the ECM. Myofibroblasts are found near a developing tumor, and after the transition to invasive breast cancer they migrate to the invading front [39] of the tumor.

3.1. Development in the absence of paracrine signaling.

To simplify the computations, we first specified the location of TECs and followed their evolution. Fig. 6 shows the different growth patterns generated by different sites of initiation of TECs along the periphery of the duct. TECs (gray circles) begin to grow from one, two, three, and all cells on the periphery of the duct in Fig. 6(A), (B), (C), (D), respectively. Although the patterns in the four cases are different at intermediate stages of development, all eventually become a solid pattern and continue to grow outward against the resistance of the stroma, which affects the further growth of the tumor. We also found different patterns when we change certain mechanical or biochemical properties, such as the adhesion strength between cells or between cells and the basal membrane, but again, occlusion was the end result.

Figure 6:

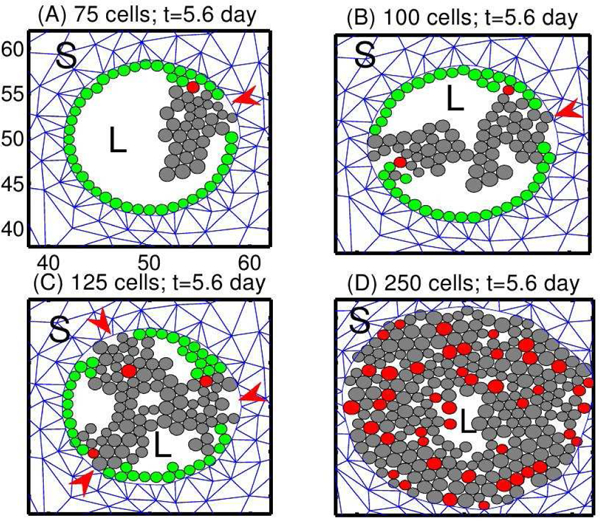
Tumor growth patterns for fixed levels of growth factors. TECs begin to grow from one, two, three or all peripheral ECs, in (A), (B), (C), and (D), resp. Red arrowheads in (A-C) indicate the initial location of TECs. Green circles are non-proliferating ECs, and red circles are the initial TECs that generate the lineage of proliferating TECs (gray circles). L = lumen in the duct structure. S = stromal tissue. From [27], with permission.

One sees in the figure that most of the ECs (green circles) remain adherent to the basal membrane on the periphery of the duct in (A-C), while future generations of TECs are displaced toward the center of the duct. When there are few TECs initially, the stress within a lineage is small except at the site of initiation, and the effect of stress on growth is small. The stress is larger at initiation sites and proliferating TECs there are subject to the reciprocal resistance force from stromal tissue in their neighborhood. In the extreme case in which all ECs are transformed to TECs initially (Fig. 6(D)), all cells are competing for space and there is a larger effect of growth on all cells, except for those at the leading edge. For the parameters used in [27], growth occurs primarily at the leading edge, which leads to an increase in the radius of the duct and a larger population of TECs at occlusion in (D), as compared with (A-C).

3.2. Breakdown of the basement membrane and invasion.

Cell-cell interactions biochemically regulated by cadherins are essential for maintenance of the integrity of the epithelial layer. The initial stage of single-cell invasion from the breast duct into the neighboring stromal tissue involves loss of adhesion with neighboring cells and reorganization of the cytoskeleton, as well as phenotypic changes in other attributes. The epigenetic and genetic changes involved characterizes a fundamental phenotypic changes, epithelial-mesenchymal transition (EMT), but certainly not all tumor cells in a migratory group are required to undergo this typical transition. Tumor cells can invade the neighboring stroma either as small group of cells (collective migration) or individuals (single cell migration), and may use enzymes for degradation of the ECM in order to facilitate movement of cells. Chemotaxis of neighboring stromal cells recruited from the tumor cells may be involved in tumor cell migration to blood vessels. In breast cancer, macrophages are stimulated by tumor-derived chemotactic signals and, in turn, assist tumor cell migration and invasion by secretion of regulatory signals such as EGF. However, we will address such details in future work.

A mathematical model for the early stage of tumor invasion into the stroma was developed in [27]. For this model, we take into consideration an active motive force for migratory cells, reaction-diffusion equations for tumor cell associated proteinase (TAP) and fibroblast-secreted proteinases (FSP), and dynamics of ECM. The cell mechanics of TEC growth in the lumen and invasion process throughout the thick layers of basal membrane describes the collective movement of the tumor cells in response to biochemical signals from stroma. To simplify the analysis we assume that only the leader cells at the invasion front generate the active force, and tumor cells behind the moving front passively follow a tunnel created by the leaders, which they can enlarge by secreting proteolytic enzymes. Leader cells at the invasion front transmit the active force directly to the stroma substrate without assistance from neighboring cells. The mechanical model can be extended to take into account active force generations by all cells behind the invasion front, but under usual conditions the cells in the interior of a moving mass do not contribute to moving the aggregate if they are not connected to the neighboring medium [4]. Therefore, in the current framework active migration of leading-edge cells at the invasion front and passive growth of the follower cells are enough to produce the collective migration of a group of invasive TECs. A schematic of the invasion model in early stages is shown in Fig. 7.

Figure 7:

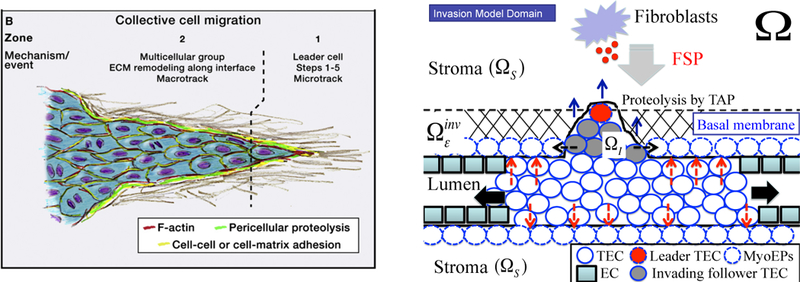
(Left) A schematic of collective cell migration in a tissue (from [7] with permission). (Right) A schematic of the invasion model used in our work. A TEC is activated (large red circle in ${\Omega }_{ϵ}^{inv}$) in response to diffusing FSP (small red circle in ${\Omega }_s$ ) and generates a microtrack for the invading front by proteolysis of the stromal tissue $\left({\Omega }_s\right).$ The follower TECs (gray circles) create the macrotrack through further proteolytic degradation of the ECM. A biochemical/mechanical coordination of those two cell types leads to collective migration (blue arrows) in the invasion region $\left({\Omega }_I\right),$ penetration of the initial barrier ${\Omega }_{ϵ}^{inv}({\Omega }_{ϵ}^{inv}$ {basal membrane + myoepithelial cells + ECM$\subset {\Omega }_s),$ and aggressive invasion whileTECs in lumen preferentially proliferate in the longitudinal direction because of low resistant forces (black arrows). Mechanical stresses acting on the intact duct wall are marked as red dashed arrows. Detailed roles of the myoepithelial cells (dashed circle) are not taken into account specifically but rather are embedded in the continuum stromal region $\left({\Omega }_{ϵ}^{inv}\right).$

In collective migration of cancer cells that infiltrate the thick ECM, the leading-edge cells at the moving front create a microtrack of locally-degraded ECM (Zone 1 in Fig. 7(left)) [7]. This microtrack is widened by the followers through a combination of proteolysis and mechanical force, leading to generation of a larger macrotrack (Zone 2 in Fig. 7(left)) [16, 14]. A new boundary between the invasion region and the continuum region (stroma) is defined by this ECM degradation and local microenvironment. We assume (i) that a TEC becomes an invasive phenotype (i.e., undergoes the EMT) when the FSP level exceeds a threshold, (ii) that leading-edge cells at the moving front creates a microtrack by secreting TAP and degrading a segment of the basal membrane, (iii) that initial infiltration is in the direction normal to the basal membrane during the initial penetration within the invasion strip (${\Omega }_{ϵ}^{inv}$ in Fig. 7).

In our modeling framework, the strong adhesion between all cells, both at the invasion front and in the moving aggregate, is prescribed so that the whole mass moves forward as a group. For a relatively weak adhesion between leading-edge cells and cells in the following mass, the cells at the moving front may infiltrate the tissue as an individual, as is observed in cell invasion of glioblastoma [23, 37, 24, 20, 21]. How this is regulated in different cancer types is poorly understood.

Overall, the key component of the invasion process are: (i) proteolytic activities of both leader and follower TECs in response to delivered FSP from CAFs in the stromal tissue (ii) occupation of the extracellular space from degradation of ECM by the proliferating followers, (iii) cellular adhesion between invasive TECs strong enough to ensure coherence of the invading group, and (iv) mechanical balance between the growing tumor cells and the reactive forces of the stromal tissue on the periphery of the invading front.

3.3. Computational results.

Fig. 8 shows the profiles of invading tumor cells and deformed stromal tissue in a longitudinal cross section of a breast duct at t= 1 h (A), 45 h (B), 90 h (C), 135 h (D), 180 h (E), 210 h (F). Proteinase diffused from a source in stromal tissue, cancer associated fibroblasts (CAFs; red ellipses in Fig. 8), stimulates TEC on the periphery of the duct, which in turn secrete TAP when the FSP level exceeds a threshold $P_s^{th}$ = 0.2. The activated TEC then initiate tumor invasion by degradation of the thick protective layers of breast duct (basal membrane + myoepithelial cells + ECM), a necessary key step for metastasis (Fig. 8C). Perturbed tensional-homeostasis by opening the gate then is followed by massive invasion of activated TEC phenotypes that essentially follow the leader cell by secreting higher levels of TAP and widening the tunnel, leading to malignant transformation of the breast (Fig. 8E-F). Local biomechanical microenvironmental changes from the mechanical stress due to the degradation and invasion processes also accelerate cell invasion and growth in the invading front and perturbed area. While growth of other TECs in the duct, except the cells at either end of the lumen, is mechanically constrained by the stromal tissue and neighboring growing cells, the invasive TECs in the invasion area are facilitated to infiltrate and proliferate.

Figure 8:

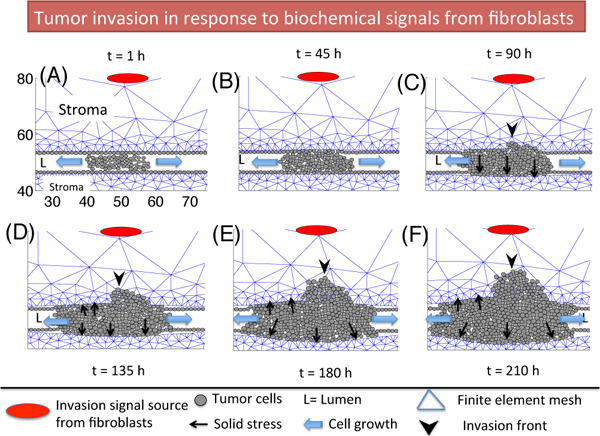
A time course of tumor invasion in response to biochemical signals (red ellipse) from tumor-assisting fibroblasts (TAFs) in stromal breast tissue at t= 1 h (A), 45 h (B), 90 h (C), 135 h (D), 180 h (E), 210 h (F). TECs on the periphery of the breast duct respond to signals from TAFs and begin to open a narrow gap and massive flow of cells follow the leader cell (black arrowhead) in invasion front in panels (C-F), leading to massive transport of TECs into the stroma and increased potential to metastasis.

4. Cell migration and proliferation in glioblastoma via the miR-451- AMPK control system.

Glioblastoma multiform (GBM) is the most aggressive form of brain cancer with a median survival time less than a year [17]. GBM is characterized by rapid proliferation and aggressive invasiveness into neighboring brain tissue [35, 23], which results in inevitable tumor recurrence after surgery [18]. We focus on the core miR-451-AMPK control system (Fig. 9A) that was shown to regulate the cell proliferation and migration experimentally [11, 10]. We first build a simplified representation in Fig. 9B from the complex signaling network in Fig. 9A by merging complex networks between CAB39/LKB1/STRAD and AMPK/MARK into one component (AMPK complex) and keeping miR-451 in one module. This results in the phenomenological equations for the miR-451 levels (M) and AMPK activities (A) in a dimensionless form [24] as follows:

$$\frac{dM}{dt}=G+\frac{k_1{k}_2^2}{k_2^2+\alpha A^2}-M,$$ (4)

$$ϵ\frac{dA}{dt}=S+\frac{k_3{k}_4^2}{k_1^2+\beta M^2}-A,$$ (5)

Figure 9:

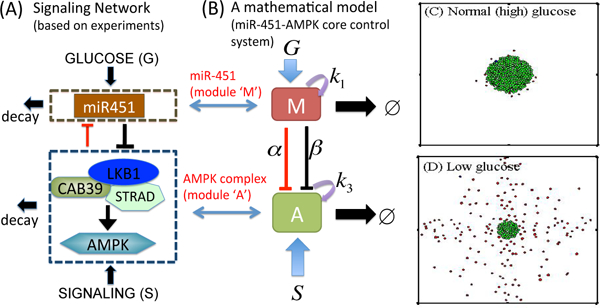
(A) miR451-AMPK signaling networks based on experimental observations [11, 10]. (B) Cartoon mathematical model [24]. (C,D) Invasion-growth pattern of a tumor spheroid in response to normal (high, G = 1.0) glucose in (C) and glucose withdrawal condition ((D), G=0.1) [21].

where G represents the signaling pathways from glucose to miR-451 and $S\text{ , }{k}_{\text{ 1}}\text{ , }{k}_{\text{2 }},k_{\text{3 }},k_{\text{4}},\alpha ,\beta ,ϵ$ are positive parameters [24]. This intracellular signaling network was incorporated into a hybrid model [21, 20] for the biochemical switches between proliferation and migration in response to metabolic stress. In the hybrid model, all glioma cells are modeled as an individual with biomechanical properties, which either grows in response to up-regulated miR-451 in high glucose conditions or migrate via down-regulation of miR-451 under a glucose withdrawal condition. The mathematical model predicts the dichotomous behaviors of glioma cells in response to various glucose levels as shown in experiments [11, 10]: (i) up-regulation of miR-451 and down-regulation of AMPK levels in response to normal glucose levels, which results in cell proliferation (see Fig. 9C). (ii) down-regulation of miR-451 and up-regulation of AMPK levels in response to glucose withdrawal, leading to cell infiltration (see Fig. 9D). (iii) there exist a bi-stability window where both proliferation and migration are idealized in response to an intermediate level of glucose. The hybrid model also predicts the cell speeds in agreement with experiments and that glioma migration depends not only on glucose availability but also on biomechanical constraints among neighboring cells [21]. An extended hybrid model [20] suggested a new therapeutic strategy, i.e., an introduction of chemoattrac- tants on the periphery of the resection site may lead to the localization of invading glioma cells back to the resected area, which will increase complete eradication of the infiltrating cells by followup surgeries.

5. Discussion.

A growing cell embedded in a tissue is subject to numerous influences from its microenvironment, and the hybrid model described herein can account for the effects of cell growth and division, stress, nutrient levels, and migration at the level of individual cells. It is well-known that numerous signal transduction networks are involved in growth and cell cycle control, but in work to date only the EGF and TGF-β signaling pathways in early breast cancer, and the miR-451-AMPK network in glioblastoma, were studied. The interactions between pathways can involve balances that determine cell fate in a subtle way, such as in the TGF-β, and SDF-1 signaling pathways involved in breast cancer invasion [2], and the HIF-miR-451-AMPK-mTOR-AKT network for regulation of cell cycle and migration in glioblastoma [1, 5, 10, 11, 40]. One of advantages of individual-based models compared to continuum models is that such an important detail can easily be integrated into the model in a very localized fashion.

One of the defining features of the hybrid model is that a cell-based description is only used in regions where it gives unique insights into tumor evolution, and the coarser continuum description is used elsewhere. In several different contexts we described tumor growth and cell infiltration in the presence of a surrounding ECM or stroma by treating the necrotic and quiescent tumor zones as continua and using a cell-based model in the proliferative area. Also, key intracellular pathways in breast cancer and glioblastoma were imbedded in the hybrid model so that they can control cell migration and proliferation in response to diffusible microenvironmental cues such as EGF/TGFβ and glucose. This unique approach essentially leads us to test numerous hypotheses which may not be explored by continuum or discrete-cell models alone. This can allow us to better understand the role of the microenvironment in the regulation of cancer progression. It should be noted that the 3D microenvironment can lead to more complex and dynamic features in cell-cell adhesion, signaling pathways, and drug resistance [36], and to investigate these we are developing a 3D hybrid model. A preliminary result from a 3D model predicts the differences in growth behavior of ECs on a solid substrate as found in [9]. In another direction, another scale has to be taken into consideration in the development of a hybrid model for viral cancer therapy, where oncolytic viruses spread, infect, and kill cancerous cells by substantial but selective replication [26].

Because a cell-based model allows for the incorporation of more cell-level detail than a continuum model, it also introduces more parameters into the model, and raises the question of whether such detail can be justified given the present knowledge of parameters in specific cases. However, much is known about the mechanical properties of individual cells and ranges for the parameters exist in the literature. Thus this component of the models is relatively well-founded. Less in known about the parameters involved in signaling networks, but this paucity is not peculiar to this class of models - it is pervasive wherever detailed models involving signal transduction are constructed. The lack of detailed parameter values does, however, indicate the necessity of applying sophisticated sensitivity analysis to determine which parameters are most important in setting a response. This process may in turn suggest experiments to determine these parameters. Moreover, the study of how various cell-level processes interact to produce a certain outcome may itself suggest new experiments to either support or disprove the theoretical predictions.