Selection Procedures for the Largest Lyapunov Exponent in Gait Biomechanics

Abstract

The present study is aimed at investigating the effectiveness of the Wolf et al. (LyE_W) and Rosenstein et al. largest Lyapunov Exponent (LyE_R) algorithms to differentiate data sets with distinctly different temporal structures. The three-dimensional displacement of the sacrum was recorded from healthy subjects during walking and running at two speeds; one low speed close to the preferred walking speed and one high speed close to the preferred running speed. LyE_R and LyE_W were calculated using four different time series normalization procedures. The performance of the algorithms were evaluated based on their ability to return relative low values for slow walking and fast running and relative high values for fast walking and slow running. Neither of the two algorithms outperformed the other; however, the effectiveness of the two algorithms was highly dependent on the applied time series normalization procedure. Future studies using the LyE_R should normalize the time series to a fixed number of strides and a fixed number of data points per stride or data points per time series while the LyE_W should be applied to time series normalized to a fixed number of data points or a fixed number of strides.

Introduction

Assessment of the nonlinear dynamics of human walking has been used to gain knowledge of the underlying motor control^17,25,30,32, the impact of various pathologies^11,16,20, the adaptations that occur due to ageing^5,16, and many others. One of the most commonly used methods for this assessment is the utilization of the largest Lyapunov exponent (LyE), which quantifies the rate of trajectory divergence or convergence in an n-dimensional state space³⁴. Applying this method, previous studies have observed altered dynamics of the center of mass displacement and acceleration and of the lower limb joint angles during human walking at speeds above and below what is preferred^{13,14,21,26,31}. Furthermore, differences in LyE have been observed in kinematic signals during walking between healthy controls and patients with peripheral neuropathy¹¹, ACL-deficient patients³⁹, intermittent claudication patients²⁰, patients with peripheral artery disease¹⁹ and unilateral transtibial amputees³⁸. LyE has also been suggested as a valid and reliable measure to differentiate the movements of fall prone individuals and controls².

Two algorithms have been primarily used to assess LyE in the literature: the Wolf et al. algorithm³⁴ and the Rosenstein et al. algorithm²². The latter algorithm was suggested as an improved version which provided a more reliable estimate of the LyE in short time series²². This statement has subsequently been debated and refuted in the literature^3,6,7. Inconsistent results have been observed when applying the two algorithms in similar experimental protocols. England and Granata¹⁴ observed increased LyE values when applying the Rosenstein et al. algorithm to lower limb joint angles across a range of walking speeds. In contrast, Raffalt and colleagues²¹ using the Wolf et al. algorithm observed a curvilinear relationship between speed and the LyE of lower limb joint angles. Additionally, Cignetti and colleagues⁶ observed inconsistent results when applying the two algorithms to the same lower limb joint angle data sets. When applying the Rosenstein et al. algorithm to center of mass movement pattern during walking, both increases^4,13 and decreases^4,26 were observed in LyE with increasing walking speed. Using the Wolf et al. algorithm, Raffalt and colleagues²¹ observed a curvilinear relationship between speed and the LyE of the sacrum acceleration. Based on the aforementioned discrepancies in the estimation of the rate of trajectory divergence, more experimental evidence is required to guide proper selection of the algorithm to be used for the calculation of the LyE.

The two algorithms work in principle similarly, quantifying the rate of divergence or convergence of nearest neighboring data points over time, however, subtle differences exist⁶. They both track the rate of exponential divergence of neighboring points on an attractor extracted from a time series. The Wolf et al. algorithm uses a reference trajectory of the attractor and follows one nearest neighbor until the separation between this point and the reference trajectory is beyond a specific limit after which the nearest neighboring point is replaced and the rate of divergence is again estimated. The rate of divergence or convergence is calculated as the average of the log of the increasing/decreasing distance between compared data points divided by the specific time the data pair was followed until a new nearest neighbor was chosen³⁴. In contrast, the Rosenstein et al. algorithm identifies multiple neighboring points and plots the log of the Euclidian distance between the points as a function of a predetermined time period. This plot is generated for all pairs of neighboring points and a mean ensemble curve is calculated. The rate of divergence or convergence is then calculated as the linear fit across the region of greatest increasing slope of the mean curve²².

In addition to the difference in computational steps between the two algorithms, previous studies have also applied different time series normalization procedures^4,13,14,20 which has been observed to affect the estimation of LyE²⁶. We have identified four different time normalization procedures used in the gait related literature:

1. The time series is cropped to keep a fixed number of data points but with a flexible number of included strides. Thus, all strides contain a varying number of data points dependent on the stride time¹³. In this manner the distance within the state space between subsequent data points on the attractor is not modified and there are an equal number of data points for analysis, however, the amount of human movement analyzed is variable due to differing number of strides.

2. The time series is cropped to keep a fixed number of strides but a flexible total number of data points. Thus, the number of data points within each stride depends on the stride time²⁰. In this manner, the original distance between subsequent data points within the state space is maintained but there is risk for individuals with very fast strides to have fewer data points available by which to select as neighboring points, thus reducing the accuracy of the nearest neighbor selection.

3. The time series is normalized to contain a fixed number of strides with fixed number of data points per time series. Thus, all strides contain a flexible number of data points dependent on the stride time relative to the mean stride time⁴. In this manner, similar to procedure 2 noted above, the distance between subsequent points in the state space will be modified. However, as the number of data points to which the time series is normalized is dependent on relative mean stride time, the magnitude of changes to distances between subsequent data points within the state space would be expected to be less.

4. The time series is normalized to contain a fixed number of strides with a fixed number of data points per stride. As a result, all strides contain the same number of data points regardless of the stride time¹⁴. In this manner, the distance between subsequent points in the state space will be modified dependent on the number of data points fixed to each stride (i.e. for fast strides the distance between data points decreases, whereas for slow strides the distance between data points increases during the normalization process).

To the best of our knowledge no experimental evidence exists to favor any of the four approaches. However, considering the increasing popularity of the usage of LyE to study nonlinear dynamics in biomechanics and motor control^27,28, this is a very important issue that needs to be addressed.

The purpose of the present study was to investigate the effectiveness of the Wolf et al. and Rosenstein et al. algorithms to differentiate data sets with distinctly different temporal structures when using four different time series normalization procedures. To fulfill this purpose, we recorded three-dimensional displacement of the sacrum from young healthy subjects who performed both walking and running at the same two speeds: one low speed which was close to the preferred walking speed (PWS) and one high speed which was close to the preferred running speed (PRS).

Based on the Dynamical System Theory, Diedrich and Warren (1995) formulated that the preferred gait mode is characterized by a stable phase relationship (i.e. walking would be a more stable mode at speeds closer to the preferred walking speed compared to running and vice versa)^9,10. Using both linear and nonlinear measures, Jordan and colleagues (2009) later supported this theory¹⁸. Accordingly, it can be assumed that the rate of movement divergence (e.g. sacrum displacements) would be less during a gait mode at a speed closer to the preferred movement speed for that particular mode (e.g. walking at low speed and running at high speed). Therefore, we predicted that the three-dimensional displacement of the sacrum during walking at the high speed would exhibit higher rates of trajectory divergence compared to running at the same speed. Likewise, we predicted that running at the low speed would exhibit a higher rate of trajectory divergence compared to walking at the same speed. The algorithm(s) and normalization procedure(s) that would confirm these predictions would be considered as the most effective method to assess the rate of trajectory divergences in a kinematic signal during locomotion.

Materials and Methods

Subjects

Ten young healthy subjects (5 males and 5 females) with a mean ± standard deviation age of 22.7 ± 3.6 years, body height of 1.75 ± 0.10 meters and body mass of 73.4 ± 14.3 kg were included in the present study. All subjects were physically active, familiar with walking and running on a treadmill and they reported no cardiovascular or neurological diseases or musculoskeletal injuries. Subjects were verbally informed of the experimental conditions and gave written consent to participate in the study. The study was approved by the Institutional Review Board of the University of Nebraska Medical Center and the study was carried out in accordance with the approved guidelines.

Protocol

The subjects completed a brief warm up session on a treadmill. Then followed a standardized protocol to establish the PWS¹³. The speed of the treadmill was gradually increased and decreased above and below what the subjects reported as a comfortable walking speed. The speed of the treadmill was blinded to the subject and the average of the speeds reported as comfortable was calculated and termed the PWS. A similar protocol was used to establish the PRS. The mean ± standard deviation of PWS and PRS was 1.25 ± 0.24 m/s and 2.46 ± 0.24 m/s, respectively. After a short rest period, the subject walked and ran for 3 minutes at a low speed of 1.79 m/s and a high speed of 2.46 m/s speeds. The order of the conditions was randomized. These speeds were chosen to represent a relative low speed close to the PWS where walking would be the preferred gait mode and a relative high speed close to PRS where running would be the preferred gait mode and to represent speeds above and below the expected walk-to-run transition speed. Furthermore, the speeds had to meet two requirements: 1) the slow speed needed to be fast enough so that running still constituted running and not a running-like motion (e.g. jumping from one leg to the other with excessively long contact phases) and 2) the high speed needed to be slow enough so that walking was possible for the subjects (i.e. having a least one foot on the ground at all time). Each trial was separated by a minimum of 1 minute of rest. Walking at the high speed was visually confirmed (i.e. that at least one foot had ground contact at all time). In case of doubt, vertical ground reaction forces recorded by force platforms embedded in the treadmill were consulted (data not included in the study).

Measurements and analyses

Three-dimensional position data of reflective markers placed on the sacrum and right toe was continuously recorded using a 12 high-speed camera system operating at 120Hz. Right toe off events were identified from abrupt change in the anterior-posterior displacements of the toe marker indicating the change from a backward to a forward motion during the contact phase. Each walking and running trial contained a different number of completed strides. Eighty strides were identified as the minimum number of completed strides for all subjects and trials. The four normalization procedures were applied to the anterior/posterior, mediolateral and vertical sacrum position signals as follows:

1. Fixed number of data points: the time series were cropped to 8000 data points.

2. Fixed number of strides: the time series were cropped to contain 80 strides.

3. Fixed number of strides and data points/time series: the time series time were normalized to contain 8000 data points using a linear spline function.

4. Fixed number of strides and data points/stride: the time series were time normalized to contain 100 data points within each stride and a total of 80 strides using a linear spline function.

The four procedures resulted in different numbers of strides, data points/stride and total number of data points for the investigated time series (see Table 1).

Table 1:

Total number of data points, data points/stride and the number of strides in the time series for each normalization procedure and each condition. The first normalization procedure cropped each time series to 8000 data points which resulted in differences in the number of data points/stride and strides between subjects and between trials. The second normalization procedure cropped each time series to 80 strides which resulted in differences in the number of data points and data points/strides between subjects and between trials. The third normalization procedure normalized each time series to included 8000 data points and 80 strides and resulted in an average number of data points/stride of 100 but with variations across the 80 strides. The average standard deviation across all subjects is presented in the table. The fourth normalization procedure normalized each time series to contain 100 data points/stride for all 80 strides.

	Data points	Data points/stride	Number of strides
Condition	Normalization procedure 1
Walk 1.79 m/s	8000	111.7 ± 7.5	71.9 ± 4.8
Run 1.79 m/s	8000	93.0 ± 5.0	86.2 ± 4.3
Walk 2.46 m/s	8000	88.0 ± 4.5	91.1 ± 4.9
Run 2.46 m/s	8000	93.2 ± 9.2	86.5 ± 7.5
	Normalization procedure 2
Walk 1.79 m/s	8840.9 ± 595.2	110.5 ± 7.4	80
Run 1.79 m/s	7375.2 ± 382.1	92.2 ± 4.8	80
Walk 2.46 m/s	6903.6 ± 338.9	86.3 ± 4.2	80
Run 2.46 m/s	7386.6 ± 738.8	92.3 ± 9.2	80
	Normalization procedure 3
Walk 1.79 m/s	8000	100 ± 1.5	80
Run 1.79 m/s	8000	100 ± 4.1	80
Walk 2.46 m/s	8000	100 ± 1.3	80
Run 2.46 m/s	8000	100 ± 1.3	80
	Normalization procedure 4
Walk 1.79 m/s	8000	100 ± 0.0	80
Run 1.79 m/s	8000	100 ± 0.0	80
Walk 2.46 m/s	8000	100 ± 0.0	80
Run 2.46 m/s	8000	100 ± 0.0	80

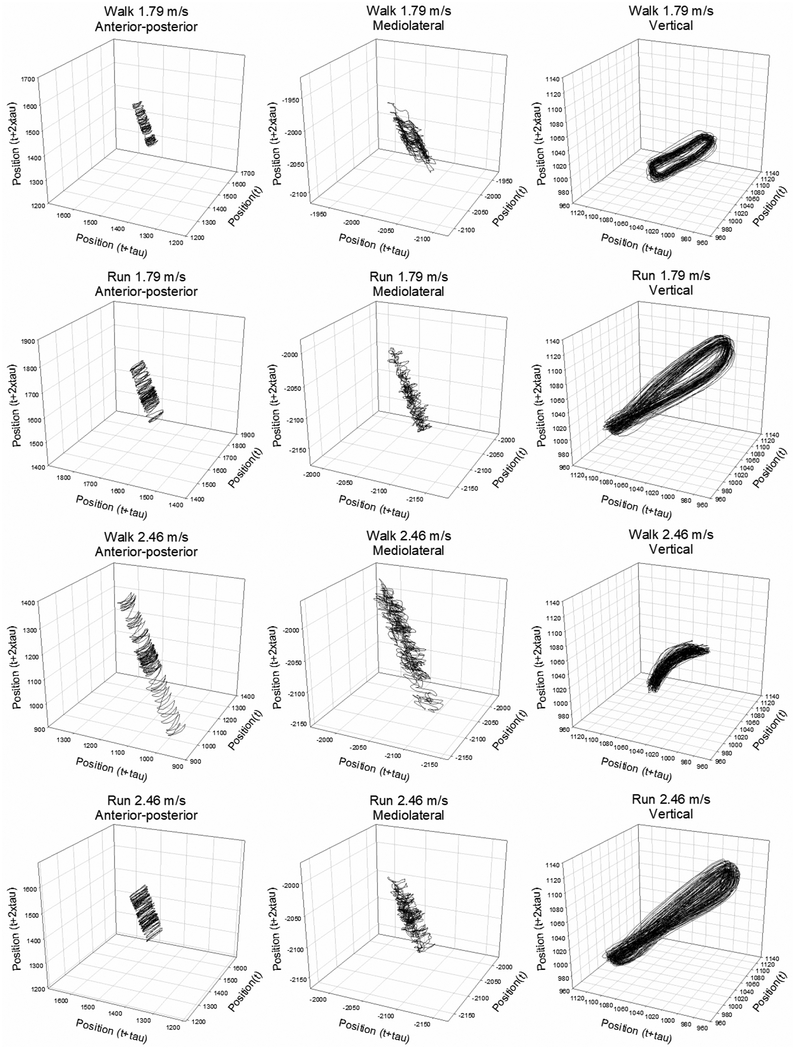
Before calculating LyE, each time series was reconstructed in state space using the method of delay embedding. Time delay and embedding dimension was calculated using the average mutual information algorithm and the false nearest neighbor algorithm^23,24,29. Across the subjects, speeds, locomotion modes and normalization procedures, the time delay and embedding dimension were on average 22.3 ± 3.2 and 4.9 ± 0.1 for the anterior/posterior position, 29.2 ± 6.0 and 4.9 ± 0.2 for the mediolateral position and 15.3 ± 0.9 and 5.1 ± 0.2 for the vertical position (the individual time delays and embedding dimensions are presented in the supplementary material). Thus, state space were reconstructed using the time delay of 22, 29 and 15 and the embedding dimension of 5, 5 and 5 for the anterior/posterior, mediolateral and vertical direction, respectively (Figure 1). To investigate the consequence of this methodological approach of averaging time delay and embedding dimension across all the time series, the calculations were also performed with the individual time delay and embedding dimension for each time series. The results are presented in the supplementary material and summarized in a result paragraph.

Figure 1:

State space reconstruction of the anterior-posterior, mediolateral and vertical displacement of the sacrum marker for the four conditions. This representation illustrates that the three signals substantially changes dynamics when changing gait mode between walk and run and when increasing or decreasing speed. Qualitatively evaluated, the trajectory dynamics during running at the low speed and walking at the high speed appear more disorganized and random compared to walking at low speed and running at high speed. This confirms the validity of the raised criteria.

The LyE was calculated in Matlab (Mathworks, Inc., Natrick, MA) using custom written scripts. Both algorithms were applied to the time series normalized with all four procedures. When applying the Rosenstein et al. algorithm, we rescaled the time-axis of the log-plots by multiplying the average stride duration for each subject and extracted the LyE exponent across the span of 0–1 strides expressed in bits/second¹⁴. Similarly, the Wolf et al. algorithm returns the outcome in bits/second^34,36.

Statistics

The performed analyses consisted of eight different LyE algorithm-time series normalization procedure combinations applied to three different variables (the three sacrum displacement directions) recorded during four different locomotion conditions (slow walking, slow running, fast walking and fast running) from ten subjects. However, the sacrum displacement data from of the fast walking trials from three subjects did not contain sufficient strides for a reliable LyE calculation and were excluded.

To investigate the effectiveness of the two algorithms and the four time series normalization procedures to differentiate the estimation of LyE, we assessed validity using a known-groups analysis approach¹⁵. We based this approach on the theory by Diedrich and Warren regarding the relationship between the gait mode and the stability of the occupied movement attractor¹⁰ and formulating four criteria related to the group average of the investigated variables:

1. Ability to return significantly higher LyE for the sacrum displacements during running at the low speed compared to walking at the low speed.

2. Ability to return significantly higher LyE for the sacrum displacements during walking at the high speed compared to running at the high speed.

3. Ability to return significantly higher LyE for the sacrum displacements during running at the low speed compared to running at the high speed.

4. Ability to return significantly higher LyE for the sacrum displacements during walking at the high speed compared to walking at the low speed.

These four criteria were evaluated using a one-way ANOVA for repeated measures. In case of a significant overall effect, a Holm-Sidak post-hoc test was applied to test the between-condition differences. Level of significance was set at 0.05. The outcome of these statistical analyses is summarized in a result paragraph and presented in full in the supplementary material.

Additionally, the sensitivity of each of the eight LyE algorithm-time series normalization procedure combination was assessed with the following procedure. Each of the four raised criteria was evaluated for each sacrum displacement direction and each subject. A raised criterion could be either confirmed (see equation 1) or rejected (see equation 2) based on the size of differences between the LyEs of the investigated time series from the compared conditions. If the difference between LyE from two compared conditions exceeded a critical limit and with the appropriate sign (according to the criterion), the criterion was confirmed. The critical limit was calculated using a modification of the Cohen’s d effect size equation with an effect size of 0.8⁸, by multiplying the pooled standard deviation of the entire group with 0.8 (see equation 3).

$$Diff(a,b)\ge 0.8\cdot s\to confirmationofcriterion$$ Equation 1:

$$Diff(a,b)\ge 0.8\cdot s\to rejectionofcriterion$$ Equation 2:

$$S=\sqrt{\frac{\left(n_1-1\right)\cdot var{1}^2+\left(n_2-1\right)\cdot var{2}^2}{n_1+n_3-2}}$$ Equation 3:

where var1 and var2 were the variance of the LyE from the two compared conditions and n₁ and n₂ were the numbers of subjects completing the two compared conditions. Finally, the percentage of confirmed criteria across all subjects was calculated for each sacrum displacement direction.

Thus, for each of the eight LyE algorithm-normalization procedure combinations applied to the three sacrum displacement signals, the four criteria were either confirmed or rejected and accompanied by a sensitivity score. All statistics were computed in Sigmaplot (Systat Software, Inc. 2014, version 13.0, Germany).

Results

A three-dimensional state space reconstruction of the anterior-posterior, mediolateral and vertical sacrum displacement for each of the four conditions is presented in Figure 1. Based on a qualitative evaluation, the trajectory dynamics during running at the low speed and walking at the high speed are more disorganized and random compared to walking at low speed and running at high speed. This qualitatively supports the validity of the raised criteria.

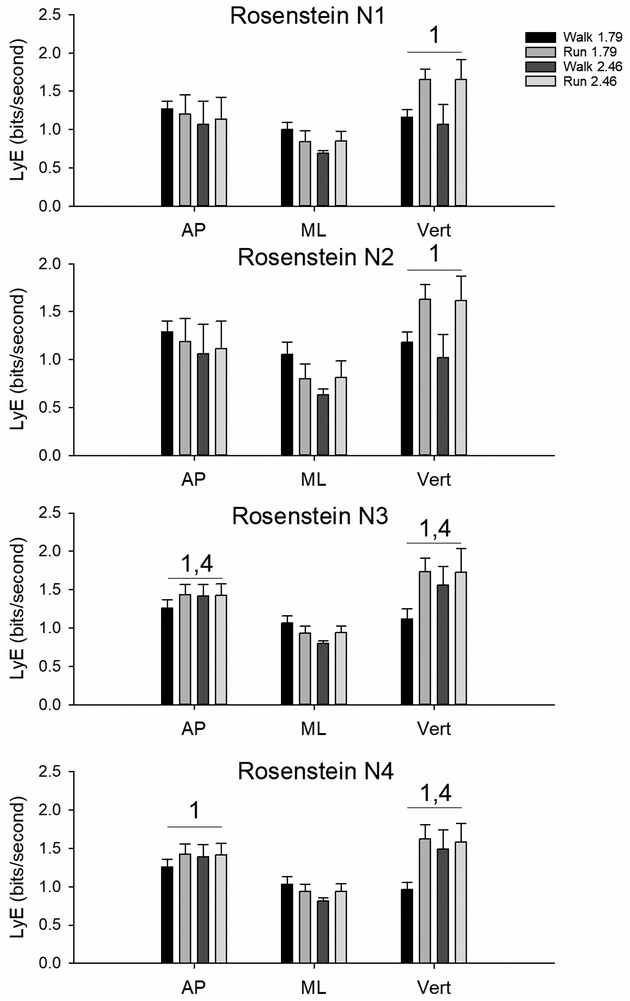
The LyE values calculated using the Rosenstein et al. algorithm are presented in Figure 2. When using the first normalization procedure (fixed number of included data points) and second normalization procedure (fixed number of included strides), only the LyE from the vertical displacement signal confirmed the first raised criterion. The third normalization procedure (fixed number of strides and data points per time series) confirmed the first and fourth raised criteria for both the anterior-posterior and vertical displacement signals. The fourth normalization procedure (fixed number of strides and data points per stride) confirmed the first raised criterion for the anterior-posterior displacement signal and the first and fourth criteria for the vertical displacement signal (Figure 2 and Table 2). On average the fourth normalization procedure showed the highest sensitivity score of 51.0% for the Rosenstein et al. algorithm. It is noteworthy that none of the normalization procedures could confirm any of the four criteria for the mediolateral displacement signal. Additionally, the sensitivity score was lowest for the mediolateral displacement signal across all normalization procedures (Table 2).

Figure 2:

Mean and standard deviation of the LyE calculated from the anterior-posterior (AP), mediolateral (ML) and vertical (Vert) displacement of the sacrum marker during the four conditions using the Rosenstein et al. algorithm and the four different normalization procedures. 1 above the bars indicates significantly higher LyE for the sacrum displacements during running at the low speed compared to walking at the low speed, 4 above the bars indicates significantly higher LyE for the sacrum displacements during walking at the high speed compared to walking at the low speed. N=10 except for walk 2.46 m/s where N=7.

Table 2:

Confirmed criteria and sensitivity for the LyE calculated with the Rosenstein algorithm for the anterior-posterior, mediolateral and vertical displacement of the sacrum marker.

	Confirmed criteria	Sensitivity (%)
Rosenstein normalization 1
Anterior-po sterior	-	35.3
Mediolateral	-	26.5
Vertical	1	41.2
Mean across direction	NA	34.3 ± 7.4
Rosenstein normalization 2
Anterior-po sterior	-	35.3
Mediolateral	-	23.5
Vertical	1	41.2
Mean across direction	NA	33.3 ± 9.0
Rosenstein normalization 3
Anterior-po sterior	1, 4	58.8
Mediolateral	-	20.6
Vertical	1, 4	55.9
Mean across direction	NA	45.1 ± 21.3
Rosenstein normalization 4
Anterior-po sterior	1	58.8
Mediolateral	-	26.5
Vertical	1, 4	67.6
Mean across direction	NA	51.0 ± 21.7

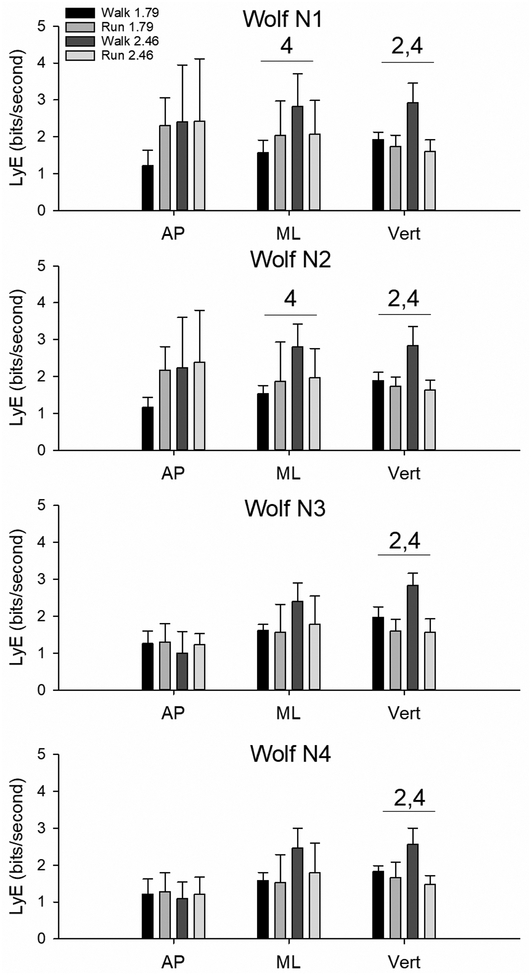
The LyE values calculated using the Wolf et al. algorithm are presented in Figure 3. When using the first normalization procedure (fixed number of included data points) and second normalization procedure (fixed number of included strides), the LyE from the mediolateral displacement signal confirmed the fourth criterion and the LyE from the vertical displacement signal confirmed the second and fourth criteria. When using the third normalization procedure (fixed number of strides and data points per time series) and the fourth normalization procedure (fixed number of strides and data points per stride), the second and fourth criteria were confirmed for the vertical displacement signal (Figure 3 and Table 3). On average the second normalization procedure showed the highest sensitivity score of 49.0% for the Wolf et al. algorithm. None of the normalization procedures could confirm any of the four criteria for the anterior-posterior displacement signal. Additionally, the sensitivity score was in general lowest for the anterior-posterior displacement signal for the four normalization procedures (Table 3). The sensitivity scores for the two LyE algorithms were fairly similar; however, the Wolf et al. algorithm was less affected by changes in the normalization procedure (Tables 2 and 3).

Figure 3:

Mean and standard deviation of the LyE calculated from the anterior-posterior (AP), mediolateral (ML) and vertical (Vert) displacement of the sacrum marker during the four conditions using the Wolf et al. algorithm and the four different normalization procedures. 2 above the bars indicates significantly higher LyE for the sacrum displacements during walking at the high speed compared to running at the high speed, 4 above the bars indicates significantly higher LyE for the sacrum displacements during walking at the high speed compared to walking at the low speed. N=10 except for walk 2.46 m/s where N=7.

Table 3:

Confirmed criteria and sensitivity for the LyE calculated with the Wolf algorithm for the anterior-posterior, mediolateral and vertical displacement of the sacrum marker.

	Confirmed criteria	Sensitivity (%)
Wolf normalization 1
Anterior-po sterior	-	38.2
Mediolateral	4	38.2
Vertical	2, 4	61.8
Mean across direction	NA	46.1 ± 13.6
Wolf normalization 2
Anterior-po sterior	-	38.2
Mediolateral	4	50.0
Vertical	2, 4	58.8
Mean across direction	NA	49.0 ± 10.3
Wolf normalization 3
Anterior-po sterior	-	44.1
Mediolateral	-	41.2
Vertical	2, 4	55.9
Mean across direction	NA	47.1 ± 7.8
Wolf normalization 4
Anterior-po sterior	-	35.3
Mediolateral	-	35.3
Vertical	2, 4	58.8
Mean across direction	NA	43.1 ± 13.6

The results from the calculations using the individual time delay and embedding dimension to reconstruct the state space are presented in the supplementary material. In general, more criteria were met when using the individual time delay and embedding dimension for both algorithms and across all the four normalization procedures (Tables 2 and 3 vs. Tables S1 and S2). Similar to using the average time delay and embedding dimension, the Rosenstein et al. algorithm with individual time delay and embedding dimension exhibited the highest sensitivity (54.9%) when the fourth normalization procedure was applied. For the Wolf et al. algorithm, the highest sensitivity was observed for the first and second normalization procedures (44.1 and 43.1%, respectively) when an individual time delay and embedding dimension were used.

Discussion

The present study aimed at investigating the effectiveness of the Rosenstein et al. and Wolf et al. algorithms to differentiate data sets with distinctly different temporal structures when using four different time series normalization procedures. While neither of the two algorithms seemed to outperform the other, the chosen normalization procedure appeared to have a substantial influence on the effectiveness of the algorithms.

The Rosenstein et al. algorithm confirmed four out of twelve criteria when the normalization procedure with fixed number of strides and data points per time series was used which was accompanied by a sensitivity score of 45.1 %. Three criteria were confirmed with a sensitivity score of 51.0 % when the normalization procedure with fixed number of strides and data points/strides was used. Thus, when using the Rosenstein et al. algorithm these two normalization procedures would provide the best results. However, while these two normalization procedures have previously been used in combination with the Rosenstein et al. algorithm to investigate the dynamics of sacrum accelerations and lower limb joint angles during walking at different speeds, they have led to different interpretations regarding stability during walking^4,14. Similar normalization procedure bias was also observed by Stenum and colleagues when applying the Rosenstein et al. algorithm in combination with three different normalization procedures to the sacrum accelerations recorded during walking at different speeds²⁶. Taken together, these observation calls for caution when comparing results from studies using different normalization procedures in combination with the Rosenstein et al. algorithm.

The Wolf et al. algorithm confirmed three out of twelve criteria when combined with either the normalization procedure using a fixed number of data points (sensitivity score of 46.1 %) or the normalization procedure using a fixed number of strides (sensitivity score of 49.0 %). This would suggest that when using the Wolf et al. algorithm, these two normalization procedures would provide the best results. Particularly, these two normalization procedures have been used in the past in combination with the Wolf et al. algorithm^{6,20,21,36,38}.

Neither of the two investigated LyE algorithms clearly outperformed the other. Thus based on the presented results, the present study cannot recommend one over the other. In a previous study, Cignetti and colleagues compared the two LyE algorithms by applying them to hip and ankle joint angles recorded from young and older adults during treadmill walking⁶. While both algorithms could differentiate the two groups and return a higher LyE from the joint angles of the older group when long time series were used, only the Wolf et al. algorithm could differentiate the groups when shorter time series were used. Furthermore, only the Wolf et al. algorithm was able to differentiate the rate of trajectory divergence in the hip and ankle joint angle, with the ankle joint exhibiting the highest LyE⁶. This inter-joint relationship with the LyE revealing a higher rate of divergence in more distal lower limb joints during walking has also been observed by several other studies using the Wolf et al. algorithm^1,21,38. In contrast, inconsistent results have been reported in the literature for the same variables when LyE was calculated with the Rosenstein et al. algorithm^6,11,12,14. Although the present study did not provide conclusive evidence for either of the two LyE algorithms, the previous observations in the literature would still favor the use of the Wolf et al. algorithm.

A crucial aspect of the LyE calculation regardless of the chosen algorithm and normalization procedure is the selection of state space reconstruction parameters^33,35. While the averaging approach is quite common^4,11,14,37 and has been associated with a relative high within-and between-session intra-class coefficients and low smallest detectable differences³³, the results presented in the supplementary material of the present study indicated that effectiveness of both algorithms tended to increased slightly when using the individual time delay and embedding dimension of each time series to reconstruct the state space. Since both approaches appear to have pros and cons and no clear consensus regarding the proper methodology exists, future studies should validate their LyE results by ensuring that the chosen state space reconstruction method did not alter the outcome significantly²¹.

To the best of our knowledge, the present study is the first to evaluate the effectiveness of the Rosenstein et al. and Wolf et al. algorithm using a ‘known-groups analysis’ approach and quantify the sensitivity of the two algorithms and the four normalization procedures. The results revealed that no more than four out of the twelve raised criteria could be confirmed when using the average time delay and embedding dimension method. No more than five criteria were confirmed for the individual time delay and embedding dimension method. Furthermore, the sensitivity scores ranged from 33.3 – 51.0 % for the average time delay and embedding dimension (35.3 – 54.9 % for the individual time delay and embedding dimension method). This low to moderate effectiveness and sensitivity could be due to three different aspects. First, the study relied on four assumptions related to the rate of trajectory divergence of the three-dimensional displacement of the sacrum: 1) the rate of trajectory during low speed running would be significantly higher compared to that during low speed running, 2) the rate of trajectory divergence would be significantly higher during high speed walking compared to high speed running, 3) the rate of trajectory divergence would be significantly higher during low speed running compared to the high speed running, and 4) the rate of trajectory divergence would be significantly higher during high speed walking compared to low speed walking. These assumptions were based on a Dynamical System Theory approach which would suggests that sacrum displacements would diverge less during a gait mode at a speed closer to the preferred movement speed for that particular mode (e.g. walking at low speed and running at high speed)^9,10,18. Since the LyE quantifies the behavior of a dynamical system and is originally derived from Chaos Theory, we found it reasonable to evaluate the performance of different LyE algorithms using criteria formulated based on Dynamical System Theory. Based on a qualitative evaluation of the three dimensional state space reconstruction presented in Figure 1, we believe that these assumptions hold true. However, the outcome of the present study would be compromised in case some or all of these assumptions are not also quantitatively true. Secondly, if these assumptions are true, the present results could also be explained by a low specificity of the LyE precluding a detection of the changes in sacrum displacement dynamics occurring when altering gait mode. Finally, despite the qualitative confirmation of our assumption, greater differences between the low and high speed for the two gait modes might be needed to significantly change the temporal structure of the kinematic signals. It could also be speculated that the use of absolute speeds and not speeds scaled to anthropometries or speeds normalized to PWS and PRS could have bias the results.

The present study had a relative small sample size which calls caution when interpreting the results. However, the original studies by Diedrich and Warren (1995, 1998)^9,10 needed only 8 subjects (4 males and 4 females) to support their theory. Similarly the study by Jorden and colleagues (2009) had 12 subjects (all females). This would suggested that the underlying phenomenon (i.e. lower rate of movement trajectory during walking at the low speed compared to running and during running at the low speed compared to walking) used in the present study is “robust” enough to be validly detected with 10 subjects.

In conclusion, the ability of two algorithms, the Rosenstein et al. and the Wolf et al., to differentiate the rate of trajectory divergence between gait kinematic signals derived from a marker placed at the sacrum and which had different temporal structures was evaluated in this study. Our results indicate that the effectiveness of the two algorithms to accomplish this task highly depends on the applied time series normalization procedure. Thus, when using the Rosenstein et al. algorithm the time series in question should be time normalized to a fixed number of strides and a fixed number of data point per stride or data points per time series. In contrast, the Wolf et al. algorithm should be applied to a normalized time series with a fixed number of data points or a fixed number of strides.