Hydroxypropyl cellulose as a green polymer for thermo-responsive aqueous foams

Hydroxypropyl cellulose (HPC) is a surface active polymer that can change its solubility as a function of temperature.

Abstract

Hydroxypropyl cellulose (HPC) is a surface active polymer that can change its solubility as a function of temperature. This makes HPC interesting for responsive foams, where macroscopic properties need to be reversibly changed on demand. Analysis of aqueous HPC foams as a function of temperature showed a moderate decrease in foam half-life time from 9000 to 4000 s, when the temperature was increased. However, within a narrow temperature range of ±2 °C a dramatic decrease in half-life time to <120 s was observed at 43 °C in the absence and at 31 °C in the presence of 0.7 M NaCl. These drastic changes are highly reversible and are associated to the lower critical solution temperatures (LCST) of HPC in aqueous solutions. In fact, dynamic light scattering experiments indicate that HPC molecules form aggregates at temperatures >31 °C (0.7 M NaCl) and >43 °C (0 M NaCl), which shrink in size when the temperature is increased further. From these results, we conclude that the LCST of 1 MDa HPC is at 43 °C when no salt is present and is at 31 °C in aqueous solutions with 0.7 M NaCl. In addition, shear rheology of bulk solutions and surface tensiometry indicate that the solution's viscosity and the surface pressure dramatically change at the respective LCSTs. Obviously, the solvent's viscosity triggers substantial changes in foam drainage at the LCST, which is shown to be the main driving force for the temperature responsiveness of HPC foams.

Introduction

Smart materials can reversibly change their physical and chemical properties as a function of external stimuli such as pressure, light, temperature, pH, magnetic or electric fields. For that reason, stimuli responsive material's have recently received considerable attention.1–3 Interesting functions are controlled drug release,4 self-repairing abilities and shape memory which can recover the materials initial structure. In this respect, aqueous foams are interesting soft materials because they allow to tailor and to tune macroscopic properties from the molecular level via structure–property relations.5–8 Thus, foams have great potential to be developed further into responsive and smart materials.

Aqueous foams responding to external stimuli such as light,5 magnetic fields9 or temperature10–13 are subject of current research. Also first multi-stimuli responsive foams are reported in previous works.14,15 A major advantage of responsive interfaces is the ability to drive materials properties such as foam stability or foamability on demand and in a non-invasive way. Photo-responsive foams are mostly based on azobenzene surfactants.5,16–18 Here, UV or blue light irradiation can trigger E to Z photo-isomerization reactions and the resulting surfactants’ conformational change can result into a different surface activity, surface tension and on larger length scales also differences in foam stability.

Fameau et al.3,10,19–22 demonstrated the possibility to switch foam stability between months and seconds with temperature by using a multilamellar tubular system consisting of 12-hydroxy stearic acid (12-HSA) mixed with hexanolamine. With this system, multi-responsive (light and temperature) properties can be reached by adding carbon black particles that absorb light and can cause local heating.15

Thermo-responsive foams and particularly foam films from poly(N-isopropylacrylamide) (PNIPAm) solutions have been studied extensively in the past.12,23–25 Depending on the molecular weight, PNIPAm has a lower critical solution temperature (LCST) of ∼32 °C.26,27 Below the LCST, the polymer is well soluble in water. Above the LCST, however, the properties of PNIPAm change and water turns to a poor solvent. The disadvantage of PNIPAm foams is their poor stability with foam life times as short as several seconds to minutes.23 For that reason, foams from PNIPAm and SDS mixtures have been investigated, which show an improved stability but have lost their responsiveness to temperature.23 Lencina et al.12 reported stable foams from mixtures of alginate-g-PNIPAm graft copolymer and DTAB, with half-life times up to one hour and thermo-responsive properties in a narrow range of surfactant concentrations.

Hydroxypropyl cellulose (HPC) has thermo-responsive properties similar to PNIPAm, but is biodegradable28 and allows for green materials chemistry. As one of the most important chemical derivatives of cellulose, HPC is used due to its hydrophilicity, phase behavior and ease of production.29 Because of non-toxic properties of HPC, it is frequently applied in food industry,30,31 pharmacy32,33 and cosmetic industry.34 In aqueous solutions, the LCST of HPC is at ∼43 °C, and this temperature can be increased or decreased by more than 25 °C e.g. by adding salt.35,36 At the LCST, HPC undergoes a volume-phase transition.36 Although HPC is an environmentally friendly surface-active polymer, to the best of our knowledge HPC as a green and thermo-responsive foaming agent has not been considered so far. For that reason, we have systematically studied the effect of temperature on the stability of HPC foams and present new information on the latter thermo-responsive properties. In order to link macroscopic with microscopic properties and to clarify the stabilization mechanism, bulk rheology, dynamic light scattering (DLS) and surface tension measurements as a function of temperature and salt concentration were performed.

Experimental

Sample preparation

Hydroxypropyl cellulose (HPC) (impurities <5 wt%, moles of substitution 4.1 mmol g^–1, LOT #MKBJ6793V) was purchased from Sigma Aldrich with an average molecular weight of 1 MDa and was used as received. NaCl (>99.9%) was purchased from VWR and used without further purification. Stock solutions were prepared by dissolving the necessary amount of HPC and NaCl in ultrapure water (18 MΩ cm; total oxidizable carbon <5 ppb), which was obtained from a Milli-Q Reference A+ (Merck, Germany) purification system. Subsequently, the stock solutions were sonicated until full dissolution was reached. With exception of DLS measurements, final polymer concentrations were kept constant at 0.5 g l^–1 in all experiments. The required glassware was cleaned with Alconox detergent solution (Sigma Aldrich) and afterwards stored in concentrated sulfuric acid (98% p.a., Carl Roth) with NOCHROMIX (Godax Labs, USA) for at least 12 h. The acid cleaned glassware was thoroughly rinsed with ultrapure water until the acid was completely removed.

Foam stability and drainage

A dynamic foam analyzer DFA100 (Krüss, Germany) was used to measure foam properties such as foam half-life time t_1/2 and drainage. Foams were produced from 55 ml sample solutions which were poured into a double walled glass column with 250 mm length and 40 mm inner diameter. To control the inner temperature, a thermostat was connected with the column. Offset temperature between column and thermostat was calibrated in reference measurements. A porous plate with pore sizes between 16 and 40 μm (P3, Schott, Germany) was fixed at the bottom of the column and ambient air was injected through the porous plate into the column and thereby homogeneously distributed over the cross section. The flow rate was set to 0.3 l min^–1 in all experiments and foams were produced by streaming air through the sample solution for 30 s. During foam formation and foam decay, the height of both foam and the liquid below the foam were monitored as a function of time. For that, an infrared LED panel was installed at one side of the column and a line sensor at the opposite side of the column. The foam height was accessible by measuring the light transmission through the glass column. In this work, the foam half-life time t_1/2 is defined as the time until the foam reaches the half of the initial height, which was established after the actual foaming process. Drainage of foams37 was studied by recording the height of the drained liquid as a function of time (raw data is shown in Fig. S2 in ESI†). In the present work, we use t_d,75 (time until 75% of the liquid has drained) which is the time between completion of the foaming process and the time where the liquid content reaches 75% of the initial height in the glass column. To avoid an influence of liquid evaporation at higher temperatures to the foam stability, the top part of the glass column was covered with Parafilm (Bemis, USA). A small hole in the Parafilm allows pressure compensation during the foaming process. Foam properties were measured at least in triplicates.

Dynamic light scattering (DLS)

All measurements were performed with a Zetasizer Nano ZSP (Malvern, UK) which was equipped with a 10 mW HeNe laser with an emission wavelength of 632.8 nm. The intensity autocorrelation function was calculated from intensity fluctuations of the scattered light which was recorded at a fixed angle of 173°. The intensity autocorrelation function g¹(t) is given by:38,39

g¹(t) = A[1 + B exp(–2Γt)] 1

Here A is the baseline, B a coherence factor that depends on experimental conditions and Γ the characteristic relaxation rate. Eqn (1) is valid for ideal solutions with monodisperse particle size distributions. For polydisperse systems g(t) contains a sum of relaxation rates Γ in the exponential function. Γ is given by:38,39

Γ = Dq² 2

with D the diffusion coefficient and 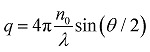the magnitude of the scattering vector. Here, λ is the laser wavelength, n₀ the refractive index of solvent and θ the scattering angle. By fitting the autocorrelation function with eqn (1) and (2), the mean relaxation time , the mean relaxation time 〈Γ〉 and average diffusion coefficient 〈 and average diffusion coefficient 〉 and average diffusion coefficient 〈D〉 can be determined. By applying the Stokes–Einstein equation can be determined. By applying the Stokes–Einstein equation

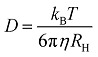3

one can calculate the average hydrodynamic radius R_H of scattered particle from of scattered particle from 〈D〉. Therefore, knowledge of the sample viscosity . Therefore, knowledge of the sample viscosity η as a function of temperature is necessary. In order to account for the temperature dependence of η we have used our results from shear rheology (see below) in the DLS analysis of R_H. To avoid a possible influence of sample's turbidity and multiple-scattering processes, the HPC concentration was decreased to 0.05 g l^–1 for DLS. Prior to each measurement, sample solutions were filtered with a 0.2 μm syringe filter. For additional information about size distributions the reader is referred to Fig. S4 in the ESI.† The solution temperature was controlled by a Peltier-element in the measurement chamber of the Zetasizer ZSP device used for DLS. Heating and cooling rates were set to a constant value of 2.9 K h^–1.

Surface tension measurements

The surface tension of HPC was determined via drop shape analysis of a pendant drop in a Profile Analysis Tensiometer – PAT1M (Sinterface, Germany). In order to control the drop temperature, the PAT1M device was connected to a thermostat WCR-8 (Witeg, Germany) and the temperature was measured with a Pt100 thermocouple close to the pendant drop. To avoid drop shrinkage which can be caused by evaporation, the drop size is measured and regulated by the tensiometer in situ. Dynamic surface tensions were obtained by drop shape analysis using the Young–Laplace equation.40 The change of density of the solvent with temperature was accounted for in our analysis. In order to the exclude the influence of temperature on the surface tension of water γ_H2O(T), the surface pressure Π was calculated:

Π(T) = γ_H2O(T) – γ_sample(T) 4

The relation between temperature and interfacial tension of pure water γ_H2O(T) was taken from Vargaftik et al.41 For each temperature, the dynamic surface tension was recorded by forming a new pendant drop until equilibrium was reached.

Bulk rheology

Experiments with bulk solutions were performed with a Physica MCR101 (Anton Paar, Austria) air bearing shear rheometer. The sample solution was placed in a cone-plate geometry (cone diameter of 25 mm, gap between cone and plate of 0.048 mm, cone angle of 2°). The temperature was controlled with a Peltier element below the plate. A fixed shear rate of 10 s^–1 was applied as this rate was previously shown to have negligible influence on the measured bulk viscosity. In fact, Bercea et al.42 observed under similar conditions (average mass, concentration and shear rate) Newtonian behavior of aqueous HPC solutions. In order to prevent evaporation of sample solution during the measurements, the cone-plate geometry was placed under a closed hood.

Results and discussion

Foam stability and drainage

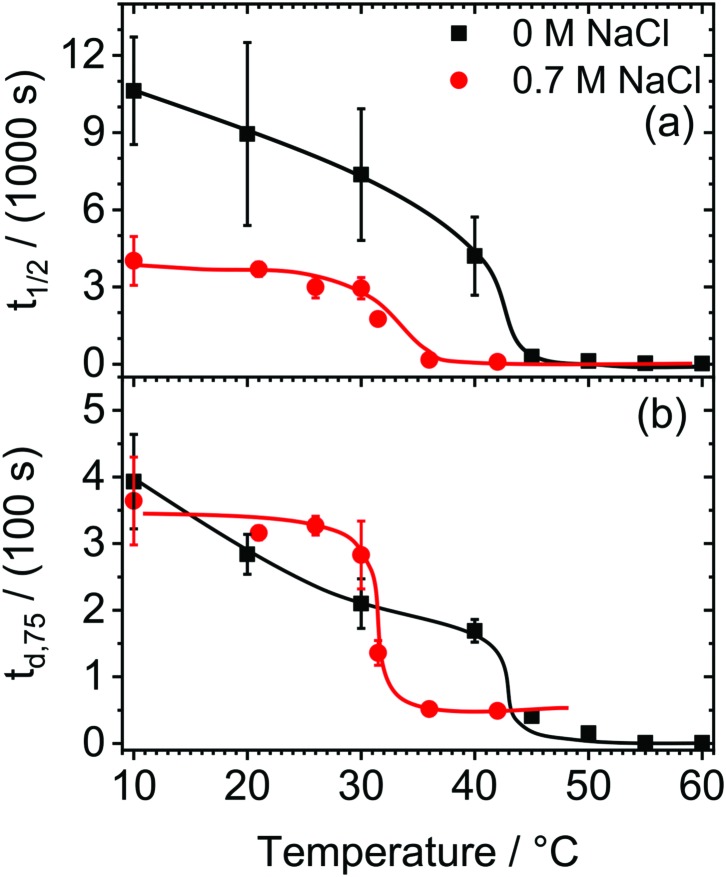
Fig. 1a shows the change in half-life time t_1/2 with temperature of HPC foams from 0.5 g l^–1 HPC aqueous solutions as well as t_1/2 in the presence of 0.7 M NaCl. For temperatures T < 20 °C, foams from HPC aqueous solutions without salt are stable and are characterized by half-life times t_1/2 of ∼9000 s. Increasing the temperature causes a decrease in t_1/2 to ∼4000 s at 40 °C. Above 43 °C, however, a dramatic decrease in foam stability within a remarkably narrow temperature range of ΔT = ±1 °C is observed (Fig. 1a). In fact, temperatures >43 °C lead to half-life times below 120 s. In the presence of 0.7 M NaCl, HPC foams are less stable as compared to salt free solutions, yet the half-life time t_1/2 is with ∼4000 s at 20 °C comparatively high and representative for stable foams (Fig. 1a). Similar to the behavior in the absence of NaCl, we observe for HPC solutions with 0.7 M NaCl a sharp drop in t_1/2, which occurs within a narrow temperature range, but at a significantly lower temperature of ∼31 °C (Fig. 1a). For temperatures >31 °C, HPC foams from 0.7 M NaCl solutions decay within <1 min.

Fig. 1. (a) Half-life time t_1/2 as a function of temperature of foams prepared from 0.5 g l^–1 hydroxypropyl cellulose (HPC) aqueous solutions with 0 (squares) and with 0.7 M NaCl (circles). (b) Time t_d,75 until 75% of the liquid content in the foam has drained as a function of temperature. In (b) squares represent the results for 0.5 g l^–1 HPC solutions without NaCl, while circles represent the HPC solutions with 0.7 M NaCl. Solid lines in (a) and (b) guide the eye.

In order to rationalize which destabilization mechanism can trigger the substantial changes in foam stabilities at the critical temperatures of 43 °C (salt free) and 31 °C (0.7 M NaCl), we will now address the foam drainage.

In Fig. 1b we present the time t_d,75 until 75% of the initial liquid content inside the foam has drained as function of temperature.

Per definition, t_d,75 can provide a qualitative correlation with the velocity of which the liquid content drains from the foam. Thus, a large t_d,75 is indicative for slow drainage while small t_d,75 values indicate fast drainage as the foam quickly loses its liquid content. Further information on the drainage of foams from HPC solutions are presented in the ESI† (Fig. S2).

From a close comparison of Fig. 1a with Fig. 1b, it becomes obvious that the change in foam stability and t_1/2 with temperature (Fig. 1a) is closely related with t_d,75 (Fig. 1b) and, therefore, also with the changes in foam drainage. In fact the relative changes in t_1/2 and t_d,75 closely follow each other and the sharp and substantial changes of both quantities are found at identical critical temperatures of 43 °C (salt-free) and 31 °C (0.7 M NaCl). Around 20 °C, a foam age of 300 s is needed to reduce the liquid content by 75% in the HPC foam from salt-free aqueous solutions (Fig. 1b). By increasing the temperature, a strong decrease in t_d,75 and thus an increase in drainage is observed. Above 43 °C (0 M NaCl) and 31 °C (0.7 M NaCl), t_d,75 drops close to zero which implies that the foam contains less than 25% of initial liquid shortly after the foaming process was completed, and which is consistent with fast drainage. Note that the critical temperatures from Fig. 1b, are identical to the critical temperatures in Fig. 1a, where also the foam stability shows dramatic changes.

Since HPC is an uncharged polymer, electrostatic forces provide only negligible contributions to the foam stability via the electrostatic disjoining pressure.43 For that reason, a reduced foam drainage caused by a high solution viscosity can be a major factor that leads to stable HPC foams, and will be discussed in detail in the following section below.

Obviously, the above described results already demonstrate that aqueous foams from HPC solution are highly responsive to temperature and show a transition from stable to unstable conditions at a critical temperature. Additions of 0.7 M NaCl can change the latter temperature substantially from 43 to 31 °C, which also demonstrates that the reported thermo-responsive properties of foam from HPC solutions can be tuned to some extent.

Characterization of bulk and interfacial properties

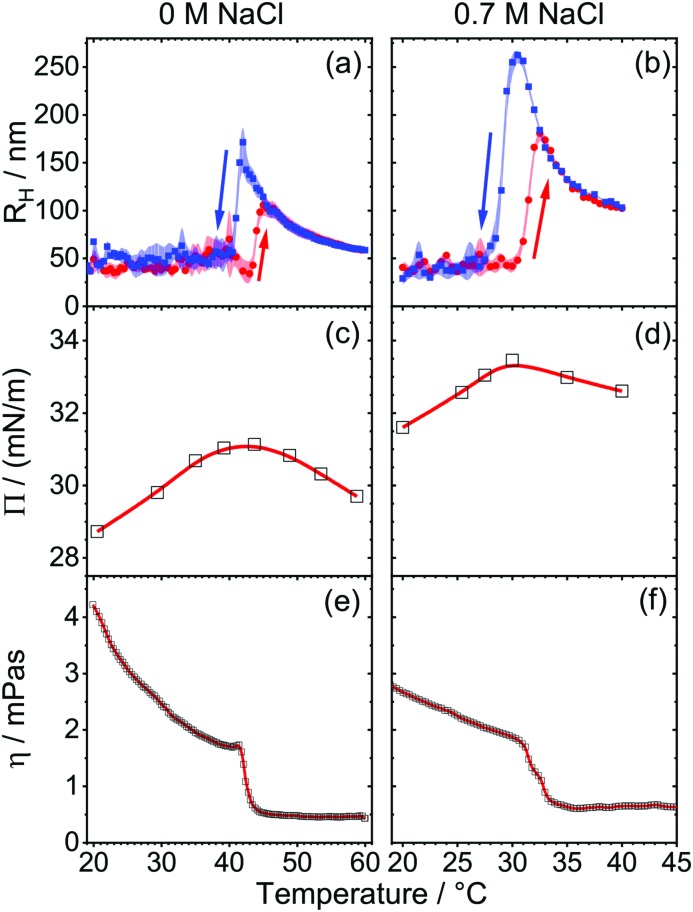
In order to link the above described foam properties to structural changes of the HPC polymer, we will now discuss the results from DLS, surface tension and shear rheology. Fig. 2a presents the mean hydrodynamic radius R_H of HPC in aqueous solutions as a function of temperature during a heating and cooling cycle. For that, the temperature dependence of the solutions viscosity was explicitly considered when the Stokes–Einstein equation (eqn (3)) was applied to calculate the mean hydrodynamic radius from the analysis of the g¹(t) intensity autocorrelation (eqn (1)) of the scattered light. In the case of salt-free solutions (Fig. 2a), temperatures below 42 °C give rise to hydrodynamic radii R_H between 25 and 50 nm. Here, the mean R_H is nearly temperature independent, but is subject to larger size fluctuations as indicated by the error margins in Fig. 2a and b. In fact, in this region the particle size distribution is also relatively broad as shown in Fig. S4 (ESI†). At a temperature of ∼43 °C, the scattered light intensity increases and the mean R_H rises abruptly to 130 nm. A similar trend was also found earlier by Gao et al.44 in their DLS experiments with similar HPC concentrations of 0.0515 g l^–1 HPC but with molecular weight equal to 0.1 MDa. In the latter system, a critical temperature of 40 °C was reported and attributed to the LCST of HPC. The slight difference in LCST maybe related to the different molecular weight (0.1 vs. 1 MDa), which can influence the LCST.

Fig. 2. Temperature dependence of aqueous HPC solutions with 0 (left, (a), (c) and (e)) and 0.7 M NaCl (right, (b), (d) and (f)): (a) and (b) of mean hydrodynamic radius R_H. HPC concentration was 0.05 g l^–1. Red circles and blue squares indicate R_H for heating and cooling temperature ramps, respectively. (c) and (d) of surface pressure of 0.5 g l^–1 HPC. Black circles indicates equilibrium measurements at a constant temperature. (e) and (f) of bulk viscosity η of 0.5 g l^–1 HPC. The red line guides the eye.

In fact, this conclusion is corroborated by our DLS results from solutions with HPC polymers having a molecular weight of 0.1 MDa (Fig. S5b in ESI†), where we find a critical temperature that is comparable to the reported value by Gao et al.44 In addition, Seurin et al.45 studied in detail the effect of the molecular weight (60 kDa, 100 kDa, 300 kDa and 1 MDa) of HPC on its LCST. The authors show that the LCST is shifted to higher temperatures when the molecular weight increase. However, this is different from what Furyk et al.46 report for PNIPAm where the LCST was 0.6 °C higher for 17.8 kDa as compared to 200 kDa.

While an abrupt change in hydrodynamic radius is expected at the LCST, the following first increase in R_H and the subsequent decrease is rather different from other thermo-responsive systems such as PNIPAm,47,48 PNIPAm gels39,49 or HPC gels.36 Previously, Gao et al.44 proposed for HPC, a transition from a hydrophilic to hydrophobic state of the polymer, which is accompanied by predominant hydrophobic interactions between the polymers which cause the formation of self-associated HPC clusters. The latter increase the average particle size, but also shrink in size when the temperature is increased even further. In contrast, PNIPAm,47,48 PNIPAm gels39,49 or HPC gels36 did not show such a behavior. In our experiments and for temperatures above 45 °C, the size distribution of HPC narrows (Fig. S4, ESI†) and the average hydrodynamic radius decreases with temperature from ∼110 nm at 45 °C to 62 nm at 60 °C (Fig. 2a). This decrease in particle size around the LCST has been observed before for other polymers and is attributed to the so-called coil-to-globule transition where the coiled polymer collapses to a more compact globular conformation in order to minimize interactions with the poor solvent.44,47,48,50,51 The driving forces of this transition are considered as a balance between hydrophilic and hydrophobic interactions between inter and intra polymer chains.36,51 Note that the HPC dispersion remains colloidal stable even if the temperature is increased above the LCST. This conclusion is supported by time-dependent measurements of R_H which are presented in Fig. S6 of the ESI.† Decreasing the temperature from 60 to 20 °C (blue squares in Fig. 2a) causes a hysteresis in the change of R_H. Compared to the change of R_H with temperature in the initial heating process, subsequent cooling of the sample solutions with an identical but negative temperature change over time lowers the apparent LCST from 43 to 41 °C. In addition, the mean hydrodynamic radius increases to ∼160 nm at these temperatures. A similar trend can be seen for other molecular weights in Fig. S5 in the ESI.†

By adding 0.7 M NaCl (Fig. 1b) the sequential trend in R_H with temperature remains similar, but we found a strong increase in the scattered light intensity at 31.5 °C which indicates a clear shift of the LCST to the latter temperature.

Previously, Xia et al.36 studied the influence of NaCl to the LCST of HPC with light scattering experiments. They reported a linear relation between salt concentration and LCST of the polymer. By adding 0.7 M NaCl the LCST was lowered to ∼30 °C which is corroborated by our results. Additionally, the mean particle radius increases up to 150 nm at 32.5 °C and shrinks by a further increase in temperature. Moreover, the hysteresis seems to be more pronounced in the presence of 0.7 M NaCl. By cooling the sample we found a rise of R_H to 250 nm and the apparent LCST at 29 °C.

The hysteresis in the change of R_H with temperature, is consistent with previous reports by Wu et al.,47,48 where the authors reported a shift in the LCST to lower temperatures (ΔT < 1 K) by cooling PNIPAm in water. Wu et al. explained this behavior by the formation of an intrachain structure during the coil-to-globule transition, which is presumably due to intrachain hydrogen bonding and also persists in the globule-to-coil transition.

The dramatic changes in the bulk hydrodynamic radius are also reflected in the properties of the air–water interfaces formed from HPC solutions. Note that in aqueous foam the air–water interface and foam films (lamella) that form from two air–water interfaces separated by a thin-liquid film are major hierarchical elements that can determine foam properties.6,52 For that reason, we have additionally addressed the behavior of the latter interfaces by determining the change of the surface pressure with temperature which is depicted in Fig. 2c and d. For HPC solutions without additional salt, a surface pressure Π of 28.7 mN m^–1 (γ = 43.8 mN m^–1) is observed at 20 °C. In previous literature,53 a surface pressure of 30.6 mN m^–1 (γ = 42 mN m^–1) at 20 °C for HPC (M_w = 750 kDa) at a similar concentration was reported. The surface pressure data are comparable, however our data shows slightly lower values which can be related to the different molecular weights of the two samples. Increasing the temperature from 20 to 42 °C, causes an increase in surface pressure because HPC is likely forced additionally to the interface by hydrophobic interaction between solvent and polymer. Around 43 °C, the surface pressure reaches a maximum value of 31 mN m^–1. Increasing the temperature further, leads to a decrease of Π to 29 mN m^–1 at 60 °C.

The presence of 0.7 M NaCl (Fig. 2d) does not change the trend in the surface pressure, but increases the absolute value of Π by 2 to 3 mN m^–1. As seen before without salt (Fig. 2c), a maximum in Π is visible at the LCST. However, the small changes of ∼2 mN m^–1 in the surface pressure around the LCST (Fig. 2c and d) cannot explain the drastic changes in the foam stability as seen in Fig. 1.

In order to reveal the origin of the major changes in foam stability at the LCST, we have performed additionally measurements on the solution's bulk viscosity, which are presented in Fig. 2e and f. In order to quantify molecular state of HPC chains we will now deploy a method that was previously reported by Bercea et al.42 Here a critical overlap parameter c·[η] = 2.4 is used to distinguish between entangled HPC macromolecules in a physical network (c·[η] > 2.4) and non-entangled isolated macromolecular coils (c·[η] < 2.4). The intrinsic viscosity [η] describes the capability of a polymer in solution to enhance viscosity and can be calculated from the empirical Mark–Houwink equation:

[η] = KMaw = 3.47 × 10^–5M_w^0.88 5

which is a function of the average mass M_w and empirical constants K and a for aqueous HPC solutions at 25 °C.42,54 Taking the latter into account, we calculated for our system a critical overlap parameter of 3.3. The latter indicates that HPC chains are forming a physical network in the solvent, which increases the bulk viscosity strongly. By increasing the temperature, the viscosity shows a gradual decrease from 4 mPa s at 20 °C to 1.7 mPa s at 40 °C. However, for temperatures >43 °C cause a substantial decrease in viscosity to 0.6 mPa s. This viscosity is actually comparable to the viscosity of neat water at these elevated temperatures.55 A similar change in bulk viscosity of HPC (M_w = 1 MDa) aqueous solutions with temperature was found earlier by Khuman et al.35 The behavior of bulk viscosity of HPC in the presence of 0.7 M NaCl is shown in Fig. 2f. The sequential trend of η as a function of temperature stays the same, while the drop in bulk viscosity is shifted to 31 °C. Additionally η is slightly decreased in a range between 20 and 30 °C compared to the pure HPC solution, which is consistent with the report by Khuman et al.35 In fact, the latter authors studied the effects of NaF on the bulk viscosity of HPC and also report that an increase in the amount of salt lowers η and the transition temperature.

Taking our above discussion of the experimental results in Fig. 1 and 2 into account, we find major changes in foam stability and drainage, surface pressure, bulk viscosity and mean hydrodynamic radii at temperatures of 43 ± 1 and 31 ± 1 °C for HPC solutions with 0 and 0.7 M NaCl, respectively. These temperatures can be attributed to the LCST of HPC in the presence and absence of NaCl and are consistent with previous studies on the LCST of HPC.35,36,44,56

Below the LCST, HPC is well solvated and surrounded by a network of water molecules because of strong hydrogen bonds interactions between polar groups of HPC and the aqueous solvent.35 The bulk viscosity is strongly increased due to kinetic and hydrodynamic interactions of entangled macromolecules. An increase in the temperature leads to a breakup of the hydrogen bonds between HPC and water molecules.35 This increases the hydrophobicity, the surface pressure and lowers the bulk viscosity of the polymer solution until the LCST is reached. At the LCST, entropy destroys the network of surrounded water molecules, the polymer phase turns insoluble in water and phase separation occurs.57 HPC turns from a hydrophilic to a hydrophobic state which causes changes in size (Fig. 2) and possibly also in the shape of the polymer. As a consequence, the physical network of the macromolecule vanishes, the polymer loses interaction with the solvent and the bulk viscosity shows a sharp decrease to the value of pure water (Fig. 2e and f). In fact, the presence of salt influences the LCST of the polymer, which is mainly linked to a salting out and salting in effect between the anions and the macromolecule.58 Kosmotropic anions like fluoride, chloride or bromide are known to be a water structure maker and destabilize the hydrogen bonds between water and the polymer which lead to a decrease of the LCST of HPC. On the other hand, chaotropic ions like iodide or thiocyanate disrupt the water structure, that can preferentially interact with the macromolecule and favour an increase in the LCST.35,57

Obviously, the origin of the changes in foam drainage and in case of HPC also of the foam stability can be directly linked to the bulk viscosity and the LCST of HPC solutions. A high viscosity prevents the foam from draining and consequently increases the foam half-life time.

Dynamic switching of foam stability

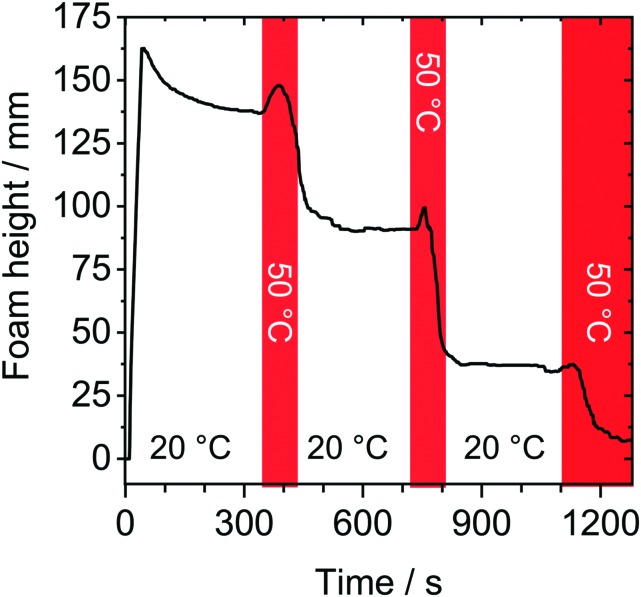
In order to show reversible thermo-responsive properties of HPC foams, we have performed foam experiments where the temperature was periodically changed between a temperature below and a temperature just above the LCST. The result of such an experiment is shown in Fig. 3. Here, red shaded areas mark a temperature change from 20 to 50 °C. The foam was produced at 20 °C and height was monitored for 300 s. A close inspection of Fig. 3 shows, that within the initial 300 s, the foam stability was high as discussed earlier (Fig. 1a). Subsequent to the 300 s waiting time with temperature set to 20 °C, the temperature was rapidly increased to 50 °C. Immediately after this temperature increase, an increase in foam height is observed. This can be explained by an increase in bubble pressure and volume with temperature. After this initial ‘induction’ time, the foam height starts to drop sharply. We point out, that rapid changes in column temperature necessarily caused a temperature gradient inside the column. Because of the latter, we observed in the temperature-switching experiments (Fig. 3), that the foam decay started at the sidewalls of the foam column as here the set temperature is reached first. Before the foam had decayed completely, the temperature was rapidly set back to 20 °C. This has caused an immediate stabilization of the foam and the foam height did not decrease considerably within the following 730 s. Subsequent to latter waiting time, temperature was set again to 50 °C. Again we observe a short initial ‘induction’ time that is followed by a substantial loss in foam height and is indicative for poor foam stability. Rapid cooling again to 20 °C, leads to a stabilized foam.

Fig. 3. Change of foam height as a function of time. Foam was prepared from 0.5 g l^–1 HPC aqueous solution and the temperature was rapidly changed from 20 to 50 °C (red shaded areas) during measurement.

The results in Fig. 3 clearly demonstrate that the thermo-responsive properties of HPC foams are highly reversible and that dynamic switching between stable and unstable conditions is possible.

Conclusions

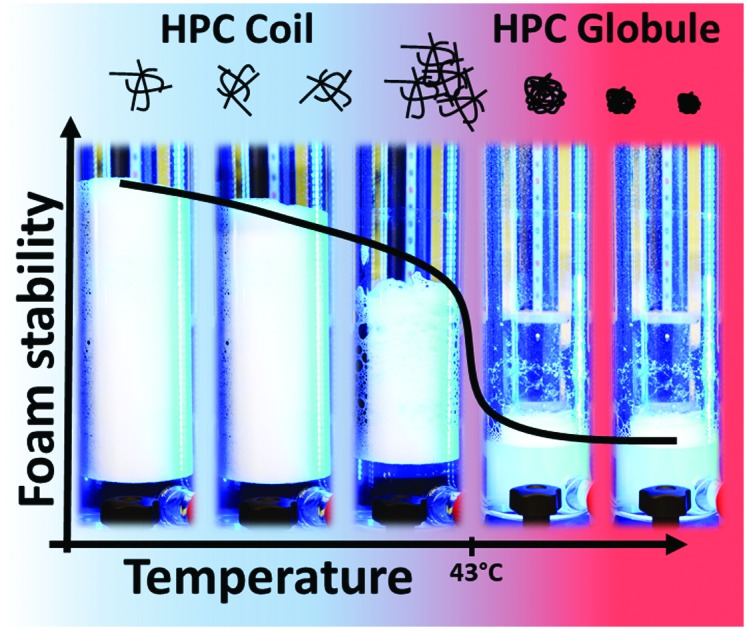
Thermo-responsive properties of foams from HPC aqueous solutions have been studied for the first time and were related to physico-chemical properties of HPC polymers in the bulk solution. Major changes in foam stability and liquid drainage occur at critical temperatures which we can attribute to the LCST of HPC. At temperatures below the LCST, HPC foams are stable for several hours. This foam stability is dominated by the high bulk viscosity and consequently slow foam drainage and can be related to an entangled physical network of polymer chains. Strong changes in foam stability, drainage, surface pressure, bulk viscosity and hydrodynamic radius occur at ∼43 °C, which is the LCST of HPC in the absence of an additional electrolyte such as NaCl. Increasing the temperature above the LCST leads to a substantial decrease in the mean hydrodynamic radius, which is attributed to a coil-to-globule transition of HPC. Because of the latter, the bulk viscosity is reduced significantly and rapid foam drainage is observed. As a consequence, the foam half-life time changes from hours below the LCST to less than a minute at temperatures above the LCST, but can be reversibly and dynamically changed back to stable conditions when the temperature is subsequently decreased below the LCST. Since the LCST can be lowered by changing the electrolyte and the ionic strength, also the related critical temperature where the foam stability changes drastically can be tuned from 43 to 31 °C.

Conflicts of interest

There are no conflicts to declare.