SAMPL6 challenge results from pK_a predictions based on a general Gaussian process model

Abstract

A variety of fields would benefit from accurate pK_a predictions, especially drug design due to the effect a change in ionization state can have on a molecule’s physiochemical properties. Participants in the recent SAMPL6 blind challenge were asked to submit predictions for microscopic and macroscopic pK_as of 24 drug like small molecules. We recently built a general model for predicting pK_as using a Gaussian process regression trained using physical and chemical features of each ionizable group. Our pipeline takes a molecular graph and uses the OpenEye Toolkits to calculate features describing the removal of a proton. These features are fed into a Scikit-learn Gaussian process to predict microscopic pK_as which are then used to analytically determine macroscopic pK_as. Our Gaussian process is trained on a set of 2,700 macroscopic pK_as from monoprotic and select diprotic molecules. Here, we share our results for microscopic and macroscopic predictions in the SAMPL6 challenge. Overall, we ranked in the middle of the pack compared to other participants, but our fairly good agreement with experiment is still promising considering the challenge molecules are chemically diverse and often polyprotic while our training set is predominately monoprotic. Of particular importance to us when building this model was to include an uncertainty estimate based on the chemistry of the molecule that would reflect the likely accuracy of our prediction. Our model reports large uncertainties for the molecules that appear to have chemistry outside our domain of applicability, along with good agreement in quantile-quantile plots, indicating it can predict its own accuracy. The challenge highlighted a variety of means to improve our model, including adding more polyprotic molecules to our training set and more carefully considering what functional groups we do or do not identify as ionizable.

1. Introduction

Accurate predictions of pK_a values are of interest in a variety of fields including pharmaceutical research, as absorption, distribution, metabolism, and toxicity can be profoundly affected by changes in ionization state [1,2]. Other key physiochemical properties, such as lipophilicity, solubility, and permeability are also ionization state dependent [3–6]. Knowing the likely ionization state of a molecule is also important as preparation for other modeling studies. For example, predictions of distribution coefficients in SAMPL5 demonstrated how dramatically free energy calculations can be affected by a choice in ionization state of a molecule [7,8]. Calculations of other biomolecular properties, such as protein ligand binding affinities, are similarly affected by choices in ionization state [9].

Because of the importance of pK_a prediction, and the difficulty of predicting pK_a values, the SAMPL challenge organizers included a pK_a prediction component in SAMPL6. Experimental macroscopic pK_as were collected for 24 drug like molecules using an established spectrophotometric technique limited to a pH range between two and twelve. As a part of follow up analysis, a few NMR experiments were performed to determine the microscopic pK_as of a select few molecules [10]. Microscopic pK_as refer to an equilibrium resulting from removing a specific hydrogen from a molecule and macroscopic pK_as describe the process of removing any hydrogen or an overall change in charge state [11,12]. All experimental data was kept secret from the public to allow participants in the challenge to make blind microscopic and macroscopic predictions for the 24 molecules. Specifically, there were three formats allowed for prediction submission:

• type I: microscopic pK_as,

• type II: fractional microstate populations as a function of pH, and

• type III: macroscopic pK_as

where microstates refer to a single tautomer of a specific charge state of a molecule. For each type of submission participants were encouraged, but not required, to submit all predictions their model generated for every molecule. SAMPL6 organizers then evaluated predictions based on experimental results for all macroscopic and a select set of microscopic pK_as [13]. Details for the challenge including experimental results, all submitted predictions, and an overview analysis are available online (github.com/MobleyLab/SAMPL6).

There are many different methods and tools for pK_a prediction, and a variety can be seen in this special issue on SAMPL6 results. These techniques vary dramatically in scope, computational cost, and accuracy. Historically, a common approach for predicting pK_a was through linear free energy relationships using empirically determined constants to relate an acid or base to a parent molecule in a known database [14,15]. A related technique, quantitative structure-property relationships (QSPR), remain popular. These incorporate a variety of molecular and atomistic descriptors [16–18]. Some of these techniques have been updated to use more advanced machine learning models such as artificial neural networks [19,20]. A variety of quantum mechanical descriptors, including partial atomic charges, have also been shown to be promising in QSPR models – due to computational cost, these methods are impractical for a general model and have only been applied to specific types of ionizable groups [6,21–23]. Quantum mechanical calculations from first principles can also be used to calculate pK_a using a thermodynamic cycle of deprotonation in the gas phase and the hydration free energy of both the protonated and deprotonated molecule [24]. QM calculations are often still limited in accuracy due to the difficulty in calculating hydration free energies of ionized molecules in implicit solvents. The most successful quantum mechanical predictions from first principles also apply an empirical linear correction factor [25,26].

Here, we introduce a new machine learning model for predicting microscopic and macroscopic pK_as. Our goal was to create a universal model which provides predictions that come with accurate estimates of their uncertainty. Most general methods for pK_a prediction build separate models for each type of ionizable group. Even predictions based on DFT calculations for model input can require specialized models for different ionizable groups [27]

In contrast, we set out to build a single general model which could predict a microscopic pK_a for any identified ionizable group. We believe that if our features, or input into the machine learning model, are based on the underlying physical and chemical properties responsible for the variation in deprotonation energy, only one model would be necessary. Artificial neural networks have been successful for predicting pK_a, but require substantial training data. We were interested in a machine learning model that could be built from less training data, but did not require an assumption about the shape of the function being fit. Gaussian process regression meets these requirements providing a model based on distributions in feature space. It also automatically incorporates an assessment of uncertainty based on how similar input data is to the training data [28]. Here, we present this new model and our results for the type I and type III components of the SAMPL6 blind challenge.

2. Computational Methods

We built a pipeline to predict the microscopic and macroscopic pK_as of a molecule starting from any molecular representation, such as a SMILES string. Our model directly predicts microscopic pK_as and then calculates macroscopic pK_as. First, we identify all ionizable groups in a molecule and iterate through them to identify all transitions between microstates. In the next step, we convert each microscopic transition into a list of quantitative features. These features are used as input into our Gaussian process regression model which predicts a pK_a for each micro-transition. The output from these steps is a list of all microscopic pK_as for each molecule. Lastly, macroscopic pK_as are analytically calculated from a thermodynamic cycle involving all microscopic transitions. Below, each of these steps is described in detail including an overview of how we trained, validated, and tested our model before the SAMPL6 challenge.

2.1. A heuristic approach is used to identify aqueous ionizable groups

The first step in processing any molecule, either for training or prediction, is to identify all microscopic transitions. Molecules, in the form of SMILES strings or any common molecular file format, are processed using OpenEye’s OEChem toolkit [29] and one reasonable tautomer of the neutral form of the molecule is chosen. A substructure search is used to identify groups that commonly ionize in water [15] as either acidic:

• any protonated oxygen atom

• any protonated aliphatic sulfur atom

• cyclopentadiene

• carbon or nitrogen between two strongly electron withdrawing groups

• arylsulfonamide nitrogens

• pyrrole-like aromatic nitrogens

• any atom with a non-dative, formal positive charge and a hydrogen

or basic:

• aliphatic nitrogen atoms, not a part of amide or sulfonamide groups

• pyridine-like aromatic nitrogens

• trivalent aliphatic phosphorous

• any atom with a non-dative, formal negative charge.

Next, we protonate all basic groups and then iterate through all ionizable groups recursively removing a proton from each in order to identify all micro-transitions. For each transition we store the protonated and deprotonated form of the molecule. OpenEye’s Omega toolkit is then used to generate a low-energy conformation for each form of the molecule [30]. Next, a list of features is calculated to describe the micro-transition between these two forms of the molecule. This feature list will then be used as input for into our Gaussian process model.

2.2. Features were chosen to describe physical characteristics

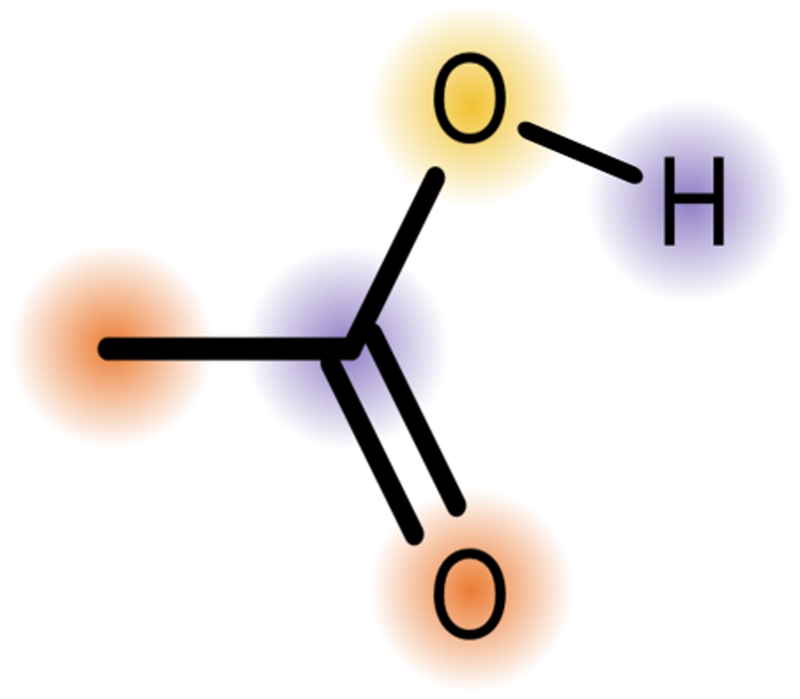
We chose features based on the chemical and physical properties that affect pK_a. The key properties chemists are trained to think about in relation to ionization are the ionizable atom, resonance, inductive effects, steric effects, and solvation. These properties affect the ability of an ionizable group to support a protonated or deprotonated state along with the associated change in formal charge. We also considered the quantum mechanical approach for calculating pK_a using a thermodynamic cycle involving the gas phase acidity and the solvation free energy of each form of the molecule. Thus, we calculate features to describe the micro-transition using the protonated and deprotonated forms of the molecule in gas and aqueous phase. Using OpenEye Toolkits we calculate a total of ten features for each transition, some for each form of the molecule and some taking differences in properties between the two forms.

• Difference in enthalpy

• Mayer Partial Bond order on the bond between hydrogen and the ionizable group

• AM1-BCC partial charges on multiple atoms, resulting in six charge-related features

• Difference of solvation free energy

• Solvent accessible surface area of the deprotonated atom

To begin, we perform a semi-empirical AM1 calculation for each microstate and then extract several properties. The first feature mirrors gas phase acidity by taking the difference in enthalpy between the protonated and deprotonated form of the molecule. For the protonated form of the molecule, the Mayer partial bond order is also calculated for the bond between the ionized atom and the hydrogen to be removed [31–33]. AM1-BCC partial charges are calculated for atoms one and two bonds away from the ionized atom [33–35]. Previous work established partial charges as a useful feature to predict pK_a on molecules. These studies used molecule sets with all the same ionizable groups considering the charge on the deprotonated and surrounding atoms [22, 23,36]. In order to apply our model to all identified ionizable groups, we needed a more general approach. We decided to consider the partial charge of (1) the deprotonated atom and the average partial charge on atoms (2) one bond and (3) two bonds away from this atom, for both the protonated and deprotonated forms of the molecule (Figure 1). This leads to six features based on the partial atomic charges. Since the AM1 calculations are performed in gas phase, the last two features attempt to capture the affect of solvation on the equilibrium. The difference in solvation free energy of the two forms of the molecule is estimated by a Poisson Boltzmann surface area calculation as implemented in OpenEye’s Szybki toolkit [37,38]. Lastly, the solvent accessible surface area around the deprotonated atom is determined with OpenEye’s Spicoli Toolkit [39–42].

Fig. 1.

We use the partial charge on the deprotonated atom (yellow) and the average partial charge on atoms one bond (purple) and two bonds (orange) away from that atom in both the protonated and deprotonated form of the molecule, making a total of six features involving partial charges.

2.3. Gaussian process regression provides a simple machine learning model

We built our Gaussian process regression model using the Python package Scikit-learn [43]. A Gaussian process is a nonparametric model which uses a Bayesian approach to sample a posterior distribution of functions [28]. There are two priors set for a Gaussian process, a mean function and a kernel (or covariance) function. As with most Gaussian process models, we set our prior mean function to zero. When initially training and validating the model, we considered a variety of the kernel functions included in Scikit-learn. To choose a kernel and optimize any required parameters, we used a three-fold cross validation method considering the root mean squared error (RMSE), mean error, and correlation coefficient of the training and validating sets (Section 2.5). The best performing kernel for our purposes was a Matérn kernel – a generalized function between the squared and absolute exponential kernels [28]. This kernel requires a preset parameter v which was optimized to 2.5 for our model. The general form of Matérn kernel is complex including a Bessel function, and with v = 2.5, our final kernel is the function:

$$k=c\left(1+\frac{\sqrt{5}d}{l}+\frac{5d^2}{3l^2}\right)\text{exp}\left(-\frac{\sqrt{5}d}{l}\right)$$ (1)

where c and l are trained constants and d is the distance between two feature vectors.

2.4. Macroscopic pK_as are calculated from microscopic transitions

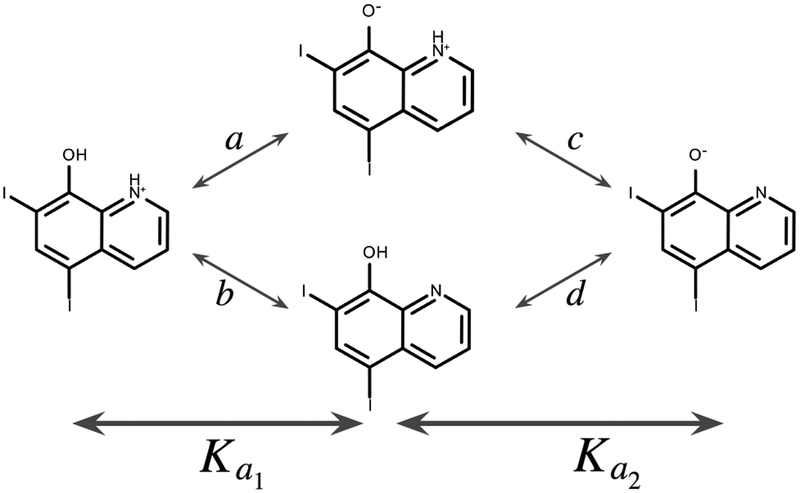
Our Gaussian process model is trained to predict microscopic pK_as which can be used to analytically calculate macroscopic pK_as. Most experimentally measured pK_as are macroscopic, providing an equilibrium constant for an overall change in total charge. These macroscopic transitions are comprised of multiple microscopic transitions, each of which consists of the removal of one specific hydrogen atom. If pK_as, or equilibrium constants, for all microscopic transitions are known, then the macroscopic pK_a can be analytically calculated using a thermodynamic cycle [15,6]. For example, for a molecule with two ionizable groups, the macroscopic K_a’s are:

$$K_{a_1}\text{ = }a\text{ + }b$$ (2)

$$K_{a_2}=\frac{1}{c}+\frac{1}{d}$$ (3)

where a and b are equilibrium constants for the first deprotonation and c and d are for the second deprotonation with the thermodynamic cycle in Figure 2. Similar, though more complex, cycles can be drawn for polyprotic molecules, allowing us to calculate macroscopic pK_as for any provided molecule.

Fig. 2.

We identify two ionizable groups in SAMPL6 compound SM22; this thermodynamic cycle shows an example of how microscopic transitions with equilibrium constants a, b, c, and d are related to macroscopic equilibrium constants ($K_{a_1}$and $K_{a_2}$).

2.5. Training, validation, and internal test sets include monoprotic and select diprotic molecules

Our training set was derived from an extensive experimental pK_a database Tony Slater curated from four original sources:

• Dissociation Constants of Organic Bases in Aqueous Solution, by D.D. Perin (3,775 molecules, 8,766 pK_as) [15];

• Dissociation Constants of Organic Acids in Aqueous Solution, by G. Kortum, W. Vogel and K. Andrussow (1,063 molecules, 2,893 pK_as) [44];

• Dissociation Constants of Organic Bases in Aqueous Solution, Supplement 1972, by D.D. Perin (4,275 molecules, 7,844 pK_as) [45];

• Ionisation Constants of Organic Acids in Aqueous Solution, by E.P. Serjeant and Boyd Dempsey (4,584 molecules, 10,912 pK_as) [46].

This is the same database used for the OpenEye application pK_a Prospector. To begin, we filtered database entries for experimental measurements which were aqueous (including removing measurements in D₂O), taken between 20 and 25 degrees Celsius, and not tagged as very uncertain. This resulted in a set of 9,890 molecules with 26,519 experimental measurements. The large number of experimental results compared to number of is not solely due to molecules with multiple pK_as; rather, it is primarily due to replicate measurements for certain molecules. In such cases we performed a weighted average, propagating the estimated uncertainties. As we are most interested in biologically relevant ionization, we also removed molecules where the experimental pK_as were outside a range of 0 to 14.

We currently use SciKit-Learn’s out-of-the-box version of Gaussian Process which assumes one expected value for each feature vector, limiting the types of we can use for training. Specifically, polyprotic molecules are not suitable for training input in this approach. Specifically, for polyprotic molecules, there is a feature vector for each microscopic transition, leading to more predicted values than experimental pK_a values. For example, there are four microscopic transitions for a diprotic molecule but only two macroscopic pK_a values. Thus, we focused our training set on instances where a microscopic transition can be directly mapped to an experimental macroscopic pK_a. The first set of molecules was perhaps the most obvious — those with only one ionizable group where the microscopic and macroscopic transition are identical. We checked that molecules we identified as having a single ionizable group also only had one experimental measurement. This resulted in 2,672 molecules. To expand the diversity of the training set we added a selection of diprotic molecules. For this set we also included molecules where we identified two ionizable groups and two experimental values were reported. Additionally, we required the difference in these two experimental pK_as be greater than three log units to assure dominance of a single microstate in estimation of the macroscopic pK_a. There were a total of 286 diprotic molecules in the database that met this requirement. For these molecules, we assumed each macroscopic pK_a was dominated by only one microscopic transition.

Before training, we removed 10% of these molecules to later serve as an internal test set, resulting in setting aside 243 monoprotic and 29 diprotic molecules, for a total of 301 data points. The training data then consisted of 2,186 monoprotic and 257 diprotic molecules. We then split the training data into thirds in order to use a three-fold cross validation method to evaluate the choice of a Gaussian process model and choose a kernel [47]. To evaluate model performance, we considered RMSE, mean error, and correlation coefficients for each training and validation set pair. We judged model performance on training and cross-validation datasets in the context of learning curves for the purposes of model and feature selection. Statistical analysis from our final cross-validation sets and internal test sets can be found in our supporting information. All training data was recombined for our final Gaussian process model used to evaluate our internal test set and make predictions for SAMPL6.

3. SAMPL6 challenge results

We predict microscopic pK_a values using a Gaussian process model trained on 2,443 mono- and diprotic molecules (2,700 data points). Physical and chemical features are calculated for the protonated and deprotonated form of the molecule using OpenEye toolkits (Section 2.2). Macroscopic pK_as are then analytically calculated from a combination of microscopic transitions (Section 2.4). We used our model to predict microscopic (type I) and macroscopic (type III) pK_as for 24 drug like molecules in the SAMPL6 blind challenge [13]. The SAMPL6 submission IDs assigned to our predictions where 6tvf8 (type I) and hytjn (type III). While DLM is a co-organizer of the challenge, none of the authors had any access to the experimental data nor any knowledge of details of the measurements until experimental values and details were publicly released to all participants. The SAMPL6 organizers also asked for optional microstate populations as a function of pH (type II). However, we elected not to participate in that portion of the challenge.

3.0.1. Predictions were matched with experiment to reduce error

In an ideal world we would have a one-to-one match when comparing predicted and experimental results, where each calculated pK_a has a corresponding experimental value. When SAMPL6 was announced, it included specification for how the experimental pK_a values would be measured. This included the limitation to perform experiments in a pH range of 2 12. Following the organizer suggestions, we included − predictions for all macroscopic pK_as our model predicted including those outside the specified experimental range. Thus, there are many molecules with fewer experimentally determined pK_as than we predicted. The organizers considered two matching algorithms and analyzed all challenge submissions with both methods. The first was a closest matching algorithm where each prediction is matched to an experimental value based on the absolute difference between them. If two predictions are paired to the same experimental value then the match with the larger absolute difference is thrown out leading to one less pair used in the analysis. To prevent the loss of data due to multiple pairings, the organizers redid the analysis using a Hungarian matching algorithm instead [48]. In the Hungarian algorithm, the absolute difference is calculated for each pair of prediction to experiment. Then the combination of pairs which reduces the absolute error for that whole molecule is retained. One potential problem in this approach is that it does not account for the natural ordering of pK_a values, meaning it is possible that the larger of two predictions could be paired with the smaller of two experimental pK_as. For example, if a molecule had two experimental pK_as 2.15 and 9.58 and a prediction reported values of 0.50 and 1.84, then the final pairs would be (9.58, 0.5) and (2.15, 1.84) as that would result in the smallest absolute error overall. In general, we believe the Hungarian approach is superior as it allows for all possible data to be included, though an ideal algorithm would restrict the order while matching. Fortunately, this reordering did not occur when our predictions were paired with experiment so we used the Hungarian matching to evaluate our performance. All analysis by organizers for all submissions can be found online (github.com/MobleyLab/SAMPL6).

3.1. Microscopic pK_a reported for type I predictions

We reported microscopic pK_as for all ionizable groups we identified in the SAMPL6 molecules. The first step for any prediction we perform is to identify ionizable groups and then iterate through those groups to find all microscopic transitions. For SAMPL6, all resonance structures of a given microstate were considered to be a single state and assigned a single identification number for the set. We matched each molecular microstate to the proper identification number using a script adapted from the SAMPL6 organizers that identifies identical resonance structures. A full table of microscopic pK_as and the script used to find their identification numbers is provided in the supplementary information.

The SAMPL6 organizers initially provided an approximate evaluation of predicted microscopic transitions using macroscopic pK_as. Organizers provided experimental macroscopic pK_as for all molecules, but experiments for microscopic pK_as were only performed for seven molecules [10]. In an attempt to provide feedback on type I predictions, organizers compared experimental data for molecules with only one experimental pK_a or two pK_as with a difference greater than 3 relative to microscopic predictions. For each molecule, the experimental values were matched to microscopic predictions that resulted in the lowest error, using the same closest and Hungarian pairing algorithms described in Section 3.0.1. These results are available for all submissions on the SAMPL6 GitHub repository [13] However, here, we have chosen to focus on analysis of directly measured microscopic predictions rather than microscopic predictions with presumed correspondence to macroscopic measurements. While many macroscopic transitions are likely dominated by a single microscopic transition, including those in section 3.1.1, we cannot know for sure that this is true for every molecule in this set. These results are highly dependent on the particular matching algorithm and no rigorous analysis of the microscopic pK_a predictions would be possible. Without evidence of which transition is dominant, this pairing does not provide constructive feedback for improving our model, thus we have chosen not to share those results here.

3.1.1. Experimental microscopic pK_as were measured for two molecules

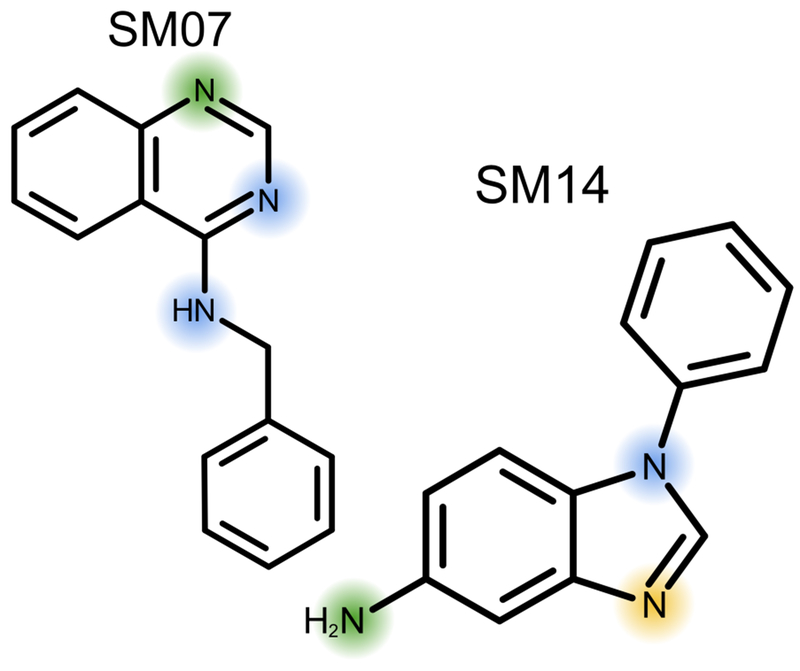
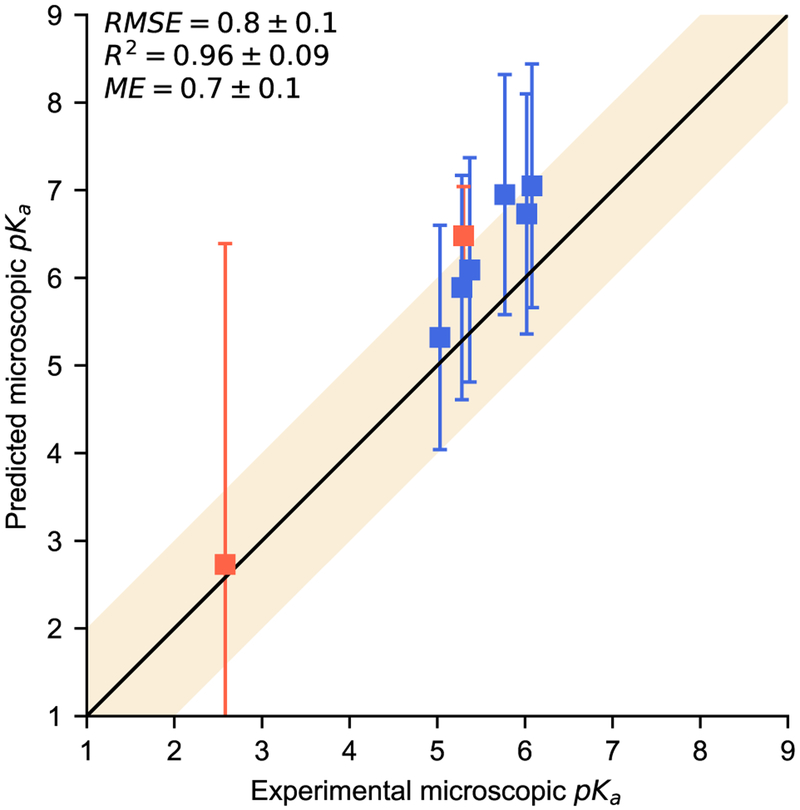
After the macroscopic pK_a values and all predictions were made public, molecules SM07 and SM14 were analyzed in an NMR experiment to determine microscopic pK_as [10]. SM14 has three nitrogens our algorithm identified as ionizable (Figure 3). The NMR results indicated the two macroscopic pK_a values were dominated by two different microscopic transitions included in our predictions (Table 1). SM07 is a 4-amino quinazoline derivative with three nitrogens our algorithm identified as ionizable (Figure 3). The NMR results indicated the macroscopic pK_a was dominated by a single microscopic transition observed for this molecule. SAMPL6 included five other molecules that are also 4-amino quinazoline derivatives. If we assume all of these molecules have a dominant microscopic transition on the same nitrogen, then we can compare a total of six predicted microscopic pK_as with experiment (Table 1). Our predictions for these microscopic transitions have reasonable correlation with the experimental values with an R² of 0.96±0.09 (Figure 4). While there appears to be a slight bias with a mean error of 0.7±0.1, all predictions were within uncertainty of experiment. Predicted uncertainties are also fairly large, greater than 1.2 for all 4-amino quinazoline derivatives. High uncertainties are expected as our training data only included molecules with one or two ionizable groups and SM14 as well as these 4-amino quinazoline derivatives would not be well represented.

Fig. 3.

NMR experiments were performed for molecules SM07 and SM14. SM07 has one microscopic transition for the protonation of the top nitrogen (green). SM14 has two microscopic transitions, first the protonation of the middle nitrogen (yellow) and then the left nitrogen (green). For both molecules, we highlight the other nitrogens we identified as ionizable (blue).

Table 1.

All NMR verified microscopic pK_as are reported. First, are those for experiments performed on molecules SM07 and SM14. The second half of the table contains molecules similar to SM07 where we assume the equivalent microscopic transition also dominates their macroscopic experimental result.

SAMPL ID	Experiment	Prediction
SM07	6.08 ± 0.01	7.05 ± 1.39
SM14	2.58 ± 0.01	2.73 ± 3.66
	5.30 ± 0.01	6.48 ± 0.56
SM02	5.03 ± 0.01	5.32 ± 1.28
SM12	5.28 ± 0.01	5.89 ± 1.28
SM09	5.37 ± 0.01	6.09 ± 1.28
SM13	5.77 ± 0.01	6.95 ± 1.37
SM04	6.02 ± 0.01	6.73 ± 1.37

Fig. 4.

Predicted microscopic pK_as are compared to experiment for six 4-amino quinazoline derivatives based on NMR experiments on molecule SM07. The shaded region region indicates agreement within 1pK_a unit.

3.1.2. Commercial models provide a reference for more of our microscopic pK_a predictions

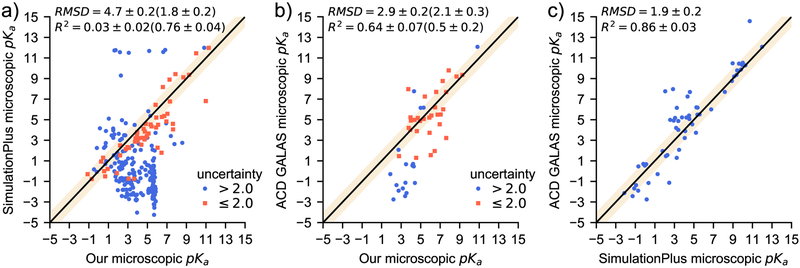
In an attempt to evaluate a wider range of microscopic pK_as, we compared our predictions with some of the top results from the macroscopic analysis. SimulationsPlus’ pK_a Predictor [20] (submission ID hdiyq) and ACD Lab’s pK_a GALAS [49] (submission ID 8qph) both performed better than our approach in the macroscopic pK_a challenge compared to experiment and provided type I predictions [13]. We will refer to these two submissions as S+ and ACD respectively. The SAMPL6 challenge instructions encouraged all participants to submit whatever microscopic pK_as their method identified. Each method we are considering for comparison here reported a different number of microscopic pK_as. Using our algorithm, we calculated 254 microscopic pK_as while, S+ reported 313 and ACD reported 65. In Figure 5, we compare our results with these two commercial products (Figure 5 a and b), then we also compare S+ and ACD predictions with each other (Figure 5c). For all three comparisons, all microscopic transitions predicted by both methods are considered. The two commercial predictions agree reasonably well with one another (RMSE of 1.9±0.2). Thus, comparing our predictions to both allowed for a more informative analysis of our microscopic pK_a predictions than comparing them to macroscopic experimental data. Our results initially seem less promising than the analysis for SM07 and SM14 discussed above with an RMSD of 4.7±0.2 compared to S+ (5a) and 2.9 ± 0.2 compared to ACD (Figure 5b). Our model is trained on a limited data set, evident in that it has a smaller dynamic range than either reference method. Therefore, large errors on predictions involving highly charged microstates are to be expected.

Fig. 5.

These plots compare microscopic pK_a predictions for all combinations of our model, SimulationPlus’ pK_a predictor and ACD Lab’s pK_a GALAS. We divide our predictions into two sets: One with predicted uncertainties less than two pK_a units (orange squares) and greater uncertainties (blue circles). The shaded region indicates an agreement within 1pK_a unit. Root Mean Squared Deviation (RMSD) and R² are reported for all pairs of points with the same statistics reported in parentheses for low uncertainty points where applicable.

If we focus on predictions with uncertainty ≤ 2.0 pK_a units, our microscopic pK_a predictions are comparable to commercially available tools. Of all the microscopic pK_a predictions submitted to SAMPL6, only about half the methods included a prediction of uncertainty. Furthermore, ours was the only submission that did not report the same uncertainty value for all predictions. In comparing our results with S+ and ACD we also considered only the points with a predicted uncertainty less than or equal to two pK_a units (Figure 5 a and b). Considering this limited set, there is a significant improvement in overall performance with RMSD’s of 1.8 ± 0.2 and 2.1 ± 0.3 compared to S+ and ACD respectively. These smaller RMSD’s show that when our method predicts a low uncertainty, it agrees with S+ and ACD as well as those two methods agree with each other. Agreement with established commercial models shows promise for our algorithm and reinforces the importance of expanding our limited training set. Additionally, the ability to predict uncertainty demonstrates the reliability of this approach. While predicting uncertainty is a critical feature for model predictions, our model still needs improvement considering S+ and ACD agree on most microscopic pK_as and both are more accurate than our method for many macroscopic ionization states.

3.2. Macroscopic pK_a reported for type III predictions

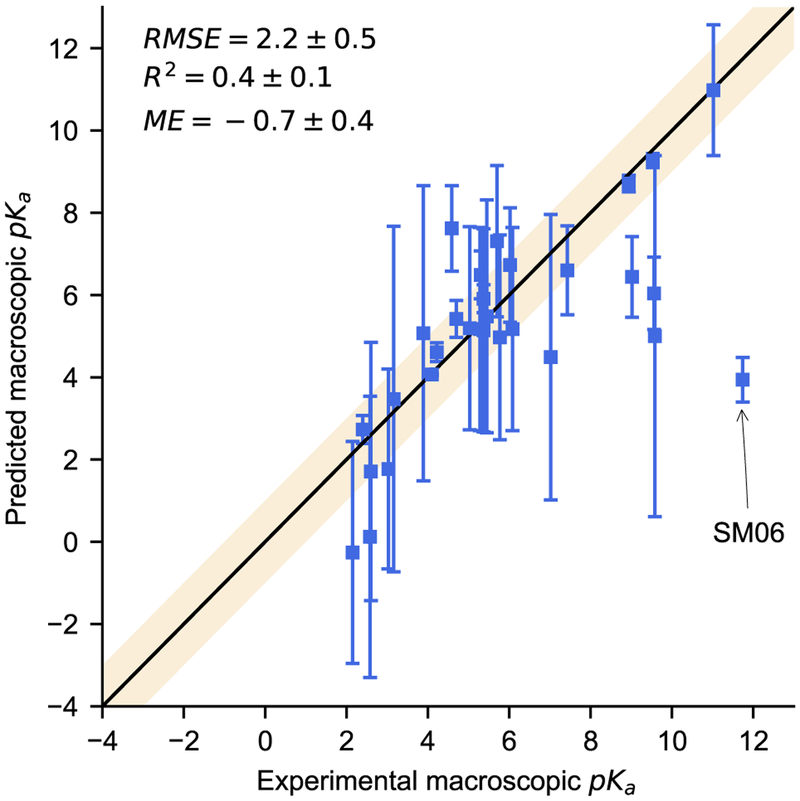
We reported macroscopic pK_a values (type III) for all molecules in SAMPL6 (Table 2). These were calculated analytically based on the microscopic pK_as determined for each molecule (Section 2.4). Using the Hungarian algorithm described in section 3.0.1, SAMPL6 organizers compared experimental results with all 34 prediction submissions using RMSE, mean error (ME), and R² correlation coefficient. Overall, we saw reasonable agreement between our predictions and experiment (Figure 6). The SAMPL6 molecules included a variety of polyprotic functional groups that are completely outside the scope of our mono- and diprotic training set. Despite this, over half (18 predictions) fall within one pK_a unit of experiment. By RMSE and ME we fall within the middle 15 predictions which cannot be easily ranked due to wide confidence intervals, determined using bootstrapping, for most participants. By correlation coefficient (R²) our method ranks very low, in the bottom five submissions, but this appears to be due to one rather extreme outlier we discuss in detail below. If we were to remove this one outlier, our ranking would improve significantly with a change in R² from 0.4±0.1 to 0.62 ± 0.09 and a shift in RMSE from 2.2±0.5 to ± 1.7 ± 0.3.

Table 2.

A list of experimental pK_as for all molecules in SAMPL6 by molecule ID and our predicted macroscopic pK_a that matches with each, based on the Hungarian matching algorithm.

SAMPL ID	Prediction	Experiment
SM01	9.27 ± 0.17	9.53 ± 0.01
SM02	5.19 ± 2.47	5.03 ± 0.01
SM03	4.49 ± 3.47	7.02 ± 0.01
SM04	6.73 ± 1.39	6.02 ± 0.01
SM05	7.62 ± 1.04	4.59 ± 0.01
SM06	1.77 ± 2.43	3.03 ±0.04
	3.94 ± 0.54	11.74 ± 0.01
SM07	5.17 ± 2.47	6.08 ± 0.01
SM08	4.61 ±0.23	4.22 ± 0.01
SM09	5.14 ± 2.47	5.37 ± 0.01
SM10	6.44 ± 0.98	9.02 ± 0.01
SM11	5.07 ± 3.59	3.89 ± 0.01
SM12	5.17 ± 2.47	5.28 ± 0.01
SM13	4.97 ± 2.49	5.77 ± 0.01
SM14	0.12 ± 3.42	2.58 ± 0.01
	6.49 ± 0.58	5.30 ± 0.01
SM15	5.42 ± 0.45	4.70 ± 0.01
	8.71 ± 0.20	8.94 ± 0.01
SM16	5.91 ± 0.34	5.37 ± 0.01
SM17	3.47 ± 4.20	3.16 ± 0.01
SM18	−0.26 ± 2.70	2.15 ± 0.02
	5.00 ± 4.39	9.58 ± 0.03
	10.98 ± 1.59	11.02 ± 0.04
SM19	6.04 ± 0.88	9.56 ± 0.02
SM20	7.31 ± 1.84	5.70 ± 0.03
SM21	4.07 ± 0.02	4.10 ± 0.01
SM22	2.73 ± 0.34	2.40 ± 0.02
	6.60 ± 1.08	7.43 ± 0.01
SM23	5.48 ± 2.83	5.45 ± 0.01
SM24	1.71 ± 3.14	2.60 ± 0.01

Fig. 6.

This plot shows our macroscopic pK_a predictions compared to experiment. The shaded region represents agreement within 1pK_a unit. The most significant outlier (SM06) is due to an acidic amide we did not identify as ionizable

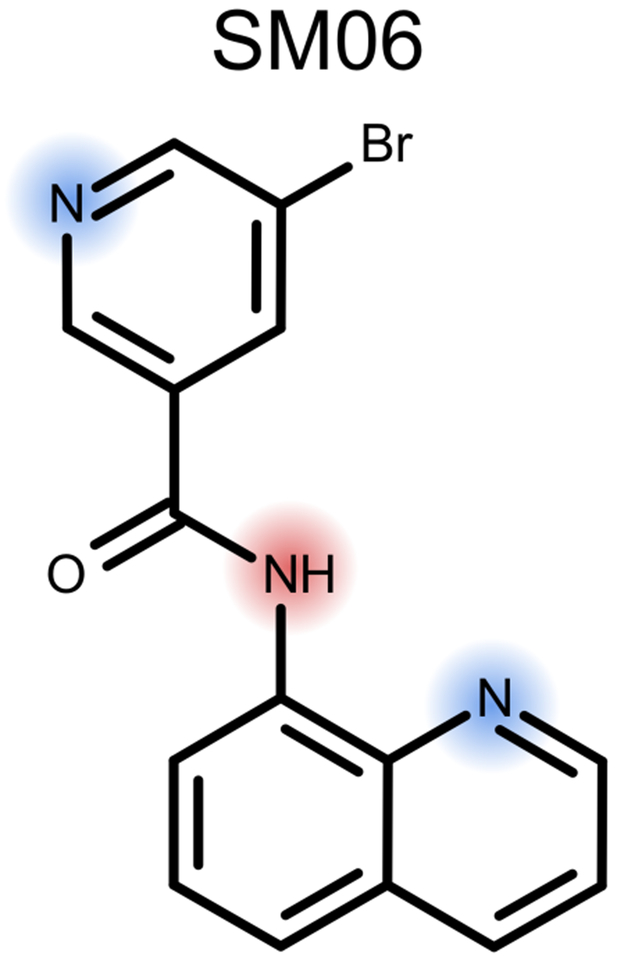
Molecule SM06 can definitely be considered an outlier, not just due to the large discrepancy between our prediction and experiment, but also due to an ionizable group we did not properly identify (Figure 7). In this case our predicted value of 3.94 ± 0.5 is matched with the experimental value 11.74 ± 0.01, as pointed out in Figure 6. This molecule contains three ionizable groups: the pyridine nitrogen base, the quinoline nitrogen base and the amide nitrogen either as a base at low pH or as an acid at high pH [50–52]. We did not train our model to treat amides as either acids or bases (Section 2.1). Our model predicted the transition from +2 to +1 to occur at a pH of 1.77 ± 2.43 and to be dominated by deprotonation of the pyridine nitrogen. It predicts +1 to +0 transition at 3.94 ± 0.54 dominated by deprotonation of the quinoline nitrogen. In order to improve our model, we consider how similar functional groups are represented in our training set and look to the literature to attempt to determine which microstate dominates at the 11.74 ± 0.01 transition. It seems probable that the deprotonation from +3 charge to +2 charge would occur well below pH2.0, outside the experimental range, and is most likely dominated by the deprotonation of a charged and doubly protonated amide. The next transitions are less immediately obvious, so we look to our training set which contains meta-substituted bromo-pyridines and carboxamide pyridines, both with pK_as in the low 3s. It also includes several monoprotic quinoline derivatives with pK_as from 4.8 − 5.5. One explanation for this large error could be that the carbonyl of the amide group could form an internal hydrogen bond stabilizing the protonated form of the quinoline and increasing its pK_a. While internal hydrogen-bonding may affect some of the features we already include, our model does not directly consider it. Adding a more explicit descriptor to capture such affects may be something we should explore as we improve our model. A more likely explanation for the error is that it is due to the amide nitrogen our model misses. Our logic for not including amides as ionizable sites in our model was because they often have a basic pK_a value less than 2.0 and an acidic pK_a value greater than 14.0. However, in this highly conjugated system, that amide nitrogen could be an important contributor to the pK_a of 11.74 ± 0.01. An analogous system to consider is N-(2-pyrimidyl)benzamide, with its second ionization measured at 11.2 [53], demonstrating that acidic amide nitrogens can have pK_a values in the appropriate range. Improving our model will likely involve conducting a more thorough investigation of which groups should be considered ionizable.

Fig. 7.

SM06 provided feedback on our ability to accurate identify ionizable groups as our method only finds two (blue), notably missing the acid amide (red)

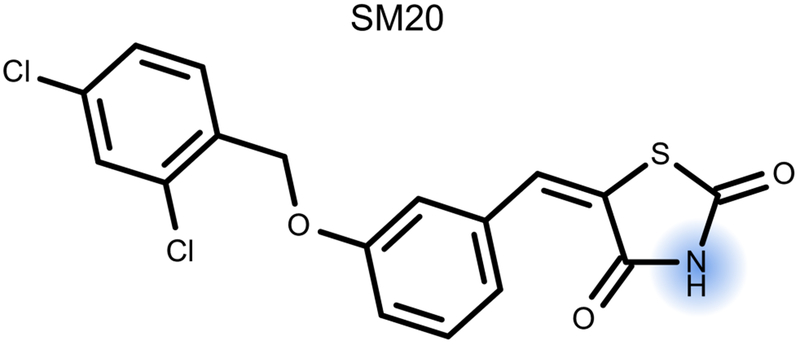
We knew going into the SAMPL6 challenge that complex polyprotic molecules would fall outside the domain of applicability for our model, however, other functional groups appear to also be poorly represented. For example, molecule SM20 has only one ionizable group, the acidic imide group (Figure 8). While our training set includes some similar functional groups, there was not a wide diversity. Specifically, none in the training set had a sulfur one bond away. This is also evident in our prediction 7.31 ± 1.84 where the large uncertainty reflects the lack of similarity between this ionizable group and our training set. Expanding our training data to include polyprotic molecules was already in our plans, but considering more complex mono- or diprotic molecules with overlapping micro-constants could also improve our model.

Fig. 8.

Our prediction for SM20 was still rather inaccurate, despite it being monoprotic (blue). This is likely due to a lack of representation of imide groups in similar environments in our training set.

An important goal in building our model was to be able to predict uncertainties which actually provide some guidance as to expected accuracy and limitations in the training data. Not all commercial products make this a priority; for example, SimulationPlus did not provide uncertainty estimates for any of their predictions. One obvious feature in our data is that the predicted uncertainties are all very large, greater than 1 pK_a unit for 19 of the matched predictions. Most of the molecules with large uncertainties are polyprotic and include functional groups outside the domain of our training set. Therefore it seems these large uncertainties are a good sign as they seem to correlate with actual error.

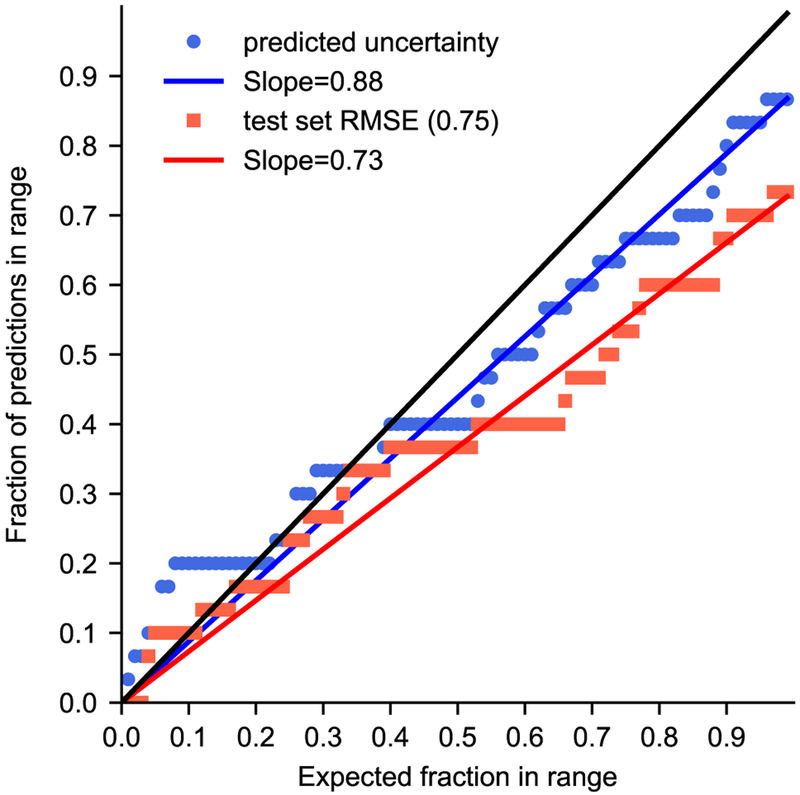
Previous SAMPL challenges have included quantile-quantile plots (QQ plots) which provide a more quantitative assessment of a participants reported model uncertainties [7,54]. QQ plots are based on the concept that actual errors should be drawn from a normal distribution, and well-predicted uncertainties should be able to predict the frequency of deviations of a given size. Thus in QQ plots, y-axis has the fraction of predicted minus experimental values that fall within a given number of uncertainties and the x-axis shows the fraction of a normal distribution within that many standard deviations. The closer the predicted uncertainties compare to a normal distribution the closer they will come to an x = y line. Thus, the slope of a regression is also often used as a part of the evaluation. We compare two possibilities for model uncertainty in our QQ plot. The first uncertainty approach we consider uses the predicted uncertainties from our Gaussian process model (blue circles in Figure 9). Another common way to report uncertainty is to assume it is the same for all predictions based on past performance of the approach. For the second set of data, we assumed the uncertainty for each predicted pK_a was equal to the RMSE for our internal test set, 0.75 (red squares in Figure 9). A method producing accurate predicted uncertainties should lead to a diagonal line on the resulting plot, with slope of 1; in this case, we find that the uncertainty model using predicted uncertainties from the Gaussian process (slope=0.87) outperforms the model with a fixed uncertainty (slope=0.73). This is promising evidence that our model is capable of predicting how its reliability varies with the chemistry being considered, rather than just its overall typical performance.

Fig. 9.

This QQ plot provides an assessment for predicted uncertainties compared to a normal distribution. Our predicted uncertainties (blue circles) out perform a fixed error of 0.75 taken from our test set RMSE (red squares), as evident by the proximity of the point to the x = y black line and a slope approaching one.

4. Conclusions

Our Gaussian process model showed promising results in the SAMPL6 challenge, but was limited by the scope of our training set. The chemical space represented in our training set was limited to mono- and diprotic (Section 2.5). Despite this limitation, we still saw fairly good agreement between our predicted macroscopic pK_as and the experimentally measured values and performed competitively compared to other participants. We rank in the top ten by RMSE (1.7 ± 0.3) after removing a single obvious outlier (Figure 6). This outlier, with an acidic amide group, highlighted a potential hole in our limited definition of ionizable groups. Improving our model will require adding groups which are often ionized outside the aqueous pK_a range, but which can be perturbed to ionize within that range. Our performance in this blind challenge is evidence that a single model trained on physically and chemically relevant features can be competitive with established methods which rely on specialized models for individual functional groups.

The other important step in improving our model will be to augment our training set with additional polyprotic molecules. Currently, the likelihood function in Scikit-learn requires one feature vector for each experimental result. Using this function, we would require a large dataset of experimental microscopic pK_as in or der to include polyprotic molecules. Generally speaking, it is easier to acquire experimental macroscopic pK_a data. Thus, a preferred approach would be to define a new likelihood function which would take advantage of the analytical relationship between microscopic and macroscopic pK_as and evaluate a set of microscopic predictions with one macroscopic value. We are confident that with this expansion we will have a general model which could predict pK_a for molecules with any combination of ionizable groups.

Evaluating microscopic pK_a predictions was limited by the availability of experimental results. For the seven molecules with NMR supported microscopic pK_as, our predicted values agreed with experiment within predicted uncertainty. This was a rather limited set of the possible microscopic transitions so we also compared our performance to top-performing commercial products. For microscopic predictions with low predicted uncertainties, our model performs well compared to SimulationPlus and ACD Labs commercial products (Figure 5). While these results are promising, this portion is a comparison of three predictive models and has not been experimentally verified. A valuable addition to future SAMPL challenges including pK_a predictions would be to expand experimental measurements to include more microscopic results when available.

We believe predictions are only valuable when they include an accurate assessment of uncertainty, otherwise downstream users have no guidance as to the reliability of such predictions and thus no confidence as to when they can usefully be used and when they should be ignored. These uncertainties are even more valuable if they are determined based on the input molecule, capturing when reliability varies with chemistry. Unfortunately, ten out of 34 type III submissions in SAMPL6 provided no uncertainties with their predictions. Perhaps requiring such predictions for every submission would improve future challenges and drive progress in this respect. From the beginning, we considered providing an uncertainty evaluation for each prediction an important component of our model. Thus, our ability to determine accurate uncertainty predictions based on input chemistry shows our model’s potential to be a successful predictive method. Previous SAMPL challenges have highlighted the importance and difficulty in accurately assessing model uncertainty for hydration free energies [54] and distribution coefficients [7]. The large error bars for ionizable sites we consider outside our domain of applicability provide evidence our uncertainty estimates are working as desired. QQ plots also support the conclusion that our model is capable of predicting its own uncertainty (Figure 9).

SAMPL6 was an opportunity to test our Gaussian process model on an external test set and our first completely blind set of predictions. Our new Gaussian process model performed semi-competitively, especially considering its limited training set compared to more established methods which participated. We look forward to incorporating important lessons from this challenge, particularly, expanding our definition of an ionizable group and improving our likelihood function to include polyprotic molecules in our next training set. Overall, SAMPL challenges provide an important service to the community allowing participants to test their predictive models in a blind manner.