Biomolecular Solvation Structure Revealed by Molecular Dynamics Simulations

Abstract

To compare ordered water positions from experiment with those from molecular dynamics (MD) simulations, a number of MD models of water structure in crystalline endoglucanase were calculated. The starting MD model was derived from a joint X-ray and neutron diffraction crystal structure, enabling the use of experimentally assigned protonation states. Simulations were performed in the crystalline state, using a periodic 2×2×2 supercell with explicit solvent. Water X-ray and neutron scattering density maps were computed from MD trajectories using standard macromolecular crystallography methods. In one set of simulations, harmonic restraints were applied to bias the protein structure toward the crystal structure. For these simulations, the recall of crystallographic waters using strong peaks in the MD water electron density was very good, and there also was substantial visual agreement between the boomerang-like wings of the neutron scattering density and the crystalline water hydrogen positions. An unrestrained simulation also was performed. For this simulation, the recall of crystallographic waters was much lower. For both restrained and unrestrained simulations, the strongest water density peaks were associated with crystallographic waters. The results demonstrate that it is now possible to recover crystallographic water structure using restrained MD simulations, but that it is not yet reasonable to expect unrestrained MD simulations to do the same. Further development and generalization of MD water models for force field development, macromolecular crystallography, and medicinal chemistry applications is now warranted. In particular, the combination of room-temperature crystallography, neutron diffraction, and crystalline MD simulations promises to substantially advance modeling of biomolecular solvation.

Graphical Abstract

INTRODUCTION

Solvent structure is very important in biomolecular simulations for medicinal chemistry applications. In protein crystallography, ordered water molecules give rise to regions of elevated solvent density. In these regions, the interactions between a solvent water molecule and the biomolecular environment are sufficiently strong to overcome the translational and rotational entropies favoring diffusion. Computational methods have been developed for modeling water to approximate the energetic contributions of such interactions^1-3. For example, ligand-binding free energies calculated from simulations are especially sensitive to the details of water structure and interactions in the immediate neighborhood of the binding site^4-5. The accuracy of these calculations depends critically on the quality of the water model. Although not a direct measure of these interactions, the ability of an MD simulation to recover experimentally determined ordered waters is a useful surrogate measure of water model quality in the biomolecular environment.

An early MD simulation of a hydrated periodic unit cell of crystalline pancreatic trypsin inhibitor marked an important step in modeling water structure⁶; however, only 19% (9 of 47) of the crystallographic waters were within 1 Å of a water density peak in the MD model. Although important studies of MD predictions of water structure followed (see review by Pettitt, Makarov, and Andrews⁷), few studies since have been carried out to validate detailed water structure predicted from MD simulations using strict comparisons to crystallography data. Higo and Nakasako⁸ compared a calculation of solution MD water density to a crystal structure of lysozyme; using a density threshold of 0.06 molecules/Å to reject peaks, approximately 60% of waters were within 1.4 Å of a MD water density peak (estimated from Table 1 and Fig. 4 in Higo and Nakasako⁸). Altan et al.⁹ used a crystalline MD approach to model water structure in Yb³⁺-substituted mannose-binding protein (MBP); at the weakest density threshold of 0.6 e⁻/ų (roughly equivalent to the above density of 0.06 molecules/ų, assuming 10 e⁻/molecule), 70% of crystallographic waters were within 1.4 Å of a MD water density peak (from Fig. 4 in Altan et al.⁹).

Table I.

Recall of crystallographic waters for the MD water models. Units are percentages (%).

	Recall of top 100 waters (all 151 waters)
	0.5 Åe	1.0 Åf	1.4 Åg
NaCl (R)a	80 (66)	94 (86)	98 (93)
Tris-Cl (R)b	77 (64)	95 (85)	98 (93)
NaCl (U,F)C	25 (21)	50 (46)	62 (56)
NaCl (U,L)d	18 (15)	42 (36)	51 (42)

^aLast 10 ns section of the restrained NaCl simulation.

^bLast 10 ns section of the restrained Tris-Cl simulation.

^cFirst 100 ns section of the unrestrained NaCl solvent MD simulation.

^dLast 100 ns section of the unrestrained NaCl solvent MD simulation.

^ePercentage of waters that have an MD peak within 0.5 Å.

^fPercentage of waters that have an MD peak within 1.0 Å.

^gPercentage of waters that have an MD peak within 1.4 Å.

Figure 4.

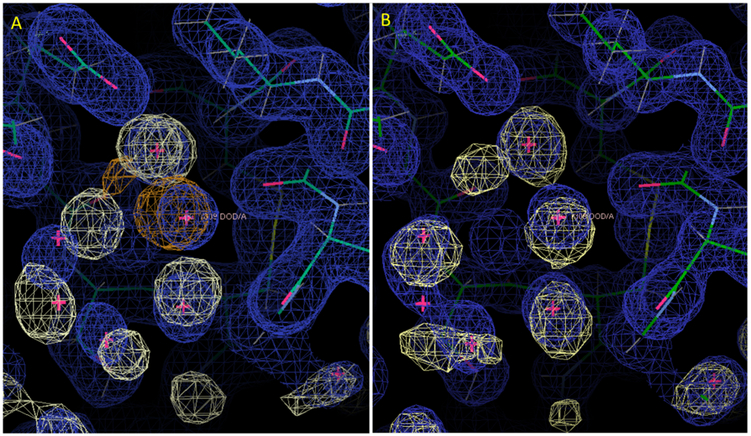
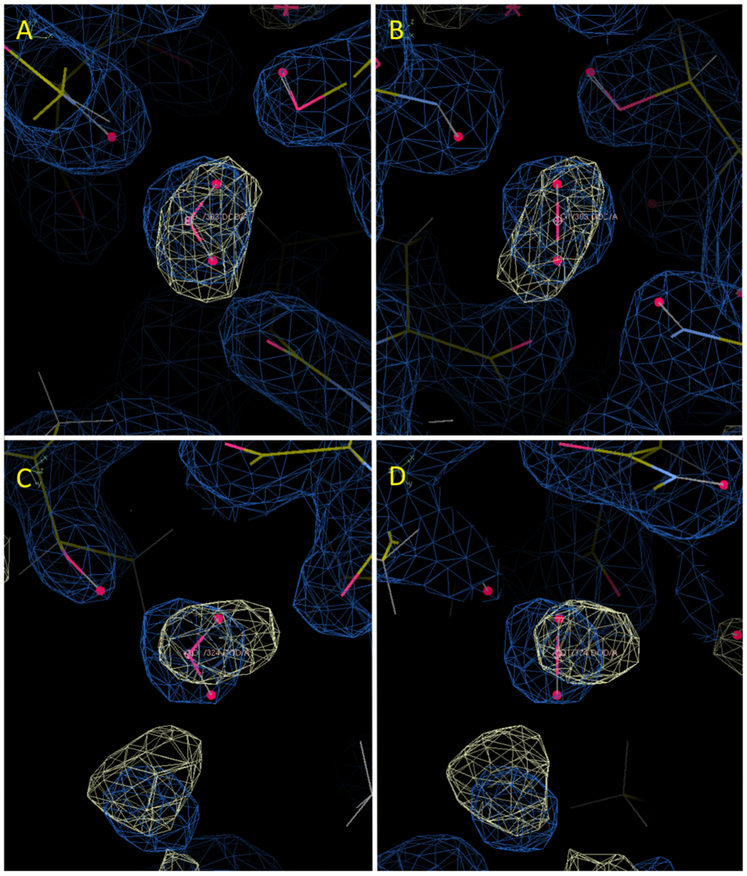
Comparison of alternative solvent models in the neighborhood of water 309. (A) Restrained NaCl model. (B) Restrained Tris-Cl model in a similar orientation. Rendering of the MD water and X-ray 2Fo-Fc maps are as in Fig. 2. Panel (A) also includes the Na+ density, rendered in orange at a level of 8-sigma. In the NaCl model (A), the position of water 309 is occupied by a Na+ ion, and there are substantial differences between the MD and crystallographic water structure nearby. In the Tris-Cl model (B), the MD water structure overlaps water 309, and the neighboring water structure is more similar between the MD and the crystallographic water structure. The panels were created using Coot³⁹.

Here we present models of water structure for endoglucanase (EG) from Phanerochaete chrysosporium, obtained using a crystalline MD approach that was designed specifically for comparisons to X-ray diffraction data¹⁰. The choice of EG as a model system addressed several issues with the related MBP study: the MBP model was derived from X-ray diffraction data, protonation states were assigned without experimental data, and the structure was obtained from crystals at 110 K rather than room temperature. In contrast, the EG crystal structure (Protein Data Bank¹¹ entry 3X2P) was obtained using both X-ray and neutron diffraction data¹². The use of neutron diffraction data enables improved modeling of water structure¹³ and the use of experimentally assigned protonation states¹⁴ (see also reviews^15-16). In addition, the EG crystal structure was obtained at room temperature. Temperature differences can influence the water structure in protein crystals, as observed using neutron diffraction¹³.

We found that MD simulations of crystalline EG with protein and ligand non-hydrogen atom restraints had very good recall of crystallographic waters, with substantial agreement between the water orientations from the neutron scattering density and the MD model. For both restrained and unrestrained simulations, the strongest water density peaks were associated with crystallographic waters. However, the unrestrained MD model had poor recall of crystallographic waters. It is therefore now possible to recover crystallographic water structure using restrained MD simulations, but it is not yet reasonable to expect unrestrained MD simulations to do the same. The amount of effort and computational resources required make it possible to apply the present approach to many other systems. Water structure appears to provide a sensitive test of MD simulations, with potential to advance force field development. Together, the combination of room-temperature crystallography, neutron diffraction, and crystalline MD simulations can improve understanding of biomolecular solvation.

METHODS

Model systems.

We prepared a modified model of the endoglucanase-cellopentaose complex from Phanerochaete chrysosporium¹². To build the model, Protein Data Bank¹¹ entry 3X2P was re-refined using the published 1.5 Å neutron and 1.0 Å X-ray diffraction data. Joint X-ray and neutron refinement was performed using phenix.refine¹⁷ version 1.14 3211. The structure was modeled using either the native form of Asn92 or the imidic acid form that was used in the published structure¹². We found insufficient crystallographic evidence to support the imidic acid form and therefore used the native form for the simulations. Protonation states for protein exchangeable H/D atoms were modeled using the neutron scattering density, considering the chemical environment. In some cases (Asp-Arg and Glu-Arg salt bridges; His residues), the model was modified with respect to Nakamura et al.¹². H/D atoms were added to waters as appropriate considering evidence from the neutron scattering density and H-bond interactions with the local environment.

Two alternative solvent models were used: water with elemental Na+ and Cl- ions (NaCl) and water with 2-Amino-2-(hydroxymethyl)propane-1,3-diol (Tris+) and Cl- ions (Tris-Cl). The Tris-Cl solvent model was developed to address the issue of ordered Na+ potentially interfering with water structure in the NaCl simulation (Results). In the NaCl model, the system was solvated with water, Na+ counterions were added to neutralize, additional Na+ and Cl- ions were added in a 1:1 ratio to match the 50 mM Tris-Cl concentration of the mother liquor. In the Tris-Cl model, the Na+ ions were replaced by explicit Tris+ ions.

The protonation state of HIS residues was determined using the neutron diffraction data (see above). On this basis, the imidazole moiety of His64 was modeled in the uncharged delta-tautomer (residue name HID), His107 and His130 were modeled in the charged tautomer (residue name HIP), and His112 was modeled in the uncharged epsilon-tautomer (residue name HIE). Deuterium atoms were modeled into the crystal structure at exchangeable hydrogen positions using an alternative conformation syntax; these were stripped from the structure, so that only the hydrogens remained. Alternative conformations of side chains were trimmed to just the “A” conformation.

The crystalline models were prepared by using the P2₁2₁2₁ space group to expand the asymmetric unit of the protein-ligand complex to the P1 unit cell and creating a 2×2×2 supercell. GROMACS¹⁸ version 5.1.4 tools were then used to prepare MD models. The protein structures were parameterized using amber99sb-ildn¹⁹, water was modeled using TIP3P²⁰, and the Tris+ was modeled using GAFF parameters²¹. The ligand was added using GLYCAM²² parameters, with appropriate edits to the amber99sb-ildn parameter files. A right rectangular simulation box was defined with dimensions a = 92.956 Å, b = 117.270 Å, c = 129.488 Å – double the unit cell dimensions.

At this point the building of the NaCl and Tris-Cl models diverged. For the NaCl model, the void volume of the crystalline system was filled with TIP3P waters (gmx solvate). To create a salt concentration reflecting the 50 mM Tris-Cl in the mother liquor, the number of solvent atoms associated with the void volume was estimated as N=62,865 using a trial solvation. Based on this number, 40 waters were replaced by Na+ ions (gmx genion). To account for the Cl- associated with the Tris+, 40 waters were replaced by Cl- ions. Then, to neutralize the system, 96 additional waters were replaced by Na+ ions, to bring the total to 136 (gmx genion).

For the Tris-Cl model, the 136 Na+ ions were replaced by explicit Tris+ ions. First, 136 Tris+ ions were added to the void volume (gmx insert-molecules). The remainder of the void was filled with TIP3P waters (gmx solvate). Then, 40 waters were replaced by Cl- ions (gmx genion).

The number of waters in each of the models was determined as the result of applying a procedure for achieving near atmospheric pressure in crystalline NVT simulations²³. Iterative application of energy minimization, NVT simulation, and solvation was performed until a mean pressure in the range (−100,+100) bar was achieved. For the NaCl model, the number of waters was increased by 2,200 to 23,258. For the Tris-Cl model, the number of waters was increased by 2,300 to 22,568.

The final compositions of the systems used for production simulations are as follows. The NaCl model had 32 copies of the protein+ligand complex; 23,258 TIP3P waters; 136 Na+ ions; and 40 Cl- ions. A total of 150,910 atoms were distributed as follows: 77,504 protein atoms; 3,456 ligand atoms; 69,774 water atoms; and 176 ions. The Tris-Cl model had 32 copies of the protein+ligand complex; 136 Tris+ ions; 22,568 waters; and 40 Cl- ions. A total of 151,424 atoms distributed as follows: 77,504 protein atoms; 3,456 ligand atoms; 2,720 Tris atoms; 67,704 water atoms; and 40 chloride ions. The NaCl model is illustrated in Fig. 1.

Figure 1.

Model of a 2×2×2 periodic supercell of crystalline EG, using the NaCl solvent model (Methods). The proteins are rendered using cartoon ribbons of various colors. The cellopentaose ligand is rendered using magenta sticks. Waters are rendered using sticks.

MD simulations.

Simulations were performed in GROMACS version 5.1.4 (NaCl model) and GROMACS version 2018 (Tris-Cl model) using the leap-frog integration method with a 2 fs time step. Fourth order holonomic LINCS constraints were used for all bonds. The Verlet neighbor list scheme was used with a cutoff of 10 Å for both electrostatics and Van der Waals interactions. Long-range electrostatics were computed using the Particle-Mesh Ewald method with cubic interpolation and a 1.2 Å grid. The modified Berendsen thermostat was used at 300 K, using velocity rescaling with a 0.1 ps time constant; the protein-ligand complex was treated as a separate temperature group from the rest of the atoms. Periodic boundary conditions were used.

For each of the systems, NVT simulations were performed in which the protein-ligand complex was harmonically restrained. The protein non-hydrogen atoms and all ligand atoms were restrained to their positions in the crystal structure itself (not the energy-minimized crystal structure) using 209.2 kJ / mol nm² spring constants, corresponding to 0.5 kcal / mol Ų. This moderate restraint addressed our concern that a stronger restraint of 1,000 kJ / mol nm² (the GROMACS default) would lead to artificial ordering at the solvent interface and a less realistic water structure²⁴. Simulations were performed for both the NaCl and Tris-Cl models. The duration for restrained simulations was 100 ns.

For the NaCl model, an unrestrained NVT simulation also was performed, without a harmonic restraint. An initial 100 ns equilibration was performed in which the protein non-hydrogen atoms and all ligand atoms were restrained to their positions in the energy minimized crystal structure using 1,000 kJ / mol nm² spring constants. This restrained equilibration was then followed by an unrestrained continuation. The continuation was performed by using the 100 ns checkpoint as a starting condition and removing the harmonic restraints. The duration of the unrestrained simulation was 1 microsecond.

Mean structure factors.

Mean structure factors were calculated for 10 ns sections of the restrained and 100 ns sections of the unrestrained MD trajectories. Results presented here correspond to the last 10 ns of the restrained and both the first and last 100 ns of the unrestrained simulations. X-ray structure factors were calculated using methods previously described¹⁰. To calculate mean structure factors for a section of a trajectory, it was divided into O(100) chunks, which were processed in parallel using a cluster of Intel(R) Xeon(R) CPU E5-2695 v4 @ 2.10GHz nodes. Prior to performing the calculation, each snapshot of the trajectory was aligned to the crystal structure using the GROMACS .tpr structure file. To do this, the .tpr file was converted to a .pdb file using gmx editconf. The .pdb file was processed to ensure the coordinates reflected the connectivity of the molecules (gmx trjconv –pbc mol). The alignment was performed using the processed .pdb file as the reference structure (gmx trjconv -fit translation –pbc nojump). Aligned structures were written as multimodel .pdb files prior to processing. These .pdb files were processed using a custom CCTBX²⁵ script to calculate the mean structure factor to 1.5 Å resolution. In the script, the complex structure factor, f_n(hkl), for each sample n is calculated at Miller indices hkl, and the mean value is calculated and output in a .mtz file. To enable comparisons to the crystal structure, the single unit cell dimensions and P2₁2₁2¹ space group were used in the .pdb CRYST1 record. Averages for longer sections of the trajectory were accumulated from sums of the smaller chunks. For the present study, a modified method was developed to calculate neutron structure factors, using the scattering tables available within CCTBX.

For the restrained simulations, the mean structure factor already was aligned with the crystal structure. For the unrestrained simulations, an alignment of the crystal structure to the simulated electron density was performed. To perform the alignment, CCP4²⁶ molrep was used, with the crystal structure as the input .pdb and the mean structure factor as the input .mtz, using both the amplitudes and phases. Because waters were stripped in the output from molrep, the crystal structure was subsequently aligned to the output molrep.pdb file, using phenix.superpose_pdbs¹⁷, yielding an aligned structure including crystallographic waters.

Quantitative comparison of MD water peaks to crystallographic waters.

Peaks in the MD water electron density were used for comparisons to the crystallographic waters. Electron density maps were computed from the mean structure factors usingphenix.mtz2map¹⁷, using the crystal structure as a reference frame. Peaks with heights sufficiently smaller than a multiple of the standard deviation of the electron density (sigma) were eliminated from comparisons. (The bulk water structure was visible at a contour level of about 0.5-sigma for the restrained simulations and about 1-sigma for the unrestrained simulations.) For the restrained simulations, peaks in excess of 3-sigma were identified using CCP4 peakmax and the positions were output as a .pdb file. For the unrestrained simulations a 2-sigma threshold was used for peak finding instead: whereas a 3-sigma threshold produced fewer than 151 waters, a 2-sigma threshold yielded a number of peaks more comparable to the restrained simulations, and yielded water envelopes similar to the restrained simulation density at 3-sigma in size and shape. The residue numbers of the 151 waters in the crystal structure were assigned in rough order of confidence. We used both the top 100 waters (residue numbers 301-400) and all 151 waters for evaluations.

A recall statistic was defined as the fraction of crystallographic waters that have a nearby peak in the simulated water density. For the recall calculation, the positions of water density peaks were compared to positions of crystallographic waters in the asymmetric unit (the protein asymmetric unit was entirely contained within the P1 water density map). A custom CCTBX python script was written to identify the peak nearest to each crystallographic water, producing a list of crystallographic waters, the matching peak, and the distance between the two. The recall was computed as the fraction of rows in the list having a distance less than a specified cutoff (0.5 Å, 1.0 Å, or 1.4 Å).

A precision statistic was defined as the fraction of peaks in the simulated water density that have a nearby crystallographic water. For the precision calculation, the water density peaks were compared to positions of crystallographic waters in the P1 unit cell. Similar to the recall calculation, a custom CCTBX python script was written to identify the crystallographic water nearest to each peak, producing a list of peaks, the matching crystallographic water from the P1 unit cell, and the distance between the two. As for the recall, the precision was computed as the fraction of rows in the list having a distance less than a specified cutoff (0.5 Å, 1.0 Å, or 1.4 Å).

The dependence of the recall and precision on the water density peak threshold was calculated first by computing the statistics using the base value mentioned above, and then by calculating the statistics for incrementally higher thresholds, up to the maximum peak height value.

RESULTS

Crystalline MD simulations.

MD simulations of crystalline endoglucanase from Phanerochaete chrysosporium were performed to determine models of water structure (Methods). The starting MD model (Fig. 1) was derived from a re-refined crystal structure (Protein Data Bank¹¹ entry 3X2P). Two alternative solvent models were used: water with elemental Na+ and Cl- ions (NaCl) and water with 2-Amino-2-(hydroxymethyl)propane-1,3-diol (Tris+) and Cl- ions (Tris-Cl). The Tris-Cl solvent model was developed to address the issue of ordered Na+ potentially interfering with water structure in the restrained NaCl simulation (see below). For each of the systems, NVT simulations were performed in which the protein-ligand complex was harmonically restrained. The duration for restrained simulations was 100 ns. For the NaCl model, an unrestrained NVT simulation also was performed, without a harmonic restraint. The duration of the unrestrained simulation was 1 microsecond.

X-ray scattering density and water positions.

Simulated electron density maps were computed from the MD trajectories (Methods). Water positions were identified using strong peaks in the simulated water density. For the restrained simulations, peaks were identified using a threshold of 3-sigma. The number of peaks found in the restrained MD water density computed from the last 10 ns section was: 963 peaks for the NaCl model, and 952 peaks for the Tris-Cl model. For the unrestrained NaCl model, peaks were identified using a threshold of 2-sigma (Methods). There were 504 peaks in the density computed from the first 100 ns section, and 331 peaks in the density computed from the last 100 ns section of the simulation. The density varied more sharply for the restrained models than for the unrestrained model. For the restrained NaCl model, sigma = 0.25 e₋/ų and mean = 0.56 e₋/ų; for the restrained Tris-Cl model, sigma = 0.24 e₋/ų and mean = 0.48 e₋/ų; for the unrestrained NaCl model, sigma = 0.15 e₋/ų and mean = 0.17 e₋/ų. A decreased sigma of the unrestrained model compared to the restrained models is consistent with the increased atomic motions of the protein and ligand, which are expected to disturb the solvent structure.

Restrained NaCl model.

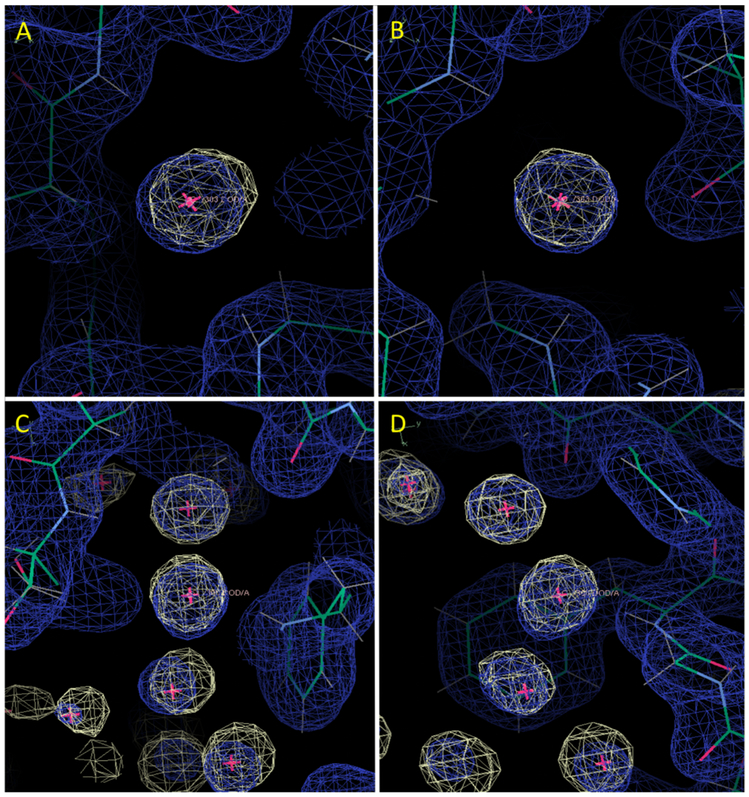
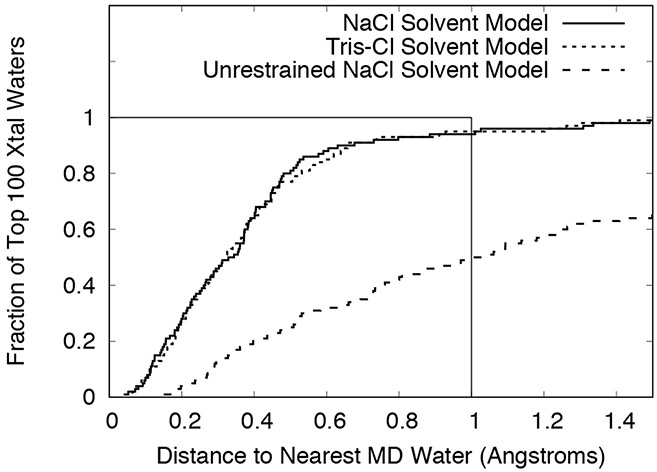
Most of the top 100 water oxygens were recovered by the restrained NaCl model simulation. For example, buried crystallographic water 303 is contained within a 3-sigma envelope of the MD water density (Fig. 2A,B). Extended networks of solvation also were reproduced, as in the neighborhood of water 305 (Fig. 2C,D). Fig. 3 (solid line) shows the cumulative distribution of distances from the top 100 crystallographic waters to the nearest MD water peak. A summary of the statistics is in Table I. Of the top 100 waters, 80% had a MD peak within 0.5 Å, 94% had a MD peak within 1 Å, and 98% had a MD peak within 1.4 Å. The waters with peaks farther than 1 Å away were: 356 (1.01 Å), 384 (1.03 Å), 387 (1.31 Å), 343 (1.34 Å), 333 (1.49 Å), and 309 (2.24 Å). Of these, water 309 is the most interesting case: it was replaced by a tightly bound Na+ ion (Fig. 4A). Water 356 is nearby and is also disturbed by the Na+ density at 309. Waters 333 and 384 are near a different peak in the Na+ density, which appears to have disturbed the water structure in the MD. Water 343 is in a region where there is an extensive water network in the MD that is largely lacking in the crystal structure. Water 387 is a discrepancy that is not obviously related to other differences between the simulation and the crystal structure.

Figure 2.

Comparison of restrained NaCl model MD water electron density to crystallographic water positions and the X-ray 2Fo-Fc map. (A) View centered on buried water 303, which is isolated from other waters. (B) The same as (A), rotated roughly 90 degrees about the y-axis (vertical). (C) View centered on water 305, part of a connected water network. (D) The same as (C), rotated roughly 90 degrees about the y-axis. The MD water density is rendered using a yellow wireframe at a level of 3-sigma. The 2Fo-Fc map is sigma-normalized and is shifted to have a mean of zero. It is rendered using a blue wireframe at a level of 1-sigma. The crystal water positions are indicated by magenta crosses. The panels were created using Coot³⁹.

Figure 3.

Cumulative distribution of distances between crystallographic waters and peaks in the MD water electron density map. The results were computed using the top 100 crystallographic waters, with residue numbers 301-400. Results for the restrained NaCl model are indicated using a solid line, results for the restrained Tris-Cl model are indicated using a dotted line, and results for the unrestrained NaCl model are indicated using a dashed line. The boxed region bounded by 1 Å on the x-axis and a fraction of 1 on the y-axis is indicated using a thin solid line.

Restrained Tris-Cl model.

Because much of the disrupted water structure in the restrained NaCl model appeared to be associated with Na+ density, simulations also were performed on a model in which the Na+ ions were replaced by Tris+ ions (Model systems). The overall recovery of crystallographic waters for the restrained Tris-Cl model was similar to the NaCl model (Fig. 3, dotted line; Table I): 77% of the top 100 crystallographic waters had a MD peak within 0.5 Å, 95% had a peak within 1 Å, and 98% had a peak within 1.4 Å. The waters with peaks farther than 1 Å away were: 343 (1.20 Å), 385 (1.26 Å), 387 (1.30 Å), 398 (1.41 Å), and 333 (1.51 Å). An examination of these cases indicates that substituting Tris+ for Na+ did address some of the water structure issues, but did not lead to an improved overall recall of crystallographic waters. Importantly, water 309, which corresponds to Na+ density in the NaCl model, does have overlapping water density for the Tris-Cl model (Fig. 4B). The nearby water 359 also has overlapping density. However, water 333 is still missing in the MD, and water 384 is only marginally within the 1 Å distance threshold (0.93 Å). Like in the NaCl model, the water network is extensively different in the neighborhood of 343. Water 385 is not visible at 1-sigma in the experimental 2Fo-Fc map and is in a region where the MD otherwise agrees well with the crystal structure; it is possible that this water was incorrectly modeled using the diffraction data alone. Water 398 also is not visible, but is in a region where the MD water structure does not correspond to ordered crystallographic waters. Like for the NaCl model, water 387 is a discrepancy that is not obviously related to other differences between the simulation and the crystal structure.

Unrestrained NaCl model.

Compared to the restrained simulation, far fewer of the top 100 crystal structure water oxygens were near MD water peaks in the unrestrained NaCl model. The agreement was highest in the first 100 ns section following the relaxation of restraints (Fig. 3, dashed line; Table I), where 25% of crystalline waters had a MD peak within 0.5 Å, 50% had a MD peak within 1 Å, and 62% had a MD peak within 1.4 Å. The agreement is poorer in the last 100 ns section (Table I only), where 18% had a MD peak within 0.5 Å, 42% had a MD peak within 1 Å, and 51% had a MD peak within 1.4 Å. This suggests that slow protein motions away from the crystal structure result in decreasing agreement with experimental water structure.

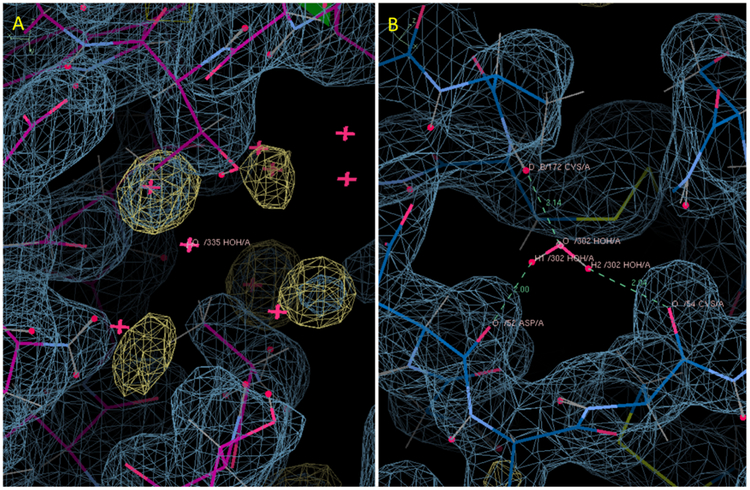
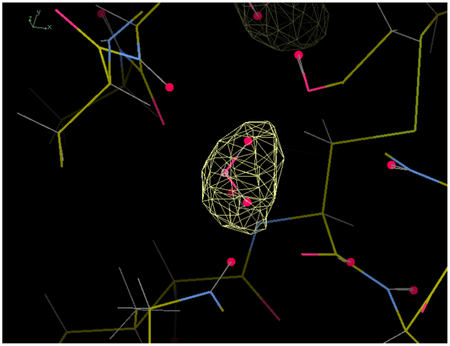
In cases where the crystalline water was not recovered by the unrestrained MD, the protein structure was not grossly inconsistent with the simulated protein electron density. A typical case is illustrated in Fig. 5A. Solvent-accessible water 335 has no nearby water MD density at 2-sigma, and two connected waters also are not recovered. The surrounding crystalline protein non-hydrogen atoms are mostly within the 1-sigma envelope of the protein MD density. Fig. 5B shows the less typical case of buried water 302, which has no nearby water MD density at 2-sigma. In this case not only is the protein MD density similar to the crystal structure, but also the water is hydrogen bonded to three sites on the surrounding protein. The lack of obvious clashes between the protein electron density and the crystalline water positions suggests that water structure is sensitive to relatively small changes in the protein environment (See Discussion).

Figure 5.

Two types of water structure discrepancy for the unrestrained MD model. (A) Solvent-accessible crystallographic water 335. MD water density is missing and some nearby waters deviate from the MD water density. (B) Buried water 302. MD water density is missing. Favorable H-bond interactions with the protein are indicated using dashed lines. In both panels, water MD density is shown using a yellow wireframe at a level of 2-sigma, and total MD density including the protein is shown using a cyan wireframe at a level of 1-sigma. The panels were created using Coot³⁹.

Recall of all 151 crystallographic waters.

Recall statistics were lower for all 151 crystallographic waters than for the top 100 crystallographic waters (Table I, values in parentheses). For the restrained NaCl model (last 10 ns section), 66% had a MD peak within 0.5 Å, 86% had a MD peak within 1 Å, and 93% had a MD peak within 1.4 Å. For the restrained Tris-Cl model (last 10 ns section), 64% had a MD peak within 0.5 Å, 85% had a MD peak within 1 Å, and 93% had a MD peak within 1.4 Å. For the unrestrained NaCl model (first 100 ns section), 21% had a MD peak within 0.5 Å, 46% had a MD peak within 1 Å, and 56% had a MD peak within 1.4 Å. It is possible that the MD model was not as accurate in the neighborhood of the last 51 waters, but it is also possible that there are more errors among the last 51 crystallographic waters than among the first 100 (See Discussion).

Precision of MD water density peaks.

Precision statistics were used to evaluate the confidence in using the MD water density peaks to predict locations of crystallographic waters (Methods). For the restrained NaCl model (last 10 ns section), 32% of the MD water density peaks had a crystallographic water within 0.5 Å, 43% had a crystallographic water within 1 Å, and 47% had a crystallographic water within 1.4 Å. For the restrained Tris-Cl model (last 10 ns section), 31% of the MD water density peaks had a crystallographic water within 0.5 Å, 43% had a crystallographic water within 1 Å, and 48% had a crystallographic water within 1.4 Å. For the unrestrained NaCl model (first 100 ns section), 16% of the MD peaks had a crystallographic water within 0.5 Å, 37% had a crystallographic water within 1 Å, and 46% had a crystallographic water within 1.4 Å.

Tradeoff between precision and recall at higher MD water densities.

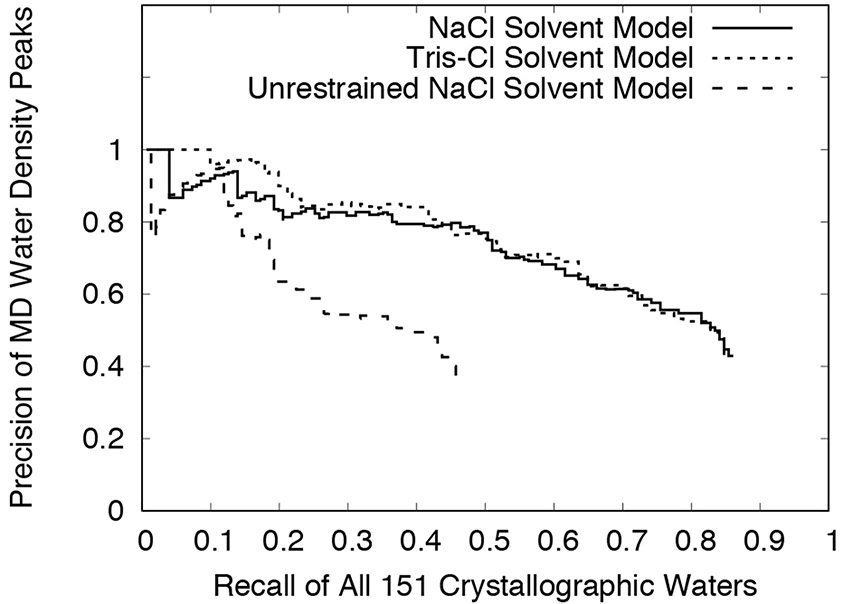
To assess whether stronger MD water density peaks were more likely to correspond to crystallographic waters, the precision was calculated for sets of peaks filtered using higher thresholds. The recall also was calculated using the higher thresholds, to determine the tradeoff in recovering crystallographic waters. The thresholds were varied in 100 uniform steps between the minimum (3-sigma for restrained and 2-sigma for unrestrained simulations) and maximum peak heights within each computed density map. For each of the simulations, the recall decreased with increasing threshold (Supporting Fig. S1A). While the recall decreased, the precision increased with increasing threshold, to a maximum of 100% (Supporting Fig. S1B). Fig. 6 shows the tradeoff between precision and recall. For a given value of recall, the precision of the NaCl and Tris-Cl models was mostly higher than the precision of the unrestrained model (the precision of the unrestrained model slightly exceeds that of the NaCl model in a band at low recall). The precision of the Tris-Cl model was similar to that of the NaCl model at lower thresholds (higher recall), and was higher than that of the NaCl model at higher thresholds (lower recall).

Figure 6.

Precision vs. recall using increasing MD water density peak thresholds. The peak threshold increases from right to left, as the recall decreases (Supporting Fig. S1). Statistics were computed using a cutoff distance of 1.0 Å. Results are shown for the last 10 ns of the NaCl and Tris-Cl solvent models, and for the first 100 ns of the unrestrained NaCl solvent model.

Neutron scattering density and water orientations.

To assess the accuracy of the water orientations in the simulations, water neutron scattering densities for the restrained NaCl model were computed (Methods) and were compared to the experimental 2Fo-Fc neutron scattering density. To calculate the simulated neutron scattering density, coordinates for water H and O atoms were extracted. Water H and O densities were individually computed using neutron scattering tables. The deuterium (D) density corresponding to the H atoms was calculated by re-normalizing the H density using the ratio of D and H scattering lengths. Finally, the water neutron scattering densities were computed as 0.8 (D density) + 0.2 (H density) + (O density), to simulate the 80% deuterium conditions of the neutron crystallography experiment.

The boomerang-like water neutron scattering density from the simulations generally aligns with the experimental 2Fo-Fc neutron scattering density; however, the simulation shows stronger ordering of H/D atoms than the experimental data, giving rise to a more extended appearance of the density. There also are examples where the orientation from the simulation differs from the experiment. An illustration of both cases is shown in Fig. 7. The orientation of water 303 (Fig. 7A,B) is reproduced by the simulation, but the H/D neutron scattering density is more ordered than in the experiment, as seen in the more extended density. The orientation of water 328 in the simulation, however, differs from the experimental model (Fig. 7C,D).

Figure 7.

Comparison of the restrained NaCl model MD water neutron scattering density to the crystallographic water orientation and the neutron 2Fo-Fc map. (A) View centered on water 303. (B) the same as (A), rotated roughly 90 degrees about the y-axis. (C) View centered on water 328. (D) the same as (C), rotated roughly 90 degrees about the y-axis. The MD model and 2Fo-Fc maps are rendered as in Fig. 2. The panels were created using Coot³⁹.

DISCUSSION

Both the recall and precision statistics for the present MD models were substantially higher than had been seen in similar MD water structure studies (compare Fig. 6 and Supporting Fig. S1 to Fig. 4 in Altan et al.⁹ and Fig. 2 in Higo and Nakasako⁸). Altan et al.⁹ found that up to 70% of 254 crystallographic waters were within 1.4 Å of a MD water peak in simulation of a unit cell of Yb³⁺-substituted mannose-binding protein. Using a similar peak height threshold, Higo and Nakasako⁸ found that 60% of 405 crystallographic waters were within 1.4 Å of a MD water peak in a solution state simulation of lysozyme. For the present EG simulation, using the top 100 waters and a distance of 1.4 Å, the recall of the restrained models is 98% (Fig. 3). Using all 151 ordered waters in the crystal structure and a distance of 1.4 Å instead, the recall of the restrained NaCl model is 93%. In addition, the maximum precision of 100% found here is greater than the maximum reported by Altan et al.⁹ (70%) and Higo and Nakasako⁸ (23%).

Only 50% of the top 100 waters and 46% of all 151 crystallographic waters were recovered within 1 Å in the first 100 ns of our simulation in NaCl solvent done without restraints on the protein. Although this recall is substantially larger than the value of 19% at 1 Å obtained for pancreatic trypsin inhibitor in van Gunsteren et al.⁶, it is much smaller than for the restrained NaCl or Tris-Cl model. Moreover, the recall is lower in the last 100 ns of the simulation. This result may indicate that current force fields are lacking or do not represent the protein in the crystal environment well, especially because we found that agreement got worse as the simulation progressed. Regardless of the cause of the inaccuracy, it is not yet reasonable to simulate an unrestrained protein, either in solution or crystalline state, and to assume that all the waters in the X-ray crystal structures would appear as ordered water density in the simulations.

Visual inspection of the environment of crystallographic waters that failed to be recovered by the unrestrained simulation revealed clues about why they might be missing. Interestingly, there were no cases where the protein density from the simulation overlapped a crystallographic water. This indicates that the protein did not directly displace the missing crystallographic waters. However, in the neighborhood of the missing waters, there were small deviations between the MD protein density and the crystal structure, disrupting entire local networks of water molecules. These observations indicate that crystalline waters were not directly displaced by the protein in the unrestrained simulation; rather, smaller displacements of the protein caused changes in water structure. A more puzzling case is buried interior water 302, which exhibits three strong hydrogen bonds to Asp52O, Cys54O, and Cys172H, as shown in Fig.5B. Despite these strong H-bonds, the MD simulation has no corresponding MD density at 2-sigma for this water. Two of the missing water H-bonds are back-filled by interactions between Cys54O and Gly161H and between Asp52O and Arg56HE; however, the fact that this water leaves does beg the question of where it went and how it got out.

The present finding that unrestrained simulations do not reproduce a high fraction of the crystallographic water structure is interesting in light of the work of Lexa and Carlson²⁴, who examined the influence of protein flexibility on the MixMD method for mapping ligand binding hot spots in hen egg-white lysozyme. In their study, simulations using limited protein flexibility identified too many hot spots, whereas a simulation with full flexibility identified a well-defined hot spot that overlapped the experimental multiple-solvent crystal structure results²⁷. They found that water density computed from an unrestrained solution state MD simulation agreed with the locations of 11 high confidence crystallographic waters not involved in crystal packing interactions. Comparing the top 11 crystallographic waters in EG with the first 100 ns of the present unrestrained simulation, all but buried water 302 (illustrated in Fig. 5) are within 1.4 Å of a MD water peak. In addition, the maximal precision values for the unrestrained and restrained MD models of EG water structure were similar (Fig. 6). The present results therefore appear to be consistent with the similar subset of results of Lexa and Carlson²⁴, which primarily was concerned with predicting hot spots.

Previous studies have used a distance of 1.4 Å to calculate the recall of crystallographic waters, corresponding to the radius of water^8-9. For the restrained EG simulations, however, waters at a distance of 1.4 Å from the peak lie outside of the 3-sigma envelope (not shown). In contrast, a distance of 1 Å, as used by van Gunsteren et al.⁶, places the water within the 3-sigma envelope of the MD water density, which is what a crystallographer might perceive as a correctly placed water. This observation suggests that using a more stringent distance threshold of 1 Å is preferred over a threshold of 1.4 Å when assessing the ability of the MD model to add information for crystallographic model building. The recovery of waters in this study was very good using the more stringent threshold of 1 Å: the restrained MD simulations recovered 94% (NaCl model) or 95% (Tris-Cl model) of the top 100 waters.

Because potential energies typically are very sensitive to small changes in atom positions, the criterion for accuracy of the water structure model might need to be even stricter for medicinal chemistry applications. In this case, the recall calculated using a distance of 0.5 Å between a water peak and the corresponding crystallographic water (or even closer) might be more appropriate. The placement of water hydrogens also can be important for ligand binding free energy calculations. Our visual comparison of the calculated and experimental neutron scattering density shows a general alignment of water orientations. Together with the high recall of water positions, this alignment suggests that water placement and orientation in networks tend to go hand in hand.

The higher recall of crystallographic waters observed here for EG compared to previous MD water studies of lysozyme⁸ and MBP⁹ might reflect an increased accuracy of the present crystalline protein MD simulations. There are major differences between the model preparation and simulation methods used here for EG and the previous MD water studies of lysozyme⁸ and MBP⁹. The lysozyme study⁸ used a solution state MD model and bears little resemblance to our study. The MBP study⁹ used a substantially different crystalline MD model. One major difference is that the MBP model used a single unit cell, and the EG model used a 2×2×2 supercell. Another is that the MBP study created a large cavity of bulk water in the unit cell through the removal of one copy of the protein, and averaged the results of four such simulations, choosing a different copy for each. In contrast, the EG simulations used all copies of the protein in the entire 2×2×2 supercell, with a number of solvent molecules tuned to achieve near atmospheric pressure. (The EG model used an NVT ensemble to ensure that the dimensions of the supercell did not vary.) The same choices made for the MD model of EG were also made for a model of staphylococcal nuclease that improved the agreement with diffuse X-ray scattering data¹⁰, providing further indirect evidence for the advantages of the present MD model preparation and simulation methods.

Other factors might also be important to explain the high recall found for the present EG study. The MBP crystal structure was derived from X-ray data at a temperature of 110 K, and the model of EG was derived from both X-ray and neutron data at 298 K. The MBP model used GROMACS assigned protonation states (with exploration of some alternatives), and the EG protonation states were assigned based on the neutron data. Backbone carbon and nitrogen atoms were fixed in the MBP simulations, with 1,000 kJ / mol nm² restraints on the remaining non-hydrogen atoms. In the EG simulation, 209.2 kJ / mol nm² restraints were used on all non-hydrogen atoms, with no additional restraints.

The number of 3-sigma peaks found in the restrained MD water density was far greater than the number of crystallographic waters (151): 963 for the restrained NaCl model, and 952 for the restrained Tris-Cl model. Many of the extra peaks in the unit cell correspond to waters in symmetry-related copies of the asymmetric unit. However, even accounting for symmetry, the precision of the MD model using the 3-sigma threshold was much less than the recall (43% precision compared to 86% recall for the NaCl model using a 1.0 Å cutoff). The excessive number of peaks indicates that the MD water structure is over-ordered, which is possibly a consequence of the harmonic restraints applied to the protein and ligand. A weaker restraint than used here (209.2 kJ / mol nm² or 0.5 kCal / mol Ų) might yield a higher precision in prediction of crystallographic waters, perhaps at the cost of recall. The number of 2-sigma peaks in the NaCl model without restraints was lower than for the restrained MD, but still higher than the number of crystallographic waters: 504 peaks in the first 100ns section, and 331 in the last 100 ns section. This means that water is less ordered in the unrestrained than in the restrained simulations, and that the ordering is less in the last 100 ns section than in the first 100 ns of the unrestrained simulation. The recall of crystalline waters in the unrestrained simulation also is substantially poorer than in the restrained simulations. The improved recall of the restrained simulations supports the previous finding that crystal structure restraints can improve predictions for crystallographic temperature factors, solid-state nuclear magnetic resonance (NMR) chemical shifts, and NMR backbone order parameters²⁸. These results indicate that the MD model, possibly including the potentials, must be improved to yield accurate predictions in the absence of any restraint.

Analysis of discrepancies revealed cases where the evidence for crystallographic waters was not clear cut from the experimental data. Indeed, overinterpretation of water structure is a common pitfall in macromolecular crystallography²⁹, and in some cases it might be unclear whether the discrepancies in this work are due to inaccuracies in the simulation or the crystal structure. The present results on EG indicate that MD models might help with this problem by providing independent evidence either for or against marginal crystallographic waters. In addition, the MD model can suggest new possible locations of waters that can then be accepted or rejected using the agreement with the diffraction data.

Filtering MD water density peaks using an increasingly high threshold decreased the recall and increased the precision of predicting crystallographic waters (Fig. 6 and Supporting Fig. S1). Until the time when the simulations and the crystallography can achieve perfect agreement, it will be necessary to consider the tradeoff between precision and recall for individual applications. For example, if the simulations are used to seek supporting evidence for crystallographic waters that have low experimental density, a high recall might be desired, calling for a low threshold. On the other hand, if the simulations are used to identify locations of tightly bound waters with high confidence, a high precision might be desired, calling for a high threshold.

Obtaining water structure information from MD simulations requires more effort and computational resources than the usual crystallography workflow. The extra cost is not excessive, however, and the approach could be applied to many other systems. The main human effort is in setting up a complete model of the crystalline protein; the effort is increased when there are missing residues that need to be modeled in the crystal structure. The MD simulation for the present systems of ~150,000 atoms proceeded at a rate of ~206 ns/day on 16 nodes of an Intel Broadwell (Xeon E5-2695 v4 @ 2.10 GHz) cluster with 36 cores per node, yielding a 100 ns trajectory within a ½ day. The same system runs at 52 ns/day on a single similar node with a NVIDIA Tesla P100 GPU, requiring two days to complete a 100 ns simulation. Routine MD simulations of water structure therefore are within reach, and might soon become a common step in crystallography workflows.

Previous studies have demonstrated the utility of using diffraction data to validate crystalline protein MD simulations^{10, 23, 30-35}. The present study indicates that water structure can be quite sensitive to relatively small changes in the protein structure. Crystalline protein water structure studies therefore have the potential to be an especially valuable tool in validating MD simulations, e.g., for force field development.

The present results suggest that the combination of room-temperature crystallography, neutron diffraction, and crystalline MD simulations has potential to increase the accuracy of biomolecular solvation models for force field development, crystallography, and medicinal chemistry. The potential value of this combination is supported by prior experimental studies. Comparative neutron diffraction experiments on concanavalin A at room temperature and 15 K revealed substantial changes in water structure upon cryocooling¹³. In addition, crystal cryocooling was observed to change side chain conformational distributions in dihydrofolate reductase³⁶. These studies highlight the importance of room temperature experiments for water structure studies. Room-temperature X-ray free-electron laser studies of the influenza M2 proton channel showed the sensitivity of the water structure to pH³⁷, indicating the potential for protonation states to influence water structure. This study highlights the advantage of using neutron diffraction experiments for determining protonation states, as prediction of pKa values is notoriously difficult³⁸. Neutron diffraction data also allow for the experimental validation of water orientations predicted by MD models, using experimentally assigned positions of the water H/D atoms.

ABBREVIATIONS

MD

molecular dynamics

MBP

Yb³⁺-substituted mannosebinding protein

EG

endoglucanase

Tris

2-Amino-2-(hydroxymethyl)propane- 1,3-diol