PCP-dependent transcellular regulation of actomyosin oscillation facilitates convergent extension of vertebrate tissue

Abstract

Oscillatory flows of actomyosin play a key role in the migration of single cells in culture and in collective cell movements in Drosophila embryos. In vertebrate embryos undergoing convergent extension (CE), the Planar Cell Polarity (PCP) pathway drives the elongation of the body axis and shapes the central nervous system, and mutations of the PCP genes predispose humans to various malformations including neural tube defects. However, the spatiotemporal patterns of oscillatory actomyosin contractions during vertebrate CE and how they are controlled by the PCP signaling remain unknown. Here, we address these outstanding issues using a combination of in vivo imaging and mathematical modeling. We find that effective execution of CE requires alternative oscillations of cortical actomyosin across cell membranes of neighboring cells within an optimal frequency range. Intriguingly, temporal and spatial clustering of the core PCP protein Prickle 2 (Pk2) is correlated to submembranous accumulations of F-actin, and depletion of Pk2 perturbs the oscillation of actomyosin contractions. These findings shed light on the significance of temporal regulation of actomyosin contraction by the PCP pathway during CE, in addition to its well-studied spatial aspects.

1. Introduction

Convergent extension (CE) is a ubiquitous process of collective cell movement that elongates the body axis in animals (Tada and Heisenberg, 2012). During convergent extension, cells rearrange by intercalating specifically in the mediolateral axis, thereby elongating the tissue in the perpendicular, anteroposterior axis (Walck-Shannon and Hardin, 2014). Two sub-cellular mechanisms have been shown to contribute to mediolateral cell intercalation (Shindo, 2017): First, mediolaterally-oriented protrusions act in a manner analogous to the leading edge of a migrating cell, driving cell intercalation via cell crawling (Shih and Keller, 1992). Second, pulsed actomyosin contractions actively shrink mediolaterally-oriented junctions (so called v-junctions, Figure S1A), thereby driving intercalation (Bertet et al., 2004, Blankenship et al., 2006, Rauzi et al., 2008). Recent work suggests that these two mechanisms act in concert in both vertebrates and Drosophila (Williams et al., 2014, Sun et al., 2017, Huebner and Wallingford, 2018).

Actomyosin contraction is the key driver of animal cell movement (Gardel et al., 2010), so understanding how the actomyosin machinery is organized during CE is an important challenge. In the context of CE, this issue is currently best understood for junction shrinking in the epithelial cells of the Drosophila germband, a key model system for studies of cell intercalation (Bertet et al., 2004, Blankenship et al., 2006). In that case, two populations of actin have been shown to act in concert: Oscillation of a pool of “medial” actin drives pulsed constriction events at the junction, and oscillations of a second pool of “junctional” actin stabilizes the newly-shortened junction (Fernandez-Gonzalez and Zallen, 2011, Rauzi et al., 2010, Sawyer et al., 2011).

Cell intercalation has also been extensively studied in the mesenchymal cells of the Xenopus gastrula mesoderm (Figure S1B)(Keller et al., 2000), though how actomyosin dynamics relate to cell intercalation in these cells is far less clear. As in the Drosophila germband, two actin populations have been described in the Xenopus mesoderm during CE. First, there is a “node-and-cable” system of actin filaments that resides superficially (i.e. 1–2 μm deep; Figure S2A, A’) and displays oscillations that are implicated in cell intercalation by cell crawling (Kim and Davidson, 2011, Pfister et al., 2016, Skoglund et al., 2008). In addition, we have described a pulsatile actin population associated with junction shrinkage deeper within the tissue (4–6 μm; Figure S2B, B’)(Shindo and Wallingford, 2014). Here, we will refer to these as the “superficial” and “deep” actin populations, respectively. The relationship between these two actomyosin populations remains unclear.

Understanding actomyosin dynamics during CE in a vertebrate is crucial, because Planar Cell Polarity (PCP) signaling is an essential regulator of cell intercalation specifically in vertebrates (Butler and Wallingford, 2017) and not in Drosophila (Zallen and Wieschaus, 2004). Moreover, CE is essential for normal neural tube closure in vertebrates and PCP genes are key genetic risk factors for human neural tube closure defects (Wallingford et al., 2013). PCP proteins control myosin phosphorylation and disruption of PCP signaling severely disrupts myosin-mediated junction shrinking in diverse tissues, including the Xenopus mesoderm (Butler and Wallingford, 2017). However, despite the wide-spread implication of actomyosin oscillation and flow in morphogenesis of invertebrates (He et al., 2010, Fernandez-Gonzalez and Zallen, 2011, Martin et al., 2009, Rauzi et al., 2010, Sawyer et al., 2011) and in migration of single vertebrate cells in culture (Huang et al., 2013, Maiuri et al., 2015), we understand little about the spatial and temporal dynamics of actomyosin and how these are influenced by PCP proteins during vertebrate collective cell movement.

In this study, we performed high-resolution, three-dimensional time-lapse imaging of actin and myosin dynamics during CE in the dorsal gastrula mesoderm of Xenopus. We adopted a mathematical modeling approach to ask how the observed patterns of actomyosin behavior may impact cell intercalation during CE. Together with the previous findings in Drosophila, our findings in silico and in Xenopus gastrulae in vivo argue that oscillatory actomyosin contraction is a general principle of cell intercalation via junction shrinking that is conserved across cell types and animals. We also show that in addition to its known role in controlling the planar orientation of actomyosin contraction, PCP signaling is required to tune the frequency of those oscillatory contractions. These results shed light on the molecular mechanisms of CE and of congenital diseases related to defective PCP signaling.

2. Results

2.1. Synchronized oscillation links intracellular actomyosin populations during convergent extension of the Xenopus mesoderm.

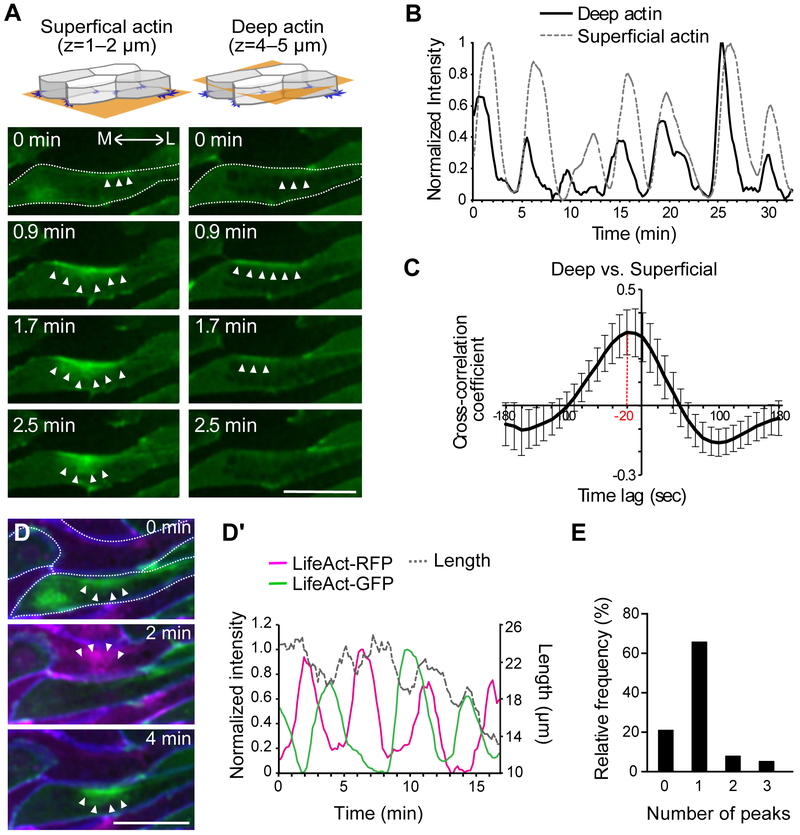
We first asked if the dynamics of the superficial “node-and-cable” system of actin filaments and the deep pulsatile actin population associated with junction shrinkage in a vertebrate CE in vivo using the dorsal mesoderm of Xenopus laevis (Figure S1C, D). Using 3D time-lapse imaging to simultaneously monitor the superficial and deep actin pools, we found that the two oscillate synchronously within individual cells during junction shrinking (Figure 1A, Movie S1). To quantify this oscillatory behavior, we identified actin flows as the peaks of normalized fluorescent intensity over time (Figure S3), and this analysis revealed that actin pulses initiated in the deep population at shrinking cell-cell junctions and then flowed to the superficial actin pool (Figure 1B). Cross-correlation of the data confirmed the synchrony of deep and superficial actin pulses, with the peak of superficial actin intensity following the peak of deep actin by ~20 seconds on average (Figure 1C, max of cross-correlation coefficient: 0.404 ± 0.154 (mean ± sd)).

Figure 1. Actomyosin oscillations during convergent extension of the Xenopus dorsal mesoderm.

(A) Mosaic expression of LifeAct-GFP (F-actin marker) allows imaging of labeled cells apposed to unlabeled cells for unambiguous assessment of actin dynamics in the superficial (left) and deep (right) actin populations. Stills from time-lapse movies show the progression of actomyosin flow across time and space (arrowheads). M: medial, L: lateral. Dotted line outlines the cell. (B) Peaks of normalized actin intensity allow quantification of actomyosin dynamics in the deep and superficial populations along contracting v-junctions from a single cell. (C) Actomyosin oscillations in deep and superficial populations are synchronous, showing a significant cross-correlation. (D, D’) Two-color labeling of F-actin in same cells in panel A with membrane-BFP reveals that oscillations along shared v-junctions (See Figure S1A) in apposed cells are out of phase; quantification of normalized intensity together with junction length over time is displayed at right. The cells are outlined with a dotted line. (E) The number of LifeAct’s peaks observed in a given cell between any two peaks occurring in an adjacent cell shows pulses in neighboring cell display a roughly one-to-one ration (See Figure S6). Scale bar = 20 μm

We previously reported that the myosin regulatory light chain 9 (Myl9) oscillates with the deep junctional pool of F-actin at the shrinking-junctions during CE (Shindo and Wallingford, 2014). When co-expressed with LifeAct-RFP, a F-actin marker, and membrane (Mem) -BFP, we found that Myl9-GFP also oscillated with F-actin in the superficial population (Figure S4A, Movie S2). Cross-correlation analysis between the intensity of Myl9-GFP and LifeAct-RFP indicated a synchronized oscillation of Myl9 and F-actin in these two populations (Figure S4A’, max of cross-correlation coefficient: 0.728766 ± 0.051 (mean ± sd)). These results suggest that oscillatory actomyosin contractions are synchronized within individual cells during CE.

2.2. Anteroposterior neighbor cells display asynchronous intercellular actomyosin oscillations during convergent extension.

Our data suggest that deep and superficial actomyosin flows are synchronized within individual cells during convergent extension, so we next asked how the flows are coordinated between neighboring cells. Because of the known relationship of anteroposterior neighbor cells in junction shrinking (Shindo and Wallingford, 2014), we used a two-color imaging approach to unambiguously assess actomyosin dynamics at the cell-cell junction between anteroposteriorly neighboring cells (Figure. S1D, S1D’). Time-lapse imaging demonstrated that actin and Myl9 flows in anteroposterior neighbors displayed asynchronous oscillations (Figure 1D, 1D’, S4B). These oscillations appeared anti-correlated in time-lapse movies (Figure 1D) and kymographs (Figure S5). However, their timing was highly variable, precluding determination of cross-correlation on average (Figure S4B’). Nonetheless, quantification of the relative timing of pulses (Figure S6) revealed a dominant one-to-one ratio of oscillations between neighboring cells (Figure 1E), suggesting a predominantly alternating relationship between neighboring cells. Thus, oscillations are synchronous between the deep and superficial actomyosin populations within each cell, but oscillations between cells are asynchronous.

2.3. Mathematical modeling suggests that asynchronous contractile oscillations with an optimal frequency increase the efficiency of convergent extension.

Understanding the significance of actomyosin dynamics in embryos is challenging because collective cell movements emerge in vivo from the coordination of actomyosin contractile systems both within cells and between cells as we observed (Guillot and Lencuit, 2013, Heisenberg and Bellaiche, 2013, Mao and Baum, 2015). In regard to this issue, mathematical modeling provides a powerful tool for understanding such complexities (Alt et al., 2017, Yu and Fernandez-Gonzalez, 2017, Inoue et al., 2016, Szabó et al., 2016). Thus, we adopted mathematical modeling as an amenable way to test for potential benefits of the spatiotemporal patterns of actomyosin oscillation for CE.

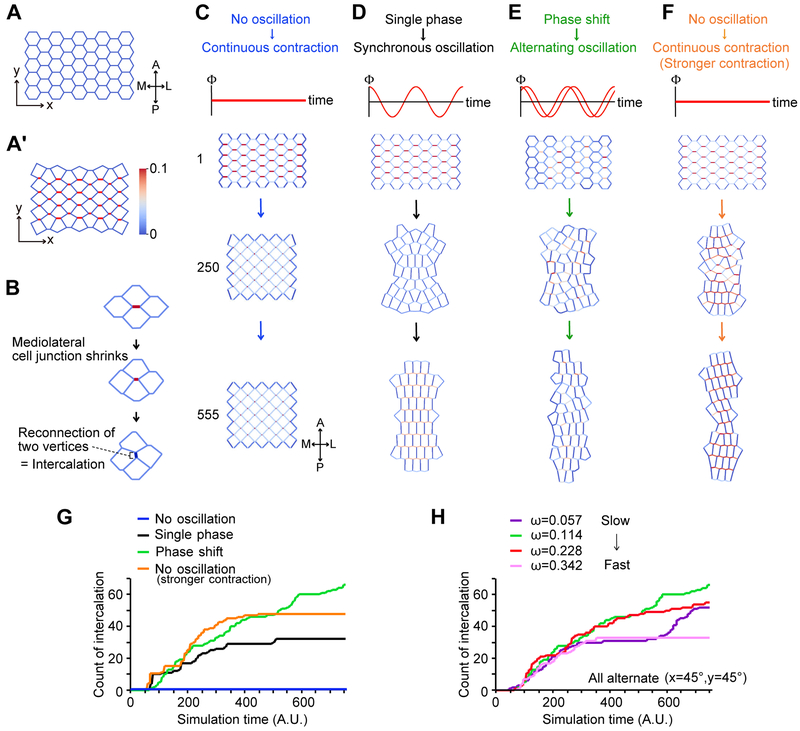
We modified the 2D vertex model, in which cell-cell junctions are modeled as two vertices and one edge shared by neighboring cells. We considered two factors, orientation and oscillation, for the line tension in the model (See method). The orientation factor limited contraction to edges aligned along the x-axis, representing the mediolateral contraction of cell-cell junctions (Figure 2A, A’). The oscillatory factor allowed us to manipulate the pattern of oscillations across multiple cells. By utilizing our modified 2D vertex model, we modeled junction shrinking with tension exerted along edges, thereby reducing the distance between vertices (Farhadifar et al., 2007, Staple et al., 2010). We then quantified the efficiency of CE by counting the number of new edges emerging after complete shrinking of a v-junction, which represents cellular intercalation (Figure 2B).

Figure 2. A 2D vertex model reveals that the alternate, carefully timed contractions are a general feature of cell intercalation.

(A) Initial cell arrangement used in the simulations. Vertical axis (x) indicates antero (A) - posterior (P), and horizontal axis (y) indicates medio (M) – lateral (L). (A’) Example of junction contractions. The cell-cell junctions aligned along the mediolateral axis (x-axis) can contract in the model. The edge color indicates the magnitude of the line tension of the cell and cell junction (red=maximum strength, blue=minimum strength). (B) Example of the junction remodeling in the simulations. After the cell-cell junction shows emergence of a new junction, and is counted as one intercalation, as shown in Figures 2G and 2H. (C) Simulation of CE with coincident, continuous contraction without oscillation generates no intercalation. Top panel shows cells at 1 simulation time t = 1 (A.U); middle panels at t = 250 and lower panels at t = 555. (D) Synchronous oscillating contractions (In-phase oscillation) generate modest intercalation. (E) Alternate oscillating contractions generate robust intercalation. (F) Continuous contraction without oscillating at 1.5 times the line tension generates modest intercalation. (G) Graph of intercalation quantified by the number of newly formed cell-cell junctions after complete v-junction shortening as shown in Figure 1B, representing the efficiency of cell intercalation. Blue: continuous contraction (Λ = 0.10); Black: Synchronous oscillation (Λ = 0.10); Green: alternating oscillation (Λ = 0.10); Orange: continuous contraction (Λ = 0.15). Frequency of oscillation is defined by angular frequency ω [radian/simulation time unit] (ω = 2π/T, See experimental procedures). For both synchronous and alternating oscillations, 2π/T is fixed to 0.114. The phase shift to generate alternating oscillation is defined by θ_x=0.7854, θ_y=0.7854 (see experimental procedure). (H) Effect of oscillating frequency on intercalation efficiency for alternating oscillation. Purple: ω = 0.057 (slowest), Green: ω = 0.114, Red: ω = 0.228, Pink: ω = 0.342 (Fastest). The phase shift is fixed to Δθ = 2.5π × 10⁻¹ for the three groups.

We first tested the significance of oscillating contractions by simulating continuous contraction of v-junctions (Figures 2C, S7A), and strikingly, cells completely failed to intercalate (Figures 2C, 2G (blue), and S7A, Movie S3). By contrast, adding a synchronous oscillation of contractions (i.e. all cells oscillate in phase, Figure S7B) resulted in substantial cell intercalation (Figures 2D, 2G (black); Movie S3). We noted that even with synchronous oscillations, the rate of cell intercalation eventually stalled, reaching a stable plateau beyond which no additional intercalation occurred (Figure 2D, 2G-black).

We therefore explored the role of contraction timing by comparing the effect of synchronous oscillations to that of alternating oscillations (Figure S7B, C). We found that alternating oscillations between neighboring cells along the y-axis (anteroposterior axis) resulted in significantly more cell intercalation than did synchronous contractions (Figures 2E, 2G-green, S7C, S7C’, Movie S3). To probe the significance of this finding, we explored the interplay of oscillation timing and contraction strength. Interestingly, increasing the force of each contraction improved intercalation even in the absence of oscillations (Figure 2F, Movie S3), but importantly, it did not overcome the eventual plateau beyond which no more intercalation occurred (Figure 2G-orange). Without oscillations, the number of cell intercalations could not overcome this plateau even if we increase the force for edge contraction (data not shown). Thus, our model suggests that alternating contraction between neighboring cells that share a shrinking junction requires less tension, which allows cells to consume lower energy to generate contractile forces for CE.

Finally, our model provided us with the means to test the significance of contraction frequency in CE. We found that when alternating contraction oscillation was very rapid, intercalation either slowed or plateaued (Figure 2H, red and pink). Decreasing contraction frequency improved intercalation (Fig 2H, green), however only up to point; at very slow contractions frequencies, the progress of intercalation became irregular, showing a double plateau (Figure 2H, purple). Taken together, these simulations suggest that asynchronous and alternating oscillation, as well as tight control of contraction frequency, is important for CE by junction shrinking.

2.4. Prickle displays both spatial and temporal patterns of localization to cell-cell junctions during CE.

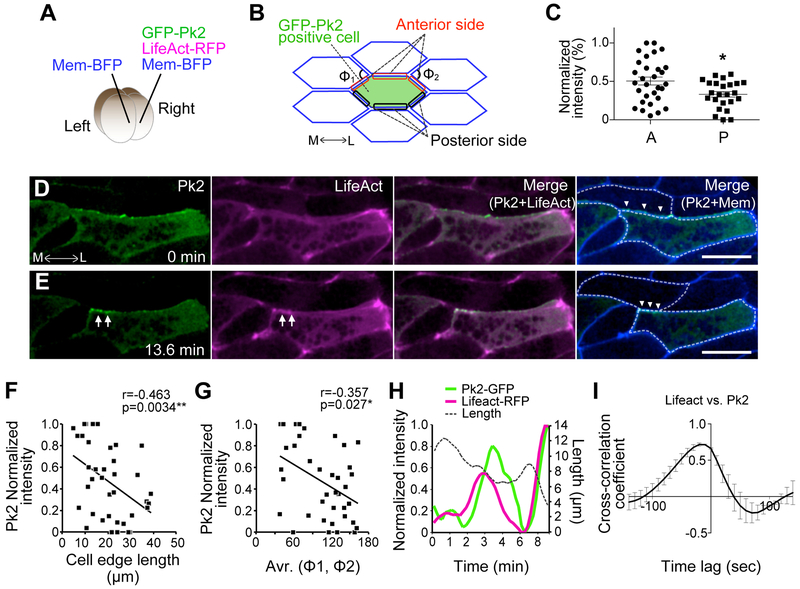
Both imaging and modeling data suggest that convergent extension requires the careful calibration of several parameters, including the frequency of contractile flows and their asynchronous coordination between neighboring cells. To explore the molecular control of these oscillations, we turned our attention to the PCP signaling network, which has been implicated in control of both deep and superficial actomyosin dynamics in the dorsal mesoderm (Kim and Davidson, 2011) (Shindo and Wallingford, 2014). In addition, we recently showed that the core PCP protein Pk2 controls CE in neural epithelial cells, where it displays a tight temporal and spatial correlation with actomyosin at shrinking junctions (Butler and Wallingford, 2018). We therefore used mosaic expression to generate labeled cells that were directly apposed to unlabeled cells in the dorsal mesoderm (Figure 3A). We then quantified the normalized fluorescence intensity at both anterior and posterior cell faces (Figure 3B, red, black). This analysis revealed that Pk2-GFP localized predominantly to the anterior face of cells engaged in CE (Figures 3C–3E, Movie S4). While this spatial localization of Pk2 is consistent with data in other cell types and organisms (Ciruna et al., 2006, Jiang et al., 2005, Ossipova et al., 2015, Yin et al., 2008), our dynamic imaging allowed us to detect additional temporal patterns.

Figure 3. Prickle2 displays temporal and spatial patterns of localization during cell intercalation.

(A) Method for mosaic expression of GFP-Pk2, LifeAct-RFP, and membrane (Mem) -BFP in a Xenopus embryo at 4 cell stage. (B) Scheme showing the cell and cell-cell junctions measured for analysis in C, F, G, and H. The angle of apices of neighboring cells attached to a shrinking junction is indicated as Φ. (C) Mean intensity of GFP-Pk2 on anterior and posterior cell cortices. [* p = 0.0282, Student’s t-test; anterior (A): n = 30, posterior (P): n = 25] (D, E) Still images from time-lapse movie of GFP-Pk2 during junction shrinkage. Images of E are 13.6 minutes after the images in D. Arrowheads indicate contracting v-junction; arrows indicate the accumulation of GFP-Pk2 at the anterior face of the contracting v-junction. (F) Correlation between GFP-Pk2 intensity and the length of cell-cell junctions. GFP-Pk2 intensity is converted to percentages in each image. (38 junctions from 2 embryos). (G) Correlation between GFP-Pk2 intensity and the angle Φ. Same numbers as (F). (H) Quantification of normalized intensity of LifeAct (magenta) and Pk2-GFP (green) together with junction length over time from single contracting cell junction. (I) Synchronous accumulation of F-actin and Pk2 is shown by cross correlation. Scale bar = 20 μm.

For example, we found that junctional Pk2-GFP intensity was elevated specifically at shrinking junctions (Figures 3D–3E). Indeed, the increased junctional Pk2 intensity was significantly correlated with decreasing junction length (Figure 3F). Moreover, Pk2 intensity was also correlated with the angle Φ (Figure 3B, 3G), a cell-shape parameter that scales with the tension exerted on shrinking junctions during intercalation (Rauzi et al., 2008, Shindo and Wallingford, 2014). Further examination of Pk2 dynamics revealed a pulsatile pattern of junctional enrichment (Figure 3H), and we detected a significant cross-correlation between Pk2 intensity and actin intensity (Figure 3I, max of cross-correlation coefficient: 0.7155 ± 0.021 (mean ± sd)). Thus, Pk2 displays both spatial and temporal patterns of localization closely relating to junction shrinking during CE. These results are significant for providing the first time-resolved information about PCP protein localization during CE in the Xenopus mesoderm.

2.5. Prickle2 controls the frequency of actomyosin oscillations.

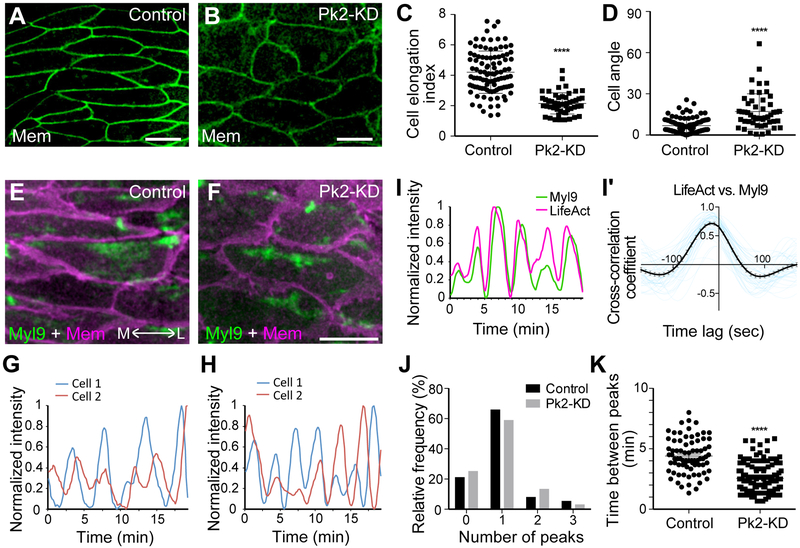
Finally, the coordinated pulsing of actomyosin and Pk2 is consistent with recent reports indicating a reciprocal relationship in which actomyosin controls PCP protein localization and PCP proteins in turn control myosin activity (Newman-Smith et al., 2015, Ossipova et al., 2015). Because we found that pulses of Pk2 were synchronized with those of F-actin, we tested the effect of Pk2 loss of function on the several parameters of actomyosin oscillation defined above (i.e. Figures 1 and 2). We knocked down Pk2 using an antisense morpholino-oligonucleotide that has been validated in both convergent extension and polarization of multiciliated cells (Butler and Wallingford, 2018, Butler and Wallingford, 2015). Pk2 knockdown disrupted both the elongation (Figures 4A, B, C) and the planar orientation (Figures 4A, B, D) of cells in the dorsal mesoderm, consistent with disruption of other core PCP proteins in dorsal gastrula mesoderm (Jessen et al., 2002, Wallingford et al., 2000). Interestingly, the effect on actomyosin was strikingly specific, as Pk2 knockdown did not eliminate oscillations (Figures 4E–4H), did not alter the tight relationship between actin and myosin (Figures 4I, 4I’), and did not disrupt the asynchronous nature of oscillations between neighboring cells (Figures 4J, S6, Movie S5). Instead, Pk2 knockdown affected the frequency of actomyosin contractions, with knockdown cells displaying an inter-peak time roughly half that of controls (Figures 4F, 4H, and 4K). Thus, our data suggest that Pk2 is required to tune the frequency of actomyosin oscillations, a parameter that our modeling suggests is essential for normal cell intercalation.

Figure 4. Prickle 2 controls the frequency of actomyosin pulses.

(A, B) Cells expressing membrane (Mem) -GFP in the Xenopus dorsal mesoderm display an elongate and aligned morphology in control (A). Pk2-KD disrupts elongation and orientation of cells (B). (C, D) Quantification of cell shapes and orientations by measuring length-width ratio (ellipticity) of each cell and cell angle from mediorateral axis, respectively. (Cell elongation index: **** p < 0.0001, Student t-test, control: n = 100 from three embryos, Pk2-KD: n = 51 from three embryos; Orientation: **** p < 0.0001, Mann Whitney U-test, control: n = 97 from three embryos, Pk2-KD: n = 51 from three embryos). (E, F) Still images from time-lapse movies of Myl9-GFP and Mem-RFP in control (E) or Pk2-KD (F). (G, H) Representative oscillations of Myl9 intensity in two apposed cells (cell1 and cell2, see Figure S4B) in a control (G) or Pk2-KD (Η). (I) Normalized intensities of Myl9-GFP and LifeAct-RFP, measured along mediolaterally aligned cell junctions in Pk2-KD embryos. (I’) Cross-correlation of normalized intensities of Myl9 and LifeAct along medioraterally aligned cell junctions in Pk2-KD embryos revealed their synchronized oscillations (black line with SE). Each blue line is from each cell junction. (J) Peaks in apposed cells generally display a one-to-one ration, suggesting a roughly asynchronous and alternate relationship between cell neighbors. To compare, the result from control embryos in Figure 1E is added. See also Figure S6. (K) Time between peaks is significantly reduced after Pk2-KD. **** p < 0.0001, Mann Whitney U-test, control: n = 76 from three embryos, Pk2-KD: n = 138 from three embryos. Scale bar = 20 μm.

3. Discussion

In this study, we link the two populations of oscillating actomyosin in a cell, previously considered to be two distinct mechanisms for vertebrate CE (Kim and Davidson, 2011, Shindo and Wallingford, 2014). The live imaging reveals the asynchronous oscillations between neighboring cells during the cell junction shrinking, that is identified as a beneficial mode for CE in the simulations. Our simulation shows the frequency of the oscillation is also critical for CE. Finally, we identify the role of the PCP protein in controlling the frequency of actomyosin oscillation.

Oscillatory actomyosin contraction is a key feature of cell movement both in individual cells and in cell collectives, and such oscillations have been extensively defined during CE of the Drosophila germ band. However, CE is a ubiquitous morphogenetic process in animals, and we know little of such oscillatory contractions in other settings. The tightly cross-correlated flows between deep and superficial actin populations in the Xenopus dorsal mesoderm we observed within single cells are reminiscent of the flows between “medial” and “junctional” actin pools described in Drosophila (Rauzi et al., 2010, Sawyer et al., 2011). The asynchronous and alternate oscillations observed here between neighboring cells in Xenopus mesoderm are likewise reminiscent of similar patterns observed in Drosophila (Fernandez-Gonzalez and Zallen, 2011). Such similarities are highly significant because intercalations studied in Drosophila occur in tightly adherent epithelial cells with a well-defined apicobasal polarity, while the mesenchymal cells observed here in Xenopus are more loosely adherent and lack obvious apical-basal polarity. Moreover, CE in the Xenopus mesoderm is entirely dependent upon intact PCP signaling (Butler and Wallingford, 2017), but the analogous process in Drosophila is independent of this signaling system (Zallen and Wieschaus, 2004). Given these dramatic differences, the results of our imaging in vivo (Figure 1) and modeling in silico (Figure 2) strongly argue that asynchronous oscillatory contraction is a general principle of cell intercalation via junction shrinking that is conserved across cell types and animals.

Our data also provide important new insights into the function of PCP signaling in vertebrate CE, which is an important issue given the implication of PCP genes in human neural tube defects (Wallingford et al., 2013). The localization and dynamics of the Pk2 are consistent with our recent observations in neural epithelial cells (Butler and Wallingford, 2018), suggesting a common spatial and temporal pattern of Pk2 localization dynamics that spans cell fates (ectoderm vs. mesoderm) and tissue types (epithelial and mesenchymal). These results are also consistent with findings that anteroposterior patterning is central to the organization of CE in both Drosophila and Xenopus (Paré et al., 2014, Ninomiya et al., 2004, Zallen and Wieschaus, 2004). Regarding the positive feedback between the PCP protein and actomyosin contractility to localize them at the cell-cell junctions in neural epithelium (Ossipova et al., 2015, Newman-Smith et al., 2015), our data support the finding that their functions are tightly linked for shrinking cell-cell junction.

Previous work has implicated PCP signaling in control of both the deep and the superficial actin populations in the Xenopus dorsal mesoderm (Kim and Davidson, 2011, Shindo and Wallingford, 2014), so our finding that actomyosin flow links these two populations is informative. In fact, disruption of the core PCP protein Dvl reduces the frequency of superficial actin contractions in these cells (Kim and Davidson, 2011), suggesting that our finding of the opposite effect following Pk2 loss of function (Figure 4) is consistent with the antagonistic relationship between these two proteins in Drosophila (Jenny et al., 2005, Tree et al., 2002). Perhaps most significantly, we show here that Pk2 displays an oscillatory pattern of junctional enrichment that correlated with that of actomyosin in mesenchymal cells of the dorsal mesoderm (Figure 3). It is notable that regulatory molecules of actin are reported as the interactome of Pk2 (Paemka et al., 2015). Although the molecular sets functioning with Pk2 to regulate oscillation frequency remain to be identified, these data suggest that the temporal patterns of PCP protein enrichment at cell-cell junction are at least as important as spatial patterns (i.e. planar asymmetry).

The mechanisms generating the alternating oscillations remain unknown. It is possible that the local interaction between the cells at the mediolaterally aligned cell junctions are involved, as a recent study combining imaging during Drosophila gastrulation and in silico approaches suggests that “asymmetric stiffness” of the two cell membrane at cell-cell junctions can attract or deplete motor proteins (Chanet et al., 2017). Adjacent contracted- and relaxed-cell membranes along the anteroposterior axis may be a basis for generating the alternating oscillations. It is also possible that the asynchronous contraction along mediolateral axis is necessary. Our model is designed to have the phase shift along both anteroposterior and mediolateral axes, raising the possibility that different timing of contractions along the mediolateral axis may also be important. This means that the alternating oscillation generates relaxed neighboring cells that can be pulled with smaller forces by the contracting cell-cell junction. The relationship between phase shift of anteroposterior and mediolateral axes will be an interesting property to investigate in the future for understanding the relationships between actomyosin oscillations and CE.

4. Materials and methods

4.1. Preparation of Xenopus embryos

Ovulation of adult Xenopus laevis females was induced by an injection of human chorionic gonadotropin. After incubating at 16 °C overnight, eggs were squeezed from the females, fertilized in vitro and dejellied in 3% cysteine (pH 7.8–8.0) at the two-cell stage. Fertilized embryos were washed and subsequently reared in 1/3 x Marc’s Modified Ringer’s (MMR) solution. To prepare the embryos for mRNA microinjections, the embryos were placed in 1/3 x MMR solution with 3% ficoll.

4.2. Plasmids and morpholino anti-sense oligonucleotides (MO)

GFP-Pk2 plasmids were constructed and designed as described previously in (Butler and Wallingford, 2015), and the Myl9-GFP plasmid in (Shindo and Wallingford, 2014). The Pk2 MO (GAACCCAAACAAACACTTACCTGTT) used disrupts splicing of the Pk2 gene (Butler and Wallingford, 2015) and severely disrupts CE of Keller explants and neural tube closure in intact Xenopus embryos; both phenotypes are rescued by co-expression of the wild-type Pk2 gene (Butler and Wallingford, 2018). Furthermore, these phenotypes are recapitulated by expression of a Pk2 dominant-negative (Butler and Wallingford, 2018) and are consistent with CE defects in a genetic mutant in the single prickle homolog in Ciona (Jiang et al., 2005).

4.3. Morpholino and mRNA microinjections

Capped mRNAs for fluorescent markers (GFP-Pk2, LifeAct-GFP, LifeAct-RFP, Myl9-GFP membrane-RFP, membrane-BFP) were synthesized using a mMessage mMachine kit (Thermo Fisher Scientific, Ambion). Morpholino (MO) or mRNA was injected into the two dorsal blastomeres targeting the dorsal marginal zone (DMZ). Pk2-MO was injected at 30 ng per blastomere. The amounts of injected mRNAs per blastomere were as follows: GFP-Pk2 [90 pg], LifeAct-GFP/RFP [60 pg], Membrane-RFP/BFP [60 pg], Myl9-GFP [20 pg].

4.4. Live imaging of Keller explants

After mRNA injection, DMZ tissues were dissected out at stage 10.5 with forceps, hair loop, and hair knives (Figure S1C). The explants were mounted onto a fibronectin (Sigma, F1141) – coated glass bottom dish in DFA (Danilchik’s for Amy) medium, and cultured at 13 °C for overnight. The explant imaging with a confocal microscope (CV1000, Yokogawa Electric Corporation) was started when the sibling embryos reached at stage 14–15. The time-lapse movie was taken every 10 sec for recording actomyosin pulsing.

4.5. Computational Simulation

We employ a 2D vertex model (Nagai T. and Honda 2001) to simulate the dynamics of multiple cells with cell rearrangement during convergent extension. In the model, cell shapes and their packing geometry are represented by a network of polygons consisting of vertices and edges. Cell rearrangement is expressed by implementing a local network topology change known as the T1 transition rule. The cell shape change is expressed by movements of vertices. The equation of motion of the i -th vertex at time t is

$$\eta \frac{d{\mathbf{r}}_i}{dt}=-{\nabla }_{i}U$$ (1)

where η is a frictional coefficient, and r_i is the position vector of the i-th vertex. The mechanical properties of the cells are expressed by an energy function U as follows.

$$U=\sum \begin{array}{c}\hfill \\ \alpha \hfill \end{array}\frac{K_{\alpha }}{2}{\left(A_{\alpha }-A_{\alpha }^{(0)}\right)}^2+\sum \begin{array}{c}\hfill \\ (i,j)\hfill \end{array}{\Lambda }_{ij}{l}_{ij}+\sum \begin{array}{c}\hfill \\ \alpha \hfill \end{array}\frac{{\Gamma }_{\alpha }}{2}{L}_{\alpha }{}^2$$ (2)

Here, the α-th cell’s area A_α, perimeter L_α, and junctional length l_ij between the i-th and j-th vertices are represented as variables. The constants K_α and Γ_α are the area elasticity and peripheral contractility, respectively. The energy function U in Eq. (2) is basically the same as suggested in (Farhadifar et al., 2007) (Staple et al., 2010), while we redefine the line tension Λ_ij as a function of time and position of vertices to take into account a preferential direction of the oscillatory constriction at each individual cell described below.

The line tension Λ_ij on the junction line between i- and j-th vertices is decomposed to two contributions: orientation and oscillatory factors.

The orientation factor, p_ij, is introduced to express the mediolateral-oriented constriction.

$$p_{ij}={\left(\frac{{\mathbf{e}}_{\mathit{x}}\cdot {\mathbf{l}}_{ij}}{l_{ij}}\right)}^2$$ (3)

Here, e_x is the unit vector in the direction of the x-axis which is defined by the mediolateral axis (x axis in Figure 2A). The junctional line vector, l_ij, is defined by the relative position vector from i-th to j-th vertices.

The oscillatory factor, Φ_α(t) is introduced to express an oscillatory contribution from the α-th cell:

$${\Phi }_{\alpha }(t)=\sin (\omega t-{\theta }_{\alpha })+1$$ (4)

Here, the angular frequency, ω, is identical for all cells where no oscillation occurs at ω = 0 (Figure S7B). The phase difference, θ_α, is defined by the initial configuration (n_x, n_y) of the α-th cell:

$${\theta }_{\alpha }=n_x\Delta \theta +n_y\Delta \theta$$ (5)

where, n_x and n_y are row and column indices for the α-th cell in the initial configuration of the cell packing, respectively. Δθ is a configuration-based phase shift where a synchronous (in-phase) oscillation is reproduced by Δθ = 0 (Figure S7B).

Supposing that the junctional line between i-th and j-th vertices is shared by the α- and α*-th cells, the line tension contributed from these two cells at the junction line is expressed as

$${\Lambda }_{ij}=p_{ij}\Lambda \left({\Phi }_{\alpha }(t)+{\Phi }_{{\alpha }^{\ast }}(t)\right),$$ (6)

where Λ corresponds to a time-averaged value of the line tension. All model constants are listed in Table 1.

Table 1.

Model parameters

Symbol	Value	Descriptions
Kα	1.0	Area elasticity of Eq. (2)
Γα	−6.0	Peripheral contractility of Eq. (2)
Λ	{0.10, 0.15}	Mean value of line tension of Eq. (6)
${\mathit{A}}_{\alpha }^{(0)}$	2.6	Cell area at stress free state of Eq. (2)
ω	{0, 0.57, 1.14, 2.28, 3.42}× 10−1	Angular frequency of Eq. (4)
Δθ	{0.0, 2.5π × 10−1}	Configuration-based phase shift of Eq. (5)
η	1.0	Friction coefficient of Eq. (1)
Δt	1.0 × 10−1	Time step size for numerical integration of Eq. (1)

4.6. Image and statistic analysis

Images were quantified by using Fiji (https://fiji.sc/) and Igor Pro. Statistic analyses were performed using Prism6, GraphPad Software, Inc. The statistic test for each analysis is described in the figure legends.

Supplementary Material

1

Figure S1. Cell movements during convergent extension in Xenopus notochord.(A) Driving force of cell intercalation along mediolateral axis during CE. Myosin light chain is phosphorylated along the cell-cell junction aligning mediolateral axis (red line, so called v-junction), and contracts the cell junction. The neighboring cells (white colored cells) are pulled by the junction contraction, then sequentially cause junctional remodeling (blue arrows). After such cell rearrangement, newly formed v-junction contracts by the actomyosin. (B) Notochord is formed during the process of gastrulation to neurulation at dorsal midline (St. 10.5-St. 18). The notochord (pink color) elongates along anteroposterior axis as blastopore closes by CE. The cells in notochord elongate and move along mediolateral axis to intercalate (cells move along the red arrows). (C) Keller explant is isolated from dorsal mesoderm at St. 10.5 Xenopus embryos for live-imaging of CE. The notochord cells in Keller explant undergo normal CE as observed in an intact whole embryo. Live imaging of the cell movement is taken by mounting the Keller explant on a glass bottom dish coated with fibronectin, and monitored with an inverted confocal microscope. The Z-plane of images in Figure 1A is around 1–2 μm from the glass (superficial), and of images in Figure 1B is taken around 4–5 μm from the glass (deep). (D) Mosaic expression of LifeAct-RFP, LifeAct-GFP, and membrane (Mem) -BFP in a 4-cell stage of Xenopus embryo. By undergoing CE, the cell populations labeled with different colors are mixed, allowing us to recognize F-actin at the cell-cell junction in both cells sharing v-junction indicated by blue box.

Figure S2. Two distinct Z-planes observed in Xenopus notochord cells to detect medial or junctional actin and myosin. (A, B) Schemes of dorsal mesoderm (notochord) cells in an isolated Keller explants. Yellow plane indicates the observed Z-plane, a superficial plane for medial actomyosin (A), and a deep plane for junctional actomyosin (B), respectively. (A’, B’) Fluorescent images of notochord cells expressing LifeAct-RFP and membrane-BFP in the superficial (A’) and deep (B’) Z-plane. Node-and-cable is visible as medial actin in the superficial plane, while junctional actin is visible more in the deep plane. White arrowheads in A’ indicate “node”, and black arrowheads in B’ indicate F-actin accumulations at the mediolaterally aligned cell junctions.

Figure S3. Normalization of measured fluorescence intensities of oscillated actin and myosin. Raw intensities of target GFP or RFP were measured along contracting v-junction (1). Moving average was calculated to smooth each line (2). To avoid effects from bleaching during taking time-lapse, baseline was subtracted using IgorPro (3). The intensities were converted to ratio (4). Note that the normalization is to compare timing of accumulations of the target proteins along single contracting v-junction, and not to compare absolute amount of each proteins.

Figure S4. Myl9 oscillations coupled with F-actin along contracting v-junctions. (A) Normalized intensities of Myl9-GFP and LifeAct-RFP in the control embryo, measured along contracting v-junction. (A’) Cross-correlation of normalized intensities of Myl9 and LifeAct along contracting v-junction revealed their synchronized oscillations (black line with SE). Each blue line is from each v-junction. (B) Normalized intensity of Myl9-GFP in adjacent cells composing contracting v-junction. (B’) Cross-correlation of normalized intensities of Myl9-GFP in adjacent cells composing contracting v-junction (black line with SE). Each blue line is from each v-junction, showing various time lags.

Figure S5. Cortical actin along mediolateral cell-cell junctions display asynchronous and alternating oscillations. Kymograph of superficial plane generated from time-lapse movie of LifeAct-RFP and membrane-BFP shown in Figure S3. Yellow box in the left panel indicates the region detected for making kymograph. Each color of arrows shows F-actin accumulations along mediolateral cell-cell junctions in each cell.

Figure S6. Quantification of alternating, asynchronous oscillations. Relative timing of pulses was quantified by counting the number of peaks in the wave (red) between the peaks in another wave (blue). If two waves are alternating as shown in left side, the number converges on 1. If two waves are unrelated as shown in right side, the number has a variety.

Figure S7. Designing 2D vertex model for comparison of different contraction modes. The graphs indicate change of oscillatory factor, Φ (Eq. 4), with respect to time in each mode. Color bar in left side of the graph is to indicate value of oscillatory factor in each cell, representing a temporal magnitude of line tension exerted by each cell. Note that the colors on the edges in the simulations show the resultant line tension exerted by neighboring two cells (Eq. 6), as shown in Figure 2A. (A) Continuous contraction without oscillation at angular frequency ω= 0 and Δθ = 0, which represents no spatiotemporal phase change as shown by gray color filling all cells uniformly. (B) Synchronous oscillation exerted by single phase, and defined by Δθ = 0. All cell contract simultaneously, represented by uniform color changes through all cells. (C) Alternate oscillation exerted by phase shift. Each cell contracts in different but coupled timing, which can generate alternate oscillation along anteroposterior axis. (C’) Example of alternating oscillation in the simulation. The cell providing force to shorten sharing edge is alternating, that can be recognized by the cell colors. Asterisk and its number indicate the cell exerting force and its magnitude to shorten mediolateral edge, respectively. The phases between the two cells are coupled, representing alternating oscillations.

2

Movie S1. Medial or junctional F-actin (green) co-expressed with membrane-BFP (magenta) during v-junction constriction. Left two panels are superficial (medial) actin, right two panels are deep (junctional) actin. Bar =10 μm. 12 frames / sec.

3

Movie S2. Alternating oscillations of medial F-actin (magenta) and Myl9 (green) with membrane-BFP (blue). From left side, merging of Myl9 and cell membrane, F-actin and cell membrane, and all three colors. Bar = 20 μm. 12 frames / sec.

4

Movie S3. Simulation of CE with different timing of contraction. (A) Coincident and continuous contraction without oscillation (Λ=0.1). (B) Synchronous contraction with oscillation (Λ=0.1). (C) Alternating oscillation (Λ=0.1). (D) Coincident and continuous contraction without oscillation, but higher line tension (Λ=0.15).

5

Movie S4. Pk2 accumulation at the shrinking v-junction. Pk2-GFP (green), LifeAct-RFP (magenta), and membrane-BFP (blue). From left side, merging of Pk2 and cell membrane, Pk2 and F-actin, and all three colors. Scale bar = 20 μm. 12 frames / sec.

6

Movie S5. Medial Myl9 pulsing (green) in control or Pk2-KD embryo. Membrane is labeled with BFP (blue). Scale bar = 20 μm. 12 frames / sec.

Highlights:

• Anteroposterior neighboring cells display asynchronous actomyosin oscillations during convergent extension in the Xenopus mesoderm.

• Mathematical modeling shows the asynchronous oscillation with an optimal frequency is important for convergent extension.

• PCP protein Prickle 2 displays both spatial and temporal patterns of localization to the contracting cell-cell junctions.

• Prickle 2 is required for controlling the frequency of actomyosin oscillations.