Revisiting volumes of lipid components in bilayers

Abstract

In addition to obtaining the highly precise volumes of lipids in lipid bilayers, it has been desirable to obtain the volumes of parts of each lipid, such as the methylenes and terminal methyls on the hydrocarbon chains and the headgroup. Obtaining such component volumes from experiment and from simulations is re-examined, first by distinguishing methods based on apparent versus partial molar volumes. While somewhat different, both these methods give results that are counterintuitive and that differ from results obtained by a more local method that can only be applied to simulations. These comparisons reveal differences in the average methylene component volume that result in larger differences in the headgroup component volumes. Literature experimental volume data for unsaturated phosphocholines and for alkanes have been used and new data have been acquired for saturated phosphocholines. Data and simulations cover extended ranges of temperature to assess both the temperature and chain length dependence of the component volumes. A new method to refine the determination of component volumes is proposed that uses experimental data for different chain lengths at temperatures guided by the temperature dependence determined in simulations. These refinements enable more precise comparisons of the component volumes of different lipids and alkanes in different phases. Finally, the notion of free volume is extended to components using the Lennard-Jones radii to estimate the excluded volume of each component. This analysis reveals that head group free volumes are relatively independent of thermodynamic phase, while both the methylene and methyl free volumes increase dramatically when bilayers transition from gel to fluid.

Graphical Abstract

1. INTRODUCTION

Many structural quantities of lipid bilayers can be classified as lateral, along the surface of the bilayer, or transversal, along the normal to the bilayer. The prime quantity for lateral structure of a simple, one component lipid bilayer, is the area per molecule A_L. Structural quantities in the transverse direction generally involve the locations relative to the center of the bilayer of various component parts of the lipid molecule and may include more than one measure. For example, thickness has been used as the hydrocarbon thickness (2D_C), or the phosphate-phosphate thickness (D_PP), or the electron density thickness (D_HH), or the steric thickness for first contact (D_B’), or the Luzzati thickness (D_B) that imagines the bilayer rearranged into a volume that consists only of lipid and no water.¹ Volume is the quantity that connects lateral and transverse structure. This is most directly obvious for the volume per lipid V_L in the relation V_L = A_LD_B/2.

Measurements of V_L are the most precise of all structural data for lipid bilayers. These data have been used to tease out component volumes, focusing on the average volume of the hydrocarbon chains, breaking down into average volumes of methylene (V_CH2) and terminal methyl (V_CH3), and methine (V_CH) in unsaturated lipids.^2–3 The volume of the headgroup (V_H) can then be obtained by subtracting the sum of the chain component volumes from V_L. Quantitative analysis of x-ray and neutron scattering data gains precision when the volumes of component parts of the lipid molecule, such as headgroup and chain volumes, are constrained from volumetric experiments.^4–5 Component volumes are also valuable for comparing simulations and experiment.⁶ More fundamentally, they enable comparisons of the lipid components in membranes of different compositions (saturated and unsaturated chains) and phases (fluid, gel, and subgel).

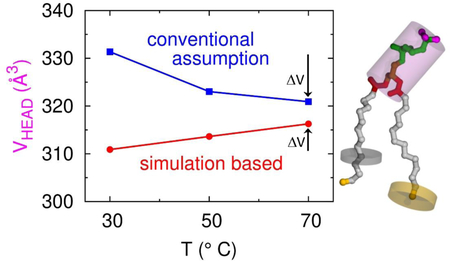
However, the estimation of component volumes from experiment has involved assumptions regarding the pooling of data, temperature dependence, and relative values of components. Different assumptions can lead to qualitatively different results. For example, inspired by data from alkanes, a component analysis recently applied to a class of monoglyceride bilayers varied the ratio r = V_CH3/V_CH2 with temperature (Harper et al., in preparation). Use of this ostensibly more realistic assumption (r has usually been fixed) resulted in the headgroup volume decreasing with increasing temperature, rather than remaining constant as inferred in previous studies of phosphocholines.^1–3 This intriguing finding seemed to beg for an explanation based on the physical chemical properties of the monoglyceride headgroup. That would have been a mistaken enterprise because when the same methodology is applied to the phosphocholines, as shown in this work, their calculated headgroup volumes also decrease with increasing temperature, indicating that there is nothing unusual about the temperature dependence of the monoglyceride headgroup.

That counterintuitive result, the headgroup volumes decreasing with increasing temperature, has led us to re-examine the assumptions in the experimental method for obtaining component volumes of lipids. A conventional method uses the highly accurate total volumes V_L(m) for lipids of different chain lengths that differ only by the number of methylenes m. The methylene component volume V_CH2 is then extracted by following the concept of apparent molar volumes defined for ordinary mixtures. We assign the acronym EXP-0 to this method and we assign SIM-0 to this method when we apply it to V_L(m) obtained from simulations. Physical chemists have long known that apparent molar volumes are less rigorous than partial molar volumes. We use the acronyms EXP-1 and SIM-1 when we apply the concept of partial molar volume to V_L(m) obtained from experiment or from simulations, respectively. Fundamentally, apparent V_CH2 does not vary with m, while partial V_CH2 can and does. Despite this difference, our results using either approach are counterintuitive when applied either to experimental data or to simulations. In contrast, results are not counterintuitive when we apply a method that will be called SIM-2. SIM-2 extracts all the component volumes directly from a single lipid bilayer simulation. However, there is insufficient information to apply this method to experiment. Instead, we propose a hybrid method, to be called EXP-SIM that uses the highly accurate experimental V_L(m) in a way that is guided by the temperature dependence obtained from simulations. This bears some resemblance to a method EXP-Small advocated by Small.⁷ For the reader’s convenience, Table 1 lists the names of the different methods of analysis in this paper along with a few phrases regarding their attributes; full descriptions are given in the sections where they are first used.

Table 1.

Characteristics of analysis methods.

Method	Data Source	Analysis
EXP-0	Experiment	Apparent molar volume for methylenes; Eq. (1)
SIM-0	Simulation	Apparent molar volume for methylenes; Eq. (1)
EXP-1	Experiment	Partial molar volume for methylenes; Eq. (2)
SIM-1	Simulation	Partial molar volume for methylenes; Eq. (2)
SIM-2	Simulation	Component volumes obtained directly8
EXP-SIM	Experiment	Equal VCH2 vs. n at T from simulations
EXP-Small	Experiment	Equal VCH2 vs. n at same relative T

In Section 2 we present new data for saturated phosphocholines and we describe how to extract apparent component volumes from it and from some literature data using the EXP-0 method. We also apply the EXP-1 to extensive literature results for the alkanes to illustrate how the EXP-0 and EXP-1 results differ. Section 3 reviews our simulation methodology including the SIM-2 method, and how the bare, hard-core, excluded volumes were obtained for the components. Simulation results are presented in Section 4 and compared to experimental results. SIM-2 finds that the headgroup volume does not decrease with increasing temperature, unlike SIM-1. SIM-2 also finds that the methylene volume decreases with increasing chain length whereas SIM-1 finds the opposite. While results of simulations can always be challenged as depending upon the parameters used in the force fields, we find that this does not affect trends with temperature. This leads to a new method EXP-SIM, introduced in Section 4.1, which combines experiment and simulation. The older EXP-Small method also used experimental data for different chain lengths at different temperatures, but at the same temperature relative to the main transition temperature.

The component volumes obtained by the analysis methods in Table 1 are similar to the volumes defined in physical chemistry for the molecular components in mixtures in the sense that they do not distinguish free volumes. After the concept of free volume was introduced to correlate with transport properties in condensed matter,⁹ it has often been used for biomembranes.^10–12 The methodology used here naturally connects to the concept of component free volumes and allows their easy estimation. The procedure begins with the calculation of excluded volumes for selected components (Section 3.3) which, when subtracted from the corresponding component volume, provide the component free volumes discussed in Sections 4 and 5.

2. EXPERIMENTAL DATA AND ANALYSIS METHODS

Standard experimental methods directly determine the total volume per lipid V_L when the lipid is in bilayers in multilamellar vesicle (MLV) form.^{2–3, 13–14} These volumes are determined when there is excess water, which then requires that the thermodynamically defined partial molar water volume V_W be the same as bulk water. Although one can imagine that water molecules intercalated in the headgroup region of the bilayer might have a different volume, this nuance is unlikely to be resolvable experimentally; we will, however, briefly address it at the end of Section 4 using simulations and find that this is not a concern.

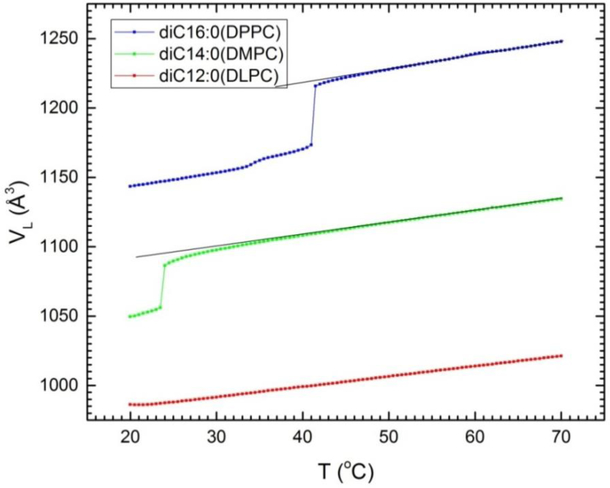
There have been many studies that have obtained V_L for many lipid bilayers. This paper uses data and results from Uhrikova et al.² and from Koenig and Gawrisch³ for a sequence of chain lengths n of di-unsaturated phosphocholine (diCn:1PC) lipids; the central diC18:1PC is often further abbreviated DOPC. We have also added new data for the saturated lipids DLPC (diC12:0PC), DMPC (diC14:0PC) and DPPC (diC16:0PC) using the DMA 5000M (Anton Paar, Ashland, Virginia) vibrating tube densimeter with lipid concentrations 5% by weight. Figure 1 plots the volume per lipid V_L as a function of temperature and a numerical data table is provided in Supplementary Information part A. Estimated uncertainties are ±2 ų except for DLPC which had reproducible values of dV/dT for those scans that didn’t have air bubbles but for which the volumes varied by as much as 10 ų. As has been previously documented,¹⁵ such offsets can occur in the DMA 5000M when applied to multilamellar dispersions of lipids that have densities considerably different from water, like DLPC in the fluid phase in the present study. We subsequently constrained the volume of the densimeter scans of DLPC in the 40–50°C range using the neutral flotation method.^{13, 16} The densimeter scans for DMPC and DPPC agreed well with earlier neutral flotation data.¹³ The scans for DMPC and DPPC exhibit the usual main phase transition and the DPPC scan also shows the lower, pre-transition at T = 35°C. This figure also shows straight lines drawn through the DMPC and DPPC data above their main phase transition. The deviation near the main transition of the data from these lines has been reported before.¹³ It indicates an anomalous pre-critical region that shows up even more dramatically in a recent study of the tilt modulus of DMPC.¹⁷

Figure 1.

Experimental volumes as a function of temperature of the saturated series of diCn:0PC lipids with n=16 (DPPC), n=14 (DMPC) and n=12 (DLPC). Deviations from the superimposed straight lines indicate anomalous behavior near and above the main phase transitions at 24.0°C for DMPC and 41.4°C for DPPC.

The experimental component volumes that are usually obtained are the average volume V_CH2 of methylene groups on the hydrocarbon chains, the volume V_CH3 of the terminal methyl of the hydrocarbon chains, the volume V_CH of any methine groups on the hydrocarbon chains, and finally, the volume of the headgroup V_H which consists of the remaining part of the lipid. For the phoshocholine (PC) lipids treated in this paper, the headgroup component contains the carboxyls on the chains, the glycerol backbone, and the phosphate and choline groups, i.e. all the atoms except for those in the methylene, methine and methyls on the hydrocarbon chains.

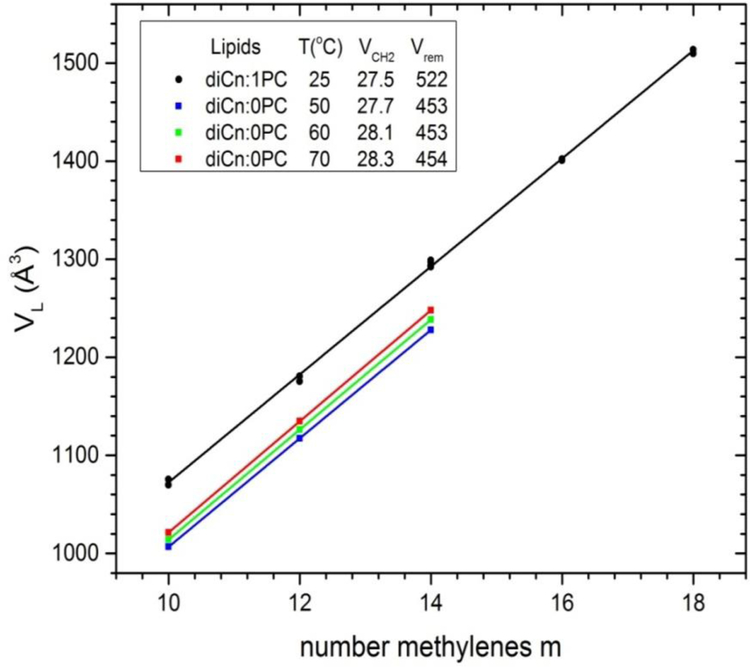
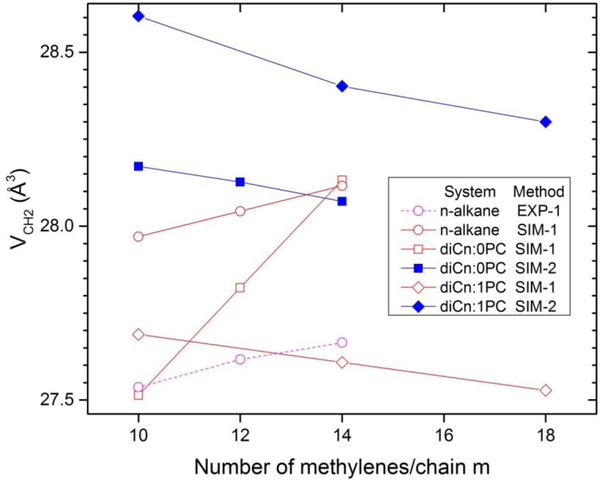
A classic (and the simplest) way to start the experimental determination of the component volumes uses plots of V_L vs number of methylenes for lipids that differ only in the number m of methylenes on the hydrocarbon chains,^{7, 18} as shown in Fig. 2. Inspired by the concept of apparent molar volumes, one writes

$${\text{V}}_L\left(m\right)={\text{V}}_L\left(0\right)+m{\text{V}}_{\text{CH}2}$$ (1)

and then the fitted slopes in Fig. 2 give twice V_CH2 (two chains/lipid) and the intercepts at m=0 give the remainder volume V_L(0) = V_rem which is the sum of V_H, 2V_CH3, and (for di-unsaturated lipids) 4V_CH. The linear fit for diCn:1PC lipids in Fig. 2 yields V_CH2 = 27.53 ų (see legend) which agrees very well with V_CH2 = 27.52 ų reported from the more exhaustive fit to a greater variety of lipids;² that study additionally partitioned the remainder volume V_rem with results 2V_CH3 = 110.1 ų, 4V_CH=88.9 ų, and V_H = 323 ų.

Figure 2.

Experimental volume V_L for unsaturated diCn:1PC lipids (circles) from Table 2 of Uhrikova et al.² and new data for saturated diCn:0PC lipids (squares) versus number m of methylenes per hydrocarbon chain. The lines show linear fits from which component CH₂ volume and the volume of the remainder V_rem were obtained with values at the temperatures shown in the legend.

However, the method of apparent molar volumes assumes that the average methylene component volume V_CH2 is the same for all m. Physical chemistry avoids such an assumption by defining the concept of partial molar volume.¹⁹ For our application, this obtains the average methylene component volume as the derivative of the volume with respect to the number of methylenes for each value of m, in our case

$${\text{V}}_{\text{CH}2}\left(m\right)={\left(\partial {\text{V}}_L\left(m\right)/\partial m\right)}_{\text{T.}}$$ (2)

This partial molecular volume method, which we call EXP-1 in this paper, does not assume that V_L(m) is a constant but allows it to depend upon chain length m. This well-defined physical chemical procedure automatically leads to the mathematically rigorous volume conserving relation V_L(m) = ∑_iN_i(m)V_i(m) summed over all components i.¹⁹ Of course, the actual molecular connectivity of the methylenes constrains m to be an integer and this makes this method not quite the same as for mixtures that consist of individual molecules and for which the concentration can be varied continuously to evaluate the partial derivative in Eq. (2). Consequently, this method is best described as inspired by the physical chemical concept of partial molecular volume.

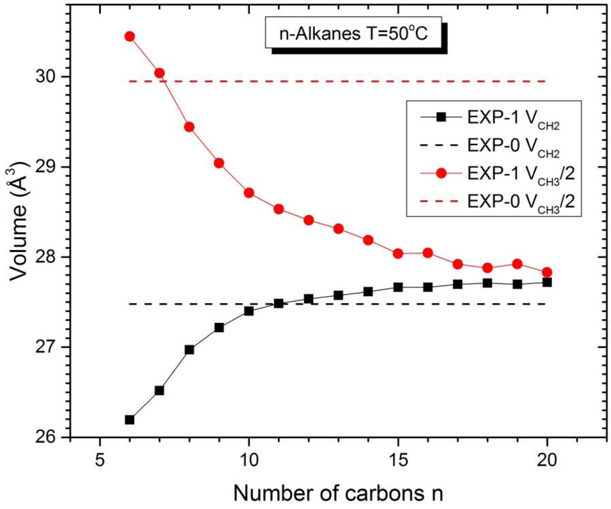
Following physical chemistry textbooks,¹⁹ obtaining EXP-1 component volumes is facilitated by plotting V_L(m)/N = v(x) where x = m/N is the effective concentration of methylenes. After taking a numerical derivative of v(x), one has V_CH2(x) = v(x) + (1-x)(dv/dx). In the case of n-alkanes, N is most naturally chosen as n = m+2 and then the methyl component volume is obtained from V_CH3(x) = v(x) - x(dv/dx). A similar procedure obtains the EXP-1 value of V_CH2 for lipids along with the volume V_rem of the remainder of the lipid molecule. For lipids, it might have seemed a priori to matter how one defines the effective concentration x; in fact, different definitions obtain the same results. While this partial molar method is clearly conceptually superior to the apparent molar method employed in Fig. 2, the actual differences in component volumes are negligible when the linear fit is confined to a narrow range in m. The best system to illustrate the chain length dependence of the methylene component volume is the n-alkanes. Extensive volume data have long been available for liquid n-alkanes^{7, 20} and have been reworked by others.^{3, 21} Fig. 3. shows EXP-1 results at T=50 C. The value obtained for V_CH3(16) is 27.68 ų compared to 27.48 ų when a linear fit is performed using all n between 6 and 20. The larger differences for V_CH3(16) stems from the fact that Eq. (1), unlike Eq. (2), does not allow total volume to be reproduced for each n. The Eq. (1) fit weights deviations for each n equally and this means that the average V_CH3 has to be closer to what Eq.(2) gives for small n because the proportion of methyls is larger for small n.

Fig. 3.

EXP-0 and EXP-1 component volumes of n-alkanes at T=50°C as a function of number of carbons n.

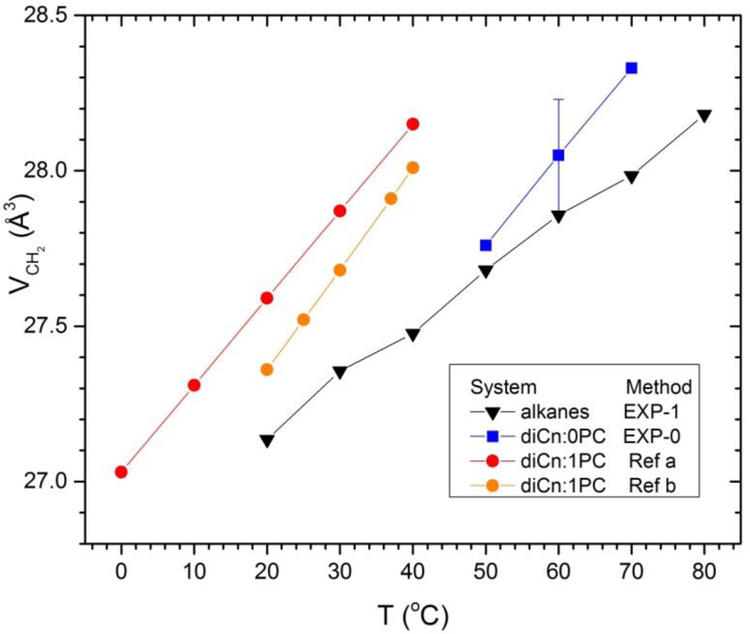
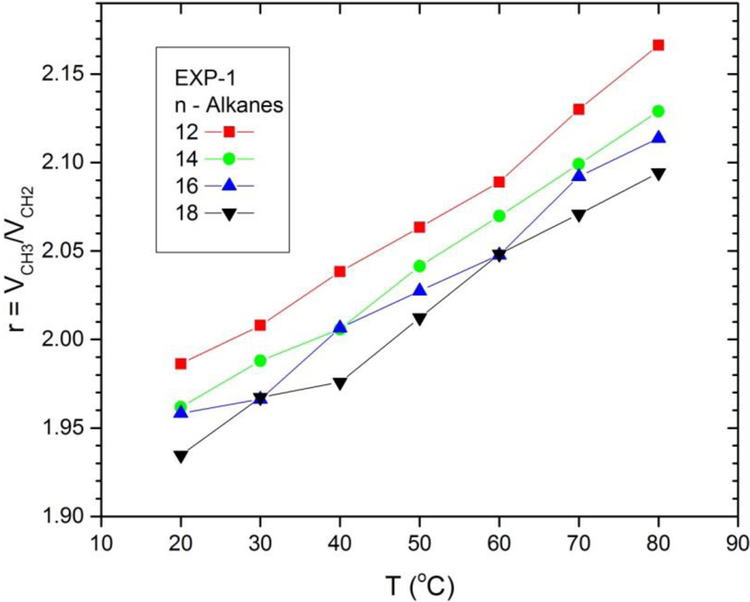
Turning to temperature dependence, Fig. 4 plots experimental values of V_CH2 as a function of temperature for alkanes, and also for our new diCn:0PC data and for literature values for diCn:1PC lipids.^2–3 For the alkanes we show values for n=16 (m=14) to compare to the saturated lipids with m=10,12,14 and the unsaturated lipids with m=10,14,18. Only one error bar is shown for the diCn:0PC data because uncertainties at different T are strongly correlated, so dV_CH2/dT has little uncertainty. All methylene volumes increase with increasing T, although somewhat faster for lipids than for alkanes, and V_CH2 is generally a bit larger for lipids than for alkanes at a given temperature. For the alkanes, the methyl volume increases more rapidly than the methylene volume, as earlier noted,^{2–3, 21} so the ratio r(T) = V_CH3(T)/V_CH2(T) increases with T as shown in Fig. 5.

Figure 4.

Temperature dependence of V_CH2 determined by EXP-1 for alkanes (n=16) and saturated lipids. Lipid results for diCn:1PC (a) are from Table 2 of Uhrikova et al.² and (b) from Table 3 of Koenig and Gawrisch.³ Original alkane volume data are from Rossini et al.²⁰

Figure 5.

Temperature dependence of r = V_CH3 /V_CH2 for alkanes by chain length determined by the EXP-1 method. Original volume data are from Rossini et al.²⁰

To reiterate, EXP-1 applied to lipids also obtains V_rem which is the sum of the volumes of the methyl, methine and headgroup components. The simplest way to separate V_rem into component volumes for saturated lipids has been to assume some value for the ratio r = V_CH3/V_CH2; a typical choice was r = 2 for saturated PCs.^{13, 22} Later, an analysis that combined volumetric and low angle x-ray data indicated r = 1.9 for gel phase DPPC.²³ Subsequently, careful fitting to many chain lengths and temperatures was performed by two groups.^2–3 Although both groups noted that the r ratio is temperature dependent for alkanes, results were given for fixed r = 2 and additionally for r = 1.9.² Those choices resulted in negligible T dependence in V_H, thereby supporting the assumptions¹³ that neither r nor V_H depends substantially upon T. Also, different fixed values of V_H were explored^2–3 to examine the uncertainty in the decomposition of V_rem into additional component volumes.

However, an increasing ratio r(T) suggested by the alkanes coupled with the EXP-1 analysis for the methylene volume requires that the lipid headgroup volume V_H(T) decreases with increasing T, not only for the monoglycerides but also for the standard PC lipids. Importantly, the EXP-1 method of analysis gives nearly equal V_CH2 for different lipid chain lengths n at the same temperature. In contrast to the physical chemistry concept that partial molar volumes should be calculated from volumes measured at the same temperature, Small proposed that volumes for different chain lengths should be plotted and analyzed as in Fig. 2, but using volumes at the same temperature relative to the transition temperature rather than at the same temperature, and that gave substantially different values for V_CH2 and r.⁷ Although it was strenuously argued that Small’s method gave inconsistent values of V_CH3,²⁴ the assumption at that time, embedded in EXP-0, that V_CH2 is the same for different chain lengths at the same temperature, might also have been flawed because longer chain lipids are more ordered and have smaller area per lipid,¹ and are therefore would likely have smaller V_CH2. Indeed, a systematic difference versus chain length was shown many years ago (Fig. 5 in Nagle & Wilkinson¹³), although that difference could have been brought to zero by assuming larger values of V_H and r. Even alkanes might be intuitively expected to pack more tightly with smaller V_CH2 with increasing chain length because there is a smaller proportion of disrupting methyls when the chains are longer. In contrast, the EXP-1 method results in increasing V_CH2 with increasing alkane chain length. To provide insight into these differences we next turn to simulations.

3. SIMULATIONS AND ANALYSIS METHODS

3.1. Basic simulation methods.

Molecular dynamics simulations were performed with the CHARMM program²⁵ and employed the domain decomposition engine²⁶ to accelerate the calculations. The C36 lipid parameters⁶ were used, with the standard CHARMM TIP3P water model.²⁷ Most initial lipid models were built with the Membrane/Bilayer Builder tool from the CHARMM-GUI web site.²⁸ The initial models were minimized with large restraints on the glycerol configuration and chain double bonds, to preserve dihedral states and prevent chiral inversion at the glycerol C2 atom. For the lowest temperatures, the initial models started with heating from 100° below the target T over 200 ps with the same restraints, and then thermally equilibrated, using 3-step Verlet for the first 1 ns of each simulation. The higher temperature runs were started using equilibrated conformations from the lowest temperature simulations. DPPC and MLG models were built de novo in a similar manner to Membrane/Bilayer Builder. The lipid with C14:1(9–10) myristoleic chains, DMOPC, required a topology definition for a new residue; it was created by analogy from the DOPC definition, as the C=C bond was in the same location. The initial model coordinates were derived from an existing well equilibrated DOPC bilayer by removing the last four C atoms from each chain, then shifting the coordinates along the bilayer normal z axis to remove the empty space. DLPC, DMPC, DOPC, and DPPC systems used long simulations from previous work²⁹ for the lowest temperature, and well equilibrated bilayers were used as starting points for the higher temperatures. The non-bonded van der Waals term in the potential used VFWSITCH truncation over the range 8–12 Å; the particle-mesh Ewald method was used for the electrostatic non-bonded term, with a grid spacing of ca. 1 Å, and κ = 0.32 or 0.34. (One simulation was run twice, once with each κ value, with no discernible differences.) An integration timestep of 1 fs was used throughout, with coordinate sets saved in the trajectory files at 1 ps intervals. Number density histograms for each atom type in the molecules were extracted from the CHARMM trajectories. Additional results of the simulations are compiled in Supplementary Information part B.

Neat fluid alkane systems of n-dodecane (nC12), n-tetradecane (nC14), and n-hexadecane (nC16) were constructed by randomly sampling molecules from low friction Langevin dynamics simulations at 303 K of a single chain, and placing the molecules on a perturbed cubic lattice. The perturbation was a small random displacement from the lattice position; the lattice grid spacing used a volume estimate based on ca. 90% of the experimental density. Each system was then energy minimized in a cubic lattice using the volume estimate appropriate for the chain length. The minimized coordinates for each of the three alkanes were used as the starting point for MD simulations at temperatures of 30, 50 and 70 °C. Each simulation began with one ns of heating and thermal equilibration via the 3-step Verlet algorithm, with heating from 100° below the target T over the first 250 ps. The simulation protocol was as above for the lipid bilayers. The systems simulated are listed in Table 2.

Table 2.

Simulation systems.

System	Chainsa	T °C	trun (ns)	Nlipids	Nwaters
DLPC	12:0	30,50,70	420,110,110	72	2880
DMPCb	14:0	30,50,70	420,110,110	72	1848
DPPC	16:0	50,70b	420,110	72	2189
DMOPC	14:1 (9–10)	25,45,65	110,110,110	80	3040
DOPCb	18:1 (9–10)	25,45,65	420,110,110	80	3040
DEPC	22:1 (13–14)	25,45,65	110,110,110	80	3600
MLG	12:0	30,50,70	110,110,110	162	2891
Alkane	12:0	30,50,70	32,32,32	560	0
Alkane	14:0	30,50,70	32,32,32	392	0
Alkane	16:0	30,50,70	32,32,32	343	0

^aBoth chains are the same; cis C=C bond positions are indicated in parentheses.

^bThese simulations had κ = 0.32, the others used κ = 0.34; DOPC at 45 °C was run with both values of κ.

3.2. Methods of analysis of simulations

We used three methods for obtaining volumes from simulations. The first two methods, SIM-0 and SIM-1, are essentially the same as EXP-0 and EXP-1, respectively, in that they use only the total lipid volumes V_L for a sequence of lipids with different numbers of methylenes m to obtain V_CH2 and V_rem. The total lipid volume is easily obtained as the volume of the simulation cell minus the volume of all the water, then divided by the number of lipids.³⁰ Equivalently, V_L was obtained by adding the component volumes determined by the second method.

The SIM-2 method is conceptually quite different. It is a well-developed method^31–32 which is now implemented as part of the SIMtoEXP software package.³⁰ SIM-2 is applied separately to a single lipid chain length at a single temperature and so, unlike the EXP-1 and SIM-1 methods, the value obtained is computationally independent of other chain lengths. Briefly, SIM-2 uses the simulated distributions of all atoms in the z direction perpendicular to the bilayer normal. It then finds the volumes of all the components, given the simulated atomic distributions, by best conserving volume along the z axis for bins consisting of x-y slices, each 0.2 Å thick in the z direction. Any parsing of the lipid into components can be accommodated by SIM-2. Unless otherwise noted, the results in this paper parse the lipid hydrocarbon chains into three components consisting of (a) chain terminal methyls, (b) chain methylenes, and (c) chain methines, if any, and the phosphocholine headgroup into four components consisting of (d) carboxyls (2 COO groups), (e) glycerol backbone (CH₂CHCH₂), (f) phosphate plus nitrogen and two connecting methylene groups, and (g) three methyl groups bonded to the nitrogen.

Fig. 6 shows typical component volume fractions as a function of z. There is only water in the regions near the ± z boundaries of the simulated box and that water exterior to the lipid bilayer determines the volume of all the water molecules. Systematic differences in the volume of a component at its different z locations results in the sum of the component volume fractions not adding precisely to unity. Coarser parsings into fewer heterogeneous components increase these deviations and finer parsings into more components increase the uncertainties in the values of the component volumes (vide infra, Figs. 13 and 14). It might also be noted that the relatively small size of the simulation box means that it is not necessary to correct for undulations which, if uncorrected, would smear the components and make their effective separation more difficult.³³ The parsing shown in Fig. 6 yields total volume fractions that deviate less than 1% from the ideal of 1 and the deviations are nearly equal in different z ranges, suggesting that there is no particular z region that would preferentially benefit from having more components. This method does not involve arbitrary decisions as to how to place boundaries between unlike atoms if Voronoi tessellation were employed. SIM-2 shares with EXP-0, SIM-0, SIM-1 and EXP-1 the feature that it focuses on space filling volume rather than allowing free volume, butSIM-2 is not based on the concepts of apparent or partial molar volumes that underlie the other methods. Rather it is based on a local summation of volumes from different components. We will henceforth describe SIM-2 as a more local method than the previous methods.

Figure 6.

Volume fractions of the components described in the text versus distance z from the center of a DLPC bilayer at T=50°C.

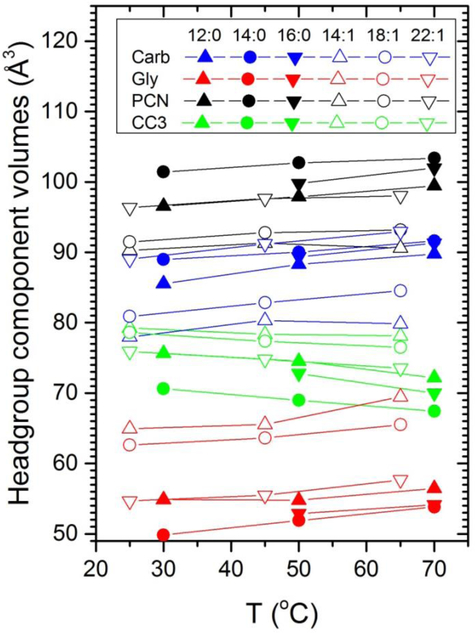
Figure 13.

Temperature dependence of the volumes of the four headgroup components obtained using SIM-2. In the legend, Carb consists of the carboxyl groups, Gly consists of the glycerol backbone, PCN consists of the phosphate plus nitrogen and two connecting methylene groups and CC3 is the three methyl groups attached to the nitrogen.

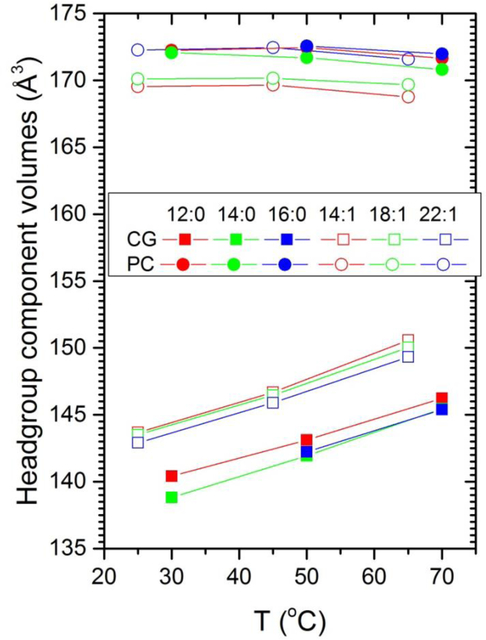
Figure 14.

Temperature dependence of the combined volume CG consisting of the carboxyl plus glycerol components shown in Fig. 13 and similarly of the PC volume consisting of the PCN plus CC3 components.

3.3. Calculation of component excluded volumes.

The calculation of a component free volume requires an estimate of the corresponding component excluded volume. The latter was carried out in two steps. First the excluded volumes of individual molecules were calculated using a grid-based method that counts occupied volume elements within a volume defined by the Lennard-Jones (L-J) radius for each atom type; the COOR SEARCH command in the CHARMM program was used here. (The L-J interaction energy between two identical particles separated by distance r is written V(r) = 4ε[(σ/r)¹²−(σ/r)⁶]where ε is the energy minimum and V equals 0 at r = σ; the L-J radius, σ/2, is therefore a natural boundary for defining an excluded volume. Values of σ are given in Supplementary Information part C.) Each selected molecule was oriented to the lab frame axes, and a bounding box was defined from the molecular extent with an added 2.5 Å buffer in all six directions. A grid with a spacing of 0.05 Å was defined within the bounding box, and the molecular volume computed as the sum of the occupied 1.25e-4 ų volume elements inside the bounding box. Ten molecules were randomly selected from simulation coordinate sets spaced 100 ps apart, using 40 ns of data for the alkanes, and 100 ns for the lipid bilayers. L-J radii are those from the CHARMM36 force field and are listed in the SI.

The second step in the calculation essentially uses the SIM-0 methodology, where the total molecular volume is replaced by the excluded molecular volume calculated in step 1. Figure S1 in the SI illustrates the procedure for alkanes. The excluded volume is highly linear when plotted vs number of methylene groups, so the component excluded volume of the methylene was calculated from the slope and that of the methyls from the y-intercept. The values are also essentially independent of temperature, consistent with the temperature-independent potentials used in CHARMM. Variation could still arise in principle from overlap of atomic volumes associated with increased gauche populations as temperature increases, but this effect was shown to be negligible. Hence, one set of excluded component volumes was used for all temperatures studied here. Component excluded volumes for methine groups and lipid head groups were obtained by calculating the molecular volumes of alkenes and lipids and subtracting the values of methylene and methyl groups obtained from the alkanes as just described.

4. SIMULATION RESULTS AND COMPARISON WITH EXPERIMENT

4.1. Methylenes on the hydrocarbon chains

Simulation results for V_CH2 for the diCn:0PC lipids are shown in Fig. 7 and compared to the EXP-1 results from Fig. 4. The EXP-0 results are statistically consistent with the SIM-1 results. (EXP-1 is not warranted due to experimental uncertainty.) Importantly, the temperature dependence is closely similar. Most importantly, the SIM-2 results are larger than the SIM-1 results. This shows that the two methods are not measuring the same quantity. Equally importantly, SIM-2 clearly obtains values of V_CH2(n) that decrease with increasing n.

Figure 7.

Comparison of V_CH2 of saturated lipids using the SIM-2 method with those obtained by EXP-1 (open squares) and those obtained by SIM-1 (filled black squares). Small open circles locate temperatures used subsequently in the EXP-SIM method.

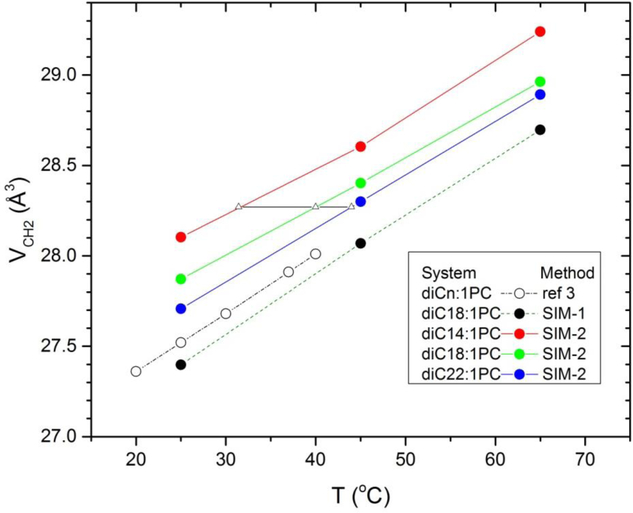
Figure 8 shows SIM-1 and SIM-2 results for V_CH2 for a sequence of diCn:1PC lipids. V_CH2 from SIM-1 is only slightly smaller than one of the literature results from Fig. 4. Most importantly, SIM-2 yields significantly larger values of V_CH2 than SIM-1, which again indicates that these two methods measure different quantities. It might be mentioned that there is a complication when obtaining the SIM-2 values in Fig. 8 because the double bond is located at the 9:10 carbon positions for n=14 and 18, which puts it halfway along the chains for n=18, but closer to the terminal methyl for n=14. For n=22, the double bond is in the 11:12 position, further from the headgroup. It is well known that the main transition temperature exhibits complex behavior with respect to the location of the double bond.³⁴ Likewise, the SIM-2 results exhibit irregular behavior in V_CH2 when the molecule is parsed in the usual way with a single component for all the chain methylenes. We have instead further parsed the methylenes in the hydrocarbon chain into two components, one for those methylenes with carbon number closer to the headgroup than the double bond and one for those methylenes closer to the terminal methyl. The volume of the methylene component closer to the terminal methyls is larger than the component closer to the headgroups by roughly 1 ų. The SIM-2 results in Fig. 8 show the average volumes for these two CH₂ components. This average indicates that V_CH2 decreases with increasing n for fixed T, similarly to the behavior of the diCn:0PC lipids in Fig. 7.

Figure 8.

Methylene volumes for the diCn:1PC lipids versus T. The SIM-2 method (colored circles) used two components. The analysis methods are indicated in the legend. The small triangles locate temperatures used in EXP-SIM.

Fig. 9 further emphasizes that the partial molar concept embedded in EXP-1 and SIM-1 does not measure the same quantity as the local SIM-2 method. For both saturated and unsaturated lipids SIM-2 obtains decreasing V_CH2 with increasing chain length. In contrast, SIM-1 obtains increasing V_CH2 with increasing m with the exception of diCn:1PC; that exception could be due to the above noted movement of the double bond with respect to the center of the chain for different chain lengths. Although this exception does not have significant differences in the n-dependence, it does have a large difference in the values obtained by SIM-1 versus SIM-2. Also shown in Fig. 9 are EXP-1 values for the alkanes. It is encouraging that they have the same m = n-2 dependence as for SIM-1, although there is an overall difference of 0.5 ų in the values consistent with small shortcomings in the force fields (see Section E of SI for further discussion.

Fig. 9.

Chain length dependence of methylene component volume for the systems and the methods in the legend. T=50°C except T=45°C for diCn:1PC lipids.

Figures 7 and 8 allow us to address the issue raised by Small⁷ of whether it would be better to compare volumes, not at the same temperature as in Eq. (2), but at the same temperature relative to the main transition temperature T_M. In Fig. 7 V_CH2 for DMPC at 50°C is the same as the V_CH2 for DPPC interpolated to 52°C. The difference in T at which the volumes are the same is somewhat smaller at the higher T and somewhat larger at the lower T when comparing DLPC and DMPC, but the overall average is about 2°C higher when adding two methylenes per chain as seen by the small open circles in Fig. 7. This is far less than the difference of 17°C in transition temperatures (T_M = 24.0° for DMPC and 41.4° for DPPC). In Fig. 8 the difference in temperature for equal volumes of diC18:1PC and diC22:1PC is 5.6°C at T= 25°C, 3.7°C at T= 45°C and 2.5°C at T= 65°C. (We ignore diC14:1PC because it is more difficult using SIM-2 to obtain robust values of V_CH2 due to the overlap of the lower CH₂ component with the terminal methyls.) Again, this is considerably less than the difference of 30.2°C in transition temperatures (T_M = −17°C for diC18:1PC and 13.2°C for diC22:1PC).

While the comparisons in the preceding paragraph indicate that EXP-0 should be applied using volumes at the same temperature rather than at the same relative temperature, they also suggest a refinement which we will call the EXP-SIM method. In this method the experimental volumes are fit as in Fig. 2, but at the temperatures at which the simulation indicates equal CH₂ volumes. For the diCn:0PC sequence shown in Fig. 7, we choose a temperature T₁₄ for n=14 and find the temperatures T₁₂ for n=12 and T₁₆ for n=16 that have the same simulated V_CH2. Then, the experimental volumes at these temperatures are fit as in Fig. 2. Numerical results using EXP-SIM are presented in Table 4 in Discussion.

Table 4.

Selected data for numerical comparison

Lipid&Method	T °C	VL (Å3)	VCH2 (Å3)	r	VH (Å3)
DMPC
EXP-1	50	1117	27.7	2.09*	337
SIM-1	50	1106	27.8	2.09*	323
SIM-2	50	1106	28.1	2.09	314
EXP-SIM	50	1117	28.0	2.09*	328
DOPC
EXP-1	40	1312	28.0	1.92*	330
SIM-1	45	1314	28.1	1.92*	335
SIM-2	45	1314	28.4	1.92	317
EXP-SIM	40	1312	28.3	1.92*	320
Hexadecane
EXP-1	50		27.7	2.03
SIM-1	50		28.1	2.28
EXP-SIM	50		27.9	1.95
EXP-Small7, 24	Trel=0		29.6	1.20

^*Fixed r values from SIM-2 result

4.2. Terminal methyls on the hydrocarbon chains

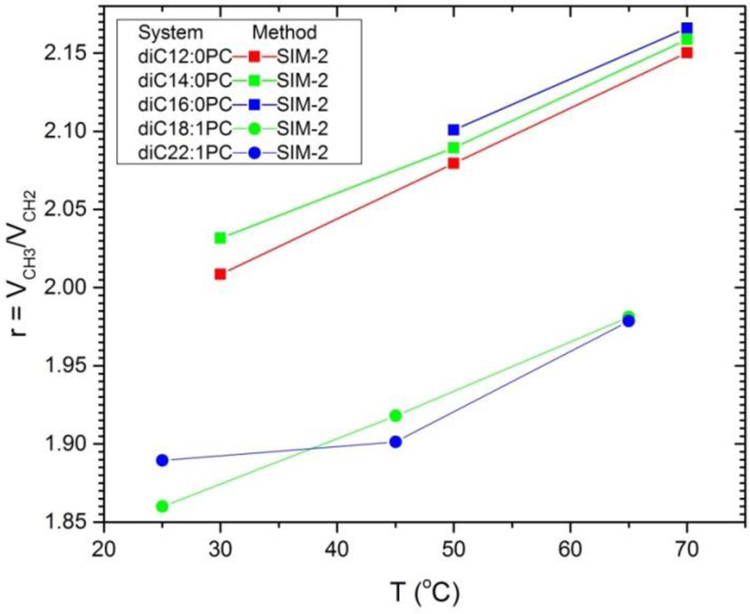
Turning next to simulated values for the terminal methyls on the hydrocarbon chains, Fig. 10 shows that simulations give very similar temperature dependence for lipids as for the experimental data for alkanes shown in Fig. 5. These results also suggest that the r ratio is smaller for the unsaturated lipids than for the saturated lipids and for the n-alkanes in Fig. 5. The highly systematic variation of r for the saturated lipids is not obtained for the unsaturated lipids, probably due to the awkward positioning of the double bond along the diCn:1PC sequence. Fig. 10 does not include SIM-1 results for r for lipids, because that would involve making assumptions about the headgroup volume, or SIM-2 results for alkanes because they cannot be obtained for isotropic liquids with no z-dependence.

Figure 10.

Temperature dependences of the ratios r of the terminal methyl volumes to the methylene volumes for saturated (squares) and unsaturated (triangles) lipids. The methods of analysis are indicated in the legend.

4.3. Headgroups

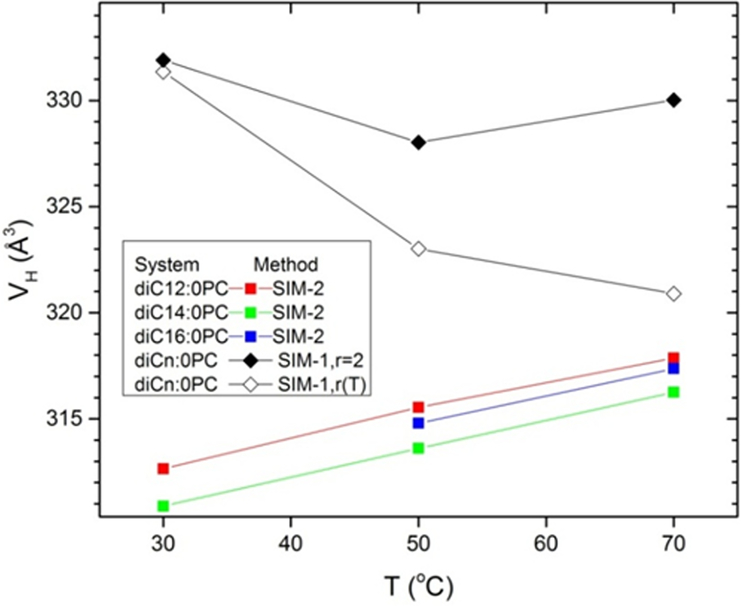
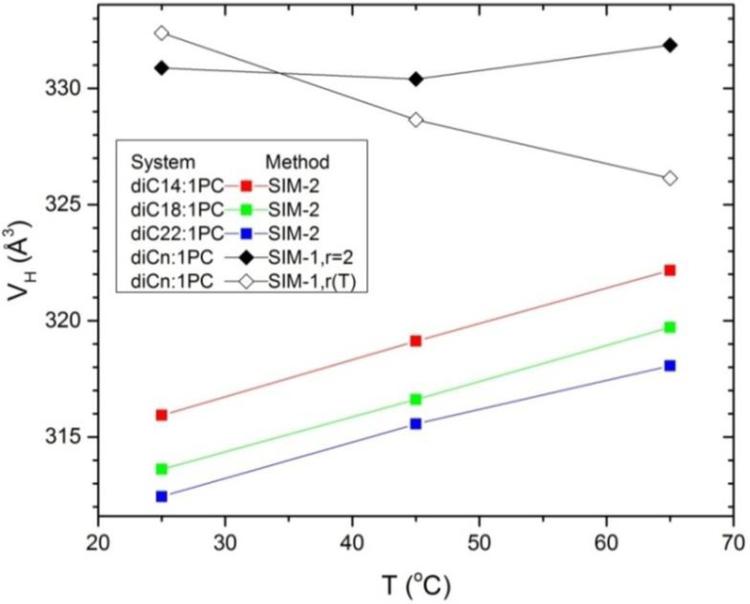
For the saturated chain sequence Fig. 11 shows that the headgroup volume V_H increases with T when analyzed using SIM-2 (squares), but that V_H is essentially constant for SIM-1 assuming r = 2 (filled diamonds) as for previous experimental analyses.^2–3 However, when the temperature dependence of r is assumed in SIM-1(open diamonds), V_H decreases with increasing T. The same behavior is observed for the unsaturated sequence of lipids as shown in Fig. 12. These SIM-2 results suggest that the decreasing headgroup volume with increasing T could be an artifact of the partial molar concept. The SIM-2 result for the temperature dependence of the headgroup volume of monolaurin glyceride (part D of Supplementary Information) is similar to those for the phosphocholines shown in Figs 11 and 12.

Fig. 11.

Temperature dependence of headgroup volume V_H for simulations of saturated lipids determined by SIM-2 (squares) and by SIM-1 with the r=2 constraint (solid diamonds) and using the simulated r(T) dependence (open diamonds).

Fig. 12.

Temperature dependence of headgroup volume V_H for simulations of diCn:1PC lipids determined by SIM-2 (squares) and by SIM-1 with the r=2 constraint (solid diamonds) and using the simulated r(T) dependence (open diamonds).

Moving on from the overall temperature dependence of the headgroups, the temperature dependence of the volumes of the components making up the headgroup may also be of some interest. While the volumes of most of the components in Fig. 13 increase with increasing T, the volume of the headgroup methyls (CC3 in Fig. 13 legend) decreases for all simulations. The trends with chain length are broadly similar for the diCn:0PC and the diCn:1PC sequences, although there are many exceptions in Fig. 13 due to the aforementioned uncertainty in obtaining robust values for component volumes using SIM-2 when the components have strongly overlapping z ranges. We note here that similar results are obtained when the PC part of the headgroup is parsed more conventionally as can be seen in Figs. S1 and S2 in a previous study.³⁵ This is because the PC headgroup is nearly parallel to the bilayer plane, so any parsing of the PC results in strongly overlapping components. These uncertainties are reduced when fewer, less overlapping, components are used as shown in Fig. 14. Figure 14 indicates that the volume of the CG group is larger for the unsaturated lipids which is consistent with their having looser packing due to their generally larger areas per lipid.^{1, 36} Also, there is little temperature dependence for the PC group, which is more fully immersed in water, than there is for the CG group.

Let us mention that, consistent with previous studies,^2–3 the SIM-2 volume of the methine component in the hydrocarbon chains of the diCn:1PC lipids, when divided by the volume of the methylene component, has negligible temperature dependence, unlike the volume ratio r for the chain terminal methyls.

Finally, we have addressed the issue of whether water in the interfacial headgroup region has the same volume as the water in the space exterior to the lipid where there is only water. For simulated DLPC at T= 50°C, 60% of the water was in the interfacial region with lipid and 40% was external to the bilayer for the unit cell shown in Fig. 6. When there is ample exterior water, SIM-2 has to find the water component volume to be that of the exterior water. However, one may truncate the distribution functions for the system at smaller values of ±z such that essentially all the lipid is contained but with no exterior water. When this was done, SIM-2 found that the component volume of water exclusively contained in the interfacial headgroup region differed insignificantly. While the volume of water in different locations might have been an interesting phenomenon, this result suggests otherwise.

4.4. Component Free Volumes.

Fig. 15 shows a representative configuration of DMPC with atoms depicted in space-filling spheres with the L-J radii (left), and with the component volumes of the headgroup and selected methyl and methylene groups depicted as transparent cylinders (right). The difference between the component volumes and component excluded volumes is the component free volume. Table 3 lists values for component volumes, component excluded volumes, and the percentage of the component volume that is free for three systems, DMPC, DOPC and n = 16 alkanes, at similar temperatures. As would be expected, the % free volume for any component is nearly the same for the different systems. The more notable result in Table 3 is that it is smallest for the head groups, and largest for the methyl groups. This is discussed further in Section 5.4.

Figure 15.

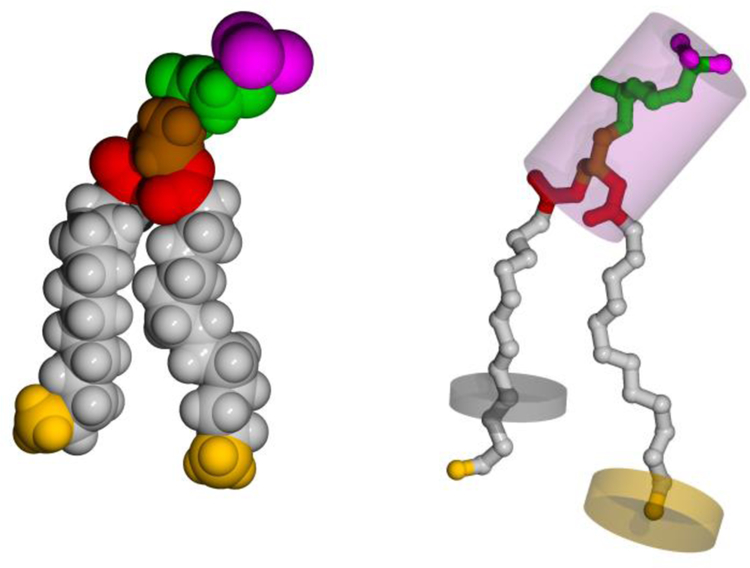
DMPC atoms shown as spheres with L-J radii (left), and as heavy atom balls and sticks with component volumes of the head group and a selected methylene and methyl in transparent cylinders superimposed (right). Chain methylenes are gray, terminal methyls are yellow, the carboxyl groups are red, the glycerol backbone is brown, the PC chain is green, and the choline methyls are magenta.

Table 3.

Selected volumes from DMPC, DOPC, and alkanes.

System	Group	Volumes (Å3)
		Component*	excluded	% free
DMPC (50 °C)	CH2	28.1	17.4	38.1
	CH3	58.7	24.3	58.4
	Head	328	250	23.8
DOPC (45 °C)	CH2	28.4	17.4	38.7
	CH3	54.5	24.2	56.6
	CH	21.9	15.2	30.6
	Head	320	250	21.9
Alkanes (50 °C)	CH2	27.7	17.4	37.2
	CH3	56.1	24.5	56.3

^*Component volumes for lipids are from SIM-2 and for n=16 alkane are from EXP-1.

5. DISCUSSION

5.1. What methodology should be used?

A central issue addressed in this paper is the accuracy of the values of the component volumes that are obtained from volume measurements. While the experimental value of the total lipid volume V_L is accurate at the 0.1% level, literature methods to obtain component volumes have employed assumptions. What we have called the EXP-1 experimental method follows the partial molar volume concept of physical chemistry in Eq. (2). EXP-0 can be thought of as an approximation to EXP-1 that follows the apparent molar volume concept in Eq. (1) as illustrated in Fig. 2. To the best of our knowledge, this distinction has not previously been made in the context of lipid or alkane component volumes. EXP-0 assumes that the average methylene volume V_CH2 is the same for all chain lengths at the same temperature for homologous lipids that differ only by the number of methylenes m. EXP-1 does not make this assumption and Fig. 3 shows that there is definite chain length dependence when applied to alkanes. There are not as many chain lengths available for homologous lipids and the experimental accuracy is lower, so it is difficult to claim m dependence for lipids from experiment; however, m dependence is found for the SIM-1 results shown in Fig. 10. Nevertheless, values obtained using Eq. (1), when constrained to the typical chain lengths available for lipids, are not much different from those obtained by the EXP-1 partial molar volume method, so the distinction between apparent and partial molar component volumes is a relatively minor concern regarding numerical values of V_CH2. While the apparent molar volume approximation in Eq. (1) has been the working assumption, often implicit, for much research, it was also once proposed that equal average methylene volume would only occur at the same temperature difference relative to the main phase transition temperature and that resulted in much larger differences.⁷ This paper uses simulations to illuminate this and further issues.

To facilitate this discussion, Table 4 displays some of our results numerically. To be succinct, only DMPC (diC14:0PC), DOPC (diC18:1PC) and hexadecane (n=16 alkane) are included. For convenience in further discussion, Table 4 labels the experimental results for the lipids as EXP-1; DMPC and DOPC are the middle members of their respective homologous sequences and then there is no practical difference with the results of EXP-0. As we rely heavily on some of the simulation results, it is appropriate first to admit that there can be differences between simulated total V_L and experiment that can be attributed to small errors in the force fields. Comparing the simulated and experimental volumes in the V_L column shows excellent agreement for DOPC, but a difference of about 1% for DMPC. However, that is not necessarily relevant for the determination of V_CH2 using SIM-1 because both SIM-1 and EXP-1 only depend on the differences in the volumes of homologous lipids with different chain lengths. Those differences with chain length are very nearly the same for experiment and simulation which is why V_CH2 is essentially the same for SIM-1 and EXP-1 for the same lipid. This means that the difference between experimental and simulated V_L is not important for the methylene volume, although it does become important for the remaining components, which motivated our new EXP-SIM method discussed below.

Before doing that, however, a more significant difference appears in Table 4. Methylene volumes using SIM-2 in Table 4 are larger by about 1% than the SIM-1 and EXP-1 values. Which value is likely to be better? The SIM-2 analysis uses detailed information about the atomic distributions, which is a wealth of information compared to just total volume measurements for a few chain lengths. The results in Figs. 7 and 8 show that homologous lipids that differ by two methylenes per chain have equal volumes only when the temperature of the longer lipid is about two degrees greater than for the shorter lipid. This doesn’t seem surprising because longer chain lengths would be expected to pack more tightly, as is well documented for the gel phase as shown by wide angle x-ray scattering.^37–38 Figure 9 shows that SIM-2 results agree with this expectation, but SIM-1 and EXP-1 results generally do not. On the other hand, EXP-1 and SIM-1 employ the partial molar volume (∂V_L/∂m), which is a well-defined physical chemical quantity that automatically leads to the volume conserving relation V_L = ∑_iN_iV_i. This is arguably superior to SIM-2 which doesn’t quite conserve volume. However, partial molar volumes do not necessarily reflect any reasonable local volume; indeed it is even negative for small concentrations of Na+ ions in water.³⁹ In this case partial molar volume accounts for the electrostriction of the nearby water. While this is technically a local effect, it is takes place over a larger region than the ion itself. By comparison, the SIM-2 method focuses on regions closer to the physical size of the components, so we describe it as a more local measure of component volume.

We therefore suggest that the SIM-2 approach is superior for obtaining the kind of local volumes for use in modeling structure using x-ray and neutron scattering data. The SIM-2 volumes are also more appropriate for comparing to local excluded volumes to obtain component free volumes. However, SIM-2 values rely exclusively on force fields subject to error. Therefore, we propose the EXP-SIM method that combines the SIM-2 and EXP-0 approaches to obtain more accurate experimental values for V_CH2. EXP-SIM applies simulation deduced temperature offsets to the highly accurate experimental V_L data. As shown by the small circles in Fig. 7, one chooses the temperature T of the middle chain length and then finds, using SIM-2, the temperature offsets ΔT_n of the other chain lengths n at which the simulated V_CH2 volumes are equal. Then, there is no difference between Eq. (1) and Eq. (2), so the experimental total lipid volume V_L for different chain lengths n is obtained at T+ΔT_n and plotted as in Fig. 2 in order to obtain V_CH2 from the slope and the remainder volume from the intercept. This use of the experimental data avoids the problem of imperfect force fields that do not match the experimental total lipid volume. Justification for using SIM-2 to obtain the ΔT_n is provided if the simulation, when analyzed with SIM-1, gives temperature dependence that agrees with experiment, as is the case for the simulations in this paper. In other words, the scale of the total volumes is tied exclusively to the scale of the experimental data while the simulations provide the temperature for equal methylene component volumes. The EXP-SIM values of V_CH2 shown in Table 4 lie between the SIM-2 and EXP values, but closer to the SIM-2 values.

5.2. Comparison of fluid phases

Table 4 also shows results for the ratio r = V_CH3/V_CH2 of chain terminal methyl volume to methylene volume obtained from the SIM-2 method. Interestingly, r is larger for DMPC than for DOPC, although the average is the often assumed value of 2. Of course, the V_H entries in Table 4 for EXP-1 and SIM-1 are larger than for SIM-2 because their V_CH2 are smaller. It is reassuring that the SIM-2 values of the headgroup volume V_H are nearly the same for DMPC and DOPC, but these values will not be accurate if the simulation gives different values of V_L than experiment. The better local values of V_H are given by EXP-SIM. For DMPC it is close to the V_H value reported for gel phase DMPC⁴⁰ and V_H for DOPC it is close to the value reported for gel phase DPPC.⁴¹ We suggest that these various values provide an estimate of the uncertainty in V_H that should be applied when fitting structural models to x-ray and neutron scattering data. Similarly, only a soft constraint that allows deviations of ±0.1 should be applied to the r value.

Table 4 also summarizes some results for the alkanes. The SIM-1 and EXP-1 values for V_CH2 are significantly different. With no head group, it is straightforward to obtain r values (e.g., see Fig. 5); the value of 2.32 from the simulation is 10% larger than experiment. Both the V_CH2 and the r results indicate an area for simulation improvement. (Such an improvement has been made for alkanes (see Supplementary Information part E), but the method has not yet been implemented for simulation of lipids.) Unfortunately, there is no way to extract component volumes using SIM-2 because that method requires orientation and alkanes are isotropic liquids. Nevertheless, Table 4 has a row for EXP-SIM for which the same ΔT_n were used as for the saturated lipids; as for the lipids this resulted in a larger V_CH2. The last row in Table 4 also shows the quite different values of V_CH2 (2 ų larger) and r (only 57% as large) using Small’s method of comparing different chain lengths at the same temperature just above the melting transition (T_rel=0).^{7, 24}

Table 4 and Figs. 4 and 9 indicate that unsaturated DOPC has somewhat larger V_CH2 than saturated DMPC, which is consistent with double bonds inducing additional disorder. Also, DMPC has slightly larger experimental V_CH2 than the alkanes according to the entries in Table 4, with even larger differences at the higher temperatures shown in Fig. 4. Apparently, the anisotropy imposed by a planar bilayer doesn’t just reduce the conformational disorder which would be expected to decrease V_CH2. We also have no explanation for the small differences in r values among DMPC, DOPC and the alkanes. Regardless, they are all close to 2 unlike the value of 1.20 obtained from the alternative EXP-Small method for the alkanes.

The initial focus of this study was on the temperature dependence of component volumes, especially of the headgroup V_H. As has been previously shown in Fig. 5, r depends on T for alkanes and our SIM-2 results are in agreement for lipids as shown in Fig. 10. When this temperature dependence is combined with the V_CH2 obtained using the methods in Eq. (1) and (2), one obtains the counterintuitive result that the headgroup volume V_H decreases with increasing T as shown in figs. 11 and 12. However, when we combine r (T) with the V_CH2 obtained using the SIM-2 method, Figs. 11 and 12 show that V_H increases normally with increasing T. Nevertheless, there is a nuance regarding what should be considered normal and counterintuitive that is exposed in Figs. 13 and 14; the volume of the PC component that is most fully hydrated has little T dependence in contrast to the more deeply buried CG component. The CG component is partially buried in the bilayer so its volume would be expected to increase normally for the same reasons that the hydrocarbon volume increases. In contrast, the PC component is relatively more completely surrounded by water which more completely fills the volume around it as temperature (and therefore area/lipid) increases. More remarkable is the decrease in the headgroup methyl component volume with increasing temperature shown in Fig. 13. Regardless, we believe that the SIM-2 method obtains the true T dependence for the local value of V_H, and that the EXP-1 method combined with an increasing r(T) misleadingly gives decreasing V_H with increasing T as a consequence of using partial molar volume values of V_CH2. This conclusion is based on the insight that simulations have provided by comparing SIM-1 and SIM-2 results in Figs. 11 and 12.

How much difference does the neglect of temperature dependence make for the values of component volumes? Interestingly, the SIM-1 results in Figs. 11 and 12 show that the assumption that r = 2 with no T dependence leads to V_H with little T dependence, which is consistent with the way that experimental volume data have been analyzed previously.^2–3 Over a 40°C range of temperature, V_H in Fig. 14 increases only about 5 ų and r in Figs. 9 and 10 increases only by about 0.1. These differences are smaller than the difference between different lipids in Table 4, so the more important uncertainties are the somewhat larger differences in r and V_H between different lipids seen in Table 4. Guidelines for these values and their uncertainties have been noted at the beginning of this subsection.

5.3. A broader perspective

While Table 4 clearly shows differences in the methylene component volume obtained by the different methods of analysis as well as for saturated versus unsaturated lipids in the fluid phase, these pale in comparison to differences between different phases of lipids and alkanes that are shown in Table 5. The fluid phase values in Table 5 are represented by the EXP-SIM results in Table 4. The contemporaneous gel phase DPPC results are obtained from data obtained to higher q than earlier studies.⁴² The range of previously reported V_CH2 values (25.3 to 25.9 ų) is substantially smaller than the difference between them and the fluid phase values in this paper. A further decrease occurs for the subgel phase of DPPC and a further decrease for a crystal phase with only two water molecules per lipid.⁴³ Turning to the r values, the alkane crystal value is smaller than the alkane fluid value obtained from EXP-SIM. The subgel values of r were previously assumed to be the same as for the alkanes.²⁴ Table 5 also has a reworked line where r was assumed to be the same as for the gel phase. This line yields a headgroup volume V_H that agrees better with other V_H in the table, in agreement with the assumption that V_H should be much less dependent upon the thermodynamic phase than V_CH2.¹

Table 5.

Comparisons with other phases

System	T (°C)	VL	VCH2	% free	r	VCH3	% free	VH	% free
DPPC Fluida	50	1232	28.0	37.9	2.09	58.5	58.6	328	23.8
Gelb	20			31.2		52.6	54.0		24.5
Subgel24	10	1144	25.3	27.5	2.08	42.5	43.1	331	28.2
Subgelc	10			27.5		49.9	51.5		24.9
Crystald	10–15	1104	24.0	21.3	1.77	39.1	38.1	348	21.6
		1104	24.0		2.08			333
		1107	22.1		1.77			319
DOPC Fluida	40	1303	28.3	38.5	1.92	54.3	55.4	320	21.9
Alkanes Fluida	50		27.9	37.6	1.95	54.4	55.5
Crystale	28		23.6	26.3	1.77	41.8	42.1
Excluded			17.4		1.39	24.2		250

^aFluid phase values are EXP-SIM entries from Table 4. Volumes are in ų.

^bNagle et al.⁴²

^cUsing alternative values of r and V_H.

^dPearson and Pascher⁴³ when constraining r and V_H as shown and water molecular volume to 30 ų.

^eUsing data for C₂₁H₄₄ from Schaerer et al.⁴⁴

The final row in Table 5 lists the Lennard-Jones component volumes. These are much smaller than the space filling volumes for the same reason that packing hard spheres together only fills precisely 74.04…% of the volume. Even when objects are packed together as tightly as possible, “free” volume must occur in the regions that cannot be in hard core contact. Table 5 includes columns for the percentage free volume of the methylene and of the headgroup. The C₂₁H₄₄ alkane crystal V_CH2 free volume (26.3%) is the analogue of the free volume of hard sphere packing. It is remarkably close to the free volume of sphere packing (25.95…%) considering the difference in shapes. The subgel free volume is only slightly greater, followed by a significant increase in the gel phase and an even larger increase for the lipid fluid phase. Compared to the baseline free volume (26.3%) of crystal alkanes, fluid phase lipids have excess free V_CH2 volumes of about 12%. In contrast, the free volume of the headgroup is relatively insensitive to the lipid phase. While this seems inconsistent with the SIM-2 temperature dependence in Figs. 11 and 12, those differences are small and within the uncertainties for V_H in Table 5. Another consideration is that the headgroups in the gel and subgel phases are less surrounded by the relatively small water molecules than in the fluid phase; small molecules surrounding an irregular large component reduces the free volume compared to packing the large components. This would balance the natural increase in volume with increasing temperature. Finally, the value of r is smaller for the crystal alkanes than for the fluid phases and it decreases even further for the L-J volumes. This makes the increases in V_CH3 free volume even greater upon fluidization than the increase in V_CH2 free volume, consistent with the more fluid terminal methyl end of the hydrocarbon chains having a greater repulsive fluctuation force that would require more free volume.

6. CONCLUSIONS

This paper elucidates different methods for obtaining component volumes of lipids. We find that the apparent and partial molar volume approaches (Eqs. (1) and (2)) combined with an increasing ratio r(T) of terminal methyl volume to methylene volume gives headgroup volume V_H that decreases with increasing T when applied to both experimental data (EXP-0 and EXP-1) and simulations (SIM-0 and SIM-1). In contrast, SIM-2, which is based on a more local analysis of component volumes, finds an increasing V_H with increasing T. There is also a difference in the chain length dependence, so the two types of method are measuring different volumes. For our best estimates of the local component volumes we introduce the EXP-SIM method which combines the highly accurate experimental results for total lipid volume with the temperature dependence obtained from simulations. While there are clear differences in the values for the component volumes obtained by the different methods, as well as clear differences between fluid phase alkanes, saturated and unsaturated phosphocholine lipids, these pale in comparison to differences in the methylene component volume between fluid phases and chain-ordered phases. In contrast, the headgroup component and free volume are not much different for different phases.