Nonparametric Bounds for the Risk Function

Abstract

Nonparametric bounds for the risk difference are straightforward to calculate and make no untestable assumptions about unmeasured confounding or selection bias due to missing data (e.g., dropout). These bounds are often wide and communicate uncertainty due to possible systemic errors. An illustrative example is provided.

Nonparametric bounds are the minimum and maximum values of the target parameter (e.g., risk difference) that are compatible with the observed data (1–3). We are often interested in bounds because, assuming we believe the observed data, these bounds provide the space in which the true but unknown parameter value must lie. The difference in the risk of an outcome if everyone in the population were treated minus the same risk if everyone were untreated is a causal risk difference, which has a possible range from −1 to 1 (4). In contrast, the associational risk difference is the difference in the risk of an outcome for those observed to be treated minus the same risk for those observed to be untreated. In observational data, the associational risk difference is point-identified (i.e., we can compute a single numerical value), but the causal risk difference is not identified without additional untestable assumptions. The causal risk difference is point-identified when treatment is assigned randomly, as in randomized experiments.

It is commonly believed that bounds on the causal risk difference (henceforth, “risk difference”) for nonrandomized data are uninformative. The logic for this belief is based on the observation that such bounds are guaranteed to have unit length and thereby always include the null hypothesis value of a zero risk difference (1). We believe this is a pessimistic perspective.

An optimist might say that such bounds cut the interval for the possible range of the risk difference in half. The bounds do so with identification conditions stemming from causal consistency (5–7) and negligible measurement bias (8) and notably do not require exchangeability of treated and untreated groups (i.e., unmeasured confounding might be present). Bounds properly reveal an ignorance interval associated with a possible lack of exchangeability that occurs in the absence of randomization (9). In expectation, ideal randomized experiments guarantee exchangeability between treatment groups by design. In such cases, the upper and lower bounds collapse to the same point.

With an important exception (1), discussions and illustrations of nonparametric bounds are typically limited to a single probability (2, 3, 10–13) rather than the set of probabilities that define a survival or risk function (14). In making such a simplification, discussions fail to address the possible uncertainty due to selection bias from missing data, such as censoring due to dropout, which affects both randomized and nonrandomized studies (15). Here we illustrate how to estimate nonparametric bounds on the risk difference function over time, which accounts for possible unmeasured confounding as well as selection bias due to missing data.

METHODS

Example data

Lau et al. (16) reported on 1,164 adult human immunodeficiency virus (HIV)-positive and acquired immune deficiency syndrome (AIDS)-free women enrolled in the Women’s Interagency HIV Study (17, 18). We illustrate here the estimation of bounds for the risks of AIDS or death according to reported baseline use of injection drugs, as well as the risk difference, over the 10-year follow-up period. We note that injection drug use in these data is prevalent at baseline, and use might change over follow-up. For pedagogical purposes, we imagine that drug use is incident and fixed over follow-up (alternatively, we wish to learn the effect of the point exposure of drug-use initiation). Specifically, we estimate the crude risk difference function and the bounds for the risk difference function.

Women were followed from December 6, 1995 (baseline), for a combined outcome of incident AIDS diagnosis or death from any cause. Of 1,164 women, 439 (38%) were classified as exposed to injection drug use based on data reported as of baseline; 672 of 1,164 women (58%) were black. The median age was 36 (quartiles: 31, 41) years at baseline, and lowest recorded CD4 count prior to baseline was 139 (quartiles: 85, 207) cells/mm³. Of the 1,164 women, 127 (11%) were lost to follow up.

Statistical methods

We assume throughout that the sample of women is effectively a random sample from the population of interest, such that we can ignore the issue of generalizability (19). We assume that the data are measured with negligible error (20), that there is no interference (21), and that exposure versions are irrelevant (5, 6). For all estimates, we present pointwise 95% confidence intervals based on a standard asymptotic normal approximation of the crude and bounded risk differences (i.e., ${\hat{b}}_L-1.96\times se({\hat{b}}_L)$ to ${\hat{b}}_U+1.96\times se({\hat{b}}_U)$, where ${\hat{b}}_L$ and ${\hat{b}}_U$ are the estimated lower and upper bounds). These confidence intervals coincide with what Vansteelandt et al. (9) call a strong uncertainty region. Next we describe the bounds.

First, assume complete follow-up data for all subjects (i.e., no dropout). Treatment (or exposure) is denoted as $A=a$, say $a=\{0,1\}$. Suppose the outcome of interest is an event time, denoted as T, where $T>0$. Let $\mathrm{\tau }$ denote the maximum follow-up length (here $\mathrm{\tau }=10$ years). Let $T(a)$ denote the potential outcome (or counterfactual) event time under treatment $A=a$. Then, by the law of total probability, the counterfactual risk at time $t$ for $a=1$, $P\left\{T\left(1\right)<t\right\}$, equals

$$\begin{array}{l}P\left\{T\left(1\right)<t|A=0\right\}P\left(A=0\right)\\ +P\left\{T\left(1\right)<t|A=1\right\}P\left(A=1\right)\end{array}$$ (1)

Likewise for $a=0$. We observe treatment $A$ and event time $T$, but we do not observe both counterfactuals $T(0)$, $T(1)$. The second probability in equation 1 is the complement of the fourth probability, both of which are identified with observed data. With a sample of $n$ subjects, we may consistently estimate $P(A=a)$ using the nonparametric estimator $\hat{P}(A=a)=n^{-1}{\sum }_{i=1}^{n}I\left(A_i=a\right)$. Under causal consistency, the third probability in equation 1 is also identified, and we may consistently estimate it similarly. In a nonrandomized study, the first probability in equation 1 is not identified without additional assumptions (e.g., exchangeability), and therefore cannot have a consistent estimator. However, the first probability may be replaced with its bounds of 0 and 1 to provide bounds for the counterfactual risks $P\{T\left(a\right)<t\}$. Note that the unidentified first probability in equation 1 is scaled by the probability of being untreated $P(A=0)$, such that the bounds on $P\{T\left(1\right)<t\}$ (or treated risk bounds) are a function of the proportion untreated (e.g., if 2/3 are treated, then the bounds for the treated risk have width 1/3). Likewise, for the untreated risk bounds. Therefore, when we take the maximal difference between the treated risk bounds and the untreated risk bounds, we have a resulting unit length.

Next let $\mathrm{\Delta }=1$ indicate an observed study event, and suppose a fraction of subjects are missing data on their event time $T$ (e.g., due to dropout), in which case, $\mathrm{\Delta }=0$. The target parameter remains $P\{T(a)<t\}$ and can now be expressed as $\sum _{\delta ,a}P\{T\left(a\right)<t|\mathrm{\Delta }=\delta ,A=a\}P(\mathrm{\Delta }=\delta ,A=a)$. Identified probabilities can be consistently estimated using nonparametric estimators, and unidentified probabilities can be replaced with bounding values, both as above. Bounds that account for both confounding and selection bias will be wider than unit interval.

All that remains is to calculate the bounds. We can operationalize the above approach as follows. For each subject, create a doppelganger (or copy) with the treatment set to its complement. For the first of 2 bounds, treated doppelgangers are immediate events at $T=\mathrm{ϵ}$ (where $\mathrm{ϵ}>0$ is smaller than the first observed event time), and untreated doppelgangers are nonevents at the end of the study period $T=\mathrm{\tau }$. Conversely, for the second of 2 bounds, treated doppelgangers are nonevents at the end of the study period and untreated doppelgangers are immediate events.

To further account for possible selection bias due to missing data (e.g., dropout), the observed data from nondoppelgangers is altered as follows. For the first of 2 bounds, treated observations with unobserved events $\mathrm{\Delta }=0$ are set to be events at the time last observed $T=t$, and untreated observations with unobserved events $\mathrm{\Delta }=0$ are set to remain nonevents with times moved to the end of the study period $T=\mathrm{\tau }$. For the second of 2 bounds the converse is undertaken. Of course, one can estimate bounds selectively accounting for possible selection bias due to missing data, while assuming treatment groups are exchangeable (i.e., no confounding), as might occur in a randomized experiment. Illustrative pseudocode is presented in the Appendix.

RESULTS

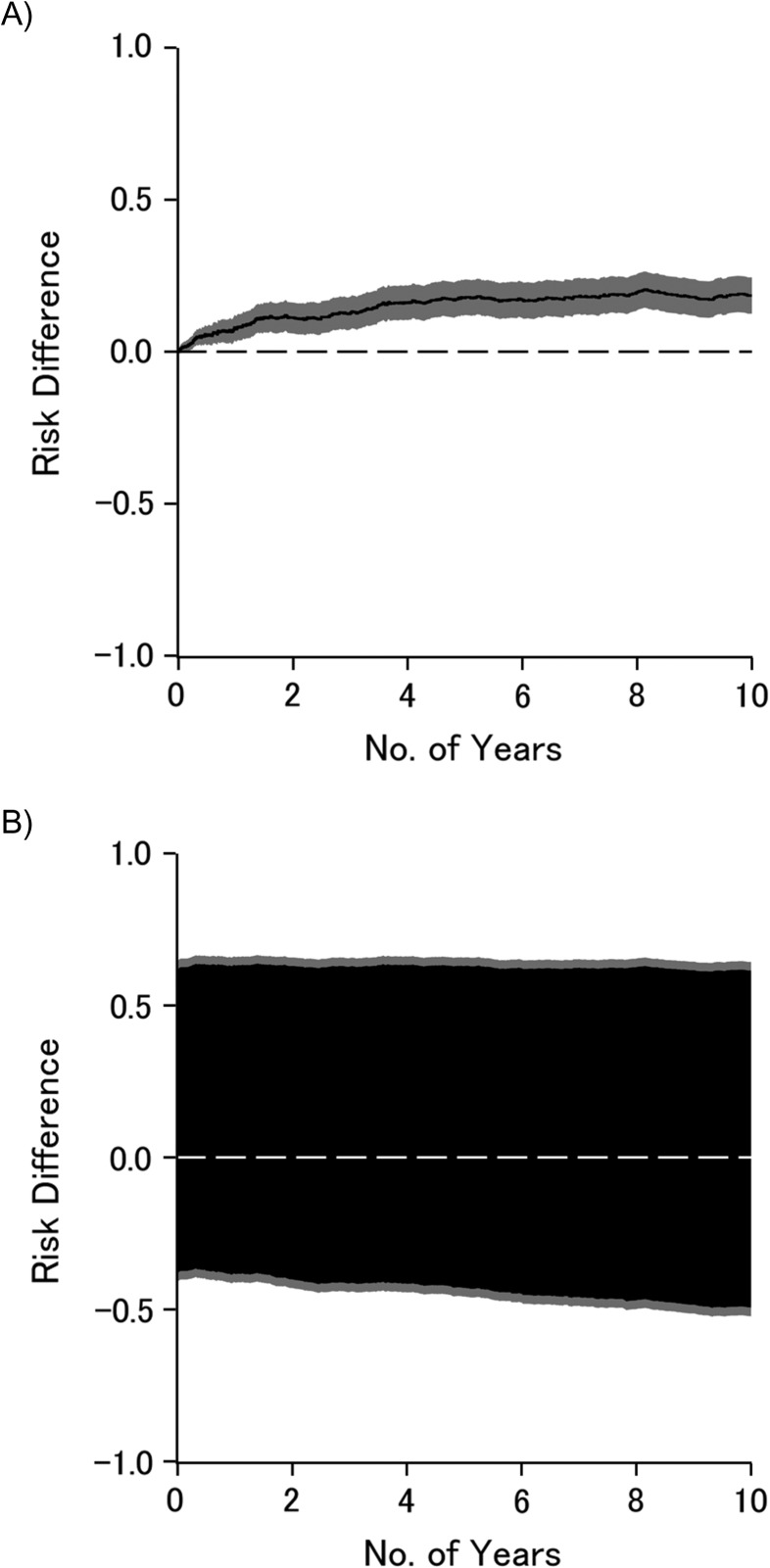
Table 1 presents estimates of the 10-year risks of AIDS diagnosis or death from any cause according to injection drug use. As can be seen, accounting for measured confounders age, race, and nadir CD4 using inverse-probability weighting did not materially alter the 10-year risks or risk difference, compared with the crude risks and risk difference. The 10-year bounded risk difference was, as expected, notably wide compared with the point estimator, which assumes no confounding or selection bias. Figure 1 illustrates the crude risk difference (Figure 1A) and the risk difference bounded for confounding and selection bias (Figure 1B) as functions of time on study; the black lines (or areas) represent point (or set) estimates, and gray areas represent the 95% confidence intervals. Briefly, the effect apparent under the strong assumption of no unmeasured confounding or selection bias weakens to become only suggestive once we allow for possible unmeasured confounding and selection bias. Other investigators provide detailed systematic exploration of how to leverage information provided in the bounds (1, 12, 22).

Table 1.

Ten-Year Risks of Diagnosis of Acquired Immune Deficiency Syndrome or Death From Any Cause According to Injection Drug Use in the Women’s Interagency HIV Study, United States, 1995–2006

Approach	No. of Participants	No. of AIDS Diagnoses or Deaths	10-Year Risk	10-Year Risk Difference	95% CI
Crude
Injection drug use	439	272	64.0	18.5	12.5, 24.5
Nonuse	725	307	45.5	0
IP-weighteda
Injection drug use	439	272	63.0	16.0	10.0, 22.1
Nonuse	725	307	47.0	0
Bounded
Injection drug use	439	272 and 1,023b	23.4 and 87.9b	−49.4 to 61.5	−52.3, 64.3
Nonuse	725	847 and 307b	72.7 and 26.4b	0

Abbreviations: AIDS, acquired immune deficiency syndrome; CI, confidence interval; HIV, human immunodeficiency virus; IP, inverse probability.

^a Accounting for race (black or not) and for age in years and nadir CD4 cell count (cells/mm³), both at baseline.

^b First and second numbers are for best and worst case for injection drug use, respectively.

Figure 1.

Difference in risk of acquired immune deficiency syndrome diagnosis or death from any cause by injection drug use, as a function of time on study, Women’s Interagency HIV Study, United States, 1995–2006. Crude results (A); bounds for confounding and selection bias (B). Black line or area is the point or set estimate, and gray area is the 95% confidence interval. HIV, human immunodeficiency virus.

DISCUSSION

What would it mean to solve the problem of unmeasured confounding? Of course, the problem of unmeasured confounding is solved already in the sense that randomized experiments provide point-identified solutions for effects of treatment assignment (23). Randomized experiments prevent unmeasured confounding; at least the ideal experiment does so in expectation. Rather, when trying to “solve the problem of unmeasured confounding,” we often mean not prevention but cure. How do we cure the problem of unmeasured confounding in nonrandomized studies? It is helpful to think about how we would do so in a randomized experiment that was broken in the sense that key data were missing. Any such prevention or cure would avoid (or at least weaken) an assumption of no unmeasured confounding, as does the randomized experiment. Such exchangeability assumptions (e.g., no unmeasured confounding, appropriate instrumental variable (24)) are the current state of the science in nonrandomized studies. Perhaps a cure would yield point-identified answers, akin to randomized experiments. Perhaps it would be folly to expect point identification without randomization or something nearly as strong.

However as soon as we relax our insistence on point identification, we have a solution in hand, albeit not widely recognized. The solution does not require any assumption about unmeasured confounding, and the solution immediately and simply allows estimates as well as confidence intervals. The solution is to provide an interval or set estimate, rather than a point estimate. Simply put, bounds are a solution to the problem of unmeasured confounding. Recalling Tukey’s apocryphal use of out-of-focus slides to convey uncertainty, in the presence of uncertainty about confounding, we have to draw our figures with a thick marker instead of a sharp pencil.

For confidence intervals, we used what Vansteelandt et al. called a strong uncertainty region (9). This strong uncertainty region is a conservative pointwise uncertainty interval for the parameter of interest, and tighter intervals with appropriate coverage can be obtained by replacing the standard multiplier by an alternative described in Vansteelandt et al. (9) and Imbens and Manski (25). For bounds that include minimum or maximum functions, such as instrumental variable bounds (26), alternative inferential methods are needed to construct valid confidence intervals (27). Here we discussed pointwise uncertainty intervals for the bounds of the risk functions; one could also entertain simultaneous uncertainty bands for the bounds of the risk function, analogous to the well-known distinction for confidence bands (28, p. 109). In some settings the width of the bounds might also be reduced by using covariates that are associated with treatment or the outcome (29).

The foremost argument against the use of bounds is that they are uninformative. That the bounds are often uninformative is itself highly informative: It is usually good to learn what one does not know! Such bounds provide a frame of reference in which the actual treatment or exposure effect lies (to the extent that data are measured without error). Such bounds also provide a logical underpinning to further refinements on analyses, such as point identification by assuming no unmeasured confounding as well as providing a space for sensitivity analyses to span. However, presenting the bounds alongside traditional point estimates provides helpful context in settings where nonrandomized data are the only feasible route to causal inference. In some settings, particularly those with either strong prior beliefs or strong preference functions, policy decisions can be grounded on set-identified bounding analyses (22).

We are not the first to call for presentation of bounds. For example, Swanson et al. conclude “If nothing else, estimating the bounds can serve as a reminder to remain humble about how much information the data really provide” (26, p. 945). Robins and Greenland argue for reporting bounds and state “Wide bounds make clear the degree to which public health decisions are dependent on merging the data with strong prior beliefs” (30, p. 457). Finally, perhaps such bounds will provide a bridge over which those conducting observational studies can communicate with colleagues conducting clinical trials with more signal and less noise.

Abbreviation

AIDS

acquired immune deficiency virus

APPENDIX

Algorithm to calculate bounds

Bound algorithm:

1. Bound 1, the worst case for treated.

2. Alter the observed record.

   • If a = 1 and ∆ = 0 then: a1 = a, ∆1 = 1, t1 = t.
   • Else if a = 0 and ∆ = 0 then: a1 = a, ∆1 = 0, t1 = τ.
   • Else if ∆ = 1 then: a1 = a, ∆1 = ∆, t1 = t.
3. Augment data with a doppelganger.

   • If a = 1 then: a1 = 1 – a, ∆1 = 0, t1 = τ.
   • Else if a = 0 then: a1 = 1 – a, ∆1 = 1, t1 = ε.

4. Adapt above steps for bound 2, the worst case for untreated.

5. Compute standard estimators for risk to the altered and augmented data.

Note: τ is the length of the study period, and ε is an arbitrarily small number (i.e., larger than 0 but smaller than the first event time).