Abstract
We introduce a number of computationally inexpensive modifications to the MM/PBSA and MM/GBSA estimators for binding free energies, which are based on average receptor-ligand interaction energies in simulations of a noncovalent complex, to improve the treatment of entropy: second- and higher-order terms in a cumulant expansion and a confining potential on ligand external degrees of freedom. We also consider a filter for snapshots where ligands have drifted from the initial binding pose. The variations were tested on six sets of systems for which binding modes and free energies have previously been experimentally determined. For some datasets, none of the tested estimators led to results significantly correlated with measured free energies. In datasets with nontrivial correlation, a ligand RMSD cutoff of 3 Å and a second-order truncation of the cumulant expansion was found to be comparable or better than the average interaction energy by several statistical metrics.
Graphical Abstract
1. Introduction
Because small molecules frequently interact with biological macromolecules through specific noncovalent interactions, fast and accurate methods for predicting binding free energies are a holy grail of computational chemistry. The most accurate methods presently available are alchemical pathway methods,1 in which a receptor-ligand complex is simulated in a series of thermodynamic states (which may be physically unrealistic) connecting end-points where the binding partners are completely decoupled or fully interacting. With cumulative improvements in force fields, sampling algorithms, and computational power, a growing number of publications have shown that alchemical pathway methods are able to accurately predict protein-ligand,2–10 and to a lesser extent, protein-protein11,12 binding free energies.
Due to the substantial computing resources required for alchemical calculations, however, free energy methods based on simulating only the end-points of the pathway — the bound and perhaps the unbound state — have been even more widely used to estimate protein-ligand13,14 and protein-protein15,16 binding free energies (Table 1).
Table 1:
The number of Web of Science search results for specific topics on September 22, 2018.
| Topic | Number of Results |
|---|---|
| “linear response approximation” and “binding” | 44 |
| “linear interaction energy” | 211 |
| “alchemical” | 453 |
| “MM/PBSA” or “MM/GBSA” | 1378 |
To our knowledge, the earliest foray in this direction was the Linear Response Approximation (LRA)17,18, which is based on a thermodynamic cycle that separates polar segments (ligand charging and uncharging) from an apolar segment (binding the uncharged ligand). As such, LRA incorporates simulations of the ligand with partial charges set to zero. More recently, de Ruiter and Oostenbrink 19 built upon LRA by using a third-order polynomial to model the electrostatic charging free energy as a function of a coupling parameter. Their third-power fitting procedure was much more consistent with alchemical calculations than LRA and another popular alternative, the Linear Interaction Energy (LIE)20–22. LIE is a simpler method that foregos simulations with the neutral ligand and instead scales average interaction energy terms (e.g. van der Waals and electrostatic) by empirical coefficients.
The popularity of all these methods has been superseded by the simpler Molecular Mechanics/Poisson-Boltzmann Surface Area (MM/PBSA) and Molecular Mechanics/Generalized Born Surface Area (MM/GBSA) methods, which unlike LIE does not require empirical coefficients. In these methods, configurational integrals are approximated using the average potential energy in a specific implicit solvent models and an entropy term based on normal modes analysis15,23. There are a number of variations of these methods based on the same general approach, but different force fields. For the calculations in this paper, the polar component of solvation free energies will be based on the generalized Born continuum dielectric model. With the understanding that the statistical estimators developed here are broadly applicable, we will, for the sake of simplicity, refer to the entire class of related methods as MM/GBSA.
Although MM/GBSA is very popular, it is less accurate than an alchemical pathway method. Its accuracy is strongly dependent on the system and parameters24, and calculated binding free energies have only weak correlation with experiment14. Genheden and Ryde 24 recently summarized 15 years of effort (including over 20 self-citations) in calibrating, testing, and validating MM/GBSA and its variants using approaches such as quantum mechanics, polarizable force fields, and improved solvation models. They concluded, sadly, that none of their attempted force field modifications gave consistent improvement. Ultimately, MM/GBSA suffers from a fatal flaw due to “severe thermodynamic approximations.”
A major thermodynamic approximation in MM/GBSA is its treatment of entropy, which is flawed both in concept and in practice. MM/GBSA entropies are an average over normal modes from multiple minima. Conceptually, this procedure will not accurately reproduce the configurational integral if the energy landscape is anharmonic or if wells overlap25,26. In practice, normal modes analysis is often computationally expensive and numerically unstable14,27,28. Hence, it is reasonably common, as in Lindström et al. 29 and Zhang et al. 30, to ignore entropy altogether. (LIE also assumes that entropy does not change upon binding31 or is subsumed into the empirical scaling factors.)
Since binding is associated with the restriction of external degrees of freedom — translation and rotation — from bulk solution into a complex, the neglect of entropy in binding processes is a severe approximation. Prior to binding, both the receptor and ligand can freely translate and rotate in solution. Afterwards, their motions are coupled such that the relative translation and rotation of the binding partners is significantly restricted. By arbitrary convention, the receptor external degrees of freedom are considered converted into complex external degrees of freedom and the ligand external degrees of freedom describe the relative positions of the binding partners. Analyses of molecular dynamics simulations suggest that complexation induces a loss of ligand external entropy with T∆S on the order of 10 kcal/mol for protein-ligand23 and 30 kcal/mol for protein-protein26 complexes. It is feasible to estimate the external entropy loss 23, but this term is rarely incorporated into end-point binding free energy calculations.
Regarding the entropy of internal degrees of freedom, it has been suggested that internal entropy may not change much upon binding23 or there are negligible differences between similar complexes32. However, later calculations showed that binding does indeed restrict the ligand conformational ensemble33. The latter assumption of negligible differences between similar complexes is invalidated by the phenomenon of enthalpy-entropy compensation, in which enthalpy decreases are often accompanied by conformational restriction that lead to a counterbalancing reduction in entropy. The prevalence of enthalpy-entropy compensation has led to the conclusion that optimizing enthalpy alone is not a useful framework in structure-based drug design34,35.
Duan et al. 36 recently introduced an approach, which they referred to as the “interaction entropy” (IE), to account for entropy in end-point binding free energy calculations. By factoring the average energy out of an exponential average, they separated energetic and entropic contributions to binding. Ultimately, however, their free energy estimates are numerically equivalent to exponential averages, which are known to be dominated by rare events37 and suffer from systematic finite-sampling error. 38
In this work, we introduce other end-point binding free energy estimators that also improve the treatment of entropy. Like IE, the modifications do not require additional simulation or expensive postprocessing beyond the standard approach. As an added benefit, they are more numerically stable than IE. The modified estimators are tested on a number of protein-ligand complexes with publicly available crystal structures and binding affinity data. Five receptors were chosen: the first bromodomain of human bromodomain-containing protein 4 (bromodomains), the farnesoid X receptor (FXR), human phenylethanolamine N-methyltransferase (hPNMT), T4 lysozyme L99A (lysozyme), and mitogen-activated protein kinase kinase kinase kinase 4 (MAP4K4). Additionally, we tested the estimators on the set of systems used in Duan et al. 36 (IE). Molecular dynamics simulations were performed starting from the crystallographic pose. A second-order cumulant expansion was found to perform equally or better than the standard MM/GBSA protocol for predicting the affinity of ligands in all six datasets. To facilitate the further testing, extension, and application of these estimators by other research groups, our main analysis script is included in the Supporting Information.
2. Theory and Computational Methods
2.1. Binding pose and affinity datasets
Data sources for each selected set of systems are shown in Table S1 of the Supporting Information. There were 7 different ligands for hPNMT, 8 for bromodomains, 9 for lysozyme, 18 for MAP4K4, 31 for FXR, and 14 for IE.
In the bromodomains and lysozyme datasets, have been directly determined by isothermal titration calorimetry. In the hPNMT, MAP4K4, and FXR datasets, there is insufficient available information to obtain an absolute . However, if x ∈ {ki, IC50} is the available binding data, then is a reasonable estimate of within an unknown additive constant C. Therefore, results from this conversion may be used to assess relative binding free energies.
2.2. Molecular simulation and potential energy calculations
The crystallographic structure of each complex was prepared for simulation using a workflow based on AmberTools 16.39 The protein was prepared with AMBER40 ff14SB.redq parameters. Using the tleap program in AmberTools, all protein residue protonation states were assigned default values. (For the purposes of comparison, we also predicted residue protonation states with PROPKA 3.041,42 at pH 7.0, as integrated in PDB2PQR 1.9.0,43 after the simulations and analysis were complete. A comparison is available in Table S2 of the Supporting Information.) Atomic radii were set with the mbondi2 option. Ligands were parametrized based on the Generalized AMBER force field44 with AM1BCC45,46 partial charges. Ligand protonation states were assigned using pkatyper (OpenEye) and partial charges calculated using the QUACPAC 1.7.0.2 toolkit (OpenEye). Chemical structures for each ligand, including assigned protonation states, are included in Figure S1 of the Supporting Information. All dynamics and energy calculations were performed with the OBC2 model47 for GBSA implicit solvent,13 with a solvent dielectric of 78.5. OpenMM 7.048,49 was used to perform Langevin dynamics simulations at 300 K for 200 ns using a timestep of 2 fs and no distance cutoff. Energies were saved every 1000 steps (2 ps), yielding 100,000 total energies per simulation.
Trajectories were prepared for postprocessing by using VMD 1.9.150 to separate coordinates of the receptor, ligand, and complex. Potential energies for the ligand, receptor, and complex were calculated using OpenMM 7.0. 48,49 Normal modes analysis was performed using the default settings of the MMPBSA.py script51 from AmberTools 16. 39
For a small subset of systems with available crystallographic structures, there were failures are different stages in the calculation: the setup workflow, normal modes analysis with default settings, or postprocessing. We did not complete analyses for these systems: 1eujj, 1hgaf, 1phif, 1sjpr, and 1txca from FXR and 1e66 from the IE data set.
2.3. Binding free energy calculations
Noncovalent binding between a receptor, R, and ligand, L, to form a complex, RL, is described by the chemical equation L + R ↔ RL. The designation of a binding partner as receptor or ligand is arbitrary, but it is conventional for the ligand to be the smaller partner. We will denote the equilibrium concentration of each of these species X by CX and specify the standard concentration C° as 1 M. The strength of a noncovalent binding process is quantified by the standard binding free energy,
| (1) |
in which kB is Boltzmann’s constant and T is the temperature, in Kelvin.
According to the statistical mechanics of noncovalent binding,1 can be related to implicit-solvent configurational integrals ZR, ZL, and ZRL,
| (2) |
| (3) |
| (4) |
where β = (kBT )−1. The coordinates rR, rL, and ξ are of the receptor, ligand, and the relative translation and orientation of the binding partners, respectively. U (·) is a potential energy that includes the gas-phase potential energy and solvation free energy. The indicator function I(ξ) is one when the receptor and ligand are complexed and zero otherwise, and J (ξ) is the Jacobian for the transformation from Cartesian coordinates into the specified coordinate system. From Equation 38 of Gilson et al. 1, if the symmetry terms are neglected and the change in molar volume upon binding is negligible, then the standard binding free energy is,
| (5) |
The 8π2 comes from integrating over degrees of freedom describing the relative orientation of the binding partners.
To account for the differences between the standard state and the binding site volume52, it is helpful to define, similarly to Gallicchio et al. 53 and Minh 54,
| (6) |
| (7) |
By adding −kBT ln (Zξ/Zξ) = 0 to Equation 5, an expression in terms of ∆Gξ can be obtained,
| (8) |
For notational simplicity we will also define GX = −kBT ln ZX for X ∈ {R, L, ξ, RL} and also,
| (9) |
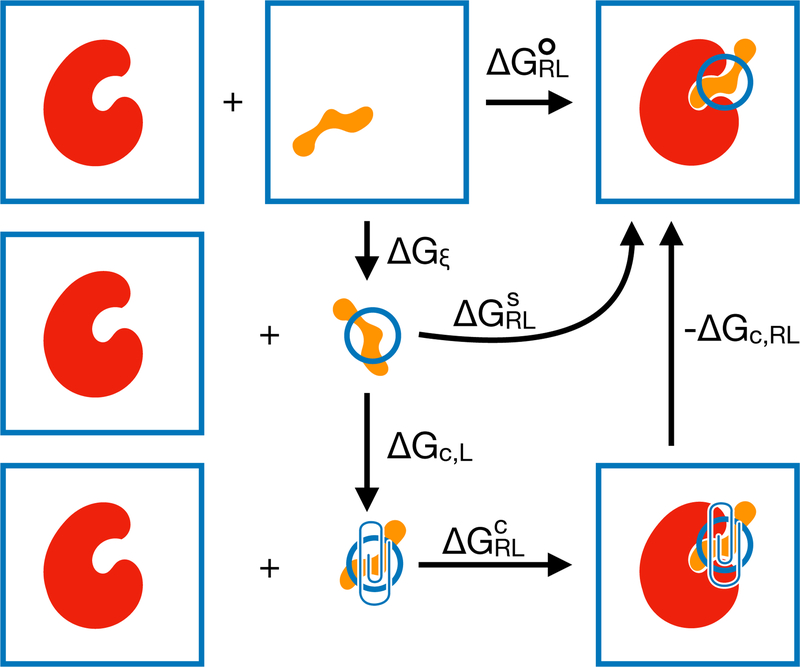
This can be interpreted as the binding free energy given that ξ are restricted to the binding site (Figure 1).
Figure 1:
Schematic thermodynamic cycle for a calculation of . The standard binding free energy (top row) is based on reference states in which both the receptor and ligand freely translate and rotate in bulk solvent. In the site-specific binding free energy (middle row), the ligand external degrees of freedom are restricted to the binding site. In the confined-ligand binding free energy (bottom row), an empirical confining potential is added to the ligand external degrees of freedom. ∆Gξ is the free energy of restricting the ligand into the binding site. ∆Gc,L and ∆Gc,RL are the free energies of adding the empirical confining potential to the ligand and complex, respectively.
2.3.1. in three-trajectory mode
Substituting the Boltzmann distribution pX(rX) = e−βU(rX )/ZX into the entropy expression leads to the energy-entropy decomposition55,
| (10) |
Expectations that involve averages over ξ also contain I(ξ) and J (ξ). Substituting Equation 10 into Equation 8 leads to the theoretical basis of MM/GBSA in three-trajectory mode55,
| (11) |
where ∆S = SRL − SR − SL − Sξ. U〈 (rξ)〉ξ is not included in Equation 11 because the potential energy U (ξ) = 0. Each thermodynamic expectation 〈…〉X is estimated from the average potential energy across the entire simulation of species X: RL for the holo ensemble of the complexed ligand and receptor; R for the apo ensemble of the receptor by itself; and L for the apo ensemble of the ligand by itself. Entropy terms are approximated by performing normal modes analysis on a few selected snapshots. Sξ = kB ln Zξ can be evalulated based on a numerical or analytical integration of Zξ. However, most MM/GBSA calculations do not consider Sξ or ∆Gξ, which may lead to a constant offset in the estimated free energies. 55
To address the conceptual and practical issues with the MM/GBSA entropy mentioned in the introduction, let us consider an alternate approach in which is expressed in terms of thermodynamic expectations. Using the identity from Zwanzig 56 in Equation 9, we obtain,
| (12) |
Each exponential average may expressed as a cumulant expansion, a power series in β 56. To the third order, this expansion is,
| (13) |
where δU ≡ U (rX)−〈U (rX)〉X. Following a procedure described by Ben-Amotz et al. 57, this same series (up to the third order) may also be derived from thermodynamic integration.
A comparison of Eqs. 11 and 13 makes it clear that the average potential energy is the first order term in a cumulant expansion and entropy can be identified as the higher order terms. Hence, a straightforward path to rigorous ∆G° estimation is to estimate the cumulants or moments of the potential energy distribution.
It is worth noting that truncating a cumulant expansion involves a trade off between accuracy and precision. If the potential energy distribution is precisely Gaussian, then a cumulant expansion may be rigorously truncated at the second order. Otherwise, the series is infinite58 and premature truncation leads to a systematic bias. Nevertheless, a low-order truncation may be beneficial due to improved numerical stability.
2.3.2. in single-trajectory mode
To reduce computational expense and to facilitate the cancellation of error, MM/GBSA is often performed in single-trajectory mode. This paper will focus on this type of calculation. In single-trajectory mode, Equation 11 is replaced by,
| (14) |
Unlike Equation 11, this expression has not hitherto been established on a firm theoretical foundation. It can be derived from Equation 11 only under the severe approximation that the probability of molecular configurations is equivalent in the apo and holo ensembles.
An alternate route to Equation 14 is a single-step perturbation from the holo to apo ensemble using an exponential average53,56,
| (15) |
where Ψ(rRL) ≡ U (rR, rL) − U (rR) − U (rL). To the third order, the cumulant expansion of Equation (15) is,
| (16) |
where Ψ ≡ Ψ(rRL) and δΨ ≡ Ψ(rRL) − 〈Ψ(rRL)〉 are used within the brackets for notational convenience. The first-order term is the average energy change and higher-order terms account for the entropy change. MM/GBSA in single-trajectory mode can be thought of as using a version of Equation 16 in which normal modes analysis substitutes for higher-order cumulants. If entropic contributions are neglected, MM/GBSA can be thought of as a first-order truncation of the equation.
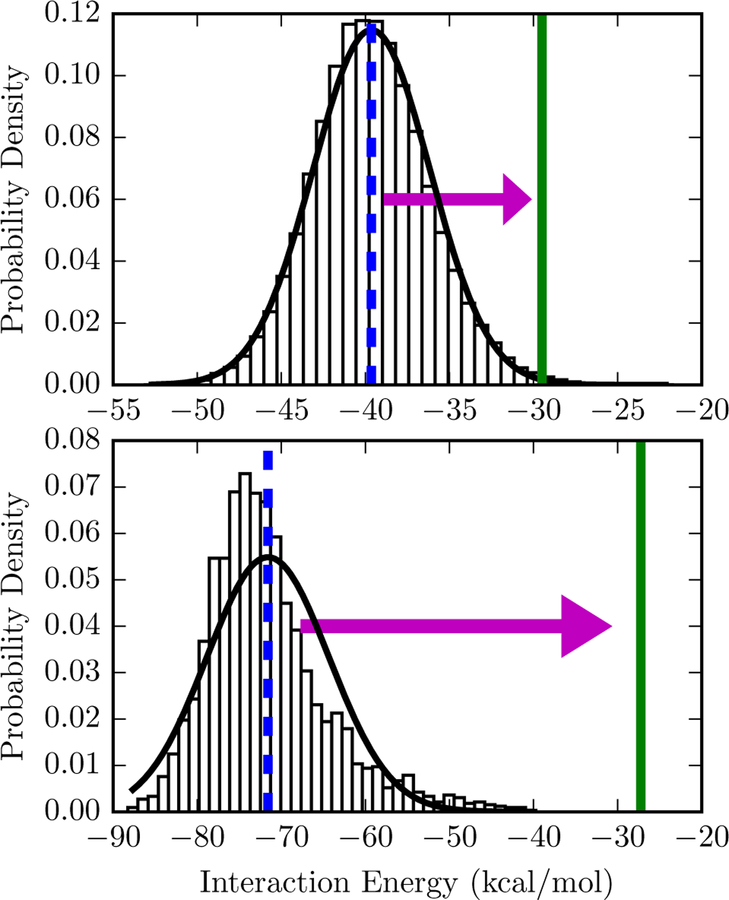
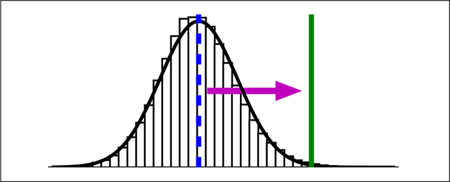
To illustrate the effect of the cumulant expansion, consider the distribution of interaction energies in Figure 2. In the top panel, a Gaussian distribution is a good fit to the data. With a first-order truncation of the expansion, the free energy estimate is at the peak of the distribution. With a second-order truncation, the free energy estimate is shifted significantly to the right, to a weaker and more physically realistic value. The histogram in bottom panel is not as well-described by a Gaussian, but a second-order truncation can nonetheless be applied as an approximation.
Figure 2: Comparison of free energy estimates for two interaction energy distributions.
The bars are a normalized histogram of interaction energies observed in a simulation of the protein-ligand complex starting from 3mxf (top) or 4ogj (bottom) in the PDB. Top: The mean interaction energy, −39.6 kcal/mol and is shown with a dashed blue vertical line. Since the standard deviation of the interaction energy is 3.5 kcal/mol, the second-order truncation of the cumulant expansion is −29.5 kcal/mol, shown with a solid green line. A Gaussian distribution based on the sample mean and standard deviation is shown as a solid black line. Bottom: The same lines and symbols are used for 4ogj. The mean interaction and standard deviation of the interaction energy is −71.59 and 7.3 kcal/mol, respectively. The second-order truncation of the cumulant expansion is −27.25 kcal/mol. Comparable figures for all systems are available in Figure S2 of the Supporting Information.
In this paper, we will compare the following choices, which we will refer to as expansion options:
a cumulant expansion, from the first to fourth order (Equation 16);
the exponential average (Equation 15); and
the sum of the mean energy and normal modes entropy (Equation 14), or MM/GBSA in single-trajectory mode.
For all the expansion options, the expectation values are estimated via a sample mean. We will subsequently use the notation  to denote the estimator for an expectation value 〈A〉.
Due to the relationship between Equations 14, 15, and 16, all of the expansion options are subject to convergence issues common to exponential averages. When computing free energy differences between two thermodynamic states using an exponential average, it is beneficial for the most highly populated regions of configuration space to overlap. 59 If there is no overlap, then configurations common to one state will have high energy in the other state and a prohibitive number of samples will be required to obtain accurate free energies. The quality of MM/GBSA-based binding free energy estimates will depend on the degree of overlap between apo and holo ensembles.
2.3.3. with a confining potential on ξ
For ligand external coordinates, there is a clear relationship between the important configuration space of the end-point ensembles: the holo ensemble is a subset of the apo ensemble. A single-step perturbation from the apo to holo ensemble of ξ would lead to many configurations with steric clashes and therefore require many samples to converge. On the other hand, sampling from the holo ensemble (as in single-trajectory MM/GBSA) should yield configurations that have reasonable energies in the apo ensemble. The holo simulation, however, is unlikely to access all of the important configuration space of the apo ensemble.
To some extent, this issue is addressed by defining an apo ensemble with a restricted binding site. Because most MM/GBSA calculations do not include a ∆Gξ term, they implicitly define a broad binding site that is equivalent to free translation and rotation in bulk solution. An apo ensemble with restrictions on ξ is more similar to the holo ensemble than an apo ensemble in bulk solution. Defining a binding site that is narrower and uniform across different ligands binding to a receptor leads to a constant shift in estimated free energies. 55 Ideally, the binding site would be defined in a way that is minimally larger than the region of ξ accessed by the bound ensemble of each ligand, leading to significant configuration space overlap between the holo and site-restricted apo ensemble.
Although it is difficult to define a minimal binding site, Ben-Shalom et al. 60 suggested that external entropy losses can be estimated by determining the binding site based on the minimum and maximum coordinates observed in different observed binding poses. They found that this range of coordinates differed from complex to complex, even among congeneric ligands binding to the same receptor (c.f. Figure 4 in their paper). While their approach to estimating translational and rotational entropy was useful for developing multiple linear regression models with higher correlation to experiment than standard MM/GBSA, they conceded that it is likely to overestimate the residual external entropy in the complex. To elaborate, they assumed that ξ is distributed uniformly, which is unlikely to be the true distribution and maximizes the entropy. Another shortcoming of their approach is that the extrema are highly sensitive to outliers.
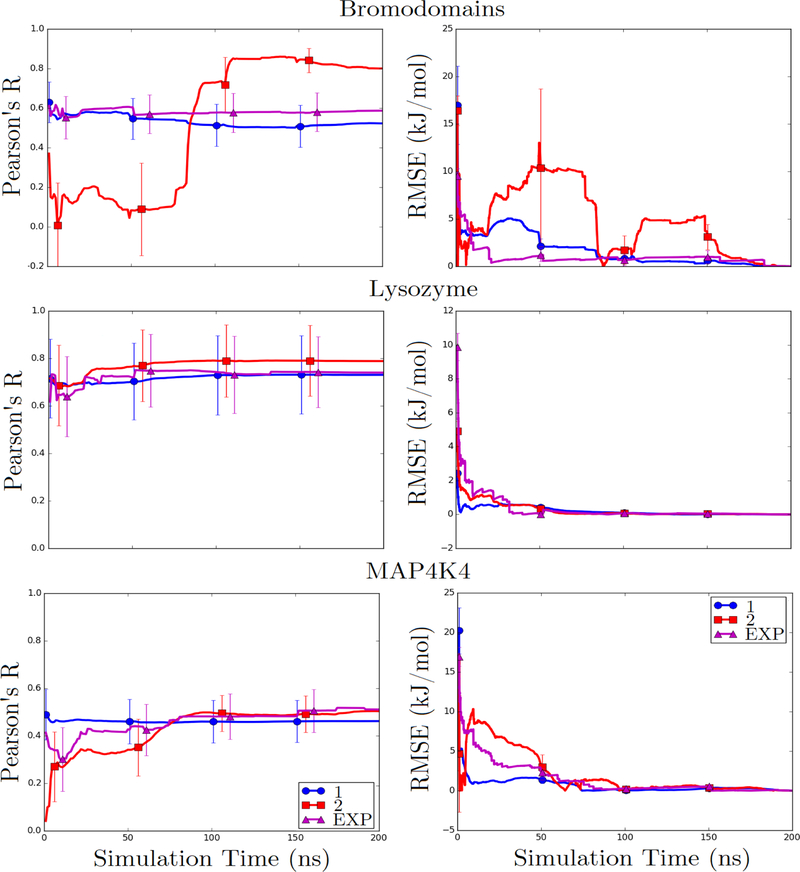
Figure 4: Pearson’s R and RMSE from the final value of calculated binding free energies as a function of time for bromodomains, lysozyme, and MAP4K4 datasets.
Calculations were performed with ligand RMSD cutoff of 3 Å, without the inclusion of ligand external entropy terms, and using three expansion options: first- and second-order cumulant expansions and an exponential average.
Here, we consider an approach to treating confinement of ligand external coordinates based on a fictitious intermediate thermodynamic state with a biasing potential on ξ (the bottom row of Figure 1). The biasing potential, which we will refer to as the confinement potential, is based on the Boltzmann inversion of a nonparametric probability density estimate. This approach is less sensitive to outliers and more accurately reflects the true residual entropy than a uniform distribution between empirically observed extrema. The intermediate thermodynamic state is fictitious in a sense that no sampling is performed in the state. Instead, free energy differences are calculated by numerical integration (∆Gc,L) or single-step free energy perturbation with or without (∆Gc,RL) reweighting. Compared to the molecular dynamics, the additional computational expense of the estimate is negligible.
External degrees of freedom were defined as three translational and three rotational degrees of freedom. To obtain these coordinates, the entire complex was first translated and rotated to align the protein α-carbons onto the crystal structure coordinates using cpptraj 17.0061. The ligand center of mass was then computed with MDTraj 1.8. 62 Translational degrees of freedom were based on the ligand center of mass. Rotational degrees of freedom were based on the ligand principal axes of rotation, calculated by:
Computing the inertial tensor using MDTraj 1.8;62
Calculating the principal axes — , , and — based on eigenvectors of the inertial tensor using numpy 1.8.1;63
Calculating proper Euler angles from the principal axes as,
where the subscripts n ∈ {1, 2, 3} indicate indices of each vector.
After obtaining the ligand center-of-mass and proper Euler angles, the binding site and confinement potential were defined as follows. For the center-of-mass:
The center-of-mass was rotated onto a new coordinate system by principal component analysis: projecting the original coordinates onto the eigenvectors of the covariance matrix. The benefit of using principal components analysis is that the new coordinates are linearly uncorrelated.
For each coordinate, the binding site of length Ld was defined as the area between the minimum and maximum with a 10% buffer on each side. d is an index for the dimension.
For each coordinate, the probability density ρ(x) as a function of position x was calculated using a Gaussian kernel density estimate (scipy.stats.gaussian kde in scipy v0.14.063). The confinement potential was defined as Uc,d(x) = −kBT ln ρd(x).
For the proper Euler angles α, βE, and γ, the binding site did not include any restrictions. The confinement potential was obtained by,
Generating a histogram H(x) with 100 bins between −π and π for α and γ and between 0 and π for β.
Obtaining a smooth and periodic density estimate by the convolution of the histogram with a Gaussian kernel. To be precise,
| (17) |
where F[·] and F−1[·] are the Fourier transform and inverse Fourier transform, respectively, and ∗ denotes the discrete convolution. The Gaussian kernel K(x) had a standard deviation of 2fπ/10 for α and γ and fπ/10 for βE, where f = n−1/5 for n data points is Scott’s factor.64 The Fourier transform (numpy.fft) and inverse Fourier transform (numpy.ifft) were performed using numpy 1.8.1.63
Defining the confinement potential as Uc,d(x) = −kBT ln ρd(x) for the dimension indexed by d.
Based on these definitions of the binding site and confinement potential, free energy differences in Figure 1 were calculated in a number of different ways. Because the binding site has no restrictions on rotation,
| (18) |
is purely based on the relative volume of translational degrees of freedom. The free energy of confining the ligand is,
| (19) |
which is based on an expectation of in the uniform distribution. Because Uc(ξ) is independent for each degree of freedom, Equation 19 can be factored into separate free energy differences. These free energy differences were estimated by numerical integration,
| (20) |
| (21) |
| (22) |
where the sums in Equations 21 and 22 are over ni histogram bin centers xi. The confinement free energy for βE differs in form because it includes a Jacobian for transformation. On the other hand, the free energy of confining the complex was calculated by a single-step perturbation from the complex to the confined complex,
| (23) |
where the outer sum is over dimensions and the inner sum is over nj observations from the holo ensemble. was calculated by using a sample mean estimator for the expectation values in Equation 16. was computed based on using importance sampling with an expression analogous to Equation 15 for a different thermodynamic state,
| (24) |
and its analogous cumulant expansion. Expectation values are estimated via a sample mean.
2.3.4. with a ligand RMSD filter
To account for the possibility of the ligand drifting away from the crystallographic binding pose, we tested an energy filter based on the ligand RMSD. The RMSD for all ligand atoms was computed using cpptraj.61 When the filter was applied, binding free energy calculations excluded energies where the corresponding ligand RMSD exceeded 3 Å, essentially excluding any non-crystallographic binding pose.
2.3.5. Synopsis of calculations
In summary, calculations were performed:
with and without a ligand RMSD filter of 3 Å.
with a correction based on the binding site volume (Equation 18), with a fictitious confining potential on ligand translation and rotation, or without a ligand external entropy correction at all; and
based on a cumulant expansion from the first to fourth order, the exponential average, or the first order truncation of the cumulant plus normal modes entropy.
To put this in context, the standard MM/GBSA protocol does not include a ligand RMSD filter, does not include a ligand external entropy correction, and is based on a first-order truncation of the cumulant expansion plus normal modes entropy.
2.4. Correlation and error statistics
The quality of estimation was assessed by a variety of statistical metrics — the Pearson R (R), Spearman ρ (ρ), Kendall τ (τ )65 correlations, as well as the root mean square error (RMSE) and adjusted RMSE (aRMSE) — relative to experimental measurements. The Spearman ρ is the Pearson R value between the rankings of variables. The Kendall τ differs from the Spearman ρ in that it considers data that may have the exact same rank. The RMSE between two series of data points {x1, x2, …, xN } and {y1, y2, …, yN } is,
| (25) |
It is not relevant to the hPNMT, and MAP4K4, and FXR datasets because absolute binding free energies have not been experimentally measured. The aRMSE is,
| (26) |
where the and are the sample mean of x and y, respectively. The aRMSE accounts for systematic deviation between the series and is useful for assessing whether relative binding free energies are accurate. In addition to the aRMSE of various statistical estimators, we also considered the aRMSE of a “dummy” estimate in which all binding free energies are assumed to have the same value.
Standard errors were calculated using bootstrapping66: for n ligands, the standard deviation was calculated for metrics estimated from 10,000 sets of n ligand free energy estimates randomly sampled with replacement from the original n estimates.
3. Results and Discussion
3.1. In some datasets, calculations achieved significant correlation with experiment
A complete table of statistical correlation and error statistics for different estimators is available in Table 2. Our actual free energy estimates are reported in Table S3 of the Supporting Information.
Table 2: Comparison between calculated and experimental for six sets of protein-ligand systems.
calculations were performed: (a) with (3) and without (∞) ligand RMSD filter of 3 Å (b) without a ligand external entropy correction (No), with a correction based on the binding site volume (Site, Equation 18), or with a fictitious confining potential on ligand translation and rotation (Yes); (c) based on a cumulant expansion truncated to the listed order (1 to 4), the exponential average (EXP), or the first order truncation of the cumulant and normal modes entropy (1 + NM). RMSE and aRMSE values are reported in kcal/mol. Standard errors are shown in parentheses.
| Set | RMSD | ξ | metric | 1 | 2 | 3 | 4 | EXP | 1 + NM |
|---|---|---|---|---|---|---|---|---|---|
| bromodomains | 3 | No | R | 0.52 (0.22) | 0.80 (0.14) | −0.18 (0.41) | −0.26 (0.28) | 0.59 (0.19) | 0.49 (0.22) |
| ρ | 0.83 (0.18) | 0.83 (0.21) | 0.33 (0.38) | −0.24 (0.35) | 0.81(0.17) | 0.83 (0.20) | |||
| τ | 0.64 (0.18) | 0.71 (0.23) | 0.21 (0.31) | −0.14 (0.24) | 0.57 (0.20) | 0.64 (0.24) | |||
| RMSE | 31.85 (6.03) | 12.05 (1.88) | 64.67 (30.29) | 395.67 (227.21) | 18.47 (3.27) | 16.76 (6.94) | |||
| aRMSE | 13.59 (5.52) | 6.16 (1.50) | 64.10 (30.58) | 374.15 (198.05) | 7.61 (2.85) | 14.01 (5.43) | |||
| Site | R | 0.53 (0.21) | 0.79 (0.15) | −0.18 (0.42) | −0.26 (0.27) | 0.60 (0.19) | 0.50 (0.22) | ||
| ρ | 0.83 (0.17) | 0.74 (0.27) | 0.33 (0.38) | −0.24 (0.32) | 0.83 (0.18) | 0.83 (0.20) | |||
| τ | 0.64 (0.18) | 0.64 (0.27) | 0.21 (0.32) | −0.14 (0.25) | 0.64 (0.18) | 0.64 (0.24) | |||
| RMSE | 29.96 (5.92) | 10.43 (1.88) | 65.21 (31.61) | 396.57 (230.25) | 16.58 (3.27) | 15.53 (6.71) | |||
| aRMSE | 13.36 (5.35) | 6.20 (1.55) | 64.35 (31.74) | 374.41 (199.26) | 7.38 (2.70) | 13.75 (5.36) | |||
| Yes | R | 0.50 (0.21) | 0.77 (0.14) | −0.19 (0.43) | −0.24 (0.34) | 0.55 (0.20) | 0.47 (0.23) | ||
| ρ | 0.83 (0.17) | 0.74 (0.23) | 0.33 (0.36) | 0.19 (0.38) | 0.81 (0.19) | 0.83 (0.19) | |||
| τ | 0.64 (0.19) | 0.57 (0.22) | 0.21 (0.30) | 0.07 (0.28) | 0.57 (0.21) | 0.64 (0.23) | |||
| RMSE | 26.44 (6.00) | 9.51 (1.96) | 51.18 (23.68) | 293.29 (167.41) | 15.12 (3.60) | 13.75 (6.36) | |||
| aRMSE | 12.94 (5.41) | 6.38 (1.45) | 50.93 (25.85) | 276.85 (150.39) | 7.64 (3.09) | 13.30 (5.49) | |||
| ∞ | No | R | 0.40 (0.28) | 0.63 (0.26) | 0.74 (0.17) | −0.28 (0.41) | 0.64 (0.19) | 0.32 (0.29) | |
| ρ | 0.60 (0.34) | 0.62 (0.34) | 0.69 (0.29) | 0.05 (0.42) | 0.81 (0.19) | 0.43 (0.37) | |||
| τ | 0.43 (0.33) | 0.50 (0.30) | 0.50 (0.27) | 0.00 (0.33) | 0.57 (0.24) | 0.29 (0.32) | |||
| RMSE | 36.19 (6.25) | 19.07 (3.65) | 29.63 (10.06) | 108.31 (36.01) | 18.62 (4.21) | 18.42 (6.52) | |||
| aRMSE | 14.42 (5.30) | 15.08 (3.26) | 29.42 (9.82) | 105.17 (32.71) | 10.43 (3.05) | 13.47 (5.22) | |||
| Site | R | 0.37 (0.26) | 0.63 (0.26) | 0.74 (0.18) | −0.29 (0.41) | 0.63 (0.19) | 0.29 (0.31) | ||
| ρ | 0.60 (0.35) | 0.62 (0.34) | 0.69 (0.30) | 0.05 (0.42) | 0.83 (0.19) | 0.43 (0.37) | |||
| τ | 0.43 (0.32) | 0.50 (0.32) | 0.50 (0.27) | 0.00 (0.34) | 0.64 (0.24) | 0.29 (0.33) | |||
| RMSE | 35.46 (6.10) | 17.95 (3.41) | 28.68 (10.04) | 108.78 (36.81) | 17.70 (3.71) | 17.57 (6.67) | |||
| aRMSE | 13.64 (5.25) | 14.02 (2.74) | 28.40 (9.31) | 105.54 (33.47) | 9.45 (2.82) | 12.73 (5.26) | |||
| Yes | R | 0.39 (0.28) | 0.44 (0.29) | 0.59 (0.20) | −0.02 (0.40) | 0.54 (0.21) | 0.30 (0.31) | ||
| ρ | 0.60 (0.34) | 0.55 (0.32) | 0.74 (0.25) | 0.26 (0.43) | 0.74 (0.23) | 0.36 (0.41) | |||
| τ | 0.43 (0.32) | 0.43 (0.28) | 0.57 (0.26) | 0.21 (0.38) | 0.50 (0.25) | 0.21 (0.35) | |||
| RMSE | 31.12 (6.04) | 16.05 (3.75) | 14.79 (4.22) | 66.35 (26.78) | 16.44 (3.66) | 14.62 (6.97) | |||
| aRMSE | 13.46 (5.51) | 10.55 (2.36) | 9.88 (2.84) | 63.48 (23.08) | 8.41 (2.93) | 12.59 (5.40) | |||
| FXR | 3 | No | R | −0.29 (0.13) | −0.01 (0.23) | −0.03 (0.14) | −0.05 (0.19) | −0.07 (0.17) | −0.28 (0.12) |
| ρ | −0.26 (0.17) | −0.19 (0.19) | 0.04 (0.18) | 0.04 (0.19) | −0.19 (0.20) | −0.24 (0.18) | |||
| τ | −0.14 (0.12) | −0.13(0.14) | 0.02 (0.12) | 0.05 (0.15) | −0.13 (0.14) | −0.15 (0.13) | |||
| aRMSE | 12.20 (2.36) | 16.47(4.72) | 49.04 (15.02) | 445.69 (143.93) | 8.43 (1.88) | 9.81 (2.13) | |||
| Site | R | −0.30 (0.15) | −0.02 (0.23) | −0.03 (0.14) | −0.05 (0.19) | −0.09 (0.18) | −0.30 (0.13) | ||
| ρ | −0.27 (0.19) | −0.20 (0.18) | 0.03 (0.19) | 0.04 (0.19) | −0.18 (0.20) | −0.23 (0.18) | |||
| τ | −0.15 (0.13) | −0.14 (0.13) | 0.01 (0.13) | 0.05 (0.13) | −0.13 (0.14) | −0.14 (0.14) | |||
| aRMSE | 12.37 (2.38) | 16.62 (4.65) | 48.99 (15.38) | 445.55 (142.03) | 8.57 (1.83) | 9.97 (2.14) | |||
| Yes | R | −0.27 (0.14) | 0.07 (0.23) | −0.16 (0.11) | 0.02 (0.18) | −0.07 (0.16) | −0.27 (0.13) | ||
| ρ | −0.22 (0.19) | −0.14 (0.20) | −0.16 (0.18) | −0.25 (0.19) | −0.03 (0.20) | −0.23 (0.18) | |||
| τ | −0.13 (0.13) | −0.08 (0.13) | −0.09 (0.13) | −0.18 (0.14) | 0.01 (0.14) | −0.11 (0.13) | |||
| aRMSE | 12.16 (1.75) | 16.31 (5.89) | 24.60 (10.28) | 953.58 (464.32) | 12.25 (1.63) | 9.57 (1.60) | |||
| ∞ | No | R | −0.24 (0.14) | −0.09 (0.20) | 0.02 (0.18) | 0.06 (0.19) | −0.06 (0.16) | −0.20 (0.14) | |
| ρ | −0.24 (0.17) | −0.15 (0.19) | 0.03 (0.19) | 0.12 (0.18) | −0.18 (0.19) | −0.21 (0.18) | |||
| τ | −0.14 (0.12) | −0.10 (0.13) | 0.02 (0.13) | 0.11 (0.14) | −0.11 (0.13) | −0.13 (0.12) | |||
| aRMSE | 11.97 (2.34) | 13.36 (2.61) | 30.92 (9.51) | 326.43 (116.68) | 8.27(1.92) | 9.64 (1.99) | |||
| Site | R | −0.25 (0.15) | −0.10 (0.21) | 0.02 (0.18) | 0.06 (0.19) | −0.08 (0.17) | −0.21 (0.14) | ||
| ρ | −0.24 (0.17) | −0.17 (0.19) | 0.03 (0.19) | 0.13 (0.19) | −0.16 (0.19) | −0.19 (0.17) | |||
| τ | −0.15 (0.12) | −0.11 (0.14) | 0.02 (0.13) | 0.11 (0.14) | −0.10 (0.13) | −0.11 (0.12) | |||
| aRMSE | 12.07 (2.33) | 13.41 (2.60) | 30.81 (8.86) | 326.34 (116.97) | 8.38 (1.83) | 9.74 (1.98) | |||
| Yes | R | −0.21 (0.16) | −0.14 (0.16) | −0.11 (0.11) | 0.10 (0.15) | −0.05 (0.17) | −0.17 (0.18) | ||
| ρ | −0.22 (0.19) | −0.11 (0.19) | −0.07 (0.18) | −0.13 (0.19) | −0.09 (0.19) | −0.22 (0.18) | |||
| τ | −0.15 (0.14) | −0.05 (0.13) | −0.02 (0.12) | −0.07 (0.13) | −0.04 (0.14) | −0.12 (0.14) | |||
| aRMSE | 12.23 (1.65) | 7.95 (1.19) | 24.23 (10.76) | 887.49 (532.79) | 12.21 (1.68) | 9.79 (1.37) | |||
| hPNMT | 3 | No | R | 0.04 (0.38) | 0.10 (0.46) | 0.30 (0.42) | −0.00 (0.49) | 0.06 (0.44) | 0.07 (0.39) |
| ρ | 0.22 (0.41) | −0.13 (0.50) | 0.22 (0.50) | 0.18 (0.51) | 0.22 (0.49) | 0.16 (0.48) | |||
| τ | 0.15 (0.35) | −0.15 (0.44) | 0.25 (0.44) | 0.25 (0.45) | 0.25 (0.45) | 0.15 (0.41) | |||
| aRMSE | 11.73 (1.95) | 7.80 (1.46) | 9.32 (1.68) | 7.69 (2.35) | 10.69 (1.84) | 10.18 (1.58) | |||
| Site | R | 0.05 (0.39) | 0.11 (0.46) | 0.32 (0.39) | 0.01 (0.49) | 0.07 (0.43) | 0.07 (0.40) | ||
| ρ | 0.22 (0.43) | 0.18 (0.48) | 0.22 (0.50) | 0.18 (0.51) | 0.22 (0.51) | 0.16 (0.48) | |||
| τ | 0.15 (0.35) | 0.15 (0.41) | 0.25 (0.44) | 0.25 (0.45) | 0.25 (0.45) | 0.15 (0.42) | |||
| aRMSE | 11.48 (1.95) | 7.56 (1.37) | 9.08 (1.68) | 7.58 (2.18) | 10.45 (1.78) | 9.95 (1.56) | |||
| Yes | R | 0.08 (0.37) | 0.04 (0.46) | 0.42 (0.36) | −0.25 (0.41) | 0.07 (0.41) | 0.11 (0.38) | ||
| ρ | 0.22 (0.43) | 0.20 (0.47) | 0.29 (0.47) | −0.42 (0.45) | 0.16 (0.48) | 0.22 (0.42) | |||
| τ | 0.15 (0.36) | 0.15(0.44) | 0.25 (0.43) | −0.25 (0.41) | 0.15 (0.40) | 0.15 (0.36) | |||
| aRMSE | 11.14 (1.81) | 6.16 (0.96) | 18.40 (4.21) | 38.29 (12.03) | 9.29 (1.48) | 9.68 (1.65) | |||
| ∞ | No | R | 0.05 (0.39) | 0.07(0.48) | 0.29 (0.41) | −0.07 (0.47) | 0.05 (0.45) | 0.09 (0.38) | |
| ρ | 0.22 (0.41) | −0.13 (0.50) | 0.22 (0.49) | 0.13 (0.50) | 0.22 (0.50) | 0.16 (0.47) | |||
| τ | 0.15 (0.34) | −0.15 (0.45) | 0.25 (0.45) | 0.15 (0.44) | 0.25 (0.43) | 0.15 (0.40) | |||
| aRMSE | 11.91 (1.92) | 7.48 (1.31) | 10.75 (1.88) | 11.03 (2.93) | 10.21 (1.64) | 10.35 (1.77) | |||
| Site | R | 0.06 (0.39) | 0.10 (0.47) | 0.31 (0.41) | −0.06 (0.48) | 0.07 (0.45) | 0.11 (0.37) | ||
| ρ | 0.22 (0.43) | 0.09 (0.51) | 0.22 (0.51) | 0.13 (0.51) | 0.22 (0.50) | 0.16 (0.47) | |||
| τ | 0.15 (0.36) | 0.05 (0.46) | 0.25 (0.43) | 0.15 (0.45) | 0.25 (0.44) | 0.15 (0.40) | |||
| aRMSE | 11.75 (1.99) | 7.19 (1.26) | 10.64 (1.94) | 10.99 (2.89) | 10.00 (1.74) | 10.24 (1.68) | |||
| Yes | R | 0.10 (0.38) | 0.01 (0.48) | 0.38 (0.33) | −0.28 (0.42) | 0.06 (0.42) | 0.15 (0.38) | ||
| ρ | 0.38 (0.36) | 0.20 (0.48) | 0.33 (0.42) | −0.47 (0.40) | 0.13 (0.53) | 0.33 (0.43) | |||
| τ | 0.25 (0.29) | 0.15 (0.45) | 0.25 (0.35) | −0.35 (0.35) | 0.15 (0.46) | 0.25 (0.36) | |||
| aRMSE | 11.70 (1.84) | 5.76 (0.90) | 21.04 (5.27) | 16.16 (4.37) | 8.63 (1.41) | 10.29 (1.92) | |||
| lysozyme | 3 | No | R | 0.73 (0.33) | 0.79 (0.31) | 0.72 (0.33) | 0.72 (0.33) | 0.74 (0.30) | 0.64 (0.34) |
| ρ | 0.43 (0.39) | 0.50 (0.39) | 0.35 (0.41) | 0.35 (0.41) | 0.47 (0.38) | 0.42 (0.38) | |||
| τ | 0.33 (0.36) | 0.33 (0.37) | 0.22 (0.38) | 0.22 (0.39) | 0.39 (0.35) | 0.33 (0.34) | |||
| RMSE | 15.86 (0.90) | 13.21 (0.84) | 12.74 (0.83) | 12.45 (0.75) | 11.96 (0.74) | 3.38 (0.64) | |||
| aRMSE | 2.83 (0.69) | 2.51 (0.62) | 2.47 (0.58) | 2.36 (0.57) | 2.20 (0.60) | 2.39 (0.55) | |||
| Site | R | 0.73 (0.34) | 0.78 (0.30) | 0.72 (0.36) | 0.71 (0.33) | 0.73 (0.33) | 0.63 (0.33) | ||
| ρ | 0.43 (0.40) | 0.50 (0.39) | 0.35 (0.40) | 0.35 (0.44) | 0.42 (0.40) | 0.32 (0.42) | |||
| τ | 0.33 (0.36) | 0.33 (0.36) | 0.22 (0.37) | 0.22 (0.37) | 0.33 (0.33) | 0.17 (0.36) | |||
| RMSE | 14.40 (0.84) | 11.76 (0.82) | 11.28 (0.80) | 11.00 (0.70) | 10.50 (0.69) | 2.47 (0.56) | |||
| aRMSE | 2.72 (0.65) | 2.40 (0.59) | 2.36 (0.54) | 2.26 (0.55) | 2.09 (0.57) | 2.29 (0.53) | |||
| Yes | R | 0.68 (0.34) | 0.76 (0.33) | 0.66 (0.40) | 0.66 (0.26) | 0.63 (0.38) | 0.58 (0.38) | ||
| ρ | 0.43 (0.39) | 0.50 (0.39) | 0.25 (0.39) | 0.63 (0.33) | 0.35 (0.40) | 0.38 (0.41) | |||
| τ | 0.33 (0.34) | 0.33 (0.36) | 0.11 (0.35) | 0.50 (0.30) | 0.22 (0.37) | 0.28 (0.35) | |||
| RMSE | 10.99 (0.82) | 9.39 (0.76) | 8.29 (0.68) | 8.92 (0.97) | 7.77 (0.72) | 3.41 (0.70) | |||
| aRMSE | 2.68 (0.58) | 2.32 (0.54) | 2.15 (0.47) | 3.79 (0.88) | 2.14 (0.48) | 2.25 (0.47) | |||
| ∞ | No | R | 0.47 (0.34) | 0.30 (0.32) | −0.04 (0.38) | 0.04 (0.33) | 0.14 (0.37) | 0.02 (0.35) | |
| ρ | 0.37 (0.34) | 0.02 (0.39) | −0.05 (0.46) | 0.17 (0.41) | −0.02 (0.40) | 0.28 (0.39) | |||
| τ | 0.28 (0.27) | 0.00 (0.31) | 0.06 (0.38) | 0.11 (0.31) | 0.06 (0.33) | 0.28 (0.33) | |||
| RMSE | 11.98 (1.42) | 30.53 (7.00) | 145.18 (38.40) | 367.41 (77.80) | 6.55(1.29) | 3.14 (1.12) | |||
| aRMSE | 5.44 (1.04) | 25.66 (4.61) | 143.30 (46.90) | 355.38 (68.35) | 6.45 (1.13) | 2.99 (0.99) | |||
| Site | R | 0.48 (0.32) | 0.29 (0.33) | −0.05 (0.36) | 0.03 (0.32) | −0.16 (0.34) | −0.26 (0.27) | ||
| ρ | 0.23 (0.40) | 0.02 (0.37) | −0.05 (0.45) | 0.17 (0.38) | −0.03 (0.42) | −0.08 (0.36) | |||
| τ | 0.17 (0.33) | 0.00 (0.31) | 0.06 (0.37) | 0.11 (0.30) | −0.06 (0.37) | −0.11 (0.27) | |||
| RMSE | 15.69 (0.77) | 24.87 (5.91) | 144.58 (40.84) | 370.10 (77.89) | 6.73 (1.20) | 7.85 (2.40) | |||
| aRMSE | 2.38 (0.61) | 21.94 (4.18) | 143.40 (47.96) | 356.87 (69.79) | 3.14 (0.79) | 5.31 (1.69) | |||
| Yes | R | 0.62 (0.40) | 0.20 (0.29) | −0.15 (0.37) | −0.16 (0.28) | 0.23 (0.37) | −0.18 (0.33) | ||
| ρ | 0.30 (0.41) | 0.07 (0.39) | −0.08 (0.45) | −0.10 (0.34) | −0.02 (0.40) | 0.23 (0.33) | |||
| τ | 0.17 (0.33) | 0.00 (0.33) | −0.06 (0.36) | −0.06 (0.25) | −0.06 (0.31) | 0.06 (0.26) | |||
| RMSE | 11.13 (0.77) | 13.72 (4.69) | 70.81 (32.09) | 134.79 (52.44) | 5.37 (0.71) | 5.79 (2.53) | |||
| aRMSE | 2.24 (0.39) | 13.70 (5.10) | 69.99 (30.78) | 113.34 (38.79) | 2.24 (0.35) | 5.67(2.38) | |||
| MAP4K4 | 3 | No | R | 0.48 (0.18) | 0.50 (0.14) | −0.17 (0.29) | −0.28 (0.17) | 0.51 (0.18) | 0.43 (0.17) |
| ρ | 0.45 (0.22) | 0.49 (0.18) | 0.17 (0.26) | −0.14 (0.26) | 0.43 (0.23) | 0.36 (0.23) | |||
| τ | 0.32 (0.18) | 0.33 (0.14) | 0.11 (0.19) | −0.10 (0.21) | 0.29 (0.17) | 0.27 (0.17) | |||
| aRMSE | 12.27 (2.71) | 8.05 (1.21) | 34.37 (15.18) | 569.24 (308.36) | 7.47 (0.88) | 12.10 (3.80) | |||
| Site | R | 0.47 (0.17) | 0.49 (0.14) | −0.18 (0.30) | −0.28 (0.19) | 0.49 (0.18) | 0.42 (0.17) | ||
| ρ | 0.45 (0.22) | 0.49 (0.17) | 0.17 (0.27) | −0.16 (0.26) | 0.40 (0.23) | 0.35 (0.23) | |||
| τ | 0.33 (0.17) | 0.33 (0.14) | 0.11 (0.19) | −0.12 (0.22) | 0.27 (0.17) | 0.25 (0.17) | |||
| aRMSE | 12.10 (2.89) | 7.98 (1.14) | 34.51 (15.10) | 569.40 (302.43) | 7.37 (0.88) | 11.90 (3.72) | |||
| Yes | R | 0.48 (0.15) | 0.44 (0.18) | 0.42 (0.20) | −0.12 (0.26) | 0.44 (0.16) | 0.44 (0.17) | ||
| ρ | 0.54 (0.20) | 0.44 (0.23) | 0.46 (0.21) | 0.09 (0.26) | 0.52 (0.21) | 0.46 (0.24) | |||
| τ | 0.40 (0.17) | 0.32 (0.19) | 0.35 (0.18) | 0.07 (0.21) | 0.39 (0.17) | 0.33 (0.18) | |||
| aRMSE | 12.69 (3.13) | 11.42 (2.40) | 15.50 (3.71) | 26.81 (10.86) | 12.21 (3.07) | 12.46 (3.91) | |||
| ∞ | No | R | 0.47 (0.17) | 0.57 (0.12) | 0.14 (0.21) | −0.26 (0.16) | 0.45 (0.18) | 0.44 (0.16) | |
| ρ | 0.39 (0.21) | 0.53 (0.18) | 0.11 (0.26) | −0.23 (0.21) | 0.45 (0.20) | 0.42 (0.21) | |||
| τ | 0.27 (0.17) | 0.39 (0.15) | 0.06 (0.20) | −0.15 (0.16) | 0.31 (0.15) | 0.31 (0.15) | |||
| aRMSE | 14.71 (2.76) | 11.82 (2.69) | 18.48 (4.46) | 59.68 (13.92) | 9.20 (1.09) | 11.57 (2.18) | |||
| Site | R | 0.46 (0.16) | 0.57 (0.13) | 0.13 (0.21) | −0.26 (0.16) | 0.45 (0.19) | 0.43 (0.17) | ||
| ρ | 0.39 (0.22) | 0.51 (0.18) | 0.10 (0.26) | −0.24 (0.20) | 0.43 (0.20) | 0.39 (0.22) | |||
| τ | 0.27 (0.16) | 0.37 (0.15) | 0.06 (0.21) | −0.16 (0.16) | 0.29 (0.15) | 0.29 (0.15) | |||
| aRMSE | 14.60 (2.70) | 11.73 (2.67) | 18.37 (4.30) | 59.73 (14.61) | 9.10 (1.08 | 11.51 (2.15) | |||
| Yes | R | 0.45 (0.16) | 0.51 (0.17) | 0.23 (0.25) | 0.18 (0.22) | 0.45 (0.17) | 0.41 (0.16) | ||
| ρ | 0.44 (0.21) | 0.50 (0.19) | 0.24 (0.25) | 0.24 (0.24) | 0.44 (0.21) | 0.35 (0.22) | |||
| τ | 0.31 (0.17) | 0.37 (0.16) | 0.19 (0.20) | 0.19 (0.20) | 0.32 (0.17) | 0.23 (0.16) | |||
| aRMSE | 14.50 (2.78) | 12.97 (2.24) | 10.93 (1.78) | 11.63 (1.86) | 13.27 (2.65) | 11.57 (2.20) | |||
| Interaction Entropy | 3 | No | R | −0.15 (0.24) | 0.07 (0.25) | 0.30 (0.21) | 0.08 (0.27) | −0.09 (0.23) | −0.18 (0.22) |
| ρ | −0.17 (0.28) | 0.08 (0.29) | 0.35 (0.26) | −0.01 (0.30) | −0.12 (0.30) | −0.18 (0.29) | |||
| τ | −0.08 (0.21) | 0.05 (0.22) | 0.23 (0.20) | −0.03 (0.23) | −0.05 (0.23) | −0.14 (0.23) | |||
| RMSE | 31.37 (3.42) | 16.88 (1.96) | 14.57 (1.95) | 66.31 (29.43) | 20.41 (2.06) | 14.45 (1.63) | |||
| aRMSE | 13.98 (1.97) | 9.28 (1.23) | 13.03 (1.97) | 66.31 (31.08) | 9.74 (1.49) | 11.37 (2.02) | |||
| Site | R | −0.13 (0.25) | 0.07 (0.24) | 0.29 (0.22) | 0.08 (0.28) | −0.07 (0.24) | −0.16 (0.21) | ||
| ρ | −0.15 (0.27) | 0.08 (0.30) | 0.35 (0.26) | 0.04 (0.30) | −0.16 (0.30) | −0.19 (0.31) | |||
| τ | −0.05 (0.21) | 0.05 (0.21) | 0.25 (0.21) | 0.01 (0.24) | −0.10 (0.22) | −0.16 (0.23) | |||
| RMSE | 25.75 (3.27) | 12.46 (1.58) | 13.79 (1.83) | 66.64 (31.45) | 15.19 (1.79) | 12.06 (1.71) | |||
| aRMSE | 14.74 (2.08) | 10.22 (1.30) | 13.79 (1.91) | 66.20 (31.82) | 10.50 (1.63) | 11.90 (2.16) | |||
| Yes | R | −0.15 (0.23) | 0.01 (0.26) | 0.27 (0.23) | 0.11 (0.28) | −0.11 (0.22) | −0.18 (0.20) | ||
| ρ | −0.21 (0.26) | 0.11 (0.28) | 0.33 (0.27) | 0.13 (0.31) | −0.09 (0.29) | −0.17 (0.30) | |||
| τ | −0.12 (0.20) | 0.08 (0.20) | 0.23 (0.20) | 0.12 (0.25) | −0.03 (0.22) | −0.14 (0.24) | |||
| RMSE | 21.86 (3.09) | 10.53 (1.10) | 14.02 (2.44) | 67.40 (30.84) | 12.39 (1.37) | 11.87 (2.33) | |||
| aRMSE | 14.39 (2.04) | 10.33 (1.26) | 13.30 (1.96) | 66.59 (29.88) | 10.43 (1.51) | 11.55 (2.08) | |||
| ∞ | No | R | −0.11 (0.25) | −0.17 (0.22) | −0.22 (0.28) | 0.09 (0.28) | −0.11 (0.25) | −0.14 (0.25) | |
| ρ | −0.13 (0.31) | −0.14 (0.28) | −0.08 (0.29) | 0.12 (0.31) | −0.20 (0.31) | −0.24 (0.29) | |||
| τ | −0.10 (0.24) | −0.12 (0.22) | −0.01 (0.23) | 0.08 (0.25) | −0.16 (0.24) | −0.19 (0.24) | |||
| RMSE | 32.71 (3.55) | 22.99 (4.69) | 25.15 (4.33) | 191.53 (69.35) | 19.06 (2.27) | 14.41 (2.27) | |||
| aRMSE | 13.79 (2.23) | 21.95 (5.88) | 25.14 (4.48) | 177.49 (58.39) | 12.28 (1.78) | 11.03 (1.80) | |||
| Site | R | −0.10 (0.24) | −0.16 (0.24) | −0.22 (0.28) | 0.10 (0.29) | −0.10 (0.25) | −0.13 (0.24) | ||
| ρ | −0.16 (0.29) | −0.14 (0.30) | −0.05 (0.30) | 0.11 (0.33) | −0.16 (0.31) | −0.25 (0.28) | |||
| τ | −0.12 (0.23) | −0.12 (0.23) | 0.01 (0.23) | 0.08 (0.25) | −0.12 (0.24) | −0.21 (0.24) | |||
| RMSE | 27.14 (3.50) | 22.42 (5.85) | 26.60 (5.63) | 188.86 (69.17) | 15.00 (1.74) | 11.52 (1.73) | |||
| aRMSE | 13.98 (2.27) | 22.41 (5.84) | 25.60 (4.52) | 177.10 (56.30) | 12.57 (1.81) | 11.15 (1.76) | |||
| Yes | R | −0.14 (0.24) | −0.17 (0.22) | −0.22 (0.26) | 0.10 (0.27) | −0.14 (0.24) | −0.17 (0.24) | ||
| ρ | −0.23 (0.29) | −0.13 (0.28) | −0.04 (0.30) | 0.16 (0.31) | −0.18 (0.29) | −0.23 (0.30) | |||
| τ | −0.14 (0.23) | −0.10 (0.21) | 0.01 (0.24) | 0.12 (0.22) | −0.12 (0.23) | −0.16 (0.24) | |||
| RMSE | 22.82 (3.50) | 23.53 (7.15) | 28.94 (6.25) | 186.42 (65.99) | 13.90 (1.61) | 11.99 (2.06) | |||
| aRMSE | 14.51 (2.28) | 22.99 (6.21) | 25.96 (4.38) | 176.17 (57.17) | 13.59 (1.96) | 11.67 (1.89) | |||
The performance of our methods in achieving consistency with experimental results was uneven. For three datasets — FXR, hPNMT, and the IE dataset from Duan et al. 36 — none of the tested estimation protocols were able to achieve significant correlation (R, ρ, or τ greater than 0.4) with experiment. For the other three datasets — bromodomains, lysozyme, and MAP4K4 — correlation was sensitive to the estimation protocol. The aRMSE was also sensitive to the estimation protocol and larger than the corresponding dummy estimate in which all binding free energies were assumed equivalent. For the six datasets, the aRMSE of dummy estimates are as follows: bromodomains (0.78 kJ/mol); FXR (1.73 kJ/mol); hPNMT (0.53 kJ/mol); lysozyme (0.71 kJ/mol); MAP4K4 (1.42 kJ/mol) and IE (3.28 kJ/mol). The comparatively high aRMSE of the end-point binding free energy estimates (Table 2) may leave an impression that the latter have limited benefit. However, the significant correlation in some datasets indicates that the calculations may be useful for rank ordering compounds and that high aRMSEs simply reflect that the slope deviates from unity.
There are several possible reasons that, for three datasets, our calculations were unable to achieve significant correlation with experiment. The usual suspects in problematic molecular simulations and calculations are sampling and force field error. Although sampling is a common issue, especially in rugged energy landscapes common to biomolecules, is it unlikely to be the major issue with our calculations because we started with a crystallographic binding pose and run for 200 ns. Indeed, a correct binding pose is no guarantee of accurate results; in the Drug Design Data Resource (D3R) Grand Challenge 2, the Kendall τ between predicted and experimental binding affinities for FXR complexes with known structure ranged from about −0.4 to 0.4.67 Force field error arises because molecular mechanics force fields only approximate quantum mechanics, inadequately accounting for local environment effects such as polarization and bond rearrangements such as protonation and tautomerization. In our simulations, more attention could have been paid to residue protonation and disulfide bonds. Analysis with PROPKA (Table S2 in the Supporting Information), completed after the initial review of our paper, suggests that one or two glutamine residues in the binding site of hPNMT are likely to be protonated and that several proteins in the IE dataset have disulfide bonds. There were no differences between PROPKA and AmberTools defaults in the bromodomains dataset and more subtle and distant differences with the lysozyme and MAP4K4 datasets. Our calculations also made the approximation of using a continuum dielectric implicit solvent model instead of an explicit solvent. Even with an explicit solvent model, however, Duan et al. 36 also did not achieve correlation with experiment any better than ours (See Table S4 in the Supporting Information for the Pearson R, Spearman ρ, and Kendall τ that we computed based on their reported results), suggesting that other factors are limiting the accuracy of our results.
Another source of error, which is the focus of the present paper, is estimation error. In the subsequent sections, we will focus on the three datasets — bromodomains, lysozyme, and MAP4K4 — that allow us to compare estimator performance.
3.2. Filtering based on ligand RMSD is beneficial
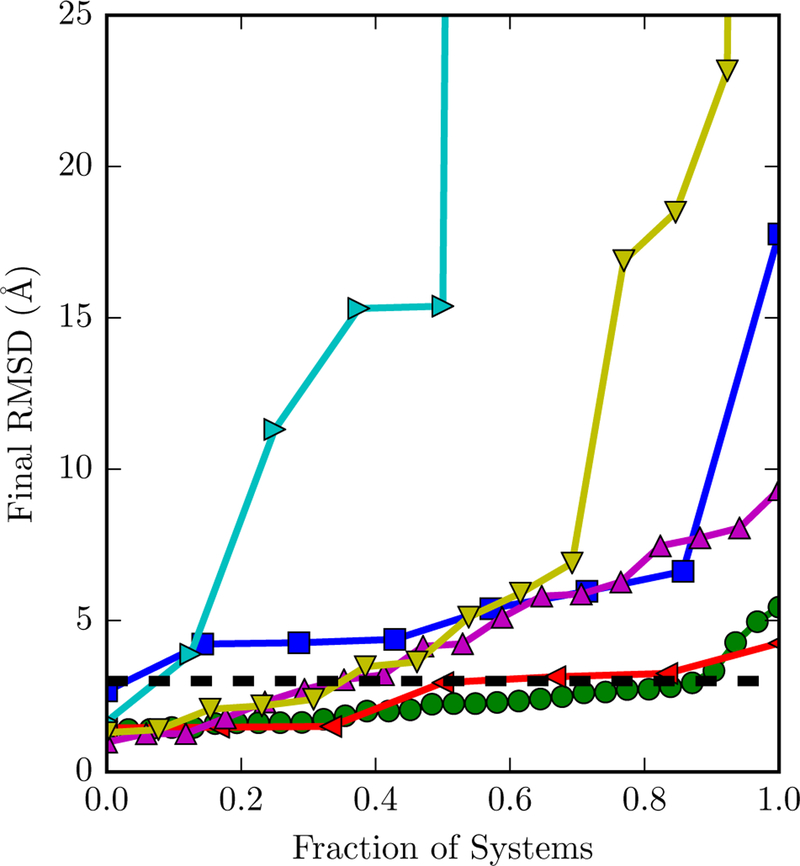
The behavior of the ligand over a 200 ns simulation is highly variable from system to system. The ligand RMSD versus time for every dataset is available in Figure S3 of the Supporting Information. Figure 3 focuses on the final RMSD at the end of each simulation. In many systems, the ligand remains close to the crystallographic pose. For example, in FXR, about 90% of simulations have a ligand RMSD of three Å or less at the end of the simulation. In others, the ligand assumes another relatively stable pose or fluctuates between a number of poses (the latter is evident in Figure S3 of the Supporting Information). In a few simulations (four for lysozyme and one for IE), the ligand completely dissociates and has a final RMSD of over 100 Å.
Figure 3: Fraction of systems with a final ligand RMSD below a certain cutoff.
The y axis is restricted to between 0 and 25 Å. The dashed line is at 3 Å, which we used as the native pose cutoff. The markers of different datasets are for bromodomains (blue squares), FXR (green circles), hPNMT (leftward triangles), lysozyme (rightwards triangles), MAPK4K (upwards triangles), and interaction entropy (downwards triangles).
There are several possible reasons for the observed alternative binding poses and ligand dissociation. Regarding the alternative binding poses, it is possible that they do exist in solution but that only the most stable form is resolved in crystal structures. Previous simulations have suggested that T4 lysozyme ligands can bind in multiple sites.68 Alternative binding poses may also be an artifact of an inaccurate force field. Regarding dissociation, it may also result from force field inaccuracy, but may simply be due to binding kinetics. Over a sufficient time scale, noncovalent binders are expected to spontaneously associate and dissociate. Such events have been observed in short molecular dynamics simulations used to build Markov state models of binding processes69–72. Compared to typical MM/GBSA simulations, which are usually shorter than 10 ns, our 200 ns simulations are much longer, making the observation of dissociation events more likely.
Regardless of the reason that ligands deviated from crystallographic poses, removing snapshots with a ligand RMSD larger than 3 Å resulted in similar of better performance compared to binding free energy estimates without an RMSD cutoff. With the bromodomain and lysozyme datasets, most correlation metrics are significantly higher and the aRMSE is lower with the RMSD-based filter compared to without the RMSD filter (Table 2). In the MAP4K4 dataset, the performance with and without the filter was similar. The benefits of the filter were evident across all six datasets, as the average ranking of Pearson R, Spearman ρ, and Kendall τ were consistently better with than without the filter (Table 3).
Table 3: Ligand RMSD filter effects.
The average rank of correlation metrics across all six datasets with a ligancd RMSD filter of 3 Å and without a filter (∞) were compared. Rankings were based on the highest value (neglecting error) among all external entropy and estimator options. The filter with the highest correlation was given rank 1, and the filter with the lower correlation was given rank 2. In the case of a tie, both filters were assigned rank 1.
| R | Ρ | Τ | |
|---|---|---|---|
| 3 Å | 1.33 | 1.17 | 1.17 |
| ∞ | 1.50 | 1.50 | 1.17 |
Although our results may suggest that including a filter based on ligand RMSD is always helpful, it is important to note that all of our simulations started from a crystallographic structure of the complex. Stringent filtering is unlikely to be beneficial if the initial binding pose is incorrect. If the binding pose is unknown, it may be useful to include a cutoff based on a distance from the receptor surface and exclude snapshots in which the ligand and receptor are no longer close.
3.3. Ligand external entropy corrections reduce error but fail to improve correlation
The sign and magnitude of the binding site volume correction and fictitious confining potential are as expected. In all cases, they are both positive, indicating that the entropic loss leads to weaker binding (Table 4 and Figure S4 in the Supporting Information). Furthermore, the magnitude of is greater than that of ∆Gξ, likely because the latter overestimates the residual external entropy in the complex. In most datasets, and ∆Gξ appear correlated (Figure S4 in the Supporting Information).
Table 4: The mean and standard deviations of free energy corrections based on ligand external entropy:
restricting the ligand to the binding site (∆Gξ) and of imposing a confining potential on translational and rotational degrees of freedom (∆Gc). The latter is based on ∆Gc = ∆Gc,L − ∆Gc,RL and does not include importance sampling effects through .
| Set | ∆Gξ | ∆Gc |
|---|---|---|
| Bromodomains | 1.98 (0.41) | 5.74 (1.05) |
| FXR | 2.20 (0.32) | 7.42 (0.92) |
| hPNMT | 2.06 (0.28) | 7.43 (1.18) |
| Lysozyme | 1.46 (0.14) | 4.94 (0.48) |
| MAP4K4 | 1.98 (0.35) | 7.33 (0.77) |
| IE | 6.96 (1.38) | 11.62 (1.28) |
Even though the external entropy corrections reduce the error, they do not increase the correlation with experiment (Tables 2 and 5). For the bromodomain and lysozyme datasets, accounting for the loss in ligand external entropy leads to a lower RMSE with respect to experiment. However, of the three options for ligand external entropy corrections, completely excluding a correction leads to the best average ranking for all three metrics.
Table 5: Assessing the effect of external entropy corrections.
The average rank of correlation metrics across all six datasets without an external entropy correction (No), with a binding site volume correction (Site), and with a fictitious potential on ξ (Yes), were compared. Rankings were based on the highest value (neglecting error) among those based on a ligand RMSD cutoff was 3 Å and all estimator options. The correction with the highest correlation was given rank 1, and the corrections with the lower correlations were given ranks 2 and 3. In the case of a tie, two correlations were assigned rank 1 and the third was asigned rank 3.
| R | ρ | τ | |
|---|---|---|---|
| No | 1.33 | 1.50 | 1.33 |
| Site | 2.17 | 1.33 | 1.50 |
| Yes | 2.33 | 2.00 | 2.17 |
These results were contrary to our expectations. Swanson et al. 23 suggested that external entropy changes are much larger and therefore more important than internal entropy changes. Indeed, we observed that the magnitude of the correction can be large, but that its variance is small. The largest standard deviation is with the IE dataset, which is based on a diverse set of receptors. For most datasets with a common receptor, standard deviations were on the order of 1 kcal/mol or less (Table 4). It may be the case that, per degree of freedom, internal entropy changes are more subtle, but accumulate to a more significant sum with larger variation between complexes.
Although our external entropy corrections may not be particularly useful in a purely physics-based free energy calculation, they may nonetheless be beneficial in a semi-empirical model. In their multiple linear regression model incorporating an external entropy correction, Ben-Shalom et al. 60 found that coefficients for entropic terms were much greater than those for enthalpic terms. Amplification of the external entropy terms makes physical sense if external entropy changes are correlated with internal entropy changes. Consideration of ∆Gc in such models may be a worthy direction for future work, but is outside the scope of this present manuscript.
3.4. The second-order cumulant expansion balances accuracy and precision
The second-order cumulant expansion leads to the most reliable correlations of all expansion options.
Across all six datasets, the second-order cumulant expansion has the first or second best average ranking for all three correlation metrics considered (Table 6). Among the three datasets where calculations are significantly correlated with experiment, the first-order expansion and exponential average have comparable correlation with experiment (Table 2). However, for the bromodomains, the Pearson R for these two estimators is significantly less than for the second-order expansion (around 0.6 opposed to 0.8) and the RMSE is much larger. The third- and fourth-order expansions significantly deteriorate correlations with experiment in the bromodomains and MAP4K4 datasets. Including the normal modes entropy reduces the RMSE but also reduces the correlation metrics.
Table 6: Assessing expansion options.
The average rank of correlation metrics across all six datasets based on different truncations of the cumulant expansion (1–4), exponential average (EXP), and the first-order cumulant expansion and normal modes entropy (1 + NM), were compared. Estimates were based on a ligand RMSD filter of 3 Å and did not include an external entropy correction. Rankings were based on the highest value (neglecting error) among all external entropy and expansion options. The estimator with the highest correlation was given rank 1, and the estimators with the lower correlations were given ranks 2 through 6. In the case of a tie between two options, both were assigned the same rank.
| R | ρ | τ | |
|---|---|---|---|
| 1 | 3.17 | 3.00 | 3.00 |
| 2 | 1.50 | 2.33 | 2.33 |
| 3 | 2.00 | 2.33 | 2.33 |
| 4 | 3.67 | 3.17 | 2.67 |
| EXP | 2.83 | 2.17 | 1.83 |
| 1 + NM | 3.67 | 3.83 | 3.50 |
The second-order cumulant expansion also reliably leads to the lowest error of all expansion options (Table 2). For bromodomains and MAP4K4, the second-order cumulant expansion has a significantly lower aRMSE than other expansion options. In the former dataset, where absolute binding free energies are available to compute the RMSE, this option leads to the lowest RMSE. In the lysozyme dataset, the aRMSE for multiple different expansion options is comparable.
The IE and MAP4K4 datasets have receptor-ligand systems in which a binding free energy estimate based on a high-order cumulant expansion is a significant outlier (2WBG in IE and MAP01 in MAP). Removing these outliers does not significantly change the outcome of our analysis. Removal of 2WBG from its dataset actually results in a lower Pearson R. Removal of MAP01 improves the Pearson R, but not to a level close to the other estimators.
The strong performance of the second-order expansion may be attributed to the fact that the majority of interaction energy distributions appear nearly Gaussian (Figure S2 of the Supporting Information). There are a few complexes that have skewed or multimodal distributions of the interaction energy or in which there are insufficient data (after filtering) to clearly define the shape of the distribution. In most datasets, however, these are exceptions rather than the rule. Due to the near-Gaussian shape of most interaction energy distributions, higher-order terms appear to add minimal benefit to accuracy while introducing significant numerical instability.
Our observation that exponential averages are superior to the first-order cumulant expansion is consistent with recent results with the IE method.36 Duan et al. 36 factored the average out of the exponential average interaction energy, leading to,
| (27) |
(This operation is equivalent to Equation 12 of prior work in solvation thermodynamics. 57) For calculations with the IE dataset, Duan et al. 36 found that protein-ligand binding free energy estimates based on IE have a lower mean absolute error relative to experimental values than the standard MM/GBSA approach. Although this expression allows for a separation of the energetic and entropic contributions to binding, the free energy estimate is numerically equivalent to Equation 15, providing evidence that the exponential average is superior to the first-order cumulant expansion.
3.5. Convergence requires variable simulation time
As evident from the Pearson R and RMSE from the final value as a function of simulation time in all three systems with significant correlation (Figure 4), the amount of simulation time for convergence is highly system-dependent. Trends are smoothest for the first-order cumulant expansion, for which both metrics change only gradually as simulation time increases and level off by about 100 ns. The second-order cumulant expansion is less stable but, except in the bromodomains dataset, also levels off by around 100 ns. Surprisingly, the instability of the Pearson R and RMSE with the bromodomain dataset is due to a relatively small change in the estimated free energy of a single system. The exponential average appears to level off sooner, around 50 ns, and is marked by sudden but relatively small jumps in the correlation.
In 1994, LIE was initially derived based on a cumulant expansion20–22 truncated at the first order. At the time, it was assumed that second- and higher-order terms would converge more slowly and the approximation was made that these terms would cancel out. In contrast with these expectations, our present results suggest that the second-order term and the exponential average do not actually converge much more slowly than the first-order term.
4. Conclusions and Future Directions
We have derived, implemented, and tested a number of modifications to the MM/GBSA estimator for binding free energies. The modifications were tested on a number of datasets with congeneric as well as diverse ligands. In some datasets, neither the MM/GBSA estimator nor any of the modifications were able to achieve significant correlation with experiment. In the others, we found that filtering snapshots with a high ligand RMSD was beneficial to both error and correlation. Although they reduced error, our proposed external entropy corrections did not improve correlation with experiment. Finally, we found that compared to a first-order cumulant expansion with or without normal modes entropy, a second-order cumulant expansion reduces error and sometimes improves correlation greatly, while never significantly reducing correlation. Including this term requires negligible additional computational expense and eliminates the necessity of costly normal modes analysis. There appears to be no downside to using the second-order cumulant truncation in place of standard MM/GBSA estimation.
The effectiveness of these estimators should still be tested for different types of models, including with explicit solvent and polarizable force fields. Comparing end-point and alchemical binding free energy calculations instead of experimental results would allow us to fully disentangle force field and estimator errors. Furthermore, because internal entropy was ignored, continued improvement of entropy terms should be pursued.
Supplementary Material
5. Acknowledgement
We thank OpenEye scientific software for providing a free academic license to their software. This research was supported by the National Institutes of Health (R15GM114781 and then R01GM127712).
Footnotes
Supporting Information Available
Details source information for the six datasets, differences between PROPKA and Amber-Tools default residue protonation states, experimental and estimated binding free energies, correlation metrics for the IE dataset, chemical structures of all ligands, interaction energy distributions for all complexes, ligand RMSE as a function of time, comparison of free energy corrections based on external entropy, and the main script for performing calculations. This material is available free of charge via the Internet at http://pubs.acs.org/.
References
- (1).Gilson MK; Given JA; Bush BL; McCammon JA The Statistical Thermodynamic Basis for Computation of Binding Affinities: A Critical Review. Bio-phys. J 1997, 72, 1047–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Michel J; Essex JW Hit Identification and Binding Mode Predictions by Rigorous Free Energy Simulations. J. Med. Chem 2008, 51, 6654–6664. [DOI] [PubMed] [Google Scholar]
- (3).Boyce SE; Mobley DL; Rocklin GJ; Graves AP; Dill KA; Shoichet BK Predicting Ligand Binding Affinity with Alchemical Free Energy Methods in a Polar Model Binding Site. J. Mol. Biol 2009, 394, 747–763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Ge X; Roux B Absolute Binding Free Energy Calculations of Sparsomycin Analogs to the Bacterial Ribosome. J. Phys. Chem. B 2010, 114, 9525–9539. [DOI] [PubMed] [Google Scholar]
- (5).Wang L; Berne BJ; Friesner RA On Achieving High Accuracy and Reliability in the Calculation of Relative Protein-Ligand Binding Affinities. Proc. Natl. Acad. Sci. USA 2012, 109, 1937–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Zhu S; Travis SM; Elcock AH Accurate Calculation of Mutational Effects on the Thermodynamics of Inhibitor Binding to P38α MAP Kinase: A Combined Computational and Experimental Study. J. Chem. Theory Comput 2013, 9, 3151–3164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Wang L; Wu Y; Deng Y; Kim B; Pierce L; Krilov G; Lupyan D; Robinson S; Dahlgren MK; Greenwood J; Romero DL; Masse C; Knight JL; Steinbrecher T; Beuming T; Damm W; Harder E; Sherman W; Brewer M; Wester R; Murcko M; Frye L; Farid R; Lin T; Mobley DL; Jorgensen WL; Berne BJ; Friesner RA; Abel R Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field. J. Am. Chem. Soc 2015, 137, 2695–2703. [DOI] [PubMed] [Google Scholar]
- (8).Aldeghi M; Heifetz A; Bodkin MJ; Knapp S; Biggin PC Accurate Calculation of the Absolute Free Energy of Binding for Drug Molecules. Chem. Sci 2016, 7, 207–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Aldeghi M; Heifetz A; Bodkin MJ; Knapp S; Biggin PC Predictions of Ligand Selectivity from Absolute Binding Free Energy Calculations. J. Am. Chem. Soc 2017, 139, 946–957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Wan S; Bhati AP; Zasada SJ; Wall I; Green D; Bamborough P; Coveney PV Rapid and Reliable Binding Affinity Prediction of Bromodomain Inhibitors: A Computational Study. J. Chem. Theory Comput 2017, 13, 784–795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Gumbart JC; Roux B; Chipot C Efficient Determination of Protein-Protein Standard Binding Free Energies from First Principles. J. Chem. Theory Comput 2013, 9, 3789–3798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Rodriguez RA; Yu L; Chen LY Computing Protein-Protein Association Affinity with Hybrid Steered Molecular Dynamics. J. Chem. Theory Comput 2015, 11, 4427–4438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Massova I; Kollman PA Combined Molecular Mechanical and Continuum Solvent Approach (MM-PBSA/GBSA) to Predict Ligand Binding. Perspect. Drug Discov 2000, 18, 113–135. [Google Scholar]
- (14).Hou T; Wang J; Li Y; Wang W Assessing the Performance of the MM/PBSA and MM/GBSA Methods. 1. The Accuracy of Binding Free Energy Calculations Based on Molecular Dynamics Simulations. J. Chem. Inf. Model 2011, 51, 69–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Wang W; Kollman PA Free Energy Calculations on Dimer Stability of the HIV Protease Using Molecular Dynamics and a Continuum Solvent Model. J. Mol. Biol 2000, 303, 567–582. [DOI] [PubMed] [Google Scholar]
- (16).Gohlke H; Kiel C; Case DA Insights into Protein-Protein Binding by Binding Free Energy Calculation and Free Energy Decomposition for the Ras-Raf and Ras-RalGDS Complexes. J. Mol. Biol 2003, 330, 891–913. [DOI] [PubMed] [Google Scholar]
- (17).Lee FS; Chu Z-T; Bolger MB; Warshel A Calculations of Antibody-Antigen Interactions: Microscopic and Semi-Microscopic Evaluation of the Free Energies of Binding of Phosphorylcholine Analogs to McPC603. Protein Eng. Des. Sel 1992, 5, 215–228. [DOI] [PubMed] [Google Scholar]
- (18).Sham YY; Chu ZT; Tao H; Warshel A Examining methods for calculations of binding free energies: LRA, LIE, PDLD-LRA, and PDLD/S-LRA calculations of ligands binding to an HIV protease. Proteins: Struct., Funct., Bioinf 2000, 39, 393–407. [PubMed] [Google Scholar]
- (19).de Ruiter A; Oostenbrink C Efficient and Accurate Free Energy Calculations on Trypsin Inhibitors. J. Chem. Theory Comput 2012, 8, 3686–3695. [DOI] [PubMed] [Google Scholar]
- (20).Åqvist J; Medina C; Samuelsson J-EE; Åqvist J; Medina C; Samuelsson JEE New Method for Predicting Binding Affinity in Computer-Aided Drug Design. Protein Eng 1994, 7, 385–391. [DOI] [PubMed] [Google Scholar]
- (21).Hansson T; Marelius J; Åqvist J Ligand Binding Affinity Prediction by Linear Interaction Energy Methods. J. Comput.-Aided Mol. Des 1998, 12, 27–35. [DOI] [PubMed] [Google Scholar]
- (22).Åqvist J; Luzhkov VB; Brandsdal BO Ligand Binding Affinities from MD Simulations. Acc. Chem. Res 2002, 35, 358–365. [DOI] [PubMed] [Google Scholar]
- (23).Swanson JMJ; Henchman RH; McCammon JA Revisiting Free Energy Calculations: A Theoretical Connection to MM/PBSA and Direct Calculation of the Association Free Energy. Biophys. J 2004, 86, 67–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Genheden S; Ryde U The MM/PBSA and MM/GBSA Methods to Estimate Ligand-Binding Affinities. Expert Opin. Drug Discovery 2015, 10, 449–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Chang C-E; Chen W; Gilson MK Evaluating the Accuracy of the Quasiharmonic Approximation. J. Chem. Theory Comput 2005, 1, 1017–1028. [DOI] [PubMed] [Google Scholar]
- (26).Minh DDL; Bui JM; Chang C.-e. A.; Jain T; Swanson JMJ; McCammon JA The Entropic Cost of Protein-Protein Association: A Case Study on Acetylcholinesterase Binding to Fasciculin-2. Biophys. J 2005, 89, L25–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Weis A; Katebzadeh K; Soderhjelm P; Nilsson I; Ryde U; Söderhjelm P; Nilsson I; Ryde U; Soderhjelm P; Nilsson I et al. Ligand Affinities Predicted with the MM/PBSA Method: Dependence on the Simulation Method and the Force Field. J. Med. Chem 2006, 49, 6596–6606. [DOI] [PubMed] [Google Scholar]
- (28).Kongsted J; Ryde U An Improved Method to Predict the Entropy Term with the MM/PBSA Approach. J. Comput.-Aided Mol. Des 2009, 23, 63–71. [DOI] [PubMed] [Google Scholar]
- (29).Lindström A; Edvinsson L; Johansson A; Andersson CD; Andersson IE; Raubacher F; Linusson A; Lindstrom A Postprocessing of Docked Protein-Ligand Complexes Using Implicit Solvation Models. J. Chem. Inf. Model 2011, 51, 267–282. [DOI] [PubMed] [Google Scholar]
- (30).Zhang X; Perez-Sanchez H; Lightstone FC A Comprehensive Docking and MM/GBSA Rescoring Study of Ligand Recognition upon Binding Antithrombin. Curr. Top. Med. Chem 2017, 17, 1631–1639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Åqvist J; Hansson T On the Validity of Electrostatic Linear Response in Polar Solvents. J. Phys. Chem 1996, 100, 9512–9521. [Google Scholar]
- (32).Martins SA; Perez MAS; Moreira IS; Sousa SF; Ramos MJ; Fernandes PA Computational Alanine Scanning Mutagenesis: MM-PBSA vs TI. J. Chem. Theory Comput 2013, 9, 1311–1319. [DOI] [PubMed] [Google Scholar]
- (33).Chang C-E; Chen W; Gilson MK Ligand Configurational Entropy and Protein Binding. Proc. Natl. Acad. Sci. USA 2007, 104, 1534–1539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Chodera JD; Mobley DL Entropy-Enthalpy Compensation: Role and Ramifications in Biomolecular Ligand Recognition and Design. Annu. Rev. Biophys 2014, 42, 121–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Geschwindner S; Ulander J; Johansson P Ligand Binding Thermodynamics in Drug Discovery: Still a Hot Tip? J. Med. Chem 2015, 58, 6321–6335. [DOI] [PubMed] [Google Scholar]
- (36).Duan L; Liu X; Zhang JZH Interaction Entropy: A New Paradigm for Highly Efficient and Reliable Computation of Protein-Ligand Binding Free Energy. J. Am. Chem. Soc 2016, 138, 5722–5728. [DOI] [PubMed] [Google Scholar]
- (37).Jarzynski C Rare Events and the Convergence of Exponentially Averaged Work Values. Phys. Rev. E 2006, 73, 46105. [DOI] [PubMed] [Google Scholar]
- (38).Zuckerman DM; Woolf TB Systematic Finite-Sampling Inaccuracy in Free Energy Differences and Other Nonlinear Quantities. J. Stat. Phys 2004, 114, 1303–1323. [Google Scholar]
- (39).Case D; Cerutti D; T.E. Cheatham I; Darden T; Duke R; Giese T; Gohlke H; Goetz A; Greene D; Homeyer N; Izadi S; Kovalenko A; Lee T; LeGrand S; Li P; Lin C; Liu J; Luchko T; Luo R; Mermelstein D; Merz K; Monard G; Nguyen H; Omelyan I; Onufriev A; Pan F; Qi R; Roe D; Roitberg A; Sagui C; Simmerling C; Botello-Smith W; Swails J; Walker R; Wang J; Wolf R; Wu X; Xiao L; York D; Kollman P AMBER 2017. University of California, San Francisco, 2017; http://ambermd.org/. [Google Scholar]
- (40).Salomon-Ferrer R; Case DA; Walker RC An Overview of the Amber Biomolecular Simulation Package. WIREs Comput. Mol. Sci 2013, 3, 198–210. [Google Scholar]
- (41).Søndergaard CR; Olsson MHM; Rostkowski M; Jensen JH Improved Treatment of Ligands and Coupling Effects in Empirical Calculation and Rationalization of pKa Values. J. Chem. Theory Comput 2011, 7, 2284–2295. [DOI] [PubMed] [Google Scholar]
- (42).Olsson MHM; Søndergaard CR; Rostkowski M; Jensen JH PROPKA3: Consistent Treatment of Internal and Surface Residues in Empirical pKa Predictions. J. Chem. Theory Comput 2011, 7, 525–537 [DOI] [PubMed] [Google Scholar]
- (43).Dolinsky TJ; Nielsen JE; McCammon JA; Baker NA PDB2PQR: An Automated Pipeline for the Setup of Poisson-Boltzmann Electrostatics Calculations. Nucleic Acids Res 2004, 32, 665–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Wang J; Wolf RM; Caldwell JW; Kollman PA; Case DA Development and Testing of a General Amber Force Field. J. Comput. Chem 2004, 25, 1157–74. [DOI] [PubMed] [Google Scholar]
- (45).Jakalian A; Bush BL; Jack DB; Bayly CI Fast, Efficient Generation of High-Quality Atomic Charges. AM1-BCC Model: I. Method. J. Comput. Chem 1999, 21, 132–146. [DOI] [PubMed] [Google Scholar]
- (46).Jakalian A; Jack DB; Bayly CI Fast, Efficient Generation of High-Quality Atomic Charges. AM1-BCC Model: II. Parameterization and Validation. J. Comput. Chem 2002, 23, 1623–41. [DOI] [PubMed] [Google Scholar]
- (47).Onufriev A; Bashford D; Case DA Exploring Protein Native States and Large-Scale Conformational Changes With a Modified Generalized Born Model. Proteins: Struct., Funct., Bioinf 2004, 55, 383–394. [DOI] [PubMed] [Google Scholar]
- (48).Eastman P; Pande VS OpenMM: A Hardware-Independent Framework for Molecular Simulations. Comput. Sci. Eng 2010, 12, 34–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Eastman P; Swails J; Chodera JD; Mcgibbon RT; Zhao Y; Beauchamp KA; Wang L.-p.; Simmonett AC; Harrigan MP; Stern CD et al. OpenMM 7: Rapid Development of High Performance Algorithms for Molecular Dynamics. PLoS Comput. Biol 2017, 13, e1005659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Humphrey W; Dalke A; Schulten K VMD - Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38 [DOI] [PubMed] [Google Scholar]
- (51).Miller BR; McGee TD; Swails JM; Homeyer N; Gohlke H; Roitberg AE MMPBSA.Py: An Efficient Program for End-State Free Energy Calculations. J. Chem. Theory Comput 2012, 8, 3314–3321. [DOI] [PubMed] [Google Scholar]
- (52).General IJ A Note on the Standard State’s Binding Free Energy. J. Chem. Theory Comput 2010, 6, 2520–2524. [DOI] [PubMed] [Google Scholar]
- (53).Gallicchio E; Lapelosa M; Levy RM Binding Energy Distribution Analysis Method (BEDAM) for Estimation of Protein-Ligand Binding Affinities. J. Chem. Theory Comput 2010, 6, 2961–2977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Minh DDL Implicit Ligand Theory: Rigorous Binding Free Energies and Thermodynamic Expectations from Molecular Docking. J. Chem. Phys 2012, 137, 104106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Gilson MK; Zhou H-X Calculation of Protein-Ligand Binding Affinities. Annu. Rev. Biophys. Biomol. Struct 2007, 36, 21–42. [DOI] [PubMed] [Google Scholar]
- (56).Zwanzig R High-Temperature Equation of State by a Perturbation Method. I. Non-polar Gases. J. Chem. Phys 1954, 22, 1420. [Google Scholar]
- (57).Ben-Amotz D; Raineri FO; Stell G Solvation Thermodynamics: Theory and Applications. J. Phys. Chem. B 2005, 109, 6866–6878. [DOI] [PubMed] [Google Scholar]
- (58).Marcinkiewicz J Sur Une Propri´et´e de La Loi de Gauß. Math. Z 1939, 44, 612–618. [Google Scholar]
- (59).Wood RH; Muhlbauer WCF; Thompson PT; Mu¨hlbauer WC; Thompson PT Systematic Errors in Free Energy Perturbation Calculations Due to a Finite Sample of Configuration Space: Sample-Size Hysteresis. J. Phys. Chem 1991, 95, 6670–6675. [Google Scholar]
- (60).Ben-Shalom IY; Pfeiffer-Marek S; Baringhaus KH; Gohlke H Efficient Approximation of Ligand Rotational and Translational Entropy Changes upon Binding for Use in MM-PBSA Calculations. J. Chem. Inf. Model 2017, 57, 170–189. [DOI] [PubMed] [Google Scholar]
- (61).Roe DR; Cheatham TE PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput 2013, 9, 3084–3095. [DOI] [PubMed] [Google Scholar]
- (62).McGibbon RT; Beauchamp KA; Harrigan MP; Klein C; Swails JM; Herna´ndez CX; Schwantes CR; Wang L-P; Lane TJ; Pande VS MD-Traj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys. J 2015, 109, 1528–1532 [DOI] [PMC free article] [PubMed] [Google Scholar]
- (63).van der Walt S; Colbert SC; Varoquaux G The NumPy Array: A Structure for Efficient Numerical Computation. Comput. Sci. Eng 2011, 13, 22–30. [Google Scholar]
- (64).Scott D Multivariate Density Estimation: Theory, Practice, and Visualization; John Wiley & Sons: New York, Chicester, 1992. [Google Scholar]
- (65).Kendall M A New Measure of Rank Correlation. Biometrika 1938, 30, 81–89. [Google Scholar]
- (66).Efron B Bootstrap Methods: Another Look at the Jackknife. Ann. Stat 1979, 7, 1–26. [Google Scholar]
- (67).Gaieb Z; Liu S; Gathiaka S; Chiu M; Yang H; Shao C; Feher VA; Walters WP; Kuhn B; Rudolph MG et al. D3R Grand Challenge 2: Blind Prediction of Protein–Ligand Poses, Affinity Rankings, and Relative Binding Free Energies. J. Comput.-Aided Mol. Des 2018, 32, 1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (68).Wang K; Chodera JD; Yang Y; Shirts MR Identifying Ligand Binding Sites and Poses Using GPU-Accelerated Hamiltonian Replica Exchange Molecular Dynamics. J. Comput.-Aided Mol. Des 2013, 27, 989–1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (69).Buch I; Giorgino T; De Fabritiis G Complete Reconstruction of an Enzyme-Inhibitor Binding Process by Molecular Dynamics Simulations. Proc. Natl. Acad. Sci. USA 2011, 108, 10184–10189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (70).Silva D-A; Bowman GR; Sosa-Peinado A; Huang X A Role for Both Conformational Selection and Induced Fit in Ligand Binding by the LAO Protein. PLoS Comput. Biol 2011, 7, e1002054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (71).Doerr S; De Fabritiis G On-the-Fly Learning and Sampling of Ligand Binding by High-Throughput Molecular Simulations. J. Chem. Theory Comput 2014, 10, 2064–2069. [DOI] [PubMed] [Google Scholar]
- (72).Kohlhoff K; Shukla D; Lawrenz M; Bowman GR; Konerding DE; Belov D; Altman RB; Pande VS Cloud-Based Simulations on Google Exacycle Reveal Ligand Modulation of GPCR Activation Pathways. Nat. Chem 2014, 6, 1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.