Abstract
The human middle temporal complex (hMT+) has a crucial biological relevance for the processing and detection of direction and speed of motion in visual stimuli. Here, we characterized how neuronal populations in hMT+ encode the speed of moving visual stimuli. We evaluated human intracranial electrocorticography (ECoG) responses elicited by square‐wave dartboard moving stimuli with different spatial and temporal frequency to investigate whether hMT+ neuronal populations encode the stimulus speed directly, or whether they separate motion into its spatial and temporal components. We extracted two components from the ECoG responses: (1) the power in the high‐frequency band (HFB: 65–95 Hz) as a measure of the neuronal population spiking activity and (2) a specific spectral component that followed the frequency of the stimulus's contrast reversals (SCR responses). Our results revealed that HFB neuronal population responses to visual motion stimuli exhibit distinct and independent selectivity for spatial and temporal frequencies of the visual stimuli rather than direct speed tuning. The SCR responses did not encode the speed or the spatiotemporal frequency of the visual stimuli. We conclude that the neuronal populations measured in hMT+ are not directly tuned to stimulus speed, but instead encode speed through separate and independent spatial and temporal frequency tuning. Hum Brain Mapp 38:293–307, 2017. © 2016 Wiley Periodicals, Inc.
Keywords: hMT+, human electrocorticography, neuronal population responses, speed encoding, visual motion
INTRODUCTION
Detection of motion is fundamental in daily life in order to distinguish changes in our environment and to accurately plan and execute movements of our own. Perception of the speed of a moving object allows us to understand and to promptly react to dynamic events in the visual scene. The speed of a moving object depends on the ratio of the change in position and the change in time between samples: the spatial and temporal frequencies of a moving object. A core region involved in detecting and processing motion in visual stimuli is a cortical region discovered almost simultaneously in macaque monkeys [Dubner and Zeki, 1971; Zeki, 1971] and referred to as V5, and in owl monkeys referred to as MT [Allman and Kaas, 1971]. MT/V5 has been extensively investigated in monkeys in terms of its retinotopic properties and selectivity for direction of moving stimuli [Allman and Kaas, 1971; Cheng et al., 1994; Dubner and Zeki, 1971; Maunsell, 1983; Maunsell and Newsome, 1987; Zeki, 2004, 2015]. However, only in recent years there has been an increasing interest in how neurons in MT encode the speed of motion.
Two different mechanisms of speed encoding have been proposed. The first proposes that MT neurons show separate and independent tuning for spatial and/or temporal frequencies of visual stimuli, such that their representation of speed encodes these stimulus properties rather than speed per se [Movshon, 1975; Tolhurst and Movshon, 1975]. Conversely, in the second proposed mechanism MT neurons encode the stimulus speed directly, rather than separating motion into its spatial and temporal components [Holub and Morton‐Gibson, 1981; Tolhurst and Movshon, 1975]. These two models give different predictions about tuning profiles for spatial and temporal frequencies in MT neurons. Direct speed tuning predicts the same preferred speed that is given by multiple combinations of spatial and temporal frequency. Different animal studies, aimed at investigating how MT encodes speed have yielded conflicting results. Recent single neuron recordings, in nonhuman primates and marmosets [Lui et al., 2007; Miura et al., 2014; Priebe et al., 2003, 2006] have shown, for example, that the majority of MT neurons exhibit separate and distinct responses for spatial and temporal frequencies, with only a small percentage displaying a speed tuning profile. Conversely, Perrone and Thiele (2001) have reported in macaque that 61% of MT cells are tuned for speed, irrespective of the spatial or temporal frequency presented. Comparable results were reported by Duijnhouwer et al. (2013).
So far these studies have only examined animal physiology. In humans, the responses to speed of motion in the human homologue of MT/V5, known as human middle temporal complex (hMT+) [Amano et al., 2009; Dumoulin et al., 2000; Tootell et al., 1995], have only been studied using functional magnetic resonance imaging (fMRI) and magnetoencephalographic (MEG) neuronal responses. Traditionally, the most widely used motion stimuli to investigate speed responses in human studies were broadband stimuli such random dots or spots of light [Chawla et al., 1998; Huk et al., 2002; Kawakami et al., 2002]. However, the broadband nature of these stimuli does not allow distinction between speed tuning or independent spatial and temporal frequency tuning. Far less attention has been focused on MT+ responses in humans to gratings moving at different speeds, and therefore different spatial and temporal frequencies. An fMRI adaptation experiment using drifting gratings provided evidence of speed tuning coding of BOLD responses over different temporal frequencies [Lingnau et al., 2009]. Conversely, Wang et al. [2003] showed, using MEG, independent spatial and temporal frequency tuning in response to gratings in hMT+. So it remains unclear whether neuronal tuning in human MT+ reflects speed tuning, independent spatial and temporal frequency tuning, or a combination of both.
The use of different types of stimuli in humans and animals also complicates hypotheses about the underlying neuronal tuning. The grating stimuli used in most animal studies contain single spatial and temporal frequencies that can be manipulated independently, allowing proper analysis of hypotheses of spatial frequency, temporal frequency and speed tuning. In human studies, random dot motion patterns and square‐wave checkerboards are more commonly used as they provide more robust responses. Square wave checkerboards has been used before during intracranial electrocorticography (ECoG) recordings in the human visual cortex and have been proven to produce a strong visually driven broadband component in the high frequency band [Harvey et al., 2013; Winawer et al., 2013]. Although checkerboard stimuli contain hard edges with contrast energy at multiple spatial and temporal frequency harmonics, they are regarded as exhibiting a single speed, being the change in edge position per second. These properties make this type of stimuli ideal in order to obtain good quality data in terms of contrast to noise ratio in the clinical setting and shorter experiment times typically employed in human ECoG studies.
ECoG in humans has recently received an increased interest since it provides a direct measure of neuronal activity in relatively small neuronal populations in the human brain. Thus, ECoG gives a unique combination of high spatial and temporal resolution that allows researchers to bridge the gap between single neuron recordings in non‐human primates and non‐invasive modalities such as MEG, EEG, and fMRI in humans. High frequency broadband (HFB) changes in the ECoG signal are particularly interesting because they reflect neuronal population spiking activity [Miller et al., 2009].
Here, we used ECoG to investigate the speed tuning properties of human MT+ neuronal populations in response to square‐wave dartboard moving with different spatial and temporal frequency combinations. We determined HFB activity in response to visual motion stimulation and used these signals to investigate whether hMT+ neuronal populations exhibit separate and independent spatial and temporal frequency tuning, or whether they encode the stimulus speed directly with selectivity to multiple combinations of spatial and temporal frequency. We further examined whether these responses to the hard edged square‐wave dartboard reflect the pattern of harmonic frequencies they contain, or are instead dominated by their fundamental frequencies. Finally, we investigated the role of ECoG signal synchronization with specific temporal frequencies of the moving stimuli in encoding the speed of motion.
MATERIALS AND METHODS
Subjects and ECoG Recordings
Four subjects (one female) underwent implantation of ECoG grids for the purpose of epilepsy monitoring. The study was approved by the medical ethical board of the Utrecht University Medical Center. All subjects gave their written informed consent to participate in the study in compliance with the Declaration of Helsinki 2013. All participants had normal or corrected‐to‐normal vision and the epileptogenic tissue did not extend to the hMT+ area under examination. Data were recorded with a 128 channels Micromed system (Treviso, Italy) at a sampling rate of 512 Hz and bandpass filtered between 0.15 and 134.4 Hz. Implanted grids had 1 cm inter‐electrode spacing and electrodes had a diameter of 2.3 mm. For each subject, electrodes were localized on a postsurgery high‐resolution computed tomography scan (Philips TomoscanSR7000) and projected on the cortical surface obtained by a pre‐surgical anatomical MRI [Branco et al., 2016; Hermes et al., 2010].
Stimuli
Visual stimuli consisted of three high‐contrast square‐wave black‐and‐white dartboard patterns presented in three separate runs. These three patterns had fundamental spatial frequencies of 0.2, 0.33 and 1 cycle/deg in the (radial) direction of motion (Fig. 2, top row). For all patterns, the fundamental spatial frequency perpendicular to the direction of motion (i.e., azimuthal) varied with eccentricity in the same way, and was 6/(eccentricity × π) cycle/deg. For each run (i.e., each spatial frequency) the square‐wave dartboard pattern expanded for 1 s from the fixation point at three temporal frequencies (1, 3, and 5 Hz randomly interleaved), alternating with stationary periods of variable length [interstimulus interval (ISI) range: 3–4.5 s]. Each spatiotemporal frequency condition was presented 18 times. For each subject, the three runs were presented in a different random order. The high signal‐to‐noise‐ratio achieved by the ECoG recordings allows us to reduce significantly the number of trials for conditions (n = 18) and to perform the task in the clinical time constraints. Due to the small size of ECoG electrodes and the proximity to the surface of the cortex, ECoG recordings require far fewer trials to reliably characterize response amplitude than EEG/MEG recordings do. The stimuli were displayed on a 1024 × 768 pixel LCD screen at a distance of 75 cm from the subject eyes. The subjects fixated on a dot located in the center of the screen that changed between green and red colour at random intervals. In order to maintain accurate fixation and consistent level of arousal during the experiment, subjects were instructed to press a button every time the fixation dot changed colour. For one subject, the button responses were not registered due to a technical issue with the trigger. Mean performance and standard deviations for the other three subjects were 89.20 ± 16.55% correct.
Figure 2.
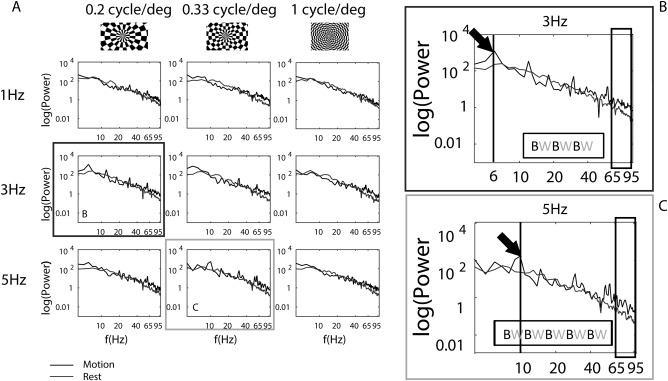
(A) Mean power spectra for the selected electrode of a representative subject in response to each spatial (columns) and temporal frequency (rows) condition of the visual motion stimuli. (B) Mean power spectra in response to 0.2 cycle/degree and 3 Hz visual motion stimulation. The spectra revealed a significant power augmentation in the HFB compared to baseline (black box) and a peak at frequencies synchronous with the contrast reversal of the moving stimuli. In particular for a temporal frequency of 3 Hz the contrast between black and white of the dartboard reversed six times. SCR peaks were thus detected at, and at multiples of, 6 Hz as indicated by the arrow. (C) Mean power spectra in response to 0.33 cycle/degree and 5 Hz visual motion stimulation. The spectra revealed as for (B) a significant increase in the HFB. The arrow indicates the peak in the spectra at 10 Hz (for the temporal frequency of 5 Hz the black and white contrast reversed 10 times). The insert in the graphs (BW) illustrated the number of times the contrast reversed.
ECoG analysis
Electrodes showing artefacts exhibited as flat signal, excessive noise or epileptic activity (judged by a neurologist) were rejected. Signals from each remaining electrode were re‐referenced to the common average of all the remaining intracranial electrodes for each subject. Power spectral density (1–134 Hz) was estimated for each trial every 1 Hz in MATLAB by Welch's periodogram‐averaging method with a 1 s window. To identify electrodes that responded to stimulus motion, we compared responses to 1 s of motion presentation (0–1 s after motion onset), and 1 s of stationary baseline (starting 1 s after the motion ceased).
For each subject, the electrodes showing hMT+ responses were selected using the following anatomical and functional criteria: (1) highest significant spectral power augmentation above baseline in the 65–95 Hz frequency range during motion presentation (paired t test, P < 0.05, Bonferroni's corrected for the number of retained electrodes), (2) location close to the established hMT+ anatomical landmarks found in the posterior part of the inferior temporal sulcus [Dumoulin et al., 2000; Wandell et al., 2007], (3) electrode location assessment by converting electrode coordinates in Montreal Neurological Institute (MNI) space using AFNI, and (4) electrode location comparison to functional activation maps obtained contrasting motion and static checkerboard of pre‐surgically 3T fMRI measurements, when available (two out four subjects). During fMRI, the subjects performed the same visual task as described above.
To quantify the responses for each spatiotemporal frequency condition of the visual motion stimuli presented, we computed the mean power spectra across the trials of each condition, for each subject. We also extracted two components from the ECoG signal: the response in the HFB, and the response at frequencies synchronous with stimulus contrast reversals (SCR response).
ECoG HFB response
To extract the neuronal population response in the HFB we filtered the data between 65 and 95 Hz using a 3rd order Butterworth filter in two directions [Hermes et al., 2012] and we calculated the log power of the analytic amplitude using the Hilbert transform. Epochs for each spatiotemporal frequency condition were extracted from the time of motion onset to 500 ms after the motion presentation ended in order to allow the signal to return to baseline. Baseline was defined as the initial 3 s before the beginning of the first trial of each run. The mean log power across the epochs of each condition was converted to z score by subtracting the mean and dividing by the standard deviation of the baseline epoch. The patterns of HFB power responses were summarized for each spatiotemporal frequency condition by extracting the area under the HFB response per condition. To investigate how the HFB area values change according to the spatial and temporal frequencies of the moving stimuli, we computed the significance of the effect by two‐way ANOVA for each subject. To identify the nature of the effect we subsequently conducted pairwise comparisons using exact statistics (permutation tests) as follows: the spatial (or temporal) frequency population to be tested for significance was calculated by the differences between the two sets of spatial (or temporal) frequencies of size n = 3 to be compared. Then values from the two sets of spatial (or temporal) frequencies were pooled and differences were calculated between all the possible randomly sampled sets of spatial (or temporal) frequencies of size n. This distribution reflected the distribution of values under the null hypothesis that spatial or temporal frequency does not affect response amplitudes. Then, one‐sided P values were computed for each pair‐wise comparison. P < 0.05 was considered to be significant.
ECoG SCR response
We identified peaks in the ECoG power spectra at multiples of the temporal frequencies of the presented stimuli. The peaks were identified at 2, 6, and 10 Hz, and the harmonics of these frequencies. We suggest that these peaks corresponded to the frequency of contrast reversals of the moving dartboards: For the temporal frequencies of 1, 3, and 5 Hz, the stimulus contrast reversed 2, 6, and 10 times per second, respectively. To quantify the intensity of the stimulus contrast reversal (SCR) peaks, we averaged trials for each spatiotemporal frequency condition in time and recomputed the power spectra. This procedure amplifies signal responses that are in phase (synchronous) during the trial, while it minimizes asynchronous signals (for instance HFB responses). Similar to the power spectra analysis above, baseline was defined as the 1 s of stationary periods starting 1 s after the motion ceased. The log of the power spectra was fit with a straight line, then for each subject we normalized the power spectra at each frequency by the fit as in Harvey et al. [2013]. Finally, to characterize the SCR response we extracted the normalized peak value at 2, 6, and 10 Hz for the 1, 3, and 5 Hz temporal frequency conditions respectively. As for the HFB responses, the effect of the spatial and temporal frequencies on the SCR responses were measured by a two‐way ANOVA, testing for differences between frequencies. Preferred frequencies were tested by a permutation analysis on the SCR responses for each subject. P < 0.05 was considered significant.
HFB analysis
We ask whether neuronal responses in hMT+ depend on speed or spatiotemporal frequency. To achieve this, we compared measured patterns of ECoG HFB responses (a measure of spiking activity) to predictions of neuronal response models tuned to both speed and spatiotemporal frequency. We reason that the neuronal response model that best predicts the measured pattern of responses best describes neuronal tuning properties. The first neuronal response model describes separate and independent responses to the spatial and temporal frequency components of the visual stimuli (Q = 0). The second describes tuning for particular speeds, i.e., predicts the same preferred speed at different spatial frequencies, with temporal frequency tuning varying in accordance with the spatial frequency (Q = 1). The third allows for a mixture of these two models, or indeed any relationship between spatial and temporal frequency tuning (Qvar).
Modeling of Square‐Wave Dartboard
We used high‐contrast square‐wave black‐and‐white moving dartboard stimuli. These elicit very strong ECoG responses that were beneficial in our clinical setting. However, square waves contain a range of harmonic spatial and temporal frequencies together with the fundamental frequencies of sine‐wave gratings. We aimed to test whether responses reflected these harmonics or were dominated by their fundamental frequencies. Therefore, we fit response models that predicted the HFB response using (1) only the fundamental frequency and (2) the sum of all harmonic frequencies present in the square wave stimulus, scaled by their respective amplitudes. We again compared which prediction best fit measured responses.
Model of Speed Encoding
We fitted the HFB responses to a variant two‐dimensional Gaussian function allowing independent tuning for spatial and temporal frequency or tuning dependent on the ratio of spatial and temporal frequencies [Lui et al., 2007; Miura et al., 2014; Priebe et al., 2006], given by the following equation:
| (1) |
where A is the HFB response peak, sfopt and tfopt are the optimal spatial and temporalfrequency and σ sf and σ tf are the bandwidths of the spatial and temporal tuning curves; where is defined as:
| (2) |
where Q is a relationship between spatial and temporal frequency preferences. The value of Q defines the spatiotemporal frequency response properties of the neuronal population tested [Priebe et al., 2003, 2006]. Neuronal populations with independent tuning for spatial and/or temporal frequencies will show non‐oriented profiles that are aligned with the vertical and horizontal axes (i.e., spatial and temporal frequency), obtained by Q = 0 in Eq. (2). Conversely, since motion speed is the ratio of temporal and spatial frequencies, neuronal populations that show tuning dependent on the ratio of spatial and temporal frequencies (i.e., direct speed encoding) will be oriented in the spatiotemporal frequency space and will be better described by an oriented profile obtained by Q = 1 [see Eq. (2)]. Other values of Q describe other relationships, such as a mixture of neurons with direct speed encoding and neurons with spatial and temporal frequency encoding within the same population.
Cross validation
Allowing Q to vary adds an extra free parameter in the model that could potentially result in an increase in variance explained compared to the Q = 0 and Q = 1 model. We therefore compared each model's goodness of fit in predicting the HFB response by computing the variance explained in cross‐validation [Klein et al., 2014; Mante et al., 2005; Zuiderbaan et al., 2012]. Here, we quantified model prediction accuracy by fitting model parameters on one half of the measured responses and evaluating how well these parameters predict the complementary half. Any parameter that varies to capture non‐repeatable (noise) responses will reduce goodness of fit.
We discarded trials (4 per subject) with low response amplitudes (less than 10% increase above baseline in 65–95 Hz responses). From the remaining trials, we selected 100 random half splits, fit Q = 0, Q = 1, and Q var models for each half split, and determined the variance explained in the complementary half. We also determined the noise ceiling; the variance explained in each split half by the measurements in the complementary half. Repeating this procedure 100 times gave distributions of model parameters, variance explained, and noise ceiling. We used means and 95% confidence intervals from these distributions to compare model fits statistically.
RESULTS
Visual Motion Elicited Responses in High Frequency Broadband and at Stimulus Contrast Reversal Frequencies in hMT+
We recorded brain activity responses to visual stimuli moving at different spatial and temporal frequencies. We selected, for each subject, the electrode within the hMT+ complex that fulfilled the selection criteria described in the section “Materials and Methods”. To confirm correct localization in the complex (MNI coordinates marked with a cross in Fig. 1), the normalized position of all selected electrodes was plotted on an average brain (Fig. 1).
Figure 1.
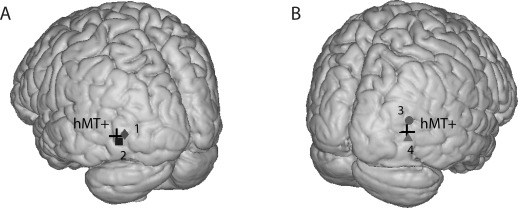
Projected significant elect rode of each subject on a normalized brain. Black cross shows the hMT+ location in the Montreal Neurological Institute (MNI) coordinates for the right (A) and left (B) hemisphere. Subjects are numbered from 1 to 4. The electrode coordinates in MNI space for each subject are: 1 = (38 90 10), 2 = (46 84 3), 3 = (34 80 18), 4 = (51 75 1).
To evaluate the overall responses of the visual stimuli we computed the mean power spectra of each spatiotemporal frequency condition for the selected electrode, for each subject (Fig. 2 for a representative subject). The spectra revealed two distinctive responses to the task: (1) a significant power augmentation in the HFB compared to baseline (Fig. 2) and (2) a peak at frequencies synchronous with the stimulus's contrast reversal (SCR) frequency (Fig. 2).
HFB Responses
Each spatiotemporal frequency condition elicited a significant power augmentation in the HFB compared to baseline (P < 0.05, Bonferroni's corrected), reflecting an increase in neuronal activity for all stimulus conditions (Fig. 2). To evaluate this neuronal response, we analyzed the HFB power over time, averaged across all the motion epochs with the same spatial and temporal frequency combination (Fig. 3). HFB responses peaked on average 87 ms after the motion onset, revealing an early transient response. HFB amplitude then decreased during motion presentation and returned to baseline about 1.5 s after motion onset (500 ms after motion offset). Notably, the shape over time of the HFB responses was synchronous with the contrast reversals found at each temporal frequency. At 1 Hz temporal frequency, the black and white dartboard has two contrast reversals per second, giving two peaks in the HFB responses (Fig. 3, first row). As the temporal frequency increases, their temporal spacing drops below the width of the HFB response waveform so the peaks become less separable (Fig. 3, second and third rows, respectively). All four subjects exhibited similar HFB response patterns.
Figure 3.
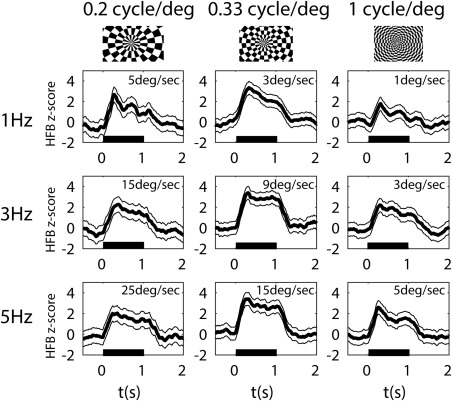
HFB (65–95 Hz) responses averaged across the 18 trials of each combination of spatial (columns) and temporal frequencies (rows) of the visual motion stimuli for a representative subject. The speed of motion (ratio of temporal to spatial frequencies) is indicated in each graph. Black horizontal bars indicate motion stimulus duration. Shaded areas represent the standard error across trials (n = 18). Top row: Representative frame for each spatial frequency of the stimuli presented.
To summarize the pattern of responses, we computed the area under the HFB responses during the 1.5 s in which we measured a power increase, for each spatiotemporal frequency condition (Fig. 4). As revealed by a two‐way ANOVA, only the effect of the spatial frequency on the HFB amplitude was significant (F(2) = 121.19, 10.28, 95.32, and 58.55 for each subject respectively, all P < 0.05). All subjects exhibited the largest response at a spatial frequency of 0.33 cycle/degree as evidence by a significant difference with adjacent frequencies (all pairwise permutation tests yielded a P value < 0.05). The temporal frequency had no preference on the HFB area value (P > 0.1 for all permutation tests). Since speed is the ratio between the spatial and the temporal frequency and the preferred temporal frequency varies with the spatial frequency the preferred speed within each sampled neuronal population differed with the spatial frequency of the moving dartboards.
Figure 4.
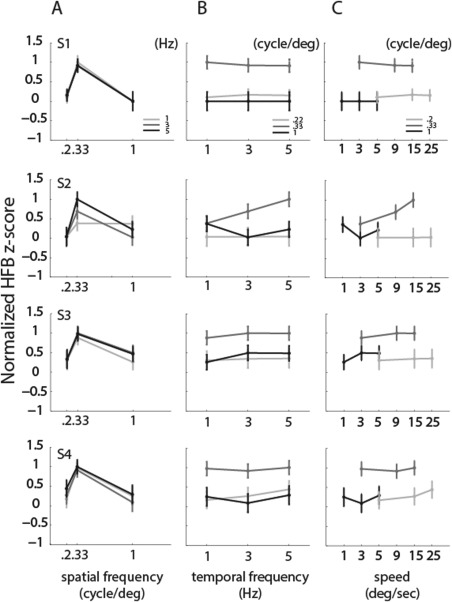
HFB response amplitudes for each fundamental spatial and temporal frequency (normalized z score). (A) Mean response amplitudes and standard errors as a function of fundamental spatial frequency. The maximum response consistently results from the presentation of the 0.33 cycles/degree stimulus. (B) Mean response amplitudes and standard errors as a function of temporal frequency. (C) Mean response amplitudes and standard errors as a function of speed, showing very different response amplitudes for the same speed carried by different spatial and temporal frequencies. Speed is defined as the ratio between the temporal (1, 3, and 5 Hz) and the spatial frequencies (0.2, 0.33, and 1 cycle/deg) of the square‐wave moving dartboard presented. Different rows show different subjects.
ECoG SCR Responses
As can been seen in Figure 2, the power spectra for particular spatial and temporal frequency combination showed SCR peaks at multiples of the contrast reversal of the visual stimuli presented. The spectra in response to 3 Hz [Fig. 2(A): second row, Fig. 2(B) in detail] display a clear peak at 6 Hz during motion, which is the second harmonic of the temporal frequency presented (a 3 Hz stimulation corresponds to 6 contrast reversals). For 5 Hz [Fig. 2(A): third row, Fig. 2(C) in detail] the spectra exhibited a larger response at 10 Hz (a 5 Hz stimulation corresponds to 10 contrast reversals). SCR peaks for 1 Hz were less pronounced (Fig. 2: first row). Peaks were also detected at multiples of the contrast reversal rate for the temporal frequencies presented. To quantify SCR peaks, we averaged trials for each condition in time and recomputed the power spectra. SCR peaks at the first harmonic of the temporal frequency of the stimuli are shown in Figure 5, as a function of spatial frequencies, temporal frequencies and speed. The SCR responses did not show a consistent pattern across subjects. Neither spatial nor temporal frequencies exhibited a frequency‐specific effect for the SCR responses (P > 0.2 for all ANOVA tests). No peaks (negative values) were detected for the highest spatial frequency of the stimuli (1 cycle/deg). Since the SCR responses did not show any particular tuning for spatial and temporal frequencies and were not always detected in our data, we did not fit tuning functions to SCR responses.
Figure 5.
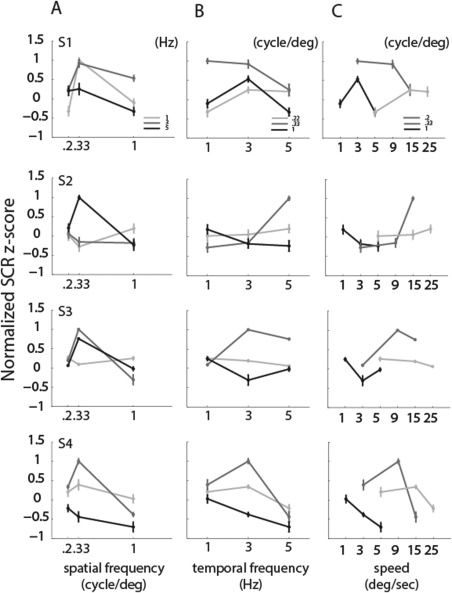
SCR response amplitudes for each fundamental spatial and temporal frequency. (A) Mean response amplitudes and standard errors as a function of fundamental spatial frequency. (B) Mean response amplitudes and standard errors as a function of temporal frequency. (C) Mean response amplitudes and standard errors as a function of speed, showing very different response amplitudes for the same speed carried by different spatial and temporal frequencies. Different rows show different subjects. SCR responses change in accordance with the spatial and temporal frequencies of the stimuli.
HFB Responses Showed Separate Tuning for Spatial and Temporal Frequency
The Gaussian models of speed encoding (Q = 0, Q = 1, and Q var) were able to characterize the tuning of HFB responses for the spatiotemporal properties of the moving dartboards. We compared each model's goodness of fit in predicting the HFB responses by computing the variance explained in cross‐validation, fitting each tuning model to a randomly selected half of the response data and evaluated fitting performance on the complementary half (see “Materials and Methods”). We estimated the responses using only the fundamental spatial and temporal frequencies present in the square‐wave dartboard stimuli, or also considering the harmonics. Figure 6(A) shows the variance explained by each model. For all subjects, the Q = 0 model explained significantly more variance than the direct speed encoding model (Q = 1, two‐sided t test, P value < 0.001 for all subjects), both when the fundamental spatiotemporal frequencies and the harmonics were included in the model [Fig. 6(A), black bars, Q = 0 and Q = 1 labels], and when only the fundamental frequencies were considered [Fig. 6(A), gray bars, Q = 0 and Q = 1 labels].
Figure 6.
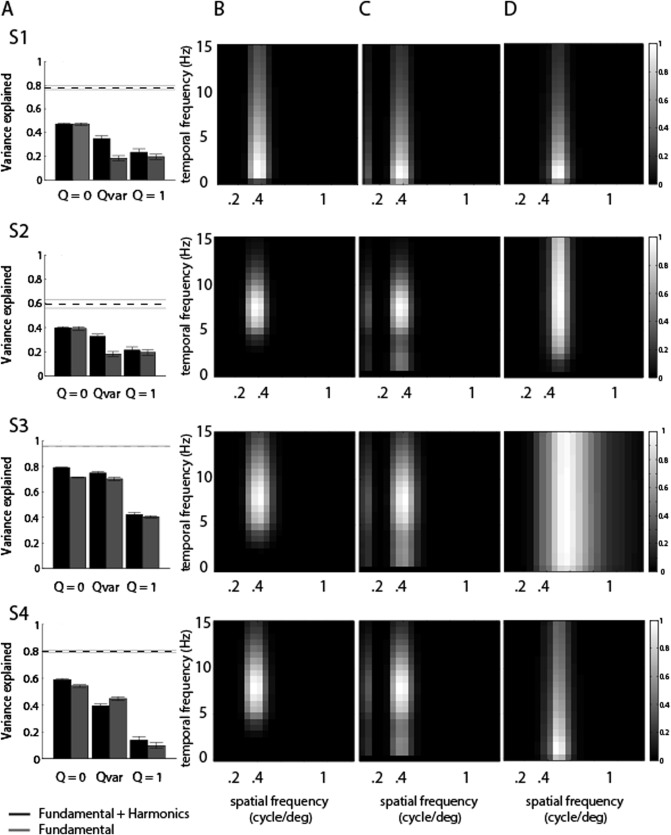
Spatial and temporal frequency tuning models capture responses to our motion stimuli. (A) The response variance explained in split‐half cross validation by Gaussian tuning models with independent spatial and temporal frequency tuning (Q = 0), any relationship between spatial and temporal frequency tuning (Q var) or tuning for speed (Q = 1). Gray bars show variance explained when the tuning model considers the fundamental stimulus frequencies only. Black bars show variance explained also considering the harmonic frequencies present in the stimulus, and explain more response variance. The dashed line shows the noise ceiling from cross validation. Error bars give 95% confidence intervals. (B) Tuning function given by the Q = 0 model that includes both the fundamental spatiotemporal frequencies and the harmonics which shows far narrower tuning widths. (C) Predicted response of the tuning function in (B) to each combination of spatial and temporal frequency of a square‐wave dartboard stimulus. (D) Tuning function given by the Q = 0 model that considers the fundamental frequencies only, which is equal to the predicted response for each spatial and temporal frequency combination. This resembles the predicted response to each spatial and temporal frequency combination shown in (C) and is artificially expanded to capture responses to harmonics.
When considering the fundamental frequencies and the harmonics, the variance explained by the Q = 0 model was also significantly higher than that explained by the Q var model [Fig. 6(A), black bars, Q = 0 and Q var labels], which allows any relationship between spatial and temporal frequency tuning (P value < 0.001 for all subjects). With the exception of Subject 3 [Fig. 6(A), gray bars, third row], the same results were found when considering only the fundamental spatiotemporal frequencies [Fig. 6(A), gray bars, Q = 0 and Q var labels]. Our crossvalidation procedure allowed the Q var model to explain less variance than the Q = 0 model, even though Q = 0 was tested in the Q var model. As Q var fitted less well than Q = 0, nonzero values for Q selected in the fitting stage predicted responses less well than Q = 0 in the validation stage. Therefore, dependencies between spatial and temporal frequency tuning functions (i.e., tilted spatio‐temporal tuning profiles) were not found in our responses indicating they primarily capture nonsystematic noise.
When the fundamental frequencies as well as the harmonic spatial and temporal frequencies were considered in our tuning models, the resulting models explained more variance than models considering the fundamental frequencies only [Fig. 6(A)]. The tuning functions that predict the responses to our stimuli are quite narrow [Fig. 6(B)], but the interactions of these tuning functions with the harmonics predict strong responses to a broader range of stimulus fundamental frequencies [Fig. 6(C)]. If responses are predicted using the fundamental frequencies only, the underlying tuning functions must become far broader to capture the strong responses at the broad range of fundamental frequencies [Fig. 6(D)], and predict the observed responses less well [Fig. 6(A)]. Therefore, harmonic frequency components underlie a significant amount of the neural responses to our square‐wave dartboard stimuli.
DISCUSSION
This study investigated the speed tuning properties in human MT+ neuronal populations in response to dartboards moving at different spatial and temporal frequency combinations, using ECoG. We found that the neuronal populations measured in hMT+ exhibit two distinct responses. The first is a HFB spectral increase in response to each spatiotemporal frequency combination. The second was a set of spectral peaks at the frequency of the stimulus's contrast reversals and their harmonics (the SCR response). We found that: (1) the HFB response (and the neuronal population activity that produces this signal), does not encode the stimulus speed directly but shows separate and independent selectivity for the spatial and temporal frequencies of the motion stimuli, (2) the SCR response was not related to speed encoding. We conclude that the neuronal populations measured in hMT+ are not directly tuned to stimulus speed, but instead encode speed through separate and independent spatial and temporal frequency tuning.
HFB Neuronal Population Responses are Tuned for Spatiotemporal Frequency
We characterized the hMT+ neuronal responses to visual motion stimuli by the HFB response component of the ECoG signal as this is the closest measure to spiking activity in single unit recordings [Manning et al., 2009; Miller et al., 2009; Ray and Maunsell, 2011]. HFB responses followed the spatiotemporal frequency properties of the dartboard presented (Fig. 4). At lower contrast reversal rates (where responses to each contrast reversal could still be distinguished from each other), we found peaks of HFB activity at the contrast reversal frequency (Fig. 3), although the amplitude of these responses was not strongly modulated by speed. Moreover, the preferred speed of the HFB responses varied when the spatial frequency of the stimulus changed (Fig. 4).
We characterized the HFB responses by comparing the ability of different speed encoding models to describe responses to all spatial and temporal frequency combinations present in the stimuli. The first describes separate and independent responses to the spatial and temporal frequency components of the visual stimuli (Q = 0). The second describes tuning for particular speeds, i.e., predicts the same preferred speed at different spatial frequencies, with temporal frequency tuning varying in accordance with the spatial frequency (Q = 1). Our hMT+ HFB responses were significantly better explained by the Q = 0 model. They exhibited selectivity for spatial and temporal frequencies independently, as opposed to evidencing direct speed tuning: the response profile in the spatiotemporal frequency space did not show the orientation predicted by direct speed tuning (Fig. 6). Moreover, no increase in the variance explained was found by fitting the HFB responses with an intermediate model that allows any relationship between spatial and temporal frequency tuning, including mixtures of both spatiotemporal encoding and direct speed tuning.
We used high‐contrast square‐wave black‐and‐white moving dartboard stimuli that are known to elicit very strong ECoG responses in the visual cortex [Winawer et al., 2013]. These strong responses were beneficial within the clinical setting of our experiments, and allowed us to detect the stimulus contrast reversal responses (SCR) to the temporal frequencies adopted in the stimuli. However, square waves dartboard contains a wider range of spatial and temporal frequencies than stimuli containing only the fundamental frequencies as sine‐wave gratings, which are more common in motion‐related animal electrophysiological studies. To address this issue, we took all the harmonic frequencies into account in the description of our stimulus used to fit the tuning models, and we also fitted tuning models using the fundamental frequencies only. Models including the harmonics predicted responses better, demonstrating that harmonic spatial and temporal frequencies contribute to the neuronal population responses we measured. However, irrespective of whether we used only the fundamental frequencies or also included the harmonics, our current data indicate that independent tuning for spatial and temporal frequency explains the responses best.
Our results are consistent with findings in both monkeys and marmosets that showed that the majority of MT neurons do not exhibit the same preferred speed at different spatial frequencies, but exhibit separate and independent tunings for the spatial and temporal frequencies of the visual stimuli [Lui et al., 2007; Miura et al., 2014; Priebe et al., 2003; Priebe and Lisberger, 2004]. These results are corroborated by an MEG study that used sine wave gratings to investigate human MT+ responses to spatial and temporal frequencies [Wang et al., 2003]. Although that study did not investigate speed tuning properties as opposed to a separable spatiotemporal mechanism, it showed neuronal responses in agreement with our data, at least in the same range of spatial and temporal frequencies investigated.
We note that our findings differ from those reported by Perrone et al. [2000] in monkeys, which describe speed tuning in the majority of neurons examined. This difference seems to depend on the criteria of classification used [Priebe et al., 2003]. Perrone and colleagues classify neurons showing any tilt in the spatiotemporal profile (Q different from zero) as speed tuned. Spatial frequency can affect speed preference in such neurons. We use a stricter criterion, where speed preference is not affected by spatial or temporal frequency. Nevertheless, our results do not show any repeatable tilt to the spatio‐temporal tuning profile at the population level: tilted models (Q var) describe our responses less well than untilted (Q = 0) models. Since ECoG electrodes record the summed activity of a population of neurons, it is possible that some neurons within this population may be tuned for speed. However, a mixture of speed tuned neurons with neurons that have separate and independent tunings for the spatial and temporal frequencies should produce an intermediate, tilted response profile.
The separable spatiotemporal properties of the recorded neuronal population in hMT+ found in this study do not correspond to those of fMRI studies in humans that investigate speed responses. Chawla et al. (1998), (1999) demonstrated a nonlinear correspondence between speed of random moving dots and blood oxygenation level‐dependent (BOLD) activity in hMT+, while Lingnau et al [2009] provided evidence of speed tuning coding of BOLD responses over different temporal frequencies. Chawla et al. used random moving dot patterns that cannot disentangle the spatial and temporal frequencies presented. Indeed, as they used the same dot sizes and densities for all speeds, spatial frequency content was constant for all speeds. Therefore, Chawla and colleagues' speed differences may reflect temporal frequency differences only. Similarly, Lingnau and colleagues use a complex fMRI adaptation paradigm to study speed and temporal frequency tuning in human visual cortex in response to drafting gratings. However, the adaptation paradigm they used to study speed tuning properties may lead to potential confounds. The speed tuning functions of neuronal populations can shift towards lower speeds with decreasing contrast [Krekelberg et al., 2006; Vintch and Gardner, 2014] and therefore the use of different contrasts in the adaptation block may lead to different populations of neurons to be tested. Attention to the stimuli due to the adaptation paradigm used may also play a role in the changes in the BOLD signal measured.
Our findings, taken together with human MEG studies and animal neurophysiological studies, support the hypothesis that the hMT+ neuronal population responses we recorded depend on the spatial structure of the stimuli. Indeed, hMT+ neuronal populations exhibit selective preferences for particular spatial frequencies. These spatial frequency preferences likely depend on the electrode location within the hMT+ complex: MT neurons' spatial frequency preferences correlate with their receptive field sizes, and medial superior temporal (MST) neurons have larger receptive fields and lower spatial frequency preferences than MT neurons [Miura et al., 2014]. We recently demonstrated that human MT and MST functional subdivisions are likely to process slow and fast speeds respectively [Gaglianese et al., 2015] which may reflect differences in receptive field size and spatial frequency preferences.
We speculate that each hMT+ neuronal population may behave as a spatial frequency filters for motion detection with different temporal tuning. This agrees with a model representation of speed that depends on the spatial frequency of the stimulus [Priebe et al., 2003, 2006]. Previous studies suggested that this mechanism is inherited from V1 cells. Speed‐tuning responses of MT neurons may emerge from non‐linear integration of neurons that prefer the same speed but exhibit different spatial and temporal frequency tuning [Priebe et al., 2006; Rust et al., 2006; Simoncelli and Heeger, 1997]. However, it has been also shown, using multimodal imaging, that motion‐driven neuronal activity in MT precedes that in V1 [Ffytche et al., 1995, 1996]. These early MT+ responses depend on a direct functional connection between the lateral geniculate nucleus and hMT+, which is modulated by the speed of the visual motion [Gaglianese et al., 2015, 2012]. Therefore, motion‐selective responses could also be inherited by direct input coming from the magnocellular geniculate cells of LGN [O'Brien et al., 2001; Sincich et al., 2004; Stepniewska et al., 1999]. Further studies using high‐density ECoG electrodes to increase the spatial resolution of our measurements could help to shed new light on this matter.
HFB and SCR Responses May Reflect Different Neuronal Populations
SCR responses were clearly affected by the spatial and temporal frequencies of the stimulus, rather than its speed. However, we did not fit tuning functions to SCR responses for several reasons. Unlike HFB responses, we do not believe SCR response amplitudes are closely linked to neural firing rates or response preferences. Moreover, SCR peaks were not always detected from our data (negative values in Fig. 5).
The difference we found between SCR and HFB responses may be explained by a recent model of ECoG signal components containing two different signal sources [Winawer et al., 2013]. This model proposes that SCR responses may capture activity from only small regions of cortical input layers. In contrast, the HFB component reflects asynchronous activity over a broader range of cortical layers, spreading from the input layer of the cortex. In light of this model, we suggest that HFB responses reflect the total response of all the hMT+ neurons underneath our ECoG electrode to moving stimuli, which can be explained by the motion‐encoding model. Conversely, SCR responses reflect only a particular stimulus feature: the synchronous response to each contrast reversal. We may also speculate that the SCR responses we measured in our data originate from direct thalamic projection to hMT+. These narrowband spectral responses locked to the temporal frequency of the visual stimuli may initiate in a relatively small region of the middle cortical input layers of hMT+ [Winawer et al., 2013], which are known to be anatomically connected with the koniocellular compartments of the dorsal LGN [Jayakumar et al., 2013; Morand et al., 2000; Sincich et al., 2004]. This part of visual information may be conveyed to hMT+ earlier than the information carried by the main pathway through V1 [Beckers and Zeki, 1995; Ffytche et al., 1995, 1996; Gaglianese et al., 2012; Raiguel et al., 1989] for a faster and possibly preconscious perception mechanism compared to the later reconstruction of fine stimuli motion details completed through V1 and carried by the HFB responses.
Methodological Considerations: Electrode Location on hMT+
ECoG provides a unique tool to investigate neuronal population responses in the human brain, but there are few limitations that must be kept in mind when using ECoG recordings. First, although the location of the electrodes is guided by the clinical requirement to identify the location of the seizure focus and therefore cannot be controlled by the scientific need for a consistent location across subjects, we are confident that the selected electrode of each subject lies in hMT+. Previous functional neuroimaging studies have defined the MT complex as the most responsive part of the human cortex when contrasting the responses to moving and stationary stimuli [Huk et al., 2002; Tootell et al., 1995; Zeki, 2015]. Similar responses are not seen in nearby areas. Anatomically, it has been shown hMT+ is reliably located in the intersection of the junction between the ascending limb of the inferior temporal sulcus and the sulcus itself in 90% of the subjects [Dumoulin et al., 2000], and similar MNI coordinates are reported in several fMRI studies. We therefore selected electrodes that exhibited the highest increases in the HFB responses to moving versus stationary stimuli and confirmed its position according to the anatomical landmark denoted by the inferior temporal sulcus, and proximity to published MNI coordinates. Moreover, in two out of four subjects the spot was validated with 3T fMRI data contrasting moving versus stationary stimuli. This combination of anatomical and functional criteria provides high confidence that our electrodes lie in hMT+. A second limitation is that ECoG electrodes only sample from small regions within hMT+ (each measures from about 5 square mm per cm of tissue), hence findings may not be representative of the whole region. Here, we did not find any foci that evidenced speed tuning in hMT+. Finally, as an inevitable aspect of the ECoG recordings, each electrode samples the aggregate activity of several 100,000 neurons, hence properties of smaller groups of neurons within this population may go unnoticed.
CONCLUSION
In conclusion, our ECoG results show that recorded neuronal population responses to visual motion stimuli in hMT+ depends on the spatiotemporal frequency properties of the presented stimuli. They exhibited distinct and independent selectivity for spatial and temporal frequencies of the visual stimuli rather than direct speed tuning. Our findings consolidate and extend previous findings in macaque and marmoset MT neurons to neuronal populations in human MT.
ACKNOWLEDGMENTS
The authors would like to thank Erik J. Aarnoutse, Frans S. S. Leijten, Cyrille H. Ferrier, Tineke Gebbink and all the clinical neurophysiology team for the experimental environment and their help in collecting the data and Dora Hermes for helpful discussion.
Disclosure: The authors declare no competing financial interests.
Contributor Information
Nick F. Ramsey, Email: n.f.ramsey@umcutrecht.nl.
Natalia Petridou, Email: a.gaglianese@umcutrecht.nl.
REFERENCES
- Allman JM, Kaas JH (1971): Representation of the visual field in striate and adjoining cortex of the owl monkey (Aotus trivirgatus). Brain Res 35:89–106. [DOI] [PubMed] [Google Scholar]
- Amano K, Wandell BA, Dumoulin SO (2009): Visual field maps, population receptive field sizes, and visual field coverage in the human MT + complex. J Neurophysiol 102:2704–2718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckers G, Zeki S (1995): The consequences of inactivating areas V1 and V5 on visual motion perception. Brain 1:49–60. [DOI] [PubMed] [Google Scholar]
- Branco MP, Gaglianese A, Hermes D, Saad Z, Petridou N, Ramsey NF (2016): Pipeline for ECoG electrode localization on brain surface: Towards a one click approach. In: Proceedings of the Sixth International Brain‐Computer Interface Meeting: BCI Past, Present, and Future. Asilomar Conference Center, Pacific Grove, CA USA: Verlag der Technischen Universitaet Graz. pp 154.
- Chawla D, Phillips J, Buechel C, Edwards R, Friston KJ (1998): Speed‐dependent motion‐sensitive responses in V5: An fMRI study. NeuroImage 96:86–96. [DOI] [PubMed] [Google Scholar]
- Cheng K, Hasegawa T, Saleem K, Tanaka K (1994): Comparison of neuronal selectivity for stimulus speed, length, and contrast in the prestriate visual cortical areas V4 and MT of the macaque monkey. J Neurophysiol 71:2269–2280. [DOI] [PubMed] [Google Scholar]
- Dubner R, Zeki SM (1971): Response properties and receptive fields of cells in an anatomically defined region of the superior temporal sulcus in the monkey. Brain Res 35:528–532. [DOI] [PubMed] [Google Scholar]
- Duijnhouwer J, Noest AJ, Lankheet MJM, van den Berg AV, van Wezel RJA (2013): Speed and direction response profiles of neurons in macaque MT and MST show modest constraint line tuning. Front Behav Neurosci 7:22 http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3616296-tool=pmcentrez?rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumoulin SO, Bittar RG, Kabani NJ, GB, Jr. , Goualher CLB Le G, Pike Evans AC (2000): A new anatomical landmark for reliable identification of human area V5/MT: A quantitative analysis of sulcal patterning. Cer Cortex 10:454–463. [DOI] [PubMed] [Google Scholar]
- Ffytche DH, Guy CN, Zeki S (1995): The parallel visual motion inputs into areas V1 and V5 of human cerebral cortex. Brain 118:1375–1394. [DOI] [PubMed] [Google Scholar]
- Ffytche DH, Guy CN, Zeki S (1996): Motion specific responses from a blind hemifield. Brain 119:1971–1982. [DOI] [PubMed] [Google Scholar]
- Gaglianese a, Costagli M, Ueno K, Ricciardi E, Bernardi G, Pietrini P, Cheng K (2015): The direct, not V1‐mediated, functional influence between the thalamus and middle temporal complex in the human brain is modulated by the speed of visual motion. Neuroscience 284:833–844. [DOI] [PubMed] [Google Scholar]
- Gaglianese A, Costagli M, Bernardi G, Ricciardi E, Pietrini P (2012): Evidence of a direct influence between the thalamus and hMT+ independent of V1 in the human brain as measured by fMRI. Neuroimage 60:1440–1447. [DOI] [PubMed] [Google Scholar]
- Harvey BM, Vansteensel MJ, Ferrier CH, Petridou N, Zuiderbaan W, Aarnoutse EJ, Bleichner MG, Dijkerman HC, van Zandvoort MJE, Leijten FSS, Ramsey NF, Dumoulin SO (2013): Frequency specific spatial interactions in human electrocorticography: V1 alpha oscillations reflect surround suppression. Neuroimage 65:424–432. [DOI] [PubMed] [Google Scholar]
- Hermes D, Miller KJ, Noordmans HJ, Vansteensel MJ, Ramsey NF (2010): Automated electrocorticographic electrode localization on individually rendered brain surfaces. J Neurosci Methods 185:293–298. http://www.ncbi.nlm.nih.gov/pubmed/19836416. [DOI] [PubMed] [Google Scholar]
- Hermes D, Miller KJ, Vansteensel MJ, Aarnoutse EJ, Leijten FSS, Ramsey NF (2012): Neurophysiologic correlates of fMRI in human motor cortex. Hum Brain Mapp 33:1689–1699. http://www.ncbi.nlm.nih.gov/pubmed/21692146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holub R A, Morton‐Gibson M (1981): Response of Visual Cortical Neurons of the cat to moving sinusoidal gratings: Response‐contrast functions and spatiotemporal interactions. J Neurophysiol 46:1244–1259. http://www.ncbi.nlm.nih.gov/pubmed/7320745. [DOI] [PubMed] [Google Scholar]
- Huk AC, Dougherty RF, Heeger DJ (2002): Retinotopy and functional subdivision of human areas MT and MST. J Neurosci 22:7195–7205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jayakumar J, Roy S, Dreher B, Martin PR, Vidyasagar TR (2013): Multiple pathways carry signals from short‐wavelength‐sensitive ('blue') cones to the middle temporal area of the macaque. J Physiol 591:339–352. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3630789-tool=pmcentrez-rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawakami O, Kaneoke Y, Maruyama K, Kakigi R, Okada T, Sadato N, Yonekura Y (2002): Visual detection of motion speed in humans: Spatiotemporal analysis by fMRI and MEG. Hum Brain Mapp 118:104–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein BP, Harvey BM, Dumoulin SO (2014): Attraction of position preference by spatial attention throughout human visual cortex. Neuron 84:227–237. http://www.ncbi.nlm.nih.gov/pubmed/25242220. [DOI] [PubMed] [Google Scholar]
- Krekelberg B, van Wezel RJA, Albright TD (2006): Interactions between speed and contrast tuning in the middle temporal area: Implications for the neural code for speed. J Neurosci 26:8988–8998. http://www.ncbi.nlm.nih.gov/pubmed/16943555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lingnau A, Wall MB, Smith AT, Ashida H (2009): Speed encoding in human visual cortex revealed by fMRI adaptation. J Vis 9:1–14. [DOI] [PubMed] [Google Scholar]
- Lui LL, Bourne J. a, Rosa MGP (2007): Spatial and temporal frequency selectivity of neurons in the middle temporal visual area of new world monkeys (Callithrix jacchus). Eur J Neurosci 25:1780–1792. http://www.ncbi.nlm.nih.gov/pubmed/17432965. [DOI] [PubMed] [Google Scholar]
- Manning JR, Jacobs J, Fried I, Kahana MJ (2009): Broadband shifts in local field potential power spectra are correlated with single‐neuron spiking in humans. J Neurosci 29:13613–13620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mante V, Frazor R. a, Bonin V, Geisler WS, Carandini M (2005): Independence of luminance and contrast in natural scenes and in the early visual system. Nat Neurosci 8:1690–1697. http://www.ncbi.nlm.nih.gov/pubmed/16286933. [DOI] [PubMed] [Google Scholar]
- Maunsell HR (1983): Functional properties of neurons in middle temporal visual area of the macaque monkey. II. Binocular interactions and sensitivity to binocular disparity. J Neurophysiol 49:1148–1167. [DOI] [PubMed] [Google Scholar]
- Maunsell JH, Newsome WT (1987): Visual processing in monkey extrastriate cortex. Annu Rev Neurosci 10:363–401. [DOI] [PubMed] [Google Scholar]
- Miller KJ, Sorensen LB, Ojemann JG, den Nijs M (2009): Power‐law scaling in the brain surface electric potential. PLoS Comput Biol 5:e1000609 http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2787015-tool=pmcentrez-rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miura K, Inaba N, Aoki Y, Kawano K (2014): Difference in visual motion representation between cortical areas MT and MST during ocular following responses. J Neurosci 34:2160–2168. http://www.ncbi.nlm.nih.gov/pubmed/24501357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morand S, Thut G, Peralta RGD, Clarke S, Khateb A, Landis T, Michel CM (2000): Electrophysiological evidence for fast visual processing through the human koniocellular pathway when stimuli move. Cer Cortex 10:817–825. [DOI] [PubMed] [Google Scholar]
- Movshon JA (1975): The velocity tuning of single units in cat striate cortex. J Physiol 249:445–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Brien BJ, Abel PL, Olavarria JF (2001): The retinal input to calbindin‐D28k‐defined subdivisions in macaque inferior pulvinar. Neurosci Lett 312:145–148. [DOI] [PubMed] [Google Scholar]
- Perrone JA, Thiele A (2001): Speed skills: Measuring the visual speed analyzing properties of primate MT. Neurons 4:4–10. [DOI] [PubMed] [Google Scholar]
- Priebe NJ, Cassanello CR, Lisberger SG (2003): The neural representation of speed in macaque area MT/V5. J Neurosci 23:5650–5661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Priebe NJ, Lisberger SG (2004): Estimating target speed from the population response in visual area MT. J Neurosci 24:1907–1916. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2553806-tool=pmcentrez-rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Priebe NJ, Lisberger SG, Movshon JA (2006): Tuning for spatiotemporal frequency and speed in directionally selective neurons of macaque striate cortex. J Neurosci 26:2941–2950. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2532672-tool=pmcentrez-rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raiguel SE, Lagae L, Guly B, Orban GA (1989): Short communications response latencies of visual cells in macaque areas V1, V2 and V5. Brain Res 493:155–159. [DOI] [PubMed] [Google Scholar]
- Ray S, Maunsell JHR (2011): Different origins of gamma rhythm and high‐gamma activity in macaque visual cortex. PLoS Biol 9:e1000610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rust NC, Mante V, Simoncelli EP, Movshon JA (2006): How MT cells analyze the motion of visual patterns. Nat Neurosci 9:1421–1431. http://www.ncbi.nlm.nih.gov/pubmed/17041595. [DOI] [PubMed] [Google Scholar]
- Simoncelli EP, Heeger DJ (1997): A model of neuronal responses in visual area MT. Vision Res 38:743–761. [DOI] [PubMed] [Google Scholar]
- Sincich LC, Park KF, Wohlgemuth MJ, Horton JC (2004): Bypassing V1: A direct geniculate input to area MT. Nat Neurosci 7:1123–1128. http://www.ncbi.nlm.nih.gov/pubmed/15378066. [DOI] [PubMed] [Google Scholar]
- Stepniewska I, Qi HX, Kaas JH (1999): Do superior colliculus projection zones in the inferior pulvinar project to MT in primates? Eur J Neurosci 11:469–480. [DOI] [PubMed] [Google Scholar]
- Tolhurst DJ, Movshon JA (1975): Spatial and temporal contrast sensitivity of neurones. Nature 257:674–675. [DOI] [PubMed] [Google Scholar]
- Tootell RBH, Reppas JB, Kwong KK, Rosen BR, Belliveaul JW, Malach R (1995): Functional analysis of human mt and related visual cortical areas using magnetic resonance imaging. J Neurosci 15:3215–3230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vintch B, Gardner JL (2014): Cortical correlates of human motion perception biases. J Neurosci Curr Issues 34:2592–2604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wandell BA, Dumoulin SO, Brewer AA (2007): Visual field maps in human cortex. Neuron 56:366–383. http://www.ncbi.nlm.nih.gov/pubmed/17964252. [DOI] [PubMed] [Google Scholar]
- Wang L, Kaneoke Y, Kakigi R (2003): Spatiotemporal separability in the human cortical response to visual motion speed: A magnetoencephalography study. Neurosci Res 47:109–116. http://linkinghub.elsevier.com/retrieve/pii/S0168010203001913. [DOI] [PubMed] [Google Scholar]
- Winawer J, Kay KN, Foster BL, Rauschecker AM, Parvizi J, Wandell BA (2013): Asynchronous broadband signals are the principal source of the BOLD response in human visual cortex. Curr Biol 23:1145–1153. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3710543-tool=pmcentrez-rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeki S (2004): Thirty years of a very special visual area, area V5. J Physiol 557:1–2. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=1665043-tool=pmcentrez-rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeki S (2015): Area V5‐a microcosm of the visual brain. Front Integr Neurosci 9:21 http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=4381624-tool=pmcentrez-rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeki SM (1971): Cortical projections from two prestriate areas in the monkey. Brain Res 34:19–35. [DOI] [PubMed] [Google Scholar]
- Zuiderbaan W, Harvey BM, Dumoulin SO (2012): Modeling center—Surround configurations in population receptive fields using fMRI. J Vis 12:15–11. [DOI] [PubMed] [Google Scholar]


