A molecular dynamics investigation of CDK8/CycC and ligand binding: conformational flexibility and implication in drug discovery

Abstract

Abnormal activity of cyclin-dependent kinase 8 (CDK8) along with its partner protein cyclin C (CycC) is a common feature of many diseases including colorectal cancer. Using molecular dynamics (MD) simulations, this study determined the dynamics of the CDK8-CycC system and we obtained detailed breakdowns of binding energy contributions for four type-I and five type-II CDK8 inhibitors. We revealed system motions and conformational changes that will affect ligand binding, confirmed the essentialness of CycC for inclusion in future computational studies, and provide guidance in development of CDK8 binders. We employed unbiased all-atom MD simulations for 500 ns on twelve CDK8-CycC systems, including apoproteins and protein–ligand complexes, then performed principal component analysis (PCA) and measured the RMSF of key regions to identify protein dynamics. Binding pocket volume analysis identified conformational changes that accompany ligand binding. Next, H-bond analysis, residue-wise interaction calculations, and MM/PBSA were performed to characterize protein–ligand interactions and find the binding energy. We discovered that CycC is vital for maintaining a proper conformation of CDK8 to facilitate ligand binding and that the system exhibits motion that should be carefully considered in future computational work. Surprisingly, we found that motion of the activation loop did not affect ligand binding. Type-I and type-II ligand binding is driven by van der Waals interactions, but electrostatic energy and entropic penalties affect type-II binding as well. Binding of both ligand types affects protein flexibility. Based on this we provide suggestions for development of tighter-binding CDK8 inhibitors and offer insight that can aid future computational studies.

Introduction

Cyclin-dependent kinases (CDKs) are among the major regulators of the cell cycle and transcription [1]. The functions of CDKs depend on binding with regulatory proteins called cyclins. CDK8 together with cyclin C (CycC), mediator complex subunit 12 (MED12) and MED13 forms a regulatory kinase module of the mediator complex [2–4], a large protein assembly that couples gene-specific transcriptional regulators to the general RNA polymerase II transcription machinery [5, 6]. A number of studies have shown that CDK8 modulates the transcriptional output from distinct transcription factors involved in oncogenic control [7]. These factors include the Wnt/β-catenin pathway, Notch, p53, and transforming growth factor β [8, 9].

CDK8 has recently attracted considerable attention after it was discovered to have key roles in oncogenesis. The gene expression of CDK8 is related to the activation of β-catenin, a core transcriptional regulator of canonical Wnt signaling in gastric cancers [10–12]. CDK8 is essential in cell proliferation in melanoma and acts as an oncogene in colon cancer in that its expression is amplified in about 60% of colorectal cancer cases [13, 14]. CDK8 gene expression is also related to prognosis in breast and ovarian cancers [15]. Additional cancer-relevant activities of CDK8 include growth factor-induced transcription [16], modulation of transforming growth factor β signaling [17] and phosphorylation of the Notch intracellular domain [18, 19].

The research on selective CDK8 ligands has started only recently but has quickly become highly active. The steroidal natural product cortistatin A was the first-reported high-affinity and selective ligand for CDK8, with IC50 value 12 nM in vitro and complete selectivity against 387 kinases [20]. The existing ligands have two categories based on the major conformations of CDK8 to which they bind. Type-I ligands bind to the DMG-in conformation (aspartate-methionine-glycine near the N-terminal region of the activation loop) and occupy the ATP-binding site. The Senexin-type, the newer CCT series, and COT series compounds, which possess 4-aminoquinazoline [21], 3,4,5-trisubstituted pyridine [22] and 6-azabenzothiophene [23] scaffolds, respectively, belong to this category. Type-II ligands bind to the DMG-out conformation and occupy mainly the allosteric site (deep pocket) and in some cases the ATP-binding site. The deep pocket is adjacent to the ATP-binding site and is accessible in CDK8 by the rearrangement of the DMG motif from the active (DMG-in) to the inactive state (DMG-out). This pocket is inaccessible in the active conformation (DMG-in), where the Met174 side-chain is reoriented to open up the ATP binding site [24]. Typical type-II CDK8 ligands are sorafenib and imatinib analogs that contain an aryl urea core [25]. Research and development of new CDK8 ligands has made significant progress in recent years, and many promising compounds were identified [26–28]. Very recently 4,5-dihydrothieno [3′, 4′:3, 4] benzo[1,2-d] isothiazole derivatives were found to have sub-nanomolar in-vitro potency (IC50: 0.46 nM) against CDK8 and high selectivity [29].

Since Scheneider et al. revealed the first crystal structure for human CDK8/CycC complexed with sorafenib (PDBID: 3RGF), in 2011 [30], a total of 25 crystal structures have been made available for this kinase system, thereby providing plenty of structural information for computational approaches to help in understand the atomistic detail of molecular functions and interactions with substrates and ligands. As compared with other CDKs, CDK8 displays additional potential recognition surfaces for interactions, possibly for recognition of MED12, MED13, or the substrates of CDK8. However, all of the crystal structures are lacking 10–20 residues within the activation loop in both the DMG-in and DMG-out conformations, suggesting that the activation loop is highly flexible. However, without structural details of this region, how its motion affects other regions of the protein is unclear and its impact on overall stability and ligand binding is unknown. In addition, although the presence of CycC is crucial in the biological function of CDK8 [30], whether CycC plays a role in ligand binding or protein stability is less clear. Therefore, it is important to gain an understanding of the effect of CycC on the dynamics of CDK8 regions, especially those near the binding sites. If the influence is negligible, CycC could be ignored, thus significantly speeding up calculations. Otherwise CycC must be included in the system to keep calculations accurate and meaningful.

Such information is not available from crystal structures, and one aspect of our study aims to elucidate this relationship. Moreover, we attempt to understand the interaction of ligands with surrounding residues, the stability of the binding modes in crystal structures, and the possibility of alternative binding modes. Computational methods such as molecular dynamics (MD) allow for complementary approaches to understand the details of structural changes during the process of ligand binding. Callegari and coworkers ranked the residence time of a series of CDK8 type-II inhibitors using metadynamics and the ranking was roughly consistent with experimental data [31]. Xu et al., with 50 ns of all-atom MD studies of human CDK8, provided insights into two-point mutations, D173A and D189N, within the activation loop by using hydrogen bond (H-bond) dynamic study of the activation loop residues and the MM/PBSA method [32].

In this study, we used all-atom unbiased MD simulations to observe the dynamics of the CDK8-CycC system both with and without bound ligands. The simulations revealed some protein regions that were significantly stabilized by the ligands and showed the effect that other regions may have on ligand binding. We examined and confirmed the importance of CycC to the stability of the CDK8 and found that it facilitates key interactions that stabilize ligand binding modes. Binding of type-I and type-II ligands to CDK8 in DMG-in and DMG-out conformations, respectively, was also simulated. By extensively studying the native bound states of these CDK8/CycC-ligand complexes as well as binding site volume changes, we developed detailed binding energy profiles for each ligand and gained insight that may help improve ligand design.

Methods

System description

The subject of this study is the CDK8 protein associated with its partner protein, CycC, along with nine inhibitors of CDK8. CDK8 has two distinct regions known as the N-lobe and the C-lobe. The binding pocket lies between these two lobes and has two regions: the allosteric site, or deep pocket, and the ATP binding site. CDK8 can be in two different conformations, DMG-in or DMG-out, based on the position of a 3-amino-acid sequence called the DMG motif comprising aspartate, methionine and glycine, which are residues 173–175 (Fig. 1). Type-I ligands bind to the DMG-in conformation and occupy the ATP binding site; type-II ligands bind the DMG-out conformation and occupy the deep pocket and the ATP binding site. CycC associates mainly with the N-lobe and has significant contacts with regions of CDK8 important to the stability of the binding pocket, such as the αC helix.

Fig. 1.

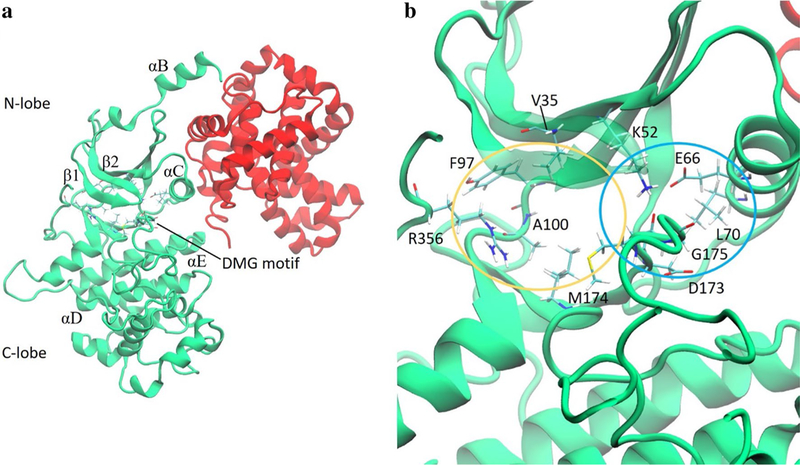
a CDK8 (green) and Cyclin C (red). b A close-up view of the binding pocket of CDK8. Residues that engage in strong interactions with type-I or type-II ligands are labeled with one-letter amino acid codes and shown in licorice. The yellow and blue ovals roughly encircle the ATP and allosteric binding sites, respectively

We studied DMG-in and DMG-out CDK8/CycC apoproteins, four type-I and five type-II (structure-kinetic relationship series, SKR) CDK8/CycC–ligand complexes. The PDB IDs of the crystal structures used as initial structures and the corresponding MD indices are listed in Table 1. We manually mutated the crystal structure 4F7N and obtained the complex of CDK8/CycC–SKR10, whose crystal structure is not available. For the CDK8/CycC apoproteins in the DMG-in conformation, we used two initial structures, 4G6L and 5CEI, with ligand 50R removed. For the DMG-out apoprotein, we used the initial structure of 4F6W, with ligand SKR1 removed. The molecular structures of the nine ligands are in Fig. 2. We retained residues 1 to 359 for CDK8 and residues ⁻2 to 257 for CycC for the MD simulations. To build the missing activation loop, we used p38 (PDB ID: 1W82 for the DMG-out conformation and PDBID: 1A9U for the DMG-in conformation) as the reference structure and constructed homology models of the CDK8 activation loop by using SWISS-MODEL [33–35]. Then we aligned residues Asp173 and Arg200 and manually added the homology model of the activation loop to CDK8. We added the other two missing loops αD-αE and αF-αG by using SWISS-MODEL with the native crystal structures as the references.

Table 1.

Initial structures and indices of MD simulations of CDk8/CycC complexes

MD index	DMG conformation	Ligand	PDB ID	Manipulation
1	DMG-In		4G6L [25]
2	DMG-In		5CEI [24]	Removal of ligand
3	DMG-In	50R	5CEI [24]
4	DMG-In	5XG	5FGK [23]
5	DMG-In	5Y6	5HBE [23]
6	DMG-In	5Y8	5HBJ [23]
7	DMG-Out		4F6W [25]	Removal of ligand
8	DMG-Out	SKR1	4F6W [25]
9	DMG-Out	SKR2	4F7L [25]
10	DMG-Out	SKR5	4F6U [25]
11	DMG-Out	SKR10	4F7N [25]	Manual ligand mutation
12	DMG-Out	SKR11	4F7N [25]

The references to the crystal structures are provided with PDB IDs

Fig. 2.

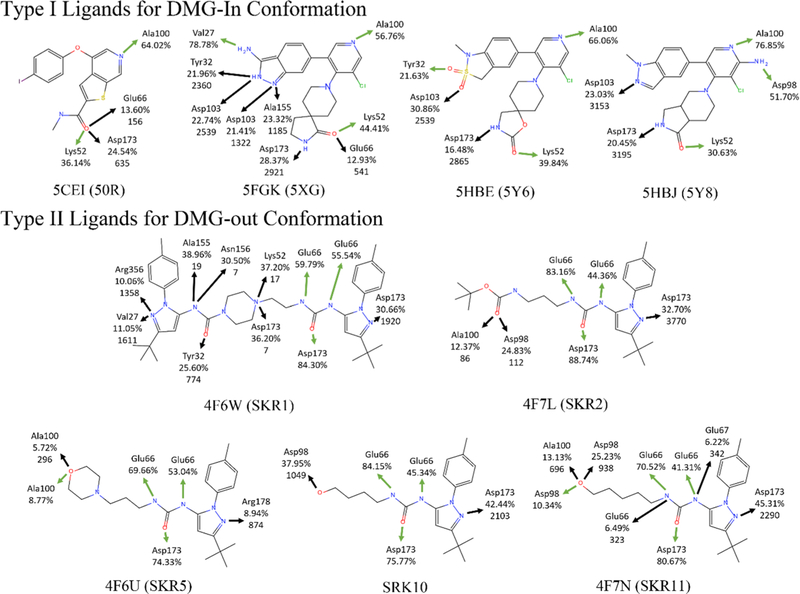
Direct H-bonds and water bridges between ligands and CDK8. Green arrows and black arrows indicate direct H-bonds and water bridges between atoms on the ligand with a residue in CDK8, respectively. The occurrence percentages of the H-bonds and water bridges are labeled below the residue name. For water bridges, numbers of observed bridge water molecules are given below the percentage

Unbiased MD simulation

The Amber 14 package with an efficient GPU implementation [36–38] was used for the MD simulations. Amber 99SB and general amber force field (GAFF) [39–41] were used for CDK8/CycC and the nine ligands, respectively. Single protonation states were used for all histidine residues according to predictions from comparing results for MCCE [42, 43], ProPKa [44, 45], and DelPhiPKa [46, 47]. Six Cl⁻ions were placed to maintain a neutral system. Minimization was performed on the hydrogen atoms, side chains and the entire protein complex for 500, 5000, and 5000 steps, respectively, and the system was then solvated with a rectangular TIP3P water box [48] such that the edge of the box was at least 12 Å away from the solutes. The system went through 1000-step water and 5000-step full-system minimization to correct any inconsistencies. Then we equilibrated the water molecules with the solutes fixed for 20 ns at 298 K in an isothermic-isobaric (NPT) ensemble. Next, we relaxed the system by slowly heating it during an equilibrium course of 10 ps at 200, 250 and 298 K. We performed the production run in an NPT ensemble with a 2-fs time step and used the Langevin thermostat [49, 50] with a damping constant of 2 ps⁻¹ to maintain a temperature of 298 K. The long-range electrostatic interactions were computed by the particle mesh Ewald method [51]. The SHAKE algorithm [52] was used to constrain water hydrogen atoms during the MD simulations. We performed 500 ns of MD production runs on each complex and the apoprotein by using CPU parallel processing and local GPU machines. We collected the resulting trajectories every 2 ps and re-saved the trajectories for analysis at intervals of 20 ps.

System dynamics and flexibility calculations

Cartesian principal component analysis

To observe major protein motions, we performed classical PCA [53–55] of α-carbon atoms in the 500-ns trajectories saved every 20 ps (25,000 frames in total). Using PCA, the complex data set of all α-carbon motions throughout the MD trajectory is reduced to its principal components (PC), the directions which contain the greatest amount of variation (largest motion). The principal components are obtained as the eigenvectors of a covariance matrix consisting of displacements of α-carbons during the trajectory. The first PC mode is the dimension of data with the largest variation, and these were saved and analyzed to reveal the dominant motions. In order to observe motions in different periods of the MD simulations, we divided the aligned 500-ns trajectories of each system into five successive 100-ns trajectories and performed PCA on α-carbon atoms of the entire system in Cartesian coordinates. We calculated the first PC modes during 0–100, 100–200, 200–300, 300–400 and 400–500 ns, instead of the first PC mode of the entirety of trajectory. In this way, distinct motions of the system occurring in these periods could be captured rather than blending the motion over all 500 ns into one mode. The average positions of the α-carbon atoms were used as a reference to compute the covariance matrix.

Root‑mean‑square fluctuation (RMSF) Calculations

The RMSF values of twelve regions of the systems were measured over the 500-ns MD trajectories. We chose regions that were distinct from one another and could plausibly have impacts on ligand binding and or the stability of the CDK8-CycC complex, such as the activation loop, αB helix, and αC helix, among others. A full illustration of the twelve regions and their tabulated RMSF values are shown in Fig. 4. The RMSF of a region is the average displacement of that region with respect to a reference position taken over the trajectory time,

$$RMSF=\sqrt{\frac{1}{T}\sum _{t=1}^T〈{\left(x_i\left(t\right)-x_{i,ref}\right)}^2〉}$$

Fig. 4.

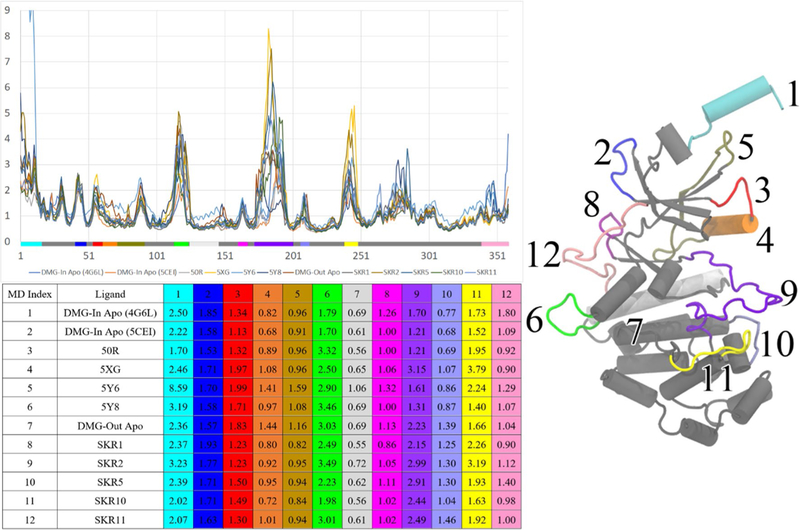
RMSF for all the studied CDK8/CycC systems. The color bar on the x-axis marks the regions of CDK8. The table beneath the plot lists the 12 regions with large motions and highlighted with colors that correspond to the color bar

where x_i(t) is the position of region i at time t, x_i,ref is the reference position of region i, and T is the time interval over which the average is taken. The reference position used here is the average position during the trajectory. The angled brackets mean that the displacement of a region is computed as the average deviation of the atoms that make up that region.

Characterization of ligand binding modes and binding energies

Hydrogen bonding analysis

Hydrogen bonds (H-bonds) contribute significantly to the binding interactions of all ligands included in this study. To understand which atoms of the ligands and CDK8 are involved in these interactions, which may provide information that can be used in the design of stronger-binding ligands, we analyzed the trajectory of each protein–ligand complex for H-bonds. In this study, an H-bond (X–H…Y) was considered formed if the distance between H and Y was < 2.5 Å and the complimentary angle of X–H…Y was < 30° (Figure S1). We used an in-house script to scan the trajectories for direct H-bonds between ligands and CDK8 as well as mediating water molecules that connect ligands and CDK8. H-bonds between ligands and different atoms on the same residue were merged into one residue–ligand H-bond formation. The occurrence (%) of a H-bond was calculated as the number of the frames containing the H-bond divided by the total frames (25,000).

Residue‑wise interactions

Further classifying the binding modes, ligand interactions with the 359 CDK8 residues were computed for each of the nine ligands studied. For each residue, we computed the sums of vdW, Coulombic, and generalized born (GB) energy terms for the ligand with the residue (E_{L + R}), the ligand alone (E_L), and the residue alone (ER), then computed the interaction energy ΔE = (E_{L + R}) − E_L − E_R. The vdW term is calculated as a Lennard-Jones potential, ${\text{E}}_{\text{vdW}}=\left(\left(A_{ij}/r_{ij}^{12}\right)-\left(B_{ij}/r_{ij}^6\right)\right)$, with A = 4εσ¹² and B = 4εσ⁶, where ε is the potential well depth in kcal/mol and σ is the distance at which the potential is zero, and r is the distance between atoms i and j. The Generalized Born energy approximates the solvation energy and was calculated using the Still model [56]. We report only residues that closely interact with the ligands in this analysis.

MM/PBSA

We used the MM/PBSA method [57] to evaluate the inter-molecular interactions between a ligand and CDK8/CycC. The method computes the energy (E) of a system from the protein (E_P), ligand (E_L) and complex (E_PL), with the interaction energy computed by Δ <E> = <E_PL> − <E_P> − <E_L>. <E> denotes the computed average energy from a given MD trajectory. The total binding energy term was computed as _EMM/PBSA = E_bonded + E_elec + E_vdW + G_PB + G_np; where E_bonded is the bonded energy, E_elec and E_vdW are electrostatic and vdW energy, G_PB is the solvation energy computed by solving the Poisson Boltzmann (PB) equation, and G_np is the nonpolar energy estimated from the solvent accessible surface area. Because <E_PL>, <E_P> and <E_L> terms were computed using the same bound state trajectory, the bonded term was canceled and is not shown in Table 2.

Table 2.

MM/PBSA energy breakdowns for the binding energy of 9 ligands with CDK8/CycC in kcal/mol

Type I
MD index	3		4		5		6
Ligand	50R		5XG		5Y6		5Y8
PDB ID	5CEI		5FGK		5HBE		5HBJ
∆EvdW	− 39.8 ± 2.8		− 45.9 ± 2.7		− 48.5 ± 2.9		− 43.9 ± 3.0
∆Eelec	− 13.0 ± 4.6		− 28.7 ± 6.4		− 24.6 ± 7.0		− 26.0 ± 5.5
∆GPB	31.2 ± 3.6		47.2 ± 5.7		48.0 ± 6.6		41.4 ± 4.9
∆Eelec+PB	18.2 ± 3.5		18.5 ± 4.3		23.4 ± 4.1		15.4 ± 3.3
∆Gnp	− 3.6 ± 0.1		− 4.2 ± 0.1		− 4.3 ± 0.1		− 4.2 ± 0.1
∆Egas	− 52.8 ± 5.7		− 74.6 ± 6.8		− 73.1 ± 8.1		− 69.9 ± 6.1
∆Gsolv	27.6 ± 3.5		43.1 ± 5.6		43.7 ± 6.6		37.3 ± 4.9
∆EMM/PBSA	− 25.2 ± 4.1		− 31.5 ± 4.1		− 29.4 ± 4.4		− 32.6 ± 3.9
∆GExpt	− 11.4		− 12.0		− 11.9		− 11.3
Type II
MD index	8	9		10		11		12
Ligand	SKR1	SKR2		SKR5		SKR10		SKR11
PDB ID	4F6W	4F7L		4F6U		4F7N		4F7N
∆EvdW	− 88.5 ± 3.4	− 62.4 ± 3.3		− 59.9 ± 4.9		− 50.6 ± 2.8		− 49.5 ± 3.0
∆Eelec	− 20.4 ± 4.1	− 20.0 ± 4.8		− 28.3 ± 7.6		− 20.9 ± 4.6		− 19.0 ± 6.0
∆GPB	66.4 ± 4.7	42.9 ± 5.0		52.6 ± 9.0		40.4 ± 5.0		38.3 ± 5.4
∆Eelec+PB	46.0 ± 4.6	22.9 ± 4.3		24.3 ± 5.2		19.6 ± 4.1		19.3 ± 4.2
∆Gnp	− 7.9 ± 0.1	− 5.8 ± 0.1		− 5.5 ± 0.1		− 4.8 ± 0.1		− 5.0 ± 0.1
∆Egas	− 108.8 ± 4.8	− 82.4 ± 5.9		− 88.2 ± 10.4		− 71.5 ± 4.6		− 68.5 ± 6.8
∆Gsolv	58.5 ± 4.7	37.0 ± 5.0		47.1 ± 9.0		35.6 ± 5.0		33.3 ± 5.4
∆EMM/PBSA	− 50.3 ± 4.7	− 45.3 ± 4.9		− 41.1 ± 5.0		− 35.9 ± 3.9		− 35.2 ± 4.5
∆GExpt	− 10.2	− 10.7		− 8.4		− 8.0		− 9.7

∆E_vdW and ∆E_elec are the van der Waals and electrostatic energy contributions, respectively, and ∆E_gas is the sum of those two terms. ∆G_PB and ∆G_np are the polar and non-polar solvation energies, respectively, and ∆G_solv is the sum of those two terms. ∆E_MM/PBSA is the binding energy predicted by MM/PBSA

Binding pocket volume analysis

We used a grid-based in-house program to evaluate the volume of the ATP binding site in order to quantify conformational change of the pocket that accompanies binding. For each conformation, we measured the minimum and maximum of the Cartesian coordinates of the α-carbons of CDK8 binding pocket residues Val27, Gly30, Glu66, Asn156 and Ile171, and divided the space determined by these coordinates into a grid with a spacing of 1 Å along the x, y and z axes. If a grid point is within 1.4 Å (radius of a water molecule) of any atoms of CDK8, it is removed. Otherwise, the grid point is kept in the space. Because the grid spacing is 1 Å, the solvent accessible volume for water of the CDK8 binding pocket is approximated by the number of grid points left over in units of Å3. The same procedure is repeated for each conformation in the trajectories.

Results and discussion

Our major areas of analysis were (i) CDK8-CycC system dynamics (ii) the effect of excluding CycC from MD simulations on dynamics and ligand binding and (iii) ligand binding modes and binding site conformational changes with the objective of developing detailed binding energy profiles for four type-I ligands and five type-II ligands (Figure S2). We first present results related the overall system dynamics and regional flexibility. The effects of CycC exclusion are presented next. We repeated MD runs on all twelve systems without the presence of CycC in order to observe the differences in dynamics. These were obtained by measuring RMSF values of twelve major regions of the system and by using PCA on sequential 100-ns portions of the 500-ns MD trajectories of all twelve systems to observe the major global motions. Next, we present binding energy profiles for all nine ligands studied. An in-house script was used to identify all hydrogen bonds (Figure S1) between CDK8 and the ligands and to find their occurrence percentages. Residue-wise interaction analysis was done for all ligand-CDK8 residue pairs to quantify electrostatic, vdW, and desolvation energies important to binding. Finally, MM/PBSA was employed to find the overall binding energies of the ligands. Binding pocket volume analysis for apoproteins and protein ligand complexes in both DMG-in and DMG-out conformations allowed us to assess how the pocket may change to accommodate ligand binding and differences caused by the orientation of the DMG motif.

To further ensure the motions observed in these simulations were not the result of random fluctuations and truly characterized the dynamics of this system, we ran secondary simulations for 200 ns for all twelve of the systems both with and without CycC. These are shorter repeats of the first simulations, run under the exact same conditions but starting with a different random number seed, so that a different trajectory is obtained. The dynamics seen in the secondary runs should recreate that seen in the primary production run and help provide assurance that the observations were not due to randomness and were not strange artifacts of any particular simulation. In our secondary simulations, the same dynamics seen in the first set of simulations was observed in all cases.

CDK8‑CycC dynamics

We examined the first PC modes of the twelve systems over five 100-ns intervals and identified five common global protein motions related to ligand binding and unbinding. These major motions were observed in both DMG conformations, with and without ligands, in all twelve systems. Figure 3 shows the five motions: (A) is a breathing motion in which the system bends and unbends about the hinge region connecting the N and C lobes; (C) is rotational motion in which the two lobes rotate back and forth relative to each other; (B) and (D) are the bending and rotational motions between CDK8 and CycC, respectively; (E) consists of the motions of the αB helix, the activation loop, and the loop connecting the αD and αE helixes. All five recurred periodically for all systems over 500 ns but never were all five found within a single 100-ns interval, showing at least 100 ns is required to fully sample system dynamics and indicating that unique motions are unlikely beyond 500 ns. Motions (A) through (D) have considerable impact on ligand binding and unbinding. Because binding sites of proteins are usually enclosed areas, global motions such as these facilitate ligand binding by opening the sites and improving accessibility. The breathing motion was found to be closely related to the binding/unbinding pathways of p38 MAP kinase [58, 59]. Motion (E) may be related to the conversion between DMG-in and DMG-out conformations [60–62]. Projecting MD trajectories onto these PC modes provide a well-defined way to cluster conformations from MD simulations and therefore can be used as a rational way for selecting conformations for molecular docking or other studies that require multiple conformations.

Fig. 3.

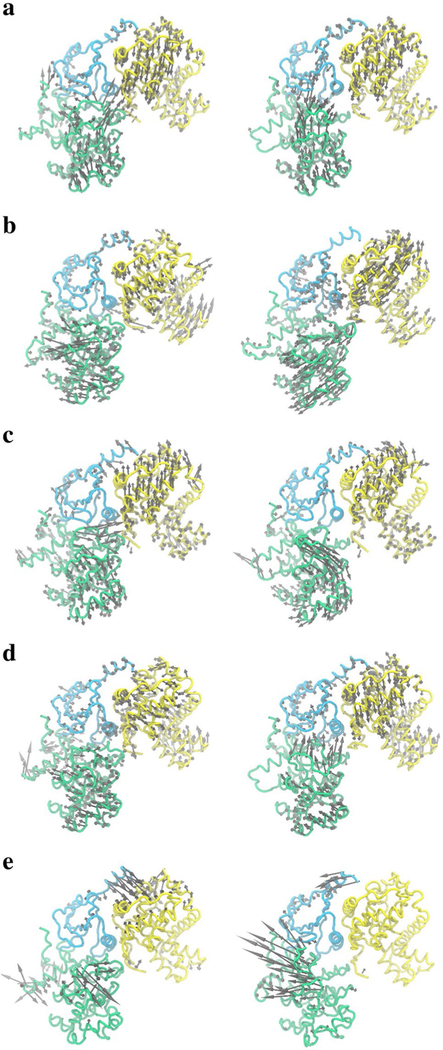
The first PC modes from Cartesian PCA of apo CDK8/CycC or CDK8/CycC-Ligand complexes using 100 ns trajectories. The breathing motion between N-lobe (cyan) and C-lobe (green) (a), breathing motion between CDK8 and Cyclin (yellow) (b), rotational motion between N-lobe and C-lobe (c), rotational motion between CDK8 and Cyclin (d), and loop motions (e) are indicated by gray arrows for DMG-In (Left) and DMG-Out (Right) conformations. The DMG-In PC modes use MD1 100–200 ns (a), MD3 0–100 ns (b), MD1 200–300 ns (c), MD5 0–100 ns (d), MD5 200–300 ns (e). The DMG-Out PC modes use MD11 100–200 ns (a), MD7 100–200 ns (b), MD11 300– 400 ns (c), MD8 100–200 ns (d), MD9 100–200 ns (e)

RMSF measurement of the 12 systems revealed the flexibility of key regions and, most notably, showed that the large motions of the activation loop do not affect binding. The RMSF plots of the 12 systems are shown in Fig. 4. For clarity, we provide the RMSF values within 12 regions of CDK8. A major difference between RMSFs of DMG-in and DMG-out conformations is in the flexibility of the activation loop (Region 9). Our DMG-in systems consistently showed smaller RMSF values for this region than DMG-out systems (1.2–1.7 vs 2.2–3.0 Å). This finding is supported by DMG-out crystal structures which, due to the higher flexibility, almost always have fewer resolved residues in the activation loop compared to DMG-in structures. Crystal structure 5FGK is missing 17 residues in the activation loop, which indicates a level of flexibility consistent with the abnormally high RMSF we observed of 3.15 Å. Our simulations have revealed that despite the different degrees of flexibility of the activation loop, both type-I and type-II ligands have stable binding conformations, as characterized in “CDK8-CycC dynamics”. Therefore, the natural dynamics of the activation loop may have very limited effects on ligand binding modes in the ATP binding site and allosteric binding site, and it may be unnecessary to consider various loop conformations in future docking-based drug development for CDK8.

Ligand binding has minor effects on the dynamics of the CDK8/CycC complex and influences DMG-in and DMG-out conformations differently. In the apo-form of CDK8, DMG-out CDK8 shows significantly more flexibility in the αC helix and activation loop areas (Fig. 4). Upon ligand binding, the αC helix of the DMG-out conformation is largely stabilized by the formation of two highly stable H-bonds via the urea linker of type-II ligands with Glu66 on the αC helix and Asp173 on β8, which leads to the activation loop. This stabilizes the binding pose of type-II ligands, in turn stabilizing the αC helix. Type-I ligands form a less stable H-bond with Lys52 (40–50% duration), which forms an H-bond with Asp173, but this interaction is also present in the apo-form CDK8, so ligand binding seems to confer no further stability. The C-terminus (region 12 in Fig. 4) is also stabilized by ligands. For the DMG-in apo-form of CDK8, the RMSF for this region can be very large depending on initial conformations and sampling, but is greatly reduced upon ligand binding by the π-stacking interaction between the ligand and Arg356. Type-II ligand SKR1 also forms this interaction and stabilizes this region. The recently discovered 4,5-dihydrothieno [3′, 4′:3, 4] benzo[1,2-d] isothiazole derivative achieved sub-nanomolar potency despite the fact that the corresponding docking study suggested this ligand had no interaction with Arg356 [29], suggesting this interaction may not be essential. Because our study showed significantly reduced CDK8 flexibility in the C-terminus due to ligand binding, investigation of ligands that avoid this interaction while maintaining the other key interactions is worthwhile and may result in ligands that produce lower entropic penalties. Except for the αC helix and C-terminus, we observed no other important stabilized regions. Ligand binding affects the dynamics of CDK8 via local, direct interactions and is unable to induce long-range or allosteric effects.

Importance of CycC to CDK8 stability and ligand binding

We performed MD simulations for the systems without CycC, and the results clearly show that CycC stabilizes CDK8 by reducing the fluctuation in the N-terminus, αC helix, and activation loop. The activation of CDKs requires the binding of cyclins and phosphorylation of Thr, Ser, and Tyr on their activation loop [63, 64]. This binding changes the conformation of CDK8 markedly [32, 64] and enables ligand binding in the allosteric site [25], which is supported by our observation that in the absence of CycC, the αC helix of CDK8 adopts an αC-out conformation, whereby Glu66 moves away from the DMG motif. By losing the H-bond from Glu66 and interactions from the entire αC helix, the allosteric binding site collapses, thereby disabling the binding of type-II ligands.

Figure S3 compares the RMSF of CDK8–50R complexes with and without CycC. Without CycC, the N-terminus of CDK8, αC helix, and activation loop have much larger RMSF values (Fig. 4). Crystal structures show that the N-terminus of CDK8 rests stably on CycC, however, in our simulations omitting CycC, the N-terminus exhibits extremely large motions, leading to a totally different conformation of this region. Crystal structures show that the αC helix is part of the binding interface of CDK8 and CycC. If CycC is absent in simulation, the αC helix has a wider range of motion and moves toward the space that CycC would normally occupy, becoming too distant form the binding site to form the characteristic H-bond via Glu66 with type-II ligands (Fig. 5). Although the activation loop is not in direct contact with CycC, the reduced motion of the N- and C-lobes and αC helix by CycC provides stability to this region as well.

Fig. 5.

Conformation change of the αB and αC helices in MD8 (apo CDK8 in DMG-out conformation) in the absence of CycC. The αB helix is in yellow, and the αC helix is in green. GLU 66 is shown in licorice

Among the three regions stabilized by CycC, the αC helix has the largest impact on ligand binding. The conformation of this helix is characterized as αC-in or αC-out according to the distance between Cα carbon atoms of Glu66 and Asp173 [65]. Structures with a short DMG-αC-helix distance (4–7.2 Å) are classified as αC-in, whereas structures with long distances (9.3–14 Å) are classified as αC-out. Structures with distances in between are classified as αC-out–like structures. Figure S4 shows this distance in MD2 and MD3 and suggests that CDK8 is usually in the αC-out conformation when CycC is absent and αC-in when CycC is present. All type-II ligands included in this study form a very strong H-bond with Glu66 on the αC-helix. This is only possible in the presence of CycC which causes CDK8 to adopt the αC-in conformation. Moreover, although the αC helix is not in direct contact with type-I ligands, it helps stabilize the binding pocket via a key salt bridge between Glu66 and Lys52. Lys52 is one of the most important residues for type-I ligand binding, providing a stable H-bond for in all cases studied here, and in this sense CycC also affects type- I ligands. In the trajectory of CDK8–5Y6 complex without CycC, 5Y6 leaves the native bound state characterized by the crystal structure and found an incorrect binding state conformation due to the absence of CycC and the unstable binding cavity (Fig. 6). In this conformation, the αC helix moves away from the ligand and the salt bridge between Lys52 and Glu66 is broken. This situation causes the beta sheets β1–2 above the binding site to move upward, providing the ligand with more room to explore the binding site. 5Y6 still keeps a V-shape but rotates by 90 degrees to pick up contacts with Tyr32 and Phe97. The MMPB/SA interaction energy (∆E_MM/PBSA) of this trajectory is − 25.5 ± 3.8 kcal/mol and is significantly weaker than its counterpart including CycC (− 29.4 ± 4.4 kcal/mol), further indicating the importance of CycC in maintaining proper binding conformations.

Fig. 6.

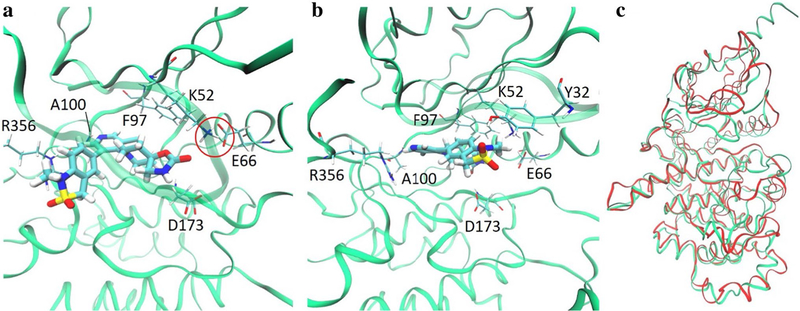
Comparison of CDK8–5Y6 complex without CycC at a 0 ns and b 200 ns. Two binding modes are observed when CycC is absent, one at 0 ns which is a typical type-I ligand binding mode, and the other at 200 ns which is partially due to loss of the important salt bridge formed between K52 and E66 (red circle in a). c Is a superposition of the two aligned trajectory frames with 0 ns in green and 200 ns in red showing the large conformational changes that occur in CycC’s absence

Ligand binding modes and binding pocket volume analysis

Our MD simulations revealed binding modes for both type- I and type-II ligands that matched crystal structures and provide a level of detail previously unavailable (Fig. 7). By calculating the binding energies of the ligands with the MM/PBSA method, we identified the driving forces behind ligand binding to CDK8. The energy breakdowns are shown in Table 2. Type-I ligands formed H-bonds with Lys52, Ala100, and Asp173 in the ATP binding site. Additionally, we found significant vdW interactions with Val27, Val35, Ile79, Tyr99, Leu158, and Arg356. Type-II ligands formed H-bonds with Asp173 and Glu66, which are stabilized by a salt bridge between Glu66 and Lys52 and experience large vdW forces with Leu69, Leu70, Ile79, Phe97, Leu142 and Ala172. Tables 2 and 3 list the strength and durations of these interactions and Figure S7 shows the patterns of H-bond formation and loss for a type-I and type-II ligand. We also computed the total solvent accessible volumes for the ATP and allosteric binding sites for all twelve systems. For type-I ligands, more contacts between ligand and protein lead to better binding affinity through vdW attractions, whereas for type-II ligands, the structural locker formed by Glu66 and Asp173 contributes more significantly. The computed volumes and a few representatives of the volume change over time are in Fig. 8. The specifics of each ligand binding mode vary and are presented in the following sections.

Fig. 7.

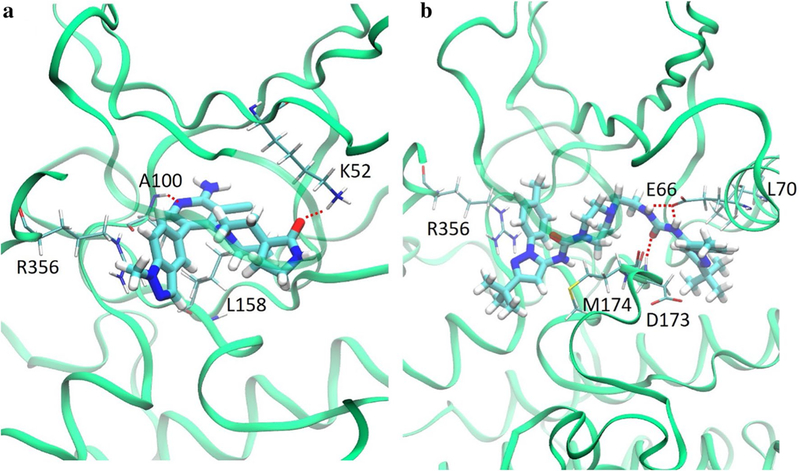
Typical binding modes for a type-I ligands and b type-II ligands with H-bonds shown by red dotted lines and the strongest-interacting residues labeled and shown in licorice

Table 3.

The major residues that have interaction energies stronger than − 1.0 kcal/mol with type I and type II ligands

Type I
MD index	3		4		5		6
Ligand	50R		5XG		5Y6		5Y8
PDB ID	5CEI		5FGK		5HBE		5HBJ
LEU158	− 2.7 ± 0.6		− 2.8 ± 0.6		− 2.7 ± 0.6		− 2.7 ± 0.6
ARG356	− 2.5 ± 0.6		− 2.7 ± 0.7		− 2.7 ± 0.7		− 3.2 ± 0.6
VAL35	− 2.4 ± 0.5		− 2.4 ± 0.6		− 2.5 ± 0.7		− 2.2 ± 0.6
LYS52	− 2.0 ± 1.2		− 3.0 ± 1.1		− 2.7 ± 0.9		− 2.6 ± 1.2
TYR99	− 1.7 ± 0.4		− 1.8 ± 0.4		− 1.6 ± 0.4		− 2.0 ± 0.5
ALA100	− 1.2 ± 0.7		− 1.2 ± 0.7		− 1.4 ± 0.6		− 1.5 ± 0.5
PHE97	− 1.0 ± 0.4		− 1.0 ± 0.4		− 1.1 ± 0.3		− 0.7 ± 0.3
TYR32	− 0.6 ± 0.6		− 2.3 ± 1.0		− 2.8 ± 1.0		− 2.0 ± 1.0
VAL27	− 1.0 ± 0.5		− 1.7 ± 0.7		− 0.9 ± 0.5		− 0.9 ± 0.5
ILE79	− 0.8 ± 0.4		− 1.1 ± 0.4		− 1.1 ± 0.4		− 0.8 ± 0.5
ASP103	+ 0.1 ± 0.6		+ 1.2 ± 0.7		+ 1.9 ± 0.8		+ 1.4 ± 0.6
Type II
MD index	8	9		10		11		12
Ligand	SKR1	SKR2		SKR5		SKR10		SKR11
PDB ID	4F6W	4F7L		4F6U		4F7N		4F7N
GLU66	− 5.2 ± 1.1	− 5.4 ± 1.2		− 4.6 ± 1.4		− 5.2 ± 1.1		− 4.4 ± 1.4
MET174	− 3.3 ± 0.8	− 2.8 ± 1.0		− 1.1 ± 0.8		− 1.4 ± 0.8		− 0.7 ± 0.8
ARG356	− 2.8 ± 0.9	− 0.1 ± 0.5		0.0 ± 0.4		0.0 ± 0.3		0.0 ± 0.3
LEU70	− 2.7 ± 0.8	− 2.7 ± 0.8		− 2.8 ± 0.8		− 2.7 ± 0.7		− 2.9 ± 0.8
LEU158	− 2.4 ± 0.8	+ 0.9 ± 0.6		− 0.6 ± 0.6		0.0 ± 0.4		0.0 ± 0.6
ASP173	− 2.0 ± 1.0	− 2.3 ± 1.0		− 1.8 ± 1.0		− 2.2 ± 1.0		− 1.7 ± 1.0
PHE97	− 1.9 ± 0.7	− 2.2 ± 0.8		− 2.3 ± 0.7		− 1.4 ± 0.8		− 1.7 ± 0.8
VAL35	− 1.9 ± 0.7	− 1.7 ± 0.8		− 1.0 ± 0.6		− 0.1 ± 0.6		− 0.3 ± 0.7
ALA172	− 1.7 ± 0.8	− 1.7 ± 0.9		− 2.0 ± 0.7		− 1.7 ± 0.7		− 1.6 ± 0.7
ILE79	− 1.7 ± 0.8	− 2.1 ± 0.9		− 2.2 ± 0.8		− 1.5 ± 0.8		− 1.8 ± 0.9
LEU69	− 1.1 ± 0.7	− 1.0 ± 0.7		− 1.0 ± 0.6		− 1.0 ± 0.7		− 1.0 ± 0.6
ARG178	0.0 ± 0.1	0.0 ± 0.3		− 1.2 ± 1.0		0.0 ± 0.2		0.0 ± 0.4
LEU142	− 0.9 ± 0.5	− 1.0 ± 0.6		− 0.9 ± 0.6		− 1.0±− 0.6		− 0.9 ± 0.7

All values are in kcal/mol. The standard deviation is marked by ±

Fig. 8.

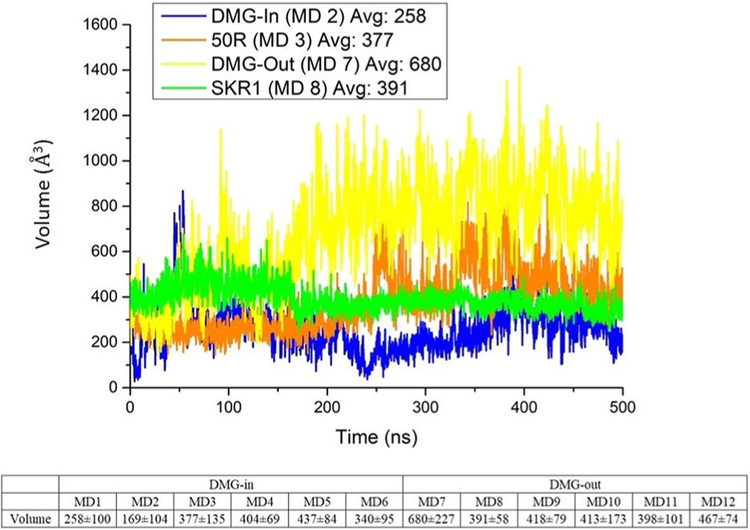
Volumes of the ATP binding site in ų. Plot: Volume change along the MD time for four selected systems; Table: average volumes with standard deviations of all 12 MD systems

Type‑I ligands

H‑bonds

Type-I ligands all share the same direct H-bonds to CDK8 at Lys52 and Ala100, but the H-bond with Ala100 has higher occurrence (56–76 vs. 38–48%) in all cases because of its position in the relatively stationary hinge region and the relative instability of the β-sheet containing Lys52 (Fig. 2). 50R has a nitrogen on the benzothiophene ring forms a H-bond with Ala100 with an occurrence of 64%, and its amide moiety forms another H-bond with Lys52. The other type-I ligands show a similar binding pattern with the ketone oxygen forming an H-bond with Lys52, and the nitrogen on the pyridine forming an H-bond with Ala100. The 3-aminoindazole moiety of 5XG forms a very highly stable H-bond with Val27, with occurrence 78%, which is a unique feature among the type-I ligands studied here.

Electrostatic, vdW, and other interactions

For all type- I ligands, the overall interaction energy is stronger with Lys52 than Ala100 due to both better vdW and electrostatic interactions despite the greater desolvation penalty. These ligands form vdW interactions (− 2.2 to − 3.2 kcal/mol) with Leu158, Arg356, Val35, and a few other residues (Table 3). Other important interactions include formation of a cation–π interaction with Arg356 by the aromatic rings of type-I ligands (Fig. 7). The benzene ring of 50R forms a cation-π interaction with Arg356 and the other three type- I ligands have the same scaffold by which the indazole or its analogue part forms the same cation-π interaction with Arg356. Type-I ligands also form some bridge water interactions with Glu66 (3 to 14%), Asp173 (25 to 38%), and some other residues, but these bridge water molecules are not very stable and are rapidly displaced by bulk water molecules. Bridge waters function as mediating water molecules that hold the interaction between the protein and ligand and may stabilize the binding pose of the ligand, but in this case are unlikely to cause any appreciable decrease in desolvation penalty since they are easily displaced [66, 67]. These interactions are not as strong as direct H-bonds but could still increase ligand binding affinity.

MM/PBSA binding energy

All type-I ligands possess a similar scaffold that occupies a nearly identical space in the ATP binding site (Figure S5) and have MM/PBSA interaction energies (ΔE_MMPBSA) of about − 25 to − 32 kcal/mol. This is the net effect of a negative vdW interaction energy term (ΔE_vdW) ranging from − 40 to − 49 kcal/mol and a positive electrostatic plus PB term (ΔE_elec+PB) from 15 to 23 kcal/mol. The vdW interaction is the major driving force for binding; the ATP binding site has a small volume in the free state and opens to accommodate the ligands which experience tight contacts once they are established. With this scaffold, these ligands have better binding affinity when the ligand is bulkier, so there may be room to further exploit this property using slightly larger type-I ligands. Figure S6 shows the relationship between binding pocket volume and experimental binding affinity.

Type‑II ligands

H‑bonds

All Type-II ligands form two strong H-bonds with Glu66 and Asp173 via the urea linker, with occurrences of roughly 90–96 and 76–93%, respectively (Fig. 2). These two H-bonds function as anchors that stabilize the type-II ligands in the allosteric binding site. The moiety that extends into the ATP binding site for SKR5 and SKR11 has a size and shape which allows these ligands to form an H-bond with Asp98 with occurrences of 8.77 and 10.34%, respectively, that is not seen with the other three type-II ligands. SKR5 has a terminal [3-(morpholine-4-yl)propyl] group that forms another H-bond with Ala100 in the hinge region. Although the occurrence of this H-bond is as low as 17%, it provides SKR5 with detectable residence time [25].

Electrostatic, vdW, and other interactions

The scaffold of all type-II ligands in the allosteric binding site is nearly identical and forms vdW interactions with Leu69 of about − 1.0 kcal/mol and with Leu70 of about − 2.8 kcal/mol. These ligands have very different structures that extend into the ATP binding site, however, and the vdW interaction in this site and structural flexibility largely account for the variability in binding affinities. SKR1 is the largest ligand and extends into and occupies the entire ATP binding site as well (Figure S5), which results in a very strong vdW interaction (ΔEvdW) with CDK8 at − 89 kcal/mol. Because ligand size roughly decreases from SKR2 to SKR11, the vdW interaction (ΔEvdW) decreases from − 62 to − 50 kcal/mol. Other differences in the ATP site moiety of type-II ligands result in variations of other interactions and may change flexibility. For example, SKR10 cannot form the H-bond with Asp98 that SKR11 can, and its absence causes the analogous part of SKR10 to fold onto the protein surface resulting in a stronger vdW interaction than SKR11.

The benzene ring of SKR1 in the ATP binding site interacts with Arg356 via cation-π stacking in the same way as type-I ligands, but it does not have contacts with the hinge region. SKR1 also forms a few stable bridge water interactions with Asn156 and Asp173. SKR2 binds similarly to SKR1 but occupies less of the ATP binding site and has less vdW interaction in that region, and rather than cation–π stacking, has vdW interaction with Arg356. In addition, the smaller structure extending into the ATP binding site is very flexible during the MD simulations, so SKR2 should have a smaller entropic penalty than SKR1.

The electrostatic plus PB term (ΔE_elec+PB) opposes the binding of type-II ligands and decreases with ligand size; however, the electrostatic term (ΔE_elec) alone is very similar among the five type-II ligands, except for SKR5. This finding indicates that the greater presence of polar functional groups in the larger type-II ligands doesn’t necessarily form favorable interactions with the binding pocket of CDK8 and that the binding of these ligands is driven by non-polar interactions.

MM/PBSA binding energies

Type-II ligands share the same scaffold, the minimal compound 7 in [25] that binds to the allosteric binding site of CDK8, but have different structures that extend into the ATP binding site, and MM/PBSA interaction energies of these ligands vary widely due to this difference. MM/PBSA calculations showed that SKR1 has stronger binding energy than SKR2, but experimental data favor SKR2 by 0.5 kcal/mol. Because entropy contributions are not considered in our MM/PBSA calculations, neglected entropic effects may account for this discrepancy. Compared with SKR1, the smaller SKR2 is less confined and retains more freedom, therefore paying less entropic penalty. In addition, RMSF measurements showed that CDK8 bound to SKR2 is more flexible than when bound with SKR1 (Fig. 4), which suggests that the protein also pays less entropy penalty bound to SKR2. SKR10 and SKR11 have less bulky structures than SKR1, SKR2, and SKR5, and thus less favorable vdW interactions with the ATP binding site, which is largely the reason for their less favorable MM/PBSA energies (Table 2).

Conclusion

In this work, we performed MD simulations for nine CDK8/CycC-ligand complexes and three CDK8/CycC apoproteins which included both DMG-in and -out conformations. Our analysis of system dynamics and flexibility shows that the highly flexible activation loop has little effect on ligand binding. Further, ligand binding stabilizes the α-C helix and C-terminus of CDK8 through direct interactions with residues in these regions but does not affect the large-scale dynamics. PCA analysis on sequential 100-ns portions of the MD trajectories revealed the range of protein global motions which are relevant to binding, such as a bending motion about the hinge region, and our simulations provide well-sampled conformations for use in future docking or MD studies.

By repeating simulations with CycC excluded, we were able to discern its stabilizing effect on the system. We found that CycC is critical to maintain the structure of CDK8 and provide proper interactions for ligand binding, namely the stabilization of Glu66 on the αC helix, which forms a critical H-bond with type-II ligands and makes an important salt bridge with Lys52, which H-bonds with type-I ligands.

Analysis of four type-I and five type-II ligand binding modes along with volume measurements of the binding pocket elucidated the protein–ligand interactions. Residues Lys52 and Ala100 form very strong H-bonds with all type-I ligands, and Asp173 and Arg356 provide highly favorable vdW interactions. Additionally, the binding pocket has a smaller volume with type-I ligands, and vdW interactions with the surrounding resides are a major driving force of binding. These ligands can reduce protein flexibility, so entropic penalties need to be taken into consideration. H-bonds may be used to optimize the enthalpic attractions, and, assuming the rigidity of the scaffold can be retained, slightly larger compounds can increase the vdW interaction to optimize the binding affinity.

Type-II ligands bind in both the allosteric and ATP binding site. They all form H-bonds with Glu66 and Asp173; the main variability in type-II binding affinities is due to the varying structures that extend into the ATP binding site. We found that larger structures extending into the ATP site result in favorable vdW interactions and H-bonds. Optimization of type-II binding affinities depends on proper design of the group extending into ATP binding site that achieves a balance between rigidity and size to keep the entropic penalty upon binding minimal while providing enough bulk to stay firmly in the binding pocket and achieve favorable vdW interactions and H-bonds.

Supplementary Material

Supporting Information

Electronic supplementary material The online version of this article (https://doi.org/10.1007/s10822-018-0120-3) contains supplementary material, which is available to authorized users.