Racioethnic Differences in the Biomechanical Response of the Lamina Cribrosa

Abstract

Glaucoma is the second leading cause of irreversible blindness in the world with a higher prevalence in those of African Descent (AD) and Hispanic Ethnicity (HE) than in those of European Descent (ED). The objective of this study was to investigate the pressure dependent biomechanical response of the lamina cribrosa (LC) in normal human donor tissues from these racioethnic backgrounds. Pressure inflation tests were performed on 24 human LCs (n=9 AD, n=6 ED, and n=9 HE) capturing the second harmonic generation (SHG) signal of collagen at 5, 15, 30, and 45 mmHg from an anterior view. A non-rigid image registration technique was utilized to determine the 3D displacement field in each LC from which 3D Green strains were calculated. The peak shear strain in the superior quadrant of the LC in those of ED was significantly higher than in those of AD and HE (p-value = 0.005 & 0.034, respectively) where ED = 0.017 [IQR = 0.012 – 0.027], AD = 0.0002 [IQR = −0.001 – 0.007], HE = 0.0016 [IQR = −0.002 – 0.012]). There were also significant differences in the regional strain heterogeneity in those of AD and HE that were absent in those of ED. This work represents, to our knowledge, the first ex-vivo study identifying significant differences in the biomechanical response of the LC in populations at increased risk of glaucoma. Future work will be necessary to assess if and how these differences play a role in predisposing those of Hispanic Ethnicity and African Descent to the onset and/or progression of primary open angle glaucoma.

Graphical abstract

1. Introduction

The lamina cribrosa (LC) is a collagenous 3D trabecular structure that supports the axons of the retinal ganglion cells (RGCs) as they egress the posterior pole of the eye. As a part of the optic nerve head (ONH), the LC acts as a barrier to maintain intraocular pressure (IOP) while also playing a key role in supporting the ocular vasculature. The LC provides passage for the retinal artery and vein and contains a network of vasculature stemming from the circle of Zinn to supply blood for cells and tissues located in the ONH [1, 2]. The biomechanical behavior of the LC has become a subject of significant interest as several studies have shown a strong correlation between LC cellular dysfunction and glaucoma [3]. Glaucoma is defined as the progressive death of RGCs and the first site of RGC axonal damage in glaucoma is believed to occur at the LC [4]. It is the second global leading cause of vision loss and it is expected to affect more than 110 million people by 2040 [5]. Several factors have been associated with one or more type of glaucoma including age [6], gender [7], elevated intraocular pressure [8, 9], ethnic background [10], family history [6], and specific medical conditions such as migraines [11], diabetes [12], hyper/ hypotension [13], hyperopia [14], and high myopia [15]. Furthermore, elevated intraocular pressure (IOP) is considered one of the primary etiologies for increased risk of development and progression of glaucoma [16, 17]. Nevertheless, studies have suggested that elevated IOP is neither necessary nor sufficient to develop glaucoma [18–20]. While many researchers have suggested a connection between elevated IOP and glaucoma in the literature, several population-based studies have found that substantial number of people with elevated IOP never develop glaucoma. Among the individuals who have been diagnosed with glaucoma, only 25% to 50% have an IOP greater than 22 mmHg. These discrepancies raise questions regarding the efficacy of IOP measurement as the sole means to diagnose glaucoma [21–23].

As such, studying the coupled relationship between IOP and tissue biomechanical response is critical to understand how the LC reacts to elevated IOP. The biomechanical response of a tissue depends on its microstructural, morphological, and mechanical properties in addition to applied loading conditions, in this case IOP. It is also understood that, in the context of mechanosensitivity, a biomechanical stimulus can trigger various deleterious cellular events. Burgoyne et al. demonstrated that mechanical stimulation can initiate the production of signaling molecules that could alter the ECM, which may be detrimental to RGC axons [24–26]. Others have suggested that variations in IOP can lead to dysregulation of homeostatic ECM turnover in the LC that may further alter the gene expression of local astrocytes and LC cells [27–34].

Imaging techniques have been used extensively to study ocular tissue biomechanics [35–37]. However, it is extremely challenging with current imaging techniques to collect the necessary information at sufficient resolution to analyze the biomechanical response of the LC in-vivo. This is primarily due to the LC’s inaccessibility and 3D complex geometry, as well as limited freedom in controlling IOP. Sigal et al. analyzed the 2D eye-specific response of the LC during ex vivo inflation testing using digital image correlation of the second harmonic generation (SHG) signal [38]. Girard et al. developed an algorithm to study 3D displacement and strain fields in the LC using OCT images [39]. They performed an in vivo experiment to investigate how lowering IOP by trabeculectomy would change strain of the ONH in glaucomatous subjects and showed that lowering IOP could significantly relieve tensile strain in the LC [40]. Midgett et al. utilized multiphoton imaging during an ex vivo LC inflation experiment and showed that in-plane LC strain components significantly change as IOP increases. This study also examined regional variations, with larger shear strain values being reported in the peripheral region of the LC [35]. Coudrillier et al. also used an ex-vivo phase contrast CT imaging method to study the full field 3D pressure-induced deformation of the porcine LC and observed large strain gradients in both transverse and sagittal planes of the LC [41]. All of these research efforts have enhanced our understanding of how the LC reacts mechanically to elevated IOP and as such how it functionally protects the axons of the RGC as the egress the posterior eye.

Race and ethnicity have been reported as risk factors for the onset and progression of glaucoma [7, 10, 42–44], with higher prevalence in groups of African descent compared to those of European descent. Higher prevalence has also been demonstrated in Hispanic ethnic groups. A few in-vivo and ex-vivo studies have demonstrated differences in the morphometry and mechanical behavior between individuals of African and European descent that could explain in-part this greater susceptibility to glaucomatous injury [45–47]. However, there has currently been no detailed report comparing the full field 3D strains in the LC of normal human donors of African descent, European descent, and Hispanic ethnicity.

The purpose of this work is therefore to quantify the biomechanical response of the normal human LC in those from various racioethnic backgrounds by acquiring 3D strain maps of the LC using nonlinear optical microscopy. More specifically, we performed ex vivo inflation tests on human LCs collecting the SHG signal of collagen from the anterior view using a multiphoton microscope at increasing levels of IOP. Digital volume correlation (DVC) was used to generate 3D displacement fields from which subsequent strain maps of the LC were calculated and compared across racioethnic background [48]. To our knowledge this study is the first to report differences in the ex-vivo LC biomechanical response in those at increased risk for POAG.

2. Methods

2.1. Study group and sample preparation

Human posterior poles were isolated from donors older than 50 years of age that self-identified as AD, ED, and HE. Eyes were acquired within 48-hour post-mortem from six different eye banks: Alabama Eye Bank in Birmingham, AL, USA; Banner Sun Health Research Institute in Sun City, AZ, USA; Donor Network of Arizona in Phoenix and Tucson, AZ, USA; Illinois Eye Bank in Chicago and Bloomington, IL, USA; Michigan Eye Bank in Ann Arbor, MI, USA; and San Diego Eye Bank in San Diego, CA, USA. The procedures in this study adhered to the tenets of the Declaration of Helsinki. The aforementioned eye banks confirmed that all subjects consented to donate tissue for research purposes. The eye banks also obtained the necessary ethical approval to use the specimens for research purposes. Our inclusion criteria for each donor sample received from the eye banks included having approximately 6mm of the optic nerve close to the lamina cribrosa. Twenty-four eyes from eighteen humans were used in this study. Detailed demographic information of the samples is shown in Table 1. Based on the medical reports we received from the eye banks, no history of glaucoma or other ocular disease was reported for the donors included in this study.

Table 1.

Demographic information for the human donors used in this study. OD-oculus dexter (right eye); OS-oculus sinister (left eye); HE-Hispanic Ethnicity; ED-European Descent; AD-African Descent; Gray shade shows donor eye pairs.

No.

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

Race

AD

HE

HE

ED

ED

ED

ED

AD

AD

AD

AD

AD

HE

AD

ED

ED

HE

HE

HE

AD

HE

HE

HE

AD

Age

70

54

54

83

77

74

70

55

55

66

66

62

64

54

89

89

58

90

90

83

80

80

95

62

Gender

M

M

M

M

M

F

M

M

M

M

M

F

M

M

F

F

M

M

M

F

M

M

M

F

Globe

OS

OD

OS

OD

OS

OD

OD

OD

OS

OD

OS

OD

OS

OS

OD

OS

OD

OD

OS

OS

OD

OS

OD

OD

All samples were received and tested within 48 hours postmortem. The sample preparation procedure used in this study was adapted from Quigley et al. [49]. The exterior scleral surface of each eye was cleaned to remove any remaining adipose, connective, and muscular tissue and bisected along its equatorial plane using a scalpel and surgical scissors. With the aid of a dissecting microscope, a microdissection procedure was performed to gently remove the choroid, retina, and prelaminar tissue from the ONH. The posterior poles then underwent a gentle digestion procedure to remove any remaining prelaminar tissue that could not be removed mechanically. Briefly, the ocular tissue was submerged in 0.25% ethylenediaminetetraacetic acid (EDTA) trypsin for 10 minutes at 37° C with gentle agitation, washed three times in fresh 1X phosphate buffered saline (PBS) solution, and a 5-minute submersion in a 1:1 0.25% EDTA-trypsin and 100 mM NaOH mixture at 37° C with gentle agitation. Tissue digestion was halted by adding an equal volume of 10% fetal bovine serum (FBS) to the solution and gently agitating for 1 minute. Finally, samples were washed in fresh 1X PBS solution three times. The mechanical microdissection procedure was repeated again to clean off any remaining prelaminar tissue. All specimens were kept moist throughout the entirety of the preparation procedure and stored in 1X PBS at 4° C to prevent tissue dehydration and/or degradation prior to imaging. All samples regardless of age, gender, or race/ethnicity received identical digestion treatment.

2.2. Mechanical testing and imaging

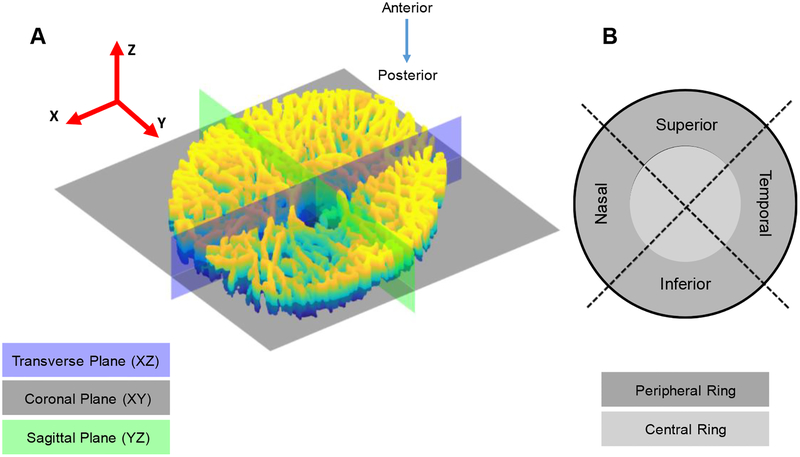
Samples were placed in a novel micro-optomechanical device consisting of an acrylic base with a cavity allowing for uninhibited posterior deformation and a metal pressure plate with a Corning No. 1 cover glass functioning as the imaging window. The cover glass was adhered above a circular opening whose diameter was 400% larger than the average maximum diameter of the human LC [50]. Four diagonal cuts along the borders of the physiological regions were made from the edge of the sclera towards the ONH, shown in Figure 1A. This was done to allow the sample to be effectively sealed via six 6–32 machine screws, shown in Figure 1B. Samples were then pressurized to four pressure levels (i.e. 5, 15, 30 and 45 mmHg). These pressure levels were selected to take in to account the non-linear biomechanical behavior of collagen present in the LC and to capture the gradual uncrimping of the collagen fibers. The pressure was regulated in a closed-loop system via feedback from a digital pressure transducer to custom software in LabVIEW 2012 (National Instruments, Austin, TX) actuating a syringe pump. A diagram of the setup is shown in Figure 1C. The samples were imaged using an Olympus BX51 upright laser-scanning microscope, shown in Figure 1D, which was coupled to a coherent 120-fs tunable pulsed titanium-sapphire laser (Chameleon ultra ii, Coherent Inc., Santa Clara, CA). The laser was centered at λ = 780 nm to efficiently visualize collagen via backscatter SHG signals. Digital images were acquired with a plan-apochromat lens with a magnification of 4X, numerical aperture = 0.28, working distance of 29.5 mm, and a pixel size of 2.41 μm in the x- and y-direction and 5 μm in the z-direction with automatic focusing. The sequential 2-D images at each 5-μm-spaced optical section were then stacked to form a volumetric dataset. The dimension of each 2D image was 1039 × 1039 pixels, and they were stored as 16 bits per pixel. An example of a mean intensity projection of the LC is shown in Figure 2. Multiphoton imaging was performed at 5, 15, 30, and 45 mmHg. Due to a loss of signal at increased imaging depth, we excluded data deeper than 200 μm from the anterior surface of the LC in our displacement and strain calculations. A 30-minute wait period was utilized at each pressure step prior to image acquisition to minimize the influence of tissue creep [35].

Figure 1.

A) Posterior poles were cut meridionally prior to insertion into the pressure inflation device. B) Samples were clamped in the pressure chamber (red arrow) and the lid was secured to maintain the pressure level during imaging. C) A LabVIEW code was developed to monitor and control the pressure level by using a syringe pump and a pressure transducer during the experiment. D) Test chamber was placed under the microscope (green arrow) and multiphoton imaging was performed at four different pressure levels imaging from the anterior view.

Figure 2.

Representative mean intensity projection of the collagen (SHG) in a human LC

2.3. Displacement and Strain Calculation

A Digital Volume Correlation (DVC) algorithm was used to compute the displacement field at increasing IOPs for each sample. A non-rigid image registration technique based on Thirion’s demon algorithm was employed to determine the displacement field. This algorithm utilized the concept of diffusing models (i.e. deformable grid), which is a robust and computationally efficient image registration approach [48, 51]. The DVC code output both the registered deformed image stack and the displacement field. A MATLAB (MathWorks, Natick, MA) code was developed based on a template matching algorithm [52] to compute the normalized cross-correlation coefficient values over many search windows between the deformed image stack acquired during the experiment (target stack) and the registered image stack (template stack) created by imposing the computed displacement field on the undeformed images. The template matching algorithm detected similarities in the texture and was independent of the voxel illumination. If two image stacks with the same size matched perfectly, the maximum cross-correlation coefficient (i.e. a value of one) occurred at the center of the target stack. We defined a normalized objective function ω(ξ) to calculate rigidity of the deformable grid (ζ) that resulted in the optimized displacement filed;

$$\omega (\zeta )=v[1-\alpha (\zeta )]+[1-v]\frac{\Vert \rho (\zeta )-C\Vert }{L}$$ (1)

where α(ζ) is the value of the maximum of the cross-correlation coefficient, C is the location of the center of the target image stack, ρ(ζ) is the location of the maximum normalized cross-correlation coefficient, L is the largest dimension of the image stack, and υ is defined as a weight coefficient set to 0.4 for all image stacks. In an ideal case, when target and template stacks are identical, ω is equal to zero. The average value of the maximum cross-correlation coefficient (α(ζ)) was 0.93 + 0.034. A design of experiments study was performed to find the value of ζ that minimized ω(ζ) for each pressure increment within each sample. The convergence criterion for ω(ζ) was 10% which translated to a maximum 10% error in the displacement field calculation. Upon completion of the displacement field validation, a 3D Gaussian low-pass filter was applied to the displacement field to minimize the effect of the noise and estimation error on the strain calculation [53].

Strain is a measure of deformation representing the displacement between particles in the body relative to a reference length. The Green strain tensor (E_ij) is defined as

$$E_{ij}=\frac{1}{2}\left(F_{ki}{F}_{kj}-{\delta }_{ij}\right)$$ (2)

where F_ij are the components of the deformation gradient tensor and δ_ij is the Kronecker delta. This tensor is not sensitive to rigid body motion. If the components of the displacement field are denoted as u_i(X₁, X₂, X₃), then the matrix of the deformation gradient tensor is:

$$\left[F_{ij}\right]=\left[u_{i,j}+{\delta }_{ij}\right]=\left[\begin{array}{ccc}1+\frac{\partial u_1}{\partial X_1}& \frac{\partial u_1}{\partial X_2}& \frac{\partial u_1}{\partial X_3}\\ \frac{\partial u_2}{\partial X_1}& 1+\frac{\partial u_2}{\partial X_2}& \frac{\partial u_2}{\partial X_3}\\ \frac{\partial u_3}{\partial X_1}& \frac{\partial u_3}{\partial X_2}& 1+\frac{\partial u_3}{\partial X_3}\end{array}\right]$$ (3)

where X_i is the coordinate of any point in the reference configuration with respect to a global right-handed Cartesian coordinate system, as shown in Figure 3A. The Z-axis was chosen to be the anterior-posterior direction and the retinal artery center was chosen as the origin of this coordinate system. Also, to investigate regional variations in the strain field, we divided the LC into the four quadrants (inferior, superior, nasal, and temporal), as well as central and peripheral regions. For each LC, we used the central artery canal as a center point and created an ellipse that was 50% from this center point to the end of the major and minor axes located on the LC. All regions are illustrated in Figure 3B. To calculate the partial derivative of the displacement field and the strain tensor, a MATLAB code which was developed by Kroon [54] based on a study performed by Adb-Elmoniem et al. [55] was employed. The numerical scheme to calculate gradient of the displacement field was a central difference for the interior data points and single sided difference along the edges of the domain. Although the strain calculation method was well tested and verified in the Adb-Elmoniem et al. work, we validated the strain calculation using synthetic data sets. Moreover, to calculate minimum detectable difference for the displacement tensor components, we imaged the same sample twice without making any changes in the imaging settings, calculating the displacement and strain fields from the resulting dataset. Theoretically, no displacement should have been detected since no pressure gradient was introduced. However, due to noise and estimation error, the displacement field and the calculated strain field were not identically equal to zero. This experiment enabled us to place a threshold to define the noise level; therefore, any detected displacement smaller than the noise level was not reported in this study. Noise levels of each displacement component were u_x= 0.79 ± 0.41 μm, u_y= 0.69 ± 0.36 μm and u_z= 0.39 ± 0.29 μm.

Figure 3.

A) Anatomical planes are shown on a segmented LC with respect to the Cartesian coordinate system. XYZ is a right-handed coordinate system with its center located at center of the retinal artery canal. B) The LC was divided into four quadrants and two rings to investigate any regional variation in strain response.

2.4. LC Porosity and size calculation

The porosity of the LC, which quantifies the fraction of void volume to total volume of tissue, was defined as the ratio of collagen volume to total LC volume. Our in-house LC segmentation code was used to create stacks of binary images that segmented LC collagen (to calculate collagen volume) [56]. We then closed the binary images morphologically and calculated total volume of the LC. These calculations were performed for each individual sample using the 5 mmHg image datasets. Values of section-dependent porosity were also generated for comparison. To determine the LC size, a least square ellipse was fitted to the LC rim which was identified by manual clicks on the maximum intensity projection of the coronal plane image set. The area of the fitted ellipse was then calculated for each sample and was compared across different racioethnic groups.

2.5. Statistical methods

A linear mixed model was employed to account for the within subject unbalanced repeated measure variability present in our data. Racioethnic group and LC section were considered as fixed effects while human subjects and eyes were included as random effects. Since the residuals of the strain data were not normally distributed [38], we used Box-Cox transformation to transform all data to normal [47]. After satisfying all requirements, we fitted the transformed data to a linear mixed model and utilized an ANOVA to identify significant differences with alpha level of 5% using a Tukey correction to adjust for multiple comparisons.

2.6. Computational resources and software

DVC calculations were done using computers with a 12-core 3.4GHz Intel Xeon E5–2643 processor with 256GB or 512GB RAM at the University of Pittsburgh Center for Research and Computing (CRC cluster). Larger datasets were processed on Large Memory (LM) nodes of the Bridges-Large machine at the Pittsburgh Supercomputing Center with up to 16-core, 3.2 GHz Intel Xeon E5–8860 v3 processors with 3TB RAM. In addition, all strain calculations were done using an Intel Xeon CPU E5–2698 v4 @2.20Hz (2 Processors) with 512GB RAM. The statistical analysis was done using scripts in R (V3.5) [57] and MATLAB (R2017a). All codes to calculate displacement field, strain field, strain smoothing, and result validation were developed in MATLAB (R2017a).

3. Results

3.1. Displacement and Strain Fields

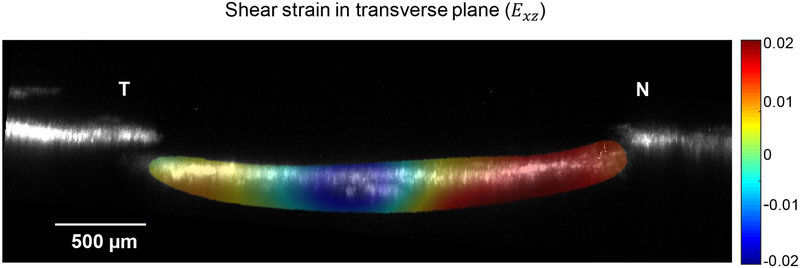
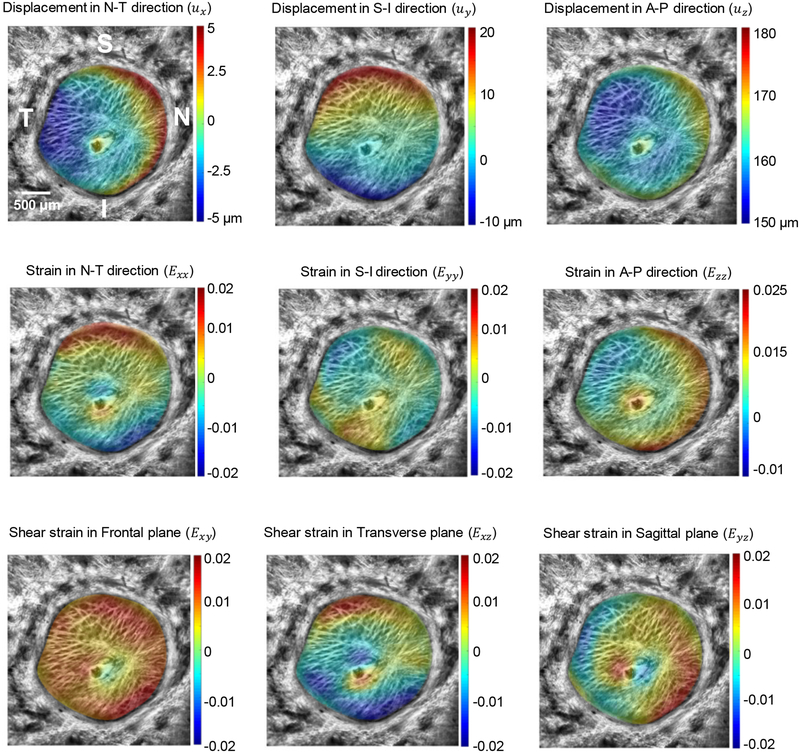
3D displacement and strain fields were calculated for each of the samples. Figure 4 illustrates the average of the shear strain component (E_xz) through the LC thickness in superior-inferior direction. Furthermore, strain and displacement components averaged through the LC thickness are depicted in this Figure 5.

Figure 4.

E_xz (strain component in the transverse plane) averaged in the superior-inferior direction for a representative sample. N and T indicate the nasal and temporal directions, respectively.

Figure 5.

Strain and displacement components averaged through the LC thickness in the second pressure step (p=30 mmHg) of a representative sample. N-T, S-I and A-P are the nasal-temporal, superior-inferior and anterior-posterior directions, respectively. The X axis is in nasal-temporal direction while the Y axis is in the superior-inferior direction.

3.2. Comparison of the strain response across the racioethnic groups

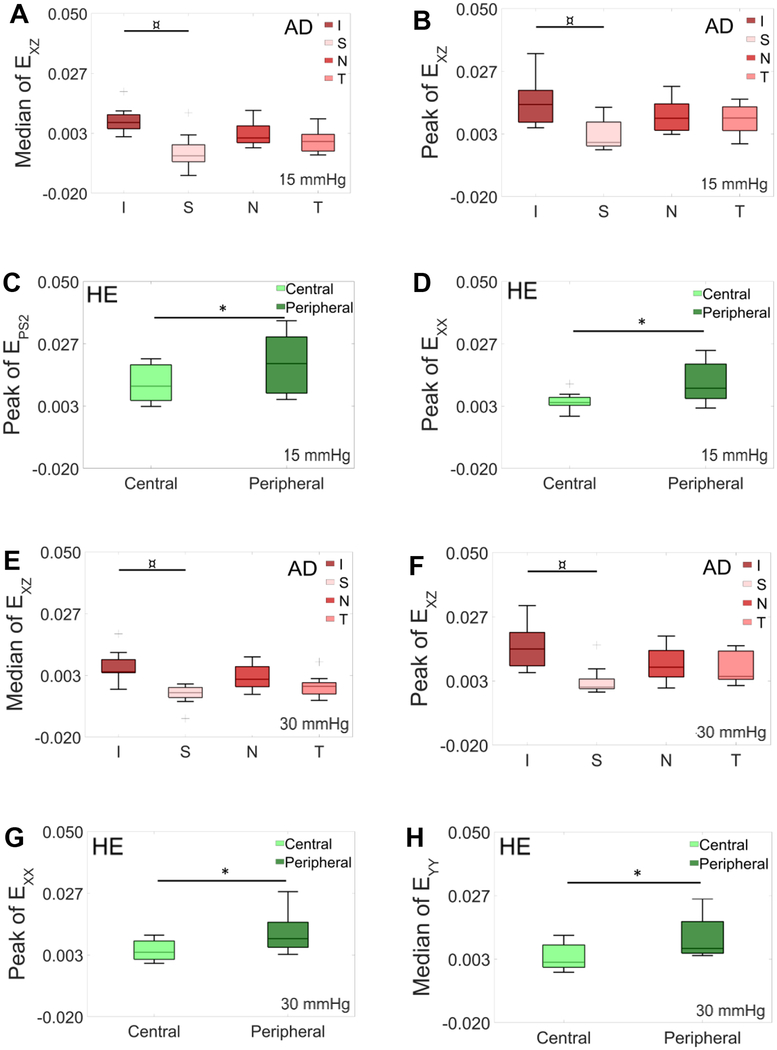
The peak and median of LC shear strains in the transverse plane were significantly different across racioethnic groups (Figure 6). Peak shear strain in the LC transverse plane at 15 mmHg was significantly higher in the ED group compared to the HE group in the entire LC (p-value=0.034), in the central ring (p-value=0.043), and in the superior quadrant (p-value=0.034). Peak E_xz in the superior quadrant of the ED group was also higher compared to that of the AD group (p-value=0.005). The median strain component in the LC coronal plane (E_xz) in the entire LC was higher in the AD than the ED group (p-value=0.030).

Figure 6.

Comparison of Green strain metrics across the racioethnic groups for strains at 15mmHg: A) Peak of E_xz in the entire LC (HE vs. ED: p-value=0.043), B) Peak of E_xz in the central ring (HE vs. ED p-value=0.039), C) Median of E_xy in the entire LC (AD vs. ED: p-value=0.0.030), D) Peak of E_xz in the superior quadrant (AD vs. ED: p-value=0.005 and HE vs. ED: p-value=0.034).

3.3. Comparison of the strain response within racioethnic groups

Significant strain heterogeneity was present in the AD (red bars) and HE (green bars) that were entirely absent in the ED group (Figure 7A–H). Specifically, peak values of strain in the nasal-temporal direction (E_xx) for the first and second pressure levels were higher in the peripheral ring than in the central ring for the HE group (p-value=0.031 and 0.0006, respectively). Additionally, peak second principal strain at 15 mmHg and the median strain in the inferior-superior direction (E_yy) at 30 mmHg were larger in peripheral region than in the central region for the HE group (p-value=0.017 and 0.025, respectively). Furthermore, for the first two pressure steps, the AD group showed larger peak and median of E_xz values in the inferior quadrant compared to the superior quadrant (p-value=0.0007 and 0.005 at 15 mmHg and p-value=0.004 and 0.008 at 30 mmHg, respectively).

Figure 7.

Comparison of strain metrics at 15 mmHg (A-D) and 30 mmHg (E-H) for the AD and HE groups (no differences were found in the ED group): A) median of E_xz (p-value = 0.005) and B) peak of E_xz (p-value= 0.0007) in different quadrants of the AD group. C) Peak of the second principal strain (p-value= 0.017) and D) peak of E_xx (p-value= 0.031) in the HE group in the central and peripheral ring. E) Median of E_xz (p-value= 0.008) and F) peak of E_xz (p-value= 0.004) in different quadrants of the AD group. G) Peak of E_xx (p-value= 0.0006) and H) median of E_yy (p-value= 0.025) in the HE group in the central and peripheral ring. Results in panels C & F showed correlation to age and should be interpreted with caution.

3.4. LC porosity and radius comparison

LC porosity did not significantly change with racioethnicity in our results. However, there was a notable increase in the variability of porosity in those of AD (Figure 8A). No significant differences were observed comparing LC size across all racioethnic groups (Figure 8B).

Figure 8.

LC A) porosity and B) area across the racioethnic group (p-value = 0.4 and =0.65 respectively)

4. Discussion

We have shown that the peak shear strain in the transverse plane (E_xz) is significantly reduced in the superior quadrant in AD and HE eyes when compared to ED. Our results also demonstrate that the median shear strain in the coronal plane (E_xy) is significantly increased in those eyes from donors of AD compared to those of ED. Interestingly, we also provide evidence that there are significant regional variations in strain in those of HE and AD that do not exist in those of ED.

A study by Quigley et al. showed that the superior and inferior regions of the LC contain larger pores with thinner connective tissue support than other regions. However, they found no statistically significant differences when comparing tissue proportion and pore size distribution across blacks and whites [49]. Other studies have shown that the proportion of connective tissue in the central region of the LC is significantly lower than that of the peripheral region [58, 59]. Our findings of higher strain values in the inferior quadrant of the AD group and peripheral ring of the HE group may be indicative of a more deformable structure in those regions for these racioethnic groups, which may stem from differences in connective tissue proportion. It is interesting to note that we found no statistically significant regional differences in the ED group while several regional variations were observed in the AD and HE strain response. This is a prominent finding as other studies have suggested that cell response to a mechanical stimuli may be more affected by local than global levels of strain [60, 61]. Strain field regional heterogeneities could stem from local differences in the LC mechanical and/or morphological properties. Further investigation is essential to better understand the origin and effect of the local strain pattern in HE and AD groups.

Fazio et al. demonstrated that in-vivo anterior lamina cribrosa surface (ALCS) displacements are significantly higher in those of ED than those of AD for small IOP elevations [45]. Girkin et al. also showed that those of AD have a thinner LC, an increased LC depth, and a thinner peripapillary sclera as compared to those of ED [47]. As the sclera is known to significantly influence the biomechanical response of the LC [62], a thinner peripapillary sclera in AD donor LCs may contribute to reduced ALCS displacements in this group and as such play a role in the reduced shear strain we observed for AD donors in this study. Girkin et al. also quantified the anterior scleral canal opening (ASCO) radius of those of AD and ED and showed that ASCO is significantly larger in those of AD compared to ED group [47]. While we did not find a significant difference in scleral canal opening for the AD vs ED groups in our study, our results of a non-significant trend of increased LC area in those of AD are consistent with this prior finding (Figure 8B). The lack of a significant difference in scleral canal opening area with race in our donor samples, coupled with the presence of race dependent differences in shear strain, suggests that size alone may not be the sole factor influencing strain values in the LC.

Although we did not find any differences in porosity across racioethnic groups, the variation in LC thickness, laminar beam orientation/thickness, collagen fibril crimp/splay, and peripapillary scleral strain are other prominent potential factors which may contribute the increased regional strain gradient in the HE and AD groups from one region to another region as compared to ED group. For instance, Tamimi et al. showed that the mean of the first principal strain in the peripapillary sclera is higher in the HE and AD groups compared to the ED group at 15 mmHg and that these differences are regionally dependent [63]. This work and that of Fazio et al. have also shown that strains in the peripapillary sclera of AD groups are reduced in comparison to ED as IOP increases [64]. These regionally dependent and race specific differences in peripapillary scleral biomechanics may have contributed to the higher regional LC strain variation in the AD and HE groups as compared to the ED group observed in this study.

Midgett and colleagues performed a LC strain analysis and found that the maximum in-plane (coronal plane) shear strain is larger in the peripheral ring compared to the central ring of human donor eyes [35]. Consistent with their findings, we showed that peak E_xx and E_xx in the HE group are significantly higher at the peripheral ring compared to the central ring. While our results did show larger peak E_xx values in the peripheral ring compared to the central ring for the other racioethnic groups, these differences were not statistically significant. This group also showed that there is no significant variation in the maximum principal strain across the different quadrants for their Caucasian donor samples, which is consistent with our result showing no regional strain variation in the ED group [35]. Taken together these studies reinforce the importance of studying the heterogeneity of strains occurring in the LC.

There are several limitations of this study. SHG signal from our multiphoton microscope reduces with depth of penetration into the LC. This fact resulted in a higher level of noise in the images close to the bottom of the stack (towards the retrolaminar region). We consistently measured the different strain metrics for 200 μm of the LC thickness to avoid noisy data. Given that our approach, as in all optical techniques, is depth limited, using a different imaging modality such as phase contrast CT may provide a better picture of the full heterogeneous strain within the entire optic nerve head. Moreover, it should be noted that all donor samples used in the HE group were male. We performed a separate statistical analysis focused on gender as a main effect in the AD and ED groups and our statistical analysis showed no significant effect related to gender in either of these groups. Nevertheless, the unintended lack of balance in gender within the HE data presented here is an important limitation to remember when interpreting the data and subsequent conclusions. In addition, some studies [65] showed the biomechanics of the left and right eyes might be different. We have also captured inter-eye differences within a donor pair. Although we have accounted for this inter-eye variability in our statistical model, a future study should compare the disparity of LC biomechanical response in the human eye pairs. Our statistical analysis did not show any significant correlation between strain metrics and age in the first pressure level (i.e. 15 mmHg). However, for the second pressure level, the central ring of HE and superior quadrant of AD showed correlation to age (Figures 7C & 7F). Therefore, caution should be taken when interpreting these two figures.

Another limitation of this study is the experiment setup. We clamped the posterior pole of each human eye into the pressure chamber. Clamping might have induced some level of strain to the tissue. However, we followed the same protocol for testing all the samples, thus the effect should be similar across all the samples. The absolute magnitude of strains reported in this study should therefore be interpreted carefully in the context of this limitation. Additionally, Sigal et al. [62] showed that the biomechanics of the LC is significantly affected by the neighboring tissues such as the peripapillary sclera and pia mater. A more inclusive experimental setup that incorporates the effect of the LC adjacent tissues may be crucial to fully understanding the coupled biomechanical response of the LC. Nevertheless, prior to this comprehensive experimental study, it is important to understand the biomechanical and morphological properties of the LC individually. Finally, the ability to SHG image the human LC from an anterior view was, in part, made possible by a short and gentle dissection procedure. Our conclusions here assume that this procedure did not differentially affect the biomechanical response of the human LC and in particular alter any pre-existing racioethnic differences present in this tissue. This caveat should be carefully considered when interpreting the results and conclusions presented in this study.

5. Conclusion

To the best of our knowledge, this is the first study that shows several significant differences in the LC biomechanical response across racioethnic groups at increased risk for POAG. We have shown that strain components in the transverse plane (E_xz) of the LC in those of ED group are significantly higher than in those of AD and HE and that strain heterogeneity is significantly increased populations at increased risk for POAG. Further investigation is necessary to determine if and how this altered biomechanical response may play a role in the initiation and/or progression of POAG.

Statement of Significance.

Glaucoma is the second leading cause of irreversible blindness in the world and occurs more frequently in those of African Descent and Hispanic Ethnicity than in those of European Descent. To date, there has been no ex-vivo study quantifying differences in the biomechanical response of the non-glaucomatous lamina cribrosa (LC) across these racioethnic backgrounds. In this work we report, for the first time, differences in the pressure dependent biomechanical response of LC across different racioethnic groups as quantified using nonlinear optical microscopy. This study lays the foundation for future work investigating if and how these differences may play a role in predisposing those at increased risk to the onset and/or progression of primary open angle glaucoma.

Appendix A. Supplementary data

A1: Pressure chamber:

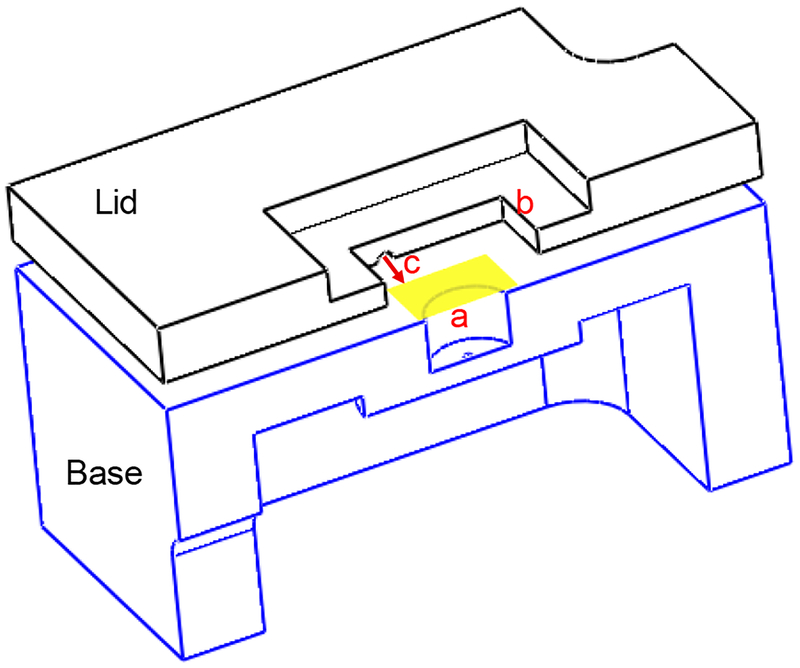
The pressure chamber was designed in SolidWorks and made of stainless steel (Type 304). The special design enabled us to simultaneously pressurize and image the anterior surface of the LC. As depicted in Figure A1, the yellow shaded area indicates the location of the sample in the chamber, each sample was placed in the chamber enabling the optic nerve stump to be positioned in the hole (a) and the imaging hatch (b) was covered with a standard cover glass to maintain the pressure. Pressure was regulated by using a syringe pump through a cylinder shaped recess (c) designed on the bottom surface of the lid.

Figure A1.

A cut view of the pressure chamber. The yellow shaded area shows the location of the LC in the chamber. The anterior surface of the LC was placed faced up in the chamber. The optic nerve stump was placed in the hole (a), pressure was regulated through recess (c) and SHG signal was collected from the hatch (b).

A2: Validation of the strain calculation code

To validate the strain calculation in our work, we defined a displacement as below (Figure A2):

$$x=2.7X+0.5Y$$

$$y=X+3.3Y$$

$$z=-3.1Z$$

Figure A2.

Red shows deformed configuration of the blue cube under the synthetic displacement field.

Manual calculation:

Right Cauchy-Green strain tensor (C_ij) is defined as:

$$C_{ij}=F_{ki}{F}_{kj}=\frac{\partial x_k}{\partial X_i}\frac{\partial x_k}{\partial X_j}=\left[\begin{array}{ccc}2.7& 0.5& 0\\ 1& 3.3& 0\\ 0& 0& -3.1\end{array}\right]\left[\begin{array}{ccc}2.7& 0.5& 0\\ 1& 3.3& 0\\ 0& 0& -3.1\end{array}\right]=\left[\begin{array}{ccc}8.29& 4.65& 0\\ 4.65& 11.14& 0\\ 0& 0& 9.61\end{array}\right]$$

$$E_{ij}^{analytical}=\frac{1}{2}\left(C_{ij}-{\delta }_{ij}\right)=\left[\begin{array}{ccc}3.6450& 2.3250& 0\\ 2.3250& 5.070& 0\\ 0& 0& 4.3050\end{array}\right]$$

The Strain code validation:

The displacement field is the only input to the strain code. Deformation gradient tensor (F_ij) and Green strain tensor (E_ij) are defined as below:

$$E_{ij}=\frac{1}{2}\left(F_{ki}{F}_{kj}-{\delta }_{ij}\right),F_{ij}=u_{i,j}+{\delta }_{ij}$$ (2&3)

For the synthetic data, Green strain tensor was calculated by using a MATLAB code:

$$E_{ij}^{computational}=\left[\begin{array}{ccc}3.64500000000001& 2.3250& 0\\ 2.3250& 5.06\overline{9}& 0\\ 0& 0& 4.3050\end{array}\right]$$

To calculate the gradient of the displacement field, gradient function from MATLAB library was used. The discretization scheme was central difference for the interior nodes and single-sided difference for the nodes on the boundary. There were two sources of the error associated with the numerical discretization: round-off error and discretization error. The total residual (ξ) was defined as:

$$\xi =\sum \left|E_{ij}^{analytical}-E_{ij}^{computational}\right|=1.73e^{-14}$$

The local truncation error is proportional to the step size of the discretization, thus we considered step size =1 μm to minimize the computational error and preserve the computational efficiency.