Mechanical Communication Acts as a Noise Filter

Summary

Cells can communicate mechanically by responding to mechanical deformations generated by their neighbors. Here, we describe a new role for mechanical communication by demonstrating that mechanical coupling between cells acts as a signaling cue that reduces intrinsic noise in the interacting cells. We measure mechanical interaction between beating cardiac cells cultured on a patterned flexible substrate and find that beat-to-beat variability decays exponentially with coupling strength. To demonstrate that such noise reduction is indeed a direct consequence of mechanical coupling, we reproduce the exponential decay in an assay where a beating cell interacts mechanically with an artificial stochastic ‘mechanical cell’. The mechanical cell consists of a probe that mimics the deformations generated by a stochastically beating neighboring cardiac cell. We show that noise reduction through mechanical coupling persists long after stimulation stops and identify microtubule integrity, NOX2, and CaMKII as mediators of noise reduction.

Graphical Abstract

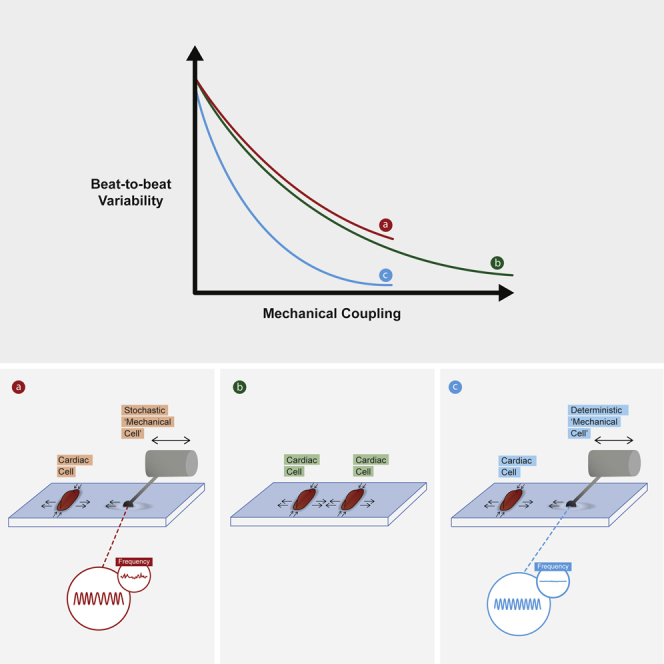
Highlights

• •Mechanical communication reduces intrinsic noise in interacting cells
• •Cardiac cell beating noise decays exponentially with the strength of mechanical coupling
• •Identical exponential decay length is obtained using a stochastic mechanical cell
• •NOX2, ROS, and CaMKII are involved in mechanical communication-induced noise reduction

Biological Sciences; Cell Biology; Physical Sciences

Introduction

It was recently established that cells are able to communicate mechanically by responding to mechanical deformations generated by their neighbors (Nitsan et al., 2016, Winer et al., 2009, Tang et al., 2011, Angelini et al., 2010, Chiou et al., 2016, Cohen and Safran, 2016, Reinhart-King et al., 2008). Exploring matrix-mediated mechanical cell-cell communication is experimentally challenging since it is difficult to isolate this specific contribution from all other modes of communication, such as electrical and chemical. However, several instances of mechanical communication through the matrix were demonstrated unequivocally. These include collective cell migration (Reinhart-King et al., 2008, Angelini et al., 2010), cell alignment (Winer et al., 2009, Engler et al., 2004), and cardiac cell beating (Nitsan et al., 2016, Chiou et al., 2016). Nevertheless, the characteristics of mechanical communication and its range, role, and ability to regulate biochemical processes within the cell are still largely unknown (Sapir and Tzlil, 2017). Cellular processes, such as protein synthesis, post-translational modification, or trafficking, undergo stochastic fluctuations—“noise”—in their levels and activities. Here we show that mechanical coupling acts as a noise filter that reduces the intrinsic noise of interacting cells.

Spontaneous beating of cardiac cells arises from self-sustained oscillations of the intercellular calcium concentration coupled to membrane depolarization-repolarization cycles (Quinn and Kohl, 2012, Maltsev and Lakatta, 2009). The beating rate is regulated by the kinetics and sensitivity of ion channels (e.g., L-type Ca²⁺ channel) and transporters (e.g., Na+/Ca²⁺ exchanger) at the plasma membrane and by calcium pumps and release channels (e.g., Ryanodine receptors [RyRs]) in the sarcoplasmic reticulum (Yang et al., 2002, Lakatta et al., 2010). Channel phosphorylation by cellular enzymes, such as protein kinase A and Ca²⁺/calmodulin-dependent protein kinase II (CaMKII), affects channel kinetics and sensitivity. The stochastic nature of these biochemical reactions and of channel opening events makes the spontaneous beating of a single cardiac cell stochastic as well (Heijman et al., 2013), with intrinsic noise manifested as variability in the time between consecutive contractions (beat-to-beat variability). Isolated spontaneously beating cardiac cells have large beat-to-beat variability that must be reduced to allow for synchronized contraction.

We have previously shown that spontaneously beating cardiac cells can be paced using a ‘mechanical cell’, which consists of a tungsten probe that mimics the deformations generated by a neighboring beating cardiac cell (Nitsan et al., 2016). There was no physical contact between the cell and the probe, and the interaction therefore was purely mechanical and mediated through propagation of deformations in the underlying substrate. However, the mechanical cell generated deterministic oscillatory deformations and cardiac cell beating is stochastic. The stochastic nature of cardiac cell beating raises several questions such as: Is beating stochasticity regulated by mechanical coupling? Can a stochastically beating cell mechanically pace its neighbor and reduce its intrinsic noise?

Here, we directly measure mechanical interaction between isolated pairs of cardiac cells cultured on a flexible substrate that enables mechanical coupling through propagation of mechanical deformations in the substrate, with no physical contact between the cells. We find that beat-to-beat variability decreases exponentially with coupling strength. To corroborate that decreased beating variability is indeed a direct consequence of mechanical coupling, we reproduce the exponential decay in an assay in which a beating cell interacts mechanically with a ‘mechanical cell’. By turning the probe into a stochastic ‘mechanical cell’, the exponential decay constant converged to that obtained for pairs of mechanically coupled living cardiac cells.

Mechanical communication cannot be regarded as a simple displacement but as a signaling cue that transmits information through a cascade of biochemical reactions. Recent theoretical work demonstrated that a signaling network can function as a filter that suppresses noise (Hinczewski and Thirumalai, 2014). We show that the propagation of the mechanical signal through the cellular signaling network does exactly that. We use a stochastic ‘mechanical cell’ to pace an isolated beating cell and reduce its beat-to-beat variability. Beating variability is reduced below the noise of the stochastic ‘mechanical cell’, and both pacing and noise reduction persist after stimulation stops, consistent with long-term modifications that occur within the cardiac cell that affect its intrinsic stochasticity. By quantitatively measuring the reduction of noise with mechanical coupling strength in the presence of different inhibitors, we could identify microtubule integrity, NOX2 (nicotinamide adenine dinucleotide phosphate-oxidase 2), and CaMKII as mediators of mechano-chemo-transduction in this case.

Results

Mechanical Coupling between Cells Reduces Beat-to-Beat Variability

Primary neonatal rat cardiac cells were cultured on either matrigel-coated or laminin-coated polyacrylamide gels with an elastic modulus of 3.8 ± 0.2 kPa as measured by atomic force microscopy. Substrate stiffness in this range was shown to support optimal spontaneous cardiac cell beating for neonatal cardiac cells in culture (Engler et al., 2008, Nitsan et al., 2016, Majkut et al., 2013). Part of the experiments were repeated with a slightly softer gel (1 ± 0.15 kPa). By incorporating 0.2-μm fluorescent beads in the polyacrylamide substrate and tracking their movement over time, we could quantify the deformation field generated by a beating cardiac cell and extract its beating signal (see Videos S1 and S2 and Figure S2). As demonstrated previously, a pair of aligned beating cells, with no physical contact between them, which reside at a distance that allows their deformation fields to overlap, synchronize their spontaneous average beating frequency (Nitsan et al., 2016). However, although the pair is synchronized in their average frequency, they go in and out of phase as a result of their beat-to-beat variability (see, for example, Figure 1 and Video S1). To study the dependence of beat-to-beat variability on the strength of mechanical coupling, we cultured cells on patterned substrates (Transparent Methods and Figure 2A). Using the patterned substrate, the dimensions of the cardiac cells and the distance between neighboring cells and their relative orientation were controlled.

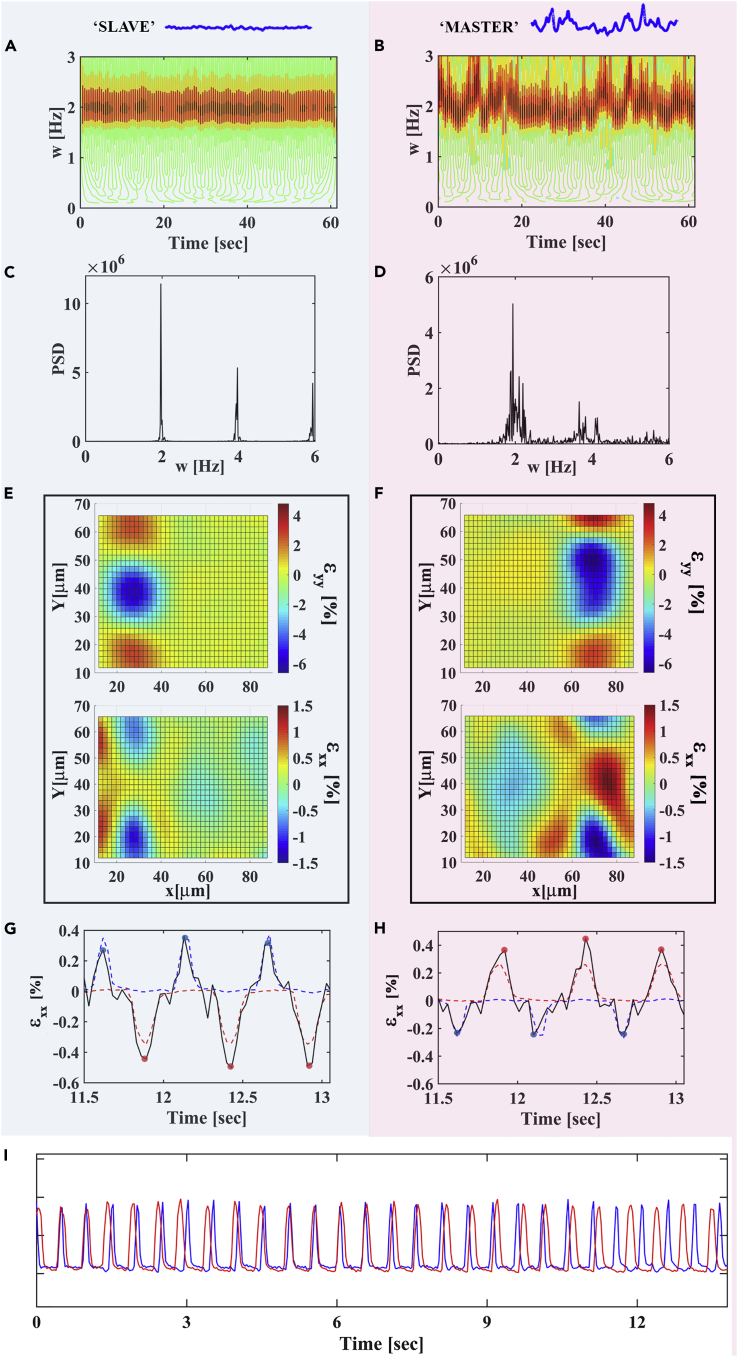
Figure 1.

Mechanical Coupling Reduces Beating Variability

A representative pair of spontaneously beating cardiac cells 20 μm apart on a flexible substrate. The average frequency is synchronized; however, the right cell is highly stochastic and weakly coupled to the left cell, while the left cell, which is strongly coupled mechanically to the right cell, beats steadily with low variability. This suggests that the left cell (‘slave’) follows the average beating frequency of the right cell (‘master’), whereas its beat-to-beat variability is reduced as a consequence of the strong coupling to the right cell. The left panel (A, C, E, and G) corresponds to the left cell, whereas the right panel (B, D, F, and H) describes the behavior of the right cell. (A) and (B) show the transient frequency vs. time calculated using wavelet analysis; (C) and (D) are the corresponding Fourier transforms (power spectral density [PSD]). (E) and (F) are the strain field generated by the beating cells along the contraction axis (y axis, top) and along the vector connecting to two cells (x axis, bottom). The strain field is shown for a time point where the neighboring cell is relaxed. (G and H), The black curve shows the average strain at the edge of the beating cell along the x axis. The blue and red curves are the normalized beating signals of the left and right cells, respectively, for a short time period where the cells beat in anti-phase (part of the signal shown in I) and are only shown to mark the time position of cell contraction. When the cells beat in anti-phase, we can differentiate between the strain generated by the cell itself and by its neighbor. The strain peaks marked with red dots result from contractions of the right cell, whereas the strain peaks marked with blue dots result from contractions of the left cell. Mechanical coupling for the left cell is calculated as χ_L = |ɛ_xx,R(x = L)/ɛ_xx,L(x = L)|, i.e., by dividing the average strain values generated by the right cell at the edge of the left cell (red dots) by the average strain generated by the left cell next to its edge (blue dots). (I), The blue and red curves are the normalized beating signals of the left and right cells, respectively, for a short time period. Videos showing the fluorescent beads in the underlying substrate (where contractions are apparent) and the calculated strain maps for this time period can be found in the Supplemental Information (Videos S1 and S2).

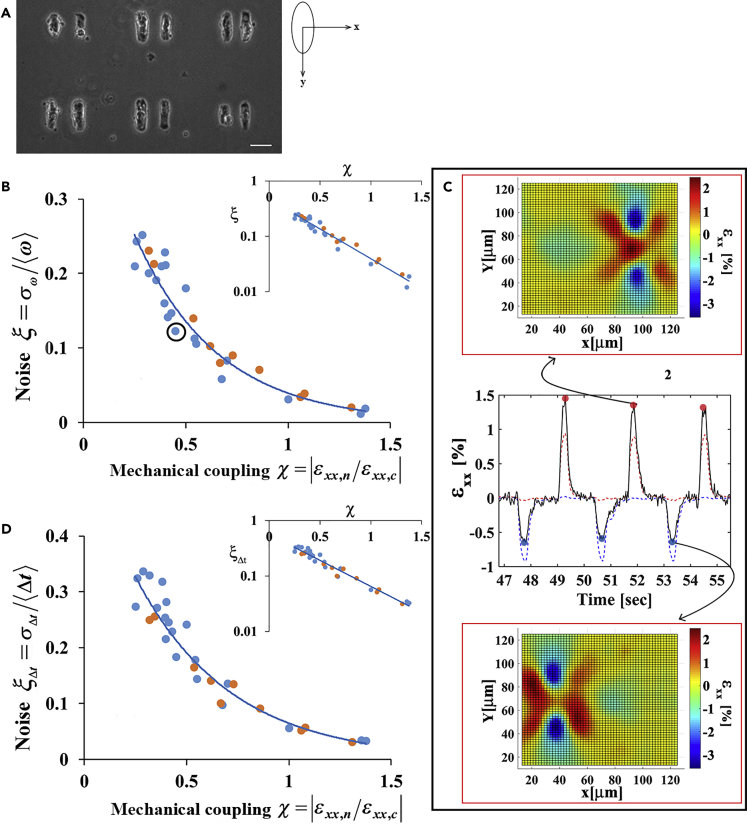
Figure 2.

Noise Is Reduced Exponentially with Mechanical Coupling

(A) A representative image of isolated pairs of cardiac cells on a pattern. Notice that there is no physical contact between the cells. Scale bar is: 50 μm. We use an axis system whereby the cells are aligned along the y axis. Using this coordination system, the contraction axis of the cell (the long axis) is the y axis and the x axis is the direction of the vector connecting the two cells. A beating cardiac cell generates deformations on a flexible substrate in the x-direction, in addition to the ones in the y-direction owing to the Poisson's effect.

(B and D) Beating noise decays exponentially with the strength of mechanical coupling to a neighboring cell. Beating noise, defined as the relative SD of the beating frequency (B) or as the relative SD of the time between consecutive beatings (D), is plotted as a function of mechanical coupling. The insets in (B) and (D) show the noise in a logarithmic scale. The decay constant in (B) and (D) is 2.43 ± 0.19 and 2.2 ± 0.14, respectively. SDs were calculated using the bootstrap method. The predictive power of the model was assessed using leave-one-out cross-validation. For both (B) and (D): the blue and orange circles represent cells that were cultured on 4 kPa and 1 kPa substrates, respectively. n = 30 cells are shown from 8 different cultures and 16 different dishes. R² values for A and B are reported in Table S1 in the Supplemental Information.

(C) Demonstration of the calculation of mechanical coupling for a representative pair of beating cardiac cells (the point marked in [B], for additional details see Figure S2). In short, the black curve shows the average strain at the edge of the beating cell in the x-direction. The blue and red curves are the normalized beating signals of the left and right cells, respectively, for a short time period in which the cells beat in anti-phase and are only shown to mark the time position of cell contraction. The strain peaks marked with red dots result from contractions of the right cell, whereas the strain peaks marked with blue dots result from contractions of the left cell. Therefore, mechanical coupling for the right cell is calculated as χ_R = |ɛ_xx,L(x = R)/ɛ_xx,R(x = R)|, i.e., by dividing the average strain values generated by the left cell at the edge of the right cell (blue dots) by the average strain generated by the right cell next to its edge (red dots). Since the strain generated by the right cell next to its edge is positive, whereas the strain generated by its neighbor is negative, we use the absolute value of this ratio. Strain maps at two time points are shown.

Video S1. Bead Displacements Generated by Beating of a Pair of Mechanically Coupled Cardiac Cells, Related to Figure 1

Time lapse imaging of the deformation field generated by a pair of beating cardiac cell on a flexible substrate. Mechanical deformations are detected by following movements of 0.2-μm fluorescent beads embedded within the gel. The corresponding strain maps are shown in Video S2. The beating noise and mechanical coupling analysis are shown in Figure 1 in the main text. The Video is played in real time. Scale bar is 10 μm.

Video S2: Strain Field Generated by Beating of a Pair of Mechanically Coupled Cardiac Cells, Related to Figure 1

Strain map along the y axis (ɛ_yy) for a pair of spontaneously beating cardiac cells cultured on a flexible substrate, 20 μm apart. The strain was calculated using the time lapse imaging of the fluorescent beads shown in Video S1. The beating noise and mechanical coupling analysis are shown in Figure 1 in the main text. For clarity, the Video is played 3-fold slower than real time. Time is shown in the green time stamp at the right corner of the video.

Spontaneously beating cardiac cells vary in their contractile amplitude, and generally, cells within a pair beat with different contraction amplitudes. In the extreme case, one of the cells contracts with an amplitude large enough to induce significant strain next to its neighbor, whereas its neighbor generates deformations that are much smaller and do not propagate all the way to the first cell. We regard this case as a ‘master’/‘slave’ behavior since only one of the cells generates strain field large enough to influence its neighbor. Surprisingly, in cases that are close to this scenario, the ‘master’ appears to contract with high beat-to-beat variability, whereas the ‘slave’ beats steadily with extremely low beat-to-beat variability (Figure 1 and Videos S1 and S2). Although it seems counter intuitive at first, the high variability of the ‘master’ cell is consistent with the high beat-to-beat variability of an isolated spontaneous beating cardiac cell in culture (Figure S1). This suggests that the slave follows the average beating frequency of the ‘master’ (Figures 1A and 1B), whereas its beat-to-beat variability is reduced as a consequence of the strong coupling to its neighbor (Figure 1). The ‘master’, on the other hand, can barely detect the strain generated by its neighbor and can therefore be thought of as a nearly isolated beating cardiac cell in culture.

This master/slave phenomenon is a limiting behavior, and in most pairs of cells, there are no clear master and slave. Nevertheless, within all pairs of cardiac cells observed (n = 30, see Figure 2), the cell that senses the deformations generated by its neighbor the most has lower beat-to-beat variability, whereas its neighbor beats more stochastically.

Noise Is Reduced Exponentially with Mechanical Coupling to a Neighboring Cell

To systematically explore the phenomenon described earlier and study the quantitative dependence of beat-to-beat variability on the strength of mechanical coupling, we define a mechanical coupling parameter that describes the level of mechanical coupling between a cardiac cell and its neighbor. Cells sense the deformation field at their edge, which is the sum of the deformations they generate and the ones generated by neighboring beating cells. The neighboring cell is expected to have a significant influence when its deformations are on the same order of magnitude or higher, as the ones generated by the cell itself. We therefore define mechanical coupling as the ratio between the deformations generated by a neighboring cell at the cell edge and those generated by the cell itself. This ratio defines how strong the perturbation generated by the neighboring cell is. More formally, we define a mechanical coupling parameter χ, such that χ = |ɛ_xx,n/ɛ_xx,c|, where ɛ_xx,n is the strain generated by the neighboring cell along the vector connecting the two cells (x axis) and ɛ_xx,c is the strain generated by the cell itself (Figures 1G, 1H, S2, and S3).

The beating noise (beat-to-beat variability) ξ was calculated as the relative standard deviation (SD) of the beating frequency, ξ = σ_ω/<ω>, where <ω>is the average beating frequency of the cell and σ_ω is the SD. An alternative definition that gave very similar results is the relative SD of the time between consecutive contractions, ξ_Δt = σ_Δt/<Δt>. Typical beating profiles and beating noise values for spontaneous beating cardiac cells in culture are shown in Figure S1.

As shown in Figure 2B, the beating noise (ξ) decays exponentially with the strength of mechanical coupling (χ) according to ξ = ae^−kχ, where k is the exponential decay constant. The inverse value of the decay constant is the value of mechanical coupling required for the noise to decay by a factor of 1/e. As such, when the decay constant is larger, the effect of mechanical communication on noise is stronger, the exponent decays faster, and a lower value of mechanical coupling is required to achieve noise reduction. The decay constant of the beating noise with the strength of mechanical coupling to a beating neighboring cell is 2.43 ± 0.19 (Figure 2B) (n = 30 cells). The same result holds when the noise is estimated using ξ_Δt with a decay constant of 2.2 ± 0.14 (n = 30 cells, Figure 2D). Mechanical coupling is determined by the deformations generated by the neighboring cells (Figure 2C). These deformations are a function of substrate stiffness, the distance between cells and beating amplitude. Since we directly measure the strain field and use it to calculate the strength of mechanical coupling, we can combine data from cells within different distances, cultured on different substrate rigidities and coatings (Figures 2 and S4). Spontaneously beating cardiac cells in culture differ in their beat-to-beat variability (Figure S1) and might in principle have different sensitivities to mechanical coupling. It is therefore not trivial that cells that belong to different pairs still fall on the same exponential curve. This result indicates that noise reduction by mechanical coupling is highly robust.

Noise Is Reduced Exponentially with Mechanical Coupling to a ‘Mechanical Cell’

To ensure that the reduction of noise is indeed a direct consequence of mechanical coupling and does not result from indirect effects, such as a change in the amount or type of secreted chemo-attractants, we used a ‘mechanical cell’ (also referred to as a mechanical probe) as previously described (Nitsan et al., 2016). In short, we replaced one of the cells with a mechanical device that consists of a tungsten probe mounted on a piezo-stage. The mechanical probe deforms the substrate such as to mimic the mechanical deformations generated by a beating cardiac cell. There is no physical contact between the cell and the probe, and the interaction therefore is solely mechanical and mediated through propagation of deformations in the underlying substrate. Figure 3A illustrates schematically the experimental setup. The mechanical interaction with the ‘mechanical cell’ was quantified in the same way it was done for two neighboring beating cells, i.e., by calculating the ratio between the strain generated at the cell edge by the probe and the strain generated by the cell itself (Figure 3B). Probe frequency was set equal to the average frequency of the beating cardiac cell to separate the effect of pacing a cardiac cell from that of noise reduction. By gradually increasing the amplitude of probe oscillations, the beating noise of the cardiac cell could be monitored as a function of the strength of mechanical interaction with the probe for the same cell. We let the cell interact with the probe for 10 minutes before recording the signal and changing the amplitude. This was done to allow the cell to reach stationary behavior. For each cell, beat-to-beat variability was found to decay exponentially with the strength of mechanical coupling (Figure 3C). Although filtering noise may affect the mean of the original signal (Rackauckas et al., 2018), the frequency of the cell and its beating amplitude did not change for different values of mechanical coupling; only the noise was reduced (Figure S5).

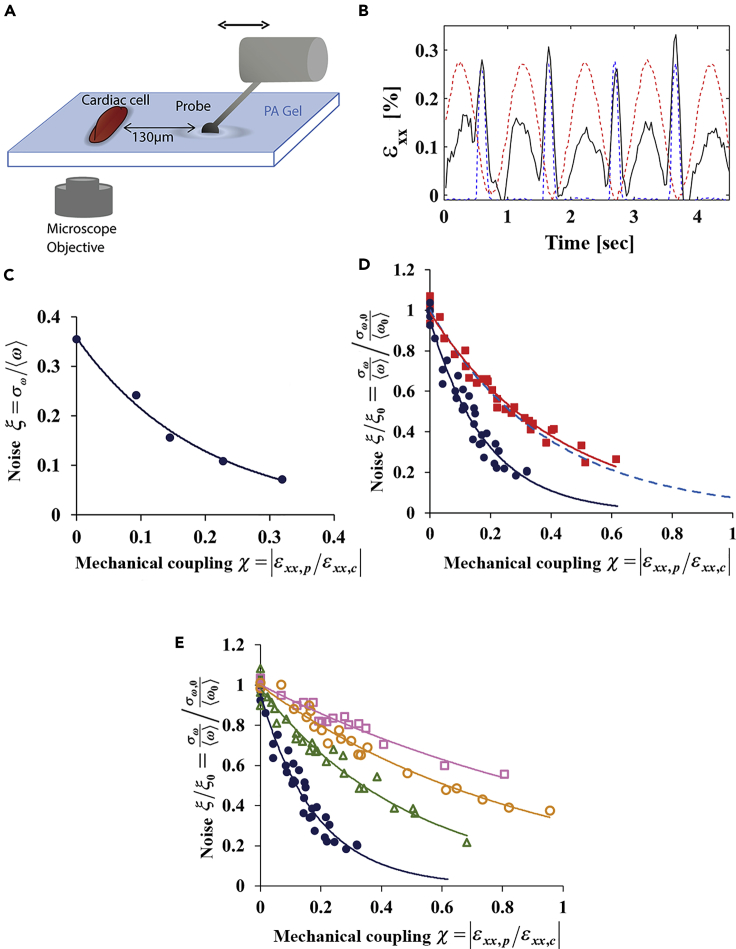
Figure 3.

Noise Is Reduced Exponentially with Increased Mechanical Coupling to a ‘Mechanical Cell’

(A) A schematic representation of the ‘mechanical cell’ setup. A tungsten probe applies an oscillatory stretch that mimics the deformations generated by a beating cardiac cell.

(B) The deformations at the edge of the cell in the direction perpendicular to the contraction axis (black curve) are generated by both the cardiac cell and the mechanical probe. The probe oscillation signal is represented by the dashed red curve, and the cell beating signal is shown in the dashed blue curve. The mechanical coupling is defined as the ratio between the strain generated by the probe at the edge of the cell and the strain generated by the cell itself, χ = |ɛ_xx,p/ɛ_xx,c|.

(C) The dependence of beating variability on the strength of mechanical interaction with a mechanical probe for a representative isolated beating cardiac cell.

(D) The dependence of beating variability, normalized to the beat-to-beat variability before probe activation, on the mechanical interaction with a deterministic mechanical probe (, blue filled circles) or with a stochastic mechanical probe (, red filled squares). The decay constant for the deterministic and stochastic probe are 5.5 ± 0.23 and 2.4 ± 0.11, respectively. The blue dashed line represents the exponential fit for the decay of beating noise with mechanical coupling within pairs of aligned cardiac cells as shown in Figure 3B. For each cell, the probe amplitude was gradually increased and beating noise was monitored as a function of the strength of mechanical interaction. For each cell, we get an exponential decay similar to the curve shown in (C). After normalization of the beat-to-beat variability, ξ, by the beating variability of the isolated cell without mechanical interaction, ξ₀ (before probe activation), all the exponential decays converge to the same exponent. Probe frequency was equal to the average frequency of the beating cardiac cell to separate the effect of pacing a cardiac cell from that of noise reduction. The experiment with the deterministic and stochastic probes was repeated for n = 11 and n = 6 isolated beating cardiac cells, respectively.

(E) The dependence of beating variability, normalized to the beat-to-beat variability before probe activation, on the mechanical interaction with a deterministic mechanical probe with no drug (, blue filled circles, decay constant: 5.5 ± 0.23, n = 11), for cells treated with 10 μM Colchicine (, green empty triangles, decay constant: 2.0 ± 0.1, n = 5), 5 μM gp91-a NOX-2-specific inhibitor (, orange empty circles, decay constant: 1.14 ± 0.05, n = 4), 10 μM Autocamtide2-related inhibitory peptide (AIP), or CaMKII inhibitor (, pink empty squares, decay constant: 0.77 ± 0.05, n = 4). R² values for C–E are reported in Table S1 in the Supplemental Information. SDs were calculated using the bootstrap method.

The exponential decays obtained for different cells all converged to the same exponential curve after normalizing with respect to the beating variability of the isolated cell before probe activation (with a decay constant of 5.5 ± 0.23, Figure 3D). This is consistent with the behavior observed for pairs of mechanically coupled cardiac cells. Again, these results demonstrate the robustness of the phenomenon of noise reduction through mechanical coupling.

Pacing and Noise Reduction of a Cardiac Cell Using a Stochastic ‘Mechanical Cell’

Interestingly, beating noise decays more rapidly with mechanical coupling when a cell interacts with a ‘mechanical cell’ compared with the decay obtained for an interaction with a living cardiac cell (Figure 3D, p < 0.0004 using linear mixed effects model with random slope). A clear difference between these assays is that the mechanical probe is deterministic, whereas the living cell is stochastic. To explore the influence of the stochastic nature of spontaneous beating on mechanical communication, we turned our mechanical probe into a stochastic mechanical cell. We did so by generating frequencies of oscillations from a Gaussian distribution with a SD comparable to the beating variability observed in isolated beating cardiac cells (Figures S1 and 4A).

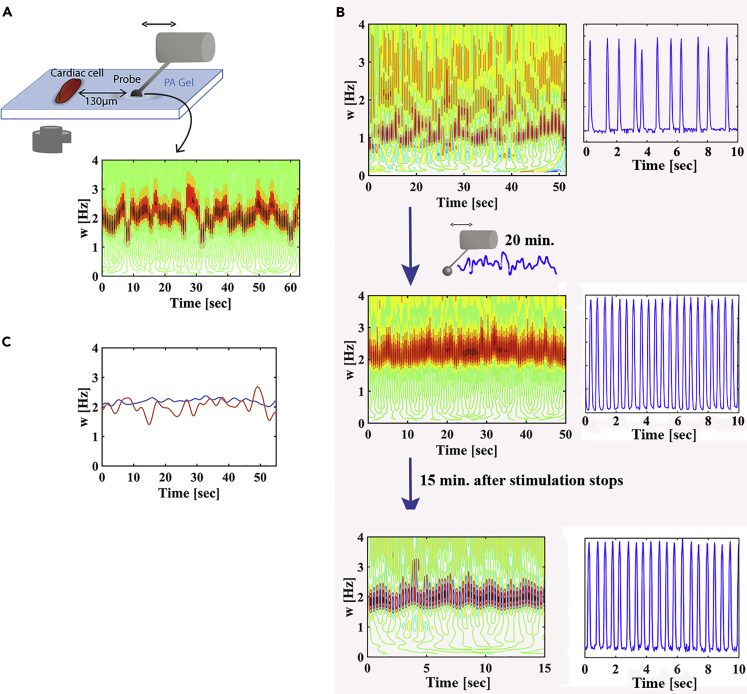
Figure 4.

Pacing and Noise Reduction of an Isolated Spontaneously Beating Cardiac Cell Using a Stochastic ‘Mechanical Cell’

(A) The signal generated by a stochastic ‘mechanical cell’ as extracted from a wavelet analysis. Probe frequencies were generated from a Gaussian distribution with an average of 2 Hz and an SD of 0.25 Hz. The mechanical coupling with the probe in this experiment was χ = 0.305. This experiment was repeated for n = 4 cells.

(B) Frequency as a function of time (left) and normalized beating signal over time (right), before mechanical stimulation (top), after 30 min of mechanical interaction with a stochastic mechanical probe (middle), and 15 min after stimulation stops (bottom). The cell initially beats at 1 Hz with a beat-to-beat variability of ξ = 0.4; after mechanical stimulation with a stochastic probe, the cell is paced to 2 Hz with a beat-to-beat variability of ξ = 0.05, lower than that of the mastering probe. These values persist after stimulation stops.

(C) The frequency of the probe (red) and of the cardiac cell (blue) in a short time window of ∼1 min after 30 min of training.

We monitored beating noise as a function of the strength of mechanical interaction with the stochastic probe while gradually increasing the probe average amplitude. Here again, the exponential decays obtained for different cells all converged to the same exponential curve after normalizing with respect to the beating variability of the isolated cell before probe activation (with a decay constant of 2.4 ± 0.11, Figure 3D). However, now, taking the cardiac cell beating stochasticity into account, it is converged to the exponential decay obtained for pairs of mechanically coupled living cardiac cells (Figure 3D).

At the beginning of the paper, we presented a master/slave behavior whereby a cell that strongly coupled mechanically to its neighbor (‘slave’) has low beat-to-beat variability as a consequence of the strong coupling and is following the average beating frequency of a highly stochastic cell (‘master’) that can barely detect its neighbor. This phenomenon raises intriguing questions. Can the steady state observed in Figure 1 be a consequence of a ‘noisy’ cell reducing the variability of a neighboring cell below its own variability? And can the ‘slave’ indeed be paced by the average frequency of a highly stochastic ‘master’? Using a stochastic ‘mechanical cell’, we can reproduce the master-slave scenario in a setup where the master identity is well defined. The ‘mechanical cell’ cannot change as a result of interaction and therefore acts as a highly stochastic master. As clearly shown in Figure 4, using the stochastic probe we were able to pace an isolated beating cardiac cell to the average oscillation frequency of the probe as well as reduce its noise below that of the probe. Moreover, after mechanical stimulation stops, the new probe-induced beating frequency and the reduced noise level persist.

The observation that the reduction in noise persists after stimulation stops suggests that the forces involved in mechanical communication induce changes in the biochemical network kinetics that governs spontaneous beating in cardiac cells. It is supported further by the fact that the noise is reduced below the noise of the master probe.

Microtubule Integrity, CaMKII, and NOX-2 Are Involved in Mechanical Coupling-Induced Noise Reduction

The relatively long time (∼10 minutes) required for noise reduction (Figure S6) and the observations that the reduction in noise persists after stimulation stops (Figures 4 and S6) and that noise is reduced below the noise of a master probe (Figure 4C) suggest that the forces involved in mechanical communication induce long-term alterations in cardiac cell spontaneous beating. Recently, it was shown that mechanical stretch triggers the production of reactive oxygen species that target Ca²⁺ signaling proteins (Prosser and Ward, 2014). This pathway was shown to often involve signaling through microtubule-dependent NADPH oxidase 2 (NOX2) and CaMKII that regulate RyR2 kinetics (Prosser and Ward, 2014, Prosser et al., 2011, Iribe et al., 2009, Jian et al., 2014 and Figure S7). To test whether this mechanotransduction pathway is involved in noise reduction, we repeated the probe assay in the presence of inhibitors for key proteins in this pathway. We again monitored beating noise as a function of the strength of mechanical interaction with the probe while gradually increasing the probe average amplitude. As shown in Figure 3E, treatment with either Colchicine, a microtubule polymerization inhibitor, or gp91ds-tat, a specific NOX-2 peptide inhibitor, interferes with beating noise reduction by mechanical coupling and reduces the decay constant from 5.5 ± 0.23 to 2.0 ± 0.1 or 1.14 ± 0.05, respectively. The largest effect occurred with Autocamtide2-related inhibitory peptide (AIP), a CaMKII-specific inhibitor, which almost eliminated the reduction in beating noise (decay constant of 0.77 ± 0.05, Figure 3E).

Discussion

Here we show that mechanical communication reduces beat-to-beat variability. We directly measure mechanical coupling and show that the noise is reduced exponentially with the strength of mechanical coupling. We demonstrate this both in pairs of mechanically coupled beating cardiac cells and in a system in which an isolated beating cardiac cell interacts mechanically with an artificial ‘mechanical cell’. The significance of this phenomenon is clearly emphasized by the cardiac cell pair presented at the beginning of the paper. These cells are synchronized at their average beating frequency; however, since one of the cells is highly stochastic they go in and out of phase. This demonstrates that noise reduction is essential to achieve synchronized phase of beating. In this paper, we studied noise reduction in spontaneously beating cells in culture. Most cells in the heart do not beat spontaneously but are paced by an electrical signal generated by pacemaker cells. However, pacemaker cells themselves beat spontaneously. Pacemaker cell beating variability is determined by the stochasticity of the biochemical network that underlies spontaneous beating (Yaniv et al., 2014). Mechanical communication may therefore be involved in the regulation of beat-to-beat variability in spontaneously beating pacemaker cells in the sinoatrial (SA) node and in synchronized pacemaker activity. In addition, mechanical communication may play a significant role in synchronized contractions during the development of the heart in early stages where electrical conduction is not fully functional (Chiou et al., 2016).

Our results indicate that the mechanism behind mechanical communication-induced noise reduction in our system requires enzymatic activity (NOX2 and CaMKII) in a pathway that was shown to regulate RyR2 kinetics (Prosser et al., 2011). To provide a possible explanation for the necessity of CaMKII activity for the reduction in noise, we would like next to discuss how changes to enzymatic activity could lead to reduced noise levels. We showed that inhibiting CaMKII interferes with noise reduction by mechanical communication. In a linear pathway (such as the one shown in Figure S7 and discussed in the literature for cardiac cell mechanosensing, which is consistent with our data), it means that CaMKII is activated by the mechanical signal (i.e., its activity is increased). For this reason, in our possible explanation we will consider how increased enzymatic activity can regulate noise in a biochemical network.

To do so, it is instructive to begin with a ‘thought experiment’. Consider a reversible reaction between two states, for example, the phosphorylated and dephosphorylated states of RyR. For simplicity, let us first think about this reaction as a simple isomerization reaction, i.e., $RyR\underset{k_{off}}{\overset{k_{on}}{\rightleftarrows }}Ry{R}_P$, where k_on and k_off are the rate constants for phosphorylation/dephosphorylation and will therefore depend on the concentration of kinase/phosphatase, respectively. Increased activity of both the kinase and phosphatase will multiply k_on and k_off by an identical factor. Therefore, in this case, at equilibrium the fraction of phosphorylated RyR will be the same. However, when the activity of the kinase and phosphatase is higher, the transition between the two states will be faster. Suppose now that we measure the average fraction of phosphorylated channels in ‘sampling windows’ of size Δt. The width of the distribution of measured average fraction values is the effective noise in the system (Figure S8C). If the kinetics is faster than Δt, during this time interval, the channel will go back and forth between phosphorylated and dephosphorylated states, essentially sampling the full equilibrium distribution within each ‘sampling window’. In this case, the average fraction measured in every sampling window is nearly identical (Figures S8B and S8C). Faster kinetics, therefore, reduces system noise as measured by the average fraction of RyR_P at discrete sampling windows. The frequency of calcium oscillations is determined by the kinetics of RyR channels, which depends on their phosphorylation state. The cell essentially “samples” the RyR_P distribution, and therefore, faster kinetics, which leads to low variability in the fraction of phosphorylated channels, will reduce the beat-to-beat variability. To demonstrate that noise reduction by increased enzyme activity (e.g., CaMKII) may occur through cardiac cells ‘sampling’ of phosphorylated RyR channel distribution, we conducted a stochastic kinetic simulation of a cardiac cell. Full details can be found in the Supplemental Information (Data S1 and Figure S9). It is important to note that this idea of how modulating enzymatic activity can regulate noise is not limited to cardiac cells. Indeed, the regulation of enzymatic activity can regulate noise in any biochemical network.

We show here directly that mechanical coupling regulates intrinsic noise in cardiac cell beating and that noise reduction by mechanical coupling is sensitive to the stochastic nature of the master cell. It is very likely that our observations extend beyond this specific biological system and that mechanical coupling also regulates intrinsic noise in other cellular systems in which mechanical communication is of importance.

Limitation of the Study

In the simulation presented in the discussion, we do not address mechanical coupling between cells. Mechanical communication is only taken into account as an increased activity of a RyR kinase (e.g., CaMKII). We use the model to discuss possible explanation for how increased enzymatic activity can regulate noise in a biochemical network. Further work is required to elucidate the detailed mechanism underlying mechanical communication-mediated noise reduction.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: April 26, 2019

Data and Software Availability

The accession number for the raw data reported in this paper is https://doi.org/10.17632/djrdcbdrn8.1.