Abstract
Key points
It is known that interception of targets accelerated by gravity involves internal models coupled with visual signals.
Non‐visual signals related to head and body orientation relative to gravity may also contribute, although their role is poorly understood.
In a novel experiment, we asked pitched observers to hit a virtual target approaching with an acceleration that was either coherent or incoherent with their pitch‐tilt.
Initially, the timing errors were large and independent of the coherence between target acceleration and observer's pitch. With practice, however, the timing errors became substantially smaller in the coherent conditions.
The results show that information about head and body orientation can contribute to modelling the effects of gravity on a moving target. Orientation cues from vestibular and somatosensory signals might be integrated with visual signals in the vestibular cortex, where the internal model of gravity is assumed to be encoded.
Abstract
Interception of moving targets relies on visual signals and internal models. Less is known about the additional contribution of non‐visual cues about head and body orientation relative to gravity. We took advantage of Galileo's law of motion along an incline to demonstrate the effects of vestibular and somatosensory cues about head and body orientation on interception timing. Participants were asked to hit a ball rolling in a gutter towards the eyes, resulting in image expansion. The scene was presented in a head‐mounted display, without any visual information about gravity direction. In separate blocks of trials participants were pitched backwards by 20° or 60°, whereas ball acceleration was randomized across trials so as to be compatible with rolling down a slope of 20° or 60°. Initially, the timing errors were large, independently of the coherence between ball acceleration and pitch angle, consistent with responses based exclusively on visual information because visual stimuli were identical at both tilts. At the end of the experiment, however, the timing errors were systematically smaller in the coherent conditions than the incoherent ones. Moreover, the responses were significantly (P = 0.007) earlier when participants were pitched by 60° than when they were pitched by 20°. Therefore, practice with the task led to incorporation of information about head and body orientation relative to gravity for response timing. Instead, posture did not affect response timing in a control experiment in which participants hit a static target in synchrony with the last of a predictable series of stationary audiovisual stimuli.
Keywords: internal model, visual motion, inclined plane, pitch, vestibular
Key points
It is known that interception of targets accelerated by gravity involves internal models coupled with visual signals.
Non‐visual signals related to head and body orientation relative to gravity may also contribute, although their role is poorly understood.
In a novel experiment, we asked pitched observers to hit a virtual target approaching with an acceleration that was either coherent or incoherent with their pitch‐tilt.
Initially, the timing errors were large and independent of the coherence between target acceleration and observer's pitch. With practice, however, the timing errors became substantially smaller in the coherent conditions.
The results show that information about head and body orientation can contribute to modelling the effects of gravity on a moving target. Orientation cues from vestibular and somatosensory signals might be integrated with visual signals in the vestibular cortex, where the internal model of gravity is assumed to be encoded.
Introduction
There is abundant evidence indicating that people can deal with complex dynamic environments even with sparse sensory information (Battaglia et al. 2013; Hamrick et al. 2016; Lacquaniti and Maioli 1989; Sanborn et al. 2013; La Scaleia et al. 2015). This indicates that successful interactions with objects in our daily routine imply an underlying model of the physical properties and forces involved, a model that can surrogate missing or ambiguous sensory information (Wolpert & Kawato 1998). Internal models are used also by other animals to intercept a moving target, such as monkeys (Streng et al. 2018), cats (Cerminara et al. 2009) and dragonflies (Mischiati et al. 2015). However, we still have an incomplete understanding of how critical elements of these internal models, such as the reference frame used to decode the effects of environmental forces, are constructed for each given task.
Gravity, as a ubiquitous force, must be a constituent part of the physical model of the environment. An internal model of gravity is required because no single sensor can distinguish between gravitational and inertial accelerations according to Einstein's equivalence principle. Indeed, an internal model of gravity has been shown to contribute to interceptions of falling targets (Lacquaniti et al. 1993; Tresilian 1997; McIntyre et al. 2001; Zago et al. 2004; Indovina et al. 2005; La Scaleia et al. 2015; Jörges and López‐Moliner 2017; Russo et al. 2017; Zago et al. 2011), optimal control of reaching movements (Gaveau et al. 2016), perceived duration of gravitational motion (Moscatelli & Lacquaniti 2011), time‐to‐passage estimates during visual self‐motion (Indovina et al. 2013), naturalness judgments of motion under gravity (La Scaleia et al. 2014b; Ceccarelli et al. 2018), interpretation of biological motion (Troje & Chang 2013; Maffei et al. 2015) and perception of the visual vertical (Van Pelt et al. 2005; De Vrijer et al. 2008).
These and other studies showed that internal estimates of both the magnitude and the direction of gravity are available for perception and action (Zago 2018). During dynamic head tilts, gravito‐inertial accelerations signalled by the otoliths (Fernandez & Goldberg, 1976) can be disambiguated by filtering the otolith signals (Mayne 1974) and/or combining them with the signals of the semicircular canals (Angelaki et al., 1999; Glasauer, 1992; Merfeld et al. 1999). As a result, even with eyes closed, generally, we do not confuse a backward pitch with a forward acceleration of the head, and we perceive the world as stable, despite frequent movements of the eyes, head and body (Snyder 1999; Day & Fitzpatrick 2005).
When the task requires aligning a visual line to the vertical in the dark, the so‐called subjective visual vertical (SVV) (Lacquaniti et al. 2015; Kheradmand & Winnick 2017), the direction of gravity is estimated by combining retinal cues about the line orientation with vestibular and somatosensory cues about head and body orientation, plus the prior assumption of an upright head orientation (Mittelstaedt 1983; Dyde et al. 2006; MacNeilage et al. 2007; De Vrijer et al. 2008).
Gravitational acceleration of objects is experienced by vision, although the visual system is poorly sensitive to image acceleration (Calderone & Kaiser, 1989; Werkhoven et al. 1992; Brouwer et al. 2002). Thus, it has been proposed that the visual effects of gravity on a moving target are interpreted by combining information about the rate of change of retinal image with binocular (stereo, vergence) and monocular (familiar size, vertical and horizontal scene contours, perspective, shading, texture gradient, lighting) cues allowing to map from the retinal to the environment frame, plus the prior assumption of Earth gravity (Zago et al. 2009).
For target interception, also vestibular and somatosensory cues about head and body orientation can help constructing a gravity reference, as occurs for the SVV task. Thus, a few previous studies have shown that the participant's posture relative to gravity direction contributes to providing a sense of ‘up’ and ‘down’ in the interception of targets moving along the vertical (Senot et al. 2005; Le Séac'h et al. 2010; Baurès & Hecht, 2011). In these studies, participants intercepted a ball approaching from above or below in a virtual scene presented with a head‐mounted stereoscopic display. Above (below) was obtained in sitting subjects (Senot et al. 2005) who pitched the head backward (forward) so as to look up (down) toward a virtual ceiling (floor), or in lying subjects (Le Séac'h et al. 2010; Baurès & Hecht, 2011) who looked up (down) when supine (prone). The interception responses turned out to be significantly earlier for downward than upward moving targets, consistent with a naïve expectation that downward motion is faster than upward motion under gravity (Senot et al. 2005; Le Séac'h et al. 2010; Baurès & Hecht, 2011). This expectation is naïve because it violates Newtonian mechanics, in accordance with which downward and upward displacements under gravity along a given vertical path have the same duration.
A role of vestibular inputs was shown with parabolic flight experiments, where the response bias reversed sign between the above and below conditions in parallel with the sign reversal of otolith signals at the transition from the hypergravity to the hypogravity phase of flight (Senot et al. 2012). Also, artificial sound‐evoked stimulation of the otolith receptors interferes with the anticipation of gravity effects during visually simulated self‐motion in the downward direction (Indovina et al. 2015) and unloading of the otoliths in the weightless conditions of space flight affects up/down asymmetries in the perception of self‐motion (de Saedeleer et al. 2013).
These previous studies demonstrated a qualitative contribution of vestibular cues about posture toward establishing a sense of up and down in the interception of targets moving along the vertical. As noted above, response timing complied with naïve rather than Newtonian physics. Therefore, it remains to be determined whether the effects of posture generalize to targets moving along oblique directions, and whether they can contribute to modelling the effects of gravity consistent with Newtonian physics, as occurs for SVV. A stringent test of the effects of head and body posture on interception timing is provided by taking advantage of Galileo's law of motion along an inclined plane (Fig. 1). A ball rolls down an incline with an acceleration a that depends on gravity g and slope β non‐linearly (a = 5/7g sinβ). If the visual scene is devoid of a reference frame, the estimate of the time of ball arrival at the interception point would be difficult because visual accelerations are poorly discriminated and the descent slope cannot be determined from visual cues (La Scaleia et al. 2014a, 2015; Tresilian & Lonergan 2002). However, in line of principle, the direction of target motion relative to gravity and therefore the slope could be estimated indirectly by combining retinal and gaze signals about the direction of target motion relative to the head with vestibular and somatosensory information about the orientation of the head relative to gravity. Estimates of gravity g and slope β would then allow anticipating the time of ball arrival correctly.
Figure 1. Visual stimuli and schematic view of the set‐up.
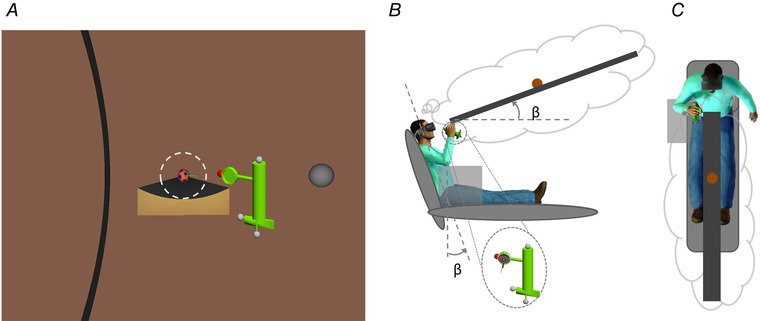
A, visual stimuli as seen by the participants. The target sphere, initially behind a lever arm, rolled forward along the gutter. Participants moved the hand‐held hitter (green) from the starting position (grey sphere) attempting to hit the sphere as soon as it arrived at the end of the gutter, so as to deviate it into a circle (arc segment shown in black). The white dashed circle (not shown in the experiments) indicates the ball at the end of the gutter. B and C, schematic lateral and top view of the set‐up. Participants’ head and torso were tilted backwards in the sagittal plane. They wore a head‐mounted display and kept the right arm on a foam box (grey) with the hand‐held hitter (green). In the bubble, the gutter is depicted at the same inclination β as that of the participant, although observers always saw the same image irrespective of their tilt. [Color figure can be viewed at wileyonlinelibrary.com]
To test this hypothesis, in the main experiments, we asked participants who were tilted backwards at different angles to hit a ball that was rolling in a gutter and approaching at different accelerations along the sightline. The scene was virtual, being presented in a head‐mounted stereoscopic display, and lacking any reference to either vertical or horizontal directions. Participants punched the ball with actual arm movements, and were provided with visual and haptic feedback about successful interceptions to increase the sense of presence in the virtual environment (Zago et al. 2004).
We used a 2 × 2 factorial design crossing ball acceleration and subject tilt (Fig. 2). The participant and the visual display were tilted backwards in the sagittal plane by 20° or 60°, whereas ball acceleration was compatible with rolling down a slope of 20° or 60°. The visual stimuli were identical at both subject tilts. Thus, for each tilt, there was one target acceleration consistent with the physical laws of a ball rolling down a surface inclined with a corresponding tilt (coherent conditions) and another acceleration inconsistent with physics (incoherent conditions). Acceleration and starting position of the ball were randomized across trials to make ball arrival time unpredictable from trial to trial, whereas the subject's tilt was blocked to provide immersiveness during the entire experimental session.
Figure 2. In a factorial design, participant's tilt (β = 20° or 60°, red and blue boxes, respectively) was crossed with ball acceleration (a = 2.397 or 6.068 m s–2, red or blue arrows respectively).
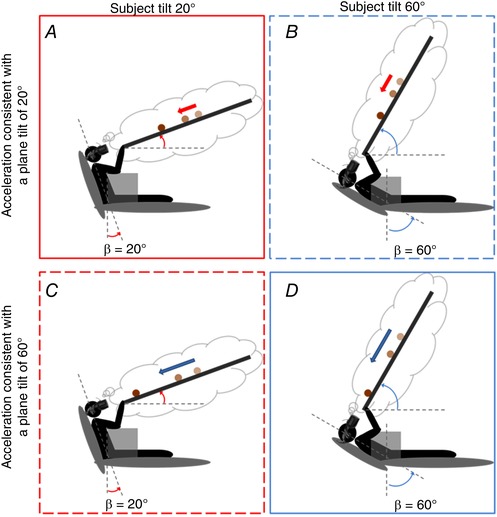
A and D (or B and C) denote conditions coherent (or incoherent) with physics. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 3 illustrates schematically the predicted timing errors (TE) of the responses. If the responses were based exclusively on visual information, they should be independent of posture (dashed lines) because the visual stimuli were the same at both subject's tilts. By contrast, if the subject tilt relative to gravity contributed to estimating the direction of target motion, it would be predicted that the responses provided by more tilted participants should be timed earlier (smaller TE values, blue continuous line) than those provided by less tilted participants (red continuous line), for a given target acceleration. This is because a ball rolling down a steeper slope typically would have a higher acceleration and should induce an observer to expect an earlier arrival time. Importantly, if subject tilt contributed quantitatively to modelling the effects of gravity on target motion, it would further be predicted that, in the coherent conditions (i.e. when ball acceleration was consistent with subject tilt), the responses should be timed more accurately (TE closer to zero) than the responses in the incoherent conditions. In the latter conditions, ball accelerations are unexpected because they are inconsistent with subject tilt, and should give rise to responses timed later when the acceleration (and final speed) is higher than the expected value (red) or to responses timed earlier when the acceleration (and final speed) is lower than the expected value (blue).
Figure 3. Theoretical TE of the interception responses at subject's tilt of 20° or 60° (red and blue, respectively).
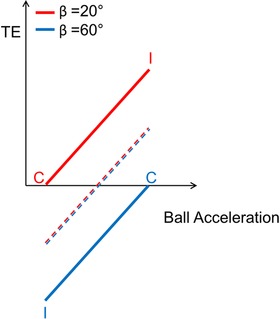
Dashed lines, TE of responses based exclusively on visual information, which was identical at both subject tilts. Continuous lines, TE of responses predicted by the hypothesis that subject tilt relative to gravity contributes to estimating the direction of target motion. When ball acceleration is coherent with subject tilt (C), TE should be closer to zero than when acceleration is incoherent with tilt (I). [Color figure can be viewed at wileyonlinelibrary.com]
A main effect of body tilt on response timing would thus be compatible with the hypothesis that head and body orientation contribute to estimating the effects of gravity on a sphere rolling along an incline. However, a main effect of body tilt might also be a result of the effects of gravity on planning and/or executing the arm movement required for interception. Indeed, previous studies showed that kinematic and dynamic features of arm movements depend on movement orientation with respect to gravity during drawing (Papaxanthis et al. 1998), pointing (Gentili et al. 2007; Pinter et al. 2012; Gaveau et al. 2016) and grasping (Verheij et al. 2013). To discriminate between the two alternatives, we ran a control experiment in which participants tilted backwards by 20° or 60° (as in the main experiments) were asked to hit a static target in synchrony with the last of a predictable series of beeps and images (Hening et al. 1988). The hypothesis that body posture affects interception timing by contributing to the estimate of target kinematics under gravity predicts that response timing should not depend on body posture in the control experiment with a static target. By contrast, the hypothesis that body posture affects interception timing because of the effects of gravity on arm movement planning and/or execution predicts that response timing should depend on body posture also in the control experiment.
Methods
Ethical approval
All participants gave written informed consent to procedures approved by the Institutional Review Board of Santa Lucia Foundation (protocol no. CE/PROG.454), in conformity with the Declaration of Helsinki regarding the use of human subjects in research.
Participants
Participants were recruited for three different sets of experiments. Interception of ball motion along a plane involved two sets of experiments: one with a between‐groups design and another one with a within‐subject design with respect to subject tilt (see Protocols). For the between‐groups protocol, 40 participants were randomly assigned to one of two groups with 20 subjects each (11 females and nine males, mean ± SD age 25 ± 5 years, in one group; 12 females and eight males, 24 ± 4 years, in the other group). The within‐subject protocol involved 8 participants (six females and two males, 23 ± 2 years). The control experiment with interception of a static target involved 20 participants (12 females and eight males, 25 ± 6 years). All participants were right‐handed (as assessed by a short questionnaire based on the Edinburgh scale), had normal or corrected‐to‐normal vision, no history of psychiatric or neurological diseases, and were naïve to the specific purpose of the experiments.
Experimental set‐up and stimuli
Participants laid on a physiotherapy bed with an adjustable backrest, so that the head and torso were tilted backwards at either 20° or 60° relative to the vertical (measured with a plumb line), whereas the lower part of the body was horizontal. They wore a head‐mounted display (HMD) (Oculus Rift DK2; Oculus VR, LLC, Menlo Park, CA, USA), where a virtual scene was rendered three‐dimensionally (3D) by XVR software (eXtreme Virtual Reality; VRMedia s.r.l., Pisa, Italy) using a Thinkpad W541 (Lenovo, Quarry Bay, Hong Kong) with a GeForce GTX 970 graphics card (NVIDIA, Santa Clara, CA, USA). Visual stimuli were shown stereoscopically with the HMD. Each screen of the HMD had a resolution of 960 × 1080 pixels, a refresh rate of 75 Hz, and a diagonal field of view of 100°. The time‐varying position of the HMD in 3D space was recorded by means of a Vicon system equipped with 10 Bonita cameras (250 Hz sampling frequency) (Oxford Metrics, Oxford, UK). Four reflective passive spherical markers were attached at the HMD front. The 3D position of the midpoint between the eyes was derived from the position of these markers measured in real time by the Vicon system. The time‐varying orientation of the HMD was measured in 3D by Oculus inertial sensors. Virtual scene update was based on the position of the midpoint between the eyes and the orientation of the head. As a result of the backrest constraint, head (HMD) tilt generally remained within ± 7° of the preset value (20° or 60°) in each experiment.
The main experiments involved the interception of ball motion along a plane. The virtual scene showed a gutter with the shape of a curved groove (length 2.85 m, width 0.2 m), with the long axis in the sagittal plane of the observer's head, along the sightline (assuming central fixation). The lower end of the gutter was at an apparent distance of 0.4 m from the eyes (Fig. 1). A target sphere (diameter 9 cm), patterned with blue pentagons (side length 1.9 cm; chromaticity co‐ordinates: x = 0.154, y = 0.042 in the CIE System, measured with a J17 LumaColor photometer; Tektronix, Beaverton, OR, USA) and orange hexagons (x = 0.567, y = 0.394), was placed over the surface and was kept in the starting position by a green lever arm. Once released by the lever rotation, the ball rolled forward along the gutter (without slipping or bouncing) toward the observer's viewpoint at a constant acceleration that depended on the trial (see Protocols), remaining centred horizontally and vertically on the screen throughout the motion on the gutter. Thus, ball rotation, disparity and expansion rate provided information about its approaching motion. In particular, the time of arrival was directly related to image dilation (Fig. 4). After exiting from the gutter, the ball fell in air under virtual gravity (9.81 m s–2 vertical acceleration). The scene background was uniformly brown (chromaticity: x = 0.425, y = 0.370). All objects were drawn with perspective geometry. Lights were non‐directional (no shadows).
Figure 4. Changes of image dilation and dilation rate.
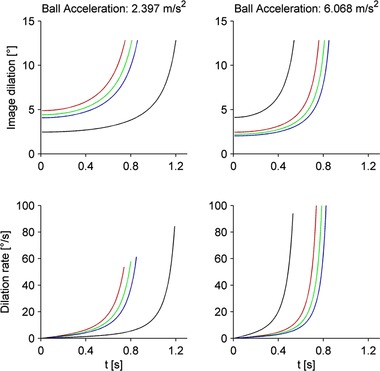
Time course of changes of image dilation (top) and dilation rate (bottom). Red, green and blue curves correspond to target motion durations of 0.75, 0.8 and 0.85 s, respectively. Black curves correspond to durations of 0.534 and 1.193 s for ball acceleration of 6.068 and 2.397 m s–2, respectively. [Color figure can be viewed at wileyonlinelibrary.com]
In the control experiments involving the interception of a static target, the virtual scene showed a transparent square box (side 9 cm; chromaticity: x = 0.388, y = 0.307) instead of the gutter. The centre of the box was placed at an apparent distance of 0.4 m from the eyes along the sagittal axis (i.e. at the same distance as the lower end of the gutter), with the frontal face parallel to the frontal plane of the observer's head. Inside the transparent box, four different 3D objects were presented seamlessly in sequence, first a ring (external diameter 9 cm, internal diameter 4.5 cm, height 1 cm) orthogonal to the sightline (assuming central fixation), then a cone with the base on the lower face of the box (diameter 9 cm, vertical height 9 cm), then a square box (side 9 cm), and finally a target sphere (diameter 9 cm). The first three objects were blue (chromaticity: x = 0.332, y = 0.265) and were displayed for 317 ms. The target sphere was red (chromaticity: x = 0.423, y = 0.344) and was displayed for 50 ms. In synchrony with the initial display of each object, 50 ms duration beeps (58 dB, 1000 Hz) were delivered by the computer sound card (Xonar DG; Asus, Taipei, Taiwan). The inter‐stimulus interval was 317 ms, so that the total duration of the audio‐visual stimuli was 1001 ms (3 × 317 ms + 50 ms). This sequence of stationary stimuli was designed not to evoke any sensation of target motion.
In all experiments, participants held in their right hand an instrumented plastic hitter, which consisted of a cylinder (diameter 3 cm, height 12 cm) with a rod (diameter 0.6 cm, height 8 cm) perpendicular to the cylinder axis. They grasped the hitter so that the rod protruded between the index and middle finger. The tip of the rod had a red sphere, 0.75 cm radius, and a vibrotactile device (C2 Tactor™; Engineering Acoustics, Casselberry, FL, USA) was attached nearby (Fig. 1, inset). Four retroreflective markers on the hitter were tracked at 250 Hz by means of the Vicon, allowing a visual rendering of the hitter in the virtual scene consistent with its time‐varying location in the real world. The Vicon, XVR and Tactor systems were networked via a user datagram protocol protocol.
Task
In each trial of the main experiments, the ball appeared at the starting position on the gutter (see Protocols). Participants had to place the tip of the hitter (red sphere) in the virtual scene within a grey sphere (diameter 4.5 cm), located in the same plane as the lower end of the gutter, at a distance of ∼30 cm to the right and ∼4.5 cm above the midpoint (Fig. 1). To reach the grey sphere, participants had to place their right elbow on a (real) foam box, with the result that the adducted upper arm was flexed by ∼45° at the shoulder, the forearm in the sagittal plane was flexed by ∼90° at the elbow, the wrist mid‐pronated, and the hand and fingers clenched around the hitter. When the tip of the hitter was inside the grey sphere, after a pseudorandom delay between 200 and 400 ms (in 50 ms steps), the ball was released by the lever arm, rolled forward and disappeared immediately after reaching the end of the gutter. Participants were asked to hit the ball as soon as it arrived at the end of the gutter with the tip of the hitter, so as to deviate the ball into a virtual circle (diameter 2 m), parallel to the direction of ball motion, 60 cm to the left of the midpoint of the end of the gutter. This required participants to hit the ball with a movement quasi‐orthogonal to the direction of ball motion.
The XVR routine computed (at 75 Hz) the instantaneous distance between the tip of the hitter and the centre of the ball. The radius of the ball was subtracted from this distance and the resulting metric was used to indicate whether or not the ball was intercepted. Thus, if this metric became null or negative, the ball was considered intercepted and participants received visual and haptic feedback about the success. For visual feedback, the ball was shown deviated to the left for 1 s. For haptic feedback, the hitter (Tactor) vibrated for 50 ms. If the interception was missed (metric >0), neither visual, nor haptic feedback were given.
In the control experiments, participants were asked to hit the static target sphere (the last object of the sequence) with the tip of the hitter, in synchrony with the last of the predictable series of beeps and images. Starting position of the arm and general procedures were similar to those in the main experiments, although, here, no performance feedback was provided to the participants to better ascertain the influence of gravity on arm movements.
Protocols
In the main experiments, we manipulated the acceleration and duration of ball motion independently of participant's tilt (Table 1). In a 2 × 2 factorial design, the participant's tilt in the sagittal plane was set at β = 20° or 60°, whereas ball acceleration a was set at 2.397 or 6.068 m s–2, corresponding to with β = 20° or 60°, respectively (Fig. 2). Therefore, there were two conditions coherent with physics: a participant tilted by 20° watching a ball accelerating at 2.397 m s–2, and a participant tilted by 60° watching a ball accelerating at 6.068 m s–2. The two conditions incoherent with physics, instead, involved a participant tilted by 20° watching a ball accelerating at 6.068 m s–2, and a participant tilted by 60° watching a ball accelerating at 2.397 m s–2. Subject tilt was blocked, whereas ball acceleration was randomized across trials.
Table 1.
Parameters of ball motion
| Case # | Ball acceleration (m s–2) | Ball motion duration (s) | Distance (m) | Speed (m s–1) |
|---|---|---|---|---|
| 1 | 2.397 | 0.750 | 0.674 | 1.797 |
| 2 | 2.397 | 0.800 | 0.767 | 1.917 |
| 3 | 2.397 | 0.850 | 0.866 | 2.037 |
| 4 | 2.397 | 1.193 | 1.707 | 2.860 |
| 5 | 6.068 | 0.750 | 1.707 | 4.551 |
| 6 | 6.068 | 0.800 | 1.942 | 4.855 |
| 7 | 6.068 | 0.850 | 2.192 | 5.158 |
| 8 | 6.068 | 0.534 | 0.866 | 3.242 |
Ball acceleration, motion duration and distance travelled were from the starting position until the end of the gutter. Speed was at the end of the gutter. Case #4 and case #8 were control conditions to match starting positions across target accelerations. Case #4 (#8) and case #5 (#3) had the same starting position but different ball acceleration.
We ran two different experimental designs with respect to subject tilt: between‐groups and within‐subject. The between‐groups protocol was designed to confirm the effect of treatment (subject tilt) without the potential contamination of carry‐over effects between sessions (related to potential long‐term effects of practice with the task). Accordingly, we randomly assigned participants to one of two groups: the first group was exposed to 20° tilt, whereas the second group was exposed to 60° tilt. The within‐subject protocol was designed to confirm the effect of tilt within individuals. Accordingly, all participants were exposed to both 20° and 60° tilts, tested in two separate sessions (counterbalanced across subjects), 15 days apart.
In each experimental session at both subject tilts, we set the starting position of the ball at one of six different values, resulting in five different values of ball motion duration from the starting position to the lower end of the gutter (Table 1). Three values of duration (0.75, 0.80 and 0.85 s) were common to both accelerations, whereas two other durations (0.534 and 1.193 s) were added to match two starting positions of the ball across the two accelerations. Overall, the combination of the manipulated variables resulted in eight different experimental conditions, denoted as cases hereafter. Case #8 at the higher acceleration matched the starting position (0.866 m) of case #3 at the lower acceleration, whereas case #5 at the higher acceleration matched the starting position (1.707 m) of case #4 at the lower acceleration. Overall, there were four motion durations (each associated with a given starting position) for each acceleration. In each session, targets were presented in consecutive sequences in which each case (two accelerations × four motion durations) was presented in random order, different from one sequence to the next. There were 15 such sequences (repetitions), resulting in a total of 120 trials.
The control experiments involving the interception of the static target followed a within‐subject protocol. Accordingly, participants were tested in two blocked sessions (20° and 60° tilts, counterbalanced across subjects). We presented the same audio‐visual stimuli for 100 repetitions at each subject tilt, so as to make the sequence fully predictable.
Before all of the experiments, participants received general instructions and familiarized with the set‐up. Participants were allowed to pause any time they wished during an experimental session, which lasted ∼35 min in the main experiments and 25 min in the control experiments.
Data analysis
We excluded a few trials (less than 1% of all trials) from the analysis as a result of the presence of artefacts or lack of subject's attention (as marked in the experiment notebook).
The 3D co‐ordinates (x, y, z) of the tip of the hitter recorded by Vicon were numerically low‐pass filtered (bidirectional, 20 Hz cut‐off, first‐order Butterworth filter). These data, as well as the positional data of the ball centre, were interpolated at 1 kHz using a cubic spline interpolation.
Success rate
For each trial, we computed the metric defined above (distance between the tip of the hitter and the centre of the sphere minus the sphere radius). We considered a hit when this metric became null or negative. The success rate was defined as the proportion of successful trials (hits) relative to the total number of trials for each experimental condition of each participant. Thus success rate was cumulated over all repetitions of each condition.
Analysis of timing and spatial errors
For each trial, we computed the hitter intersection point as the position where the trajectory of the hitter tip intercepted, for the first time, the sagittal plane tangent to the ball surface facing the hitter (i.e. the right side of the ball). The ball intersection point was the position of the ball when its surface first reached the minimum distance relative to the hitter intersection point (La Scaleia et al. 2015). Hitter and ball intersection times were defined as the time samples when the corresponding intersection points were reached. We then computed the timing error (TE) as the difference between the hitter intersection time and the ball intersection time. Accordingly, a positive (negative) value of TE corresponded to a response later (earlier) than that theoretically expected if the hitter tip arrived at the intersection time at the same time as the ball. We computed the spatial error as the Euclidean distance between the hitter intersection point and the ball intersection point minus the ball radius.
For the control experiments, we computed the arrival time of the hitter as the time when it first reached the minimum distance relative to the surface of the target sphere. TE was defined as the difference between the hitter arrival time and the time when the target first appeared.
Analysis of hand kinematics
For both the main and control experiments, we considered the time‐varying position of the tip of the hitter, which was differentiated to compute the tangential velocity as v T = . Movement onset was computed according to a algorithm described previously (La Scaleia et al. 2015). First, we normalized the tangential velocity to the maximum: v = v T/v max; then, going back from the sample at which v = 1, we defined the first sample for which v < 0.08 is the onset time. Movement duration was defined as the interval between the onset time of hand movement and the arrival time at the hitter intersection point.
Statistical analysis
The main statistical analyses involved the trials at the three motion durations (0.75, 0.80 and 0.85 s) that were common to both accelerations. The trials at the two other durations (0.534 and 1.193 s) were included in a separate analysis, as a control for the effect of starting position.
Repeated measures (RM)‐ANOVA was conducted on continuous outcome variables (i.e. timing error, duration and maximum speed of hand movements); instead, for the binary response (i.e. success rate), we used the generalized linear mixed model (GLMM) (Jaeger, 2008).
RM‐ANOVA
Results are given as the mean ± SD, and uncertainty is reported using the 95% confidence interval (CI). Statistical differences between conditions were assessed using RM‐ANOVA with ball acceleration, motion duration and repetition as within‐subjects factors, and subject tilt as a between‐subjects factor for the between‐groups protocol. For the within‐subject protocol, subject tilt was a within‐subjects factor (in addition to ball acceleration, motion duration and repetition), whereas session order was the between‐subjects factor. For the control experiments, RM‐ANOVA had subject tilt and repetition as within‐subjects factors, and session order as between‐subjects factor. The degrees of freedom for the within‐subjects comparisons were corrected (Greenhouse‐Geisser) in case of deviance from sphericity. Whenever RM‐ANOVA detected a significant difference (α = 0.05), we performed post hoc Bonferroni corrections for multiple comparisons. Effect size was assessed as partial eta‐squared (ηp 2).
GLMM
Success rate is reported as quartiles (median and interquartile range, IQR). We assessed how success rate depended on the experimental conditions by means of the GLMM (Moscatelli et al. 2012), which separates the overall variability into a fixed component and a random component, and assumes that the response variable has a binomial distribution. The fixed component estimates the experimental effects, whereas the random component estimates the heterogeneity between participants. We considered the following model:
In this model, the logit transform of the probability that participant j hit the ball in trial i is equal to a linear combination of fixed and random effect predictors. Specifically, A is the dummy variable for the acceleration (A = 0 or 1 for 2.397 or 6.068 m s–2, respectively), S is the dummy variable for the subject tilt (S = 0 or 1 for 20° and 60°, respectively), T × A is the interaction between ball motion duration and acceleration, and A × S is the interaction between ball acceleration and subject tilt. δk are the fixed effects coefficients, u jk are the random effects coefficients. For the within‐subjects protocol, the model also included the dummy variable O for the experimental session order (O = 0 or 1 for first session or second session, respectively). The significance of fixed effect parameters was assessed by means of Wald statistics. We selected each GLMM model from a pool of nested models based on the Bayesian information criterion (Schwarz 1978).
We performed data preprocessing with custom software in MATLAB (MathWorks, Natick, MA, USA) and statistical analyses with MATLAB, SPSS (IBM Corp., Armonk, NY, USA) and the R software environment (R Development Core Team, 2011; R Foundation for Statistical Computing, Vienna, Austria) with the lme4, lmerTest and MERpsychophysics packages.
Results
Main experiments: between‐groups protocol
In this experimental series, two groups of participants were asked to intercept ball motion along a plane: one group at 20° body tilt, and the other one at 60° tilt.
Success rate
The success rate computed over all repetitions was quite variable, although it was comparable in the two groups of participants, irrespective of their tilt (20° or 60°) (Fig. 5 A). Instead, success rate was higher in the coherent conditions (when ball acceleration was physically compatible with subject tilt) than in the incoherent conditions (when acceleration was incompatible with tilt) (Fig. 5 B).
Figure 5. Interception success rate in the between‐groups protocol.
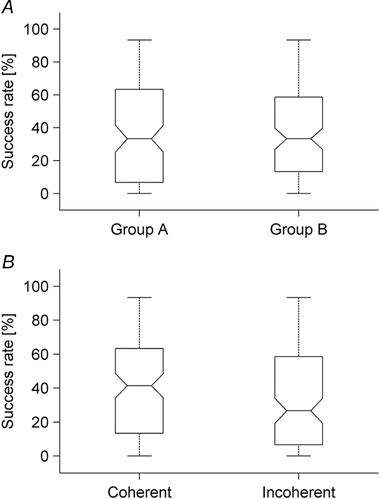
A, results plotted separately for each group of participants, group A and B tilted by 20° and 60°, respectively (20 participants × three motion durations × two ball accelerations in each group). B, results plotted separately for the conditions coherent or incoherent with physics (40 participants × three motion durations in each plot). In the box‐and‐whisker plots, the bottom and top of the boxes correspond to the lower and upper quartile, respectively, and define the IQR. The notch displays the 95% CI of the median and the whiskers extend to the lowest and highest data points.
To assess the dependence of success rate on the experimental variables in a statistically robust manner, we used the GLMM (Table 2). This analysis showed that the success rate did not depend significantly on group (or equivalently subject tilt). Instead, the success rate depended significantly on ball acceleration, being greater with the lower (2.397 m s–2) acceleration than with the higher (6.068 m s–2) acceleration (median = 60%, IQR = 27 and median = 13%, IQR = 27 for the two ball accelerations, respectively, two groups × three motion durations × 20 subjects, n = 120). It also depended significantly on motion duration, although only for the higher acceleration when success rate was larger for the higher motion duration (0.850 s). In addition, we found a statistically significant interaction between acceleration and subject tilt, with the success rate being higher in the coherent conditions than in the incoherent conditions (median success rate = 41%, IQR = 50 and 27% IQR = 51, respectively, for the coherent and incoherent conditions).
Table 2.
Success rate for the between‐groups protocol
| Intercept | Acceleration | Subject tilt | Acceleration (2.397 m s–2): motion duration | Acceleration (6.068 m s–2): motion duration | Acceleration: subject tilt | |
|---|---|---|---|---|---|---|
| Coefficient | 0.418 | –7.095 | ‐0.268 | 0.061 | 5.133 | 1.102 |
| P value | 0.679 | 3.490 × 10–5 *** | 0.311 | 0.961 | 0.002** | 0.005** |
All coefficients of the GLMM for the fixed factors in the model used to fit the score reached by participants and the relative P value values are shown (subject tilt = 20°, ball acceleration = 2.397 m s–2 are the baseline).
* P < 0.05.
** P < 0.01.
*** P < 0.001.
Response timing
Table 3 shows that, according to RM‐ANOVA, timing errors TE depended significantly on several experimental variables. In particular, the responses were timed significantly earlier for the lower acceleration than the higher acceleration (by 49 ± 26 ms, mean ± SD, n = 120, pooling the results across motion durations and participants). The timing errors were not stationary during an experiment but depended significantly on repetitions, tending to decrease with practice. Figure 6 plots TE values averaged over participants, considering the three matched motion durations in each repetition (see Methods). It can be seen that the effect of practice was different in the coherent conditions vs. the incoherent conditions because the mean TE converged toward zero for both subject tilts in the former case, whereas the mean TE remained conspicuous for both tilts in the latter case.
Table 3.
Timing error (matched ball motion durations) for the between‐groups protocol
| Factors | F (d.f.) | P value | ηp 2 |
|---|---|---|---|
| Acceleration (A) | 162.700 (1,38) | 0.000*** | 0.811 |
| Motion duration (T) | 1.186 (1.977,75.107) | 0.311 | 0.030 |
| Repetition (R) | 5.365 (4.145,157.499) | 0.000*** | 0.124 |
| Subject tilt (S) | 5.186 (1,38) | 0.028* | 0.120 |
| A × S | 0.136 (1,38) | 0.714 | 0.004 |
| T × S | 0.242 (1.977,75.107) | 0.783 | 0.006 |
| R × S | 1.537 (4.145,157.499) | 0.192 | 0.039 |
| A × T | 23.541 (1.906,72.444) | 0.000*** | 0.383 |
| A × T × S | 4.234 (1.906,72.444) | 0.020* | 0.100 |
| A × R | 19.700 (7.615,289.382) | 0.000*** | 0.341 |
| A × R × S | 1.253 (7.615,289.382) | 0.270 | 0.032 |
| T × R | 8.809 (14.688,558.143) | 0.000*** | 0.188 |
| T × R × S | 1.580 (14.688,558.143) | 0.076 | 0.040 |
| A × T × R | 5.484 (14.405,547.386) | 0.000*** | 0.126 |
| A × T × R × S | 1.238 (14.405,547.386) | 0.241 | 0.032 |
RM‐ANOVA on TE considering two accelerations (A) × three motion durations (T) × 15 repetitions (R) as within‐subjects factors and subject tilt (S) as a between‐subjects factor.
* P < 0.05.
** P < 0.01.
*** P < 0.001.
Figure 6. Effect of practice on timing errors in the between‐groups protocol.
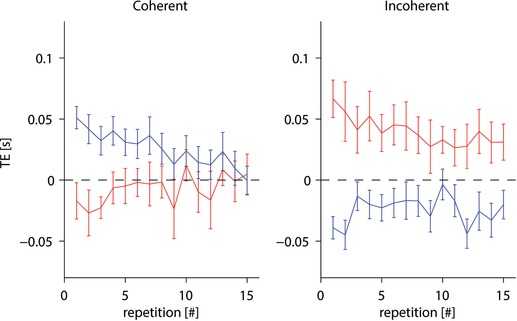
Mean (± 95% confidence interval over all 20 participants) plotted as a function of repetition separately for the coherent conditions (left) and incoherent conditions (right). Results for subjects tilted by 20° and 60° are shown in red and blue, respectively. Only trials with the three motion durations matched across target accelerations are included. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 7 compares the mean TE computed over the first four repetitions with the mean TE computed over the last four repetitions. RM‐ANOVA (two accelerations × three motion durations as within‐subjects factors, two subject tilts as a between‐subjects factor) over the first four repetitions showed that TE at the beginning of the experiment was independent of tilt (Table 4). Moreover, the mean TE values over these repetitions were significantly different from zero for both ball accelerations and both subject tilts (paired t tests, n = 20 participants, P < 0.05, corrected for multiple comparisons). By contrast, RM‐ANOVA carried over the last four repetitions showed that TE at the end of the experiment depended significantly on tilt (Table 4), the responses being timed generally earlier when participants were tilted by 60° than when they were tilted by 20°. Moreover, the mean TE values over these repetitions were significantly different from zero in the incoherent conditions (P < 0.002, corrected for multiple comparisons), although they did not differ significantly from zero in the coherent conditions (P < 0.08, uncorrected for multiple comparisons). Very similar results were obtained by considering the first three repetitions or the last three repetitions, instead of four repetitions.
Figure 7. Comparison of TE repetitions.
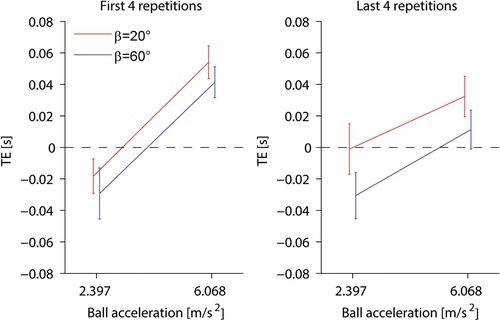
Comparison of TE averaged over the first four repetitions (left) with TE averaged over the last four repetitions (right) in the between‐groups protocol. Mean TE (± 95% confidence interval over all 20 participants) for subjects tilted by 20° and 60° are shown in red and blue, respectively. Only trials with the three motion durations matched across target accelerations are included. [Color figure can be viewed at wileyonlinelibrary.com]
Table 4.
Timing error on first and last four repetitions for the between‐groups protocol
| Factors | Acceleration (A) | Motion duration (T) | Subject tilt (S) | A × S | A × T | T × S | A × T × S | |
|---|---|---|---|---|---|---|---|---|
| First four repetitions | F (d.f.) | 230.323 | 3.550 | 2.809 | 0.031 | 11.012 | 2.961 | 3.947 |
| (1,38) | (1.98, 75.20) | (1,38) | (1,38) | (1.95, 73.96) | (1.98, 75.20) | (1.95, 73.96) | ||
| P value | 0.000*** | 0.034* | 0.102 | 0.861 | 0.000*** | 0.058 | 0.024* | |
| ηp 2 | 0.858 | 0.085 | 0.069 | 0.001 | 0.225 | 0.072 | 0.094 | |
| Last four repetitions | F | 86.524 | 0.276 | 7.986 | 1.096 | 5.197 | 1.664 | 0.831 |
| (1,38) | (1.88, 71.44) | (1,38) | (1,38) | (1.78, 67.76) | (1.88, 71.44) | (1.78, 67.76) | ||
| P value | 0.000*** | 0.746 | 0.007** | 0.302 | 0.01* | 0.198 | 0.428 | |
| ηp 2 | 0.695 | 0.007 | 0.174 | 0.028 | 0.12 | 0.042 | 0.021 |
RM‐ANOVA on TE on first or last four repetitions considering two accelerations (A) × three motion durations (T) as within‐subjects factors and subject tilt (S) as a between‐subjects factor.
* P < 0.05.
** P < 0.01.
*** P < 0.001.
Considering individual results, we found that the mean of the absolute values of TE over the last four repetitions was smaller (i.e. smaller timing errors) in the coherent conditions than the corresponding value in the incoherent conditions in 13 of 20 participants tilted by 20° and 15 of 20 participants tilted by 60°.
Matching the initial ball positions
To match the three durations (0.75, 0.80 and 0.85 s) of ball motion between the two conditions of lower and higher acceleration, the corresponding initial positions of the ball and the distance travelled prior to reaching the interception point necessarily differed. However, the protocol also included two cases (durations of 0.534 and 1.193 s), randomly assorted with the other ones, which matched two starting positions across the two accelerations (see Methods). As a control for the effect of starting position, we separately analysed the trials of these two cases along with those at the corresponding starting position for each acceleration (i.e. cases #3 and #8, cases #4 and #5) (Table 1). Table 5 shows the details of RM‐ANOVA results. Figure 8 plots mean TE values for these cases as a function of repetition. These plots indicate a trend with practice roughly similar to that shown in Fig. 6, with a better convergence toward zero error for the coherent conditions than the incoherent conditions. Furthermore, considering these experimental conditions, RM‐ANOVA computed over the first/last four repetitions confirmed the previous results, in particular showing that TE at the beginning of the experiment was independent of tilt, whereas at the end of the experiment it depended significantly on tilt, the responses being timed generally earlier when participants were tilted by 60° than when they were tilted by 20° (Table 6), similar to the results reported in Table 4.
Table 5.
Timing error (matched starting positions) for the between‐groups protocol
| Factors | F (d.f.) | P value | ηp 2 |
|---|---|---|---|
| Acceleration (A) | 410.623 (1,38) | 0.000*** | 0.915 |
| Starting position (SP) | 12.309 (1,38) | 0.001** | 0.245 |
| Repetition (R) | 12.148 (5.28,200.74) | 0.000*** | 0.242 |
| Subject tilt (S) | 3.079 (1,38) | 0.087 | 0.075 |
| A × S | 1.522 (1,38) | 0.225 | 0.039 |
| SP × S | 1.694 (1,38) | 0.201 | 0.043 |
| R × S | 1.107 (5.28,200.74) | 0.359 | 0.028 |
| A × SP | 0.084 (1,38) | 0.774 | 0.002 |
| A × SP × S | 0.829 (1,38) | 0.368 | 0.021 |
| A × R | 14.804 (8.03,305.03) | 0.000*** | 0.280 |
| A × R × S | 0.939 (8.03,305.03) | 0.485 | 0.024 |
| SP × R | 9.885 (8.41,319.76) | 0.000*** | 0.206 |
| SP × R × S | 0.803 (8.41,319.76) | 0.606 | 0.021 |
| A × SP × R | 9.729 (8.98,341.11) | 0.000*** | 0.204 |
| A × SP × R × S | 0.974 (8.98,341.11) | 0.461 | 0.025 |
RM‐ANOVA on TE considering two accelerations (A) × two starting positions (SP) × 15 repetitions (R) as within‐subjects factors and subject tilt (S) as a between‐subjects factor.
* P < 0.05.
** P < 0.01.
*** P < 0.001.
Figure 8. Effect of practice on timing errors.
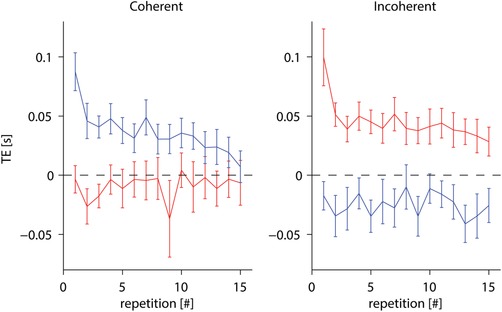
Effect of practice on timing errors, in the between‐groups protocol, in the trials with matched initial position of the target across accelerations (cases #3 and #8, cases #4 and #5) (Table 1) (same format as in Fig. 6). [Color figure can be viewed at wileyonlinelibrary.com]
Table 6.
Timing error on first and last four repetitions (matched starting positions) for the between‐groups protocol
| Factors | Acceleration (A) | Starting position (SP) | Subject tilt (S) | A × S | A × SP | SP × S | A × SP × S | |
|---|---|---|---|---|---|---|---|---|
| First four repetitions | F (d.f.) | 456.458 (1,38) | 11.166 (1,38) | 1.356 (1,38) | 0.875 (1,38) | 4.930 (1,38) | 0.948 (1,38) | 0.514 (1,38) |
| P value | 0.000*** | 0.002** | 0.251 | 0.355 | 0.032* | 0.337 | 0.478 | |
| ηp 2 | 0.923 | 0.227 | 0.034 | 0.023 | 0.115 | 0.024 | 0.013 | |
| Last four repetitions | F | 161.221 (1,38) | 10.157 (1,38) | 5.620 (1,38) | 1.803 (1,38) | 1.613 (1,38) | 0.483 (1,38) | 3.414 (1,38) |
| P value | 0.000*** | 0.003** | 0.023* | 0.187 | 0.212 | 0.491 | 0.072 | |
| ηp 2 | 0.809 | 0.211 | 0.129 | 0.045 | 0.041 | 0.013 | 0.082 |
RM‐ANOVA on TE on first or last four repetitions considering two accelerations (A) × two starting positions (SP) as within‐subjects factors and subject tilt (S) as a between‐subjects factor.
* P < 0.05.
** P < 0.01.
*** P < 0.001.
Characteristics of hand movements
All participants hit the virtual ball with very small spatial errors [median = 0.09 cm, 0–0.46 cm (25th to 75th percentile), n = 3575, pooling the results across all repetitions, motion durations and participants, after exclusion of rejected trials]. Mean ± SD duration of hand movements was 0.157 ± 0.09 s (n = 1785) and 0.172 ± 0.09 s (n = 1790) for participants tilted by 20° and 60°, respectively. Mean ± SD maximum speed was 4.41 ± 1.41 m s–1 and 4.0 ± 1.3 m s–1 for participants tilted by 20° and 60°, respectively. Neither movement duration, nor maximum speed differed significantly between the two groups of participants (Table 7). Instead, these movement parameters depended significantly on ball acceleration. On average, hand movements aimed at balls descending with the higher acceleration were faster and lasted less than those aimed at balls with lower acceleration. However, these movement parameters changed with practice, tending to converge to similar values toward the end of the experiment, irrespective of ball acceleration (Fig. 9).
Table 7.
Characteristics of hand movements for the between‐groups protocol
| Motion duration | Maximum speed | |||||
|---|---|---|---|---|---|---|
| Factors | F (d.f.) | P value | ηp 2 | F (d.f.) | P value | ηp 2 |
| Acceleration (A) | 85.38 (1,38) | 0.000*** | 0.692 | 78.31 (1,38) | 0.000*** | 0.673 |
| Motion duration (T) | 6.87 (1.93,73.24) | 0.002** | 0.153 | 1.55 (1.99,75.46) | 0.219 | 0.039 |
| Repetition (R) | 2.53 (6.20,235.63) | 0.020* | 0.063 | 3.42 (4.16,157.97) | 0.009** | 0.082 |
| Subject tilt (S) | 0.91 (1,38) | 0.345 | 0.023 | 1.49 (1,38) | 0.230 | 0.038 |
| A × S | 0.05 (1,38) | 0.827 | 0.001 | 3.06 (1,38) | 0.088 | 0.075 |
| T × S | 0.76 (1.93,73.24) | 0.467 | 0.020 | 0.58 (1.99,75.46) | 0.564 | 0.015 |
| R × S | 1.04 (6.20,235.63) | 0.397 | 0.027 | 1.18 (4.16,157.97) | 0.322 | 0.030 |
| A × T | 12.13 (1.92,72.83) | 0.000*** | 0.242 | 5.36 (1.90,72.19) | 0.008** | 0.124 |
| A × T × S | 0.38 (1.92,72.83) | 0.678 | 0.010 | 1.82 (1.90,72.19) | 0.171 | 0.046 |
| A × R | 2.31 (8.55,324.91) | 0.018* | 0.057 | 10.94 (8.96,340.45) | 0.000*** | 0.223 |
| A × R × S | 0.46 (8.55,324.91) | 0.894 | 0.012 | 1.25 (8.96,340.45) | 0.261 | 0.032 |
| T × R | 1.67 (12.16,462.19) | 0.070 | 0.042 | 2.99 (14.40,547.24) | 0.000*** | 0.073 |
| T × R × S | 0.80 (12.16,462.19) | 0.651 | 0.021 | 1.24 (14.40,547.24) | 0.235 | 0.032 |
| A × T × R | 1.38 (12.00,453.08) | 0.172 | 0.035 | 1.14 (13.87,526.90) | 0.323 | 0.029 |
| A × T × R × S | 1.25 (12.00,453.08) | 0.243 | 0.032 | 1.32 (13.87,526.90) | 0.191 | 0.034 |
RM‐ANOVA on characteristics of hand movements (motion duration and maximum speed) considering two accelerations (A) × three motion durations (T) × 15 repetitions (R) as within‐subjects factors and subject tilt (S) as a between‐subjects factor.
* P < 0.05.
** P < 0.01.
*** P < 0.001.
Figure 9. Effect of practice on hand movement.

Effect of practice on hand movement duration (left) and maximum speed (right) in the between‐groups protocol. Mean TE (± 95% confidence interval over all 40 participants) for target acceleration of 2.397 and 6.068 m s–2 are shown in black and grey, respectively. Only trials with the three motion durations matched across target accelerations are included.
Summary
The results with the between‐groups protocol showed that the interception responses at the end of the experiments conformed to the theoretical predictions depicted in Fig. 3, being timed more accurately around ball arrival in the coherent conditions than in the incoherent conditions.
Several observations further indicate that the effects of coherence on performance were a genuine result of participant's tilt rather than a by‐product of group membership. Thus, overall success rate, duration and maximum speed of hand movements, as well as the timing errors over the first few repetitions were comparable between the two groups. Nevertheless, to further corroborate the conclusions, we also carried out a within‐subject protocol.
Main experiments: within‐subject protocol
In this experimental series, all participants were exposed to both 20° and 60° tilts, tested in two separate sessions (counterbalanced across subjects) 15 days apart. Table 8 reports the results of GLMM on the success rate. As in the case of the between‐groups experiments, also the within‐subjects experiments revealed a significant effect of ball acceleration, the success rate being higher with the lower ball acceleration than with the higher ball acceleration. We also observed a significant effect of session order, success rate in the second session being higher than in the first one (median = 28%, IQR = 21 and median = 39%, IQR = 25 for the first and second session, respectively, three motion durations × eight subjects, n = 24). This global improvement of the interception performance was indicative of a long‐term learning process carrying over from the first session onto the second one, and precluded in‐depth analyses of the time course of changes in the interception responses, as shown in Fig. 6 for the between‐groups experiments.
Table 8.
Success rate for the within‐subject protocol
| Intercept | Acceleration | Subject tilt | Motion duration | Experimental session order | |
|---|---|---|---|---|---|
| Coefficient | 1.344 | –2.640 | –0.254 | –1.473 | 0.570 |
| P value | 0.339 | 1.350 × 10–6 *** | 0.065 | 0.372 | 3.380 × 10‐5 *** |
All coefficients of the GLMM for the fixed factors in the model used to fit the score reached by participants and the relative P value are shown [subject tilt = 20°, ball acceleration = 2.397 m s–2 and Session Order ‘first (I)’ are the baseline].
Figure 10 compares the mean TE computed at the start of each session (first four repetitions of session 1 and first four repetitions of session 2) with the mean TE computed at the end of each session (last four repetitions of session 1 and last four repetitions of session 2). RM‐ANOVA (two subject tilts × two accelerations × three motion durations as within‐subjects factors, two session orders as between‐subjects factor) on the first four repetitions showed that TE was independent of tilt (Table 9), whereas the same statistical analysis carried over the last four repetitions of each session showed that TE at the end of the experiment depended significantly on tilt (Table 9). In particular, we found that, on average, the responses at the end of the experiment were timed later relative to ball arrival when participants were less tilted (20°) than when they were more tilted (60°), when ball acceleration was higher (6.068 m s–2) than when it was lower (2.397 m s–2) and in session order 20° to 60° than session order 60° to 20°.
Figure 10. Timing errors in the within‐subject protocol.
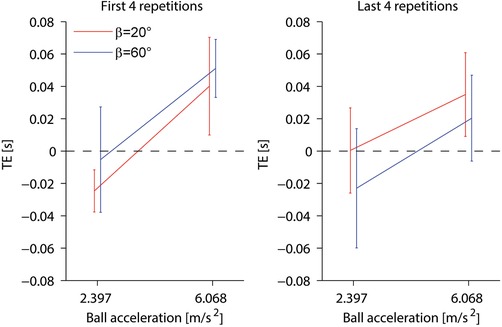
Mean TE over the first four repetitions (left) with TE averaged over the last four repetitions (right) (± 95% confidence interval over all eight participants) for blocks with the subjects tilted by 20° and 60° are shown in red and blue, respectively. Only the trials with the three motion durations matched across target accelerations are included. [Color figure can be viewed at wileyonlinelibrary.com]
Table 9.
Timing error on first and last 4 repetitions for the within‐subject protocol
| First four repetitions | Last four repetitions | |||||
|---|---|---|---|---|---|---|
| Factors | F (d.f.) | P value | ηp 2 | F (d.f.) | P value | ηp 2 |
| Subject tilt (S) | 1.469 (1,6) | 0.271 | 0.197 | 8.573 (1,6) | 0.026* | 0.588 |
| Acceleration (A) | 26.960 (1,6) | 0.002** | 0.818 | 23.090 (1,6) | 0.003** | 0.794 |
| Motion duration (T) | 0.891 (1.521,9.124) | 0.150 | 0.136 | 0.100 (1.75,10.51) | 0.883 | 0.016 |
| Session block order (B) | 3.662 (1,6) | 0.104 | 0.379 | 6.673 (1,6) | 0.042* | 0.527 |
| S × B | 0.064 (1,6) | 0.809 | 0.011 | 0.937 (1,6) | 0.371 | 0.135 |
| A × B | 0.238 (1,6) | 0.643 | 0.038 | 0.001 (1,6) | 0.971 | 0.000 |
| T × B | 0.557 (1.521,9.124) | 0.545 | 0.085 | 1.145 (1.75,10.51) | 0.347 | 0.160 |
| S × A | 1.220 (1,6) | 0.312 | 0.169 | 2.175 (1,6) | 0.191 | 0.266 |
| S × A × B | 19.941 (1,6) | 0.004** | 0.769 | 3.349 (1,6) | 0.117 | 0.358 |
| S × T | 1.516 (1.97,11.85) | 0.259 | 0.202 | 0.043 (1.26,7.58) | 0.891 | 0.007 |
| S × T × B | 1.214 (1.97,11.85) | 0.331 | 0.168 | 2.064 (1.26,7.58) | 0.193 | 0.256 |
| A × T | 1.866 (1.23,10.37) | 0.216 | 0.237 | 3.441 (1.85,11.13) | 0.071 | 0.364 |
| A × T × B | 0.079 (1.23,10.37) | 0.836 | 0.013 | 1.732 (1.85,11.13) | 0.222 | 0.224 |
| S × A × T | 0.189 (1.73, 10.37) | 0.801 | 0.031 | 0.095 (1.37,8.25) | 0.840 | 0.016 |
| S × A × T × B | 1.268 (1.73, 10.37) | 0.316 | 0.174 | 0.209 (1.37,8.25) | 0.735 | 0.034 |
RM‐ANOVA on TE considering two subject tilts (S) × two accelerations (A) × three motion durations (T) as within‐subjects factors and Session Block Order (B) as between‐subjects factor.
* P < 0.05.
** P < 0.01.
*** P < 0.001.
Figure 10 shows that, on average, the interception responses at the end of the experimental sessions conformed to the theoretical predictions of Fig. 3 also in the within‐subjects protocol, being timed more accurately around ball arrival in the coherent conditions than in the incoherent conditions, although the effect was not statistically significant for the 60° tilt.
Considering individual results, we found that the mean of the absolute values of TE over the last four repetitions was smaller (i.e. smaller timing errors) in the coherent conditions than the corresponding value in the incoherent conditions in seven of eight participants.
Control experiments
Here, participants were asked to hit a static target in synchrony with the last of a predictable series of beeps and images. They were exposed to both 20° and 60° tilts, tested in two separate sessions, in a counterbalanced order.
Success rate
The GLMM analysis, using subject tilt and session order as factors, showed that success rate did not depend significantly on any factors or interaction (P > 0.27). In particular, median success rate was 20% (IQR = 10) and 19% (IQR = 14), respectively, for the subject tilted by 20° or 60°.
Response timing
Figure 11 B compares the mean timing errors obtained with the two body tilts. TE did not depend significantly on subject tilt (F 1,18 = 0.23, P = 0.6, ηp 2 = 0.01). In particular, the mean TE was 14 ms [CI = (–12 to 41 ms), n = 20 subjects] and 18 ms [CI = (–17 to 52 ms), n = 20 subjects] for a subject tilt of 20° or 60°, respectively. Both mean values fall within the theoretical margin of error corresponding to the display interval of the target sphere (0–50 ms). Figure 11 C plots mean TE values for the two body tilts as a function of repetition. Although a slight trend with practice is noted, this was similar in the two tilt conditions. Moreover, the effect of repetition on TE was not statistically significant (F 11.85,213.30 = 1.517, P = 0.12, ηp 2 = 0.08), nor did TE depend significantly on session order (F 1,18 = 0.254, P = 0.6, ηp 2 = 0.01) or any interactions (P > 0.05).
Figure 11. Control experiment.
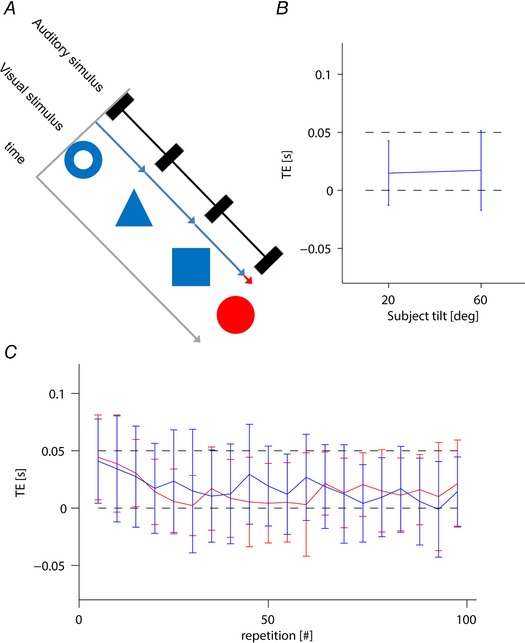
A, stimuli. The predictable series of stationary images (visual stimulus) and beeps (auditory stimulus) presented to participants. The blue and red arrows indicate the display duration of corresponding object. Participants were asked to hit the static target sphere (the last object of the sequence) in synchrony with the last of the predictable series of beeps. B, mean TE (± 95% confidence interval over all 20 participants) for subjects tilted by 20° and 60°. C, mean TE as a function of repetition for subjects tilted by 20° and 60° (red and blue, respectively). For clarity, each data point represents the average (± 95% confidence interval over all 20 participants) of five consecutive trials. In (B) and (C), black dashed lines represent the theoretical margin of error corresponding to the duration of the target sphere (0–50 ms). [Color figure can be viewed at wileyonlinelibrary.com]
We also evaluated the TE at the beginning or at the end of each session, considering the first or the last four repetitions of session 1 and the first or the last four repetitions of session 2. RM‐ANOVA (subject tilt as within‐subjects factor and session order as between‐subjects factor) showed that TE over the first four repetitions did not depend significantly on subject tilt (F 1,18 = 0.23, P = 0.64, ηp 2 = 0.01), session order (F 1,18 = 0.003, P = 0.96, ηp 2 = 0.0001) and their interaction (F 1,18 = 0.89, P = 0.36, ηp 2 = 0.05). Similarly, TE of the last four repetitions did not depend significantly on subject tilt (F 1,18 = 0.40, P = 0.53, ηp 2 = 0.02), session order (F 1,18 = 0.098, P = 0.76, ηp 2 = 0.005) and their interaction (F1,18 = 0.540, P = 0.47, ηp 2 = 0.03).
By contrast, the hand motion duration depended significantly on subject tilt (F 1,18 = 11.078, P = 0.0037, ηp 2 = 0.002); in particular, it was 209 ms [CI = (184–234 ms)] and 231 ms [CI = [205–258 ms)] at 20° and 60°, respectively. Hand motion duration did not depend significantly on any other factors or interactions (P > 0.10). Also maximum speed depended significantly on subject tilt (F 1,18 = 11.078, P = 0.0037, ηp 2 = 0.38); in particular, it was 2.22 m s–1 [CI = (1.91–2.53 m s–1)] and 1.96 m s–1 [CI = (1.73–2.19 m s–1)] at 20° and 60°, respectively. Maximum speed did not depend significantly on any other factors or interactions (P > 0.18).
In sum, body posture affected significantly arm kinematics but not interception timing when hitting a static target.
Discussion
The hypothesis and the findings
In the main experiments, participants were asked to hit a ball rolling on a surface viewed stereoscopically in a head‐mounted display. Because the ball approached along the sightline and the scene did not include any reference about either vertical or horizontal directions, the surface slope could not be estimated from visual information. However, participants were tilted in the sagittal plane by 20° or 60°, whereas ball acceleration (2.397 or 6.068 m s–1) was compatible with rolling down a slope of 20° or 60°. In theory, therefore, vestibular and somatosensory information about the orientation of the head relative to gravity could help estimating the visual direction of ball motion relative to gravity and therefore the descent slope because the direction of ball motion was head‐fixed. This hypothesis predicts that the interception performance should be more accurate when ball acceleration is coherent with subject tilt than when it is incoherent (Fig. 3).
Consistent with this hypothesis, we found that the global success rate computed over all repetitions was significantly higher in the coherent conditions than in the incoherent conditions. However, the performance measured in terms of timing errors was not stationary throughout the experiment, although it tended to improve with practice, significantly more so for the coherent conditions than the incoherent conditions. Initially, the timing errors were large and independent of the coherence between acceleration and subject tilt. This is what would be expected if the responses were based exclusively on visual information because the visual stimuli were identical at both subject tilts. At the end of the experimental session, however, the timing errors were substantially smaller in the coherent conditions than the incoherent ones. This was true for the average of the responses in the last four repetitions over all participants, as well as for the same average parameter computed in individual participants in the majority of them. Moreover, the results did not depend on the distance travelled by the ball prior to interception, as shown by the trials where the starting position was matched between the lower and the higher acceleration.
The results also conformed to another important prediction stemming from the hypothesis. In particular, if subject tilt relative to gravity contributed to estimating the direction of target motion relative to gravity, the responses provided by more tilted participants should be timed earlier than those provided by less tilted participants, for a given target acceleration. This is because a ball rolling down a steeper slope typically is more strongly accelerated, inducing an observer to expect an earlier arrival time. Indeed, although, at the beginning of the experiment, we found that the response timing was independent of posture, at the end, the responses were timed significantly earlier when participants were tilted by 60° than when they were tilted by 20°. Therefore, practice with the task led to incorporation of postural information about head and body tilt relative to gravity for response timing.
The hypothesis that body posture affects interception timing by contributing to the estimate of target kinematics under gravity predicts that response timing should not depend on body posture when the target to be intercepted is motionless. To test this prediction, we ran a control experiment in which participants tilted backwards by 20° or 60° were asked to hit a static target in synchrony with the last of a predictable series of stationary audio‐visual stimuli. We found that body posture affected significantly arm kinematics, consistent with previous studies on the effects of gravity on arm movements (Papaxanthis et al. 1998, Pinter et al. 2012; Gentili et al. 2007; Verheij et al. 2013; Gaveau et al. 2016), although it did not affect interception timing even after extensive practice.
In the main experiments, we also found a robust effect of ball acceleration on the responses. Thus, overall success rate was much lower when ball acceleration was higher than when it was lower. This result is consistent with the well‐established notion that fast targets are more difficult to intercept than slow ones (Port et al. 1997; Tresilian & Lonergan 2002). Moreover, the responses were timed significantly later for the higher acceleration than the lower acceleration, also consistent with previous results (Bosco et al. 2012).
The observed bias of the responses as a function of target acceleration confirms that participants were unable to rely on online visual measurements of acceleration in order to time the interceptions. Indeed, it is well known that the visual system poorly estimates image accelerations (Werkhoven et al. 1992; Perrone and Thiele 2001; Brouwer et al. 2002). Motor timing generally does not take into account arbitrary accelerations, being based on first‐order optical parameters such as the dilation rate or the tau‐variable (Bootsma et al. 1997; Port et al. 1997; Engel and Soechting 2000; Senot et al. 2003; Brenner and Smeets, 2015; Zago et al. 2009). Instead, the present results are consistent with the idea that the interception responses were timed based on a model of the effects of gravity on a ball rolling down a descent, whose slope was estimated indirectly from postural orientation.
Comparison with previous work
As detailed in the Introduction, a few previous studies investigated the effects of posture on target interception (Senot et al. 2005; Le Séac'h et al. 2010; Baurès & Hecht, 2011). In these previous studies, the virtual scene included visually polarized cues that helped defining Up and Down directions relative to physical gravity. Nevertheless, the results showed that subject posture relative to gravity direction provided a major contribution to the sense of up and down in timing interception of targets moving along the vertical, although the effects were more consistent with naïve physics than with Newtonian physics. In Baurès & Hecht (2011), the effect of posture became apparent only when the last segment of target trajectory was occluded for a prolonged time (2.5 s), consistent with a dominant cognitive influence. In these previous studies, there was no appreciable effect of practice on interception timing, even when visual feedback about the performance was provided to the participants (Senot et al. 2005; Le Séac'h et al. 2010). However, repetitions of the same condition were limited to five in the latter studies. Moreover, the responses were provided by means of a button press and there was no haptic feedback.
In the present experiments, the visual scene lacked any polarized cues, and the only cues about target motion direction could be derived indirectly from the tilted posture of the participants. There were 15 repetitions of each experimental case, which allowed for practice effects to come to light. Moreover, the participants hit the target by means of actual arm movements and received haptic feedback, in addition to visual feedback. Therefore, during the experiment, the punching movement and the haptic feedback could have created a unitary reference frame between the real and the virtual world, thus reinforcing the coherent conditions. In this regard, it has previously been shown that the interception of targets accelerated by gravity is much better in the presence of real punching movements and haptic feedback from contact with the target than when interception is obtained by clicking a mouse‐button and without haptic feedback (Zago et al. 2004).
One may wonder why the influence of a prior about gravity direction became most evident at the end of the experiment rather than at the outset. We consider that, in the absence of direct visual cues about gravity direction as in the present experiments, a gravitational reference for the visual stimuli could only be built and refined progressively with practice with the task. Accordingly, the effects on response timing built up progressively and were seen best at the end of the experiment.
Our findings show that the effects of posture extend beyond a mere sense of up and down directions, and involve targets moving along oblique directions. Moreover, the results are compatible with the hypothesis that posture contributes quantitatively to modelling the effects of gravity, giving rise to interception responses that are consistent with Newtonian dynamics. Indeed, in the coherent trials where target acceleration coincided with that of a ball rolling down a slope with the same inclination as the participant's tilt, performance feedback and practice with the task led to fairly accurate responses (Brenner et al. 2016; Leow et al. 2016). In the incoherent trials, instead, the discrepancy between predicted and actual target kinematics led to significant timing errors, which were only partially corrected with practice. Therefore, performance errors were more salient in the coherent than the incoherent conditions (Jiang et al. 2018).
Effects of body posture relative to gravity have been previously shown also for arm pointing movements. Thus, Le Seac'h & McIntyre (2007) reported that arm kinematics changed as a function of body roll (i.e. vertical posture vs. reclined on the side). Scotto di Cesare et al. (2014) showed that, when subjects point toward a visual target during slow pitch of the body and/or visual scene, the pattern of spatial errors was compatible with a gravity‐centred reference frame. In our experiments, the general characteristics (duration, speed) of arm movements directed to hit the ball did not depend on body posture, although they showed a trend with practice.
Sloped trajectories have been previously used in various interception tasks (La Scaleia et al. 2014a, 2015; Tresilian & Lonergan 2002). In particular, de Rugy et al. (2012) studied the interception of balls rolling down paths with variable slope and showed that internal models predict the effects of complex, varying accelerations when they result from lawful interactions with the environment.
Estimates of body and gravity directions
The good performance after practice in the coherent conditions demonstrates that postural cues about the orientation of the subject in space effectively contributed to constructing a gravity reference for the control of target interception. Although our experimental manipulations were insufficient to determine their relative weight, egocentric cues also contributed in addition to gravicentric cues. This was shown by the statistically significant main effect of subject tilt on timing errors, independently of target acceleration (and therefore coherence), in both the between‐groups and the within‐subject protocols.
Different sensory organs can signal the orientation of the head and body with respect to gravity. Thus, static tilt of the head changes the component of the gravitational shear force acting in the plane of the maculae, and affects background activity and dynamic sensitivity of otolith afferents with regular discharge (Fernandez & Goldberg, 1976). In addition, somatosensory receptors (in the skin, muscles and tendons) and visceral receptors (in the kidneys, vena cava) can contribute to a sense of body orientation by monitoring contact forces between the body and the environment. Finally, the efference copy of the motor commands for reaching the target also may have contributed to a gravity reference in our experiments. Indeed, the muscle effort required to support the outstretched limb against gravity differed when participants were tilted by 20° or 60°.
We argued that postural cues helped estimating the visual direction of ball motion relative to gravity and therefore the descent slope. In this regard, previous studies about the SVV are pertinent. Most such studies assessed SVV in the roll plane. Although the estimates of the visual vertical are very accurate with the participant in the upright position (<2° errors), small roll tilts of the body (<30°) may result in limited overshoots (so called E‐effect) and large tilts (>60°) generally result in more appreciable undershoots (A‐effect) (e.g. Kaptein and Van Gisbergen, 2004; Tarnutzer et al. 2009; Vingerhoets et al. 2009). When a peripheral visual frame is added when testing SVV, A‐effects at large body tilts tend to decrease relative to when SVV is tested without the frame (Vingerhoets et al. 2009).
A few studies assessed SVV in the pitch plane, thus being comparable to the situation of the present experiments. Ebenholtz (1970) tested SVV in the anteroposterior direction with the subject pitched backwards in 15° steps, up to 90° tilt. Small (<5°) overshoots were reported at 15°, 30° and 45° pitch, with small undershoots (<5°) at 60° and slightly larger undershoots (6–12°) for greater tilts. Bortolami et al. (2006) assessed the subjective vertical using haptic matches, and their regression parameters indicate that the vertical was undershot by <1° at 20° backward pitch and <2° at 60°. Bringoux et al. (2004) studied the perceived gravity‐referenced eye level, which corresponds to the subjective Earth‐referenced horizon. For participants pitched backwards by 20–30°, the errors remained within 4°, similarly to the previous results of Schöne (1964). In sum, the constant errors in assessing the direction of gravity or the horizontal with a visual or haptic match are small at body tilts comparable to those of the present experiments.
Furthermore, the estimates of the direction of visual motion follow a pattern very similar to that of SVV. De Vrijer et al. (2008) asked laterally tilted subjects to align the direction of random dots motion (30% coherence) with the direction of gravity in darkness. They found that, at ≤60° tilts, the errors in both SVV and motion estimate were small (<10°), although the errors became substantial at >60° tilts, indicative of incomplete compensation for large body tilts. Claassen et al. (2016) reported that the coherence threshold for detecting the direction of random dots motion was significantly lower when both subject position and motion direction were congruent with gravity.
According to current views, the direction of gravity is estimated by combining retinal cues about the line orientation with static vestibular and somatosensory cues about body orientation, plus the prior assumption of an upright body orientation (Mittelstaedt 1983; Dyde et al. 2006; MacNeilage et al. 2007; De Vrijer et al. 2008; Lacquaniti et al. 2015; Alberts et al. 2016; Kheradmand & Winnick 2017). Also, the perception of static body tilt results from multisensory fusion, vestibular inputs being integrated with proprioceptive inputs (Bringoux et al. 2016), although the perception of body orientation is considered to be independent of the perception of vertical direction, with systematic errors smaller than those in SVV (Kaptein & Van Gisbergen, 2004; Kheradmand & Winnick 2017).
Putative neural substrates
Neuroimaging (Indovina et al. 2005; Ferri et al. 2016, 2013; Maffei et al. 2010, 2015; Miller et al. 2008), transcranial magnetic stimulation (Bosco et al. 2008; Delle Monache et al. 2017) and lesion studies (Maffei et al. 2016) in humans have shown that the effects of gravity on a visual target motion elicit neural responses in a distributed cortical‐subcortical network, including the vestibular cortex, putamen, thalamus, cerebellum and vestibular nuclei (Lacquaniti et al. 2013). In particular, the vestibular cortex integrates visual, vestibular and somatosensory signals in a widely distributed network, mainly localized in the temporal, parietal and insular cortices (Lopez & Blanke 2011). Also, SVV tasks engage temporo‐parietal‐insular cortices (Fiori et al. 2015; Kheradmand & Winnick 2017), although temporal and spatial processing of gravity may not necessarily co‐localize in the same regions (Maffei et al. 2016).
Detailed electrophysiological studies in monkeys have shown that neurons carrying signals of head and body orientation relative to gravity, independent of visual landmarks, can be found in several brain regions, including the brainstem, cerebellum, thalamus, temporal, parietal and insular cortices (Angelaki et al. 2004; Chen et al. 2011; Laurens et al. 2013, 2016). Several of these neurons use internal models of physics to disentangle gravitoinertial cues (Angelaki et al. 2004) or visual motion cues for target interception (Cerminara et al. 2009; Streng et al. 2018).
Conclusions
We have shown that vestibular and somatosensory cues about head and body orientation in space contribute to model the effects of gravity on a target moving with different accelerations, in the absence of visual landmarks. This work adds to the existing knowledge about the fusion of multisensory cues with internal models of physics. This fusion affords reliable estimates of orientation of ourselves and external objects in space, as well as successful interactions with the environment, even in the presence of ambiguous sensory information.
The protocols that we used in the present study may have translational relevance to test the role of visual–vestibular integration in patients with peripheral or central vestibular dysfunctions. Thus, Maffei et al. (2016) showed that some such patients have a reduced ability to discriminate natural from unnatural gravitational acceleration for the interception of targets moving along the vertical. However, the diagnostic power would be enhanced considerably by assessing the patients with targets moving along variable slopes (de Rugy et al. 2012) and by tilting the patient relative to gravity to test visual–vestibular integration directly.
Additional information
Competing interests
The authors declare that they have no competing interests.
Author contributions
The work was performed at the Laboratory of Neuromotor Physiology, IRCCS Fondazione Santa Lucia. BLS conceived the research, performed the experiments and analysed the data. MZ contributed to the methodology. All authors contributed to the design of the work, interpretation of the data and the drafting of the work. All authors approved the final version of the manuscript submitted for publication, agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved, and that all persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.
Funding
This work was supported by the Italian Ministry of Health (IRCCS Fondazione Santa Lucia Ricerca corrente), the Italian Space Agency (grants I/006/06/0 and 2014‐008‐R.0), the Italian University Ministry (PRIN grant 2015HFWRYY_002) and Horizon 2020 Robotics Program from the European Commission (ICT‐23‐2014 under Grant Agreement 644 727‐CogIMon). The funders had no role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Acknowledgements
We thank Drs Andrea d'Avella, Yuri P. Ivanenko, Vincenzo Maffei and Alessandro Moscatelli for critically reading a previous version of this work, as well as anonymous reviewers for their helpful suggestions after the first submission. We thank Franco Tecchia and Giovanni Avveduto for support with the development of the experimental set‐up.
Biography
Barbara La Scaleia received a degree in Aerospace Engineering in 2003 from the University of Rome ‘La Sapienza’, Italy and a PhD in Neurosciences from the University of Rome Tor Vergata, Italy. She is currently a researcher at the Laboratory of Visuomotor Control and Gravitational Physiology at Fondazione Santa Lucia. Her work focuses mainly on visuomotor control and motion perception in humans. For her research, she develops her own multisensory virtual reality set‐ups

Edited by: Janet Taylor & Diego Contreras
This is an Editor's Choice article from the 1 April 2019 issue.
References
- Alberts BBGT, Selen LPJ, Bertolini G, Straumann D, Medendorp WP & Tarnutzer AA (2016). Dissociating vestibular and somatosensory contributions to spatial orientation. J Neurophysiol 116, 30–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angelaki DE, McHenry MQ, Dickman JD, Newlands SD & Hess BJ (1999). Computation of inertial motion: neural strategies to resolve ambiguous otolith information. J Neurosci 19, 316–327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angelaki DE, Shaikh AG, Green AM & Dickman JD (2004). Neurons compute internal models of the physical laws of motion. Nature 430, 560–564. [DOI] [PubMed] [Google Scholar]
- Battaglia PW, Hamrick JB & Tenenbaum JB (2013). Simulation as an engine of physical scene understanding. Proc Natl Acad Sci U S A 110, 18327–18332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baurès R & Hecht H (2011). The effect of body posture on long‐range time‐to‐contact estimation. Perception 40, 674–681. [DOI] [PubMed] [Google Scholar]
- Bootsma RJ, Fayt V, Zaal FTJM & Laurent M (1997). On the information‐based regulation of movement: what Wann (1996) may want to consider. J Exp Psychol Hum Percept Perform 23, 1282–1289. [Google Scholar]
- Bortolami SB, Pierobon A, DiZio P & Lackner JR (2006). Localization of the subjective vertical during roll, pitch, and recumbent yaw body tilt. Exp Brain Res 173, 364–373. [DOI] [PubMed] [Google Scholar]
- Bosco G, Carrozzo M & Lacquaniti F (2008). Contributions of the human temporoparietal junction and MT/V5+ to the timing of interception revealed by transcranial magnetic stimulation. J Neurosci 28, 12071–12084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bosco G, Delle Monache S & Lacquaniti F (2012). Catching what we can't see: manual interception of occluded fly‐ball trajectories. PLoS ONE 7, e49381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner E, Rodriguez IA, Muñoz VE, Schootemeijer S, Mahieu Y, Veerkamp K, Zandbergen M, van der Zee T & Smeets JB (2016). How can people be so good at intercepting accelerating objects if they are so poor at visually judging acceleration? Iperception 7, 2041669515624317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner E & Smeets JBJ (2015). How people achieve their amazing temporal precision in interception. J Vis 15, 1–21. [DOI] [PubMed] [Google Scholar]
- Bringoux L, Scotto Di Cesare C, Borel L, Macaluso T & Sarlegna FR (2016). Do visual and vestibular inputs compensate for somatosensory loss in the perception of spatial orientation? insights from a deafferented patient. Front Hum Neurosci 10, 181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bringoux L, Tamura K, Faldon M, Gresty MA & Bronstein AM (2004). Influence of whole‐body pitch tilt and kinesthetic cues on the perceived gravity‐referenced eye level. Exp Brain Res 155, 385–392. [DOI] [PubMed] [Google Scholar]
- Brouwer A‐M, Brenner E & Smeets JBJ (2002). Perception of acceleration with short presentation times: can acceleration be used in interception? Percept Psychophys 64, 1160–1168. [DOI] [PubMed] [Google Scholar]
- Calderone JB & Kaiser MK (1989). Visual acceleration detection: effect of sign and motion orientation. Percept Psychophys 45, 391–394. [DOI] [PubMed] [Google Scholar]
- Ceccarelli F, La Scaleia B, Russo M, Cesqui B, Gravano S, Mezzetti M, Moscatelli A, d’ Avella A, Lacquaniti F & Zago M (2018). Rolling motion along an incline: visual sensitivity to the relation between acceleration and slope. Front Neurosci. 12:406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cerminara NL, Apps R & Marple‐Horvat DE (2009). An internal model of a moving visual target in the lateral cerebellum. J Physiol 587, 429–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen A, DeAngelis GC & Angelaki DE (2011). A comparison of vestibular spatiotemporal tuning in macaque parietoinsular vestibular cortex, ventral intraparietal area, and medial superior temporal area. J Neurosci 31, 3082–3094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Claassen J, Bardins S, Spiegel R, Strupp M & Kalla R (2016). Gravity matters: motion perceptions modified by direction and body position. Brain Cogn 106, 72–77. [DOI] [PubMed] [Google Scholar]
- Day BL & Fitzpatrick RC (2005). The vestibular system. Curr Biol 15, R583–586. [DOI] [PubMed] [Google Scholar]
- Delle Monache S, Lacquaniti F & Bosco G (2017). Differential contributions to the interception of occluded ballistic trajectories by the temporoparietal junction, area hMT/V5+, and the intraparietal cortex. J Neurophysiol 118, 1809–1823.7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Rugy A, Marinovic W & Wallis G (2012). Neural prediction of complex accelerations for object interception. J Neurophysiol 107: 766–771. [DOI] [PubMed] [Google Scholar]
- De Saedeleer C, Vidal M, Lipshits M, Bengoetxea A, Cebolla AM, Berthoz A, Cheron G & McIntyre J (2013). Weightlessness alters up/down asymmetries in the perception of self‐motion. Exp Brain Res 226, 95–106. [DOI] [PubMed] [Google Scholar]
- De Vrijer M, Medendorp WP & Van Gisbergen JaM (2008). Shared computational mechanism for tilt compensation accounts for biased verticality percepts in motion and pattern vision. J Neurophysiol 99, 915–930. [DOI] [PubMed] [Google Scholar]
- Dyde RT, Jenkin MR & Harris LR (2006). The subjective visual vertical and the perceptual upright. Exp Brain Res 173, 612–622. [DOI] [PubMed] [Google Scholar]
- Ebenholtz SM (1970). Perception of the vertical with body tilt in the median plane. J Exp Psychol 83, 1–6. [DOI] [PubMed] [Google Scholar]
- Engel KC & Soechting JF (2000). Manual tracking in two dimensions. J Neurophysiol 83, 3483–3496. [DOI] [PubMed] [Google Scholar]
- Fernandez C & Goldberg JM (1976). Physiology of peripheral neurons innervating otolith organs of the squirrel monkey. I. Response to static tilts and to long‐duration centrifugal force. J Neurophysiol 39, 970–984. [DOI] [PubMed] [Google Scholar]
- Ferri S, Pauwels K, Rizzolatti G & Orban GA (2016). Stereoscopically observing manipulative actions. Cereb Cortex 26, 3591–3610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiori F, Candidi M, Acciarino A, David N & Aglioti SM (2015). The right temporoparietal junction plays a causal role in maintaining the internal representation of verticality. J Neurophysiol 114, 2983–2990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaveau J, Berret B, Angelaki DE & Papaxanthis C (2016). Direction‐dependent arm kinematics reveal optimal integration of gravity cues. eLife, 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gentili R, Cahouet V, & Papaxanthis C (2007). Motor planning of arm movements is direction‐dependent in the gravity field. Neuroscience, 145, 20–32. [DOI] [PubMed] [Google Scholar]
- Glasauer S (1992). Interaction of semicircular canals and otoliths in the processing structure of the subjective zenith. Ann NY Acad Sci 656, 847–849. [DOI] [PubMed] [Google Scholar]
- Hamrick JB, Battaglia PW, Griffiths TL & Tenenbaum JB (2016). Inferring mass in complex scenes by mental simulation. Cognition 157, 61–76. [DOI] [PubMed] [Google Scholar]
- Hening W, Favilla M & Ghez C (1988). Trajectory control in targeted force impulses. Exp Brain Res 71, 116–128. [DOI] [PubMed] [Google Scholar]
- Indovina I, Maffei V, Bosco G, Zago M, Macaluso E & Lacquaniti F (2005). Representation of visual gravitational motion in the human vestibular cortex. Science 308, 416–419. [DOI] [PubMed] [Google Scholar]
- Indovina I, Maffei V, Pauwels K, Macaluso E, Orban GA & Lacquaniti F (2013). Simulated self‐motion in a visual gravity field: sensitivity to vertical and horizontal heading in the human brain. NeuroImage 71, 114–124. [DOI] [PubMed] [Google Scholar]
- Indovina I, Mazzarella E, Maffei V, Cesqui B, Passamonti L & Lacquaniti F (2015). Sound‐evoked vestibular stimulation affects the anticipation of gravity effects during visual self‐motion. Exp Brain Res 233, 2365–2371. [DOI] [PubMed] [Google Scholar]
- Jaeger TF (2008). Categorical data analysis: away from ANOVAs (transformation or not) and towards logit mixed models. J Mem Lang 59, 434–446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang W, Yuan X, Yin C & Wei K (2018). Visuomotor learning is dependent on direction‐specific error saliency. J Neurophysiol 120, 162–170. [DOI] [PubMed] [Google Scholar]
- Jörges B & López‐Moliner J (2017). Gravity as a strong prior: implications for perception and action. Front Hum Neurosci 11, 203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaptein RG & Van Gisbergen JAM (2004). Interpretation of a discontinuity in the sense of verticality at large body tilt. J Neurophysiol 91, 2205–2214. [DOI] [PubMed] [Google Scholar]
- Kheradmand A & Winnick A (2017). Perception of upright: multisensory convergence and the role of temporo‐parietal cortex. Front Neurol 8, 552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacquaniti F, Bosco G, Gravano S, Indovina I, La Scaleia B, Maffei V & Zago M (2015). Gravity in the brain as a reference for space and time perception. Multisensory Res 28, 397–426. [DOI] [PubMed] [Google Scholar]
- Lacquaniti F, Bosco G, Indovina I, La Scaleia B, Maffei V, Moscatelli A & Zago M (2013). Visual gravitational motion and the vestibular system in humans. Front Integr Neurosci 7, 101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacquaniti F, Carrozzo M & Borghese NA (1993). The role of vision in tuning anticipatory motor responses of the limbs In Multisensory Control of Movement, ed. Berthoz A, pp. 379–393. Oxford University Press, Oxford. [Google Scholar]
- Lacquaniti F & Maioli C (1989). Adaptation to suppression of visual information during catching. J Neurosci 9, 149–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- La Scaleia B, Lacquaniti F & Zago M (2014a). Neural extrapolation of motion for a ball rolling down an inclined plane. PLoS ONE 9, e99837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- La Scaleia B, Zago M & Lacquaniti F (2015). Hand interception of occluded motion in humans: a test of model‐based vs. on‐line control. J Neurophysiol 114, 1577–1592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- La Scaleia B, Zago M, Moscatelli A, Lacquaniti F & Viviani P (2014b). Implied dynamics biases the visual perception of velocity. PLoS ONE 9, e93020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurens J, Kim B, Dickman JD & Angelaki DE (2016). Gravity orientation tuning in macaque anterior thalamus. Nat Neurosci 19, 1566–1568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurens J, Meng H & Angelaki DE (2013). Neural representation of orientation relative to gravity in the macaque cerebellum. Neuron 80, 1508–1518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Séac'h ABL, Senot P & McIntyre J (2010). Egocentric and allocentric reference frames for catching a falling object. Exp Brain Res 201, 653–662. [DOI] [PubMed] [Google Scholar]
- Le Seac'h AB & McIntyre J (2007). Multimodal reference frame for the planning of vertical arms movements. Neurosci Lett 423, 211–215. [DOI] [PubMed] [Google Scholar]
- Leow LA, de Rugy A, Marinovic W, Riek S & Carroll TJ (2016). Savings for visuomotor adaptation require prior history of error, not prior repetition of successful actions. J Neurophysiol 116, 1603–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez C & Blanke O (2011). The thalamocortical vestibular system in animals and humans. Brain Res Rev 67, 119–146. [DOI] [PubMed] [Google Scholar]
- MacNeilage PR, Banks MS, Berger DR & Bülthoff HH (2007). A Bayesian model of the disambiguation of gravitoinertial force by visual cues. Exp Brain Res 179, 263–290. [DOI] [PubMed] [Google Scholar]
- Maffei V, Indovina I, Macaluso E, Ivanenko YP, A Orban G & Lacquaniti F (2015). Visual gravity cues in the interpretation of biological movements: neural correlates in humans. NeuroImage 104, 221–230. [DOI] [PubMed] [Google Scholar]
- Maffei V, Macaluso E, Indovina I, Orban G & Lacquaniti F (2010). Processing of targets in smooth or apparent motion along the vertical in the human brain: an fMRI study. J Neurophysiol 103, 360–370. [DOI] [PubMed] [Google Scholar]
- Maffei V, Mazzarella E, Piras F, Spalletta G, Caltagirone C, Lacquaniti F & Daprati E (2016). Processing of visual gravitational motion in the peri‐sylvian cortex: evidence from brain‐damaged patients. Cortex 78, 55–69. [DOI] [PubMed] [Google Scholar]
- Mayne R (1974). A systems concept of the vestibular organs In Vestibular System Part 2: Psychophysics, Applied Aspects and General Interpretations, Handbook of Sensory Physiology, Vol 6/2, ed. Kornhuber HH, pp. 493–580. Springer, Berlin. [Google Scholar]
- McIntyre J, Zago M, Berthoz A & Lacquaniti F (2001). Does the brain model Newton's laws? Nat Neurosci 4, 693–694. [DOI] [PubMed] [Google Scholar]
- Merfeld DM, Zupan L & Peterka RJ (1999). Humans use internal models to estimate gravity and linear acceleration. Nature 398, 615–618. [DOI] [PubMed] [Google Scholar]
- Miller WL, Maffei V, Bosco G, Iosa M, Zago M, Macaluso E & Lacquaniti F (2008). Vestibular nuclei and cerebellum put visual gravitational motion in context. J Neurophysiol 99, 1969–1982. [DOI] [PubMed] [Google Scholar]
- Mischiati M, Lin H‐T, Herold P, Imler E, Olberg R & Leonardo A (2015). Internal models direct dragonfly interception steering. Nature 517, 333–338. [DOI] [PubMed] [Google Scholar]
- Mittelstaedt H (1983). A new solution to the problem of the subjective vertical. Naturwissenschaften 70, 272–281. [DOI] [PubMed] [Google Scholar]
- Moscatelli A & Lacquaniti F (2011). The weight of time: gravitational force enhances discrimination of visual motion duration. J Vis 11. [DOI] [PubMed] [Google Scholar]
- Moscatelli A, Mezzetti M & Lacquaniti F (2012). Modeling psychophysical data at the population‐level: the generalized linear mixed model. J Vis 12. [DOI] [PubMed] [Google Scholar]
- Papaxanthis C, Pozzo T, Vinter A, & Grishin A (1998). The representation of gravitational force during drawing movements of the arm. Exp Brain Res 120, 233–242. [DOI] [PubMed] [Google Scholar]
- Perrone JA & Thiele A (2001). Speed skills: measuring the visual speed analyzing properties of primate MT neurons. Nat Neurosci 4, 526–532. [DOI] [PubMed] [Google Scholar]
- Pinter IJ, van Soest AJ, Bobbert MF, & Smeets JBJ (2012). Do we use a priori knowledge of gravity when making elbow rotations? Exp Brain Res 217, 163–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Port NL, Lee D, Dassonville P & Georgopoulos AP (1997). Manual interception of moving targets. I. Performance and movement initiation. Exp Brain Res 116, 406–420. [DOI] [PubMed] [Google Scholar]
- Russo M, Cesqui B, La Scaleia B, Ceccarelli F, Maselli A, Moscatelli A, Zago M, Lacquaniti F & d’ Avella A (2017). Intercepting virtual balls approaching under different gravity conditions: evidence for spatial prediction. J Neurophysiol 118, 2421–2434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanborn AN, Mansinghka VK & Griffiths TL (2013). Reconciling intuitive physics and Newtonian mechanics for colliding objects. Psychol Rev 120, 411–437. [DOI] [PubMed] [Google Scholar]
- Schoene H (1964). On the role of gravity in human spatial orientation. Aerosp Med 35, 764–772. [PubMed] [Google Scholar]
- Scotto Di Cesare C, Sarlegna FR, Bourdin C, Mestre DR & Bringoux L (2014). Combined influence of visual scene and body tilt on arm pointing movements: gravity matters! PLoS ONE 9, e99866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Senot P, Prévost P & McIntyre J (2003). Estimating time to contact and impact velocity when catching an accelerating object with the hand. J Exp Psychol Hum Percept Perform 29, 219–237. [PubMed] [Google Scholar]
- Senot P, Zago M, Lacquaniti F & McIntyre J (2005). Anticipating the effects of gravity when intercepting moving objects: differentiating up and down based on nonvisual cues. J Neurophysiol 94, 4471–4480. [DOI] [PubMed] [Google Scholar]
- Senot P, Zago M, Le Séac'h A, Zaoui M, Berthoz A, Lacquaniti F & McIntyre J (2012). When up is down in 0g: how gravity sensing affects the timing of interceptive actions. J Neurosci 32, 1969–1973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder L (1999). This way up: illusions and internal models in the vestibular system. Nat Neurosci 2, 396–398. [DOI] [PubMed] [Google Scholar]
- Streng ML, Popa LS & Ebner TJ (2018). Modulation of sensory prediction error in Purkinje cells during visual feedback manipulations. Nat Commun 9, 1099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz G (1978). Estimating the dimension of a model. Ann Stat 6, 461–464. [Google Scholar]
- Tarnutzer AA, Bockisch C, Straumann D & Olasagasti I (2009). Gravity dependence of subjective visual vertical variability. J Neurophysiol 102, 1657–1671. [DOI] [PubMed] [Google Scholar]
- Tresilian JR (1997). Revised tau hypothesis: a consideration of Wann's (1996) analyses. J Exp Psychol Hum Percept Perform 23, 1272–1281. [Google Scholar]
- Tresilian JR & Lonergan A (2002). Intercepting a moving target: effects of temporal precision constraints and movement amplitude. Exp Brain Res 142, 193–207. [DOI] [PubMed] [Google Scholar]
- Troje NF & Chang DHF (2013). Shape‐independent processing of biological motion In People Watching: Social, Perceptual, and Neurophysiological Studies of Body Perception, ed. Johns KL. & Shiffar M, pp. 82–100. Oxford University Press, Oxford. [Google Scholar]
- Van Pelt S, Van Gisbergen JaM & Medendorp WP (2005). Visuospatial memory computations during whole‐body rotations in roll. J Neurophysiol 94, 1432–1442. [DOI] [PubMed] [Google Scholar]
- Verheij R, Brenner E, & Smeets JBJ (2013). Gravity affects the vertical curvature in human grasping movements. J Mot Behav, 45, 325–332. [DOI] [PubMed] [Google Scholar]
- Vingerhoets RaA, De Vrijer M, Van Gisbergen JaM & Medendorp WP (2009). Fusion of visual and vestibular tilt cues in the perception of visual vertical. J Neurophysiol 101, 1321–1333. [DOI] [PubMed] [Google Scholar]
- Werkhoven P, Snippe HP & Toet A (1992). Visual processing of optic acceleration. Vision Res 32, 2313–2329. [DOI] [PubMed] [Google Scholar]
- Wolpert DM & Kawato M (1998). Multiple paired forward and inverse models for motor control. Neural Netw 11, 1317–1329. [DOI] [PubMed] [Google Scholar]
- Zago M (2018). Perceptual and motor biases in reference to gravity In Spatial Biases in Perception and Cognition, ed. Hubbard T, pp. 156–166. Cambridge University Press, Cambridge. [Google Scholar]
- Zago M, Bosco G, Maffei V, Iosa M, Ivanenko YP & Lacquaniti F (2004). Internal models of target motion: expected dynamics overrides measured kinematics in timing manual interceptions. J Neurophysiol 91, 1620–1634. [DOI] [PubMed] [Google Scholar]
- Zago M, McIntyre J, Senot P & Lacquaniti F (2009). Visuo‐motor coordination and internal models for object interception. Exp Brain Res 192, 571–604. [DOI] [PubMed] [Google Scholar]
- Zago M, La Scaleia B, Miller WL & Lacquaniti F (2011). Coherence of structural visual cues and pictorial gravity paves the way for interceptive actions. J Vis 11, 13. [DOI] [PubMed] [Google Scholar]


