Defining the Specificity of Carbohydrate–Protein Interactions by Quantifying Functional Group Contributions

Abstract

Protein–carbohydrate interactions are significant in a wide range of biological processes, disruption of which has been implicated in many different diseases. The capability of glycan-binding proteins (GBPs) to specifically bind to the corresponding glycans allows GBPs to be utilized in glycan biomarker detection or conversely to serve as targets for therapeutic intervention. However, understanding the structural origins of GBP specificity has proven to be challenging due to their typically low binding affinities (mM) and their potential to display broad or complex specificities. Here we perform molecular dynamics (MD) simulations and post-MD energy analyses with the Poisson–Boltzmann and generalized Born solvent models (MM-PB/GBSA) of the Erythrina cristagalli lectin (ECL) with its known ligands, and with new cocrystal structures reported herein. While each MM-PB/GBSA parametrization resulted in different estimates of the desolvation free energy, general trends emerged that permit us to define GBP binding preferences in terms of ligand substructure specificity. Additionally, we have further decomposed the theoretical interaction energies into contributions made between chemically relevant functional groups. Based on these contributions, the functional groups in each ligand can be assembled into a pharmacophore comprised of groups that are either critical for binding, or enhance binding, or are noninteracting. It is revealed that the pharmacophore for ECL consists of the galactopyranose (Gal) ring atoms along with C6 and the O3 and O4 hydroxyl groups. This approach provides a convenient method for identifying and quantifying the glycan pharmacophore and provides a novel method for interpreting glycan specificity that is independent of residue-level glycan nomenclature. A pharmacophore approach to defining specificity is readily transferable to molecular design software and, therefore, may be particularly useful in designing therapeutics (glycomimetics) that target GBPs.

Graphical Abstract

INTRODUCTION

The recognition of glycans present on cell surfaces as glycoconjugates lies at the heart of a number of biological processes in animals, plants, and microorganisms.¹ Non-covalent glycan–protein interactions are involved in cellular adhesion, innate immunity, bacterial, and viral infection, as well as plant defense mechanisms and other processes.^2–7 Glycan-binding proteins (GBPs), such as lectins, adhesins, toxins, antibodies, carbohydrate-binding modules, are often multimers that possess the ability to cross-link cells, which is essential for cell signaling,⁸ and the disruption of recognition can lead to conditions such as delay in muscle fiber development. The multimeric structure of most carbohydrate-binding proteins serves also to enhance the apparent affinity of binding processes through avidity effects.⁹ The affinity of monomeric carbohydrate–protein interactions is typically weaker than micromolar, and yet, the specificity appears to arise primarily from the structure of monomeric complexes.¹⁰

Much of our understanding of carbohydrate recognition has come from crystallographic studies of plant lectins, because these proteins are often relatively stable, crystallize readily, and have a wide range of receptor specificities. More recently, glycan array screening has been widely applied to define specificity. However, the specificity of lectins¹¹ and anti-carbohydrate antibodies¹² can appear complex. Nevertheless, plant lectins have found widespread use as affinity reagents in the separation and characterization of oligosaccharides and glycoconjugates¹³ and are often employed in staining and histochemistry of cells and tissues.^14–16 For example, the legume lectin from Erythrina cristagalli (ECL) is widely used as a reagent for the detection of terminal galactopyranose (Gal) residues in glycans (its canonical specificity is for Gal), yet it also binds to N-acetylgalactosamine (GalNAc) and fucosylated Gal (Fucα1–2Gal). Although its function in the legume is unknown, understanding the complex specificity of lectins, such as ECL, is fundamental to the rational design of diagnostic and therapeutic agents that target specific glycans.¹⁷

Numerous experimental methods have been used to quantify the affinity of GBP–carbohydrate interactions, including isothermal titration calorimetry (ITC), NMR spectroscopy, microscale thermophoresis (MST), biolayer interferometry (BLI), surface plasmon resonance (SPR), frontal affinity chromatography (FAC), and ELISA-based assays. Data from different experimental techniques can result in conflicting definitions of specificity, depending on the sensitivity of the method and on the presence or absence of avidity effects. This is particularly clear in the case of weak interactions, which may be observed by NMR¹⁸ or MST¹⁹ but not by glycan array screening.^20,21 Given the widespread use of glycan array screening, it has become the de facto method for defining the specificity of GBPs and, yet, often requires amplification of the signal through multimerization of the protein analyte.²² Although glycan array screening is a high throughput method capable of screening hundreds of glycans, it is often unable to detect weak monomeric interactions and does not provide structural insights into the origin of the observed specificity and cross-reactivity. While site-directed mutagenesis of the protein²³ or chemical modification of ligand²⁴ can be used to probe the mode of binding in the past, protein crystallography is by far the most widely used method to define the binding mode. However, crystallography often employs high ratios of ligand to a protein, and the ligand is typically only a small fragment of the intact glycan, leading to questions as to the biological relevance of the cocomplex.²⁵ Given the high flexibility of glycans, it is not surprising then that these complex macromolecules are resistant to crystallization, making it difficult to determine the molecular structures for all but the simplest glycan fragments. Thus, experimental techniques alone can prove to be insufficient to understand the mechanism of low-affinity carbohydrate recognition. However, when these techniques are coupled with computational analyses, it can lead to an improved grasp of the underlying reasons behind the specificity of carbohydrate–protein interactions.

From a structural perspective, binding to the protein requires the carbohydrate to form interactions (hydrogen bonds, van der Waals contacts, hydrophobic contacts) that are specific in terms of geometry and charge complementarity. Discrimination between potential binders depends on differences in affinity, which depends on the strengths of individual interatomic (or interfunctional group) interactions. However, it is challenging to quantify these interactions experimentally, as any physical alteration to the protein (such as a point mutation) or to the ligand (such as a chemical modification) could perturb more than the local interaction, aside from the significant effort that may be required. Thus, an opportunity exists to exploit computational methods to estimate the energetic contributions made by individual interacting groups. There are a number of theoretical methods capable of estimating receptor–ligand affinities with varying levels of accuracy and computational cost,²⁶ including thermodynamic integration (TI),^26,27 free energy perturbation (FEP),^28,29 replica exchange, linear interaction energy (LIE),^30–32 and MM-PB/GBSA (molecular mechanics Poisson–Boltzmann/ generalized Born surface area).^33,34 While equilibrium methods such as TI and FEP are generally more accurate than end-point methods like MM-GBSA, achieving sufficient conformational sampling is only practical for TI/FEP calculations if the ligands differ only slightly in structure; calculating the binding energy difference between ligands that differ by one or more monosaccharide is currently impractical. In contrast, MM-PB/GBSA methods are less size-limited, and by default are therefore the methods most widely applied for predicting the energetics of carbohydrate–protein complexes. Although the absolute interaction energies from MM-GBSA analyses typically overestimate the experimental binding free energies, the relative interaction energies can be useful in identifying structural features responsible for the observed experimental affinities.³⁵ Each GBSA approximation varies in the mathematical form of the energy function and on the type and number of interacting molecules included in the developmental training set. The training set for developing GB^HCT consisted of small molecules.³⁶ The GB methods GB₁^OBC and GB₂^OBC were attempts to improve on GB^HCT and included proteins and peptides.³⁷ Both GBn₁ and GBn₂ only used proteins and peptides.^38,39 None of the GB methods to date have included any carbohydrate–protein complexes, and thus, we chose not to focus on their ability to reproduce the absolute binding energies of the ligands but, rather, to examine their abilities to identify and quantify the relative contributions to binding made by specific interacting functional groups.

Here we perform molecular dynamics (MD) simulations of complexes of ECL with six ligands: lactose^40,41 (Galβ1–4Glcβ, Lac, 1), epi-lactose (Galβ1–4Manβ, Epilac, 2), N-acetyllactosamine (Galβ1–4GlcNAcβ, LacNAc, 3), N,N-diacetyllactosamine (GalNAcβ1–4GlcNAcβ, LacDiNAc, 4), fucosylated lactose (Fucα1–2Galβ1–4Glcβ, FucLac, 5),⁴⁰ and fucosylated N-acetyllactosamine (Fucα1–2Galβ1–4GlcNAcβ, FucLacNAc, blood group H trisaccharide, 6) (Figure 1). The MM-GBSA method is then used to compute absolute affinities, as well as inter-residue and intergroup interaction energies. This approach enables us to identify key components of the ligand that are responsible for the observed experimental specificity and to quantify their relative contributions. In addition, we report a novel crystal structure of ECL in complex with N-acetyllactosamine and epi-lactose, and new experimental affinities for seven di- or trisaccharides. From a theoretical perspective, the results illustrate the current accuracy limitations of the computational methods.

Figure 1.

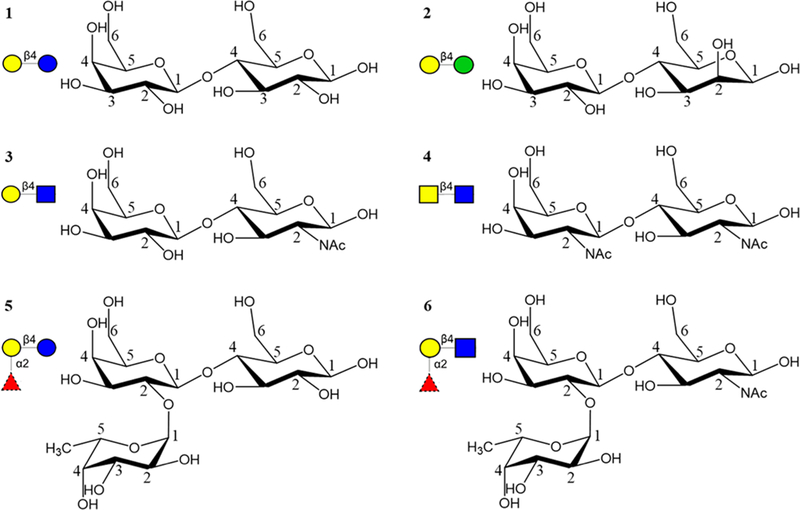
Six different ligands, i.e., Lac (1, top left), Epilac (2, top right), LacNAc (3, middle left), LacDiNAc (4, middle right), Fuclac (5, bottom left), and FuclacNAc (6, bottom right) that interact with ECL. The monosaccharides are represented in SNFG notation⁴⁶ as Gal yellow circle, Glc blue circle, Man green circle, GlcNAc blue square, GalNAc yellow square, and Fuc red triangle.

The results from the present analysis provide an explanation for the observed specificity of ECL in terms of a substructure of ligand features, leading to the definition of a ligand pharmacophore that explains the inhibitory power of a range of reported monosaccharides.⁴² The ability to computationally detect glycan pharmacophores should advance both the engineering of GBPs with modified ligand specificities⁴³ and conversely, the development of glycomimetic therapeutics.^44,45

MATERIALS AND METHODS

Crystallization.

A sample of ECL was dissolved in 100 mM NaCl, 20 mM HEPES pH 7.5, 0.1 mM CaCl₂, and 0.1 mM MnCl₂ to a concentration of ∼7 mg/mL. About 1 h prior to crystallization, the solution of ECL was combined with the aqueous solution, 0.25 mM, of the particular ligand at a molar ratio of 1:10 (ECL:ligand). Crystals were grown by the vapor diffusion at 20–22 °C using the sitting drop method. For ECL with N-acetyl-_D-lactosamine complex screening with QIA-GEN’s the JCSG Core I Suite resulted in diffraction quality crystals of pyramidal shape from several conditions: no. 10, 12, 13, 20, 22, and 31. The best crystals were obtained from either 0.2 M calcium acetate hydrate or potassium sodium tartrate and 20% PEG 3350, corresponding to conditions 20 and 22. The crystals grew from 1 μL sitting drop Intelli-Plates. Co-crystals of ECL with epi-lactose were obtained from 10 μL drops in microbridges using well solutions containing 0.2 M calcium acetate, 0.1 M HEPES pH 7.5, 14–16% PEG 3350.

Data Collection.

For both complexes, X-ray crystallo-graphic data were collected from frozen crystals at 100 K. Prior to data collection crystals were placed in a cryoprotectant solution composed of 75% well solution and 25% glycerol and then flash cooled by immersion in liquid nitrogen. For ECL-N-acetyl-_D-lactosamine complex diffraction data were collected using an ADSC Quantum 315r detector at the Advanced Photon Source (APS) on the ID19 beamline SBC-CAT to 1.9 Å resolution. For ECL-epi-lactose cocrystal crystallographic data were collected to 2.2 Å using a Rigaku HomeFlux system, equipped with a MicroMax-007 HF generator, Osmic VariMax optics, and an RAXIS-IV++ image-plate detector. X-ray diffraction data were collected, integrated and scaled using HKL3000 software suite.⁴⁷ The structure was solved by molecular replacement using CCP4 suite.⁴⁸ The structure of the binary complex of ECL with lactose (PDB ID 1UZY)⁴¹ was used as a starting model with all waters, ligands including the N-linked glycosylated saccharide, and metal ions removed. Refinement was completed using the phenix.refine program in the PHENIX⁴⁹ suite and the resulting structure analyzed with molprobity.⁵⁰ The structures were built and manipulated with program Coot,⁵¹ whereas the figures were generated using the PyMol molecular graphics software (v.1.5.0.3; Schrödinger LLC). A summary of the crystallographic data and refinement is given in Table 1.

Table 1.

X-ray Crystallographic Data-Collection and Refinement Statistics^a

	ECL-2	ECL-3
beamline/facility	Rigaku HighFlux HomeLab/ ORNL	SBC-CAT 19ID/ APS
space group	P65	P65
cell dimensions:
a, b, c (Å)	134.95, 134.95, 81.79	134.67, 134.67, 81.21
α, β, γ (deg)	90, 90, 120	90, 90, 120
resolution (Å)	40.00–2.20 (2.28–2.20)	44.08–1.90 (1.93–1.90)
Rmerge (%)b	8.50 (49.60)	6.80 (46.10)
I/σI	13.1 (2.1)	38.4 (4.4)
no. reflections measured	42764 (4263)	65144 (3227)
completeness (%)	98.8 (98.8)	99.2 (98.1)
redundancy	3.3 (3.1)	6.7 (5.8)
Rwork/Rfree (%)	18.14/20.42	22.17/26.36
no. atoms (non-H)	4142	4274
water molecules	296	394
rmsd bonds (Å)	0.003	0.007
rmsd bond angles (deg)	0.684	1.188
PDB ID	6AQ5	6AQ6

^aData in parentheses is for the highest resolution shell.

^bRmerge = å|I – ⟨I⟩|/å⟨I⟩.

BLI Binding Experiment.

ECL (cat. no.: L-1140, Vector Lab, Burlingame, CA, USA), 3 (cat. no.: A7791, Sigma-Aldrich, St. Louis, MO, USA), 1 (cat. no.: 61339, Sigma-Aldrich, St. Louis, MO, USA), 2 (cat. no.: G0886, Sigma-Aldrich, St. Louis, MO, USA), 5 (cat. no.: OF06739, Carbosynth Limited, Berkshire, UK), 6 (provided by the Consortium for Functional Glycomics), and 7 (cat. no.: 22150, Sigma-Aldrich, St. Louis, MO, USA) were purchased from their commercial resources. Biotinylated glycan Galβ1–4GlcNAcβ-OCH₂CH₂CH₂NH-biotin (LacNAc-biotin) was received as a gift from Dr. Nicolai Bovin. ECL was weighted and dissolved in the ECL buffer: 10 mM HEPES, 15 mM NaCl, 0.1 mM CaCl₂, and 0.1 mM MnCl₂ buffered at pH 7.4, at 25 °C.

Protein BLI Direct Binding Assay (K_D,surface).

Ligand (LacNAc-biotin) was loaded onto streptavidin biosensors (SA, cat. no.: 18–5019, Pall ForteBio Corp., Menlo Park, CA, USA) at 1 μM for 1800 s. Then the loaded LacNAc biosensors were dipped into 0.1 μM EZ-link Hydrazide-Biocytin (biocytin, cat. no.: 28020, Thermo Scientific, Rockford, IL, USA) for blocking the possible unoccupied biotin-SA binding sites for 1800 s. The immobilization of ligand onto SA biosensors resulted in ∼0.3 nm loading signal under this condition. ECL direct binding K_D (LacNAc biosensor surface KD) was measured using a BioLayer Interferometer (BLI) Octet Red 96 system (Pall ForteBio Corp., Menlo Park, CA, USA) and data acquired using ForteBio Data Acquisition 8.2 software (Pall ForteBio Corp., Menlo Park, CA, USA). The protein direct binding experiment was performed for 600 s for association and 1800 s for dissociation in ECL buffer. ECL was prepared in 2-fold serial dilution in ECL buffer from 0–50 μM, in the replicates of three. The surface K_D (K_{D,surfaceLacNAcbiosensor}) was calculated to be 0.92 μM with a standard deviation of 0.02 μM from triplicate measurements using the ForteBio Data Analysis 8.2 software (Pall ForteBio Corp., Menlo Park, CA, USA) assuming a 1:1 binding model.

Protein BLI Inhibition (IC₅₀) Assay and K_D Derivation.

ECL protein was prepared at 2 μM in ECL buffer. Eight compounds were tested in the inhibition assay including six inhibitors: 1, 2, 3, 5, 6 (present as the β-azido glycoside), and a non-ECL binder 7. All the compounds were prepared in 2-fold serial dilution in ECL buffer from 0,1.25, 2.5, 5, 10, 20, 40, and 80 mM. A 100 μL portion of 2 μM ECL, 20 μL of prepared inhibitor/nonbinder at its concentration, and 80 μL of ECL buffer were mixed and incubated at room temperature for 1 h. ECL inhibition assay was performed on Octet Red 96 at baseline time 120 s, association time 600 s, and dissociation time 1800 s at shaker speed 1000 rpm at room temperature, in replicates of three. IC₅₀ was calculated by using three-parameter dose–response inhibition model in GraphPad Prism 7 (GraphPad, La Jolla, CA, USA). Solution K_D values for each inhibitor were calculated from the equation: K_D,solution = IC₅₀/(1 + [ECL]/K_D,surface).⁵² IC₅₀ values and associated BLI sensorgrams are reported in Table S1 and Figure S1, respectively; inhibition curves are shown in Figure S2.

Molecular Dynamics.

Crystal structures of ECL in complex with 1, 2, 3 and 5, along with the 3D models of 4 and 6 in complex with ECL were used for performing MD simulations. The GLYCAM-Web server (www.glycam.org) was used to generate 3D structures of 4 and 6, which were then superimposed on 3 and 5 respectively to get the complex structures. All the waters of crystallization and ions were retained, while the N-glycan at N113 was removed from the crystal structures, retaining only N113. The missing hydrogen atoms were added to the protein and crystal waters using the Reduce tool, provided by AMBERTOOLS (58), which also sets the protonation state of HIS residues, and detects and corrects flipped amide or imidazole groups in the side chains of ASN, GLN, and HIS residues. The ionization states of the ionizable side chains (ASP, GLU, ARG, LYS) were set appropriately for a neutral pH, and kept in that state throughout the simulation. Hydrogen atoms in the ligand were assigned from the GLYCAM06 monosaccharide structure files using the tLeap module of AMBERTOOLS. These structures were then minimized in vacuo to get rid of any steric clashes by steepest descent (SD) minimization for 5000 steps followed by 20 000 steps of conjugate gradient (CG) minimization. The net charge on the systems were neutralized by adding counterions (6 Na⁺ ions), followed by solvation in a truncated octahedral box with pre-equilibrated TIP3P water molecules, using the tLEAP module provided by AMBER-TOOLS. Initially, the water molecules were allowed to relax around the solute, by performing SD minimization (5000 steps) followed by CG minimization (20 000 steps), while the solute atoms were restrained (500 kcal/mol-Ų). The final stage of minimization was performed without any restraints using the same SD/CG steps involved in the previous stage. Each system was then heated from 5 to 300 K over a span of 50 ps using Langevin thermostat (ntt = 3), under NVT conditions followed by a 1 ns equilibration under NPT conditions using the pmemd.cuda version of AMBER14.⁵³ The simulations were performed using the ECL monomer (extracted from the homodimer), therefore positional restraints (10 kcal/mol-Ų) were applied to the Cα atoms in the protein backbone. Nonbonded interactions were truncated at a cutoff of 8.0 Å and long-range electrostatic interactions were calculated using the PME algorithm.⁵⁴ The MD simulations were performed under the same conditions as equilibration for 100 ns.

Binding Affinity and Entropy Calculations.

Absolute binding affinity and per-residue contributions⁵⁵ were carried out on 100 000 snapshots extracted evenly from 100 ns of MD simulation using a single trajectory method with the MMPBSA.py.MPI module of AMBER.⁵⁶ The net binding energies (and entropies) were computed as the difference between those for the complex minus those for the protein and ligand. Quasi-harmonic (QH) entropies were calculated using the cpptraj module of AMBERTOOLS⁵⁷ and extrapolated to an infinite simulation period by fitting a linear regression curve to entropy as a function of inverse simulation period⁵⁸ (Figure S4). Three different sets of snapshots were obtained by extracting every third frame from a 100 ns simulation, starting from a different initial frame, generating three independent extrapolated entropies, which were then averaged to estimate the error range. For comparison to the single-trajectory approach employed to compute the QH entropies, in the case of lactose, three independent 100 ns simulations were performed, and the average entropy and standard deviation computed. The resulting average extrapolated entropy (−14.9) was found to be close to the value from the single extrapolated trajectory entropy (−14.4). The triplicate values do give a larger standard deviation (0.8) compared to the single trajectory value (0.01). Thus, for the sake of computational efficiency, the single trajectory approach was employed for the other ligands. Normal mode (NM) entropy calculations were performed using the MMPBSA.py.MPI module. The maximum number of minimization steps and criteria were set to 10 000 and 0.001, respectively. As normal-mode analysis is exceptionally computationally costly, it was performed using 100 snapshots from the simulation.⁵⁹ Nevertheless, a trial calculation using 250 snapshots from a simulation of ECL in complex with 1 resulted in a net NM entropy value (−19.2 kcal/mol) comparable to that from 100 snapshots (−19.0 kcal/mol). Conformational entropies associated with changes in the glycosidic torsion angle distributions that occur upon binding were computed using the Karplus–Kushick (KK) approach.

RESULTS

Specificity of ECL.

ECL is a legume lectin with Galβ1–4GlcNAc as the preferred binding motif. A number of experimental studies have been performed to determine and compare the affinity of ECL for various monosaccharides and sugars.^40,60 Binding studies performed here using BLI compare well with reported values obtained by ITC^40,60 and show that lactose (Galβ1–4Glcβ, 1), epi-lactose (Galβ1–4Manβ, EpiLac, 2), and fucosylated lactose (Fucα1–2Galβ1–4Glcβ, FucLac, 5) are equivalent binders, while the introduction of an N-acetyl moiety into the Glc residue enhances affinity, as in N-acetyllactosamine (Galβ1–4GlcNAcβ, LacNAc, 3) and 2′-fucosyl-N-acetyllactosamine (Fucα1–2Galβ1–4GlcNAcβ, FucLacNAc, Blood group H trisaccharide, 6) (Table 2). Neither cellobiose (Glcβ1–4Glcβ, 7) nor maltose (Glcα1–4Glcβ, 8) shows any measurable affinity for ECL. Interestingly, data from glycan array screening of ECL indicates that 1 and 5 are nonbinders, while only 3, 6, and GalNAcβ1–4GlcNAcβ (LacDiNAc, 4) are binders.⁶¹ The false negative binding observed in the glycan array data for 1 and 5 may indicate the relative weakness of the binding of these ligands and suggests a need for caution when employing glycan array screening to define glycan-binding specificity for low-affinity ligands. While affinity measurements can indicate which regions of the ligand may be important for binding, a detailed rationalization can best be obtained from examination of the 3D structures of the complexes.

Table 2.

Binding Parameters Determined by BLI Compared to Reported Values

ligand	KD (mM)	ΔG (kcal/mol)	reference ΔG40,60,a	reference ΔG40,60,b
1	0.32 (0.02)c	–4.83 (0.04)	–4.9 (0.2)	–4.8 (<0.1)
2	0.21 (0.01)	–5.08 (0.02)
3	0.08 (0.01)	–5.66 (0.04)	–5.5 (0.1)
5	0.22 (0.01)	–5.04 (0.06)		–4.8 (<0.1)
6	0.032 (0.01)	–6.21 (0.14)
D-Gal				–4.0 (<0.1)

^aExperiments performed by isothermal titration calorimetry (ITC) at 27 °C.

^bExperiments performed by ITC at 25 °C.

^cStandard deviations shown in parentheses.

Crystal Structure of ECL in Complex with 2 and 3.

To study the structural effects of the ligand binding, the crystal structure of ECL bound to EpiLac and LacNAc was determined at 2.2 and 1.9 Å resolution respectively (Table 1). The electron density maps clearly demonstrate binding of 2 and 3 in the combining site (Figure 2B and C). The X-ray structures of native ECL, two in complex with Lac (PDB ID 1UZY, 1GZC) and one with FucLac (PDB ID 1GZ9) were determined previously.^40,41 All ECL crystal structures indicate that there is only one binding site per monomer, which is characterized by a shallow groove. All the ligands occupy the same binding site with Gal and Glc residues residing in equivalent positions in each of the complexes (Figure 2). Assuming that all of the known ligands bind ECL in a similar fashion with Gal in the binding pocket, 3D models of 4 and 6 in complex with ECL were created. 3D structures for 4 and 6 ligands were retrieved from the GLYCAM-Web server (www.glycam.org), and models for their complexes with ECL were generated by superimposing the coordinates for the ring atoms on to those present in the complex with 3 and 5 respectively (Figure 2D and F).

Figure 2.

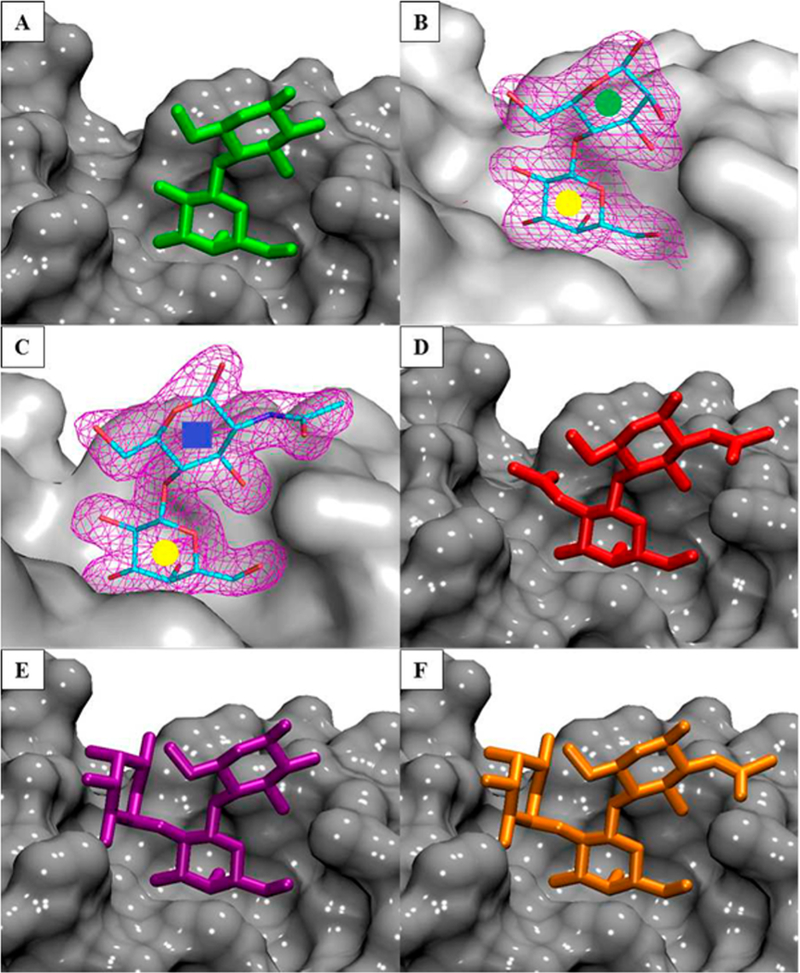
(A, B, C, E) Cocrystal structures of ECL in complex with ligands 1, 2, 3, and 5. (D, F) Modeled structure of ECL in complex with ligands 4 and 6. The protein is shown as a gray surface, and the ligands are shown as sticks. Representative 2F_o – F_c electron density maps (purple mesh at the 1.3σ level) are depicted for ligands 2 (B) and 3 (C) colored by atom type; carbon is cyan, nitrogen is blue, and oxygen is red.

The binding site for the Gal residue is formed by A88, D89, G107, and N133, which are highly conserved among related legume lectins⁶² and participate in four important H-bond interactions with the sugar. In this hydrogen-bonding network, carboxylic oxygen atoms of D89 form two equivalently strong hydrogen bonds with O4 and O3 of Gal and are H-bond acceptors, whereas both the main chain NH of G107 and NH₂ group of N133 are H-bond donors in their weaker interactions with O3 of Gal. Relative to 1, the fucosyl residue in 5, and the N-acetyl group in 3, 4, and 6 form additional hydrogen bonds and van der Waals contacts with the protein (Figure 3).

Figure 3.

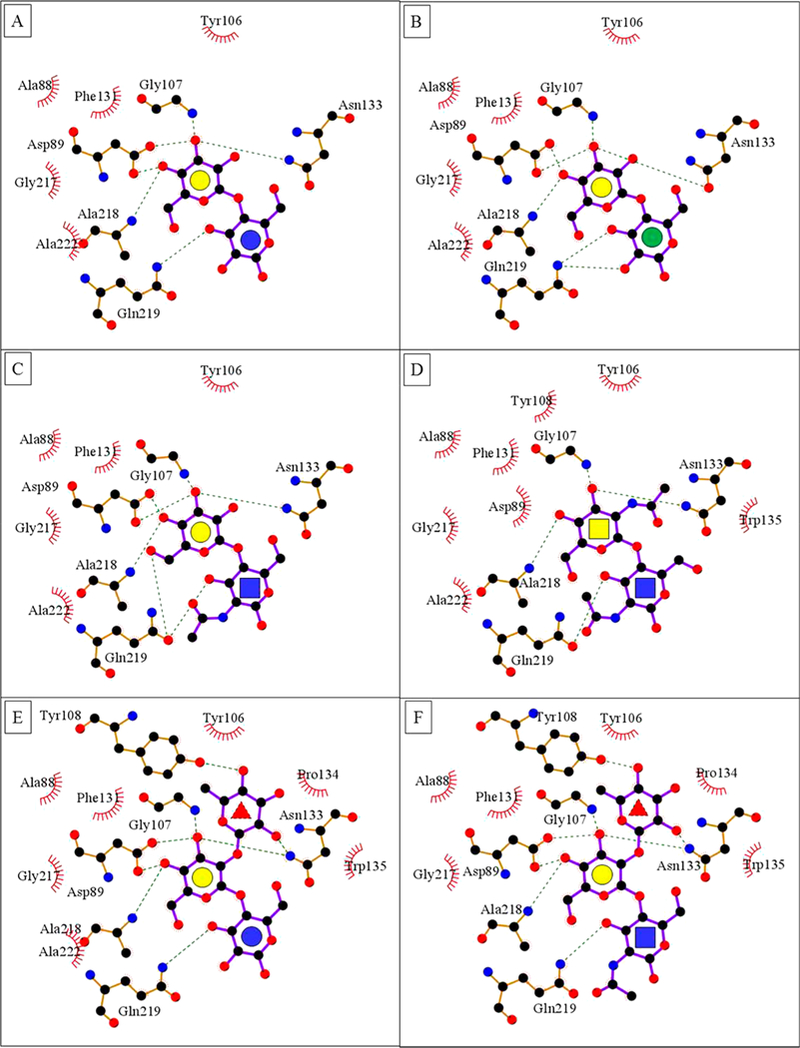
(A–F) LigPlot⁶³ contacts between the amino acids in the binding pocket of ECL and ligands 1–6. The red brackets show hydrophobic contacts, and green dotted lines show hydrogen bonds. The monosaccharides are represented as Gal yellow circle, Glc blue circle, Man green circle, GlcNAc blue square, GalNAc yellow square, and Fuc red triangle.

It is notable that despite the presence of presumably favorable interactions with the fucosyl residue, the affinity of 5 is not significantly different than 1, while ECL possesses about 3-fold higher affinity and more favorable enthalpy for 3, suggesting a need to examine the interaction energies in detail. 3D structures alone can provide at best only a qualitative guide to the impact of any given intermolecular interaction on the affinity of the ligand. Computational simulations, employing accurate 3D structures, can permit structure–function relationships to be derived that include the critical contributions from molecular motion, solvation, and entropy.

Structural Basis of Ligand Recognition.

To examine and compare the stabilities and strengths of the interactions of each of the ligands with ECL, each complex was subjected to molecular dynamics (MD) simulation (100 ns) with backbone restraints (10 kcal/mol-Ų) in the presence of explicit water, using the AMBER12SB/GLYCAM06j^64,65 force field. The ligand–protein complexes remained stable over the course of the simulations (average ligand displacement RMSD 1 = 0.86 Å, 2 = 0.83 Å, 3 = 1.03 Å, 4 = 1.09 Å, 5 = 0.85 Å, 6 = 0.97 Å; average dihedral angle for glycosidic linkages from the MD simulation remain within the standard deviation of the averages from all the known PDB structures calculated using glytorsion at http://www.glycosciences.de/tools/glytorsion/ (Table S2)), which signified that the trajectories were equilibrated and appropriate for further analysis. Consistent with the crystal structures, each of the ligands formed stable hydrogen bonds between the O3/O4 hydroxyl groups of Gal and residues D89, N133, and A218 (Tables S3 and S4). In 5 and 6, the Fuc-O2 group maintained its hydrogen bond with the side chain of N133. A hydrogen bond between the O3 group in the terminal reducing monosaccharide residue (Glc, Man, GlcNAc) in 1–6 was also observed but found to be significantly more stable in the case of GlcNAc. Although a hydrogen bond is present between Gal-O3 and G107 in all the crystal structures, it was not highly occupied over the course of the simulations. Similarly, the hydrogen bond between Fuc-O4 and Y108 in 5, present in the crystal structure, only formed occasionally during the simulation.

Quantification of Per-Residue Contributions to Affinity.

Five different generalized Born (GBSA) desolvation free energy parametrizations (GB^HCT, igb = 1;³⁶ GB ^OBC, igb = 2;³⁷ GB₂^OBC, igb = 5;³⁷ GBn₁ , igb = 7;³⁸ GBn_2, igb = 8³⁹), as well as a Poisson–Boltzmann (PBSA) model using mbondi radii were employed to estimate binding affinities of all the six complexes. Amino acids making significant interactions with the ligand were identified on the basis of their individual contributions to the total interaction energy, considering only the residues that contribute greater than 0.5 kcal/mol, which confirmed all of the expected interactions. Each PB/GBSA model predicts similar (within approximately 2.2 kcal/mol) per-residue binding energies with 1 for interactions that do not involve hydrogen-bonds (A88, A222, F131, G217, P134, W135, Y106, and Y108). For hydrogen bond forming residues, this is not the case. For example, according to GBn₁ desolvation model N133 makes a negligible contribution to binding (–0.06 kcal/mol), despite the fact that this residue is involved in a stable hydrogen bond with the ligand. The most significant per-residue variation was seen in the predicted strength of the interaction with D89, which ranged from –7.7 to +8.5 kcal/mol. As a charged residue that makes a stable hydrogen bond with the ligand, D89 would be expected to contribute significantly to binding, whereas the GBn₂ and PBSA desolvation methods both predicted its interaction to be unfavorable. Based on these observations, the GBn₁, GBn₂, and PBSA models were eliminated from further consideration, leaving GB^HCT, GB₁^OBC, and GB₂^OBC for additional analysis (Figure S5). Furthermore, as was presumed, binding affinity analysis performed using all the GBSA models was unable to rank the ligands in correct order, while PBSA model ranked every ligand correctly (Tables S5–S10, Figure S6). Therefore, absolute binding affinities and entropy effects were not a focus of this study and are discussed in the Supporting Information.

In addition, stabilizing nonpolar (van der Waals) interactions were observed between the Fuc residue and Y106, Y108, P134, and W135, which were confirmed by contact analyses of the crystal structure. Nonpolar contacts were also observed in the presence of the GlcNAc residue, stabilizing its interaction with Q219. While the presence of the GalNAc residue introduced favorable van der Waals contacts with N133, it also introduced electrostatic repulsions, reducing the overall contribution of N133 to the binding. The significance of some of these residues (A88, Y106, F131, A218, D89, N133, and Q219, among others) has been confirmed experimentally by point mutations on a closely related protein called Erythrina corallodendron lectin (ECorL).⁶⁶

On the basis of the current definition of glycan specificity, ECL is a Gal/GalNAc specific legume lectin.⁶⁷ As expected, from the perspective of the ligand, the Gal/GalNAc residues were found to be the main contributors to binding, accounting for more than 65% of the interaction energy in all cases. According to GB₁^OBC and GB₂^OBC models, the Fuc residue in 5 and 6 contributed less than 6%, consistent with the observation that fucosylation impacts the affinity only marginally (the GB^HCT model estimated the contribution from Fuc to be as high as 18.6%). The Glc and Man residues contributed less than 6.4%, while the presence of NAc group in the GlcNAc residue brings its contribution up to just over 8.6% in 3, 4, and 6 (Figure 4). Despite their general utility, per-residue interaction energies include the contributions from all atoms in the interacting residues and, so, do not provide direct measures of the strengths of specific interactions.

Figure 4.

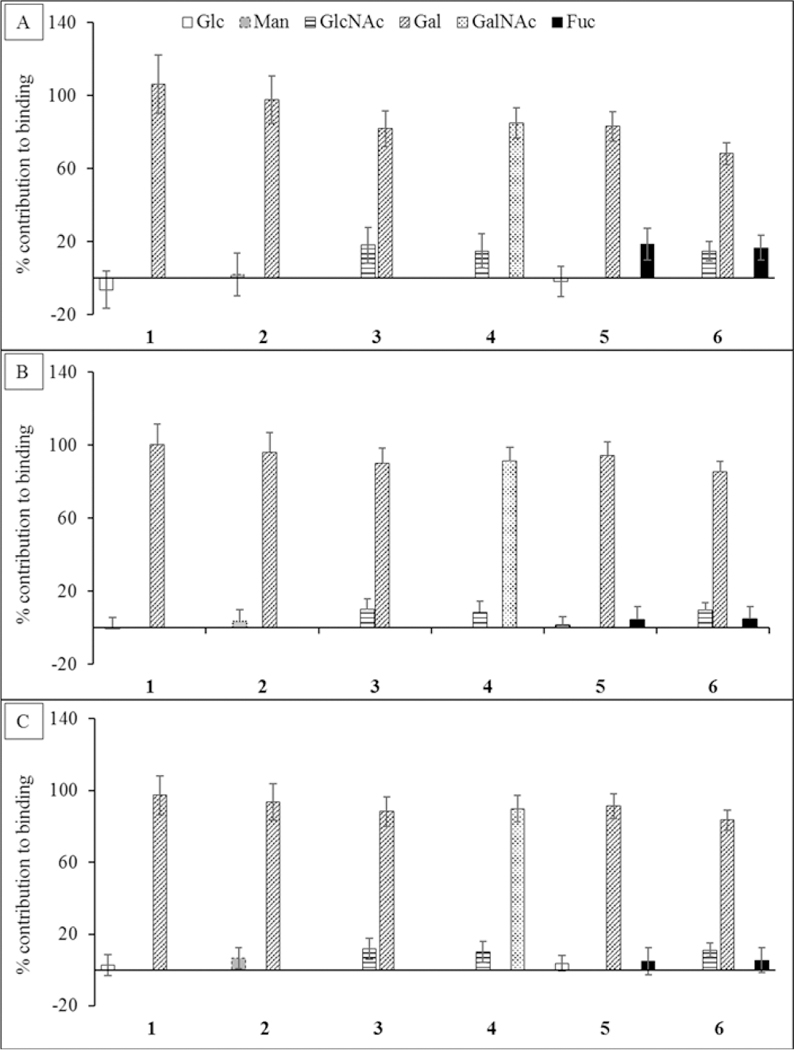
Percentage contribution to the total ΔG made by each monosaccharide in each ligand. The calculations were performed using three different desolvation models: (A) GB^HCT, (B) GB₁^OBC, and (C) GB2^OBC. In each ligand the Gal or GalNAc residue contributes the most to the total affinity.

Quantification of Per-Functional Group Contributions to Affinity.

Using pairwise decomposition of the interaction energy, with per-atom and per-residue decomposition of the ligand and the protein respectively, the strength of all the hydrogen bonds was estimated and compared. Desolvation models GB₁OBC and GB₂OBC showed that Asp89 forms two favorable hydrogen bonds (contributing over −2.4 kcal/mol) with Gal/GalNAc (O3 and O4), whereas GB^HCT model was unable to capture the interaction accurately, by either underestimating its strength or by determining it to be unfavorable (between −1.2 and 0.2 kcal/mol), eliminating the GB^HCT model from further study. Only GB₁^OBC and GB₂^OBC presented comparable results for each of the individual interactions (Figure 5).

Figure 5.

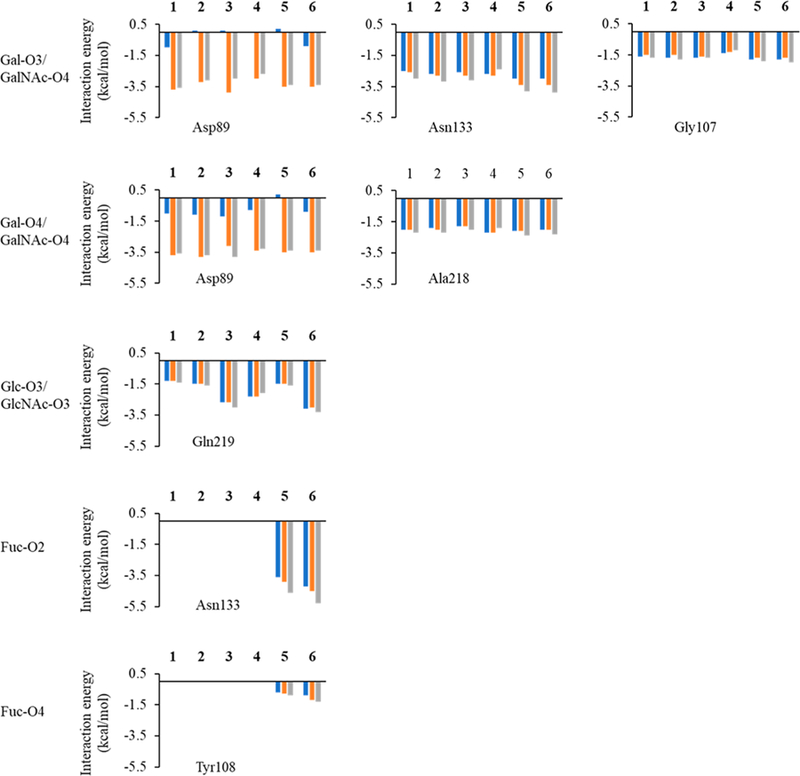
Interaction energies of per-hydroxyl group of the sugar interacting with different protein residues from the MD simulation of all of the six ECL-ligand complexes. The Gal in ligand 1 is substituted by GalNAc in ligand 4, so Gal-O3/O4 in 1 corresponds to GalNAc-O3/O4 in 4. The Glc in ligand 1 is substituted by Man in ligand 2, so Glc-O3 in 1 represents Man-O3 in 2. The Glc in ligand 1 has been substituted by GlcNAc in ligands 3 and 4, so Glc-O3 in 1 represents GlcNAc-O3 in 3 and 4. The blue bars indicate interaction energies calculated using GB^HCT (igb = 1) desolvation parameters, while orange bars indicate calculations performed using GB₁^OBC (igb = 2) and values represented by gray bars were calculated using GB₂^OBC (igb = 5) parameters.

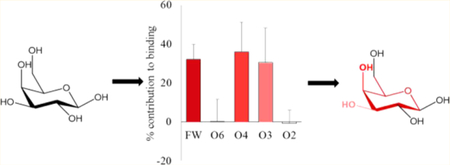
The assumption that the carbohydrate specificity of GBPs can be defined by the monosaccharide residues, fails to identify the underlying 3D structural features responsible for it. Not all exocyclic groups in a monosaccharide are equal participants in the interaction. Combining the per-atom decomposition values into contributions from individual functional groups (hydroxyl, NAc, etc.) clearly revealed which of the functional groups in the ligand were most critical for binding (Figure S7). Six functional groups were created for the Gal/GalNAc residue (four exocyclic hydroxyls, the NAc, and the ring structure including C6, which we refer to as the monosaccharide framework). The functional-group analysis showed that the main contribution to binding came from electrostatic interactions with the O3 and O4 hydroxyl groups (O3 over 25%, O4 over 20%) along with van der Waals contacts from the framework atoms of the Gal/GalNAc residue (over 18%) (Figure 6). The NAc moiety enhanced the interaction by contributing about 1 kcal/mol. It was also evident that some functional groups do not participate (such as the O6 and O2 hydroxyl groups of Gal/GalNAc residues). This approach provides an objective method to quantify features of the ligand that are critical/enhancing/unimportant for binding. Based on these observations it can be deduced that the conformation of the groups contributing most to the binding defines the minimum 3D motif required for that protein–ligand interaction.

Figure 6.

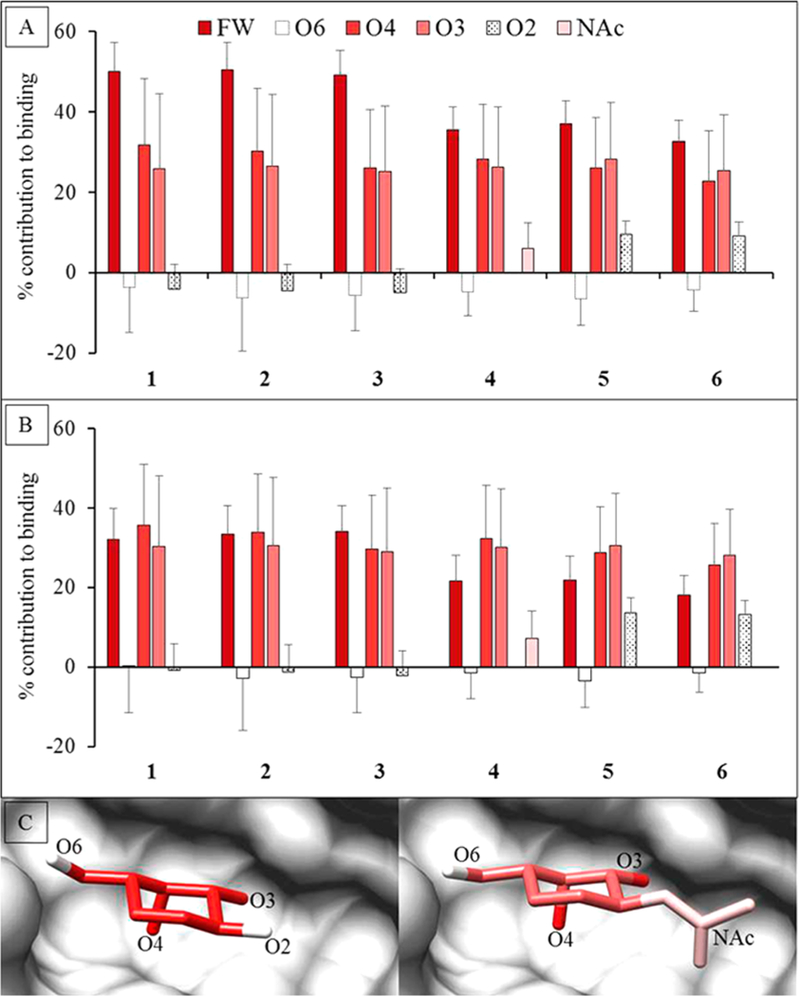
Percentage contribution to the total ΔG made by specific functional groups in the Gal or GalNAc residues. The calculations were performed using two different desolvation models. (A) GB₁^OBC and (B) GB₂^OBC. The three most important contributors to binding are the ring framework (FW) atoms, and hydroxyl groups O3 and O4. (C) Image of the D-Gal residue in Lac (1) (left) and D-GlcNAc in LacDiNAc (4) (right) interacting with ECL (gray surface). The per-functional group contribution to binding, where red to white indicates higher to lower contribution (using GB₂^OBC (igb = 5) parameters).

Carbohydrate 3D Pharmacophore.

The precise 3D spatial arrangement of functional groups in a ligand required for binding to a protein is often defined as a pharmacophore. As is evident from the present binding assays (Table 2), combined with the theoretical per-functional group contributions to binding (Figure 5), the 3D pattern that emerges as the pharmacophore required for binding to ECL is the spatial orientation of the O3 and O4 hydroxyl groups in the Gal/ GalNAc residue along with the atoms forming the terminal ring structure. This implies that molecules that mimic the pharmacophore should be able to bind to ECL, provided that no unfavorable interactions are introduced. This observation is fully consistent with the present data, as well as with ECL inhibition data reported for a range of monosaccharides by Wu et al.⁴² (Figure 7). The pharmacophore analysis predicts the binding preference of ECL in decreasing order as D-Gal ≈ D-GalNAc > D-Fuc > L-Ara > L-Rha > D-Man > D-Glc ≈ D-GlcNAc > D-Ara = L-Fuc. The poor inhibitors either lost hydrogen bond opportunities due to changes in functional group configurations (D-Glc, D-GlcNAc, L-Fuc) or formed unfavorable steric collisions (D-Ara, L-Fuc); as clashes were introduced or as the differences from the pharmacophore increased, inhibitory power decreased relative to D-Gal.

Figure 7.

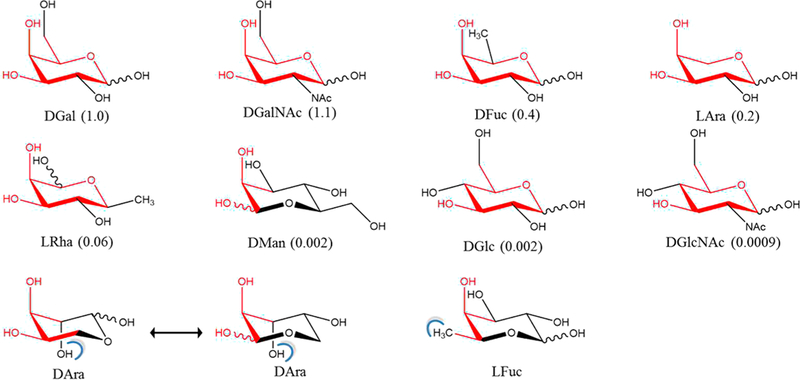
Relative ability of monosaccharides to inhibit the binding of ECL to the human asialo α1-acid glycoprotein. Relative inhibitory potentials derived from IC₅₀ values are shown in parentheses.⁴² Pharmacophore positions are indicated in red and steric clashes (determined by Chimera⁶⁸) are shown as blue brackets, based on alignment of the monosaccharides onto the Gal residue in the ECL cocrystal with lactose. The rings are oriented so as to most clearly show the similarity to D-Gal.

DISCUSSION

Lectins typically display weak (mM) binding affinities and their specificities can appear complex, particularly when defined in terms of monosaccharide-based motifs.⁶⁹ Here we introduce an alternative definition of binding motifs based on the observation that specificity arises from unique 3D arrangements of interacting groups at the stereocenters in the ligand and may comprise contributions from more than one monosaccharide. Altering the configurations at these chiral centers significantly changes the interaction with a protein, which suggests that proteins are typically specific for diastereomers. By understanding these spatial requirements, the specificity of a lectin may be defined by a subset of ligand atomic features. The ability to detect and computationally quantify these interactions and to use this information to define specificity has been illustrated here using the lectin ECL.

The affinity of ECL for a range of di- and trisaccharides has been quantified previously by ITC^40,60 and here further using a competitive assay measured by BLI,⁷⁰ which agree well with each other. As expected, the MM-GBSA calculations were unable to reproduce these absolute binding energies and trends for the ligands. Among the desolvation models used PBSA performed the best at ranking the ligand affinities. The results from binding free energy analyses employing different desolvation models, along with entropy calculations indicated that improvements need to be made in the current desolvation models. It would likely be beneficial to recalibrate the current GB/PB methods by including carbohydrate–protein interactions.⁷¹

Although no combination of solvation or entropy models led to an adequate agreement with the absolute experimental binding energies, much insight into the contributions from individual residues could be gained from a per-residue energy decomposition analysis. Most of GB/PB models identified the same set of key protein and ligand residues. However, a large variation in the contribution was seen for the negatively charged residue D89, which varied from −7.7 to +8.4 kcal/mol (Table 3). PBSA and GBn₂ desolvation models predicted the contribution from D89 to be highly unfavorable, despite the fact that crystallographic data shows that it forms hydrogen bonds with the Gal residue of the ligand, and earlier mutational studies have shown D89 to be essential for binding. While GBn₁ model could successfully identify D89 as one of the residues favorable for binding, it appears to underestimate the contribution from another essential residue (N133).⁶⁶

Table 3.

Impact of Desolvation Free Energy on Per-Residue MM-PB/GBSA Values^a

	GBHCT (igb = 1)	GB1OBC(igb = 2)	GB2OBC(igb = 5)	GBn1 (igb = 7)	GBn2 (igb = 8)	PBSA
Residues Forming Hydrogen Bonds with the Ligand
A218	−3.30	−2.63	−2.45	−1.34	−2.97	−2.98
D89	−1.54	−5.25	−6.77	−7.72	3.93b	8.45
G107	−1.30	−0.75	−0.71	−0.28	−1.32	−1.73
N133	−1.81	−0.95	−0.91	−0.06	−0.55	−2.15
Q219	−2.92	−2.23	−2.25	−1.57	−2.26	−2.04
Residues Involved in Other Interactions with the Ligand
A88	−0.88	−0.64	−0.54	−0.49	−1.13	−1.41
A222	−0.42	−0.45	−0.46	−0.66	−0.41	−0.32
F131	−2.07	−2.36	−2.53	−2.52	−2.22	−0.54
G217	−1.32	−0.32	−0.17	0.67	−0.49	−1.49
P134	−0.15	−0.19	−0.21	−0.13	−0.17	−0.14
W135	−0.03	−0.13	−0.24	−0.44	−0.09	−0.37
Y106	−2.51	−1.70	−1.68	−1.78	−2.22	−2.86
Y108	0.02	−0.08	−0.12	−0.19	−0.13	−0.17

^aEnergies in kcal/mol.

^bNumbers in bold represent residues with structurally inconsistent values.

As is common practice, all the calculations were performed with a dielectric constant of unity (ϵ = 1). It has however been suggested that using a higher dielectric value may be appropriate for systems where charge polarization is likely to be important.⁷² Given the extreme sensitivity of the contribution from D89 to the PB/GBSA model, a value of ϵ = 4 was also examined. As expected, increasing ϵ proportionally decreased the interaction energies between polar groups (Table S11), while leaving nonpolar interactions largely unaffected. However, the larger dielectric value did not correct the poor performance of the PBSA or GBn₂ models with D89. While several desolvation models showed good correlations with the experimental affinity data, when the per-residue interaction energies were examined, only the GB₁^OBC and GB₂^OBC models were consistently in agreement with expectations based on affinity data from point mutagenesis, and with the observed interactions in cocrystal structures.

By further decomposing the binding free energies on the per-group basis, it was possible to quantify the strengths of key interactions, such as hydrogen bonds (Tables S3 and S4). Such an analysis can be particularly useful in predicting or rationalizing the effects of protein mutations on ligand affinity. Conversely, this information can be crucial from the perspective of inhibitor design. A per-group energy analysis permits the identification of functional groups in each ligand that are responsible for the specificity of the interactions. The lack of participation of the Glc-O2 group explains why epimerizing 1 at C2 (i.e., converting it to a mannose in 2) resulted in equivalent binding affinities. Similarly, the O2 group of the Gal residue does not make a significant contribution to binding, thus its modification should also be tolerated, provided no new steric clashes arise. The ability to modify the ligand at the Gal-O2 position was confirmed by the binding of 4, 5, and 6. Conversely, modification of groups with a high contribution (O3 and O4 groups of Gal residue) should significantly affect the binding. For example, replacing Gal residue with its O4 epimer i.e. Glc, resulting in cellobiose (Glcβ1–4Glcβ, 7) should hamper its interaction with ECL, as demonstrated experimentally (Figures S1–S3).

Based on the range of strengths of their interactions, the functional groups could be characterized as critical, enhancing, or noninteracting. Critical groups are essential for achieving measurable affinity and define the pharmacophore. Enhancing groups improve the strength of the interaction relative to that of the pharmacophore, but are not required for binding, while noninteracting groups can be altered with no effect on binding, if doing so does not introduce unfavorable steric or electrostatic repulsions. The ability to rank the functional groups in terms of their importance to binding can be used to design novel ligands and can aid in explaining the specificity and affinity of different ligands for a protein.

By defining the glycan pharmacophore structurally, and separating it from residue-based nomenclature, it is possible to represent the pharmacophore in a number of alternative chemoinformatic formats. One such format is known as the Simplified Molecular Input Line Entry System (SMILES),⁷³ another is the IUPAC International Chemical Identifier (InChI).⁷⁴ SMILES and InChI strings are readily transferable between many software packages, facilitate the detection of similar features, and convert back to 3D structures.

CONCLUSION

Here the performance of six reported GB/PB methods, with entropy contributions from three independent methods was examined. Because of a lack of a carbohydrate specific GB/PB model or even a model that included carbohydrates in its development, it was not particularly surprising that none of the approaches, either with or without entropic corrections, reproduced the absolute experimental affinities. By performing per-residue energy decompositions on each data set, we were able to identify anomalies, such as theoretically unfavorable interactions that are known to be experimentally essential for affinity, leading us to eliminate certain GB/PB combinations from further study. Ultimately, we found that, despite weaknesses in reproducing absolute interaction energies, two methods (IGB2 and IGB5 with NM entropies) were able to correctly rank the ligand affinities and gave chemically sensible per-residue or per-functional group interaction energies. As there is a charged residue in the binding pocket of ECL, the impact of varying the internal dielectric constant was also examined⁷⁵ and found to be beneficial.

ABBREVIATIONS

GBP

glycan-binding proteins

ECL

Erythrina cristagalli lectin

MD

molecular dynamics

MM

molecular mechanics

MM-PB/GBSA

molecular mechanics Poisson–Boltzmann/generalized Born surface area

PDB

Protein Data Bank

RMSD

root mean square deviation

ITC

isothermal titration calorimetry

BLI

biolayer interferometry

SD

steepest descent

CG

conjugate gradient

QH

quasi-harmonic

NM

normal mode

KK

Karplus–Kushick

SMILES

Simplified Molecular Input Line Entry System

InChI

International Chemical Identifier