On the Bayesian interpretation of the harmonic mean p-value

I read with much interest the article by Wilson (1) on the harmonic mean $p$-value (HMP) for combining statistical significance tests. I congratulate the author on a thorough discussion of this proposal. However, I would like to point out that Good (2) had suggested the HMP already in 1958 (see also refs. 3 and 4 and references therein). Good (2) distinguishes tests in parallel from tests in series, where the latter lead to Fisher’s method while the former lead to the HMP. Both Good (ref. 2, p. 804) and Wilson (section 5 of supporting information for ref. 1) use the theorem of weighted averages of Bayes factors (5) to derive the HMP. Good’s argument is based on his empirical observation that the Bayes factor against the null hypothesis is approximately equal to $1/\left(\gamma p\right)$, where $p$ is the $p$-value and $\gamma$ is between 3⅓ and 30. The weighted average of these Bayes factors then leads to the weighted HMP. However, this approximation is quite crude since the Bayes factor is not necessarily monotonically related to the $p$-value (section 3 of ref. 6) and can even support the null hypothesis when a $p$-value would lead to its rejection (section 4.4 of ref. 7).

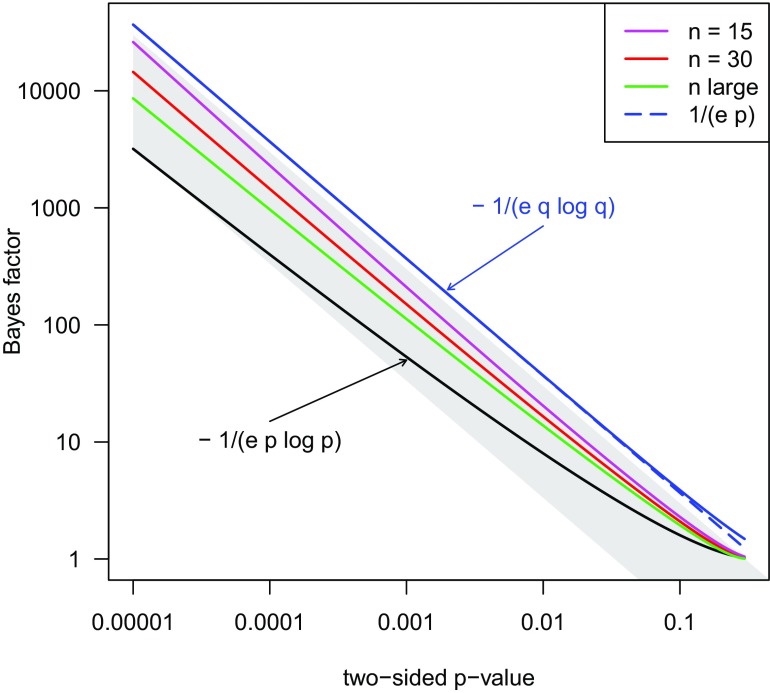
Wilson uses a Beta($\xi <1$, 1) distribution for the $p$-value under the alternative to derive optimal weights for the HMP. This class is suitable for local alternatives and leads to the popular $-1/\left\{ep\hspace{0.17em}\log \left(p\right)\right\}$ upper bound on the Bayes factor against the null (8). However, the derivation in Wilson (1) requires that all tests have good power, where Bayes factors based on simple alternatives are more appropriate and may give larger Bayes factors than $-1/\left\{ep\hspace{0.17em}\log \left(p\right)\right\}$ (6) (Fig. 1). Similar results can be obtained for one-sided $p$-values using the pCalibrate R package.

Fig. 1.

Bounds on the Bayes factor against the null as a function of the two-sided $p$-value. The bounds for small sample size $n$ are based on the $t$-distribution, for large $n$ on the standard normal distribution. Good’s range of Bayes factors $1/\left(\gamma \hspace{0.17em}p\right)$ where 3⅓ $<\gamma <30$ is represented in gray.

A promising alternative for well-powered studies is the class of Beta(1, $\kappa >1$) distributions (section 2.3 of ref. 6). The Bayes factor against the null is then bounded by $-1/\left\{eq\hspace{0.17em}\log \left(q\right)\right\}$ where $q=1-p$. This bound is also shown in Fig. 1 and is always above the bounds for the Bayes factors based on simple alternatives. For $p<0.1$ the $-1/\left\{eq\hspace{0.17em}\log \left(q\right)\right\}$ bound can be well approximated by $1/\left(e\hspace{0.17em}p\right)$, where $e\approx 2.72$ is remarkably close to Good’s lower limit 3⅓ for $\gamma$. This bound is a monotone function of the $p$-value and suggests a modification of Good’s argument to justify the HMP: If $1/\left(e{p}_i\right)$ is an upper bound for the Bayes factor for all $p$-values $p_i$ considered, then

$$\text{maxBF}=\frac{1}{e}\sum _i\frac{{\mu }_i}{p_i}$$

is an upper bound for the model-averaged Bayes factor, where ${\mu }_i$ are the prior probabilities of the alternatives. Direct transformation of the HMP $\stackrel{\circ }{p}$ with weights ${\mu }_i$ to $1/\left(e\stackrel{\circ }{p}\right)$ would give the same bound, which shows that the HMP with weights ${\mu }_i$ is compatible with an evidential interpretation of $p$-values using bounds on the Bayes factor.