Anomalous quantum criticality in the electron-doped cuprates

Significance

Understanding the normal state in superconducting cuprates is crucial to the understanding of origin of the superconductivity. It has been conjectured that many properties of the cuprates arise from proximity to a quantum critical doping. Here, by measuring the low-temperature normal-state thermopower in n-type La_2−xCe_xCuO₄, we observe a quantum critical $S/T$ versus $\text{ln}\left(1/T\right)$ behavior over an unexpectedly wide doping range x = 0.15 − 0.17. Above a Fermi surface reconstruction at x = 0.14, the slope of S/T scales with T_C, suggesting a link between the critical fluctuations and the superconductivity. In contrast to other quantum critical systems, the presence of quantum criticality over an extended doping range provides a clue to the connection between quantum criticality and superconductivity.

Abstract

In the physics of condensed matter, quantum critical phenomena and unconventional superconductivity are two major themes. In electron-doped cuprates, the low critical field (H_C2) allows one to study the putative quantum critical point (QCP) at low temperature and to understand its connection to the long-standing problem of the origin of the high-T_C superconductivity. Here we present measurements of the low-temperature normal-state thermopower (S) of the electron-doped cuprate superconductor La_2−xCe_xCuO₄ (LCCO) from x = 0.11–0.19. We observe quantum critical $\mathit{S}/\mathit{T}$ versus $\mathbf{l}\mathbf{n}\left(\mathbf{1}/\mathit{T}\right)$ behavior over an unexpectedly wide doping range x = 0.15–0.17 above the QCP (x = 0.14), with a slope that scales monotonically with the superconducting transition temperature (T_C with H = 0). The presence of quantum criticality over a wide doping range provides a window on the criticality. The thermopower behavior also suggests that the critical fluctuations are linked with T_C. Above the superconductivity dome, at x = 0.19, a conventional Fermi-liquid $\mathit{S}\propto \mathit{T}$ behavior is found for $\mathit{T}\le$ 40 K.

A quantum critical point (QCP) arises when a continuous transition between competing phases occurs at zero temperature. The existence of a QCP has been suggested in a variety of exotic materials, in particular under the superconducting dome in high-T_C copper oxides (cuprates) (1). In strongly correlated materials displaying antiferromagnetic (AFM) order, such as heavy fermions, cuprates, and iron pnictides, quantum criticality is an important theme for understanding the low-temperature physics and the superconductivity. In these materials it is believed that quantum fluctuations influence the physical properties over a wide temperature region above QCP. In this region the system shows a marked deviation from conventional Landau Fermi-liquid (FL) behavior. The superconductivity (SC) in the cuprates may be governed by proximity to a QCP, although exactly how is still a mystery despite many years of intense research on these materials (1–3). In hole-doped cuprates, a QCP has been found to be associated with the disappearance of the pseudogap phase (4–6), a phase of unknown origin. The electron-doped cuprates have a less complex doping-phase diagram and a much lower upper-critical field (7), which allows the T → 0 K normal state to be studied over the entire phase diagram. The absence of pseudogap physics, and other unidentified competing phases, allows the QCP to be attributed to the disappearance of AFM as doping is increased away from the Mott insulating state at x = 0 (8). However, the relation between quantum criticality and the normal-state behavior of the n-type (and p-type) cuprates is still an important open question.

In the past, the transport properties of the n-type cuprates near the AFM QCP have been studied primarily by electrical resistivity and Hall effect measurements (8, 9) and Shubnikov–de Hass oscillations (10, 11). These experiments, along with angle-resolved photoemission spectroscopy (ARPES) (12, 13), have given strong evidence for a Fermi surface reconstruction (FSR) at this AFM QCP, at a doping just above the optimal doping for superconductivity. In this article, we provide a surprising insight on the quantum criticality via thermoelectric measurements in the field-driven normal state of the electron-doped cuprate La_2−xCe_xCuO₄ (LCCO), for doping above and below the purported QCP. The temperature dependence of the thermopower at low temperatures provides a distinctive signature of quantum critical behavior (14).

Results and Discussion

The Seebeck coefficient (also known as thermopower) is a quantity that measures the energy dependence of the conductivity. The Seebeck coefficient is related to the electric field generated by a thermal gradient in the absence of a charge current and is defined as S = $\mathrm{\Delta }V/\mathrm{\Delta }T$, where $\mathrm{\Delta }V$ is the voltage and $\mathrm{\Delta }T$ is the temperature difference (15). The thermopower basically measures the entropy per mobile particle. The thermopower of a normal metal contains two contributions. One is related to the energy-dependent electronic parameters near the Fermi energy (E_F) and at low temperature is proportional to T/E_F. Another contribution is the phonon drag contribution, which is most important in the temperature region where a typical phonon wavelength is comparable to the Fermi wavelength and phonon–electron scattering is predominant. At the lower temperature of our present experiments the phonon drag contribution can be ignored (15).

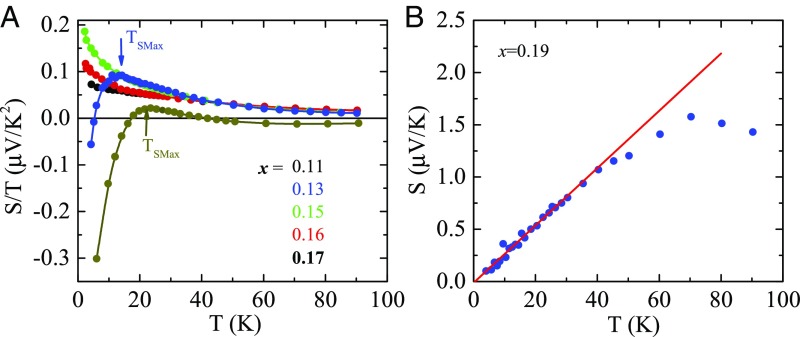
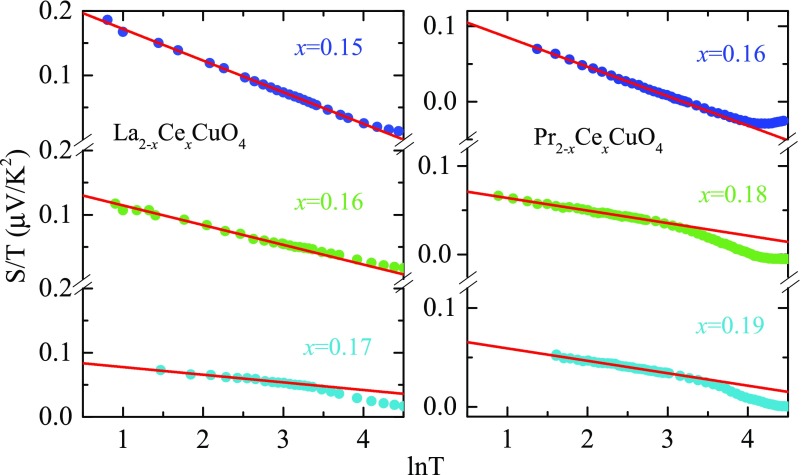
Our normal-state thermopower (S) measurements have been carried out from 2 to 80 K on LCCO thin films with doping from x = 0.11 to 0.17 in a magnetic field of H > H_C2. Detailed information on the thermopower measurement technique is given in SI Appendix (see ref. 7 for details). Fig. 1A presents the data for S (T) in the normal state below 80 K plotted as $S/T$ versus T for x = 0.11–0.17. Similar data are found for several films at each doping. For x = 0.11 and 0.13, $S/T$ displays a strong temperature dependence and below a temperature T_Smax becomes increasingly negative. This shows that electrons dominate the low-temperature normal-state thermopower for these dopings. The peak in $S/T$ decreases from T_Smax ∼ 27 K for x = 0.11 to T_Smax ∼ 15 K for 0.13. In Fig. 2 we show the data of Fig. 1A plotted as $S/T$ vs. ln T for the doping x = 0.15, 0.16, and 0.17. For all these dopings, the low-temperature behavior of S/T goes as ln (1/T), with a deviation away from this behavior at higher temperature.

Fig. 1.

(A) Seebeck coefficient (S) of LCCO for different concentrations, plotted as $S/T$ versus temperature T, measured at a magnetic field of 11 T for x = 0.11–0.17. T_Smax denotes the temperature below which $S/T$ decreases at low temperatures reaching negative values for x = 0.11 and 0.13. For x = 0.11 and 0.13 $S/T$ decreases below 26.5 and 13 K, respectively. For 0.15, 0.16, and 0.17 $S/T$ shows increasing behavior at low temperature. (B) S versus T for overdoped LCCO, x = 0.19 at zero field. The solid line is the fit to $S\propto T$ down to lowest measuring temperature, 4 K (see text).

Fig. 2.

Normal-state Seebeck coefficient for LCCO films x ≥ 0.14 and PCCO films with x ≥ 0.16, plotted as $S/T$ vs. $\text{ln}\hspace{0.17em}T$. The solid lines are a linear fit to the data. For all of the films $S/T$ exhibits $–\text{ln}\hspace{0.17em}T$ dependence down to the lowest measured temperature of around 2 K for LCCO and 3 K for PCCO.

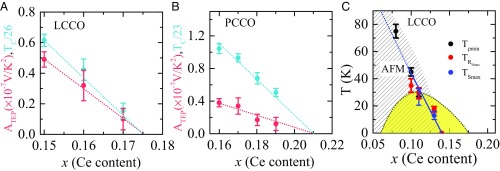
The dramatic change in the sign and magnitude of $S/T$ from the overdoped to underdoped region at 4 K is consistent with the Hall effect (16), where the 4 K value of R_H is observed to change from negative for x < 0.14 to positive above x > 0.14. As shown in Fig. 3C the normal-state Hall resistivity maxima $T_{R_{Hmax}}$ (the temperature below which Hall coefficient starts to fall) and T_Smax lie on the same line, which is the estimated FSR line, T_FSR. The T_FSR separates the large, hole-like, FSR from the reconstructed FS. In the T-x phase diagram, commensurate (π, π) spin density wave modulations have been inferred from in-plane angular magnetoresistance (AMR) measurements (17) below the FSR doping at x = 0.14. The AMR is found at doping above where long-range AFM order is claimed to end (∼0.08 in LCCO) (18), suggesting that AMR is sensitive to short-range magnetic correlations. All dramatic changes in the transport properties are observed at 0.14 doping and not at 0.08. A similar behavior is found for other n-type cuprates (8–13, 19). In addition, quantum oscillation (11) and ARPES (20) measurements have seen evidence for the reconstructed FS for x < 0.14. Further such measurements are needed to verify the existence of the large hole-like FS for x > 0.14, as suggested by our thermopower and Hall experiments. In summary, the experimental evidence to date suggests that for LCCO there is a QCP at x = 0.14 driven by short-range AFM order.

Fig. 3.

Doping dependence of A_TEP (slope of the data in Fig. 2). (A and B) A_TEP (red circles) and T_C (divided by the SC transition temperature of the optimal doped 0.11 sample, 26 K for LCCO and 23 K for PCCO; blue circles) for different dopings of LCCO and PCCO. The error bars in T_C are the standard deviation over many samples of each doping. The error bars in A_TEP are a convolution of standard deviations in the values of the slopes for different temperature ranges of fitting. (C) Temperature vs. doping phase diagram of LCCO. The black line denotes the SC transition temperature as a function of concentration and the yellow region denotes the SC dome. T_ρmin and T_RHmax are the normal-state in-plane resistivity minima and normal-state in-plane Hall resistivity maxima, respectively (19). The solid blue line (ending at x = 0.14) represents the FSR line separating the large FS from the reconstructed FS. The nearly similar values of T_RHmax, and T_Smax for x = 0.11 and 0.13 samples are evidence for the FSR. The shaded regime represents AFM region (17, 18).

One expects that fluctuations associated with this QCP at T = 0 K will impact transport (and other properties) at finite temperatures above the QCP (2). The most studied of these transport properties is the non-FL resistivity ($\rho \sim T^n$, with n < 2) at low temperatures (21, 22). In addition, in some heavy fermion materials a non-FL logarithmic temperature dependence of the low-temperature thermopower has also been observed near a magnetic QCP. For example, the thermopower in the heavy fermion YbRh₂Si₂ shows the logarithmic increase $S/T=\log \left(T/\stackrel{\sim }{T}\right)$ with $\stackrel{\sim }{T}=3$ K in the QCP regime (23) and in CeCoIn₅ the normal state S/T is observed to vary as ln T near the field-induced QCP (24).

This non–Fermi-liquid (NFL) behavior of S (T) has been interpreted to result from low-energy quasi-2D spin fluctuations associated with an AFM QCP (14). In this theory, the thermopower is given by

$$S\propto \frac{1}{e}\left(\frac{g_0^2\mathcal{N}\prime \left(0\right)}{{\mathit{ϵ}}_F{\omega }_S\mathcal{N}\left(0\right)}\right)T\hspace{0.17em}\text{ln}\left({\omega }_S/\delta \right),$$ [1]

where $\mathcal{N}\left(0\right)$ is the density of states at the Fermi energy ${\mathit{ϵ}}_F$, $g_0^2$ is the coupling between the electrons and the spin fluctuations, and ${\omega }_S$ is the energy of the spin fluctuations. Here δ measures the deviation from the critical point $\left[\delta =\text{Γ}\left(p-p_c\right)+T\right]$, where p depends on experimental parameters like doping, pressure, or magnetic field that can be tuned to the critical point. As shown in ref. 14, when T is greater than zero, the thermopower is given by $S/T\propto A\hspace{0.17em}\text{ln}\left(1/T\right)$ in proximity to the QCP, where $A=1/e\left(\frac{g_0^2\mathcal{N}\prime \left(0\right)}{{\mathit{ϵ}}_F{\omega }_S\mathcal{N}\left(0\right)}\right)$. Away from the critical point the thermopower shows a cross-over to an FL behavior $S/T\propto \text{constant}$ as T decreases.

Our thermopower data shown in Fig. 2 are in qualitative agreement with the Paul and Kotliar theory (14) at least down to 2 K. Experimentally, we find $S/T=A_{TEP}\ln \left(1/T\right)$ over a wide doping range, not just at the QCP, with no sign of a low-temperature deviation toward S/T being constant at any doping (here $A_{TEP}$ is defined as our experimental slope of S/T versus logarithmic T). This suggests an “anomalous quantum criticality” in LCCO with a quantum critical region from x ≥ 0.14 to the end of the SC dome at x_c ∼ 0.175. Above x_c we find conventional FL behavior $S/T\propto \text{constant}$ at x = 0.19 (Fig. 1B). To better understand the anomalous critical behavior in LCCO we have reanalyzed our prior thermopower data of the electron-doped cuprate, Pr_2−xCe_xCuO₄ (PCCO) measured in the normal state (25). Fig. 2 presents the temperature dependence of S/T vs. ln T for PCCO down to 3 K with doping x = 0.16, 0.17, and 0.19 at 9 T. The S/T shows a ln (1/T) dependence down to the lowest measured temperature for all of the doping and a deviation away from the ln (1/T) behavior at higher temperature. Thus, the normal-state thermopower of PCCO and LCCO has a slope A_TEP that scales monotonically with the change of T_C for different doping as shown in Fig. 3. So, this behavior appears to be universal in the electron-doped copper oxides. Our data are supported by the low-temperature normal-state resistivity behavior for LCCO, where for x = 0.15, 0.16, and 0.17 the resistivity varies linearly with temperature down to 20 mK (21). So, the breadth of the critical region in LCCO (and PCCO) suggests that the physics in the electron-doped cuprates is associated with an extended quantum phase.

In Fig. 3 A and B, we show the coefficient $A_{TEP}\left(x\right)$ of the $S/T$ logarithmic T dependence, obtained from fits to the low temperature regions with $S/T\propto \ln \left(1/\text{T}\right)$, as a function of doping for both LCCO and PCCO. A significant discovery of this work is that $A_{TEP}\left(x\right)$ decreases with T_C as x increases and goes to zero at the doping where SC ends. From the discussion of theoretical Eq. 1, we will assume that $A_{TEP}\left(x\right)=A$. Therefore, if Eq. 1 is valid for our data, then $A_{TEP}\left(x\right)$ depends mainly on the strength, g, of the coupling between the electrons and the spin fluctuations. Therefore, the strength of this coupling appears to be directly linked to the electron pairing (and hence the magnitude of T_C) in the n-type cuprates.

Fig. 1B presents our thermopower data for a non-SC of LCCO (x = 0.19, i.e., beyond the SC dome). In a conventional FL, we expect the low-temperature thermopower to follow (15)

$$S=\frac{{\pi }^2}{3}\frac{k_B}{e}\frac{T}{T_F}.$$ [2]

We use our data to estimate the Fermi temperature and the Fermi energy $\left(T_F={\mathit{ϵ}}_F/k_B\right)$ from the slope of S vs. T. We find ϵ_F ∼ 10,000 K⁻¹, which is in agreement with prior estimates for n-type cuprate from other experiments (27). The abrupt change in low-temperature thermopower behavior from non-SC, x = 0.19, to the lower SC dopings suggests that there is a dramatic change in the normal ground state in LCCO at the end of the SC dome (x_c). Prior evidence for an anomalous critical behavior at x_c has been reported (27), but the origin of this critical physics is not yet understood. This is now under investigation.

Summary

We have discovered an unexpected behavior of the low-temperature thermopower $\left[S/T\propto \text{ln}\left(1/\text{T}\right)\right]$ in the normal state of the electron-doped cuprate LCCO over an extended doping regime (x) above the FS reconstruction at x = 0.14. This suggests an anomalous quantum critical behavior in this system. Significantly, the magnitude of the slope of the logarithmic-in-T thermopower scales with the superconducting T_C, with both going to zero at the end of the SC dome. This suggests an intimate link between the quantum critical fluctuations and the Cooper pairing. We find a similar behavior in another n-type cuprate, PCCO, strongly indicating that this is a universal behavior in the electron-doped cuprates.

Materials and Methods

The measurements have been performed on c-axis-oriented LCCO thin films for the optimally doped (x = 0.11), and overdoped (x = 0.13, 0.15, 0.16, and 0.17) compositions. The thin films were deposited on (100) SrTiO₃ (10 × 5 mm²) substrates by a pulsed-laser deposition (PLD) technique utilizing a KrF excimer laser as the exciting light source (7) at a temperature of 700 °C and at an oxygen partial pressure of 230 mTorr. The thickness of the films used for this study is typically between 150 and 200 nm. The quality of the films was determined by the lowest residual resistivity of the samples and the SC transition width (∆T_C) calculated from the imaginary part of the ac susceptibility peak. The targets of the compounds for the PLD were prepared by the solid-state reaction method using 99.999% pure La₂O₅, CeO₅, and CuO powders. Details regarding the electronic measurements are provided in SI Appendix.