Regulation of T cell expansion by antigen presentation dynamics

Significance

Antigen-specific T cells proliferate multiple times during an immune reaction to fight against disease. This expansion of T cells must be carefully regulated to ensure an effective defense while avoiding autoimmunity. One challenge to regulation is that the initial size of antigen-specific T cell clones can be quite variable. Intriguingly, a recent study in mice found that the fold expansion of a T cell clone depends as an inverse power law on its initial size. We propose a simple mathematical model that naturally yields the observed power law relation. Our model accounts for multiple experiments on T cell proliferation, suggests optimal vaccination protocols, and highlights dynamics of presented antigen as a key regulator of the size of an immune response.

Abstract

An essential feature of the adaptive immune system is the proliferation of antigen-specific lymphocytes during an immune reaction to form a large pool of effector cells. This proliferation must be regulated to ensure an effective response to infection while avoiding immunopathology. Recent experiments in mice have demonstrated that the expansion of a specific clone of T cells in response to cognate antigen obeys a striking inverse power law with respect to the initial number of T cells. Here, we show that such a relationship arises naturally from a model in which T cell expansion is limited by decaying levels of presented antigen. The same model also accounts for the observed dependence of T cell expansion on affinity for antigen and on the kinetics of antigen administration. Extending the model to address expansion of multiple T cell clones competing for antigen, we find that higher-affinity clones can suppress the proliferation of lower-affinity clones, thereby promoting the specificity of the response. Using the model to derive optimal vaccination protocols, we find that exponentially increasing antigen doses can achieve a nearly optimized response. We thus conclude that the dynamics of presented antigen is a key regulator of both the size and specificity of the adaptive immune response.

During an immune reaction, antigen-specific lymphocytes proliferate multiple times to form a large pool of effector cells. T cell expansion must be carefully regulated to ensure efficient response to infections while avoiding immunopathology. One challenge to regulation is that the number of naive T cells specific to any given antigen is biased by the VDJ recombination machinery and thymic selection (1), and the total number of T cells specific to an antigen further depends on previous infections with the same or similar pathogens (2). As a result, there are large variations in the number of precursor cells before an immune response. How does the adaptive immune system properly regulate its lymphocyte expansion given varying precursor numbers?

In a study by Quiel et al. (3), transgenic ${\mathrm{C}\mathrm{D}\mathrm{4}}^{+}$ T cells specific for a peptide from cytochrome C were adoptively transferred into mice. The number of transgenic T cells was then tracked in response to immunization with cytochrome C (Fig. 1A). It was found that fold expansion of the transgenic T cells depends as an inverse power law on the number of transferred precursor cells (Fig. 1B). Here, we propose a simple mathematical model to describe the dynamics of T cell expansion. We show that the power law behavior arises naturally when T cell proliferation is limited by decaying antigen availability, and we predict how the power law exponent is related to the rates of lymphocyte proliferation/death and of antigen decay. Our proposal adds to previous modeling efforts to explain the surprising power law relation in terms of negative feedback regulation (4) or the active depletion (also known as grazing) of peptide–MHCs (pMHCs) by T cells (5). Furthermore, in contrast to these previous studies, which did not explore the effect of T cell affinity for antigen and neglected the role of antigen decay, our model readily explains the dependence of T cell expansion on antigen affinity (6) and on the kinetics of antigen administration (7). We thus identify the dynamics of presented antigen as a key regulator of the size of an immune response.

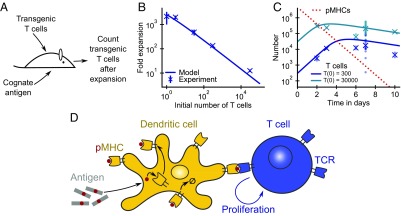
Fig. 1.

Limitation of T cell expansion by antigen decay can explain the power law dependence of fold expansion on the initial number of cognate T cells. (A) Transfer of transgenic T cell clones into recipient mice allows for monitoring of T cell proliferation in vivo in response to cognate antigen stimulation (3, 6). (B and C) Comparison of experimental data from ref. 3 with model predictions. (B) Factor of expansion at day 7 as a function of the number of precursor T cells (crosses, geometric mean; error bars, $\pm$SE). (C) T cell and pMHC number vs. time for 300 and 30,000 initial transgenic T cells (crosses, geometric mean; dots, individual mice). (D) Schematic of the model. Dendritic cells take up antigens, process them into short peptides, and present these on MHCs on their surfaces. T cells bind to pMHCs via TCRs. Recognition of cognate pMHC stimulates T cells to proliferate, and continual antigen stimulation is needed to maintain proliferation. Turnover of pMHCs leads to decay of presented peptides over time. Fitted model parameters and asymptotic SEs: $\alpha =1.5\pm 0.3$/d, $\mu =1.2\pm 0.5$/d, $\delta =0.22\pm 0.21$/d, and $C\left(0\right)=10^{6.7\pm 1.1}$. We fixed $K=0.0$ (upper bound from fit $\simeq 700$).

Results

A Simple Model Explains Power Law Dependence of Fold Expansion on Precursor Number.

We propose a minimal model of T cell expansion in which T cell proliferation is regulated by the level of presented cognate antigen (Fig. 1D). Our model has two experimentally motivated features: T cells proliferate at a saturated rate at high pMHC concentrations (3), and pMHC turnover leads to decaying antigen levels over time (8, 9). We describe the dynamics of the number of specific T cells, $T$, and cognate pMHCs, $C$, using the equations

$$\frac{\mathrm{d}T}{\mathrm{d}t}=\alpha \frac{TC}{K+T+C}-\delta T$$ [1]

$$\frac{\mathrm{d}C}{\mathrm{d}t}=-\mu C.$$ [2]

Eq. 1 describes a population of T cells that proliferate at rate $\alpha C/\left(K+T+C\right)$ and die at rate $\delta$. The rate of proliferation depends on how much antigenic stimulus the average T cell receives, which depends on the amount of presented antigen, the number of competing T cells, and a parameter $K$ related to the affinity of the T cells for the antigen. The functional form of the proliferation rate can be motivated mechanistically under the presumption that proliferation is proportional to the number of T cells bound to pMHCs (10) (SI Appendix, SI Text, section 1). From a phenomenological perspective, the proliferation term in Eq. 1 captures the effective dependence of proliferation on the various parameters. When antigen is abundant, all specific T cells receive sufficient stimulus and proliferate at a maximal rate $\alpha$. By contrast, when T cell numbers are large compared with the level of antigen, the proliferation rate is proportional to $C$, because antigen becomes limiting. Finally, low-affinity antigens (large $K$) can drive proliferation but only at sufficiently high antigen concentrations. Considering the limit of small $T$ shows that $K$ sets the concentration of antigen at which the proliferation rate is one-half of its maximum. The parameter $K$ thus represents the overall functional avidity of the T cells for the antigen, which depends approximately linearly on the dissociation rate of an individual T cell receptor (TCR) from a pMHC complex (11).

Eq. 2 describes how the number of presented antigens decays over time (with the initial pMHC number established through a prior relatively fast process of antigen uptake and processing). This decay, which has been measured directly in experiments (8, 9), is mediated by a number of mechanisms, most prominently the turnover of MHCs by ubiquitylation (12) and the apoptosis of activated antigen-presenting cells (13). As we show below, the changing level of presented antigens implied by this decay plays a key role in regulating T cell expansion.

Given the simplicity of the model, we can readily understand its dynamics. Assume that, for small times, the amount of pMHCs is saturating for T cell binding, $C\left(t\right)\gg K$ and $C\left(t\right)\gg T\left(t\right)$, so that T cells proliferate exponentially, $T\left(t\right)\simeq T\left(0\right)e^{\left(\alpha -\delta \right)t}$. Exponential proliferation proceeds until the pMHC concentration $C\left(t\right)\simeq C\left(0\right)e^{-\mu t}$ decays below the saturation level. This occurs at a transition time $t^{\star }$ when one of two conditions for saturation is no longer fulfilled [i.e., when $C\left(t^{\star }\right)\approx T\left(t^{\star }\right)$ or when $C\left(t^{\star }\right)\approx K$, whichever comes first]. The former case implies a slowdown of expansion due to competition among T cells for antigen binding, and the latter implies a slowdown due to the limited affinity of the T cells for the antigen (with a cross-over between the two as shown in SI Appendix, Fig. S1).

We first consider the competition-limited regime, in which the characteristic time $t^{\star }$ is set by $C\left(t^{\star }\right)\approx T\left(t^{\star }\right)$, which together with Eqs. 1 and 2, implies

$$t^{\star }=\frac{1}{\alpha -\delta +\mu }\ln \frac{C\left(0\right)}{T\left(0\right)}.$$ [3]

After this time, proliferation of T cells rapidly slows down as pMHC levels continue to decline. Neglecting the small additional T cell proliferation plus decay beyond this time (SI Appendix, Fig. S2), the peak fold expansion is given by

$$\frac{T\left(t^{\star }\right)}{T\left(0\right)}\approx {\left(\frac{C\left(0\right)}{T\left(0\right)}\right)}^{\left(\alpha -\delta \right)/\left(\alpha -\delta +\mu \right)}.$$ [4]

Thus, the model naturally yields an inverse power law dependence of T cell amplification $T\left(t^{\star }\right)/T\left(0\right)$ on the initial T cell population $T\left(0\right)$. Additionally, Eq. 3 predicts an earlier occurrence of the peak in the population size at higher precursor numbers.

Both of these robust predictions of the model hold true in the experimental data of Quiel et al. (3) (Fig. 1). Moreover, as shown in Fig. 1B, the model can quantitatively account for the experimental data on the relationship between the number of precursor transgenic ${\mathrm{C}\mathrm{D}\mathrm{4}}^{+}$ T cells and fold expansion—here defined as the number of transgenic T cells at day 7 divided by the number of transgenic T cells at day 0—as well as for the time courses of transgenic T cell population sizes (Fig. 1C). The few parameters of the model can be readily inferred from the data. The rate of decay of T cell numbers after their peak sets $\delta$. The initial rate of increase of T cell number is given by $\alpha -\delta$, which sets $\alpha$. The experimentally observed power law exponent of $\approx -0.5$ implies that $\alpha -\delta \approx \mu$, from which we can infer $\mu$. We obtain an upper limit on the saturation constant $K$ from the observation that the power law holds down to the smallest experimental precursor numbers (Fig. 1B), as the scaling would have broken down if the condition $K\ll C\left(t^{\star }\right)$ was not fulfilled for the smallest precursor numbers (SI Appendix, Fig. S3). Finally, the model naturally recapitulates the observed biphasic time course of T cell expansion: exponential proliferation at early times followed by a cross-over into a phase of more slowly exponentially decreasing T cell numbers.

Importantly, our model makes concrete predictions regarding how the fold expansion depends on system parameters. For example, according to Eq. 4, it predicts the dependence of the power law exponent of fold expansion on the rates of T cell proliferation/decay and antigen decay. It also predicts a uniform increase in fold expansion if $C\left(0\right)$ is increased. This has been observed experimentally (figure 5A in ref. 3): an increase in either the antigen dose or the number of antigen-presenting cells leads to a uniform multiplicative increase of fold expansion across precursor numbers.

Our model further predicts that a transfer of the same number of transgenic T cells after a time delay $t_{\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{y}}$ relative to antigen administration will lead to a smaller fold expansion. During the time delay, pMHC decays, which implies that $C\left(t_{\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{y}}\right)$ is lower than at the time of antigen administration ($t=0$) by a factor of $e^{-t_{\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{y}}\mu }$. Fold expansion scales with the antigen concentration at the time of transfer (Eq. 4). Thus, the fold expansions in the delayed transfer and simultaneous transfer experiments are related by $T\left(t_{\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{y}}^{\star }\right)/T\left(t_{\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{y}}\right)\approx e^{-t_{\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{y}}\mu \left(\alpha -\delta \right)/\left(\alpha -\delta +\mu \right)}T\left(t^{\star }\right)/T\left(0\right)$ (i.e., fold expansion is lower by a factor that is exponential in the time delay) (SI Appendix, Fig. S4). In contrast, if antigen grazing dominates as a source of early pMHC loss (5), then a later transfer of T cells should not impact fold expansion. Time delay experiments thus provide a means to ascertain how much antigen loss is due to T cell-independent mechanisms and how much is due to grazing.

Our model formulation has been kept deliberately simple to highlight our proposed explanation for the power law relation observed in ref. 3: namely, competition among an exponentially increasing number of T cells for an exponentially decreasing number of pMHC complexes. The model can be extended in a number of ways without altering the basic behavior. First, one might ask how the results change for a more complicated dynamics of the pMHC number that includes the initial uptake and processing of antigen by the antigen-presenting cells as was done in ref. 5. A simple analysis shows that the power law scaling continues to hold as long as there is no new processing of antigen into pMHC for times larger than the smallest $t^{\star }$ (SI Appendix, SI Text, section 2). Second, one can modify the dynamical equations to include the added effect of T cell grazing of antigen (5, 14, 15) while keeping the other aspects of the model intact (SI Appendix, SI Text, section 3). Simulations and mathematical analysis of this modified decay plus grazing model show that it exhibits similar dynamics and can also fit the experimental data. Both models have in common the same robust mechanism for generating a power law: T cells proliferate at a constant rate until the exponential decay of cognate pMHCs causes proliferation to cease.

Dependence of T Cell Expansion on Antigen Affinity.

T cells only respond to ligands that bind sufficiently strongly to their TCR, which is the basis of the specificity of the adaptive immune system. Above this binding threshold, there is a large range of possible affinities that can stimulate T cell expansion. How does the affinity of a T cell clone for the pMHC, as typically measured by a dissociation constant, affect its expansion? In our model, affinity is captured by the parameter $K$, which is equal to the concentration of free pMHC at which the proliferation rate of the T cells is half-maximal in the noncompetitive regime. Clearly, affinity is important whenever pMHC concentrations are near or below $K$. Applying our model to affinity-limited expansion in the context of a pMHC concentration that is decreasing over time makes specific predictions about how T cell proliferation depends on affinity. Additionally, we demonstrate that affinity can play an important role in expansion for mixtures of T cells of different affinities even if pMHC concentrations are higher than all $K$ values.

When proliferation of T cells is limited by their antigen affinity, low-affinity T cells stop proliferating earlier, and consequently, their fold expansion is smaller. In contrast to the competitive regime (Eq. 3), the characteristic time $t^{\star }$ at which exponential proliferation stops is now set by $C\left(t^{\star }\right)\approx K$. This yields a logarithmic dependence of $t^{\star }$ on the binding constant

$$t^{\star }=\frac{1}{\mu }\ln \left(C\left(0\right)/K\right),$$ [5]

and we find that the fold expansion scales as

$$\frac{T\left(t^{\star }\right)}{T\left(0\right)}\approx {\left(C\left(0\right)/K\right)}^{\left(\alpha -\delta \right)/\mu }$$ [6]

(i.e., as an inverse power law with respect to $K$).

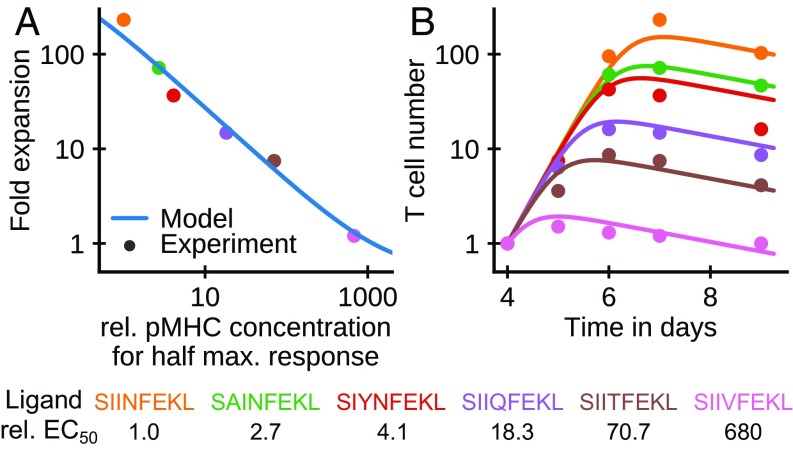
Zehn et al. (6) have studied the effect of antigen affinity on ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell expansion using adoptive transfer experiments. Assuming that Eq. 1 also describes the dynamics of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells, Eqs. 5 and 6 make testable predictions for how the timing and magnitude of the peak expansion should depend on affinity in these experiments. In their study, the expansion of transgenic OT-1 T cells was tracked in response to an infection by Listeria monocytogenes. Different strains of the bacterium were engineered to express altered ligands with different affinities for the transgenic T cells. This experimental design allowed direct study of how T cell expansion depends on antigen affinity in vivo. A reanalysis of the published data confirms our model predictions that the fold expansion depends as a power law on antigen affinity (Fig. 2A, data points) and that peak population sizes are reached earlier when affinity is lower (Fig. 2B, data points). Moreover, our model can fit the data quantitatively. To this end, we set $K$ to the experimentally determined concentration of pMHC (${\mathrm{E}\mathrm{C}}_{50}$) needed for one-half of T cells to show a detectable IFN-$\gamma$ response (Fig. 2). We then fit the rates $\alpha ,\mu ,\delta$ as well as the day 4 pMHC concentration $C\left(4\right)$ and T cell number $T\left(4\right)$ to the time course data. In the affinity-limited regime, the denominator in Eq. 1 can be approximated by $K+C$, which makes the equation linear in $T$ and thus, independent of the relative T cell and pMHC numbers. Since the $K$ values are taken from the measured ${\mathrm{E}\mathrm{C}}_{50}$ values, the curves have no free parameters to adjust independent of each other. Nevertheless, the fitted model closely reproduces both the observed dependence of the fold expansion on the affinity (Fig. 2A) and the full time courses of T cell numbers for different affinities (Fig. 2B).

Fig. 2.

Limitation of T cell expansion by antigen decay can account for the power law dependence of fold expansion on affinity. (A and B) Comparison of data from an experiment with L. monocytogenes strains expressing different antigens (see legend for their amino acid sequence) (6) with model predictions. (A) Factor of expansion of the transgenic T cells at day 7 relative to day 4 vs. the relative concentration of different pMHCs needed to elicit half-maximal IFN-$\gamma$ response from the T cells (${\mathrm{E}\mathrm{C}}_{50}$ relative to antigen SIINFEKL’s $\sim 8\hspace{0.17em}\mathrm{p}M$). (B) T cell number vs. time for the different strains. Fitted model parameters and asymptotic SE: $\alpha =2.47\pm 0.13$/d, $\mu =3.1\pm 0.3$/d, $\delta =0.23\pm 0.06$/d, $C\left(4\right)=10^{3.22\pm 0.17}$, and $T\left(4\right)=0.92\pm 0.10$. The number of transgenic T cells is calculated from their fraction $f$ of total T cells as $f/\left(1-f\right)$, with the number at day 4 set to 1. $K$ was set equal to the relative ${\mathrm{E}\mathrm{C}}_{50}$ values of the different ligands.

So far, we have considered proliferation of a clone of T cells with a particular affinity for the pMHCs. However, the preinfection T cell repertoire specific to an antigen is typically broad, with many different T cell clones of different affinities participating. How does the presence of other T cells of different affinities affect proliferation of a particular T cell clone? Following ref. 10, we generalize our competitive binding model to multiple T cell populations of varying affinities (SI Appendix, SI Text, section 1). When pMHCs are abundant, the presence of other T cells with different affinities does not change proliferation of individual clones (SI Appendix, Eq. S20). However, when T cells are competing for antigens, high-affinity T cells enjoy preferential binding to antigen, with the magnitude of the preference set by the affinity ratio (SI Appendix, Eq. S21). Interestingly, this implies that, even for pMHC concentrations well above all T cell affinities, the higher-affinity T cells proliferate much faster (Fig. 3).

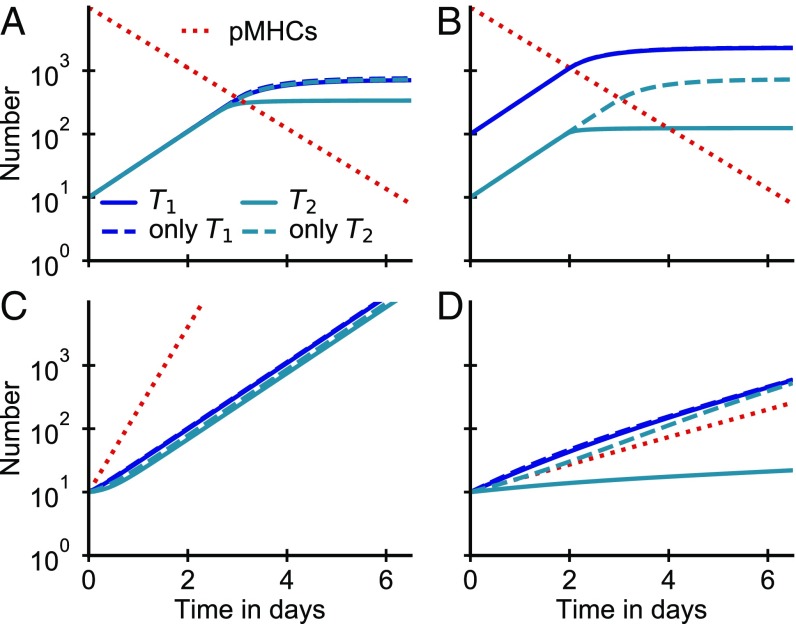
Fig. 3.

High-affinity T cells can outcompete low-affinity T cells for access to pMHCs, even when pMHC concentrations exceed all T cell affinities. (A–D) Comparisons of the time courses of expansion of mixtures of two types of T cells with high, $K_1=1$, and low, $K_2=10$, affinities (solid curves) with the expansion of the T cells on their own (dashed curves). (A and B) Proliferation driven by a large but exponentially decreasing number of pMHCs ($\mu =1.1$) starting from equal (A) and unequal (B) initial T cell numbers. (C and D) Proliferation driven by a small but exponentially increasing number of pMHCs mimicking antigen dynamics early in an infection [$C\left(t\right)\propto e^{\gamma t}$]. Competition outcome depends strongly on whether pMHC levels increase faster ($\gamma =3$; C) or slower $\gamma$ = (0.5; D) than T cells proliferate. Parameters: $\alpha =1.2$ and $\delta =0$.

How differential proliferation of T cells of different affinities affects overall fold expansion depends on both the onset and the extent of the competitive regime. For example, consider the dynamics of two T cell clones with relatively high and low affinities for the same pMHC antigen (Fig. 3). If the pMHC concentration declines from a very high saturating initial level, most of the expansion happens before the onset of competition, and therefore, the overall difference in fold expansion is low (Fig. 3A). However, high-affinity T cells can still effectively shut off proliferation of a smaller population of low-affinity T cells before these would stop proliferating on their own, resulting in a lowered fold expansion of the low-affinity T cells (Fig. 3B). In the experiments of Zehn et al. (6), the transgenic T cell clones expanded to comparable numbers at day 4 when stimulated by antigens with different affinities (Fig. 2B), which suggests that affinity did not play a major role in the first 4 d of expansion. In our model, initial T cell expansion is independent of affinity as long as the pMHC concentration rises quickly to levels that saturate proliferation for all T cells (Fig. 3C). By contrast, if pMHC concentration rises more slowly than the maximum rate of T cell proliferation, high-affinity T cells can outcompete low-affinity T cells for pMHCs and thereby, suppress expansion of the low-affinity T cells (Fig. 3D).

In summary, the same model used to explain the power law dependence of expansion on initial cell numbers for ${\mathrm{C}\mathrm{D}\mathrm{4}}^{+}$ T cells is also able to quantitatively explain the effect of affinity on ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell expansion. The two experiments reveal limiting cases of the model: competition limited vs. affinity limited. In between these limiting cases, the effects of antigen affinities, T cell numbers, and pMHC concentrations combine in interesting ways to differentially influence T cell expansion.

Dependence of T Cell Expansion on Antigen Kinetics.

A recent experimental study with mice (7) has shown that spreading vaccine antigen administration into multiple smaller doses instead of using a single larger dose can increase ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell responses. Is our model consistent with this observed dependence of T cell expansion on antigen dosing?

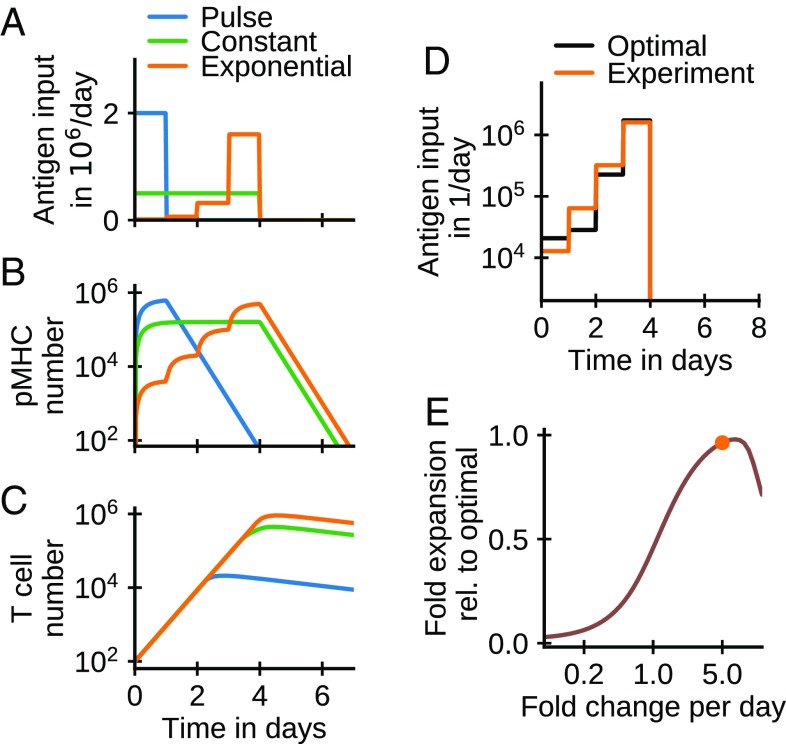
To address this question, we add a time-varying antigen input rate $\nu \left(t\right)$ to Eq. 2 (Materials and Methods, Eq. 8). We simulate the system of equations for three cases with equal total antigen input but different schedules (Fig. 4A): (i) a single antigen pulse of 1-d length, (ii) constant input over 4 d, and (iii) exponentially increasing input over 4 d. These inputs lead to markedly different pMHC levels over time (Fig. 4B). To mimic the experimental protocol of ref. 7, we analyze the impact of these different pMHC kinetics on T cell numbers at day 6 (Fig. 4C). We find that the exponentially increasing input leads to the largest T cell expansion (orange curve in Fig. 4C), ahead by a factor of two relative to constant antigen dosing (green curve in Fig. 4C) and the single-shot protocol (blue curve in Fig. 4C). While the experiment shows a larger fold advantage of the exponential protocol over the constant protocol, our model correctly predicts the observed order of response amplitudes. Our model provides a simple explanation for the different potencies of the protocols. Early on when T cell numbers are very low, even low pMHC concentrations are sufficient for all T cells to proliferate at their maximal rate. Later on, as T cell numbers increase, competition of T cells for pMHC can limit their expansion. Ideally, pMHC levels should rise in tandem with T cells to minimize competition and maximize stimulation at all times. By contrast, dosing schedules with high levels of pMHCs at early times are wasteful of the finite antigen budget: While initial pMHC levels are higher than needed for full T cell stimulation, these levels decay to become insufficient to stimulate the rising T cell population at later times. The exponentially increasing input protocol better synchronizes antigen levels with T cell proliferation and therefore, leads to a higher fold expansion. Indeed, we find that an optimized daily dose protocol is close to the experimentally used exponential protocol (Fig. 4D) using the derived parameters for CD8⁺ T cells from Fig. 2. It is worth noting that the experimental choice of fivefold increases of dose per day (7) is surprisingly close to optimal among exponential protocols (Fig. 4E).

Fig. 4.

Impact of antigen kinetics on T cell proliferation. (A) Antigen input schedules: single pulse, constant input, and exponentially increasing input (increase each day by fivefold as in ref. 7). (B) Dynamics of pMHCs. (C) Dynamics of T cells. (D) The optimal schedule is close to the experimentally used exponential schedule. The antigen input schedule over 4 d that optimizes fold expansion at day 6 was computed numerically using a projected gradient algorithm (16). (E) Fold expansion for exponential schedules as a function of the fold increase per day, with the experimental schedule indicated by the dot. Parameters: $\alpha$, $\mu$, and $\delta$ as in Fig. 2; $K=10$; $C\left(0\right)=0,T\left(0\right)=100$; and total administered antigen is $2\cdot 10^6$.

Discussion

Prompted by the surprising observation of a power law dependence of T cell fold expansion on initial cell numbers (3), we developed a simple mathematical model in which T cell proliferation is stimulated by a dynamically changing number of cognate pMHC molecules and showed that it naturally yields the observed power law. We then explored more generally how T cell numbers, TCR affinity for antigen, and the dynamics of pMHC presentation combine to regulate T cell expansion in different regimes. Testing these results against other experimental datasets, we found that our model correctly predicts a power law dependence of T cell expansion on affinity for low-affinity antigens (6), a quantitative relationship that had not previously been appreciated. With regard to vaccination, our model furthermore predicts the observed enhanced efficacy of stretching a fixed total antigen dose over several days (7) and provides testable predictions for how to optimize antigen dosing.

The core of our model is that T cell expansion is regulated by dynamically changing levels of presented antigens. The dynamics of pMHCs is assumed to be characterized by a fast processing of antigens by antigen-presenting cells followed by a slower decay. The first assumption of rapid processing seems well justified for the subcutaneous injection of antigens used in ref. 3 but might be more questionable in ref. 6, where live replicating bacteria are used, as this might lead to continued processing of new antigens by dendritic cells. However, as the bacterial load declines rapidly after reaching a peak at 3 d postinfection (17, 18), newly generated pMHCs likely play a small role compared with the turnover of the already presented pMHCs at the late stages of infection analyzed in Fig. 2. The second assumption of the decay of presented pMHCs is experimentally well supported (8, 9) and has a known mechanistic basis (12, 13). Furthermore, our inferred decay constants are within the range of decay constants reported for different antigens bound to dendritic cells (8) and are also roughly compatible with direct measurements of the decrease of the stimulatory capacity of antigen-presenting cells in transgenic mice after switching off inducible antigen production (9). One limitation of our model, particularly for replicating antigens, is that we have neglected any influence of the epitope-specific pMHC density on the surface of an antigen-presenting cell, which may also play a role in determining T cell stimulation and expansion (19).

The kinetics of antigen administration has been shown to influence the magnitude of T cell (7) and B cell (20) immune responses. This finding has implications for the rational design of vaccination strategies (21), but open questions remain regarding how to optimize dosing for high magnitude of response and/or high affinity of the responding cells (20). Our modeling suggests that exponentially increasing doses are close to optimal for maximizing the magnitude of T cell response. We further find that selection for higher affinity is strongest when T cells compete for antigen stimulation. Selection for affinity is thus predicted to be more stringent for lower or more slowly increasing antigen levels and for larger or faster growing prior T cell populations. This could have important implications for patterns of immunodominance in primary vs. secondary infections: In secondary infections, competition is expected to be stronger, as preexisting memory cells specific to the pathogen are usually present in higher numbers and can also proliferate faster.

Looking ahead, our model could be further extended to make it more realistic. Including single-cell stochasticity could help clarify how reproducible population-level expansion arises despite stochasticity at the single-cell level (22) and would also allow connections to recent experimental studies, which have revealed substantial heterogeneity of the immune responses of single cells (23). Furthermore, the model could be extended to account for the diverse compartments (different lymph nodes, the spleen, different tissues) (2) and T cell subtypes (4) involved in an immune response. Spatial or cellular heterogeneity can create separate niches in which T cells compete for proliferation and survival, which may provide another layer of regulation of T cell expansion.

Among the open questions raised in our study, we highlight two. First, other than regulating T cell expansion during an acute infection, how else might antigen presentation levels influence T cell populations, and do they play a role in thymic selection or the dynamics of naive T cells competing for self-antigens? Specifically, recent work in ecology (24) suggests that T cell grazing, which consumes antigens, could allow for the coexistence of a diverse naive repertoire despite competition for self-antigens. Second, regulation of T cell population dynamics can be achieved by tuning of system parameters. For example, smart control of the lifetime of presented pMHC complexes could induce the “right” amount of T cell amplification. Might system parameters have evolved to be close to optimal, and/or could some parameters also be regulated during an immune response to provide a robust response to infections while avoiding autoimmunity?

Materials and Methods

Experimental Studies.

We used previously published data from refs. 3 and 6. In both studies, transgenic T cells were transferred into recipient mice, and their expansion in response to antigenic stimulation was subsequently studied. Quiel et al. (3) studied the response of 5C.C7 ${\mathrm{C}\mathrm{D}\mathrm{4}}^{+}$ T cells to a subcutaneous administration of pigeon cytochrome C and lipopolysaccharide. The number of transgenic T cells was determined by quantitative real-time PCR calibrated against a reference with known T cell numbers. Zehn et al. (6) used OT-1 ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells specific to an ovalbumin peptide. They injected into the mice L. monocytogenes expressing either wild-type ovalbumin or altered ovalbumin with specific amino acid substitutions in the antigenic region. The percentage of transgenic T cells within the spleen of mice was quantified by flow cytometry to measure the relative expansion of transferred vs. endogenous cells. To assess T cell affinity for the different ligands, they were stimulated with RMA-S cells loaded with different doses of antigen for 5 h. T cell responses were assessed by IFN-$\gamma$ staining and quantified by the peptide dose needed for half-maximal response probability.

Model Equations.

We consider deterministic birth–death-type models for the dynamics of the T cell population, $T$, and the concentration of pMHCs, $C$, of the following form:

$$\frac{\mathrm{d}T}{\mathrm{d}t}=\alpha \left(T,C,K\right)T-\delta T,$$ [7]

$$\frac{\mathrm{d}C}{\mathrm{d}t}=\nu \left(t\right)-\mu \left(T,C,K\right)C.$$ [8]

By binding to pMHCs, T cells are stimulated to proliferate at a rate $\alpha \left(T,C,K\right)$, which can depend on the availability of antigen, competition with other T cells, and a parameter $K$ related to the affinity of the TCR for pMHC (SI Appendix, SI Text, section 1). T cells die at a rate $\delta$. The uptake of antigen and its processing lead to a time-varying influx $\nu \left(t\right)$ of pMHCs (SI Appendix, SI Text, section 2). The pMHC complexes decay at a rate $\mu \left(T,C,K\right)$, which may depend on T cell numbers (SI Appendix, SI Text, section 3). In the text, we make a number of simplifying assumptions regarding the functions $\alpha$, $\nu$, and $\mu$, variations of which are considered in SI Appendix, SI Text, sections 1–3. Numerically, we simulate these equations as described in SI Appendix, SI Text, section 4.